Enhancing Traffic Sustainability: An Analysis of Isolation Intersection Effectiveness through Fixed Time and Logic Control Design Using VisVAP Algorithm
Abstract
1. Introduction
2. Related Works
3. Material and Methodology
3.1. Overview of the Methodology
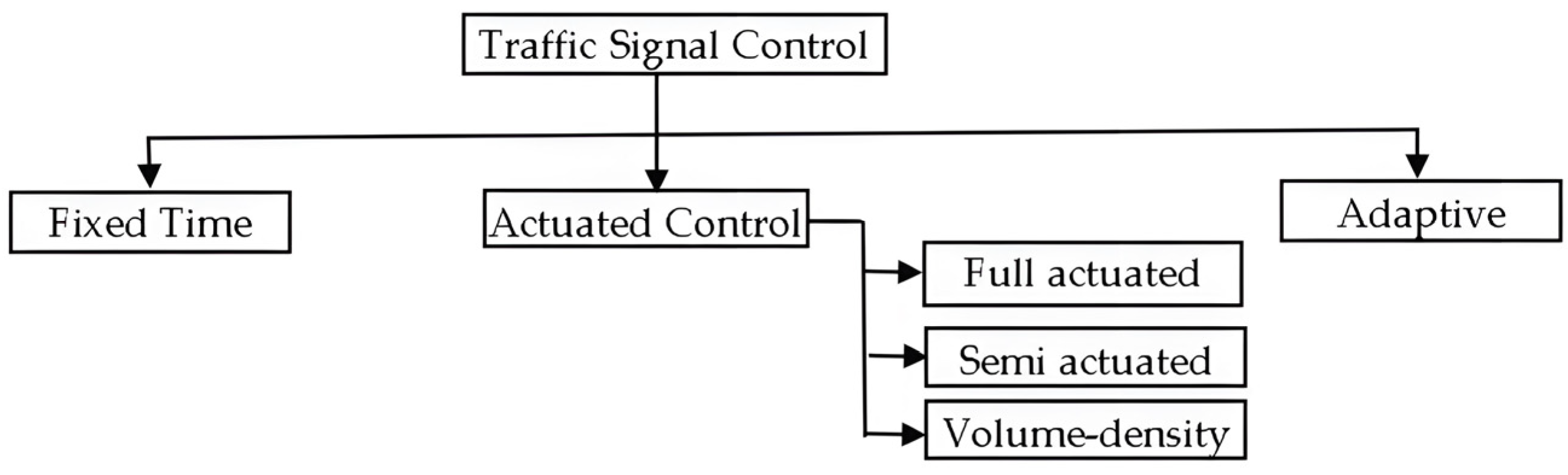
3.2. Methods of Traffic Signal Controls
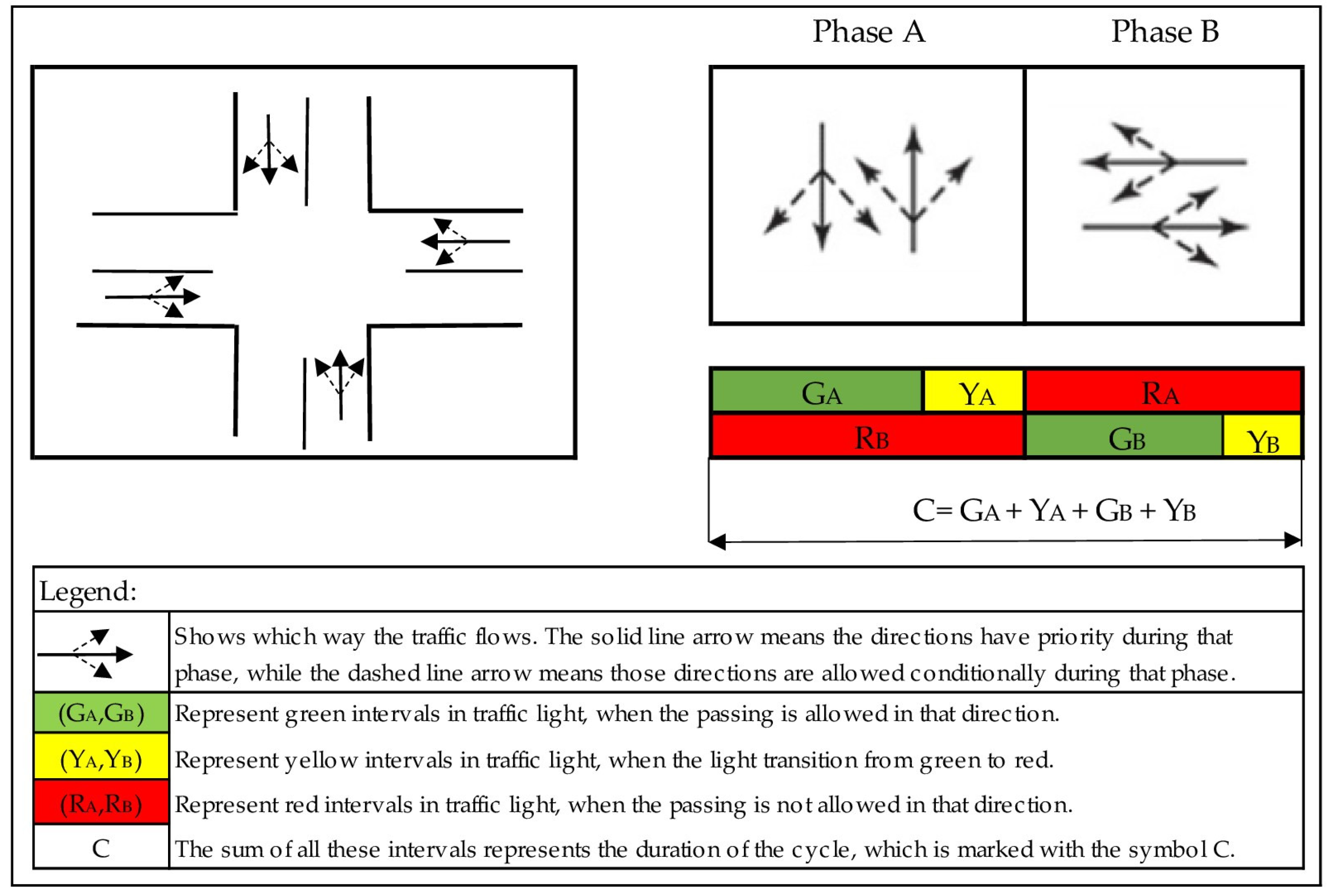
3.2.1. Fixed Time Traffic Signal Control (FTSC)
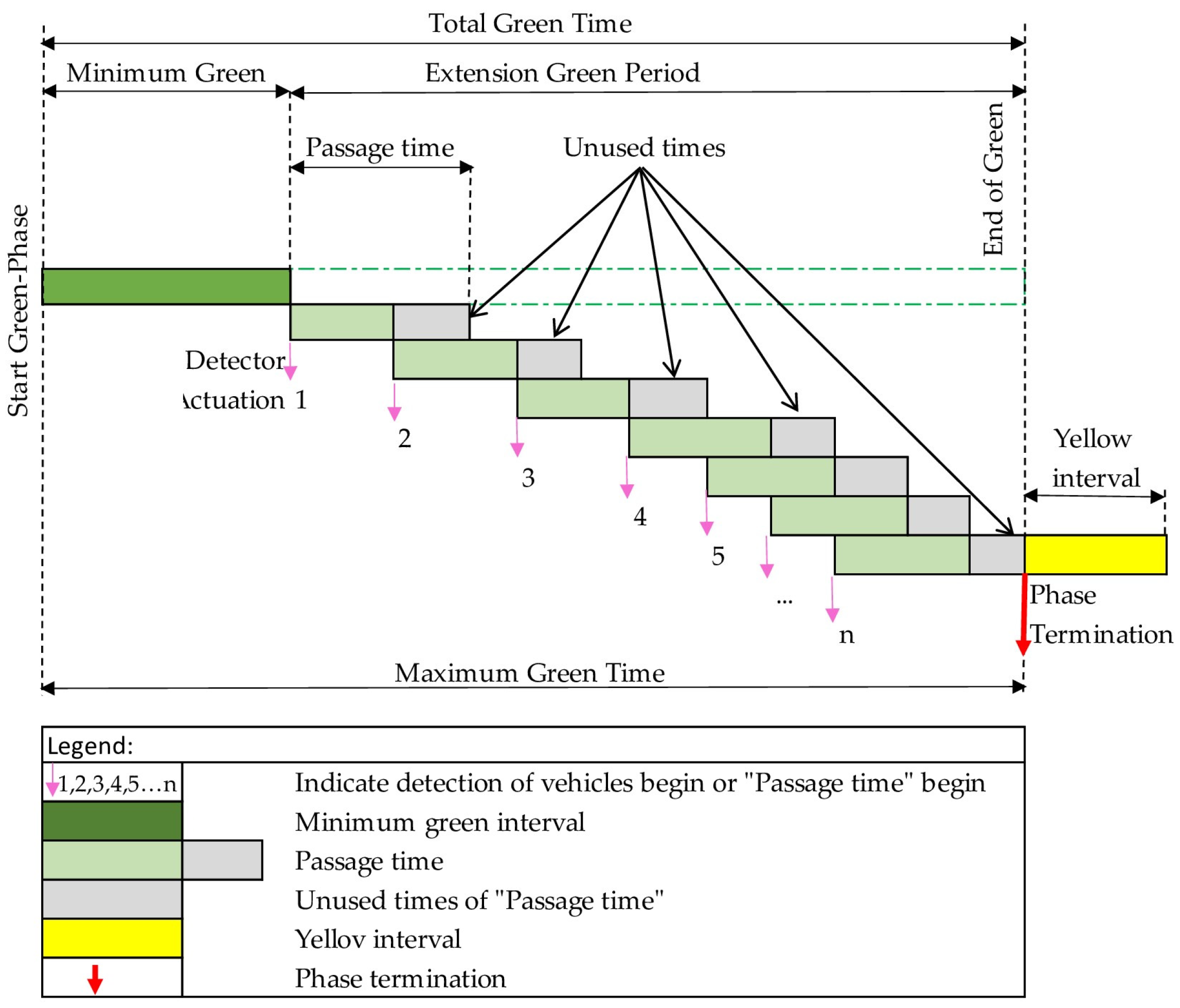
3.2.2. Semi Actuated Traffic Signal Control (SATSC)
- setting the predetermined initial length of the green interval and the additional passage time intervals, when necessary, results in maintaining a constant state or increasing the phase duration until the maximum is reached,
- setting the predetermined initial length of the green interval and additional passage time intervals, resulting in the predetermined duration of the phase.

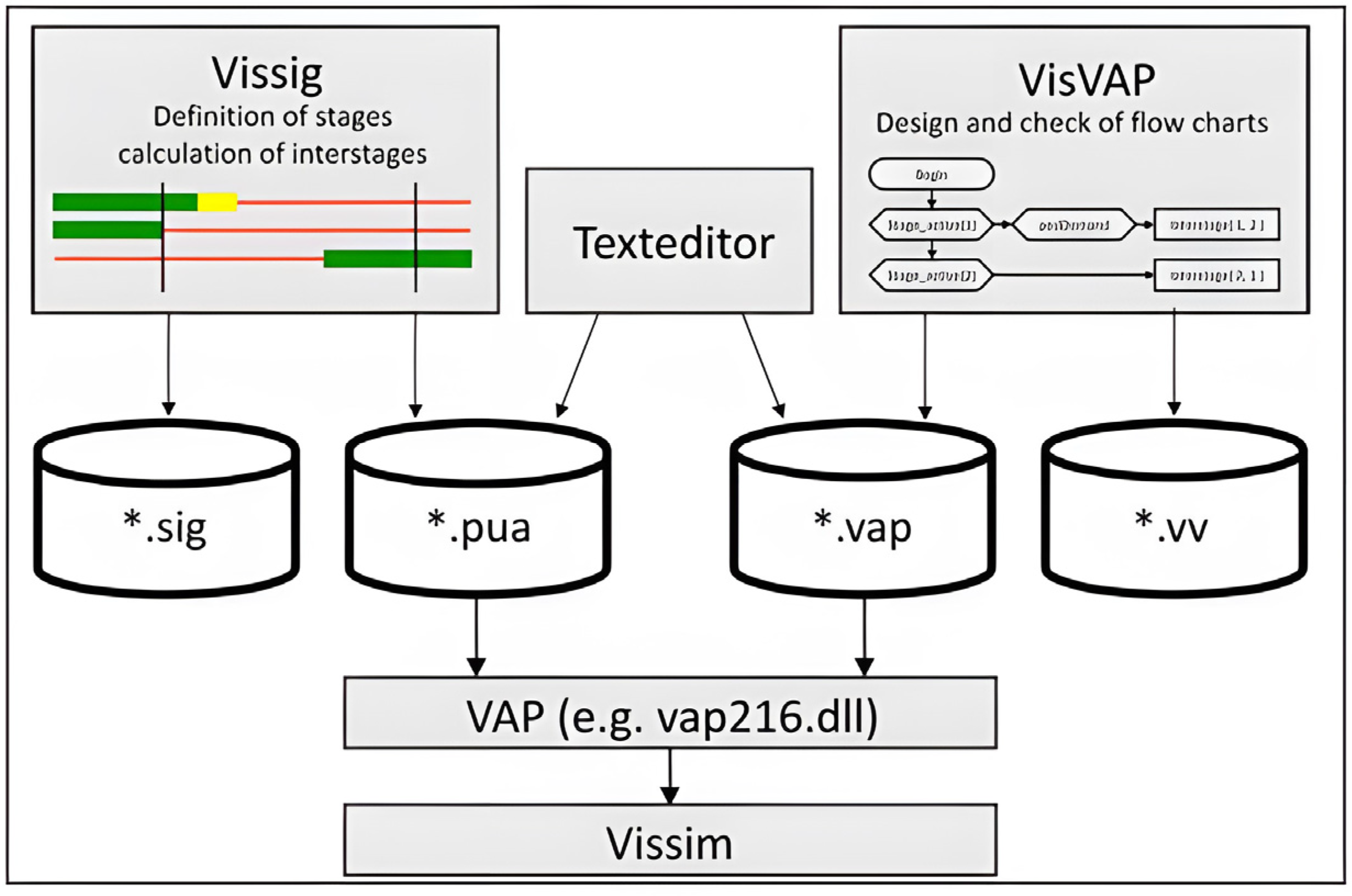
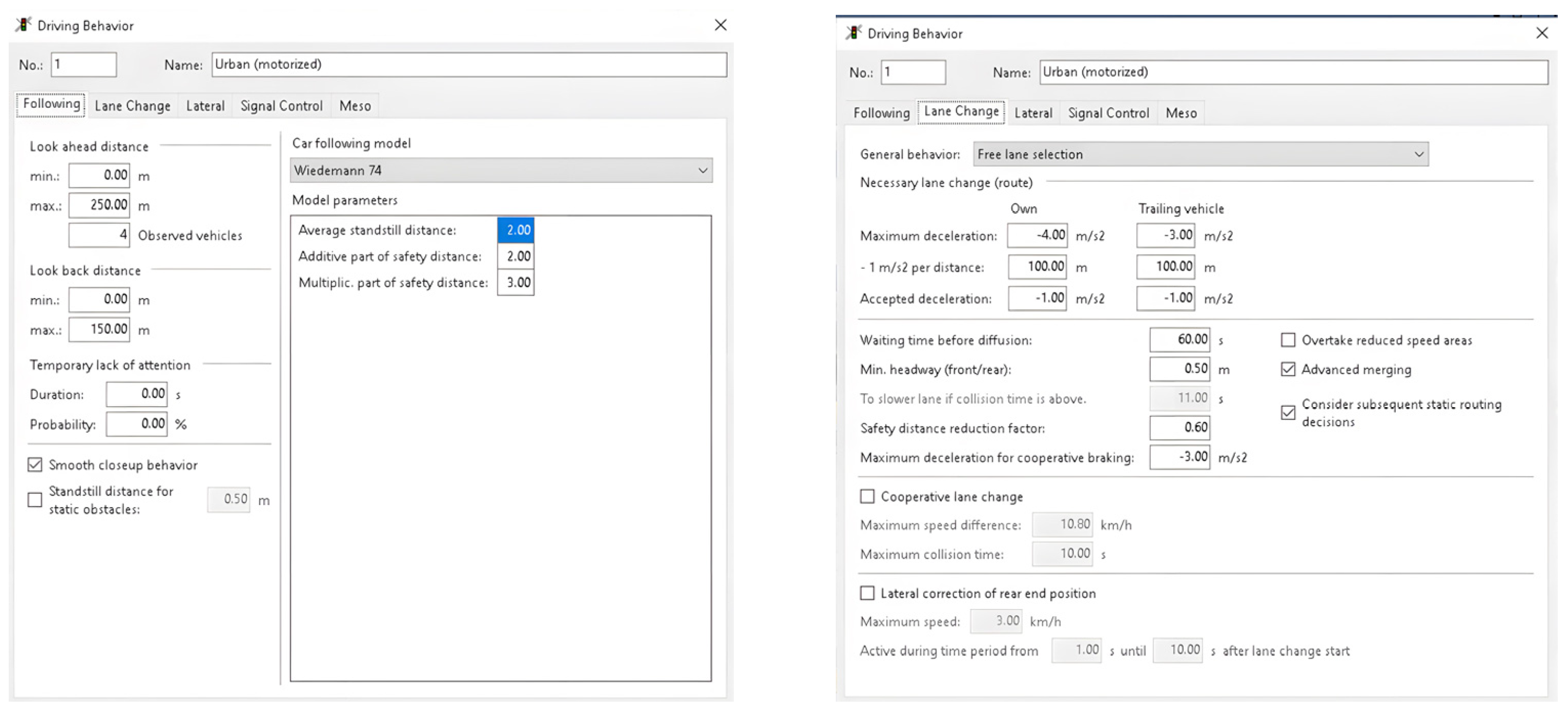
3.3. Tools
4. Model Development
4.1. Study Area and Data Description
4.2. Methodology of Model Development
4.2.1. Model Developed According to the FTSC Strategy
4.2.2. Model Developed According to the SATSC Strategy
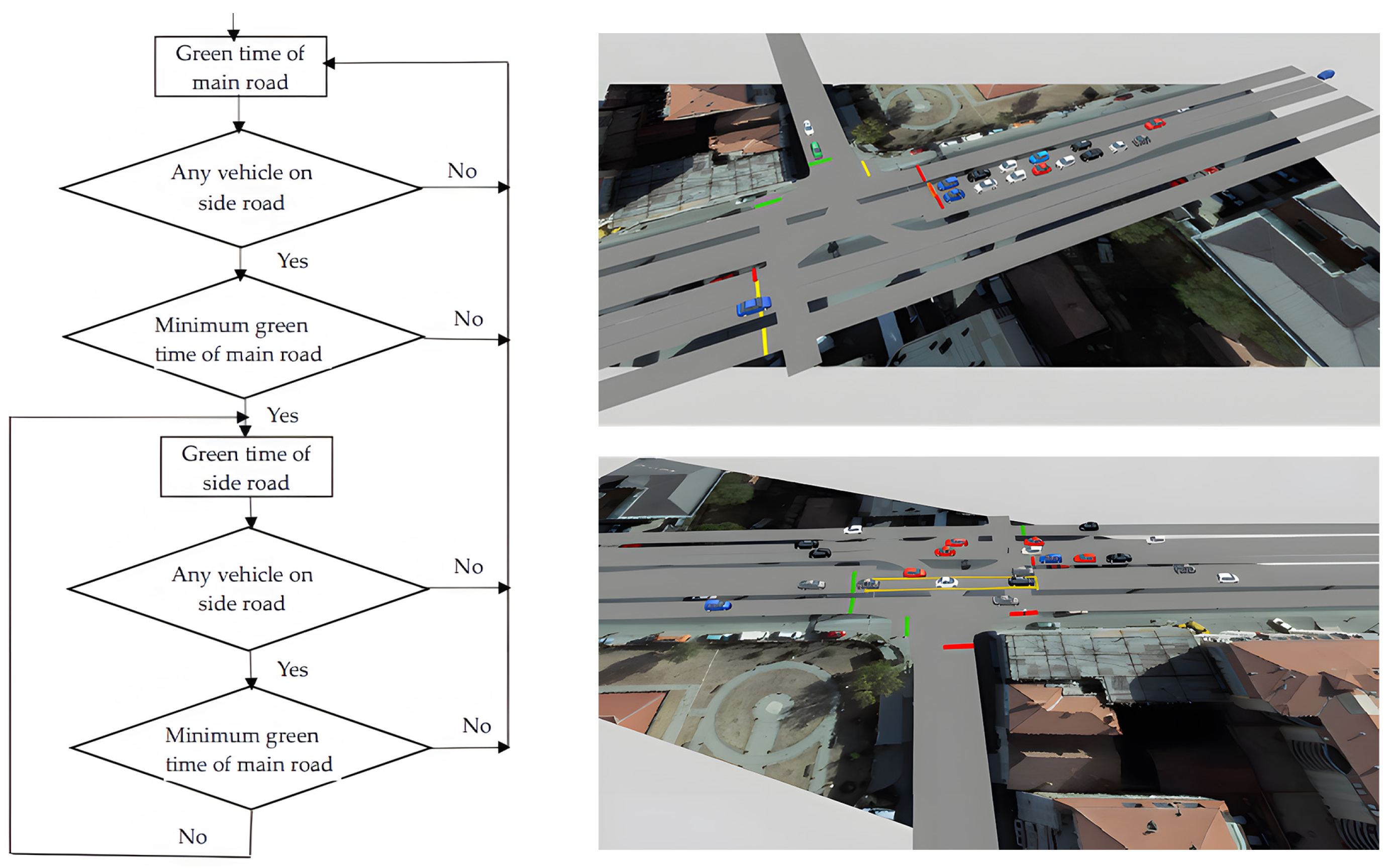
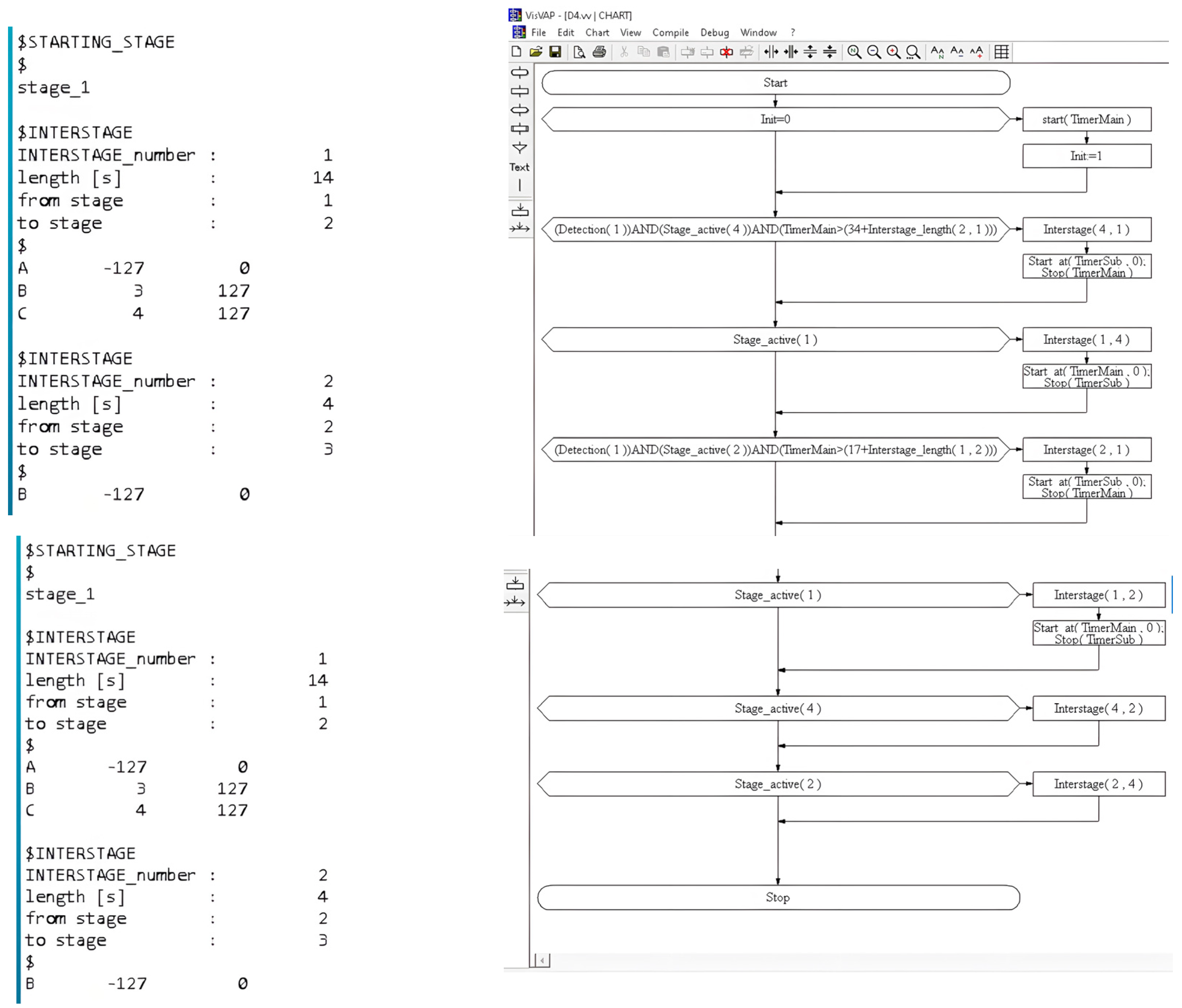
4.2.3. Logic Design Control
5. Results and Discussion
5.1. Queue Lengths and Delay as a Performance Indicator
5.2. Discussion of the Results Regarding Queue Length
5.3. Discussion of the Results Regarding Delays
5.4. Comparison of Results Based on Performance Indicators
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, H.; He, R.; Jia, X. Estimation and Analysis of Vehicle Exhaust Emissions at Signalized Intersections Using a Car-Following Model. Sustainability 2019, 11, 3992. [Google Scholar] [CrossRef]
- Holguín-Veras, J.; Leal, J.A.; Sánchez-Diaz, I.; Browne, M.; Wojtowicz, J. State of the art and practice of urban freight management: Part I: Infrastructure, vehicle-related, and traffic operations. Transp. Res. Part A Policy Pract. 2018, 137, 360–382. [Google Scholar] [CrossRef]
- Blokpoel, R.; Hausberger, S.; Krajzewicz, D. Emission optimized control and speed limit for isolated intersections. IET Intell. Transp. Syst. 2017, 11, 174–181. [Google Scholar] [CrossRef]
- Kim, M.; Schrader, M.; Yoon, H.-S.; Bittle, J.A. Optimal Traffic Signal Control Using Priority Metric Based on Real-Time Measured Traffic Information. Sustainability 2023, 15, 7637. [Google Scholar] [CrossRef]
- Stoilova, K.; Stoilov, T. Model Predictive Traffic Control by Bi-Level Optimization. Appl. Sci. 2022, 12, 4147. [Google Scholar] [CrossRef]
- Ni, D. Pre-Timed Signal Timing. In Signalized Intersections-Fundamentals to Advance Systems; Springer: Cham, Switzerland, 2020; pp. 99–126. [Google Scholar] [CrossRef]
- Truong, L.T.; Currie, G.; Wallace, M.; De Gruyter, C. Analytical approach to estimate delay reduction associated with bus priority measures. IEEE Intell. Transp. Syst. Mag. 2017, 9, 91–101. [Google Scholar] [CrossRef]
- Mei, Z.; Tan, Z.; Zhang, W.; Wang, D. Simulation analysis of traffic signal control and transit signal priority strategies under Arterial Coordination Conditions. Simulation 2019, 95, 51–64. [Google Scholar] [CrossRef]
- Tamannaei, M.; Fazeli, M.; Chamani Foomani Dana, A.; Mansourianfar, H. Transit Signal Priority: Proposing a Novel Algorithm to Decrease Delay and Environmental Impacts in BRT Route Intersections. Int. J. Transp. Eng. 2019, 7, 153–169. [Google Scholar] [CrossRef]
- Traffic Signal Timing Manual-Second Edition. Chapter 5. Basic Signal Timing Procedure and Controller Parameters; Department of Transportation, Federal Highway Administration: Washington, DC, USA. Available online: https://ops.fhwa.dot.gov/publications/fhwahop08024/chapter5.htm (accessed on 6 September 2023).
- Sustainable Urban Mobility Plan of City of Fushe Kosovo; Institute for Science and Technology (INSI Sh.p.k) and Municipality of Fushe Kosovo: Prishtine, Kosovo, 2021.
- Fouladvand, M.E.; Sadjadi, Z.; Shaebani, M.R. Optimized Traffic Flow at a Single Intersection: Traffic Responsive Signalization. J. Phys. A Math. Gen. 2004, 37, 561–576. [Google Scholar] [CrossRef]
- Wiering, M.; Vreeken, J.; van Veenen, J.; Koopman, A. Simulation and Optimization of Traffic in a City. In Proceedings of the IEEE Intelligent Vehicles Symposium, Parma, Italy, 14–17 June 2004; pp. 453–458. [Google Scholar] [CrossRef]
- Chowdhury, A.; Karmakar, G.; Kamruzzaman, J.; Das, R.; Newaz, S.H.S. An Evidence Theoretic Approach for Traffic Signal Intrusion Detection. Sensors 2023, 23, 4646. [Google Scholar] [CrossRef]
- Hao, R.; Wang, L.; Ma, W.; Yu, C. Estimating Signal Timing of Actuated Signal Control Using Pattern Recognition under Connected Vehicle Environment. Promet Traffic Transp. 2021, 33, 153–163. [Google Scholar] [CrossRef]
- Zhu, S.; Guo, K.; Guo, Y.; Tao, H.; Shi, Q. An Adaptive Signal Control Method with Optimal Detector Locations. Sustainability 2019, 11, 727. [Google Scholar] [CrossRef]
- Akcelik, R. Estimation of Green Times and Cycle Time for Vehicle-Actuated Signals; Transportation Research Record 1457; Sage: Atlanta, GA, USA, 1994; pp. 63–72. Available online: https://onlinepubs.trb.org/Onlinepubs/trr/1994/1457/1457-008.pdf (accessed on 22 November 2023).
- Kim, J.T.; Courage, K.G. Evaluation and Design of Maximum Green Time Settings for Traffic-Actuated Control. Transp. Res. Rec. 1852, 2003, 246–255. [Google Scholar] [CrossRef]
- Wu, J.; Liu, P.; Tian, Z. Operational analysis of the contraflow left-turn lane design at signalized intersections in China. Transp. Res. Part C Emerg. Technol. 2016, 69, 228–241. [Google Scholar] [CrossRef]
- Robert, O.; Peter, W. Delay-Time Actuated Traffic Signal Control for an Isolated Intersection. Proceedings 90st Annual Meeting Transportation Research Board (TRB). 2011. Available online: https://trid.trb.org/view/1092084 (accessed on 22 November 2023).
- Zhang, G.H.; Wang, Y.H. Optimizing minimum and maximum green time settings for traffic actuated control at isolated intersections. IEEE Trans. Intell. Transp. Syst. 2011, 12, 164–173. [Google Scholar] [CrossRef]
- Shiri, M.J.S.; Maleki, H.R. Maximum Green Time Settings for Traffic-Actuated Signal Control at Isolated Intersections Using Fuzzy Logic. Int. J. Fuzzy Syst. 2017, 19, 247–256. [Google Scholar] [CrossRef]
- Webster, F.V. Traffic Signal Settings; Technical Paper No. 39; Road Research Laboratory, Her Majesty Stationary Office: London, UK, 1958. [Google Scholar]
- Akcelik, R. Time-Dependent Expressions for Delay, Stop Rate and Queue Length at Traffic Signals; Internal Report AIR367-1; Australian Road Research Board: Melbourne, Australia, 1980; Available online: https://api.semanticscholar.org/CorpusID:14676799 (accessed on 1 October 2023).
- Highway Capacity Manual; Transportation Research Board of the National Academies: Washington, DC, USA, 2010.
- Rathinavel, N.; Duraisamy, S.; Karuppanan, G.; Swaminathan, N. Design of Vehicle Actuated Signal using Simulation. Građevinar 2014, 66, 635–642. [Google Scholar] [CrossRef]
- Wang, X.B.; Yin, K.; Liu, H. Vehicle actuated signal performance under general traffic at an isolated intersection. Transp. Res. Part C Emerg. Technol. 2018, 95, 582–598. [Google Scholar] [CrossRef]
- Roess, R.; Prassas, E.S.; McShane, W.R. Traffic Engineering, 4th ed.; Pearson/Prentice Hall: Old Bridge, NJ, USA, 2011. [Google Scholar]
- Shahgholian, M.; Gharavian, D. Advanced Traffic Management Systems: An Overview and A Development Strategy. arXiv 2018, arXiv:1810.02530. [Google Scholar]
- Gao, J.; Shen, Y.; Liu, J.; Ito, M.; Shiratori, N. Adaptive Traffic Signal Control: Deep Reinforcement Learning Algorithm with Experience Replay and Target Network. arXiv 2017, arXiv:1705.02755. [Google Scholar]
- Guo, Y.; Ma, J. An Improved Actuated Signal Control of Intersection Based on VISVAP. In Proceedings of the 2016 International Conference on Sensor Network and Computer Engineering, Xi’an, China, 8–10 July 2016; Atlantis Press: Dordrecht, The Netherlands, 2016; pp. 123–128, ISSN 2352-5401. [Google Scholar] [CrossRef]
- Maadi, S.; Stein, S.; Hong, J.; Murray-Smith, R. Real-Time Adaptive Traffic Signal Control in a Connected and Automated Vehicle Environment: Optimisation of Signal Planning with Reinforcement Learning under Vehicle Speed Guidance. Sensors 2022, 22, 7501. [Google Scholar] [CrossRef] [PubMed]
- Toledo, T.; Balasha, T.; Keblawi, M. Optimization of Actuated Traffic Signal Plans Using a Mesoscopic Traffic Simulation. J. Transp. Eng. Part A Syst. 2020, 146. [Google Scholar] [CrossRef]
- Tomar, I.; Indu, S.; Pandey, N. Traffic Signal Control Methods: Current Status, Challenges, and Emerging Trends. Proc. Data Anal. Manag. 2022, 1, 151–163. [Google Scholar]
- Eom, M.; Kim, B.-I. The traffic signal control problem for intersections: A review. Eur. Transp. Res. Rev. 2020, 12, 50. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine; Urbanik, T.; Tanaka, A.; Lozner, B.; Lindstrom, E.; Lee, K.; Quayle, S.; Beaird, S.; Tsoi, S.; Ryus, P.; et al. Signal Timing Manual, 2nd ed.; The National Academies Press: Washington, DC, USA, 2015. [Google Scholar] [CrossRef]
- Ni, D. Traffic Signal Coordination. In Signalized Intersections-Fundamentals to Advance Systems; Springer: Cham, Switzerland, 2020; pp. 291–326. [Google Scholar] [CrossRef]
- Traffic Control Systems Handbook: Chapter 8. System Control; Department of Transportation, Federal Highway Administration: Washington, DC, USA. Available online: https://ops.fhwa.dot.gov/publications/fhwahop06006/chapter_8.htm (accessed on 5 October 2023).
- Majstorovic, Ž.; Tišljaric, L.; Ivanjko, E.; Caric, T. Urban Traffic Signal Control under Mixed Traffic Flows: Literature Review. Appl. Sci. 2023, 13, 4484. [Google Scholar] [CrossRef]
- Traffic Signal Timing Manual-Second Edition. Chapter 7. Local Controllers; Department of Transportation, Federal Highway Administration: Washington, DC, USA. Available online: https://ops.fhwa.dot.gov/publications/fhwahop06006/chapter_7.htm (accessed on 25 October 2023).
- Qadri, S.S.S.M.; Gökçe, M.A.; Öner, E. State-of-art review of traffic signal control methods: Challenges and opportunities. Eur. Transp. Res. Rev. 2020, 12, 55. [Google Scholar] [CrossRef]
- Wang, X.; Wu, X.; Liu, J. Optimization Models of Actuated Control Considering Vehicle Queuing for Sustainable Operation. Sustainability 2022, 14, 8998. [Google Scholar] [CrossRef]
- Madrigal Arteaga, V.M.; Pérez Cruz, J.R.; Hurtado-Beltrán, A.; Trumpold, J. Efficient Intersection Management Based on an Adaptive Fuzzy-Logic Traffic Signal. Appl. Sci. 2022, 12, 6024. [Google Scholar] [CrossRef]
- Simõesa, M.L.; Ribeiroa, I.M. Global optimization and complementarity for solving a semi-actuated traffic control problem. Procedia Soc. Behav. Sci. 2011, 20, 390–397. [Google Scholar] [CrossRef]
- Awadallah, F. Yellow and All-red Intervals: How to Improve Safety and Reduce Delay. Int. J. Traffic Transp. Eng. 2013, 3, 159–172. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine; McGee, H.; Moriarty, K.; Eccles, K.; Liu, M.; Gates, T.; Retting, R. Guidelines for Timing Yellow and All-Red Intervals at Signalized Intersections; The National Academies Press: Washington, DC, USA, 2012. [Google Scholar] [CrossRef]
- Ni, D. Level of Service of Traffic Signalized Intersections. In Signalized Intersections-Fundamentals to Advance Systems; Springer: Cham, Switzerland, 2020; pp. 157–178. [Google Scholar] [CrossRef]
- Roess, R.; Prassas, E.S.; Mcshane, W. Traffic Engineering, 5th ed.; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2021; ISBN 13: 9780137518784. [Google Scholar]
- Chen, Z.-M.; Liu, X.-M.; Wu, W.-X. Optimization Method of Intersection Signal Coordinated Control Based on Vehicle Actuated Model. Math. Probl. Eng. 2015, 2015, 749748. [Google Scholar] [CrossRef]
- Feng, S.; Ci, Y.; Wu, L.; Zhang, F. Vehicle Delay Estimation for an Isolated Intersection under Actuated Signal Control. Math. Probl. Eng. 2014, 2014, 356707. [Google Scholar] [CrossRef]
- Ni, D. Controllers and Detectors. In Signalized Intersections-Fundamentals to Advance Systems; Springer: Cham, Switzerland, 2020; pp. 179–209. [Google Scholar] [CrossRef]
- Cakici, Z.; Murat, Y.S.; Aydin, M.M. Design of an Efficient Vehicle-Actuated Signal Control Logic for Signalized Intersections. Sci. Iran. 2021, 29, 1059–1107. [Google Scholar] [CrossRef]
- Mathew, T.V. Signalized Intersections Delay Models. Lecture Notes in Transportation System Engineering. 2017. Available online: https://www.civil.iitb.ac.in/tvm/nptel/572_Delay_A/web/web.html (accessed on 20 September 2023).
- Manual of Uniform Traffic Control Devices for Streets and Highways 2009 Edition, including Revision 1 date May 2012, Revision 2 date May 2012, Revision 3 date July 2022. U.S Department of Transportation, Federal Highway Administration: Washington, DC, USA. Available online: https://mutcd.fhwa.dot.gov/pdfs/2009/pdf_index.htm (accessed on 10 September 2023).
- Jin, J.; Ma, X. A group-based traffic signal control with adaptive learning ability. Eng. Appl. Artif. Intell. 2017, 65, 282–293. [Google Scholar] [CrossRef]
- Gregurić, M.; Ivanjko, E.; Mandžuka, S. The Use of Cooperative Approach in Ramp Metering. Promet Traffic Transp. 2016, 28, 11–22. [Google Scholar] [CrossRef]
- Pandža, H.; Vujić, M.; Ivanjko, E. A VISSIM Based Framework for Simulation of Cooperative Ramp Metering. In Proceedings of the International Scientific Conference ZIRP 2015: Cooperation Model of the Scientific and Educational Institutions and the Economy, Zagreb, Croatia, 12 May 2015; pp. 151–162. [Google Scholar]
- PTV—Planung Transport Verkehr AG. VISVAP User Manual; PTV: Düsseldorf, Germany, 2005. [Google Scholar]
- Ziemska, M. Exhaust Emissions and Fuel Consumption Analysis on the Example of an Increasing Number of HGVs in the Port City. Sustainability 2021, 13, 7428. [Google Scholar] [CrossRef]
- Ziemska-Osuch, M.; Osuch, D. Modeling the Assessment of Intersections with Traffic Lights and the Significance Level of the Number of Pedestrians in Microsimulation Models Based on the PTV Vissim Tool. Sustainability 2022, 14, 8945. [Google Scholar] [CrossRef]
- VISSIM User’s Guide. PTV (Planung Transport Verkehr) VISSIM 8.0. 2014. Available online: http://www.et.byu.edu/~msaito/CE662MS/Labs/VISSIM_530_e.pdf (accessed on 15 July 2023).
- PTV—Planung Transport Verkehr AG. VisVAP 2.16 User Manual; PTV: Düsseldorf, Germany, 2007. [Google Scholar]











| Orientations | No. of Lane | Movement | Latidude | Longitude | Wide of Lane | No. of Traffic Light | Phase | Signal Group |
|---|---|---|---|---|---|---|---|---|
| South aproach | Lane 1 | through | 42.639813 | 21.100996 | 4 m | 4 | B | SG3 |
| Lane 2 | through | 42.639827 | 21.100953 | 3.1 m | 3 | B | SG3 | |
| Lane 3 | through | 42.639843 | 21.100944 | 3.1 m | 2 | B | SG3 | |
| Lane 4 | left | 42.639862 | 21.100934 | 2.1 m | 5 | C | SG2 | |
| East aproach | Lane 5 | through | 42.640049 | 21.101476 | 3.2 m | 8 | B | SG4 |
| Lane 6 | through | 42.640074 | 21.101452 | 3.2 m | 7 | B | SG4 | |
| Lane 7 | through/right | 42.640113 | 21.101416 | 4.1 m | 6 | B | SG4 | |
| West aproach | Lane 8 | left/right | 42.640125 | 21.101085 | 4.6 m | 1 | A | SG1 |
| No. of Phases | Signal Group | Green Time G (s) | Yellow Time Y (s) | Red Time R (s) | Cycle Length C (s) |
|---|---|---|---|---|---|
| Phase A | SG1 (lane 8) | 21 | 3 | 68 | |
| Phase B | SG2 (lane 4) and SG3 (lanes 1,2,3) | 7 65 | 3 3 | 82 24 | 92 |
| Phase C | SG3 (lanes 1,2,3) and SG4 (lanes 5,6,7) | 65 55 | 3 3 | 24 34 |
| No. of Phases | Signal Group | Green Time G (s) | Yellow Time Y (s) | Unit Extension U (s) | Red Time R (s) | Cycle Length C (s) |
|---|---|---|---|---|---|---|
| Phase A | SG1 (lane8) | Gmin = 5 | 3 | U = 3 | R = 26 | |
| Phase B | SG3 (lanes 1,2,3) and SG4 (lanes 5.6.7) | Gmax = 10 Gmax = 10 | 3 3 | not applicable | R = 8 R = 21 | Cmin = 26 |
| Phase C | SG3 (lanes 1,2,3) and SG2 (lane 4) | Gmax = 10 Gmax = 10 | 3 3 | not applicable | R = 8 R = 21 | Cmax = 34 |
| Type of Control | Queue Lengths (m) | Delays (s) |
|---|---|---|
| FTSC | 33.08 | 9.32 |
| SATSC | 19.31 | 4.50 |
| Improvement | 39.6% | 51.3% |
| Advantages | Disadvantages |
|---|---|
| Can be effectively used in a coordinated signaling system in a road corridor | Continuous demand and low flows from the secondary road cause excessive delays on the main road if the parameters of the maximum green interval and passage time are not appropriately set |
| Enables the reduction of delays on the main road during periods of light traffic | Detectors should be used on secondary roads, thus requiring their installation and continuous maintenance |
| They do not require detectors for the main road, and as a result, traffic flow is not compromised in their absence | Controllers are much more complex than those with fixed times, increasing maintenance costs |
| The main road is always supplied with the green interval, except in the presence of vehicles on the secondary road | A dedicated phase for the secondary road takes a specific minimum interval within the cycle timing whenever there is the presence of vehicles |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duraku, R.; Boshnjaku, D. Enhancing Traffic Sustainability: An Analysis of Isolation Intersection Effectiveness through Fixed Time and Logic Control Design Using VisVAP Algorithm. Sustainability 2024, 16, 2930. https://doi.org/10.3390/su16072930
Duraku R, Boshnjaku D. Enhancing Traffic Sustainability: An Analysis of Isolation Intersection Effectiveness through Fixed Time and Logic Control Design Using VisVAP Algorithm. Sustainability. 2024; 16(7):2930. https://doi.org/10.3390/su16072930
Chicago/Turabian StyleDuraku, Ramadan, and Diellza Boshnjaku. 2024. "Enhancing Traffic Sustainability: An Analysis of Isolation Intersection Effectiveness through Fixed Time and Logic Control Design Using VisVAP Algorithm" Sustainability 16, no. 7: 2930. https://doi.org/10.3390/su16072930
APA StyleDuraku, R., & Boshnjaku, D. (2024). Enhancing Traffic Sustainability: An Analysis of Isolation Intersection Effectiveness through Fixed Time and Logic Control Design Using VisVAP Algorithm. Sustainability, 16(7), 2930. https://doi.org/10.3390/su16072930




