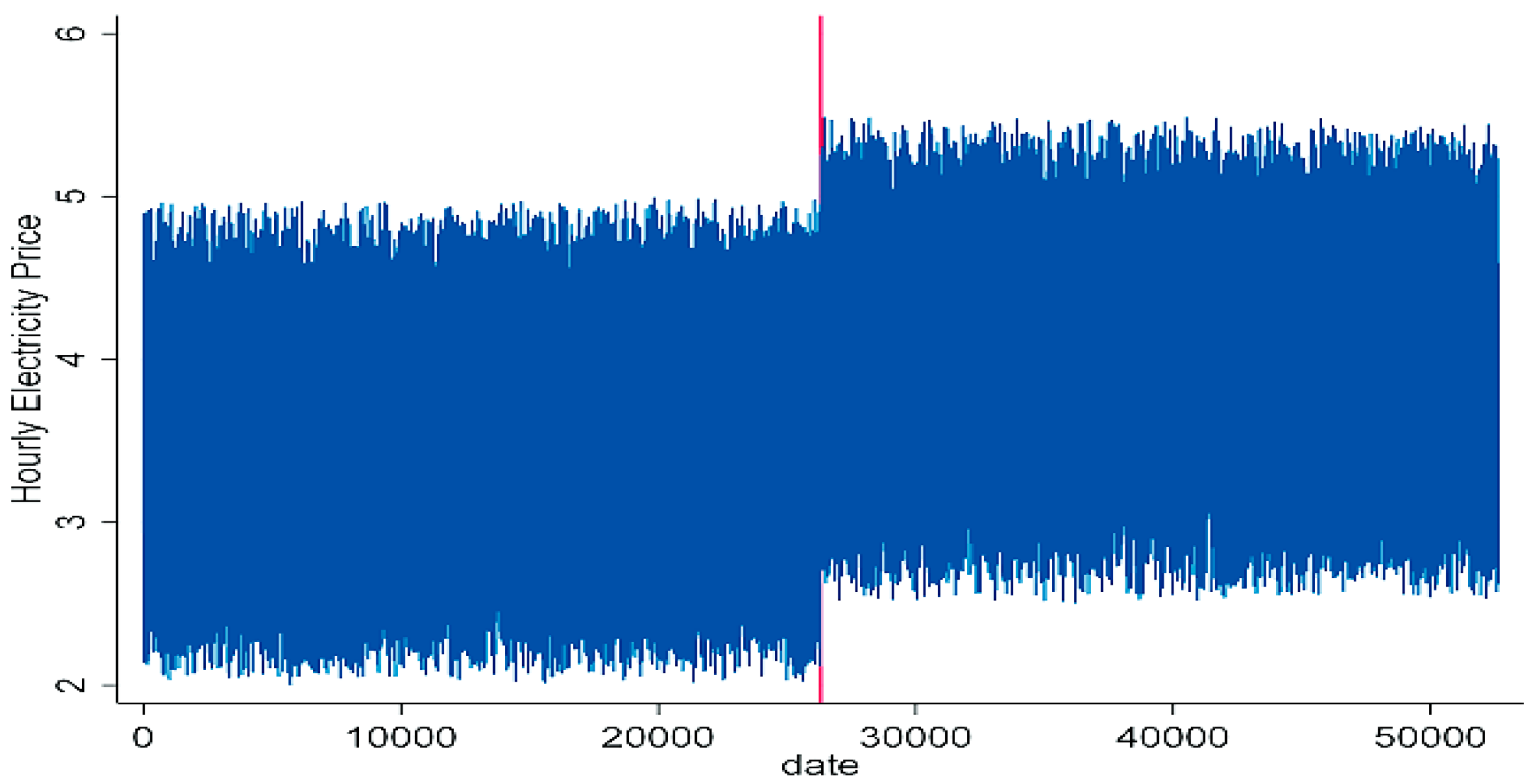
A total of 52,614 observations collected over six years were used to estimate the number of GARCH models. It should be emphasized that the reason for the negative electricity prices is a period of high costs and low profits, and outliers, often caused by unexpected shocks, provide valuable information about the market dynamics and help to refine the model’s predictions.
5.1. Results of Symmetric GARCH Model
The results of estimating the symmetric ARCH
, GARCH
, and asymmetry terms specifications TGARCH
, EARCH
, EGARCH
, considering
p = 0 and q = 2, stand for the number of lags of variances to be included in the models, which are reported in
Table 4 and
Table 5. The GARCH error parameter, also known as the error terms of the ARCH component, measures the persistence and volatility of the shocks in the time series. Since the probability of its coefficient (except the constant) is less than 0.05, the error term has a normal distribution. This case means that the estimated parameters significantly affect the model’s outcome. Significant coefficients indicate a strong relationship between past shocks and the level of volatility observed in today’s market. In this case, the GARCH model captures the tendency of high- or low-volatility periods to persist over time and their potential impact on future volatility levels. When the coefficient is less than one, it implies that shocks have a lasting impact on the volatility of the financial time series. The market does not quickly revert to the initial level. Thus, shocks have a sustained effect on the conditional variance.
The electricity market in Portugal is particularly vulnerable to external shocks, such as changes in energy prices or supply disruptions, which may have a long-term effect on the conditional variance in electricity markets. The impact of energy shocks on financial stability can lead to sharp rises in electricity prices and increased volatility, affecting energy companies, financial agents, and central banks involved in safeguarding Portugal’s electricity market’s financial stability and pricing dynamics. High volatility can introduce uncertainty for market participants, including consumers, producers, and policymakers, and may impact investment decisions and long-term planning. Diversifying energy sources and enhancing energy security are crucial strategies to mitigating the impact of external shocks on market stability.
Market participants react more strongly to minor shocks during periods of high persistence. This situation suggests that the market is more sensitive to even minor disturbances. However, when the parameter is greater than one, this indicates that as the parameter increases, the impact of past shocks on future volatility decreases, leading to a quicker return to the average level of volatility.
5.2. Results of the Asymmetric GARCH Model
In contrast to traditional ARCH models, the GARCH model recognizes that the effects of shocks do not immediately disappear but persist over time, considering the impact of past shocks on future volatility. The EGARCH model’s empirical results often contribute to a more accurate representation of market dynamics.
Positive developments, such as strong economic indicators, successful corporate earnings reports, or favorable policy announcements, often instill confidence in investors and market participants. When we have lower volatility, positive developments reassure investors and market participants the following day, increasing confidence in the overall economic outlook. On the other hand, negative news appears to have the opposite effect, causing an increase in volatility the next day.
The EGARCH variance equation indicates that the impact of positive shocks on volatility differs from negative shocks. The estimated coefficient is −0.026, and it implies that, on average, for each unit increase in the lagged standardized residual () the log conditional variance decreases by 0.026 units. A negative coefficient suggests an asymmetric response to shocks. In EGARCH models, this implies that the impact of negative shocks on volatility is greater than that of positive shocks. In other words, negative shocks have a more pronounced effect on increasing volatility than positive shocks.
The relationship between negative news and increased volatility is a common trend observed across different markets and can serve as a valuable indicator for understanding how adverse information influences market dynamics. Acknowledging the relationship between negative news and volatility is essential for investors to navigate uncertain market environments successfully. By being informed of the latest developments and observing how the market responds to adverse news, investors can better navigate volatile conditions and potentially capitalize on opportunities.
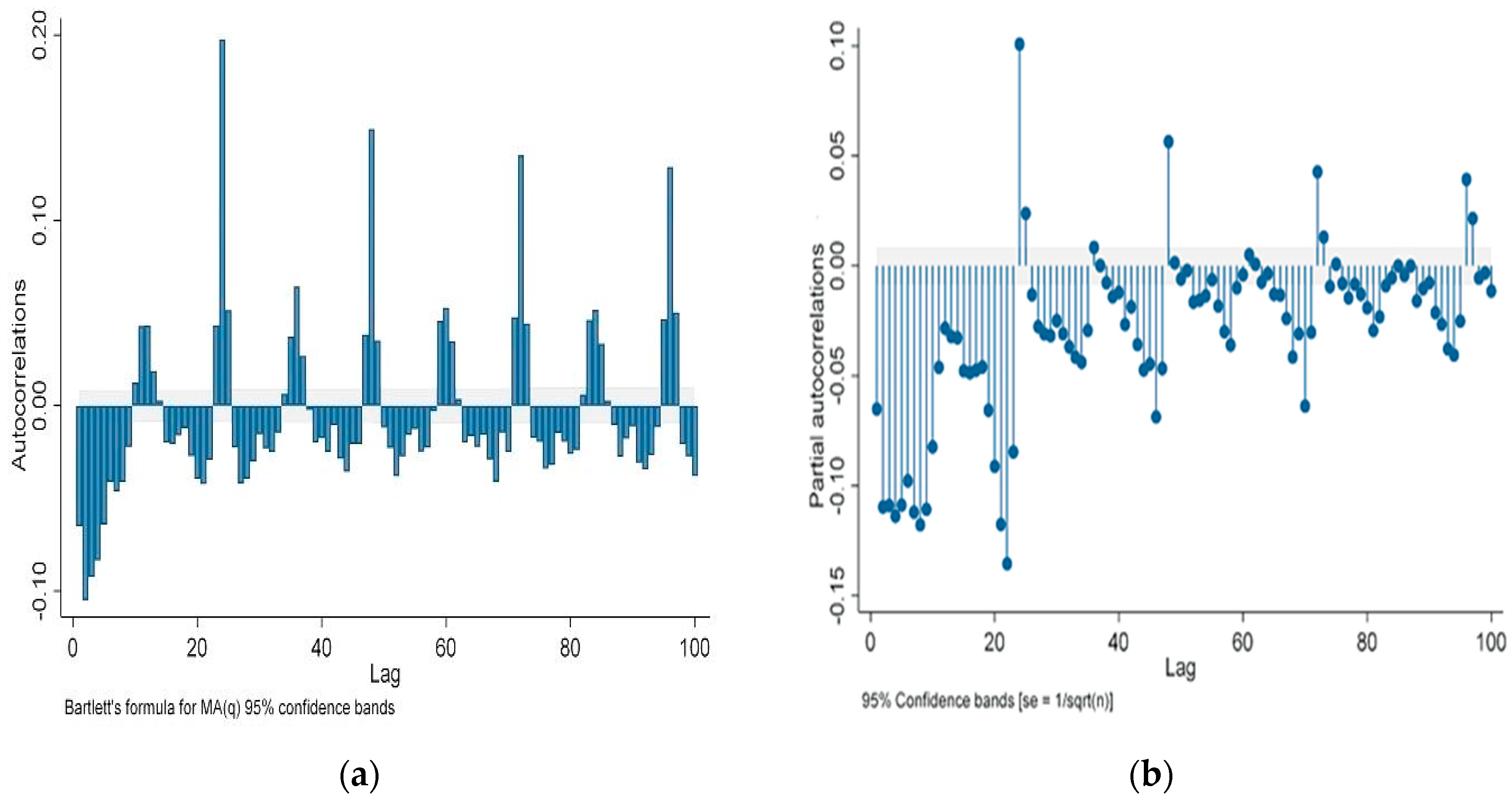
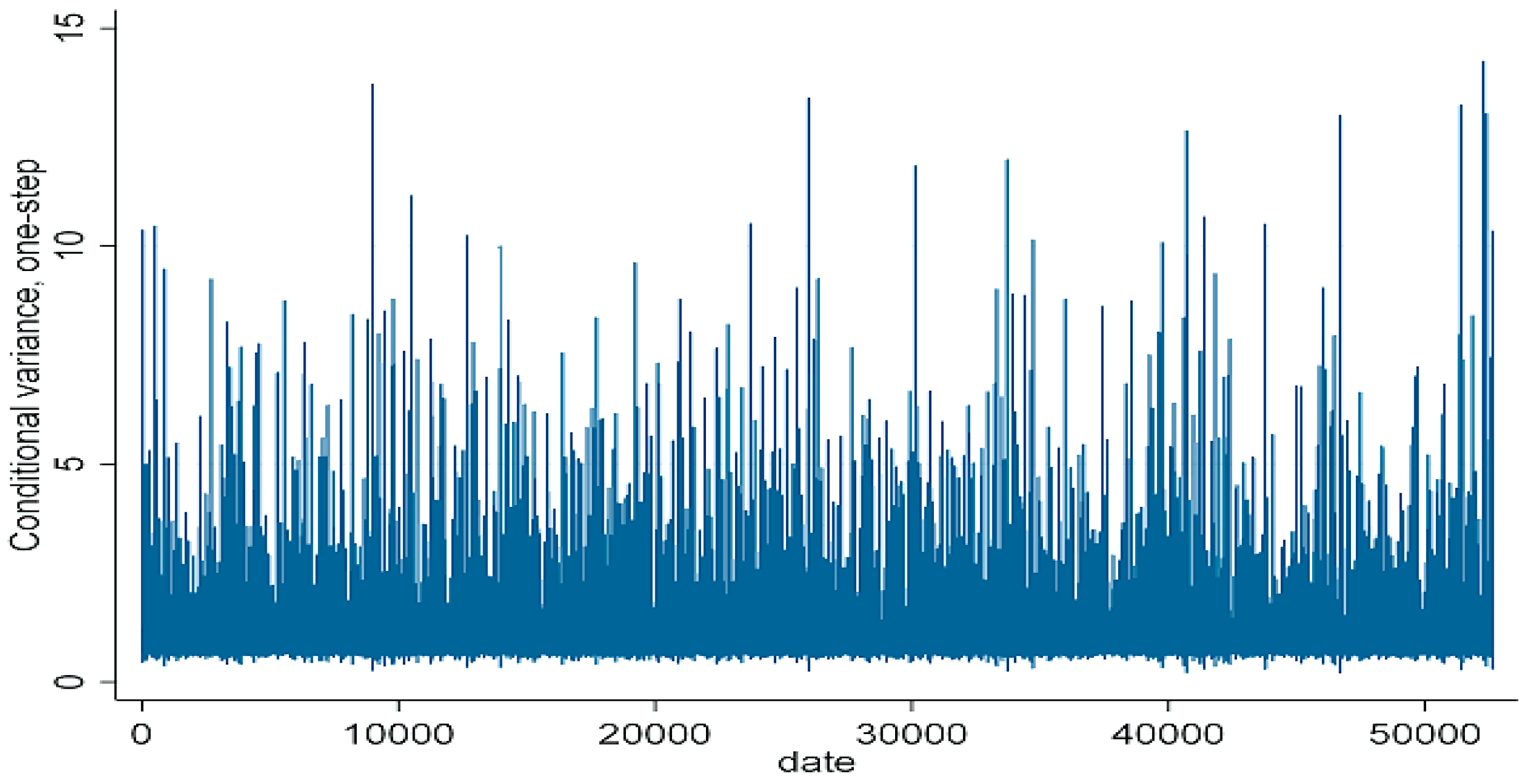
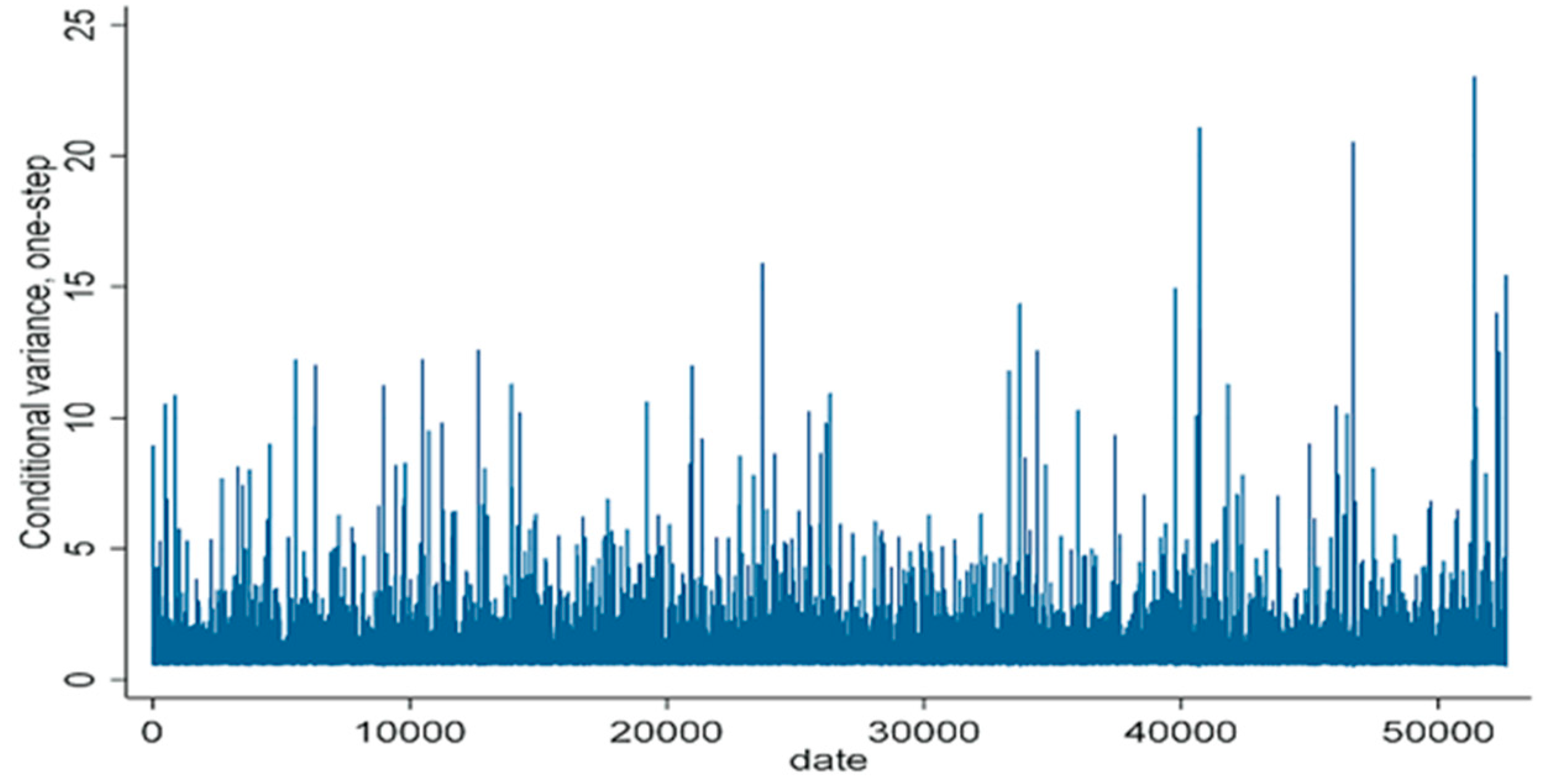
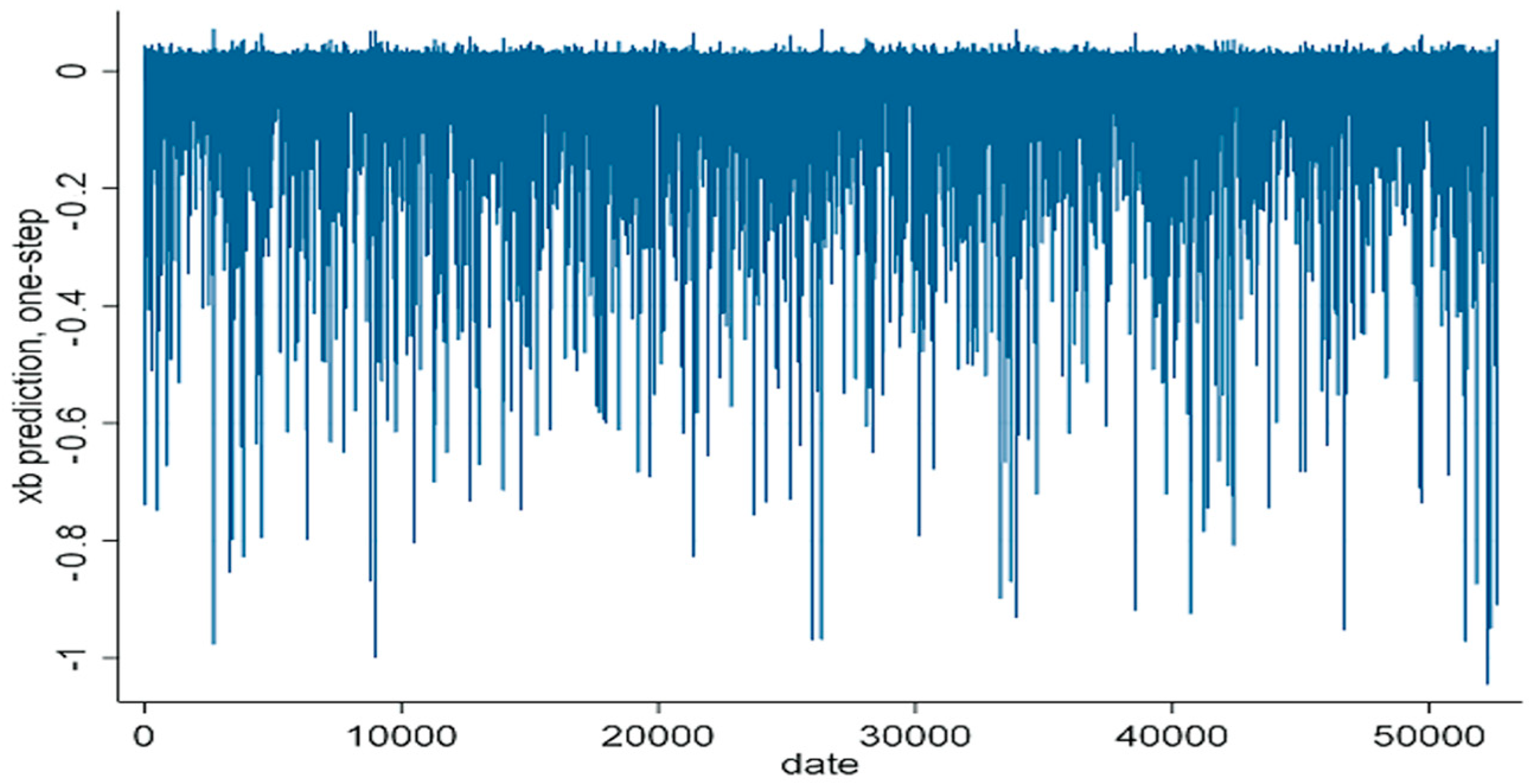
Figure 3,
Figure 4,
Figure 5 and
Figure 6 illustrate the ARIMA and GARCH models. This model can eliminate excessive peaks in data fluctuations and provide a more accurate representation of the different levels of volatility experienced in the data. The graphs demonstrate that the market is sensitive to unforeseen events because unexpected news can significantly affect the stability of the price variable and lead to rapid and sometimes substantial price changes. This case suggests that although these models can provide valuable predictions, many factors can influence market dynamics, and that the models may not capture all of these complexities. Erdogdu [
40] finds that unexpected events, such as political instability, natural disasters, or market changes, are the leading cause of increased volatility in financial markets, which causes rapid and often unpredictable price changes. These fluctuations can be positive or negative. For example, positive fluctuations may occur in response to favorable economic initiatives that stimulate consumer spending. This situation can lead to increased demand and a price rise.
5.3. Results of Markov-Switching Model
Markov-switching models are statistical tools used to analyze time series data where a process is used to transition between states. The model separately estimates each state’s parameters (such as mean and variance). The duration of each state is considered, representing how long the time series stays within a specific regime before transitioning to another. Transition probabilities indicate the possibility of moving from one state to another, and regime changes help to understand how different factors or events influence the behavior of the time series. The breaking points in the time series data represent the moments when the regime switches occur. Identifying these breaking points is crucial for understanding market conditions or changes in the economic environment.
Table 6 presents the results for each state’s mean and the constant error variance. The notation
refers to the possibility of transitioning from one state
to another
in a single step. The constant coefficient (C) for each state provides insight into the mean or average price value within that state. State 1 is represented by p11, which is the predicted probability of remaining in State 1 throughout future periods. It averages 3.255%, while the actual value is 0.603. This case indicates that the model predicts a relatively high likelihood of remaining in State 1. State 2 is represented by p12, which indicates the predicted probability of transitioning from State 1 to State 2 in the next period. It is calculated as 0.603 − 0.381 = 0.22. In this case, State 2 has a higher mean value than State 1, with a mean value of 4.232%. The statement indicates that the probability of remaining in State 1 is higher than that of transitioning to State 2. When there is a higher probability of staying in State 1, the system is less likely to move to State 2 in the next step. If State 1 represents a stable condition where supply and demand are balanced, it is more likely to persist. Supply and demand dynamics, weather conditions, and market regulations or changes in the supply and demand for electricity could influence average prices, and a less stable economy might lead to a transition to higher average prices (State 2).
The Schwarz Bayesian information criteria (SBIC) only applies to stationary models; they cannot be used to evaluate the serial correlation variable in this case. It is essential to consider alternative criteria, such as the Akaike information criterion (AIC) or the Hannan–Quinn information criterion (HQIC), for assessing the serial correlation in nonstationary models. Therefore, the nonstationary model excludes the incorporation of the 2.06 SBIC. The Akaike information criterion (AIC) is commonly used to evaluate the quality of a model by balancing the goodness of fit with the complexity of the model. A value of 2.06 indicates a relatively small amount of missed information in the model, making it a reliable tool for analysis or prediction tasks.
The Hannan–Quinn information criterion (HQIC) is an alternative to the Akaike information criterion (AIC) that balances bias and variance in model selection. Burnham and Anderson [
41] found that HQIC was not asymptotically efficient. This situation means that while HQC may perform well in certain situations, it may not always be the most accurate or reliable method for model selection. It is crucial to consider the strengths and limitations of each criterion.
They analyze AR parameters and volatility regimes in a Markov-switching model. In this case, State 2 is characterized by higher volatility (0.297%) compared to State 1 (0.223%), making it more sensitive to recent shocks. The AR coefficients for States 1 and 2 indicate that the shocks’ impact will slowly disappear. This finding means that even small changes in the market can potentially have more pronounced effects on asset prices. As a result, disturbances experienced in State 1 will have a lasting impact on the system. The value of sigma () is an important parameter as it assesses the impact of the volatility or standard deviation of the data within each state on the overall model accuracy. A higher sigma value indicates a larger fluctuation in the data, while a lower sigma value is associated with smaller fluctuation patterns in the long term. The sigma value in State 2 is lower (0.439) than in State 1 (0.492), implying that short-term shocks may have a significant impact when the system is in State 1. However, when the system transitions to State 2, these shocks tend to have a smaller and more manageable impact over the long term.
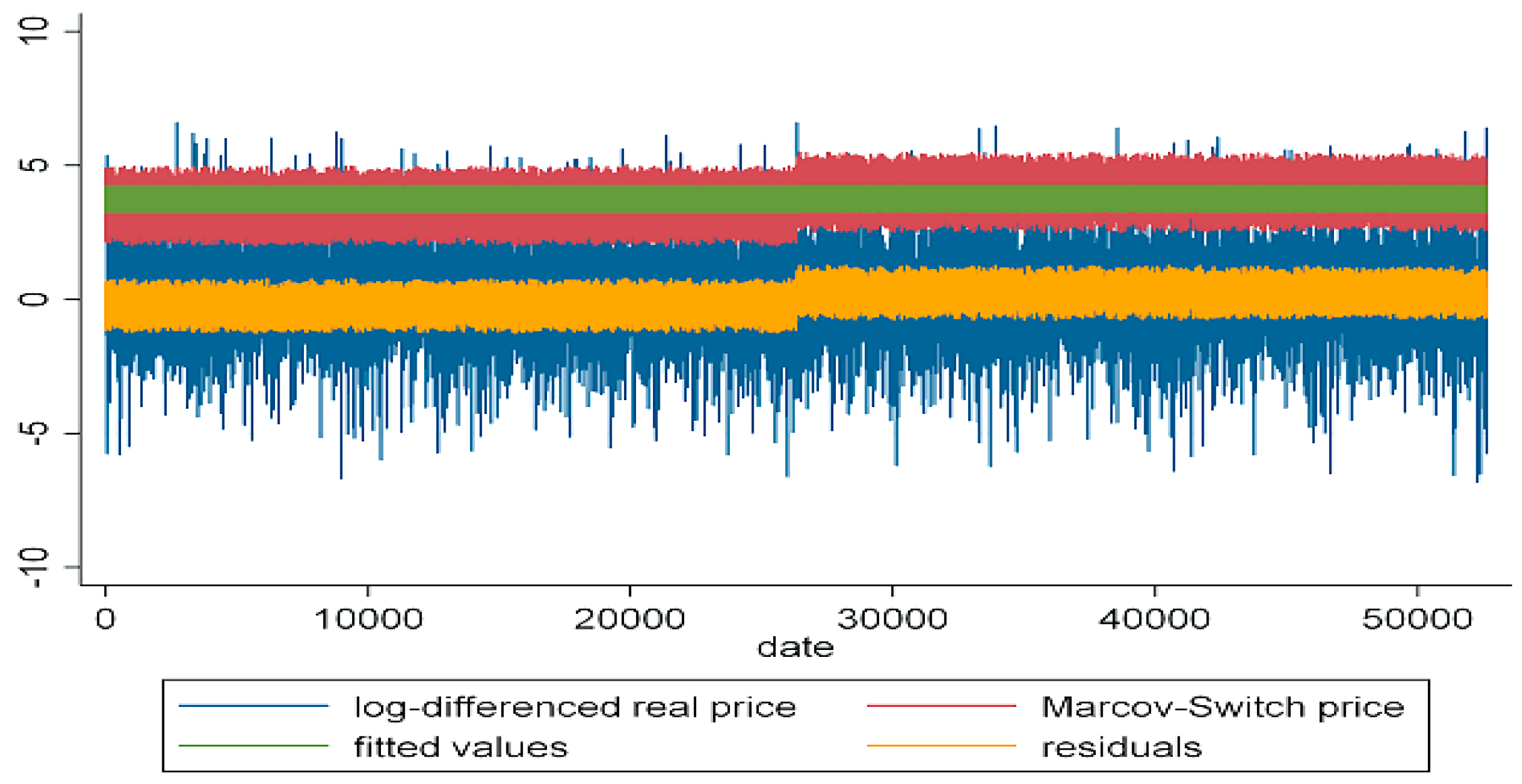
Figure 7 illustrates specific pricing patterns that could characterize two distinct states during specific periods when electricity prices remain constant. An extensive innovation during a low-volatility period will cause an earlier transition to the high-volatility regime. These distinct states are not short-lived but persist for a considerable duration, suggesting that once a trend or significant volatility is established in electricity markets, it tends to continue before transitioning to a different regime and affecting the transition. Markets may experience periods of stability (low volatility) compared to periods of turbulence and uncertainty (high volatility). These transitions are often associated with changes in market dynamics, economic conditions, or external events.
In
Figure 8, the plot of filtered probabilities is used to identify crisis periods that affect market indices. This analysis provides information about the timing and duration of these crises and helps determine specific points when regime switching occurs, particularly in periods of market instability. Being in State 1 may lead to financial losses during fluctuating times due to unpredictable market fluctuations. Remaining in State 1 could result in missed opportunities for growth, as other states may offer more favorable conditions. State 2 provides enhanced protection and stability, reducing the risk of potential damage during uncertain periods.
The model’s predictive performance is evaluated by comparing the fitted price values (predicted values) and residual values (the differences between predicted and actual values) with the actual data. The filtered probabilities can capture trends in the data. This approach enhances the precision of estimating the target variable compared to relying on limited or incomplete information.
Figure 9 represents that although there is a GARCH influence on prices, the statement was not sustained in the long run. As prices return to normal levels, it is essential to consider other factors that may contribute to price fluctuations in the long run.
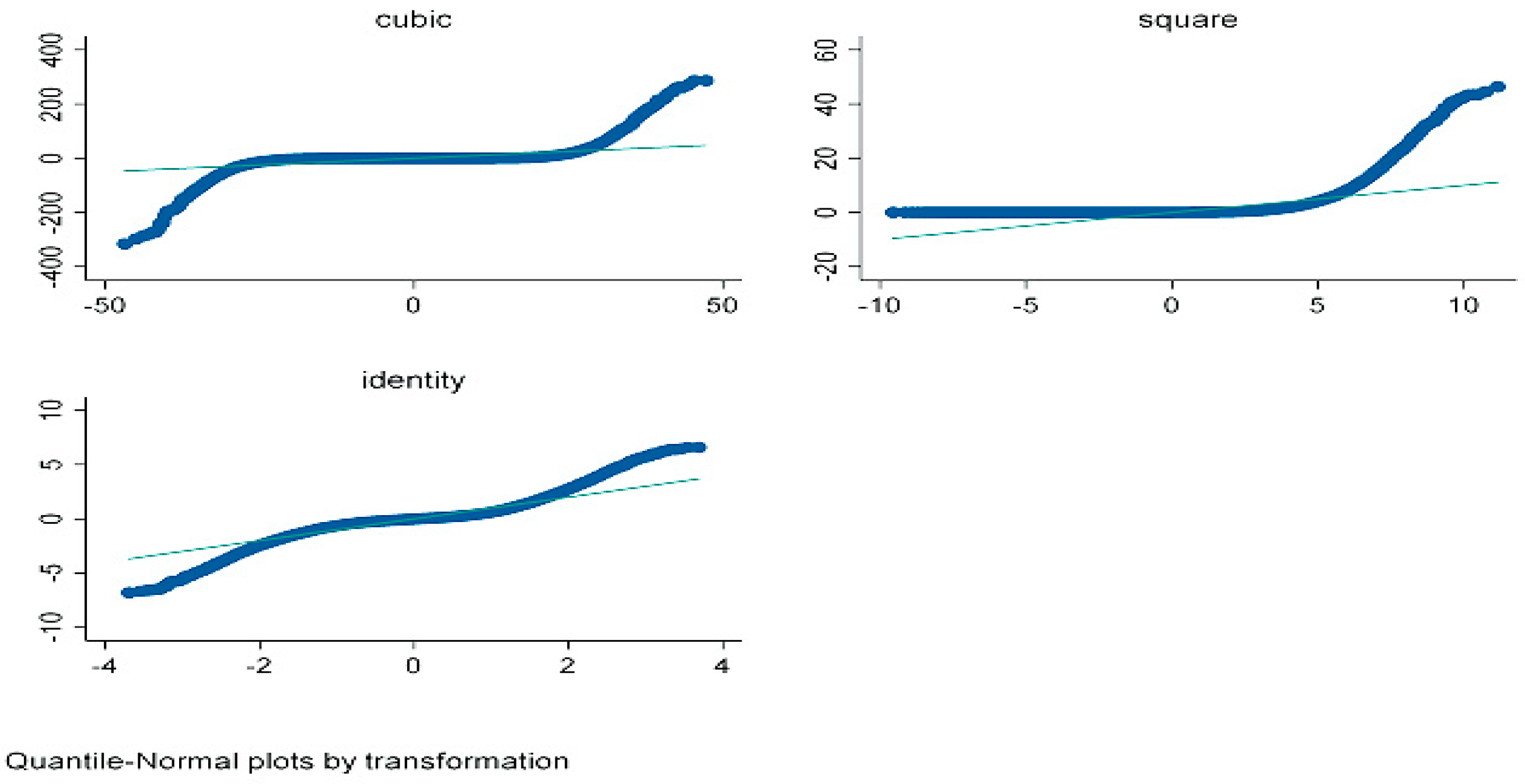
Figure 10 examines the residuals and the differences between the observed and predicted values. Plotting the residuals can help assess whether outliers or influential data points disproportionately affect the model. If the spread of residuals is not constant across all levels of the predictor variable, it may exhibit a pattern that influences the occurrence of price spikes in different directions. Skewness impacts statistical measures, and some observations are related to positive and negative price spikes. Skewness measures the asymmetry of a distribution, with positive skewness indicating a longer right tail and negative skewness indicating a longer left tail. The mention of positive price spikes being associated with high demand or limited supply, and of negative price spikes with oversupply or decreased demand, suggests that there are distinct patterns in the behavior of the data.
Regarding Quantile–Quantile (QQ) graphs, they help assess the normality of a dataset. Extreme values in high-frequency data might result in spikes or outliers in a QQ plot. It is crucial to consider the context and purpose of the analysis to determine whether these extreme values significantly impact the overall interpretation of the data. The QQ plot in
Figure 10 supports the non-normality assumption, indicating heteroscedasticity in electricity prices.
Figure 11 identifies peaks representing significant seasonal frequencies in the price time series. Koopman et al. [
42] propose an approach to improve efficiency in modeling seasonal variance. Incorporating these hourly dummy variables allows for more accurate predictions of seasonal patterns and better resource allocation optimization. This method can be advantageous in industries where demand fluctuates significantly throughout the day, such as transportation or hospitality. This approach improves efficiency, accuracy, and reliability by simplifying the model and reducing the risk of overfitting.