Optimal Design of Grid-Connected Hybrid Renewable Energy System Considering Electric Vehicle Station Using Improved Multi-Objective Optimization: Techno-Economic Perspectives
Abstract
1. Introduction
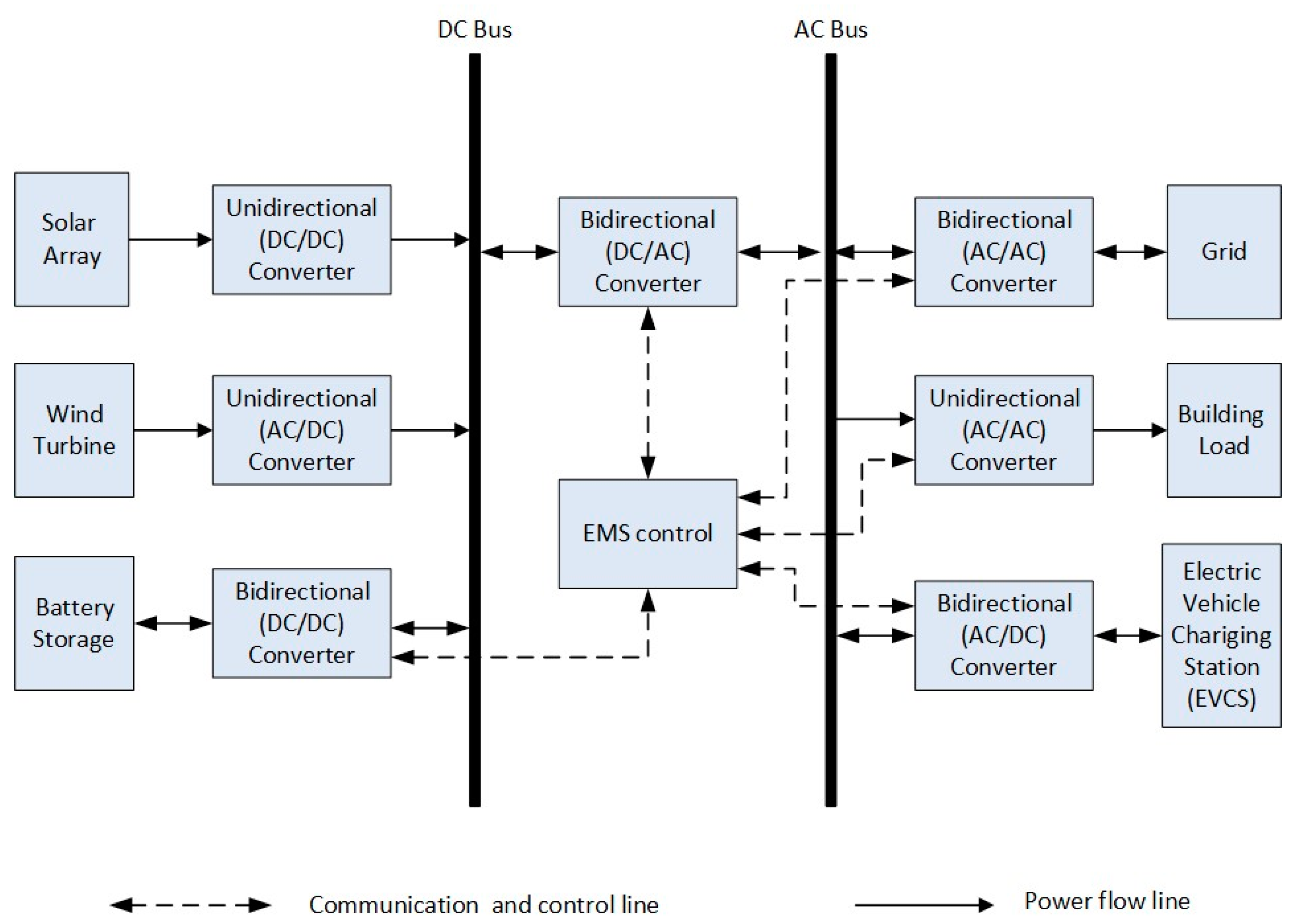
2. Mathematical Modeling of the Grid-Connected PV/WT/Battery System Combined with EVCS Using Vehicle-to-Grid (V2G) Technique
2.1. Photovoltaic Panel Mathematical Modeling
2.2. Wind Turbine Mathematical Modeling
2.3. Battery Mathematical Modeling
2.4. Converter Mathematical Modeling
2.5. The Grid Mathematical Modeling
2.6. Mathematical Modeling of Electric Vehicle Charging Station
3. Date Collection and Renewability–Economic–Technical Assessments
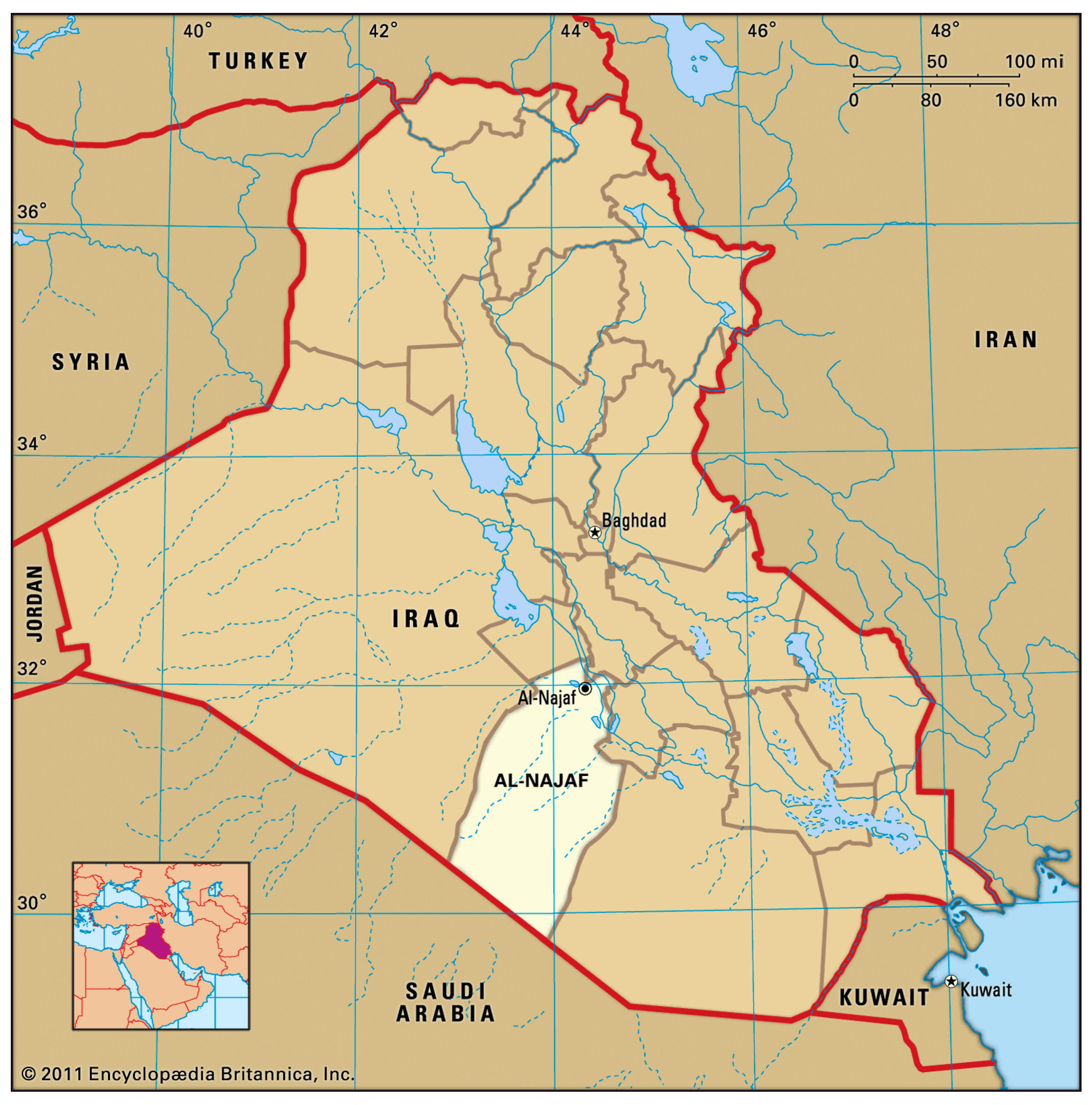
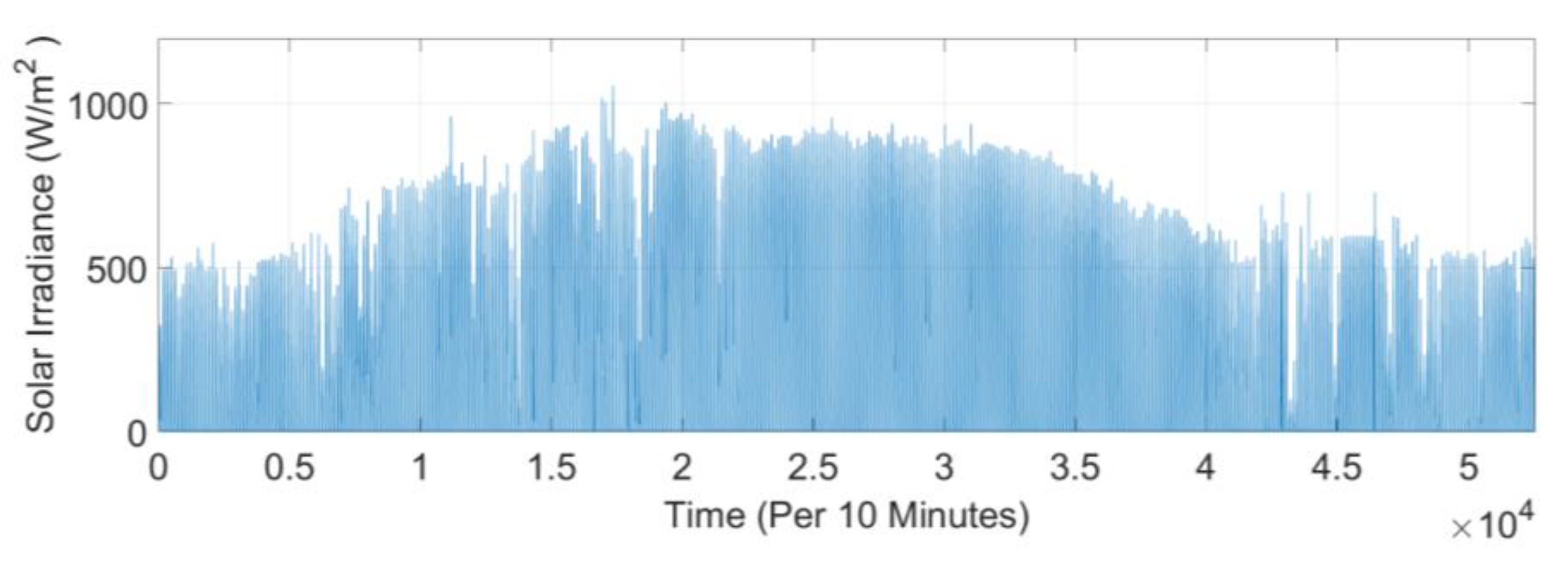
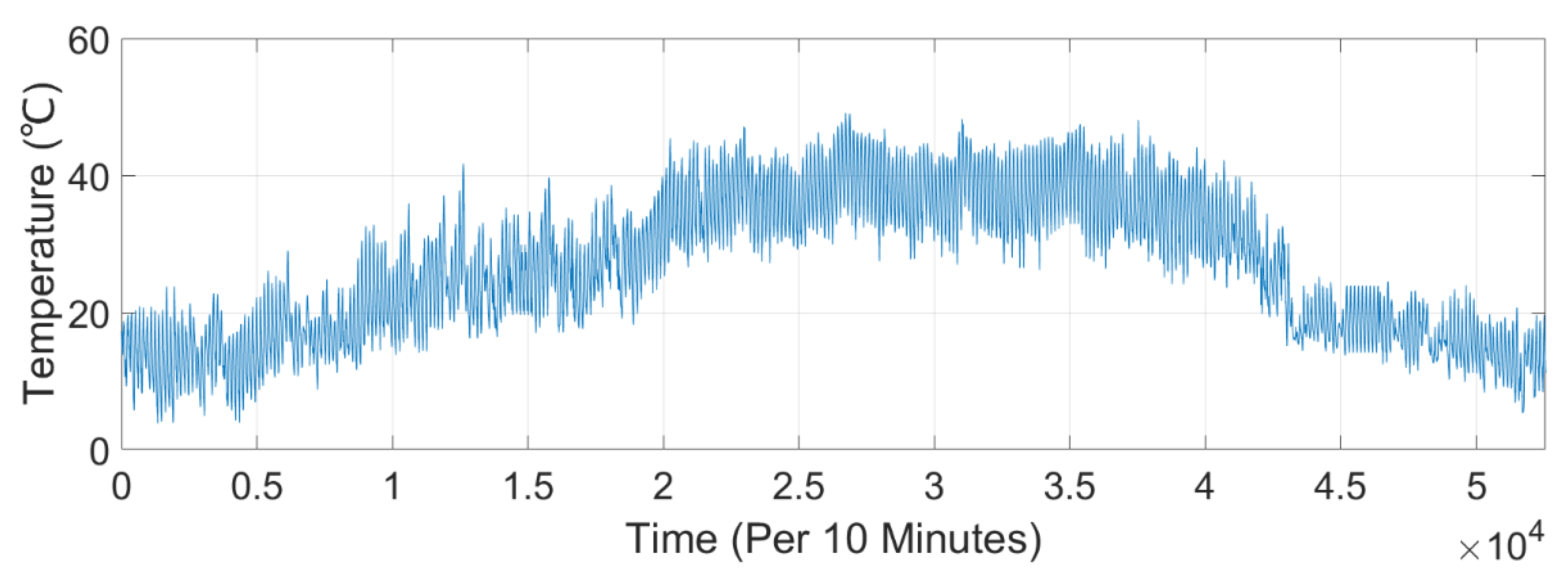
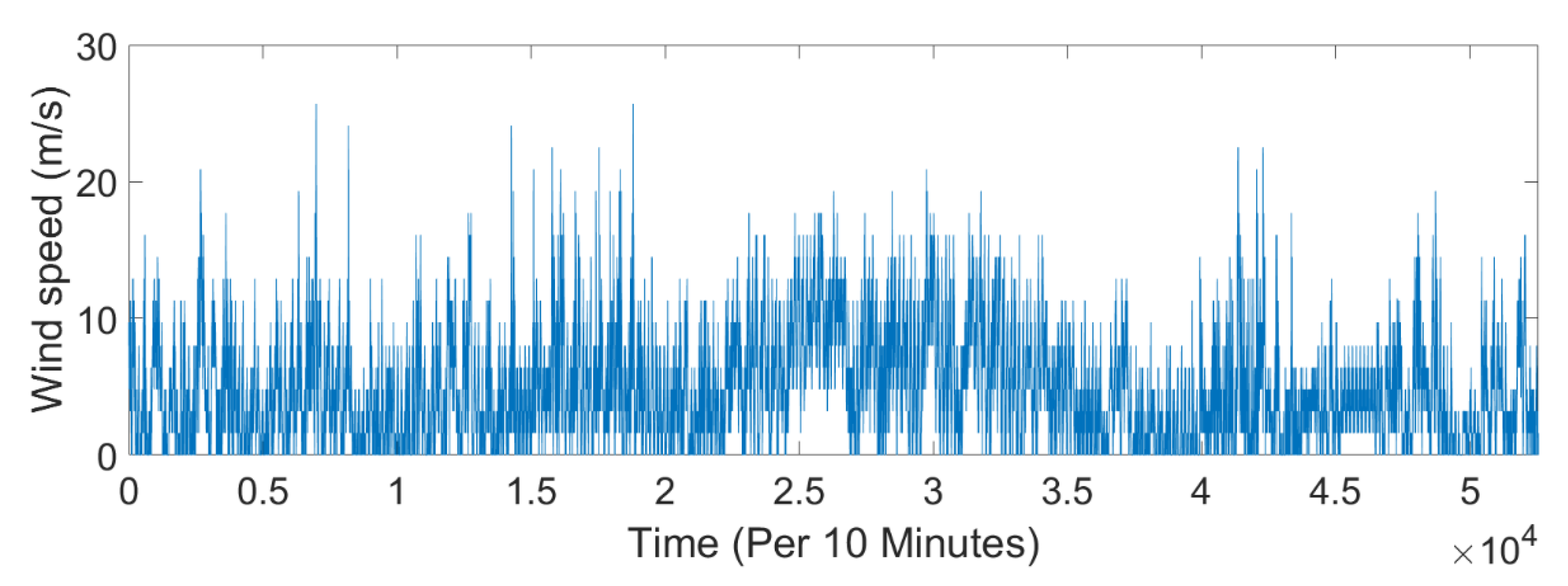
3.1. The Study Site and Load Profile
3.1.1. Al-Najaf Governorate in Iraq
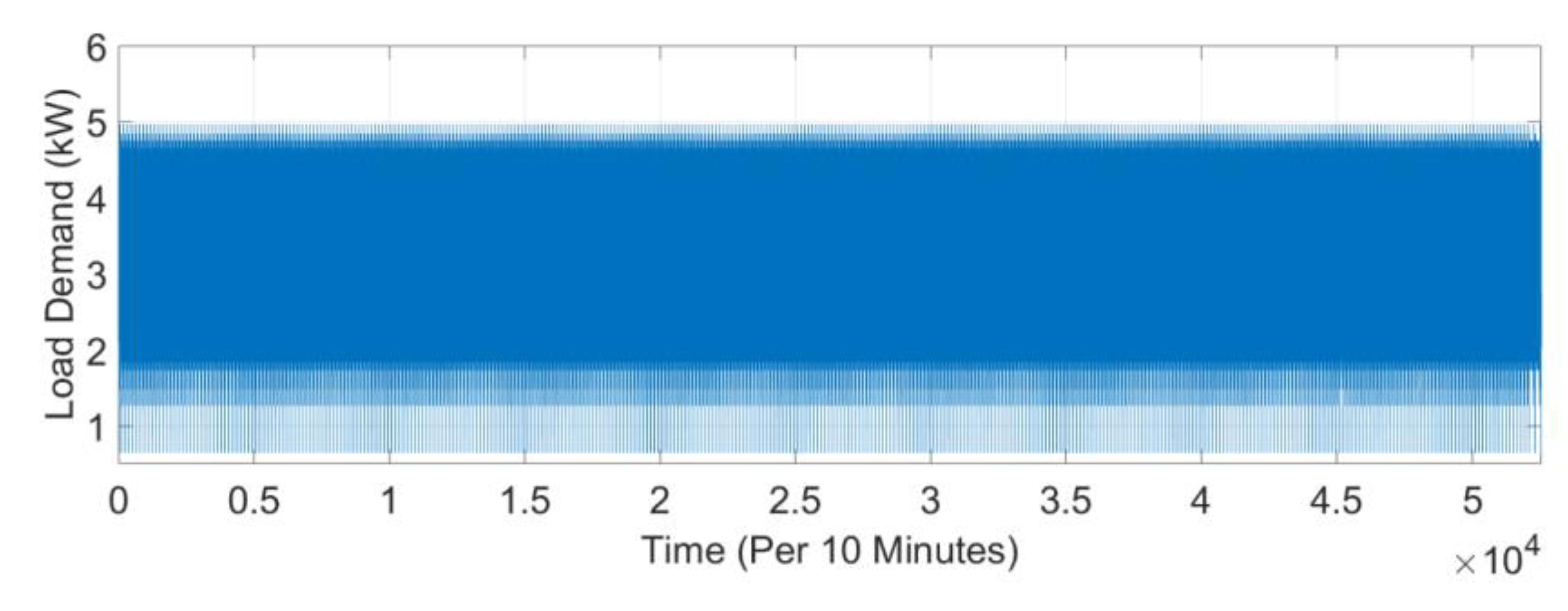
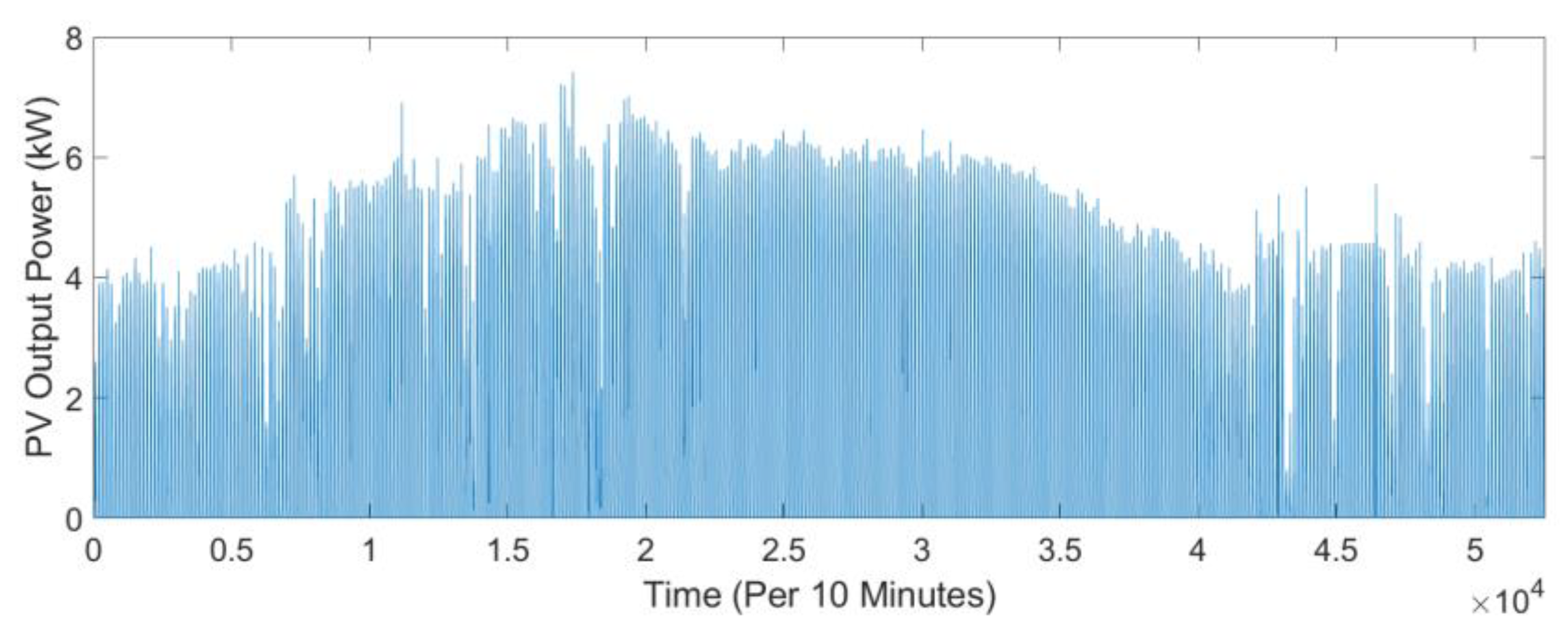
3.1.2. Load Profile
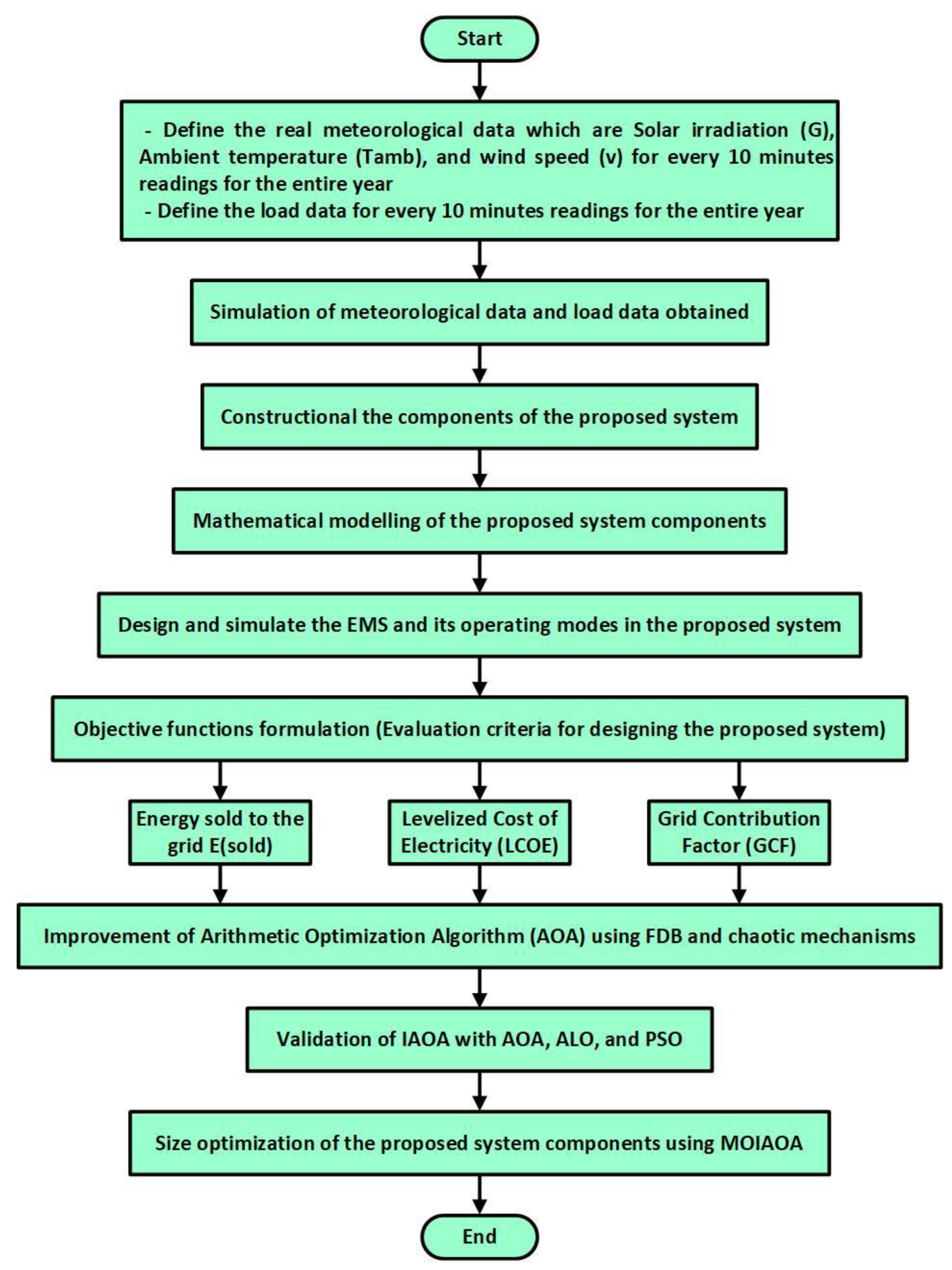
3.2. Objective Function Formulation
3.2.1. Levelized Cost of Electricity (LCOE)
3.2.2. Grid Contribution Factor (GCF)
3.2.3. Energy Sold to the Grid (
4. The Proposed Methodology for Sizing of the Grid-Connected PV/WT/Battery/EVCS System
4.1. Energy Management Strategy and Its Scenarios in the Proposed System
- Operating Mode 1: Renewable energy sources (photovoltaic and wind power) supply power for running the system and charging the battery and the electric vehicle.
- Operating Mode 2: The battery supplies power for load and electric vehicle charging if there is no grid and insufficient RESs.
- Operating Mode 3: The main grid supplying power for electric vehicle charging (Buying–Charging–G2V) when batteries and RESs are not available and grid demand is required. The power flow will be unidirectional.
- Operating Mode 4: The electric vehicle supplying power for the grid (V2G–Sell–Discharging) when grid demand is high and batteries and RESs are unavailable. The flow of power will be bidirectional. The proposed operation modes of RB-EMS for the proposed system are listed in Table 2.
4.2. Arithmetic Optimization Algorithm (AOA)
4.2.1. Inspiration
4.2.2. Initialization Phase
4.2.3. Exploration Phase
4.2.4. Exploitation Phase
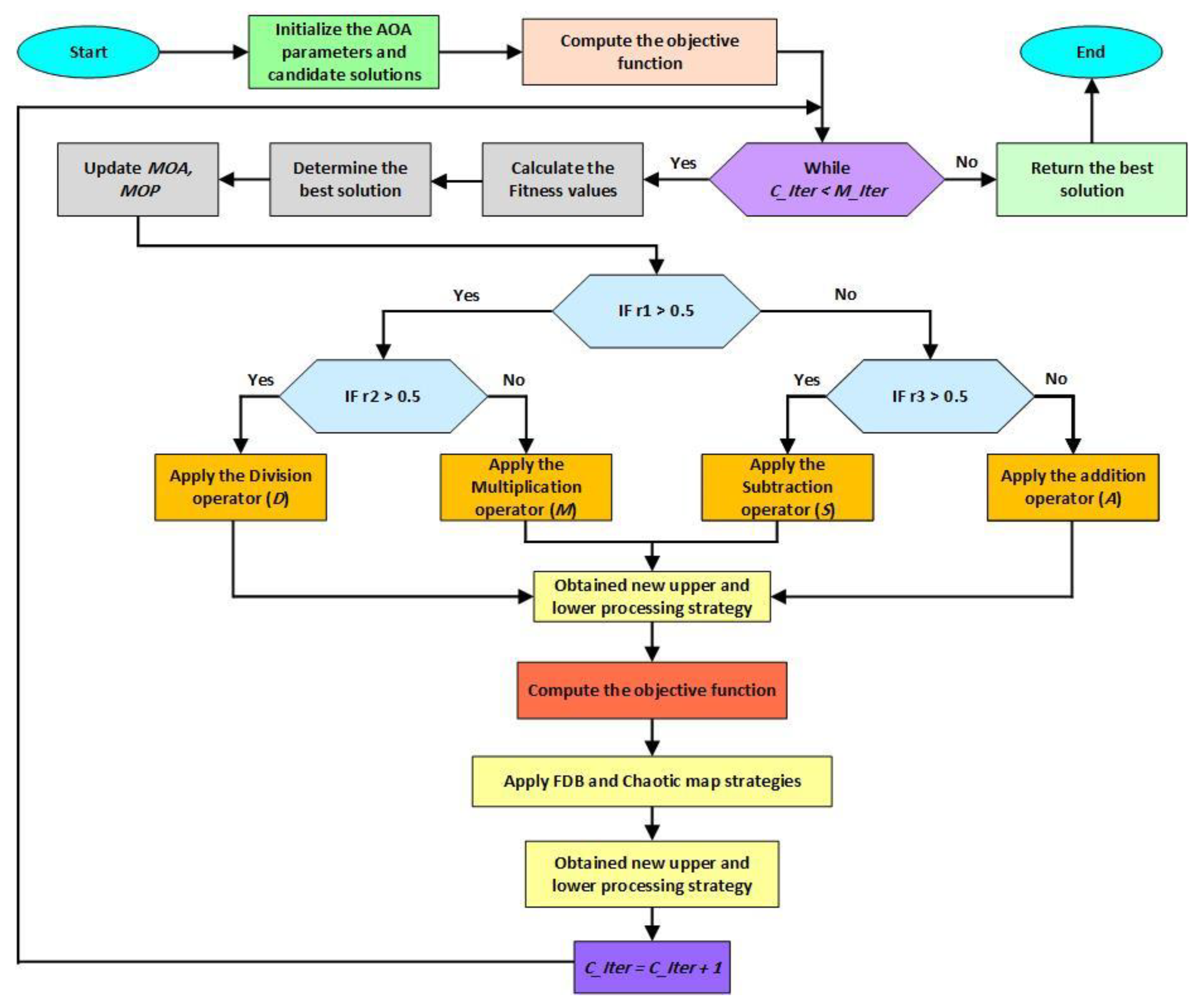
4.3. The Proposed Improved Arithmetic Optimization Algorithm (IAOA)
- FDB Strategy
- Chaotic map tactic
- Handling upper and lower boundaries
4.4. The Proposed MOIAOA Method
5. Results and Discussion
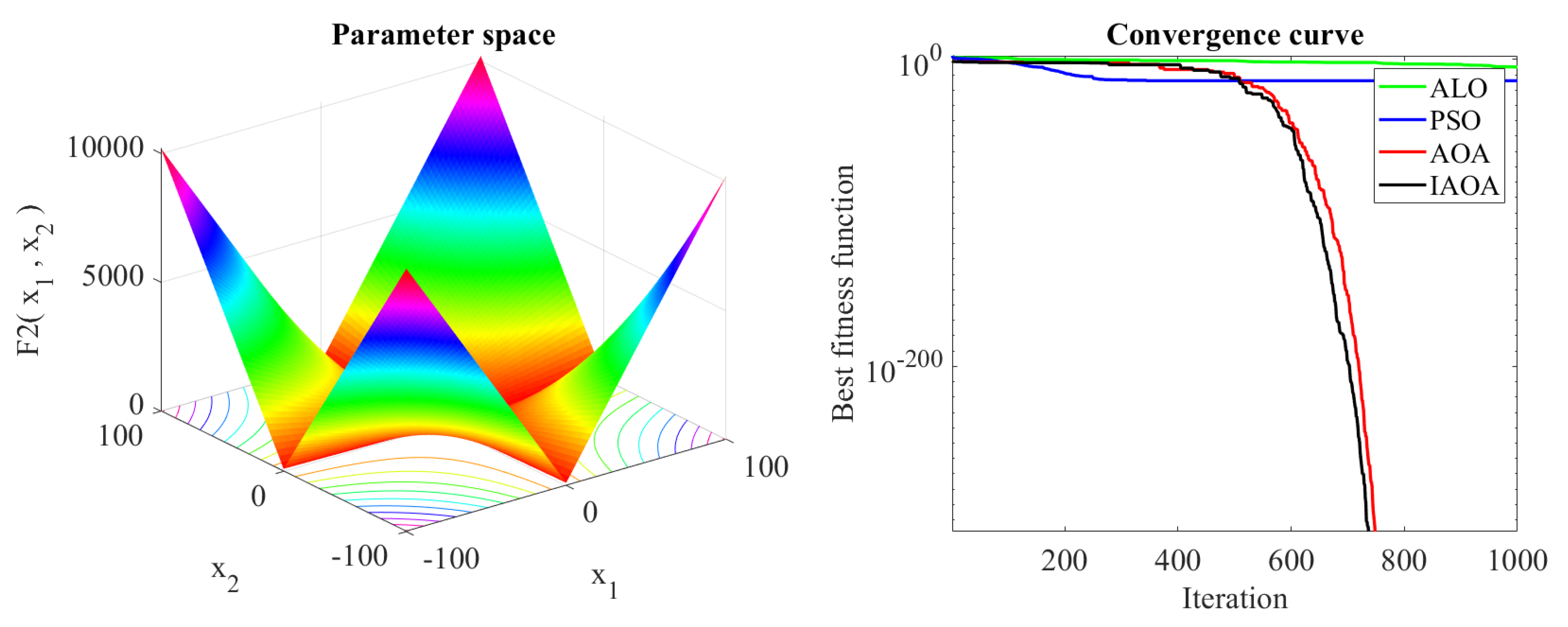
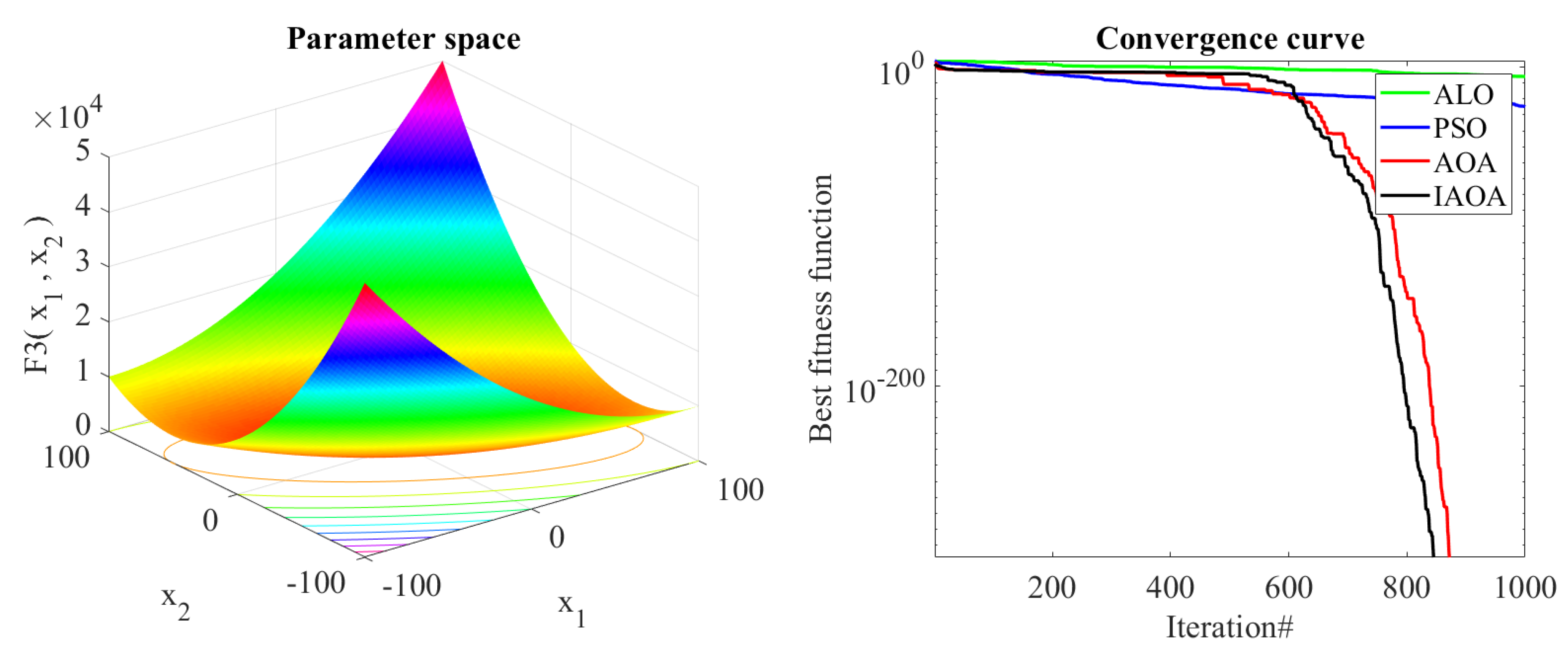
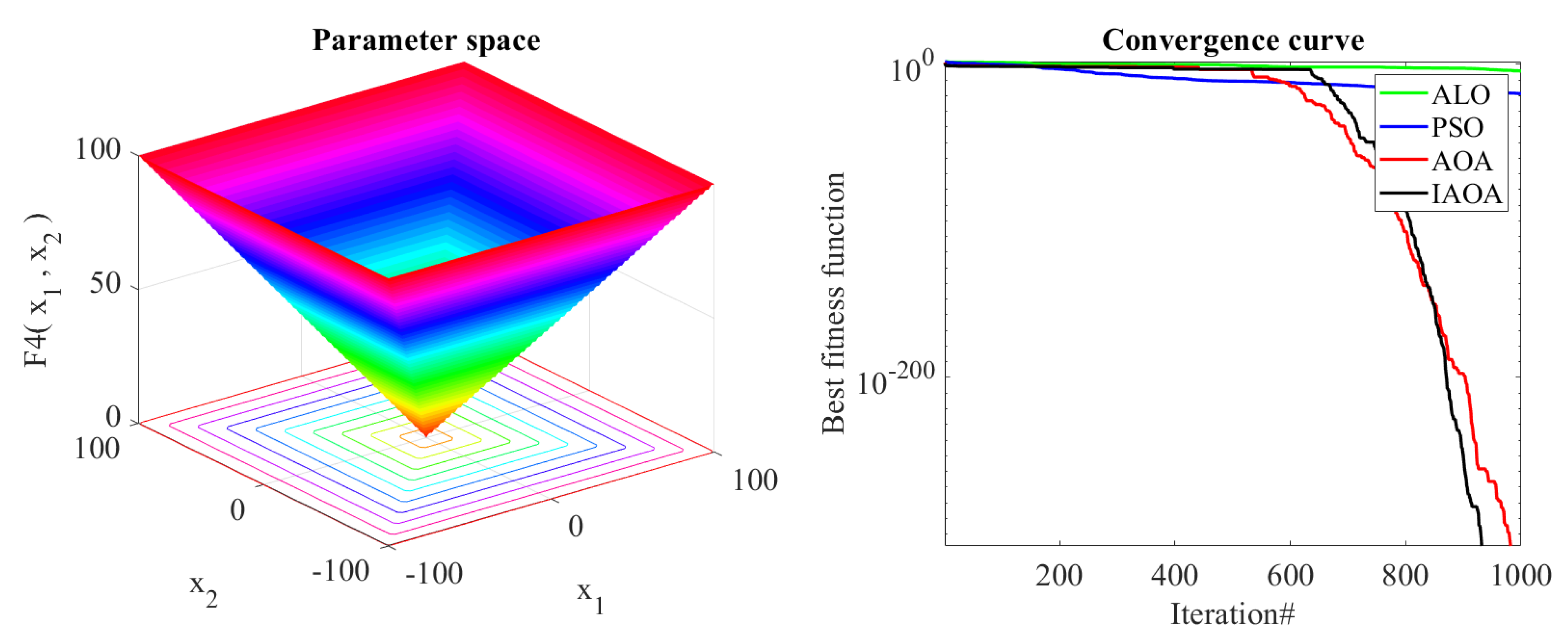
5.1. Performance Comparison between the Proposed IAOA and AOA, PSO, ALO
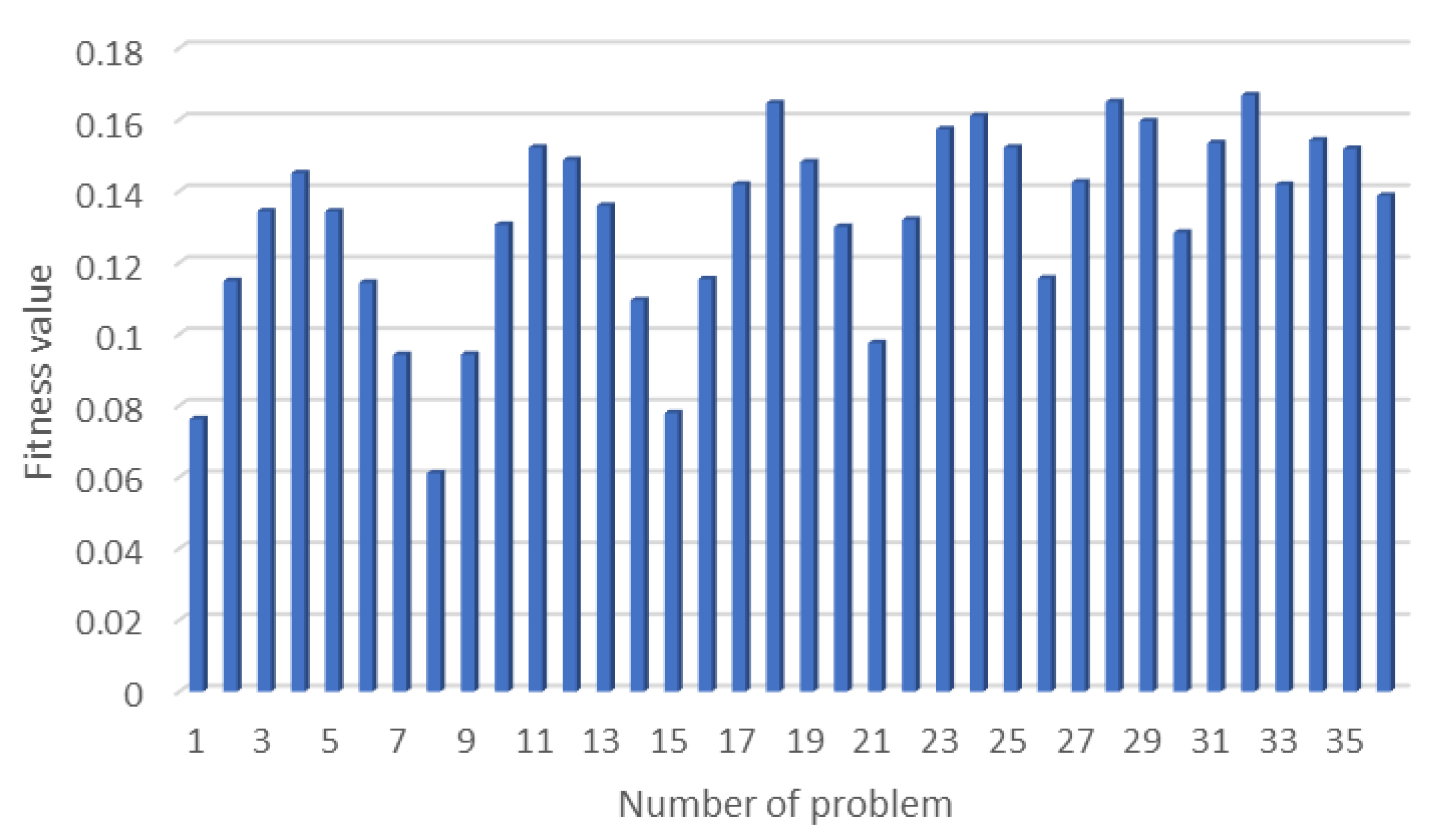
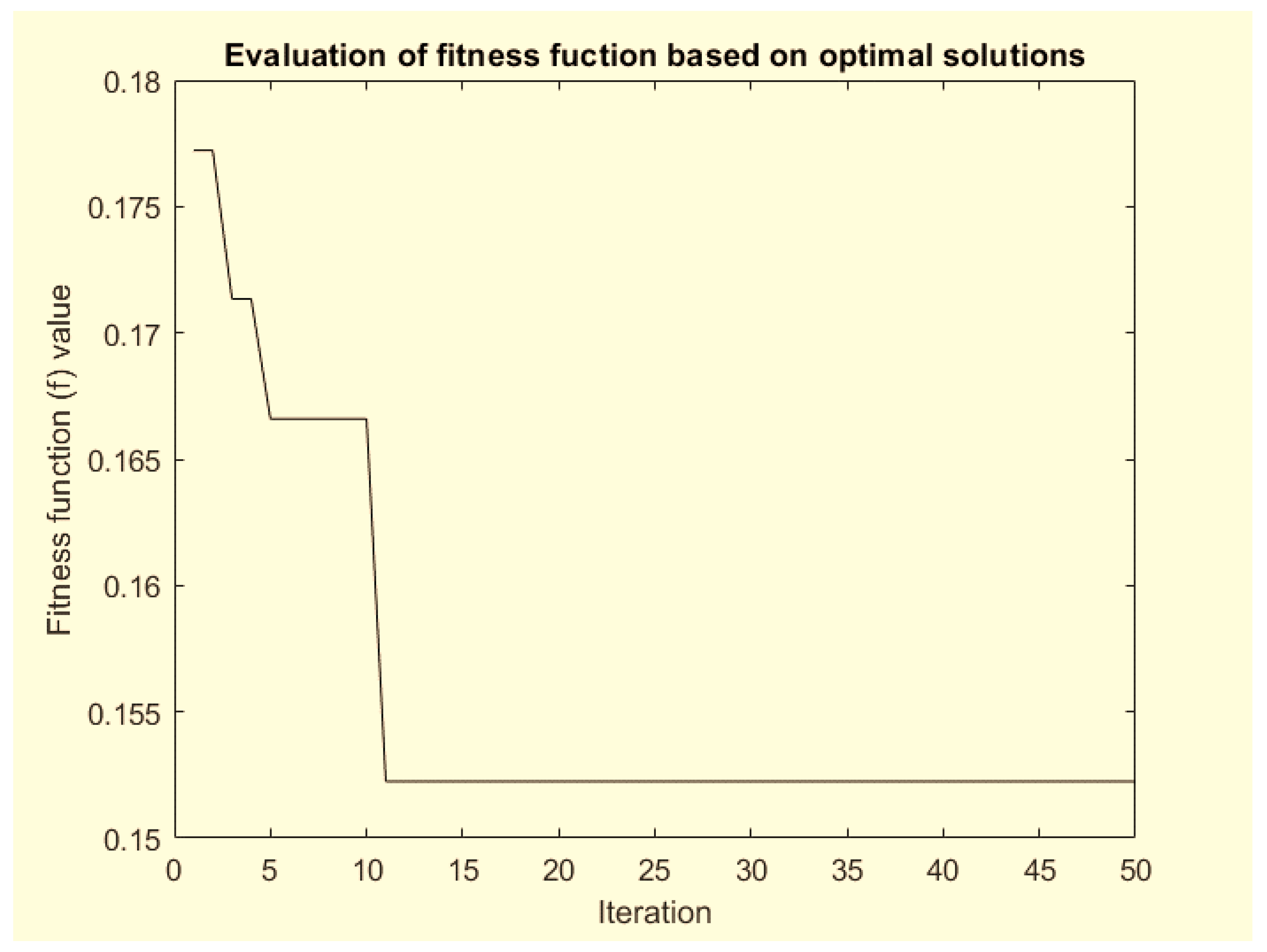
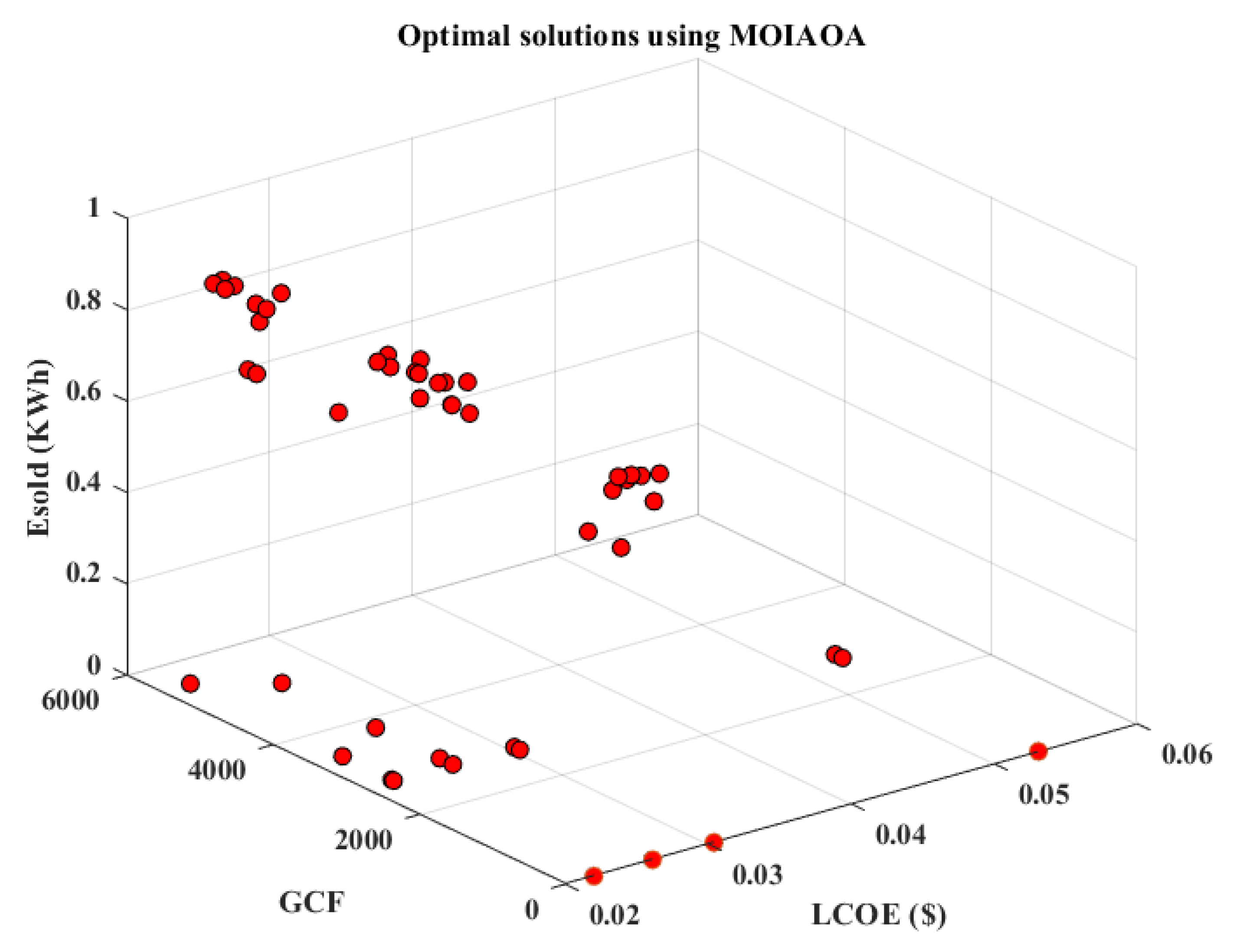
5.2. Results of the MIAOA
6. Conclusions and Future Direction
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| The annual energy sold to the grid | |
| WT | Wind turbine |
| EV | Electric Vehicle |
| EVCS | electric vehicle charging station |
| NS | Non-Scale |
| PSO | Particle swarm optimization |
| ALO | Ant Lion Optimizer |
| EMS | Energy Management Strategy |
| AOA | Arithmetic optimization algorithm |
| HRES | Hybrid renewable energy system |
| MOO | Multi-objective optimization |
| STC | Standard Test Condition |
| The output power generated from PV | |
| Solar irradiance | |
| Rated power for PV | |
| NOCT | The nominal operating cell temperature |
| cut-in speed of the WT | |
| cut-out speed of the WT | |
| Rated power of the WT | |
| Rated wind speed of the WT | |
| The generated output power of the WT | |
| BSS | Battery Storage System |
| DOD | The depth of discharge |
| The station rated capacity | |
| The power factor | |
| The amount of charging slots for each EV | |
| The overload factor for cover overloading in transients | |
| The maximum power rate of each EV | |
| The inverter rating | |
| The peak load demand | |
| BT | Battery |
| X | a collection of initialized solutions |
| Rand | a random variable in the range [0, 1] |
| and | the upper and lower limits of the problem |
| MOA ( | the value at the t th iteration |
| the maximum number of iterations | |
| randomly generated number that is conditioned between the D and M operations | |
| and | the upper and lower limits |
| ε | a tiny integer value |
| a randomly generated number that serves as a denotation for the A and S operators | |
| FF | Fitness Function |
| PV | photovoltaic |
| RESs | Renewable energy sources |
| LCOE | Levelized Cost of Energy |
| V2G | Vehicle-to-grid |
| STC | Standard Test Conditions |
| RB-EMS | Rule-Based Energy Management Strategy |
| GCF | Grid Contribution Factor |
| REF | Renewable Energy Fraction |
| NPC | Economic criterion of net present cost |
| IAOA | Improved arithmetic optimization algorithm |
| MOIAOA | Multi-objective improved arithmetic optimization algorithm |
| Temperature coefficient | |
| The cell temperature as reference temperature | |
| The ambient temperature | |
| Capacity of the battery | |
| The daily average load demand | |
| AD | the autonomy days |
| v1, v2 | The wind speed |
| h | hub height |
| The reference height anemometer | |
| The power-law exponential known as wind gradient, Hellmann exponent, or friction coefficient | |
| SOC | State of Charge |
| The battery’s output of electricity | |
| The total power generated by PV | |
| The total power generated by WT | |
| The total energy demand | |
| The inverter efficiency | |
| The self-discharge rate of the battery | |
| Battery efficiency | |
| The feed-in tariff rate | |
| The cost of selling energy | |
| The cost of buying electricity from the grid | |
| The per hour summation of annually buying electricity from the grid for one year | |
| MOA | Math Optimizer Accelerated |
| the current iteration | |
| Max & Min | The accelerated function’s maximum and lowest values are denoted by Max and Min (Maximum and minimum values of the MOA function) |
| a control variable set | |
| MOP | Math Optimizer Probability |
| a sensitive control parameter set | |
| FDB | Fitness–distance balance |
References
- Ali, S.; Zheng, Z.; Aillerie, M.; Sawicki, J.-P.; Péra, M.-C.; Hissel, D. A Review of DC Microgrid Energy Management Systems Dedicated to Residential Applications. Energies 2021, 14, 4308. [Google Scholar] [CrossRef]
- Ali, A.; Shaaban, M.F.; Awad, A.S.A.; Azzouz, M.A.; Lehtonen, M.; Mahmoud, K. Multi-Objective Allocation of EV Charging Stations and RESs in Distribution Systems Considering Advanced Control Schemes. IEEE Trans. Veh. Technol. 2023, 72, 3146–3160. [Google Scholar] [CrossRef]
- Das, R.; Wang, Y.; Putrus, G.; Kotter, R.; Marzband, M.; Herteleer, B.; Warmerdam, J. Multi-objective techno-economic-environmental optimization of electric vehicle for energy services. Appl. Energy 2020, 257, 113965. [Google Scholar] [CrossRef]
- Ahmadi, S.E.; Kazemi-Razi, S.M.; Marzband, M.; Ikpehai, A.; Abusorrah, A. Multi-objective stochastic techno-economic-environmental optimization of distribution networks with G2V and V2G systems. Electr. Power Syst. Res. 2023, 218, 109195. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Yang, H.; Shan, K. Hybrid renewable energy applications in zero-energy buildings and communities integrating battery and hydrogen vehicle storage. Appl. Energy 2021, 290, 116733. [Google Scholar] [CrossRef]
- Eriksson, E.; Gray, E.M. Optimization and integration of hybrid renewable energy hydrogen fuel cell energy systems—A critical review. Appl. Energy 2017, 202, 348–364. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Fazlhashemi, S.S.; Javadi, H.; Taghvaei, M. Multi-objective day-ahead energy management of a microgrid considering responsive loads and uncertainty of the electric vehicles. J. Clean. Prod. 2020, 267, 121562. [Google Scholar] [CrossRef]
- Jia, S.; Kang, X.; Cui, J.; Tian, B.; Xiao, S. Hierarchical stochastic optimal scheduling of electric thermal hydrogen integrated energy system considering electric vehicles. Energies 2022, 15, 5509. [Google Scholar] [CrossRef]
- Zhang, Q.; Ding, J.; Li, G. Optimal operation of PV-diesel-battery MG based on fuzzy comprehensive evaluation. In Proceedings of the 2018 Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 10–12 April 2018; pp. 1–5. [Google Scholar]
- Saffari, M.; Misaghian, M.S.; Flynn, D.; Kia, M.; Vahidinasab, V.; Lotfi, M.; Catalão, J.P.; Shafie-Khah, M. Multi-objective optimization of an active distribution system using normalised normal constraint method. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Jannati, J.; Nazarpour, D. Multi-objective scheduling of electric vehicles intelligent parking lot in the presence of hydrogen storage system under peak load management. Energy 2018, 163, 338–350. [Google Scholar] [CrossRef]
- Ahmed, H.Y.; Ali, Z.M.; Refaat, M.M.; Aleem, S.H.A. A Multi-Objective Planning Strategy for Electric Vehicle Charging Stations towards Low Carbon-Oriented Modern Power Systems. Sustainability 2023, 15, 2819. [Google Scholar] [CrossRef]
- Tan, B.; Chen, H. Multi-objective energy management of multiple microgrids under random electric vehicle charging. Energy 2020, 208, 118360. [Google Scholar] [CrossRef]
- Hosseinnia, H.; Nazarpour, D.; Talavat, V. Multi-objective optimization framework for optimal planning of the microgrid (MG) under employing demand response program (DRP). J. Ambient Intell. Humaniz. Comput. 2019, 10, 2709–2730. [Google Scholar] [CrossRef]
- Kataoka, R.; Shichi, A.; Yamada, H.; Iwafune, Y.; Ogimoto, K. Comparison of the economic and environmental performance of V2H and residential stationary battery: Development of a multi-objective optimization method for homes of EV owners. World Electr. Veh. J. 2019, 10, 78. [Google Scholar] [CrossRef]
- Wu, G.; Yi, C.; Xiao, H.; Wu, Q.; Zeng, L.; Yan, Q.; Zhang, M. Multi-objective Optimization of Integrated Energy Systems Considering Renewable Energy Uncertainty and Electric Vehicles. IEEE Trans. Smart Grid 2023, 14, 4322–4332. [Google Scholar] [CrossRef]
- Stojkovic, J. Multi-objective optimal charging control of electric vehicles in pv charging station. In Proceedings of the 2019 16th International Conference on the European Energy Market (EEM), Ljubljana, Slovenia, 18–20 September 2019; pp. 1–5. [Google Scholar]
- De Schepper, E.; Van Passel, S.; Lizin, S.; Vincent, T.; Martin, B.; Gandibleux, X. Economic and environmental multi-objective optimization to evaluate the impact of Belgian policy on solar power and electric vehicles. J. Environ. Econ. Policy 2016, 5, 1–27. [Google Scholar] [CrossRef]
- Zeynali, S.; Rostami, N.; Feyzi, M. Multi-objective optimal short-term planning of renewable distributed generations and capacitor banks in power system considering different uncertainties including plug-in electric vehicles. Int. J. Electr. Power Energy Syst. 2020, 119, 105885. [Google Scholar] [CrossRef]
- Ahmadi-Nezamabad, H.; Zand, M.; Alizadeh, A.; Vosoogh, M.; Nojavan, S. Multi-objective optimization based robust scheduling of electric vehicles aggregator. Sustain. Cities Soc. 2019, 47, 101494. [Google Scholar] [CrossRef]
- Yang, Z.; Ghadamyari, M.; Khorramdel, H.; Alizadeh, S.M.S.; Pirouzi, S.; Milani, M.; Banihashemi, F.; Ghadimi, N. Robust multi-objective optimal design of islanded hybrid system with renewable and diesel sources/stationary and mobile energy storage systems. Renew. Sustain. Energy Rev. 2021, 148, 111295. [Google Scholar] [CrossRef]
- Foroozandeh, Z.; Ramos, S.; Soares, J.; Vale, Z. Energy management in smart building by a multi-objective optimization model and pascoletti-serafini scalarization approach. Processes 2021, 9, 257. [Google Scholar] [CrossRef]
- Coelho, V.N.; Coelho, I.M.; Coelho, B.N.; Cohen, M.W.; Reis, A.J.; Silva, S.M.; Souza, M.J.; Fleming, P.J.; Guimaraes, F.G. Multi-objective energy storage power dispatching using plug-in vehicles in a smart-microgrid. Renew. Energy 2016, 89, 730–742. [Google Scholar] [CrossRef]
- Soares, J.; Ghazvini, M.A.F.; Vale, Z.; de Moura Oliveira, P. A multi-objective model for the day-ahead energy resource scheduling of a smart grid with high penetration of sensitive loads. Appl. Energy 2016, 162, 1074–1088. [Google Scholar] [CrossRef]
- Han, W.; Zhang, J.; Chen, L. Multi-Objective Optimal Dispatch of Smart Grid by Estimating Available Capacity of EV Aggregators. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 1299–1303. [Google Scholar]
- Panda, N.K.; Paterakis, N.G. A multi-objective optimization model for the quantification of flexibility in a large business park. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021; pp. 1–6. [Google Scholar]
- Gholami, K.; Karimi, S.; Anvari-Moghaddam, A. Multi-objective stochastic planning of electric vehicle charging stations in unbalanced distribution networks supported by smart photovoltaic inverters. Sustain. Cities Soc. 2022, 84, 104029. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Esmaili, M.; Mohammadkhani, N. Stochastic multi-objective energy management in residential microgrids with combined cooling, heating, and power units considering battery energy storage systems and plug-in hybrid electric vehicles. J. Clean. Prod. 2018, 195, 301–317. [Google Scholar] [CrossRef]
- Zhu, J.; Jin, Y.; Zhu, W.; Lee, D.-K.; Bohlooli, N. Multi-objective planning of micro-grid system considering renewable energy and hydrogen storage systems with demand response. Int. J. Hydrog. Energy 2023, 48, 15626–15645. [Google Scholar] [CrossRef]
- Sharafi, M.; ElMekkawy, T.Y.; Bibeau, E.L. Optimal design of hybrid renewable energy systems in buildings with low to high renewable energy ratio. Renew. Energy 2015, 83, 1026–1042. [Google Scholar] [CrossRef]
- Murray, P.; Carmeliet, J.; Orehounig, K. Multi-objective optimization of power-to-mobility in decentralised multi-energy systems. Energy 2020, 205, 117792. [Google Scholar] [CrossRef]
- Zhang, Y.; Le, J.; Liao, X.; Zheng, F.; Liu, K.; An, X. Multi-objective hydro-thermal-wind coordination scheduling integrated with large-scale electric vehicles using IMOPSO. Renew. Energy 2018, 128, 91–107. [Google Scholar] [CrossRef]
- Luo, C.; Huang, Y.-F.; Gupta, V. Stochastic dynamic pricing for EV charging stations with renewable integration and energy storage. IEEE Trans. Smart Grid 2017, 9, 1494–1505. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- “Kyocera KD325GX-LFB (325 W) Solar Panel”, SolarDesignTool. Available online: http://www.solardesigntool.com/components/module-panel-solar/Kyocera/2788/KD325GX-LFB/specification-data-sheet.html (accessed on 4 June 2023).
- Mouli, G.C.; Bauer, P.; Zeman, M. System design for a solar powered electric vehicle charging station for workplaces. Appl. Energy 2016, 168, 434–443. [Google Scholar] [CrossRef]
- Bhatti, A.R.; Salam, Z. A rule-based energy management scheme for uninterrupted electric vehicles charging at constant price using photovoltaic-grid system. Renew. Energy 2018, 125, 384–400. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W.; Lau, K.Y. Optimal sizing of an autonomous photovoltaic/wind/battery/diesel generator microgrid using grasshopper optimization algorithm. Sol. Energy 2019, 188, 685–696. [Google Scholar] [CrossRef]
- Diaf, S.; Diaf, D.; Belhamel, M.; Haddadi, M.; Louche, A. A methodology for optimal sizing of autonomous hybrid PV/wind system. Energy Policy 2007, 35, 5708–5718. [Google Scholar] [CrossRef]
- Bhandari, B.; Poudel, S.R.; Lee, K.-T.; Ahn, S.-H. Mathematical modeling of hybrid renewable energy system: A review on small hydro-solar-wind power generation. Int. J. Precis. Eng. Manuf. -Green Technol. 2014, 1, 157–173. [Google Scholar] [CrossRef]
- Al-Kharbosy, M.E.H. Enhancement Protection and Operation of the Doubly Fed Induction Generator during Grid Fault. Master’s Thesis, South Valley University-Qena-Egypt, Qena, Egypt, 2012. [Google Scholar]
- Borhanazad, H.; Mekhilef, S.; Ganapathy, V.G.; Modiri-Delshad, M.; Mirtaheri, A. Optimization of micro-grid system using MOPSO. Renew. Energy 2014, 71, 295–306. [Google Scholar] [CrossRef]
- Poompavai, T.; Kowsalya, M. Control and energy management strategies applied for solar photovoltaic and wind energy fed water pumping system: A review. Renew. Sustain. Energy Rev. 2019, 107, 108–122. [Google Scholar] [CrossRef]
- Leone, C.; Longo, M.; Fernández-Ramírez, L.M.; García-Triviño, P. Multi-Objective Optimization of PV and Energy Storage Systems for Ultra-Fast Charging Stations. IEEE Access 2022, 10, 14208–14224. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W.; Yiew, L.K.; Ayop, R.; Tan, W.-S. A rule-based energy management scheme for long-term optimal capacity planning of grid-independent microgrid optimized by multi-objective grasshopper optimization algorithm. Energy Convers. Manag. 2020, 221, 113161. [Google Scholar] [CrossRef] [PubMed]
- Maleki, A.; Khajeh, M.G.; Ameri, M. Optimal sizing of a grid independent hybrid renewable energy system incorporating resource uncertainty, and load uncertainty. Int. J. Electr. Power Energy Syst. 2016, 83, 514–524. [Google Scholar] [CrossRef]
- Kaabeche, A.; Ibtiouen, R. Techno-economic optimization of hybrid photovoltaic/wind/diesel/battery generation in a stand-alone power system. Sol. Energy 2014, 103, 171–182. [Google Scholar] [CrossRef]
- Chang, W.-Y. The state of charge estimating methods for battery: A review. Int. Sch. Res. Not. 2013, 2013, 953792. [Google Scholar] [CrossRef]
- RELiON Batteries, Rechargable Deep Cycle Lithium Batteries Rb75 12.8. 2020. Available online: https://relionbattery.com/products/lithium/application/electric-vehicles (accessed on 14 May 2023).
- Singh, S.; Singh, M.; Kaushik, S.C. Feasibility study of an islanded microgrid in rural area consisting of PV, wind, biomass and battery energy storage system. Energy Convers. Manag. 2016, 128, 178–190. [Google Scholar] [CrossRef]
- Natesan, C.; Ajithan, S.K.; Chozhavendhan, S.; Devendiran, A. Power management strategies in microgrid: A survey. Int. J. Renew. Energy Res. 2015, 5, 334–340. [Google Scholar]
- Barakat, S.; Ibrahim, H.; Elbaset, A.A. Multi-objective optimization of grid-connected PV-wind hybrid system considering reliability, cost, and environmental aspects. Sustain. Cities Soc. 2020, 60, 102178. [Google Scholar] [CrossRef]
- Arancibia, A.; Strunz, K. Modeling of an electric vehicle charging station for fast DC charging. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–6. [Google Scholar]
- AL-Hasnawi, D.M.H. Experimental Study the Effect of Ambient Temperature on the Performance of Photovoltaic System Work with MPPT Charge Controller in Technical Engineering College of Najaf; Southern Technical University: Basra Governorate, Iraq, 2018. [Google Scholar]
- Wirth, H.; Schneider, K. Recent Facts about Photovoltaics in Germany; Fraunhofer Ise: Freiburg im Breisgau, Germany, 2015; p. 92. [Google Scholar]
- Bartolucci, L.; Cordiner, S.; Mulone, V.; Santarelli, M.; Ortenzi, F.; Pasquali, M. PV assisted electric vehicle charging station considering the integration of stationary first-or second-life battery storage. J. Clean. Prod. 2023, 383, 135426. [Google Scholar] [CrossRef]
- Duman, A.C.; Erden, H.S.; Gönül, Ö.; Güler, Ö. A home energy management system with an integrated smart thermostat for demand response in smart grids. Sustain. Cities Soc. 2021, 65, 102639. [Google Scholar] [CrossRef]
- Alsharif, A.; Tan, C.W.; Ayop, R.; Dobi, A.; Lau, K.Y. A comprehensive review of energy management strategy in Vehicle-to-Grid technology integrated with renewable energy sources. Sustain. Energy Technol. Assess. 2021, 47, 101439. [Google Scholar] [CrossRef]
- Tran, D.-D.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; Van Mierlo, J.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Moura, S.; Yin, X.; Pickert, V. Stochastic control of smart home energy management with plug-in electric vehicle battery energy storage and photovoltaic array. J. Power Sources 2016, 333, 203–212. [Google Scholar] [CrossRef]
- Hussain, M.T.; Sulaiman, D.N.B.; Hussain, M.S.; Jabir, M. Optimal Management strategies to solve issues of grid having Electric Vehicles (EV): A review. J. Energy Storage 2021, 33, 102114. [Google Scholar] [CrossRef]
- Lorestani, A.; Gharehpetian, G.B.; Nazari, M.H. Optimal sizing and techno-economic analysis of energy- and cost-efficient standalone multi-carrier microgrid. Energy 2019, 178, 751–764. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.-H.; Javaid, M.S.; Shaaban, Y.A.; Shahriar, M.S.; Ramli, M.A.M.; Latreche, Y. Decomposition based multiobjective evolutionary algorithm for PV/Wind/Diesel Hybrid Microgrid System design considering load uncertainty. Energy Rep. 2021, 7, 52–69. [Google Scholar] [CrossRef]
- Ridha, H.M.; Hizam, H.; Mirjalili, S.; Othman, M.L.; Ya’acob, M.E.; Ahmadipour, M. Innovative hybridization of the two-archive and PROMETHEE-II triple-objective and multi-criterion decision making for optimum configuration of the hybrid renewable energy system. Appl. Energy 2023, 341, 121117. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Duman, S.; Kahraman, H.T.; Sonmez, Y.; Guvenc, U.; Kati, M.; Aras, S. A powerful meta-heuristic search algorithm for solving global optimization and real-world solar photovoltaic parameter estimation problems. Eng. Appl. Artif. Intell. 2022, 111, 104763. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Aras, S.; Gedikli, E. Fitness-distance balance (FDB): A new selection method for meta-heuristic search algorithms. Knowl. -Based Syst. 2020, 190, 105169. [Google Scholar] [CrossRef]
- Ridha, H.M.; Gomes, C.; Hizam, H.; Ahmadipour, M.; Heidari, A.A.; Chen, H. Multi-objective optimization and multi-criteria decision-making methods for optimal design of standalone photovoltaic system: A comprehensive review. Renew. Sustain. Energy Rev. 2021, 135, 110202. [Google Scholar] [CrossRef]
- Zeng, H.B.; Liu, X.G.; Wang, W.; Xiao, S.P. New results on stability analysis of systems with time-varying delays using a generalized free-matrix-based inequality. J. Frankl. Inst. 2019, 356, 7312–7321. [Google Scholar] [CrossRef]




| Components | Parameter | Value | Unit |
|---|---|---|---|
| Wind Turbine (WT) | Rated Power of Wind Turbine ) | 1 | kW |
| Cut-in speed (Vcin) | 3 | m/s | |
| Cut-out speed (Vco) | 20 | m/s | |
| Rated wind speed (Vrat) | 11 | m/s | |
| Capital cost (per kW) | 2300 | USD | |
| Replacement cost (per kW) | 1500 | USD | |
| O & M cost (per kW) [operation + maintenance] | 2 | USD/vr | |
| Hub height | 50 | M | |
| Overall efficiency | 26 | % | |
| Lifetime | 20 | years | |
| Solar (PV) | Rated power (Ps r) | 325 | W |
| Derating factor (f loss) | 88 | % | |
| Capital cost (per kW) | 1200 | USD | |
| Replacement cost (per kW) | 1200 | USD | |
| O & M cost (per kW) | 4 | USD/yr | |
| Lifetime | 20 | years | |
| Battery | kVAh or kWh capacity | 6 | kWh |
| Minimum state of charge (SOCmin) | 30 | % | |
| Maximum state of charge (SOCmax) | 100 | % | |
| Round trip efficiency (gbatt) | 92 | % | |
| Capital cost (per unit battery) | 167 | USD | |
| Replacement cost (per unit) | 67 | % | |
| M & O cost (per unit) | 1.67 | USD/yr | |
| Lifetime | 5 | years | |
| Nominal battery capacity | 41 | Ah | |
| Battery capacity | 75 | Ah | |
| Rectifier (grec) and inverter (ginv) | Efficiency | 97% | |
| Installation and capital cost (per kW) | 127 | USD/yr | |
| O & M cost (per kW) | 1 | USD/yr | |
| Lifetime | 20 | years | |
| General Requirement | Interest rate | 6% | |
| Project life (N) | 20 | years | |
| EVs Capacity in kWh | 20 | kWh | |
| Utility prices: | |||
| Power export price to utility (selling) | 0.015 | USD/kWh | |
| Power import price from utility (purchasing) | 0.013 | USD/kWh | |
| Optimization of lower and upper bounds | Solar | 1200 | 1 |
| Wind | 1000 | 15 | |
| Battery | 1000 | 1 |
| Rule No. | Modes | IF | THEN |
|---|---|---|---|
| 1 | RESs | ||
| 2 | BT | ||
| 3 | Charge (G2V) | ||
| 4 | Discharge (V2G) |
| Benchmark Function | Dim | Range | Optimal Value |
|---|---|---|---|
| 10 | [−100, 100] | 0 | |
| 10 | [−100, 100] | 0 | |
| 10 | [−10, 10] | 0 | |
| 10 | [−5.12, 5.12] | 0 |
| Function | Algorithm | Best Value | Worst Value | Average Value | STD |
|---|---|---|---|---|---|
| ALO | 1.6291 | 8.8636 | 4.0018 | 1.9334 | |
| PSO | 8.2671 | 2.5752 | 1.2876 | 5.7582 | |
| AOA | 0 | 0 | 0 | 0 | |
| IAOA | 0 | 0 | 0 | 0 | |
| ALO | 1.1730 | 0.4850 | 0.0254 | 0.1082 | |
| PSO | |||||
| AOA | 0 | 0 | 0 | 0 | |
| IAOA | 0 | 0 | 0 | 0 | |
| ALO | 1.1878 | 0.0025 | 1.8484 | 5.4351 | |
| PSO | 1.4774 | 4.0204 | 2.0227 | 8.9870 | |
| AOA | 0 | 0 | 0 | 0 | |
| IAOA | 0 | 0 | 0 | 0 | |
| ALO | 5.1427 | 0.0027 | 4.3189 | 5.8547 | |
| PSO | |||||
| AOA | 0 | 1.1591 × 10−186 | 5.7954 × 10−188 | 0 | |
| IAOA | 0 | 1.7994 × 10−250 | 8.9970 × 10−252 | 0 |
| W1 | W2 | W3 | WT | PV | Bat | f | LCOE | GCF | Elapsed Time (Seconds) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.8 | 0.1 | 1 | 31 | 138 | 0.0762 | 2.37 × 10−2 | 0.0171 | 0.8596 | 4956.680489 |
| 0.1 | 0.7 | 0.2 | 1 | 32 | 108 | 0.1149 | 2.37 × 10−2 | 0.0171 | 0.8596 | 5536.762598 |
| 0.1 | 0.6 | 0.3 | 4 | 18 | 100 | 0.1344 | 2.33 × 10−2 | 0.0274 | 0.8337 | 4827.420494 |
| 0.1 | 0.5 | 0.4 | 1 | 18 | 93 | 0.145 | 0.022 | 0.8377 | 0 | 3438.61148 |
| 0.1 | 0.4 | 0.5 | 1 | 14 | 73 | 0.1343 | 0.0261 | 0.8376 | 0 | 2909.015921 |
| 0.1 | 0.3 | 0.6 | 1 | 13 | 63 | 0.1144 | 0.0304 | 0.8375 | 0 | 2731.221521 |
| 0.1 | 0.2 | 0.7 | 1 | 11 | 49 | 0.0942 | 0.0531 | 0.8371 | 0 | 2678.625856 |
| 0.1 | 0.1 | 0.8 | 1 | 12 | 106 | 0.0611 | 0.022 | 0.8377 | 0 | 5521.751529 |
| 0.2 | 0.7 | 0.1 | 6 | 27 | 70 | 0.0943 | 0.022 | 0.8377 | 0 | 2740.512867 |
| 0.2 | 0.6 | 0.2 | 4 | 22 | 147 | 0.1306 | 0.0237 | 0.0171 | 0.8596 | 4810.072815 |
| 0.2 | 0.5 | 0.3 | 1 | 20 | 91 | 0.1522 | 0.0237 | 0.0171 | 0.8596 | 3293.332732 |
| 0.2 | 0.4 | 0.4 | 2 | 15 | 63 | 0.1487 | 0.0253 | 0.0012 | 0.8475 | 3465.500523 |
| 0.2 | 0.3 | 0.5 | 1 | 15 | 83 | 0.1359 | 0.0531 | 0.8371 | 0 | 2780.494461 |
| 0.2 | 0.2 | 0.6 | 1 | 14 | 63 | 0.1095 | 0.022 | 0.8377 | 0 | 2766.968238 |
| 0.2 | 0.1 | 0.7 | 1 | 12 | 56 | 0.0779 | 0.0261 | 0.8376 | 0 | 3786.031941 |
| 0.3 | 0.6 | 0.1 | 5 | 31 | 59 | 0.1154 | 0.0216 | 0.1136 | 0.7579 | 3414.903356 |
| 0.3 | 0.5 | 0.2 | 3 | 24 | 68 | 0.1419 | 0.0233 | 0.0274 | 0.8337 | 2633.810036 |
| 0.3 | 0.4 | 0.3 | 1 | 19 | 103 | 0.1646 | 0.0237 | 0.0171 | 0.8596 | 5378.376291 |
| 0.3 | 0.3 | 0.4 | 1 | 15 | 56 | 0.1481 | 0.0246 | 0.0035 | 0.8554 | 2637.907928 |
| 0.3 | 0.2 | 0.5 | 1 | 12 | 63 | 0.13 | 0.0304 | 0.8375 | 0 | 2654.862484 |
| 0.3 | 0.1 | 0.6 | 1 | 12 | 56 | 0.0975 | 0.0261 | 0.8376 | 0 | 5068.761916 |
| 0.4 | 0.5 | 0.1 | 5 | 31 | 59 | 0.132 | 0.0243 | 0.0069 | 0.8475 | 3235.824878 |
| 0.4 | 0.4 | 0.2 | 4 | 12 | 56 | 0.1573 | 0.0239 | 0.0738 | 0.7026 | 4983.926465 |
| 0.4 | 0.3 | 0.3 | 1 | 16 | 63 | 0.161 | 0.0253 | 0.0012 | 0.8475 | 2682.447224 |
| 0.4 | 0.2 | 0.4 | 2 | 8 | 33 | 0.1522 | 2.66 × 10−2 | 7.34 × 10−5 | 0.8409 | 3272.623188 |
| 0.4 | 0.1 | 0.5 | 3 | 1 | 2 | 0.1156 | 0.0261 | 0.8376 | 0 | 2731.882521 |
| 0.5 | 0.4 | 0.1 | 3 | 24 | 68 | 0.1425 | 0.0262 | 0.0119 | 0.7838 | 2762.613745 |
| 0.5 | 0.3 | 0.2 | 1 | 19 | 68 | 0.1649 | 0.0239 | 0.0738 | 0.7026 | 5103.018621 |
| 0.5 | 0.2 | 0.3 | 1 | 15 | 52 | 0.1595 | 0.0246 | 0.0035 | 0.8554 | 5587.216803 |
| 0.5 | 0.1 | 0.4 | 3 | 1 | 1 | 0.1284 | 0.0246 | 0.0035 | 0.8554 | 2951.953591 |
| 0.6 | 0.3 | 0.1 | 5 | 17 | 42 | 0.1534 | 0.0262 | 0.0119 | 0.7838 | 2522.240268 |
| 0.6 | 0.2 | 0.2 | 5 | 7 | 25 | 0.1668 | 0.0266 | 7.34 × 10−5 | 0.8409 | 2629.085911 |
| 0.6 | 0.1 | 0.3 | 3 | 1 | 2 | 0.1418 | 2.46 × 10−2 | 3.50 × 10−3 | 0.8554 | 2904.915789 |
| 0.7 | 0.2 | 0.1 | 8 | 6 | 17 | 0.1542 | 0.0262 | 0.0119 | 0.7838 | 2771.440828 |
| 0.7 | 0.1 | 0.2 | 4 | 3 | 11 | 0.1518 | 0.0266 | 7.34 × 10−5 | 0.8409 | 5176.083577 |
| 0.8 | 0.1 | 0.1 | 5 | 10 | 4 | 0.1387 | 0.0246 | 3.50 × 10−3 | 0.8554 | 5424.871393 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Sahlawi, A.A.K.; Ayob, S.M.; Tan, C.W.; Ridha, H.M.; Hachim, D.M. Optimal Design of Grid-Connected Hybrid Renewable Energy System Considering Electric Vehicle Station Using Improved Multi-Objective Optimization: Techno-Economic Perspectives. Sustainability 2024, 16, 2491. https://doi.org/10.3390/su16062491
Al-Sahlawi AAK, Ayob SM, Tan CW, Ridha HM, Hachim DM. Optimal Design of Grid-Connected Hybrid Renewable Energy System Considering Electric Vehicle Station Using Improved Multi-Objective Optimization: Techno-Economic Perspectives. Sustainability. 2024; 16(6):2491. https://doi.org/10.3390/su16062491
Chicago/Turabian StyleAl-Sahlawi, Ameer A. Kareim, Shahrin Md. Ayob, Chee Wei Tan, Hussein Mohammed Ridha, and Dhafer Manea Hachim. 2024. "Optimal Design of Grid-Connected Hybrid Renewable Energy System Considering Electric Vehicle Station Using Improved Multi-Objective Optimization: Techno-Economic Perspectives" Sustainability 16, no. 6: 2491. https://doi.org/10.3390/su16062491
APA StyleAl-Sahlawi, A. A. K., Ayob, S. M., Tan, C. W., Ridha, H. M., & Hachim, D. M. (2024). Optimal Design of Grid-Connected Hybrid Renewable Energy System Considering Electric Vehicle Station Using Improved Multi-Objective Optimization: Techno-Economic Perspectives. Sustainability, 16(6), 2491. https://doi.org/10.3390/su16062491










