Abstract
Battery swapping station (BSS) technology can provide electric taxis (ETs) with more economical and high-efficiency operating services. However, the battery-swapping market needs to be more organized due to unpredictable swapping periods for ETs, resulting in more requirements for batteries of BSSs needing multiple batteries simultaneously. To address these challenges, this paper first analyzed two operation patterns of taxis to estimate the demand for swapping ETs. Then, an optimal capacity model of BSS is proposed to optimize the battery capacity of BSSs to meet the swapping demand of ETs. Finally, a genetic algorithm (GA) is utilized to solve the proposed model. The real operating data of taxis with GPS routes in Chengdu city are used as a case study to validate the proposed method. The results show that the proposed method could obtain the optimal battery capacity of a BSS and improve the economic benefits of BSSs.
1. Introduction
Electric vehicles (EVs) with lower tailpipe emissions, high energy efficiencies, and lower driving costs are becoming a significant alternative to traditional vehicles. Developing the electric vehicle industry and charging infrastructure has become a current trend [1]. Battery swapping technology is a promising solution that allows for high-efficiency replenishment by exchanging depleted batteries for fully charged ones due to its short swapping time [2]. Electric taxis (ETs) have been introduced for transportation sector electrification. Charging time will affect the revenue of individual ETs. Thus, BSSs are suitable for ETs. The State Grid Corporation of China has constructed several BSSs for ETs and EBs in Beijing, Shanghai, Hangzhou, Qingdao, and other cities in recent years [3].
However, there is little literature regarding the capacity optimization of BSSs for ETs [4,5]. A day-ahead dispatching model based on robust optimization has been proposed in [6], which uses inventory robust optimization and multi-band robust optimization to solve the uncertainty of demand and electricity prices. A dynamic programming model has been used to determine the optimal number of batteries for a swap station problem in [7], and the purchase and charging schedule were optimized to minimize the total costs. A coordinated charging strategy for BSS has been proposed to minimize daily charging costs in [8], including the economic cost and the revenue of participating in grid services. The authors of [9] proposed a battery-swapping method for scheduling idle taxis to swap batteries through a real-time algorithm. A charging load forecasting method of BSSs considering various uncertainties of EVs has been proposed to estimate the uncontrolled energy consumption of BSSs [10]. The authors of [10,11] used the historical operation data of ETs for a later analysis. The authors of [11] studied the BSS’s scheduling problem to minimize the charging cost and meet the fully charged battery demand by optimizing the charging processes of the charging bays. The authors of [12] constructed a real-time battery swap pricing model for ETs. The authors of [13] analyzed the impact of swapping price on the operation of BSSs, and the results showed that a reasonable swapping price can smooth the load curve and reduce system losses. In [14], a Monte Carlo simulation was used to analyze the service capability and profitability of charging stations and BSSs for taxis and buses. An optimal schedule of battery charging in a BSS for electric buses has also been studied to meet the swap battery demand of electric buses [15]. The BSS in the above-mentioned research can not only achieve fast charging but can also flexibly participate in the operation of the power system to provide grid services. An economic dispatch model of BSSs with wind power has been proposed to bring more benefits to the system in [16].
This study aims to identify the optimal capacity of a BSS for ETs considering the operating cost and profits of the BSS. During peak hours, a swapping station may experience congestion, resulting in longer waiting times for ET users. The BSS needs to ensure a sufficient inventory to meet users’ needs when ETs arrive at the BSS by accurately predicting its users’ battery-swapping demands. An insufficient or excessive capacity can adversely affect the BSS’s operational efficiency. It is imperative to improve the efficiency of BSSs and their benefits by optimizing the battery capacity of BSSs.
This research contributes to filling the gap in the literature by providing insights into the optimal capacity of BSSs to meet the demand of electric taxis. In this paper, data mining is used to obtain the operating patterns of EVs based on the taxi operation data of Chengdu in China. The battery capacity demands and the operations of the BSS are analyzed in different operation patterns based on the operational data. Then, this paper proposes a capacity optimization model of a BSS for ETs considering driving distance and the operating patterns of ETs. The objective of the proposed model is to maximize the profits of BSSs while meeting ETs’ charging demands. Finally, a genetic algorithm (GA) is used to obtain the optimal capacity of BSSs and the optimal operational patterns for ETs.
The rest of the paper is organized as follows: In Section 2, the EV operation patterns based on data mining are analyzed to obtain the BSS capacity demand in different operation patterns. In Section 3, an optimal model considering the revenue and expenditure of the BSS is proposed to determine the capacity of the BSS. Simulation results are analyzed in Section 4. Finally, the paper is concluded in Section 5.
2. Operation Analysis of a BSS
2.1. Data Mining of Taxi Operation
The daily driving distance and trajectory of taxis have a high level of certainty and similarity. Historical driving data of taxis can serve as an operational foundation for ETs [17], influenced by social and economic factors. ETs utilizing battery swapping technology can be fully charged in just a few minutes, without considering the long charging duration. Due to technical and battery manufacturing standards, BSSs are usually operated to serve their own brand of cars by car manufacturers. ETs usually use the same type of cars. Planning routes for ETs is challenging due to their profit-oriented nature. To estimate the swap battery demand of a BSS, this paper utilizes data mining to obtain the mobility patterns of taxis. Generally, the number of BSSs in a city is limited, and they are usually located in areas with lower land costs. The uneven temporal and spatial distribution of taxi charging demands can be alleviated through the dynamic pricing of BSSs, which is not the focus of this paper. Therefore, this paper focuses on the optimization capacity of a BSS because the number of BSSs in a city is limited due to economic factors.
The operational data of taxis in Chengdu are analyzed. Chengdu is located in the southwest of China. More than 13,500 taxis’ GPS data from 6:00 to 24:00 were collected, which included vehicle labels, latitude and longitude coordinates, passenger information, and collection time. Firstly, redundant and abnormal GPS data were removed. Each GPS coordinate needed to be within the urban area (103.7109 E–104.4140 E, 30.3222 N–30.9375 N). Considering possible GPS errors, the distance between the two points was not allowed to exceed 1 km.
Figure 1 shows the distribution of the taxi driving distance from 6:00 to 24:00. The distribution of taxi driving distance ranges from 300 to 400 km, showing a normal distribution. Figure 2 shows the distribution of the taxi driving distance in different periods. The driving distance of taxis presents a normal distribution except for the operation data at 6:00, because ET users usually have a rest at night. The daily traveling distance of taxis will be longer in the actual operation timeframe because Figure 1 only contains the operating data from 6:00 to 24:00. To simplify the computation, it is assumed that the daily driving distance of ETs has a normal distribution.
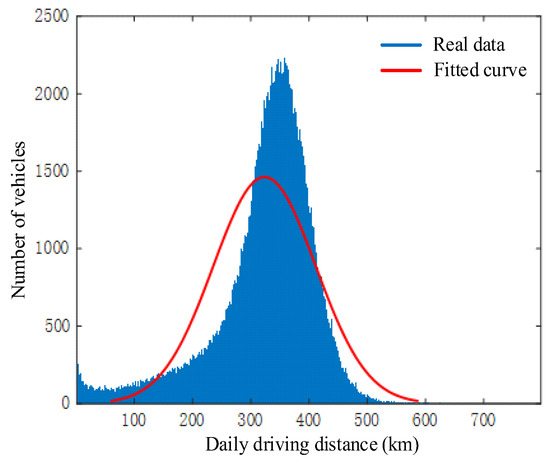
Figure 1.
Distribution of daily driving distance of taxis.
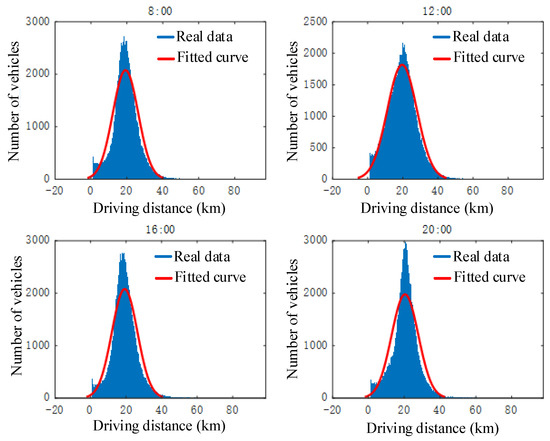
Figure 2.
Distribution of hourly taxi driving distance.
2.2. Operation Analysis of a BSS
The swapping battery process can be completed within a few minutes, which is similar to that of fuel taxis. Thus, the driving pattern of fuel taxis is assumed to be the same as that of ETs. In general, there are two operation patterns for ETs, namely, single shift and double shift. A single shift means that taxis are driven over 24 h without rest. A double shift means that the operation period of taxis is divided into daytime and night periods. In the daytime period (6:00–22:00), all taxis are running, while 30–40% of taxis run in the night period (23:00–5:00).
Based on the driving distance of taxis, the state of charge (SOC) of ETs can be calculated as follows:
where is the electricity consumption rate of ETs, 13 kWh/100 km in this paper. is the rated battery capacity of ETs, 50 kWh in this paper. is the driving distance that is generated by the Monte Carlo method. is the SOC of ETs at time . The initial SOC of ETs is randomly distributed between 0.2 and 0.95. The SOC of ETs is limited by maximum and minimum values to avoid overcharging and over-discharging. When the SOC of ETs is lower than the threshold, ETs will swap battery storage. Exhausted batteries are charged in the BSS immediately, with a charging power of 21 kW [18].
- Pattern I: Electric taxis run all day
In pattern I, ETs are running all day. The ETs with a battery-swapping mode can be operated for 24 h ignoring the charging times. The simulation starts at 7:00 and lasts 100 days. The average value of the 100-day simulation results is shown in Table 1 and Figure 3.

Table 1.
The total demand and the average demand of batteries of the BSS in pattern I.
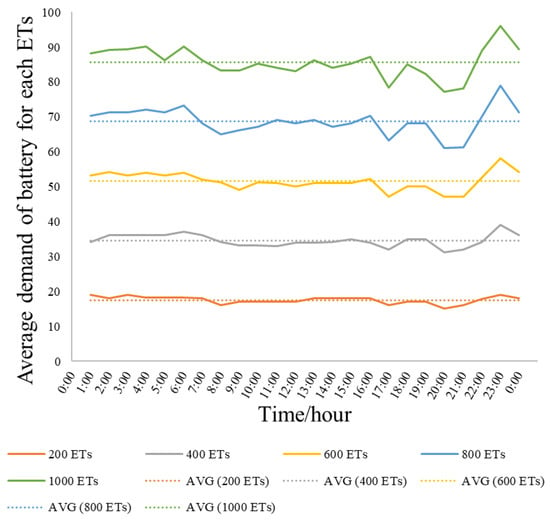
Figure 3.
The demand for batteries of a BSS in pattern I.
- Pattern II: Not all electric taxis operate all day
In pattern II, all ETs participate in the operation in the daytime period, but only 30–40% of the ETs participate in the operation in the night period due to a significant decrease in the travel demand of people. The simulation starts at 7:00 and lasts 100 days.
Figure 4 and Table 2 show the hourly swapping battery demand of ETs in the pattern II model. The results show that the total daily demand for the BSS in pattern II is lower than that in pattern I because some ETs in pattern II stop running and charge at night. After 7:00, the demand for the BSS gradually increases. The period of 11:00–16:00 is that of peak demand for the BSS, and it needs a large number of batteries to meet the demand. Meanwhile, a large amount of batteries of the BSS is charging at the same time, which may cause overload and huge charging costs.
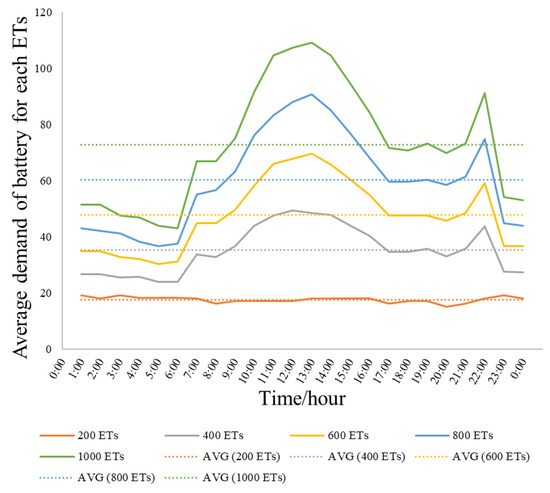
Figure 4.
The demand for batteries of the BSS in pattern II.

Table 2.
The total demand and the average demand for batteries of the BSS in pattern II.
The different operation pattern of ETs has a significant influence on the demand for the BSS, which is related to the economic development of a city and the living habits of residents. The ratio of vehicles operating all day in pattern II is a reasonable assumption based on the operating data.
2.3. Operation Analysis of a BSS
The BSS is used as an energy supply station for ETs. The BSS must have sufficient batteries to meet the demand for swapping batteries while maximizing its profits. When an ET arrives at the BSS, the battery is swapped. The swapped battery is stored and charged to provide services for other ETs at the BSS. It is assumed that the charging power is 21 kW. This means that a battery of 50 kWh with a SOC of 20–45% will be fully charged within an average duration of 90 min. Figure 5 shows the battery charging timing sequence [19]. The yellow zone indicates the stage of the battery. The green zone indicates that the battery is available for battery-swapping services.
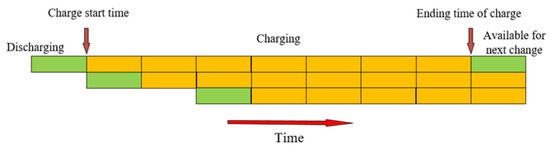
Figure 5.
Charging time sequence.
Figure 6 shows the operation of the BSS with 40 batteries to serve 300 ETs in pattern I and pattern II. The negative value in Figure 6 means that the BSS cannot meet the demand for swapping batteries in the current period, while the positive value means that there is an available number of batteries for battery-swapping services for ETs. In pattern I, the charging power of the BSS shows a smooth curve ranging from 650 to 840 kW. The average charging power of the BSS is 756 kW. The battery inventory cannot fully satisfy the demand for swapping, which is mainly concentrated during the night period. Although there are shortages, the value is lower than that of pattern II. In contrast, the average charging power of the BSS is 840 kW, which is 11% larger than that of pattern I. The battery shortage is mainly concentrated during the peak demand for the BSS at 11:00–15:00. There is a slight increase at 22:00, and then it decreases at 23:00, which is the second peak demand timeframe for the BSS. The first peak demand for the BSS starts at 10:00, and there is another battery swap demand after 12 h of operation, but the number of ETs decreases in pattern II after 23:00.
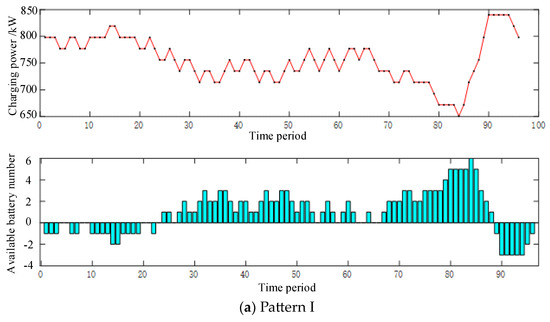

Figure 6.
The comparison of charging power and the usage of the BSS in patterns I and II.
Figure 7 shows the operation of the BSS with 300 ETs under different battery inventories. With increasing battery inventory, the charging power will increase. When the number of batteries reaches 45, the available battery number is always positive. It means that the BSS can meet the swapping demand of ETs. In pattern II, the battery inventory cannot fully satisfy the demand of the BSS. The more battery inventory the BSS contains, the more demand can be satisfied during the peak demand timeframe. Meanwhile, a large amount of battery surplus will occur during the valley demand. There are different perspectives between ET users and investors in the BSS. For users, they want more batteries that can provide a better service. Conversely, the investor believes that more batteries not only increase the investment cost but also lead to insufficient battery utilization during the valley demand for the BSS. Therefore, the tradeoff between the inventory of the BSS and the number of ETs is key to promoting BSS development.
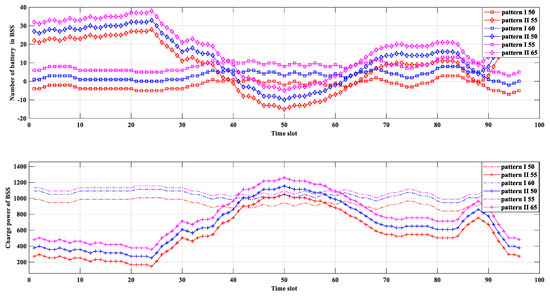
Figure 7.
The comparison of battery usage and charging power of the BSS between two battery inventory scales.
3. Capacity Optimization for a BSS
The BSS can provide battery-swapping services for ETs. The objective function of capacity optimization of the BSS is to maximize the BSS’s income, including the battery investment costs, the battery operational costs, the battery charging costs, the battery degradation costs, the battery recycling income, and the battery swapping income. The objective function of the capacity optimization of the BSS can be formulated as follows:
where F represents the overall construction and operational costs of the BSS. f is the total revenue of the BSS.
where the first part of Equation (3) is the investment cost of the batteries. is the purchase cost of a battery. is the number of batteries stored in the BSS that are used for battery swapping. is the number of batteries providing power for ETs. The second part of Equation (3) is the construction cost of the BSS, including the cost of land construction and charging facilities. is the fixed construction cost of the battery. The third part of Equation (3) is the operation and maintenance (O&M) cost of the BSS. is the O&M cost of the BSS in the t-th year. The fourth part of Equation (3) is the charging cost of the BSS. is the charging power in time h and year t under the BSS with n battery inventory and ETs. is the electricity price in time h. is the scheduling period of one day with 24 h. is the lifetime of the battery.
where is the monthly battery rental fee in m-th month. is the battery swapping income for a single exchange. is the number of ETs demanding battery swapping in time h. The third part of Equation (4) is the recycling income of the battery. is the depreciation rate of the battery. The fourth part of Equation (4) is the penalty cost when the BSS cannot meet the demand for swapping. is the shortage number of batteries in time h. is the penalty price for a BSS that cannot provide the battery swapping service.
where Equation (5) is used to calculate the shortage number of batteries at time h. is the available number of batteries at time h.
The optimization model of the BSS needs to meet the following constraints:
where constraint (6) is used to ensure that the shortage rate of the battery is within 5–10% to improve the service quality of the BSS. Constraint (7) limits the battery inventory of the BSS.
The GA is a randomized search algorithm for solving complex optimization problems inspired by natural selection and biological evolution. The GA was developed by Holland to search for the global optimum value of an optimization problem [20]. GA is one of the most popular optimization technologies that is currently used in power system optimization. Generally, a GA includes three steps: selection, crossover, and mutation. The detailed introduction and modeling of the GA can be found in [21]. Because a global optimum value is not granted, the solution is obtained by the average solutions from multiple simulations [22].
4. Case Study
The proposed model is verified in this section. The purchase cost is 9285 USD for a 50 kW·h battery. The fixed investment for a battery is 7143 USD. The time-variable electricity price is 0.17 USD/kW·h during the peak period, 0.05 USD/kW·h during the valley period, and 0.12 USD/kW·h in other periods. The swapping battery cost is 16 USD. The rental cost of a battery is 71.5 USD/month. The depreciation rate of the battery is assumed to be 0.2. The annual O&M cost rate is 2% of the investment cost of the battery.
The proposed approach is studied in two cases with different operation patterns. One case is modeled without the penalty cost of the BSS to the maximum profit of the BSS, ignoring service quality. The other one is modeled with the penalty cost of the BSS to consider the service quality of the BSS. The proposed approach is studied in two cases with two operation patterns. This model is solved using GA. The key parameters are shown in Table 3.

Table 3.
The key parameters in GA.
A. The results considering the penalty cost of the BSS
Table 4 shows the optimization results using the penalty price constraints with different operation patterns. It can be seen from Table 4 that the total profits in pattern I are significantly higher than those in pattern II. The optimal capacity of pattern II is higher than that of pattern I when serving the same ETs. In pattern I, with the increase in the number of ETs, there is an increase in the total revenue of the BSS. However, the relationship between the total revenue and the number of ETs is highly irregular in pattern II. The daily demand of pattern I is higher than that of pattern II, but the demand in pattern II is unevenly distributed, requiring a large number of batteries to satisfy the swapping demand during the peak period. Table 5 shows the demand satisfaction rate of ET battery swapping. To improve the profitability of the BSS, the demand satisfaction rate of the battery swap station in the two operation patterns is 100%, which can meet all the battery swapping needs.

Table 4.
Optimal capacity and profit of the BSS.

Table 5.
The demand satisfaction rate of the BSS.
Figure 8 shows the income and cost of the BSS in the two operation patterns. The swapping battery income is the most important factor in the two cases. The purchase cost of the batteries and the charging costs are the main costs of the BSS in the two cases. Thus, it is important to optimize the charging decisions of the BSS over the same day. There is no significant difference in the battery purchase cost when serving the same number of ETs in pattern I and pattern II.
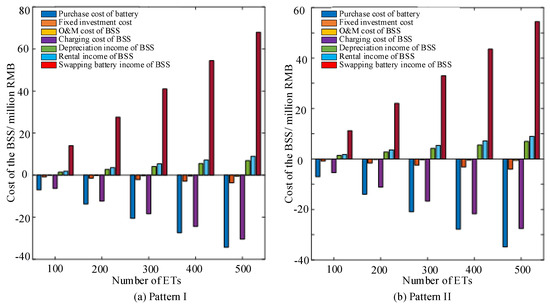
Figure 8.
The income and expenditure of the BSS.
Figure 9 shows the operation of the BSS serving 300 ETs. The demand for the BSS is satisfied by the 43 batteries in pattern I. Although there is a certain amount of battery inventory surplus in pattern I, the surplus number in each period is within 10. In pattern II, there is no shortage of batteries during the peak period of battery swapping, and the batteries of the BSS can fully meet the demand for battery swapping. However, there is a large surplus of batteries during other periods, and the overall surplus reaches 1692. In the valley period of the battery swap demand, by reducing the charging power of the BSS, the charging cost can be effectively reduced, thereby improving the overall income of the BSS.

Figure 9.
The operations of the BSS in pattern I and pattern II.
B. The results without considering the penalty cost of the BSS
Considering the rest time of the drivers, the demand for the BSS will be reduced accordingly. Therefore, a proportional constraint is used to determine the optimal capacity of the BSS. In the proportional constraint, the BSS only needs to satisfy the swapping demand ranging from 90% to 95%. The constraint (6) is to ensure that the shortage rate of the battery is within 5–10% to improve the service quality of the BSS. The optimization result of the BSS in this proportional constraint is shown in Table 6.

Table 6.
Optimal capacity and profit of the BSS.
Table 7 shows the demand satisfaction rate of the BSS with proportional constraints. The demand satisfaction rates are above 93%. The main revenue of the BSS is the swapping battery income. Although the investment of the BSS can be reduced partly, the total revenue is not as good as the price penalty in pattern I. However, the total profits of the BSS show an irregular trend in pattern II. Therefore, the proportional constraints can be used to appropriately increase the benefits of the BSS in pattern II.

Table 7.
The demand satisfaction rate of the BSS in pattern I.
Table 8 shows the comparison of the capacity and income of the BSS under the two cases. It can be concluded that, under the proportional constraint, the optimal battery inventory and revenue of the BSS show a downward trend compared with the price constraint, but the difference in battery inventory is not obvious. In the case of the proportional constraint, although the initial construction cost of the BSS can be reduced, the decrease in the demand satisfaction rate will cause a reduction in the battery swap income.

Table 8.
Comparison of capacity and income of the BSS under the two cases.
5. Conclusions
To obtain the optimal capacity of the BSS, this paper first analyzes the operational data of taxis to obtain the operation characteristics of ETs. Secondly, the demand for swapping batteries is calculated in different operation patterns of ETs. Finally, the capacity optimization model of the BSS considering the income and cost of the BSS is proposed. The GA algorithm is used to find the optimal battery capacity of the BSS. The results show that the profit of the BSS in pattern I is higher than that in pattern II. The total profits of the BSS are mainly affected by the purchase cost of batteries, the charging cost, and the battery swapping income. The charging cost in pattern II is lower than in pattern I. It is important to optimize the charging profiles of the BSS to reduce the charging costs. This paper mainly analyzes the investment and operation of BSSs from the aspect of economic factors. The proposed model and the results will provide investors with a model for evaluating the investment and operation of BSSs. There are some limitations in this paper. The location of the BSS is not considered. Moreover, this paper does not consider the impact of driving characteristics, weather conditions, and road conditions on the energy consumption rate of ETs. These are future research directions.
Author Contributions
Conceptualization, Y.Z.; methodology, Y.Z.; validation, B.L., S.X.; formal analysis, B.L., S.X.; investigation, B.L. and S.X.; resources, J.Z. and G.W.; data curation, J.Z. and G.W.; writing—original draft preparation, S.X. and B.L.; writing—review and editing, S.X. and B.L.; visualization, S.X. and B.L.; supervision, Y.Z. and B.L.; project administration, Y.Z.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Specific Research Project of Guangxi for Research Bases and Talents (2022AC21257).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sukkrajang, K.; Duangsoithong, R.; Chalermyannont, K. Trade Distance and Price Model for Electric Vehicle Charging Using Blockchain-Based Technology. In Proceedings of the 2021 18th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Mai, Thailand, 19–22 May 2021; IEEE: Chiang Mai, Thailand, 2021; pp. 964–967. [Google Scholar] [CrossRef]
- Zeng, L.; Chen, S.-Z.; Tang, Z.; Tian, L.; Xiong, T. An Electric Vehicle Charging Method Considering Multiple Power Exchange Modes’ Coordination. Sustainability 2023, 15, 10520. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, K.; Qin, X.; Li, Y.; Liu, H.; Cheng, X. Annual Report on Electric Vehicle Charging Infrastructure Development in China 2016-2017; China Electric Vehicle Charging Infrastructure Promotion Alliance (EVCIPA): Beijing, China, 2020. Available online: https://www.nea.gov.cn/136376732_14978397401671n.pdf (accessed on 16 November 2023).
- Sandhya, P.; Nisha, G.K. Review of Battery Charging Methods for Electric Vehicle. In Proceedings of the 2022 IEEE International Conference on Signal Processing, Informatics, Communication and Energy Systems (SPICES), Thiruvananthapuram, India, 10–12 March 2022; IEEE: Thiruvananthapuram, India, 2022; pp. 395–400. [Google Scholar] [CrossRef]
- Rajkumar, S.; Nagaveni, P.; Amudha, A.; Siva Ramkumar, M.; Emayavaramban, G.; Selvaganapathy, T. Optimizing EV Charging in Battery Swapping Stations with CSO-PSO Hybrid Algorithm. In Proceedings of the 2023 8th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 1–3 June 2023; IEEE: Coimbatore, India, 2023; pp. 1566–1571. [Google Scholar] [CrossRef]
- Sarker, M.; Pandzic, H.; Ortega-Vazquez, M. Optimal Operation and Services Scheduling for an Electric Vehicle Battery Swapping Station. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; IEEE: Denver, CO, USA, 2015; pp. 901–910. [Google Scholar] [CrossRef]
- Worley, O.; Klabjan, D. Optimization of Battery Charging and Purchasing at Electric Vehicle Battery Swap Stations. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; IEEE: Chicago, IL, USA, 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, H.; Guo, C.; Ren, J.; Sheng, J. A Coordinated Charging Strategy on Battery Swapping Station in Microgrid Considering Battery to Grid. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; IEEE: Chengdu, China, 2019; pp. 3322–3326. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, W.; Huang, L.; Wei, Z.; Liu, H.; Stankovic, J.A. Toward Urban Electric Taxi Systems in Smart Cities: The Battery Swapping Challenge. IEEE Trans. Veh. Technol. 2018, 67, 1946–1960. [Google Scholar] [CrossRef]
- Dai, Q.; Cai, T.; Duan, S.; Zhao, F. Stochastic Modeling and Forecasting of Load Demand for Electric Bus Battery-Swap Station. IEEE Trans. Power Deliv. 2014, 29, 1909–1917. [Google Scholar] [CrossRef]
- Tan, X.; Qu, G.; Sun, B.; Li, N.; Tsang, D.H.K. Optimal Scheduling of Battery Charging Station Serving Electric Vehicles Based on Battery Swapping. IEEE Trans. Smart Grid 2019, 10, 1372–1384. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, X. Battery Swap Pricing and Charging Strategy for Electric Taxis in China. Energy 2018, 147, 561–577. [Google Scholar] [CrossRef]
- Azeem, F.; Irshad, B.; Zidan, H.A.; Narejo, G.B.; Hussain, M.I.; Manzoor, T. Design and Analysis of a Peak Time Estimation Framework for Vehicle Occurrences at Solar Photovoltaic and Grid-Based Battery-Swappable Charging Stations. Sustainability 2023, 15, 16153. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Yu, Z.; Zhu, X.; Shi, D. A Monte Carlo Simulation Approach to Evaluate Service Capacities of EV Charging and Battery Swapping Stations. IEEE Trans. Ind. Inform. 2018, 14, 3914–3923. [Google Scholar] [CrossRef]
- You, P.; Yang, Z.; Zhang, Y.; Low, S.H.; Sun, Y. Optimal Charging Schedule for a Battery Switching Station Serving Electric Buses. IEEE Trans. Power Syst. 2016, 31, 3473–3483. [Google Scholar] [CrossRef]
- Gao, Y.-J.; Zhao, K.-X.; Wang, C. Economic Dispatch Containing Wind Power and Electric Vehicle Battery Swap Station. In Proceedings of the PES Transmission and Distribution Conference and Exposition 2012, Orlando, FL, USA, 7–10 May 2012; IEEE: Orlando, FL, USA, 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, H.; Huang, H.; Ni, X.; Zeng, W. Revealing Spatial-Temporal Characteristics and Patterns of Urban Travel: A Large-Scale Analysis and Visualization Study with Taxi GPS Data. ISPRS Int. J. Geo-Inf. 2019, 8, 257. [Google Scholar] [CrossRef]
- Adegbohun, F.; Von Jouanne, A.; Lee, K. Autonomous Battery Swapping System and Methodologies of Electric Vehicles. Energies 2019, 12, 667. [Google Scholar] [CrossRef]
- Amiri, S.S.; Jadid, S.; Saboori, H. Multi-Objective Optimum Charging Management of Electric Vehicles through Battery Swapping Stations. Energy 2018, 165, 549–562. [Google Scholar] [CrossRef]
- Lorenz, E.; Hurka, J.; Heinemann, D.; Beyer, H.G. Irradiance Forecasting for the Power Prediction of Grid-Connected Photovoltaic Systems. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 2–10. [Google Scholar] [CrossRef]
- Alhijawi, B.; Awajan, A. Genetic Algorithms: Theory, Genetic Operators, Solutions, and Applications. Evol. Intell. 2023. [Google Scholar] [CrossRef]
- Guzman Razo, D.E.; Müller, B.; Madsen, H.; Wittwer, C. A Genetic Algorithm Approach as a Self-Learning and Optimization Tool for PV Power Simulation and Digital Twinning. Energies 2020, 13, 6712. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).