Numerical Study on Effects of Flow Channel Length on Solid Oxide Fuel Cell-Integrated System Performances
Abstract
1. Introduction
2. Description of SOFC-Integrated System
2.1. Description of the SOFC Model
- (1)
- The SOFC unit cell operates steadily, and the electrochemical reactions reach equilibrium.
- (2)
- The cathode and anode are constructed from homogeneous and isotropic porous materials.
- (3)
- In the anodic electrochemical reaction, only hydrogen gas participates.
- (4)
- SOFCs maintain consistent flow rates at the cathode and anode inlets over different lengths, and the inlet gas pressure is supplied by a compressor.
- (5)
- Gas pressure at the anode and cathode outlet is equivalent to the standard atmospheric pressure in the SOFC. Furthermore, the model operates at standard atmospheric pressure.
- (6)
- The SOFC gas inlet temperature and operating temperature are both set at 800 °C.
- (7)
- Anode and cathode outlet temperatures are computed from the model.
- (8)
- All gases are ideal gases in SOFC.
2.1.1. Electrochemical Reaction
2.1.2. Model Parameter Settings
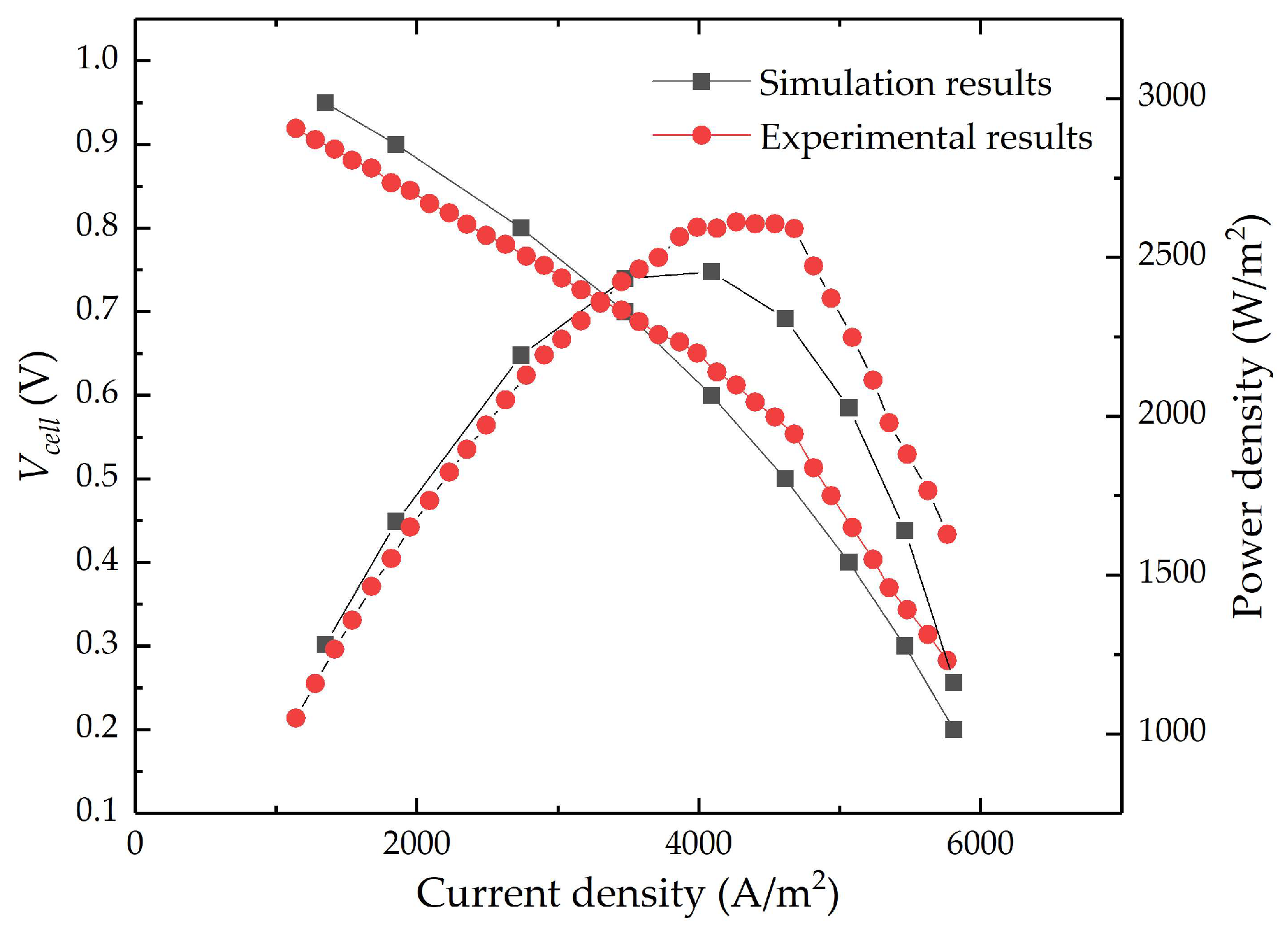
2.1.3. SOFC Model Validation
2.2. Description of Other Equipment Models in the Integrated System
3. System Performance Evaluation Indicators
4. Results and Analysis
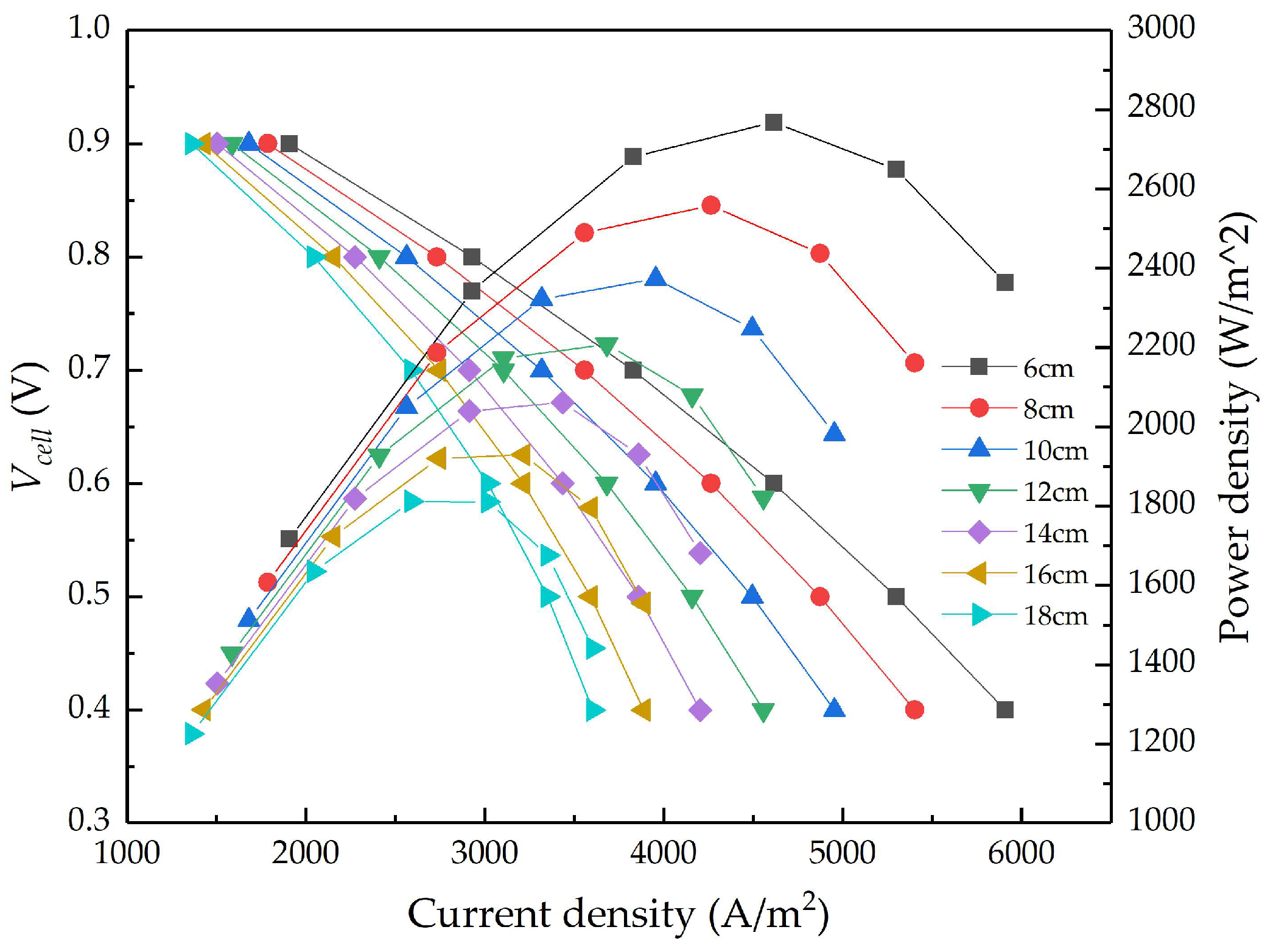
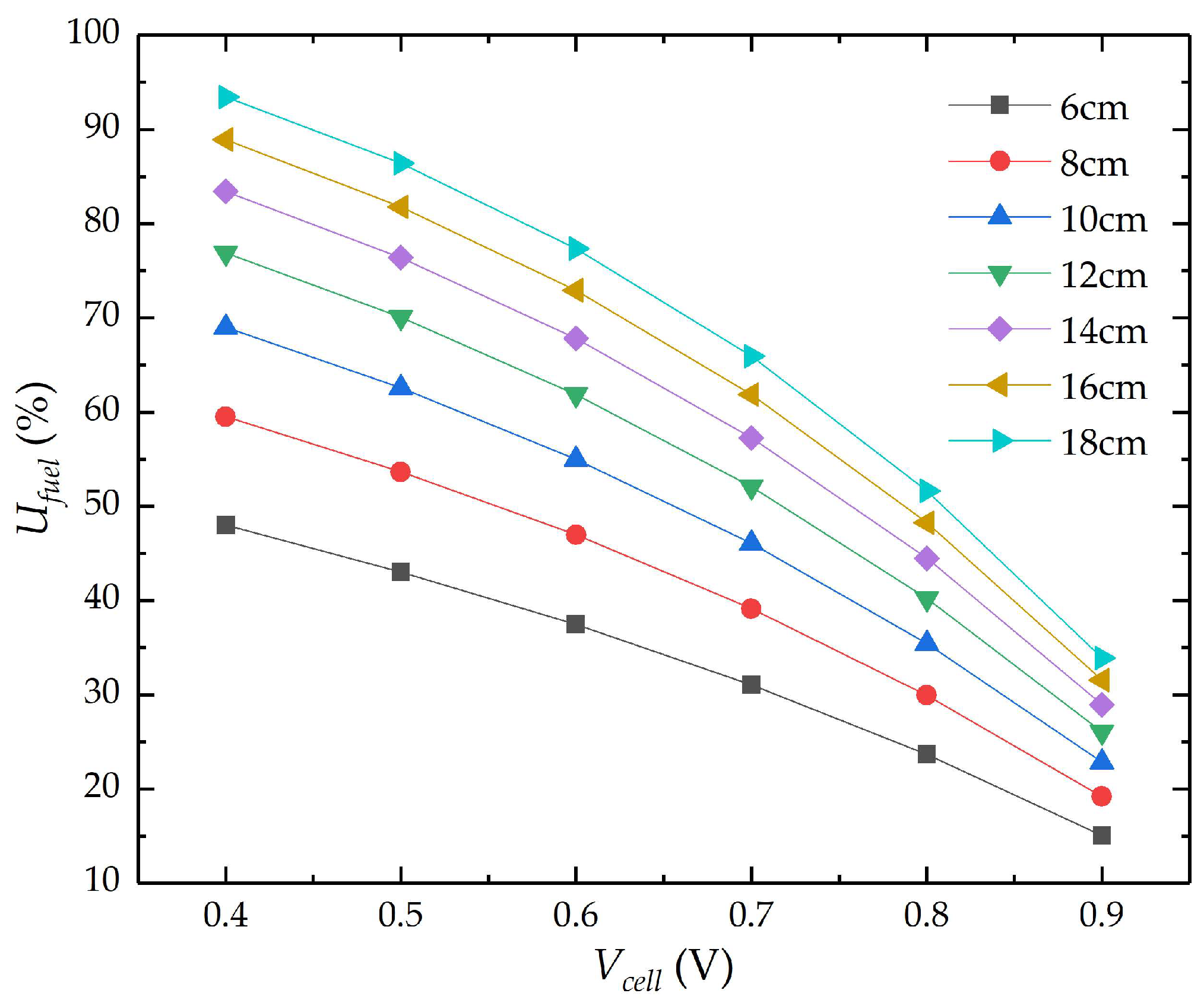
4.1. Influence of Different Flow Channel Lengths on SOFC Stack
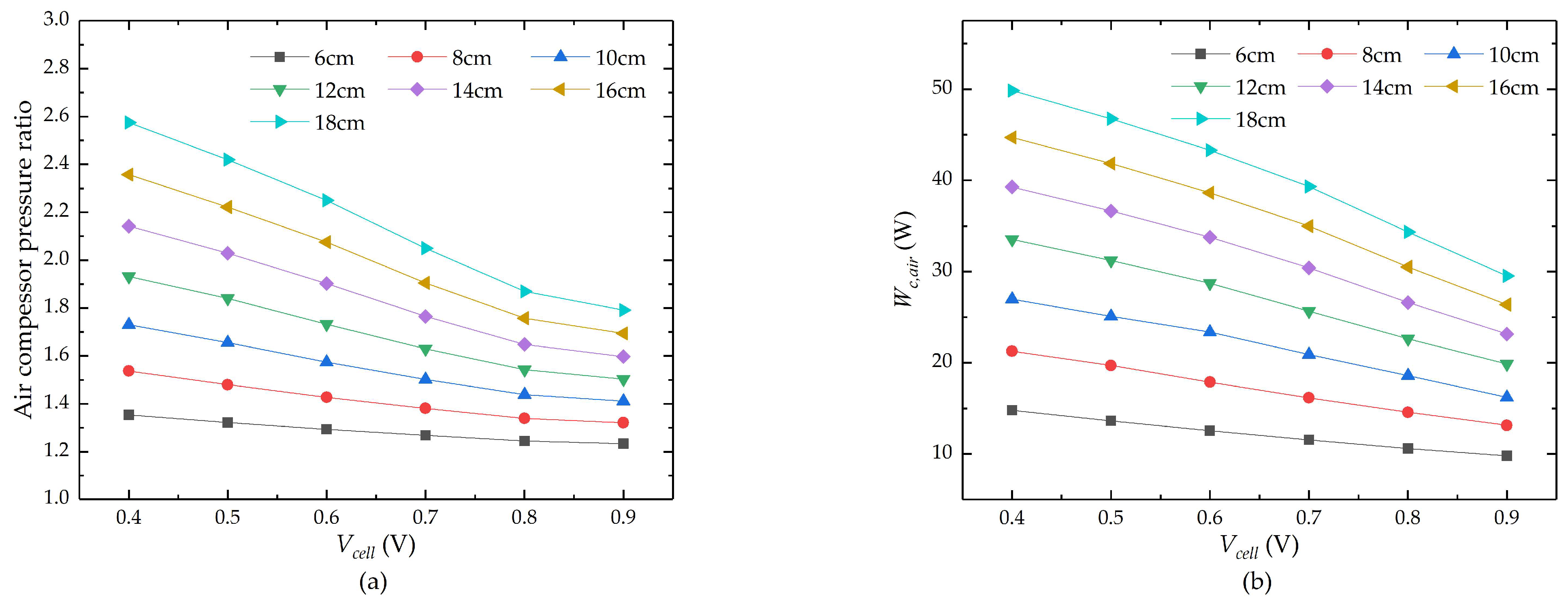
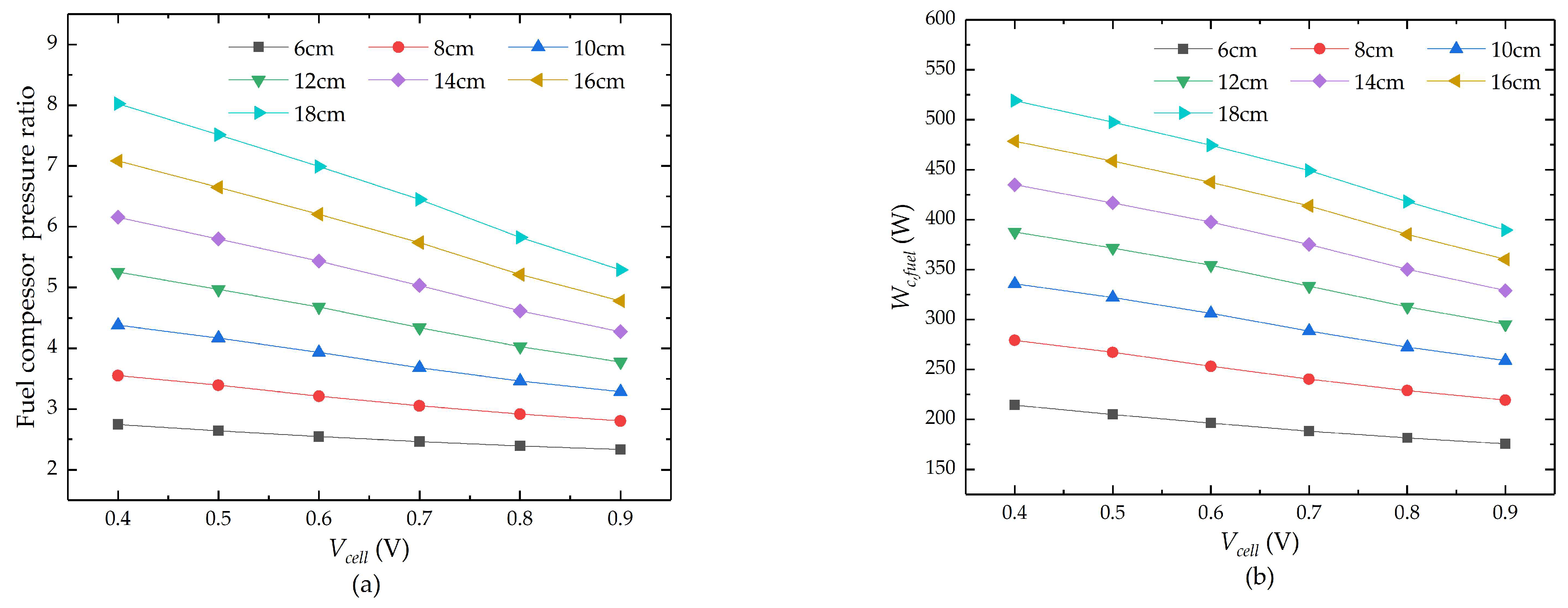
4.2. Influence of Different Flow Channel Lengths on Compressor
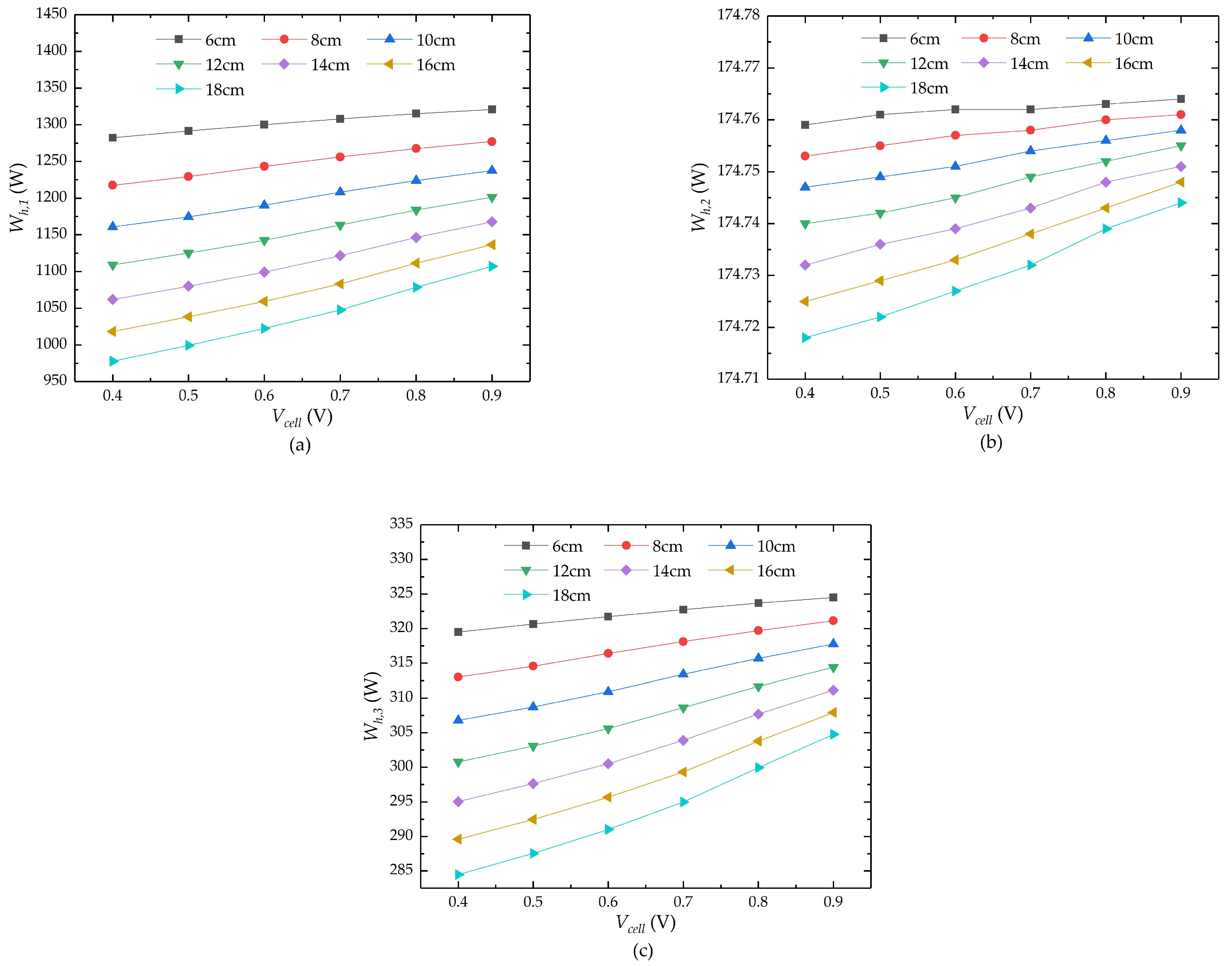
4.3. Influence of Different Flow Channel Lengths on Heat Exchangers
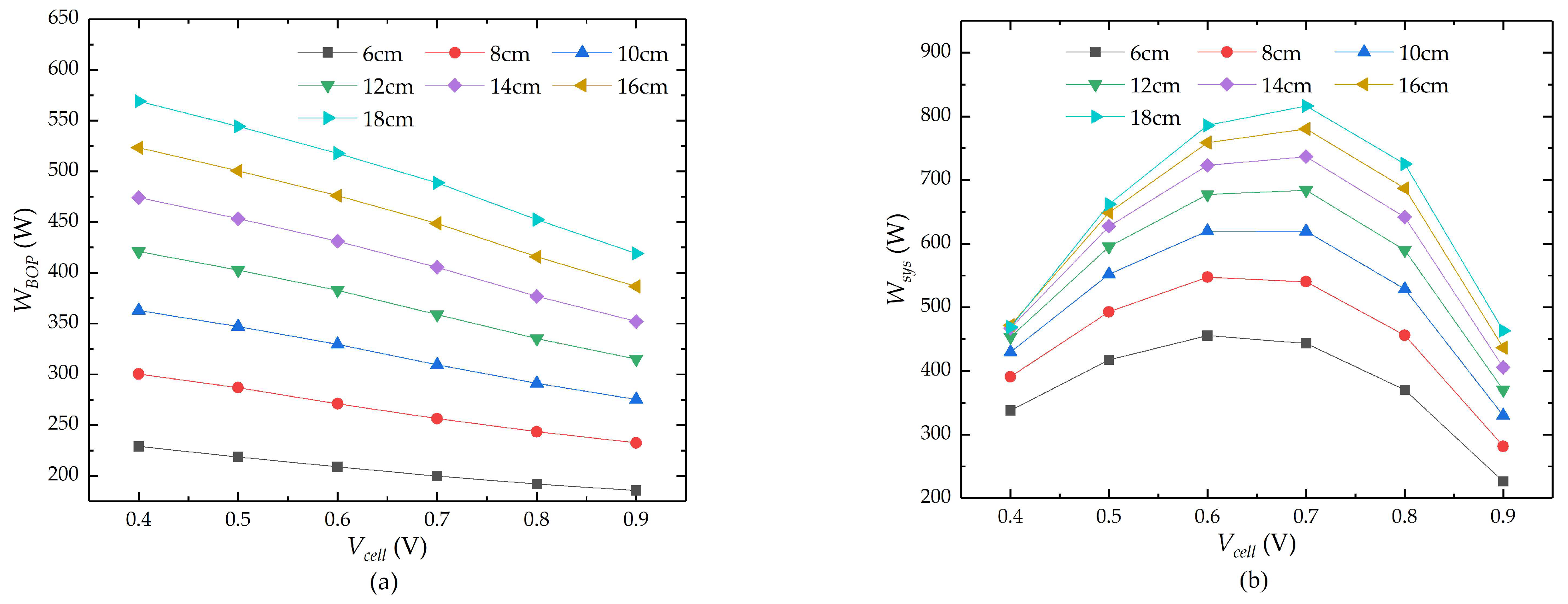
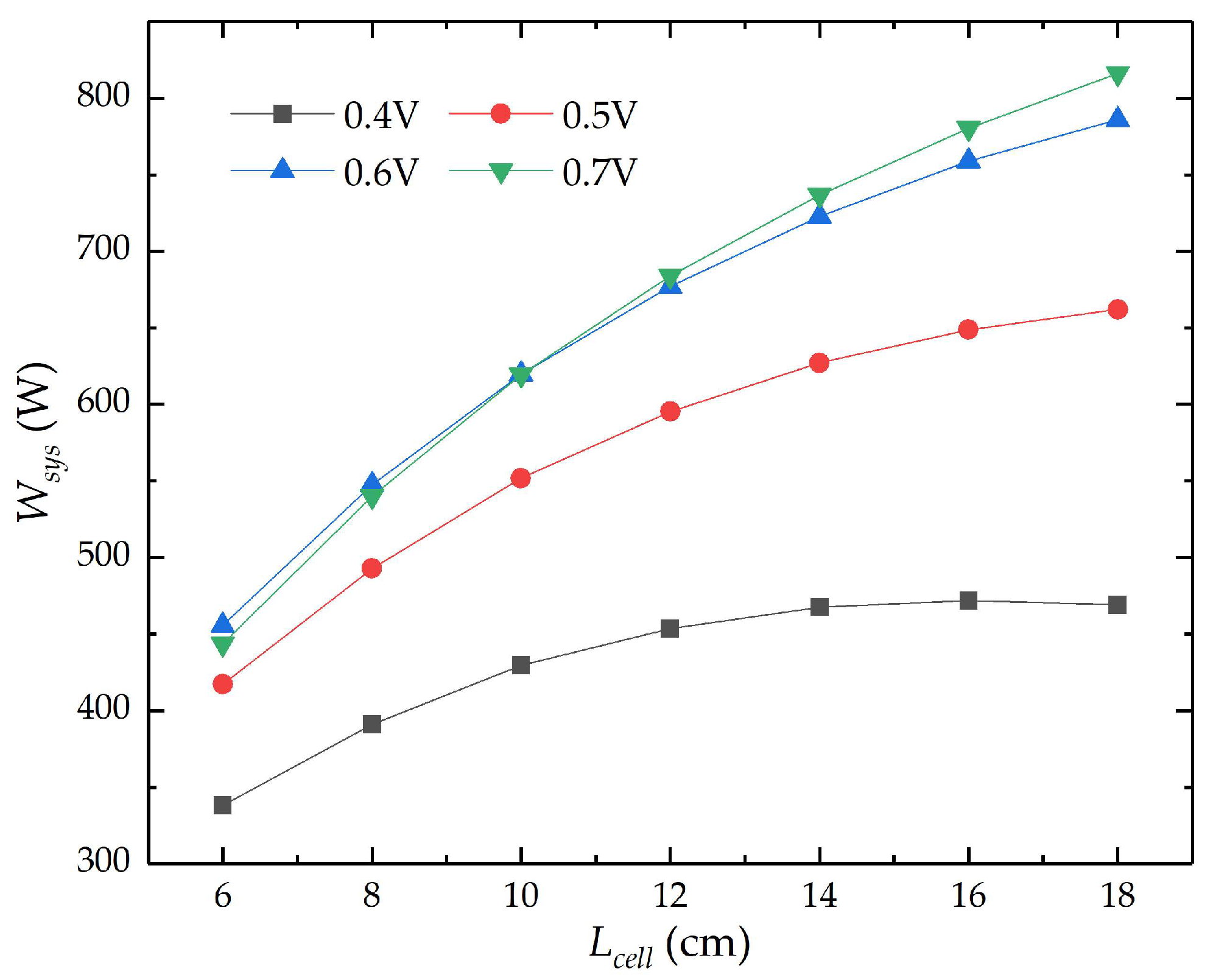
4.4. System Performances Analysis
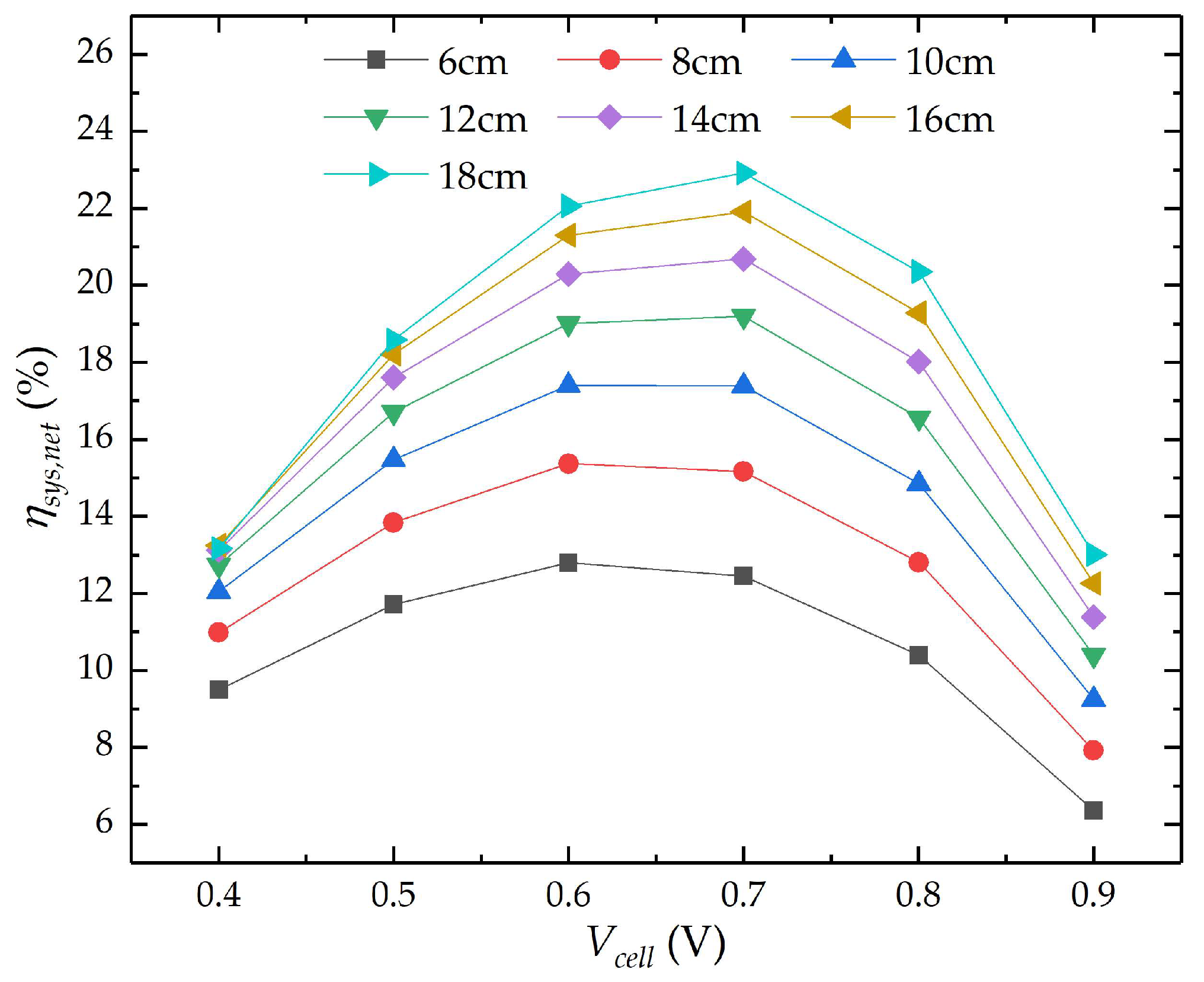
4.4.1. Maximum Net Electrical Power of the System
4.4.2. Maximum Net Electrical Efficiency of the System
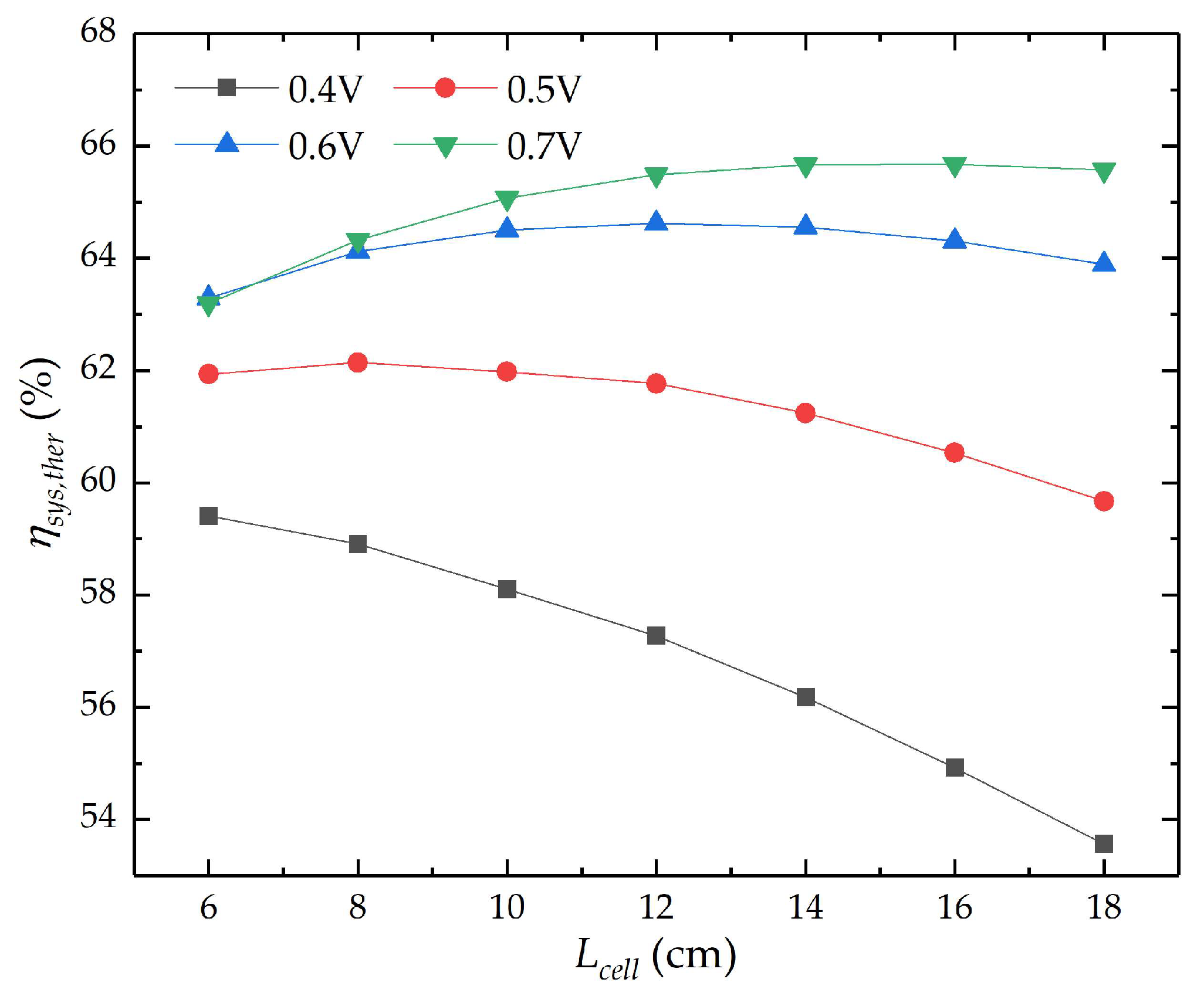
4.4.3. Maximum Thermoelectric Efficiency of the System
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar Yadav, A.; Sinha, S.; Kumar, A. Comprehensive review on performance assessment of solid oxide fuel cell-based hybrid power generation system. Therm. Sci. Eng. Prog. 2023, 46, 102226. [Google Scholar] [CrossRef]
- Vinchhi, P.; Khandla, M.; Chaudhary, K.; Pati, R. Recent advances on electrolyte materials for SOFC: A review. Inorg. Chem. Commun. 2023, 152, 110724. [Google Scholar] [CrossRef]
- Meng, Q.S.; Han, J.T.; Kong, L.J.; Liu, H.; Zhang, T.; Yu, Z.T. Thermodynamic analysis of combined power generation system based on SOFC/GT and transcritical carbon dioxide cycle. Int. J. Hydrog. Energy 2017, 42, 4673–4678. [Google Scholar] [CrossRef]
- Deng, M.L.; Liu, J.Y.; Zhang, X.S.; Li, J.S.; Fu, L.R. Energy and Parameter Analysis of SOFC System for Hydrogen Production from Methane Steam Reforming. J. Therm. Sci. 2022, 31, 2088–2110. [Google Scholar] [CrossRef]
- Zeng, Z.Z.; Qian, Y.P.; Zhang, Y.J.; Hao, C.K.; Dan, D.; Zhuge, W.L. A review of heat transfer and thermal management methods for temperature gradient reduction in solid oxide fuel cell (SOFC) stacks. Appl. Energy 2020, 280, 19. [Google Scholar] [CrossRef]
- Atif Mahmood, M.; Nawaz Chaudhary, T.; Farooq, M.; Salman Habib, M.; Maka, A.O.M.; Usman, M.; Sultan, M.; Shiung Lam, S.; Chen, B. Sensitivity analysis of performance and thermal impacts of a single hydrogen fueled solid oxide fuel cell to optimize the operational and design parameters. Sustain. Energy Technol. Assess. 2023, 57, 103241. [Google Scholar] [CrossRef]
- Zhu, P.; Wu, Z.; Yang, Y.; Wang, H.; Li, R.; Yang, F.; Zhang, Z. The dynamic response of solid oxide fuel cell fueled by syngas during the operating condition variations. Appl. Energy 2023, 349, 121655. [Google Scholar] [CrossRef]
- Iliev, I.K.; Gizzatullin, A.R.; Filimonova, A.A.; Chichirova, N.D.; Beloev, I.H. Numerical Simulation of Processes in an Electrochemical Cell Using COMSOL Multiphysics. Energies 2023, 16, 7265. [Google Scholar] [CrossRef]
- Cai, W.; Yuan, J.; Zheng, Q.; Yu, W.; Yin, Z.; Zhang, Z.; Pei, Y.; Li, S. Numerical Investigation of Heat/Flow Transfer and Thermal Stress in an Anode-Supported Planar SOFC. Crystals 2022, 12, 1697. [Google Scholar] [CrossRef]
- Mueller, M.; Klinsmann, M.; Sauter, U.; Njodzefon, J.-C.; Weber, A. High Temperature Solid Oxide Electrolysis—Technology and Modeling. Chem. Ing. Tech. 2023, 96, 143–166. [Google Scholar] [CrossRef]
- Cui, D.A.; Ji, Y.L.; Chang, C.; Wang, Z.; Xiao, X.; Li, Y.T. Influence of structure size on voltage uniformity of flat tubular segmented-in-series solid oxide fuel cell. J. Power Sources 2020, 460, 6. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Y.; Liu, J.; Xiang, M.; Sun, B.; Ya, Y.; Guo, Z.; Cheng, X. Effects of bipolar plate flow channel configuration on thermal-electric performance of direct ammonia solid oxide fuel cell: Part I—Numerical study of channel section geometry. Int. J. Hydrog. Energy 2024, 50, 765–785. [Google Scholar] [CrossRef]
- An, Y.-T.; Ji, M.-J.; Hwang, H.-J.; Eugene Park, S.; Choi, B.-H. Effect of cell-to-cell distance in segmented-in-series solid oxide fuel cells. Int. J. Hydrog. Energy 2015, 40, 2320–2325. [Google Scholar] [CrossRef]
- Park, J.M.; Kim, D.Y.; Baek, J.D.; Yoon, Y.J.; Su, P.C.; Lee, S.H. Effect of Electrolyte Thickness on Electrochemical Reactions and Thermo-Fluidic Characteristics inside a SOFC Unit Cell. Energies 2018, 11, 473. [Google Scholar] [CrossRef]
- Mushtaq, U.; Kim, D.-W.; Yun, U.-J.; Lee, J.-W.; Lee, S.-B.; Park, S.-J.; Song, R.-H.; Kim, G.; Lim, T.-H. Effect of cathode geometry on the electrochemical performance of flat tubular segmented-in-series (SIS) solid oxide fuel cell. Int. J. Hydrog. Energy 2015, 40, 6207–6215. [Google Scholar] [CrossRef]
- Sinha, A.A.; Sanjay; Ansari, M.Z.; Shukla, A.K.; Choudhary, T. Comprehensive review on integration strategies and numerical modeling of fuel cell hybrid system for power & heat production. Int. J. Hydrog. Energy 2023, 48, 33669–33704. [Google Scholar]
- Peng, J.; Zhao, D.; Xu, Y.; Wu, X.; Li, X. Comprehensive Analysis of Solid Oxide Fuel Cell Performance Degradation Mechanism, Prediction, and Optimization Studies. Energies 2023, 16, 788. [Google Scholar] [CrossRef]
- Zhao, Y.R.; Sadhukhan, J.; Lanzini, A.; Brandon, N.; Shah, N. Optimal integration strategies for a syngas fuelled SOFC and gas turbine hybrid. J. Power Sources 2011, 196, 9516–9527. [Google Scholar] [CrossRef]
- Huang, S.L.; Yang, C.; Chen, H.; Zhou, N.N.; Tucker, D. Coupling impacts of SOFC operating temperature and fuel utilization on system net efficiency in natural gas hybrid SOFC/GT system. Case Stud. Therm. Eng. 2022, 31, 12. [Google Scholar] [CrossRef]
- Ameri, M.; Mohammadi, R. Simulation of an atmospheric SOFC and gas turbine hybrid system using Aspen Plus software. Int. J. Energy Res. 2013, 37, 412–425. [Google Scholar] [CrossRef]
- Doherty, W.; Reynolds, A.; Kennedy, D. Computer simulation of a biomass gasification-solid oxide fuel cell power system using Aspen Plus. Energy 2010, 35, 4545–4555. [Google Scholar] [CrossRef]
- Ni, T.M.; Si, J.W.; Gong, X.H.; Zhang, K.; Pan, M.Z. Thermodynamic and economic analysis of a novel cascade waste heat recovery system for solid oxide fuel cell. Energy Convers. Manag. 2022, 259, 14. [Google Scholar] [CrossRef]
- Hussain, J.; Ali, R.; Akhtar, M.N.; Jaffery, M.H.; Shakir, I.; Raza, R. Modeling and simulation of planar SOFC to study the electrochemical properties. Curr. Appl. Phys. 2020, 20, 660–672. [Google Scholar] [CrossRef]
- Qiao, Y.X.; Fan, C.; Sun, K.N. Multiphysics Simulation of a Solid Oxide Fuel Cell Based on COMSOL Method. In Proceedings of the 5th International Conference on Advances in Energy, Environment and Chemical Science (AEECS), Shanghai, China, 26–28 February 2021; EDP Sciences: Les Ulis, France, 2021. [Google Scholar]
- Yakabe, H.; Ogiwara, T.; Hishinuma, M.; Yasuda, I. 3-D model calculation for planar SOFC. J. Power Sources 2001, 102, 144–154. [Google Scholar] [CrossRef]
- Khazaee, I.; Rava, A. Numerical simulation of the performance of solid oxide fuel cell with different flow channel geometries. Energy 2017, 119, 235–244. [Google Scholar] [CrossRef]
- Lee, S.; Park, M.; Kim, H.; Yoon, K.J.; Son, J.W.; Lee, J.H.; Kim, B.K.; Choi, W.; Hong, J. Thermal conditions and heat transfer characteristics of high-temperature solid oxide fuel cells investigated by three-dimensional numerical simulations. Energy 2017, 120, 293–305. [Google Scholar] [CrossRef]
- Milewski, J.; Świrski, K.; Santarelli, M.; Leone, P. Advanced Methods of Solid Oxide Fuel Cell Modeling; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Patcharavorachot, Y.; Arpornwichanop, A.; Chuachuensuk, A. Electrochemical study of a planar solid oxide fuel cell: Role of support structures. J. Power Sources 2008, 177, 254–261. [Google Scholar] [CrossRef]
- Chatrattanawet, N.; Saebea, D.; Authayanun, S.; Arpornwichanop, A.; Patcharavorachot, Y. Performance and environmental study of a biogas-fuelled solid oxide fuel cell with different reforming approaches. Energy 2018, 146, 131–140. [Google Scholar] [CrossRef]
- Janardhanan, V.M.; Deutschmann, O. CFD analysis of a solid oxide fuel cell with internal reforming: Coupled interactions of transport, heterogeneous catalysis and electrochemical processes. J. Power Sources 2006, 162, 1192–1202. [Google Scholar] [CrossRef]
- Rosner, F.; Rao, A.; Samuelsen, S. Economics of cell design and thermal management in solid oxide fuel cells under SOFC-GT hybrid operating conditions. Energy Convers. Manag. 2020, 220, 112952. [Google Scholar] [CrossRef]
- Oryshchyn, D.; Harun, N.F.; Tucker, D.; Bryden, K.M.; Shadle, L. Fuel utilization effects on system efficiency in solid oxide fuel cell gas turbine hybrid systems. Appl. Energy 2018, 228, 1953–1965. [Google Scholar] [CrossRef]
- Rosner, F.; Rao, A.; Samuelsen, S. Thermo-economic analyses of solid oxide fuel cell-gas turbine hybrids considering thermal cell gradients. J. Power Sources 2021, 507, 230271. [Google Scholar] [CrossRef]
- Sadeghi, M.; Jafari, M.; Hajimolana, Y.S.; Woudstra, T.; Aravind, P.V. Size and exergy assessment of solid oxide fuel cell-based H2-fed power generation system with alternative electrolytes: A comparative study. Energy Convers. Manag. 2021, 228, 113681. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Z.; Ni, M. Management, Modeling of a novel SOFC-PEMFC hybrid system coupled with thermal swing adsorption for H-2 purification: Parametric and exergy analyses. Energy Convers. Manag. 2018, 174, 802–813. [Google Scholar] [CrossRef]
- Akkaya, A.V.; Sahin, B.; Erdem, H.H. Exergetic performance coefficient analysis of a simple fuel cell system. Int. J. Hydrog. Energy 2007, 32, 4600–4609. [Google Scholar] [CrossRef]
- Ilbas, M.; Kumuk, B. Numerical modelling of a cathode-supported solid oxide fuel cell (SOFC) in comparison with an electrolyte-supported model. J. Energy Inst. 2019, 92, 682–692. [Google Scholar] [CrossRef]
- Ferguson, J.R.; Fiard, J.M.; Herbin, R. Three-dimensional numerical simulation for various geometries of solid oxide fuel cells. J. Power Sources 1996, 58, 109–122. [Google Scholar] [CrossRef]
- Celik, A.N. Three-dimensional multiphysics model of a planar solid oxide fuel cell using computational fluid dynamics approach. Int. J. Hydrog. Energy 2018, 43, 19730–19748. [Google Scholar] [CrossRef]
- Hajimolana, S.A.; Hussain, M.A.; Daud, W.; Soroush, M.; Shamiri, A. Mathematical modeling of solid oxide fuel cells: A review. Renew. Sust. Energ. Rev. 2011, 15, 1893–1917. [Google Scholar] [CrossRef]
- Akhtar, N.; Decent, S.P.; Loghin, D.; Kendall, K. A three-dimensional numerical model of a single-chamber solid oxide fuel cell. Int. J. Hydrog. Energy 2009, 34, 8645–8663. [Google Scholar] [CrossRef]
- Andersson, M.; Yuan, J.L.; Sundén, B. SOFC modeling considering electrochemical reactions at the active three phase boundaries. Int. J. Heat Mass Transf. 2012, 55, 773–788. [Google Scholar] [CrossRef]
- Kanno, D.; Shikazono, N.; Takagi, N.; Matsuzaki, K.; Kasagi, N. Evaluation of SOFC anode polarization simulation using three-dimensional microstructures reconstructed by FIB tomography. Electrochim. Acta 2011, 56, 4015–4021. [Google Scholar] [CrossRef]
- Wang, X.S.; Lv, X.J.; Weng, Y.W. Performance analysis of a biogas-fueled SOFC/GT hybrid system integrated with anode-combustor exhaust gas recirculation loops. Energy 2020, 197, 17. [Google Scholar] [CrossRef]
- Campanari, S. Thermodynamic model and parametric analysis of a tubular SOFC module. J. Power Sources 2001, 92, 26–34. [Google Scholar] [CrossRef]





| Parameter | Value | Unit | Symbol |
|---|---|---|---|
| Channel width | 2 | mm | wch |
| Rib width | 2 | mm | wrib |
| Anode thickness | 0.15 | mm | tan |
| Electrolyte thickness | 0.1 | mm | tel |
| Cathode thickness | 0.1 | mm | tca |
| Gas channel height | 2 | mm | hch |
| Flow channel length | 60–180 | mm | Lcell |
| Number of cells | 1000 | - | Ncell |
| Parameter | Value | Unit |
|---|---|---|
| Anode electric potential | 0 | V |
| Cathode electric potential | 0.4–0.9 | V |
| Anode air velocity | 0.8 | m/s |
| Cathode air velocity | 3 | m/s |
| Anode mass fraction | H2:H2O = 0.4:0.6 | - |
| Cathode mass fraction | O2:N2 = 0.15:0.85 | - |
| Anode fuel outlet | 0 | Pa |
| Cathode fuel outlet | 0 | Pa |
| Cell operating temperature | 800 | ℃ |
| Cell operating pressure | 101.32 | kPa |
| Parameter | Value | Unit | Symbol | References |
|---|---|---|---|---|
| Anode electronic conductivity | 2149.2 | S/m | [39] | |
| Cathode electronic conductivity | 5093 | S/m | [39] | |
| Electrolyte ionic conductivity | 2.2669 | S/m | [39] | |
| Anodic transfer coefficient of anode | 0.5 | [40] | ||
| Anodic transfer coefficient of cathode | 3.5 | [40] | ||
| Anode activation energy | 6.54 × 1011 | 1/(Ω∙m2) | [26,41] | |
| Cathode activation energy | 2.35 × 1011 | 1/(Ω∙m2) | [26,41] | |
| Exchange current density of anode | 4637.4 | A/m2 | [26] | |
| Exchange current density of cathode | 1166.2 | A/m2 | [26] | |
| The specific surface area of anode | 102,500 | 1/m | [42] | |
| The specific surface area of cathode | 102,500 | 1/m | [42] | |
| Electrolyte volume fraction | 0.7 | - | [43] | |
| porosity | 0.4 | - | [26,44] |
| Parameter | Value | Unit | References |
|---|---|---|---|
| Porosity of anode | 0.4 | - | [26,44] |
| Porosity of cathode | 0.4 | - | [26,44] |
| Permeability of anode | 1.76 × 10−11 | m2 | [26] |
| Permeability of cathode | 1.76 × 10−11 | m2 | [26] |
| Parameter | Value | Unit | References |
|---|---|---|---|
| Anode heat capacity | 450 | J/(kg∙k) | [43] |
| Cathode heat capacity | 430 | J/(kg∙k) | [43] |
| Electrolyte heat capacity | 470 | J/(kg∙k) | [43] |
| Anode density | 3310 | kg/m2 | [45] |
| Cathode density | 3030 | kg/m2 | [45] |
| Electrolyte density | 5160 | kg/m2 | [45] |
| Thermal conductivity of the anode | 11 | W/(m∙k) | [43] |
| Thermal conductivity of the cathode | 6 | W/(m∙k) | [43] |
| Thermal conductivity of electrolyte | 2.7 | W/(m∙k) | [43] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, J.; Fu, L.; Wang, Q. Numerical Study on Effects of Flow Channel Length on Solid Oxide Fuel Cell-Integrated System Performances. Sustainability 2024, 16, 1643. https://doi.org/10.3390/su16041643
Liu Y, Liu J, Fu L, Wang Q. Numerical Study on Effects of Flow Channel Length on Solid Oxide Fuel Cell-Integrated System Performances. Sustainability. 2024; 16(4):1643. https://doi.org/10.3390/su16041643
Chicago/Turabian StyleLiu, Yuhang, Jinyi Liu, Lirong Fu, and Qiao Wang. 2024. "Numerical Study on Effects of Flow Channel Length on Solid Oxide Fuel Cell-Integrated System Performances" Sustainability 16, no. 4: 1643. https://doi.org/10.3390/su16041643
APA StyleLiu, Y., Liu, J., Fu, L., & Wang, Q. (2024). Numerical Study on Effects of Flow Channel Length on Solid Oxide Fuel Cell-Integrated System Performances. Sustainability, 16(4), 1643. https://doi.org/10.3390/su16041643






