Optimizing Water-Light Complementary Systems for the Complex Terrain of the Southwestern China Plateau Region: A Two-Layer Model Approach
Abstract
:1. Introduction
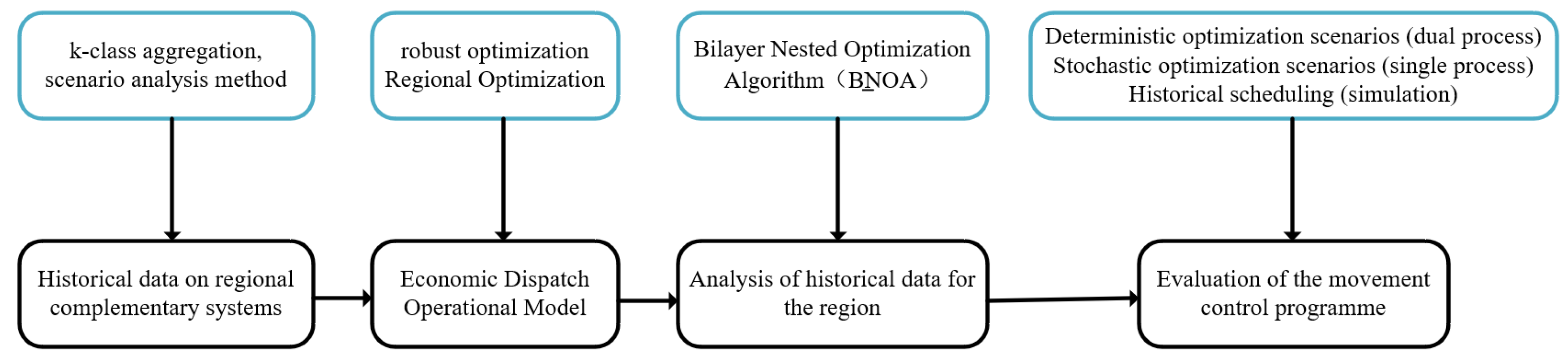
2. Research Methodology
2.1. Summarize
2.2. Economic Scheduling Model Based on Robust Optimization
2.2.1. Photovoltaic
2.2.2. Hydropower Modeling
Objective Function
Constraints
- (a)
- Crew dynamics limitations
- (b)
- Head constraints
- (c)
- Reservoir characterization constraints
- (d)
- Hydropower unit output constraints
- (e)
- Water balance constraints
- (f)
- Hydropower plant flow constraints
- (g)
- Hydropower plant hydraulic linkage constraints
- (h)
- Reservoir capacity constraints
- (i)
- Load balancing constraints
- (j)
- Rotating space constraints
- (k)
- Constraints on unit output rise and fall
- (l)
- Minimum start/stop constraints
- (m)
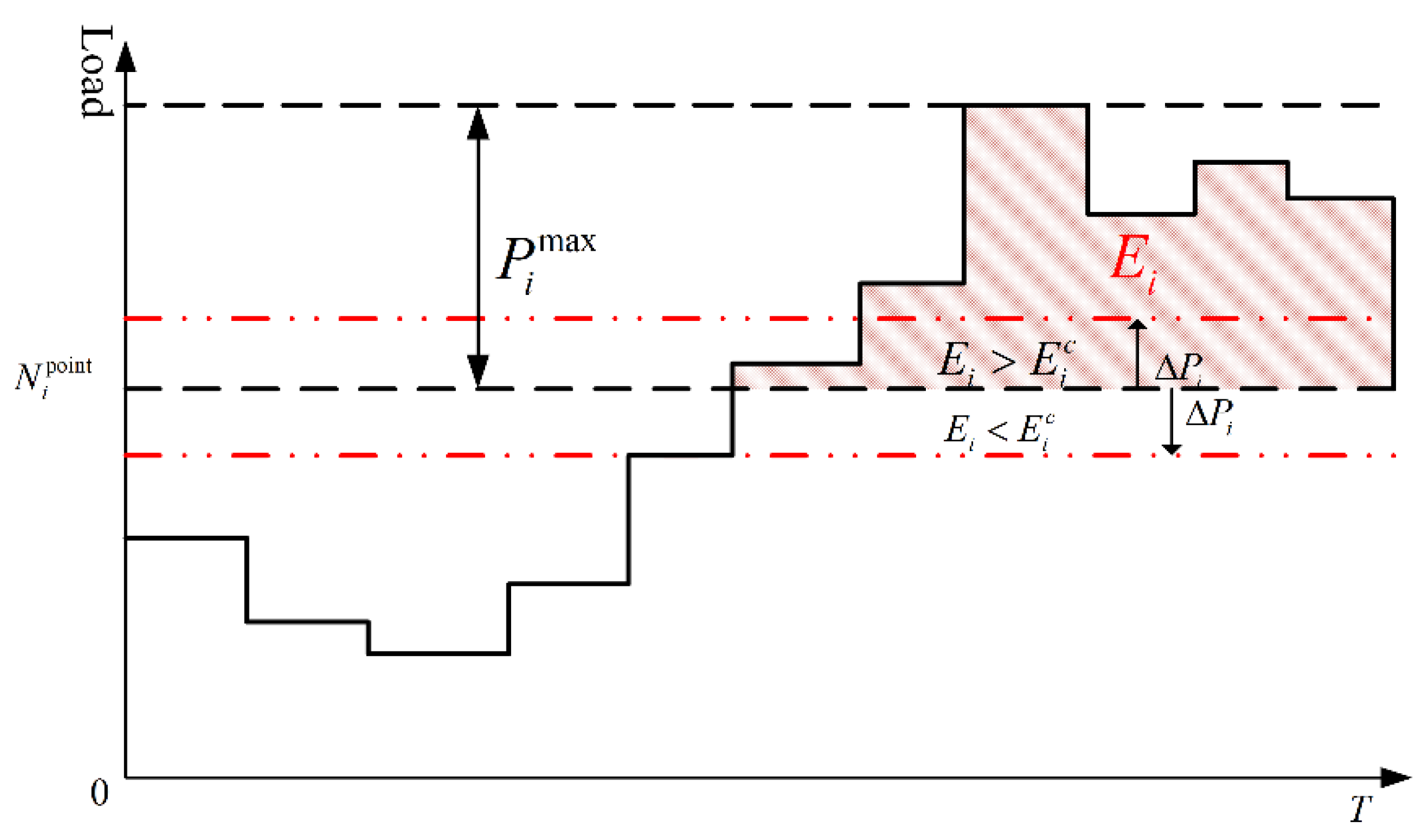
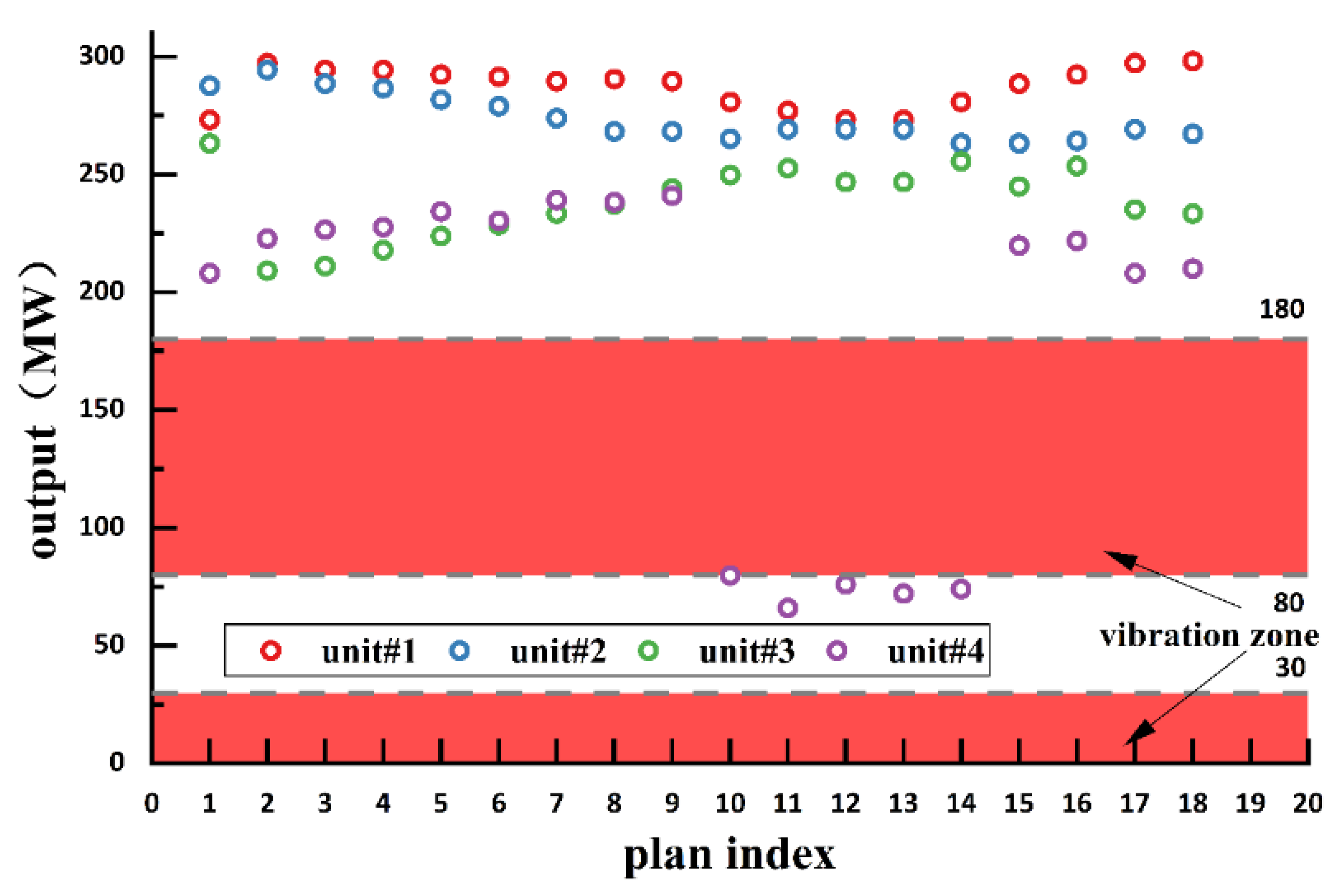
- Restraint of the vibration zone of the unit
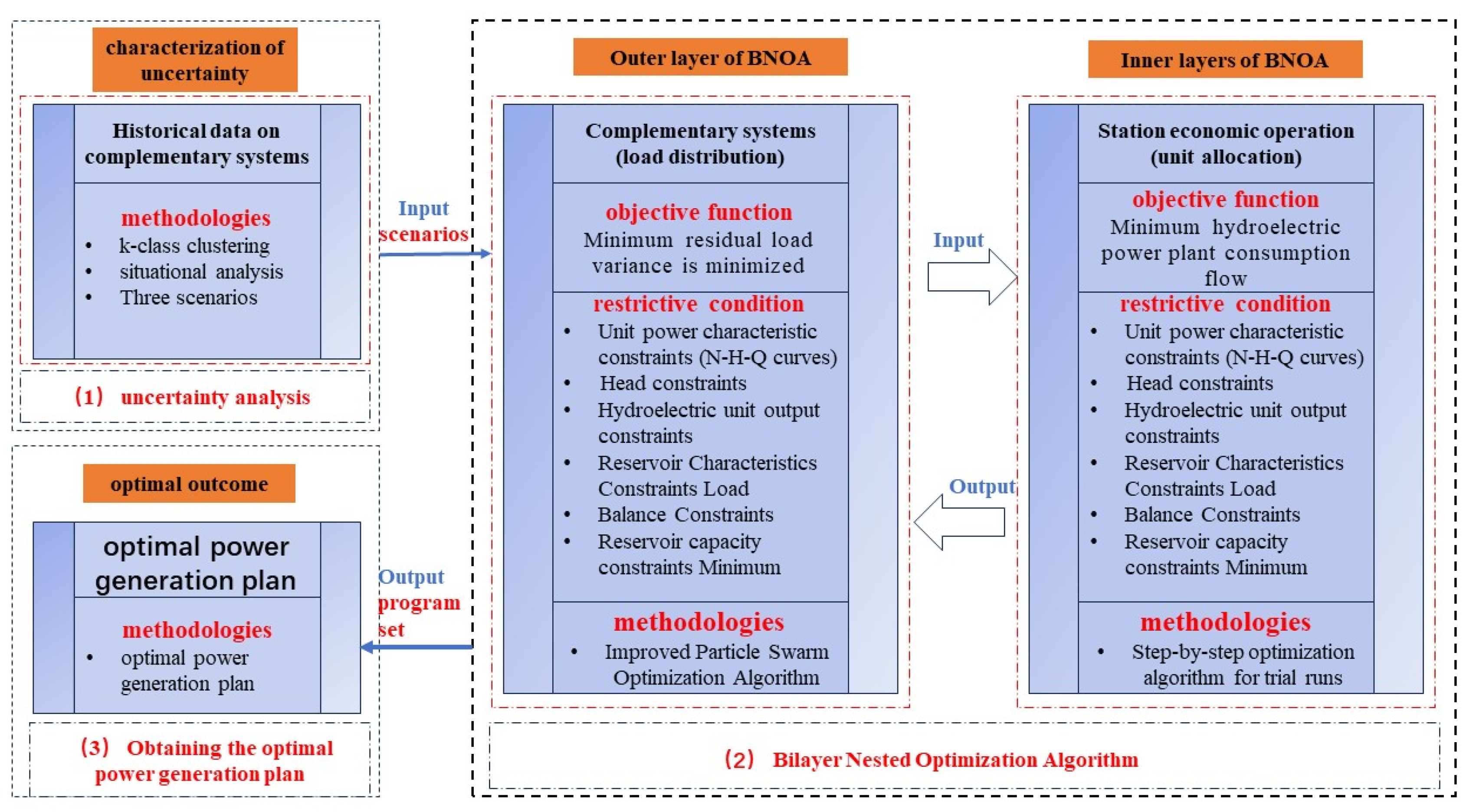
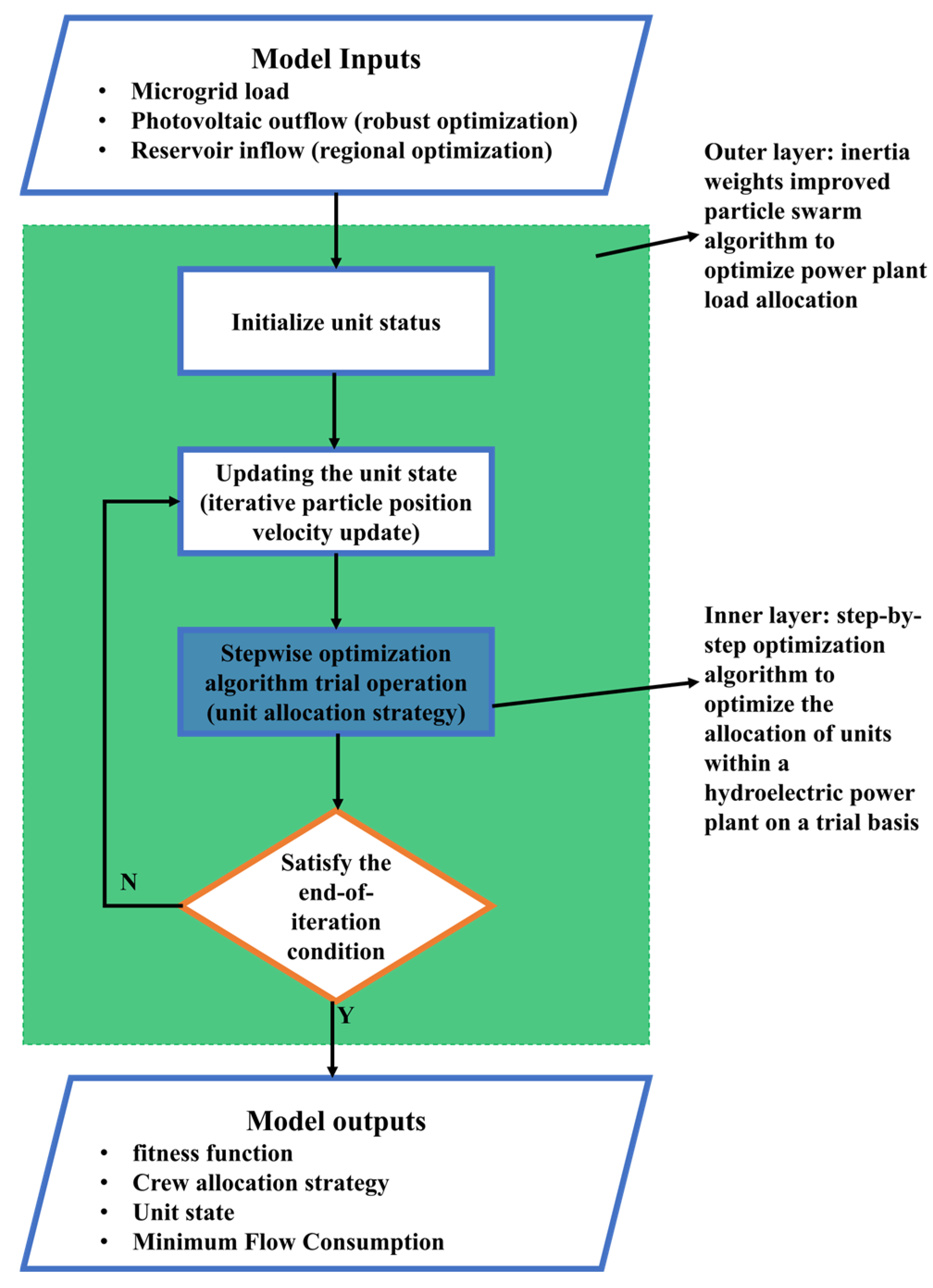
2.3. Double-Level Nested Optimization Algorithm Based on Economic Dispatching Model
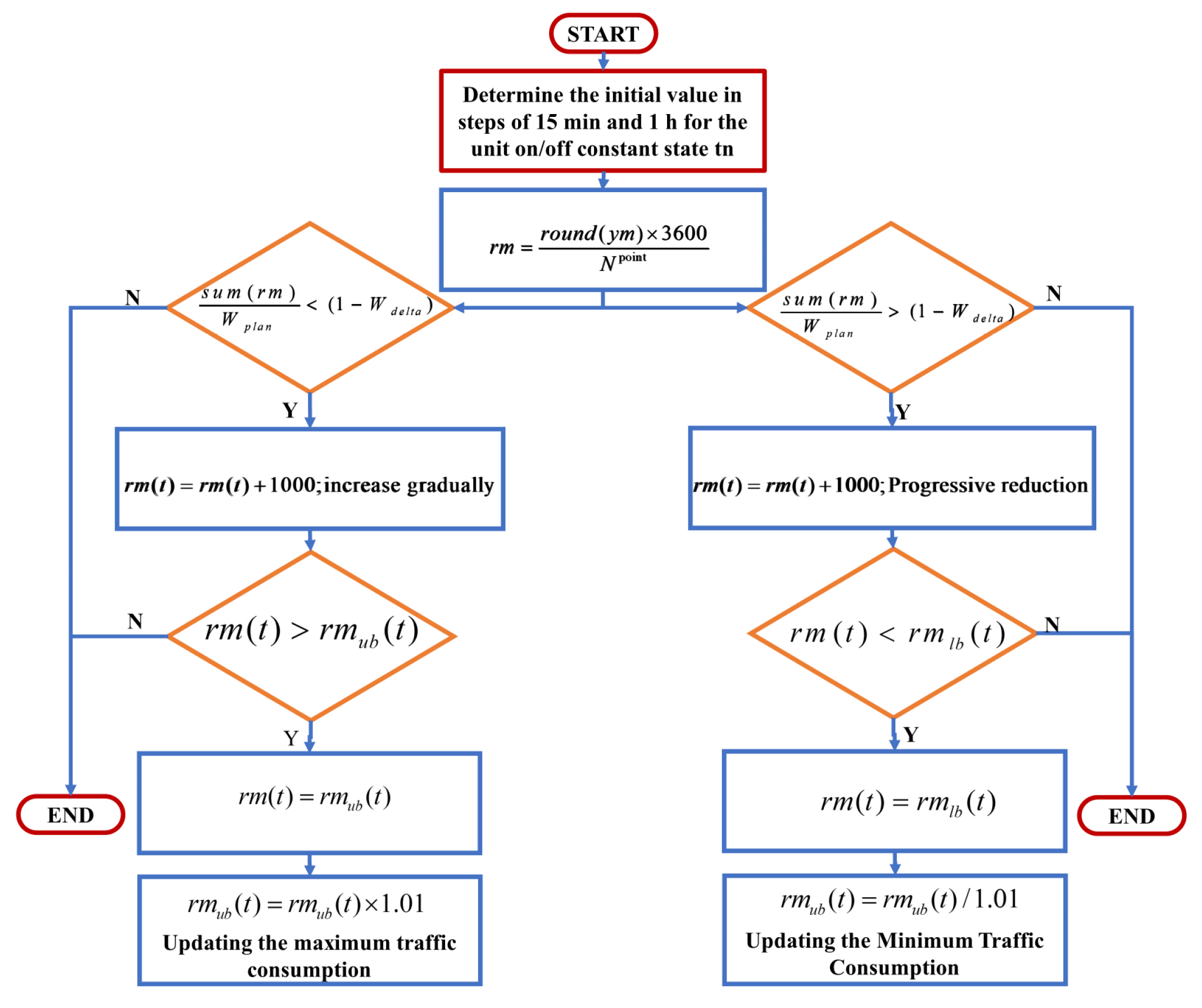
2.3.1. Outer Layer Optimization (Economic Operation Modeling to Address the “Electricity to Water” Problem)
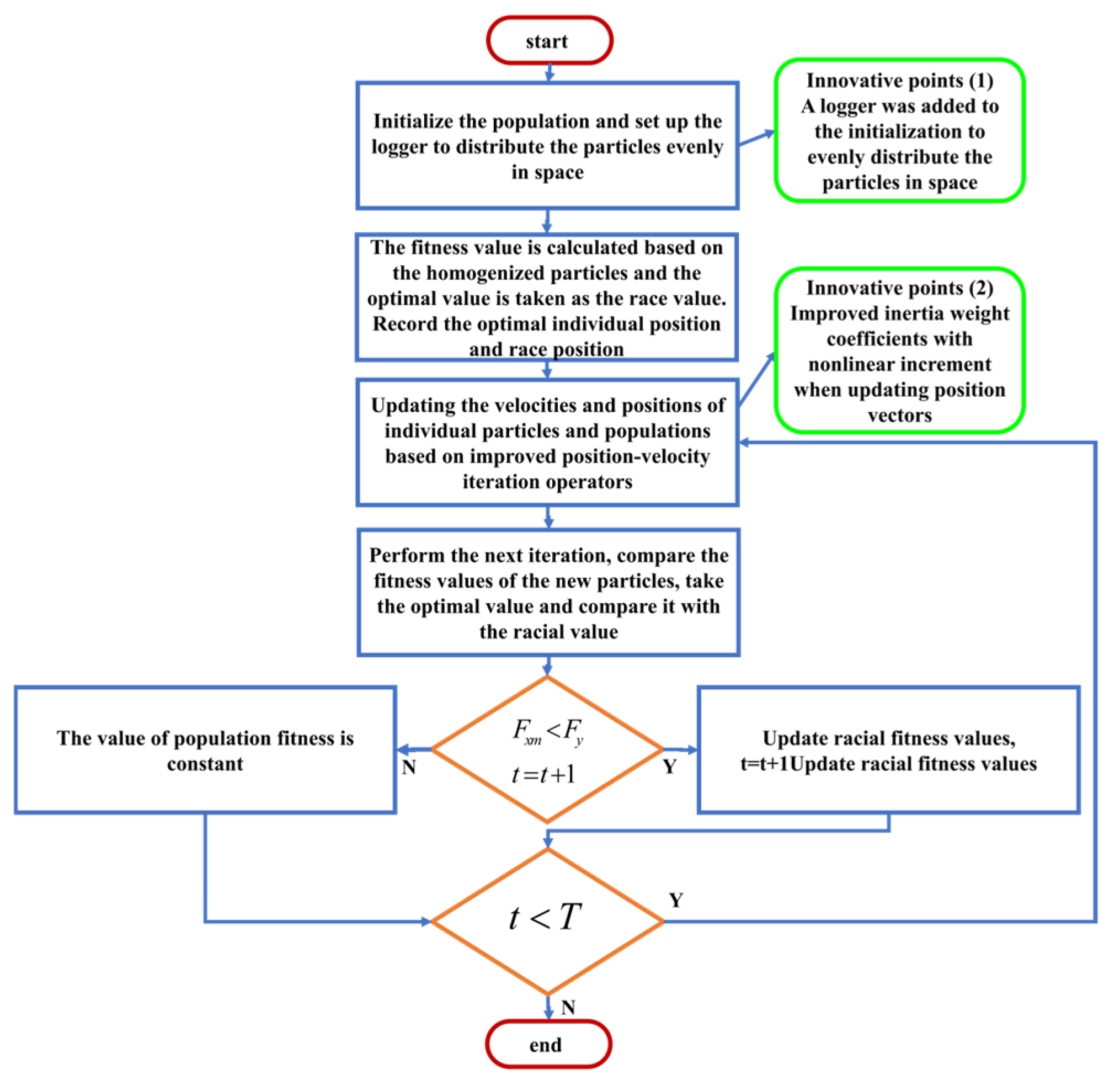
- (1)
- A recorder is introduced to the original model to distribute initial particles uniformly in space D rather than having random particle positions, effectively preventing optimization from falling into local optima.
- (2)
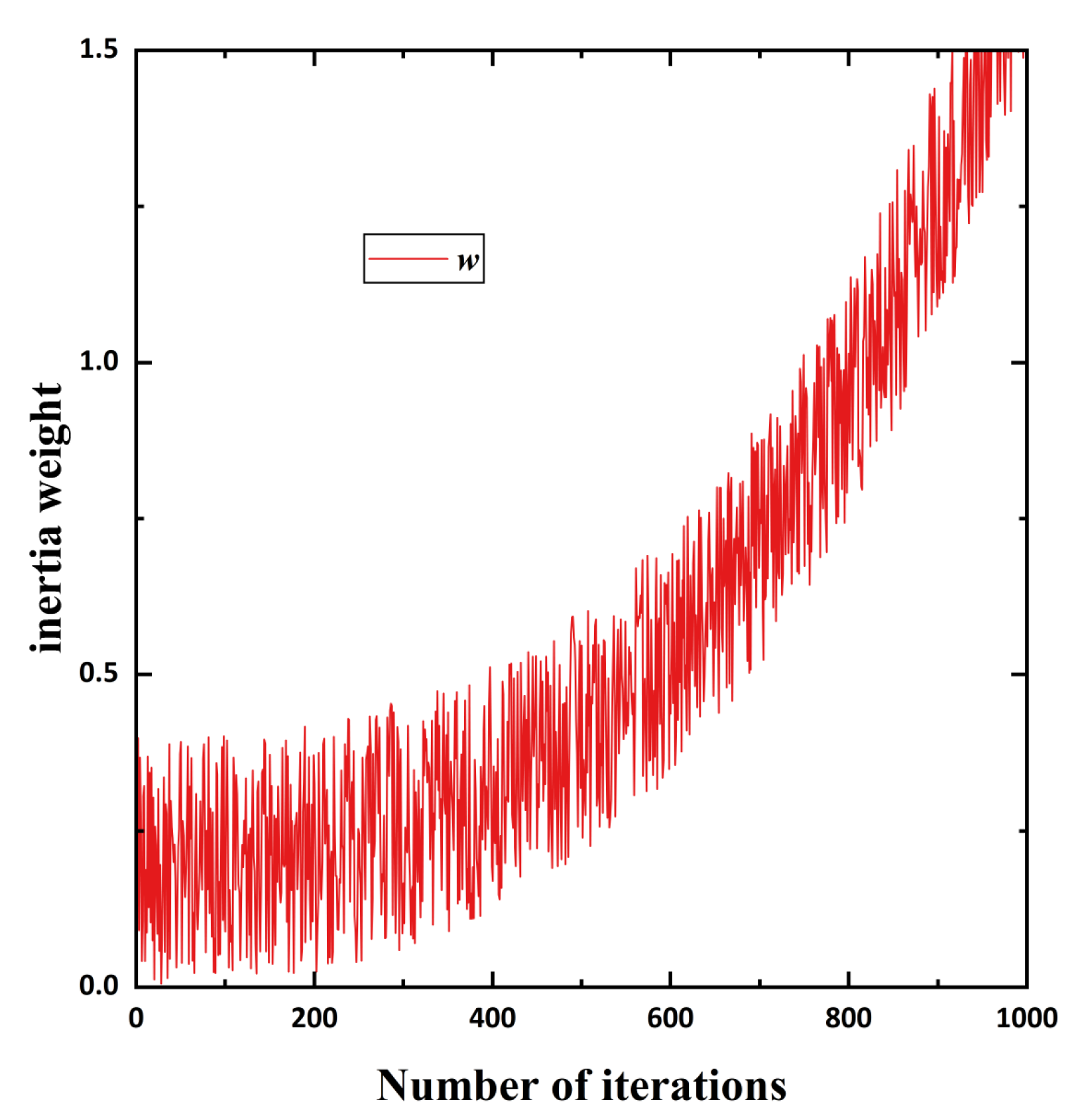
- To balance the global exploration and local development ability of PSO, this study proposes an improved PSO algorithm with inertia weights. It transforms the linearly decreasing variable of inertia weights into a nonlinear inertia weight, as depicted in Figure 6.
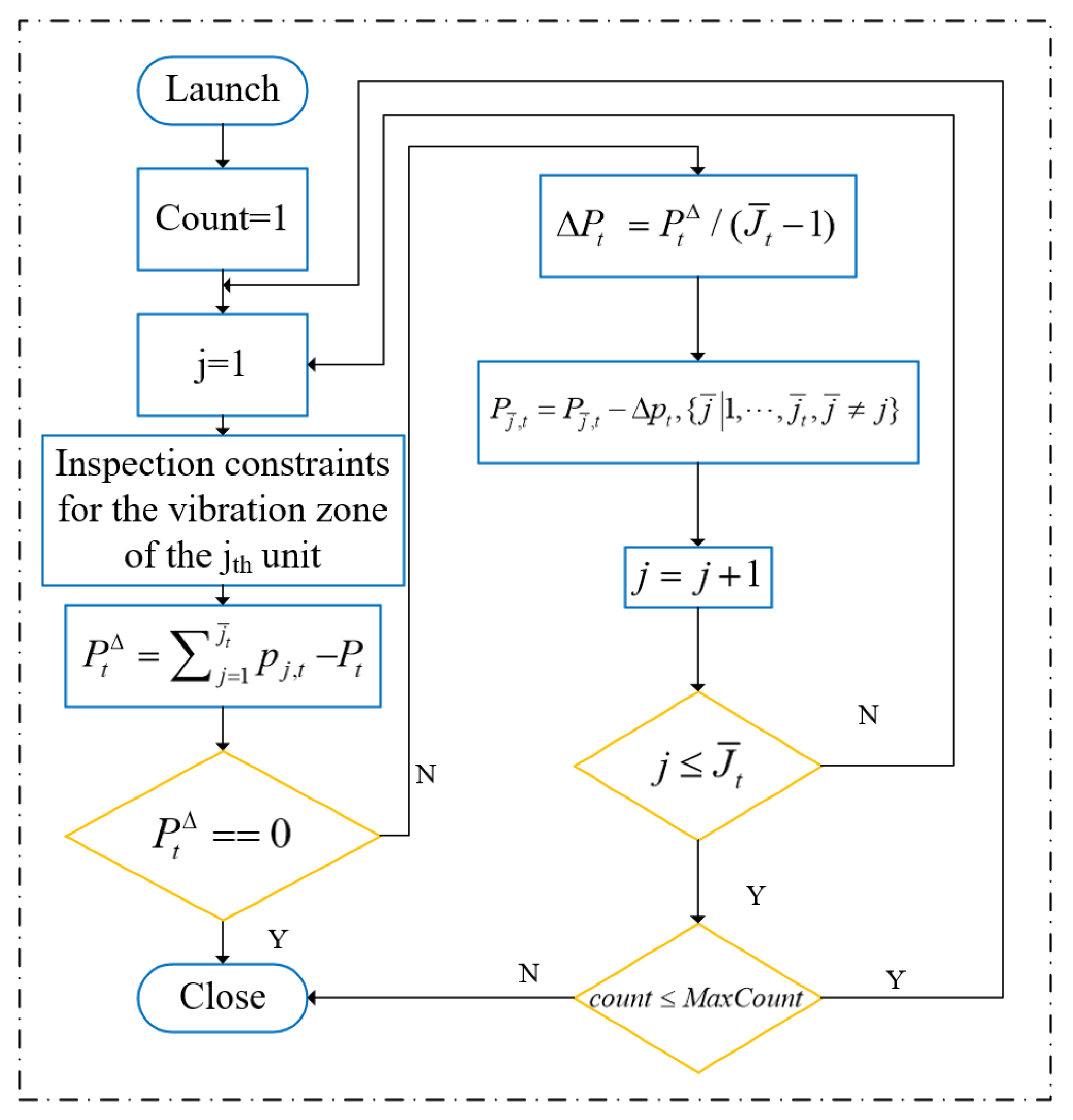
2.3.2. Inner Layer Optimisation (Optimisation of Hydroelectric Units)
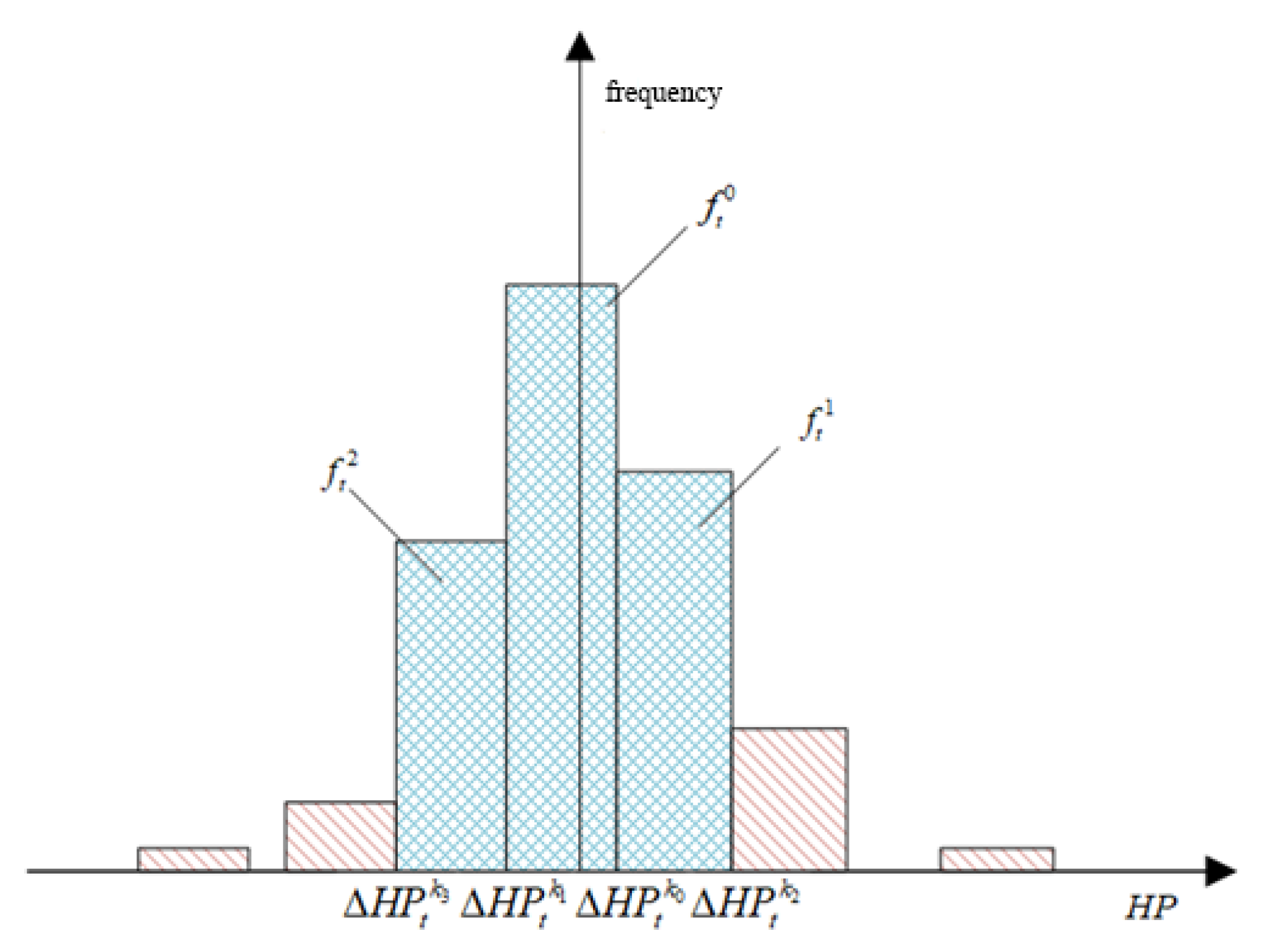
Hydroelectric Power Plant Output Scenarios and Time Sequences
The Inner-Layer Optimization Models for Hydroelectric Power Plants Incorporate Specific Strategies
- (1)
- The inner layer optimizes the load distribution strategy across units using SOAT Operational. Unit load distribution is modeled with a stepwise optimization algorithm (SOA), treating each unit as a stage, and the input unit number represents the stage variable (d = 1, 2,…, N) for the facing stage of the residual phase. The output after the stage can be considered the unit’s overall output. Consequently, the state transfer equation of the SOA model is as follows:
- (2)
- When considering hydropower units, the unit on/off state variable (us) constitutes a two-dimensional coding, altering the conventional coding strategy of optimizing only the number of units. This change involves optimizing the time nodes and the number of units when the hydropower unit models are not the same as signified by:
- (3)
- The load factor ηi of the hydropower plant is calculated, linking to the planned daily power generation and the maximum output of the hydropower plant, :
- (4)
- The objective function of the unit combination model is established following the Bellman optimization principle. The recursive form, as shown in Equation (33), is employed:
Trial Operational
3. Case Studies
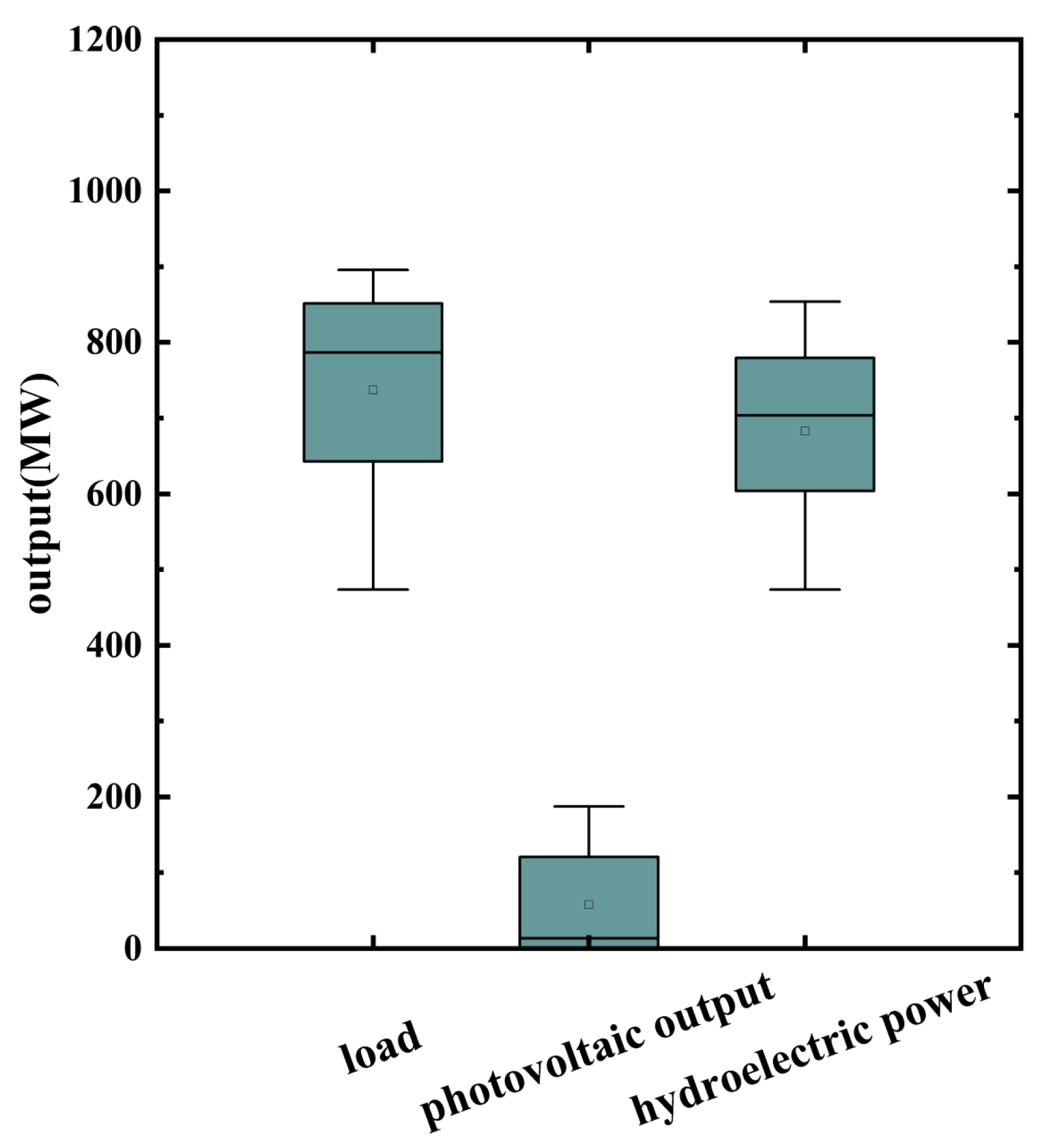
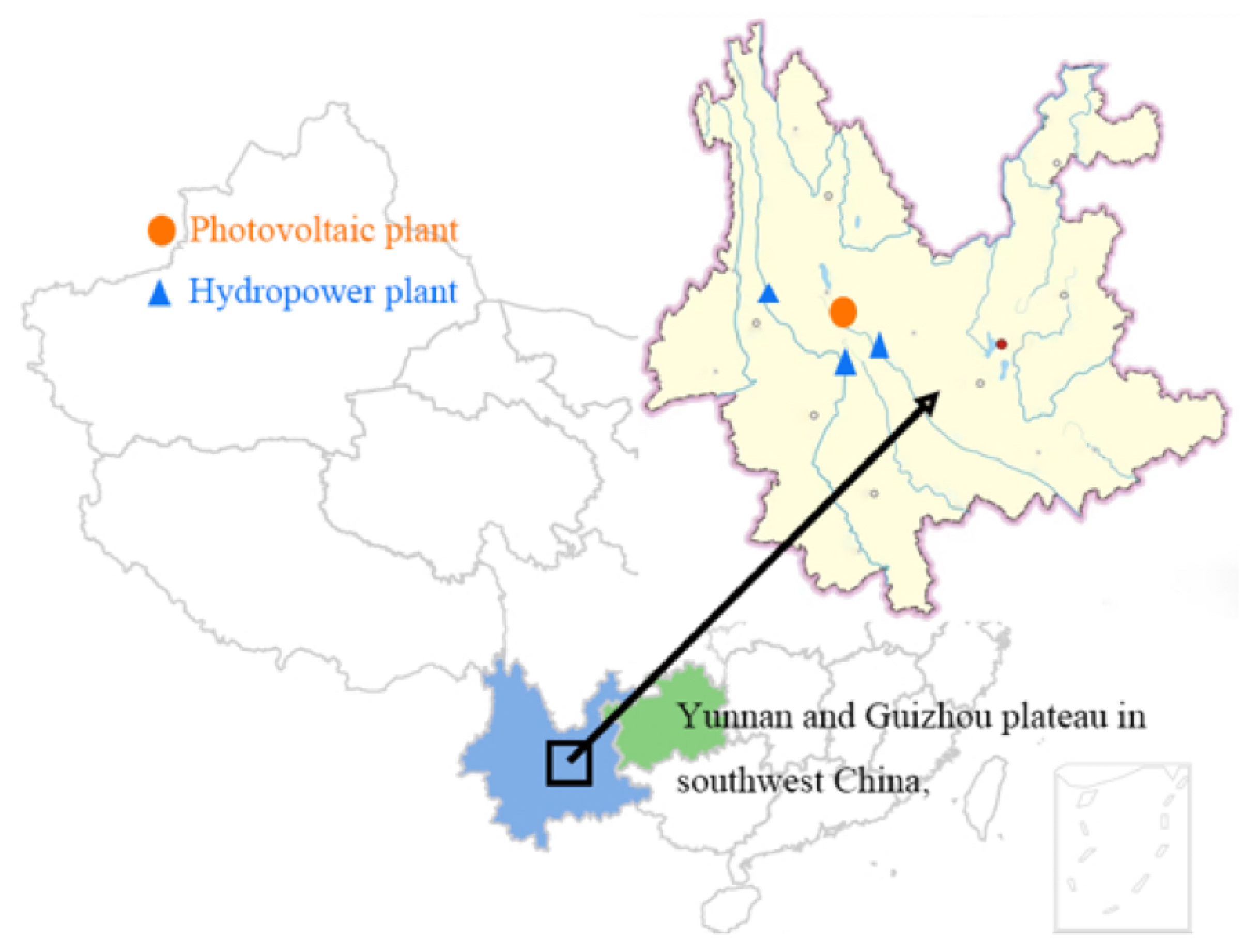
3.1. Partial Parameterization of the Power Station and Multi-Scenario Settings
- 1.
- River hydro units (UNIT#1–4) output sequence from 1 March 2016 to 31 March 2016, at a 1-h resolution.
- 2.
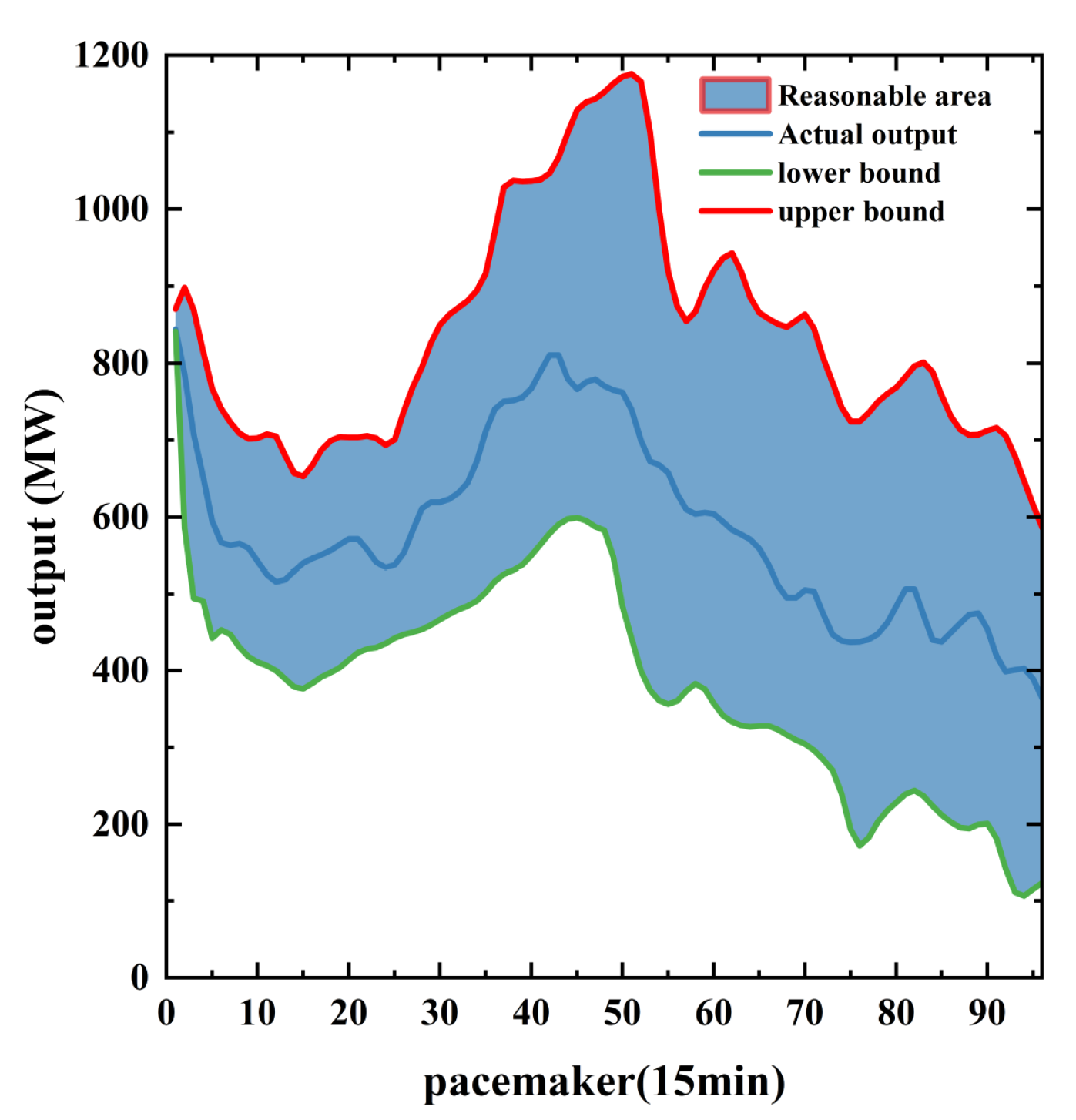
- Sequence of PV output from PV power plants in the region spanning 1 April 2013 to 1 April 2014, with a 15-min resolution.
- 3.
- Output sequence on 15 June 2016, at a 1-min resolution for the water-photovoltaic (WPV) power plants in the region, consisting of 1200 MW of hydropower and 200 MW of photovoltaics.
- 4.
- Reservoir inflow runoff sequence from January 1956 to December 2011 at a monthly resolution.
3.2. Program Parameter Design
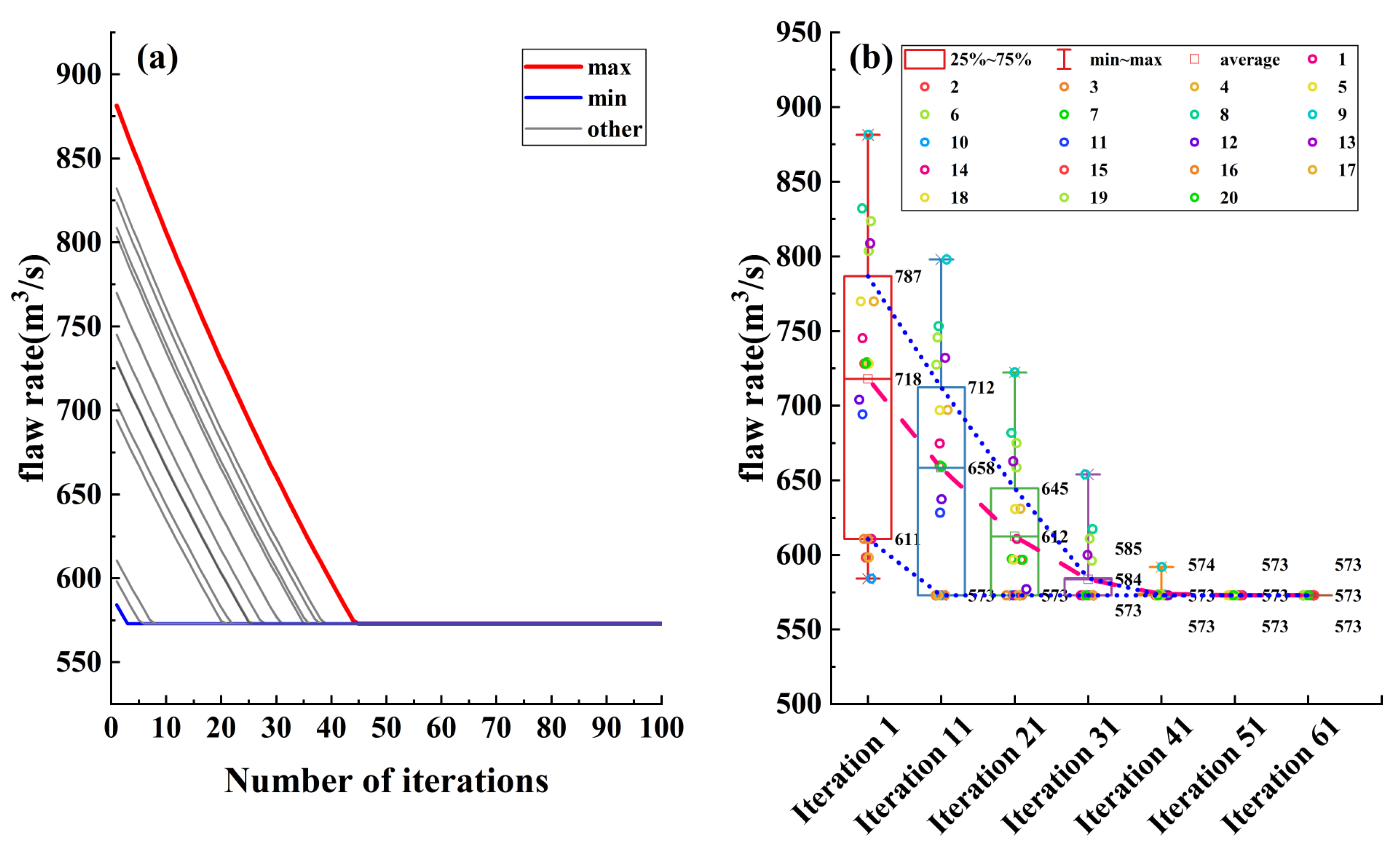
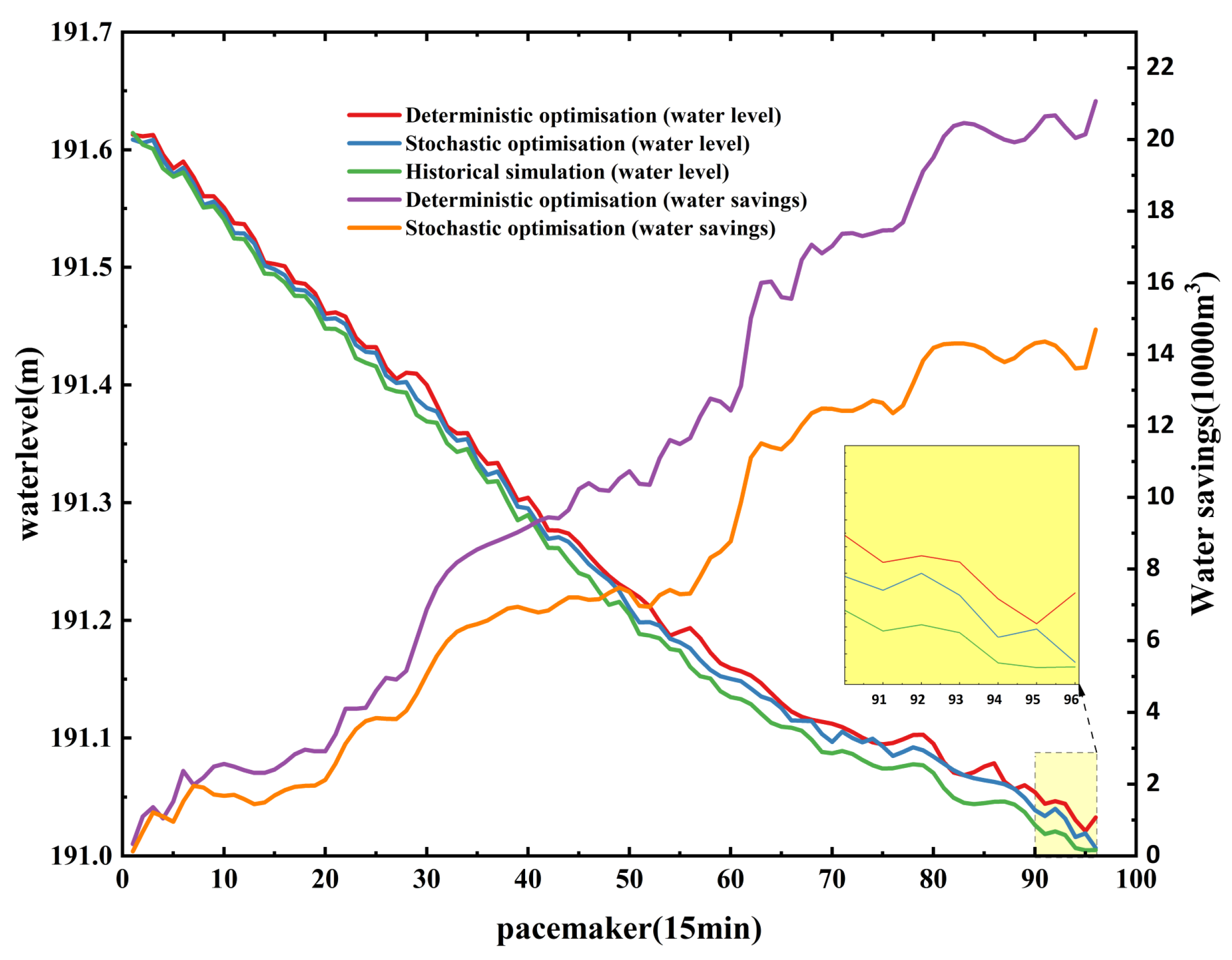
3.3. Effectiveness Analysis of Double Nested Algorithms
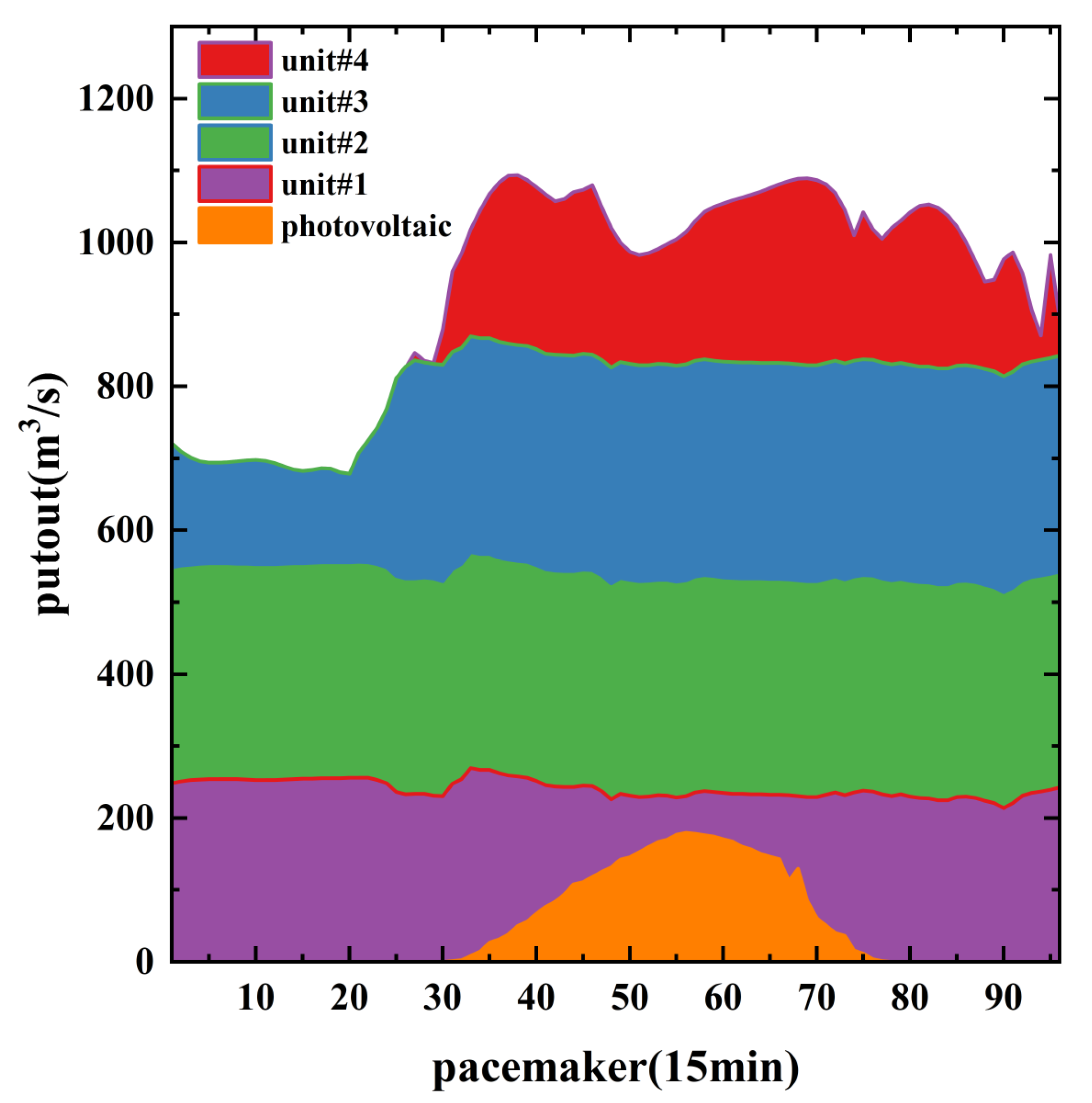
4. Comparison of Three Dispatch Scenarios for Individual Cases
5. Conclusions
- (1)
- In a complementary system, the uncertainty in photovoltaic output and inflow runoff can complement each other by optimizing and adapting in a double-layer nested model.
- (2)
- The water head range, output range, and vibration range of the hydropower station influence the adjustable range of the unit. A small change in water consumption can bring about a significant change in the adjustable range. The proposed two-dimensional coding strategy effectively handles the continuous start/stop constraints of the unit, significantly reducing the number of optimization variables and achieving dimensionality reduction.
- (3)
- The proposed double-layer nested optimization algorithm effectively generates an economic operation plan within a short time. By trial-computing the inner-layer optimization results, a daily dispatch plan with 384 optimized variables can be obtained in just 5 min.
- (4)
- Compared with historical dispatch simulation scenarios, the deterministic optimization and stochastic optimization scenarios reduced water consumption by 1.7% and 1.2% respectively. This not only confirms the superiority of the model but also demonstrates the advantages of coupling photovoltaic and runoff prediction for short-term water dispatching, resulting in a complementary gain effect for water and light.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| IPSO-SOAT | Improved Particle Swarm Optimization Algorithm with Weight Coefficients-Stepwise Optimization Algorithm Trial Operational Model |
| PV | Photovoltaic |
| HES | Hybrid Energy System |
| UC | Unit Combination |
| RO | Robust Optimization |
| BNOA | Bilayer Nested Optimization Approach |
| pn | Photovoltaic prediction, Uncertain Characterization of PV Output Force (MW) |
| pf | Typical daily values after clustering of photovoltaic historical data (MW) |
| e | Optical prediction error values, following a normal distribution (MW) |
| F | Objective function for economic dispatch operations (m) |
| μn,t | On/off status of the unit, n is a 0–1 variable (1 for unit on, 0 for unit off) |
| rm,n,t | Consumption rate of the nth PV unit at time slot t for the mth PV scenario (m) |
| Δt | Stepsize (scheduling time slot length) (min) |
| Hydroelectric unit transient output at time period t of the mth scenario (MW) | |
| hm,t | Head at time period t of the mth scene (m) |
| head loss (m) | |
| Water level before runoff to hydroelectric plants (m) | |
| Water level after runoff from hydroelectric plants (m) | |
| vm,t | Storage capacity at the beginning of time period t (m3) |
| vm,t+1 | Storage capacity at the end of time period t (m3) |
| It | Average incoming flow in time period t |
| Upper limit of the flow rate into the reservoir of the hydropower plant in time period t (m3/s) | |
| Lower limit of the flow rate into the reservoir of the hydropower plant in time period t (m3/s) | |
| Qt | Incoming flow at hydroelectric power station at time period t (m3/s) |
| v− | Lower limit of hydroelectric power plant capacity (m3) |
| v+ | Upper limit of hydroelectric power plant capacity (m3) |
| LPt | spinning reserve margin (MW) |
| ΔP | Upper speed limit for unit raising/lowering (MW) |
| k | Time code |
| SUN | Minimum on-line time of the unit |
| SDN | Maximum online time of the unit |
| sun,k | Unit power-on action (1 for power on, 0 for power off) |
| sdn,k | Unit shutdown action (1 for shutdown, 0 for power on) |
| Lower limit of unit vibration zone (MW) | |
| Upper limit of unit vibration zone (MW) | |
| The velocity of the ith particle in the d-dimension (m/s) | |
| Position of the ith particle in d-dimension (one solution of the objective function) | |
| w | Inertia weighting factor |
| r1 | Self-learning factor |
| r2 | Group Learning Factor |
| Hydroelectric power output at time t in the nth sample scenario (MW) | |
| Hydroelectric output fluctuations at time t in the nth sample scenario (MW) | |
| Hpe | Hydroelectric Power Plant Expected Output Scenario Set (MW) |
| Upper boundary value of hydroelectric power plant output in Stepsize t (MW) | |
| Lower boundary value of hydropower plant output in Stepsize t (MW) | |
| NT | The algorithm optimizes the total number of variables |
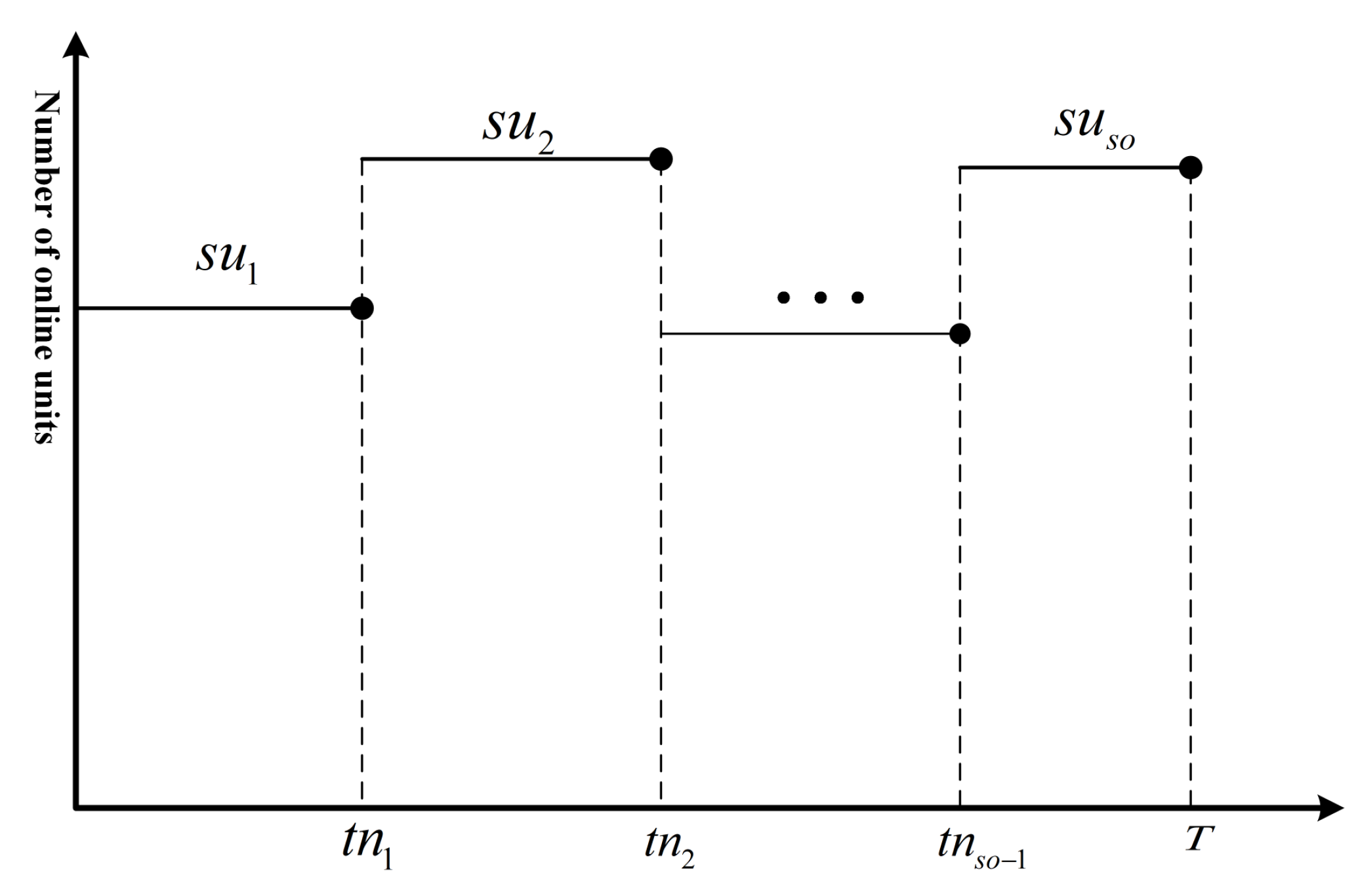
| ouT | Number of units on-line in each dispatch period during the entire dispatch period T |
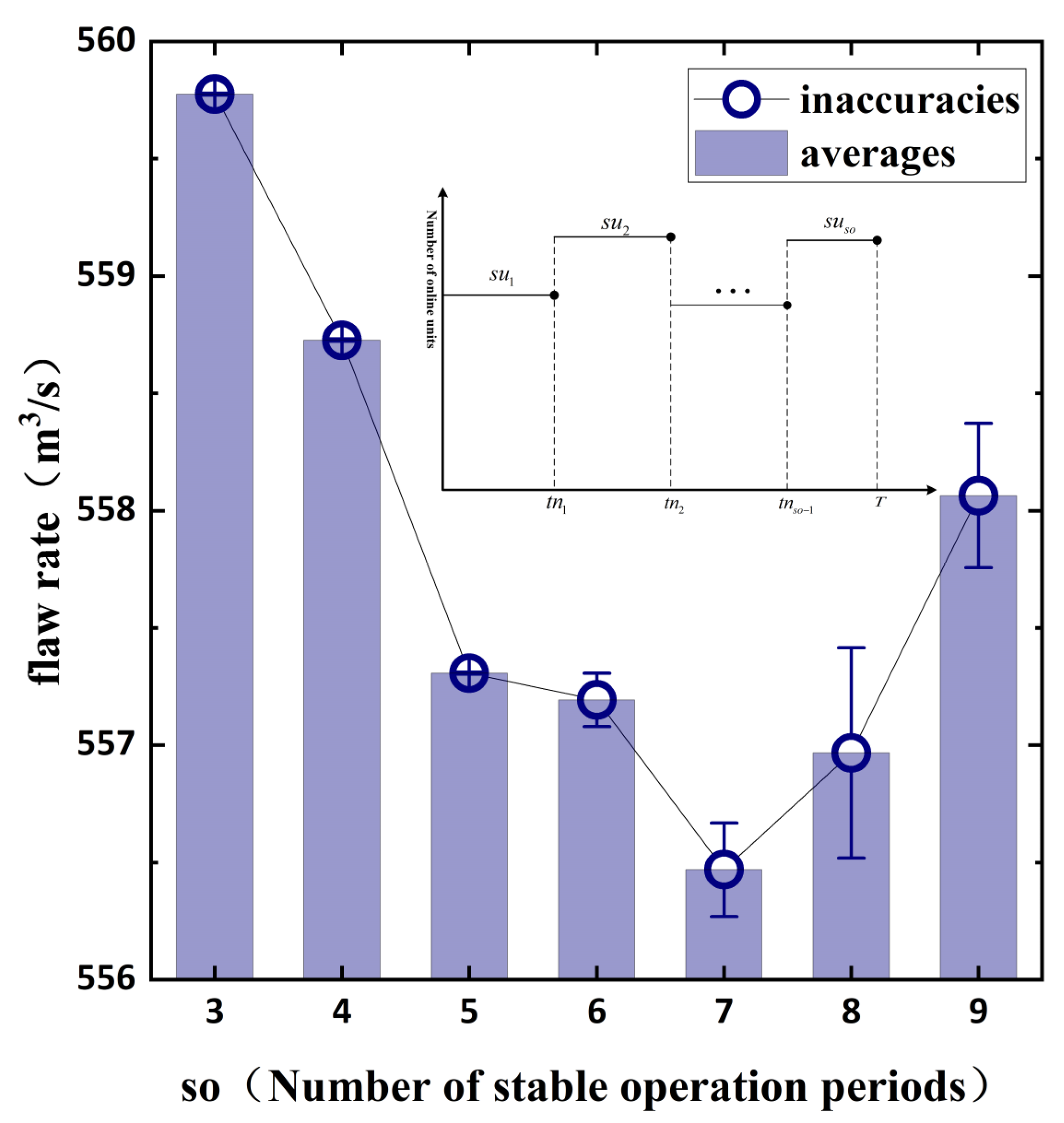
| so | Total number of consecutive periods during the scheduling period in which the number of units in operation remains unchanged |
| tnso | Indicates the time node at which the state of the unit is about to change |
| suso | Indicates the number of online units for each stabilization period. |
| total output | |
| frph(pd,t,ht) | Generation water consumption flow rate of unit j when net load is pd,t and net head is ht |
References
- Zhou, X.; Chen, S.; Lu, Z.; Huang, Y.; Ma, S.; Zhao, Q. Technology Features of the New Generation Power System in China. Proc. CSEE 2018, 38, 1893–1904. [Google Scholar]
- Kober, T.; Schiffer, H.W.; Densing, M.; Panos, E. Global energy perspectives to 2060—WEC’s World Energy Scenarios 2019. Energy Strategy Rev. 2020, 31, 100523. [Google Scholar] [CrossRef]
- Wang, D.D.; Sueyoshi, T. Climate change mitigation targets set by global firms: Overview and implications for renewable energy. Renew. Sustain. Energy Rev. 2018, 94, 386–398. [Google Scholar] [CrossRef]
- Tafuni, A.; Giannotta, A.; Mersch, M.; Pantaleo, A.M.; Amirante, R.; Markides, C.N.; De Palma, P. Thermo-economic analysis of a low-cost greenhouse thermal solar plant with seasonal energy storage. Energy Convers. Manag. 2023, 288, 117123. [Google Scholar] [CrossRef]
- Ma, X.; Zhai, Y.; Zhang, T.; Yao, X.; Hong, J. What changes can solar and wind power bring to the electrification of China compared with coal electricity: From a cost-oriented life cycle impact perspective. Energy Convers. Manag. 2023, 289, 117162. [Google Scholar] [CrossRef]
- Guo, Y.; Ming, B.; Huang, Q.; Wang, Y.; Zheng, X.; Zhang, W. Risk-averse day-ahead generation scheduling of hydro–wind–photovoltaic complementary systems considering the steady requirement of power delivery. Appl. Energy 2022, 309, 118467. [Google Scholar] [CrossRef]
- Tian, C.C. Function Remolding of Hydropower Systems for Carbon Neutral and Its Key Problems. Autom. Electr. Power Syst. 2021, 45, 29–36. [Google Scholar]
- Nematollahi, O.; Hoghooghi, H.; Rasti, M.; Sedaghat, A. Energy demands and renewable energy resources in the Middle East. Renew. Sustain. Energy Rev. 2016, 54, 1172–1181. [Google Scholar] [CrossRef]
- Luo, S.; Hu, W.; Huang, Q.; Han, X.; Chen, Z. Optimization of Photovoltaic/Small Hydropower/Pumped Storage Power Station System Sizing under the Market Mechanism. Trans. China Electrotech. Soc. 2020, 35, 2792. [Google Scholar]
- Braff, W.A.; Mueller, J.M.; Trancik, J.E. Value of storage technologies for wind and solar energy. Nat. Clim. Chang. 2016, 6, 964–969. [Google Scholar] [CrossRef]
- Guo, S.; Liu, Q.; Sun, J.; Jin, H. A review on the utilization of hybrid renewable energy. Renew. Sustain. Energy Rev. 2018, 91, 1121–1147. [Google Scholar] [CrossRef]
- Yanmei, Z.; Shijun, C.; Guangwen, M.; Xiaoyan, H.; Liang, W. Short-Term Complementary Operation of Hydro-Photovoltaic Integrated System Considering Power Generation and Output Fluctuation. Trans. China Electrotech. Soc. 2020, 35, 2769–2779. [Google Scholar]
- Ashok, S. Optimised model for community-based hybrid energy system. Renew. Energy 2007, 32, 1155–1164. [Google Scholar] [CrossRef]
- Zou, S.; Zhang, N.; Wei, B. A capacity optimization and scheduling scheme of a multi-energy complementary power station considering energy trading. Front. Energy Res. 2023, 11, 1194139. [Google Scholar] [CrossRef]
- Wang, S.; Jia, R.; Shi, X.; An, Y.; Huang, Q.; Guo, P.; Luo, C. Hybrid Time-Scale Optimal Scheduling Considering Multi-Energy Complementary Characteristic. IEEE Access 2021, 9, 94087–94098. [Google Scholar] [CrossRef]
- Li, J.; Luo, G.; Li, T.; Gao, L.; Liang, X.; Hu, J.; Cao, Y.; Qi, L.; Liu, X.; Huo, M. Impact on traditional hydropower under a multi-energy complementary operation scheme: An illustrative case of a ‘wind–photovoltaic–cascaded hydropower plants’ system. Energy Strategy Rev. 2023, 49, 101181. [Google Scholar] [CrossRef]
- Li, H.; Liu, P.; Guo, S.; Ming, B.; Cheng, L.; Yang, Z. Long-term complementary operation of a large-scale hydro-photovoltaic hybrid power plant using explicit stochastic optimization. Appl. Energy 2019, 238, 863–875. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, J.; Liu, G.; Mo, L.; Wang, Y.; Jia, B.; He, F. Multi-plan formulation of hydropower generation considering uncertainty of wind power. Appl. Energy 2020, 260, 114239. [Google Scholar] [CrossRef]
- Zhu, F.; Zhong, P.; Xu, B.; Liu, W.; Wang, W.; Sun, Y.; Chen, J.; Li, J. Short-term stochastic optimization of a hydro-wind-photovoltaic hybrid system under multiple uncertainties. Energy Convers. Manag. 2020, 214, 112902. [Google Scholar] [CrossRef]
- Shayan, M.E.; Najafi, G.; Ghobadian, B.; Gorjian, S.; Mazlan, M. A novel approach of synchronization of the sustainable grid with an intelligent local hybrid renewable energy control. Int. J. Energy Environ. Eng. 2023, 14, 35–46. [Google Scholar] [CrossRef]
- Shayan, M.E.; Najafi, G.; Ghobadian, B.; Gorjian, S.; Mamat, R.; Ghazali, M.F. Multi-microgrid optimization and energy management under boost voltage converter with Markov prediction chain and dynamic decision algorithm. Renew. Energy 2022, 201, 179–189. [Google Scholar] [CrossRef]
- Shou-ren, Z. Development and utilization of hydropower resources in China: Opportunity and challenges. J. Hydraul. Eng. 2007, 1, 9350. [Google Scholar]
- Yi, J.; Labadie, J.W.; Stitt, S. Dynamic Optimal Unit Commitment and Loading in Hydropower Systems. J. Water Res. Plan. Man. 2003, 129, 388–398. [Google Scholar] [CrossRef]
- Anoune, K.; Bouya, M.; Astito, A.; Abdellah, A.B. Sizing methods and optimization techniques for PV-wind based hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2018, 93, 652–673. [Google Scholar] [CrossRef]
- Chen, L.; Ge, L.; Wang, D.; Zhong, W.; Zhan, T.; Deng, A. Multi-objective water-sediment optimal operation of cascade reservoirs in the Yellow River Basin. J. Hydrol. 2022, 609, 127744. [Google Scholar] [CrossRef]
- Yuan, X.; Yu, H.; Liang, J.; Xu, B. A novel density peaks clustering algorithm based on K nearest neighbors with adaptive merging strategy. Int. J. Mach. Learn. Cybern. 2021, 12, 2825–2841. [Google Scholar] [CrossRef]
- Salomon, S.; Avigad, G.; Fleming, P.J.; Purshouse, R.C. Active Robust Optimization: Enhancing Robustness to Uncertain Environments. IEEE Trans. Cybern. 2014, 44, 2221–2231. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.T. Generating robust and flexible job shop schedules using genetic algorithms. IEEE Trans. Evolut. Comput. 2003, 7, 275–288. [Google Scholar] [CrossRef]
- Wiesmann, D.; Hammel, U.; Back, T. Robust design of multilayer optical coatings by means of evolutionary algorithms. IEEE Trans. Evolut. Comput. 1998, 2, 162–167. [Google Scholar] [CrossRef]
- Qiu, H.; Gu, W.; Xu, X.; Pan, G.; Liu, P.; Wu, Z.; Wang, L. A Historical-Correlation-Driven Robust Optimization Approach for Microgrid Dispatch. IEEE Trans. Smart Grid 2021, 12, 1135–1148. [Google Scholar] [CrossRef]
- Mahdi, M.; Xueqian, S.; Gai, Q.; Basirialmahjough, M.; Yuan, H. Improving robustness of water supply system using a multi-objective robust optimization framework. Environ. Res. 2023, 232, 116270. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Guo, T.; Tian, Q.; Nojavan, S. Optimal robust scheduling of energy-water nexus system using robust optimization technique. Comput. Chem. Eng. 2021, 155, 107542. [Google Scholar] [CrossRef]
- Nag, K.; Pal, T.; Mudi, R.K.; Pal, N.R. Robust Multiobjective Optimization with Robust Consensus. IEEE Trans. Fuzzy Syst. 2018, 26, 3743–3754. [Google Scholar] [CrossRef]
- San, L.C.; Fulong, L. Press Conference of the National Energy Administration on the Energy Situation in the First Half of the Year. In Proceedings of the China National Energy Administration Routine Press Conference, Beijing, China, 1 July 2022. [Google Scholar]
- Yousri, D.; Farag, H.E.Z.; Zeineldin, H.; El-Saadany, E.F. Integrated model for optimal energy management and demand response of microgrids considering hybrid hydrogen-battery storage systems. Energy Convers. Manag. 2023, 280, 116809. [Google Scholar] [CrossRef]
- Prasanna, A.; Dorer, V.; Vetterli, N. Optimisation of a district energy system with a low temperature network. Energy 2017, 137, 632–648. [Google Scholar] [CrossRef]
- Brentan, B.M.; Carpitella, S.; Izquierdo, J.; Luvizotto, E.; Meirelles, G. District metered area design through multicriteria and multiobjective optimization. Math. Method Appl. Sci. 2022, 45, 3254–3271. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, G.; Zhou, J.; Dai, R.; Yu, F. Optimal planning strategy for energy internet zones based on interval optimization. Energy Rep. 2020, 6, 1255–1261. [Google Scholar] [CrossRef]
- Zhang, Y.; Lian, J.; Ma, C.; Yang, Y.; Pang, X.; Wang, L. Optimal sizing of the grid-connected hybrid system integrating hydropower, photovoltaic, and wind considering cascade reservoir connection and photovoltaic-wind complementarity. J. Clean. Prod. 2020, 274, 123100. [Google Scholar] [CrossRef]
- Ming, B.; Liu, P.; Guo, S.; Zhang, X.; Feng, M.; Wang, X. Optimizing utility-scale photovoltaic power generation for integration into a hydropower reservoir by incorporating long- and short-term operational decisions. Appl. Energy 2017, 204, 432–445. [Google Scholar] [CrossRef]
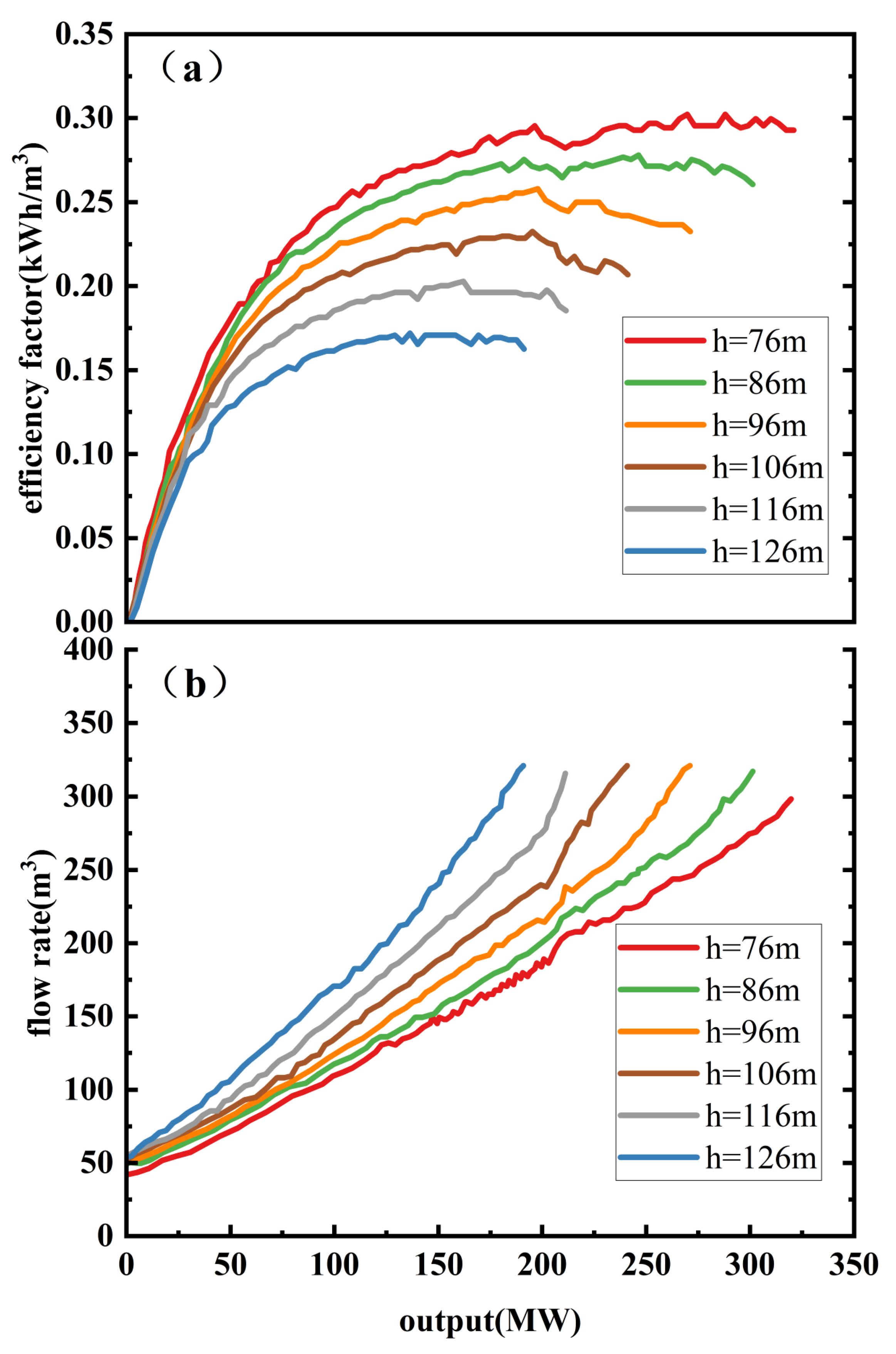
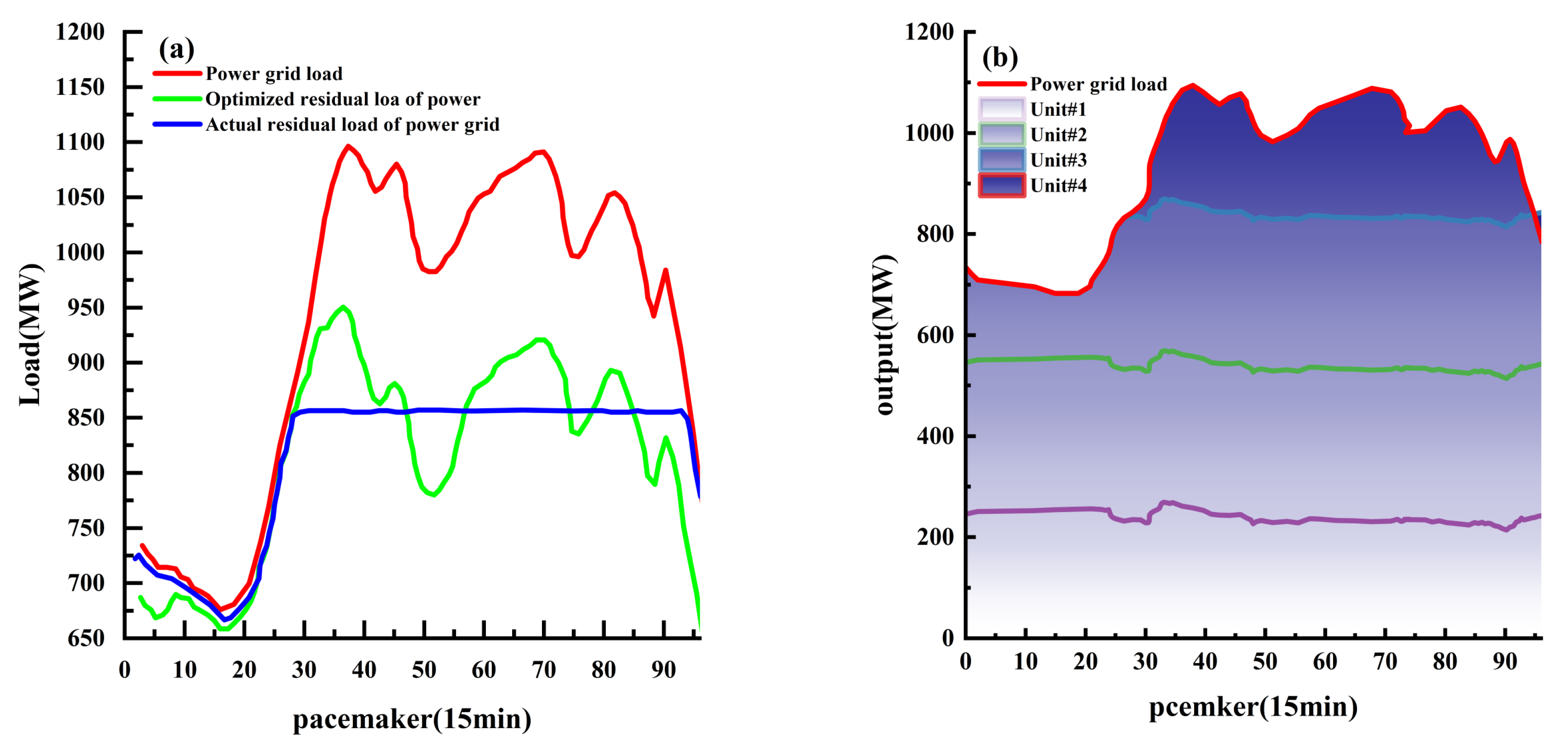
| Power Plant | Regulating Capacity | Installed Capacity (MW) | Normal/Dead Water Level (m) | Maxi/Min Discharge (m3/s) | Max/Min Head (m) | Unit Vibration Limit (MW) |
|---|---|---|---|---|---|---|
| power plants | year | 300 × 4 | 200/161.2 | 340 × 4/0 | 121.5/80.7 | (0–30) U (80, 180) |
| Parameter Category | Symbol | Value | Unit |
|---|---|---|---|
| Min. start-up time | 1 | [h] | |
| Min. stopping time | 1 | [h] | |
| Climbing speed of output | 10 | [MW/s] | |
| Spinning reserve | 80 | [MW] | |
| Vibration zone upper limit | 30.180 | [MW] | |
| The lower limit of the vibration zone | 0.80 | [MW] | |
| The upper limit of unit output | 0 | [MW] | |
| The lower limit of the unit | 300 | [MW] |
| Statistical Counts | Deterministic Optimization | Stochastic Optimization |
|---|---|---|
| 1 | 572.6 | 574.1 |
| 2 | 572.7 | 574.6 |
| 3 | 572.6 | 574.1 |
| 4 | 573.1 | 574.6 |
| 5 | 572.5 | 574.5 |
| 6 | 572.4 | 574.7 |
| 7 | 572.1 | 574.2 |
| 8 | 572.8 | 574.9 |
| 9 | 573.4 | 573.3 |
| 10 | 573.8 | 574.9 |
| 11 | 573.4 | 574.4 |
| 12 | 573.8 | 575.0 |
| 13 | 572.6 | 573.1 |
| 14 | 573.2 | 574.1 |
| 15 | 572.9 | 574.6 |
| 16 | 573.0 | 573.1 |
| 17 | 572.4 | 573.3 |
| 18 | 572.5 | 574.0 |
| 19 | 572.8 | 574.3 |
| 20 | 572.3 | 574.7 |
| average | 572.8 | 574.2 |
| statistics | 0.5 | 0.6 |
| average ± statistics | 572.8 ± 0.5 | 574.2 ± 0.6 |
| Evaluation Metrics | Historical Scheduling (Simulation) | Deterministic Optimization Scheduling | Stochastic Optimization Scheduling |
|---|---|---|---|
| Total water consumption (100,000 m3) | 49.49 | 48.65 | 48.86 |
| Probability of non-vibration zone operation (%) | 91.2 | 100 | 100 |
| Load standby fulfillment probability (%) | 83.6 | 100 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Luo, Z.; Luo, N.; Zhang, X.; Chao, H.; Dai, L. Optimizing Water-Light Complementary Systems for the Complex Terrain of the Southwestern China Plateau Region: A Two-Layer Model Approach. Sustainability 2024, 16, 292. https://doi.org/10.3390/su16010292
Hu Z, Luo Z, Luo N, Zhang X, Chao H, Dai L. Optimizing Water-Light Complementary Systems for the Complex Terrain of the Southwestern China Plateau Region: A Two-Layer Model Approach. Sustainability. 2024; 16(1):292. https://doi.org/10.3390/su16010292
Chicago/Turabian StyleHu, Zhikai, Zhumei Luo, Na Luo, Xiaoxv Zhang, Haocheng Chao, and Linsheng Dai. 2024. "Optimizing Water-Light Complementary Systems for the Complex Terrain of the Southwestern China Plateau Region: A Two-Layer Model Approach" Sustainability 16, no. 1: 292. https://doi.org/10.3390/su16010292
APA StyleHu, Z., Luo, Z., Luo, N., Zhang, X., Chao, H., & Dai, L. (2024). Optimizing Water-Light Complementary Systems for the Complex Terrain of the Southwestern China Plateau Region: A Two-Layer Model Approach. Sustainability, 16(1), 292. https://doi.org/10.3390/su16010292







