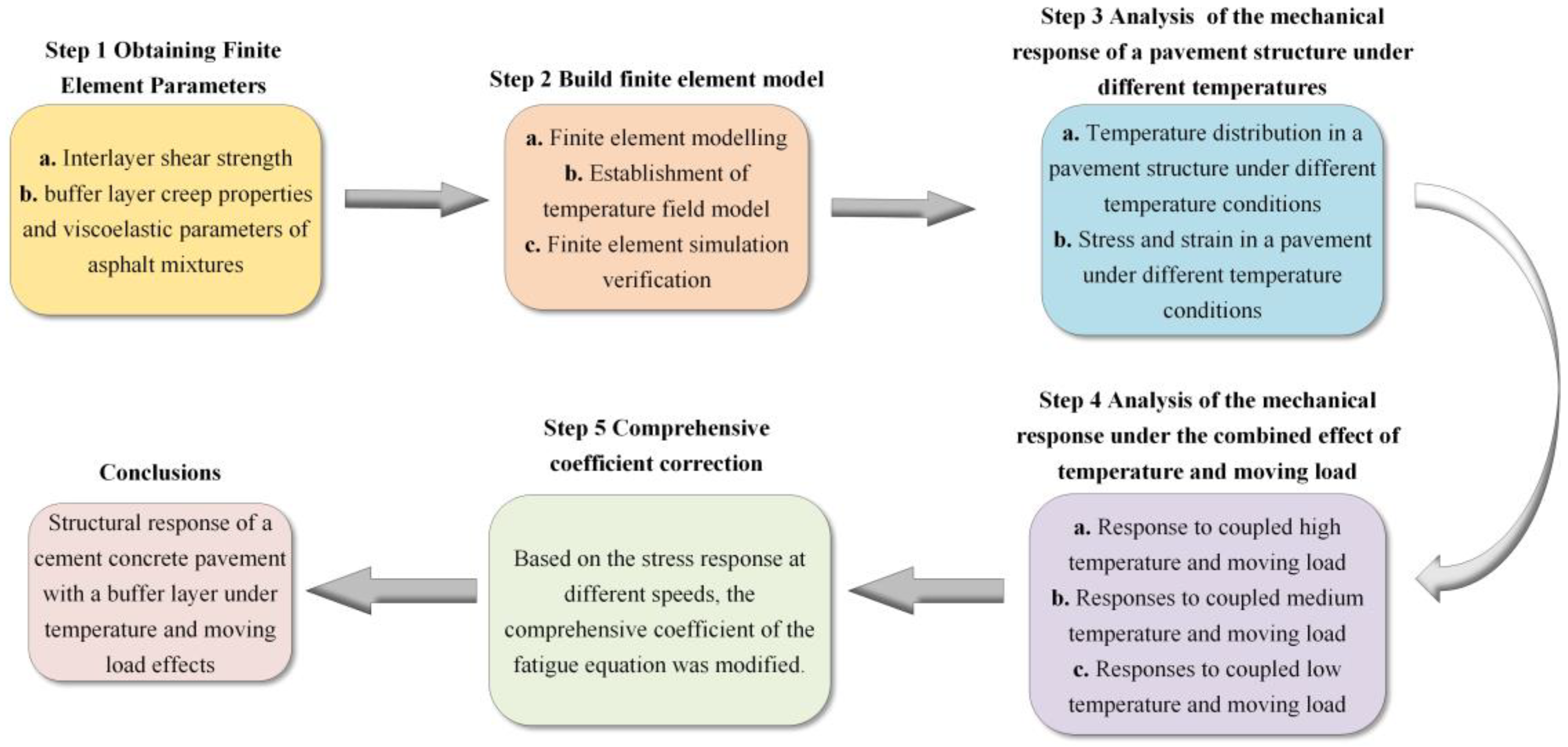
Figure 1.
Flowchart of the research.
Figure 1.
Flowchart of the research.
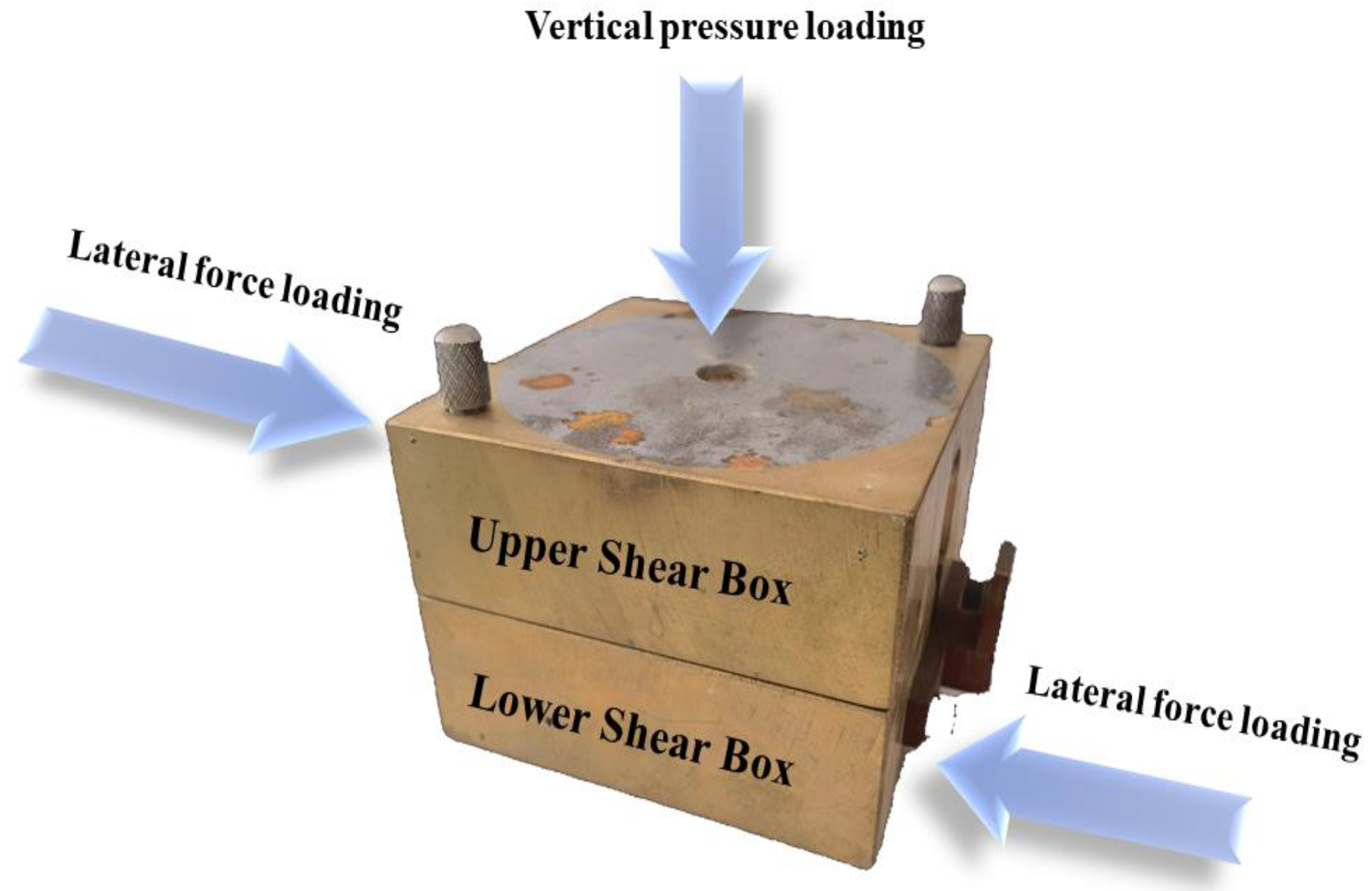
Figure 3.
Shearing principle diagram.
Figure 3.
Shearing principle diagram.
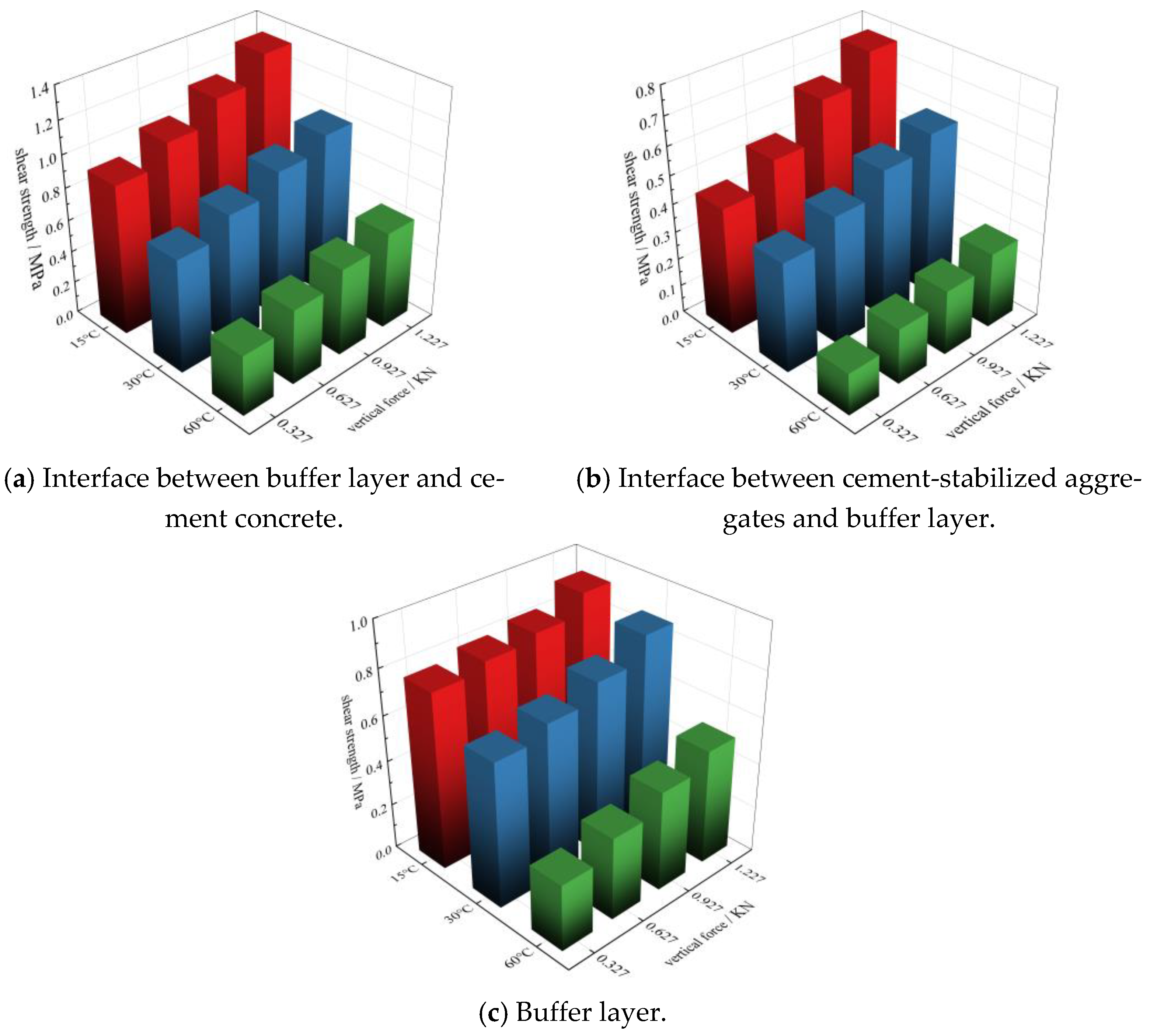
Figure 4.
Shear strength.
Figure 4.
Shear strength.
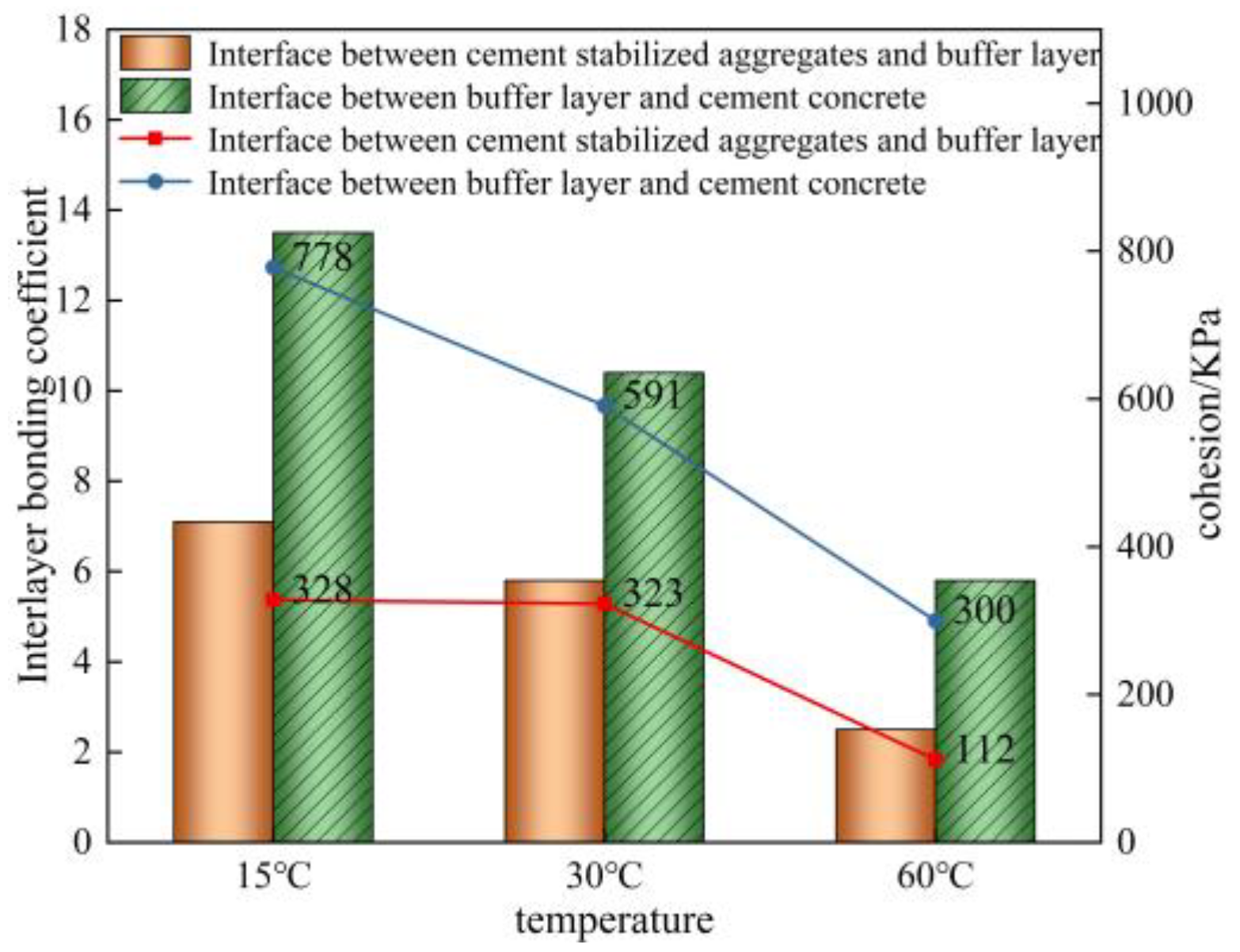
Figure 5.
Interlayer bonding coefficient and cohesion.
Figure 5.
Interlayer bonding coefficient and cohesion.
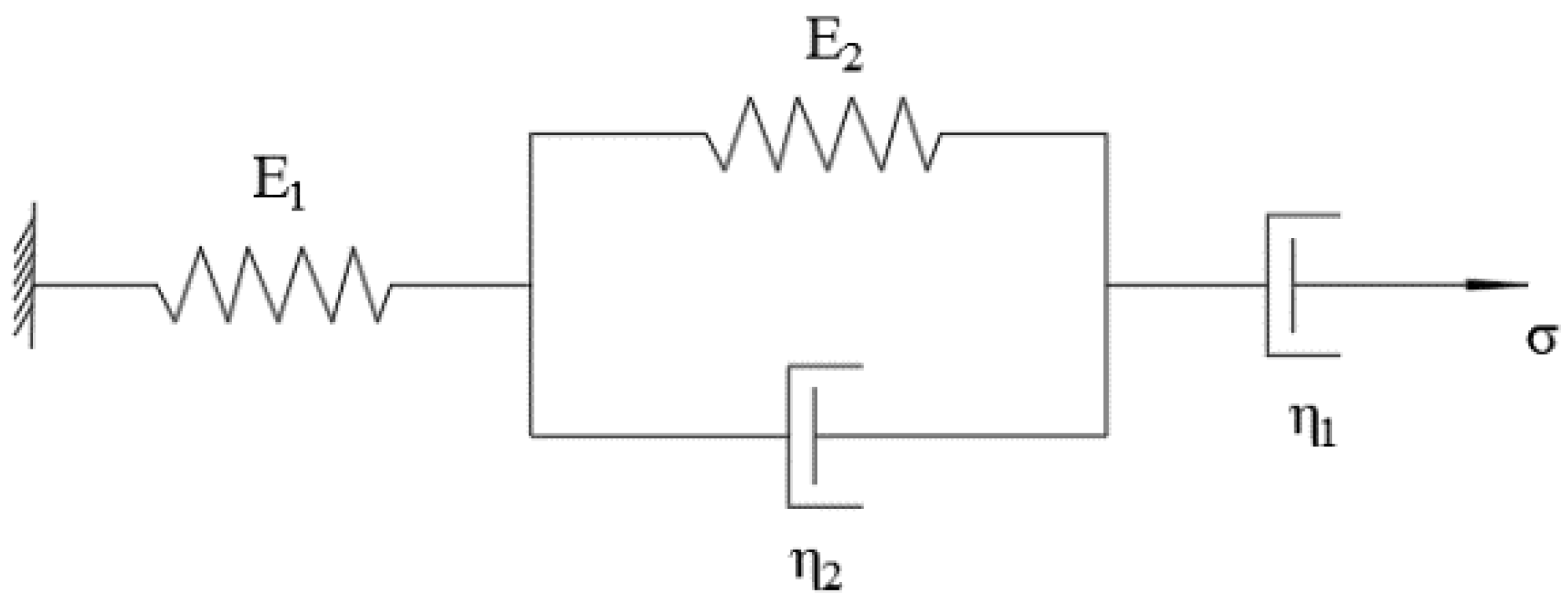
Figure 6.
Uniaxial dynamic creep test.
Figure 6.
Uniaxial dynamic creep test.
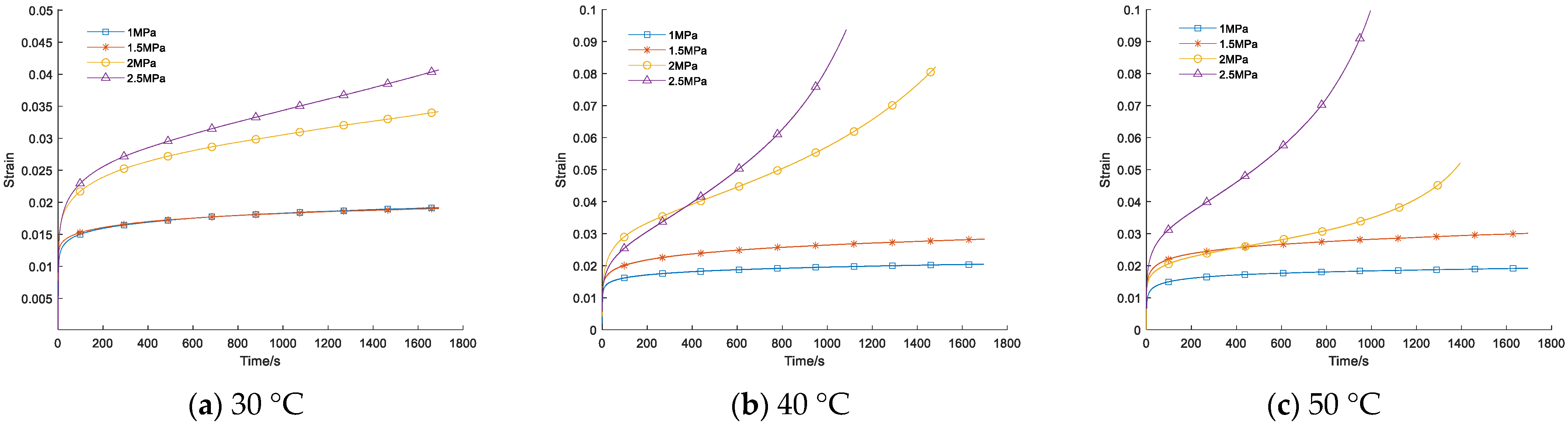
Figure 7.
Dynamic creep test results.
Figure 7.
Dynamic creep test results.
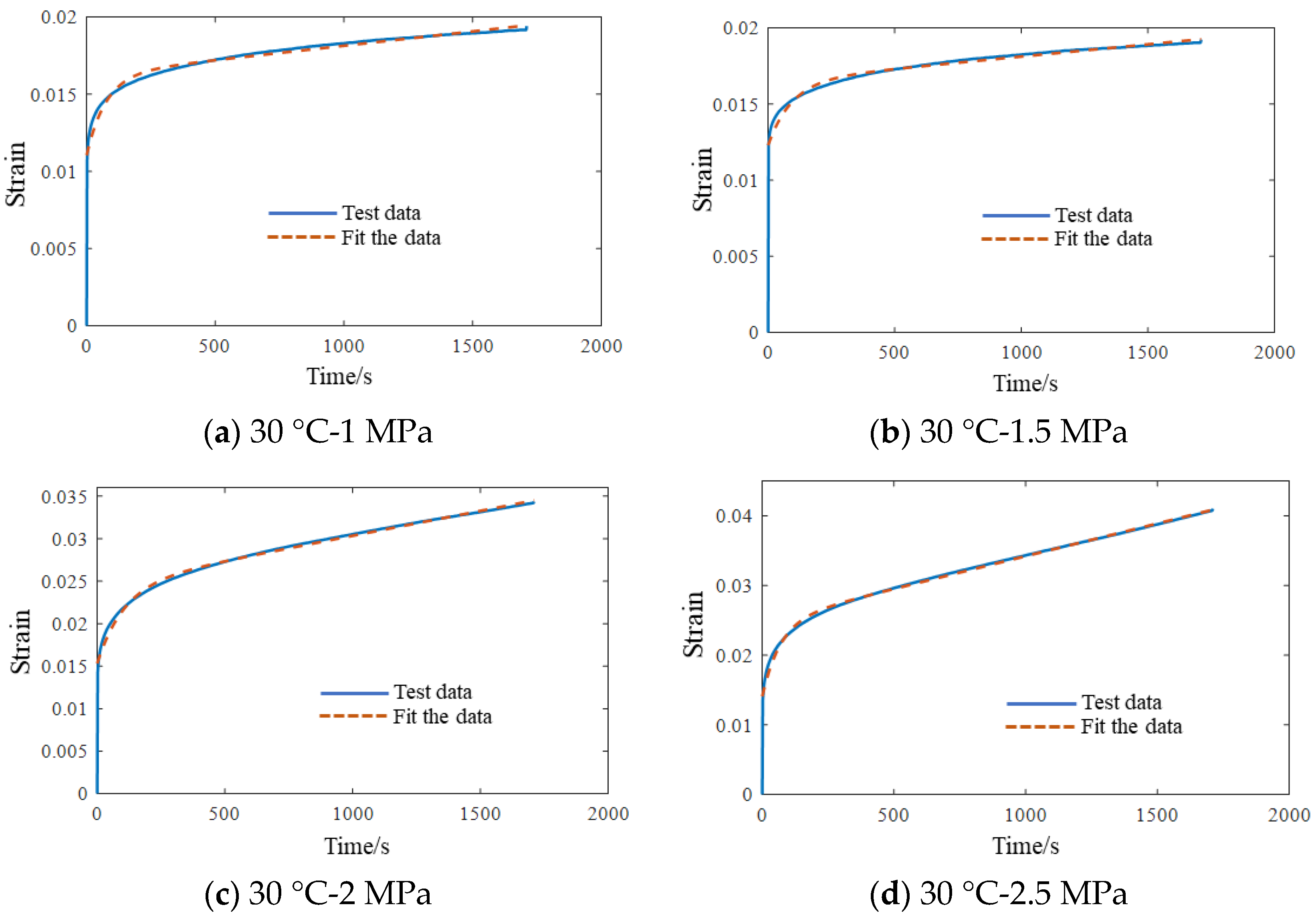
Figure 9.
Comparison of experimental data and fitting curve.
Figure 9.
Comparison of experimental data and fitting curve.
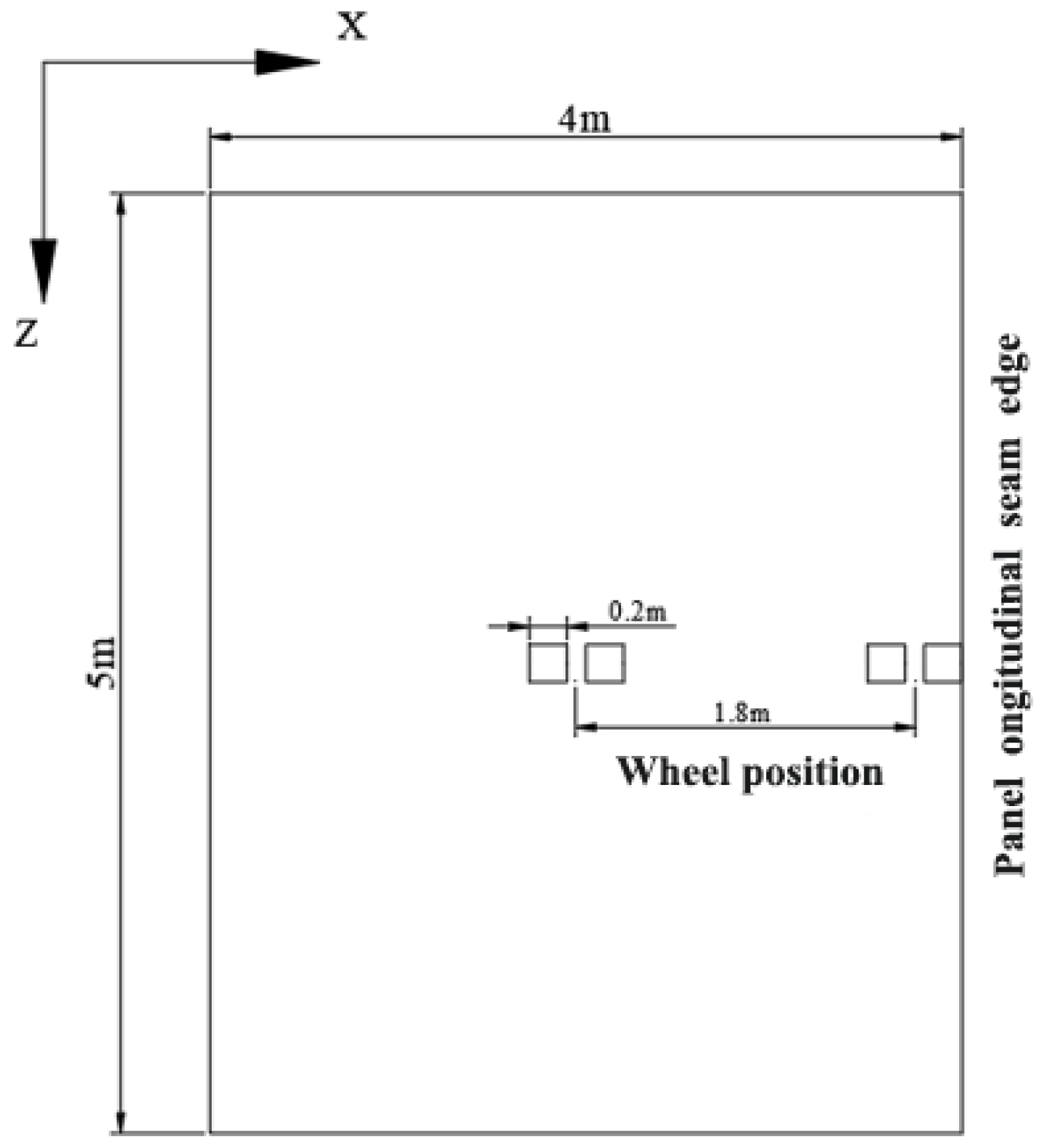
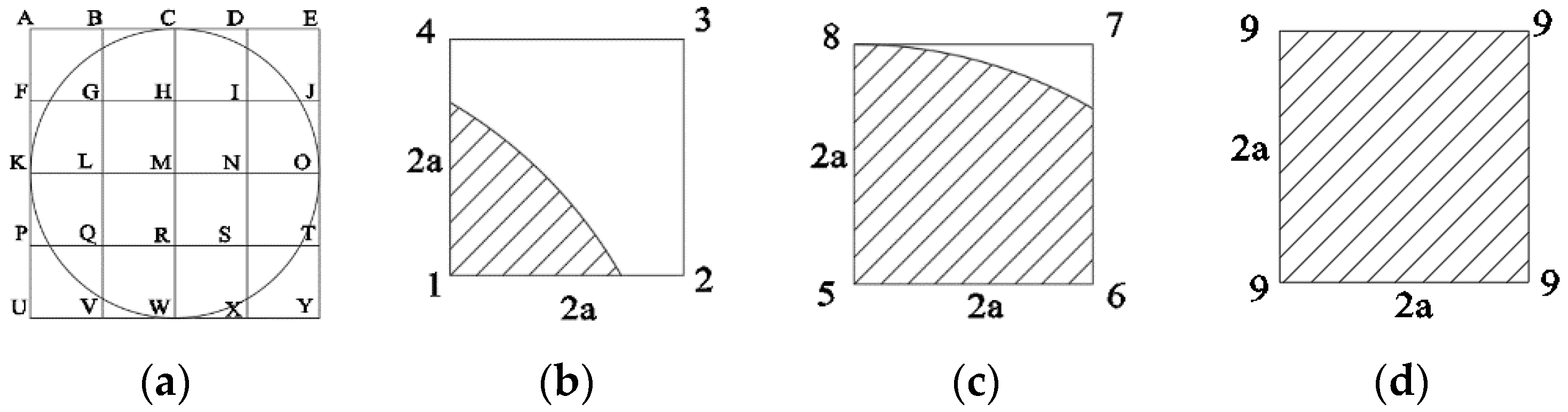
Figure 10.
Load location schematic.
Figure 10.
Load location schematic.
Figure 11.
Equivalent nodal force calculation schematic.
Figure 11.
Equivalent nodal force calculation schematic.
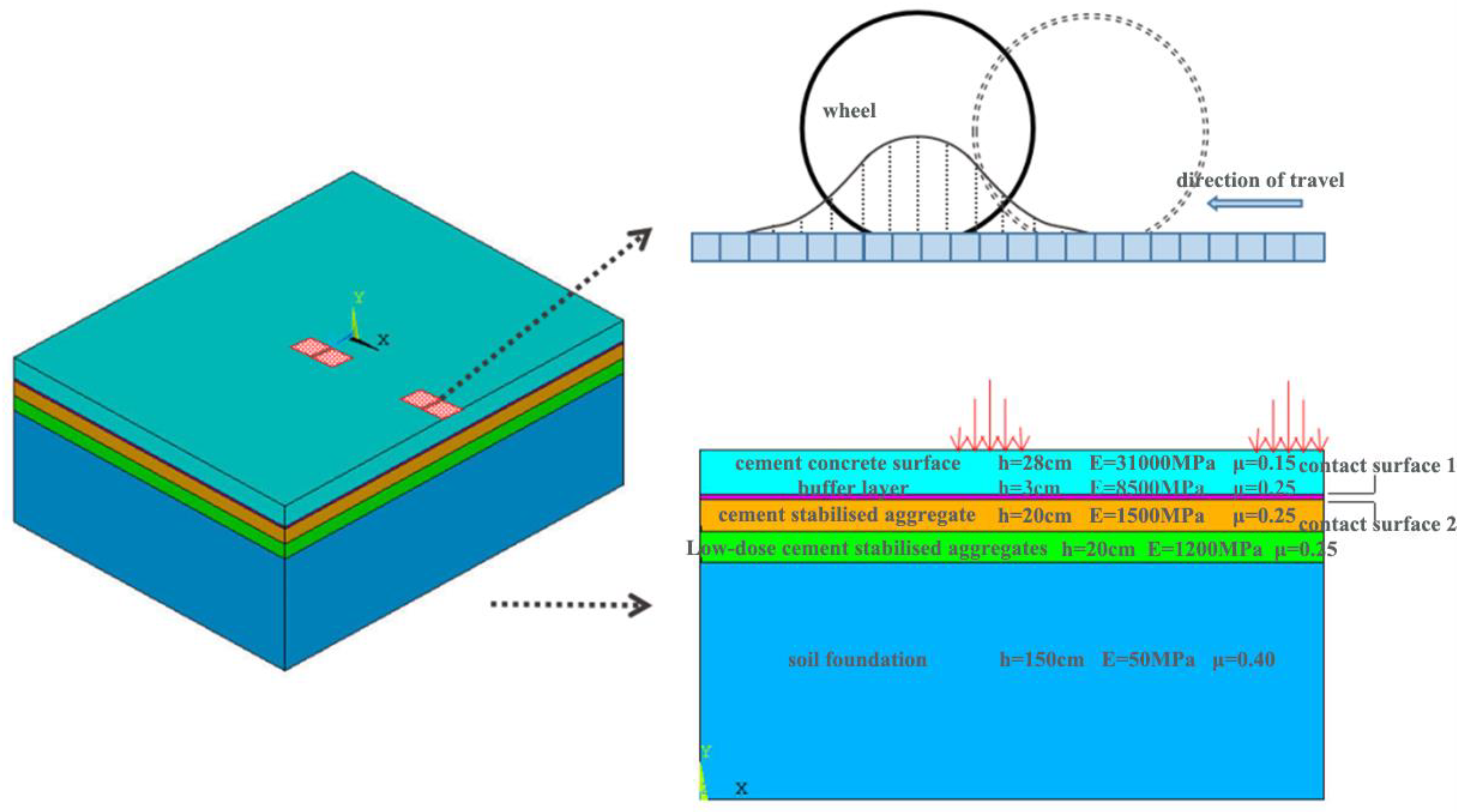
Figure 12.
Finite-element modelling and load forms.
Figure 12.
Finite-element modelling and load forms.
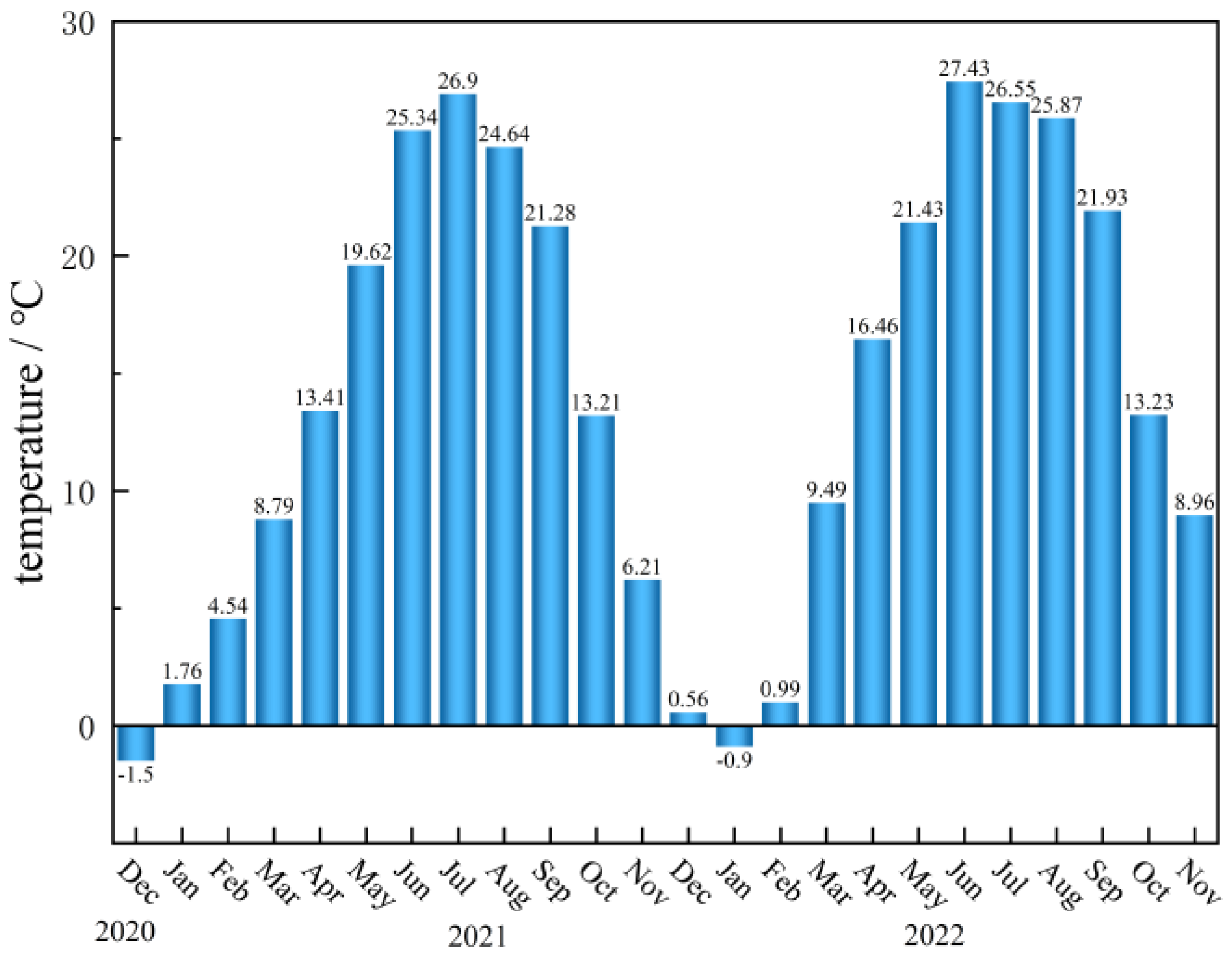
Figure 13.
Average near-surface temperature from December 2020 to November 2022.
Figure 13.
Average near-surface temperature from December 2020 to November 2022.
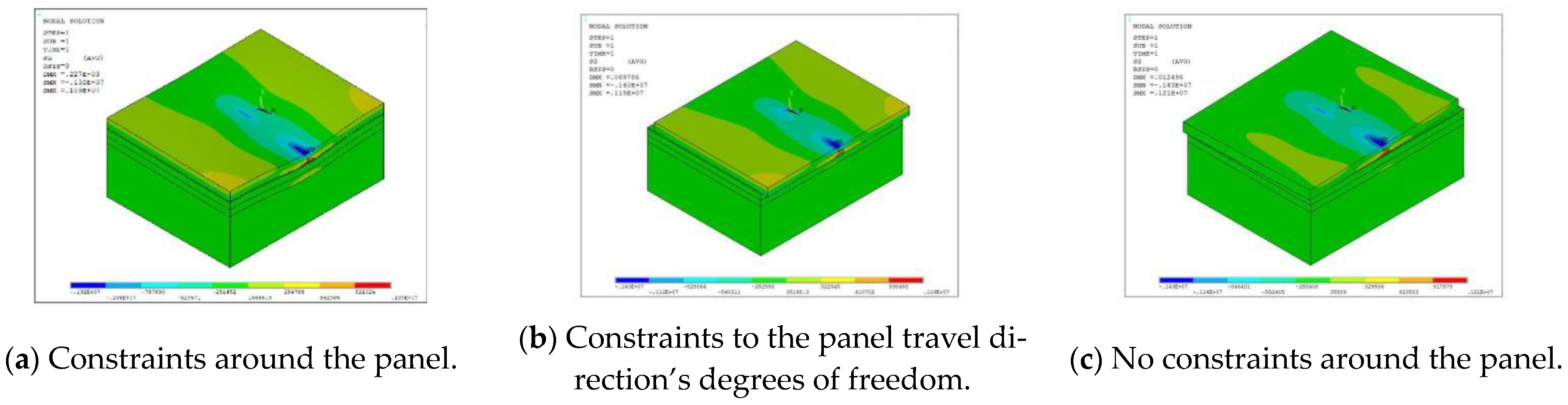
Figure 14.
Stress-distribution diagram under three kinds of panel constraints.
Figure 14.
Stress-distribution diagram under three kinds of panel constraints.
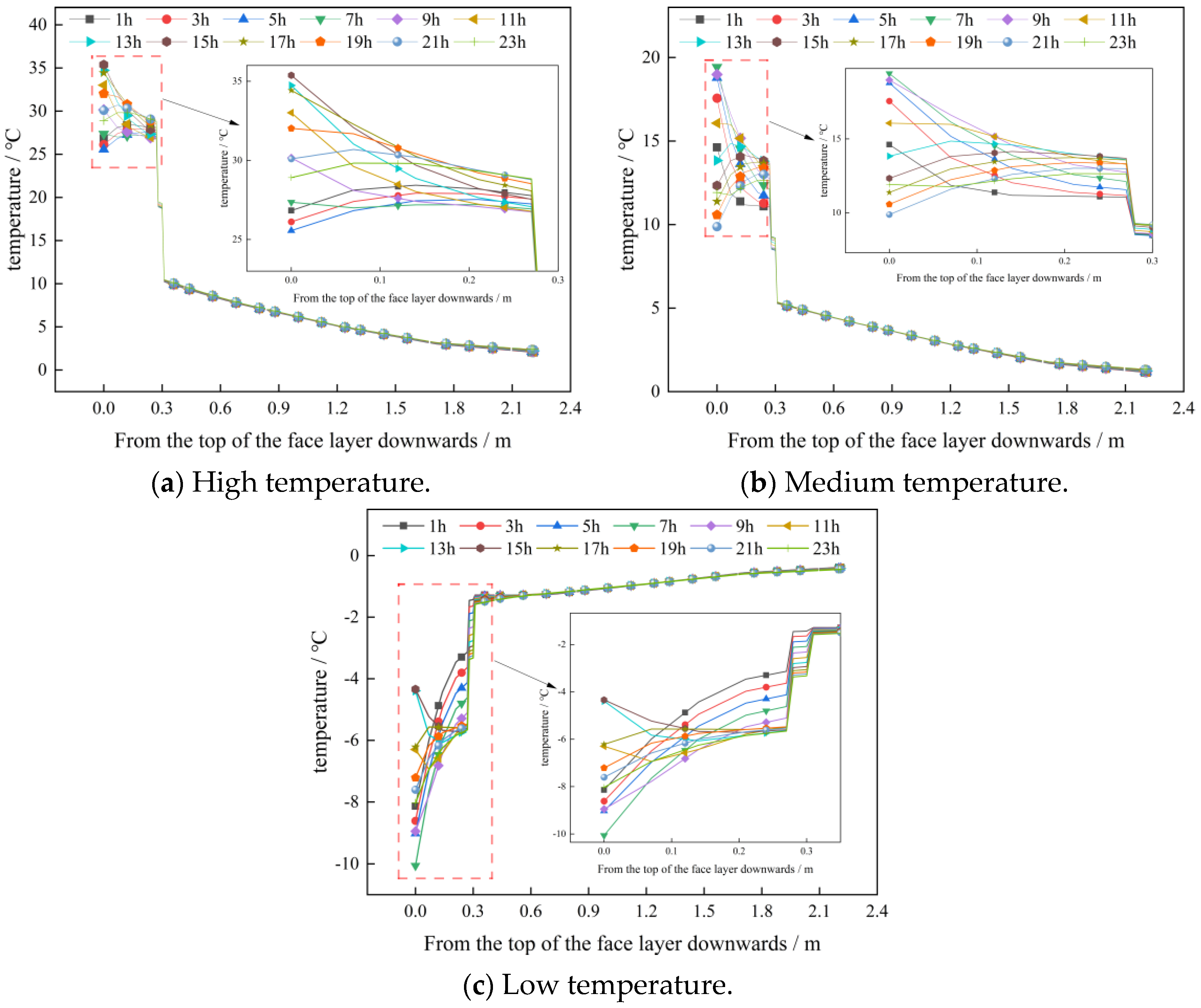
Figure 15.
Temperature change curve of pavement structure.
Figure 15.
Temperature change curve of pavement structure.
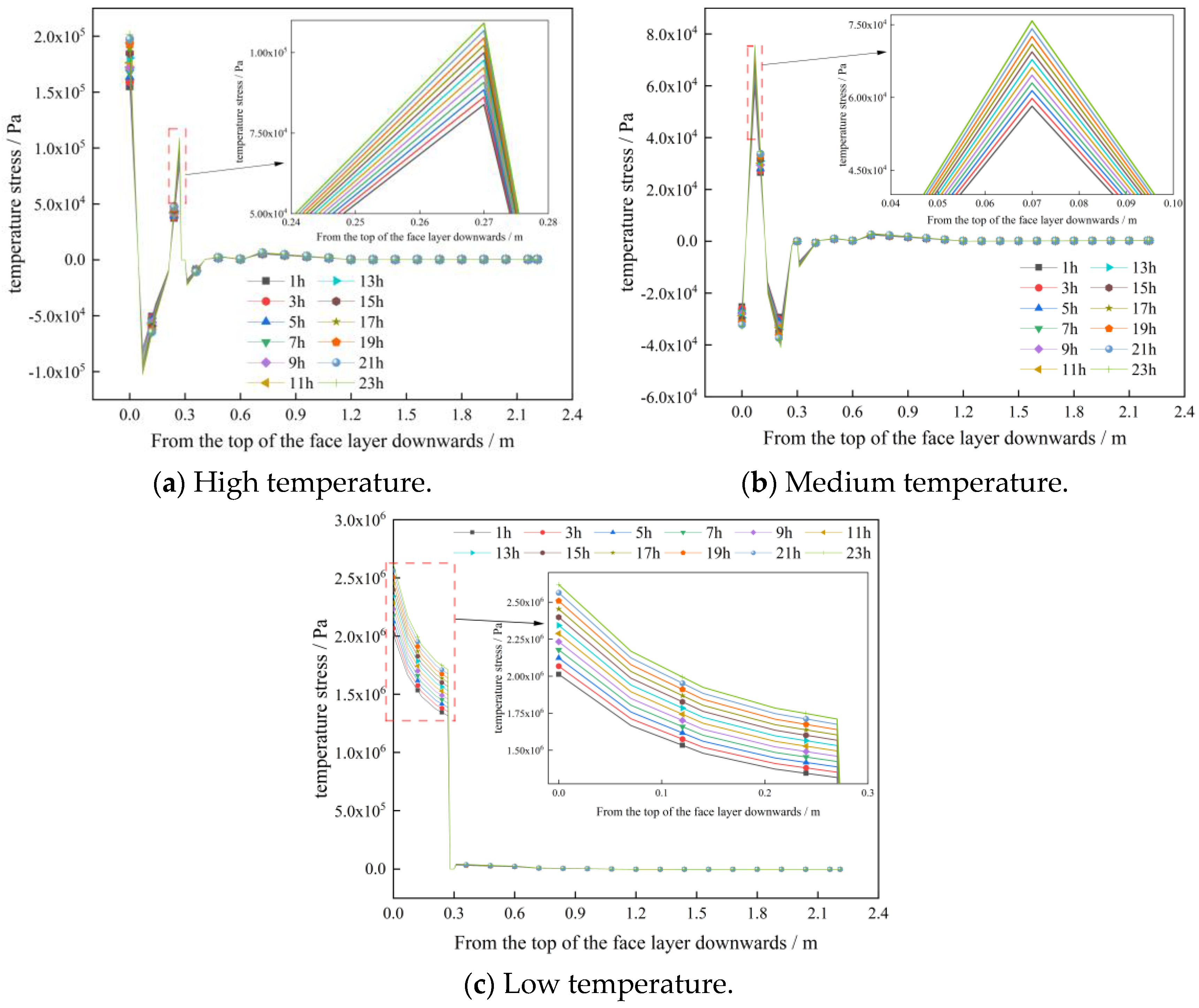
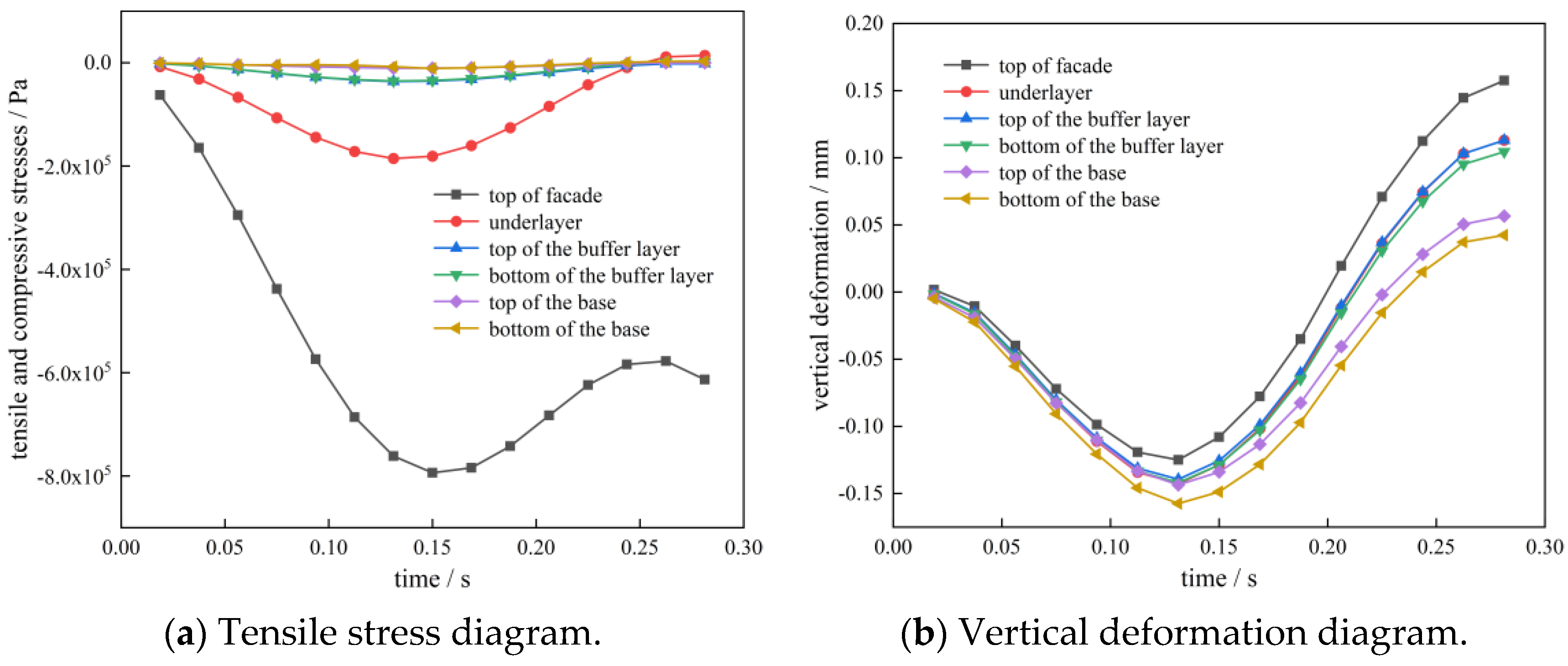
Figure 16.
Stress variation curve of pavement structure.
Figure 16.
Stress variation curve of pavement structure.
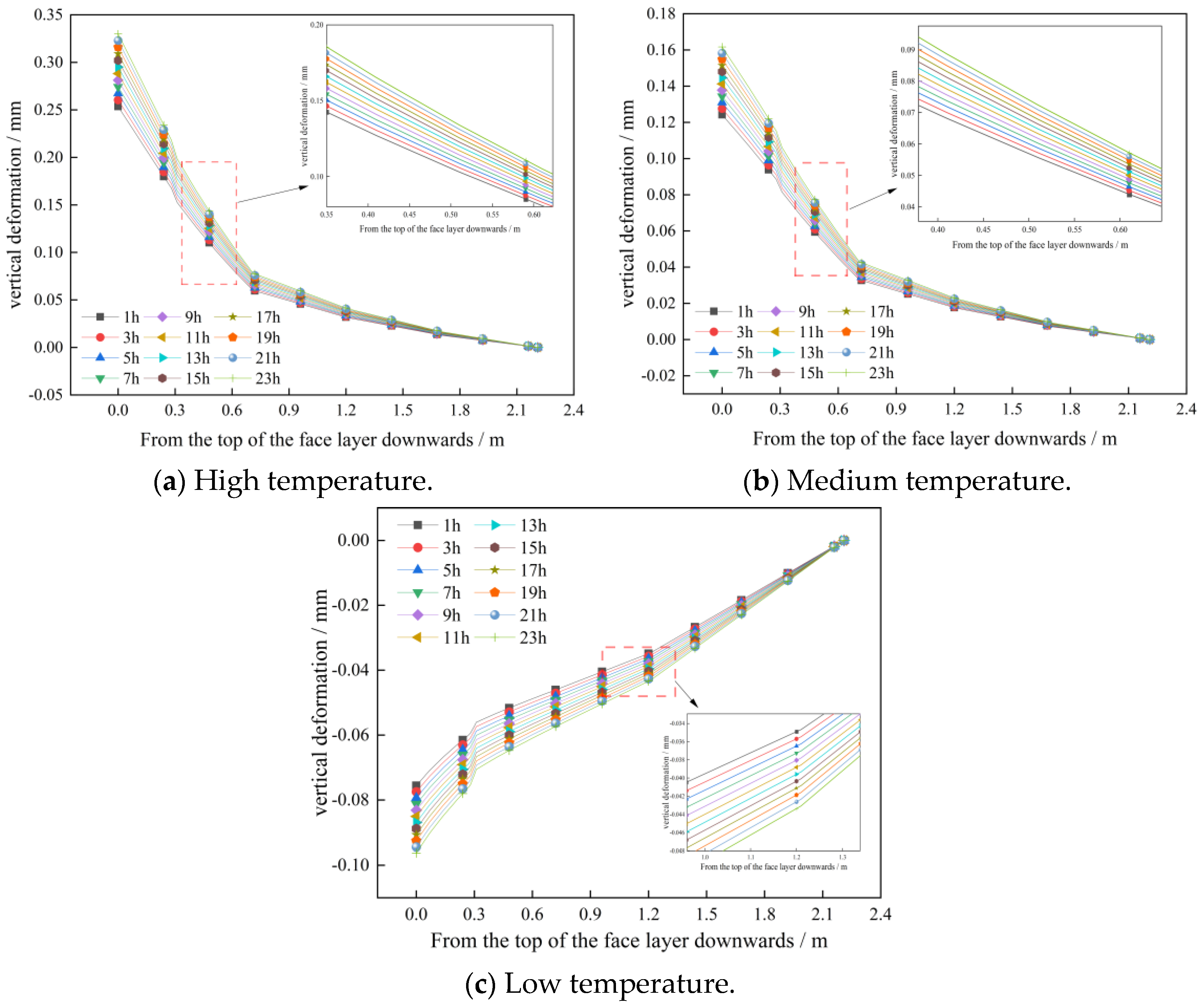
Figure 17.
Strain change curve for the pavement structure.
Figure 17.
Strain change curve for the pavement structure.
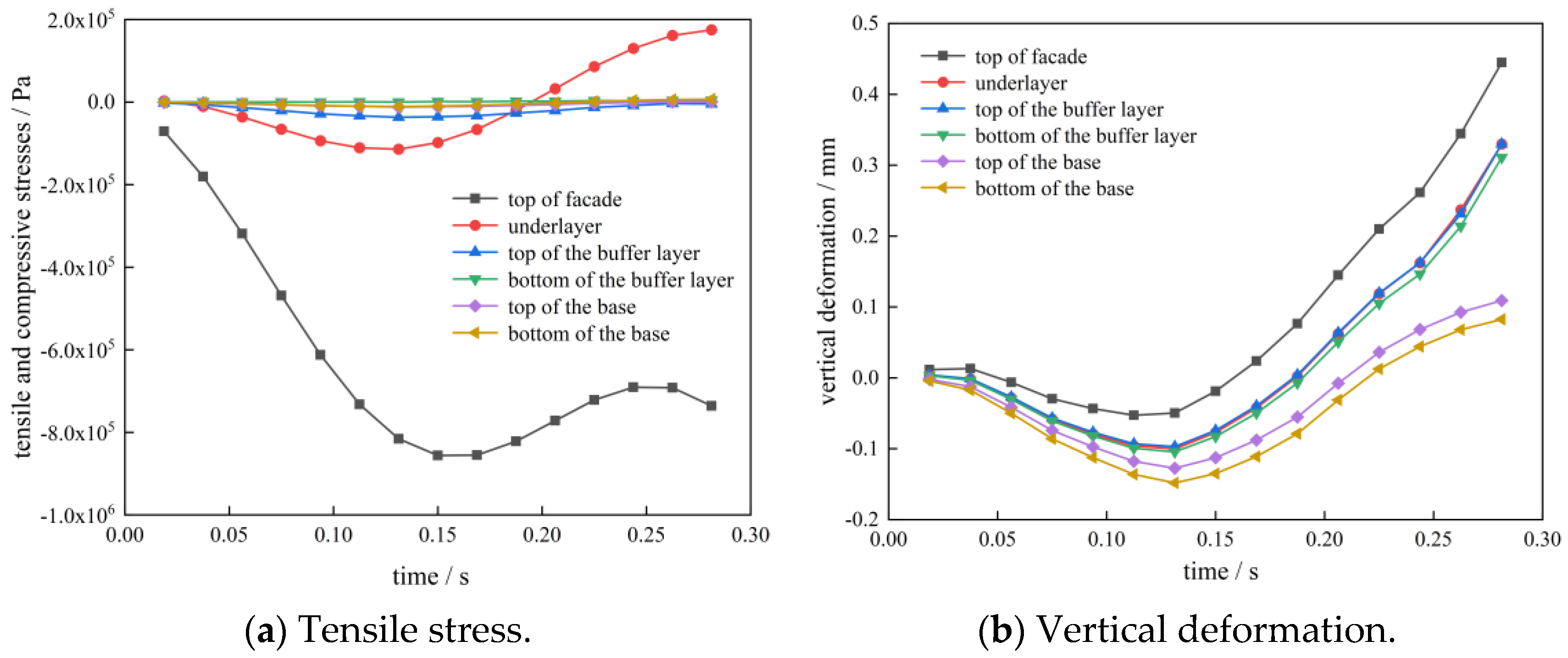
Figure 18.
Stress–strain curves under high temperature coupled with moving loads.
Figure 18.
Stress–strain curves under high temperature coupled with moving loads.
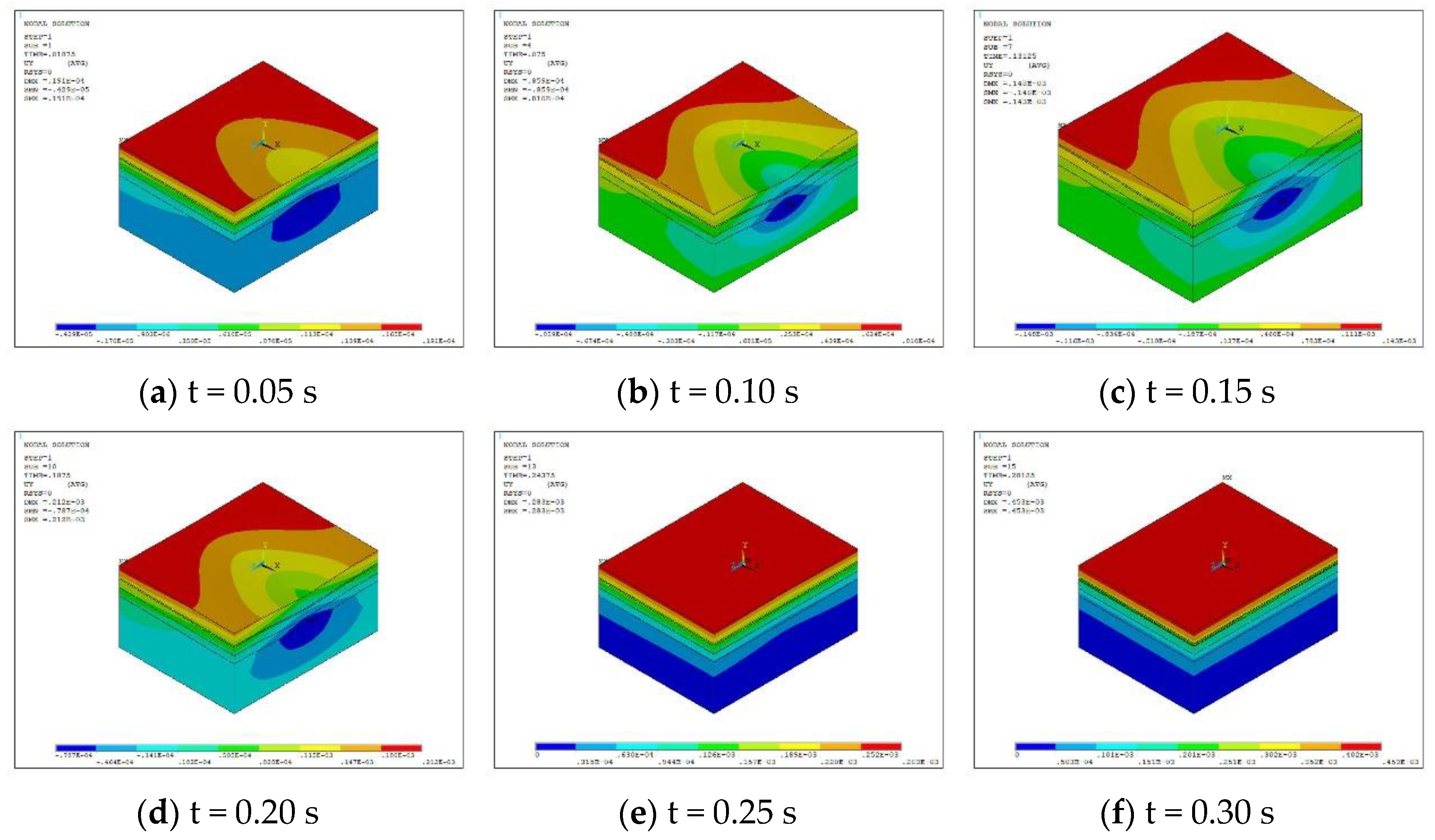
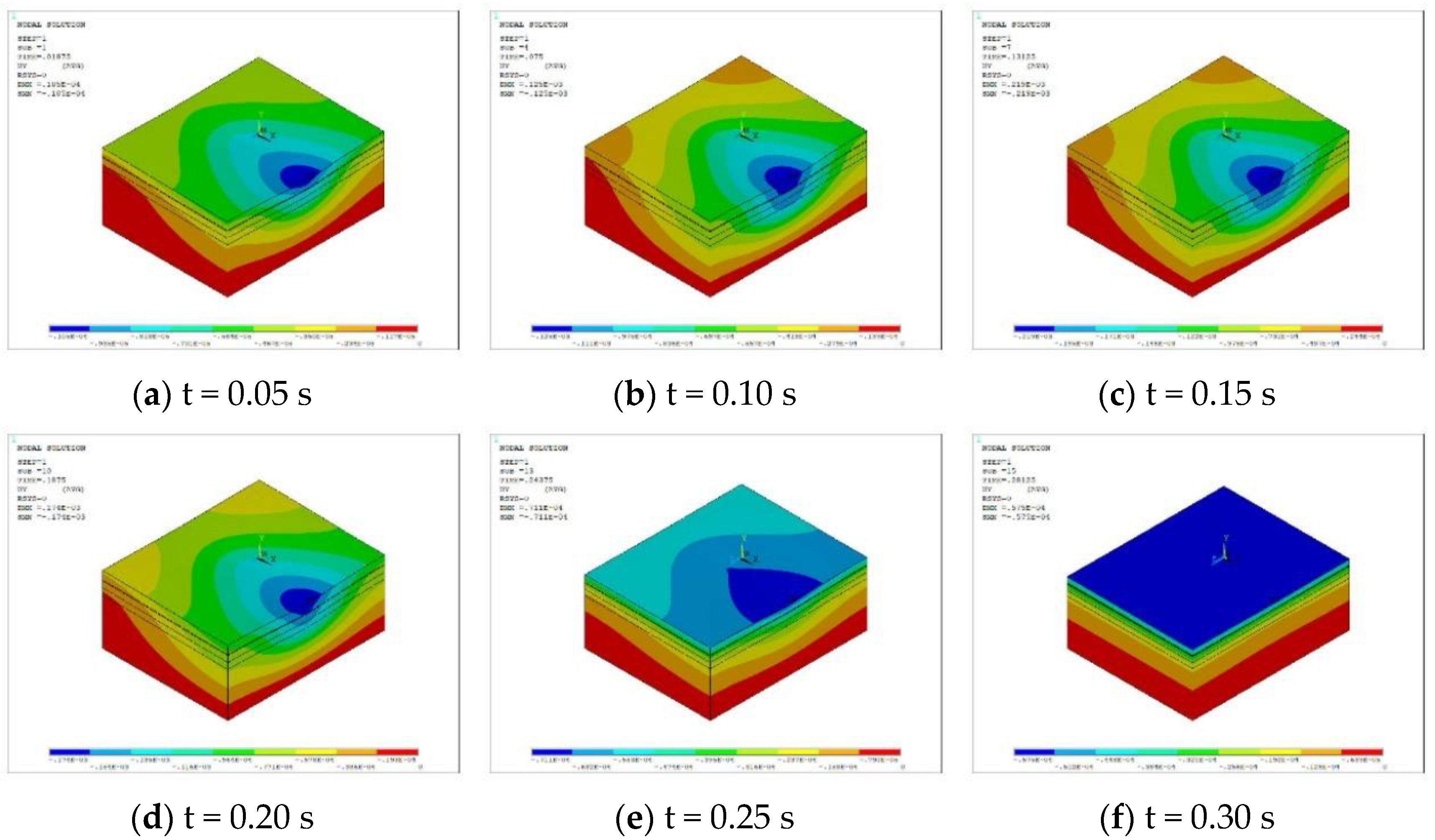
Figure 19.
Deformation cloud diagram under the coupling of high temperature and moving load.
Figure 19.
Deformation cloud diagram under the coupling of high temperature and moving load.
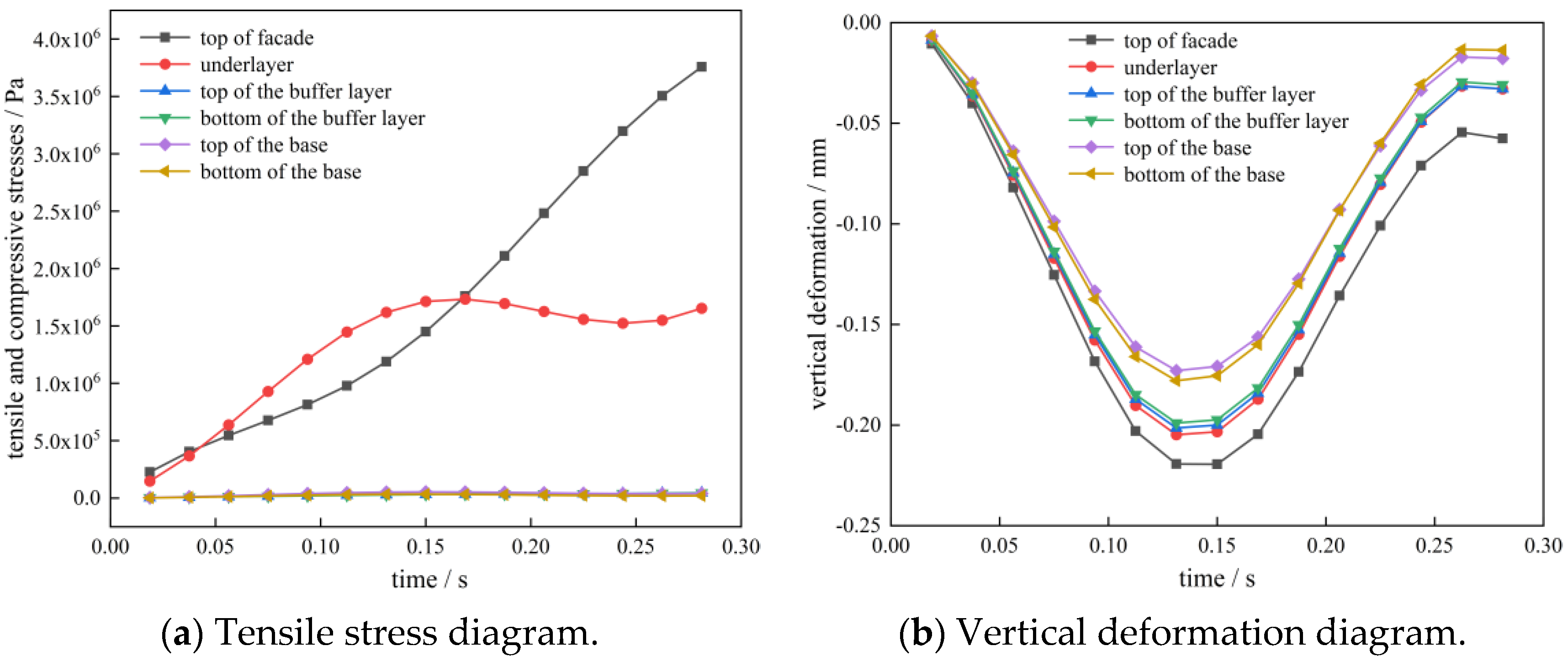
Figure 20.
Stress–strain curves of medium temperature with moving loads.
Figure 20.
Stress–strain curves of medium temperature with moving loads.
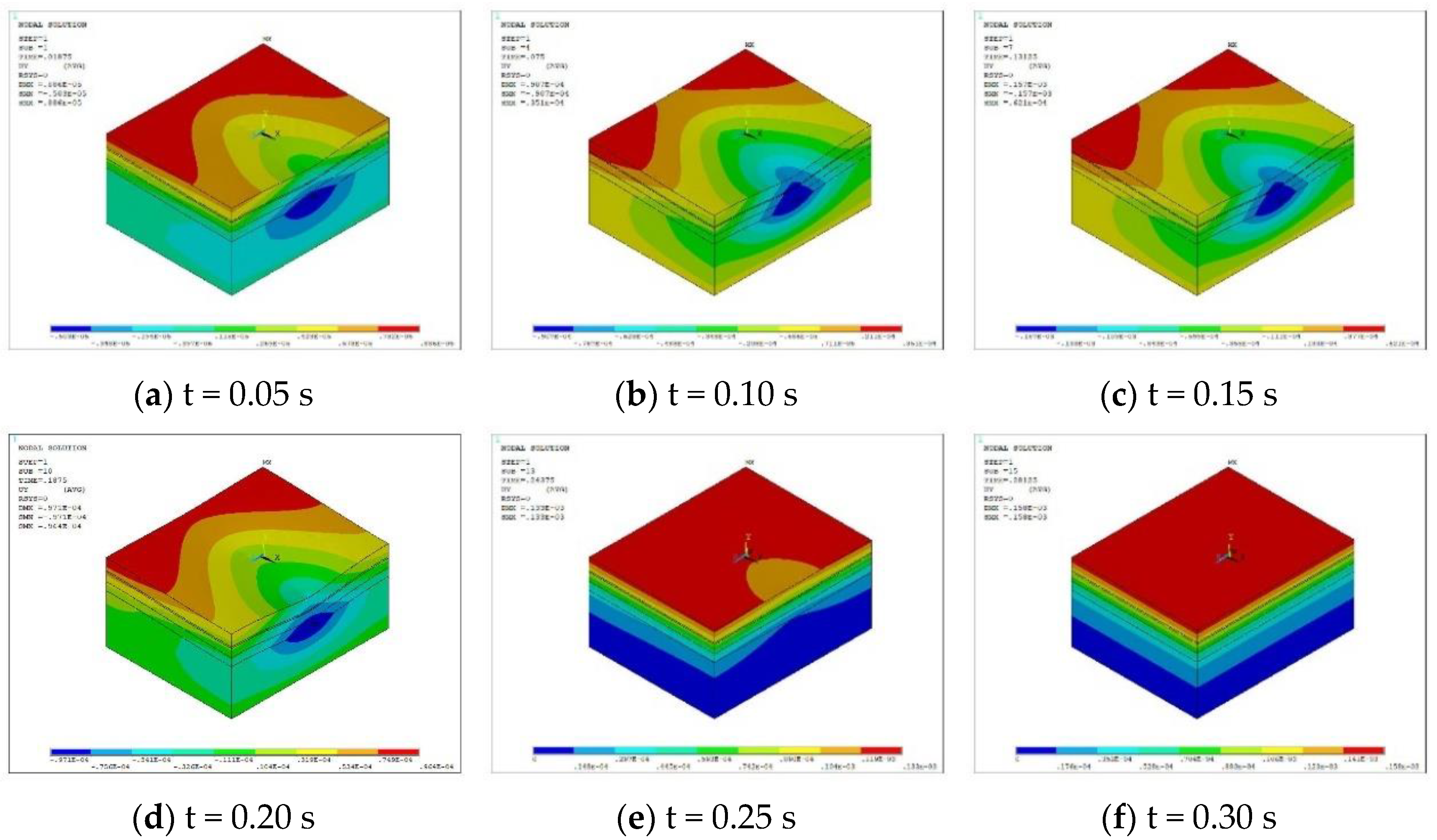
Figure 21.
Deformation cloud diagram under the coupling of medium temperature and moving load.
Figure 21.
Deformation cloud diagram under the coupling of medium temperature and moving load.
Figure 22.
Stress–strain curves of low temperature coupled with moving loads.
Figure 22.
Stress–strain curves of low temperature coupled with moving loads.
Figure 23.
Deformation cloud diagram under the coupling of low temperature and moving load.
Figure 23.
Deformation cloud diagram under the coupling of low temperature and moving load.
Table 1.
Mix proportions of cement concrete surface layer.
Table 1.
Mix proportions of cement concrete surface layer.
| Material | Water | Cement | Sand | Pebble |
|---|
| Amount/(kg/m3) | 165 | 430 | 561 | 1244 |
Table 2.
AC-10 buffer layer.
Table 2.
AC-10 buffer layer.
| Type of Grading | Mass Percentage (%) Passing through the Following Sieve Holes (mm) |
|---|
| 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 |
|---|
| AC-10 | Limit | 100 | 100 | 75 | 58 | 44 | 32 | 23 | 16 | 8 |
| Lower limit | 100 | 90 | 45 | 30 | 20 | 13 | 9 | 6 | 4 |
| Synthetic grade | 100 | 96.8 | 52.5 | 35.3 | 24.6 | 16.7 | 12.6 | 8.4 | 6.3 |
Table 3.
Cement-stabilized gravel gradation.
Table 3.
Cement-stabilized gravel gradation.
| Type of Grading | Mass Percentage (%) Passing through the Following Sieve Holes (mm) |
|---|
| 19 | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 |
|---|
| C-B-2 | Limit | 100 | 93 | 86 | 72 | 45 | 31 | 22 | 15 | 10 | 7 | 5 |
| Lower limit | 100 | 88 | 76 | 59 | 35 | 22 | 13 | 8 | 5 | 3 | 2 |
| Synthetic grade | 100 | 90.5 | 81 | 65.5 | 40 | 26.5 | 17.5 | 11.5 | 7.5 | 5 | 3.5 |
| Actual gradation value | 100 | 100 | 100 | 100 | 61.1 | 40.5 | 26.7 | 17.6 | 11.5 | 7.6 | 3.8 |
Table 4.
Composition of cement-stabilized crushed stone mixture.
Table 4.
Composition of cement-stabilized crushed stone mixture.
| Composition | Crushed Stone:Sand | Cement Content (%) | Moisture Content (%) |
|---|
| Dosage ratio | 61:39 | 6 | 7 |
Table 5.
Combined shear specimen program.
Table 5.
Combined shear specimen program.
| Combined Program | Height of Each Level (cm) | Sheared Surface |
|---|
| Cement-Stabilized Aggregates | Buffer Layer | Cement Concrete |
|---|
| Option 1 | 6 | 2 | 4 | Cement-stabilized aggregates in contact with buffer layer |
| Option 2 | 4 | 2 | 6 | Buffer layer in contact with concrete |
| Option 3 | 6 | 2 | 6 | Buffer layer |
Table 6.
Prony series calculation results.
Table 6.
Prony series calculation results.
| Temperature (°C) | Loading (MPa) | α1 | α2 | τ1 | τ2 |
|---|
| 30 | 1 | 0.6743 | 0.3257 | 8769.4252 | 50.9225 |
| 1.5 | 0.7411 | 0.2589 | 10,289.4169 | 69.4683 |
| 2 | 0.6139 | 0.3861 | 4214.8417 | 64.7026 |
| 2.5 | 0.5540 | 0.4460 | 2673.2983 | 38.6277 |
| 40 | 1 | 0.6678 | 0.3322 | 8827.4209 | 43.8048 |
| 1.5 | 0.6428 | 0.3572 | 6631.7981 | 72.5826 |
| 2 | 0.3594 | 0.6406 | 851.6299 | 6.9557 |
| 2.5 | 0.2479 | 0.7521 | 410.2973 | 1.9592 |
| 50 | 1 | 0.5998 | 0.4002 | 9473.2413 | 41.1912 |
| 1.5 | 0.6283 | 0.3717 | 6849.1315 | 54.1239 |
| 2 | 0.2413 | 0.7587 | 497.2264 | 1.9139 |
| 2.5 | 0.3085 | 0.6915 | 1325.1377 | 2.5628 |
Table 7.
Pavement structure material parameters.
Table 7.
Pavement structure material parameters.
| Structural Layer | Thicknesses (cm) | Modulus of Elasticity (MPa) | Poisson’s Ratio | Density (kg·m−3) | Thermal Conductivity
(W/(m·°C)) | Specific Heat Capacity (J/(kg·°C)) | Thermal Expansion (1/°C) |
|---|
| Cement concrete surface | 28 | 31,000 | 0.15 | 2450 | 1.3 | 879 | 1 × 10−5 |
| Buffer layer | 3 | 8500 | 0.25 | 2350 | 1.0 | 894 | 2 × 10−5 |
| Cement-stabilized aggregates | 20 | 1500 | 0.25 | 2000 | 1.2 | 817 | 2 × 10−5 |
| Low-dose cement-stabilized aggregate base | 20 | 1200 | 0.25 | 2300 | 1.2 | 817 | 2 × 10−5 |
| Soil foundation | 150 | 50 | 0.4 | 1800 | 1.2 | 1020 | 5 × 10−6 |
Table 8.
Superposition method and equivalent load of the node force.
Table 8.
Superposition method and equivalent load of the node force.
| Load Points | A/E/U/Y | B/D/F/J/P/T/V/X | C/K/O/W | G/I/Q/S | H/L/N/R | M |
|---|
| Node stacking method | 3 | 4 + 7 | 8 + 8 | 1 + 6 + 6 + 9 | 9 + 5 + 5 + 9 | 4 × 9 |
| Loading(N) | 30 | 481 | 884 | 1817 | 2032 | 2040 |
Table 9.
Correspondence between vehicle loading frequency and vehicle speed.
Table 9.
Correspondence between vehicle loading frequency and vehicle speed.
| Vehicle loading frequency (Hz) | 25 | 20 | 10 | 5 | 2 | 1 | 0.5 |
| Speed (km/h) | 137.2 | 109.7 | 54.9 | 27.4 | 11 | 5.5 | 2.7 |
Table 10.
Hot weather (20 June 2022) near-surface temperature.
Table 10.
Hot weather (20 June 2022) near-surface temperature.
| Times | Near-Surface Temperature (°C) | Times | Near-Surface Temperature (°C) | Times | Near-Surface Temperature (°C) |
|---|
| 00:00 | 24.8 | 08:00 | 33.63 | 16:00 | 38.7 |
| 01:00 | 24.47 | 09:00 | 36.65 | 17:00 | 36.52 |
| 02:00 | 24.53 | 10:00 | 38.88 | 18:00 | 33.4 |
| 03:00 | 24.3 | 11:00 | 40.53 | 19:00 | 30.91 |
| 04:00 | 24.03 | 12:00 | 41.97 | 20:00 | 29.32 |
| 05:00 | 23.55 | 13:00 | 42.66 | 21:00 | 28.71 |
| 06:00 | 26.08 | 14:00 | 42.14 | 22:00 | 27.96 |
| 07:00 | 29.83 | 15:00 | 40.96 | 23:00 | 27.48 |
Table 11.
Moderate weather (1 May 2022) near-surface temperature.
Table 11.
Moderate weather (1 May 2022) near-surface temperature.
| Times | Near-Surface Temperature (°C) | Times | Near-Surface Temperature (°C) | Times | Near-Surface Temperature (°C) |
|---|
| 00:00 | 16.59 | 08:00 | 24.05 | 16:00 | 9.2 |
| 01:00 | 19.94 | 09:00 | 21.89 | 17:00 | 8.83 |
| 02:00 | 22.71 | 10:00 | 17.93 | 18:00 | 8.42 |
| 03:00 | 24.81 | 11:00 | 13.87 | 19:00 | 7.97 |
| 04:00 | 26.02 | 12:00 | 12.5 | 20:00 | 7.47 |
| 05:00 | 26.48 | 13:00 | 11.3 | 21:00 | 6.98 |
| 06:00 | 26.35 | 14:00 | 10.45 | 22:00 | 9.19 |
| 07:00 | 25.54 | 15:00 | 9.39 | 23:00 | 14.78 |
Table 12.
Cold weather (30 December 2020) near-surface temperature.
Table 12.
Cold weather (30 December 2020) near-surface temperature.
| Times | Near-Surface Temperature (°C) | Times | Near-Surface Temperature (°C) | Times | Near-Surface Temperature (°C) |
|---|
| 00:00 | −9.88 | 08:00 | −12.06 | 16:00 | −5.65 |
| 01:00 | −10.09 | 09:00 | −8.99 | 17:00 | −8.32 |
| 02:00 | −10.31 | 10:00 | −6.63 | 18:00 | −9.04 |
| 03:00 | −10.53 | 11:00 | −4.66 | 19:00 | −9.62 |
| 04:00 | −10.74 | 12:00 | −3.31 | 20:00 | −9.81 |
| 05:00 | −10.94 | 13:00 | −2.66 | 21:00 | −9.84 |
| 06:00 | −12.8 | 14:00 | −2.84 | 22:00 | −10.02 |
| 07:00 | −13.08 | 15:00 | −3.83 | 23:00 | −10.11 |
Table 13.
Recommended values of heat exchange coefficients at different wind speeds.
Table 13.
Recommended values of heat exchange coefficients at different wind speeds.
| Air velocity (m/s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | …… |
| Heat exchange coefficient (W/m2·°C) | 9.4 | 13.2 | 16.8 | 20.6 | 24.3 | 28 | 31.7 | 35.4 | 39.1 | 42.8 | 46.5 | …… |
Table 14.
Road surface heat exchange coefficient for hot weather (20 June 2022).
Table 14.
Road surface heat exchange coefficient for hot weather (20 June 2022).
| Times | Air Velocity (m/s) | Heat Exchange Coefficient (W/m2·°C) | Times | Air Velocity (m/s) | Heat Exchange Coefficient (W/m2·°C) |
|---|
| 00:00 | 1.11 | 13.507 | 12:00 | 0.38 | 10.806 |
| 01:00 | 1.74 | 15.838 | 13:00 | 0.36 | 10.732 |
| 02:00 | 2.14 | 17.318 | 14:00 | 0.76 | 12.212 |
| 03:00 | 2 | 16.8 | 15:00 | 0.44 | 11.028 |
| 04:00 | 1.67 | 15.579 | 16:00 | 0.01 | 9.437 |
| 05:00 | 1.44 | 14.728 | 17:00 | 1.5 | 14.95 |
| 06:00 | 1.39 | 14.543 | 18:00 | 2.06 | 17.022 |
| 07:00 | 1.03 | 13.211 | 19:00 | 2.67 | 19.279 |
| 08:00 | 0.66 | 11.842 | 20:00 | 2.82 | 19.834 |
| 09:00 | 0.19 | 10.103 | 21:00 | 2.74 | 19.538 |
| 10:00 | 0.46 | 11.102 | 22:00 | 2.7 | 19.39 |
| 11:00 | 0.8 | 12.36 | 23:00 | 2.71 | 19.427 |
Table 15.
Road surface heat exchange coefficient for moderate weather (1 May 2022).
Table 15.
Road surface heat exchange coefficient for moderate weather (1 May 2022).
| Times | Air Velocity (m/s) | Heat Exchange Coefficient (W/m2·°C) | Times | Air Velocity (m/s) | Heat Exchange Coefficient (W/m2·°C) |
|---|
| 00:00 | 2.67 | 19.279 | 12:00 | 1.69 | 15.653 |
| 01:00 | 2.22 | 17.614 | 13:00 | 1.75 | 15.875 |
| 02:00 | 1.27 | 14.099 | 14:00 | 1.61 | 15.357 |
| 03:00 | 1.24 | 13.988 | 15:00 | 1.37 | 14.469 |
| 04:00 | 0.57 | 11.509 | 16:00 | 1.29 | 14.173 |
| 05:00 | 0.12 | 9.844 | 17:00 | 1.67 | 15.579 |
| 06:00 | 0.02 | 9.474 | 18:00 | 1.67 | 15.579 |
| 07:00 | 0.48 | 11.176 | 19:00 | 1.48 | 14.876 |
| 08:00 | 0.62 | 11.694 | 20:00 | 1.27 | 14.099 |
| 09:00 | 0.72 | 12.064 | 21:00 | 1.12 | 13.544 |
| 10:00 | 0.97 | 12.989 | 22:00 | 1.24 | 13.988 |
| 11:00 | 1.83 | 16.171 | 23:00 | 1.02 | 13.174 |
Table 16.
Road surface heat exchange coefficient for cold weather (30 December 2020).
Table 16.
Road surface heat exchange coefficient for cold weather (30 December 2020).
| Times | Air Velocity (m/s) | Heat Exchange Coefficient (W/m2·°C) | Times | Air Velocity (m/s) | Heat Exchange Coefficient (W/m2·°C) |
|---|
| 00:00 | 3.76 | 23.312 | 12:00 | 4.23 | 25.051 |
| 01:00 | 3.65 | 22.905 | 13:00 | 4.14 | 24.718 |
| 02:00 | 3.61 | 22.757 | 14:00 | 3.92 | 23.904 |
| 03:00 | 3.74 | 23.238 | 15:00 | 3.72 | 23.164 |
| 04:00 | 3.63 | 22.831 | 16:00 | 3.33 | 21.721 |
| 05:00 | 3.44 | 22.128 | 17:00 | 2.04 | 16.948 |
| 06:00 | 2.4 | 18.28 | 18:00 | 1.23 | 13.951 |
| 07:00 | 2.2 | 17.54 | 19:00 | 0.53 | 11.361 |
| 08:00 | 2.14 | 17.318 | 20:00 | 0.05 | 9.585 |
| 09:00 | 2.9 | 20.13 | 21:00 | 0.25 | 10.325 |
| 10:00 | 3.78 | 23.386 | 22:00 | 0.42 | 10.954 |
| 11:00 | 4.08 | 24.496 | 23:00 | 0.65 | 11.805 |
Table 17.
Validation of simulation analysis results.
Table 17.
Validation of simulation analysis results.
| Type of Constraint | Simulation Analysis Results (MPa) | Normative Calculations (MPa) [26] | Relative Error (%) |
|---|
| Constraints around the panel | 1.09 | 1.051 | 3.7 |
| Constraints to the panel travel direction’s degrees of freedom | 1.19 | 13.2 |
| No constraints around the panel | 1.21 | 15.2 |
Table 18.
Maximum tensile and horizontal shear stresses at different vehicle speeds.
Table 18.
Maximum tensile and horizontal shear stresses at different vehicle speeds.
| Type of Road | Speed (km/h) | Maximum Tensile Stress (Pa) | Maximum Horizontal Shear Stress (Pa) |
|---|
| - | 0 | 819,177 | 160,100 |
| Low-grade roads | 30 | 873,397 | 170,841 |
| 40 | 898,354 | 175,298 |
| 50 | 912,525 | 178,027 |
| 60 | 926,458 | 180,466 |
| High-grade roads | 40 | 873,161 | 170,385 |
| 50 | 881,928 | 173,990 |
| 60 | 900,641 | 175,531 |
| 70 | 916,189 | 179,604 |
| 80 | 922,953 | 180,609 |
Table 19.
Comprehensive coefficient ().
Table 19.
Comprehensive coefficient ().
| Class of Road | Motorway | Class I Roads | Class II Roads | Class III and IV Roads |
|---|
| 1.10 | 1.05 | 1.00 | 0.95 |
Table 20.
Recommended values of the comprehensive coefficient ().
Table 20.
Recommended values of the comprehensive coefficient ().
| Class of Road | Low-Grade Roads | High-Grade Roads |
|---|
| Speed (km/h) | 30 | 40 | 50 | 60 | 40 | 50 | 60 | 70 | 80 |
| 1.07 | 1.10 | 1.11 | 1.13 | 1.07 | 1.08 | 1.10 | 1.12 | 1.13 |