Study of Heat Transfer Characteristics and Economic Analysis of a Closed Deep Coaxial Geothermal Heat Exchanger Retrofitted from an Abandoned Oil Well
Abstract
1. Introduction
2. Abandoned Oil Well Structure and Working Principles of a CGHE
3. Development of Numerical Heat Transfer Model
3.1. Model Assumptions
- The thermal properties of ground, pipe, water, and backfilling material are dependent on their specific temperatures.
- The properties of the ground are homogeneous in each ground layer.
- The penetration of groundwater is neglected.
- The lateral and bottom boundaries of the borehole model are set to be temperature constant.
- The geothermal heat flux in the ground is assumed to be uniform and constant.
3.2. Initial and Boundary Conditions
3.3. Heat Transfer Governing Equation
3.4. Numerical Discretization
3.5. Equation Solving Algorithm
3.6. Model Validation
4. Thermal Performance Analysis of the Retrofitted CGHE
4.1. Parameter Settings of the Retrofitted CGHE
4.2. Average Heat Extraction Rate in the Heating Season
4.3. Orthogonal Test Scheme Design and Test Results
4.4. Analysis of Orthogonal Test Results
5. Case Study and Economic Analysis
5.1. Actual Operation of the Ground Source Heat Pump (GSHP) System with Retrofitted CGHE
5.2. Initial System Investment
- (1)
- Drilling cost
- (2)
- Pipe material cost
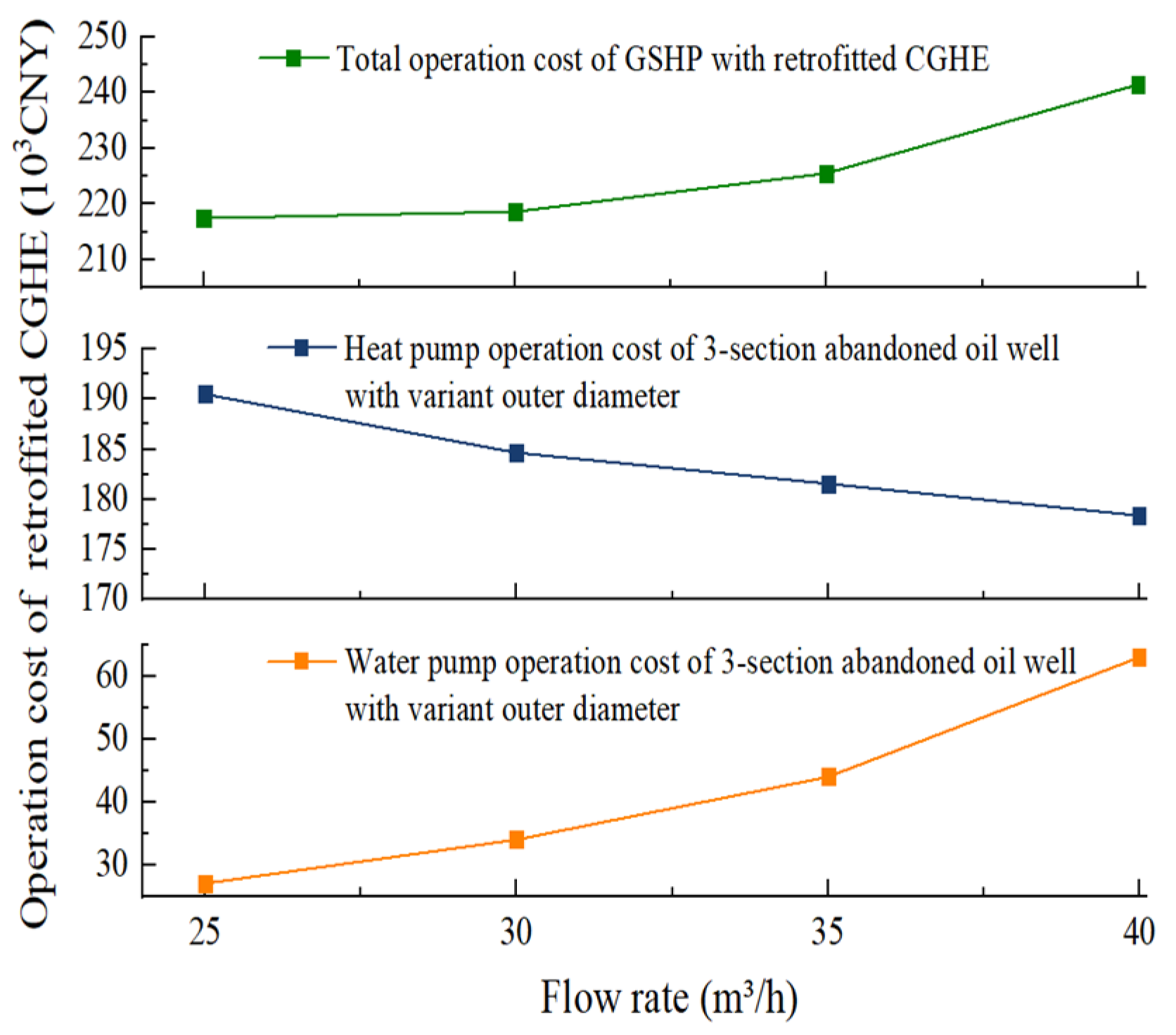
5.3. Total Operation Cost of the GSHP System with Retrofitted CGHE
- (1)
- Water pump cost
- (2)
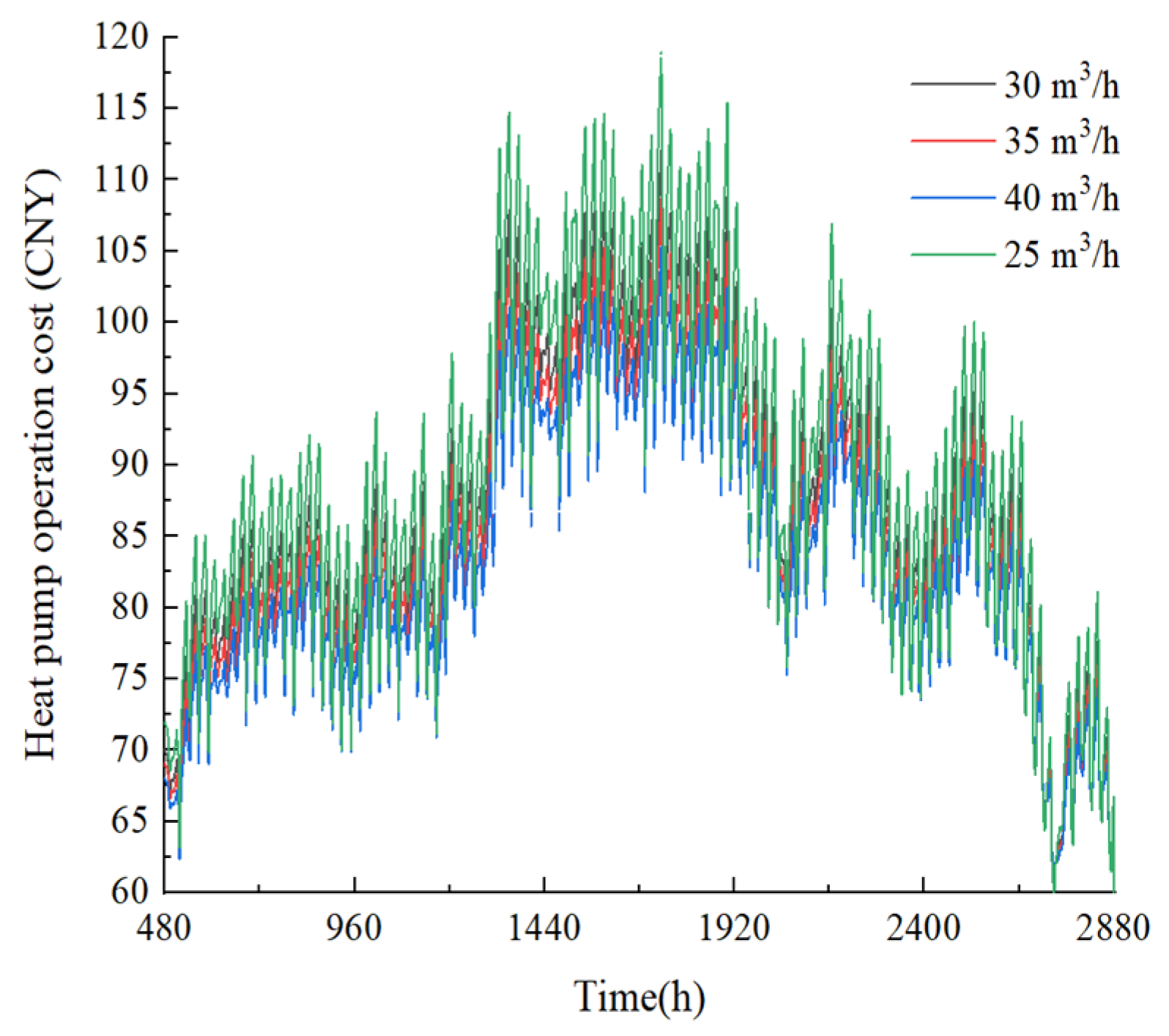
- Heat pump operation cost
6. Conclusions
- (1)
- A sensitive analysis was carried out by using the orthogonal experimental method to investigate the influence of four critical variables on the thermal performance of CGHE. The results show that the inlet water temperature plays the most important role in heat extraction rates, followed by types of CGHE retrofitted from abandoned wells, flow rate, and inner tube thermal conductivity.
- (2)
- An economic analysis of the retrofit, considering the operation costs of the water pump and heat pump, was performed. Given the fact that the CGHE in this study was retrofitted from the abandoned oil wells, the drilling cost can be reduced by up to CNY 1800 thousand. The pump operation cost of CGHE retrofitted from three-section abandoned oil wells is significantly increase with the increase in the flow rate, while the heat pump operation cost decreases because the COP increases.
- (3)
- This study integrates actual project considerations to determine the most appropriate circulation flow based on building load requirements. From an economic perspective, a flow rate of 35 m³/h is selected as the optimal choice, which aligns with both the economic efficiency and operation stability of the middle and deep CGHEs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AOGW | abandoned oil and gas wells |
| CGHE | coaxial geothermal heat exchanger |
| DBHE | deep borehole heat exchanger |
| EGS | enhanced geothermal systems |
| FDM | finite difference method |
| FVM | finite volume method |
| GSHP | ground source heat pump |
Nomenclature
| a | thermal diffusivity (m2/s) |
| c, cf, cg | specific heat capacity of the circulating fluid (J/(kg·K)) |
| C, C1, C2 | heat capacity of the circulating fluid (J/(m·K)) |
| d, do, di, d1i, d1o, d2i, d2o | pipe diameter (m) |
| pf | frictional pressure drops (Pa) |
| ps | local pressure drops (Pa) |
| Hj | bottom coordinate of the j-layer |
| k, kg, kp1, kp2 | thermal conductivity (W/(m·K)) |
| qg | geothermal heat flux (W/m2) |
| h1, h2, ha | convective heat transfer coefficients (W/(m2·K)) |
| K, K1, K2 | height of the equivalent coarse grain (m) |
| l | pipe length (m) |
| M | circulating fluid flow rate (kg/s) |
| P | power consumption (W) |
| Q | total heat transfer rate of the CGHE (W) |
| r | radial coordinate (m) |
| rb | borehole radius (m) |
| rbnd | the radius of the radial boundary (m) |
| R1, R2 | thermal resistance ((m·k)/W) |
| ta | ambient air temperature (°C) |
| u | average section velocity (m/s) |
| v | kinematic viscosity (m2/s) |
| ρ, ρf, ρg | density (kg/m3) |
| λ | friction factor |
References
- Li, J.; Zhu, T.; Li, F.; Wang, D.; Bu, X.; Wang, L. Performance Characteristics of Geothermal Single Well for Building Heating. Energy Eng. 2021, 118, 517–534. [Google Scholar] [CrossRef]
- Rubio-Maya, C.; Ambríz Díaz, V.M.; Pastor Martínez, E.; Belman-Flores, J.M. Cascade Utilization of Low and Medium Enthalpy Geothermal Resources—A Review. Renew. Sustain. Energy Rev. 2015, 52, 689–716. [Google Scholar] [CrossRef]
- Davis, A.P.; Michaelides, E.E. Geothermal Power Production from Abandoned Oil Wells. Energy 2009, 34, 866–872. [Google Scholar] [CrossRef]
- Lund, J.W.; Toth, A.N. Direct Utilization of Geothermal Energy 2020 Worldwide Review. Geothermics 2021, 90, 101915. [Google Scholar] [CrossRef]
- Jia, L.; Lu, L.; Chen, J.; Han, J. A Novel Radiative Sky Cooling-Assisted Ground-Coupled Heat Exchanger System to Improve Thermal and Energy Efficiency for Buildings in Hot and Humid Regions. Appl. Energy 2022, 322, 119422. [Google Scholar] [CrossRef]
- Jia, L.; Lu, L.; Chen, J. Exploring the Cooling Potential Maps of a Radiative Sky Cooling Radiator-Assisted Ground Source Heat Pump System in China. Appl. Energy 2023, 349, 121678. [Google Scholar] [CrossRef]
- Chmielowska, A.; Tomaszewska, B.; Sowida, A. The Utilization of Abandoned Petroleum Wells in Geothermal Energy Sector. Worldwide Trends and Experience. In Proceedings of the E3S Web of Conferences, Krynica, Poland, 12–14 June 2020; Volume 154, p. 05004. [Google Scholar] [CrossRef]
- Morita, K.; Bollmeier, W.S.; Mizogami, H. Analysis of the Results from the Downhole Coaxial Heat Exchanger (DCHE) Experiment in Hawaii. Trans. Geotherm. Resour. Counc. 1992, 16, 17–23. [Google Scholar]
- Morita, K.; Bollmeier, W.S.; Mizogami, H. An Experiment to Prove the Concept of the Downhole Coaxial Heat Exchanger (DCHE) in Hawaii. Geothermal Res. Council Trans. 1992; 16, 9–16. [Google Scholar]
- Kohl, T.; Brenni, R.; Eugster, W. System Performance of a Deep Borehole Heat Exchanger. Geothermics 2002, 31, 687–708. [Google Scholar] [CrossRef]
- Kohl, T.; Salton, M.; Rybach, L. Data Analysis of the Deep Borehole Heat Exchanger Plant Weissbad (Switzerland). In Proceedings of the World Geothermal Congress, Kyushu-Tohoku, Japan, 28 May–10 June 2000. [Google Scholar]
- Nian, Y.-L.; Cheng, W.-L. Insights into Geothermal Utilization of Abandoned Oil and Gas Wells. Renew. Sustain. Energy Rev. 2018, 87, 44–60. [Google Scholar] [CrossRef]
- Cheng, W.-L.; Li, T.-T.; Nian, Y.-L.; Xie, K. Evaluation of Working Fluids for Geothermal Power Generation from Abandoned Oil Wells. Appl. Energy 2014, 118, 238–245. [Google Scholar] [CrossRef]
- Cheng, W.-L.; Liu, J.; Nian, Y.-L.; Wang, C.-L. Enhancing Geothermal Power Generation from Abandoned Oil Wells with Thermal Reservoirs. Energy 2016, 109, 537–545. [Google Scholar] [CrossRef]
- Cui, G.; Ren, S.; Zhang, L.; Ezekiel, J.; Enechukwu, C.; Wang, Y.; Zhang, R. Geothermal Exploitation from Hot Dry Rocks via Recycling Heat Transmission Fluid in a Horizontal Well. Energy 2017, 128, 366–377. [Google Scholar] [CrossRef]
- Caulk, R.A.; Tomac, I. Reuse of Abandoned Oil and Gas Wells for Geothermal Energy Production. Renew. Energy 2017, 112, 388–397. [Google Scholar] [CrossRef]
- Gharibi, S.; Mortezazadeh, E.; Hashemi Aghcheh Bodi, S.J.; Vatani, A. Feasibility Study of Geothermal Heat Extraction from Abandoned Oil Wells Using a U-Tube Heat Exchanger. Energy 2018, 153, 554–567. [Google Scholar] [CrossRef]
- Kujawa, T.; Nowak, W.; Stachel, A.A. Utilization of Existing Deep Geological Wells for Acquisitions of Geothermal Energy. Energy 2006, 31, 650–664. [Google Scholar] [CrossRef]
- Templeton, J.D.; Ghoreishi-Madiseh, S.A.; Hassani, F.; Al-Khawaja, M.J. Abandoned Petroleum Wells as Sustainable Sources of Geothermal Energy. Energy 2014, 70, 366–373. [Google Scholar] [CrossRef]
- Fang, L.; Diao, N.; Shao, Z.; Zhu, K.; Fang, Z. A Computationally Efficient Numerical Model for Heat Transfer Simulation of Deep Borehole Heat Exchangers. Energy Build. 2018, 167, 79–88. [Google Scholar] [CrossRef]
- Song, X.; Wang, G.; Shi, Y.; Li, R.; Xu, Z.; Zheng, R.; Wang, Y.; Li, J. Numerical Analysis of Heat Extraction Performance of a Deep Coaxial Borehole Heat Exchanger Geothermal System. Energy 2018, 164, 1298–1310. [Google Scholar] [CrossRef]
- Saadi, M.S.; Gomri, R. Investigation of Dynamic Heat Transfer Process through Coaxial Heat Exchangers in the Ground. Int. J. Hydrogen Energy 2017, 42, 18014–18027. [Google Scholar] [CrossRef]
- Yang, M.; Li, X.; Deng, J.; Meng, Y.; Li, G. Prediction of Wellbore and Formation Temperatures during Circulation and Shut-in Stages under Kick Conditions. Energy 2015, 91, 1018–1029. [Google Scholar] [CrossRef]
- Bu, X.; Ma, W.; Li, H. Geothermal Energy Production Utilizing Abandoned Oil and Gas Wells. Renew. Energy 2012, 41, 80–85. [Google Scholar] [CrossRef]
- Yekoladio, P.J.; Bello-Ochende, T.; Meyer, J.P. Design and Optimization of a Downhole Coaxial Heat Exchanger for an Enhanced Geothermal System (EGS). Renew. Energy 2013, 55, 128–137. [Google Scholar] [CrossRef]
- Beier, R.A.; Acuña, J.; Mogensen, P.; Palm, B. Transient Heat Transfer in a Coaxial Borehole Heat Exchanger. Geothermics 2014, 51, 470–482. [Google Scholar] [CrossRef]
- Nian, Y.-L.; Cheng, W.-L. Evaluation of Geothermal Heating from Abandoned Oil Wells. Energy 2018, 142, 592–607. [Google Scholar] [CrossRef]
- Bertani, R. Geothermal Power Generation in the World 2010–2014 Update Report. Geothermics 2016, 60, 31–43. [Google Scholar] [CrossRef]
- Winterton, R.H.S. Where did the Dittus and Boelter equation come from? Int. J. Heat Mass Transfer 1998, 41, 809–810. [Google Scholar] [CrossRef]
- Gnielinski, V. On Heat Transfer in Tubes. Int. J. Heat. Mass. Transf. 2013, 63, 134–140. [Google Scholar] [CrossRef]
- Jia, L.; Lu, L.; Cui, P.; Chen, J.; Pan, A. A Novel Study on Influence of Ground Surface Boundary Conditions on Thermal Performance of Vertical U-Shaped Ground Heat Exchanger. Sustain. Cities Soc. 2024, 100, 105022. [Google Scholar] [CrossRef]
- Rao, Z.; Li, M.; Li, M.; Liu, P.; Zhao, L.; Lv, Y. Deep casing-buried pipe heat exchanger heat-economic analysis and application. J. Cent. South Univ. (Nat. Sci. Ed.) 2022, 53, 4749–4761. [Google Scholar]
- Miansari, M.; Valipour, M.A.; Arasteh, H.; Toghraie, D. Energy and Exergy Analysis and Optimization of Helically Grooved Shell and Tube Heat Exchangers by Using Taguchi Experimental Design. J. Therm. Anal. Calorim. 2020, 139, 3151–3164. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, Y.; Hu, C. Buried pipe diameter selection of ground source heat pump. HVAC Units 2012, 42, 114–117. [Google Scholar]
- Gan, X.; Pei, J.; Pavesi, G.; Yuan, S.; Wang, W. Application of Intelligent Methods in Energy Efficiency Enhancement of Pump System: A Review. Energy Rep. 2022, 8, 11592–11606. [Google Scholar] [CrossRef]
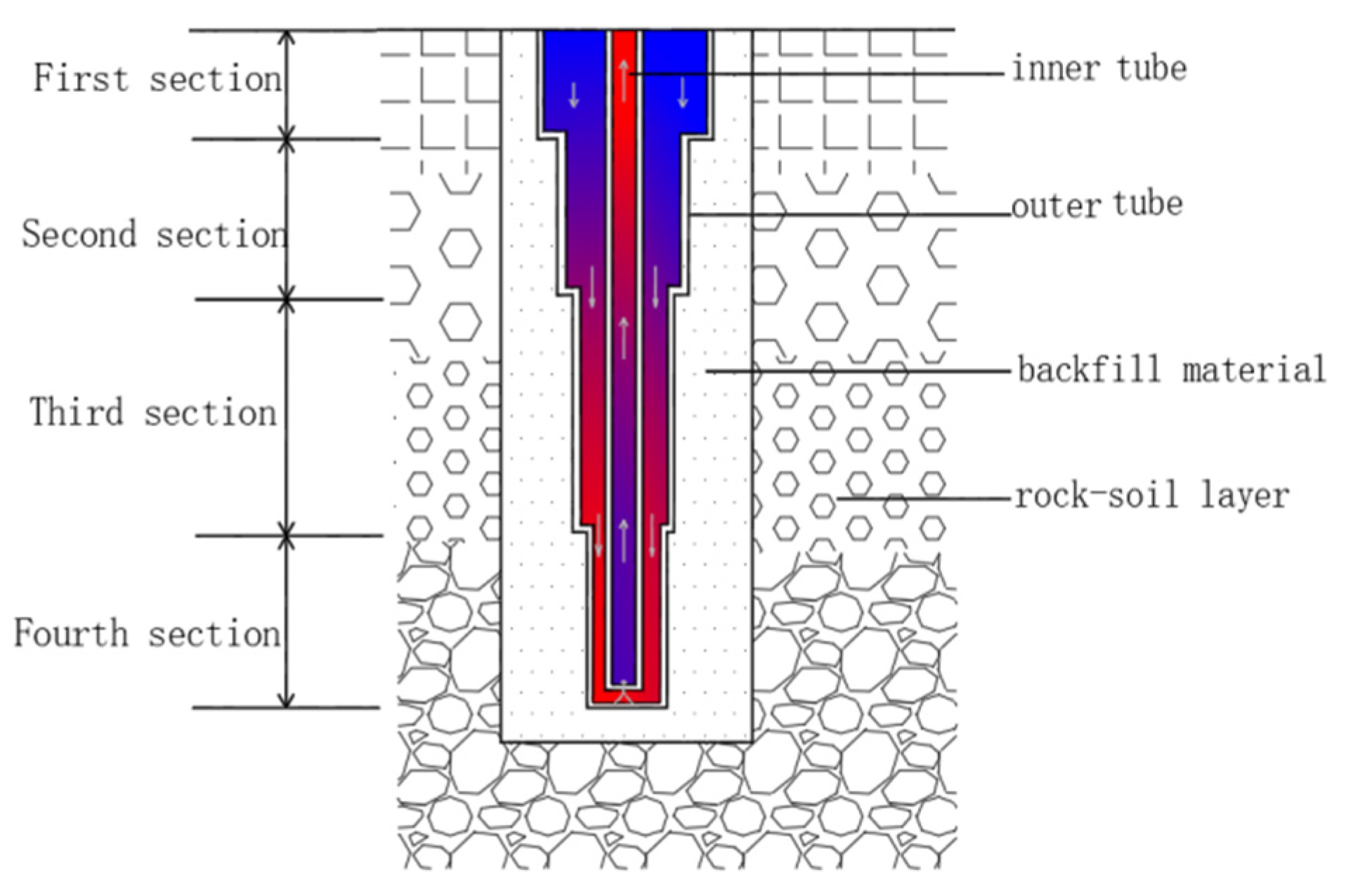

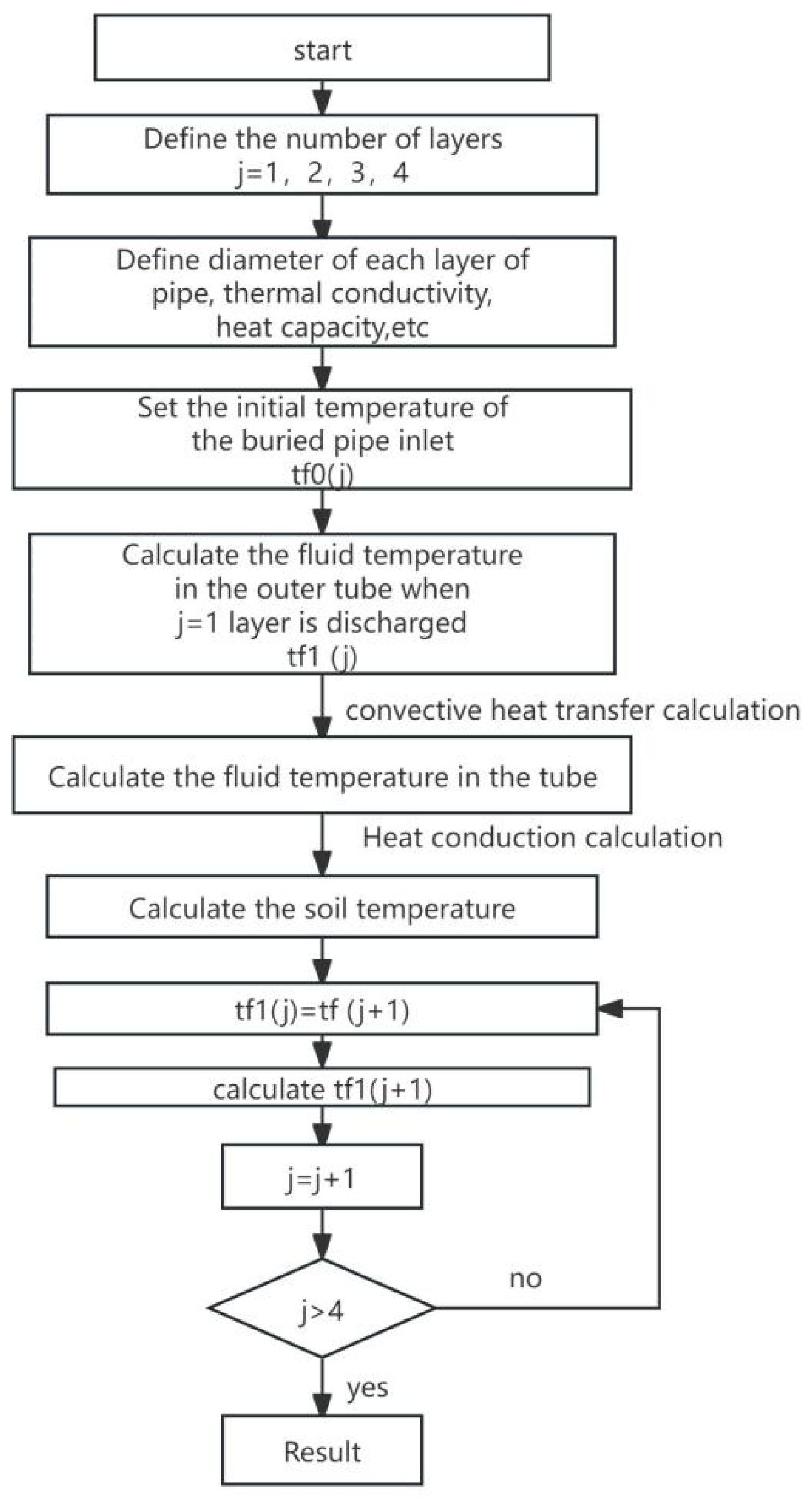



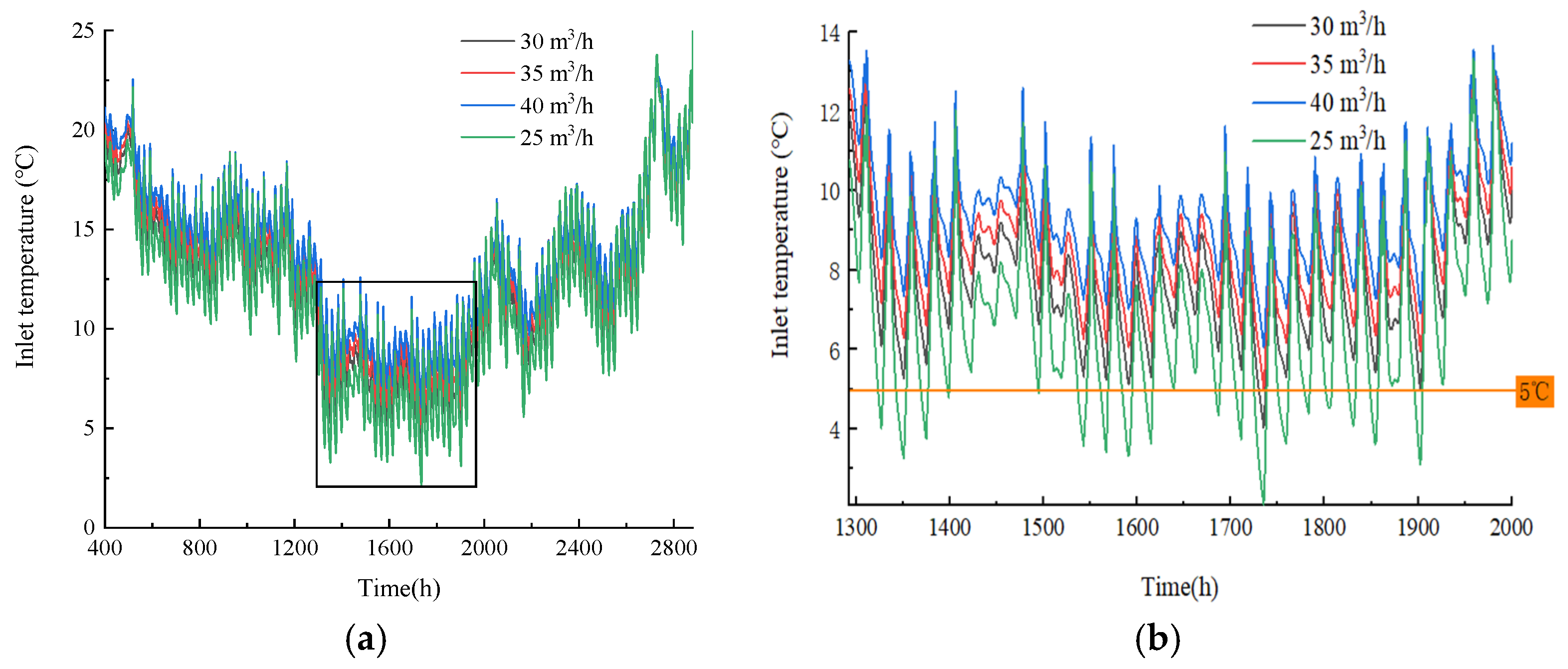


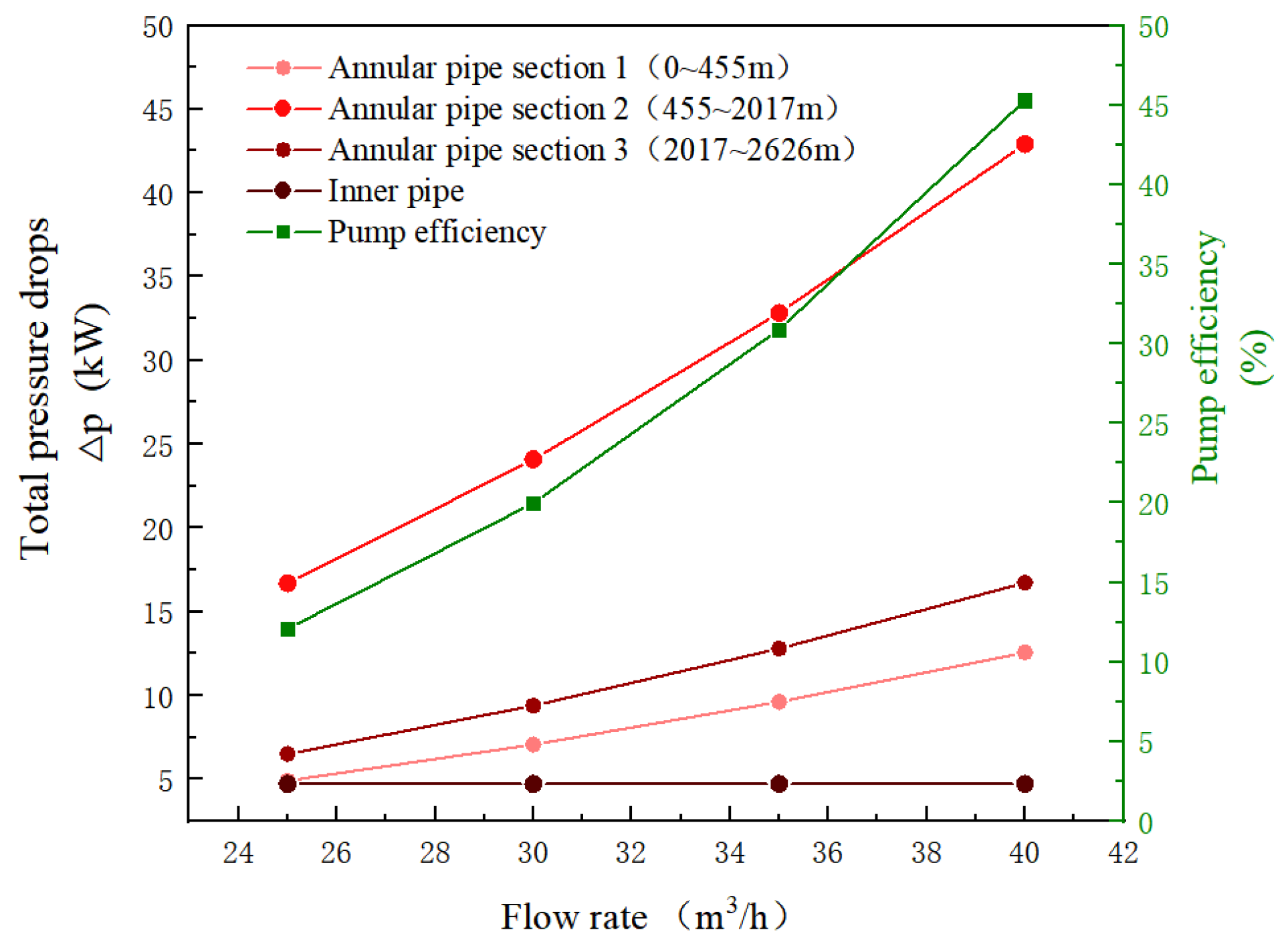

| No. | Length of Borehole (m) | Borehole Diameter (m) | External Diameter of the Outer Pipe (m) | Inner Diameter of the Outer Pipe (m) | k of the Ground W/(m·K) | Specific Heat Capacity 106J/(Nm3·K) |
|---|---|---|---|---|---|---|
| First section | 0~455 | 0.44 | 0.34 | 0.32 | 2.8 | 1.10 |
| Second section | 455~2017 | 0.31 | 0.24 | 0.23 | 2.8 | 1.93 |
| Third section | 2017~2626 | 0.22 | 0.18 | 0.16 | 3.0 | 1.41 |
| Forth section | 2626~2829 | 0.15 | 0.14 | 0.12 | 3.5 | 2.24 |
| Operating Condition | Modeling Parameter | |||
|---|---|---|---|---|
| A: Configuration of CGHE Retrofitted from Abandoned Oil Wells | B: Inlet Temperature | C: Flow Rate | D: Thermal Conductivity of Inner Pipe kp2 | |
| (°C) | (m³/h) | (W/(M·K)) | ||
| 1 | 4-section with variant do of 2829 m | 5 | 25 | 0.17 |
| 2 | 4-section with variant do of 2829 m | 10 | 30 | 0.25 |
| 3 | 4-section with variant do of 2829 m | 15 | 35 | 0.34 |
| 4 | 4-section with variant do of 2829 m | 20 | 40 | 0.43 |
| 5 | 3-section with variant do of 2626 m | 5 | 30 | 0.34 |
| 6 | 3-section with variant do of 2626 m | 10 | 25 | 0.43 |
| 7 | 3-section with variant do of 2626 m | 15 | 40 | 0.17 |
| 8 | 3-section with variant do of 2626 m | 20 | 35 | 0.25 |
| 9 | 4-section with constant do of 2829 m | 5 | 35 | 0.43 |
| 10 | 4-section with constant do of 2829 m | 10 | 40 | 0.34 |
| 11 | 4-section with constant do of 2829 m | 15 | 25 | 0.25 |
| 12 | 4-section with constant do of 2829 m | 20 | 30 | 0.17 |
| 13 | 3-section with constant do of 2626 m | 5 | 40 | 0.25 |
| 14 | 3-section with constant do of 2626 m | 10 | 35 | 0.17 |
| 15 | 3-section with constant do of 2626 m | 15 | 30 | 0.43 |
| 16 | 3-section with constant do of 2626 m | 20 | 25 | 0.34 |
| Operating Condition | Combination of Factors | Average Heat Extraction (kW) |
|---|---|---|
| 1 | A1B1C1D1 | 422.18 |
| 2 | A1B2C2D2 | 385.94 |
| 3 | A1B3C2D2 | 344.84 |
| 4 | A1B3C3D3 | 305.00 |
| 5 | A2B1C2D3 | 383.09 |
| 6 | A2B2C1D4 | 324.62 |
| 7 | A2B3C4D1 | 319.11 |
| 8 | A2B4C3D2 | 269.08 |
| 9 | A3B1C3D4 | 420.76 |
| 10 | A3B2C4D3 | 394.05 |
| 11 | A3B3C1D2 | 326.41 |
| 12 | A3B4C2D1 | 301.88 |
| 13 | A4B1C4D2 | 393.67 |
| 14 | A4B2C3D1 | 349.02 |
| 15 | A4B3C2D4 | 292.01 |
| 16 | A4B4C1D3 | 247.68 |
| Analysis of Range | A | B | C | D |
|---|---|---|---|---|
| n1 | 364.5 | 404.9 | 330.2 | 348.0 |
| n2 | 324.0 | 363.4 | 340.7 | 343.8 |
| n3 | 360.8 | 320.6 | 345.9 | 342.4 |
| n4 | 320.6 | 280.9 | 353.0 | 335.6 |
| Ri | 43.9 | 124 | 22.7 | 12.5 |
| Performance Parameter | Number |
|---|---|
| Nominal heating capacity | 500 kW |
| Designed inlet and outlet water temperatures of the evaporator | 15/7 °C |
| Design inlet and outlet water temperatures of the condenser | 40/45 °C |
| Nominal power consumption | 115 kW |
| Rated COP | 4.48 |
| Pipe Type | Hydraulic Diameter (m) | Re | Pr | Nu | h (W/m2·K) |
|---|---|---|---|---|---|
| Annular pipe section 1 | 0.32 | 16,287.79 | 9.02 | 112.02 | 315.78 |
| Annular pipe section 2 | 0.23 | 20,760.25 | 9.02 | 136.02 | 705.69 |
| Annular pipe section 3 | 0.16 | 25,844.40 | 9.02 | 162.07 | 2113.49 |
| Inner pipe | 0.09 | 83,431.80 | 9.02 | 413.88 | 2819.27 |
| Pipe Type | Fitted Curve | |
|---|---|---|
| Annular pipe section 1 | y = 79.86 ± 15 + (9.43 ± 0.4) × x | y: convection heat transfer coefficient (W/m2·K) x: flow rate (m3/h) |
| Annular pipe section 2 | y = 178.53 ± 34 + (21.07 ± 1.0) × x | |
| Annular pipe section 3 | y = 548.87 ± 162 + (62.40 ± 4.9) × x | |
| Inner pipe | y = 712.90 ± 135 + (84.19 ± 4.0) × x | |
| Buried Depth | 1000 m | 1500 m | 2000 m | 2500 m | 3000 m |
|---|---|---|---|---|---|
| Drilling cost (103CNY) | 600 | 900 | 1200 | 1500 | 1800 |
| Buried Depth | 1000 m | 1500 m | 2000 m | 2500 m | 3000 m |
|---|---|---|---|---|---|
| Pipe material cost (103CNY) | 440 | 660 | 880 | 1100 | 1320 |
| Pipe Type | Fitted Curve | |
|---|---|---|
| Annular pipe section 1 | y = −8.07 ± 0.82 + (0.51 ± 0.02) × x | y: total pressure drop (m) x: flow rate (m3/h) |
| Annular pipe section 2 | y = −27.69 ± 2.82 + (1.75 ± 0.09) × x | |
| Annular pipe section 3 | y = −10.80 ± 1.10 + (0.68 ± 03) × x | |
| Inner pipe | y = 4.72 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.-J.; Jia, L.-R.; Zhang, W.-S.; Yu, M.-Z.; Zhao, X.-D.; Cui, P. Study of Heat Transfer Characteristics and Economic Analysis of a Closed Deep Coaxial Geothermal Heat Exchanger Retrofitted from an Abandoned Oil Well. Sustainability 2024, 16, 1603. https://doi.org/10.3390/su16041603
Liu R-J, Jia L-R, Zhang W-S, Yu M-Z, Zhao X-D, Cui P. Study of Heat Transfer Characteristics and Economic Analysis of a Closed Deep Coaxial Geothermal Heat Exchanger Retrofitted from an Abandoned Oil Well. Sustainability. 2024; 16(4):1603. https://doi.org/10.3390/su16041603
Chicago/Turabian StyleLiu, Rui-Jia, Lin-Rui Jia, Wen-Shuo Zhang, Ming-Zhi Yu, Xu-Dong Zhao, and Ping Cui. 2024. "Study of Heat Transfer Characteristics and Economic Analysis of a Closed Deep Coaxial Geothermal Heat Exchanger Retrofitted from an Abandoned Oil Well" Sustainability 16, no. 4: 1603. https://doi.org/10.3390/su16041603
APA StyleLiu, R.-J., Jia, L.-R., Zhang, W.-S., Yu, M.-Z., Zhao, X.-D., & Cui, P. (2024). Study of Heat Transfer Characteristics and Economic Analysis of a Closed Deep Coaxial Geothermal Heat Exchanger Retrofitted from an Abandoned Oil Well. Sustainability, 16(4), 1603. https://doi.org/10.3390/su16041603







