Enhancing Sustainability in Marine Structures: Nonlinear Energy Sink for Vibration Control of Eccentrically Stiffened Functionally Graded Panels Under Hydrodynamic Loads
Abstract
:1. Introduction
2. Materials and Methodology
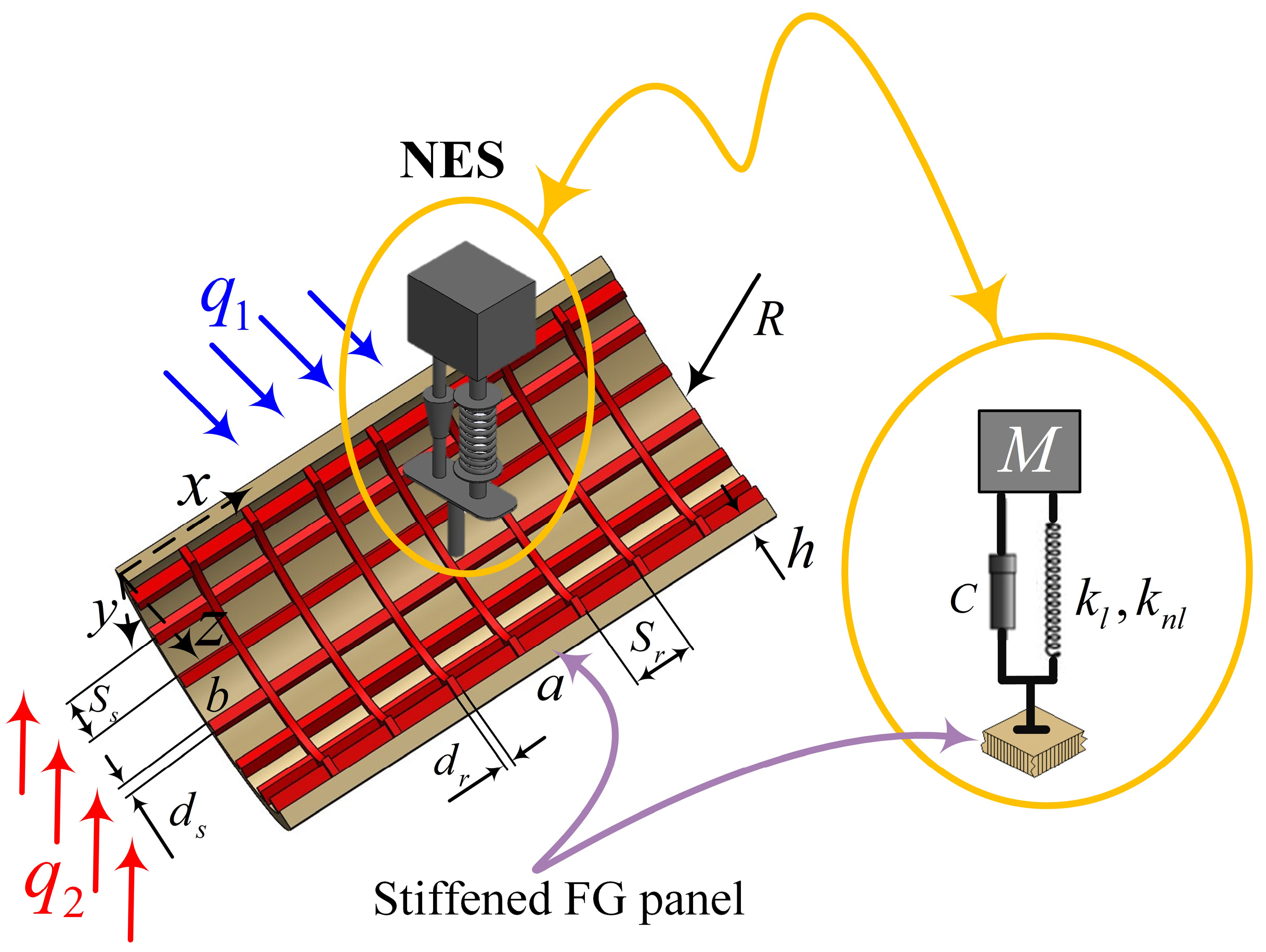
2.1. ESFG Panels with NES
- FG panels:
- FG stiffeners:
2.2. Governing Equations
- FG panels:
- FG stiffeners:
- Resultant forces:
- Resultant moments:
2.3. Dynamic Galerkin Approach
2.4. Free Vibration Analysis
2.5. P-T Method
3. Numerical Results
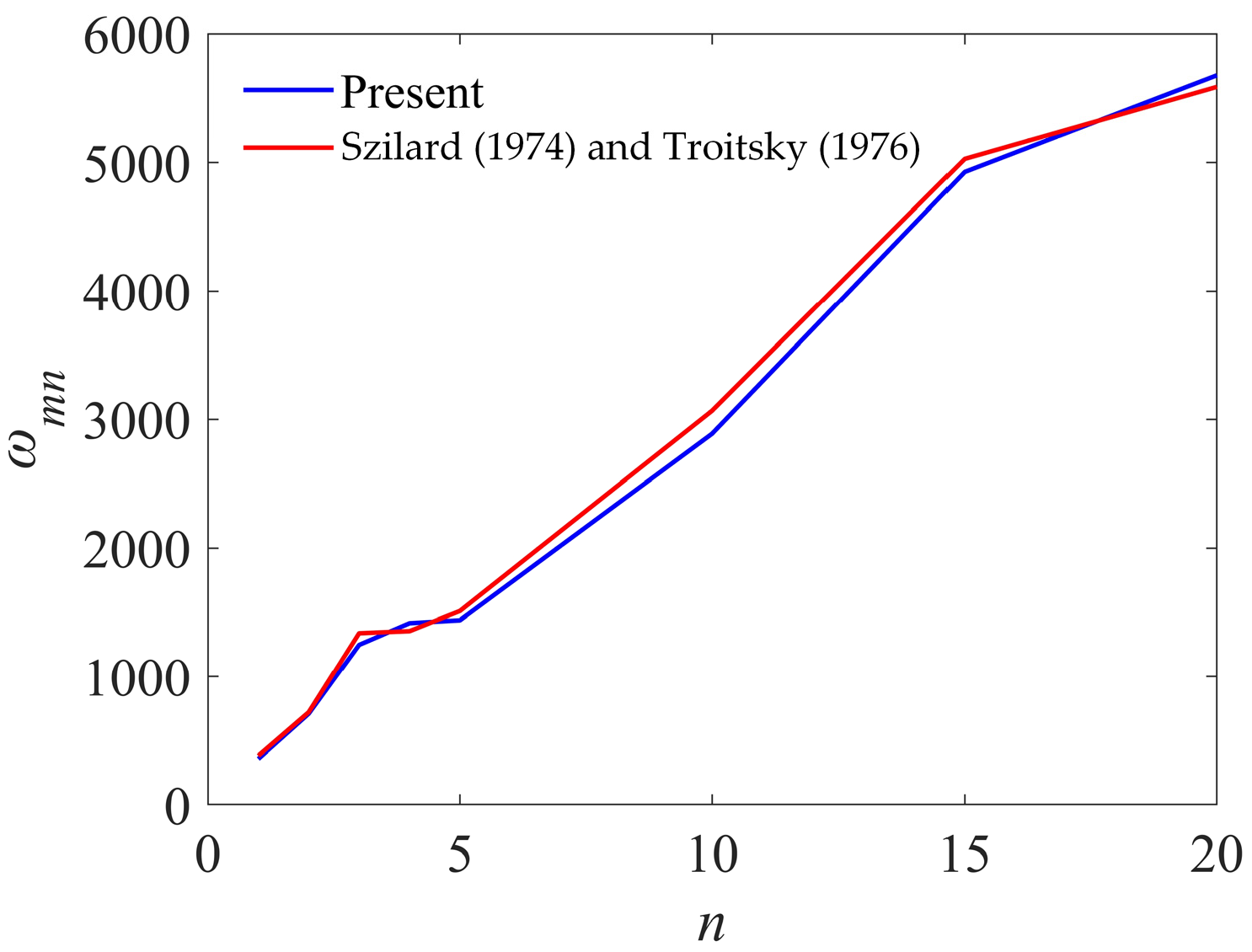
3.1. Validation of the Present Study
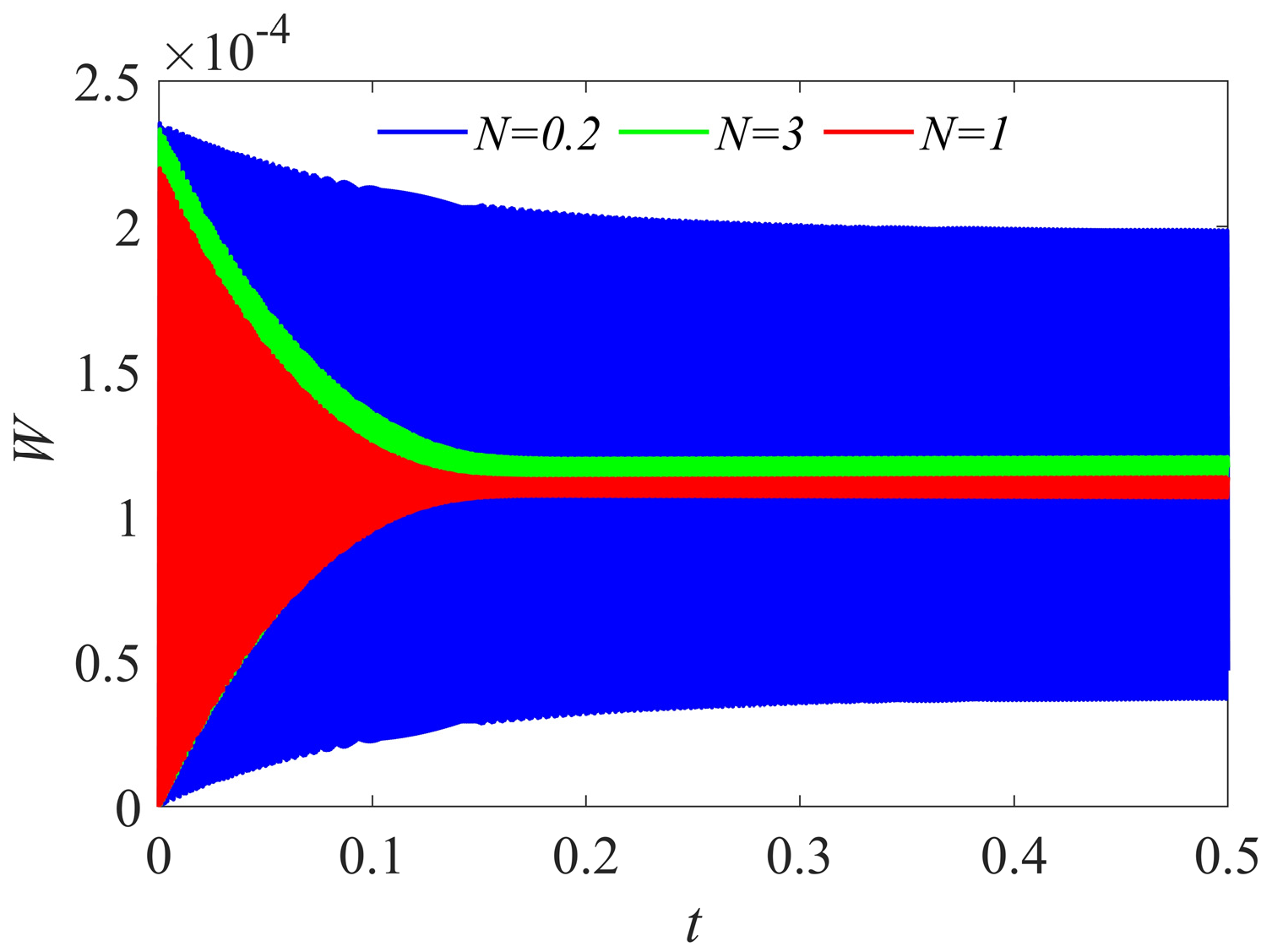
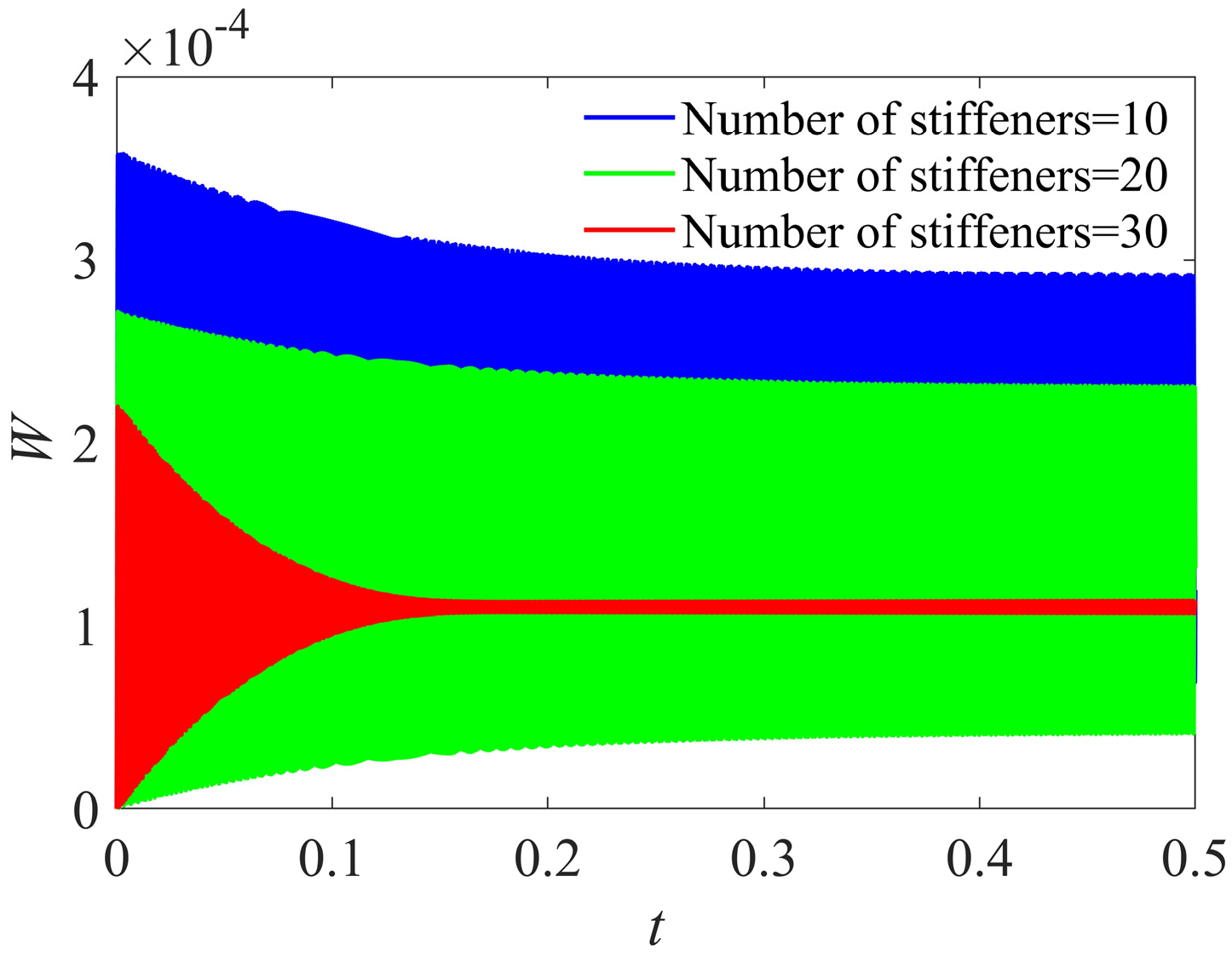
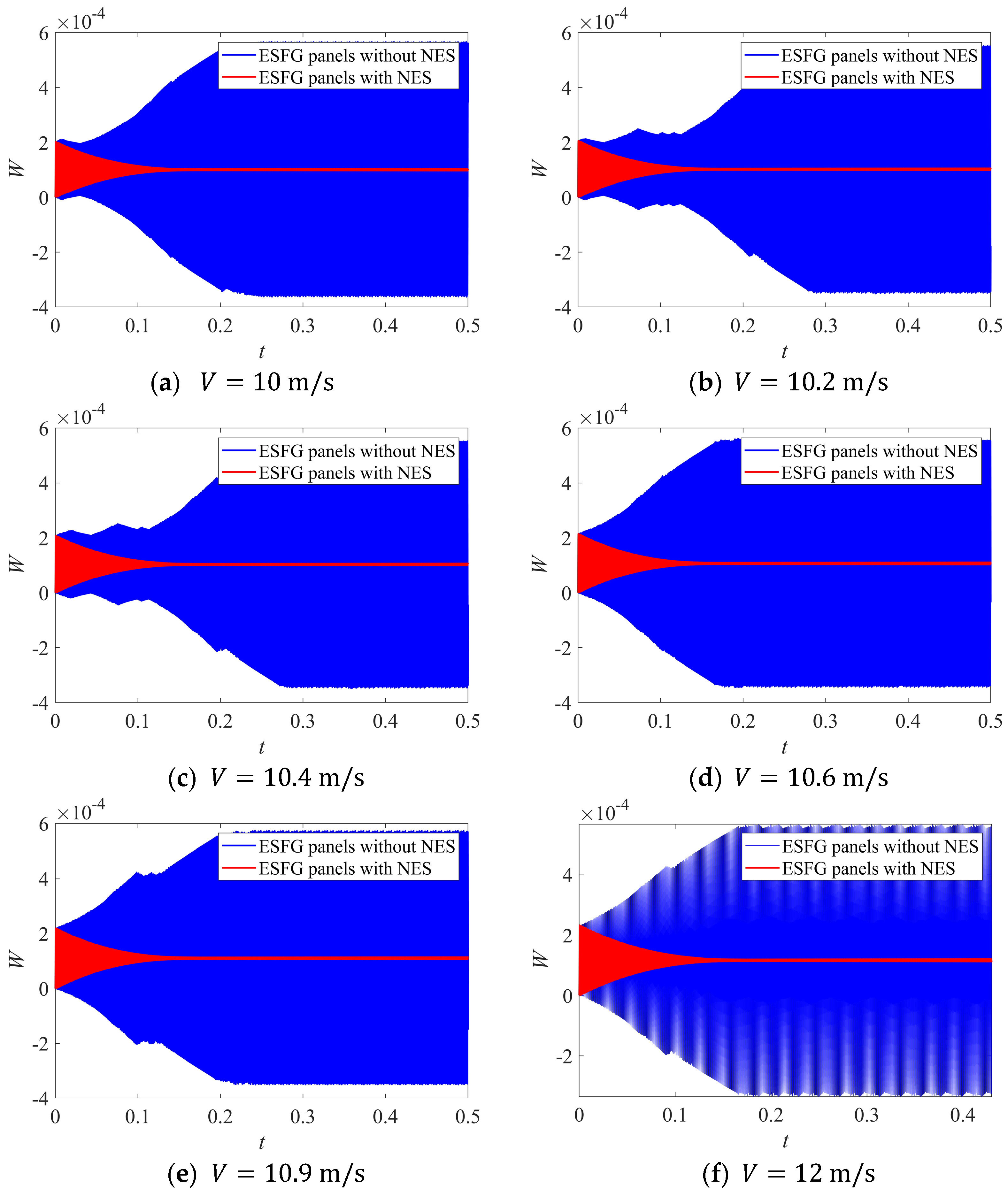
3.2. Vibration Behaviors of ESFG Panels
4. Conclusions
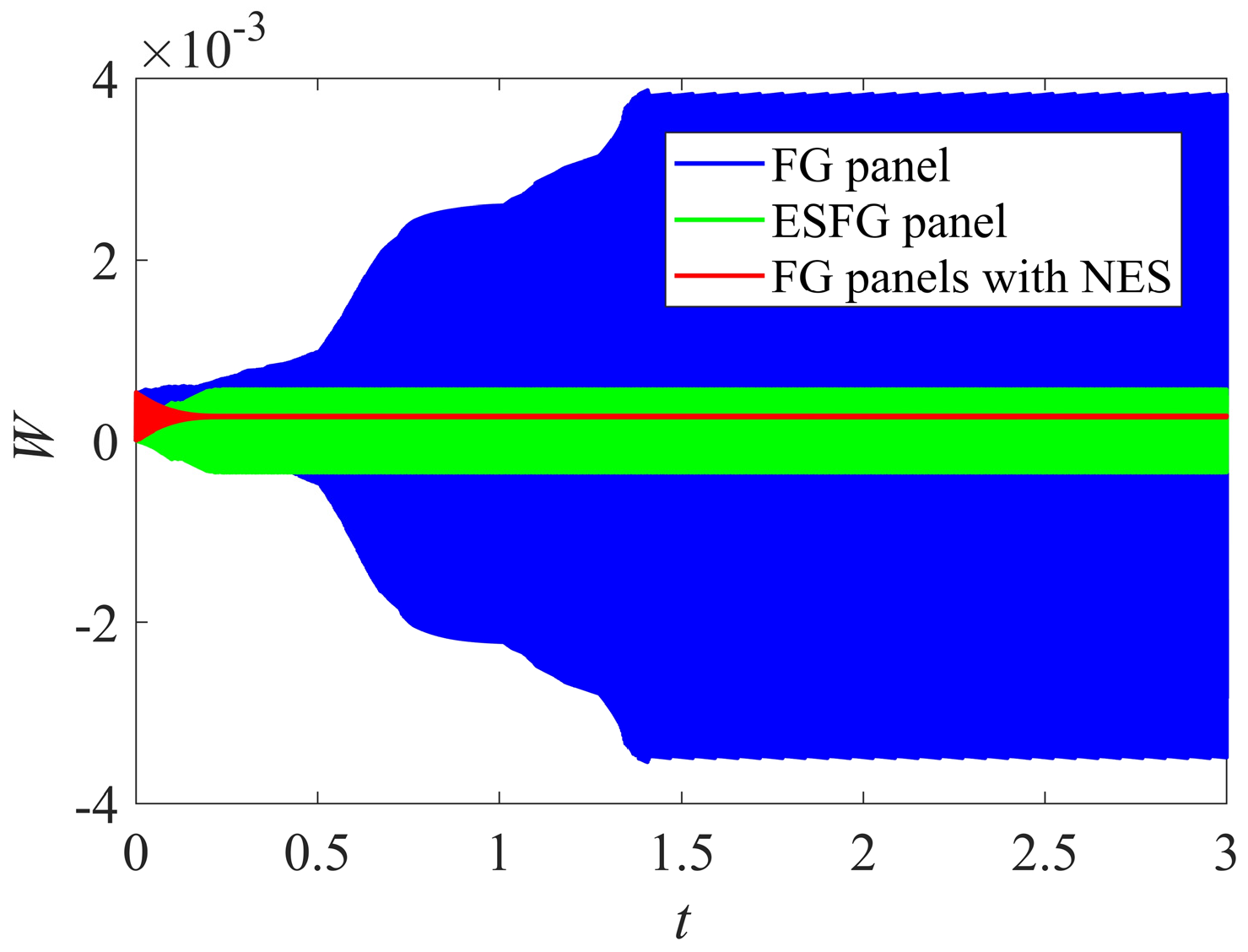
- The FG stiffeners significantly reduce the amplitude of nonlinear vibrations of the FG panels; however, the NES absorber has an even greater effect on reducing the vibration amplitude than the FG stiffeners.
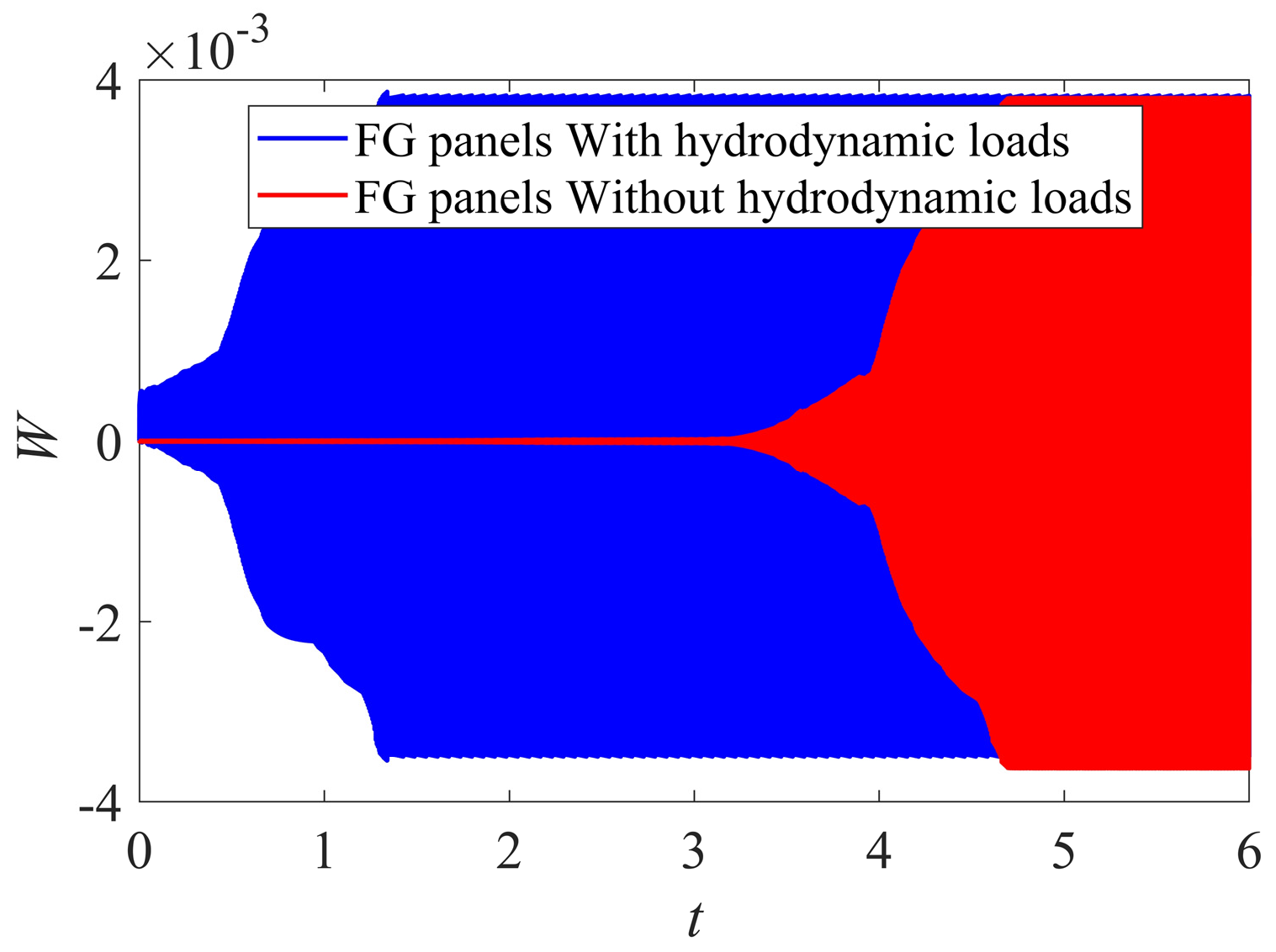
- Using the NES absorber for the ESFG panels under hydrodynamic lift and drag loads for various velocities can effectively decrease the vibrational energy and consequently leads to increasing the service life of marine structures.
- The maximum deflection of the ESFG panels under hydrodynamic lift and drag loads is substantially reduced by positioning the NES absorber at the center of the panels.
- When the material properties of both the stiffeners and panels are FG, the maximum deflection of the ESFG panels is substantially reduced. Additionally, when the material properties of the panel and stiffeners approach those of ceramic and metal, respectively, the vibration amplitude is lower than when the material properties of the panel and stiffeners approach those of metal and ceramic, respectively.
- Increasing the number of stiffeners effectively decreases vibrational energy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shen, H.S.; Xiang, Y.; Lin, F. Nonlinear vibration of functionally graded graphene-reinforced composite laminated plates in thermal environments. Comput. Methods Appl. Mech. Eng. 2017, 319, 175–193. [Google Scholar] [CrossRef]
- Civalek, Ö.; Baltacıoglu, A.K. Free vibration analysis of laminated and FGM composite annular sector plates. Compos. Part B Eng. 2019, 157, 182–194. [Google Scholar] [CrossRef]
- Gao, K.; Gao, W.; Chen, D.; Yang, J. Nonlinear free vibration of functionally graded graphene platelets reinforced porous nanocomposite plates resting on elastic foundation. Compos. Struct. 2018, 204, 831–846. [Google Scholar] [CrossRef]
- Ye, C.; Wang, Y.Q. Nonlinear forced vibration of functionally graded graphene platelet-reinforced metal foam cylindrical shells: Internal resonances. Nonlinear Dyn. 2021, 104, 2051–2069. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Zhang, W. Vibration and flutter characteristics of GPL-reinforced functionally graded porous cylindrical panels subjected to supersonic flow. Acta Astronaut. 2021, 183, 89–100. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Ghaedsharaf, M. Three-dimensional free vibration of laminated cylindrical panels with functionally graded layers. Compos. Struct. 2014, 108, 894–904. [Google Scholar] [CrossRef]
- Khoa, N.D.; Anh, V.M.; Duc, N.D. Nonlinear dynamic response and vibration of functionally graded nanocomposite cylindrical panel reinforced by carbon nanotubes in thermal environment. J. Sandw. Struct. Mater. 2021, 23, 852–883. [Google Scholar] [CrossRef]
- Sheng, G.G.; Wang, X. Nonlinear vibration control of functionally graded laminated cylindrical shells. Compos. B Eng. 2013, 52, 1–10. [Google Scholar] [CrossRef]
- Arefi, M.; Ghasemian Talkhunche, G. Higher-order vibration analysis of FG cylindrical nano-shell. Eur. Phys. J. Plus 2021, 136, 154. [Google Scholar] [CrossRef]
- Jafari Niasar, M.; Jafari, A.A.; Irani Rahaghi, M.; Mohammadrezazadeh, S. Active control of free and forced vibration of a rotating FG cylindrical shell via FG piezoelectric patches. Mech. Based Des. Struct. Mach. 2024, 52, 3900–3924. [Google Scholar] [CrossRef]
- Rahman, N.; Alam, M.N.; Junaid, M. Active vibration control of composite shallow shells: An integrated approach. J. Mech. Eng. Sci. 2018, 12, 3354. [Google Scholar] [CrossRef]
- Quoc, T.H.; Van Tham, V.; Tu, T.M. Active vibration control of a piezoelectric functionally graded carbon nanotube-reinforced spherical shell panel. Acta Mech. 2021, 232, 1005–1023. [Google Scholar] [CrossRef]
- Selim, B.A.; Liu, Z.; Liew, K.M. Active vibration control of functionally graded graphene nanoplatelets reinforced composite plates integrated with piezoelectric layers. Thin-Walled Struct. 2019, 145, 106372. [Google Scholar] [CrossRef]
- Al-Furjan, M.S.H.; Yin, C.; Shen, X.; Kolahchi, R.; Zarei, M.S.; Hajmohammad, M.H. Energy absorption and vibration of smart auxetic FG porous curved conical panels resting on the frictional viscoelastic torsional substrate. Mech. Syst. Signal Process. 2022, 178, 109269. [Google Scholar] [CrossRef]
- Bich, D.H.; Ninh, D.G. Research on dynamical buckling of imperfect stiffened three-layered toroidal shell segments containing fluid under mechanical loads. Acta Mech. 2017, 228, 711–730. [Google Scholar] [CrossRef]
- Wang, T.; Gao, W.; Zou, X.; Shen, Z.; Huang, H.; Zhang, X.; Liu, B. Applying a thermodynamic-based method to reveal the failure laws of CFRP stiffened plates. Mech. Adv. Mater. Struct. 2024, 1–16. [Google Scholar] [CrossRef]
- Xu, J.; Guo, Y.; He, Z.; Li, Z.; Liu, G.; He, Y. Simplified analytical method for predicting the large deformation of stiffened plates with initial cracks under repeated impacts. Ocean Eng. 2024, 304, 117886. [Google Scholar] [CrossRef]
- Azzara, R.; Filippi, M.; Carrera, E. Rotordynamic analyses of stiffened cylindrical structures using high-fidelity shell models. Mech. Adv. Mater. Struct. 2024, 31, 11677–11686. [Google Scholar] [CrossRef]
- Langley, R.S. A dynamic stiffness technique for the vibration analysis of stiffened shell structures. J. Sound Vib. 1992, 156, 521–540. [Google Scholar] [CrossRef]
- Shi, D.; Zhang, H.; Ding, Y.; Yang, C.; Cheng, T. The modeling method for vibration characteristics analysis of composite laminated rotationally stiffened shell. PLoS ONE 2024, 19, e0299586. [Google Scholar] [CrossRef]
- Nayak, A.N.; Bandyopadhyay, J.N. Dynamic response analysis of stiffened conoidal shells. J. Sound Vib. 2006, 291, 1288–1297. [Google Scholar] [CrossRef]
- Zheng, C.; Yang, Y.; Yu, W.; Chen, S.; Zhang, L.; Zhao, S. Study on Scaled Model with Distortion of Free Vibration of Longitudinal Ring-Stiffened Large Thin-walled Cylindrical Shell. Lat. Am. J. Solids Struct. 2024, 21, e549. [Google Scholar] [CrossRef]
- Duc, N.D.; Kim, S.E.; Manh, D.T.; Nguyen, P.D. Effect of eccentrically oblique stiffeners and temperature on the nonlinear static and dynamic response of S-FGM cylindrical panels. Thin-Walled Struct. 2020, 146, 106438. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, D.; Sharma, K. An analytical investigation on linear and nonlinear vibrational behavior of stiffened functionally graded shell panels under thermal environment. J. Vib. Eng. Technol. 2021, 9, 2047–2071. [Google Scholar] [CrossRef]
- Minh, T.Q.; Nam, V.H.; Duc, V.M.; Hung, V.T.; Ly, L.N.; Phuong, N.T. Nonlinear vibration and dynamic buckling responses of stiffened functionally graded graphene-reinforced cylindrical, parabolic, and sinusoid panels using the higher-order shear deformation theory. ZAMM-J. Appl. Math. Mech. Z. Angew. Math. Mech. 2024, 104, e202300580. [Google Scholar] [CrossRef]
- Aghamaleki, S.B.; Fakoor, M.; Hashemian, A.H. Damped Vibration and Optimization of the Geometrical Parameters of FG Stiffened Cylindrical Shells Resting on Elastic Foundation Using GA. Int. J. Struct. Stab. Dyn. 2024, 24, 2450264. [Google Scholar] [CrossRef]
- Ahmadi, H.; Foroutan, K. Active vibration control of nonlinear stiffened FG cylindrical shell under periodic loads. Smart Struct. Syst. Int. J. 2020, 25, 643–655. [Google Scholar]
- Wang, H.L.; Wang, X.; Ding, H. Low frequency multimode vibration suppression of floating raft system based on NES cells. Mar. Struct. 2024, 96, 103629. [Google Scholar] [CrossRef]
- Song, H.; Dong, M.; Gu, L. Research on Efficient Suspension Vibration Reduction Configuration for Effectively Reducing Energy Consumption. Sustainability 2024, 16, 4208. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, C.; Yu, M.; Huang, Z. Lightweight Design of Vibration Control Devices for Offshore Substations Based on Inerters. Sustainability 2024, 16, 3385. [Google Scholar] [CrossRef]
- Hu, H.; Zhong, R.; Wang, Q.; Shi, X. Spectro-geometry dynamic analysis of FG-GPLRC cylindrical shell with periodically embedded dynamic vibration absorbers. Thin-Walled Struct. 2024, 203, 112243. [Google Scholar] [CrossRef]
- Foroutan, K.; Ahmadi, H. Effect of dynamic absorber on the nonlinear vibration of SFG cylindrical shell. Adv. Aircr. Spacecr. Sci. 2020, 7, 291–308. [Google Scholar]
- Duc, N.D.; Hadavinia, H.; Van Thu, P.; Quan, T.Q. Vibration and nonlinear dynamic response of imperfect three-phase polymer nanocomposite panel resting on elastic foundations under hydrodynamic loads. Compos. Struct. 2015, 131, 229–237. [Google Scholar] [CrossRef]
- Brush, D.O.; Almroth, B.O. Buckling of Bars, Plates and Shells; Mc Graw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Bich, D.H.; Van Dung, D.; Nam, V.H. Nonlinear dynamical analysis of eccentrically stiffened functionally graded cylindrical panels. Compos. Struct. 2012, 94, 2465–2473. [Google Scholar] [CrossRef]
- Dai, L. Nonlinear Dynamics of Piecewise Constant Systems and Implementation of Piecewise Constant Arguments; World Scientific Publishing Co.: Hackensack, NJ, USA, 2008. [Google Scholar]
- Chorfi, S.M.; Houmat, A. Non-linear free vibration of a functionally graded doubly-curved shallow shell of elliptical plan-form. Compos. Struct. 2010, 92, 2573–2581. [Google Scholar] [CrossRef]
- Alijani, F.; Amabili, M.; Karagiozis, K.; Bakhtiari-Nejad, F. Nonlinear vibrations of functionally graded doubly curved shallow shells. J. Sound Vib. 2011, 330, 1432–1454. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded shallow shells according to a 2D higher-order deformation theory. Compos. Struct. 2008, 84, 132–146. [Google Scholar] [CrossRef]
- Soedel, W. Vibration of Sheels and Plates; Marcel Dekker: New York, NY, USA, 1981. [Google Scholar]
- Shen, H.S.; Xiang, Y. Nonlinear vibration of nanotube-reinforced composite cylindrical shells in thermal environments. Comput. Method Appl. Mech. Eng. 2012, 213, 196–205. [Google Scholar] [CrossRef]
- Deb Nath, J.M. Dynamics of Rectangular Curved Plates. Doctoral Dissertation, University of Southampton, Hampshire, UK, 1969. [Google Scholar]
- Chern, Y.C.; Chao, C.C. Comparison of natural frequencies of laminates by 3-D theory, part II: Curved panels. J. Sound Vib. 2000, 230, 1009–1030. [Google Scholar] [CrossRef]
- Bardell, N.S.; Mead, D.J. Free vibration of an orthogonally stiffened cylindrical shell, Part I: Discrete line simple supports. J. Sound Vib. 1989, 134, 29–54. [Google Scholar] [CrossRef]
- Szilard, R. Theory and Analysis of Plates; Prentice-Hall: Hoboken, NJ, USA, 1974. [Google Scholar]
- Troitsky, M.S. Stiffened Plates; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Matveev, K. Hydrofoils and Advanced Marine Vehicles. Available online: http://hydrofoil.org/ (accessed on 10 November 2024).



| Present | Alijani et al. [37] | Matsunaga [38] | Chorfi and Houmat [39] | ||
|---|---|---|---|---|---|
| FG plate | |||||
| 0 | 1 | 0.0456 | 0.0456 | 0.0430 | 0.0442 |
| 0.5 | 0.0506 | 0.0506 | 0.0492 | 0.0490 | |
| FG cylindrical panel | |||||
| 0.5 | 1 | 0.0501 | 0.0501 | 0.0485 | 0.0490 |
| 0.5 | 0.0553 | 0.0553 | 0.0535 | 0.0540 | |
| Present | Soedel [40] | Shen and Xiang [41] | Nath [42] | Chern and Chao [43] | Bardell and Mead [44] | |||
|---|---|---|---|---|---|---|---|---|
| 2.4384 | 1.2190 | (1,1) | 162.2 | 163.7 | 163.2 | 163.9 | 161.4 | 163.1 |
| 1.2192 | 0.7112 | (1,2) | 182.0 | 182.1 | 181.7 | 182.2 | 180.8 | 181.6 |
| Drag (N) | Lift (N) | |
|---|---|---|
| 12 | 4416.1 | 129,529 |
| 10.9 | 5130.6 | 121,090 |
| 10.6 | 5243.2 | 117,836 |
| 10.4 | 6165.6 | 114,204 |
| 10.2 | 5380.6 | 112,730 |
| 10 | 5550.8 | 110,537 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foroutan, K.; Torabi, F. Enhancing Sustainability in Marine Structures: Nonlinear Energy Sink for Vibration Control of Eccentrically Stiffened Functionally Graded Panels Under Hydrodynamic Loads. Sustainability 2024, 16, 11111. https://doi.org/10.3390/su162411111
Foroutan K, Torabi F. Enhancing Sustainability in Marine Structures: Nonlinear Energy Sink for Vibration Control of Eccentrically Stiffened Functionally Graded Panels Under Hydrodynamic Loads. Sustainability. 2024; 16(24):11111. https://doi.org/10.3390/su162411111
Chicago/Turabian StyleForoutan, Kamran, and Farshid Torabi. 2024. "Enhancing Sustainability in Marine Structures: Nonlinear Energy Sink for Vibration Control of Eccentrically Stiffened Functionally Graded Panels Under Hydrodynamic Loads" Sustainability 16, no. 24: 11111. https://doi.org/10.3390/su162411111
APA StyleForoutan, K., & Torabi, F. (2024). Enhancing Sustainability in Marine Structures: Nonlinear Energy Sink for Vibration Control of Eccentrically Stiffened Functionally Graded Panels Under Hydrodynamic Loads. Sustainability, 16(24), 11111. https://doi.org/10.3390/su162411111