Dynamic Response Study of Coral Reef Revetment Project Under Extreme Wave Action
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Experimental Procedure
3. Results
3.1. Analysis of Average Overtopping Volume
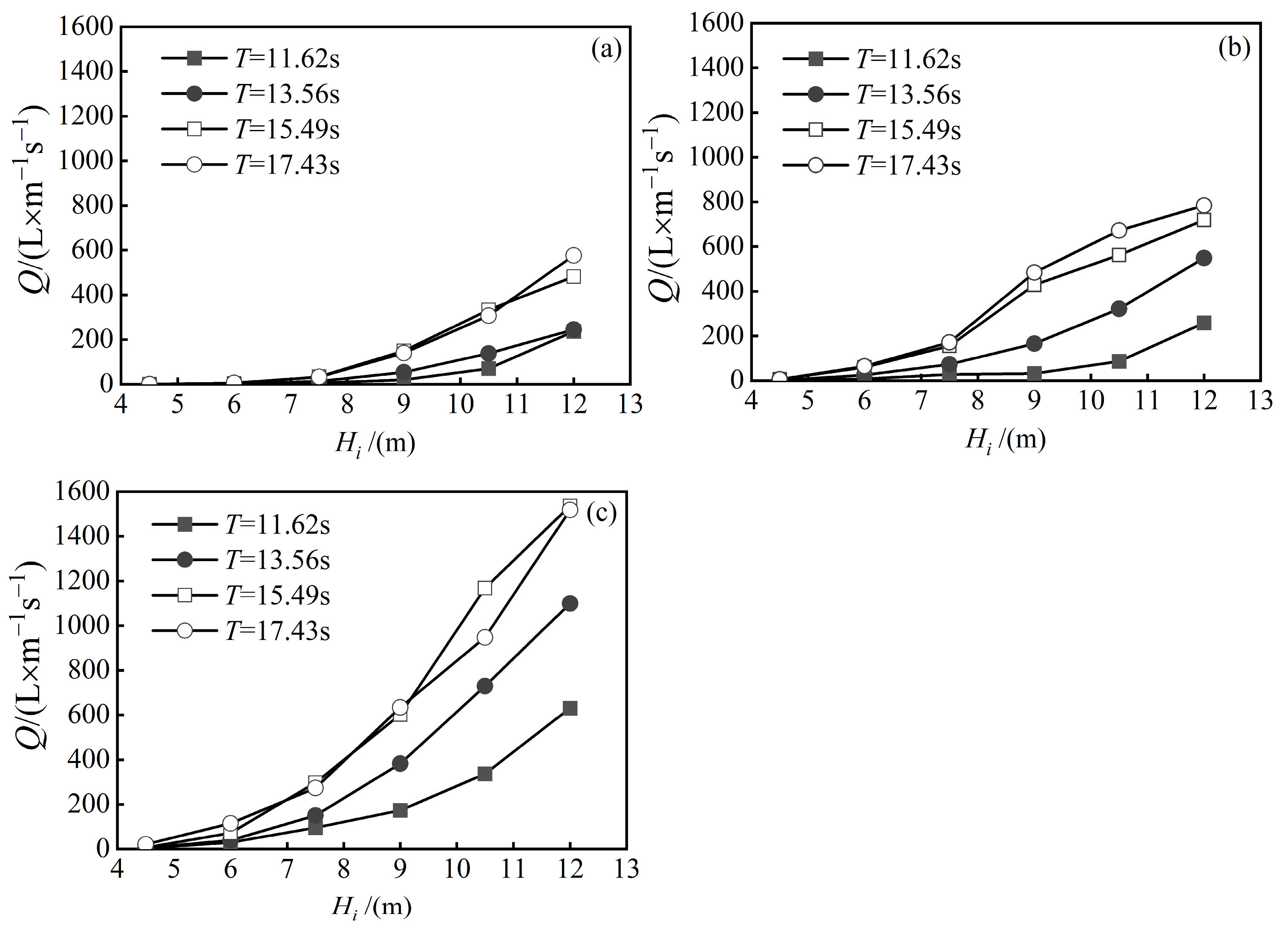
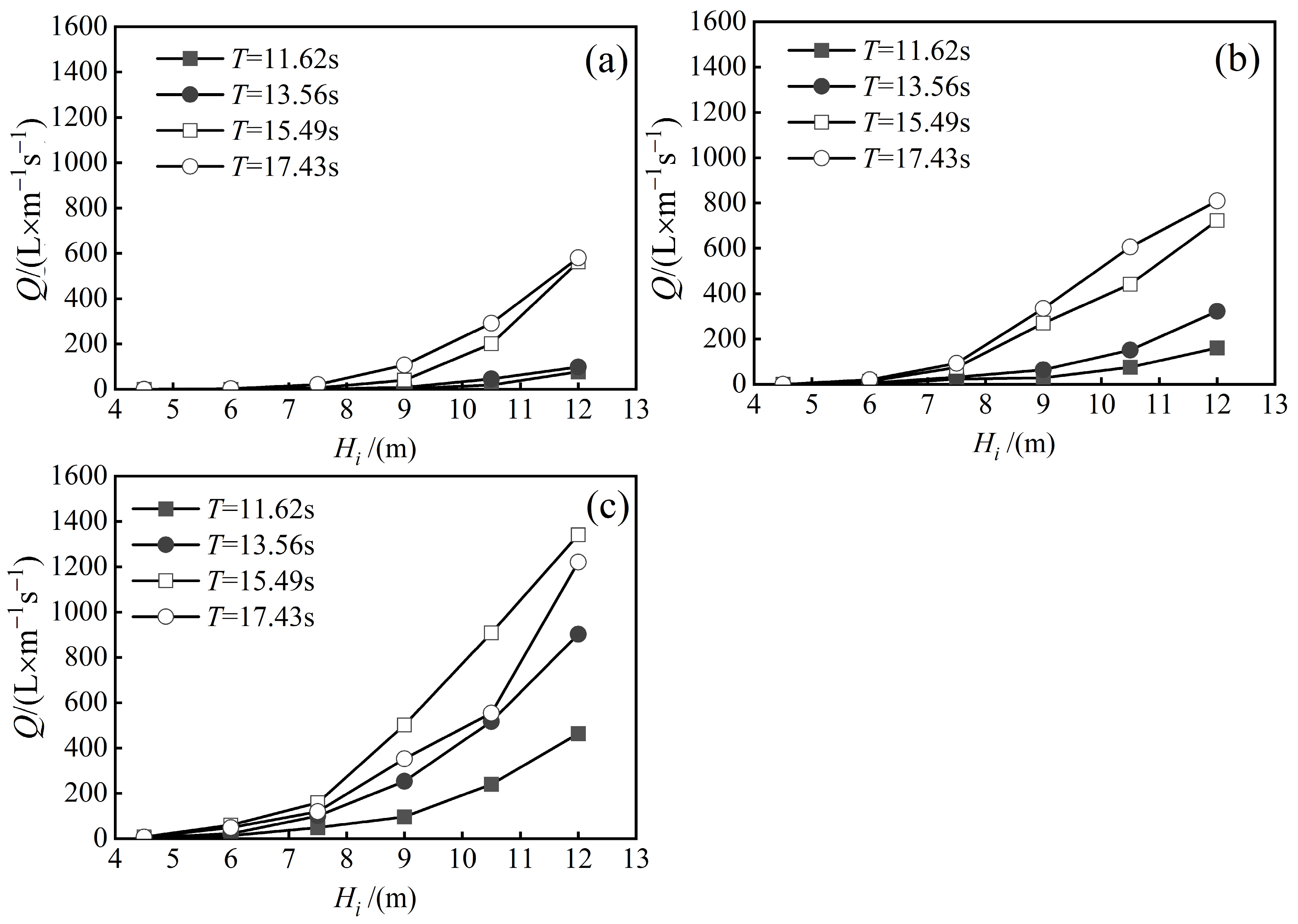
3.1.1. The Influence of Incident Wave Height and Period on Overtopping
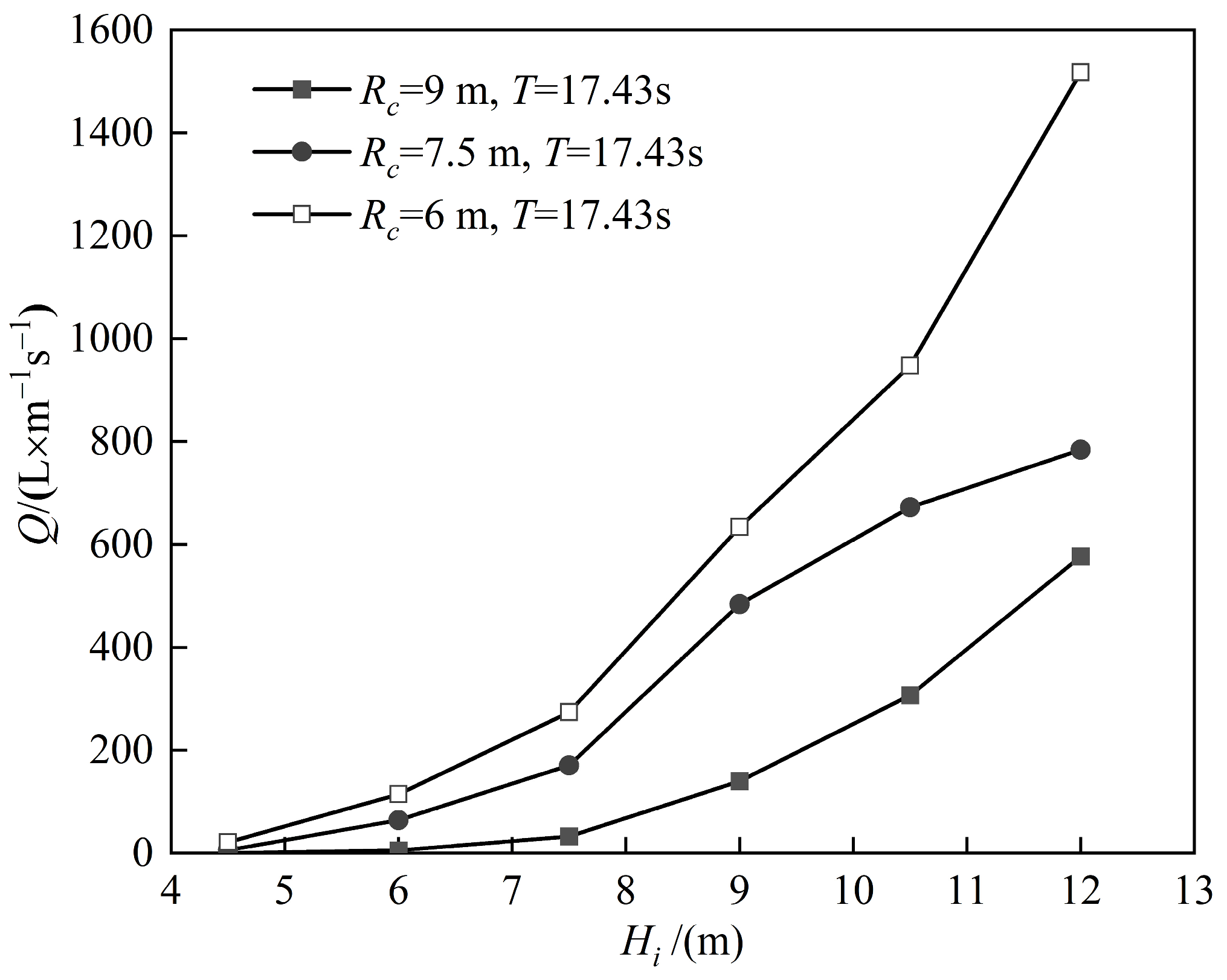
3.1.2. The Influence of Freeboard Height on Overtopping
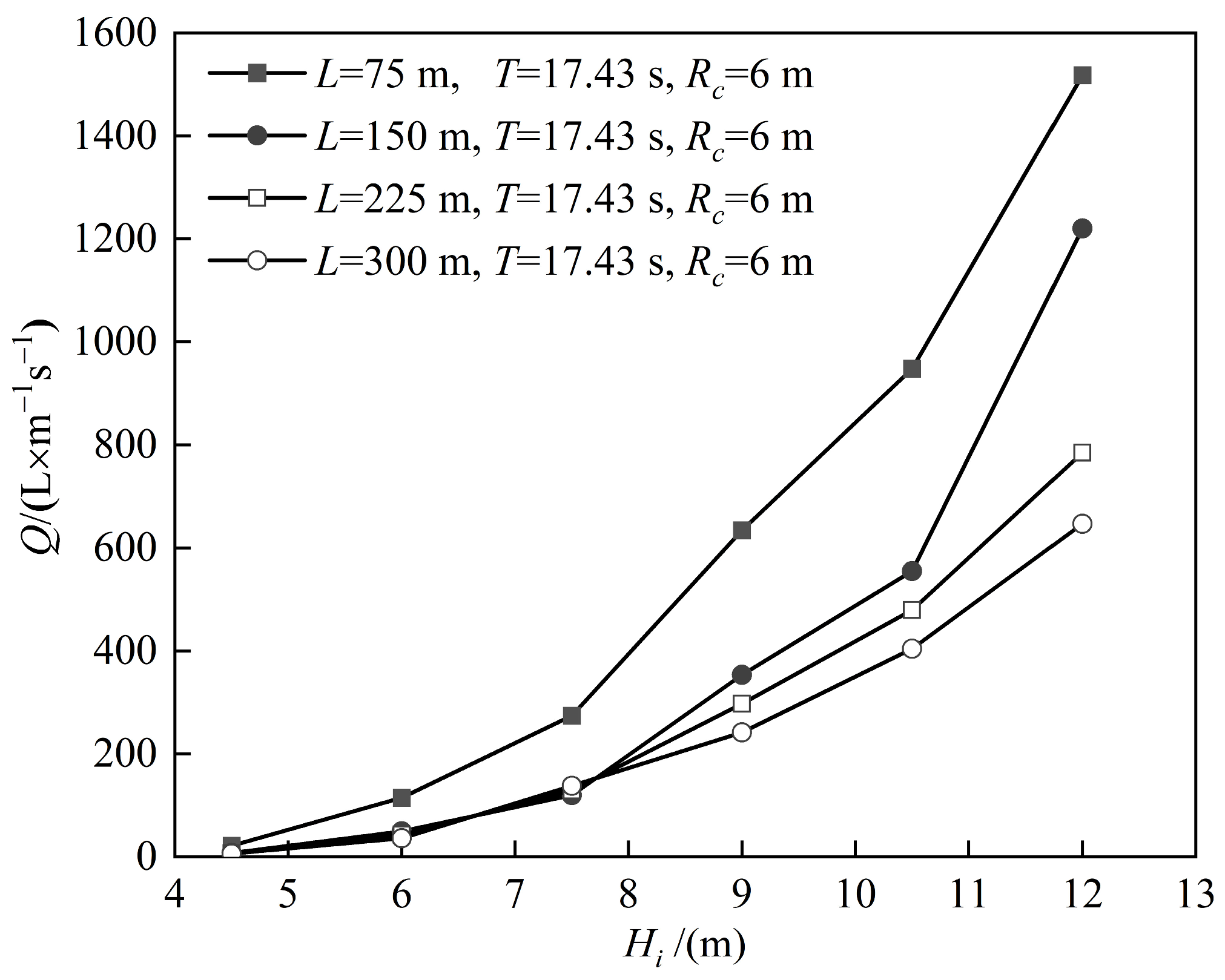
3.1.3. The Influence of the Location of the Revetment Project on Overtopping
3.1.4. The Influence of Wave Steepness on Overtopping
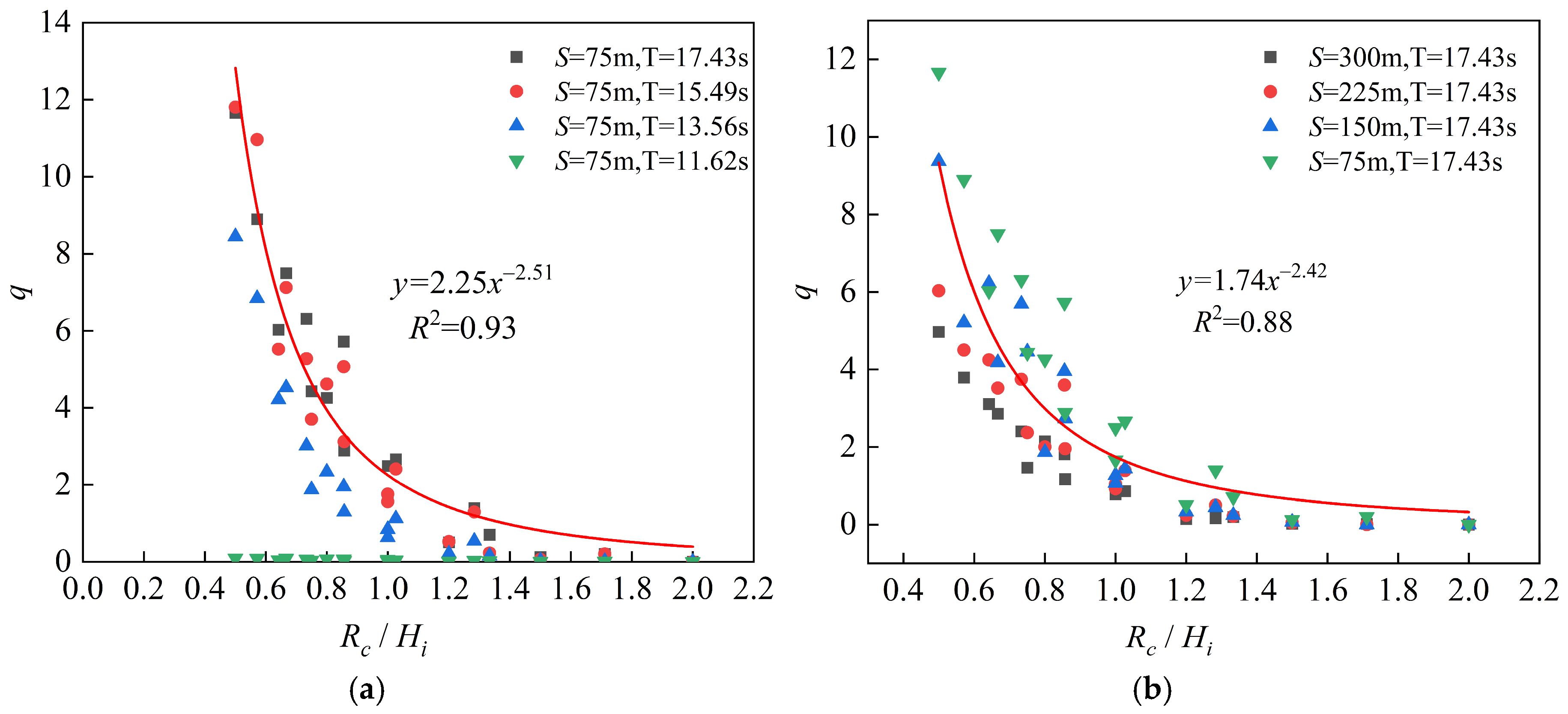
3.1.5. The Influence of Relative Freeboard Height on Overtopping
3.2. Analysis of Seawall Wave Pressure
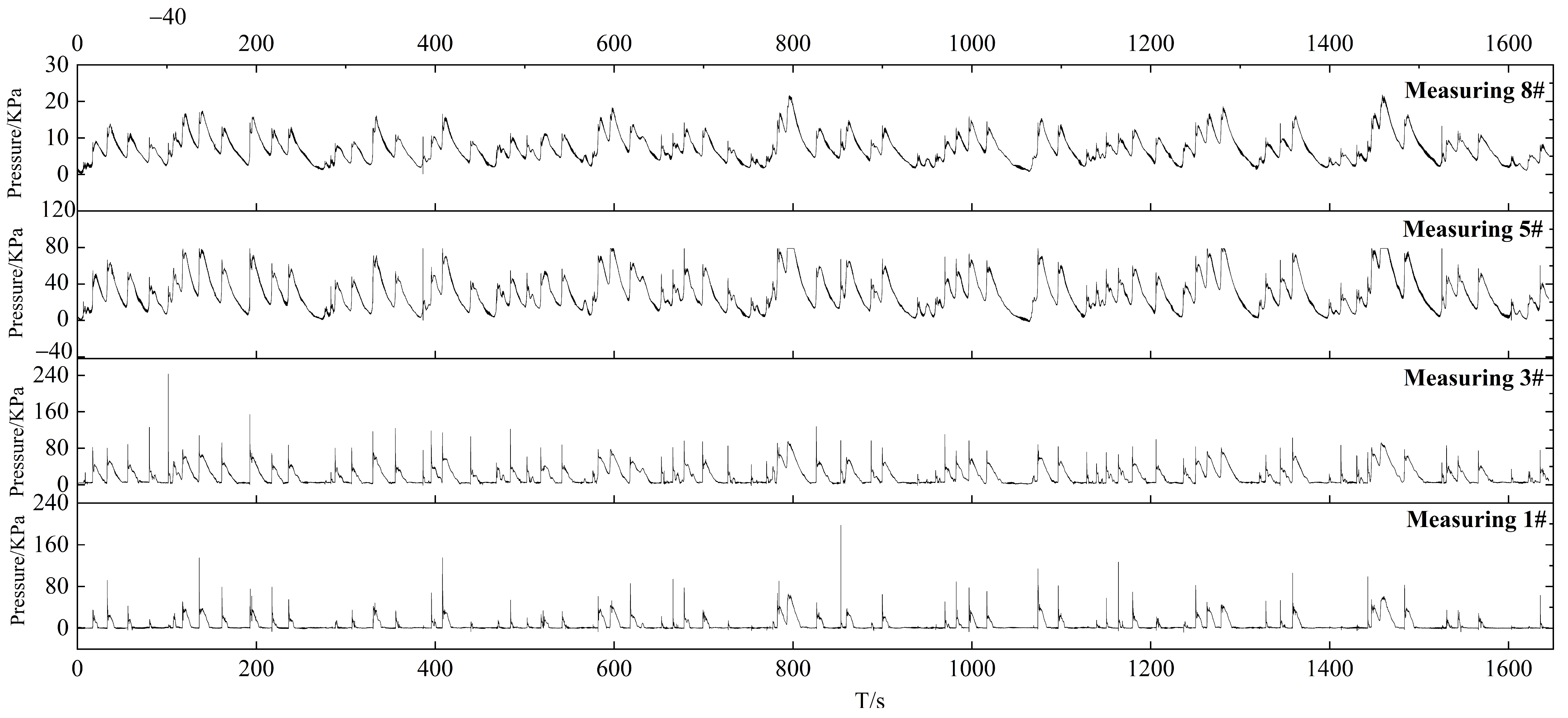
3.2.1. Pressure Varies with Time
3.2.2. The Influence of Incident Wave Height on Wave Pressure
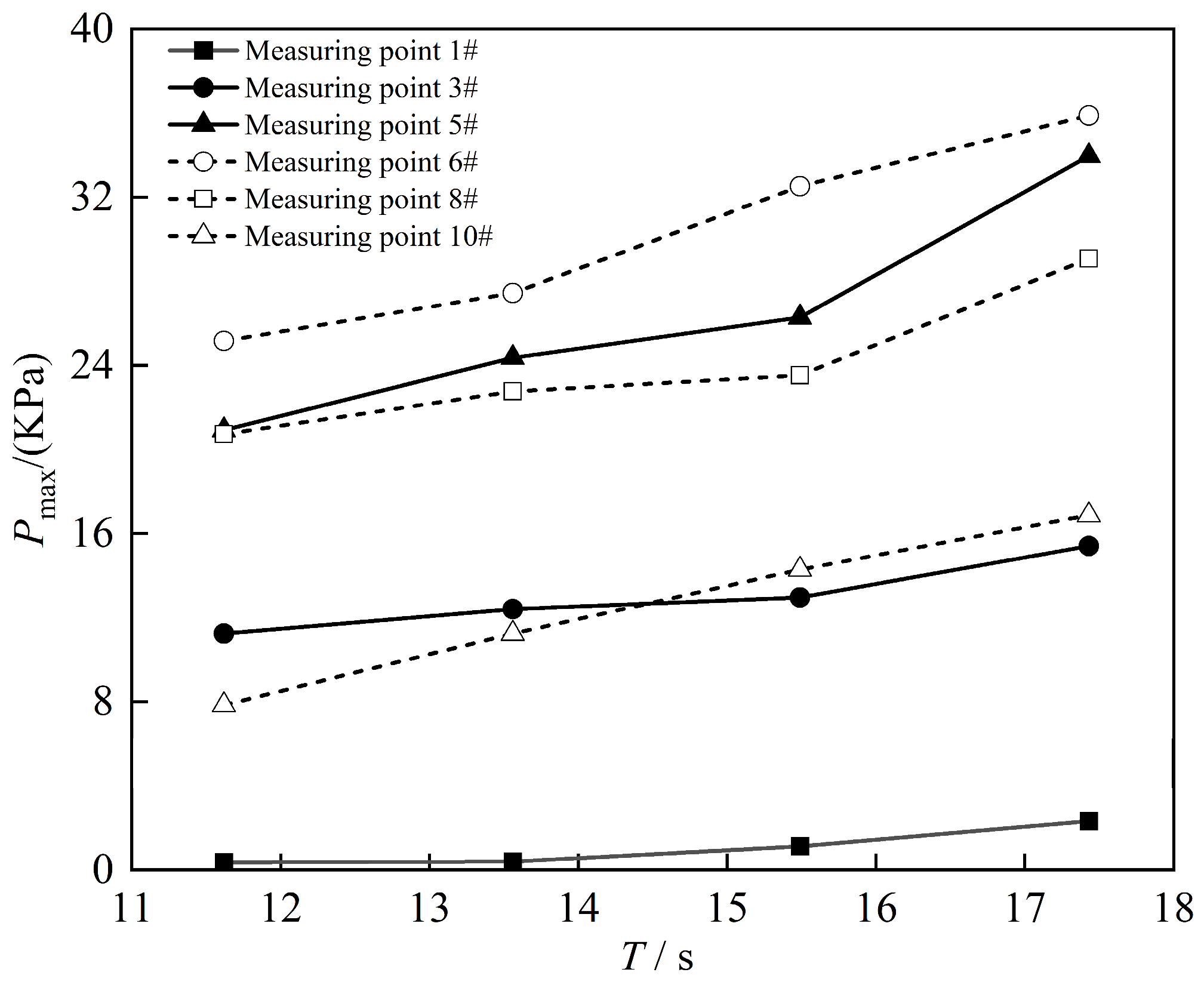
3.2.3. The Influence of Incident Wave Period on Wave Pressure
3.2.4. The Influence of Freeboard Height on Wave Pressure
3.2.5. The Influence of the Location of the Revetment Project on Wave Pressure
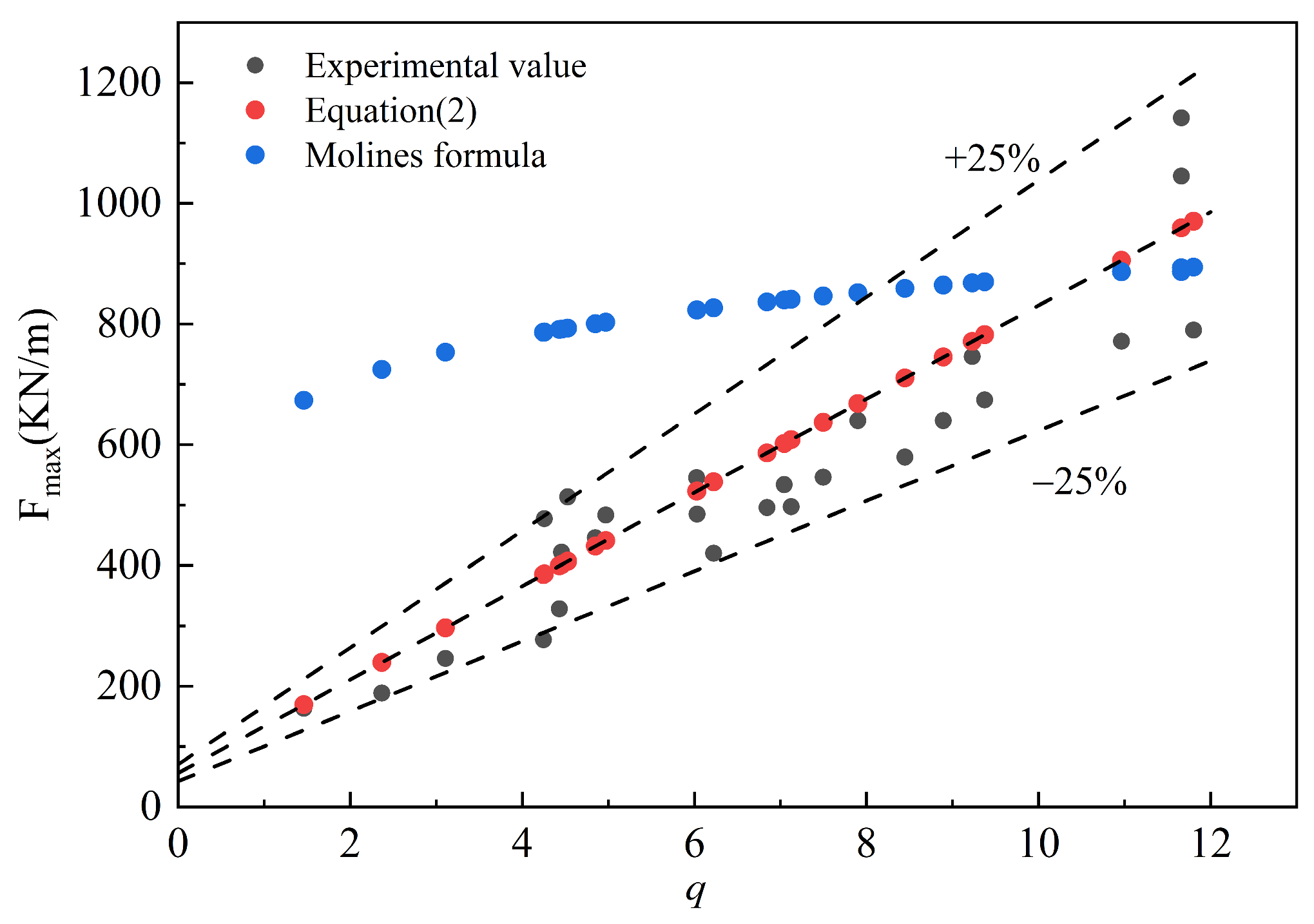
3.2.6. Comprehensive Analysis of Average Wave Overtopping Volume and Seawall Wave Force
4. Discussion
5. Conclusions
- (1)
- The average wave overtopping and the wave force on the seawall of the revetment project increase with the increase in incident wave period and wave height.
- (2)
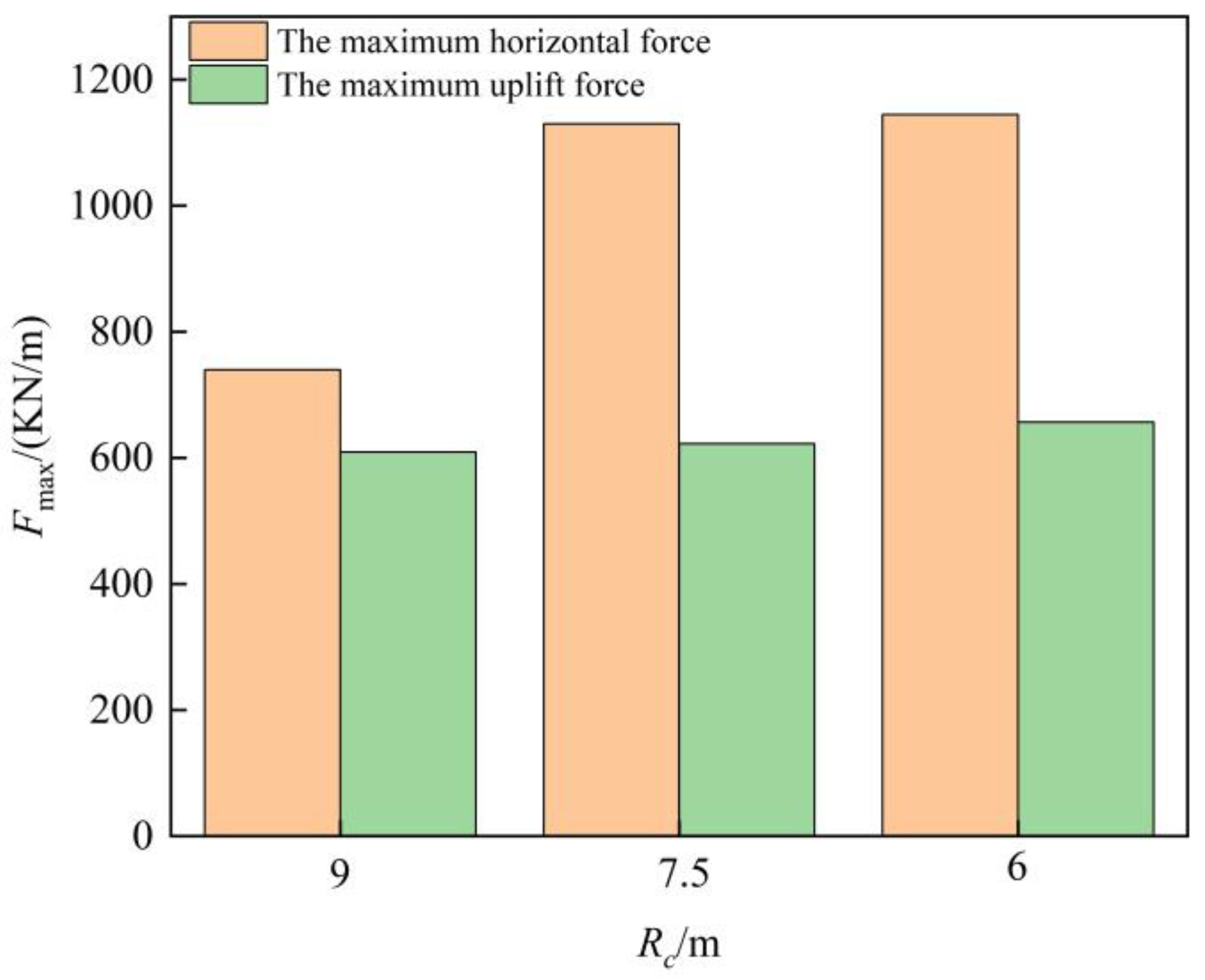
- The average wave overtopping and the wave force on the seawall of revetment projects are inversely proportional to the freeboard height of the seawall. Specifically, when the relative freeboard height (Rc/Hi) is greater than 2, the wave overtopping is 0. When Rc/Hi is less than 2, the dimensionless average wave overtopping decreases exponentially with the increase in relative freeboard height.
- (3)
- The average wave overtopping and the wave force on the seawall of revetment projects are directly proportional to the proximity of the revetment project to the reef edge. The closer the revetment project is to the reef edge, the greater the average wave overtopping and the wave force on the seawall.
- (4)
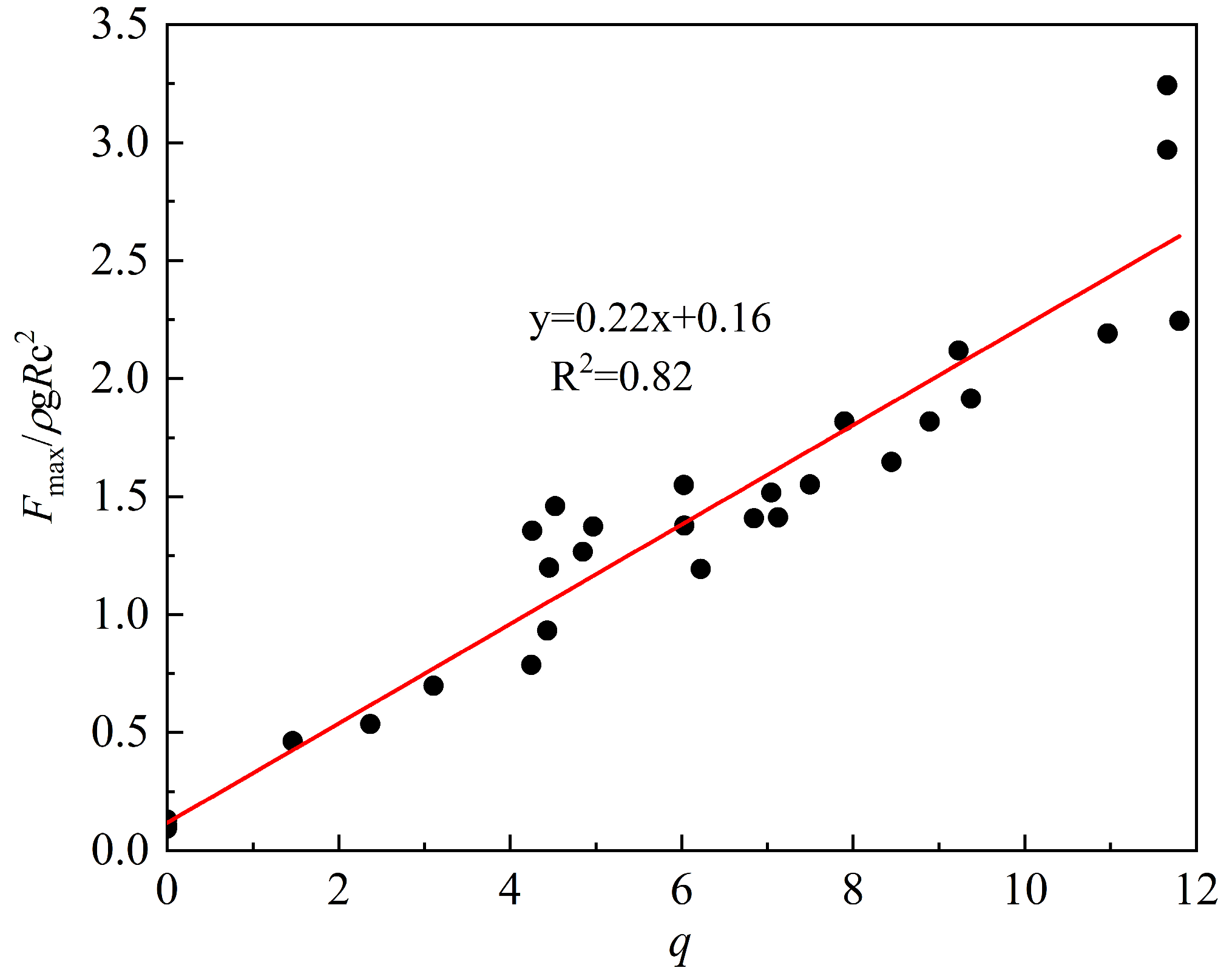
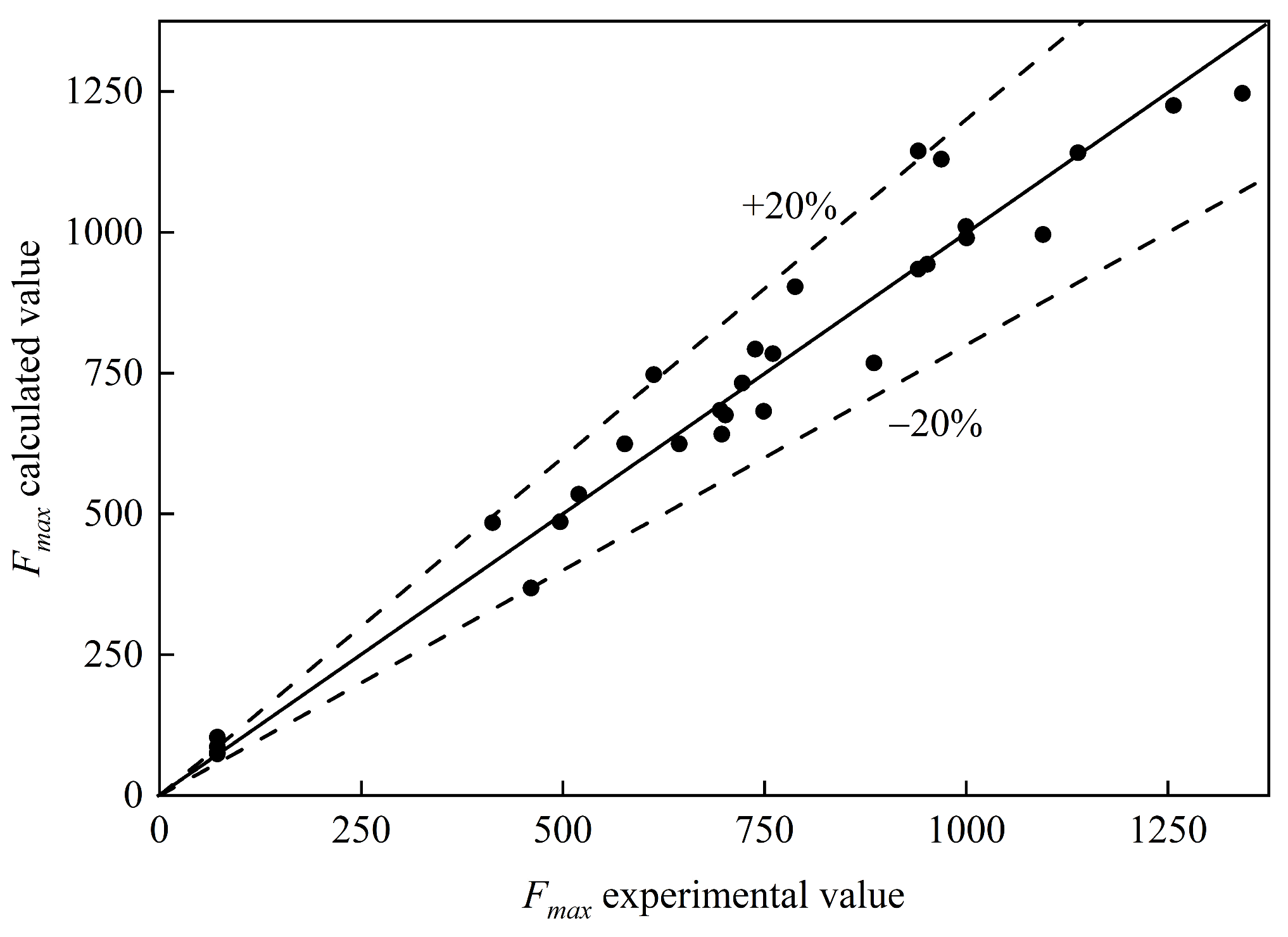
- In coral reef terrains, there exists a linear relationship between the dimensionless mean wave overtopping volume and the dimensionless maximum wave force in revetment projects. The wave force on the seawall can be directly calculated using the overtopping volume, with the calculation formula being as follows: fmax = Fmax/ρgRc2 = 0.22() + 0.16.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pedersen, J. Wave Forces and Overtopping on Seawalls of Rubble Mound Breakwaters. Ph.D. Thesis, Aalborg Universitetsforlag, Aalborg, Denmark, 1996. [Google Scholar]
- Nrgaard, J.Q.H.; Andersen, T.L.; Burcharth, H.F. Wave loads on rubble mound breakwater seawalls in deep and shallow water wave conditions. Coast. Eng. 2013, 80, 137–147. [Google Scholar] [CrossRef]
- Goda, Y. Estimation of the rate of irregular wave overtopping of seawalls. Rep. Port Harb. Res. Inst. 1970, 9, 3–41. [Google Scholar]
- Cecioni, C.; Franco, L.; Bellotti, G. Wave forces on breakwater seawalls: Physical model tests and improvement of prediction. In Proceedings of the International Conference of Coastal Structures, Hannover, Germany, 29 September–2 October 2019. [Google Scholar]
- Han, X.; Dong, S. Interaction between medium-long period waves and smoothed mound breakwater with seawall based on experiments and multi-phase simulations. Ocean Eng. 2023, 279, 114576. [Google Scholar] [CrossRef]
- Molines, J.; Bayón, A.; Gómez-Martín, M.E.; Medina, J.R. Numerical study of wave forces on seawalls of mound breakwaters with parapets. J. Mar. Sci. 2020, 8, 276. [Google Scholar]
- Han, X.; Dong, S.J. Wave Force on the seawall of Rubble Mound Breakwaters at Intermediate Depths. J. Ocean Univ. China 2023, 22, 53–64. [Google Scholar] [CrossRef]
- Chen, S.; Chen, H.; Zhao, H.; Zheng, J.; Zhang, C. Experimental study on wave forces acting on seawalls over coral reef terrain in a large flume. J. Hohai Univ. (Nat. Sci.) 2019, 47, 65–70. (In Chinese) [Google Scholar]
- Meer, J.W.V.D.; Janssen, J.P.F.M. Wave run-up and wave overtopping at dikes. In Wave Forces on Inclined and Vertical Wall Structures; American Society of Civil Engineers: New York, NY, USA, 1995. [Google Scholar]
- Ward, D.L.; Ahrens, J.P. Overtopping Rates for Seawalls; Army Engineer Research and Development Center (ERDC): Vicksburg, MS, USA, 1992. [Google Scholar]
- JTS 145-2015; Hydrological Code for Port and Waterway Engineering. Ministry of Transport of the People’s Republic of China: Beijing, China, 2015. (In Chinese)
- Xia, Y.; Li, H.; Shen, R. Analysis and research on allowable overtopping criteria for port engineering. Ocean Eng. 2013, 31, 104–109. (In Chinese) [Google Scholar]
- Pillai, K.; Etemad-Shahidi, A.; Lemckert, C.J.C.E. Wave overtopping at berm breakwaters: Experimental study and development of prediction formula. Coast. Eng. 2017, 130, 85–102. [Google Scholar] [CrossRef]
- Molines, J.; Ripoll, E.; Gómez-Martín, M.E.; Medina, J.R. Individual Wave Overtopping Volumes on Mound Breakwaters. Phys. Model. Coast. Eng. Sci. 2024, 159, 103703. [Google Scholar] [CrossRef]
- Yoo, D.-H.; Lee, Y.-C.; Kim, D.-S.; Lee, K.-H. An Experimental Study on the Estimation Method of Overtopping Discharge at the Rubble Mound Breakwater Using Wave-Overtopping Height. J. Navig. Port Res. 2024, 48, 192–199. [Google Scholar]
- Chen, S.; Wang, Z.; Zhang, C.; Chen, H.; Zheng, J. Experimental Study on Overtopping of Vertical Breakwaters over Coral Reef Terrain in a Large Flume. Chin. Sci. Bull. 2019, 64, 10. (In Chinese) [Google Scholar] [CrossRef]
- Miyaguni, T.; Matayoshi, S.; Nakaza, E.; Uza, T. Wave overtopping rate of a sea-wall on coral reef flat. Jpn. Soc. Civ. Eng. 2010, 24, 951–956. [Google Scholar]
- Molines, J.; Herrera, M.P.; Medina, J.R. Estimations of wave forces on seawalls based on wave overtopping rates. Coast. Eng. 2018, 132, 50–62. [Google Scholar] [CrossRef]
- Formentin, S.M.; Palma, G.; Zanuttigh, B.J.C.E. Integrated assessment of the hydraulic and structural performance of seawalls on top of smooth berms. Coast. Eng. 2021, 168, 103951. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Song, J.; Chi, S.; Zhao, S.; Qi, H.; Shi, J. Tide-modulated wave characteristics and breaking regimes in the intertidal zone of a dissipative beach. Ocean Eng. 2022, 266, 113055. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Zhao, S.; Qi, H.; Cai, F.; Zheng, J.J. Equilibrium configurations of sandy-muddy transitional beaches on South China coasts: Role of waves in formation of sand-mud transition boundary. Coast. Eng. 2024, 187, 104401. [Google Scholar] [CrossRef]

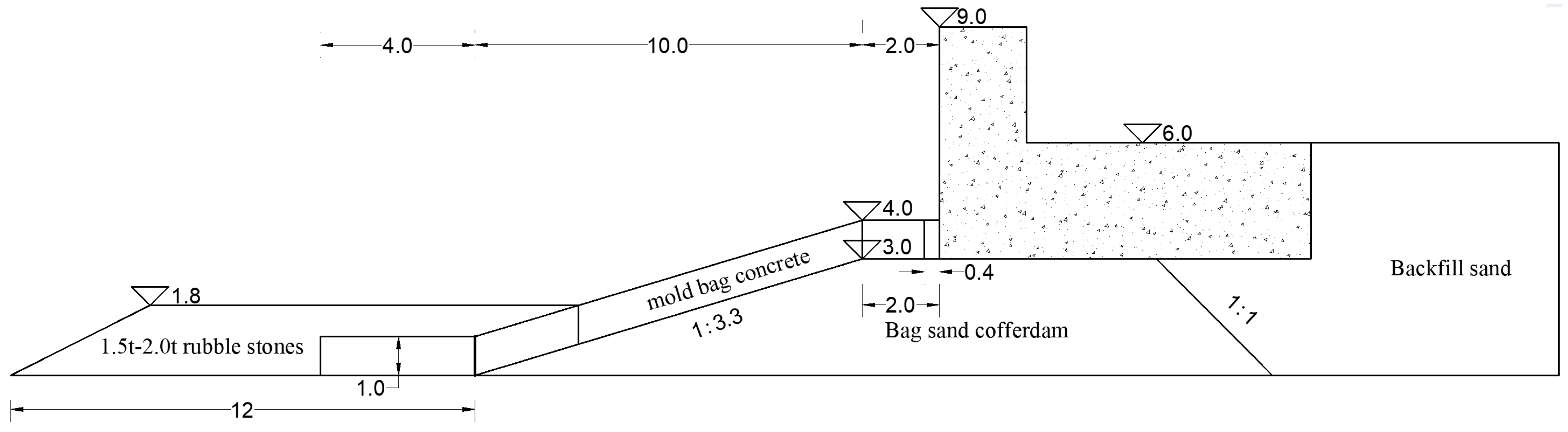

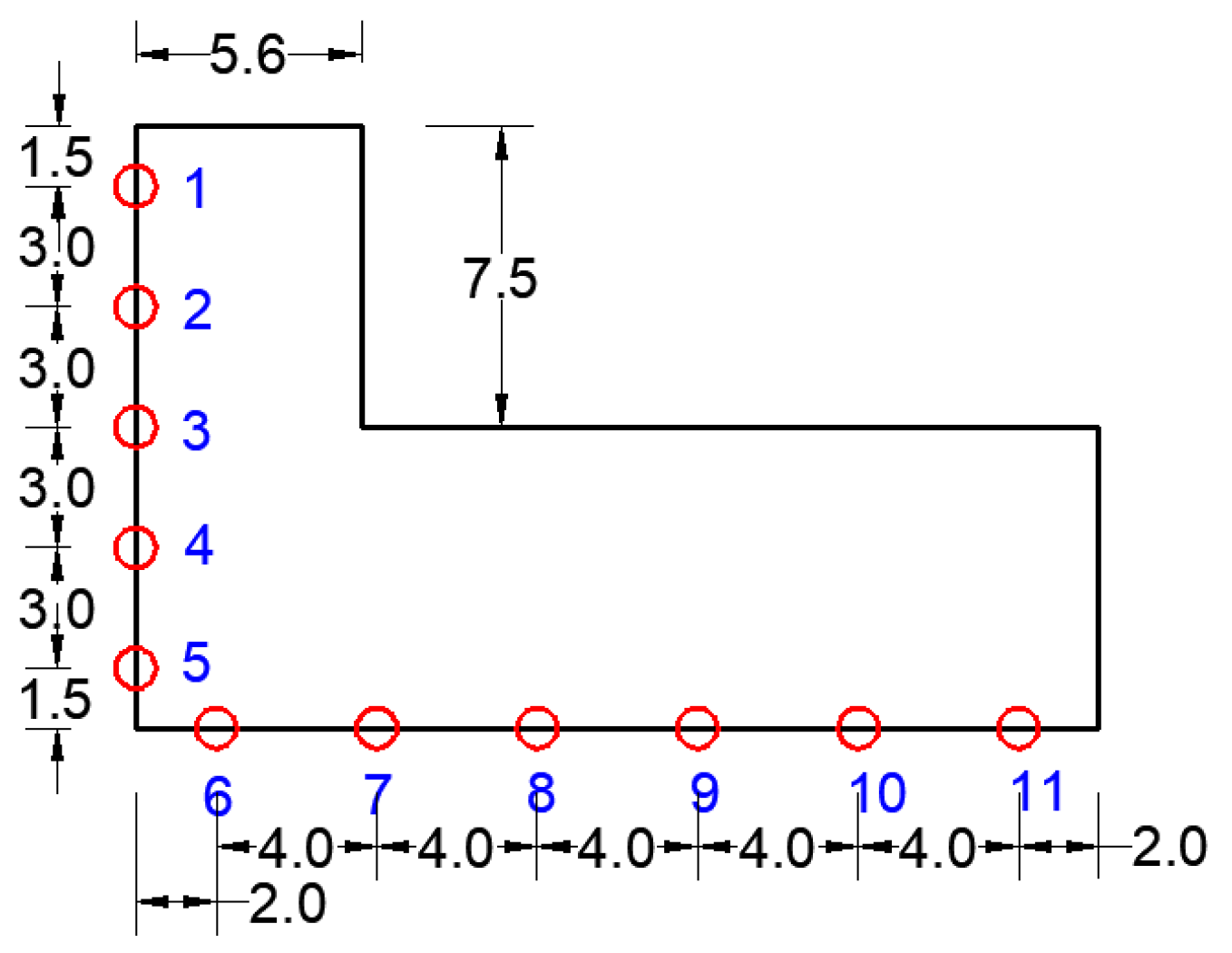



| Reef Flat Water Depth h/m | Freeboard Height Rc/m | Distance Between Revetment Project and Reef Edge S/m | Wave Type | Significant Wave Height Hi/m | Average Period T/s |
|---|---|---|---|---|---|
| 0 1.5 3 | 9 7.5 6 | 75 150 225 300 | Irregular waves (JONSWAP spectrum) | 4.5 6 7.5 9 10.5 12 | 11.62 13.56 15.49 17.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Chen, S.; Chen, H.; Nie, Z.; Qi, Z.; Duan, Z. Dynamic Response Study of Coral Reef Revetment Project Under Extreme Wave Action. Sustainability 2024, 16, 9939. https://doi.org/10.3390/su16229939
Hu J, Chen S, Chen H, Nie Z, Qi Z, Duan Z. Dynamic Response Study of Coral Reef Revetment Project Under Extreme Wave Action. Sustainability. 2024; 16(22):9939. https://doi.org/10.3390/su16229939
Chicago/Turabian StyleHu, Jielong, Songgui Chen, Hanbao Chen, Zhichao Nie, Zuoda Qi, and Zihao Duan. 2024. "Dynamic Response Study of Coral Reef Revetment Project Under Extreme Wave Action" Sustainability 16, no. 22: 9939. https://doi.org/10.3390/su16229939
APA StyleHu, J., Chen, S., Chen, H., Nie, Z., Qi, Z., & Duan, Z. (2024). Dynamic Response Study of Coral Reef Revetment Project Under Extreme Wave Action. Sustainability, 16(22), 9939. https://doi.org/10.3390/su16229939








