Assessing Regional Economic Performance in Romania Through Panel ARDL and Panel Quantile Regression Models
Abstract
1. Introduction
2. Literature Review
3. Methodology and Data Collection
3.1. Data Stationarity
3.1.1. LLC Panel Unit Root Test
3.1.2. IPS Panel Unit Root Test
3.1.3. Fisher-Type Panel Unit Root Tests
3.2. Panel ARDL
3.3. Panel Quartile Regression
3.4. Granger Panel Causality Test
4. Results and Discussions
4.1. Input Data Analysis
4.2. Empirical Results
4.3. Comparison across Quantiles
5. Conclusions and Policy Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Definition |
| LLC panel unit root test | Levin, Lin and Chu test |
| IPS test | Im, Pesaran, and Shin test |
| ADF | Augmented Dickey–Fuller |
| pARDL | Panel Autoregressive Distributed Lag |
| ECT | Error Correction Term |
| PQR | Panel Quantile Regression |
| OLS | Ordinary Least Squares |
| GDPR | Regional Gross Domestic Product |
| CTCRD | Research and Development Expenditure |
| IT | IT Equipment in the Administration of Public and Private University Education Unit |
| FCL | Number of Universities |
| NMPS | Average Number of Employees |
References
- Peng, B.; Sheng, X.; Wei, G. Does Environmental Protection Promote Economic Development? From the Perspective of Coupling Coordination between Environmental Protection and Economic Development. Environ. Sci. Pollut. Res. 2020, 27, 39135–39148. [Google Scholar] [CrossRef] [PubMed]
- Zakari, A.; Oluwaseyi Musibau, H. Sustainable Economic Development in OECD Countries: Does Energy Security Matter? Sustain. Dev. 2023, 32, 1337–1353. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, H. Green Connection to the World: Building Regional Responsible Sustainable Development Strategies. Sustain. Dev. 2024, 32, 3555–3568. [Google Scholar] [CrossRef]
- Cai, J.; Chen, Q.; Zhang, Z. Balancing Environmental Sustainability and Economic Development: Perspectives from New Structural Economics. Sustainability 2024, 16, 1124. [Google Scholar] [CrossRef]
- Balan, M. Estimating Economic and Social Regional Disparities in Romania. Academia Brâncuși 2018, 3, 5–18. [Google Scholar]
- Russu, C. Aspects of Regional Development in Romania. Econ. Isights Trends Chall. 2014, III, 25–32. [Google Scholar]
- Goschin, Z. Regional Growth in Romania after Its Accession to EU: A Shift-Share Analysis Approach. Procedia Econ. Financ. 2014, 15, 169–175. [Google Scholar] [CrossRef]
- Otoiu, A.; Titan, E. Socio-Economic Convergence in the EU at National and Regional Level. Procedia Econ. Financ. 2015, 23, 1090–1095. [Google Scholar] [CrossRef]
- Pridham, G. Romania and EU Membership in Comparative Perspective: A Post-Accession Compliance Problem?—The Case of Political Conditionality. Perspect. Eur. Politics Soc. 2007, 8, 168–188. [Google Scholar] [CrossRef]
- Dornean, A. Main Factors and Implications of Policies Implemented in Romania in the Context of the Current Global Crisis. Procedia Soc. Behav. Sci. 2012, 58, 454–463. [Google Scholar] [CrossRef][Green Version]
- Moussis, N. Guide to European Policies, 12th revised ed.; European Study Service: Brussels, Belgium, 2007; ISBN 978-2-930119-42-x. [Google Scholar]
- Gavriluţ, D.; Bădulescu, D.; University of Oradea, Romania; Jaganjac, J.; University “‘Vitez’” Bosnia and Herzegovina. The role of R&D sector on fostering economic growth. Insights from romania. In Proceedings of the 17th International Management Conference “Management Beyond Crisis: Rethinking Business Performance”, Bucharest, Romania, 2–3 November 2023. [Google Scholar]
- Kocsis, L.Z. The Importance of the Development of Industry in Romania and Its Development Potential. RETP 2024, 19, 56–76. [Google Scholar] [CrossRef]
- Androniceanu, A.; Georgescu, I.; Nica, E.; Popescu, G. A Computational Analysis of the Romanian Interregional Policy. In Proceedings of the 31st International Business Information Management Association Conference (IBIMA), Milan, Italy, 25–26 April 2018; pp. 1952–1962. [Google Scholar]
- Androniceanu, A.; Georgescu, I. Regional Policy in Romania: Main Changes and Dilemmas of Practice; London Scientific: London, UK, 2018; ISBN 978-0-9954618-5-7. [Google Scholar]
- Behrens, K.; Thisse, J.-F. Regional Economics: A New Economic Geography Perspective. Reg. Sci. Urban Econ. 2007, 37, 457–465. [Google Scholar] [CrossRef]
- Bailey, D.; Clark, J.; Colombelli, A.; Corradini, C.; De Propris, L.; Derudder, B.; Fratesi, U.; Fritsch, M.; Harrison, J.; Hatfield, M.; et al. Regions in a Time of Pandemic. Reg. Stud. 2020, 54, 1163–1174. [Google Scholar] [CrossRef]
- Martin, R.; Sunley, P. Regional Economic Resilience: Evolution and Evaluation. In Handbook on Regional Economic Resilience; Bristow, G., Healy, A., Eds.; Edward Elgar Publishing: Cheltenham, UK, 2020; ISBN 978-1-78536-086-2. [Google Scholar]
- Trippl, M.; Fastenrath, S.; Isaksen, A. Rethinking Regional Economic Resilience: Preconditions and Processes Shaping Transformative Resilience. Eur. Urban Reg. Stud. 2024, 31, 101–115. [Google Scholar] [CrossRef]
- Gumpert, M. Regional Economic Disparities under the Solow Model. Qual. Quant. 2024, 58, 1017–1037. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, R.; Sun, M.; Zhang, L.; Li, X.; Meng, L.; Wang, Y.; Liu, Q. Regional Sustainable Development Strategy Based on the Coordination between Ecology and Economy: A Case Study of Sichuan Province, China. Ecol. Indic. 2022, 134, 108445. [Google Scholar] [CrossRef]
- Szopik-Depczyńska, K.; Cheba, K.; Bąk, I.; Kędzierska-Szczepaniak, A.; Szczepaniak, K.; Ioppolo, G. Innovation Level and Local Development of EU Regions. A New Assessment Approach. Land Use Policy 2020, 99, 104837. [Google Scholar] [CrossRef]
- Ferreira, C.; Broughton, K.; Broadhurst, K.; Ferreira, J. Collaborative Innovation in a Local Authority—‘Local Economic Development-by-Project’? Public Manag. Rev. 2024, 26, 1405–1423. [Google Scholar] [CrossRef]
- Ma, R.; Sun, J.; Yin, J. Research on the Impact Mechanism of Smart City Construction on Economic Growth—An Analysis Based on the Schumpeterian Innovation Theory Framework. Systems 2024, 12, 251. [Google Scholar] [CrossRef]
- Shi, Y.; Jiang, Y.; Xie, C.; Li, C. Regional Innovation and Sustainable Development Interplay: Analyzing the Spatial Externalities of Domestic Demand in the New Development Paradigm. Sustainability 2024, 16, 2365. [Google Scholar] [CrossRef]
- Pusz, M.; Jonas, A.E.G.; Deutz, P. Knitting Circular Ties: Empowering Networks for the Social Enterprise-Led Local Development of an Integrative Circular Economy. Circ. Econ. Sust. 2024, 4, 201–232. [Google Scholar] [CrossRef]
- Anda, M.I.; Gabriela, B.; Nicolae, E.; Rehman, A. Economic Growth Drivers in Romania: Evidence from a NARDL Analysis. Sustainability 2023, 15, 5916. [Google Scholar] [CrossRef]
- Chiriță, N.; Ciurea, C.; Nica, I.; Delcea, C. Exploring Academic Networks in the Fields of Cybernetics and Economics: A Bibliometric Analysis of the Economic Computation and Economic Cybernetics Studies and Research Journal. ECECSR 2024, 58, 307–322. [Google Scholar] [CrossRef]
- Gurgu, E.; Frăsineanu, D.; Simbotin, G. How Creative Sectors Can Contribute to the Sustainable Developemnt of Romania. Ann. Spiru Haret Univ. Econ. Ser. 2024, 24, 1–27. [Google Scholar]
- Deng, P.; Lu, S.; Xiao, H. Evaluation of the Relevance Measure between Ports and Regional Economy Using Structural Equation Modeling. Transp. Policy 2013, 27, 123–133. [Google Scholar] [CrossRef]
- Park, J.S.; Seo, Y.-J. The Impact of Seaports on the Regional Economies in South Korea: Panel Evidence from the Augmented Solow Model. Transp. Res. Part E Logist. Transp. Rev. 2016, 85, 107–119. [Google Scholar] [CrossRef]
- Chen, Z. Measuring the Regional Economic Impacts of High-Speed Rail Using a Dynamic SCGE Model: The Case of China. Eur. Plan. Stud. 2019, 27, 483–512. [Google Scholar] [CrossRef]
- Kauppila, P.; Karjalainen, T.P. A Process Model to Assess the Regional Economic Impacts of Fishing Tourism: A Case Study in Northern Finland. Fish. Res. 2012, 127–128, 88–97. [Google Scholar] [CrossRef]
- Madsen, B.; Jensen-Butler, C. Theoretical and Operational Issues in Sub-Regional Economic Modelling, Illustrated through the Development and Application of the LINE Model. Econ. Model. 2004, 21, 471–508. [Google Scholar] [CrossRef]
- Charalampidis, I.; Karkatsoulis, P.; Capros, P. A Regional Economy-Energy-Transport Model of the EU for Assessing Decarbonization in Transport. Energies 2019, 12, 3128. [Google Scholar] [CrossRef]
- Mushtaq, S.; Cockfield, G.; White, N.; Jakeman, G. Modelling Interactions between Farm-Level Structural Adjustment and a Regional Economy: A Case of the Australian Rice Industry. Agric. Syst. 2014, 123, 34–42. [Google Scholar] [CrossRef]
- Garidzirai, R.; Muzindutsi, P.-F. A Panel ARDL Analsis of the Productivity of Key Economic Sectors Contributing to Local Economic Growth in an Emerging Country. Stud. Univ. Babes-Bolyai Oeconomica 2020, 65, 39–53. [Google Scholar] [CrossRef]
- Sadik-Zada, E.R.; Loewenstein, W.; Hasanli, Y. Production Linkages and Dynamic Fiscal Employment Effects of the Extractive Industries: Input-Output and Nonlinear ARDL Analyses of Azerbaijani Economy. Miner. Econ. 2021, 34, 3–18. [Google Scholar] [CrossRef]
- Qalandarovna Abdurakhmanova, G.; Jeong, J.Y.; Rakhimjon Ugli Oqmullayev, R.; Utkir Ugli Karimov, M. The Impact of Tourism on Employment and Economic Growth in Uzbekistan: An ARDL Bounds Testing Approach. In Proceedings of the 5th International Conference on Future Networks & Distributed Systems, Dubai, United Arab Emirates, 15–16 December 2021; ACM: New York, NY, USA, 2021; pp. 431–439. [Google Scholar]
- Levin, A.; Lin, C.-F.; James Chu, C.-S. Unit Root Tests in Panel Data: Asymptotic and Finite-Sample Properties. J. Econom. 2002, 108, 1–24. [Google Scholar] [CrossRef]
- Im, K.S.; Pesaran, M.H.; Shin, Y. Testing for Unit Roots in Heterogeneous Panels. J. Econom. 2003, 115, 53–74. [Google Scholar] [CrossRef]
- Maddala, G.S.; Wu, S. A Comparative Study of Unit Root Tests with Panel Data and a New Simple Test. Oxf. Bull. Econ. Stat. 1999, 61, 631–652. [Google Scholar] [CrossRef]
- Payne, J.E.; Lee, J.; Islam, M.T.; Nazlioglu, S. Stochastic Convergence of per Capita Greenhouse Gas Emissions: New Unit Root Tests with Breaks and a Factor Structure. Energy Econ. 2022, 113, 106201. [Google Scholar] [CrossRef]
- Babar, H.; Hamid, K.; Rasheed, M.; Rasool, F.; Saeed, M.Y. Do Macroeconomic Factors Are Interlinked with Stock Markets in Asian Emerging Economies. A Panel Data Approach. Int. J. Bus. Econ. Aff. 2024, 9, 42–51. [Google Scholar] [CrossRef]
- Kiran Baygin, B.; Çil, N. Persistence of Shocks on Non-Renewable and Renewable Energy Consumption: Evidence from 15 Leading Countries with Fourier Unit Root Test. Environ. Dev. Sustain. 2023, 26, 5915–5934. [Google Scholar] [CrossRef]
- Kilinc-Ata, N.; Barut, A.; Citil, M. Do Military Expenditures Have an Impact on the Adoption of Renewable Energy in OECD Nations? Evidence from a Panel Cointegration Test Approach. IJESM 2024. [Google Scholar] [CrossRef]
- Kathuria, K.; Kumar, N. Examining the Dynamics of India’s Major Exchange Rates Using Fourier Nonlinear Quantile Unit Root Test. Asia-Pac. Financ. Markets 2024, 1–16. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. Journal of the American Statistical Association 1979, 74, 427–431. [Google Scholar] [CrossRef]
- Choi, I. Unit Root Tests for Panel Data. J. Int. Money Financ. 2001, 20, 249–272. [Google Scholar] [CrossRef]
- Kaur, N.; Singh, B. Dynamics of Resource Allocation–Firm Performance Relationship: Panel Autoregressive Distributed Lag Approach. Manag. Decis. Econ. 2024, 45, 3663–3676. [Google Scholar] [CrossRef]
- Epo, B.N.; Tapche Ndam, Y.F.; Abiala, A.M. Knowledge Economy and Financial Development in Developing Countries: Evidence from a Panel Autoregressive Distributed-Lag (ARDL) Approach. J. Knowl. Econ. 2024, 1–55. [Google Scholar] [CrossRef]
- Ghazouani, T.; Maktouf, S. Impact of Natural Resources, Trade Openness, and Economic Growth on CO2 Emissions in Oil-exporting Countries: A Panel Autoregressive Distributed Lag Analysis. In Natural Resources Forum; Blackwell Publishing Ltd: Oxford, UK, 2023. [Google Scholar] [CrossRef]
- Ben Abdallah, A. The Relationship Between Trade Openness, Foreign Direct Investment Inflows, and Economic Growth in Middle East and North of Africa Region: Autoregressive Distributed Lag Model vs. Vector Error Correction Model. J. Knowl. Econ. 2024, 15, 1118–1141. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Shin, Y. Cointegration and Speed of Convergence to Equilibrium. J. Econom. 1996, 71, 117–143. [Google Scholar] [CrossRef]
- Zardoub, A. Exploring the Links between Financial Flows and Economic Growth: A Panel ARDL Approach. PRR 2023, 7, 90–104. [Google Scholar] [CrossRef]
- Hidthiir, M.H.B.; Ahmad, Z.; Junoh, M.Z.M.; Yusof, M.F.B. Dynamics of Economic Growth in ASEAN-5 Countries: A Panel ARDL Approach. Discov. Sustain. 2024, 5, 145. [Google Scholar] [CrossRef]
- Sek, S.K.; Sim, K.Y.; Mukherjee, D. Panel ARDL and NARDL Models: Role of Agriculture in Economic Growth in Selected Asian Countries. In Applied Econometric Analysis Using Cross Section and Panel Data; Mukherjee, D., Ed.; Contributions to Economics; Springer Nature Singapore: Singapore, 2023; pp. 471–503. ISBN 978-981-9949-01-4. [Google Scholar]
- Mehmood, K.; Tauseef Hassan, S.; Qiu, X.; Ali, S. Comparative Analysis of CO2 Emissions and Economic Performance in the United States and China: Navigating Sustainable Development in the Climate Change Era. Geosci. Front. 2024, 15, 101843. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K.F. Quantile Regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Baffour Gyau, E.; Li, Y.; Adu, D. Investigating the Impact of ICT on Transport-Based CO2 Emissions: Empirical Evidence from a Quantile Cointegration Regression Analysis. Environ. Sci. Pollut. Res. 2023, 31, 4606–4629. [Google Scholar] [CrossRef] [PubMed]
- Işık, C.; Bulut, U.; Ongan, S.; Islam, H.; Irfan, M. Exploring How Economic Growth, Renewable Energy, Internet Usage, and Mineral Rents Influence CO2 Emissions: A Panel Quantile Regression Analysis for 27 OECD Countries. Resour. Policy 2024, 92, 105025. [Google Scholar] [CrossRef]
- Elmonshid, L.B.E.; Sayed, O.A.; Awad Yousif, G.M.; Eldaw, K.E.H.I.; Hussein, M.A. The Impact of Financial Efficiency and Renewable Energy Consumption on CO2 Emission Reduction in GCC Economies: A Panel Data Quantile Regression Approach. Sustainability 2024, 16, 6242. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- National Institute of Statistics Statistical Data. Available online: https://insse.ro/cms/en (accessed on 9 October 2024).
- Ministry of Finance. 2003 Regular Report on Romania’s Progress Towards Accession. Available online: https://mfinante.gov.ro/documents/35673/228074/regular_report2003.pdf (accessed on 15 October 2024).

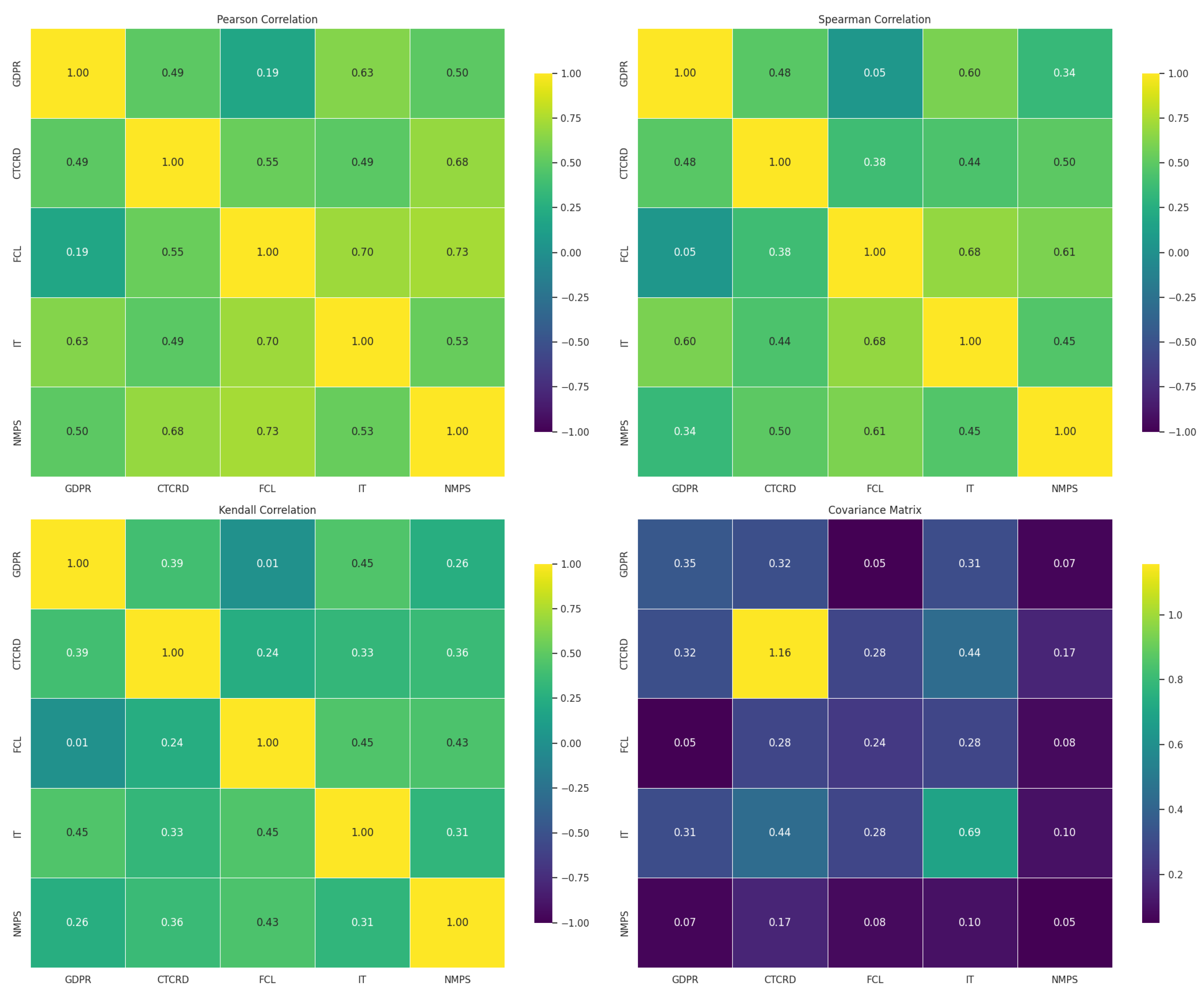


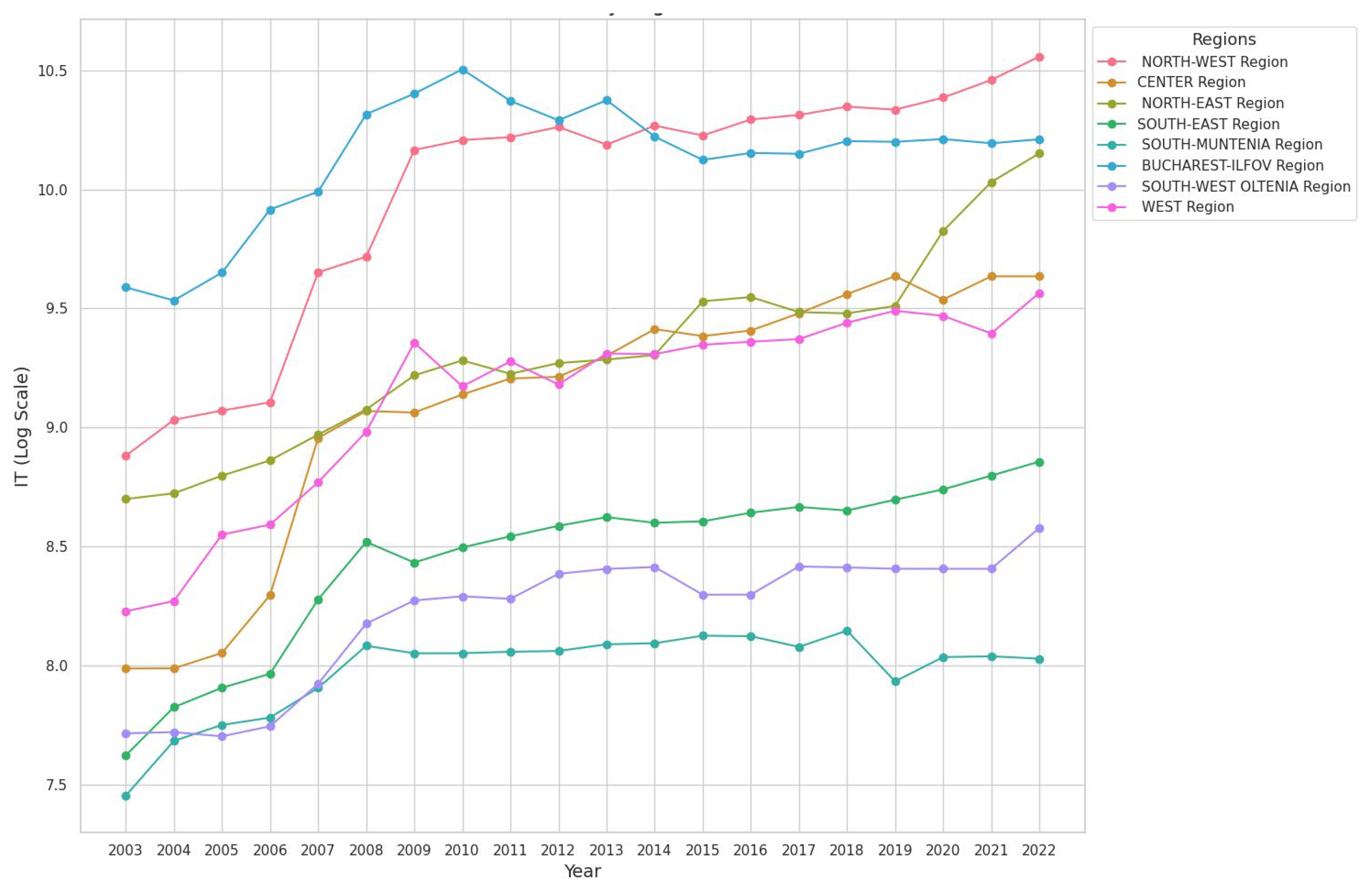
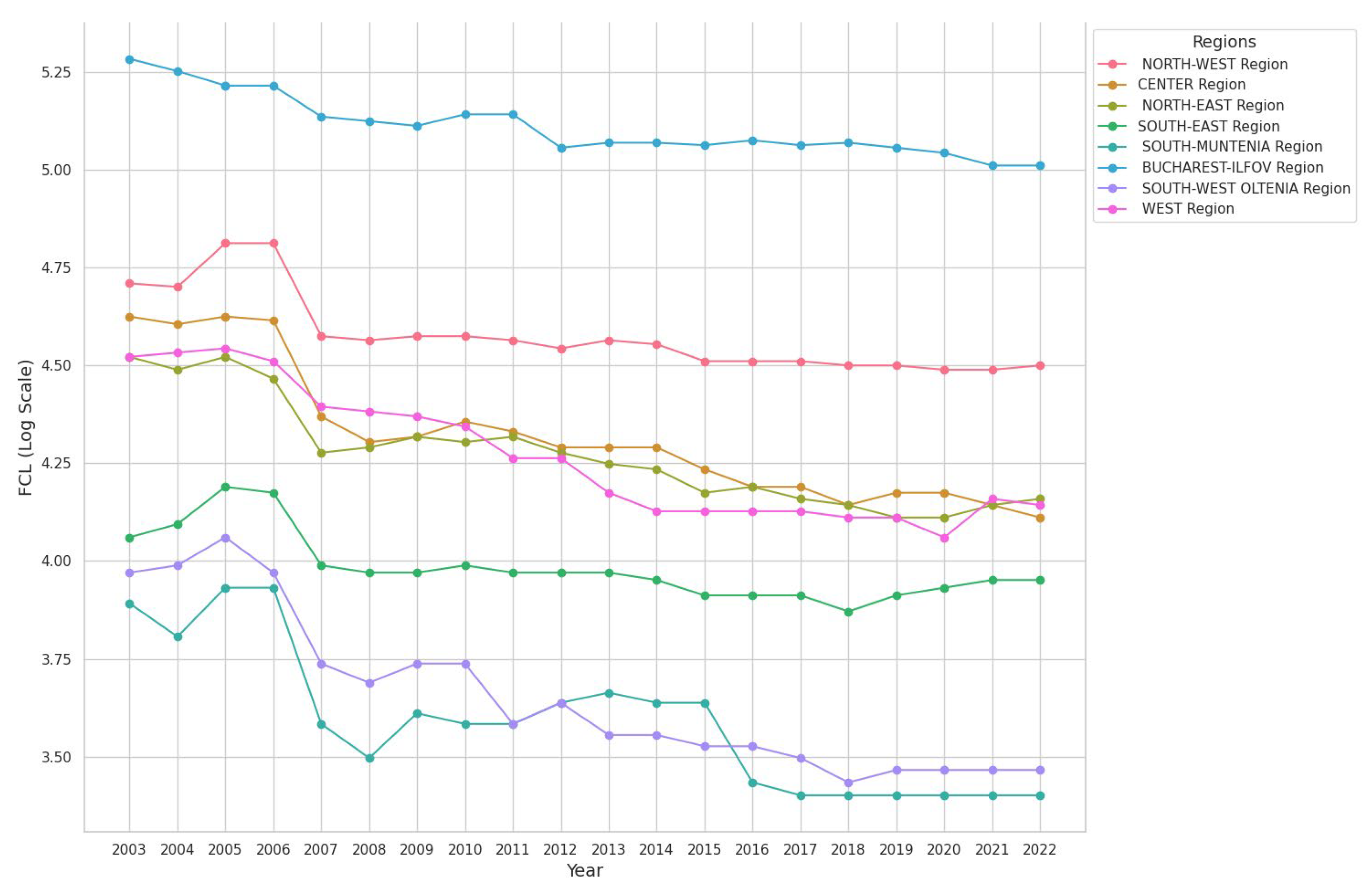
| First Author; Year; Journal; Reference | Scope | Methodology | Key Findings | Relevance to Regional and Local Economy |
|---|---|---|---|---|
| Deng, P.; 2013; Transport Policy; [30] | This study explores the relationship between ports (port demand and supply, port value-added activity) and the regional economy from a logistics perspective, providing decision support for decision makers. | Structural equation modeling (SEM) approach using samples from the five coastal port clusters in China. | The results showed that port supply positively influences port demand and that port value-added activities have a positive impact on the regional economy; however, port demand and supply did not have significantly positive effect on the regional economy. | The study highlights the impact of port activities on the regional economy and provides directions for decision makers in port development planning. |
| Park, J.S.; 2016; Transportation Research Part E: Logistics and Transportation Review; [31] | The study investigates the economic impact of seaports on regions in Korea using an econometric analysis based on the extended Solow model. | Econometric analysis based on panel data covering all regions in Korea between 2000 and 2013. | Econometric analysis shows that cargo ports without sufficient traffic hinder regional economic growth while cargo ports contribute to regional economic growth only when traffic is sufficient. Container port activities have a positive impact on regional economic growth and investment in ports indirectly leads to economic growth. | The study provides a clear understanding of the role of ports in the economic growth of Korea’s regions, suggesting the importance of adequate port traffic and indirect investment in ports. |
| Chen, Z.; 2019; European Planning Studies; [32] | The study analyzes the regional economic impact of high-speed rail (HSR) infrastructure development in China using a dynamic and spatial computable general equilibrium framework. | Dynamic and spatial computable general equilibrium modeling framework based on real data from 2002 to 2013. | The development of HSR infrastructure in China has had a positive regional economic impact. Real GDP growth boosted by rail infrastructure investment was significant in the South-West but lower in the developed eastern regions. Contributions to economic growth come mainly from increased productivity in the rail transport sector and the stimulating effect of rail infrastructure investments. | The study provides insights into the impact of HSR infrastructure on regional economies and suggests that infrastructure investment can spur economic growth, particularly in less developed regions. |
| Kauppila, P.; 2012; Fisheries Research; [33] | The study analyzes the regional economic impact of recreational fishing tourism, with an emphasis on the development of a procedural model applicable in rural areas. | Development of a procedural model based on existing statistics to assess regional economic impact, with practical applicability and low data collection costs. | The proposed model calculates regional economic indicators for fishing tourism, being applied in the area of the Iijoki river in Finland. Although it ignores multiplicative effects, it provides a simple and efficient method of analysis. | The study contributes to the understanding of the impact of fishing tourism on the local and regional economy, providing a practical tool for planners and researchers, with the potential to revitalize rural areas. |
| Madsen, B.; 2004; Economic Modelling; [34] | The study analyzes the links between the regional economy and activities at the sub-regional level, focusing on disaggregated general equilibrium models applied to transport costs and bridge tolls in Denmark. | Using the sub-regional disaggregated general equilibrium model, called LINE, to assess the impact of changes in transport costs on economic activity. | The study highlights the fact that traditional economic models at the regional level fail to capture the fundamental economic mechanisms at the sub-regional level. The application of the model shows how changes in transport costs influence economic activity at the sub-regional level in Denmark. | The relevance of this study lies in clarifying how sub-regional economic changes, such as transport costs, can influence the regional economy, providing a better understanding of economic linkages at different spatial levels. |
| Charalampidis, I.; 2019; Energies; [35] | The study presents a new macroeconomic–regional model (GEM-E3-R) for assessing the impact of transport sector restructuring on regional economies in the EU in the context of the EU’s decarbonization strategy. | A computable general equilibrium (CGE) model with two layers: one at the national level (multi-sectoral, multi-country) and one at the regional level, which assesses the impact of the restructuring of the transport sector using a dynamic agglomeration–dispersion mechanism and a gravity model for inter-regional flows. | The restructuring of the transport sector, in particular the electrification of car mobility and the use of advanced biofuels, will generate positive economic effects on regional economies in the EU, with differentiations depending on the industrial structure and the ability of regions to adopt new technologies. | The study highlights the importance of infrastructure investment and new technologies in the transport sector for regional development, providing a rigorous assessment of the long-term economic impact of the EU’s decarbonization strategy. |
| Mushtaq, S.; 2014; Agricultural Systems; [36] | The study investigates farm-level structural adjustments and their impact on regional economies in Australia in the context of climate change and water use policy reforms, with a focus on the rice industry. | Integrating empirical evidence on farm-level structural adjustments with a regional computable general equilibrium (CGE) model to assess the sectoral and regional impacts of climate change and water use policy. | The study shows that the existing diversity in agricultural production has allowed adaptations at the farm level, but additional water loss and the adoption of less intensive production methods will reduce the net number of agricultural businesses, which will affect rice production at the regional level. The negative impacts on the regional economy are partially offset by the redistribution of resources at the national level. Relocating rice production to the north would require strong government support. | The study highlights the impact of water use policies and climate change on regional economies, highlighting the need for government support to adapt the rice industry to the new conditions. |
| Garidzirai, R; 2020; Studia Universitatis Babes-Bolyai Oeconomica; [37] | The research examines the principal industries that might foster local economic development in South Africa, notwithstanding the general economic stagnation. | A Panel-Distributed Autoregressive Model (ARDL) using PMG, MG, and DFE estimators on annual data from 1996 to 2015 to analyze productivity effects in six sectors. | Productivity in the construction, transport, trade, manufacturing and finance sectors positively influences long-term economic growth, while productivity in mining and tourism has a negative effect. In the short term, all sectors, except trade and transport, contribute positively to local economic growth. | The study identifies sectors that can boost local economic growth in South Africa and recommends investment in infrastructure and skills development in mining and tourism to boost regional productivity. |
| Sadik-Zada, E.R.; Mineral Economics; [38] | The study analyzes the production linkages and employment effects of the oil sector on the rest of the Azerbaijani economy, using input–output tables for the years 2006, 2008 and 2009. | Input–output analysis of output and job creation multipliers followed by a nonlinear distributed autoregressive (ARDL) model for assessing the long-run effects of oil revenues on employment. | Despite advanced infrastructure and local content policies, the integration of the oil sector into the domestic economy is weak, and production and job creation multipliers have declined slightly after 3 years of exponential growth in oil production. Investments in the processing, construction, and network industries have the largest output linkages, and agriculture, education, health and the public sector have the largest job creation effect. | The study highlights the impact of oil revenues on job creation in Azerbaijan and suggests the need for additional investment in oil-related industries to boost regional manufacturing linkages. |
| Abdurakhmanova, G.Q.; 2021; Proceedings of the 5th International Conference on Future Networks and Distributed Systems; [39] | The study investigates the influence of tourism on employment and economic growth in Uzbekistan using empirical data from 1991 to 2020. | An autoregressive distributed model (ARDL) to analyze the long- and short-run connections between global tourism arrivals, employment, and real GDP. | The results show a close relationship between tourism, employment, and economic growth in Uzbekistan, with a unidirectional causality from tourism to economic growth. The increase in the number of international tourists has a positive impact on the economy and employment. | The study highlights the strategic role that tourism can play in boosting regional economic growth and employment, suggesting that Uzbekistan could achieve economic prosperity by supporting the tourism sector. |
| GDPR | CTCRD | FCL | IT | NMPS | |
|---|---|---|---|---|---|
| Mean | 11.15 | 12.40 | 4.22 | 9.03 | 13.13 |
| Median | 11.16 | 12.34 | 4.17 | 9.07 | 13.14 |
| Maximum | 12.71 | 15.53 | 5.28 | 10.55 | 13.71 |
| Minimum | 9.73 | 10.65 | 3.40 | 7.45 | 12.72 |
| Std. Dev. | 0.59 | 1.07 | 0.48 | 0.83 | 0.22 |
| Skewness | 0.05 | 0.75 | 0.25 | 0.11 | 0.65 |
| Kurtosis | 3.04 | 3.20 | 2.48 | 1.85 | 3.50 |
| Jarque–Bera | 0.08 | 15.68 | 3.48 | 9.01 | 12.98 |
| Probability | 0.95 | 0.00 | 0.17 | 0.01 | 0.00 |
| At Levels | |||||
|---|---|---|---|---|---|
| GDPR | CTCRD | FCL | IT | NMPS | |
| Unit root (Common Unit Root Process) | |||||
| LLC | −5.41 *** (0.00) | 1.68 (0.92) | −7.16 *** (0.00) | −5.60 *** (0.00) | −1.43 * (0.07) |
| Unit root (Individual Root Process) | |||||
| IPS | −2.02 ** (0.02) | −1.72 ** (0.04) | −3.28 *** (0.00) | −4.65 *** (0.00) | −1.07 (0.14) |
| ADF Fisher Chi-Square | −26.18 * (0.05) | 43.34 *** (0.00) | 40.18 *** (0.00) | 58.73 *** (0.00) | 18.33 (0.30) |
| At first difference | |||||
| Unit root (Common Unit Root Process) | |||||
| LLC | −5.38 *** (0.00) | −9.17 *** (0.00) | −10.54 *** (0.00) | −6.84 *** (0.00) | −4.78 *** (0.00) |
| Unit root (Individual Root Process) | |||||
| IPS | −4.07 *** (0.00) | −9.06 *** (0.00) | −7.84 *** (0.00) | −6.65 *** (0.00) | −4.73 *** (0.00) |
| ADF-Fisher Chi-Square | 43.69 *** (0.00) | 98.68 *** (0.00) | 82.53 *** (0.00) | 70.87 *** (0.00) | 50.10 *** (0.00) |
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
|---|---|---|---|---|
| Long-run equation | ||||
| CTCRD | 0.05 | 0.04 | 1.38 | 0.17 |
| FCL | −1.09 | 0.26 | −4.17 | 0.00 *** |
| IT | 0.53 | 0.09 | 5.43 | 0.00 *** |
| NMPS | 4.40 | 0.24 | 17.90 | 0.00 *** |
| Short-run equation | ||||
| COINTEQ01 | −0.32 | 0.04 | −6.73 | 0.00 *** |
| D (GDPR (−1)) | −0.36 | 0.16 | −2.11 | 0.03 ** |
| D(CTCRD) | −0.03 | 0.01 | −2.39 | 0.01 *** |
| D (CTCRD (−1)) | −0.04 | 0.01 | −2.85 | 0.00 *** |
| D(FCL) | −0.07 | 0.13 | −0.57 | 0.56 |
| D (FCL (−1)) | −0.28 | 0.08 | −3.24 | 0.00 *** |
| D(IT) | −0.26 | 0.09 | −2.80 | 0.00 *** |
| D (IT (−1)) | −0.12 | 0.09 | −1.35 | 0.18 |
| D(NMPS) | 0.42 | 0.20 | 2.02 | 0.04 ** |
| D (NMPS (−1)) | −0.25 | 0.23 | −1.10 | 0.27 |
| C | −15.55 | 2.37 | −6.54 | 0.00 *** |
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
|---|---|---|---|---|
| CTCRD | 0.08 | 0.06 | 1.33 | 0.18 |
| FCL | −1.09 | 0.12 | −8.75 | 0.00 *** |
| IT | 0.69 | 0.04 | 14.06 | 0.00 *** |
| NMPS | 0.62 | 0.05 | 11.38 | 0.00 *** |
| Pseudo R-squared | 0.53 | Mean dependent var | 11.15 | |
| Adjusted R-squared | 0.52 | S.D. dependent var | 0.59 | |
| S.E. of regression | 0.38 | Objective | 14.19 | |
| Quantile dependent var | 10.79 | Restr. objective | 30.69 | |
| Sparsity | 0.79 | |||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
|---|---|---|---|---|
| CTCRD | 0.18 | 0.05 | 3.15 | 0.00 *** |
| FCL | −0.84 | 0.09 | −8.52 | 0.00 *** |
| IT | 0.52 | 0.07 | 6.92 | 0.00 *** |
| NMPS | 0.57 | 0.04 | 13.83 | 0.00 *** |
| Pseudo R-squared | 0.50 | Mean dependent var | 11.15 | |
| Adjusted R-squared | 0.49 | S.D. dependent var | 0.59 | |
| S.E. of regression | 0.31 | Objective | 18.25 | |
| Quantile dependent var | 11.15 | Restr. objective | 36.65 | |
| Sparsity | 0.58 | |||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
|---|---|---|---|---|
| CTCRD | 0.27 | 0.06 | 4.19 | 0.00 *** |
| FCL | −0.73 | 0.16 | −4.36 | 0.00 *** |
| IT | 0.41 | 0.09 | 4.25 | 0.00 *** |
| NMPS | 0.53 | 0.05 | 9.90 | 0.00 *** |
| Pseudo R-squared | 0.48 | Mean dependent var | 11.15 | |
| Adjusted R-squared | 0.47 | S.D. dependent var | 0.59 | |
| S.E. of regression | 0.38 | Objective | 15.18 | |
| Quantile dependent var | 11.53 | Restr. objective | 29.59 | |
| Sparsity | 0.84 | |||
| Variable | Coefficient | Std. Error | z-Statistic | Prob. | [95% Confidence Interval] |
|---|---|---|---|---|---|
| CTCRD | 0.01 | 0.01 | 0.19 | 0.00 *** | [−0.04, 0.04] |
| FCL | −0.31 | 0.06 | −2.96 | 0.00 *** | [−0.52, −0.10] |
| IT | −0.02 | 0.02 | −0.58 | 0.26 | [−0.08, 0.04] |
| NMPS | 0.50 | 0.05 | 16.00 | 0.00 *** | [0.85, 1.09] |
| Constant | −3.14 | 0.68 | −8.04 | 0.00 *** | [−10.99, −6.68] |
| Null Hypothesis | F-Statistic | Prob. | Conclusion |
|---|---|---|---|
| CTCRD does not Granger cause GDPR | 17.20 | *** | |
| GDPR does not Granger cause CTCRD | 32.04 | *** | |
| FCL does not Granger cause GDPR | 22.86 | *** | |
| GDPR does not Granger cause FCL | 3.54 | 0.06 ** | |
| IT does not Granger cause GDPR | 2.15 | 0.14 | |
| GDPR does not Granger cause IT | 7.87 | 0.00 *** | |
| NMPS does not Granger cause GDPR | 38.15 | *** | |
| GDPR does not Granger cause NMPS | 5.91 | 0.01 *** | |
| FCL does not Granger cause CTCRD | 2.84 | 0.09 * | |
| CTCRD does not Granger cause FCL | 14.84 | 0.00 *** | |
| IT does not Granger cause CTCRD | 19.08 | *** | |
| CTCRD does not Granger cause IT | 1.08 | 0.29 | |
| NMPS does not Granger cause CTCRD | 10.41 | 0.00 *** | |
| CTCRD does not Granger cause NMPS | 0.73 | 0.39 | |
| IT does not Granger cause FCL | 7.27 | 0.00 *** | |
| FCL does not Granger cause IT | 15.50 | 0.00 *** | |
| NMPS does not Granger cause FCL | 2.13 | 0.14 | |
| FCL does not Granger cause NMPS | 1.89 | 0.17 | |
| NMPS does not Granger cause IT | 2.49 | 0.12 | |
| IT does not Granger cause NMPS | 2.53 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgescu, I.; Nica, I.; Delcea, C.; Chiriță, N.; Ionescu, Ș. Assessing Regional Economic Performance in Romania Through Panel ARDL and Panel Quantile Regression Models. Sustainability 2024, 16, 9287. https://doi.org/10.3390/su16219287
Georgescu I, Nica I, Delcea C, Chiriță N, Ionescu Ș. Assessing Regional Economic Performance in Romania Through Panel ARDL and Panel Quantile Regression Models. Sustainability. 2024; 16(21):9287. https://doi.org/10.3390/su16219287
Chicago/Turabian StyleGeorgescu, Irina, Ionuț Nica, Camelia Delcea, Nora Chiriță, and Ștefan Ionescu. 2024. "Assessing Regional Economic Performance in Romania Through Panel ARDL and Panel Quantile Regression Models" Sustainability 16, no. 21: 9287. https://doi.org/10.3390/su16219287
APA StyleGeorgescu, I., Nica, I., Delcea, C., Chiriță, N., & Ionescu, Ș. (2024). Assessing Regional Economic Performance in Romania Through Panel ARDL and Panel Quantile Regression Models. Sustainability, 16(21), 9287. https://doi.org/10.3390/su16219287









