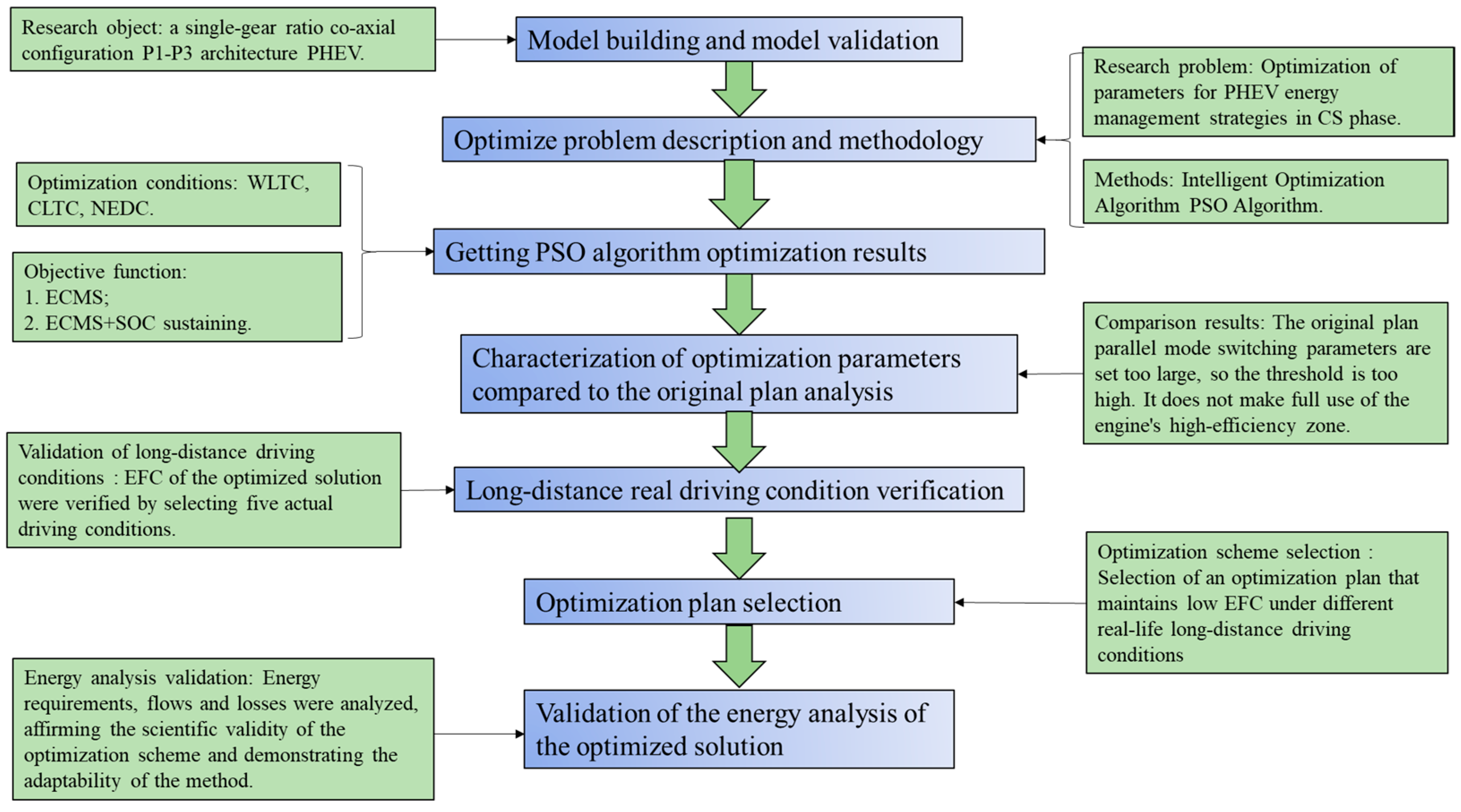
Optimization of Energy Management Strategy of a PHEV Based on Improved PSO Algorithm and Energy Flow Analysis

Abstract

Single-gear-ratio plug-in hybrid vehicles (SRPHEVs) are favored by major manufacturers due to their excellent energy-saving potential, simple structure, ease of maintenance and control, great cost-saving potential, and the benefits of vehicle lightweighting. Implementing an energy management strategy (EMS) is the key to realizing the energy-saving potential of PHEVs. In this paper, based on a newly developed coaxial configuration, P1-P3 SRPHEV, with the purpose of reducing PHEV fuel consumption, the advantages of various methods were synthesized. An improved intelligent optimization algorithm, the Particle Swarm Optimization (PSO) algorithm, was used to find the optimal rule-based strategy parameters. The PSO algorithm could be easily adjusted to the parameters and obtains the desired results quickly. Different long-distance speed profiles tested under real-world driving cycle (RDC) conditions were used to validate the fuel savings. And an energy flow analysis was conducted to further investigate the reasons for the algorithm optimization. The results show that the optimization plans of the PSO algorithm in different cycle conditions can improve the equivalent fuel consumption of vehicles in different long-distance conditions. Considering the optimization effect of the equivalent fuel consumption and actual fuel consumption, the best case of the equivalent fuel consumption is improved by 2.98%, and the actual fuel consumption is improved by 2.37%. Through the energy flow analysis, it is found that the energy-saving effect of the optimization plan lies in the following principle: lowering the parallel mode switching threshold to increase the parallel mode usage time and to reduce the fuel–mechanical–electrical transmission path loss, resulting in increasing the energy utilization of the whole vehicle.

1. Introduction

Hybrid electric vehicles have become the current focus of the research and development of major manufacturers because of their great potential for energy saving and carbon reduction [1]. The power systems of plug-in hybrid electric vehicles (PHEVs) are equipped with high-capacity power batteries which can be recharged through the power grid to bring out the advantages of pure electric vehicles, and, at the same time, they can realize multi-mode operation to improve adaptability and solve the range anxiety of pure electric vehicles by depending on the characteristics of HEVs [1,2,3], which has made PHEVs become the mainstream through various manufacturers and universities. Research on fuel economy improvement and cost saving has become the focus [4].

The energy-saving advantages of HEVs not only depend on the design of the powertrain, but also on the design of the energy management strategy parameters [5,6,7]. The energy management strategies (EMS) of HEVs are mainly categorized as follows:

(1)

Rule-based energy management strategy [8]: The rule-based energy management strategy is the type of strategy that can be realized on the whole vehicle in a large area for practical utilization [9]. This strategy adopts logic switching judgment to realize the switching of different driving strategies. The advantage of this strategy is that the computation burden is small, easy to realize, and more reliable [10]. However, the disadvantage is that the parameter settings depend on the experience of experts and engineers;

(2)

Optimization-based energy management strategies [11,12,13,14,15,16,17,18]: optimization-based energy management strategies are divided into global optimization and local optimization [11]. Global optimization can achieve the optimal solution under the condition of knowing the working conditions in advance, such as in the use of dynamic programming algorithms [12,13,14], which do not rely on the experience of experts and can obtain the optimal strategy. They are also suitable for different working conditions, but global optimization algorithms, such as dynamic programming, require a lot of time for computation [14,15]. To solve this problem, a study has developed a rapid DP algorithm that can save 78% of the computation time used by the traditional DP algorithm [16]. The combination of ADP (adaptive dynamic programming) and neural networks can further improve the accuracy of the energy management strategy, but the structure becomes more complex as a result [17]. A study has been conducted to address the similarities between different of bus driving characteristics, and the adaptability of the DP strategy is adapted by using an algorithm called the one-step look-ahead rollout algorithm to adjust the DP strategy in real-time [18]. Further, the current real-time optimization methods, such as PMP (Pontryagin’s minimum principle) and the ECMS (equivalent consumption minimization strategy), are expected to solve this problem [19,20,21];

(3)

Prediction-based energy management strategies [22,23]: prediction-based energy management strategies use the information from current intelligent transportation systems such as GPSs (global positioning systems) and GISs (geographic information systems) as inputs and use methods such as MPC (model predictive control) to construct constrained optimization problems in a finite time domain [23,24]. MPC is a type of rolling optimization, which is one of the commonly used methods in the current control area [25,26]. The method relies on model accuracy and the accurate prediction of future states;

(4)

Learning-based energy management strategies [27,28,29,30]: with the development of AI (Artificial Intelligence), machine learning integrated into HEV energy management strategy methods is gradually coming to the forefront of the current research [27]. Learning-based energy management strategies use deep reinforcement learning and other methods to learn the data of the whole vehicle during driving and environmental interaction [31,32]. Determining the optimal policy can be conducted through a trial-and-error approach and by applying reward judgments [33]. In recent years, a considerable number of deep reinforcement learning-based energy management strategies have been proposed, and these have achieved close to the global optimum of energy saving results [34]. There are also methods that combine prediction and neural network learning methods to achieve the study of energy management strategies [35], with the advantages of adaptability and learning ability, but with obvious disadvantages, such as the demand of large number of datasets, which are realistically difficult to obtain [27]. Outputting the pre-optimization results of different driving modes into the reinforcement learning framework in advance can improve the performance and learning speed of machine learning [36]. This approach maybe can further be used in a real vehicle.

Therefore, these methods each have their own advantages and disadvantages, and the simples and easiest to install on a whole vehicle is the rule-based strategy, while other strategies are limited by the computational capability and speed, which makes it difficult to install them on a real vehicle.

The energy flow analysis method is an effective way to analyze the energy use and loss of the whole vehicle, which helps to study the direction of the energy consumption of the whole vehicle, causes, as well as the direction of energy saving [37]. Such a method is not only used in PBEVs (pure-battery electric vehicles) [38,39], but also in ICEVs (internal combustion engine vehicles) and PHEVs [37,40,41]. Payri et al. [40] established a detailed energy balance test and energy flow analysis method which was utilized in a direct injection diesel engine. In a dynamic study, Duan et al. [41] explored the cold-start energy consumption of a vehicle equipped with a gasoline engine under the NEDC cycle and found that the energy flow distribution is largely influenced by the operating conditions. The effect of alternative fuels on engine energy flow has also been investigated in several papers on a variety of alternative fuels [42,43,44]. Xie et al. [39] developed a microsimulation model using the concept of digital twins to investigate the energy flow and factors affecting the range of a pure electric vehicle with single-pedal characteristics. Du et al. [45] investigated the energy flow and factors affecting the range of a plug-in series-parallel hybrid vehicle for a configuration and control strategy, and they also tested and analyzed the energy consumption characteristics in the CD (charge depleting) phase and CS (charge sustaining) phase. Lv et al. [46] analyzed the effect of braking energy recovery on the energy flow of a pure electric vehicle.

Hybrid vehicles can realize lower transmission gear ratios in hybrid models because the electric motor can work in a very low speed range and provide high torque. Single-gear-ratio hybrid vehicles have the advantages of lower transmission costs, simple control difficulty, being lightweight, and so on.

Based on a newly designed PHEV with single-gear-ratio transmission, this paper discusses an optimization method for energy management strategy parameters based on the optimization of energy management strategy in the CS period of this PHEV. The research idea framework of this paper is shown in Figure 1. The PHEV in this paper exhibits the P1-P3 architecture with single-gear-ratio transmission, which can realize multi-mode driving switching through the clutch, in which the engine and P1 adopt the coaxial configuration and the transmission mechanical efficiency between the two parts is higher. In this paper, we will combine the two approaches of the rule-based and optimization-based methods. Firstly, considering the practical limitations, the main investigated part is the rule-based energy management strategy, which adopts the improved PSO algorithm to seek the optimal parameters of the energy management strategy to ensure the economy of the whole vehicle and to get rid of the limitations of the experts’ experience. Considering that the algorithm optimization prevents a single search from falling into local optimization and that the selection of a single optimization condition is not representative enough, the WLTC, CLTC, and NEDC are selected as the optimization conditions, and different objective functions are selected for the combination of plans. Five long-distance working conditions (>70 km) measured under RDE (real driving emission) test conditions are selected for fuel consumption verification. Subsequently, the selected optimal plan characteristics that can maintain a lower equivalent fuel consumption under different working conditions are analyzed. The energy demand and energy flow of the original plan and the low-equivalent fuel consumption plan are studied to explain the energy-saving mechanism of the optimization results of the PSO algorithm, and the relationship between the energy loss value and the amount of fuel consumption are further analyzed to explain the next step in EMS energy efficiency optimization. A comparison between the research in this paper and the existing research is listed in

Table 1. Comparison of existing research and this research.

Existing Research	Research in This Paper
Fast global optimization methods are still some way off from actual vehicle use [16,18]. The use of predictive control-based and learning-based energy management strategies can obtain the optimal solution and improve the applicability of the strategy, but it needs to rely on real-time data or a lot of data for learning, and the computational requirement is large [20,27,28,31,32,33,34,35].	Former strategy parameters optimization does not require high computational demand based on rule-based strategy, and the algorithm is simple and easy to operate. The strategy obtained from optimization can save energy on different driving styles and has good adaptability.
Intelligent optimization algorithms are used to find the optimal rule-based energy management strategy parameters and power system parameters [8], but the selected working conditions are single and unrepresentative.	Combining a variety of cycling conditions and objective functions to prevent the optimization results from being unrepresentative.
Considering the energy management strategy of integrated working conditions with multiple combinations of cyclic conditions to improve the adaptability of the energy management strategy [47], but the proposed energy management strategies are all based on the condition that the SOC does not change.	Adopting representative cycling conditions as the optimal working conditions; and verifying the energy-saving effect based on RDC (long distance Real Driving Cycling) with different styles. And comparing the difference between considering SOC maintenance with regulation constraint and not considering SOC maintenance.
Energy flow analysis method to analyze the energy utilization efficiency of different segments of pure electric vehicles/hybrid electric vehicles under different working conditions to further explore the direction of energy conservation [37,39,46].	Comparative analysis of the energy utilization of the whole vehicle by using energy flow analysis, explaining the reasons for energy saving by optimization with algorithm.
Single-gear ratio PHEVs to reduce the difficulty of strategic control.	Single-gear ratio PHEV with coaxial configuration of engine and P1 motor for higher transmission efficiency. Multi-mode driving via clutch for good mode-adaptability.

.

2. Modeling and Simulation Methods

2.1. Research Object

In this paper, a P1-P3-architecture coaxially arranged series-parallel plug-in hybrid vehicle equipped with a single-gear-ratio transmission is selected as the object, as shown in Figure 2, which includes a 1.5 L naturally aspirated hybrid special engine, a clutch, two motors (P1 position and P3 position), a single-gear-ratio transmission, a final reduction drive and differential, and two front-driving wheels. Among them, the P1 motor and engine belong to the coaxial structure with high mechanical transmission efficiency. The whole vehicle and power-related parameters are summarized in

Table 2. Specifications of the research vehicle.

Parameter	Value	Unit
Vehicle mass	1700	kg
Assumed passenger mass	150	kg
Vehicle resistance coefficient f0	111.1	N
Vehicle resistance coefficient f1	0.736	N/(km/h)
Vehicle resistance coefficient f2	0.0308	N/(km/h)2
Tire radius	0.331	m
Number of transmission gears (forward)	1	-
Engine type	Inline-four engine	-
Engine rated power	82	kW
Motor type	Permanent magnetic synchronous	-
P1 motor rated power	99.5	kW
P3 motor rated power	100.5	kW
Battery package capacity	65	Ah
Battery package nominal voltage	350	V

.

2.2. Powertrain Modeling

The engine and motor modeling are based on MAP. Figure 3a,b show the MAP, which is shown as plots of the efficiency and fuel consumption rate of the engine, and the optimal load rate operating line of the engine is labeled on the plots. From Figure 3, it can be seen that the engine optimal line is distributed in the region where the load factor is around 80%, so the engine needs to work in this region to maximize the fuel utilization. The MAP plots of the motor efficiencies of the P1 motor and the P3 motor, and the efficiency of the MCU (motor control unit) integrated in the PEU, are show in Figure 4 and Figure 5, respectively. It can be seen that both the motor controller and the motor are less efficient in the lower speed range. Because of the coaxial configuration, P1’s rotation speed is more than 1000 rpm, which prevents it from working in the lower efficiency range.

Figure 6 shows the graphs of HVB (high-voltage battery) single-cell resistance and open-circuit voltage versus the SOC (state of charge). From Figure 6, it can be seen that the battery open-circuit voltage and internal resistance values are closely related to the battery SOC, and a too-low SOC will lead to a sharp increase in the internal resistance of the battery discharge and a sharp decrease in the open-circuit voltage, causing the battery discharge capacity to be greatly reduced.

2.3. The Vehicle Energy Flow Model Building

In order to analyze the energy-saving mechanisms of different strategy parameters, the energy flow module analysis is applied to the whole vehicle modeling process. In this paper, Equations (1)–(17) (

Table 3. Summary of calculation methods for whole-vehicle energy flow analysis.

Part	Parameter	Equation	No
Vehicle longitudinal dynamics	Vehicle coasting force	$F_{\mathit{coasting}}=f0+f1v_{vehicle}+f2v_{vehicle}^2$	(1)
	Longitudinal dynamics equation	$F_{\mathit{power}}{- F}_{\mathit{brake}}{=F}_{\mathit{coasting}}{+m}_{\mathit{vehicle}}{\mathit{gsin}\theta +m}_{\mathit{vehicle}}{a}_{\mathit{vehicle}}$	(2)
	Power equation	$P_{\mathit{force}}{=\mathit{Fv}}_{\mathit{vehicle}}$	(3)
Engine	Engine brake power	$P_{\mathit{engine}}={\displaystyle \frac{T_{\mathit{engine}}{n}_{\mathit{engine}}}{9550}}$	(4)
	Fuel combustion power	$P_{\mathit{fuel}}{=\mathit{LHV}}_{\mathit{fuel}}{\stackrel{·}{m}}_{\mathit{fuel}}$	(5)
P1 and P3 motor	Motor power	$P_{\mathit{motor}}={\displaystyle \frac{T_{\mathit{motor}}{n}_{\mathit{motor}}}{9550}}$	(6)
	Motor loss	$P_{\mathit{loss}\_\mathit{motor}}=\left\{\begin{array}{c}\left(1-{\eta }_{motor}\right)\left|P_{motor}\right|, T_{motor}<0\\ \left({\displaystyle \frac{1}{{\eta }_{motor}}}-1\right)\left|P_{motor}\right|, T_{motor}\ge 0\end{array}\right.$	(7)
	Motor PEU loss	$P_{\mathit{loss}\_\mathit{PEU}}=\left\{\begin{array}{c}\left(1-{\eta }_{PEU}\right){\eta }_{motor}\left|P_{motor}\right|, T_{motor}<0\\ \left({\displaystyle \frac{1}{{\eta }_{PEU}}}-1\right){\displaystyle \frac{1}{{\eta }_{motor}}}\left|P_{motor}\right|, T_{motor}\ge 0\end{array}\right.$	(8)
HVB	HVB brake power	$P_{\mathit{bat}}{=P}_{P1\_\mathit{to}\_\mathit{elec}}{+P}_{P3\_\mathit{to}\_\mathit{elec}}+{\displaystyle \frac{P_{\mathit{LVD}}}{{\eta }_{\mathit{LVD}}}}$	(9)
	HVB current	$I_{\mathit{bat}}={\displaystyle \frac{U_{OC}-\sqrt{U_{oc}^2-4P_{bat}{R}_{bat\_int}}}{2R_{bat\_int}}}$	(10)
	HVB terminal voltage	$U_{\mathit{terminal}}{=U}_{\mathit{oc}}-I_{\mathit{bat}}{R}_{\mathit{bat}\_\mathit{int}}$	(11)
	HVB efficiency	${\eta }_{\mathit{bat}}={\displaystyle \frac{\mathit{min}\left(U_{\mathit{oc}}{,U}_{\mathit{terminal}}\right)}{\mathit{max}\left(U_{\mathit{oc}}{,U}_{\mathit{terminal}}\right)}}$	(12)
	HVB power	$P_{\mathit{bat}\_\mathit{total}}{=U}_{\mathit{oc}}{I}_{\mathit{bat}}$	(13)
	HVB brake power	$P_{bat}{=U}_{\mathit{terminal}}{I}_{\mathit{bat}}$	(14)
Brake system	Brake recovery power	$P_{\mathit{brake}\_\mathit{recovery}}{=F}_{P3}{v}_{\mathit{vehicle}},\mathit{brake} \mathit{mode} \mathit{on}$	(15)
	Brake loss power	$P_{hydraulic\_brake\_loss}=F_{hydraulic\_brake}{v}_{vehicle}$	(16)
Mechanical	Powertrain loss	$P_{mechanical\_loss}={\displaystyle \frac{T_{input}{n}_{input}}{9550}}\left(1-{\eta }_{mechanical}\right)$	(17)

) are used to calculate the energy flow and loss of the powertrain, driveline, and braking system during the driving process, and the corresponding energy values are the integrals of the corresponding power equations in the time domain. Explanations of the parameters in the table are listed in the Abbreviations section at the end of the article.

It should be noted that:

• When the motor torque is negative, it indicates that the motor is dragged by the external torque;
• The brake power of HVBs (Equation (9)) has been calculated in terms of the power consumption of low-voltage devices: ${\displaystyle \frac{P_{\mathit{LVD}}}{{\eta }_{\mathit{LVD}}}}$, where $P_{\mathit{LVD}}$ is the power consumed by the LVDs (low-voltage devices) and ${\eta }_{\mathit{LVD}}$ is the average conversion efficiency of the LVDs;
• Brake recovery is only performed by the P3 motor, and brake losses are only calculated in terms of the hydraulic brake losses. The rest of the loss has been calculated in terms of the motor loss and mechanical loss;
• Because the P1 motor and engine are arranged coaxially, the transfer efficiency is very high, and for comprehensive considerations, only the mechanical loss of the transmission and the final drive reduction are calculated in terms of the mechanical loss.

2.4. Energy Management Strategy Settings

This PHEV is divided into five operating modes, including pure electric drive mode, series mode, direct engine drive mode, full load mode, and energy recovery mode. The application scenarios and possible energy flow patterns of different modes are summarized in

Table 4. The summary of different drive modes.

Drive Mode	Schematic of Energy Flow	Application Scenarios
Pure electric		Used when battery SOC is high, power demand is low, and vehicle speed is low
Direct engine		The clutch is engaged and the engine intervenes in the drive for higher speed conditions. The P1 motor is responsible for recovering energy from the engine and the P3 motor is responsible for providing additional energy requirements to keep the engine operating point near the optimal operating line.
Series		Used when SOC is reduced to a certain level, power demand is not high, and speed is low.
Full load		Used at higher speed, under conditions of high overall-vehicle power demand, and when hardware requirements permit.
Energy recovery		When the vehicle is decelerating, it is necessary to judge the vehicle speed and the current battery SOC status to decide whether to use the P3 motor to recover kinetic energy, and the remaining braking force demand is provided by the hydraulic brake system.

. The energy flow patterns differ from each other in different modes.

Combining the characteristics of the energy flow patterns of the whole vehicle, the above five modes are combined into four modes, which are the pure electric mode, series mode, parallel mode, and brake energy recovery mode. According to the application scenarios and the limitation of the engine application scenarios based on the single-gear-ratio transmission, the RB (rule-based) energy management strategy, as shown in Figure 7, is initially formed, and takes into account the state switching of the HVB. The HVB state is divided into the power mode and the charge mode, which are formulated with reference to the CD stage and CS stage characteristics based on the PHEV [6,8,37,48]. A typical CDCS EMS is shown in Figure 8. When the HVB SOC is in range (SOC_min, SOC_max), the vehicle works in the CS stage. The HVB is in the power mode (HVB-mode = 1) when the battery SOC is high and needs to be recharged when the battery SOC is low (HVB-mode = 0). The list of parameters included in the control strategy and the explanation of the parameters are shown in

Table 5. Parameters of energy management strategy.

Parameter	Unit	Description
vswitch	kph	Minimum velocity threshold for parallel mode opening
vbrake	kph	Minimum velocity allowed for braking energy recovery
SOCmin	-	Lower SOC bound of CS stage
SOCmax	-	Upper SOC bound of CS stage
Tswitch	Nm	Minimum wheel torque for parallel mode opening
HVB-mode	-	Label for determining whether the high-voltage battery is in a discharge or charge state

.

The value of T_switch is judged according to the HVB state. HVB-mode characterizes the HVB state. If the battery is in the high SOC state (HVB-mode = 1), it is assumed that the electric power is derived from the external power grid, so the battery power is used preferentially, and the judging principle of T_switch is based on the P3 motor maximum torque. If the battery is in the low SOC state (HVB-mode = 0), the engine needs to intervene frequently for charging, so the judgment principle of T_switch is based on the engine optimal torque, which is a function of the engine speed. The switch logic is shown in Figure 9, and the coefficient k1 or k2 are assigned to the equation as shown in Equation (18). The parameters are listed in the Abbreviations section at the end of the article.

$$T_{\mathit{switch}}=\left\{\begin{array}{c}{T}_{p3\_\mathit{max}}{R}_{P3\_\mathit{to}\_\mathit{wheel}}{k}_1, \mathit{HVB}-\mathit{mode}=1\\ T_{\mathit{eng}\_\mathit{opt}}{R}_{\mathit{engine}\_\mathit{to}\_\mathit{wheel}}{k}_2, \mathit{HVB}-\mathit{mode}=0\end{array}\right.$$

(18)

The HVB state logic is shown in the green box in Figure 7 and in Figure 8. The HVB-mode is 1 when the SOC power is high, and the initial battery state is 1 during the CS phase. When the SOC is lower than the lower bound of the CS state SOC_min, the battery state is transformed to 0. The battery mode is switched to 1 again when the SOC is higher than the upper bound of the CS state SOC_max. Based on the characteristics of PHEVs, the external power grid can be selected for charging when the car stops. If there is no condition for external charging, the next startup will be in the CS range. From Figure 7, it can be seen that the series mode is not turned on when HVB-mode equals 1; on the contrary, the pure electric mode is not turned on when HVB-mode equals 0.

2.5. The Optimization Method

The PSO algorithm has a fast convergence speed and good robustness in terms of optimization, and the parameters of the algorithm are easy to adjust [49]. Therefore, the PSO algorithm is selected as an optimization tool. The PSO parameter settings adopted in this paper are based on those in the literature [50], and the algorithm parameters are set as shown in

Table 6. The parameters of the PSO.

Parameter	Description	Values
Genmax	Max iteration number for PSO	300
Pop-size	Swarm size	40
Kiner	Inertia weight	$0.9-\left(0.9-0.4\right){\displaystyle \frac{Ge{n}_{current}}{Ge{n}_{max}}}$
Kcogn	Swarm cognitive behavior	$2.75-\left(2.75-1.25\right){\displaystyle \frac{Ge{n}_{current}}{Ge{n}_{max}}}$
Ksoci	Swarm social behavior	$0.5-\left(0.5-2.25\right){\displaystyle \frac{Ge{n}_{current}}{Ge{n}_{max}}}$
Vmax	Population max velocity, popmax is upon boundary and popmin is low boundary	${\displaystyle \frac{po{p}_{max}-po{p}_{min}}{100}}$
Vmin	Population min velocity	$-{\displaystyle \frac{po{p}_{max}-po{p}_{min}}{100}}$

. The maximum number of iterations is 300, and the number of particles is 40. Combined with the characteristics of the PSO algorithm, the inertia weights are set to decay linearly with the increase in the number of iterative steps in the range of [0.4, 0.9]. The accelerating factor of the individual behavior of the particles linearly decays in the range of [1.25, 2.75], and the particle social behavior acceleration factor increases linearly in the range of [0.5, 2.25]. The maximum and minimum particle velocities are limited to 1% of the overall range of each parameter. The literature [50] shows that this parameter setting method can obtain a faster convergence speed and more accurate optimization results. In order to confirm that the improved PSO algorithm of reference [50] has an advantage over the conventional algorithm, the improved PSO, GWO, (grey wolf optimizer) and conventional GA (genetic algorithm) are set as comparison groups. The difference in convergence performance is shown in Figure 10, and a comparison of the different algorithms’ optimization search results is shown in

Table 7. Final solution results of different algorithms.

	vswitch	SOCmin	SOCmax	vbrake	k1	k2	Fitness
	(kph)	(%)	(%)	(kph)
Unimproved PSO	54.30	22.02	29.22	7.00	0.62	0.45	297.43
Improved PSO	54.14	22.02	30.16	7.14	0.72	0.50	297.47
GWO	53.13	22.02	31.28	7.05	0.40	0.40	297.42
GA	43.00	22.01	28.35	7.27	0.76	0.42	297.47

. The driving cycle is NEDC, and the max iteration is 300. It can be noticed from Figure 10 that the improved PSO algorithm does converge faster, even though the fitness effect of the random initial solution is worse. From Table 7, there is very little difference in the algorithmic fitness results. Therefore, in this paper, the improved PSO algorithm in the literature [50] is used.

2.6. The Objective Functions

The optimization objective aims to reduce fuel consumption; however, the optimization results from considering only the engine fuel consumption are still not representative and do not take into account the electric power system conversion losses, so reference is made to the objective function of the strategy of ECMS. Unlike previous studies which consider the difference between the battery charge with discharge efficiencies, the equivalent fuel consumption by the battery in this paper is only considered as including the charge process, because the battery energy comes only from the engine in the CS stage. The J1 and J2 objective functions describe the battery equivalent fuel consumption based on the aspect of the battery total power, instead of on the aspect of motor power. The electric power flow from the engine is shown in Figure 11. A penalty term limiting the change in SOC is added to the objective function of J2 (Equation (20)) to compare the effect on the optimization results of the requirement of no change in SOC as specified in the demand of test regulations. The relevant objective function formulas are included in

Table 8. The different optimization objective functions.

Target Function Description	Formula	No
HVB power equivalent fuel consumption	$\mathrm{J}1={\displaystyle {\displaystyle \sum }_{i=1}^{\mathit{time}\_\mathit{length}}}\left({\stackrel{·}{m}}_{\mathit{fuel}}+{\displaystyle \frac{P_{\mathit{bat}\_\mathit{total}}}{{\eta }_{\mathit{bat}\_\mathit{char}}{\eta }_{\mathit{eng}\_\mathit{aver}}{\eta }_{p1\_\mathit{total}\_\mathit{aver}}{\mathit{LHV}}_{\mathit{fuel}}}}\right)$	(19)
HVB power equivalent fuel consumption + SOC sustaining	$\mathrm{J}2={\displaystyle {\displaystyle \sum }_{i=1}^{\mathit{time}\_\mathit{length}}}\left({\stackrel{·}{m}}_{\mathit{fuel}}+{\displaystyle \frac{P_{\mathit{bat}\_\mathit{total}}}{{\eta }_{\mathit{bat}\_\mathit{char}}{\eta }_{\mathit{eng}\_\mathit{aver}}{\eta }_{p1\_\mathit{total}\_\mathit{aver}}{\mathit{LHV}}_{\mathit{fuel}}}}\right)+k\left|{\mathit{SOC}}_{\mathit{end}}{-\mathit{SOC}}_{\mathit{init}}\right| ,$ $k \mathrm{is} \mathrm{very} \mathrm{large}$	(20)

, with J1 (Equation (19)) considering the equivalent fuel consumption from the battery power, and J2 incorporating a penalty term for sustaining electric power, with k set to a very large number. Other parameters are listed in the Abbreviations section at the end of the article.

2.7. Model Validation

For validating the following performance of the model, the electric consumption in the pure electric mode, and the fuel consumption data in the power maintenance mode, the real vehicle data of the small-capacity battery version (15.6 Ah) are used. The test cycle is the WLTC, and the test method follows the standard GB/T 19753-2021 [51]. The validation results show that the vehicle model has good speed following performance, as shown in Figure 12. The errors of simulated electric consumption and simulated fuel consumption under the WLTC conditions are less than 5%, which is within the error tolerance, as shown in

Table 9. The model electric consumption and fuel consumption validation.

Parameters	Experimental Results	Simulation Results	Error
Electric consumption	2.85 kW·h	2.94 kW·h	1.9%
Fuel consumption	4.75 L/100 km	4.63 L/100 km	2.5%

; therefore, the model can be used for subsequent analytical investigations.

3. Results and Discussions

3.1. The Optimization Parameters

According to the energy management strategy setting and optimization tasks described in the previous section, the types of optimization parameters and range of optimization parameters that we selected are preliminarily determined on the basis of analyzing the characteristics of the whole vehicle and the energy management strategy, as shown in

Table 10. The optimized parameter original values and optimization range settings.

Parameters	Description	Original	Range
Vswitch	Min velocity that allows parallel mode on	70 kph	[40, 90] kph
SOCmin	Min HVB SOC for CS period	20%	[20%, 24%]
SOCmax	Max HVB SOC for CS period	28%	[26%, 35%]
Vbrake	Min velocity that allows brake recovery on	7 kph	[7, 20] kph
k1	Coefficient of demand torque for parallel mode on when HVB-mode equals to 1 (Formula (18))	0.7	[0.4, 1]
k2	Coefficient of demand torque for parallel mode on when HVB-mode equals to 0 (Formula (18))	1	[0.4, 1]

.

3.2. The Selection of Optimization Working Cycles and Validation Working Conditions

To ensure the credibility of the optimization results and prevent the influence of different optimization conditions, the WLTC (world light vehicle test cycle), CLTC (China light-duty vehicle test cycle), and NEDC (new European driving cycle) are selected as the global conditions for parameter optimization, of which the NEDC and WLTC have been used in China’s emission regulations. The CLTC is a driving cycle that is more suitable for China’s actual driving conditions, and was analyzed by China Automotive Technology and Research Center Co, Ltd. and compiled by GPS data from many vehicles and cities. The speed–time profiles of these three driving cycles are shown in Figure 13.

Five driving conditions according to the requirements of the RDE (real driving emission) test, which were actually tested in the Yangtze River Delta region of China, were selected as the validation conditions. The speed–time profiles of the relevant driving conditions are shown in Figure 14, and the statistical feature of each test condition is shown in

Table 11. Features of selected validation working cycles.

	RDC1	RDC2	RDC3	RDC4	RDC5
Length (km)	73.81	76.79	72.14	71.57	74.13
Times (s)	6063	5981	5550	5607	5549
Average velocity (km/h)	43.83	46.22	46.79	45.95	48.09
Max velocity (km/h)	119.00	115.00	117.00	119.00	128.00
Max acceleration (m/s2)	2.78	8.05	2.38	3.33	2.78
Max deceleration (m/s2)	−2.66	−9.06	−2.50	−2.50	−2.78
Average acceleration (m/s2)	0.48	1.07	0.47	0.65	0.61
Average deceleration (m/s2)	−0.42	−0.97	−0.43	−0.50	−0.52
Urban condition percentage (%)	65.30	64.60	64.80	65.30	63.10
Highway condition percentage (%)	34.70	35.40	35.20	34.70	36.90
Acceleration time percentage (%)	31.90	12.20	31.70	33.10	32.00
Deceleration time percentage (%)	36.60	13.50	35.10	42.80	37.70
Constant speed time percentage (%)	17.00	62.00	21.10	11.20	18.20
Stopping time percentage (%)	14.50	12.30	12.10	12.90	12.10

, from which it can be seen that RDC2 is the most aggressive condition, and that the other conditions are of average intensity, reflecting the influence of the driver’s driving style. The proportion of urban driving conditions and the proportion of high-speed driving conditions remain at a relatively consistent level, which largely represents the actual driving conditions of China’s roads in the Yangtze River Delta region.

3.3. PSO Optimization Results

The three working conditions and two objective functions are combined with each other, and the six plans are listed in

Table 12. The combination of PSO algorithm optimization plans.

Combination of Optimization Plan	Plan No
Original plan	0
WLTC + HVB power equivalent fuel consumption (J1)	1
CLTC + HVB power equivalent fuel consumption (J1)	2
NEDC + HVB power equivalent fuel consumption (J1)	3
WLTC + HVB power equivalent fuel consumption + SOC sustaining (J2)	4
CLTC + HVB power equivalent fuel consumption + SOC sustaining (J2)	5
NEDC + HVB power equivalent fuel consumption + SOC sustaining (J2)	6

, in which the original plan is listed as No. 0, and the other plans are numbered sequentially from No. 1 to No. 6.

PHEVs use both grid electric power and engine battery charging electric power, and the cost of the former is heavily dependent on the cost of the grid power price, which exhibits high volatility. The cost of using electricity from the grid is significantly lower than the cost of using fuel for charging, so the fuel consumption in the CS stage greatly affects the economy of PHEVs. Based on the CS stage, the initial SOC of the battery is set to 24%, which is within the CS stage.

The optimization results of the PSO algorithm for the EMS parameters of each plan are shown in

Table 13. Optimization results of PSO algorithm for EMS parameters of each plan.

Plan No	0	1	2	3	4	5	6
vswitch (kph)	70.0	40.0	40.0	54.1	73.0	63.4	66.7
SOCmin (%)	20.0	22.5	21.8	22.0	23.1	21.4	21.9
SOCmax (%)	28.0	27.7	29.3	30.2	27.2	29.2	29.4
vbrake (kph)	7.0	7.0	7.0	7.1	10.7	9.6	15.8
k1	0.70	0.45	0.53	0.72	0.58	0.61	0.60
k2	1.00	0.40	0.40	0.50	0.65	0.61	0.76

. From the optimization results, it can be seen that:

• The speed threshold v_switch for the parallel mode being on is larger than the original plan only in plan 4, and all other plans are smaller than the original plan;
• The difference between the upper and lower bounds of the optimization parameter of the SOC reflects the optimal range of the SOC change in the power maintenance phase, and the optimization results show that the difference between the upper and lower bounds of different plans is very small;
• The v_brake is closed to the lower bound of the optimization, which is 7 kph;
• The k1 and k2 optimization results are both smaller than those of the original plan.

These results show that the torque threshold for the parallel mode in the original plan is set too large, and the utilization rate of the high-efficiency region of the engine is too small. The optimal plans try to reduce the torque threshold for parallel mode entrance within an acceptable range.

Table 14. The AFC and EFC of different plans under optimization working cycle.

Plan No		Plan No
		0	1	2	3	4	5	6
WLTC	AFC	3.74	4.77	4.44	4.74	4.53	4.46	4.83
	EFC	4.42	4.19	4.19	4.26	4.53	4.33	4.40
CLTC	AFC	2.15	4.34	3.78	4.17	5.56	3.77	4.39
	EFC	3.70	3.70	3.71	3.76	3.86	3.77	3.88
NEDC	AFC	1.79	4.69	3.43	3.91	5.85	3.20	3.95
	EFC	3.88	3.87	3.74	3.77	4.06	3.84	3.95

shows the AFC (actual fuel consumption) and EFC (equivalent fuel consumption) calculation results of the different plans under the WLTC, CLTC, and NEDC. It can be found that the fuel consumption results for the cycle conditions over a short distances lead to a big difference between the AFC and EFC. The reason for this is that the distance is too short, and the pure electric mode + parallel mode of driving are used for a long time at the beginning of the trip. The original plan (plan 0) focuses only on the AFC, so the AFC is much smaller than the EFC, but the optimization plan (plan 1~6) adopts the EFC as the objective function optimization, which is done to ensure that the EFC is the smallest, although this results in the AFC increasing and the excessive energy from the engine going into the battery system when the energy conversion efficiency is high, thus improving the energy utilization rate overall. Therefore, the energy-saving effects of the optimized schemes need to be verified under actual driving cycle conditions.

3.4. Verification of Energy-Saving Effect of PSO Optimization Plan

The EFC is verified using the optimization results of the above six plans, and the AFC, EFC, and OPTR (optimization rate), compared with the original plan, are shown in

Table 15. AFC and OPTR for each optimization plan.

Plan No		RDC1	RDC2	RDC3	RDC4	RDC5
0	AFC	4.24	5.06	4.52	4.21	4.23
1	AFC	4.26	4.87	4.41	4.70	4.21
	OPTR (%)	−0.61	3.79	2.37	−11.79	0.40
2	AFC	4.09	5.11	4.43	4.57	4.57
	OPTR (%)	3.59	−0.99	1.97	−8.67	−8.09
3	AFC	4.06	4.93	4.29	4.65	4.70
	OPTR (%)	4.30	2.65	5.09	−10.43	−11.15
4	AFC	4.14	5.18	4.60	4.34	4.16
	OPTR (%)	2.19	−2.37	−1.73	−3.09	1.54
5	AFC	4.61	5.38	4.23	4.50	4.54
	OPTR (%)	−8.71	−6.38	6.37	−6.99	−7.34
6	AFC	4.69	5.43	4.99	4.50	4.58
	OPTR (%)	−10.72	−7.25	−10.38	−7.03	−8.31

and

Table 16. EFC and OPTR for each optimization plan.

Plan No		RDC1	RDC2	RDC3	RDC4	RDC5
0	EFC	4.21	4.97	4.43	4.62	4.58
1	EFC	4.08	4.91	4.29	4.49	4.54
	OPTR (%)	3.04	1.15	2.98	2.82	0.76
2	EFC	4.20	4.82	4.34	4.48	4.47
	OPTR (%)	0.29	2.96	1.83	3.03	2.42
3	EFC	4.22	4.92	4.39	4.52	4.51
	OPTR (%)	−0.14	1.07	0.70	2.01	1.46
4	EFC	4.19	5.02	4.39	4.60	4.55
	OPTR (%)	0.36	−1.07	0.88	0.35	0.61
5	EFC	4.19	4.95	4.43	4.56	4.54
	OPTR (%)	0.50	0.34	−0.05	1.34	0.94
6	EFC	4.30	5.08	4.51	4.69	4.66
	OPTR (%)	−2.07	−2.11	−1.81	−1.60	−1.79

, respectively. From the EFC data (Table 15), The following can be concluded:

• Most of the optimization results are reduced relative to the EFC of the original plan, but some of the optimization results show deterioration of the EFC in some of the validation conditions;
• Because the electric power sustaining strategy (objective function J2) is a requirement of the test regulations, comparing the optimization of the electric power sustaining strategy (plan 4~6) with the non-electric power sustaining strategy (plan 1~3), it can be seen that the optimization of the electric power sustaining plan is optimal under the regulations’ test requirements but is not the best under the validated RDC conditions. Further, the EFC and the AFC have not been greatly improved, and are even deteriorated compared with the plan 0;
• The EFC using the battery power consumption (objective function J1) takes into consideration the direct conversion of the electric power in real time, which better reflects the actual energy conversion. Therefore, the plans (1, 2, and 3) with J1 as their objective function can almost always achieve improvement of the EFC under the validation conditions, which has better universality, and the AFC (Table 14) also improves under most of the validation conditions. In the RDC3 validation conditions, the optimization result of plan 1 is better. The EFC is improved by 2.98%, and the AFC is also improved by 2.37%.

3.5. Comprehensive Selection of Optimization Plan

The optimization plan is selected through the analysis of the optimization rate of the EFC and AFC under different validation conditions. Considering that the five actual driving cycles are all from the random test conditions that meet the RDE test conditions, it is assumed that the five conditions representing the actual driving conditions have equal probability of occurring during the actual driving process, and, therefore, each of the weights is equal. The AOPTRs (average optimization rate) of the EFC and AFC were calculated and are shown in Figure 15. Through comparison, it is found that optimization plans 1 and 2, which use the WLTC and CLTC as optimization conditions and ECMS as the objective function (J1), can obtain the best average EFC AOPTR, which indicates that both plans can obtain a higher energy utilization rate under different driving conditions. Comparison reveals that plan 1 has larger optimization rate of the average AFC, which means that it can take into account the adaptability of the working conditions, the energy utilization, and the actual fuel consumption. Although the AFC is slightly higher than that of the original plan, the extra energy is stored in the HVB when the energy conversion efficiency is high. Therefore, plan 1 is selected as the optimized energy management strategy.

3.6. The Comparison Between Original Plan and Optimum Plans Based on Energy Flow

In order to investigate the reasons for the energy savings of the parameter optimizations of the energy management strategy relative to the original plan, an energy flow analysis of the original and optimized plan 1 is performed.

Firstly, the distribution of the working time of each mode of the powertrain of the original plan and the selected plan 1 are investigated, and the selected evaluation conditions are RDC1, RDC2, and RDC5, which represent the mild and lower-speed driving, aggressive driving, and mild and higher-speed driving conditions, respectively. The calculated results of the proportion of time for each driving mode are shown in Figure 16.

It can be seen from Figure 16 that:

• The duration of the parallel mode of the optimization plan is increased significantly, because the series mode has multi-process energy loss and the economy of long-term use is poor. The optimization plan increases the proportion of parallel mode use;
• From the EFC calculation results (Table 16), it can be seen that, in order to achieve the effect of fuel saving, the use of the series mode should be reduced under the conditions of vehicle speed permission;
• The brake recovery mode in the RDC2 condition has a shorter duration, which is because this condition is more aggressive, the process of reaching the predetermined speed is faster, and the proportion of uniform speed time is longer;
• The RDC5 condition has the largest percentage of use of the recovery mode because RDC5 is in deceleration for the largest percentage of the time, the deceleration rate is small, and more energy can go to the brake recovery system.

The results of the driving energy demand for the different evaluation conditions are shown in Figure 17. Since the coasting energy demand is divided into driving and braking phases (coasting resistance is greater than 0 when the vehicle speed is greater than zero), the coasting resistance energy of the two phases is counted separately. The results show that:

• During the acceleration and uniform speed phase (drive period), the acceleration energy demand of the mild driving mode (RDC1 and RDC5) accounted for a higher proportion, and, during the aggressive driving (RDC2), the drive phase coasting resistance loss accounted for a larger proportion;
• In the braking phase (deceleration), the coasting resistance loss of aggressive driving is lower, but the whole-vehicle deceleration loss accounts for a larger proportion of 35.6%, and this part of the energy loss will be transferred to the braking system;
• Coasting resistance energy is the energy loss of the body and tire resistance in the process of driving. Under the conditions RDC1, RDC2, and RDC5, the total coasting resistance loss is 25,060 kJ, 26,620 kJ, and 27,490 kJ, respectively. This part of the energy loss cannot be recycled, and it will be listed as the total loss of the body. The total loss of the body is closely related to the average vehicle speed, and therefore depends more on the traffic conditions;
• The energy exchange at the wheel end is the key to the coupling of the powertrain system and the body system, and so the acceleration energy and deceleration energy are directly coupled with the wheel end. This part of the energy flow analysis needs to be combined with the energy flow analysis of the powertrain system.

The energy flow and loss of each link under each working condition are shown in Figure 18, with the effective energy transfer path in red, the recovered energy transfer path in green, and the energy loss value in purple. It can be seen that:

• The biggest difference between the original plan and the optimized plan is the P1 motor output energy and transmission loss energy, indicating that the original plan tends to be in the series mode for a longer time;
• The P3 motor output energy under the optimized plan is smaller, and the motor loss is also smaller, indicating that the optimized plan tends to give priority to the use of direct engine driving under the CS stage;
• The value of the P1 motor directly delivering power to the P3 battery under the optimization plan is greatly reduced, indicating that the use percentage of the series mode is reduced, and that the P3 motor is more inclined to obtain energy from the battery.

Combined with the previous operating mode time statistics (Figure 16), it can be summarized that the basic principle of the PSO algorithm in finding the optimal optimization plan is that prioritizing use of the parallel mode will lead to less loss processes and will reduce the loss of electrical multi-stage transmission.

4. Conclusions

Based on the parameter optimization problem of EMS in the CS phase of a newly designed P1–P3 PHEV with a single-gear-ratio and coaxial configuration, an improved intelligent optimization algorithm, PSO, is used to find the optimal rule-based EMS parameter combinations. Different driving styles for long-distance driving conditions extracted from real driving conditions are used to validate the energy-saving effects of the optimized EMS parameter combinations, and energy flow analysis is used to explain the energy-saving mechanisms. The main research results are as follows.

• The intelligent optimization algorithm, PSO, is used to optimize the rule-based EMS, which can not only reduce the dependence on expert knowledge but can also obtain the optimal parameters plan and reduce the trial-and-error cost of the preliminary design stage. At the same time, in order to prevent the algorithm from falling into local optimality and the working conditions selected for optimization not being representative enough, two different objective functions and three optimal working conditions are set to be combined to form six comparative plans. The energy-saving effect of the different plans is verified through extracted actual driving conditions (RDC) compared to the initial control group. The results show that the energy-saving effect of the best optimal combination brings a 2.98% improvement in the EFC and 2.37% in the AFC (plan 1, RDC3). Since the PHEV fuel consumption test regulation requires the battery SOC to remain unchanged, it is found that the optimal plan that meets the regulatory test conditions does not lead to an improvement in energy efficiency and deterioration in the AFC under real-world driving conditions;
• The energy-saving effects of different optimization plans for real driving are obtained by taking the average value, and the EFC AOPTR under the optimal parameter combination is determined to be 2.15% (plan 1). Plan 1 is selected as the best plan. The energy flow analysis method is used to calculate the energy flow in each link, and the energy flow results of the initial control group and those of the best plan are compared. It is found that the optimal best plan by the improved PSO algorithm tends to reduce the use of the series mode, and the percentage of the series mode use time under different driving styles has been reduced by 6–18%. The optimized plan appropriately reduces the frequency of P3 motor and P1 motor usage by lowering the access thresholds (v_switch, k1, k2) for the parallel mode, therefore reducing the electrical losses and saving the overall vehicle energy utilization in the CS phase. The energy-saving principle of the PSO algorithm optimization lies in reducing the usage time of the series mode and reducing the electrical losses by using the reduced access thresholds of the parallel mode;
• The methodology used in this paper avoids the use of global optimization algorithms with high computational requirements, and also avoids deep reinforcement learning methods that require a large number of learning samples to be collected before the design stage, so that the optimized parameters can be directly inputted into the EMS controller of the whole vehicle for subsequent application. At the same time, the research idea adopted in this paper avoids the possibility of falling into the local optimum when using heuristic algorithms, instead verifying the effectiveness of the optimization method through actual driving conditions. The direction of fuel consumption reduction is analyzed, which provides a direction for the optimization of the parameters of the energy management strategy.

For future optimization, the energy management strategy optimization method described in this paper, which combines energy flow and actual driving conditions, can be extended to other vehicle projects. First of all, the optimization methods used in this paper do not require high computational requirements. Secondly, when solving multi-parameter optimization, intelligent optimization algorithms have the advantages of being easy to operate, fast to compute, and credible in terms of their results compared with other methods. Finally, the actual driving cycle and energy flow analysis methods used in this paper can be extended to whole-vehicle thermal management optimization, energy management/thermal management co-optimization, etc.