Research on Optimal Driving Torque Control Strategy for Multi-Axle Distributed Electric Drive Heavy-Duty Vehicles

Abstract

Multi-axle distributed electric drive heavy-duty vehicles have the characteristics of high transmission efficiency, strong maneuverability, and good passability, making them widely used in large cargo transportation. However, the current driving torque control strategies of multi-axle distributed electric drive heavy-duty vehicles lack comprehensive consideration of their longitudinal and lateral dynamic characteristics, making it difficult to comprehensively optimize multiple performances such as power economy, comfort, and stability. In order to solve the above problems, This work focuses on a five-axle distributed electric drive heavy-duty vehicle. Firstly, given the differences in dynamics between two-axle vehicles and multi-axle vehicles, the dynamic model of the multi-axle distributed electric drive heavy-duty vehicle and its critical components is constructed. Then, by analyzing the characteristics of power economy, comfort, and stability of the multi-axle distributed electric drive heavy-duty vehicle, an optimal driving torque control strategy based on multiple performance coordination is proposed. Finally, on the hardware-in-the-loop (HiL) platform, the performance of the optimal driving torque control strategy proposed in this paper is verified by using the China Heavy-Duty Commercial Vehicle Test Cycle for Truck (CHTC-HT) and a straight-line acceleration driving condition on a split friction road. The simulation test results show that, compared with the traditional torque average distribution strategy, the proposed optimal driving torque control strategy can reduce the energy consumption rate by 3.45% in CHTC-HT. The strategy is attributed to the driving torque distribution based on the vehicle’s optimal instantaneous energy consumption, and vehicle comfort is also ensured by the driving mode switching frequency suppression. Subsequently, the vehicle’s stability on the split friction road is effectively improved by the torque coordination compensation strategy. This control strategy significantly improves the comprehensive performance of multi-axle distributed electric drive heavy-duty vehicles.

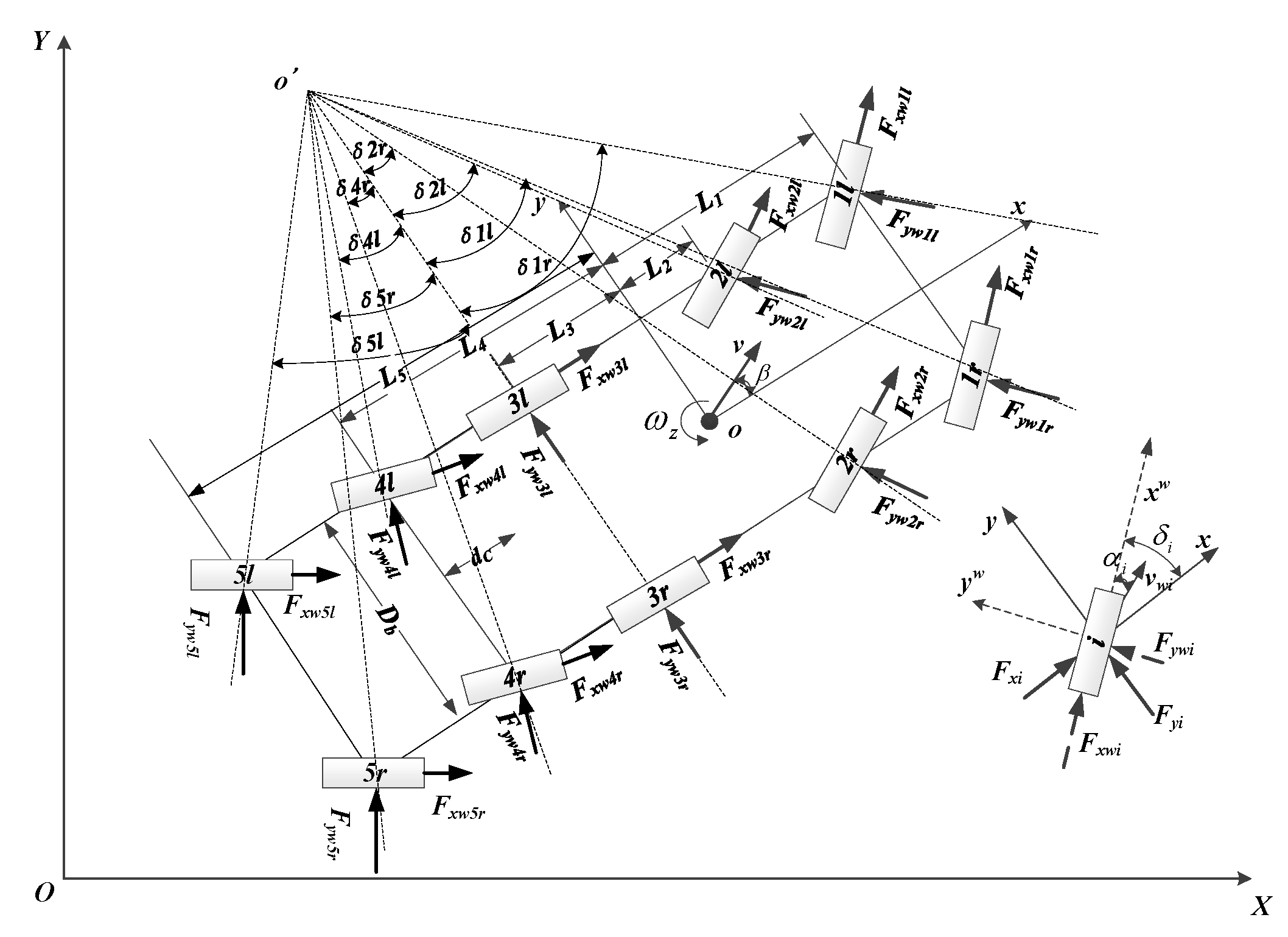
1. Introduction

As global energy shortages and environmental pollution problems become increasingly severe, electric vehicles, with their advantages of cleanliness and high efficiency, have become an essential technology for governments to save energy and reduce emissions. They have begun to be widely promoted and popularized worldwide in recent years. Multi-axle distributed electric drive heavy-duty vehicles in the commercial vehicle sector are characterized by their high control flexibility, short transmission chain, compact structure, high transmission efficiency, and optimal space layout utilization [1,2]. As a result, they have emerged as the preferred vehicles for transporting large and specialized freight, garnering increasing attention from researchers in recent years. However, due to the participation of multiple motors in driving, multi-axle distributed electric drive heavy-duty vehicles have over-driving characteristics, numerous constraints, and strong nonlinear coupling of vehicle longitudinal–lateral–vertical motion behaviors. They still face theoretical and technical challenges in vehicle dynamics control and driving economy control [3]. Therefore, how to optimize the driving torque according to the dynamic characteristics of multi-axle distributed electric drive heavy-duty vehicles has become a problem that needs to be solved in the field of multi-axle vehicle control.

Regarding the driving torque of multi-axle vehicles, existing research can be roughly divided into three categories: multi-axle vehicle dynamic control, multi-axle vehicle economic torque distribution, and multi-axle vehicle stability control.

In terms of torque distribution for multi-axle vehicle economy, Fan et al. conducted a series of studies on the drive of three-axle electric drive vehicles and used a composite method to optimize the driving torque distribution coefficient of each axle, thereby improving the efficiency of the motor drive system and the drive economy of the whole vehicle [4]. Zhong Heng et al. [5] proposed a coordinated distribution control strategy for the driving force of multi-axle vehicles based on a working condition adaptive identification algorithm, which can distribute failure mode torque according to the failure state of the vehicle power source while improving the economy and reliability of multi-axle vehicles. Li Junqiu et al. [6] proposed an energy-saving control strategy for a multi-axle electric drive vehicle based on drive mode switching. By selecting the number and position of the wheels involved in the drive in real-time, the wheel hub motor works in the high-efficiency zone, thereby reducing vehicle energy consumption. Qiao Shuaipeng et al. [7] proposed a torque distribution control strategy for the multi-axle electric drive vehicle based on the optimal efficiency of the motor system, which improved the vehicle economy by 9.18% compared with the average driving torque distribution strategy. Jing Liqiang et al. [8] proposed a torque distribution control method for multi-axle electric vehicles using the Deep Deterministic Policy Gradient (DDPG) algorithm for deep reinforcement learning optimization, which optimized the vehicle’s energy consumption under different steering conditions. Taking into account the advantage of reconfigurable control for a certain 8 × 8 in-wheel motor-driven wheel vehicle, Zhang Rui proposed a hierarchical vehicle dynamics and energy-saving optimization integrated coordinated control strategy to improve the efficiency of the entire drive system while meeting the vehicle’s handling stability [9]. Ragheb et al. [10] analyzed the wheel-soil interaction mechanics, off-road vehicle dynamic simulation, and torque management strategy of multi-wheeled off-road vehicles, and proposed an active torque distribution system to optimize traction and yaw control to achieve high efficiency and high stability of multi-wheeled off-road vehicles. Oh et al. [11] used a model predictive control (MPC) algorithm to optimize the steering control of a multi-axle crane. By building a simplified crane model and considering the driver’s intention, the MPC algorithm calculated the optimal steering angle for each axle to minimize the turning radius and reduce the driver’s steering effort, thereby improving steering efficiency and dynamic stability.

In terms of dynamic control, Yang Guibing et al. [12] constructed a driving force optimization control algorithm that includes pre-distribution control based on each axle load, drive anti-skid control, and driving force redistribution based on vehicle status, realizing the optimal slip rate estimation and anti-skid control under variable adhesion coefficient road, improving the vehicle’s climbing performance, straight-line acceleration performance, and passability on obstacle roads. Bao Yutong et al. [13] proposed a coordinated anti-skid control strategy for 12 × 12 multi-axle distributed drive vehicles, which significantly reduces the model complexity and improves the slip control accuracy by 30% using the Hierarchical Linear Quadratic Regulator (HLQR) scheme. Given the driving ability weakening and passability reduction when multi-axle distributed vehicles are under failure conditions on off-road terrain, Chu Wenbo et al. [14] proposed a coordinated driving force distribution control strategy to ensure the vehicle’s longitudinal driving ability. In order to reduce the problem of reduced reliability of multi-axle vehicle power control caused by parameter changes, Xiaofei Pei [15] presented a joint estimation of the vehicle’s state and parameters based on the dual unscented Kalman filter and developed a real-time parameter estimator to implement the simultaneous estimation of the vehicle’s state and parameters. Luoquan Li [16] proposed a hierarchical drive allocation strategy for dynamically coordinating vehicle performance. The upper layer uses a sliding mode variable structure control algorithm based on adaptive error to determine the expected additional yaw moment of the vehicle, and the lower layer uses a fuzzy controller and quadratic programming algorithm to optimize the driving torque of each wheel, thereby improving the comprehensive performance of distributed drive multi-axle vehicles under various working conditions. Williams [17] created a dynamic model of multi-axle vehicles with any number of steerable axles by expanding the yaw plane model and integrating rolling dynamics and multi-axle steering functions. This model is designed to predict and control the dynamics of multi-axle vehicles, thereby enhancing their maneuverability and stability. Bogomolov et al. [18] proposed a method for calculating the normal reaction forces of each axle of a multi-axle vehicle and developed a general mathematical model for determining the horizontal coordinates of the elastic center of the vehicle body. This method takes into account the design characteristics of the vehicle suspension and shows through example analysis that this method can significantly affect the geometric characteristics of the adhesion utilization curve and complies with UN/ECE regulations. Healy [19] proposed a velocity vector algorithm for multi-axle electric vehicles, which can estimate the wheel and axle speeds of each electric drive axle according to different steering modes and vehicle geometry. The algorithm is applicable to a variety of vehicle configurations, which is of great significance to improving the vehicle’s traction, maneuverability, and passenger comfort, and provides a theoretical basis for the design and control of transmission system components.

In terms of multi-axle vehicle stability control, Wang Weichen et al. [20] proposed a fuzzy collaborative control method for assisted driving of multi-axle distributed electric drive vehicles based on the Linear Time-Varying Model Predictive Control (LTV-MPC). By designing a multi-objective coordination algorithm based on the human–machine collaboration index and the stability weight adjustment coefficient, the human–machine conflict was alleviated, and the vehicle’s handling stability and energy efficiency were improved. Li Zhichao et al. [21] proposed a path-tracking control strategy for autonomous multi-axle electric vehicles based on Nonlinear Model Predictive Control (NMPC). Considering the high-fidelity nonlinear dynamic model of the vehicle, the nonlinear characteristics of the tires, and other constraints, a fast solution algorithm based on the projected gradient and augmented Lagrangian method was designed to effectively improve the vehicle’s safety and stability while tracking the target path. Wang Zhifu et al. [22] established a dynamic mathematical model of an 8 × 8 wheel hub motor-driven vehicle with 26 degrees of freedom using Matlab/Simulink and verified the model’s performance and the effect of the handling stability control strategy through closed-loop simulation. Huang Wei et al. [23] established a multi-axle steering vehicle model with two degrees of freedom and conducted a handling stability simulation of a three-axle special vehicle in the ADAMS multi-body dynamics model, highlighting the influence of the lateral stabilizer bar on handling stability. Wang Yunchao [24] conducted experimental analysis on multi-axle steering vehicles based on the existing vehicle handling stability test methods and developed corresponding test methods. By establishing a linear planar dynamical model of multi-articulated vehicles with multiple axles, Aoki [25] employed stability factors coupled with numerical computations to scrutinize the non-oscillatory stability during steady-state steering and lane-changing maneuvers, and analyzed the steering sensitivity and off-tracking behaviors, as well as the consequential impact of multi-axle configurations on vehicle stability. Kushwaha [26] developed a 4-DOF linear yaw plane model to analyze the yaw dynamics of a seven-axle trailer–semitrailer combination vehicle. The steering response and tire force distribution at different speeds were studied through simulation and experimental verification, along with methods to improve handling stability at low speeds using command steering law.

The aforementioned research has effectively improved the performance of multi-axle vehicles in terms of economic control, dynamic control, and stability control, and has provided a solid research foundation for the comprehensive control of multiple performances of multi-axle electric drive vehicles. However, for multi-axle distributed electric drive heavy-duty vehicles, their driving modes can include single-axle drive, two-axle drive, and multi-axle drive. Under certain steady-state driving conditions or minor acceleration conditions, the vehicle’s driving power requirements can be satisfied by merely adopting non-all axle drive modes such as single-axle drive or two-axle drive mode, and the power loss of the drive system will be reduced by increasing the load of the working motor, ultimately improving the efficiency of the electric drive system and the vehicle’s economy. Therefore, according to the vehicle’s power requirements under different driving conditions, determining the number of drive axles and the corresponding torque distribution of each axle to achieve optimal vehicle economy has become an important research topic in the field of multi-axle electric drive vehicle drive control. In addition, parameters such as velocity and axle load of multi-axle electric drive vehicles often change greatly, and the road conditions are diverse; the vehicle stability is prone to decrease because wheels slip under certain low-adhesion and high-torque conditions. Therefore, how to control the driving force of each wheel on different road adhesions based on the dynamic characteristics of multi-axle distributed electric drive heavy-duty vehicles is currently also an important research focus on vehicle stability.

This paper takes a five-axle distributed electric drive heavy-duty vehicle as the research object. The wheels on each axle are connected to the drive motor through a fixed speed ratio reducer. The purpose of this research is to develop an optimal strategy for the driving torque distribution of each axle to improve the vehicle’s power economy, comfort, and stability under different working conditions. The main contribution of this paper lies in optimizing the distribution of torque of each axle under specific required torque by combining the dynamic characteristics of multi-axle vehicles, improving the efficiency of the vehicle’s overall electric drive system, formulating corresponding strategies to suppress the decrease in comfort caused by the torque switching of different axles, and improving the vehicle stability when driving on complex roads through torque compensation, thereby providing a theoretical basis for energy-saving, comfort, and safety control in distributed electric drive multi-axle heavy-duty vehicles.

The remaining parts of this paper are as follows: Section 2 constructs the dynamic model of the multi-axle distributed electric drive heavy-duty vehicle and its key components, providing a theoretical basis for the control optimization of driving torque; Section 3 introduces the optimal driving torque control strategy for multi-axle distributed electric drive heavy-duty vehicles based on multiple performance coordination, focusing on the driving torque reference allocation strategy based on the optimal vehicle’s instantaneous energy consumption, the comfort control strategy based on the suppression of the drive mode switching frequency, and the torque coordination compensation strategy based on drive anti-slip; Section 4 conducts hardware-in-the-loop simulations of the CHTC-HT and an open-road straight-line acceleration driving condition on a split friction road to verify the effect of the proposed drive control strategy; and Section 5 is the conclusion.

2. Construction of Dynamics Model of Multi-Axle Distributed Electric Drive Heavy-Duty Vehicle and Its Key Components

2.1. Vertical Load Model of Each Wheel

The static wheel load of a multi-axle vehicle is generally calculated by the static axle load of each axle. However, different from the dynamics of two-axle vehicles, the method of calculating the statically determinate problem of ordinary two-axle vehicles cannot be used since the static axle load calculation for a multi-axle vehicle is an over-determined problem [27]. Therefore, the displacement method is used to calculate the static axle load of each axle in this paper. Assuming that the loads on the left and right wheels are equal under static conditions, the body of the multi-axle vehicle is abstracted into a single-track force-bearing rigid rod [21]. The rigid rod is in an equilibrium state due to vehicle gravity and the wheels’ normal force. The system composed of tires and suspension is abstracted into a spring system with a stiffness of K_i. The force analysis of the axle load calculated by the displacement method is shown in Figure 1. In Figure 1, the spring system deforms under the action of the gravitational force mg. Due to the varying distances L_i from the vehicle centroid to each axle, the compression amount Δh_is of the spring system on each axle is different. Ultimately, the sum of the vertical deformation forces F_zis on the five axles equals the vehicle gravitational force mg, and the entire system is in a state of force equilibrium.

According to Hooke’s law, the static vertical deformation of each axle [28] is as follows:

$$\Delta h_{is}={\displaystyle \frac{F_{zis}}{K_i}}, \left(i=1,2,\cdots ,5\right)$$

(1)

where $i=1~5$ represents the i-th axle; Δh_is and K_i are the static vertical deformation and the stiffness of the spring system for the i-th axle in mm, respectively; F_zis represents the vertical reaction of the ground of the i-th axle in N. From the force equilibrium on the z-axle and the zero resultant moments on the y-axle of the vehicle body, we can get the following:

$$\left\{\begin{array}{c}{\displaystyle \sum _{i=1}^5{F}_{zis}=mg}\\ {\displaystyle \sum _{i=1}^5\left(F_{zis}·L_i\right)=0}\end{array}\right.,(i=1,2,\cdots ,5)$$

(2)

where m is the vehicle mass in kg; g is gravitational acceleration, its value is 9.8 m/s²; L_i is the horizontal distance of the i-th axle to the mass center in m. Then, according to the geometric relationship shown in Figure 1, the deformation equation can be obtained:

$${\displaystyle \frac{\Delta h_{1s}-\Delta h_{2s}}{\Delta h_{1s}-\Delta h_{is}}}={\displaystyle \frac{L_1-L_2}{L_1-L_i}},\left(i=3,4,5\right)$$

(3)

where Δh_1s, Δh_2s, and Δh_is represent vertical suspension deflection of the 1st axle, 2nd axle, and i-th axle in m, respectively. It should be noted that in the calculation of Equations (2) and (3), when the i-th axle is located in front of the center of mass, L_i takes a positive value, and when the i-th axle is located behind the center of mass, L_i takes a negative value. Combining Equations (1)–(3), we can obtain a five-variable linear equation system about F_zis by eliminating the intermediate variables Δh_is and K_i. Next, substituting the known algebraic value L_i into it, we can obtain the static load F_zis of each axle [28]:

$$F_{zis}={\zeta }_i·mg,\left(i=1,2,\cdots 5\right)$$

(4)

In the formula, the constant coefficient ${\zeta }_i$ is the static load coefficient of the i-th axle. Under static conditions, the loads on the left and right wheels are equal, so the static load of a wheel on the i-th axle is as follows:

$$F_{zijs}={\displaystyle \frac{1}{2}}{F}_{zis},\left(i=1,2,\cdots 5; j=1,2\right)$$

(5)

where j = 1 represents the left, and j = 2 represents the right, so F_zijs is the static load of a wheel on the i-th axle in N. Therefore, the maximum driving force of each wheel provided by the ground adhesion conditions is

$$F_{wij\_\max }=\phi ·F_{zijs}$$

(6)

where F_{wij_max} is the maximum driving force of the j-th wheel on the i-th axle in N; $\varphi$ is the ground adhesion coefficient.

In order to prevent wheel slippage caused by excessive motor driving force, the wheel torque provided by the corresponding motor should satisfy the following:

$$T_{wij}\le F_{wij}·r=\phi ·F_{zijs}·r$$

(7)

where T_wij is the torque of the j-th wheel on the i-th axle in N·m; F_wij is the force of the j-th wheel on the i-th axle in N; $r$ is the wheel radius in m.

2.2. Body Model

Since multi-axle vehicles have complex longitudinal and lateral forces because more wheels are in contact with the ground, their body force model becomes more complex [29]. As shown in Figure 2, by analyzing the forces and moments acting on the vehicle, the differential equation of motion in the body coordinate system can be established using Euler’s law of motion.

• The vehicle longitudinal motion equation [29] is as follows:

  $$m(\stackrel{·}{v_x}-v_y{\omega }_z)={\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{F}_{xwij}\cos {\delta }_{ij}}}-{\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{F}_{ywij}\cos {\delta }_{ij}}}-F_R;\hspace{1em}\hspace{1em}i=1,2,\cdots ,5;j=1,2$$

  (8)

  where v_x is the longitudinal velocity in the vehicle coordinate system in m/s; v_y is the lateral velocity in the vehicle coordinate system in m/s; ω_z is the angular velocity of rotation around the z-axle in the vehicle coordinate system in rad/s; F_xwij and F_ywij are the longitudinal force and the lateral force of the j-th wheel on the i-th axle in N, respectively; δ_ij is the steering angle of the j-th wheel on the i-th axle in rad; F_R represents the driving resistance in N, as shown in Formula (9):

  $$F_R=mg{f}_r\cos {\alpha }_{grade}+mg\sin {\alpha }_{grade}+{\displaystyle \frac{1}{2}}{C}_{D}A{\rho }_a{v}_x^2$$

  (9)

  where f_r is the rolling resistance coefficient, which is mainly related to the road surface; α_grade is the slope angle in rad; C_D is the air resistance coefficient; A is the windward area in m²; ρ_a is the air density, which is generally taken as 1.2258 N·s²·m⁻⁴.
• The lateral motion equation of the vehicle body [29] is as follows:

  $$m(\stackrel{·}{v_x}+v_x{\omega }_z)={\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{F}_{xwij}\sin {\delta }_{ij}}}+{\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{F}_{ywij}\cos {\delta }_{ij}}};\hspace{1em}\hspace{1em}i=1,2,\cdots ,5;j=1,2$$

  (10)
• The yaw motion equation of the vehicle body [29] is as follows:

  $$\begin{array}{cc}{I}_z{\stackrel{·}{\omega }}_z=& {\displaystyle \frac{B}{2}}{\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2[{(-1)}^j{F}_{xwij}\cos {\alpha }_{ij}+{(-1)}^{j+1}{F}_{ywij}\sin {\alpha }_{ij}]}+{\displaystyle \sum _{i=1}^2{\displaystyle \sum _{j=1}^2{L}_i(F_{xwij}\cos {\alpha }_{ij}+F_{ywij}\sin {\alpha }_{ij})}}}\\ & -{\displaystyle \sum _{i=3}^5{\displaystyle \sum _{j=1}^2{L}_i(F_{xwij}\cos {\alpha }_{ij}+F_{ywij}\sin {\alpha }_{ij})}+{\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{M}_{zij}};i=1,2,\cdots ,5;j=1,2}}\end{array}$$

  (11)

  where I_z is the moment of inertia of the vehicle rotating around the z-axle in kg·m²; α_ij is the wheel slip angle of the j-th wheel on the i-th axle in rad; B is the wheelbase in m; M_zij is the self-aligning torque of the j-th wheel on the i-th axle in N·m.

2.3. Motor System Model

The empirical modeling method is adopted to construct an inner rotor permanent magnet synchronous motor model. The external characteristics and efficiency data of the motor are calibrated through relevant experiments, and then the external characteristic curve formula of the motor is fitted through data. Finally, a single-drive motor satisfies the following relationship:

$$T_{mij}=\left\{\begin{array}{l}{T}_{m\max }\hspace{1em}\hspace{1em}\begin{array}{cc}& n_{mij}\le n_b\end{array}\\ 9550P_{m\max }/n_{mij}\begin{array}{cc}& n_{mij}>n_b\end{array}\end{array}\right.$$

(12)

where T_mmax is the maximum output torque of a single motor in N·m; P_mmax is the power of a single motor in kW; n_b is the motor base speed in r/min; n_mij is the speed of the j-th motor on the i-th axle in r/min.

The motor output shaft is transmitted to the wheels through the reducer, and the final output torque and speed can be expressed as follows:

$$\left\{\begin{array}{c}{T}_{wij}=T_{mij}·i_0·{\eta }_{ij}\\ n_{wij}=n_{mij}·i_0\end{array}\right.$$

(13)

where i₀ is the fixed transmission ratio of the reducer; ${\eta }_{ij}$ represents the transmission efficiency of the reducer.

Due to factors such as inertia, communication delay, and gap, the motor output torque has certain dynamic characteristics, which can be expressed by a second-order transfer function [30]:

$$T_{mij}={\displaystyle \frac{1}{1+2\xi s+2{\xi }^2{s}^2}}{e}^{-\tau s}{T}_{cmdij}$$

(14)

where T_cmij is the target torque issued by the vehicle controller in N·m; $\xi$ and $\tau$ are parameters determined by motor performance and communication delay.

2.4. Tire Slip Angle and Slip Rate Model

The slip rate and sideslip angle of heavy-duty vehicle tires are coupled with each other, and the longitudinal force and lateral force have a greater impact on the vehicle’s dynamic performance. Therefore, the magic formula model based on the “Pac 2022_315/80 R22.5” is established as the tire model in this paper, which can be applied to complex working conditions such as steady-state steering conditions, single/double lane change conditions, and split road conditions for heavy-duty vehicles.

For multi-axle distributed drive vehicles, the independent control of each wheel’s torque results in different slip rates, which can significantly affect the vehicle’s lateral–longitudinal stability. Therefore, based on the comprehensive consideration of the tire’s sideslip angle, slip rate, and road adhesion coefficient, the longitudinal velocity and lateral velocity of the wheel center are as follows:

$$\left\{\begin{array}{c}{u}_{ij}=v_x\pm {\displaystyle \frac{{\omega }_{z}B}{2}}\\ v_{ij}=v_y\pm L_i{\omega }_z\end{array}\right.$$

(15)

where u_ij and v_ij are the longitudinal velocity and lateral velocity of the j-th wheel on the i-th axle in m/s, respectively; ω_zB/2 is caused by yaw motion—when j = 1, its value is negative, and when j = 2, its value is positive; L_iω_z is caused by yaw motion. The term is positive for the first two axles (i = 1, 2) located in front of the vehicle’s center of mass, and for the rear three axles (i = 3, 4, 5) located behind the vehicle’s center of mass, the term is negative. Therefore, in the wheel coordinate system $o^w-x^w{y}^w{z}^w$, there is

$$v_{wxij}=u_{ij}\cos {\delta }_{ij}+v_{ij}\sin {\delta }_{ij}$$

(16)

where v_wxij is the velocity of the wheel center along the $x^w$ direction of the corresponding tire coordinate system for the j-th motor on the i-th axle in m/s. The wheel slip rate under driving conditions [13] is as follows:

$${\lambda }_{ij}={\displaystyle \frac{{\omega }_{ij}r-v_{wxij}}{\max ({\omega }_{ij}r,v_{wxij})}}$$

(17)

where λ_ij is the wheel slip rate of the j-th motor on the i-th axle. The longitudinal and lateral slip rates of the wheels [13] are as follows:

$$\left\{\begin{array}{c}{\lambda }_x={\lambda }_{ij}\cos {\delta }_{ij}\\ {\lambda }_y={\lambda }_{ij}\sin {\delta }_{ij}\end{array}\right.$$

(18)

where ${\lambda }_x$ and ${\lambda }_y$ are the longitudinal and lateral slip rates of the tire, respectively. The wheel slip angle is as follows:

$${\alpha }_{ij}={\delta }_{ij}-\arctan {\displaystyle \frac{v_{ij}}{u_{ij}}}$$

(19)

3. Optimal Driving Torque Control Strategy for Multi-Axle Distributed Electric Drive Heavy-Duty Vehicles Based on Multiple Performance Coordination

Since multi-axle distributed electric drive heavy-duty vehicles have characteristics such as large axle load changes, diverse driving modes, and variable adhesion performance, an optimal driving torque control strategy is proposed in this paper based on the coordination of multiple performances such as power economy, comfort, and stability. The control strategy is divided into three modules: power economy module, comfort module, and stability module. Among them, the power economy control module mainly determines the driving mode by optimizing the instantaneous energy consumption under the constraints of each axle wheel adhesion according to the vehicle driving state and the driver’s control signal; that is, it determines the number and the driving torque distribution of working axles through the optimization algorithm. The comfort control module reduces the switching caused by different driving modes of the power economy module, to ensure the vehicle’s comfort. Finally, the stability control module mainly makes the slip rate of the driving wheel within a stable range by controlling each motor torque under various road adhesion and load changes, thereby improving the vehicle’s stability.

The power economy module, comfort module, and stability module are controlled by the distribution of the torque of the left and right drive motors on each axle. The control strategy is based on the torque distribution of the power economy module, which can determine the efficient and economic torque distribution when the vehicle is driving under various working conditions. This benchmark torque distribution is the basis for the torque distribution of the other two control modules. However, the torque distribution of the power economy module may cause frequent torque switching between different axles, which in turn causes a decrease in driving comfort. Therefore, in order to slow down the decrease in comfort, this paper develops a comfort control strategy based on driving mode switching frequency suppression to reduce the vehicle jerk caused by driving mode switching. In addition, the power economy distribution makes it difficult to ensure vehicle stability under some complex road conditions. Especially, the low adhesion coefficient road surface easily causes some wheel torque changes, which further increases vehicle lateral force and deteriorates vehicle stability. Therefore, a torque coordination compensation strategy based on dynamics and stability is developed in this paper, which can adjust the torque of the left and right motors on a specific axle to address the impact of lateral interference forces on vehicle stability.

3.1. Driving Torque Benchmark Distribution Strategy Based on the Vehicle’s Optimal Instantaneous Energy Consumption

In general, the higher the efficiency of the vehicle’s electric drive system, the lower the vehicle’s energy consumption. Therefore, the essence of improving the economy of electric drive vehicles is to improve the efficiency of the vehicle’s electric drive system [31]. Generally speaking, the high-efficiency area of the motor is mostly concentrated in the high-speed or high-torque range. By optimizing the motor torque distribution, the motor working point can be moved to the high-speed and high-torque range, thereby improving the working efficiency of the motor and ultimately improving the vehicle’s economy.

The five-axle distributed electric drive heavy-duty vehicle studied in this paper has five drive modes: single-axle drive, dual-axle drive, three-axle drive, four-axle drive, and five-axle drive. Different drive modes correspond to different power distribution methods, which greatly affect the power and energy consumption of the vehicle. Therefore, provided that the total demand torque is met, the control strategy aims to improve the efficiency of the electric drive system by increasing the load of the working motor, which can be achieved by reasonably increasing or reducing the number of drive shafts. Specifically, this paper takes the instantaneous energy consumption as the goal and optimizes the multi-axle vehicle drive mode and the driving torque distribution of the working axles under multiple constraints, such as vehicle velocity, motor speed, axle load change, and road adhesion. This ultimately achieves the improvement of the vehicle economy. The specific process is as follows:

3.1.1. Optimization Variables and Objective Function

The required driving torque has a certain relationship with the accelerator pedal opening signal, where the accelerator pedal consists of a free stroke and an effective stroke. The accelerator pedal opening α_ap can be expressed as follows:

$${\alpha }_{ap}={\displaystyle \frac{\epsilon -{\epsilon }_0}{{\epsilon }_{\max }-{\epsilon }_0}}$$

(20)

where α_ap represents the accelerator pedal opening; ε₀, ε, and ε_max represent the accelerator pedal’s empty travel, effective travel, and maximum travel, respectively. To reduce the control difficulty, this paper adopts a linear correlation scheme between the total required driving torque and the accelerator pedal opening. Therefore, the relationship between the total required driving torque and the accelerator pedal is as follows:

$$T_{req}={\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{T}_{mij}({\alpha }_{ap},n_{mij})}};\hspace{1em}\hspace{1em}i=1,2,\cdots 5;j=1,2$$

(21)

where T_req is the total required driving torque in N·m, which is the total output torque of each drive motor of the electric vehicle; $T_{mij}({\alpha }_{ap},n_{mij})$ represents the torque of the j-th motor on the i-th axle in N·m. In this state, the total required power is as follows:

$$P_{mech}={\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{P}_{mech,mij}}}={\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{\omega }_{mij}{T}_{ij}({\alpha }_{ap},n_{mij});}}\hspace{1em}\hspace{1em}i=1,2,\cdots 5;j=1,2$$

(22)

where $P_{mech}$ is the total mechanical power of the driving motor in kW; P_{mech,m ij} is the mechanical power of the j-th motor on the i-th axle in kW. Then, the motor speed was converted to the international standards:

$${\omega }_{mij}={\displaystyle \frac{2\pi n_{mij}}{60}};\hspace{1em}\hspace{1em}i=1,2,\cdots ,5;j=1,2$$

(23)

where ${\omega }_{mij}$ is the rotational speed of the j-th motor on the i-th axle in rad/s. The motor’s mechanical power is used to overcome various driving resistances and is the vehicle’s effective work power. However, the motor also generates some loss of power due to iron loss, copper loss, friction loss, etc. Therefore, the total motor power should equal the sum of the motor’s mechanical part and the motor loss power, that is

$$P_t=P_{mech}+P_{loss}={\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2(P_{mech,mij}+P_{loss,mij});}}\hspace{1em}\hspace{1em}i=1,2,\cdots ,5;j=1,2$$

(24)

where P_t is the total power of the drive motor in kW; P_loss is the total loss of power of the drive motor in kW; P_loss,mij is the mechanical power of the j-th motor on the i-th axle in kW. The motor loss energy is dissipated into the air in the form of heat. In motor mode, the motor power loss is as follows:

$$P_{loss,mij}=\left\{\begin{array}{cc}{P}_{mech,mij}·(1/{\eta }_{mij}(T_{mij},{\omega }_{mij})-1),& T_{mij}>T_{mij0},{\omega }_{mij}>{\omega }_{mij0}\\ {\omega }_{mij0}·T_{mij}·(1/{\eta }_{mij}(T_{mij},{\omega }_{mij})-1),& T_{mij}>T_{mij0},0<{\omega }_{mij}<{\omega }_{mij0}\end{array}\right.\hspace{1em}\hspace{1em}i=1,2,\cdots ,5;j=1,2$$

(25)

where T_mij0 and ω_mij0 are the torque and speed corresponding to the minimum data point of the motor map characteristic for the j-th motor on the i-th axle, respectively; η_mij(T_mij, ω_mij) is the efficiency of the j-th motor on the i-th axle at a specific speed and torque, which is generally obtained through the motor calibration test.

The key to improving the efficiency of multi-axle distributed electric drive vehicles is to reduce the power loss of the working motor. Therefore, by optimizing the torque distribution and motor of each axle, the total power of the drive motor P_t used to overcome the resistance to vehicle motion and various losses can be reduced, so that the vehicle economy can be optimized. This paper selects the driving force distribution coefficient of each shaft as the optimization variable, so

$$\left\{\begin{array}{cc}\stackrel{\rightharpoonup }{\kappa }=({\kappa }_1,{\kappa }_2,\cdots ,{\kappa }_5)& \\ {\displaystyle \sum _{i=1}^5{\kappa }_i=1,}& i=1,2,\cdots ,5\end{array}\right.$$

(26)

where κ_i is the torque distribution coefficient of each axle, and its value range is 0 ≤ κi ≤ 1. On this basis, the total power of the drive motor under the distribution of the driving force of each axle is obtained as follows:

$$P_t(\stackrel{\rightharpoonup }{\kappa })={\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2\frac{{\kappa }_i{T}_{req}{\omega }_{mij}}{2i_0}}}+{\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{P}_{loss,mij}({\kappa }_i)}};\hspace{1em}\hspace{1em}i=1,2,\cdots ,5;j=1,2$$

(27)

where $P_t(\stackrel{\rightharpoonup }{\kappa })$ is the total power of all drive motors under κ_i in kW; P_loss,i(κ_i) is the motor loss power of the i-th axle under κ_i in kW. $P_t(\stackrel{\rightharpoonup }{\kappa })$ is taken as the optimization objective function.

3.1.2. Constraint Condition

The torque distribution of each axle should not exceed the maximum torque of the motors of that axle, and the working motor speed can not exceed its maximum speed. Otherwise, the motor will heat seriously and even be damaged. Thus, the following constraints must be met:

$$\left\{\begin{array}{c}{n}_{mij}\le n_{mij\_\max }\\ {\kappa }_i{T}_{req}\le 2T_{mij\_\max }(n_{mij})\end{array}\right.$$

(28)

where n_{mij_max} is the maximum speed of the j-th motor on the i-th axle in r/min; T_{mij_max}(n_mij) is the maximum external characteristic torque of the motor at the speed of n_{mij_max} in N∙m.

In addition, the torque distribution of each axle is subject to the wheel adhesion limit of the corresponding axle, and its adhesion cannot exceed the road adhesion coefficient. Therefore, the adhesion constraint obtained under the vertical load constraint of each axle is as follows:

$$C_{\phi i}={\displaystyle \frac{{\kappa }_i{T}_{req}}{F_{zis}r}}\le \phi ;\hspace{1em}\hspace{1em}i=1,2,\cdots ,5$$

(29)

where C_φi is the wheel adhesion coefficient of the i-th axle; φ is the road adhesion coefficient.

3.1.3. Optimization Model

Ultimately, the optimization model of instantaneous energy consumption power can be expressed as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\min :\hfill & \begin{array}{cc}{P}_t(\stackrel{\rightharpoonup }{\kappa })={\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2\frac{{\kappa }_i{T}_{req}{\omega }_{mij}}{2i_0}}}+{\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{P}_{loss,mij}({\kappa }_i)}};\hfill & \end{array}\end{array}\hfill \\ \begin{array}{c}\begin{array}{cc}\begin{array}{cc}S.t.:\hfill & \begin{array}{cc}\begin{array}{cc}\begin{array}{ccc}& & \end{array}& \end{array}& \end{array}{n}_{mij}\le n_{mij\_\max }\end{array}\hfill & \begin{array}{ccc}\begin{array}{cc}\begin{array}{ccc}& & \end{array}& \end{array}& & \end{array}\\ \begin{array}{cc}& \begin{array}{cc}& \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& \end{array}\end{array}\end{array}{\kappa }_i{T}_{req}\le 2T_{mij\_\max }(n_{mij})& \begin{array}{cc}& \end{array}\end{array}\\ {\displaystyle \frac{{\kappa }_i{T}_{req}}{F_{zis}r}}\le \phi \end{array}\end{array}\right.\hspace{1em}\hspace{1em}i=1,2,\cdots ,5;j=1,2$$

(30)

Since the above optimization model is a convex optimization problem with inequality constraints, the Lagrangian slack variable method is used to solve the optimization problem in this paper. Through the optimization process, the torque distribution ratio of each axle corresponding to the optimal instantaneous energy consumption power under different velocities and different demand torques can be quickly obtained, and it is used as the reference torque distribution ratio. The torque distribution ratio can minimize the energy consumption of the electric drive system and achieve an optimal vehicle economy.

3.2. Comfort Control Strategy Based on Driving Mode Switching Frequency Suppression

The driving torque distribution strategy based on optimal instantaneous energy consumption can improve the vehicle’s economy, but it will also cause more changes in working axles and motor torques. Generally speaking, the torque rise rate is less than the torque unloading rate for a permanent magnet synchronous motor. The increase or decrease in the number of working motors during the driving mode switching process will also cause torque fluctuations. Furthermore, when the required torque fluctuates near the driving mode switching surface, the vehicle driving mode will switch frequently, which will cause frequent starts/stops and frequent torque changes of different driving motors. As a result, the vehicle comfort will decrease because of the frequent fluctuations in the driving torque. To reduce the comfort problem caused by frequent switching of driving modes, this paper develops a driving mode switching suppression control strategy that combines continuous single-axle driving mode non-switching, short-term mode frequent switching elimination based on the timing module threshold, and mode switching boundary filtering based on the double threshold values of the accelerator pedal opening and vehicle speed, thereby improving the vehicle comfort.

3.2.1. Non-Switch Strategy on Continuous Single-Axle Drive Mode

During the drive mode switching process, the drive axles and driving torque distribution change with the motors on different axles being connected and disconnected; as a result, the vehicle’s comfort is affected by these changes. The jerk of mode switching is as follows:

$$j_s={\displaystyle \frac{1}{{\delta }_{r}rm}}\times {\displaystyle \frac{d[2{\displaystyle \sum _{i=1}^5{T}_i({\alpha }_{ap},n_i)}-F_{R}r]}{dt}},i=1,2,\cdots ,5$$

(31)

where $j_s$ is the jerk strength in m/s³; δ_r is the vehicle’s rotational mass conversion coefficient, δ_r >1.

According to the literature [32], speed, torque, and coordinated control time are the main influencing factors of the switching among different drive modes, and the coordinated control time is the most significant impact factor. In all switching modes, the growth rate of the access motor torque will be significantly lower than the decline rate of the exit motor torque on continuous single-axle drive mode, resulting in a longer coordinated control time of the access and exit of the motor torque. Thus, the jerk on the switching in continuous single-axle drive mode is the most serious. In addition, the efficiency of different motor drives in the single-axle drive mode is low, so there will not be significant energy consumption even if higher-efficiency motors are not used. The specific control process is as follows:

Let κ_p(t) denote the torque coefficient assigned to the p-th axle (p is an integer from 1 to 5, representing different axes) at any time t, if

$$\begin{array}{cc}{\kappa }_P(t)=1\&{\kappa }_P(t)=1;& \forall q\ne p,q\in \left\{1,2,3,4,5\right\}\end{array}$$

(32)

and if the multi-axle vehicle is in a single-axle drive mode at this time, the torque coefficient assigned to the p-th axle at the next moment t + 1 is as follows:

$${\kappa }_P(t+1)=1;\hspace{1em}\hspace{1em}\exists K_s(t+1)=1\&s\ne p,s\in \left\{1,2,3,4,5\right\}$$

(33)

Through the above strategy, when operating in a single-axle drive mode, the vehicle will continue using the previous single-axle drive mode rather than switching to another axle’s single-drive mode, even if the latter would result in lower instantaneous energy consumption. It will reduce the jerk caused by switching in single-axle drive mode, thereby improving vehicle comfort.

3.2.2. Frequent Switch Exclusion of Short-Length Mode Based on the Time Module Threshold

When the multi-axle vehicle works in a short-duration mode, the vehicle may switch frequently between different driving modes, thus affecting the vehicle’s comfort. This paper uses a method combining timing filtering and the shortest time limit to reduce the frequent switch caused by the short-duration mode. Assuming $\stackrel{\rightharpoonup }{\kappa }(t)$ is the torque distribution mode of the multi-axle distributed electric drive heavy-duty vehicle at time t, and T₀ is the time threshold for filtering the short-term driving modes, which is generally determined based on the data of model debugging and actual vehicle operation, ${\overline{K}}_f(t)$ is the final torque distribution mode after filtering out the short-term driving mode at time t, that is

$${\stackrel{\rightharpoonup }{\kappa }}_f(t)=\left\{\begin{array}{cc}\stackrel{\rightharpoonup }{\kappa }(t-1),& \Delta t<T_0\\ \stackrel{\rightharpoonup }{\kappa }(t),& \Delta t\ge T_0\end{array}\right.$$

(34)

where Δt represents the difference between the current driving mode and the previous driving mode. If Δt is less than the threshold value T₀, the current driving mode is ignored, and the previous driving mode is maintained. If Δt is greater than or equal to the threshold value T₀, the current driving mode is applied. This method can effectively filter out the driving modes that are less than a given threshold, avoiding the vehicle comfort decline caused by frequently switching on short-term driving modes.

3.2.3. Mode Switching Boundary Filtering Strategy Based on the Accelerator Pedal Opening Threshold and Velocity Threshold

When signals such as the accelerator pedal opening and velocity fluctuate within a small range near the switching boundary value, frequent switching of the driving torque mode can occur. However, in order to ensure good dynamic response characteristics, the fluctuations of these signals cannot be directly eliminated. Based on a comprehensive analysis of various factors, the accelerator pedal opening and velocity are selected as the threshold values to remove unnecessary signal spikes near the threshold, thereby achieving the purpose of suppressing frequent mode switching. A first-order delay filter is used to filter the accelerator pedal signal and the velocity signal, that is

$$\left\{\begin{array}{c}{\alpha }_{ap}(k)=(1-Q){\alpha }_{ap}(k-1)+Qx(k)\\ v(k)=(1-Q)v(k-1)+Qx(k)\end{array}\right.$$

(35)

where α_ap(k) and v(k) are the current filter output values of the accelerator pedal opening and velocity, respectively; α_ap(k − 1) and v(k − 1) are the previous filter output values of the accelerator pedal opening and velocity, respectively; x(k) is the current sampling value; Q is the filter coefficient, satisfying Q = T/(T + τ), where T is the sampling period and τ is the time constant of the digital filter. This filtering strategy can avoid the frequent switching of the driving torque mode caused by the small signal fluctuation near the switching boundary and improve comfort while ensuring the vehicle’s dynamic response.

3.3. Torque Coordination Compensation Strategy Based on Dynamics and Stability

According to automobile theory, when the wheel slip rate is controlled within the range of about 0.2, the wheel can be in the optimal slip rate area with relatively large longitudinal and lateral forces. However, when the slip rate is greater than 0.2, the wheel will be in an unstable zone because the longitudinal force of the tire decreases, and the lateral adhesion deteriorates. When driving on a low-adhesion road, the multi-axle distributed electric drive heavy-duty vehicle may experience simultaneous slip of multiple wheels and easily enter an unstable state since each wheel is connected to the motor. Therefore, in order to control wheel slip and approximate the generalized longitudinal and yaw moments, the torque coordination control target is determined by the vehicle state and the driver’s intention in this paper. Then, an active set algorithm is used to control the wheel driving torque, thereby reducing the power loss and instability caused by the torque coordination compensation process.

3.3.1. Determination of Control Objectives

According to the driver’s intention and vehicle status, the current main goal is to maintain driving ability or to keep the vehicle stable as much as possible. The specific judgment rules are shown as follows:

$$\left\{\begin{array}{c}\delta <\overline{\delta } \& v<\overline{v} \mathrm{Dynamic} \mathrm{coordination}\\ \delta >\overline{\delta } | v>\overline{v} \mathrm{Stability} \mathrm{coordination}\end{array}\right.$$

(36)

where δ is the steering wheel angle in rad; v is the vehicle velocity in m/s; $\overline{\delta }$ and $\overline{v}$ are the set threshold values. When the wheel angle and velocity are both small, the vehicle does not easily lose stability, so the goal of dynamic coordination is to improve the longitudinal driving requirements as much as possible under the premise of reducing the constraint of the additional torque generated. Therefore, according to the torque coordination compensation, the longitudinal force requirement constraint should be fully or partially met. Consequently, the longitudinal force of all wheels will be close to the driver’s longitudinal force requirement.

$${\displaystyle \sum _{i=1}^5{\displaystyle \sum _{j=1}^2{F}_{xwij}·\cos {\delta }_{ij}=}}{F}_{xreq}$$

(37)

where F_xreq is the driver’s required longitudinal force in N.

In addition, if the vehicle is prone to instability situations such as large turning angles or high-velocity conditions, the required yaw moment should be preferentially met as much as possible through torque coordination compensation, but it is at the cost of losing some longitudinal dynamics. Thus, the yaw moment generated by the longitudinal force needs to be close to the driver’s requirements, that is

$${\displaystyle \sum _{i=1}^5{F}_{xwi2}·\cos {\delta }_{i2}-}{\displaystyle \sum _{i=1}^5{F}_{xwi1}·\cos {\delta }_{i1}=\frac{M_{zreq}}{B/2}}$$

(38)

3.3.2. Torque Comprehensive Coordination Compensation Strategy Process Based on Dynamics and Stability

In view of achieving the determination of the control target, the active set algorithm is adopted to formulate the torque coordination compensation strategy. Mainly, the starting execution set $W_k(t)$ at time t takes the active set $W_k(t-T_s)$ of the previous moment, and the starting feasible point $u_k^0(t)$ takes the feasible point $u_k(t-T_s)$ of the previous moment. The specific torque coordination compensation is divided into dynamic compensation strategy and stability compensation strategy.

The logic of the dynamic compensation coordination strategy is shown in Figure 3. The main principle is to make full use of the driving torque of the normal wheel ${\mu }_{\lambda ij}=0$ to compensate for the torque of slip loss. First, the same-side torque compensation is performed. In order to improve the tire margin, the torque of slip control loss is evenly distributed to each wheel until the same-side wheel is saturated. Then, after the same-side wheel is saturated, the opposite-side torque compensation is performed until all wheels are saturated.

The logic of the stability compensation coordination strategy is shown in Figure 4. The main principle is to reduce the undesired yaw moment by increasing the wheel torque of the same side or reducing the wheel torque of the opposite side. First, the torque compensation on the same side is performed. In order to increase the tire margin, it is evenly distributed to each wheel until the capacity of the wheel on the same side is saturated. After the wheel on the same side is saturated, the motor torque on the opposite side is reduced until the yaw moment meets the requirements.

4. Results and Discussion of Hardware-in-the-Loop Simulation

In order to verify the performance of the proposed optimal driving torque control strategy (ODTCS), a hardware-in-the-loop simulation platform of the multi-axle distributed electric drive heavy-duty vehicle was built, as shown in Figure 5. The HiL platform mainly consists of three parts: a host computer (capable of supporting the Windows 7 or Windows 10 operating systems), the Speedgoat HiL Simulator (which can be chosen from the Baseline, Mobile, or Performance options), and the VCU. The software environment of this HiL platform is Matlab/Simulink (R 2014a or later versions). The host computer is mainly used to run the five-axle electric drive vehicle dynamics model developed by Matlab/Simulink. Then, the vehicle dynamics model compiled into a real-time vehicle model is deployed to the Speedgoat HiL Simulator through Ethernet. The real-time vehicle dynamics model can provide real-time parameters for VCU testing. Next, the optimal driving torque control strategy proposed in this paper is also developed using Simulink and deployed to the VCU (Vehicle Control Unit) via rapid code generation technology. The control signals and vehicle status signals are transmitted through the CAN Bus between the VCU and the Speedgoat HiL Simulator. Based on the hardware-in-the-loop platform, the CHTC-HT with continuous, multiple speed characteristics and multiple power requirements is selected in this paper to evaluate the performance of the power economy module and the comfort module in the control strategy. Subsequently, a split friction road with different adhesion coefficients between the left and right wheels is selected as the test road surface, and the acceleration driving in a straight line is selected to verify the effect of the control strategy proposed in this paper for the stability control module, which specifically addresses lateral force interference. Besides, the specific parameters of the vehicle studied in this paper are shown in

Table 1. Vehicle-related parameters used.

Parameter	Value
Length × Width × Height/m	16.7 × 3 × 3
Center of mass height/m	1.4
Curb weight/kg	19,000
Gross weight/kg	47,000
Distance between each axle and centroid/m	6.7/4.4/0/−2.4/−4.8
Windward area/m2	7.62
Wind resistance coefficient	0.85
Wheel rolling radius/m	0.59
Reducer reduction ratio	10.81
Maximum torque of a single motor/N·m	1100
Maximum power of a single motor/kW	110
Rated power of a single motor/kW	80

.

4.1. Simulation Results for CHTC-HT

The driving conditions of the multi-axle distributed electric drive heavy-duty vehicle have many acceleration, constant velocity, deceleration, and other situations, so the performance of the drive control strategy should be verified by a cycle condition with complex velocity ranges. Therefore, the CHTC-HT is selected as the cycle condition, which includes three velocity ranges: low velocity, medium velocity, and high velocity. This condition can accurately reflect the performance of heavy-duty vehicles under various driving conditions on China’s roads. In addition, to intuitively illustrate the performance of the proposed control strategy, the Equal Torque Distribution Control Strategy (ETDCS) is used as a comparison group, which verifies the performance of the optimal driving torque control strategy by comparing working efficiency, SOC, energy consumption, and so on.

As shown in Figure 6, although there are many accelerations, constant velocity phases, and decelerations in CHTC-HT, the multi-axle distributed electric drive heavy-duty vehicle can always follow the desired velocity well and maintain good dynamics performance by adopting the optimal driving torque control strategy proposed in this paper. Figure 7 shows the motor torque of each axle in CHTC-HT, where, since CHTC-HT does not consider vehicle lateral force, the torques of the left and right motors on each axle are equal. Accordingly, to simplify the results, the motor torques such as “torque of motor 1, torque of motor 3, torque of motor 5, torque of motor 7, and torque of motor 9”, which are the left motor torques of Axle 1, Axle 2, Axle 3, Axle 4, and Axle 5, respectively, are selected to compare the torque changes on each axle. By comparing with the data in Figure 7a,b, it can be observed that, in some low-torque demand segments such as medium/low velocity or small acceleration, some motors’ torques (such as that of motor 1) when using ODTCS proposed in this paper are much larger than when using ETDCS, thus ODTCS can increase the load of some motors in CHTC-HT. Subsequently, motors’ working points on some axles (such as the 1st axle and the 7th axle) in Figure 8a have significantly moved towards the high-efficiency range when using ODTCS compared with those when using ETDCS in Figure 8b. The reason is that the motor torque on some axles (such as the 1st axle and the 7th axle) has been greatly improved in some low-torque demand segments by using ODTCS, so the motor working efficiency improves, accompanied by an increase in the motor load rate.

As detailed in Figure 9, the SOC value at the end of CHTC-HT is 58% when using ODTCS proposed in this paper, which is 0.59% higher SOC than that when using ETDCS. Meanwhile, it can be observed from Figure 10 that there is 2291 kJ less energy consumption when using ODTCS than when using ETDCS, so the energy consumption rate is reduced by 3.45% by using ODTCS proposed in this paper. These results indicate that the vehicle economy is improved according to the optimal instantaneous energy consumption strategy when using ODTCS proposed in this paper. In addition, it can be identified from Figure 11 that, at some moments, the vehicle jerk when using ODTCS is slightly greater than that when using ETDCS, which is a minor deficit caused by the switching of the driving mode when ODTCS is applied. However, the maximum jerk when using ODTCS does not exceed 8 m/s³ in CHTC-HT, which is less than the allowable comfort range of 10 m/s³. Therefore, the vehicle’s comfort is also ensured by using ODTCS.

Overall, for the multi-axle electric drive heavy-duty vehicle, the optimal driving torque control strategy proposed in this paper can optimize the torque distribution of the motors on each axle under a specific required torque and reduce the vehicle energy consumption by improving the working efficiency of the motors on each axle. Simultaneously, vehicle jerks can be reduced through the drive mode switching suppression strategy. Ultimately, by adopting the optimal driving torque control strategy proposed in this paper, the vehicle’s economy can be improved while the vehicle’s comfort is ensured.

4.2. Simulation Results for Straight-Line Acceleration Driving on Split Friction Road

In order to verify the vehicle stability when driving on complex roads, a split friction road comprising high adhesion and low adhesion surfaces is used as the test road. Simultaneously, a straight-line acceleration driving with an initial velocity of 18 km/h and a steering wheel angle input of 0 is selected to assess the impact of lateral force disturbances on vehicle stability. For the split friction road considered in this paper, the road adhesion coefficient of the left is initially 0.8, which drops to 0.2 after 2 s, and the road adhesion coefficient of the right is constant at 0.8. Moreover, ETDCS is still selected as the comparison group strategy to evaluate performance.

As illustrated in Figure 12, the OTDCS proposed in this paper has a lower longitudinal velocity than ETDCS. This demonstrates that a small amount of longitudinal velocity performance is sacrificed when the stability torque coordination compensation strategy is activated in this simulation test. Data in Figure 13 suggest that the lateral displacement when using ETDCS is larger than that when using OTDCS. The primary cause is that ETDCS cannot coordinate the torque of the two side wheels and results in a large lateral force torque because of the difference between the left and right wheels, whereas OTDCS can reduce the torque difference by adjusting the motor torque of the left and right side, effectively reducing the lateral force. Furthermore, Figure 14 shows that the yaw rate when using ETDCS is also larger than that when using OTDCS, which proves that the torque difference between the left and right wheel can be reduced effectively by using OTDCS, thereby effectively reducing the lateral force and improving driving stability.

As shown in Figure 15, the vehicle’s center of mass slip angle and its rate of change are smaller when using ODTCS compared to ETDCS, indicating better maneuverability and stability. As shown in Figure 16 and Figure 17, when the left wheel enters the low-adhesion road, the adhesion provided by the left ground cannot meet the wheel’s demand. The left motor torque shows a slow downward trend when using ETDCS due to the reduction of ground adhesion, and the corresponding left wheel slip rate increases sharply to 0.6 because transitioning from a high adhesion coefficient road to a low adhesion coefficient road can cause a large overshoot of the wheel slip rate. However, the ODTCS proposed in this paper can actively reduce the driving torque of the left motor when the vehicle enters the low-adhesion road, so that the left wheel slip rate is controlled to about 0.2 (pink dotted line in Figure 17) by quickly reducing the wheel driving force on the low-adhesion road. Thus, the wheel slip rate is controlled in a stable range, and the vehicle’s stability is effectively improved.

5. Conclusions

The driving torque control of multi-axle distributed electric drive heavy-duty vehicles is of great significance for improving the vehicle’s power economy, comfort, and stability. Hence, we considered the approach used for multi-axle vehicles in several works such as [7,9,14,15] and compared the advantages and disadvantages of the control strategies in these works regarding energy-saving optimization, dynamics integrated control, stability control, etc. However, we found that most previous studies only focused on controlling one or two performance aspects, making it difficult to achieve the optimal coordination of multi-axle vehicles in terms of power economy, comfort, and stability. Based on the exploration mentioned above, combined with the dynamic characteristics of multi-axle distributed electric drive heavy-duty vehicles, an optimal driving torque control strategy based on the comprehensive coordination of power economy, comfort, and stability is proposed in this paper. In this control strategy, the power economy control module mainly optimizes the vehicle’s instantaneous energy consumption based on the vehicle driving state and the driver’s control signal under the constraint condition, which can achieve the optimal torque distribution for economy, and serves as the torque reference distribution strategy. The comfort control module aims to reduce the comfort issues caused by the switching of different driving modes in the torque reference distribution strategy, and the vehicle comfort is guaranteed by controlling the jerk generated in the drive mode switching process. The stability control module aims to control the torque of each motor so that the wheel slip rate under various complex road conditions is controlled within a stable range and the vehicle stability can be improved. Finally, the performance of the proposed optimal driving torque control strategy was verified through a hardware-in-the-loop simulation system. The results show that compared with the traditional torque average distribution strategy, the proposed optimal driving torque control strategy can reduce the energy consumption rate by 3.45% in CHC-HT while ensuring vehicle comfort, and the wheel slip rate on the low-adhesion road under the straight-line acceleration condition on the split friction road can always be controlled within a stable range.

However, the control strategy proposed in this work focused solely on the dynamics of multi-axle vehicles for torque distribution, without considering the impact of advanced on-board intelligent equipment on vehicle control. In the future, with the rapid advancement of intelligence in commercial vehicles, the vehicle real-time status and road conditions can be easily obtained by using advanced on-board sensors, and the precise control of the multi-axle vehicle chassis in the horizontal, longitudinal, and vertical directions can also be easily achieved. Therefore, the lateral–longitudinal–vertical chassis dynamics domain control technology based on the fusion of multi-source information will become one of the key directions of future research on multi-axle distributed electric drive heavy-duty vehicles.