Optimal Machine Learning Model to Predict Demolition Waste Generation for a Circular Economy
Abstract
1. Introduction
- Designing a model for predicting the volumes of recycling and landfill DW by considering the characteristics of DW generated from old structures within redevelopment zones.
- Testing various potential subprediction models by determining optimal hyperparameters (HPs) and employing different algorithms.
- Analyzing the factors affecting the volumes of recycling and landfill DW generated.
- Proposing an optimal ML model for forecasting the volumes of recycling and landfill DW by evaluating the performance of training, validation, and testing models.
2. Literature Review on ML-Based Models and Application
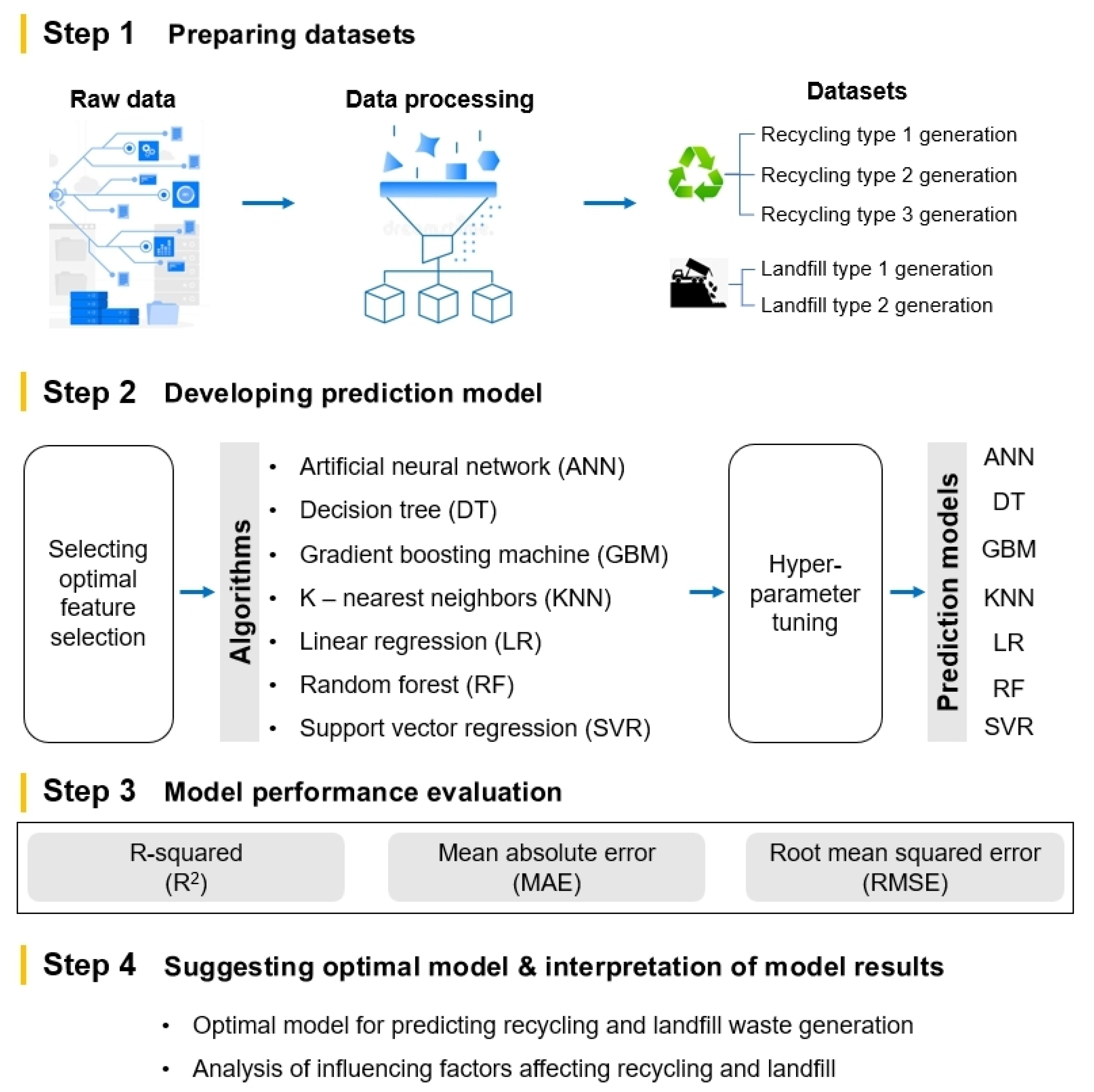
3. Methods and Materials
3.1. Data Collection and Preprocessing
3.2. Model Development
3.2.1. Variable Selection
3.2.2. Hyperparameter Tuning
3.3. Performance Metrics for Model Verification
4. Results and Discussion
4.1. Assessment of Models
4.2. Prediction Performance of Optimal Model and Comparison with Existing Models
4.3. Variable Importance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hossein, A.H.; AzariJafari, H.; Khoshnazar, R. The role of performance metrics in comparative LCA of concrete mixtures incorporating solid wastes: A critical review and guideline proposal. Waste Manag. 2022, 140, 40–54. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Chen, J. Computer vision for solid waste sorting: A critical review of academic research. Waste Manag. 2022, 142, 29–43. [Google Scholar] [CrossRef]
- Chen, D.M.-C.; Bodirsky, B.L.; Krueger, T.; Mishra, A.; Popp, A. The world’s growing municipal solid waste: Trends and impacts. Environ. Res. Lett. 2020, 15, 074021. [Google Scholar] [CrossRef]
- Statista. 2023. Available online: https://www.statista.com/topics/4983/waste-generation-worldwide/#topicOverview (accessed on 8 August 2024).
- Ma, W.; Hao, J.L. Enhancing a circular economy for construction and demolition waste management in China: A stakeholder engagement and key strategy approach. J. Clean. Prod. 2024, 450, 141763. [Google Scholar] [CrossRef]
- Ginga, C.P.; Ongpeng, J.M.C.; Daly, M.K.M. Circular Economy on Construction and Demolition Waste: A Literature Review on Material Recovery and Production. Materials 2020, 13, 2970. [Google Scholar] [CrossRef] [PubMed]
- López Ruiz, L.A.; Roca Ramón, X.; Gassó Domingo, S. The circular economy in the construction and demolition waste sector—A review and an integrative model approach. J. Cleaner Prod. 2020, 248, 119238. [Google Scholar] [CrossRef]
- Hao, J.; Di Maria, F.; Chen, Z.; Yu, S.; Yu, W.; Di Sarno, L. Comparative study of construction and demolition waste management in China and the European Union. Detritus 2020, 13, 114–121. [Google Scholar] [CrossRef]
- Duan, H.; Miller, T.R.; Liu, G.; Tam, V.W.Y. Construction debris becomes growing concern of growing cities. Waste Manag. 2019, 83, 1–5. [Google Scholar] [CrossRef]
- Purchase, C.K.; Al Zulayq, D.M.; O’Brien, B.T.; Kowalewski, M.J.; Berenjian, A.; Tarighaleslami, A.H.; Seifan, M. Circular economy of construction and demolition waste: A literature review on lessons, challenges, and benefits. Materials 2021, 15, 76. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.D.; Macchion, L. Risk management in green building: A review of the current state of research and future directions. Environ. Dev. Sustain. 2023, 25, 2136–2172. [Google Scholar] [CrossRef]
- Nasir, M.H.A.; Genovese, A.; Acquaye, A.A.; Koh, S.C.L.; Yamoah, F. Comparing linear and circular supply chains: A case study from the construction industry. Int. J. Prod. Econ. 2017, 183, 443–457. [Google Scholar] [CrossRef]
- Oluleye, B.I.; Chan, D.W.; Saka, A.B.; Olawumi, T.O. Circular economy research on building construction and demolition waste: A review of current trends and future research directions. J. Clean. Prod. 2022, 357, 131927. [Google Scholar] [CrossRef]
- Mahpour, A. Prioritizing barriers to adopt circular economy in construction and demolition waste management. Resour. Conserv. Recycl. 2018, 134, 216–227. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, L.; Sang, P. Exploring the restrictive factors for the development of the construction waste recycling industry in a second-tier Chinese city: A case study from Jinan. Environ. Sci. Pollut. Res. Int. 2023, 30, 46394–46413. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Wang, Y.; Liu, F.; Zhang, Y. Development of a hybrid model to predict construction and demolition waste: China as a case study. Waste Manag. 2017, 59, 350–361. [Google Scholar] [CrossRef]
- Katz, A.; Baum, H. A novel methodology to estimate the evolution of construction waste in construction sites. Waste Manag. 2011, 31, 353–358. [Google Scholar] [CrossRef]
- Hoque, M.M.; Rahman, M.T.U. Landfill area estimation based on solid waste collection prediction using ANN model and final waste disposal options. J. Cleaner Prod. 2020, 256, 120387. [Google Scholar] [CrossRef]
- Ma, S.; Zhou, C.; Chi, C.; Liu, Y.; Yang, G. Estimating physical composition of municipal solid waste in China by applying artificial neural network method. Environ. Sci. Technol. 2020, 54, 9609–9617. [Google Scholar] [CrossRef]
- Yu, Y.; Yazan, D.M.; Bhochhibhoya, S.; Volker, L. Towards circular economy through industrial symbiosis in the Dutch construction industry: A case of recycled concrete aggregates. J. Cleaner Prod. 2021, 293, 126083. [Google Scholar] [CrossRef]
- Abbasi, M.; El Hanandeh, A. Forecasting municipal solid waste generation using artificial intelligence modelling approaches. Waste Manag. 2016, 56, 13–22. [Google Scholar] [CrossRef]
- Yazdani, M.; Kabirifar, K.; Frimpong, B.E.; Shariati, M.; Mirmozaffari, M.; Boskabadi, A. Improving construction and demolition waste collection service in an urban area using a simheuristic approach: A case study in Sydney, Australia. J. Cleaner Prod. 2021, 280, 124138. [Google Scholar] [CrossRef]
- Lu, W.; Long, W.; Yuan, L. A machine learning regression approach for pre-renovation construction waste auditing. J. Cleaner Prod. 2023, 397, 136596. [Google Scholar] [CrossRef]
- Lu, W.; Lou, J.; Webster, C.; Xue, F.; Bao, Z.; Chi, B. Estimating construction waste generation in the Greater Bay Area, China using machine learning. Waste Manag. 2021, 134, 78–88. [Google Scholar] [CrossRef] [PubMed]
- Akanbi, L.A.; Oyedele, A.O.; Oyedele, L.O.; Salami, R.O. Deep Learning Model for Demolition Waste Prediction in a Circular Economy. J. Cleaner Prod. 2020, 274, 122843. [Google Scholar] [CrossRef]
- Cha, G.-W.; Moon, H.-J.; Kim, Y.-C. Comparison of random forest and gradient boosting machine models for predicting demolition waste based on small datasets and categorical variables. Int. J. Environ. Res. Public Health 2021, 18, 8530. [Google Scholar] [CrossRef] [PubMed]
- Cha, G.-W.; Moon, H.J.; Kim, Y.-C. A hybrid machine-learning model for predicting the waste generation rate of building demolition projects. J. Cleaner Prod. 2022, 375, 134096. [Google Scholar] [CrossRef]
- Coskuner, G.; Jassim, M.S.; Zontul, M.; Karateke, S. Application of artificial intelligence neural network modeling to predict the generation of domestic, commercial and construction wastes. Waste Manag. Res. 2021, 39, 499–507. [Google Scholar] [CrossRef] [PubMed]
- Gulghane, A.; Sharma, R.L.; Borkar, P. A formal evaluation of KNN and decision tree algorithms for waste generation prediction in residential projects: A comparative approach. Asian J. Civ. Eng. 2024, 25, 265–280. [Google Scholar] [CrossRef]
- Hu, R.; Chen, K.; Chen, W.; Wang, Q.; Luo, H. Estimation of construction waste generation based on an improved on-site measurement and SVM-based prediction model: A case of commercial buildings in China. Waste Manag. 2021, 126, 791–799. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.; Alimi, W.; Assaggaf, R.; Salami, B.A.; Oladapo, E.A. An overview of factors influencing the properties of concrete incorporating construction and demolition wastes. Constr. Build. Mater. 2023, 367, 130307. [Google Scholar] [CrossRef]
- Cha, G.-W.; Park, C.-W.; Kim, Y.-C.; Moon, H.J. Predicting Generation of Different Demolition Waste Types Using Simple Artificial Neural Networks. Sustainability 2023, 15, 16245. [Google Scholar] [CrossRef]
- Abdallah, M.; Abu Talib, M.A.; Feroz, S.; Nasir, Q.; Abdalla, H.; Mahfood, B. Artificial intelligence applications in solid waste management: A systematic research review. Waste Manag. 2020, 109, 231–246. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Wang, J.; Xu, X. Machine learning in construction and demolition waste management: Progress, challenges, and future directions. Autom. Constr. 2024, 162, 105380. [Google Scholar] [CrossRef]
- Nguyen, X.C.; Nguyen, T.T.H.; La, D.D.; Kumar, G.; Rene, E.R.; Nguyen, D.D.; Chang, S.W.; Chung, W.J.; Nguyen, X.H.; Nguyen, V.K. Development of machine learning-based models to forecast solid waste generation in residential areas: A case study from Vietnam. Resour. Conserve. Recy. 2021, 167, 105381. [Google Scholar] [CrossRef]
- Opitz, D.; Maclin, R. Popular ensemble methods: An empirical study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Galiano, V.R.; Panday, P.; Neeti, N. An evaluation of bagging, boosting, and random forests for land-cover classification in Cape Cod, Massachusetts, USA. GIScience Remote Sens. 2012, 49, 623–643. [Google Scholar] [CrossRef]
- Al Martini, S.; Sabouni, R.; Khartabil, A.; Wakjira, T.G.; Shahria Alam, M.S. Development and strength prediction of sustainable concrete having binary and ternary cementitious blends and incorporating recycled aggregates from demolished UAE buildings: Experimental and machine learning-based studies. Constr. Build. Mater. 2023, 380, 131278. [Google Scholar] [CrossRef]
- Jayasinghe, T.; Wei Chen, B.; Zhang, Z.; Meng, X.; Li, Y.; Gunawardena, T.; Mangalathu, S.; Mendis, P. Data-driven shear strength predictions of recycled aggregate concrete beams with/without shear reinforcement by applying machine learning approaches. Constr. Build. Mater. 2023, 387, 131604. [Google Scholar] [CrossRef]
- Xu, A.; Chang, H.; Xu, Y.; Li, R.; Li, X.; Zhao, Y. Applying artificial neural networks (ANNs) to solve solid waste-related issues: A critical review. Waste Manag. 2021, 124, 385–402. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Statist. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Qi, C.; Tang, X. Slope stability prediction using integrated metaheuristic and machine learning approaches: A comparative study. Comput. Ind. Eng. 2018, 118, 112–122. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Guo, G.; Wang, H.; Bell, D.; Bi, Y.; Greer, K. KNN Model-Based Approach in Classification. In On the Move to Meaningful Internet Systems 2003: CoopIS, DOA, and ODBASE; Lecture Notes in Computer Science, Meersman, R., Tari, Z., Schmidt, D.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2888, pp. 986–996. [Google Scholar]
- Zuo, W.; Zhang, D.; Wang, K. On kernel difference-weighted k-nearest neighbor classification. Pattern Anal. Appl. 2008, 11, 247–257. [Google Scholar] [CrossRef]
- Huang, J.-C.; Ko, K.-M.; Shu, M.-H.; Hsu, B.-M. Application and comparison of several machine learning algorithms and their integration models in regression problems. Neural Comput. Appl. 2020, 32, 5461–5469. [Google Scholar] [CrossRef]
- Ogutu, J.O.; Schulz-Streeck, T.; Piepho, H.-P. Genomic selection using regularized linear regression models: Ridge regression, lasso, elastic net, and their extensions. BMC Proc. 2012, 6, S10. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, G.; Huang, Y.; Sun, J.; Aslani, F.; Nener, B. Modelling uniaxial compressive strength of lightweight self-compacting concrete using random forest regression. Constr. Build. Mater. 2019, 210, 713–719. [Google Scholar] [CrossRef]
- Deng, C.X.; Xu, L.X.; Li, S. Classification of Support Vector Machine and Regression Algorithm; INTECH Open Access Publisher: London, UK, 2010. [Google Scholar]
- Tran, V.Q.; Dang, V.Q.; Ho, L.S. Evaluating compressive strength of concrete made with recycled concrete aggregates using machine learning approach. Constr. Build. Mater. 2022, 323, 126578. [Google Scholar] [CrossRef]
- Soliman, O.S.; Mahmoud, A.S. A classification system for remote sensing satellite images using support vector machine with non-linear kernel functions. In Proceedings of the 8th International Conference on Informatics and Systems (INFOS), Giza, Egypt, 14–16 May 2012; p. BIO-181. [Google Scholar]
- DeCastro-García, N.; Muñoz Castañeda, Á.L.; Escudero García, D.; Carriegos, M.V. Effect of the sampling of a dataset in the hyperparameter optimization phase over the efficiency of a machine learning algorithm. Complexity 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Cheng, J.; Dekkers, J.C.M.; Fernando, R.L. Cross-validation of best linear unbiased predictions of breeding values using an efficient leave-one-out strategy. J. Anim. Breed. Genet. 2021, 138, 519–527. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Garrick, D.J.; Fernando, R.L. Efficient strategies for leave-one-out cross validation for genomic best linear unbiased prediction. J. Anim. Sci. Biotechnol. 2017, 8, 38. [Google Scholar] [CrossRef]
- Shao, Z.; Er, M.J. Efficient leave-one-out cross-validation-based regularized extreme learning machine. Neurocomputing 2016, 194, 260–270. [Google Scholar] [CrossRef]
- Cha, G.-W.; Kim, Y.-C.; Moon, H.J.; Hong, W.-H. New approach for forecasting demolition waste generation using chi-squared automatic interaction detection (CHAID) method. J. Cleaner Prod. 2017, 168, 375–385. [Google Scholar] [CrossRef]
- Singh, T.; Uppaluri, R.V.S. Machine learning tool-based prediction and forecasting of municipal solid waste generation rate: A case study in Guwahati, Assam, India. Int. J. Environ. Sci. Technol. 2023, 20, 12207–12230. [Google Scholar] [CrossRef]
- Wu, Z.; Ann, T.W.; Shen, L.; Liu, G. Quantifying construction and demolition waste: An analytical review. Waste Manag. 2014, 34, 1683–1692. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, W.; Liu, J. Regional differences and driving factors of construction and demolition waste generation in China. Eng. Constr. Archit. Manag. 2022, 29, 2300–2327. [Google Scholar] [CrossRef]
- Wang, Z.; Han, F.; Xia, B.; Liu, J.; Zhang, C. Regional differences and heterogeneity of construction and demolition waste with economic growth: Evidence from China. Constr. Manag. Econ. 2023, 41, 44–59. [Google Scholar] [CrossRef]
- Liu, J.; Wu, P.; Jiang, Y.; Wang, X. Explore potential barriers of applying circular economy in construction and demolition waste recycling. J. Clean. Prod. 2021, 326, 129400. [Google Scholar] [CrossRef]




| Building Characteristics | Count | |
|---|---|---|
| Project | A | 81 |
| B | 69 | |
| Usage | Residential | 135 |
| Residential and commercial | 15 | |
| Structure | Reinforced concrete | 81 |
| Concrete block | 5 | |
| Concrete brick | 35 | |
| Wood | 29 | |
| Wall type | Block | 121 |
| Brick | 22 | |
| Soil | 7 | |
| Roof type | Roofing tile | 74 |
| Slab | 27 | |
| Slab and roofing tile | 33 | |
| Slab and slate | 3 | |
| Slate | 13 | |
| No. of floors | 1 | 114 |
| 2 | 36 | |
| Equipment type | A | 35 |
| B | 86 | |
| C | 29 |
| Classification | Maximum | Minimum | Mean |
|---|---|---|---|
| Floor area (m2) | 295.22 | 52.42 | 133.14 |
| Recycling 1 (mineral) (kg) | 402,040.25 | 35,540.20 | 126,319.07 |
| Recycling 2 (combustible) (kg) | 28,546.88 | 721.50 | 8834.02 |
| Recycling 3 (metals) (kg) | 30,011.73 | 143.90 | 6500.95 |
| Landfill 1 (specified waste) (kg) | 6642.72 | 0.00 | 659.86 |
| Landfill 2 (mixed waste) (kg) | 68,651.98 | 6421.80 | 24,066.29 |
| Algorithms | Prediction Model | Considered HP Title | Selected HP |
|---|---|---|---|
| ANN | Recycling 1 (R 1) | Activation function, no. of neurons, regularization, iteration | ReLu, 12, 30, 70 |
| Recycling 2 (R 2) | ReLu, 12, 30, 70 | ||
| Recycling 3 (R 3) | ReLu, 12, 30, 70 | ||
| Landfill 1 (L 1) | ReLu, 25, 30, 40 | ||
| Landfill 2 (L 2) | ReLu, 20, 30, 70 | ||
| DT | R 1 | Min_samples_split, criterion, max_depth | 3, 11, 4 |
| R 2 | 3, 11, 4 | ||
| R 3 | 3, 11, 4 | ||
| L 1 | 2, 6, 2 | ||
| L 2 | 3, 11, 4 | ||
| GBM | R 1 | n_estimators, criterion, max_depth, learning rate | 20, 2, 2, 0.25 |
| R 2 | 25, 3, 2, 0.25 | ||
| R 3 | 15, 2, 2, 0.20 | ||
| L 1 | 15, 2, 2, 0.25 | ||
| L 2 | 25, 2, 2, 0.25 | ||
| KNN | R 1 | No. of neighbors, metric, weight | 3, Manhattan, distance |
| R 2 | 3, Manhattan, distance | ||
| R 3 | 3, Manhattan, distance | ||
| L 1 | 2, Manhattan, distance | ||
| L 2 | 3, Manhattan, distance | ||
| LR | R 1 | Regularization method, alpha value | Ridge, 1 |
| R 2 | Ridge, 1 | ||
| R 3 | Ridge, 1 | ||
| L 1 | Ridge, 1 | ||
| L 2 | Ridge, 1 | ||
| RF | R 1 | n_estimators, criterion, max_depth, max_features | 35, 2, 9, 8 |
| R 2 | 35, 2, 9, 8 | ||
| R 3 | 35, 2, 9, 8 | ||
| L 1 | 35, 2, 11, 8 | ||
| L 2 | 35, 2, 9, 6 | ||
| SVR | R 1 | C, epsilon, kernel type (gamma, coefficient, degree) | 20, 0.35, Polynomial (2, 8, 2) |
| R 2 | 20, 0.3, Polynomial (0.9, 9.5, 2) | ||
| R 3 | 20, 0.35, Polynomial (1, 8, 2) | ||
| L 1 | 9, 0.3, Polynomial (1, 8, 2) | ||
| L 2 | 20, 0.35, Polynomial (1, 8, 2) |
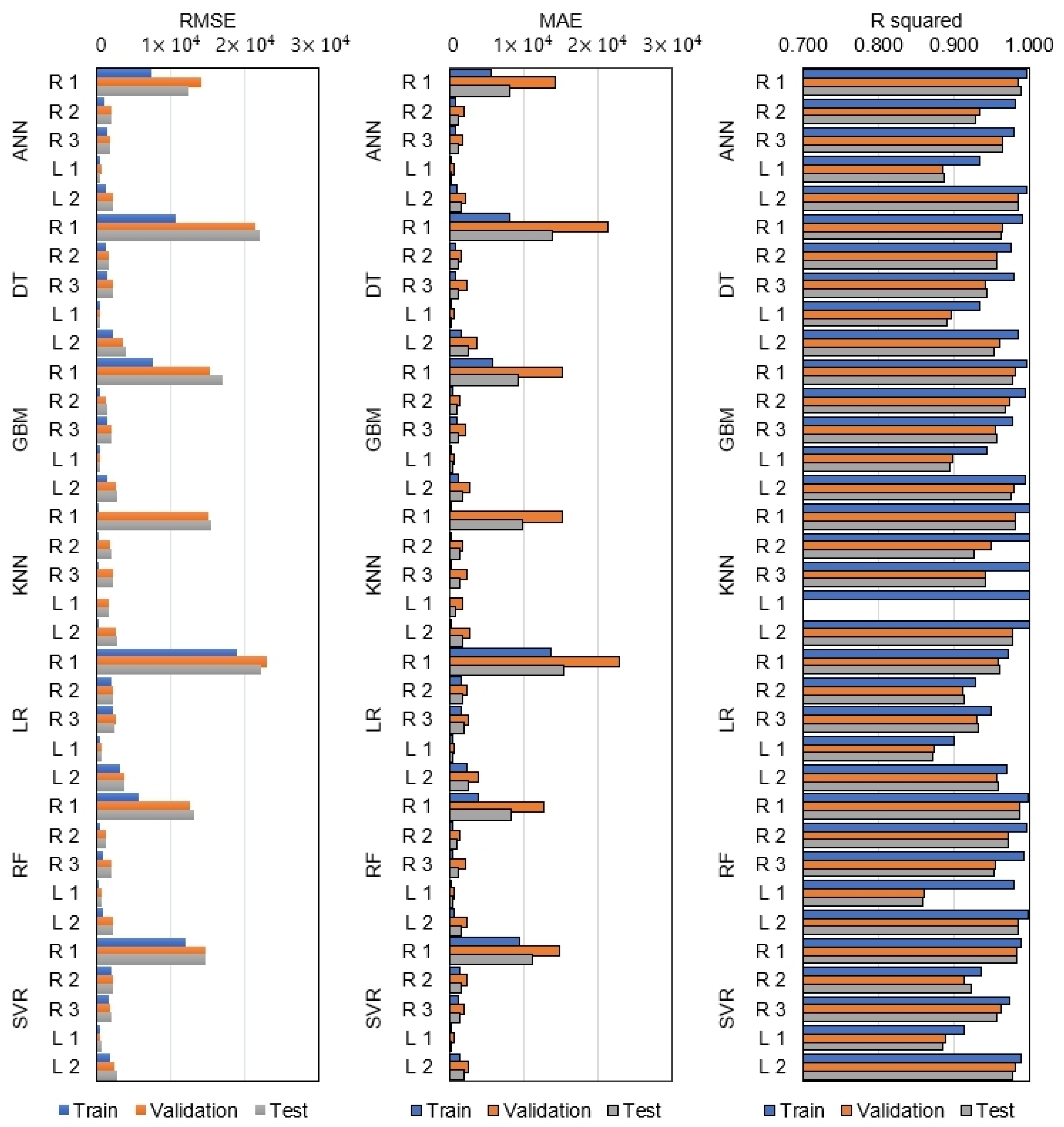
| Algorithm | RMSE | MAE | R-Squared | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training | Validation | Test | Training | Validation | Test | Training | Validation | Test | |
| ANN | 2288.30 | 4122.32 | 3902.50 | 1615.91 | 4122.32 | 2385.03 | 0.977 | 0.951 | 0.950 |
| DT | 3175.80 | 5865.85 | 6063.40 | 2268.70 | 5865.85 | 3730.36 | 0.973 | 0.944 | 0.941 |
| GBM | 2245.96 | 4320.19 | 4740.58 | 1682.68 | 4320.19 | 2649.89 | 0.981 | 0.957 | 0.954 |
| KNN | 33.69 | 4685.90 | 4832.75 | 3.89 | 4685.90 | 2978.30 | 1.000 | 0.776 | 0.779 |
| LR | 5366.72 | 6404.70 | 6242.79 | 3874.35 | 6404.70 | 4354.99 | 0.944 | 0.926 | 0.927 |
| RF | 1626.83 | 3770.25 | 3838.40 | 1070.55 | 3770.25 | 2421.08 | 0.993 | 0.951 | 0.951 |
| SVR | 3560.72 | 4359.81 | 4420.18 | 2679.40 | 4359.81 | 3222.35 | 0.960 | 0.946 | 0.945 |
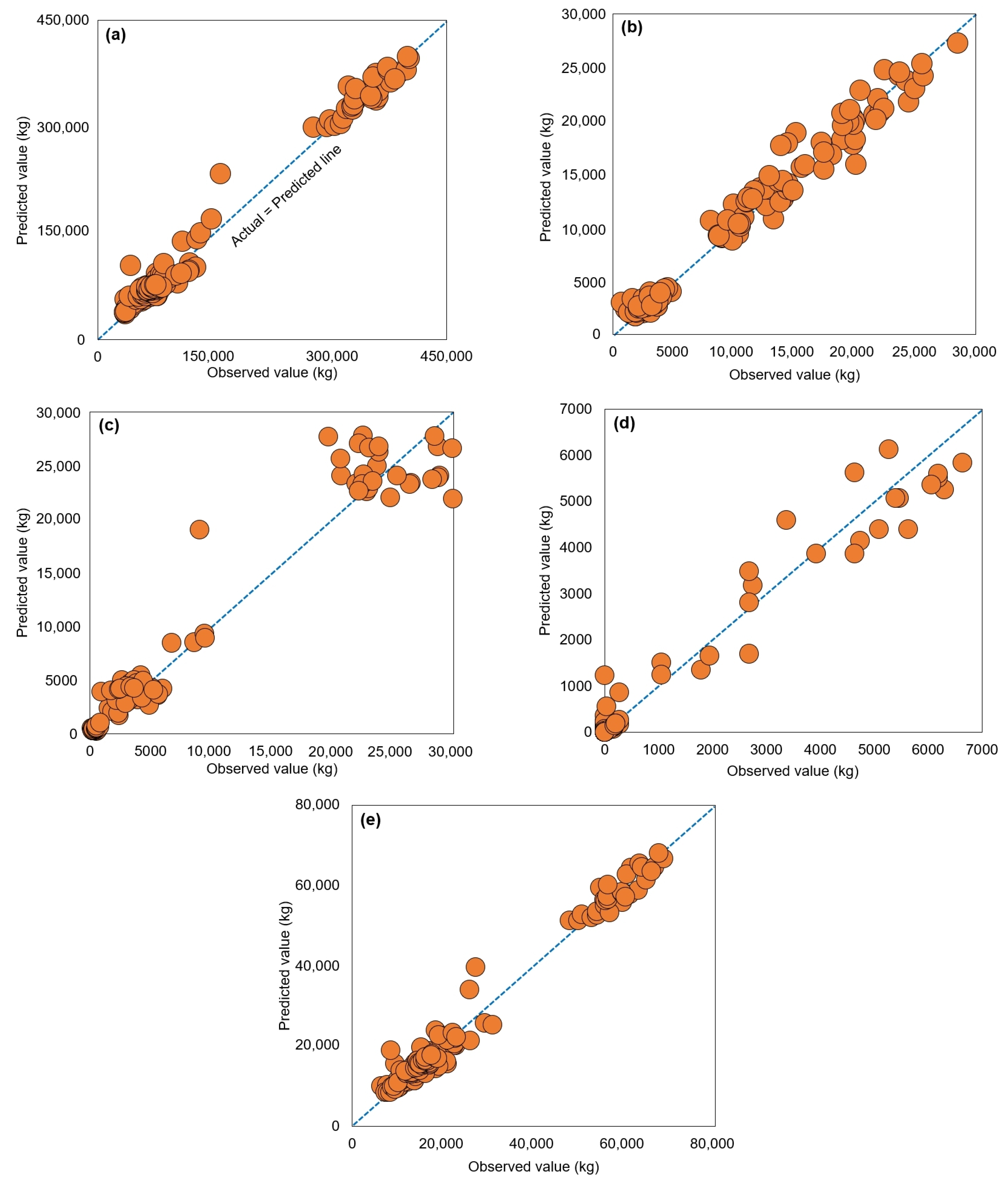
| Model Type | Training | Validation | Test | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R-Squared | RMSE | MAE | R-Squared | RMSE | MAE | R-Squared | |
| R 1 | 5692.29 | 3838.75 | 0.997 | 13,100.86 | 8326.42 | 0.987 | 12,670.48 | 8158.93 | 0.987 |
| R 2 | 486.62 | 350.45 | 0.996 | 1266.54 | 862.93 | 0.972 | 1271.18 | 851.98 | 0.972 |
| R 3 | 792.42 | 414.48 | 0.993 | 2044.36 | 1119.73 | 0.953 | 2004.55 | 1063.50 | 0.954 |
| L 1 | 232.78 | 105.66 | 0.980 | 620.71 | 285.36 | 0.858 | 617.64 | 291.14 | 0.860 |
| L 2 | 930.01 | 643.42 | 0.997 | 2159.55 | 1510.98 | 0.986 | 2287.41 | 1574.08 | 0.984 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cha, G.-W.; Park, C.-W.; Kim, Y.-C. Optimal Machine Learning Model to Predict Demolition Waste Generation for a Circular Economy. Sustainability 2024, 16, 7064. https://doi.org/10.3390/su16167064
Cha G-W, Park C-W, Kim Y-C. Optimal Machine Learning Model to Predict Demolition Waste Generation for a Circular Economy. Sustainability. 2024; 16(16):7064. https://doi.org/10.3390/su16167064
Chicago/Turabian StyleCha, Gi-Wook, Choon-Wook Park, and Young-Chan Kim. 2024. "Optimal Machine Learning Model to Predict Demolition Waste Generation for a Circular Economy" Sustainability 16, no. 16: 7064. https://doi.org/10.3390/su16167064
APA StyleCha, G.-W., Park, C.-W., & Kim, Y.-C. (2024). Optimal Machine Learning Model to Predict Demolition Waste Generation for a Circular Economy. Sustainability, 16(16), 7064. https://doi.org/10.3390/su16167064







