Wind Speed Forecasting Based on Phase Space Reconstruction and a Novel Optimization Algorithm
Abstract
:1. Introduction
2. Methodology
2.1. Singular Spectrum Analysis
2.2. Phase Space Reconstruction
2.3. Cascade Backpropagation Network
2.4. Recurrent Neural Network
2.5. Gated Recurrent Unit
2.6. Convolutional Neural Network Combined with Recurrent Neural Network
3. The Proposed GPSOGA Optimization Algorithm
3.1. Particle Swarm Optimization
3.2. Genetic Algorithm
3.3. Global Elite Opposition-Based Learning Strategy
3.4. The Proposed Optimization Algorithm
| Algorithm 1: The pseudo code of the proposed GPSOGA algorithm. |
| Objective function: /* and denote actual value and forecasting value respectively. */ Input: Training set and validation set Output: Optimal weight coefficients of corresponding forecasting models Parameters: —maximum iterations —current iteration —dimensions of particles —number of particles , —a random value in [0, 1] —particle velocity —particle position —the maximum value of particle position —the minimum value of particle position —maximum of particle velocity —The best position of the searching particle in the population —the crossover probability —the mutation probability —agent position generated by GEOLS Initialize the position () of each particle according to , , and Initialize fitness and speed () of each particle according to WHILE : DO The position of each particle is encoded in binary FOR EACH : DO IF DO A particle is randomly selected from the population as the mother, and a value is randomly selected in the DNA length, and the DNA sequence after the value of the mother is assigned to . END IF IF DO A random location of DNA is chosen to reverse it END IF END FOR The position of each particle is decoded in decimal Calculate elite agent position by Equations (13)–(15). IF DO END IF FOR EACH : DO Each particle updates its and by Equations (11) and (12) IF DO ELIF DO END IF IF DO END IF END FOR END WHILE RETURN |
4. The Proposed SSA-GPSOGA-NNCT Algorithm
5. Experiment Results and Analysis
5.1. Dataset Information
5.2. Evaluation Criteria
5.3. Comparison Models and Their Parameters
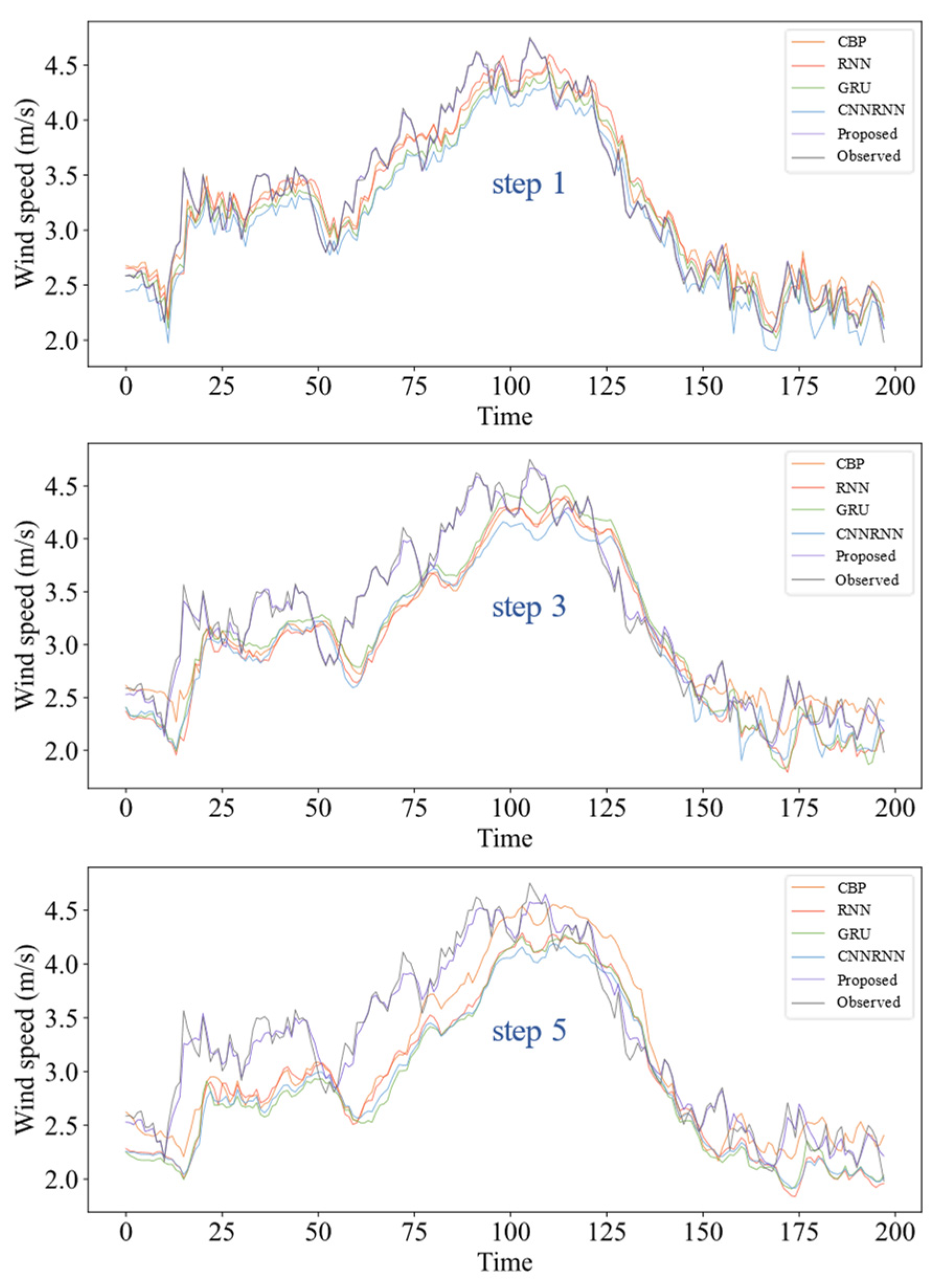
5.4. Experiment I
5.5. Experiment II
5.6. Experiment III
5.7. Experiment IV
6. Discussion
6.1. Diebold–Mariano Test
6.2. Akaike’s Information Criterion
6.3. Nash–Sutcliffe Efficiency Coefficient
7. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Perry, S. Wind energy for sustainable development: Driving factors and future outlook. J. Clean. Prod. 2021, 289, 125779. [Google Scholar]
- WWEA. WWEA Half-Year Report 2023: Additional Momentum for Windpower in 2023; WWEA: Bonn, Germany, 2023. [Google Scholar]
- IEA. World Energy Outlook 2022; IEA: Paris, France, 2022. [Google Scholar]
- Arndt, C.; Arent, D.; Hartley, F.; Merven, B.; Mondal, A.H. Faster than you think: Renewable energy and developing countries. Annu. Rev. Resour. Econ. 2019, 11, 149–168. [Google Scholar] [CrossRef]
- Rockström, J.; Gaffney, O.; Rogelj, J.; Meinshausen, M.; Nakicenovic, N.; Schellnhuber, H.J. A roadmap for rapid decarbonization. Science 2017, 355, 1269–1271. [Google Scholar] [CrossRef] [PubMed]
- Damousis, I.G.; Dokopoulos, P. A fuzzy expert system for the forecasting of wind speed and power generation in wind farms. In Proceedings of the PICA 2001. Innovative Computing for Power-Electric Energy Meets the Market. 22nd IEEE Power Engineering Society. International Conference on Power Industry Computer Applications (Cat. No. 01CH37195), Sydney, NSW, Australia, 20–24 May 2001; IEEE: Piscataway, NJ, USA, 2001. [Google Scholar]
- Attig-Bahar, F.; Ritschel, U.; Akari, P.; Abdeljelil, I.; Amairi, M. Wind energy deployment in Tunisia: Status, drivers, barriers and research gaps—A comprehensive review. Energy Rep. 2021, 7, 7374–7389. [Google Scholar] [CrossRef]
- Yang, Q.; Huang, G.; Li, T.; Xu, Y.; Pan, J. A novel short-term wind speed prediction method based on hybrid statistical-artificial intelligence model with empirical wavelet transform and hyperparameter optimization. J. Wind Eng. Ind. Aerodyn. 2023, 240, 105499. [Google Scholar] [CrossRef]
- Karan, S.; Panigrahi, B.K.; Shikhola, T.; Sharma, R. An imputation and decomposition algorithms based integrated approach with bidirectional LSTM neural network for wind speed prediction. Energy 2023, 278, 127799. [Google Scholar]
- Yang, Z.; Dong, S. A novel decomposition-based approach for non-stationary hub-height wind speed modelling. Energy 2023, 283, 129081. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, S.; Zhao, N.; Xin, J.; Wu, B. Short-term wind speed prediction using time varying filter-based empirical mode decomposition and group method of data handling-based hybrid model. Energy Convers. Manag. 2020, 220, 113076. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J.; Xiao, L. A hybrid approach based on the Gaussian process with t-observation model for short-term wind speed forecasts. Renew. Energy 2017, 114, 670–685. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Tan, J.; Zhang, K. A composite framework coupling multiple feature selection, compound prediction models and novel hybrid swarm optimizer-based synchronization optimization strategy for multi-step ahead short-term wind speed forecasting. Energy Convers. Manag. 2020, 205, 112461. [Google Scholar] [CrossRef]
- Neshat, M.; Nezhad, M.M.; Abbasnejad, E.; Mirjalili, S.; Tjernberg, L.B.; Garcia, D.A.; Alexander, B.; Wagner, M. A deep learning-based evolutionary model for short-term wind speed forecasting: A case study of the Lillgrund offshore wind farm. Energy Convers. Manag. 2021, 236, 114002. [Google Scholar] [CrossRef]
- Xiong, D.; Fu, W.; Wang, K.; Fang, P.; Chen, T.; Zou, F. A blended approach incorporating TVFEMD, PSR, NNCT-based multi-model fusion and hierarchy-based merged optimization algorithm for multi-step wind speed prediction. Energy Convers. Manag. 2021, 230, 113680. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H.; Song, J. Deep belief network based k-means cluster approach for short-term wind power forecasting. Energy 2018, 165, 840–852. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Kong, C.; Chen, B. A new prediction method based on VMD-PRBF-ARMA-E model considering wind speed characteristic. Energy Convers. Manag. 2020, 203, 112254. [Google Scholar] [CrossRef]
- Liu, D.; Ding, L.; Bai, Y.-L. Application of hybrid model based on empirical mode decomposition, novel recurrent neural networks and the ARIMA to wind speed prediction. Energy Convers. Manag. 2021, 233, 113917. [Google Scholar] [CrossRef]
- Jiang, Z.; Che, J.; Wang, L. Ultra-short-term wind speed forecasting based on EMD-VAR model and spatial correlation. Energy Convers. Manag. 2021, 250, 114919. [Google Scholar] [CrossRef]
- Singh, S.; Mohapatra, A. Repeated wavelet transform based ARIMA model for very short-term wind speed forecasting. Renew. Energy 2019, 136, 758–768. [Google Scholar]
- Pazikadin, A.R.; Rifai, D.; Ali, K.; Malik, M.Z.; Abdalla, A.N.; Faraj, M.A. Solar irradiance measurement instrumentation and power solar generation forecasting based on Artificial Neural Networks (ANN): A review of five years research trend. Sci. Total. Environ. 2020, 715, 136848. [Google Scholar] [CrossRef] [PubMed]
- Salcedo-Sanz, S.; Ortiz-García, E.G.; Pérez-Bellido, Á.M.; Portilla-Figueras, A.; Prieto, L. Short term wind speed prediction based on evolutionary support vector regression algorithms. Expert Syst. Appl. 2011, 38, 4052–4057. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, L.; Qin, H.; Liu, Y.; Wang, C.; Yu, X.; Yin, X.; Li, J. Wind speed prediction method using shared weight long short-term memory network and Gaussian process regression. Appl. Energy 2019, 247, 270–284. [Google Scholar] [CrossRef]
- Wei, D.; Wang, J.; Niu, X.; Li, Z. Wind speed forecasting system based on gated recurrent units and convolutional spiking neural networks. Appl. Energy 2021, 292, 116842. [Google Scholar] [CrossRef]
- Gao, Z.; Li, Z.; Xu, L.; Yu, J. Dynamic adaptive spatio-temporal graph neural network for multi-node offshore wind speed forecasting. Appl. Soft Comput. 2023, 141, 110294. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, J.; Dong, Y.; Wu, J. Combined forecasting models for wind energy forecasting: A case study in China. Renew. Sustain. Energy Rev. 2015, 44, 271–288. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, Z.; Zhang, K.; Mao, W.; Ma, Y.; Fan, X. A combined model based on CEEMDAN and modified flower pollination algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 136, 439–451. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Li, Q.; Ji, A. Design and research of hybrid forecasting system for wind speed point forecasting and fuzzy interval forecasting. Expert Syst. Appl. 2022, 209, 118384. [Google Scholar] [CrossRef]
- Niu, X.; Wang, J. A combined model based on data preprocessing strategy and multi-objective optimization algorithm for short-term wind speed forecasting. Appl. Energy 2019, 241, 519–539. [Google Scholar] [CrossRef]
- Jian, H.; Lin, Q.; Wu, J.; Fan, X.; Wang, X. Design of the color classification system for sunglass lenses using PCA-PSO-ELM. Measurement 2022, 189, 110498. [Google Scholar] [CrossRef]
- Leon, A.S.; Bian, L.; Tang, Y. Comparison of the genetic algorithm and pattern search methods for forecasting optimal flow releases in a multi-storage system for flood control. Environ. Model. Softw. 2021, 145, 105198. [Google Scholar] [CrossRef]
- Lv, H.; Chen, X.; Zeng, X. Optimization of micromixer with Cantor fractal baffle based on simulated annealing algorithm. Chaos Solitons Fractals 2021, 148, 111048. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Yengejeh, R.J.; Davami, A.H. Building energy optimization using grey wolf optimizer (GWO). Case Stud. Therm. Eng. 2021, 27, 101250. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.K.; Chakraborty, R.; Saha, M. An enhanced whale optimization algorithm for large scale optimization problems. Knowl.-Based Syst. 2021, 233, 107543. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Wei, X. A hybrid wind speed forecasting model based on phase space reconstruction theory and Markov model: A case study of wind farms in northwest China. Energy 2015, 91, 556–572. [Google Scholar] [CrossRef]
- He, P.; Fang, Q.; Jin, H.; Ji, Y.; Gong, Z.; Dong, J. Coordinated design of PSS and STATCOM-POD based on the GA-PSO algorithm to improve the stability of wind-PV-thermal-bundled power system. Int. J. Electr. Power Energy Syst. 2022, 141, 108208. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Li, Z.; Yang, H.; Li, H. Design of a combined system based on two-stage data preprocessing and multi-objective optimization for wind speed prediction. Energy 2021, 231, 121125. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, C.; Zhang, G. A combined forecasting system based on modified multi-objective optimization and sub-model selection strategy for short-term wind speed. Appl. Soft Comput. 2020, 94, 106463. [Google Scholar] [CrossRef]
- Arteche, J.; García-Enríquez, J. Singular spectrum analysis for signal extraction in stochastic volatility models. Econ. Stat. 2017, 1, 85–98. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Li, C.; Tan, J. Multi-step short-term wind speed forecasting approach based on multi-scale dominant ingredient chaotic analysis, improved hybrid GWO-SCA optimization and ELM. Energy Convers. Manag. 2019, 187, 356–377. [Google Scholar] [CrossRef]
- Lin, L.; Li, M.; Ma, L.; Baziar, A.; Ali, Z.M. Hybrid RNN-LSTM deep learning model applied to a fuzzy based wind turbine data uncertainty quantization method. Ad Hoc Netw. 2021, 123, 102658. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Xue, X.; Saeed, A.; Hu, X. Short-term wind speed interval prediction based on ensemble GRU model. IEEE Trans. Sustain. Energy 2019, 11, 1370–1380. [Google Scholar] [CrossRef]
- Nachaoui, M.; Afraites, L.; Laghrib, A. A regularization by denoising super-resolution method based on genetic algorithms. Signal Process. Image Commun. 2021, 99, 116505. [Google Scholar] [CrossRef]
- Feng, Y.; Lan, C.; Briseghella, B.; Fenu, L.; Zordan, T. Cable optimization of a cable-stayed bridge based on genetic algorithms and the influence matrix method. Eng. Optim. 2022, 54, 20–39. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wang, R.; Luo, Q. Elite opposition-based flower pollination algorithm. Neurocomputing 2016, 188, 294–310. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, Z.; Li, C.; Li, R. A novel combined forecasting system for air pollutants concentration based on fuzzy theory and optimization of aggregation weight. Appl. Soft Comput. 2020, 87, 105972. [Google Scholar] [CrossRef]
- Tsvetkova, O.; Ouarda, T.B. Use of the Halphen distribution family for mean wind speed estimation with application to Eastern Canada. Energy Convers. Manag. 2023, 276, 116502. [Google Scholar] [CrossRef]
- Lu, Y.; Li, T.; Hu, H.; Zeng, X. Short-term prediction of reference crop evapotranspiration based on machine learning with different decomposition methods in arid areas of China. Agric. Water Manag. 2023, 279, 108175. [Google Scholar] [CrossRef]
- Mojgan, S.; Khayamim, R.; Ozguven, E.E.; Dulebenets, M.A. Sustainable decisions in a ridesharing system with a tri-objective optimization approach. Transp. Res. Part D 2023, 125, 103958. [Google Scholar]
- Chen, M.; Tan, Y. SF-FWA: A Self-Adaptive Fast Fireworks Algorithm for effective large-scale optimization. Swarm Evol. Comput. 2023, 80, 101314. [Google Scholar] [CrossRef]
- Dulebenets, M.A. An Adaptive Polyploid Memetic Algorithm for scheduling trucks at a cross-docking terminal. Inf. Sci. 2021, 565, 390–421. [Google Scholar] [CrossRef]
- Singh, E.; Pillay, N. A study of ant-based pheromone spaces for generation constructive hyper-heuristics. Swarm Evol. Comput. 2022, 72, 101095. [Google Scholar] [CrossRef]






| Dataset | Min. | Median | Max. | Mean | Std. |
|---|---|---|---|---|---|
| Dataset 1 | 0.3530 | 2.6625 | 5.5810 | 2.7703 | 1.1196 |
| Dataset 2 | 0.3540 | 4.0460 | 9.7100 | 3.9389 | 1.7143 |
| Dataset 3 | 0.3640 | 1.7760 | 5.1360 | 1.8342 | 0.8890 |
| Dataset 4 | 0.3620 | 4.0540 | 11.8100 | 4.4091 | 2.2651 |
| Experiments | Comparison Models |
|---|---|
| Experiment I | CBP |
| RNN | |
| GRU | |
| CNNRNN | |
| Experiment II | SSA-CBP |
| SSA-RNN | |
| SSA-GRU | |
| SSA-CNNRNN | |
| Experiment III | SSA-SA-NNCT |
| SSA-ACO-NNCT | |
| SSA-GA-NNCT | |
| SSA-PSO-NNCT | |
| Experiment IV | EMD-GPSOGA-NNCT |
| CEEMDAN-GPSOGA-NNCT |
| Model | Parameters | Values |
|---|---|---|
| CBP, RNN, GRU | Number of neurons in hidden layers | 100 |
| Size of batch | 32 | |
| Epochs of training | 200 | |
| CNNRNN | Number of kernels in the CNN layer | 10 |
| Number of parallel filters in the CNN layer | 100 | |
| Number of neurons in the RNN layer | 100 | |
| Size of batch | 32 | |
| Epochs of training | 200 | |
| CEEMDAN | Noise standard deviation | 0.05 |
| Number of realizations | 50 | |
| Maximum sifting iterations | 300 | |
| PSR | Reconstruction dimension d | 10 |
| Time delay τ | 1 | |
| SA, ACO, GA, PSO, GPSOGA | Maximum iterations | 100 |
| Number of searching individuals | 60 |
| Step 1 | Step 3 | Step 5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAPE | MAE | MSE | MAPE | R2 | MAE | MSE | MAPE | ||||
| Dataset 1 | CBP | 0.1589 | 0.0378 | 5.1632 | 0.9323 | 0.2851 | 0.1292 | 8.6159 | 0.8687 | 0.3372 | 0.1818 | 10.1662 | 0.8746 |
| RNN | 0.1692 | 0.0439 | 5.3300 | 0.9213 | 0.3245 | 0.1643 | 10.0029 | 0.9059 | 0.3860 | 0.2335 | 11.6739 | 0.8822 | |
| GRU | 0.1715 | 0.0475 | 5.2373 | 0.9149 | 0.3016 | 0.1364 | 9.3970 | 0.8558 | 0.4250 | 0.2827 | 12.7851 | 0.8940 | |
| CNNRNN | 0.1644 | 0.0424 | 5.0308 | 0.9240 | 0.3315 | 0.1645 | 10.1096 | 0.9055 | 0.4153 | 0.2654 | 12.4034 | 0.8250 | |
| Proposed | 0.0156 | 0.0004 | 0.5067 | 0.9991 | 0.0435 | 0.0031 | 1.4294 | 0.9943 | 0.0767 | 0.0093 | 2.4493 | 0.9833 | |
| Dataset 2 | CBP | 0.4909 | 0.4779 | 12.0881 | 0.9251 | 0.5755 | 0.6228 | 15.4712 | 0.9023 | 0.6482 | 0.7939 | 16.8649 | 0.8754 |
| RNN | 0.3465 | 0.2119 | 9.6922 | 0.9667 | 0.5300 | 0.4997 | 14.1149 | 0.9216 | 0.5960 | 0.6569 | 15.8675 | 0.8969 | |
| GRU | 0.3812 | 0.2208 | 11.3245 | 0.9653 | 0.4902 | 0.4158 | 14.8632 | 0.9347 | 0.8043 | 1.2173 | 19.5752 | 0.8090 | |
| CNNRNN | 0.3753 | 0.2184 | 10.7489 | 0.9657 | 0.5214 | 0.4452 | 16.5091 | 0.9301 | 0.6590 | 0.7657 | 17.776 | 0.8799 | |
| Proposed | 0.0453 | 0.0038 | 1.2235 | 0.9994 | 0.1028 | 0.0191 | 2.9543 | 0.9969 | 0.1819 | 0.0551 | 5.6233 | 0.9913 | |
| Dataset 3 | CBP | 0.1710 | 0.5057 | 14.9385 | 0.8639 | 0.3470 | 0.1876 | 30.9241 | 0.8433 | 0.4278 | 0.2868 | 38.6148 | 0.9005 |
| RNN | 0.1655 | 0.0500 | 15.5006 | 0.8682 | 0.4089 | 0.2524 | 32.7434 | 0.8725 | 0.3569 | 0.2188 | 36.4308 | 0.8501 | |
| GRU | 0.1683 | 0.0516 | 15.1504 | 0.8579 | 0.3047 | 0.1529 | 31.3265 | 0.9131 | 0.3348 | 0.1912 | 34.3368 | 0.8674 | |
| CNNRNN | 0.1898 | 0.0622 | 18.2551 | 0.8872 | 0.3011 | 0.1596 | 28.2073 | 0.8576 | 0.3361 | 0.1887 | 31.6548 | 0.8503 | |
| Proposed | 0.0182 | 0.0006 | 1.5909 | 0.9960 | 0.0444 | 0.0034 | 3.9608 | 0.9769 | 0.0816 | 0.0113 | 7.1916 | 0.9247 | |
| Dataset 4 | CBP | 0.9881 | 1.5249 | 18.4462 | 0.9408 | 1.2373 | 2.5485 | 23.8929 | 0.8998 | 1.3806 | 3.1115 | 27.0739 | 0.8672 |
| RNN | 0.9936 | 1.609 | 19.2608 | 0.921 | 1.2226 | 2.5561 | 23.4273 | 0.898 | 1.3625 | 3.1363 | 25.7829 | 0.8614 | |
| GRU | 0.981 | 1.504 | 18.2036 | 0.8457 | 1.2335 | 2.641 | 24.1534 | 0.878 | 1.3605 | 3.0157 | 25.7006 | 0.8898 | |
| CNNRNN | 1.0329 | 1.6885 | 18.7101 | 0.9023 | 1.2194 | 2.4893 | 23.2502 | 0.8137 | 1.3369 | 2.9483 | 25.1321 | 0.9056 | |
| Proposed | 0.1025 | 0.0204 | 1.8978 | 0.9951 | 0.3071 | 0.1669 | 5.6554 | 0.9606 | 0.486 | 0.3986 | 8.8072 | 0.9061 | |
| Step 1 | Step 3 | Step 5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAPE | MAE | MSE | MAPE | R2 | MAE | MSE | MAPE | ||||
| Dataset 1 | SSA-CBP | 0.0642 | 0.0063 | 2.0743 | 0.9885 | 0.1502 | 0.0317 | 5.2032 | 0.9431 | 0.1556 | 0.0339 | 5.1781 | 0.9392 |
| SSA-RNN | 0.0169 | 0.0005 | 0.5440 | 0.9990 | 0.0996 | 0.0127 | 3.0550 | 0.9772 | 0.1059 | 0.0174 | 3.4444 | 0.9688 | |
| SSA-GRU | 0.0222 | 0.0008 | 0.7247 | 0.9985 | 0.0823 | 0.0098 | 2.7254 | 0.9822 | 0.1514 | 0.0325 | 4.5651 | 0.9417 | |
| SSA-CCNRNN | 0.0255 | 0.0010 | 0.8192 | 0.9981 | 0.0925 | 0.0124 | 3.0497 | 0.9778 | 0.1094 | 0.0179 | 3.4357 | 0.9679 | |
| Proposed | 0.0156 | 0.0004 | 0.5067 | 0.9991 | 0.0435 | 0.0031 | 1.4294 | 0.9943 | 0.0767 | 0.0093 | 2.4493 | 0.9833 | |
| Dataset 2 | SSA-CBP | 0.3461 | 0.2700 | 6.9472 | 0.9576 | 0.6016 | 1.0297 | 9.9864 | 0.8385 | 0.4961 | 0.5266 | 9.8678 | 0.9174 |
| SSA-RNN | 0.0654 | 0.0076 | 1.8038 | 0.9987 | 0.1882 | 0.051 | 5.4475 | 0.9920 | 0.2131 | 0.0746 | 6.4870 | 0.9882 | |
| SSA-GRU | 0.0736 | 0.0116 | 1.9255 | 0.9981 | 0.1762 | 0.0485 | 5.3744 | 0.9923 | 0.2562 | 0.1386 | 6.1579 | 0.9782 | |
| SSA-CCNRNN | 0.1975 | 0.1067 | 4.1492 | 0.9832 | 0.1915 | 0.0963 | 4.0609 | 0.9848 | 0.2686 | 0.1413 | 7.6861 | 0.9778 | |
| Proposed | 0.0453 | 0.0038 | 1.2235 | 0.9994 | 0.1028 | 0.0191 | 2.9543 | 0.9969 | 0.1819 | 0.0551 | 5.6233 | 0.9913 | |
| Dataset 3 | SSA-CBP | 0.0313 | 0.0015 | 2.9107 | 0.9899 | 0.0899 | 0.0123 | 8.9501 | 0.9181 | 0.1830 | 0.0438 | 14.2863 | 0.8796 |
| SSA-RNN | 0.0178 | 0.0008 | 1.6445 | 0.9946 | 0.0689 | 0.0073 | 6.6673 | 0.9514 | 0.1189 | 0.0217 | 9.5569 | 0.8558 | |
| SSA-GRU | 0.0338 | 0.0017 | 3.2008 | 0.9881 | 0.0554 | 0.0053 | 4.9410 | 0.9644 | 0.1015 | 0.0181 | 8.6586 | 0.8797 | |
| SSA-CCNRNN | 0.0328 | 0.0018 | 3.3472 | 0.9877 | 0.0787 | 0.0095 | 6.6068 | 0.9370 | 0.1033 | 0.0172 | 8.7949 | 0.8857 | |
| Proposed | 0.0182 | 0.0006 | 1.5909 | 0.9960 | 0.0444 | 0.0034 | 3.9608 | 0.9769 | 0.0816 | 0.0113 | 7.1916 | 0.9247 | |
| Dataset 4 | SSA-CBP | 0.1273 | 0.0299 | 2.3410 | 0.9929 | 0.4083 | 0.2986 | 7.8789 | 0.9296 | 0.6538 | 0.6985 | 12.4793 | 0.8354 |
| SSA-RNN | 0.1525 | 0.0403 | 2.7375 | 0.9904 | 0.3893 | 0.3003 | 7.2788 | 0.9292 | 0.5687 | 0.5375 | 10.6628 | 0.8734 | |
| SSA-GRU | 0.1314 | 0.0324 | 2.3346 | 0.9923 | 0.3551 | 0.2318 | 6.6904 | 0.9453 | 0.5641 | 0.5485 | 10.2898 | 0.8708 | |
| SSA-CCNRNN | 0.1982 | 0.6830 | 3.7835 | 0.9839 | 0.3435 | 0.2021 | 6.2534 | 0.9524 | 0.6505 | 0.6932 | 11.2917 | 0.8367 | |
| Proposed | 0.1025 | 0.0204 | 1.8978 | 0.9951 | 0.3071 | 0.1669 | 5.6554 | 0.9606 | 0.4860 | 0.3986 | 8.8072 | 0.9061 | |
| Step 1 | Step 3 | Step 5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAPE | MAE | MSE | MAPE | R2 | MAE | MSE | MAPE | ||||
| Dataset 1 | SSA-SA-NNCT | 0.1306 | 0.0239 | 4.2301 | 0.9571 | 0.0551 | 0.0049 | 1.7708 | 0.9911 | 0.1240 | 0.0262 | 3.9866 | 0.9529 |
| SSA-ACO-NNCT | 0.0174 | 0.0006 | 0.5682 | 0.9989 | 0.1480 | 0.0348 | 4.3457 | 0.9376 | 0.0803 | 0.0101 | 2.6024 | 0.9818 | |
| SSA-GA-NNCT | 0.0308 | 0.0016 | 2.7731 | 0.9889 | 0.0621 | 0.0056 | 2.0409 | 0.9899 | 0.1329 | 0.0261 | 4.2545 | 0.9532 | |
| SSA-PSO-NNCT | 0.0158 | 0.0005 | 0.5135 | 0.9991 | 0.0440 | 0.0033 | 1.4468 | 0.9941 | 0.0801 | 0.0098 | 2.5816 | 0.9824 | |
| Proposed | 0.0156 | 0.0004 | 0.5067 | 0.9991 | 0.0435 | 0.0031 | 1.4294 | 0.9943 | 0.0767 | 0.0093 | 2.4493 | 0.9833 | |
| Dataset 2 | SSA-SA-NNCT | 0.1951 | 0.0709 | 4.7473 | 0.9888 | 0.3792 | 0.2458 | 9.3127 | 0.9614 | 0.3039 | 0.1646 | 7.9633 | 0.9741 |
| SSA-ACO-NNCT | 0.1147 | 0.0214 | 2.9277 | 0.9966 | 0.1601 | 0.0518 | 3.8252 | 0.9918 | 0.2014 | 0.0713 | 5.7130 | 0.9888 | |
| SSA-GA-NNCT | 0.0972 | 0.0227 | 2.1252 | 0.9964 | 0.3573 | 0.2134 | 7.8370 | 0.9665 | 0.3476 | 0.2597 | 7.6108 | 0.9592 | |
| SSA-PSO-NNCT | 0.0518 | 0.0051 | 1.3954 | 0.9991 | 0.1060 | 0.0214 | 2.9977 | 0.9966 | 0.1863 | 0.0560 | 5.7998 | 0.9912 | |
| Proposed | 0.0453 | 0.0038 | 1.2235 | 0.9994 | 0.1028 | 0.0191 | 2.9543 | 0.9969 | 0.1819 | 0.0551 | 5.6233 | 0.9913 | |
| Dataset 3 | SSA-SA-NNCT | 0.0406 | 0.0028 | 3.5775 | 0.9808 | 0.0509 | 0.0047 | 4.4664 | 0.9687 | 0.0964 | 0.0149 | 8.3017 | 0.9009 |
| SSA-ACO-NNCT | 0.0199 | 0.0007 | 1.7773 | 0.9952 | 0.0513 | 0.0045 | 4.7902 | 0.9699 | 0.0861 | 0.0123 | 7.4389 | 0.9179 | |
| SSA-GA-NNCT | 0.1491 | 0.0422 | 2.7625 | 0.9900 | 0.0539 | 0.0051 | 4.6864 | 0.9657 | 0.0924 | 0.0133 | 7.7894 | 0.9116 | |
| SSA-PSO-NNCT | 0.0197 | 0.0007 | 1.6873 | 0.9953 | 0.0489 | 0.0041 | 4.2658 | 0.9727 | 0.0842 | 0.0116 | 7.1622 | 0.9228 | |
| Proposed | 0.0182 | 0.0006 | 1.5909 | 0.9960 | 0.0444 | 0.0034 | 3.9608 | 0.9769 | 0.0816 | 0.0113 | 7.1916 | 0.9247 | |
| Dataset 4 | SSA-SA-NNCT | 0.1496 | 0.0395 | 2.8636 | 0.9906 | 0.3494 | 0.2039 | 6.8123 | 0.9519 | 0.5185 | 0.4460 | 9.4389 | 0.8949 |
| SSA-ACO-NNCT | 0.1062 | 0.0214 | 1.9928 | 0.9949 | 0.3187 | 0.1748 | 6.1091 | 0.9588 | 0.4936 | 0.4069 | 8.9811 | 0.9041 | |
| SSA-GA-NNCT | 0.1491 | 0.0422 | 2.7625 | 0.9900 | 0.3403 | 0.2011 | 6.1707 | 0.9526 | 0.5308 | 0.4846 | 9.6930 | 0.8858 | |
| SSA-PSO-NNCT | 0.1066 | 0.0215 | 1.9808 | 0.9949 | 0.3120 | 0.1669 | 5.7963 | 0.9606 | 0.5069 | 0.4333 | 9.0767 | 0.8979 | |
| Proposed | 0.1025 | 0.0204 | 1.8978 | 0.9951 | 0.3071 | 0.1669 | 5.6554 | 0.9606 | 0.4860 | 0.3986 | 8.8072 | 0.9061 | |
| Step 1 | Step 3 | Step 5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAPE | MAE | MSE | MAPE | R2 | MAE | MSE | MAPE | ||||
| Dataset 1 | EMD-GPSOGA-NNCT | 0.0678 | 0.0073 | 2.2451 | 0.9869 | 0.0955 | 0.0141 | 3.0810 | 0.9746 | 0.1080 | 0.0186 | 3.5666 | 0.9665 |
| CEEMDAN-GPSOGA-NNCT | 0.5403 | 0.4525 | 10.2478 | 0.8934 | 0.1002 | 0.0157 | 3.2823 | 0.9718 | 0.1287 | 0.0260 | 4.2743 | 0.9533 | |
| Proposed | 0.0156 | 0.0004 | 0.5067 | 0.9991 | 0.0435 | 0.0031 | 1.4294 | 0.9943 | 0.0767 | 0.0093 | 2.4493 | 0.9833 | |
| Dataset 2 | EMD-GPSOGA-NNCT | 0.3035 | 0.1399 | 10.0201 | 0.9780 | 0.3914 | 0.2299 | 13.2703 | 0.9639 | 0.4955 | 0.3701 | 16.4526 | 0.9410 |
| CEEMDAN-GPSOGA-NNCT | 0.2212 | 0.0835 | 6.2285 | 0.9868 | 0.3587 | 0.1992 | 11.9113 | 0.9687 | 0.4392 | 0.2878 | 15.2696 | 0.9548 | |
| Proposed | 0.0453 | 0.0038 | 1.2235 | 0.9994 | 0.1028 | 0.0191 | 2.9543 | 0.9969 | 0.1819 | 0.0551 | 5.6233 | 0.9913 | |
| Dataset 3 | EMD-GPSOGA-NNCT | 0.0933 | 0.0193 | 8.7657 | 0.8715 | 0.1307 | 0.0365 | 11.7078 | 0.8578 | 0.1512 | 0.0478 | 13.8153 | 0.8831 |
| CEEMDAN-GPSOGA-NNCT | 0.0834 | 0.0140 | 7.5605 | 0.9069 | 0.1455 | 0.0401 | 12.9240 | 0.8339 | 0.1524 | 0.0402 | 13.5900 | 0.8334 | |
| Proposed | 0.0182 | 0.0006 | 1.5909 | 0.996 | 0.0444 | 0.0034 | 3.9608 | 0.9769 | 0.0816 | 0.0113 | 7.1916 | 0.9247 | |
| Dataset 4 | EMD-GPSOGA-NNCT | 0.5534 | 0.4928 | 10.3445 | 0.8839 | 0.7939 | 1.0773 | 14.9112 | 0.8462 | 0.8545 | 1.2587 | 16.2717 | 0.8435 |
| CEEMDAN-GPSOGA-NNCT | 0.5543 | 0.4951 | 10.2425 | 0.8833 | 0.7760 | 1.0356 | 14.1822 | 0.8561 | 0.9265 | 1.4638 | 16.7090 | 0.8552 | |
| Proposed | 0.1025 | 0.0204 | 1.8978 | 0.9951 | 0.3071 | 0.1669 | 5.6554 | 0.9606 | 0.4860 | 0.3986 | 8.8072 | 0.9061 | |
| Dataset 1 | Dataset 2 | Dataset 3 | Dataset 4 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Step 1 | Step 3 | Step 5 | Step 1 | Step 3 | Step 5 | Step 1 | Step 3 | Step 5 | Step 1 | Step 3 | Step 5 | ||
| Experiment I | CBP | 9.275 | 10.205 | 10.004 | 6.853 | 6.521 | 6.493 | 7.92 | 10.189 | 9.130 | 9.056 | 9.266 | 8.843 |
| RNN | 7.764 | 9.308 | 10.171 | 7.469 | 6.722 | 6.357 | 6.326 | 10.788 | 8.699 | 9.502 | 8.871 | 8.179 | |
| GRU | 8.455 | 9.822 | 10.738 | 9.937 | 6.775 | 7.671 | 6.474 | 8.622 | 8.633 | 8.888 | 8.489 | 8.601 | |
| CNNRNN | 9.495 | 10.595 | 10.722 | 9.553 | 7.794 | 6.696 | 7.35 | 7.855 | 8.664 | 9.053 | 9.088 | 8.702 | |
| Experiment II | SSA-CBP | 9.295 | 12.117 | 9.866 | 7.187 | 6.721 | 6.858 | 5.025 | 6.966 | 11.857 | 5.041 | 5.078 | 5.399 |
| SSA-RNN | 2.803 | 11.511 | 6.452 | 5.019 | 8.051 | 3.691 | 2.024 | 6.495 | 7.875 | 5.985 | 4.760 | 3.296 | |
| SSA-GRU | 4.829 | 8.776 | 9.577 | 4.849 | 7.709 | 5.123 | 4.610 | 4.882 | 5.634 | 3.602 | 3.728 | 4.467 | |
| SSA-CNNRNN | 6.186 | 9.033 | 8.046 | 5.68 | 5.256 | 5.411 | 4.959 | 8.408 | 6.591 | 8.086 | 3.809 | 6.779 | |
| Experiment III | SSA-SA-NNCT | 13.121 | 8.378 | 6.505 | 7.027 | 7.111 | 4.789 | 7.022 | 3.886 | 4.081 | 5.669 | 2.083 | 2.747 |
| SSA-ACO-NNCT | 3.694 | 6.014 | 2.313 | 8.169 | 4.787 | 3.145 | 2.410 | 4.019 | 2.412 | 1.702 | 1.901 | 1.803 | |
| SSA-GA-NNCT | 11.231 | 6.174 | 6.895 | 4.643 | 7.965 | 5.188 | 5.696 | 3.942 | 2.700 | 4.455 | 2.632 | 2.906 | |
| SSA-PSO-NNCT | 1.653 | 1.689 | 1.975 | 4.108 | 1.880 | 2.097 | 1.971 | 3.443 | 2.821 | 1.723 | 1.834 | 3.241 | |
| Experiment IV | EMD-GPSOGA | 9.393 | 8.238 | 5.061 | 11.38 | 9.618 | 8.977 | 4.531 | 5.273 | 4.828 | 9.399 | 6.858 | 6.047 |
| CEEMDAN-GPSOGA | 9.421 | 8.172 | 6.696 | 8.316 | 9.893 | 9.168 | 6.119 | 6.913 | 5.542 | 9.748 | 6.314 | 6.631 | |
| Dataset1 | Dataset2 | Dataset3 | Dataset4 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Step 1 | Step 3 | Step 5 | Step 1 | Step 3 | Step 5 | Step 1 | Step 3 | Step 5 | Step 1 | Step 3 | Step 5 | ||
| Experiment I | CBP | −442.5 | −199.1 | −131.5 | 59.8 | 112.3 | 160.3 | −384.3 | −125.3 | −41.3 | 285.9 | 391.2 | 430.8 |
| RNN | −412.6 | −151.5 | −82.0 | −101.2 | 68.6 | 122.8 | −386.9 | −66.6 | −94.8 | 297.6 | 391.8 | 432.3 | |
| GRU | −397.1 | −188.3 | −44.1 | −93.0 | 32.3 | 244.9 | −380.8 | −165.8 | −121.5 | 279.4 | 398.3 | 424.6 | |
| CNNRNN | −351.4 | −151.3 | −56.6 | −95.2 | 45.8 | 153.2 | −343.6 | −157.3 | −124.2 | 284.3 | 386.6 | 420.1 | |
| Experiment II | SSA-CBP | −794.2 | −476.9 | −463.6 | −53.2 | 211.8 | 79.0 | −1078.6 | −663.9 | −413.3 | −488.8 | −33.3 | 135.0 |
| SSA-RNN | −1294.7 | −658.5 | −595.8 | −757.7 | −383.2 | −307.9 | −1202.8 | −767.4 | −551.9 | −429.4 | −32.2 | 83.1 | |
| SSA-GRU | −1204.5 | −707.8 | −472.0 | −675.0 | −393.0 | −185.2 | −1047.4 | −829.3 | −587.8 | −472.9 | −83.4 | 87.1 | |
| SSA-CNNRNN | −1151.0 | −663.2 | −590.5 | −236.9 | −257.3 | −181.4 | −1039.5 | −716.0 | −598.0 | −325.4 | −110.6 | 133.5 | |
| Experiment III | SSA-SA-NNCT | −532.7 | −458.6 | −514.5 | −317.9 | −71.8 | −151.1 | −951.4 | −854.9 | −626.1 | −433.4 | −108.8 | 46.2 |
| SSA-ACO-NNCT | −1265.7 | −845.8 | −702.5 | −554.6 | −379.9 | −316.6 | −1229.2 | −862.1 | −663.4 | −555.2 | −139.3 | 28.0 | |
| SSA-GA-NNCT | −508.2 | −819.9 | −515.5 | −543.3 | −99.8 | −60.9 | −1034.9 | −836.5 | −648.9 | −420.7 | −111.5 | 62.6 | |
| SSA-PSO-NNCT | −1309.3 | −924.9 | −709.8 | −835.6 | −554.7 | −364.4 | −1230.6 | −882.0 | −675.8 | −554.0 | −148.5 | 40.4 | |
| Experiment IV | EMD-GPSOGA | −767.6 | −636.5 | −582.0 | −183.3 | −85.0 | 9.2 | −574.8 | −449.2 | −396.0 | 65.9 | 220.8 | 251.6 |
| CEEMDAN-GPSOGA | −768.0 | −615.9 | −516.3 | −285.5 | −113.4 | −40.6 | −638.7 | −430.6 | −430.2 | 66.8 | 212.9 | 281.5 | |
| Proposed | −1318.9 | −933.0 | −719.7 | −896.9 | −576.9 | −367.8 | −1262.3 | −915.2 | −680.6 | −564.0 | −148.4 | 23.9 | |
| Dataset 1 | Dataset 2 | Dataset 3 | Dataset 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Step 1 | Step 3 | Step 5 | Step 1 | Step 3 | Step 5 | Step 1 | Step 3 | Step 5 | Step 1 | Step 3 | Step 5 | ||
| Experiment I | CBP | 0.932 | 0.769 | 0.675 | 0.925 | 0.902 | 0.875 | 0.664 | 0.243 | 0.901 | 0.647 | 0.400 | 0.267 |
| RNN | 0.921 | 0.706 | 0.582 | 0.967 | 0.922 | 0.897 | 0.668 | 0.673 | 0.450 | 0.626 | 0.398 | 0.261 | |
| GRU | 0.915 | 0.756 | 0.494 | 0.965 | 0.935 | 0.809 | 0.658 | 0.131 | 0.267 | 0.659 | 0.378 | 0.290 | |
| CNNRNN | 0.893 | 0.706 | 0.525 | 0.966 | 0.930 | 0.880 | 0.587 | 0.577 | 0.250 | 0.650 | 0.414 | 0.306 | |
| Experiment II | SSA-CBP | 0.989 | 0.943 | 0.939 | 0.958 | 0.839 | 0.917 | 0.990 | 0.918 | 0.710 | 0.993 | 0.930 | 0.835 |
| SSA-RNN | 0.993 | 0.977 | 0.969 | 0.995 | 0.992 | 0.988 | 0.995 | 0.951 | 0.856 | 0.990 | 0.929 | 0.873 | |
| SSA-GRU | 0.996 | 0.982 | 0.942 | 0.998 | 0.992 | 0.978 | 0.988 | 0.964 | 0.880 | 0.992 | 0.945 | 0.871 | |
| SSA-CNNRNN | 0.998 | 0.978 | 0.968 | 0.983 | 0.985 | 0.978 | 0.988 | 0.937 | 0.886 | 0.984 | 0.952 | 0.837 | |
| Experiment III | SSA-SA-NNCT | 0.957 | 0.938 | 0.953 | 0.989 | 0.961 | 0.974 | 0.981 | 0.969 | 0.901 | 0.991 | 0.952 | 0.895 |
| SSA-ACO-NNCT | 0.998 | 0.991 | 0.982 | 0.997 | 0.992 | 0.989 | 0.995 | 0.970 | 0.918 | 0.993 | 0.959 | 0.864 | |
| SSA-GA-NNCT | 0.951 | 0.990 | 0.953 | 0.996 | 0.967 | 0.959 | 0.987 | 0.966 | 0.912 | 0.990 | 0.953 | 0.886 | |
| SSA-PSO-NNCT | 0.996 | 0.991 | 0.982 | 0.997 | 0.994 | 0.989 | 0.995 | 0.973 | 0.923 | 0.994 | 0.951 | 0.899 | |
| Experiment IV | EMD-GPSOGA | 0.987 | 0.975 | 0.967 | 0.978 | 0.964 | 0.942 | 0.872 | 0.758 | 0.683 | 0.884 | 0.746 | 0.704 |
| CEEMDAN-GPSOGA | 0.987 | 0.972 | 0.953 | 0.987 | 0.969 | 0.955 | 0.907 | 0.734 | 0.733 | 0.883 | 0.756 | 0.655 | |
| Proposed | 0.999 | 0.994 | 0.983 | 0.999 | 0.997 | 0.991 | 0.996 | 0.977 | 0.925 | 0.995 | 0.961 | 0.906 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Chen, Y.; Zang, Y. Wind Speed Forecasting Based on Phase Space Reconstruction and a Novel Optimization Algorithm. Sustainability 2024, 16, 6945. https://doi.org/10.3390/su16166945
He Z, Chen Y, Zang Y. Wind Speed Forecasting Based on Phase Space Reconstruction and a Novel Optimization Algorithm. Sustainability. 2024; 16(16):6945. https://doi.org/10.3390/su16166945
Chicago/Turabian StyleHe, Zhaoshuang, Yanhua Chen, and Yale Zang. 2024. "Wind Speed Forecasting Based on Phase Space Reconstruction and a Novel Optimization Algorithm" Sustainability 16, no. 16: 6945. https://doi.org/10.3390/su16166945
APA StyleHe, Z., Chen, Y., & Zang, Y. (2024). Wind Speed Forecasting Based on Phase Space Reconstruction and a Novel Optimization Algorithm. Sustainability, 16(16), 6945. https://doi.org/10.3390/su16166945





