Tracking the Dynamics and Uncertainties of Soil Organic Carbon in Agricultural Soils Based on a Novel Robust Meta-Model Framework Using Multisource Data
Abstract
1. Introduction
- Process-based simulation models, e.g., such as MIcrobial-MIneral Carbon Stabilization model (MIMICS, [21]), DeNitrification-DeComposition model (DNDC, [22]), and Environmental Policy Integrated Climate model (EPIC [23,24,25,26,27,28,29]), which represent key dynamic processes affecting soil nutrients, land emissions, and productivity (yields);
2. Modeling SOC Dynamics: Process-Based vs. Statistical Models
2.1. SOC Analysis and Modeling
2.2. Modeling SOC Dynamics: Processed-Based vs. Statistical Models
2.2.1. Process-Based EPIC Model
2.2.2. Statistical and Machine Learning Models
2.2.3. Statistical and Machine Learning Models
3. Estimating SOC Level Dependencies on Land Practices and Climate Changes
3.1. Experimental Design
3.2. Data
3.3. Machine Learning Quantile Regression Meta-Model
3.3.1. Linear Regression Model
3.3.2. Quantile Regression (QR) Model
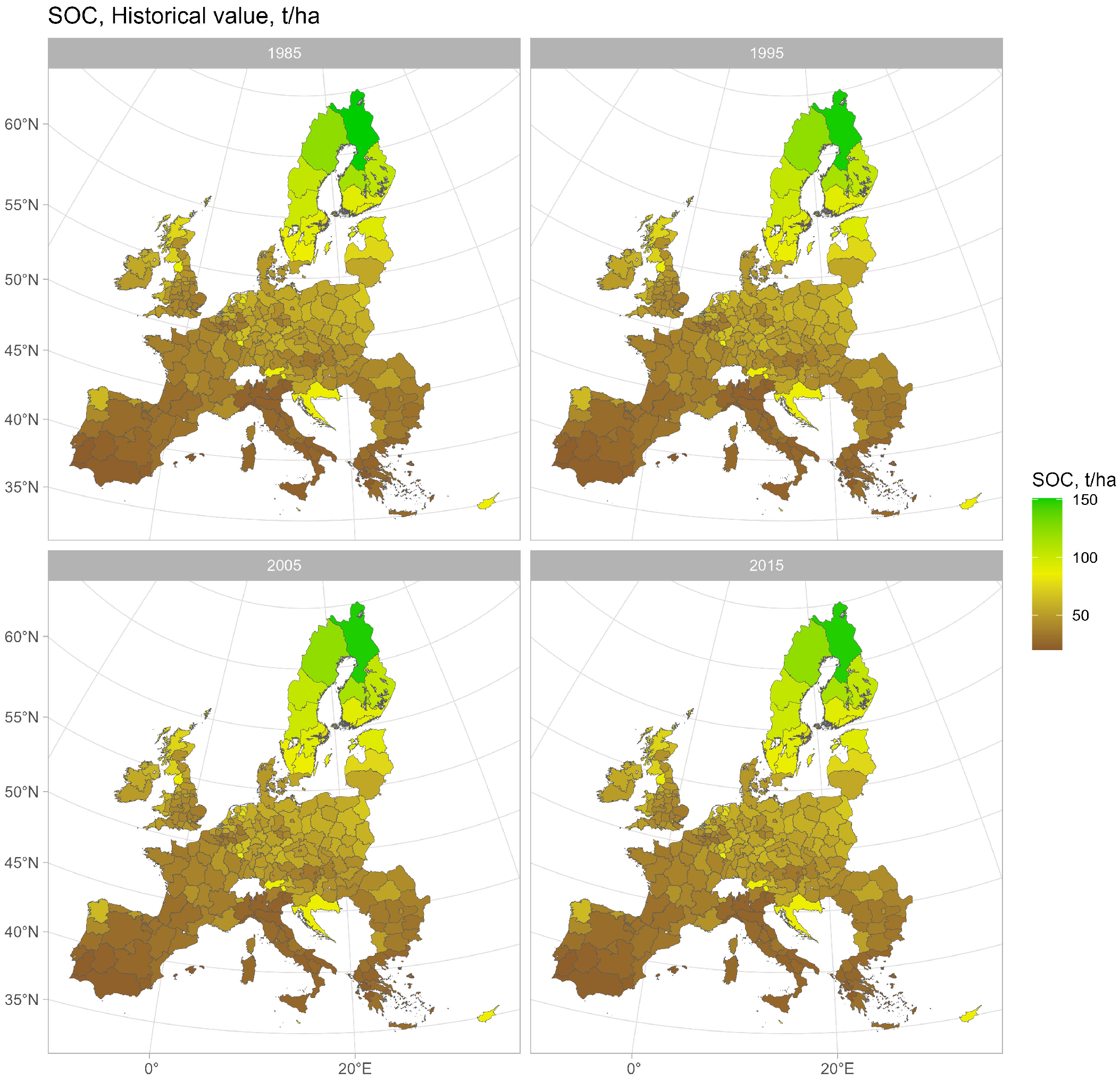
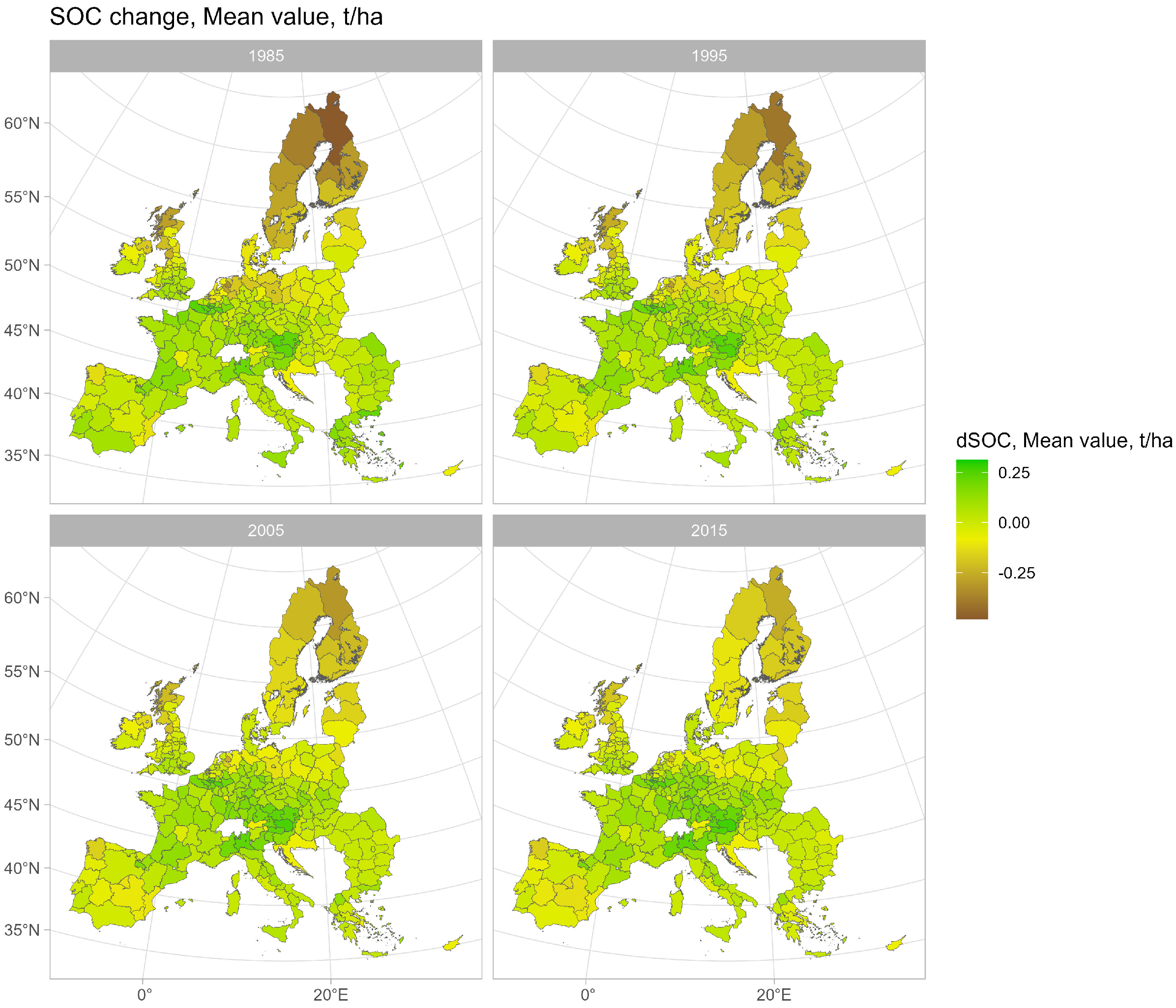
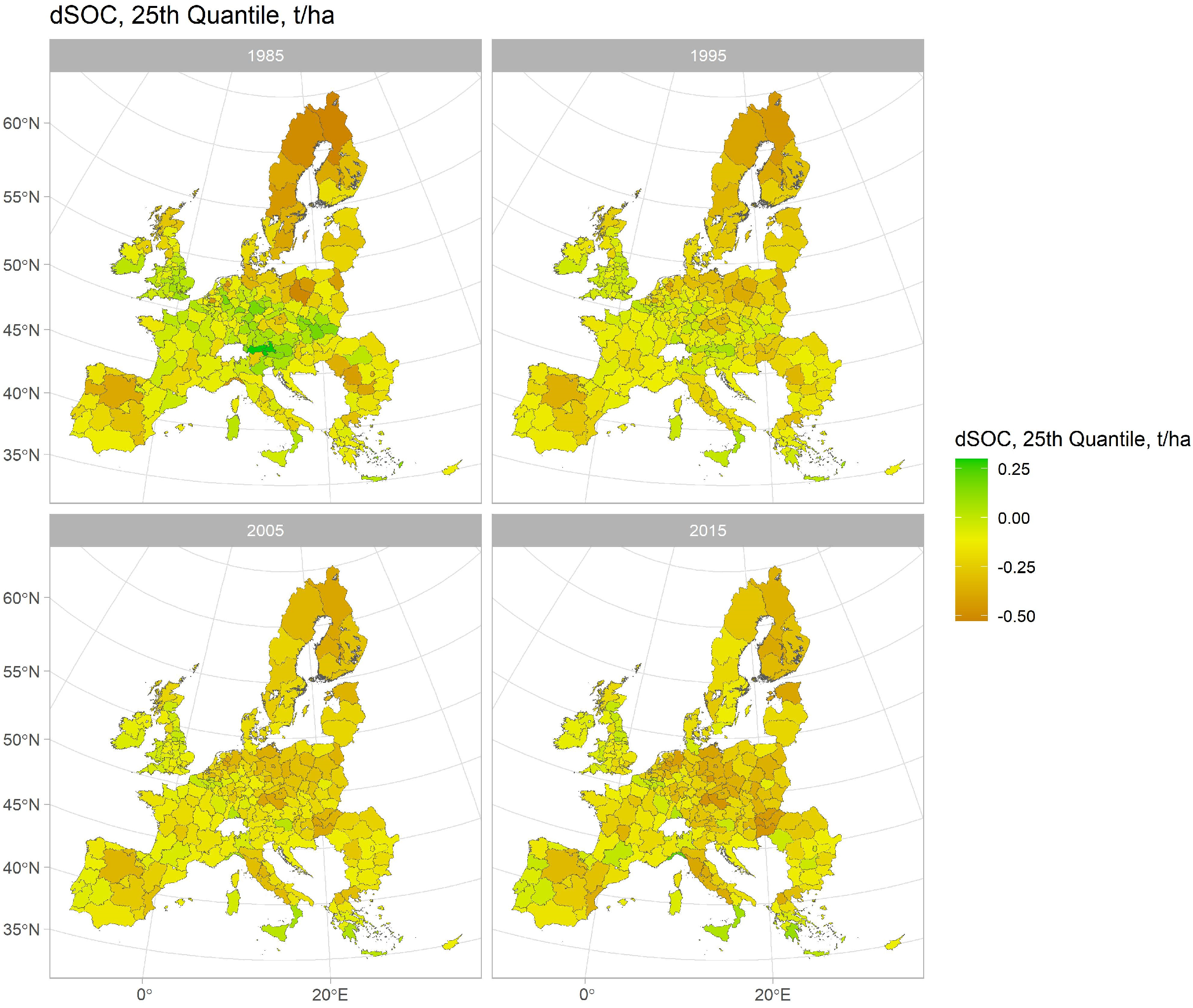
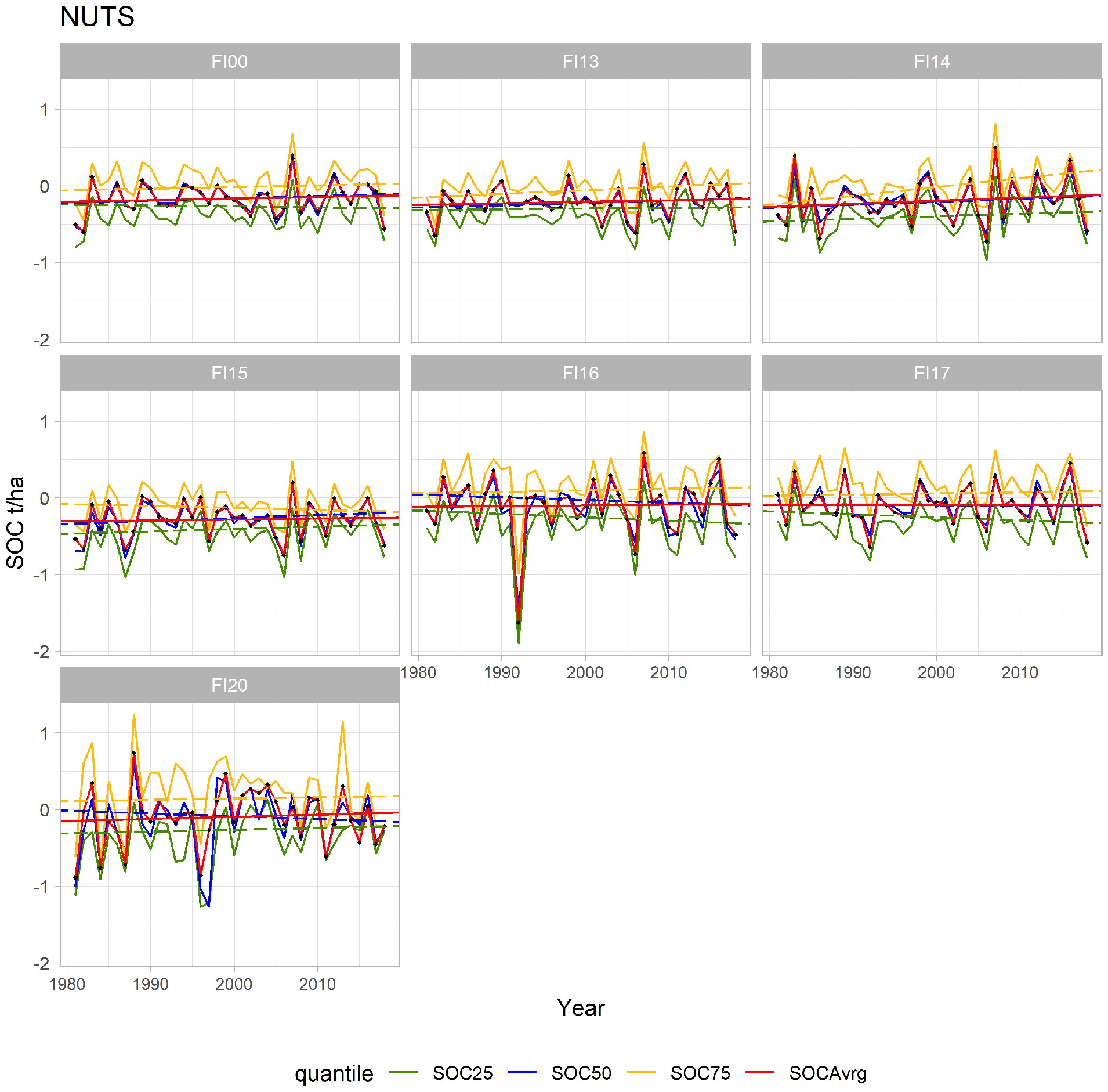
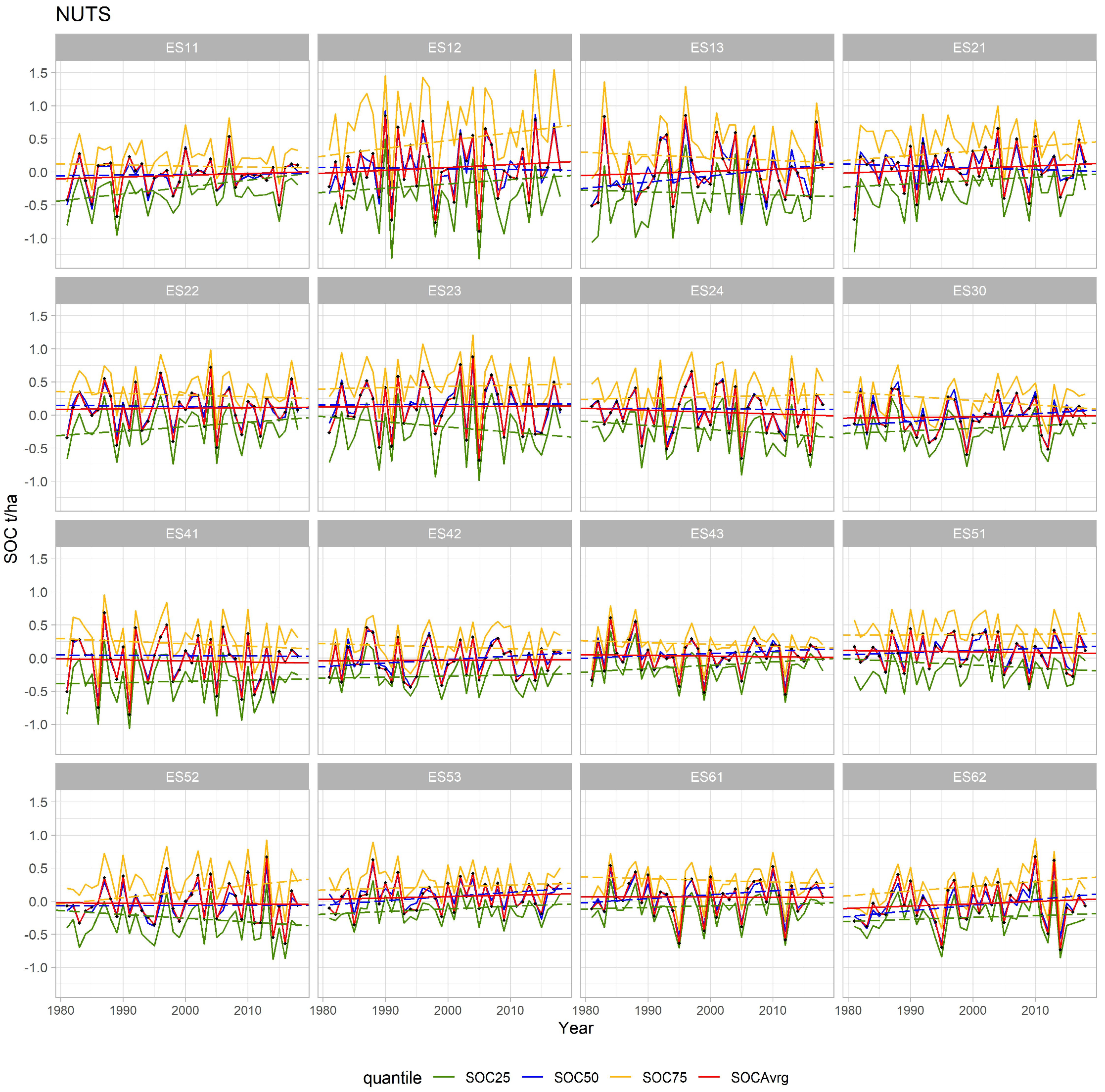
4. Selected Results
Results Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alexander, P.; Paustian, K.; Smith, P.; Moran, D. The economics of soil C sequestration and agricultural emissions abatement. Soil 2015, 1, 331–339. [Google Scholar] [CrossRef]
- Batjes, N.H. Mitigation of atmospheric CO2 concentrations by increased carbon sequestration in the soil. Biol. Fertil. Soils 1988, 27, 230–235. [Google Scholar] [CrossRef]
- Batjes, N.H.; Ribeiro, E.; Van Oostrum, A. Standardized soil profile data to support global mapping and modelling (WoSIS snapshot 2019). Earth Syst. Sci. Data Discuss. 2019, 12, 299–320. [Google Scholar] [CrossRef]
- Amelung, W.; Bossio, D.; de Vries, W.; Kögel-Knabner, I.; Lehmann, J.; Amundson, R.; Bol, R.; Collins, C.; Lal, R.; Leifeld, J.; et al. Towards a global-scale soil climate mitigation strategiy. Nat. Commun. 2020, 11, 5427. [Google Scholar] [CrossRef]
- Cowie, A. Guidelines for Land Degradation Neutrality. A report prepared for the Scientific and Technical Advisory Panel of the Global Environment Facility, 2020. Available online: https://catalogue.unccd.int/1474_LDN_Technical_Report_web_version.pdf (accessed on 10 May 2024).
- Panagos, P.; Montanarella, L. Soil thematic strategy: An important contribution to policy support, research, data development and raising the awareness. Curr. Opin. Environ. Sci. Health 2018, 5, 38–41. [Google Scholar] [CrossRef]
- Panagos, P.; Montanarella, L.; Barbero, M.; Schneegans, A.; Aguglia, L. Soil priorities in the European Union. Geoderma Reg. 2022, 29, e00510. [Google Scholar] [CrossRef]
- Álvaro-Fuentes, J.; Easter, M.; Paustian, K. Climate change effects on organic carbon storage in agricultural soils of northeastern Spain. Agric. Ecosyst. Environ. 2012, 155, 87–94. [Google Scholar] [CrossRef]
- Schimel, D.S.; Braswell, B.H.; Holland, E.A.; McKeon, R.; Ojima, D.S.; Painter, T.H.; Parton, W.J.; Townsend, A.R. Climatic, edaphic, and biotic controls over storage and turnover of carbon in soils. Glob. Biogeochem. Cycles 1994, 8, 279–293. [Google Scholar] [CrossRef]
- Wu, Z.T.; Dijkstra, P.; Koch, G.W.; Peñuelas, J.; Hungate, B.A. Responses of terrestrial ecosystems to temperature and precipitation change: A meta-analysis of experimental manipulation. Glob. Chang. Biol. 2011, 17, 927–942. [Google Scholar] [CrossRef]
- Poll, C.; Marhan, S.; Back, F.; Niklaus, P.A.; Kandeler, E. Field-scale manipulation of soil temperature and precipitation change soil CO2 flux in a temperate agricultural ecosystem. Agric. Ecosyst. Environ. 2013, 165, 88–97. [Google Scholar] [CrossRef]
- USDA Natural Resources Conservation Service. Carbon to Nitrogen Ratios in Cropping Systems. 2011. Available online: https://www.nrcs.usda.gov/conservation-basics/natural-resource-concerns/soil/soil-science (accessed on 1 February 2024).
- Carbon to Nitrogen Ratio (C:N). Soil Health Nexus. Available online: https://soilhealthnexus.org/resources/soil-properties/soil-chemical-properties/carbon-to-nitrogen-ratio-cn/ (accessed on 8 July 2024).
- Rocci, K.S.; Lavallee, J.M.; Stewart, C.E.; Cotrufo, M.F. Soil organic carbon response to global environmental change depends on its distribution between mineral-associated and particulate organic matter: A meta-analysis. Sci. Total Environ. 2021, 793, 148569. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Rocci, K.S.; Lehmann, A.; Rillig, M.C. Nitrogen increases soil organic carbon accrual and alters its functionality. Glob. Chang. Biol. 2023, 29, 1971–1983. [Google Scholar] [CrossRef] [PubMed]
- Manzoni, S.; Taylor, P.; Richter, A.; Porporato, A.; Ågren, G.I. Environmental and stoichiometric controls on microbial carbon-use efficiency in soils. New Phytol. 2012, 196, 7991. [Google Scholar] [CrossRef]
- Nakhavali, M.A.; Lauerwald, R.; Regnier, P.; Friedlingstein, P. Predicting future trends of terrestrial dissolved organic carbon transport to global river systems. Earth’s Future 2024, 12, e2023EF004137. [Google Scholar] [CrossRef]
- Zhu, K.; Ran, H.; Wang, F.; Ye, X.; Niu, L.; Schulin, R.; Wang, G. Conservation tillage facilitated soil carbon sequestration through diversified carbon conservation. Agric. Ecosyst. Environ. 2022, 337, 108080. [Google Scholar] [CrossRef]
- Aditi, K.; Abbhishek, K.; Chander, G.; Singh, A.; Thomas Falk, T.; Mequanint, M.B.; Cuba, P.; Anupama, G.; Mandapati, R.; Nagaraji, S. Assessing residue and tillage management options for carbon sequestration in future climate change scenarios. Curr. Res. Environ. Sustain. 2023, 5, 100210. [Google Scholar] [CrossRef]
- Havlík, P.; Schneider, U.A.; Schmid, E.; Boettcher, H.; Fritz, S.; Skalský, R.; Aoki, K.; de Cara, S.; Kindermann, G.; Kraxner, F.; et al. Global land-use implications of first and second generation biofuel targets. Energy Policy 2011, 39, 5690–5702. [Google Scholar] [CrossRef]
- Kyker-Snowman, E.; Wieder, W.R.; Frey, S.D.; Grandy, A.S. Stoichiometrically coupled carbon and nitrogen cycling in the MIcrobial-MIneral Carbon Stabilization model version 1.0 (MIMICS-CN v1.0). Geosci. Model Dev. 2020, 13, 4413–4434. [Google Scholar] [CrossRef]
- Li, C.; Frolking, S.; Frolking, T.A. A model of N2O evolution from soil driven by rainfall events: 1. Model structure and sensitivity. J. Geophys. Res. 1992, 97, 9759–9776. [Google Scholar] [CrossRef]
- Balkovič, J.; Madaras, M.; Skalsky, R.; Folberth, C.; Smatanova, M.; Schmid, E.; van der Velde, M.; Kraxner, F.; Obersteiner, M. Verifiable soil organic carbon modelling to facilitate regional reporting of cropland carbon change: A test case in the Czech Republic. J. Environ. Manag. 2020, 274, 111206. [Google Scholar] [CrossRef]
- Balkovič, J.; van der Velde, M.; Schmid, E.; Skalský, R.; Khabarov, N.; Obersteiner, M.; Stürmer, B.; Xiong, W. Pan-European crop modelling with EPIC: Implementation, up-scaling and regional crop yield validation. Agric. Syst. 2013, 120, 61–75. [Google Scholar] [CrossRef]
- Jones, C.A.; Dyke, P.T.; Williams, J.R.; Kiniry, J.R.; Benson, V.W.; Griggs, R.H. EPIC: An operational model for evaluation of agricultural sustainability. Agric. Syst. 1991, 37, 341–350. [Google Scholar] [CrossRef]
- Jones, R.J.A.; Hiederer, R.; Rusco, E.; Loveland, P.J.; Montanarella, L. Estimating organic carbon in the soils of Europe for policy support. Eur. J. Soil. Sci. 2015, 56, 655–671. [Google Scholar] [CrossRef]
- Jones, J.W.; Antle, J.M.; Basso, B.; Boote, K.J.; Conant, R.T.; Foster, I.; Godfray, H.C.J.; Herrero, M.; Howitt, R.E.; Janssen, S.; et al. Toward a new generation of agricultural system data, models, and knowledge products: State of agricultural systems science. Agric. Syst. 2017, 155, 269–288. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.R.; Jones, C.A.; Dyke, P.T. A modelling approach to determining the relationship between erosion and soil productivity. Trans. ASAE 1984, 27, 129–144. [Google Scholar] [CrossRef]
- Williams, J.R. The erosion productivity impact calculator (EPIC) model: A case history. Phil. Trans. Roy. Soc. 1990, 329, 421–428. [Google Scholar]
- Drummond, S.T.; Sudduth, K.A.; Joshi, A.; Birrell, S.J.; Kitchen, N.R. Statistical and neural methods for site-specific yield prediction. Trans. ASAE 2003, 46, 5. [Google Scholar] [CrossRef]
- Van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction usingmachine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. Forest Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Micale, F.; Genovese, G. Methodology of the MARS Crop Yield Forecasting System; Statistical data collectoin, processing and analysis; EUR.; No. 21291 EN/4; EC: Luxenburg, 2004; Volume 4, ISBN 9789289481830. [Google Scholar]
- Zayani, H.; Fouad, Y.; Michot, D.; Kassouk, Z.; Baghdadi, N.; Vaudour, E.; Lili-Chabaane, Z.; Walter, C. Using Machine-Learning Algorithms to Predict Soil Organic Carbon Content from Combined Remote Sensing Imagery and Laboratory Vis-NIR Spectral Datasets. Remote Sens. 2023, 15, 4264. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Jones, J.W.; Hatfield, J. The Agricultural Model Intercomparison and Improvement Project (AgMIP): Protocols and pilot studies. Agric. For. Meteorol. 2013, 170, 166–182. [Google Scholar] [CrossRef]
- Schlenker, W.; Roberts, M.J. Nonlinear effects of weather on corn yields. Rev. Agr. Econ. 2006, 28, 391–398. [Google Scholar] [CrossRef]
- Izaurralde, R.C.; Williams, J.R.; McGill, W.B.; Rosenberg, N.J.; Jakas, M.C.Q. Simulating soil C dynamics with EPIC: Model description and testing against long-term data. Ecol. Modell. 2006, 192, 362–384. [Google Scholar] [CrossRef]
- Causarano, H.J.; Doraiswamy, P.C.; McCarty, G.W.; Hatfield, J.L.; Milak, S.; Stern, A.J. EPIC Modeling of Soil Organic Carbon Sequestration in Croplands of Iowa; USDA-ARS/UNL Faculty: Washington, DC, USA, 2008; p. 1363. Available online: https://digitalcommons.unl.edu/usdaarsfacpub/1363 (accessed on 24 April 2024).
- Ermolieva, T.; Ermoliev, Y.; Havlik, P.; Lessa-Dersi-Augustynczik, A.; Kahil, T.; Balkovic, J.; Skalsky, R.; Folberth, C.; Knopov, P.S.; Wang, G. Connections between robust statistical estimation, robust decision making withtwo-stage stochastic optimization, and robust machine learning problems. Cybern. Syst. Anal. 2023, 59, 33–47. [Google Scholar] [CrossRef]
- Ermolieva, T.; Havlik, P.; Derci Augustynczik, A.L.; Boere, E.; Frank, S.; Kahil, T.; Wang, G.; Balkovič, J.; Skalský, R.; Folberth, C.; et al. A Novel Robust Meta-Model Framework for Predicting Crop Yield Probability Distributions Using Multisource Data. Cybern. Syst. Anal. 2023, 59, 844–858. [Google Scholar] [CrossRef]
- Liu, T.; Wang, L.; Feng, X.; Zhang, J.; Ma, T.; Wang, X.; Liu, Z. Comparing soil carbon loss through respiration and leaching under extreme precipitation events in arid and semiarid grasslands. Biogeosciences 2018, 15, 1627–1641. [Google Scholar] [CrossRef]
- Ermolieva, T.; Havlík, P.; Ermoliev, Y.; Mosnier, A.; Obersteiner, M.; Leclere, D.; Khabarov, N.; Valin, H.; Reuter, W. Integrated management of land use systems under systemic risks and security targets: A Stochastic Global Biosphere Management Model. J. Agric. Econ. 2016, 67, 584–601. [Google Scholar] [CrossRef]
- Ermolieva, T.; Havlik, P.; Frank, S.; Kahil, T.; Balkovic, J.; Skalsky, R.; Ermoliev, Y.; Knopov, P.S.; Borodina, O.M.; Gorbachuk, V.M. A Risk-Informed Decision-Making Framework for Climate Change Adaptation through Robust Land Use and Irrigation Planning. Sustainability 2022, 14, 1430. [Google Scholar] [CrossRef]
- FAO. Global Soil Partnership: RECSOIL, Recarbonization of Global Agricultural Soils; FAO: Rome, Italy, 2023; Available online: https://www.fao.org/global-soil-partnership/areas-of-work/recsoil/what-is-soc/en/ (accessed on 20 December 2023).
- Liptzin, D.; Norris, C.E.; Cappellazzi, C.B.; Bean, G.M.; Cope, M.; Greub, K.L.H.; Rieke, E.L.; Tracy, R.W.; Aberle, E.; Ashworth, A.; et al. An evaluation of carbon indicators of soil health in long-term agricultural experiments. Soil Biol. Biochem. 2022, 172, 108708. [Google Scholar] [CrossRef]
- European Commission. A Soil Deal for Europe; European Commission: Brussels, Belgium, 2021; Available online: https://research-and-innovation.ec.europa.eu/document/download/1517488e-767a-4f47-94a0-bd22197d18fa_en?filename=soil_mission_implementation_plan_final.pdf (accessed on 20 December 2023).
- Oldfield, E.E.; Bradford, M.A.; Wood, S.A. Global meta-analysis of the relationship between soil organic matter and crop yields. SOIL 2019, 5, 15–32. [Google Scholar] [CrossRef]
- Bruni, E.; Guenet, B.; Clivot, H.; Kaetterer, T.; Martin, M.; Virto, I.; Chenu, C. Defining quantitative targets for topsoil organic carbon stock increase in European croplands: Case studies with exogenous organic matter inputs. Front. Environ. Sci. 2020, 10, 824724. [Google Scholar] [CrossRef]
- Goidts, E.; van Wesemael, B. Regional Assessment of Soil Organic Carbon Changes under Agriculture in Southern Belgium (1955–2005). Geoderma 2007, 141, 341–354. [Google Scholar] [CrossRef]
- Meersmans, J.; Van Wesemael, B.; Goidts, E.; Van Molle, M.; De Baets, S.; De Ridder, F. Spatial Analysis of Soil Organic Carbon Evolution in Belgian Croplands and Grasslands, 1960-2006. Spat. Anal. Soil Org. Carbon Evol. 2011, 17, 466–479. [Google Scholar] [CrossRef]
- Smith, P.; Smith, J.U.; Powlson, D.S.; McGill, W.B.; Arah, J.R.M.; Chertov, O.G.; Coleman, K.; Franko, U.; Frolking, S.; Jenkinson, D.S.; et al. A comparison of the performance of nine soil organic matter models using datasets from seven long-term experiments. Geoderma 1997, 81, 153–225. [Google Scholar] [CrossRef]
- Guo, L.; Falloon, P.; Coleman, K.; Zhou, B.; Li, Y.; Lin, E.; Zhang, F. Application of the RothC model to the results of long-term experiments on typical upland soils in northern China. Soil Use Manag. 2007, 23, 63–70. [Google Scholar] [CrossRef]
- Gilhespy, S.L.; Anthony, S.; Cardenas, L.; Chadwick, D.; del Prado, A.; Li, C.; Misselbrook, T.; Rees, R.M.; Salas, W.; Sanz-Cobena, A.; et al. First 20 years of DNDC (DeNitrification DeComposition): Model evolution. Ecol. Model. 2014, 292, 51–62. [Google Scholar] [CrossRef]
- Li, C. Biogeochemical concepts and methodologies: Development of the DNDC model. Quat. Sci. 2001, 2, 89–99. [Google Scholar]
- Li, C.; Frolking, S.; Harriss, R. Modeling carbon biogeochemistry in agricultural soils. Glob. Biogeochem. Cycles 1994, 8, 237–254. [Google Scholar] [CrossRef]
- Parton, W.J.; Schimel, D.S.; Cole, C.V.; Ojima, D.S. Analysis of factors controlling soil organic matter levels in Great Plains grasslands. Soil Sci. Soc. Am. J. 1987, 51, 1173–1179. [Google Scholar] [CrossRef]
- Parton, W.J.; Scurlock, J.M.O.; Ojima, D.S.; Gilmanov, T.G.; Scholes, R.J.; Schimel, D.S.; Kirchner, T.; Menaut, J.-C.; Seastedt, T.; Garcia Moya, E.; et al. Observations and modelling of biomass and soil organic matter dynamics for the grassland biome worldwide. Glob. Biogeochem. Cycles 1993, 7, 785–809. [Google Scholar] [CrossRef]
- Müller, C.; Elliott, J.; Chryssanthacopoulos, J.; Arneth, A.; Balkovic, J.; Ciais, P.; Deryng, D.; Folberth, C.; Glotter, M.; Hoek, S.; et al. Global Gridded Crop Model evaluation: Benchmarking, skills, deficiencies and implications. Geosci. Model Dev. Discuss. (GMDD) 2016, 1–39. [Google Scholar] [CrossRef]
- Lembaid, I.; Moussadek, R.; Mrabet, R.; Bouhaouss, A. Soil organic carbon changes under alternative climatic scenarios and soil properties using DNDC model as a semi-arid Mediterranean environment. Climate 2022, 10, 23. [Google Scholar] [CrossRef]
- Kahil, M.T.; Dinar, A.; Albiac, J. Modeling water scarcity and droughts for policy adaptation to climate change in arid and semiarid regions. J. Hydrol. 2015, 522, 95–109. [Google Scholar] [CrossRef]
- Kahil, M.T.; Connor, J.D.; Albiac, J. Efficient water management policies for irrigation adaptation to climate change in Southern Europe. Ecol. Econ. 2015, 120, 226–233. [Google Scholar] [CrossRef]
- Schnecker, J.; Baldaszti, L.; Gündler, P.; Pleitner, M.; Sandén, T.; Simon, E.; Spiegel, F.; Spiegel, H.; Malo, C.U.; Zechmeister-Boltenstern, S.; et al. Seasonal dynamics of soil microbial growth, respiration, biomass, and carbon use efficiency in temperate soils. Geoderma 2023, 440, 116693. [Google Scholar] [CrossRef]
- Zheng, Q.; Hu, Y.; Zhang, S.; Noll, L.; Böckle, T.; Dietrich, M.; Herbold, C.W.; Eichorst, S.A.; Woebken, D.; Richter, A.; et al. Soil multifunctionality is affected by the soil environment and by microbial community composition and diversity. Soil Biol. Biochem. 2019, 136, 07521. [Google Scholar] [CrossRef] [PubMed]
- Pietikäinen, J.; Pettersson, M.; Bååth, E. Comparison of temperature effects on soil respiration and bacterial and fungal growth rates. FEMS Microbiol. Ecol. 2005, 52, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Burke, I.C.; Yonker, C.M.; Parton, W.J.; Cole, C.V.; Schimel, D.S.; Flach, K. Texture, Climate, and Cultivation Effects on Soil Organic Matter Content in U.S. Grassland Soils. Soil Sci. Soc. Am. J. 1989, 53, 800. [Google Scholar] [CrossRef]
- Haddad, A.N. Evaluating the Relationship between Soil Texture and Soil Organic Carbon across California Grasslands. Soil Clay Content Soil Carbon 2017. Available online: https://nature.berkeley.edu/classes/es196/projects/2017final/HaddadA_2017.pdf (accessed on 4 January 2024).
- Bengough, A.G.; Bransby, M.F.; Hans, J.; McKenna SJRoberts, T.J.; Valentine, T.A. Root responses to soil physical conditions; growth dynamics from field to cell. J. Exp. Bot. 2006, 57, 437–447. [Google Scholar] [CrossRef]
- Soldatova, E.; Krasilnikov, S.; Kuzyakov, Y. Soil organic matter turnover: Global implications from δ13C and δ15N signatures. Sci. Total Environ. 2023, 912, 169423. [Google Scholar] [CrossRef]
- Wang, C.; Kuzyakov, Y. Soil organic matter priming: The pH effects. Glob. Chang. Biol. 2023, 30, e17349. [Google Scholar] [CrossRef] [PubMed]
- Mahal, N.K.; Osterholz, W.R.; Miguez, F.E.; Poffenbarger, H.J.; Sawyer, J.E.; Olk, D.C.; Archontoulis, S.V.; Castellano, M.J. Nitrogen Fertilizer Suppresses Mineralization of Soil Organic Matter in Maize Agroecosystems. Front. Ecol. Evol. 2019, 7, 59. [Google Scholar] [CrossRef]
- Smit, M.J.; van Leeuwen, E.S.; Florax, R.J.G.M.; de Groot, H.L.F. Rural development funding and agricultural labour productivity: A spatial analysis of the European Union at the NUTS2 level. Ecol. Indic. 2015, 59, 6–18. [Google Scholar] [CrossRef]
- Scholtz, R.; Tarasovičová, Z.; Balkovič, J.; Schmid, E.; Fuchs, M.; Moltchanova, E.; Kindermann, G.; Scholtz, P. GEOBENE Global Database for Bio-Physical Modeling. GEOBENE Project 2008. Available online: https://geo-bene.project-archive.iiasa.ac.at/files/Deliverables/Geo-BeneGlbDb10(DataDescription).pdf (accessed on 1 June 2023).
- Werner, M. Shuttle Radar Topography Mission (SRTM), Mission overview. J. Telecom. 2001, 55, 75–79. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Lilly, A.; Nemes, A.; Le Bas, C. Development and use of a database of hydraulic properties of Europen soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
- Jones, R.J.A.; Hiederer, R.; Rusco, E.; Loveland, P.J.; Montanarella, L. The Map of Organic Carbon in Topsoils in Europe, Version 1.2, September 2003: Explanation of Special Publication Ispra 2004 No.72 (S.P.I.04.72); European Soil Bureau Research Report 2004, No.17, EUR 21209 EN, 26pp. and 1 map in ISO B1 format; Office for Official Publications of the European Communities: Luxembourg, 2003. [Google Scholar]
- IFA; IFD; IPI; PPI; FAO. Fertiliser Use by Crop; FAO: Rome, Italy, 2002. [Google Scholar]
- Wriedt, G.; van der Velde, M.; Aloe, A.; Bouraoui, F. A European irrigation map for spatially distributed agricultural modelling. Agric. Water Manag. 2009, 96, 771–789. [Google Scholar] [CrossRef]
- Rodríguez-Lado, L.; Martínez-Cortizas, A. Modelling and mapping organic carbon content of topsoils in an Atlantic area of southwestern Europe (Galicia, NW-Spain). Geoderma 2015, 245–246, 65–73. [Google Scholar] [CrossRef]
- Evans, C.D.; Monteith, D.T.; Cooper, D.M. Long-term increases in surface water dissolved organic carbon: Observations, possible causes and environmental impacts. Environ. Pollut. 2005, 137, 55–71. [Google Scholar] [CrossRef]
- Chen, Z.; Wei, X.; Ni, X.; Wu, F.; Liao, S. Changing presipitation effect on forest soil carbon dynamics is driven by different attributes between dry and wet areas. Geoderma 2023, 429, 116279. [Google Scholar] [CrossRef]
- Poeplau, C.; Bolinder, M.A.; Eriksson, J.O.; Lundblad, M.; Kätterer, T. Increasing organic carbon stocks in Swedish agricultural soils due to unexpected socio-economic drivers. Geophys. Res. Abstr. 2015, 17, EGU2015-9264. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ermolieva, T.; Havlik, P.; Lessa-Derci-Augustynczik, A.; Frank, S.; Balkovic, J.; Skalsky, R.; Deppermann, A.; Nakhavali, M.; Komendantova, N.; Kahil, T.; et al. Tracking the Dynamics and Uncertainties of Soil Organic Carbon in Agricultural Soils Based on a Novel Robust Meta-Model Framework Using Multisource Data. Sustainability 2024, 16, 6849. https://doi.org/10.3390/su16166849
Ermolieva T, Havlik P, Lessa-Derci-Augustynczik A, Frank S, Balkovic J, Skalsky R, Deppermann A, Nakhavali M, Komendantova N, Kahil T, et al. Tracking the Dynamics and Uncertainties of Soil Organic Carbon in Agricultural Soils Based on a Novel Robust Meta-Model Framework Using Multisource Data. Sustainability. 2024; 16(16):6849. https://doi.org/10.3390/su16166849
Chicago/Turabian StyleErmolieva, Tatiana, Petr Havlik, Andrey Lessa-Derci-Augustynczik, Stefan Frank, Juraj Balkovic, Rastislav Skalsky, Andre Deppermann, Mahdi (Andrè) Nakhavali, Nadejda Komendantova, Taher Kahil, and et al. 2024. "Tracking the Dynamics and Uncertainties of Soil Organic Carbon in Agricultural Soils Based on a Novel Robust Meta-Model Framework Using Multisource Data" Sustainability 16, no. 16: 6849. https://doi.org/10.3390/su16166849
APA StyleErmolieva, T., Havlik, P., Lessa-Derci-Augustynczik, A., Frank, S., Balkovic, J., Skalsky, R., Deppermann, A., Nakhavali, M., Komendantova, N., Kahil, T., Wang, G., Folberth, C., & Knopov, P. S. (2024). Tracking the Dynamics and Uncertainties of Soil Organic Carbon in Agricultural Soils Based on a Novel Robust Meta-Model Framework Using Multisource Data. Sustainability, 16(16), 6849. https://doi.org/10.3390/su16166849





_Nakhavali.png)




