Analysis of the Decoupling between Urban Economic Development and Transportation Carbon Emissions in China: Empirical Evidence from 284 Cities

Abstract

The proposal of China’s “double carbon target” means that China is trying to realize the decoupling between economic development and carbon emissions. Based on the dual perspectives of velocity decoupling and quantitative decoupling, this paper systematically analyzes the decoupling state between transportation carbon emissions and economic development in 284 Chinese cities from 2006 to 2020 by using the Tapio decoupling model and the environmental Kuznets curve model. The results show the following: (1) From the perspective of velocity decoupling, most China’s cities have initially realized the decoupling state of transportation carbon emissions and urban economic development, entering the stage of weak decoupling, but not yet into the stage of strong decoupling, which indicates the decoupling level still needs to be improved. In space, the regions with high decoupling levels show the spatial differentiation characteristics of more in the east and middle, and less in the west. (2) From the perspective of quantitative decoupling, the relationship between urban transportation carbon emissions and economic development presents an inverted U-shaped EKC curve in China, and all cities have basically not crossed the inflection point and not entered the absolute decoupling state, but are in the trend of evolving to the quantitative decoupling state. This conclusion also verifies the view that velocity decoupling is generally in the weak decoupling stage. (3) The quantitative decoupling analysis also shows that urban population density, urban road density and per capita private car ownership all can worsen transportation carbon emissions, while public transport efficiency is the key driving forces for industrial carbon emission reduction. This study will help policymakers and practitioners to better understand the decoupling relationship between urban economic development and transportation carbon emissions in China, so as to formulate a strategy that fits China’s characteristics to achieve the “double carbon target” for transportation sector.

1. Introduction

Climate change has become one of the greatest global challenges of the 21st century. Relevant studies show that greenhouse gas emissions caused by human activities are the main cause of global warming, and carbon dioxide is one of the main greenhouse gases [1]. Therefore, with the increasing prominence of global warming and climate change, reducing carbon emissions has become the common responsibility of governments and international organizations. As the world’s largest developing country, China’s carbon emission reduction work plays a crucial role in improving the grim situation of global climate change. In the past decade, China has formulated a series of policy measures to try to realize the decoupling of economic growth and carbon emissions [2]. Although it has achieved some results, it still faces severe challenges. In 2020, in order to accelerate the reduction in emissions from all sectors of society, the Chinese government has proposed a grand “dual carbon target”.

Obviously, the realization of this goal depends on the joint efforts of all walks of life, especially the key industry that affects the national travel, material transportation and circulation—the transportation sector. As a basic industry of the national economy, transportation has the characteristics of high energy consumption and high emissions, and has even become the third emission source after power heating and industrial buildings. Due to the acceleration of urbanization, the improvement of residents’ living standards and the diversification of travel modes, the control of transportation carbon emissions would become particularly difficult [3,4]. In addition, the current low-carbon level in China’s transportation sector is still generally low, and due to large differences in economic development, technical level, energy structure, ecological efficiency and other aspects, the decoupling level of urban transportation carbon emissions and economic development may be uneven, which seriously restricts the orderly development of transportation carbon emission reduction work. In this context, how to accelerate the decoupling goal of the urban transportation sector has become a key topic that the society and the country pay extensive attention to and need to solve as soon as possible.

In fact, the topic of decoupling has been widely used to analyze the relationship between environmental quality and economic growth at the national, provincial and municipal levels [5,6,7]. Decoupling analysis is helpful to explore the relationship between economic growth and carbon emissions, and provide practical solutions for realizing low-carbon development. In the field of transportation, from the perspective of research methods, the relevant research mainly includes two categories [8]:

(1)

Using the Environment Kuznets Curve (EKC) model, the fluctuation relationship between transportation carbon emissions with economic growth is studied to verifying the existence of EKC theory. For example, based on data in the period of 1971–2011, Alshebry et al. [9] used Autoregressive Distributed Lag and the Granger causality test to verify the EKC hypothesis of transportation CO₂ and economic growth in Saudi Arabia, which found that there is no inverse “U” type nonlinear relationship between them. Kharbach et al. [10] analyzed the relationship between road transportation CO₂ and economic growth in Morocco, confirming the existence of the EKC curve. Amin et al. [11] analyzed the EKC model and found that renewable energy, economic growth and urbanization have a one-way causal relationship with the carbon emissions of the transportation sector in Europe. On the other hand, based on data from 30 provinces in China, Guo et al. [12] confirmed that there is an inverted U-shaped EKC curve relationship between provincial economic growth and transportation carbon emissions. In addition, some scholars also combined the EKC model with other methods to predict the carbon emissions of the transportation sector. For example, Huang et al. [13] proposed a nonlinear multivariate gray prediction model based on EKC in view of the realistic characteristics of incomplete statistics of carbon emissions data of the transportation sector, considering factors such as economy, population and energy.

(2)

The relationship between transportation carbon emissions and economic growth was discussed with the help of decoupling models, including the Tapio decoupling model, Kaya identity and log-mean variance index (LMDI) decomposition model. Jiang et al. [14] combined the decomposition technology with decoupling analysis and decomposed the traffic decoupling index into five different aspects to analyze the key driving factors of the decoupling of CO₂ emissions related to different transportation modes and transportation turnover. Liu et al. [8] adopted the Tapio decoupling model and LMDI decomposition model to conduct decoupling research on energy-related carbon emissions for transportation and gross domestic product (GDP) from the national and provincial levels. Similar to the study by Liu et al. [8], Zhang et al. [15] explored the decoupling relationship between provincial transportation carbon emissions and economic development in the Yellow River Basin, and believed that there were significant differences in the influencing factors between the “upstream region” and the “downstream region”. Based on the Tapio decoupling model, Foster et al. [16] discussed the differences between the decoupling state of transport carbon emissions and economic growth in low-, middle- and high-income countries. On the whole, it is generally believed that with the technological progress, the adjustment of energy structure and the guidance of government policies, the carbon emissions of the transportation sector are expected to achieve decoupling from economic growth [17]. In addition, some scholars analyze the decoupling relationship between negative externalities of cargo transport and economic growth from the perspective of sustainable development of the transportation system [18]. For instance, Loo and Banister [19] explored the potential and reality of transport decoupling in 15 major countries since 1990 by measuring changes in all three elements of sustainable development (economic, environmental and social).

On the whole, many scholars have investigated the decoupling state and its internal attribution of economic growth and transportation carbon emissions in China or different provinces. However, on the one hand, it is generally ignored to carry out more fine-scale research from the perspective of the city. As the main battlefield of economic development [4], cities are important places for carbon emissions, and the decoupling between economy and carbon emissions often shows significant geographical differences [20], especially for China, a large country with a vast territory, where the differences may be more significant. This means that there may be obvious spatial differentiation between urban economic development and transportation carbon emissions. At the same time, cities are the underlying administrative units of various policies in China, and the realization of transportation carbon emission reduction policies and targets needs to be finally implemented by each city. Therefore, exploring the decoupling between economic development and transportation carbon emissions from the perspective of cities is necessary, which plays important roles in formulating transportation emission reduction policies suitable for each city.

On the other hand, few scholars have integrated EKC and decoupling models into a unified framework for analysis, which can actually reflect the decoupling trend between urban economic development and transportation carbon emissions from different perspectives. The former reflects the decoupling in terms of total volume, also known as “quantitative decoupling” or “absolute decoupling”. By using EKC, Wang and Kim [21] explored whether there is absolute decoupling between income and carbon emissions, using the United States as a research sample. The latter reflects the decoupling of the degree of growth, which can be considered as a kind of “velocity decoupling”, and the two methods also can verify each other. That is to say, the research included those in the unified framework which can reflect the decoupling of urban economic development and transportation carbon emissions more systematically. In addition, previous studies generally used transportation carbon emissions calculated based on China’s energy consumption statistics, which did not include private car data, which may cause the conclusions obtained to be inconsistent with the facts.

In this regard, this study adopts a set of comprehensive transportation carbon emissions data, integrates a Tapio decoupling model and EKC model into a unified framework, and then uses 284 of China’s cities as research objects to provide a more detailed scale study on the decoupling relationship between urban transportation carbon emissions and economic development. Compared with previous studies, the innovations of this paper are as follows: First, different from previous studies that mainly focus on the national, provincial or single city of China, this paper concentrates on 284 cities in China and provides quantitative analysis on a more detailed scale. Second, this paper systematically discusses the decoupling relationship between urban transportation carbon emissions and economic development from the dual perspectives of “velocity decoupling” and “quantitative decoupling”, which is conducive to expand the content and framework of previous research on transportation carbon emissions. We hope that this study can provide references and suggestions for government departments to realize the decoupling of economic and transportation carbon emissions at the city level.

2. Research Methods and Data Sources

2.1. Velocity Decoupling: Tapio Decoupling Model

The Tapio decoupling model developed by Tapio [22] is usually used to analyze the internal action mechanism and future development trend between economic growth and carbon emission [23], which actually reflects the relationship between economic growth and carbon emission growth, showing a kind of “velocity decoupling”. Compared with the OECD decoupling factor model and IGT model based on the IPAT equation, the Tapio decoupling model has the advantages of lower sensitivity and higher stability [24]. Therefore, this paper selects the Tapio decoupling model to empirically analyze the degree of velocity decoupling between transportation carbon emissions and economic development in 284 cities in China. The expression is as follows:

$$D{E}_{i,t}={\displaystyle \frac{\left(C{E}_{i,t}-C{E}_{i,t-1}\right)/C{E}_{i,t-1}}{\left(GD{P}_{i,t}-GD{P}_{i,t-1}\right)/GD{P}_{i,t-1}}}={\displaystyle \frac{\Delta C{E}_{i,t}/C{E}_{i,t-1}}{\Delta GD{P}_{i,t}/GD{P}_{i,t-1}}}$$

(1)

where i and t denote the city and time, respectively; DE is the decoupling elasticity index between urban transportation carbon emission and economic development, and CE is the transportation carbon emission; GDP denotes the measure index of economic development level of city.

Furthermore, to comprehensively clarify the decoupling between urban transportation carbon emissions and economic development in China, following the ideas of Lantz and Lantz and Feng [25] and Dogan and Turkekul [26], this paper also constructs and measures the decoupling index (PDE) between per capita transportation carbon emissions (PCE) and per capita GDP (PGDP), and its specific formula is as follows:

$$PD{E}_{i,t}={\displaystyle \frac{\left(PC{E}_{i,t}-PC{E}_{i,t-1}\right)/PC{E}_{i,t-1}}{\left(PGD{P}_{i,t}-PGD{P}_{i,t-1}\right)/PGD{P}_{i,t-1}}}={\displaystyle \frac{\Delta PC{E}_{i,t}/PC{E}_{i,t-1}}{\Delta PGD{P}_{i,t}/PGD{P}_{i,t-1}}}$$

(2)

In fact, Tapio [22] not only proposed the above index, but also, based on the research of Vehmas et al. [27], clearly defined the concept of decoupling, the difference of decoupling, coupling and negative decoupling combined with the relationship between environment and economy (i.e., EKC theory), and then broke them into eight decoupling stages (see

Table 1. Decoupling stage of transportation carbon emission and economic development.

Decoupling Stage		$\mathit{D}\mathit{E}$$\mathbf{/}\mathit{P}\mathit{D}\mathit{E}$	$\mathbf{\Delta }\mathit{C}\mathit{E}\mathbf{/}\mathbf{\Delta }\mathit{P}\mathit{C}\mathit{E}$	$\mathbf{\Delta }\mathit{G}\mathit{D}\mathit{P}\mathbf{/}\mathbf{\Delta }\mathit{P}\mathit{G}\mathit{D}\mathit{P}$
Negative decoupling	Expansion negative decoupling	≥1.2	+	+
	Weak negative decoupling	(0, 0.8)	−	−
	Strong negative decoupling	(−∞, 0)	+	−
Decoupling	Strong decoupling	(−∞, 0)	−	+
	Weak decoupling	(0, 0.8)	+	+
	Recessive decoupling	≥1.2	−	−
Coupling	Expansion coupling	(0.8, 1.2)	+	+
	Recessive coupling	(0.8, 1.2)	+	+

), which has been widely adopted in numerous subsequent papers, such as Liu and Feng [8], Wang et al. [28], Chen et al. [29] and Hossain and Chen [30]. Referring to those research papers, this paper also divides the decoupling into eight stages as shown in Table 1 for the convenience of analysis.

2.2. Quantitative Decoupling: EKC Model

Since Panayotou [31] and Grossman and Krueger [32] proposed the EKC theory, that is, the inverted U-shaped relationship between environmental quality and per capita income, many scholars have conducted empirical analysis to verify this relationship by using an EKC model (a quadratic model). In fact, the model determines whether there is quantitative decoupling between economic development and carbon emissions through the relationship between the total amount, and whether it has reached the stage of absolute decoupling at present. When the economic development passes the inflection point of an inverted U-shaped curve, carbon emissions show a downward trend with the economy growth, reflecting in the quantitative decoupling relationship or absolute decoupling.

Therefore, this paper adopts the EKC model to discuss the quantitative decoupling between urban economic development and transportation carbon emissions. In order to eliminate the influence of heteroscedasticity and multicollinearity as much as possible, this paper conducts logarithmic processing on all variables, and the regression coefficient of the independent variable after processing can be regarded as the elastic coefficient of the dependent variable, which has good economic and application significance. The specific model, denoted as model (1), is constructed is as follows:

$$LNC{E}_{it}={\alpha }_0+{\alpha }_{1}LNGD{P}_{it}+{\alpha }_2{\left(LNGD{P}_{it}\right)}^2+{\displaystyle \sum {\beta }_{i}LN{X}_{it}}+{\epsilon }_{it}$$

(3)

where ${\alpha }_0$ is the constant term; ${\alpha }_1$ and ${\alpha }_2$ are the estimated coefficients of the first and second terms of GDP, respectively; $X_{it}$ represents control variables, that is, other factors affecting transportation carbon emissions; ${\epsilon }_{it}$ represents a random error term. Similar to velocity decoupling, this paper also constructs a quantitative decoupling EKC model between per capita transportation carbon emissions and per capita GDP, denoted as model (2), as follows:

$$LNPC{E}_{it}={\gamma }_0+{\gamma }_{1}LNPGD{P}_{it}+{\gamma }_2{\left(LNPGD{P}_{it}\right)}^2+{\displaystyle \sum {\lambda }_i{X}_{it}}+{\epsilon }_{it}$$

(4)

According to the value range of estimate coefficient, the relationship between urban traffic carbon emissions and economic development can be generally divided into the following five categories (using model (1) as example):

(1) When ${\alpha }_1={\alpha }_2=0$, it indicates that there is no long-term change relationship between urban transportation carbon emissions and economic development; (2) when ${\alpha }_1>0$ and ${\alpha }_2=0$, it indicates that urban transportation carbon emissions and urban economy show a monotonously increasing trend, and the EKC curve is reflected as a “J” shape; (3) if ${\alpha }_1<0$ and ${\alpha }_2=0$, the EKC curve is embodied as the inverted “J” type; (4) when ${\alpha }_1<0$ and ${\alpha }_2>0$, the carbon emission of urban transportation presents a change trend of “first decreasing and then rising”, with the development of urban economy, and the EKC curve is reflected as a “U” shape; (5) when ${\alpha }_1>0$ and ${\alpha }_2<0$, urban transportation carbon emission presents a change trend of “first rising and then decreasing” with urban economic development, and the EKC curve is reflected as an inverted “U” shape.

3. Indicator Selection and Data Source

Referring to previous studies [12,17], CO₂ emission for the transportation industry is adopted to reflect the transportation carbon emissions. Economic development is represented by the GDP of a city. At the same time, in order to provide the accuracy of the estimation results, four control variables are selected into model (1) and model (2) as follows:

(1)

Urban population density (PDN). Many previous studies have confirmed that population density is a crucial factor affecting transportation carbon emissions [33,34]. The increase in urban population density can aggravate the demand for transportation, and then worsen the carbon emissions, showing an adverse impact. The ratio of population to urban area is adopted to measure PDN in this article.

(2)

Urban road density (RDN), which is evaluated by the ratio of urban road area to the population following the research of Aljoufie [35]. RDN not only reflects the urban form but also characterizes the development level of urban transport infrastructure. Some scholars believe that it has a positive impact on transportation carbon emissions [36], while some hold the opposite view [34]. The authors argue that RND will lead to greater transportation demand and further aggravate transportation carbon emissions in China, that is, a positive relationship is predicted.

(3)

Public transport operating efficiency (PTE), reflecting the operation quality of urban public transport, which is evaluated by the average passenger volume of public transport vehicles per unit. Public transport plays an important role in urban transportation. Since new energy vehicles have been promoted at a very early age in China, as an efficient and environmentally friendly mode of transportation, their operation quality certainly has a significant impact on urban transportation carbon emissions.

(4)

Per capita private car ownership (PRC). One of the main contributors of transport carbon emissions is private cars, since most of them use gasoline or diesel, which can produce a lot of CO₂. Therefore, the more PRC, the more transport carbon emissions.

In addition, due to the lack of data of some prefecture-level cities, league and autonomous prefectures, this paper finally selects 284 prefecture-level cities in China from 2006 to 2020 as research samples to explore the decoupling relationship between urban economic development and transportation carbon emissions. The specific cities are shown in Figure 1. Among them, the transportation carbon emission data come from the Multi-resolution Emission Inventory model for climate and air pollution research of the MEIC team of Tsinghua University (http://meicmodel.org.cn/, accessed on 12 April 2024). This database is a comprehensive and detailed database covering the carbon emission of all means of transportation, including private cars and operational vehicles. The remaining data are derived from the China City Statistical Yearbook over the years. In order to eliminate the influence of price factors, the GDP is uniformly converted into the GDP of constant price based on the year 2000. In addition, for some missing data, the interpolation method is used to complete the samples.

4. Results and Discussion

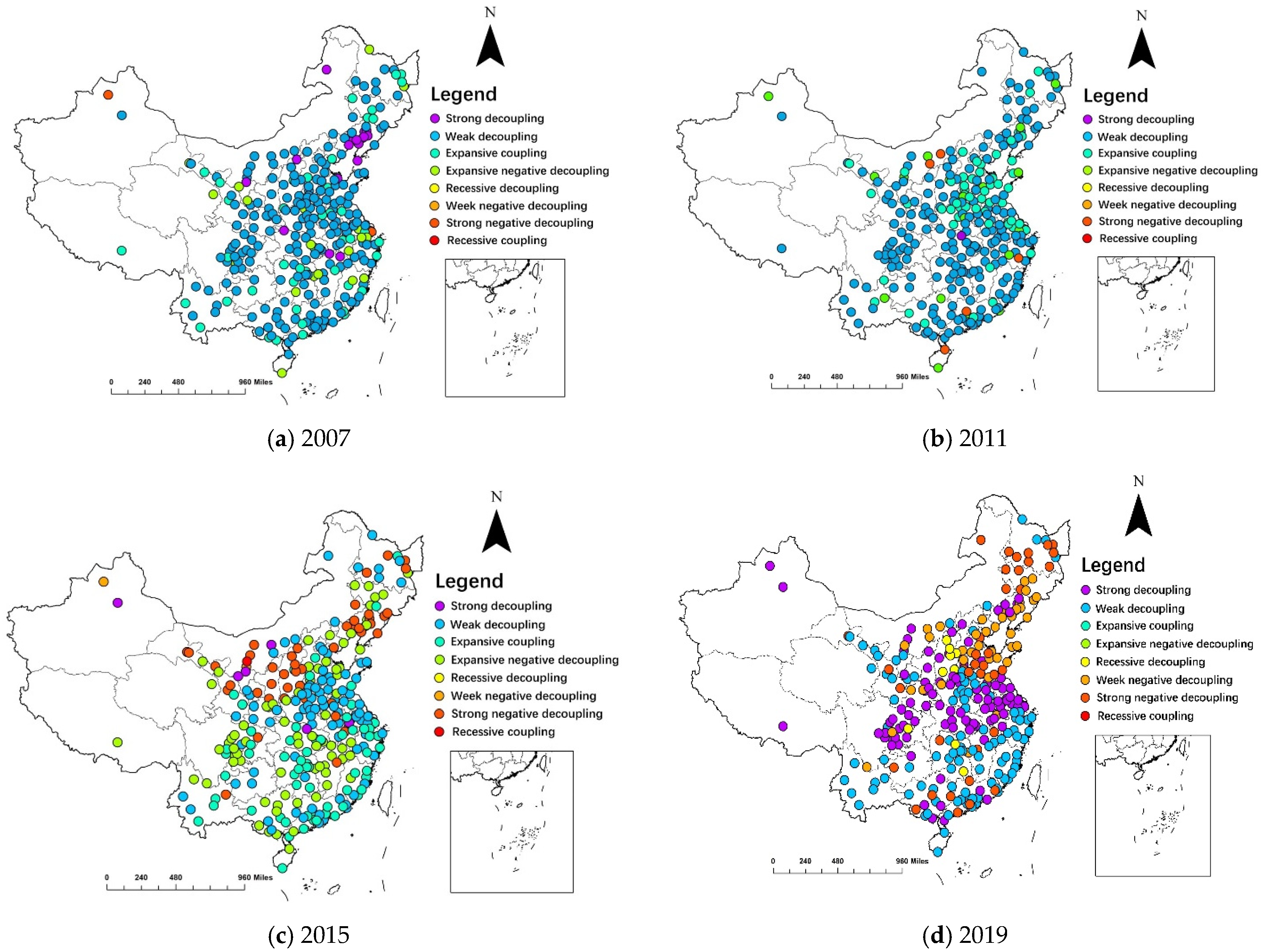
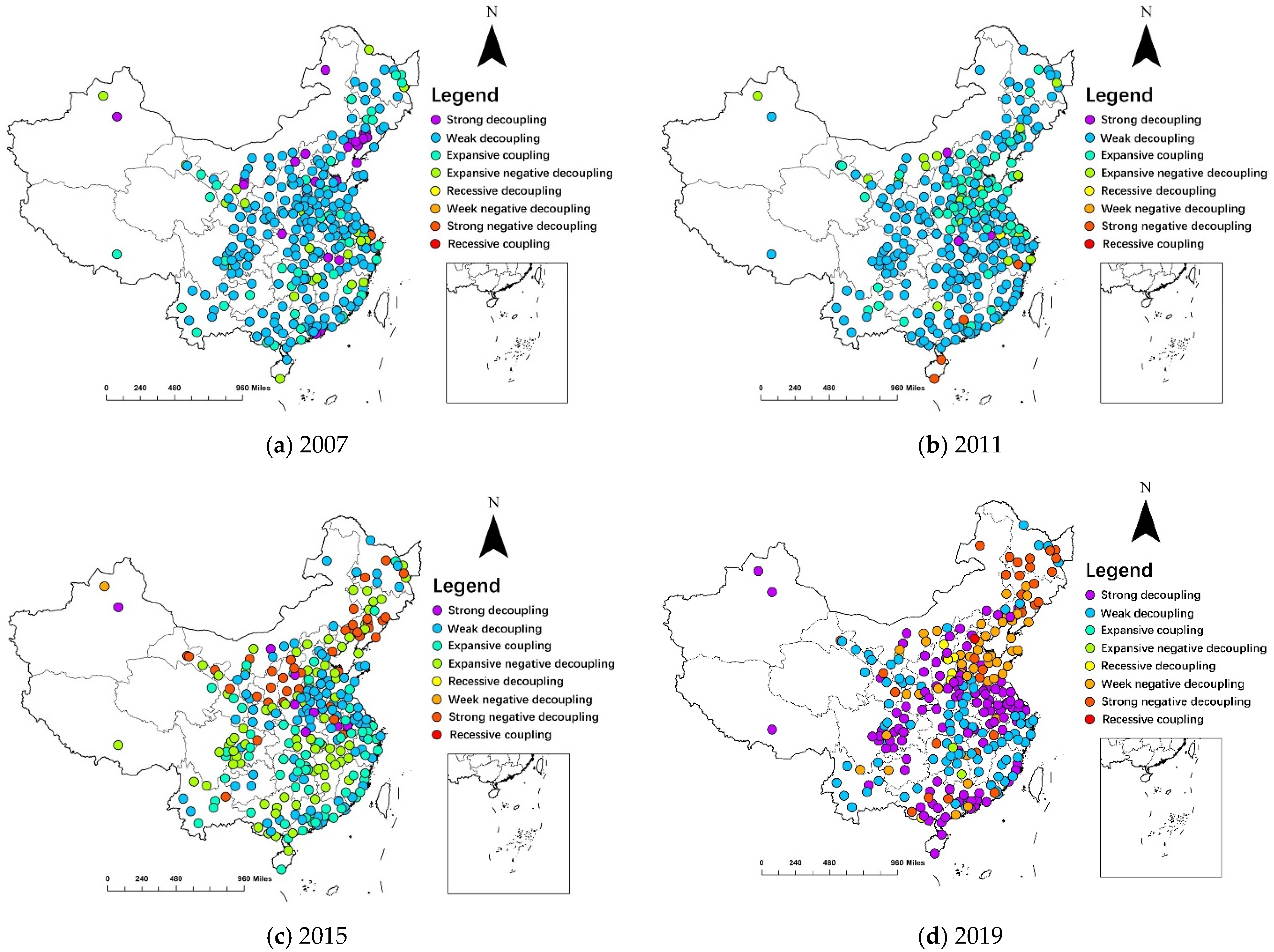
4.1. Velocity Decoupling State Analysis

4.1.1. Decoupling State Analysis in Time Dimension

In order to more clearly show the decoupling state between transportation carbon emissions and GDP, as well as that between per capita transport carbon emissions and per capita GDP, this paper draws the decoupling state space evolution charts for 2007, 2011, 2015 and 2019 using ARCGIS, as shown in Figure 1 and Figure 2. Among them, it should be noted that ① Since the Tapio index is calculated based on the growth of carbon emission and GDP, as shown in Equation (1), we can only obtain the velocity decoupling index from 2007 to 2020, while the Tapio index in 2006 is missing. Therefore, this paper shows the decoupling state in 2007, rather than that in 2006. ② Due to the impact of epidemic policies, most urban transportation is restricted, which means that the obtained data are not representative, so that 2019 is chosen as the sample year for analysis rather than 2020.

Figure 2 reflects the decoupling between urban transportation carbon emissions and GDP. Combining it with the measurement results, it can be found that, except for 2015, the number of cities in the weak and strong decoupling stage between transportation carbon emissions and GDP in each year is basically stable at about 200. Among them, 217, 202 and 198 cities reached the weak or strong decoupling stages in 2007, 2011 and 2019, respectively, where the proportion of cities in the weak decoupling stage is generally larger, accounting for 70.97% of the total number of cities in the weak decoupling stage and the strong decoupling stage from 2007 to 2019. In addition, in 2020, affected by the epidemic policy, most cities had strict travel control, and transportation demand is significantly reduced, resulting in a large number of cities temporarily jumping to the stage of strong decoupling. This indicates that, in most Chinese cities, although the worsening speed of transportation carbon emissions is significantly lower than the economic growth rate, showing a good development trend and a good decoupling trend, economy development will still lead to the deterioration of transportation carbon emissions. Therefore, more efforts should be made to promote the absolute decoupling of the two.

Figure 3 is the decoupling between per capita urban transportation carbon emissions and per capita GDP. It can be seen that except for 2015, the number of cities in the weak and strong decoupling stages between per capita transportation carbon emissions and per capita GDP in each year is also about 200. Among them, there are 218, 202 and 198 in 2007, 2011 and 2019, accounting for 76.76%, 71.13% and 69.72% of the total number of cities, respectively. Meanwhile, from 2007 to 2017, the above cities mainly concentrated in the weak decoupling stage, on average accounting for 74.51% of the total number of cities in the weak decoupling and strong decoupling stage. In 2018, 2019 and 2020, the number of cities in the strong decoupling stage evolved to 245, 114 and 191, respectively, accounting for 75.86% on average among three years. This indicates that, from a per capita perspective, the decoupling elasticity of economic and transportation carbon emissions in most Chinese cities begin to change from positive to negative, that is, with the growth of per capita economic development level, per capita transportation carbon emissions show a downward trend.

In addition, China’s 284 cities can be divided into three categories according to the change in the decoupling state between urban transportation carbon emissions and economic development:

(1)

Decoupling stable cities, whose decoupling characteristics are as follows: During the study period, although there are a few years of transient expansion coupling and even the expansion negative decoupling phenomenon, the time of strong or weak decoupling state of such cities is at least 10 years, and the decoupling state remains stable on the whole. In terms of spatial distribution, these cities are relatively dispersed. In terms of a weak or strong decoupling stage, there are 32 cities in the eastern region, 46 cities in the central region, and 43 cities in the western region. In terms of the decoupling between per capita transportation carbon emissions and per capita GDP, it is mainly concentrated in 23 provinces such as Beijing, Anhui and Fujian, including 30 cities in the eastern region, 47 cities in the central region and 44 cities in the western region for weak decoupling as well as strong decoupling.

(2)

Decoupling relatively stable cities: During the study period, some years show expansion coupling and even expansion negative decoupling, but over the past 7 years and less than 10 years, strong or weak decoupling states are shown, the decoupling state is relatively stable, and has the potential to further improve. According to the decoupling state of urban transportation carbon emissions and GDP, such cities are distributed in 17 provinces, including Guangdong, Jiangsu, Shanghai, Yunnan and Zhejiang. Among them are 66 cities in the eastern region, 50 cities in the central region and 40 cities in the western region, showing the characteristics of decreasing in number in the eastern central region and the western region. According to the decoupling between per capita transportation carbon emissions and per capita GDP, the spatial distribution of these cities also showed a descending gradient trend in the east, central and western regions. Among them are 69 cities in the eastern region, 49 cities in the central region and 39 cities in the western region.

(3)

Decoupling unstable cities: During the research period, the years for the cities to achieve strong decoupling and weak decoupling states are less than 7 years, and most years show expansion coupling and even expansion negative decoupling, and the decoupling state is relatively unstable. According to the decoupling index of transportation carbon emission and GDP and per capita transportation carbon emission and per capita GDP, these cities are mainly located in Heilongjiang, Hebei, Gansu and Jilin provinces, among which there is one city in the eastern region, four cities in the central region and one city in the western region, which are generally located in the central region.

In general, from 2006 to 2020, the number of decoupled relatively stable state cities in China is the largest, followed by decoupled stable state cities, and decoupled unstable state cities are the least. It is worth noting that although most cities are in a relatively stable state of decoupling in terms of stage, in recent years, with the implementation of relevant emission reduction policies, the coupling state of economy and transportation carbon emissions has shown a gradually improving trend, and the development of green transportation is on the rise, but its sustainable level still needs to be further improved.

4.1.2. Decoupling State Analysis in Spatial Dimension

Table 2. Quantitative distribution of decoupling state between urban transportation carbon emissions and GDP.

	Weak Decoupling	Expansion Coupling	Expansion Negative Decoupling	Strong Decoupling
China	273	2	3	6
Eastern China	99	0	0	1
Middle China	94	2	2	2
Western China	80	0	1	3

and

Table 3. Quantitative distribution of decoupling state between urban per capita transportation carbon emissions and per capita GDP.

	Weak Decoupling	Expansion Coupling	Expansion Negative Decoupling	Strong Decoupling
China	259	3	3	19
Eastern China	91	0	0	9
Middle China	91	3	2	4
Western China	77	0	1	6

show the quantitative distribution of decoupling between urban transportation carbon emissions and GDP, as well as per capita transportation carbon emissions and per capita GDP in different regions (China, eastern, middle and western China) from 2006 to 2020, respectively. As can be seen from Table 2, the decoupling state between carbon emissions from urban transportation and GDP from 2006 to 2020 includes four types in China: weak decoupling, expansion coupling, expansion negative decoupling and strong decoupling, where weak decoupling is the dominant state. Specifically, the number of cities in the weak decoupling state is 99 in the east, 94 in the central region and 80 in the west, accounting for 99%, 94% and 95.2% of the total number of cities in the three regions in turn.

According to Table 3, the decoupling state between urban per capita transportation carbon emissions and per capita GDP from 2006 to 2020 also includes the same four types as mentioned above, where the weak decoupling state is also dominant, among which 91 cities are in the east, 91 are in the central region and 77 are in the west. It successively accounted for 91%, 91% and 91.7% of the total number of the three major regional cities. This indicates that most cities in China have initially realized the decoupling of transportation carbon emissions and economic development during the study period. However, from the perspective of the level of decoupling, the state of strong decoupling has not yet been reached, and the degree of decoupling is still low, meaning that there is still a certain distance from the transportation sector to achieve a higher level of green and low-carbon development. Therefore, we should further strengthen the planning and construction of low-carbon transportation infrastructure, pay attention to improving the technical level, widely popularize the application of new energy transportation and always maintain the sustainable development path of carbon reduction and emission reduction to avoid the phenomenon of a “double hook”. In addition, from the perspective of space, the regions with a high level of decoupling still show a greater trend in the eastern and central regions, and less so in the western regions.

4.2. Quantitative Decoupling State Analysis

In order to effectively identify the quantitative decoupling state between transportation carbon emissions and economic development by using the EKC model as shown in model (1) and model (2), the Pesaran cross-sectional dependence (CD) test proposed by Pesaran [37,38] is conducted in the first step, aiming to identify the existence of cross-section dependence, which may lead to biased estimation results [39] and thus affect the accuracy of research conclusions.

Table 4. Cross-sectional dependency test.

	CD-Test	p-Value	Mean $\mathit{\rho }$	Mean Abs ($\mathit{\rho }$)
LNCE	673.3090	0.0000	0.8700	0.8800
LNPCE	598.4370	0.0000	0.7700	0.8000
LNGDP	738.7990	0.0000	0.9500	0.9500
LNGDP2	737.0730	0.0000	0.9500	0.9500
LNPGDP	725.8420	0.0000	0.9300	0.9400
LNPGDP2	578.1600	0.0000	0.7400	0.8200
LNPDN	487.2650	0.0000	0.6300	0.6900
LNRDN	495.3950	0.0000	0.6400	0.6900
LNPTE	264.7170	0.0000	0.3400	0.4500
LNPRC	700.4590	0.0000	0.9000	0.9300

displays the results of the CD test, where all the CD test statistics pass the test at the 1% significance level, confirming the existence of the cross-section dependence.

In the next step, the panel unit root test is carried out to avoid the spurious regression problem caused by non-stationary data. However, due to the existence of cross-section dependence, traditional unit root tests, such as the augmented Dickey Fuller (ADF) and Phillips–Perron (PP) tests, are not applicable, so this paper employs the cross-sectional ADF (CADF) test developed by Pesaran [40] to verify the stationarity of every variable, with the results shown in

Table 5. Cross-sectionally ADF (CADF) test.

	Level		First Difference
	Constant	Constant and Trend	Constant	Constant and Trend
LNCE	−3.0750 ***	−2.9030 ***	−3.1360 ***	−3.0970 ***
LNPCE	−2.7690 ***	−2.7390 ***	−2.9920 ***	−2.9020 ***
LNGDP	−1.9610 ***	−2.6250 ***	−2.6990 ***	−2.9720 ***
LNGDP2	−1.9100 ***	−2.5860 ***	−2.6680 ***	−2.8100 ***
LNPGDP	−1.7910	−2.2420	−2.3150 ***	−2.5400 ***
LNPGDP2	−1.5800	−1.7080	−2.8790 ***	−3.3050 ***
LNPDN	−2.1940 ***	−2.4130 ***	−2.5470 ***	−2.7890 ***
LNRDN	−1.7740	−1.9990	−2.1960 ***	−2.3510 *
LNPTE	−2.3960 ***	−2.6180 ***	−2.7860 ***	−2.5980 ***
LNPRC	−2.4820 ***	−2.5340 ***	−2.9270 ***	−2.6890 ***

Note: *** and * represent significance levels of 1% and 10%, respectively.

. It shows that although most variables are stationary, a small number of variables, such as LNPGDP, LNGDP² and LNRDN, have unit roots. In contrast, the first differences I(1) of all variables are stationary, implying that long-run relationships as well as cointegration tests can be suitably carried out.

Furthermore, three panel cointegration test methods proposed by Kao [41], Pedroni [42,43] and Westerlund [44] are employed, where the cross-sectional dependence is also subtracted, with the results displayed in

Table 6. Panel cointegration tests.

Test		Model (1)	Model (2)
		Statistic	Statistic
Kao (1999) [41]	Modified Dickey–Fuller t	−11.0674 ***	−8.4141 ***
	Dickey–Fuller t	−22.9048 ***	−18.9287 ***
	Augmented Dickey–Fuller t	−13.1649 ***	−11.0119 ***
	Unadjusted modified Dickey–Fuller t	−13.7588 ***	−13.9590 ***
Pedroni (1999, 2004) [42,43]	Unadjusted Dickey–Fuller t	−23.9335 ***	−21.3800 ***
	Modified Phillips–Perron t	25.5316 ***	25.6745 ***
	Phillips–Perron t	−34.0027 ***	−33.1854 ***
	Augmented Dickey–Fuller t	−32.0745 ***	−30.7439 ***
Westerlund (2005) [44]	Variance ratio	6.8264 ***	7.3494 ***

Note: The latter two tests also take into account the time trend. *** represents significance levels of 1%.

. Whether for model (1) or model (2), the statistics have passed the significance test of 1%, indicating that there is a long-term relationship between urban transportation carbon emissions and economic development in China, and it is appropriate to study the quantitative decoupling of the two. In addition, this article also conducts the VIF test, Wald test and Wooldridge test. Among them, the first test shows that the VIF of each variable is less than 10, indicating that there is no serious multicollinearity in the model, while the latter two tests reject the null hypothesis, suggesting that the model has intra-group and inter-group heteroscedasticity.

In view of the above test results, this paper adopts the Ordinary Least Squares method with Driscoll–Kraay standard errors (DKOLS) to estimate model (1) and model (2), which can solve the problems of cross-sectional correlation, heteroscedasticity and autocorrelation according to Hoechle et al. [45] and is widely employed in the current literature, such as Pablo-Romero et al. [46].

Table 7. The estimate results of model (1) and model (2).

	LNCE [Model (1)]		LNPCE [Model (2)]
	(1)	(2)	(3)	(4)
	DKOLS RE	DKOLS FE	DKOLS RE	DKOLS FE
LNGDP	0.2860 **	0.4088 ***
	(0.1156)	(0.0785)
LNGDP2	0.0340 ***	−0.0174 ***
	(0.0077)	(0.0062)
LNPGDP			0.2791 ***	0.3187 ***
			(0.0305)	(0.0240)
LNPGDP2			−0.0181 ***	−0.0508 ***
			(0.0052)	(0.0047)
LNPDN	−0.2593 ***	0.0366 **	0.0172	0.0597 ***
	(0.0314)	(0.0175)	(0.0158)	(0.0125)
LNRDN	0.0371	0.0181 ***	0.1353 ***	0.0376 ***
	(0.0246)	(0.0050)	(0.0171)	(0.0071)
LNPTE	−0.0273 ***	−0.0153 ***	−0.0421 ***	−0.0015
	(0.0094)	(0.0045)	(0.0082)	(0.0056)
LNPRC	0.1942 ***	0.0700 ***	0.3315 ***	0.0774 ***
	(0.0170)	(0.0114)	(0.0137)	(0.0151)
Constant	11.1977 ***	12.4322 ***	9.4025 ***	8.4023 ***
	(0.3173)	(0.2112)	(0.0677)	(0.0702)
F test	5383.4500 ***	64.4400 ***	2469.4300 ***	157.1200 ***
Hausman test	27.3600 ***		3335.1500 ***
R-squared	0.7693	0.8429	0.6686	0.7979
Observations	4260	4260	4260	4260

Note: The corresponding standard error is in parentheses. *** and ** represent significance levels of 1% and 5%, respectively.

shows the estimate results of DKOLS with the random and fixed effect, where model (1) reflects the relationship between total transportation carbon emissions and GDP and model (2) represents the relationship between per capita transportation carbon emissions and per capita GDP. The Hausman tests all significantly reject the null hypothesis, indicating that the fixed effect is more suitable than the random effect; therefore, further analysis will be conducted according to the results in columns (2) and (4) of Table 7.

According to column (2) and (4) of Table 7, it can be found that the coefficients of LNGDP and LNGDP² are 0.4088 and −0.0174, respectively, and the coefficients of LNPGDP and LNPGDP² are 0.3187 and −0.0508, respectively, which both pass the test at the significance level of 1%. This implies that the relationship between transportation carbon emissions and GDP, as well as per capita transport carbon emissions and per capita GDP, both show an inverted U-shaped curve, which indicates that China’s transportation carbon emissions and economic development have an obvious quantitative decoupling state in the long run. That is, when the level of economic development exceeds a certain inflection point, at this time, with the improvement in economic development level, the total carbon emission of urban transportation and its per capita carbon emission will show a downward trend, showing a decoupling trend, that is, quantitative decoupling.

Referring to Pablo-Romero et al. [46] and Frodyma et al. [47], the turning point of the inverted U-shaped curve can be measured by $\exp (-{\alpha }_1/2{\alpha }_2)$, with the corresponding points being 126,389.8710 million yuan and 23.0303 ten thousand yuan per person for GDP and PGDP, respectively. Combining with the inflection point of decoupling, it can be found that the current cities have basically not crossed the inflection point, indicating that the current number of cities is not absolutely decoupled, which is similar to the conclusion obtained from velocity decoupling—although most cities in China have achieved a weak decoupling between economic development and transportation carbon emissions, they have not reached a strong decoupling state. On the whole, the conclusions of quantitative decoupling and velocity decoupling have been mutually verified, which confirms the analysis conclusion of urban transportation decoupling characteristics in this paper. Meanwhile, it can be determined that at present, the decoupling relationship between urban transportation carbon emissions and economic development in China is still in a “dilemma” and has not yet entered a “win-win zone”. Special attention should be paid to the strictness of transportation carbon emission reduction policies, as well as enhancing one’s vigilance on its greater negative impact on economic development.

At the same time, from the perspective of control variables, the results from column (2) and (4) of Table 7 are basically consistent. ➀ The coefficient of urban population density (PDN) is significantly positive, indicating that the continuous expansion of PDN will increase transportation carbon emissions, in which the conclusion is consistent with the view of Din et al. [48]. The increase in population density will lead to more transportation demand and even worsen urban traffic congestion, thus exacerbating carbon emissions from the transportation sector. ➁ The coefficients of urban road density (RDN) are 0.0181 and 0.0376 and both pass the test at the significance level of 1%, indicating that the expansion of RDN is not conducive to carbon emission reduction in the transportation industry. More road area per capita means the gradual improvement in urban transport infrastructure, which will lead to greater travel demand and then will increase industry carbon emissions. ➂ The coefficients of public transport operating efficiency (PTE) pass the test at the significance level of 1% in column (2) of Table 7, and are negative, meaning that public transport operating efficiency has a negative relationship with transport carbon emissions. The improvement in the efficiency of the public transport operation can attract more urban residents to switch from private cars to public transport. However, public transport has the characteristics of strong carrying capacity and high efficiency, and new energy (electric) vehicles are widely used in China. Therefore, the improvement of PTE can obviously improve the low-carbon development of the transportation industry. ➃ The coefficient of per capita private car ownership (PRC) is significantly positive, indicating that the increasing number of private cars will continue to worsen the current situation of transportation carbon emissions, which is closely related to the fact that private cars are still dominated by fuel vehicles during the study period in China.

5. Conclusions and Policy Recommendations

How to decouple economic growth and traffic carbon emissions has always been an urgent issue of national and social attention. Although many studies have analyzed the decoupling state of economic growth and transportation carbon emissions in different periods and regions in China, there is still a lack of comprehensive evaluation of the decoupling level of transportation carbon emissions and economic development at the city level, and the analysis of velocity decoupling and quantity decoupling into a unified framework for discussion. In order to systematically quantify the decoupling relationship between urban transportation carbon emissions and economic development, based on the Tapio decoupling and the EKC model, this paper deeply explores the decoupling relationship between 284 cities in China during 2006–2020 from the dual perspectives of velocity decoupling and quantitative decoupling. The main conclusions are as follows:

(1) From the perspective of velocity decoupling, most cities in China have initially realized the weak decoupling between transportation carbon emissions and economic growth during the research period, but have not reached the stage of strong decoupling, and there are mainly three kinds of evolution: stable decoupling, relatively stable decoupling and unstable decoupling. Most of the cities are in a relatively stable state of decoupling, and multiple decoupling states appear alternately in many cities. In terms of space, regions with a high level of decoupling still show a tendency in the east and central regions to be greater, and to a lesser extent in the west regions. (2) From the perspective of quantitative decoupling, the relationship between economic growth and transportation carbon emissions presents an inverted U-shaped EKC curve, but the current cities have basically not crossed the inflection point and achieved absolute decoupling. In other words, the decoupling relationship between China’s urban transportation carbon emissions and economic development is still in a “dilemma”, and has not yet entered the “win-win zone”, and is in the transition process towards a win-win situation. (3) The quantitative decoupling results also show that urban population density, urban road density and per capita private car ownership are all important factors leading to the increase in urban transport carbon emissions; the efficiency of public transport operation is the key driver for reducing carbon emissions in urban transport.

Based on the above conclusions, this paper believes that the development of low-carbon transportation should be promoted from the following aspects: ① It takes into account economy and emission reduction, increasing traffic emission reduction efforts and implementing a variety of supply and demand strategies such as traffic structure optimization and adjustment, transportation technology upgrading, transportation vehicle replacement and travel demand guidance, so as to promote effective and high-quality emission reduction in the transportation industry and realize the “double carbon” goal of the industry as soon as possible. ② It strengthens transportation carbon emission reduction control according to local conditions in areas with low decoupling levels, and tries to explore new traffic emission reduction strategies and policy systems. ③ Starting from a multi-path model, taking urban development, public transportation and new energy as the starting point, relying on various strategies such as government tax relief, research and development subsidies, transportation subsidies, vigorously developing compact towns and bus cities, rapidly promoting the promotion and application of new energy vehicles and realizing the full coverage of new energy private cars as soon as possible should be adapted, so as to effectively promote the development of low-carbon transportation.