Efficient Operation Algorithm of UAVs for Tourist Safety: Case of the Hallasan Mountain Trail in Jeju Island

Abstract

Tourist safety is one of the most important factors for tourists when choosing a tourism destination. Jeju Island’s Hallasan Mountain Trail is a trail that connects the mid-slope of Hallasan, the main mountain on Jeju volcanic island, and boasts very beautiful scenery. However, tourist safety has become an issue as accidents continue to occur every year. In this study, an efficient operation algorithm that can minimize the total cost with a mixed-integer linear programming (MILP) model is developed, considering the introduction of a UAV patrol system on the Hallasan Mountain Trail, which is difficult to access by vehicles. The application of different speeds for patrol and nonpatrol routes, the selection of candidate sites for UAV stations with easy vehicle access, and the sensitivity analysis of patrol speed and maximum operation time considering the performance improvement of UAVs are the contributions of this study. The results show that stations are installed as close as possible to the trail courses and that lower-performance UAVs are utilized that can patrol the trail courses at a given time. The sensitivity analysis also confirmed that the total cost can be minimized by reducing the number of stations and UAVs or replacing higher-performance UAVs with lower-performance UAVs.

1. Introduction

With the spread and endemicity of COVID-19, tourists’ tourism preferences have changed significantly [1]. The Korea Tourism Organization (KTO) used the slogan “Every moment of daily life is travel” when announcing the 2023 tourism trend using big data. KTO presented six themes based on each letter of the alphabet in the word “MOMENT”: Meet the local, Outdoor/leisure travel, Memorable time in rural, Eco-friendly travel, Need for longer stay, and Trip to enjoy hobbies. One of these is a trail that allows people to leisurely enjoy the open natural environment. Trails were popular even before the COVID-19 outbreak, but they are one of the travel patterns that quickly revived even during the COVID-19 pandemic, and are becoming more popular after COVID-19 became endemic [2]. In Korea, various trails are being built in each region, and trails have been built or are scheduled to be built in almost all tourist destinations in Korea. Many people are looking for trails all over the country, and overtourism is a concern in the case of some famous places [3].

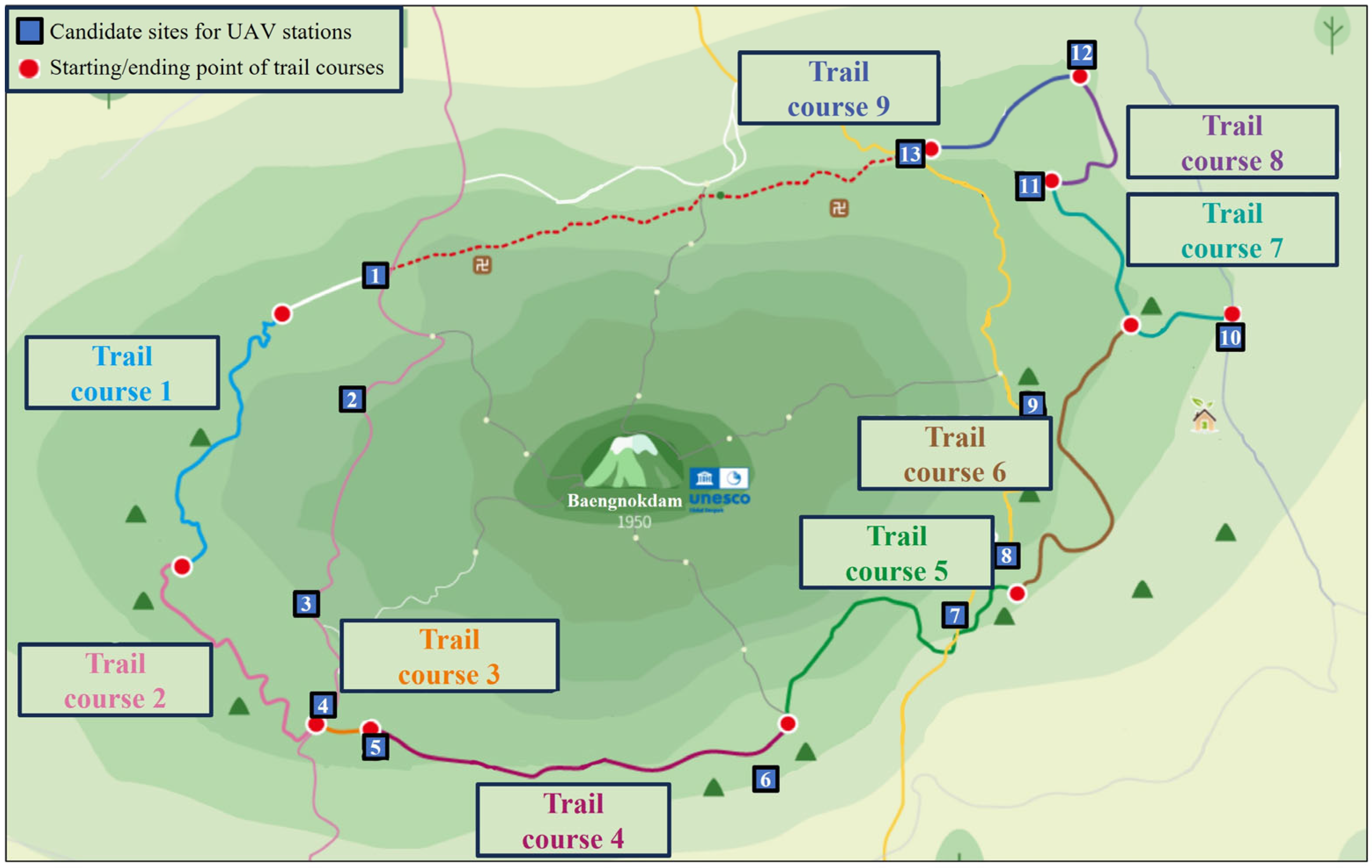
Jeju Island’s Hallasan Mountain Trail is a trail that connects the mid-slope of Hallasan, the main mountain on Jeju volcanic island, and boasts very beautiful scenery. It is a representative trail on Jeju Island along with the Jeju Olle Trail, which connects the coastal area. As shown in Figure 1, most areas of the Hallasan Mountain Trail are heavily forested, and most areas are difficult to access by vehicle rather than on foot. In Korea, because security is very stable, violent crimes rarely occur even in places where there is not much traffic, such as the Hallasan Mountain Trail. However, cases of patients suffering from acute diseases, fractures, etc., or people becoming lost and in distress may occasionally occur. In these cases, quick evacuation and rescue for treatment are necessary, but due to the nature of the mountain trail, there are areas where cell phones cannot be used, so a system for the safety of tourists is essential [4].

Therefore, this study aims to address the tourist safety system using UAVs (unmanned aerial vehicles) in the Hallasan Mountain Trail. Since the UAVs system is currently being used in various fields such as environmental monitoring [5], civil security [6], and traffic safety [7], as well as tourism [8], it can ensure sufficient usability for tourist safety, and has recently been widely used for recreational purposes such as shows using drones. Although traditional monitoring systems such as CCTV exist, large cost investments are required in mountainous terrain that vehicles cannot access, such as the Hallasan Mountain Trail, so UAVs are being used as a new system to monitor tourist safety [9].

The contributions of this study considering existing references are as follows. First of all, this study reflected actual situations as much as possible and utilized actual data. The actual physical distance and location information of the Hallasan Mountain Trail were used, and the candidate site for installing the UAV station was also set to exist on a road accessible by vehicles. In addition, the cost structure required to introduce the UAVs system was well designed, and a formula was developed to facilitate reflection when additional cost factors need to be considered in the future. Currently, the installation cost of the UAV station, UAV purchase cost according to UAV performance, and operating cost according to UAV operation are considered, but if additional costs need to be considered, they can be easily reflected. Moreover, differences in UAV performance and resulting operational characteristics were taken into consideration. When a UAV moves to a specific point on the trail for a monitoring mission, it moves at the highest speed, and when performing an actual monitoring mission, it moves at a predetermined speed. Additionally, when a UAV takes on a mission, it can start from the start point of a specific trail and move to the end point, and an algorithm was developed to decide whether to perform a monitoring mission for the next trail at that point or return to the station.

2. Literature Review

UAVs are being widely utilized across various industries due to their relatively low operational costs compared to conventional transportation methods and their ability to easily access areas that humans or traditional transport vehicles may struggle to reach. Particularly, they are extensively utilized in the logistics industry such as parcel delivery services and in disaster-stricken areas affected by fires, earthquakes, and other natural disasters.

The VRP (vehicle routing problem) of UAVs for delivery tasks is different from that of existing conventional vehicles. This is due to constraints such as battery capacity or payload weight of UAVs, making it challenging to visit multiple points at once for delivery tasks [10]. Therefore, it is imperative to consider these characteristics in research related to routing problem of UAVs. Kim et al. [11] proposed a routing algorithm to derive the optimal round-trip route for delivering goods from warehouses to customers using UAVs. The optimal route was determined considering the maximum range and payload of the UAVs, with the aim of minimizing total travel distance. Yuan et al. [12] addressed the delivery scheduling problem of heterogeneous logistics UAVs with varying payload capacities, maximum flight times, and flight speeds. Since VRP is traditionally known as an NP-hard problem, they proposed a GA (genetic algorithm)-based solution framework to solve the problem. To evaluate the performance of the proposed algorithm, numerical experiments were conducted and compared with the results obtained from SA (simulated annealing) and GLS (greedy local search). Using both conventional trucks and UAVs simultaneously for delivery has been proven to be advantageous in terms of operation cost, CO₂ emissions, and delivery time compared to using trucks or UAVs alone [13]. Chen et al. [14] conducted research on the scenario where UGVs (unmanned ground vehicles) carry both UAVs and delivery parcels on road networks. UAVs are deployed from UGVs to delivery parcels to customers. They proposed an algorithm combining ACO (ant colony optimization) and GA. In the first step, ACO was used to explore the UGV’s route, while in the second step, GA was adopted to derive the UAV’s route. Jeon et al. [15] addressed the routing problem when UAVs perform both delivery and pickup tasks simultaneously. The UAVs are deployed from ground vehicles with parcels and they deliver them to customers. After completing the delivery tasks, the UAVs can visit other customers to pick up parcels before returning to the ground vehicle. It is also possible for the UAVs to perform delivery or pickup tasks individually. They developed heuristic algorithms to solve large-scale problems and evaluated the algorithms through multiple numerical experiments. Munawar et al. [16] suggested utilizing UAVs to deliver self-diagnostic kits to potential COVID-19 patients and collect samples for testing. The objective was to minimize time and carbon emissions, deriving the optimal number of UAVs and routes. Applying four algorithms (greedy, intra-route, inter-route, and tabu) revealed that the tabu algorithm yielded the best solution.

UAVs can be effectively utilized in areas inaccessible to humans or conventional transportation methods. When UAVs are deployed for disaster response, such as detecting wildfires or conducting search and rescue operations in disaster-stricken areas, it is crucial to rapidly survey all points within the area. Therefore, routing plans for UAVs in disaster areas require considerations distinct from those for delivery tasks. Calamoneri et al. [17] addressed the use of UAVs for identifying people in need in areas affected by natural disasters. Due to the constraint on battery capacity, UAVs cannot cover large areas in a single trip and should repeatedly move between the base and search areas to cover all affected areas. Therefore, they studied the multidepot, multitrip vehicle problem to search the entire area in the shortest time. Ribero et al. [18] investigated the utilization of UAVs for search and rescue mission in emergency or post-disaster situations. Due to the urgent nature of these situations, they considered the use of mobile charging stations to avoid UAVs flying long distances for recharging purposes to fixed charging stations. They derived the optimal routes for UAVs and mobile charging stations to minimize the normalized weighted sum of the costs of UAVs and mobile charging stations, as well as the travel time for UAVs. Ozkan & Kilic [19] proposed an algorithm and mathematical model for generating routes for UAVs to detect wildfires. The routing problems for UAVs typically emphasize deriving routes that can complete visits to required points in the shortest time. However, considering the dynamic and probabilistic perspective of wildfire detection, revisiting the same points repeatedly may be important.

UAVs are widely used for patrol and surveillance tasks. Patrol and surveillance operations require continuous and repetitive monitoring and should be able to cover all necessary areas. Therefore, a routing plan should be developed considering these characteristics. Rajan et al. [20] addressed the routing problem when UAVs perform patrol tasks for data-gathering purposes. The UAVs depart from a source and arrive at a destination, visiting designated targets along the way to collect information. Information at the targets is obtained probabilistically, and if the collected information is insufficient, supplementary targets need to be visited additionally. Therefore, they derived patrol routes that minimize the cost of additional visits. Ko and Song [8] addressed the scenario where UAVs patrol tourist attractions to protect assets and tourists. They segmented patrol tasks into multiple levels of difficulty and categorized UAVs into tiers based on their performance. Considering that the scope of patrol tasks varies according to the UAV tier, they conducted a more realistic study. The objective was to minimize the sum of UAV purchase costs and total travel distance. The optimal UAV procurement plans and operation schedule were derived. Ko and Song [9] developed the optimal CCTV installation locations and operation schedules for UAV patrols to efficiently monitor and enhance security at tourist attractions. While surveillance via CCTV is a prominent safety measure, the collaboration with UAV patrols was suggested due to the limited coverage of CCTV. Relative security priorities were set considering peak tourist hours at each tourist point, and the validity of the proposed model was verified through a case study in the Nice region of France. Yang et al. [21] dealt with the collaboration of multiple UAVs and police car for patrolling. They classified patrol areas based on risk levels, ensuring that high-risk areas are patrolled by ground vehicles. Considering three objective functions ((1) minimizing patrol and deployment costs of police car and UAVs, (2) minimizing differences in UAV patrol workload, (3) minimizing differences in patrol workload for police cars), they derived patrol routes for UAVs and police cars at designated points, as well as launch and recovery locations for UAVs. In addition, various studies related to UAV patrol systems have been conducted, such as a UAV-based forest fire patrol path planning strategy [22], UAV patrolling for wildfire monitoring by a dynamic Voronoi tessellation on satellite data [23], a study on multi-UAV cooperative path planning for complex patrol tasks in large cities [24], etc.

As reviewed in previous studies, research on UAV routing should significantly consider different perspectives based on the intended application. This study utilizes actual data of the Hallasan Mountain Trail such as distance and location information and derives the location of UAV stations and the route of UAVs for patrol purposes. Additionally, the candidate sites for installing UAV stations are selected to be accessible to ground vehicles, and the speed of UAVs is set differently for simple travel and patrols to enhance operational feasibility. There are many studies on route planning for UAVs, but most of them derive routes that visit each point in the presence of multiple points. In contrast, in this study, a route is derived for patrolling along a trail course rather than visiting specific points. In addition, to ensure the quality of monitoring, when patrolling the trail course, the UAV operates at a low and constant speed, regardless of the maximum speed of the UAV, and when traveling between UAV stations and the trail course other than patrolling, the UAV operates at the maximum speed of the UAV. In other words, this study reflects that UAVs are not traveling at a constant speed, but at different speeds depending on the situation. These are the main differences between this study and previous studies.

3. Model Development

3.1. Problem Description

In this study, we tried to develop an efficient operation algorithm for the patrol using UAVs on tourist trails with the objective of minimizing the total cost of the UAV system by reflecting the situation of providing patrol service using UAVs on tourist trails that are difficult to access by vehicles. The total cost of the UAV system is calculated as the sum of the installation cost of UAV stations, purchase cost of UAVs, and maintenance cost of UAVs (weighted by flight distance). To understand the problem situation easily, it is assumed that the patrol system using UAVs is introduced on the Hallasan Mountain Trail in Jeju Island, South Korea. Figure 2 shows the Hallasan Mountain Trail. The trail is a forest path with a total length of 70.8 km, and it has nine courses in a counterclockwise direction, from the first course starting in the northwest to the ninth course ending in the northeast [25]. The course from the northeast to the northwest is currently unopened. There are accidents on the Hallasan Mountain Trail every year, such as tourists becoming lost, injured, or falling down due to illness. To respond to these accidents, regular patrols are required, but the Hallasan Mountain Trail is not accessible to vehicles and must be patrolled by humans. It requires a lot of manpower to patrol all nine trail courses regularly. CCTV could be one solution, but it has the disadvantage that it can only monitor the area around the installed location. Therefore, this study aims to derive an efficient operation strategy for the introduction of a system that monitors and patrols the Hallasan Mountain Trail from the sky using UAVs.

The patrol process is as follows: (1) The UAV departs from a UAV station and moves to the starting point of each course; (2) The UAV patrols from the starting point to the ending point of the course; (3) The UAV returns to the UAV station where it started and recharges. UAVs can patrol multiple courses in a row and then return to the UAV station, or they can patrol a single course and then return to the UAV station. UAVs move at the maximum speed of each UAV when traveling from the UAV station to the starting point of the course, from the ending point of the course to the UAV station, and from the ending point of one course to the starting point of another course. However, to maintain the same patrol quality, UAVs are assumed to patrol each course at the same speed. The starting and ending points of each course may or may not overlap, depending on the course, so there are 11 starting and ending points in total. Several types of UAVs with different maximum speeds are considered, each of which must return to the station from which it departed to recharge after patrol for a certain amount of time, and it is assumed that each course requires one patrol every hour.

There are some factors to consider when installing UAV stations. The first is accessibility to the station. The station will need to be staffed to monitor the UAV’s patrol video and to maintain and inspect the UAV. If the station is located in a place that is inaccessible to vehicles, it will be difficult for engineers to visit. Therefore, to ensure vehicle accessibility to the station, potential UAV station locations are selected alongside two-lane roads. The second is the proximity to the trail course. Before the start of a patrol, the UAV needs to travel from the station to the starting point of the trail course, and after the end of the patrol, the UAV needs to travel from the ending point of the trail course to the station for charging and inspection. If the distance between the station and the trail course is long, it requires a UAV with a higher maximum speed or a longer maximum operation time. This leads to increased operational costs. Therefore, UAV station candidates should be located close to the trail course for efficient operation. Many potential UAV station locations fulfill these conditions, but for simplicity of analysis, 13 potential UAV station locations are selected for this study.

3.2. Notations

In this study, a mathematical-model-based optimization technique is applied to derive an optimal operation system for the patrol of tourist trails using UAVs. To develop the mathematical model, notations to represent a set of decision variables, parameters, and index sets are defined in Nomenclature.

3.3. Mathematical Model

Equation (1) is the objective function that minimizes the total cost of the UAV system. The total cost is the sum of the installation cost of UAV stations, the purchase cost of UAVs, and the maintenance cost of UAVs weighted by flight distance. The flight distance is calculated by summing the UAV’s patrol distance and nonpatrol travel distance. When a UAV’s movement is represented by $x_{q,u,k,k\prime }$, if node $k$ is a trail course, it is traveling from the ending point of that course, and if node $k\prime$ is a trail course, it is traveling to the starting point of that course. If it travels to the starting point of a trail course, it patrols from that point to the ending point of that course.

$$\begin{array}{c}Minimize {\displaystyle \sum _{i\in I}}{y}_i·ps+{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{u\in U}}{z}_{q,u}·p{u}_q+w\hfill \\ \hfill ·\left({\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{u\in U}}{\displaystyle \sum _{k\in K}}{\displaystyle \sum _{j\in J}}{x}_{q,u,k,j}·r_j+{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{u\in U}}{\displaystyle \sum _{k\in K}}{\displaystyle \sum _{k\prime \in K}}{x}_{q,u,k,k\prime }·t_{k,k\prime }\right)\end{array}$$

(1)

Equations (2)–(4) describe the flight path of the UAV for patrolling. Equation (2) shows that the UAV must depart from the station to patrol. Equation (3) indicates that once the UAV arrives at a trail course, it must move to another course or station after patrolling. Equation (4) represents that after patrolling, the UAV must return to the station from which it departed.

$${\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{j\in J}{x}_{q,u,k,j}\le M·{\displaystyle \sum }_{i\in I}{\displaystyle \sum }_{j\in J}{x}_{q,u,i,j}\hspace{1em}\hspace{1em}\forall q\in Q,\forall u\in U$$

(2)

$${\displaystyle \sum }_{k\in K}{x}_{q,u,k,j}={\displaystyle \sum }_{k\in K}{x}_{q,u,j,k}\hspace{1em}\hspace{1em}\forall q\in Q,\forall u\in U,\forall j\in J$$

(3)

$${\displaystyle \sum }_{j\in J}{x}_{q,u,i,j}={\displaystyle \sum }_{j\in J}{x}_{q,u,j,i}\hspace{1em}\hspace{1em}\forall q\in Q,\forall u\in U,\forall i\in I$$

(4)

Equations (5)–(7) are related to time constraints. Equation (5) indicates that all trail courses must be patrolled once per hour. Equation (6) represents that the sum of the UAV’s nonpatrol travel time and patrol time must not exceed the maximum operation time after full charge. Equation (7) shows that the UAV can depart from the station once per hour.

$${\displaystyle \sum }_{q\in Q}{\displaystyle \sum }_{u\in U}{\displaystyle \sum }_{k\in K}{x}_{q,u,k,j}=1\hspace{1em}\hspace{1em}\forall j\in J$$

(5)

$${\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{k\prime \in K}{x}_{q,u,k,k\prime }·t_{k,k\prime }/d_q+{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{j\in J}{x}_{q,u,k,j}·r_j/ds\le ot\hspace{1em}\hspace{1em}\forall q\in Q,\forall u\in U$$

(6)

$${\displaystyle \sum }_{i\in I}{\displaystyle \sum }_{j\in J}{x}_{q,u,i,j}\le 1\hspace{1em}\hspace{1em}\forall q\in Q,\forall u\in U$$

(7)

Equations (8) and (9) show the relationship between the decision variables. Equation (8) indicates that a station must be installed at a candidate site for UAVs to depart from or arrive at the station. Equation (9) represents that UAVs must be purchased to be operational. Equations (10)–(12) show that the decision variables $x_{q,u,k,k\prime }$, $y_i$, and $z_{q,u}$ are binary variables with values of 0 or 1.

$$y_i·M\ge {\displaystyle \sum }_{q\in Q}{\displaystyle \sum }_{u\in U}{\displaystyle \sum }_{j\in J}{x}_{q,u,i,j}+{\displaystyle \sum }_{q\in Q}{\displaystyle \sum }_{u\in U}{\displaystyle \sum }_{j\in J}{x}_{q,u,j,i}\hspace{1em}\hspace{1em}\forall i\in I$$

(8)

$$z_{q,u}·M\ge {\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{k\prime \in K}{x}_{q,u,k,k\prime }\hspace{1em}\hspace{1em}\forall q\in Q,\forall u\in U$$

(9)

$$x_{q,u,k,k\prime }=\left\{0,1\right\}\hspace{1em}\hspace{1em}\forall u\in U,\forall k\in K,\forall k\prime \in K$$

(10)

$$y_i=\left\{0,1\right\}\hspace{1em}\hspace{1em}\forall i\in I$$

(11)

$$z_{q,u}=\left\{0,1\right\}\hspace{1em}\hspace{1em}\forall q\in Q,\forall u\in U$$

(12)

4. Numerical Experiment

4.1. Parameters Setting

The Hallasan Mountain Trail consists of nine courses, each of which has a different length [25]. There are 13 candidate sites for UAV stations. The cost of installing a station is assumed to be the same, at USD 10,000, regardless of the location. Three different performance UAVs with maximum speeds of 30 m/s, 20 m/s, and 10 m/s are considered, with prices of USD 1300, USD 1000, and USD 900, depending on the performance. The UAVs travel at maximum speed for nonpatrol travel, but patrol at a speed of 5 m/s. They can operate for up to 2700 s (45 min) and require 900 s (15 min) of charging time. The values of the system parameters and index sets can be found in

Table 1. System parameters.

Symbol	Value
$r_j$	{8700, 8000, 2300, 11,300, 11,500, 9400, 10,000, 3000, 6600}
$p{u}_q$	{1300, 1000, 900}
$d_q$	{30, 20, 10}
$ps$	10,000
$w$	1
$ds$	5
$ot$	2700
$M$	1,000,000

and

Table 2. Index sets.

Symbol	Value
$I$	{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}
$J$	{Course 1, Course 2, Course 3, Course 4, Course 5, Course 6, Course 7, Course 8, Course 9}
$K$	{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, Course 1, Course 2, Course 3, Course 4, Course 5, Course 6, Course 7, Course 8, Course 9}
$U$	{1, 2, 3, 4, 5, 6, 7, 8, 9}
$Q$	{High, Medium, Low}

. The system parameters for UAVs are set by referring to plans for introduction of a UAV patrol system on the Hallasan Mountain Trail.

Table 3. Latitude and longitude of candidate UAV station sites and trail courses.

Candidate Sites	Latitude	Longitude	Starting Point	Latitude	Longitude	Ending Point	Latitude	Longitude
Site 1	33.409257	126.476542	Course 1	33.396661	126.459438	Course 1	33.345612	126.444188
Site 2	33.377355	126.468404	Course 2	33.345612	126.444188	Course 2	33.312009	126.457448
Site 3	33.338165	126.454421	Course 3	33.312009	126.457448	Course 3	33.310409	126.473168
Site 4	33.312067	126.457343	Course 4	33.310409	126.473168	Course 4	33.318742	126.563469
Site 5	33.308685	126.472794	Course 5	33.318742	126.563469	Course 5	33.339056	126.626991
Site 6	33.307900	126.569880	Course 6	33.339056	126.626991	Course 6	33.392909	126.642250
Site 7	33.337823	126.610336	Course 7	33.392909	126.642250	Course 7	33.422984	126.626052
Site 8	33.351997	126.622241	Course 8	33.422984	126.626052	Course 8	33.440253	126.630150
Site 9	33.378588	126.625973	Course 9	33.440253	126.630150	Course 9	33.430917	126.596845
Site 10	33.394945	126.684806
Site 11	33.423092	126.626073
Site 12	33.440434	126.630343
Site 13	33.431168	126.596489

shows the latitude and longitude of the candidate sites for UAV stations and the latitude and longitude of the starting and ending points of trail courses [26]. The distance between nodes ($t_{k,k\prime }$) is calculated as a Euclidean distance using the latitude and longitude values. When a UAV departs from a trail course, it means that it finishes patrolling that course and leaves from the ending point to another node, and when it arrives at a trail course, it means that it arrives at the starting point of that course and starts patrolling.

4.2. Results

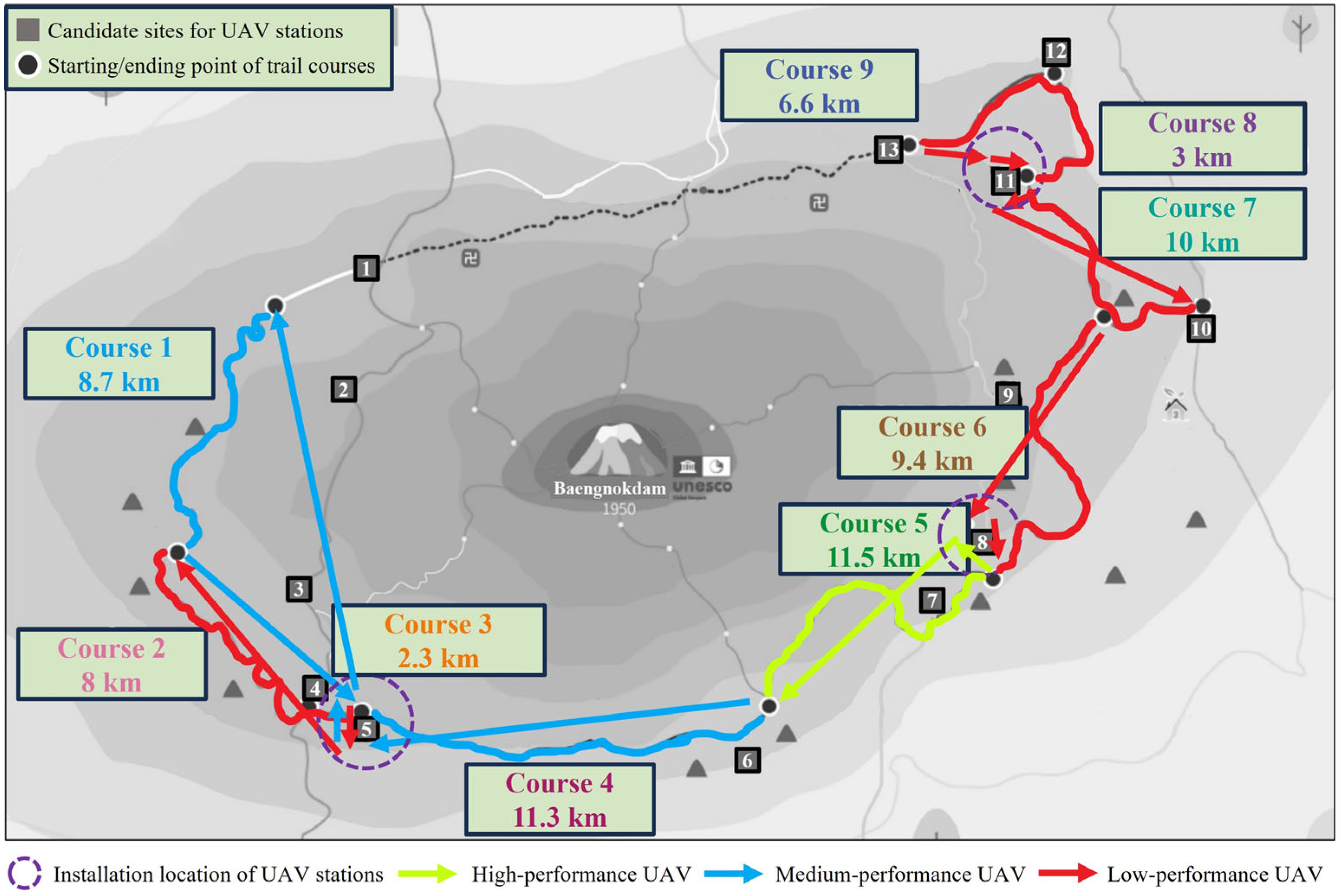
In this study, a mixed-integer linear programming (MILP) algorithm is used. To derive the optimal solution, it utilizes IBM ILOG CPLEX Optimization Studio 22.1.1. This method is widely used in scheduling research in the field of logistics and smart factories, and it has been proven in many studies that the solutions derived are optimal. The results can be seen in Figure 3. UAV stations are installed in three candidate sites: 5, 8, and 11. A total of seven UAVs are used for patrolling: one high-performance UAV, two medium-performance UAVs, and four low-performance UAVs. Looking at the flight path, the medium-performance UAV departs from the station at Site 5 to patrol Course 1 and returns, the low-performance UAV departs to patrol Courses 2 and 3 and returns, and another low-performance UAV departs to patrol Course 4 and returns. From the station at Site 8, the high-performance UAV departs to patrol Course 5 and returns, and the medium-performance UAV departs to patrol Course 6 and returns. From the station at Site 11, two low-performance UAVs depart, one to patrol Course 7 and the other to patrol Courses 8 and 9, and return.

UAV stations are installed in the closest proximity to the trail course among several candidate sites. The farther away the station is from the trail course, the longer flight distance it will require, which increases the cost. The performance of the UAVs used for patrolling depends on their ability to return from patrols within the maximum operation time. Courses 5 and 4 are 11,500 m and 11,300 m long, respectively, and are among the longest of the nine trail courses. UAVs patrolling Course 5 need to have high performance to complete the flight within the maximum operation time, while for Course 4, medium-performance UAVs can complete the patrol within the maximum operation time. Both the length of the trail course and the distance to the station affect the operating time. Course 1 is only 8700 m long, but the distance to the station is long, so a medium-performance UAV is required, while Course 6 is 9400 m long, but the distance to the station is short, so a low-performance UAV can patrol it.

4.3. Sensitivity Analysis

In the numerical experiment, it is assumed that the patrol speed of the UAV along the trail course is constant at 5 m/s, regardless of the performance of the UAV. This is so that the UAV can patrol while maintaining the quality of patrol monitoring. Patrolling at too high a speed may cause the UAV to miss problematic situations on the trail course. If the patrol monitoring performance of the UAV improves, then patrolling at a faster speed will not degrade the quality of patrol monitoring. In this section, the sensitivity analysis of increasing the patrol speed due to improved monitoring performance is performed. The optimal operation strategy of the UAV patrol system is compared when the patrol speed is increased from 5 m/s to 10 m/s in 0.5 m/s increments. As the patrol speed increases, the UAVs can cover more distance in a given time. The results of the sensitivity analysis for patrol speed changes are shown in

Table 4. Sensitivity analysis of patrol speed changes.

Patrol Speed (m/s)	Total Cost ($)	Number of UAVs			Number of UAV Stations (Sites)
		High	Medium	Low
5 m/s	159,901	1	2	4	3 (5, 8, 11)
5.5 m/s	157,757	1	1	5	3 (3, 8, 11)
6 m/s	157,457	0	2	5	3 (3, 8, 11)
6.5 m/s	156,413	1	0	6	3 (3, 8, 11)
7 m/s	149,689	1	1	4	3 (4, 8, 11)
7.5 m/s	149,102	2	1	2	2 (5, 8)
8 m/s	148,039	1	2	2	2 (4, 8)
8.5 m/s	147,468	1	2	2	2 (5, 8)
9 m/s	137,268	2	1	1	2 (5, 9)
9.5 m/s	136,968	1	2	1	2 (5, 9)
10 m/s	134,290	2	1	1	1 (11)

and Figure 4. Since the goal is to minimize the total cost, increasing the patrol speed results in fewer UAV stations and fewer UAVs. At a patrol speed of 7.5 m/s, the number of stations is reduced to two, and at a patrol speed of 10 m/s, the number of stations is reduced to one. Similarly, as the patrol speed increases, the number of UAVs decreases, but in some cases, the number of UAVs remains the same. Even if the number of UAVs is the same, the system can lower the cost by using low- or medium-performance UAVs instead of high-performance UAVs, or low-performance UAVs instead of medium-performance UAVs.

After all, an improvement in the monitoring performance of UAVs can increase the patrol speed, which shows that a more efficient system can be operated. As the cost-effectiveness of patrol systems using UAVs improves, more places will be able to utilize them. However, there is one factor that cannot be overlooked and that is the ability of the monitoring personnel. It is essential to have monitoring personnel check the monitoring video of the UAVs when utilizing UAV patrol systems. If the monitoring performance of the UAV is improved and the patrol speed is increased, the monitoring personnel must be able to accurately recognize the problematic situation through the monitoring video to respond to the accident situation. In other words, it is not just the performance of the UAV that is important, but the ability of the monitoring personnel is also important, and it is necessary to support the training of the monitoring personnel.

After the UAVs patrol trail courses, they must be charged and inspected, and the maximum operating time and charging/inspection time depends on the performance of the UAVs. In the numerical experiment, it is assumed that the UAVs patrol for 2700 s (45 min) every hour, which is the maximum operation time, and charge and inspect for the remaining 900 s (15 min). This section examines how the optimal operation strategy of the UAV patrol system would change if the maximum operation time is varied. The results of varying the maximum operation time in 60 s (1 min) intervals from the original value of 2700 s are shown in

Table 5. Sensitivity analysis of maximum operation time.

Maximum Operation Time (s)	Total Cost ($)	Number of UAVs			Number of UAV Stations (Sites)
		High	Medium	Low
2520	No feasible.
2580	160,301	2	2	3	3 (5, 8, 11)
2640	160,201	2	1	4	3 (5, 8, 11)
2700	159,901	1	2	4	3 (5, 8, 11)
2760	157,757	1	1	5	3 (3, 8, 11)
2820	157,757	1	1	5	3 (3, 8, 11)
2880	157,757	1	1	5	3 (3, 8, 11)
2940	157,757	1	1	5	3 (3, 8, 11)
3000	157,457	0	2	5	3 (3, 8, 11)
3060	157,457	0	2	5	3 (3, 8, 11)
3120	157,357	0	1	6	3 (3, 8, 11)

and Figure 5. With the maximum operation time of 2520 s, there is no optimal solution because there is a trail course that cannot be patrolled in the given time. As the maximum operation time increases, it can be seen that medium-performance UAVs replace the patrols on the trail course that were previously patrolled by high-performance UAVs, and low-performance UAVs replace the patrols on the trail course that were previously patrolled by medium-performance UAVs. When the maximum operation time increases from 2760 s to 2820 s, 2880 s, and 2940 s, the results are the same because it is not possible to replace the patrols on the trail course with lower-performance UAVs. However, unlike the previous sensitivity analysis on patrol speed, the number of UAV stations is not affected. It is expected that the number of UAV stations would be affected if the patrol intervals were longer, and the maximum operation time of the UAVs increased.

After all, an improvement in the battery performance of UAVs can increase the maximum operation time, which leads to more efficient system operation. The increase in the maximum operation time would not reduce the total number of UAVs or the number of UAV stations, unlike the case of the increase in patrol speed identified earlier. This is because the numerical example in this study assumes a patrol speed of 5 m/s and a patrol is required every hour. Due to these assumptions, an increase in the maximum operation time is not enough to reduce the total number of UAVs or the number of UAV stations. Instead, it lowers the total cost by making it possible to substitute higher-performance UAVs with higher maximum speeds for lower-performance UAVs with lower maximum speeds. This cost-effectiveness through improved battery performance will lead to the use of UAVs in more places. However, it is important to be cautious about the information provided by UAV manufacturers about maximum operation time. The maximum operation time in the specifications provided by the manufacturer is what is expected under ideal conditions, and in the process of actual operation, the maximum operation time can be significantly reduced. This can have a significant impact on the operation of the patrol system. Therefore, it is necessary to conduct a sufficient trial period to understand the exact performance of the UAV before implementing a system utilizing UAVs.

5. Conclusions

In this study, we investigated the optimal operation strategy of a system for UAVs to patrol trails that are difficult to access by vehicles for tourist safety. The optimal operation strategy that minimizes the total cost was derived by considering UAVs with different performances and multiple UAV station candidate sites on the Hallasan Mountain Trail in Jeju Island, South Korea. As a result of the study, first, it was confirmed that the UAV station should be installed at the potential sites located as close as possible to the trail course, as expected before the study. The closer the distance between the UAV station and the trail course, the shorter the total distance traveled by the UAVs, which leads to an efficient operation of the UAV patrol system. Second, it was found that UAVs with higher performance are not always selected for operation. If the performance of a UAV does not enable it to patrol additional trail courses, the lower-performance UAV that can patrol the same course is selected for operation. This choice also leads to the efficient operation of the UAV patrol system. In addition, two sensitivity analyses were conducted. First, we compared the change in the optimal operation strategy as the patrol speed of the UAVs is increased to consider the improvement in the monitoring quality. Second, we compared the change in the optimal operation strategy as the maximum operation time of the UAVs was varied to consider the improvement in the energy efficiency of the UAVs. It was found that as the performance of the UAVs improved, the minimization of the total cost was achieved by reducing the number of UAV stations and UAVs or replacing higher-performance UAVs with lower-performance UAVs.

The implications of this study are as follows. First, while most of the previous studies on UAV patrol routes for tourist safety or tourism security have focused on routes to visit specific points, this study aimed to derive routes to travel along a patrol course, rather than simply deriving routes to visit specific points. The different speeds were applied to differentiate between routes that patrol the trail course and routes that simply travel nonpatrol. Second, the candidate sites for UAV stations were selected based on vehicle accessibility. Vehicle accessibility of stations is required for the maintenance of UAVs. Since most of the Hallasan Mountain Trail is inaccessible to vehicles, candidate sites that are easily accessible to vehicles and close to the trail courses were selected. Third, the sensitivity analyses were conducted for changes in patrol speed and maximum operation time, considering that the performance of UAVs is constantly improving. We identified the impact of patrol speed and maximum operation time on the UAV patrol system.

The limitations of this study are the following. First, the patrol intervals on all trail courses are the same. Each trail course has different levels of risk and popularity. The more popular or dangerous trail courses have a higher risk of accidents, so they need to be patrolled more frequently. In future research, we will consider these factors and apply different patrol intervals to different trail courses. Second, the patrol speed is consistent even though the monitoring environment may be different for specific sections of each trail course. Certain sections are difficult to monitor due to trees, and others are easy to monitor due to unobstructed views. To achieve consistent monitoring quality, the patrol speed needs to be different for each section, considering the specific situation of these sections. In future research, we will examine the situation of each section and study a system that patrols each section of the trail course at different speeds. Third, since the Hallasan Mountain Trail is a mountain road, the height of the UAV’s travel path can vary greatly, but we did not consider the altitude. Like many previous UAV path studies, we only studied the path in two dimensions, but in future studies, we will study the path in three dimensions, including altitude. Fourth, we did not consider the crash risk of UAVs. As mentioned earlier, the Hallasan Mountain Trail is a mountain road; there are many tree-covered sections, and the crash risk must be considered when using UAVs for patrolling in such sections. In this case, not only is there a crash risk for UAVs, but it can also be difficult to monitor accurately. CCTV could be a good complement. In future studies, we will consider using a combination of UAVs and CCTV for patrol monitoring.