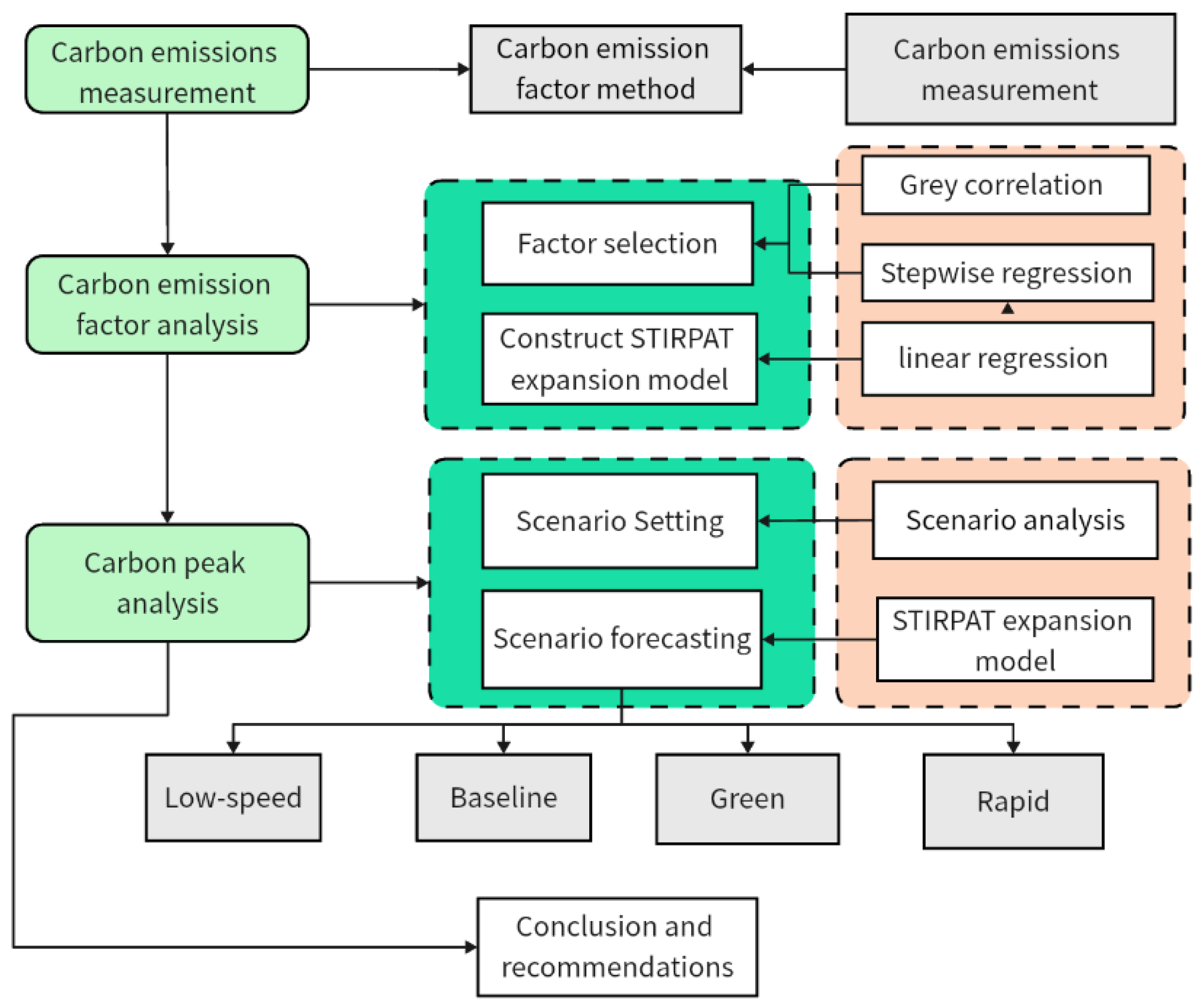
Analysis of Influencing Factors and Prediction of the Peak Value of Industrial Carbon Emission in the Sichuan-Chongqing Region

Abstract

The greenhouse effect has a negative impact on social and economic development. Analyzing the factors influencing industrial carbon emissions and accurately predicting the peak of industrial carbon emissions to achieve carbon peak and carbon neutrality is therefore vital. The annual data from 2000 to 2022 were used to study the influencing factors of carbon emission and the path of carbon emission reduction. In this study, the gray correlation method and stepwise regression method were used to explore the effective factors that met the significance test and the STIRPAT expansion model was constructed to analyze the characteristics and influencing factors of industrial carbon emissions in the Sichuan-Chongqing region. Finally, the changing trend of regional industrial carbon emissions is predicted by scenario analysis and four development scenarios are set up, which show that (1) from 2000 to 2022, the change in total industrial carbon emissions in Sichuan Province and Chongqing Municipality presents an inverted U-shaped trend, reaching a phased peak in 2013 and 2014, respectively, then declining and then rising again after 2018. (2) Industrial scale foreign trade dependence and population are the effective factors of industrial carbon emission in Sichuan, and all have positive effects. Energy structure and per capita income are the effective factors in Chongqing, showing negative and positive effects, respectively. (3) Analysis of four scenarios shows that the time range of the industrial carbon peak in the Sichuan-Chongqing region is 2030–2035 and that its peak height ranges from 81.98 million tons to 87.64 million tons. Among them, the green development scenario is the most consistent path to achieve the carbon peak as soon as possible; in this case, industrial carbon emissions will peak in 2030, in line with the national target time, and the lowest peak level of 81.98 million tons. The suggestions in this paper are continuously optimizing the energy structure, adjusting the industrial scale, and accelerating scientific and technological progress to achieve sustainable development.

1. Introduction

With the Paris Agreement proposed in November 2016, the world is expected to achieve carbon neutrality between 2050 and 2100 and it is expected that countries will transition to a low-carbon economy. The scope of China’s economy is still expanding due to the country’s rapid economic development and the expansion of its production activities. There is a tight relationship between energy usage, carbon emissions, and economic progress. Increased energy consumption and a sharp rise in carbon emissions are encouraged by rapid economic expansion. China is the world’s largest carbon emitter, with CO₂ emissions surpassing that of the United States in 2006, according to figures from the China Carbon Accounting Database [1].

In September 2020 during the 75th session of the UN General Assembly, China declared that it would raise its nationally determined contributions (NDCS), enact more robust laws and regulations, work toward reaching a peak in carbon dioxide emissions by 2030, and become carbon neutral by 2060.

With the in-depth implementation of its manufacturing power strategy, its industrial scale continues to rapidly grow, becoming another important source of carbon emissions. With the continuous progress and development of the Sichuan-Chongqing region, the region has become an important economic center, a scientific and technological innovation center, and a new highland of reform and opening up with national influence, which has promoted the continuous vigorous development of industries in the region. Increasing industrial energy consumption has also accelerated the rate of carbon emissions, which has caused an increasingly serious impact on the environment of the Sichuan-Chongqing region. Therefore, it is important to strengthen industrial energy conservation and reduce emissions in the Sichuan-Chongqing area.

This paper makes some contributions to the previous research in three aspects. First, the academic community has conducted systematic research on the influencing factors and peak prediction of carbon emissions in China and some provinces and cities. However, the research on industrial carbon emission in Sichuan and Chongqing region, which is the main economic area in southwest China, is relatively small in scale and has not been analyzed according to the characteristics and actual conditions of different provinces and cities. Second, when analyzing the influencing factors of carbon emissions, many scholars inevitably choose to include multiple influencing factors into the same model, which leads to serious multicollinearity and statistical insignificance problems, and each factor has a different degree of influence, so it is necessary to study the main influencing factors in the Sichuan and Chongqing region. Third, there are few studies on whether the Sichuan and Chongqing areas’ industrial carbon emissions can reach the target before the national carbon peak time, so it is necessary to analyze and discuss it in the basic situation and find an effective carbon reduction path suitable for the region within the target time frame. Hence, the analysis is based on the mentioned aspects in this study.

2. Research Status

In response to the issue of carbon emissions, many scholars at home and abroad have conducted many empirical analyses on the following three aspects: carbon emission measurement methods, analysis of carbon emission influencing factors, and carbon emission prediction methods.

2.1. Carbon Emissions Measurement Methods

At present, there are many methods for measuring carbon emissions, including the carbon emission coefficient, input–output, and carbon footprint methods provided by the IPCC. Wei et al. measured their carbon emissions and used the carbon emission coefficient method to examine the spatial features of land-use carbon emissions over the previous 20 years in different districts and counties in Gansu Province from the perspectives of the carbon ecological support coefficient and per capita carbon footprint [2]. Chu et al. used the IPCC’s carbon emission coefficient approach to assess greenhouse gas emissions from agriculture that are not carbon-based at the province level in a thorough manner [3]. To estimate overall agriculture net carbon emissions, Zhang and Cai employed the economy-water-carbon coefficient technique, the IPCC carbon emissions accounting method, and the environmental input–output model [4]. Using an enhanced input–output model, Qi et al. estimated CO₂ and air pollutant emission leakages at the provincial level in China in 2012 and 2017 based on dispersed dyes’ carbon footprint [5]. Li et al. evaluated the possible environmental damage caused by carbon emissions from the textile industry [6]. Shen et al. forecasted the carbon emissions of the olefin industry worldwide and in China under different development scenarios based on the carbon footprint of different olefin routes [7].

At present, China’s statistics on energy consumption at the provincial level are not sufficiently comprehensive and the carbon emission coefficient method requires less data, making it more suitable for the measurement of carbon emissions from energy consumption at the provincial level.

2.2. Application of the STIRPAT Model in Influencing Factors of Carbon Emission

Many scholars have decomposed the factors that influence carbon emissions. For instance, Panos et al. carried out a factor decomposition of per capita CO₂ based on the expanded Kaya model, which includes employment rate, energy mix, carbon intensity of GDP, economic growth of labor productivity, and carbon intensity of fossil fuel consumption [8]. Using a Tobit regression model, Liu et al. investigated the critical factors influencing the coordinated reduction in carbon emissions and air pollutants (APCE). They found that, while the degree of opening to the outside world mitigated this effect, economic growth, industrial structure, and green technology innovation increased the cost-plus rate of addressing APCE [9].

The STIRPAT model has been used by many scholars in the field of the decomposition and prediction of carbon emission-influencing factors. Tang et al. used the extended STIRPAT model to analyze countermeasures and suggestions for carbon emissions in China’s metal smelting industry, identifying population, coal consumption, urbanization rate, total metal output, carbon intensity, proportion of secondary industries, and per capita GDP as important factors affecting carbon emissions [10]. Cai et al. adopted the novel STIRPAT model to explore ways to reduce carbon emissions from the perspective of household consumption and assessed the impact of major factors such as carbon emission intensity, consumption structure, per capita consumption, and population on indirect household carbon emissions, finding that the energy intensity of economic industries is an important factor affecting carbon emission intensity [11]. Wei et al. employed a combination of the Tapio decoupling and STIRPAT models to conduct an analysis, leading to the conclusion that there exists a strong decoupling and weak decoupling relationship between agricultural and animal husbandry economic development and carbon emissions [12].

Based on the analysis and understanding of the factors influencing carbon emissions, it was found that the energy structure and foreign trade have a certain impact on carbon emissions. For example, Wu et al. utilized the extended STIRPAT model to examine the correlation between CO₂ emissions and various driving factors, such as resident population, economic level, technological level, and urbanization level. The study yielded a reasonable prediction of future CO₂ emissions in Qingdao [13]. Li et al. used the extended STIRPAT model to empirically test the impact of the energy structure and digital economy on carbon emissions using data [14]. Liu et al. [15] believe that the energy structure is a factor promoting carbon emissions and provides a basis for carbon emission reduction and energy consumption reduction in the transportation industry [15].

2.3. Application of the STIRPAT Model in Predicting Carbon Emissions

The theories, methods, and assumptions used by different scholars differ and the obtained results differ within the range of reasonable estimation. Currently, STIRPAT, LEAP, LDMI, and scenario prediction models are widely used to predict future total carbon emissions. Most scholars use a combination of models and scenario predictions to forecast regional carbon emissions.

Kong et al. [16] conducted a scenario analysis to predict and analyze the total carbon emissions of Shandong Province from 2020 to 2050. The findings indicate that, under three different development scenarios, Shandong Province is capable of reaching a carbon peak during the period of 2030–2035. Furthermore, there are variations in both the timing and magnitude of the carbon peak across the different scenarios [16]. Yan et al. conducted a scenario analysis using the STIRPAT model. Their empirical results confirmed the Environmental Kuznets Curve (EKC) relationship and revealed the impact of changes in population structure and urbanization on plastic pollution [17]. Feng et al. utilized a combination of LMDI and LEAP models to forecast the carbon emissions of industrial park groups within an economic development zone in Yancheng, spanning from 2020 to 2035, under both baseline and low-carbon scenarios. The findings indicate that the third scenario, as per the low-carbon scenario, is deemed most suitable for park development [18]. Zeng et al. [19] conducted a study on different peaking scenarios and found that the Yangtze River Delta urban agglomeration, as a whole, is capable of achieving carbon peaking on time under three simulation paths. However, it is important to note that the specific cities within the region will experience significantly different peaking conditions due to varying policy guidance [19]. Wu et al. utilized the extended STIRPAT model and established three different scenarios to simulate carbon emissions from China’s power industry from 2020 to 2040. The findings indicate that carbon emissions are projected to reach their peak before 2030, specifically in 2029, with a peak range of approximately 4.95 billion tons [20]. Hou et al. used scenario analysis to design three different development scenarios and the results showed that only under the coordinated development scenario could Shanxi’s high energy-consuming manufacturing industry reach the carbon peak in 2030, whereas the carbon emission curves of the other two scenarios did not reach the peak [21]. Zhang et al. simulated seven scenarios to predict the changing trend of carbon emissions in the Xi’an operation stage. The results show that the crude development scenario fails to reach its peak, whereas the comprehensive optimized development scenario will reach its peak in 2040, and the remaining scenarios will reach their peak in 2050 [22]. Ning et al. conducted simulations and predictions on the carbon peak time, peak value, and emission reduction potential of cities and urban agglomerations under various scenarios. The findings indicate that Hohhot and Baotou are projected to reach their carbon peaks in 2033 and 2031, respectively, under the baseline scenario. In contrast, other regions and urban agglomerations are not expected to reach their carbon peaks until 2035 [23].

Overall, the researchers identified the dominant factors of carbon emissions in different regions by using the STIRPAT model, suggesting that it is highly practical. It not only helps to decompose the factors that affect carbon emissions but also includes multiple index factors into the equation at the same time and can be used as an effective model in the prediction of carbon emissions, which is conducive to subsequent research.

This study takes the Sichuan-Chongqing region as the research area and uses the carbon emission coefficient method to estimate the industrial carbon emissions of Sichuan Province and Chongqing Municipality. The degree of correlation between the selected potential variables was quantitatively described by the gray correlation method. The influencing factors were accurately analyzed by stepwise regression and the effective factors with significant significance were retained. A STIRPAT extended model was constructed and a linear regression method was used to calculate the model. Finally, the peak time and value of industrial carbon emissions in the two regions were predicted based on a prediction model of industrial carbon emissions and scenario analysis. The following Figure 1 represents the overall structure of this article.

3. Industrial Carbon Emission Measurement

3.1. Carbon Emission Measurement Methods

This study adopted a top-down approach to calculate industrial carbon emissions in the Sichuan-Chongqing region from 2000 to 2022. The carbon emission coefficients of various energy sources were obtained from the IPCC Guidelines for National Greenhouse Gas Emission Inventory and raw coal, coke, crude oil, gasoline, kerosene, fuel oil, natural gas, and electricity consumption representing carbon emissions were selected [24].

At present, this method is mainly used by the IPCC, domestic Ministry of Ecology and Environment, and other authoritative institutions.

$${\mathrm{C}}_{\mathrm{i}}^{\mathrm{t}}=\sum {\mathrm{E}}_{\mathrm{i}}^{\mathrm{t}}\times {\mathrm{F}}_{\mathrm{i}}\times {\mathsf{\beta }}_{\mathrm{i}}$$

(1)

${\mathrm{C}}_{\mathrm{i}}^{\mathrm{t}}$ is the carbon dioxide emissions produced by the consumption of i energy in year t of the industrial sector, ${\mathrm{E}}_{\mathrm{i}}^{\mathrm{t}}$ is the physical consumption of i energy in the t year of the industrial department, ${\mathrm{F}}_{\mathrm{i}}$ is the reference coefficient of i energy converted into standard coal, and ${\mathsf{\beta }}_{\mathrm{i}}$ is the standard carbon emission coefficient of i energy.

3.2. Industrial Carbon Emission Measurement Results

Based on the calculation of industrial carbon emissions in the Sichuan-Chongqing region from 2000 to 2022, it was determined that the total industrial carbon emissions of Sichuan Province and Chongqing Municipality will change due to energy consumption, as shown in

Table 1. Carbon emissions from energy consumption by industry.

Sichuan Province						Chongqing Municipality
Year	Coal	Oils	Natural Gas	Electricity	Total	Year	Coal	Oils	Natural Gas	Electricity	Total
2000	32.62	0.61	0.30	1.30	34.84	2000	7.51	0.08	0.11	0.31	8.01
2001	34.90	0.69	0.32	1.44	37.35	2001	7.87	0.07	0.12	0.45	8.51
2002	29.17	0.48	0.42	1.80	31.87	2002	7.70	0.07	0.13	0.40	8.30
2003	38.74	0.63	0.44	2.07	41.88	2003	9.66	0.09	0.13	0.49	10.37
2004	39.47	0.84	0.35	1.71	42.37	2004	11.07	0.12	0.13	0.49	11.81
2005	41.76	0.92	0.37	1.84	44.88	2005	12.36	0.14	0.15	0.55	13.21
2006	45.24	1.27	0.46	2.22	49.19	2006	14.89	0.24	0.16	0.63	15.93
2007	49.80	1.45	0.45	2.38	54.09	2007	17.95	0.27	0.20	0.77	19.17
2008	52.45	2.05	0.46	2.39	57.34	2008	19.84	0.25	0.22	0.93	21.24
2009	60.38	2.04	0.55	2.64	65.61	2009	21.59	0.24	0.22	1.00	23.05
2010	57.66	2.14	0.72	3.02	63.54	2010	25.87	0.27	0.25	1.18	27.57
2011	57.91	2.57	0.57	3.90	64.95	2011	28.43	0.27	0.25	1.31	30.27
2012	61.16	2.68	0.43	3.99	68.26	2012	26.13	0.26	0.30	1.36	28.05
2013	60.32	5.05	0.74	4.06	70.17	2013	27.47	0.29	0.30	1.48	29.54
2014	57.07	7.68	0.64	3.87	69.26	2014	28.87	0.29	0.33	1.63	31.12
2015	47.75	10.53	0.62	3.65	62.55	2015	28.14	0.34	0.37	1.70	30.56
2016	43.87	4.31	0.77	3.64	52.59	2016	26.51	0.36	0.42	1.70	28.99
2017	40.39	4.52	0.80	3.75	49.46	2017	24.21	0.33	0.42	1.69	26.65
2018	38.92	3.69	0.87	4.16	47.64	2018	23.56	0.25	0.40	1.71	25.91
2019	40.35	4.28	0.97	4.45	50.05	2019	24.70	0.25	0.39	1.75	27.09
2020	39.23	4.19	1.01	4.84	49.26	2020	23.12	0.24	0.44	1.74	25.54
2021	40.83	4.49	1.13	5.53	51.98	2021	22.19	0.21	0.49	1.92	24.82
2022	40.85	4.51	1.13	5.62	52.11	2022	23.28	0.19	0.53	1.95	25.95

(Unit: Mt) and Figure 2 below.

According to Figure 2, the analysis of industrial carbon emissions in Sichuan and Chongqing region from 2000 to 2022 shows that carbon emissions have increased from 42.85 million tons in 2000 to 78.05 million tons in 2022, with an average annual growth rate of 3.73%. Overall, carbon emissions exhibited an inverted U-shaped development trend, which is in line with the environmental Kuznets theory. This is primarily because the adjustment of energy use has led to a constant change in industrial carbon emissions in the region. At the same time, it should be noted that the Sichuan-Chongqing region has begun to pay attention to carbon emission reduction and the development of the low-carbon economy.

The estimated results in Table 1 show that the total carbon emissions of Sichuan Province increased from 34.84 million tons in 2000 to 52.11 million tons in 2022, with an average annual rate of change of 2.25%. From 2000 to 2013, carbon emissions increased rapidly, with an average annual rate of change of 7.80%, whereas from 2014 to 2018, carbon emissions decreased significantly, with an average annual rate of change of −11.34%. The total carbon emission of Chongqing increased from 8.01 million tons in 2000 to 25.95 million tons in 2022, with an average annual rate of change of 10.18%. During 2000–2014, carbon emissions increased rapidly, with an average annual rate of change of 20.61%, and from 2015 to 2018, carbon emissions decreased annually, with an annual rate of change of −5.97%. Based on the analysis of carbon emission changes in the two places, it is found that the overall development trend of carbon emission in Sichuan Province and Chongqing Municipality from 2000 to 2022 presents an inverted U-shape and the decrease in coal consumption and the increase in natural gas and electricity consumption in the two regions are the direct causes of carbon emission changes. In addition, in 2014, with The State Council of China on the “2014–2015 Energy Conservation and Emission Reduction and Low Carbon Development Action Plan” issued, Sichuan Province and Chongqing actively responded to the policy call, increased the adjustment of industrial structure, accelerated economic transformation and upgrading, and began to show a significant decline in carbon emissions from that year. Therefore, the promulgation of relevant governance policies will lead to constant changes in total regional industrial carbon emissions.

3.3. Data Source Description

In this study, data on the industrial fossil energy consumption, population, per capita income, industrial added value, and total import and export volumes of Sichuan Province and Chongqing from 2000 to 2022 were obtained from the China Statistical Yearbook, Chongqing Statistical Yearbook, Sichuan Statistical Yearbook, and China Energy Statistical Yearbook from 2001 to 2023. Data on energy intensity and energy structure were calculated according to the proportion of clean energy to total energy consumption, total energy consumption, and regional GDP, respectively.

4. Analysis of Influencing Factors of Industrial Carbon Emission

4.1. Construct STIRPAT Extension Model

The STIRPAT model is a nonlinear model based on the classical environmental pressure equation (IPAT). The basic STIPAT model equation is as follows:

$$\mathrm{I}=\mathsf{\alpha }{\mathrm{P}}^{\mathrm{b}}{\mathrm{A}}^{\mathrm{c}}{\mathrm{T}}^{\mathrm{d}}\mathrm{e}$$

(2)

Among them, I represents regional industrial carbon emissions; P represents population; A represents per capita income, indicating economic level; T represents the technical level; and $\mathsf{\alpha }$ is a constant term. b, c, and d represent the elastic coefficients of the above three, respectively, and e is the errors of the entire model.

According to Equation (2), the STIRPAT model exhibited better plasticity and adaptability. To analyze industrial carbon emissions in the Sichuan-Chongqing area more comprehensively, more independent variables were introduced. Based on existing references, the technology level was broken down into energy structure and energy intensity indicators [25] and then industrial-scale and foreign trade dependence were introduced. Therefore, the model is expanded to

$$\mathrm{I}=\mathsf{\alpha }{\mathrm{P}}^{\mathrm{b}}{\mathrm{A}}^{\mathrm{c}}{\mathrm{E}}^{\mathrm{d}}{\mathrm{N}}^{\mathrm{f}}{\mathrm{I}\mathrm{S}}^{\mathrm{g}}{\mathrm{F}\mathrm{D}}^{\mathrm{h}}\mathrm{e}$$

(3)

Table 2. The meaning, measurement method, and selection basis of specific indicators.

Index	Indicator Meaning	Index Measurement	Selection Basis
P	Population	Total resident population at year-end (100 million)	The growth of urban population increases the total energy consumption, thus increasing the total carbon emission and carbon emission intensity [13]
A	Per capita income	Regional GDP per capita (ten thousand yuan)	Rapid economic development changes people’s consumption structure and affects carbon emission level and carbon intensity [10]
E	Energy structure	Clean consumption/Total energy consumption (104 tons)	The use of clean energy can effectively reduce the consumption of fossil energy, thus reducing the carbon emission intensity and pollutant emission level [14]
N	Energy intensity	Total energy consumption/GDP (104 tons/billion yuan)	Energy intensity reflects the economic benefits of energy utilization and becomes an important contributing factor to curbing the growth of carbon emissions [11]
IS	Industrial scale	Industrial added value/GDP (100 million yuan)	Industrial scale adjustment not only affects the overall industrial development but also affects the industrial structure, thus affecting the total carbon emission and carbon intensity [26]
FD	Foreign trade dependence	Total imports and exports/GDP (100 million yuan)	Rapid economic development has enhanced import and export trade, increased the output of capital-intensive and technology-intensive products, and significantly increased carbon emissions of various countries due to trade frictions [13]

Tips: Clean energy means natural gas plus electricity.

lists the meanings and measurement methods for the specific indicators. d, f, g and h are elastic coefficients, indicating that when other factors remain unchanged; E, N, IS and FD change by 1%, respectively and I will change by d%, f%, g%, and h%, respectively.

According to relevant data from the Chongqing Statistical Yearbook and Sichuan Statistical Yearbook from 2001 to 2023, the potential influencing factors involved were sorted and

Table 3. Specific values of each influencing factor.

Sichuan Province								Chongqing Municipality
Year	LnP	LnA	LnE	LnN	LnIS	LnFD	LnP	LnA	LnE	LnN	LnIS	LnFD
2000	−0.183	−0.702	−2.541	0.535	−1.211	−3.062	−1.256	−0.449	−2.533	−0.094	−1.040	−2.648
2001	−0.205	−0.621	−2.517	0.517	−1.217	−2.954	−1.263	−0.343	−2.267	−0.121	−1.046	−2.722
2002	−0.209	−0.529	−2.147	0.280	−1.222	−2.684	−1.268	−0.213	−2.339	−0.272	−1.043	−2.868
2003	−0.201	−0.421	−2.282	0.423	−1.189	−2.576	−1.272	−0.071	−2.371	−0.198	−1.010	−2.636
2004	−0.212	−0.255	−2.478	0.260	−1.153	−2.543	−1.275	0.089	−2.481	−0.229	−0.982	−2.397
2005	−0.197	−0.125	−2.462	0.186	−1.076	−2.535	−1.274	0.094	−2.462	−0.250	−0.979	−2.409
2006	−0.202	0.036	−2.368	0.113	−1.021	−2.368	−1.270	0.208	−2.515	−0.192	−0.908	−3.424
2007	−0.207	0.260	−2.397	−0.011	−0.997	−2.320	−1.267	0.383	−2.507	−0.213	−0.941	−2.184
2008	−0.206	0.450	−2.446	−0.146	−0.954	−2.078	−1.259	0.589	−2.423	−0.323	−0.992	−2.150
2009	−0.200	0.553	−2.473	−0.118	−0.926	−2.096	−1.252	0.829	−2.437	−0.365	−0.990	−2.480
2010	−0.218	0.753	−2.301	−0.338	−0.896	−1.987	−1.243	1.033	−2.458	−0.374	−1.007	−2.196
2011	−0.215	0.961	−2.116	−0.507	−0.912	−1.810	−1.223	1.238	−2.456	−0.507	−1.010	−1.572
2012	−0.213	1.086	−2.159	−0.586	−0.933	−1.723	−1.212	1.359	−2.338	−0.711	−0.994	−1.105
2013	−0.210	1.186	−2.124	−0.674	−0.945	−1.738	−1.200	1.464	−2.311	−0.775	−1.004	−0.966
2014	−0.206	1.269	−2.150	−0.788	−0.993	−1.740	−1.190	1.565	−2.260	−0.847	−1.002	−0.753
2015	−0.199	1.312	−2.021	−1.023	−1.039	−2.105	−1.181	1.655	−2.194	−0.957	−1.049	−1.093
2016	−0.192	1.394	−1.939	−1.178	−1.122	−2.231	−1.168	1.766	−2.124	−1.130	−1.117	−1.381
2017	−0.188	1.522	−1.851	−1.372	−1.198	−2.042	−1.157	1.848	−2.057	−1.309	−1.174	−1.429
2018	−0.184	1.642	−1.726	−1.518	−1.244	−1.888	−1.151	1.924	−2.044	−1.392	−1.237	−1.331
2019	−0.180	1.716	−1.702	−1.547	−1.259	−1.876	−1.143	2.006	−2.068	−1.438	−1.282	−1.360
2020	−0.178	1.758	−1.616	−1.600	−1.286	−1.749	−1.137	2.058	−2.009	−1.546	−1.274	−1.302
2021	−0.178	1.866	−1.544	−1.648	−1.247	−1.626	−1.136	2.162	−1.894	−1.679	−1.263	−1.144
2022	−0.177	1.911	−1.533	−1.690	−1.252	−1.649	−1.135	2.186	−1.917	−1.652	−1.277	−1.177

was obtained.

To calculate the undetermined coefficients, the nonlinear model was converted into a log-linear model, as follows:

lnI = lnα + blnP + clnA + dlnE + flnN + glnIS + hlnFD + lne

(4)

Factor analysis of potential influencing factors, with regard to Sichuan Province and Chongqing Municipality, the KMO test values of 0.643 and 0.811, respectively, the value of 0.6–0.8 are suitable for factor analysis, and Bartlett’s test of the household straight is less than 0.001, indicating that there is a correlation between the variables. Based on this, the variables were subjected to a gray correlation analysis and stepwise regression.

4.2. Model Analysis

4.2.1. Unit Root Test

In our study, we use the extended STIRPAT model to estimate industrial carbon emissions in the Sichuan-Chongqing region. Stationarity tests are performed using enhanced Dickey-Fuller (ADF) tests. If the sequence is not stationary, first-order difference processing must be performed, and if the first-order differential sequence is still unstable, second-order differential processing must be performed, and stationarity testing must be performed until the data are stationary. The analysis found that the data of Chongqing showed better stationarity after 2002, so the analysis of Chongqing in this paper is based on the data analysis from 2002 to 2022, the analysis of Sichuan in this paper is based on the data analysis from 2000 to 2022.

Table 4. The results of the unit root test. (D denotes the first-order difference and DD denotes the second-order difference).

Sichuan Province								Chongqing Municipality
Variable	AIC Value	1% Critical Value	5% Critical Value	10% Critical Value	t	p	Stationarity	AIC Value	1% Critical Value	5% Critical Value	10% Critical Value	t	p	Stationarity
LnI	−30.336	−3.77	−3.005	−2.643	−1.895	0.334	nonstationary	−40.163	−3.964	−3.085	−2.682	−2.966	0.038 **	stationary
LnP	−109.355	−4.069	−3.127	−2.702	−1.451	0.558	nonstationary	−104.441	−3.809	−3.022	−2.651	0.629	0.988	nonstationary
LnA	−49.354	−4.012	−3.104	−2.691	−1.367	0.598	nonstationary	−70.514	−4.138	−3.155	−2.714	−3.078	0.028 **	stationary
LnE	−37.314	−4.069	−3.127	−2.702	0.093	0.966	nonstationary	−37.118	−3.809	−3.022	−2.651	0.615	0.988	nonstationary
LnN	−34.792	−3.77	−3.005	−2.64	−0.002	0.958	nonstationary	−33.037	−3.964	−3.085	−2.682	−2.593	0.094 *	stationary
LnIS	−56.332	−4.069	−3.127	−2.702	−1.494	0.537	nonstationary	−63.266	−4.138	−3.155	−2.714	0.396	0.981	nonstationary
LnFD	−39.781	−4.069	−3.127	−2.702	−6.573	0.000 ***	stationary	−27.431	−4.138	−3.155	−2.714	−3.031	0.032 **	stationary
DLnI	−29.796	−4.138	−3.155	−2.714	−1.537	0.515	nonstationary	−36.146	−4.223	−3.189	−2.73	−2.333	0.162	nonstationary
DLnP	−172.713	−4.138	−3.155	−2.714	−26.606	0.000 ***	stationary	−97.182	−4.223	−3.189	−2.73	1.096	0.995	nonstationary
DLnA	−41.589	−3.788	−3.013	−2.646	−2.216	0.201	nonstationary	−73.639	−4.223	−3.189	−2.73	−3.078	0.028 **	stationary
DLnE	−43.625	−4.138	−3.155	−2.714	−2.323	0.165	nonstationary	−79.031	−4.223	−3.189	−2.73	−14.412	0.000 ***	stationary
DLnN	−32.068	−3.788	−3.013	−2.646	−5.957	0.000 ***	stationary	−28.174	−3.859	−3.042	−2.661	−2.738	0.068 *	stationary
DLnIS	−48.301	−3.788	−3.013	−2.646	−1.632	0.466	nonstationary	−61.326	−4.138	−3.155	−2.714	−1.026	0.744	nonstationary
DLnFD	−32.291	−4.138	−3.155	−2.714	−0.742	0.836	nonstationary	−12.994	−4.223	−3.189	−2.73	0.245	0.975	nonstationary
DDLnI	−23.874	−3.809	−3.022	−2.651	−10.241	0.000 ***	stationary	−24.673	−3.889	−3.054	−2.667	−7.323	0.000 ***	stationary
DDLnP	−97.862	−4.069	−3.127	−2.702	−3.464	0.009 ***	stationary	−96.739	−3.889	−3.054	−2.667	−3.524	0.007 ***	stationary
DDLnA	−39.662	−3.833	−3.031	−2.656	−5.259	0.000 ***	stationary	−45.413	−3.964	−3.085	−2.682	−4.351	0.000 ***	stationary
DDLnE	−24.829	−3.889	−3.054	−2.667	−4.078	0.001 ***	stationary	−28.295	−3.924	−3.068	−2.674	−4.126	0.001 ***	stationary
DDLnN	−29.006	−3.809	−3.022	−2.651	−10.404	0.000 ***	stationary	−26.44	−3.889	−3.054	−2.667	−7.199	0.000 ***	stationary
DDLnIS	−44.6	−3.809	−3.022	−2.651	−5.279	0.000 ***	stationary	−55.369	−4.138	−3.155	−2.714	−4.894	0.000 ***	stationary
DDLnFD	−29.03	−4.138	−3.155	−2.714	−5.566	0.000 ***	stationary	−14.352	−4.223	−3.189	−2.73	−3.224	0.019 **	stationary

Note: ***, **, and * represent the significance level of 10%, 5%, and 1%, respectively.

shows that the ADF value of the second-order differential sequence of each variable exceeds the significance threshold of 1% and reaches a stationary state.

4.2.2. Gray Correlation Analysis

Gray correlation analysis is used to analyze the correlation between the characteristic series and the parent series [27] and the gray correlation score method is used to calculate the correlation between the above six variables and total carbon emissions. The main steps are as follows:

(1)

The reference series $X_0\left(k\right)$ is the total industrial carbon emissions from 2000 to 2022 and comparison series $X_q\left(k\right)$ is the indicator of each influencing factor;

(2)

Dimensionless processing of data. The total industrial carbon emissions and their influencing factors have different unit attributes, some of which are numerical and some of which are ratios; direct comparisons between them require standardization of the data into dimensions;

(3)

The resolution coefficient $\delta$ is set to 0.5, the result is accurate to four decimal places, and the correlation degree is obtained using Formulas (5) and (6).

$$r=\frac{\frac{min}{q}\frac{min}{k}\left|X_0\left(k\right)-X_q\left(k\right)\right|+\frac{max}{q}\frac{max}{k}\left|X_0\left(k\right)-X_q\left(k\right)\right|}{\left|X_0\left(k\right)-X_q\left(k\right)\right|+\frac{max}{q}\frac{max}{k}\left|X_0\left(k\right)-X_q\left(k\right)\right|}$$

(5)

$$R=\frac{1}{n}{\sum }_{k=1}^{n}r$$

(6)

In Equations (5) and (6), q represents the influencing factor, k represents the year, and r represents the degree of correlation between the influencing factors and industrial carbon emissions and indicates the degree of correlation between the influencing factors. The results are summarized in

Table 5. Gray relational degree table among variables.

Sichuan Province								Chongqing Municipality
	LnI	LnP	LnA	LnE	LnN	LnIS	LnFD		LnI	LnP	LnA	LnE	LnN	LnIS	LnFD
LnI	1							LnI	1
LnP	0.837	1						LnP	0.854	1
LnA	0.554	0.557	1					LnA	0.566	0.527	1
LnE	0.830	0.922	0.564	1				LnE	0.857	0.939	0.606	1
LnN	0.529	0.521	0.815	0.523	1			LnN	0.580	0.535	0.815	0.543	1
LnIS	0.880	0.887	0.591	0.866	0.585	1		LnIS	0.788	0.831	0.651	0.814	0.653	1
LnFD	0.885	0.893	0.56	0.919	0.555	0.579	1	LnFD	0.844	0.678	0.507	0.725	0.502	0.574	1

. The greater the degree of correlation, the greater the influence of the influencing factor on industrial carbon emissions, and vice versa. When the gray correlation degree between the two influencing factors was greater than 0.9, multicollinearity between the two factors was determined and the influencing factors with little correlation with industrial carbon emissions could be eliminated.

According to the data analysis, the factors influencing the degree of industrial carbon emissions correlation in Sichuan Province, in descending order, were foreign trade dependence, industrial scale, population, energy structure, per capita income, and energy intensity. In Chongqing, energy structure, population, foreign trade dependence, industrial scale, energy intensity, and per capita income are ranked in that order. If the degree of correlation was greater than 0.9, multicollinearity existed between two factors. It is found that the correlation degree between the population and energy structure in Sichuan Province is 0.922; in fact, even the correlation degree between the energy structure and foreign trade dependence in Sichuan Province is 0.919 but the correlation degree between the population and industrial carbon emissions is greater than the correlation degree between the energy structure and industrial carbon emissions, so the energy structure is excluded. Similarly, the correlation between population and energy structure in Chongqing is 0.939 but the correlation degree between energy structure and industrial carbon emissions is greater than that between population and industrial carbon emissions, meaning the population was excluded. The remaining factors were preliminarily identified as useful influencing factors for each province and city.

4.2.3. Stepwise Regression

In this paper, the step-up screening method is used to make certain improvements on the basis of the forward approach. When a variable is introduced, it is first checked as to whether the variable causes significant changes in the model (F-value). If significant changes occur, the T-value is carried out on all variables. When a newly introduced variable is not significant or the original introduced variable no longer changes significantly due to the newly added variable, this variable is excluded to ensure that only significant variables are included in the regression equation before each new variable is introduced. Finally, an optimal set of variables is obtained.

According to the data analysis in Table 5, the foreign trade dependence had the highest degree of correlation with industrial carbon emissions in Sichuan Province, which was first selected into the model and constructed as Model 1. At this time, there were four explanatory variables outside Model 1 and the variable with the second-highest degree of correlation was introduced into the model for regression. Based on Model 1, industrial scale was selected and the results showed that the revised R² was 0.931, the T-value of the industrial scale was 10.303, and the p-value was 0.000, which was less than p = 0.10. The industrial scale is retained after the significance test. Then, the population with the third correlation degree was selected and the results showed that the revised R² = 0.939, T-value of the energy structure was 1.909, and p-value was 0.071, which is less than p = 0.10. Thus, the population was selected. The remaining two variables were brought into regression in turn and the results showed that the T-values of per capita income and energy intensity were 1.770 and −0.943, respectively, and the p-values were 0.094 and 0.358, respectively; the per capita income passed statistical tests while the energy intensity did not. However, the p-values of the population changed to 0.390 after the addition of per capita income, making it insignificant. In addition, the correlation between per capita income and industrial carbon emissions was weaker than that between population and industrial carbon emissions; it also makes foreign trade dependence appear weak significance. Therefore, per capita income was excluded. Therefore, the effective factors affecting industrial carbon emissions in Sichuan Province are industrial scale, foreign trade dependence, and population.

It can be seen from the data in Table 5 that energy structure had the highest correlation with industrial carbon emissions in Chongqing and it was first selected into the model and constructed as Model 2. Currently, four explanatory variables outside Model 2 are successively brought into the model for regression according to the degree of correlation. Based on Model 2, foreign trade dependence was selected for the statistical significance test. The results show that for the revised R² = 0.603, the T-value of foreign trade dependence was 4.818 and the p-value was 0.000, which was less than p = 0.10. However, the p-values of the energy structure changed to 0.344 after the addition of foreign trade dependence, making it insignificant. In addition, the correlation between foreign trade dependence and industrial carbon emissions was weaker than that between energy structure and industrial carbon emissions; therefore, foreign trade dependence was excluded. The industrial scale with the third-degree correlation was then selected for the statistical significance test. The results showed that the revised R² = 0.123, the T-value of the industrial scale was 0.806, and the p-value was 0.431, showing insignificant statistics; thus, the industrial scale was excluded. At this time, energy intensity and per capita income are brought into the model and this showed that energy intensity was statistically significant (t = −5.946, p = 0.000) and that per capita income passed the statistical significance test (t = 22.386, p = 0.000). Comparing the fitting effects of the two models adding energy intensity or per capita income, it is found that the R² and F values of the model adding energy intensity (R² = 0.851, F = 23.61) are much smaller than the two values after adding per capita income (R² = 0.986, F = 308.27), indicating that adding per capita income makes the model more reliable. If both factors are added, the energy structure will be not significant (p = 0.247). The final factors affecting industrial carbon emissions in Chongqing were energy structure and per capita income. After gray correlation analysis and stepwise regression, the formulas are as follows.

• Sichuan Province:

LnI = Lnα + bLnFD + cLnIS +dLnP+ Lne

(7)

• Chongqing Municipality

LnI = Lnα + bLnE + cLnA + Lne

(8)

4.2.4. Co-Integration Test and Multicollinearity Test

(1)

EG test

The EG test is to test the co-integration relationship between two or more higher-order single integral variables and makes judgments by analyzing the stationarity of the residual after regression. If the null hypothesis is rejected (p < 0.05), there is a co-integration relationship. The effective variables of Sichuan and Chongqing after gradual regression are tested and the results are shown in

Table 6. Results of cointegration test.

Sichuan Province				Chongqing Municipality
		t-Statistic	Prob.			t-Statistic	Prob.
ADF test		−6.143479	0.0000	ADF test		−3.723464	0.0009
Test critical values	1% level	−2.674290		Test critical values	1% level	−2.699769
	5% level	−1.957204			5% level	−1.961409
	10% level	−1.608175			10% level	−1.606610

. The p-values of Sichuan Province and Chongqing are 0.0000 and 0.0009, respectively, indicating that the co-integration test is passed.

(2)

Multicollinearity test

Multiple variables influence each other, which may lead to multicollinearity problems in time-series data. Variance inflation factor (VIF) analysis was performed for each variable and multicollinearity between variables was judged by the VIF value. The results in

Table 7. Argument VIF value.

Sichuan Province		Chongqing Municipality
	VIF		VIF
lnFD	1.440	LnE	3.356
LnIS	3.257	LnA	3.356
LnP	3.222

show that the VIF value of each variable in both Sichuan and Chongqing is less than 10; the model is not affected by multicollinearity among the variables and the obtained results are reliable.

4.2.5. Linear Regression Analysis

The OLS regression model is a statistical analysis method used to determine the interdependent quantitative relationships between two or more variables. The QLS linear regression was performed using Equations (7) and (8). At this time, the p value of the F-test was 0.000, which was less than the 1% significance level, and the model showed significance, indicating that there was a regression relationship between the independent and dependent variables. Simultaneously, the goodness of fit R² and F values of the modified model were 0.948 and 114.34 (Sichuan) and 0.972 and 308.27 (Chongqing), respectively, and the specific regression values are listed in

Table 8. OLS regression analysis results.

Area	Variables	B	Std. Error	Beta	t	p	R2	F
Sichuan Province	Adjust R2 = 0.939						0.948	114.343 (0.000 ***)
	Constant	1.896	0.424		4.467	0.000 ***
	LnFD	0.309	0.033	0.593	9.41	0.000 ***
	LnIS	1.19	0.153	0.738	7.782	0.000 ***
	LnP	2.986	1.564	0.18	1.909	0.071 *
Chongqing Municipalit	Adjust R2 = 0.968						0.972	308.273 (0.000 ***)
	Constant	−6.495	0.35		−18.551	0.000 ***
	LnE	−1.791	0.139	−0.938	−12.893	0.000 ***
	LnA	0.784	0.035	1.628	22.386	0.000 ***

Note: *** and * represent the significance level of 10% and 1%, respectively.

.

In Sichuan Province, if the industrial scale changes by 1%, industrial carbon emissions change by 1.19%. An increase in the proportion of the added value of the secondary industry to the gross national product at the industrial scale will promote the production of total carbon dioxide emissions. Judging from the current development situation in Sichuan Province, the industrial structure has changed from being dominated by secondary industries to tertiary industries and the substantial increase in tertiary industries will also increase the carbon emissions. Therefore, upgrading the industrial structure of Sichuan Province will change the industrial carbon emissions.

The level of foreign trade dependence has a positive impact on industrial carbon emissions in Sichuan Province, with a contribution rate of 0.309, indicating that an improvement in foreign trade will promote industrial carbon emissions. During the processes of importing and exporting products and economic development, a large amount of energy needs to be invested to create an output, especially for capital- and technology-intensive products. The greater the output, the greater the total industrial carbon emissions. But at the same time, the economic development brought about by foreign trade has promoted technological progress, thus effectively improving the efficiency of energy use and reducing industrial carbon emissions caused by excess energy consumption.

The p-value of the population is 2.986, which indicates that the population does present a weak significant effect on industrial carbon emissions in Sichuan and it is possible to control industrial carbon emissions by limiting the number of the population. It is found that an increase in population will also increase the number of industrial employees, which means that industries, especially the manufacturing industry, continue to develop rapidly, resulting in an increase in energy demand and industrial carbon emissions. Carbon emissions lead to the deterioration of the environment, bring ecological persecution, and endanger primary industries, thus falling into the population growth trap.

The contribution rate of energy structure to Chongqing is −1.791, showing a reverse effect, indicating that energy consumption dominated by clean energy instead of coal has reduced the total amount of industrial carbon emissions. Sichuan Province has gradually changed its economic development mode from extensive to intensive, the high-energy-consuming coal industry has gradually decreased, the high-tech and tertiary industries have accelerated development, and the industrial structure has been optimized and adjusted. The energy consumption has been reduced and the energy efficiency has improved. Accelerating the transformation of fossil fuel energy into clean energy has become a direction for realizing a low-carbon economy in Chongqing.

Per capita income had a relatively lesser impact on industrial carbon emissions in Chongqing, with a contribution rate of 0.784. When the level of industrial development in a country or region is low, the level of industrial carbon emissions is also low; however, with the improvement in the per capita income level, that is, the improvement in the industrial development level, the level of industrial carbon emissions will increase along with economic growth. When industrial development reaches a certain level, that is, after the per capita income reaches a certain critical point, with further improvement in the per capita income level, the industrial carbon emission level begins to decline, which is manifested as the gradual slowing down of the industrial carbon emission level and the gradual improvement in high carbon emission pressure.

4.2.6. Model Heteroscedasticity and Validity Test

(1)

Heteroscedasticity test

The white test results in

Table 9. Results of the heteroscedasticity test.

Sichuan Province		Chongqing Municipality
White Test		White Test
χ2	p	χ2	p
14.759	0.098	3.866	0.569

show that the p-values of both regions are greater than 0.05 and the null hypothesis shows that there is no heteroscedasticity in the model that is accepted, indicating that there is no heteroscedasticity problem.

(2)

Validity test

The relevant variables were substituted into the regression equation to obtain the simulated industrial carbon emissions of Sichuan Province from 2000 to 2022 and Chongqing Municipality from 2002 to 2022 and then the simulated values were fitted and compared with the actual carbon emissions of each year, as shown in Figure 3 below. The general trend is consistent, indicating that the prediction model is empirically significant. Therefore, this model was adopted to predict industrial carbon emissions in the two regions.

5. Forecast of Peak Industrial Carbon Emissions

5.1. Scenario Design

To estimate industrial carbon emissions in Sichuan Province and Chongqing Municipality from 2023 to 2040, four scenarios of low-speed, baseline, green, and rapid development were set based on documents such as the 13th and 14th Five-Year Plans of Sichuan Province and Chongqing Municipality and the existing literature [28,29]. Three change rates of low-, medium-, and high-speed growth were used to predict each influencing factor. For more details, please refer to

Table 10. Combination setting of different development scenarios.

Sichuan Province				Chongqing Municipality
Scenario combination	FD	IS	P	E	A
Low-speed development scenario	Low speed	Low speed	Low speed	Low speed	Low speed
Baseline development scenario	Moderate speed	Moderate speed	Moderate speed	Moderate speed	Moderate speed
Green development scenario	Low speed	High speed	Moderate speed	High speed	Low speed
Rapid development scenario	High speed	Moderate speed	High speed	Moderate speed	High speed

.

From the perspective of the Sichuan Province. (1) In a low-speed development scenario, the rate of change in each influencing factor increases at a low speed; that is, strict control of the movement of people in the region and the foreign trade speed is appropriately slowed down to reduce the overall industrial carbon emissions. (2) Baseline development scenario: In the case that existing policy conditions do not change, the change in all factors is set to “medium” as its baseline development situation. (3) Green development scenario: With the help of stricter environmental regulations to eliminate backward production capacity, the adjustment of the industrial scale can be accelerated. Slowing down the speed of foreign trade and strictly controlling the growth rate of the population are advised. (4) Rapid development scenario: The industrial scale adjustment speed is moderate. The strengthening of foreign trade promotes rapid economic development; population growth soared as rapid economic development and attracted more people to the region but it led to an uncontrolled increase in carbon emissions, having a serious impact on the environment.

From the perspective of Chongqing, (1) in a low-speed development scenario, the region’s overall economy is developing at a low rate and energy structure and per capita income is growing at a low rate. (2) Benchmark development scenario: In the case that the existing economic development and energy policy conditions do not change, the change in all factors is set as “medium” as its benchmark development situation. (3) The green development scenario focuses on the introduction of low-carbon technologies and the replacement of fossil energy with existing clean energy and renewable energy, thus promoting rapid changes in the energy structure and overall regional per capita income growth is stable. (4) Rapid development scenario: For the purpose of economic development, while implementing the existing energy policy, we should strengthen regional economic coordination and innovation to achieve an increase in per capita income.

The industrial carbon emission scenario parameters of relevant influencing factors in Sichuan Province and Chongqing Municipality were set, which were specifically described as follows. The specific values can be seen in

Table 11. The main parameters of each scenario are set.

Sichuan Province						Chongqing Municipality
	Year	Low-Speed Development Scenario	Baseline Development Scenario	Green Development Scenario	Rapid Development Scenario		Year	Low-Speed Development Scenario	Baseline Development Scenario	Green Development Scenario	Rapid Development Scenario
Industrial scale	2023–2025	−0.70%	−0.85%	−1.00%	−0.85%	Energy structure	2023–2025	0.90%	1.00%	1.10%	1.00%
	2026–2030	−1.00%	−1.15%	−1.30%	−1.15%		2026–2030	1.50%	1.60%	1.70%	1.60%
	2031–2035	−1.30%	−1.45%	−1.60%	−1.45%		2031–2035	2.10%	2.20%	2.30%	2.20%
	2036–2040	−1.60%	−1.75%	−1.90%	−1.75%		2036–2040	2.70%	2.80%	2.90%	2.80%
Population	2023–2025	0.12%	0.15%	0.15%	0.18%	Per capita income	2023–2025	5.50%	6.00%	5.50%	6.50%
	2026–2030	0.10%	0.13%	0.13%	0.16%		2026–2030	5.00%	5.50%	5.00%	6.00%
	2031–2035	0.08%	0.11%	0.11%	0.14%		2031–2035	4.50%	5.00%	4.50%	5.50%
	2036–2040	0.06%	0.09%	0.09%	0.12%		2036–2040	4.00%	4.50%	4.00%	5.00%
Foreign trade dependence	2023–2025	3.00%	3.50%	3.00%	4.00%
	2026–2030	3.50%	4.00%	3.50%	4.50%
	2031–2035	4.00%	4.50%	4.00%	5.00%
	2036–2040	4.50%	5.00%	4.50%	5.50%

.

(1)

Setting the scenario parameters for Sichuan Province

1.

Industrial scale

In the 14th Five-Year Plan and the outline of 2035 vision goals, it is pointed out that the cost and burden of manufacturing should be reduced, the structural upgrading of the secondary industry should be promoted, and the development of high-tech service industries should be emphasized. The goal is to achieve the added value of strategic emerging industries, accounting for more than 17% of the GDP by 2035. Combined with the study of Qichao et al. the study predicts that the primary industry will account for 5.0%, the secondary industry for 31.7%, and the tertiary industry for 63.3% in 2025 in Sichuan Province [30]. The proportion of secondary industry in the total economic volume of Sichuan Province shows a trend of fluctuating decline, indicating that the internal structure of the secondary industry in Sichuan Province is in the process of constant adjustment and transformation. Therefore, it is set that the average annual decline rate of the value-added of the secondary industry in GDP is −0.7% at low-speed growth, −0.85% at moderate-speed growth, and −1.0% at high-speed growth. The rate of decline was 0.3% every five years.

2.

Population

Macroeconomic factors include the population, urbanization rate, GDP, and industrial structure. The population factor is the key control object of government departments. Under the baseline scenario, the population develops according to the expected planning target. With the deepening of the scenario, the population growth rate gradually slows down. According to the Medium and Long Term Plan of Population Development of Sichuan Province, “the permanent population will reach about 84.3 million by 2025 and 84.7 million by 2030”, so the average annual growth rate of the population is set at 0.12% under the low growth rate. The average annual growth rate of medium-speed and high-speed growth is 0.15% and 0.18%, respectively. The rate of decline decreased by 0.2% every five years.

3.

Foreign trade dependence

According to the Sichuan-Chongqing regional planning document, the import and export trade of the Shuangcheng economic circle in the Sichuan-Chongqing region continues to increase and the economy is booming, which means that the degree of opening up will also increase. Referring to the foreign trade statistics document of the Sichuan Provincial government, it is mentioned that “Sichuan’s foreign trade exports in 2021 will be 570.87 billion yuan, an increase of 22.7% over the previous year; Imports reached 380.49 billion yuan, up 10.8% over the previous year. Compared with 2019, Sichuan’s foreign trade import and export, export and import increased by 40.1%, 46.2% and 31.8% compared with the previous year, respectively.” Therefore, the average annual growth rates of total imports and exports in the GDP are 3%, 3.5%, and 4% under low-, moderate-, and high-speed growth, respectively. The growth rate increased by 0.5% every five years.

(2)

Setting scenario parameters in Chongqing

1.

Energy structure

The “Action Plan for carbon Peak before 2030” points out that it is necessary to optimize the energy structure, reduce the use of coal and other fossil energy, promote the development of new energy, and improve energy efficiency. According to the “14th Five-Year Plan for Chongqing Energy Development (2021–2025)”, the expected growth rate of the proportion of non-fossil energy consumption, the proportion of coal consumption, and the proportion of natural gas consumption in 2020–2025 under the goal of energy green transformation is 4.1%, −4.3%, and 4.3% respectively. The average annual growth rate of clean energy use in total energy consumption of Chongqing is 0.9%, 1.0%, and 1.1% under low-, moderate-, and high-speed growth, respectively. The growth rate has increased by 0.6% every five years.

2.

Per capita income

According to the “14th Five-Year Plan” of Chongqing and the outline of the 2035 Vision Goal”, it is required that “the economy will continue to grow steadily, and the per capita GDP will change from 79,000 yuan in 2020 to 102,000 yuan in 2025”. The expected goal was achieved by calculating that the average annual growth rate of Chongqing would remain at 5.82%. According to Wen et al. China’s per capita GDP growth will gradually slow from to 2015–2040 but the average annual growth rate should be between 5.8% and 6.2% [31]. Therefore, the average annual growth rate of per-capita income was set at 5.5%, 6.0%, and 6.5% for low-, medium-, and high-speed growth, respectively. The growth rate decreased by 0.5% every five years.

5.2. Peak Prediction Results and Analysis

Based on the prediction models of industrial carbon emissions in Sichuan Province and Chongqing Municipality combined with four development scenarios, this study calculates industrial carbon emission trends from 2023 to 2040 in the Sichuan-Chongqing region under different scenarios and obtains the peak time of industrial carbon in this region under different scenarios. The calculation results are shown in the Figure 4 below.

Future carbon emissions in Sichuan and Chongqing were predicted using the STIRPAT extended model and scenario analysis method. The predicted results are as follows.

In Sichuan Province, social and economic development is relatively slow under the low-speed development scenario. In this scenario, the time of the industrial carbon peak is approximately 2030 and the peak carbon emission is approximately 54.24 million tons. In the baseline development scenario, social and economic development are stable for a long time in which the industrial carbon peak time is approximately 2030 and the peak carbon emission is approximately 54.49 million tons. In the green development scenario, social and economic development will bear the pressure of energy conservation and emission reduction, the industry will assume more responsibility for emission reduction, and foreign trade will be controlled. In this scenario, the time for industrial carbon to peak is approximately 2025 and the peak carbon emission is 53.36 million tons. In the rapid development scenario, with rapid social and economic growth, rapid foreign trade dependence, industrial scale expansion, and the movement of the population may not be limited; the industrial carbon peak time is approximately 2035 and the peak carbon emissions are 56.06 million tons.

From the perspective of Chongqing, the regional economy will increase slowly in the low-speed development scenario. In this scenario, the peak time for industrial carbon emissions is approximately 2030 and the peak carbon emissions are approximately 29.74 million tons. In the baseline development scenario, social and economic development and the regional per capita income remained stable for a long time. In this scenario, the peak time of industrial carbon emissions will be approximately 2030 and the peak carbon emissions will be approximately 30.20 million tons. In the green development scenario, a strict energy policy will be carried out and speed up the use of clean energy. In this scenario, the industrial carbon peak will occur in approximately 2030 and the peak carbon emission will be 28.91 million tons. In a rapid development scenario, owing to the advantages of regional industrial economic development, the per capita income and economic trade will grow rapidly and consume large amounts of energy. In this scenario, the peak time for industrial carbon emissions is approximately 2035 and the peak carbon emissions are 31.58 million tons.

It can be seen from the forecast results that the forecast development trend of regional industrial carbon emissions in 2023–2040 is still in line with the environmental Kuznets law. Moreover, there were some differences in the realization time and peak height of the industrial carbon peak between Sichuan Province and Chongqing under different scenarios.

Combined with the forecasts of Sichuan Province and Chongqing Municipality, it was found that the total industrial carbon emissions in the Sichuan-Chongqing region will peak at different times according to different scenarios. Under the scenario of low speed, baseline, green, and rapid development, the time of industrial carbon peaking in the Sichuan-Chongqing region is about 2030, 2030, 2030, and 2035 and the corresponding peak carbon emissions are 83.97 million tons, 84.70 million tons, 81.98 million tons, and 87.64 million tons, respectively. The trend of industrial carbon emissions in the Sichuan-Chongqing region from 2000 to 2040 shows a double-hump pattern and the absolute carbon emissions at large humps are larger than those at small humps. The analysis shows that the continuous development of the regional economy, rapid innovation in technology, increase in per capita income, continuous increase in regional population, the establishment of regional enterprises, and inflow of foreign capital lead to rapid industrial development, all of which have a positive impact on regional development; therefore, carbon emissions will continue to rise. However, based on the existing policy situation, although there will be a phased peak of carbon emissions, the total absolute amount will decrease. Therefore, the continuous implementation of a low-carbon economy and the choice of a green development scenario will also be the future direction of the Sichuan-Chongqing region.

6. Conclusions and Recommendations

6.1. Conclusions

(1)

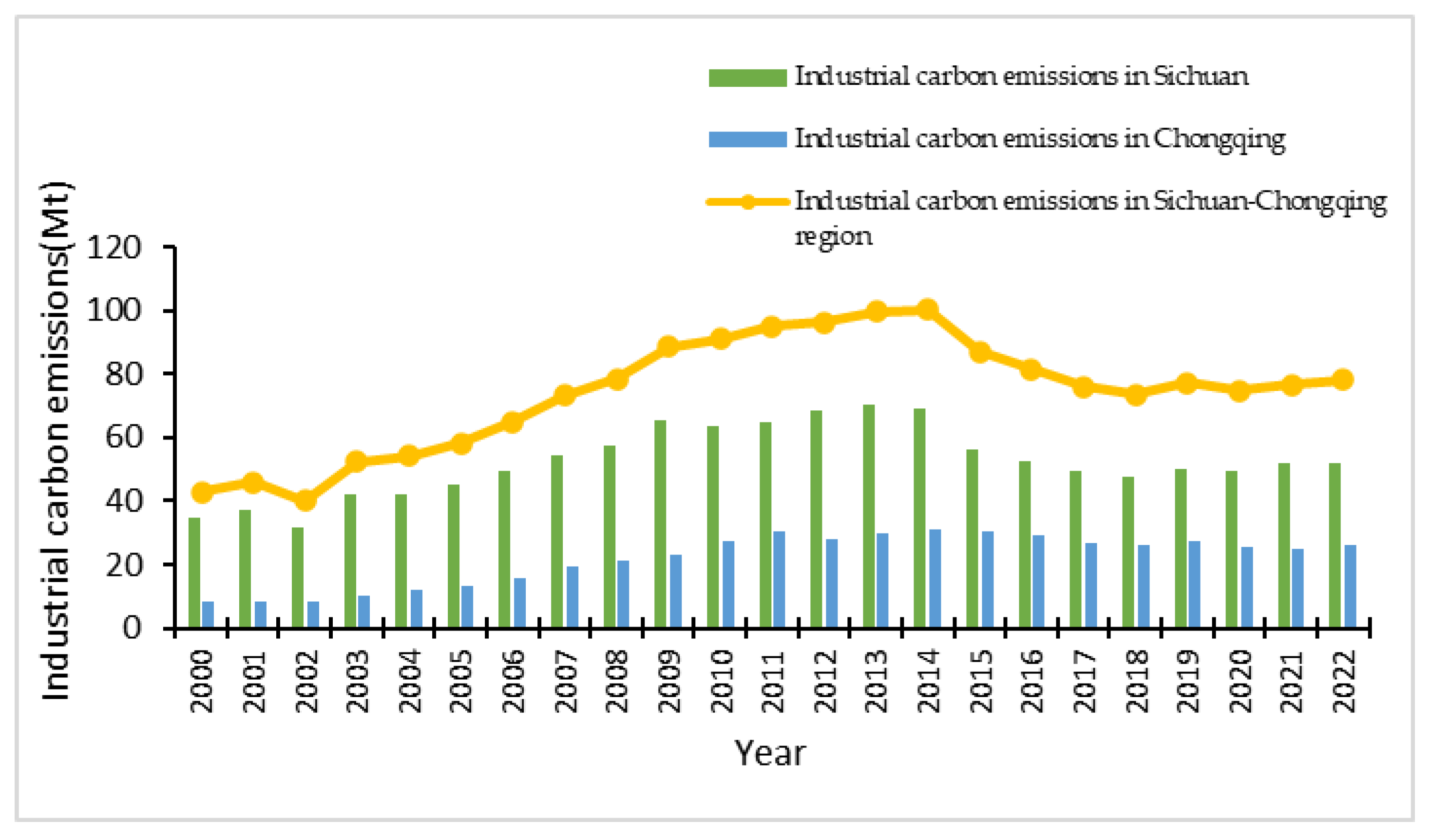
In the analysis of temporal changes in carbon emissions from energy consumption in Sichuan Province and Chongqing Municipality, carbon emissions from energy consumption in the two regions increased at a high rate from 2000 to 2014 and peaked in 2013 and 2014, respectively. After 2014, China introduced carbon emissions reduction policies to control the growth of carbon emissions. From 2015 to 2018, total industrial carbon emissions declined and the growth rate of industrial carbon emissions showed stable volatility in the following years. In 2022, the industrial consumption of coal, oil, natural gas, and electricity in Sichuan Province will account for 73.25%, 5.16%, 1.82%, and 19.77%, respectively, whereas those in Chongqing in the same year will account for 84.49%, 0.40%, 1.63%, and 13.07%, respectively. This indicates that coal remains the main source of industrial energy consumption in Sichuan and Chongqing. Therefore, accelerating the optimization of the energy structure and promoting the use of clean energy have become future development directions for the Sichuan-Chongqing region;

(2)

Retaining the effective factors that have a strong correlation with carbon emission by the grey degree of correlation and stepwise regression method, the extended STIRPAT model was constructed and the model fit well. The results of OLS show that the industrial scale has the highest contribution rate to industrial carbon emissions in Sichuan Province, followed by foreign trade dependence and population. It should be noticed that although the influence of population factors is large, the significance is low. All factors have a positive impact on regional carbon emissions and the influence degrees are 1.19, 0.309, and 2.986, respectively. Energy structure has the highest contribution rate to industrial carbon emissions in Chongqing, followed by per capita income. The energy structure has a negative effect on carbon emission while the per capita income has a positive effect; this shows that the increased use of clean energy can achieve industrial carbon emission reduction well and the influence degrees are −1.791 and 0.784, respectively;

(3)

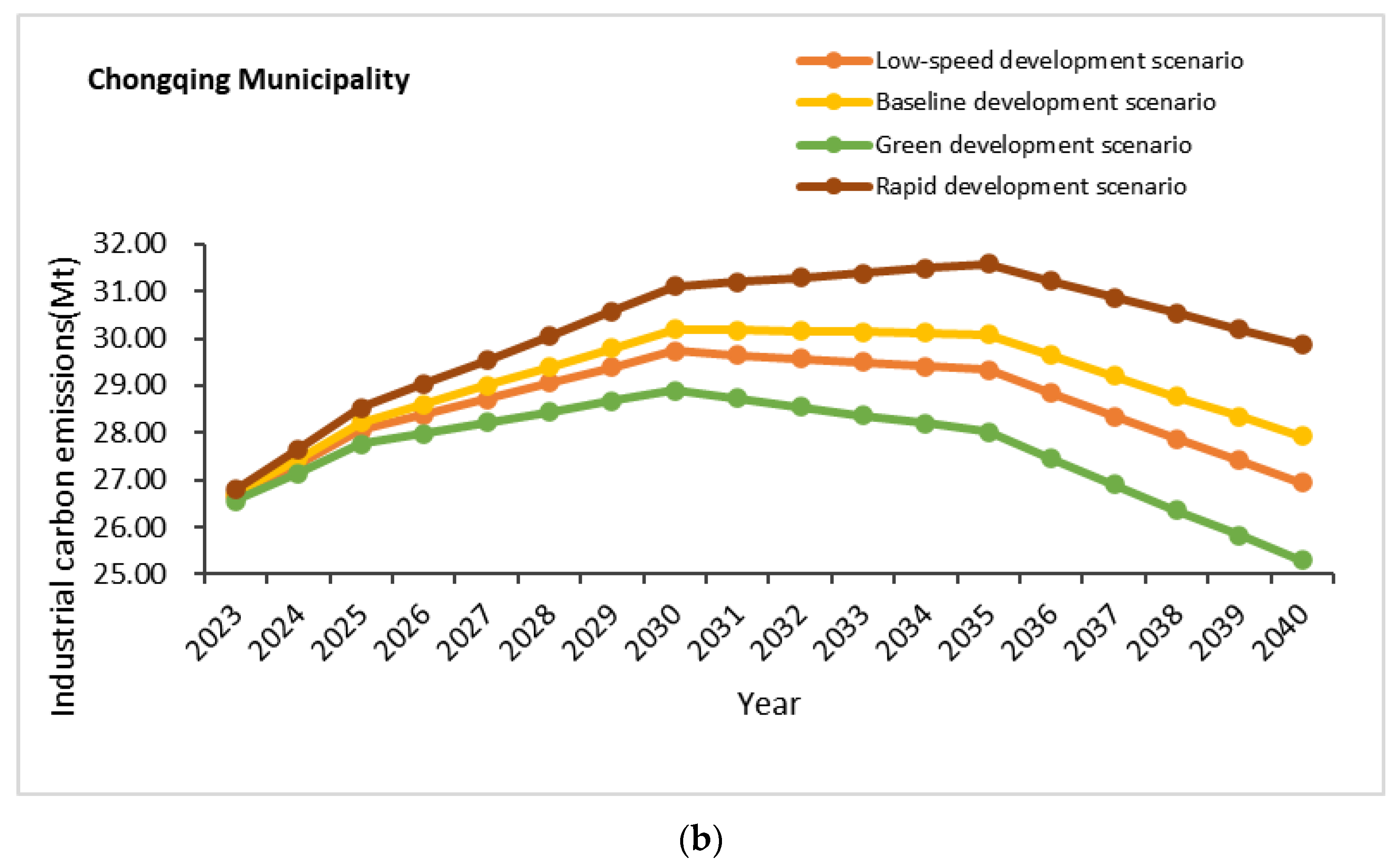
Four development scenarios were established using scenario analysis and the extended STIRPAT model was used to predict the total industrial carbon emissions of the two regions during 2023–2040. Under the low-speed and baseline development scenarios, both Sichuan and Chongqing will reach their peaks in 2030 and the peak carbon emissions are 54.24 (Sichuan, low-speed), 54.49 (Sichuan, baseline-speed), 29.74 (Chongqing, low-speed), and 30.20 (Chongqing, baseline-speed), respectively. Whereas, under the high-speed development scenario, they will reach their peaks in 2035 and the peak carbon emissions are 56.06 (Sichuan, high-speed), and 31.58 (Chongqing, high-speed), respectively. In the green development scenario, Chongqing will reach its peak in 2030 and Sichuan will reach its peak in 2025 and the peak carbon emissions are 28.91 (Chongqing, Green-speed) and 53.36 (Sichuan, Green-speed), respectively. In the case of low speed, baseline, and green and rapid development, the Sichuan-Chongqing region will reach its peak in 2030, 2030, 2030, and 2035 and the peak level is 83.97 Mt, 84.70 Mt, 81.98 Mt, and 87.64 Mt, respectively.

(4)

Overall, the change in total carbon emissions in Sichuan and Chongqing presents a double hump-shaped development trend from 2000 to 2040; however, the peak value may be a phased peak. When the optimization speed of the regional energy structure is accelerated and the reduction in energy consumption intensity is increased, industrial carbon emissions will return to the downward trend; however, when economic development is rapid, there is no reasonable optimization of energy structure and industrial scale adjustment and industrial carbon emissions will return to the upward trend. Therefore, if the two regions want to complete the carbon compliance task within a specified time, they must choose a green development scenario, that is, continuously optimizing the energy structure, adjusting the industrial scale, and accelerating scientific and technological progress to achieve high economic development and low carbon emissions.

6.2. Recommendations

(1)

Construction of green and low carbon pipe control application system in the Sichuan-Chongqing region includes carbon emission monitoring and evaluation of key energy-using enterprises, carbon emission data of key products throughout their life cycle, online monitoring of key energy-using equipment, supporting enterprises to build data-driven production methods and enterprise management models, and promoting smart energy management and carbon emission management information systems;

(2)

Support the application of renewable electricity in electric heating kilns and other fields, promote the exploration, development, and utilization of natural gas, accelerate the planning and construction of hydropower, wind power, and photovoltaic power generation, and build a clean, low-carbon, safe, and efficient energy system;

(3)

Strengthen the evaluation of cleaner production for projects with high energy consumption and high emissions. New and rebuilt projects should reach advanced levels of cleaner production and enterprises that exceed standards and total emissions and consume high energy will be included in the mandatory cleaner production audit list in accordance with the law;

(4)

Continue to optimize and adjust the industrial structure, resolutely curb the blind development of energy-intensive and high-emission projects, and carry out green digital transformation and upgrading of energy-intensive and high-emission industries such as petroleum processing, coking, and nuclear fuel processing.

6.3. Discussions

6.3.1. Discussion Result Analysis

In this paper, it is concluded that the carbon emission reduction path is the most suitable for industrial carbon emission in the Sichuan and Chongqing areas under the condition of green development. Compared with the studies of other scholars, it is found that the influencing factors have different degrees of influence in different regions. For example, Lian et al.’s [32] result shows that population is the factor that has the greatest impact on carbon emission in Fujian Province and that its optimization scenario (similar to the green development scenario in this paper) is the most suitable path for carbon emission reduction in this region. Liao et al.’s [33] research shows that energy structure is the most influential factor for carbon emission in Sichuan Province and its low-carbon and energy-saving scenario is the most suitable path for carbon emission reduction in this region. Zhu et al. [28] show that energy intensity is the factor that has the greatest impact on the carbon emission of the tourism industry in Jiangxi Province and its low-carbon scenario is the most suitable path for carbon emission reduction in the tourism industry in this region. From the examples of the three scholars, it is analyzed that controlling population flow, realizing effective adjustment of industrial structure and energy structure, and increasing the use of clean energy can reduce total carbon emissions and achieve low-carbon sustainable development.

6.3.2. Major Contribution

The main contribution of this paper is to study the trend of industrial carbon emissions in the Sichuan-Chongqing region, which is an important economic development region in Southwest China, explore the effective influencing factors in this region, and use gray correlation degree analysis to indirectly eliminate factors with multicollinearity, which has certain innovation. Moreover, it aims to conduct a basic prediction analysis to explore whether industrial carbon emissions in this region reach the peak within the target time, to find a carbon reduction path suitable for regional development.

6.3.3. Study Limitation

(1)

The first limitation of the study is the error and significance of the data. In this paper, the total industrial carbon emission is estimated by the carbon emission coefficient method, which is an indirect estimation form, so there may be little difference between the actual value and the estimated value. Moreover, the calculated factors are not all strong and significant (p < 0.01) and the analyzed situation may need to be demonstrated in combination with the actual situation;

(2)

The second limitation is the lack of comparisons across multiple cities. This paper only takes the characteristics and prediction of industrial carbon emission in Sichuan and Chongqing as the research object. However, other cities in southwest China have not been analyzed and compared and few cities have been studied;

(3)

The third limitation is the lack of discussion on other influencing factors, such as the impact of urbanization rate, and the specific discussion on the factors excluded in the paper has not been performed.

6.3.4. Future Research Direction

The future research direction can be explored by improving the limitations mentioned above and more accurate methods can be selected and calculated for carbon emissions in the research field. All the influencing factors involved are analyzed to determine which factors have the highest contribution rate, so as to find targeted problems for improvement. Then, several urban agglomerations were analyzed, such as Yunnan Province, which is developed in tourism, in Guizhou Province, which borders Chongqing, and the carbon emission forms of the studied cities were compared to find out the carbon emission reduction direction suitable for the southwest region.