Provincial Coal Flow Efficiency of China Quantified by Three-Stage Data-Envelopment Analysis

Abstract

The exploration of regional variations in coal flow efficiency (CFE) in China and the collaborative strategies for emission reduction are vital for accelerating the progress of ecological civilization within the coal industry and achieving an optimal allocation of coal resources. To unveil the evolutionary traits of actual CFE and its decomposition, this study employs a current technology based on a combined super-efficient measure (SBM), global SBM, the stochastic frontier approach (SFA), and the global Malmquist–Luenberger index (GML) model on panel data from 2010 to 2021 across 30 provinces in China. The research conclusions are as follows. First, significant efficiency gaps are observed among provinces, showcasing superior performance in the north and east regions. Moreover, the impact of environmental factors and random disruptions on individual slack variables varies, resulting in a decrease of 0.18 and 0.43 in the CFE of source-area and sink-area when these factors are not taken into account. Thirdly, a clear distinction emerges between the technical efficiency change index (EC) and the best-practice gap change index (BPC). Lastly, the CFE displays regional disparities marked by an upward trajectory and fluctuating patterns resembling a “W” shape.

1. Introduction

China heavily relies on coal as its principal energy source, playing a crucial role in fueling its economic expansion and significantly contributing to greenhouse gas emissions. Figure 1 shows that China has coal reserves of 2078.85 billion tons, representing 13.3% of global reserves. Despite a decline from 68.5% in 2012 to 56.2% in 2022, coal remains China’s dominant energy source and is expected to maintain this position [1]. Recognizing the strategic significance of coal for national energy security, the spatial and temporal incongruities between its resource distribution and consumption demand give rise to regional coal resource allocation, leading to the development of coal flow fields and the establishment of regional energy interconnections. The flow pattern of coal resources and the dynamics of supply and demand have long been central priorities in the realms of transportation and energy. The “Outline of the Fourteenth Five-Year Plan for the National Economic and Social Development of the People’s Republic of China and the Visionary Goals for the Year 2035” places strong emphasis on driving forward an energy revolution, constructing a clean, low-carbon, secure, and efficient energy system, and enhancing energy supply security [2]. Consequently, fostering regional coal flow while mitigating carbon emissions is an imperative step toward constructing an ecologically sustainable coal industry.

China possesses ample energy resources; nevertheless, their spatial distribution is distinctly uneven, characterized by a disparity in the distribution of the rich in the north and poor in the south, and more in the east and less in the west. The high share of coal consumption has become a bottleneck in improving energy efficiency, according to a report by the World Wide Fund for Nature (WWF) [3]. To overcome this bottleneck, scholars are focusing on improving coal resource utilization efficiency [4,5,6], researching low-carbon coal logistics development, and transforming the coal industry to be more environmentally friendly [7,8]. However, these endeavors solely consider specific phases of the coal resource life cycle from processing to consumption, disregarding regional coal allocation in China and the intricate structural features of the coal life cycle as a resource flow system.

Scholars have primarily focused on optimizing flow patterns, matching supply demand, driving mechanisms, and predicting coal flow direction to address the resource flow problem. Wang and Zhao [9] analyze carbon-based energy resource flow nodes at industrial and regional levels, pinpoint limitations in current research, and suggest academic enhancements for theoretical research and methodology integration. Others focus on the supply-and-demand pattern of coal resources and propose improvements in transport construction [10,11]. Song and Wang [12] investigate global coal supply-and-demand distributions and trade scenarios and introduce the “field” theory to analyze coal flow characteristics and fundamental flow patterns. Liu [13] developed an optimization model for coal resource flow in China, focusing on aligning coal supply and demand to evaluate the transaction rationality between coal producers and consumers. In terms of spatial analysis, Chong et al. [14] analyzed the variation in coal consumption in China by utilizing the logarithmic mean splitting index to study the distributional map of China’s coal flow consumption. Mou and Li [15] used linear programming methods to quantitatively study the direction and quantity of coal flow in China and analyzed the impacts of future coal supply zone shifts. Mischke and Xiong [16] used Sankey diagrams to analyze China’s energy supply, transformation, and end use. Wang et al. [17] used a field theory to study changes in spatial and temporal patterns of coal resource flow in the world and their causes. Interregional studies on CFE have primarily focused on analyzing the flow rate and flow direction from the perspective of coal supply, studying the influence of different factors [18], or discussing the transportation network from the perspective of coal supply area and the segmentation of the supply–demand relationship in specific target markets [19]. Efficiency is typically indicative of the proportionality between input and output factors [20]. Recent research defines the CFE as the ratio of input and output economic value factors in a region due to the coal flow. Zhang and Zhao [21] measure the CFE in different regions with the help of the DEA method and use the coupled coordination model to measure the relationship between flow efficiency and industrial structure. Based on an analysis of China’s coal production and consumption pattern, as well as the inter-regional supply–demand balance, Che et al. [22] used exploratory spatial data analysis to analyze the spatial correlation characteristics of coal consumption in each region of China.

The importance of energy efficiency is growing across various sectors, requiring in-depth scholarly attention. The fuzzy evaluation method and hierarchical analysis are commonly used techniques for efficiency assessment. However, prioritizing signals can be challenging due to subjectivity, potentially leading to unjust evaluation results. The DEA approach is a statistical technique that evaluates input–output efficiency without assumptions regarding distribution or functional form. It does not require parameter estimation or functional linkage. Model weights are determined through mathematical programming, removing subjectivity [23]. The DEA model has been extensively expanded and applied in energy efficiency research. Wang and Su [24] used an SBM approach to study regional energy efficiency and emission reduction from a green development perspective. Liu et al. [25] used the SBM method to study total factor energy efficiency in the western region, while this research used an integrated SBM model to comprehensively evaluate the production efficiency of listed companies in the coal industry [26]. Moreover, a modified SBM model was proposed, which takes undesirable outputs into account. Liu [27] assessed the energy efficiency of China’s Pearl River Delta by constructing an SBM model, considering undesired outputs. Li and Cui [28] analyzed the efficiency of China’s regional coal industry using an undesired output SBM model. DEA has limitations, as it does not account for random errors or external environmental factors, assuming a homogenized external environment that may affect real values. To address this, the SBM-SFA-SBM model integrates the SBM model with the three-stage DEA model [29]. With the maturity and development of the three-stage DEA model, it has become a popular tool for measuring industrial or energy efficiency [30,31]. Li et al. [32] measured total factor carbon emissions efficiency using a three-stage SBM-DEA model with undesired outputs, while Xu and Zhao [33] measured the efficiency of regional low-carbon innovation networks in China using an improved J-SBM three-stage DEA model.

The literature research shows that although substantial research has been conducted on optimizing resource flow and patterns, there is no consensus or established criteria for evaluating CFE. Current studies largely use the traditional DEA model, leading to a bias in efficiency assessment. These analyses fail to consider the variations in coal flow patterns across different regions, the discrepancies in the measurement of CFE across different regions, and the intricate interplay between environmental factors and random disturbances on CFE. In comparison to prior studies, the primary motivations and contributions of this paper are outlined as follows: Firstly, this paper delves into the examination of CFE in diverse functional regions through the lens of sustainable development. The analysis of CFE serves as a bridge connecting ecology and economics, contributing towards the optimization of China’s coal resource flow pattern in a low-carbon manner and propelling sustainable development initiatives forward. Secondly, this research combines the SBM model with the three-stage DEA approach, explicitly considering CO₂ emissions as an undesirable output. This methodology solves the ranking issue present when all decision-making units (DMUs) cannot be distinctly ordered. Moreover, it refines the input and output data, employing the SFA model, which mitigates the influences of environmental variables and random fluctuations, thus revealing the true efficiency levels. This modification holds substantial relevance in the literature on enhancing regional CFE, representing a novel contribution to the discourse on resource optimization within the sustainability paradigm. Lastly, this study explores the variations in CFE among different regions and analyzes the underlying variables that drive these changes. It serves as a crucial foundation for the precise creation of low-carbon sustainable strategies for coal. Figure 2 shows the research framework of this paper.

The remainder of this paper is organized as follows: Section 2 offers the methodology and data sources used in this paper. Section 3 presents the main research results, including the flow efficiency analysis and exponential decomposition. The conclusions and discussions are summarized in Section 4.

2. Methods and Data

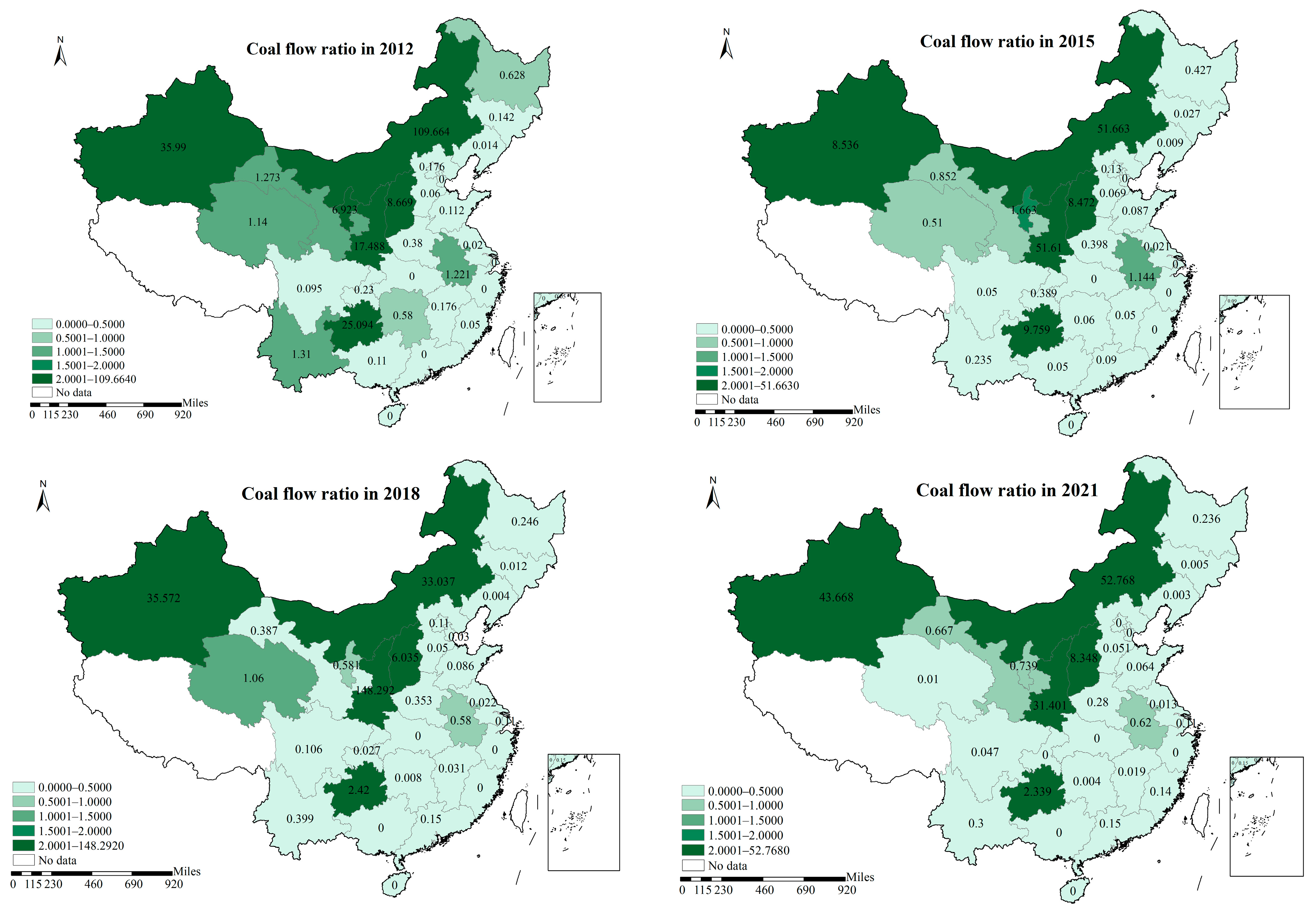
2.1. Regional Functional Division of Coal Flow

In economics, the liquidity ratio is the proportion of an enterprise’s current assets to its current liabilities. This paper applies the classification method of flow types of petroleum resources to measure the flow tendency of coal resources in each region using the coal flow ratio, which is the ratio of regional coal output to regional coal input. The formula is as follows:

$$C_i=\frac{V_i}{U_i}$$

(1)

where $V_i$ represents the coal output of a certain period in the region, and $U_i$ is the coal input of this period. When the value of $C_i$ is larger, it indicates that the coal output of the region is stronger, and it is the source-area; when $C_i$ tends toward 0, it indicates that the inflow of the region is stronger, and it is the sink-area; and when $C_i$ is close to 1, it indicates a transit-area with a balanced coal output and input.

2.2. Super-SBM-Undesired Model

In the conventional SBM model, the efficiency value of most DMUs is 1, and the comparison between these DMUs cannot be made. Tone [34] proposed a super-SBM model to measure the effective DMUs of SBM, compensating for the inability to calculate efficiency values for all DMUs. The discussion is carried out under the premise that DMUs are effective, and the production possibility set $P$ is defined by the detachable point $(x_0,y_0)$ of $\left(X,Y\right)$. The formula used is as follows:

$$P\backslash \left(x_0,y_0\right)=\left\{\left(\overline{x},\overline{y}\right)\right|\overline{x}\ge \mathrm{X}\mathsf{\lambda },\overline{y}\le Y\mathsf{\lambda },\overline{y}\ge 0,\mathsf{\lambda }\ge 0\}$$

(2)

Defining $\overline{P}\backslash \left(x_0,y_0\right)$ as a subset of $P\backslash \left(x_0,y_0\right)$. Supposing $X>0,\lambda >0$, $\overline{P}\backslash \left(x_0,y_0\right),P\backslash \left(x_0,y_0\right)$ are nonempty. The calculation formula of $\overline{P}\backslash \left(x_0,y_0\right)$ is shown in Equation (3):

$$\overline{P}\backslash \left(x_0,y_0\right)=P\backslash \left(x_0,y_0\right)=\cap \left\{\overline{x}\ge x_0,\overline{y}\le y_0\right\}$$

(3)

The super-SBM model is presented as follows:

$$\begin{array}{l}{\delta }^{*}=min\frac{\frac{1}{m}{{\displaystyle \sum }}_{i=1}^m\frac{\overline{x}}{x_{i0}}}{\frac{1}{S}{{\displaystyle \sum }}_{r=1}^s\frac{\overline{y_r}}{y_{r0}^g}}\\ S.T.\left\{\begin{array}{c}\overline{x}\ge X\lambda \\ \overline{y}\le Y\lambda \\ \overline{x}\ge x_0 and \overline{y}\le y_0\\ \overline{y}\ge 0,\lambda \ge 0\end{array}\right.\end{array}$$

(4)

When environmental factors are considered, environmental pollutants are added to the input–output framework as undesired outputs. Based on the above method of introducing undesired output into the SBM model, the undesired output is introduced into the super-SBM model.

The production possibility set $P^{\prime }$ is defined by the detachable point $(x_0,y_0^g,y_0^b)$ of $\left(X,Y\right)$. This is discussed as follows

$$P^{\prime }\backslash \left(x_0,y_0^g,y_0^b\right)=\left\{\left(\overline{x},\overline{y_0^g},\overline{y_0^b}\right)\right|\overline{x}\ge X\lambda ,\overline{y^g}\le Y^g\lambda ,\overline{y^b}\ge Y^b\lambda ,\overline{y}\ge 0,\lambda \ge 0$$

(5)

Defining $\overline{P^{\prime }\backslash }\left(x_0,y_0^g,y_0^b\right)$ as a subset of $P^{\prime }\backslash \left(x_0,y_0^g,y_0^b\right)$.

Suppose $X>0,\lambda >0$, $\overline{P^{\prime }\backslash }\left(x_0,y_0^g,y_0^b\right),P^{\prime }\backslash \left(x_0,y_0^g,y_0^b\right)$ are nonempty. The calculation formula of $\overline{P^{\prime }\backslash }\left(x_0,y_0^g,y_0^b\right)$ is presented as follows:

$$\overline{P^{\prime }\backslash }\left(x_0,y_0^g,y_0^b\right)=P^{\prime }\backslash \left(x_0,y_0^g,y_0^b\right)=\cap \left\{\overline{x}\ge x_0,\overline{y}\le y_0\right\}$$

(6)

The super-SBM-undesired model is constructed as follows:

$$\begin{array}{l}{\alpha }^{*}=min\frac{\frac{1}{m}{{\displaystyle \sum }}_{i=1}^m\frac{\overline{x}}{x_{i0}}}{1+\frac{1}{S_1+S_2}({{\displaystyle \sum }}_{r=1}^{S_1}\frac{S_r^g}{y_{r0}^g}+{{\displaystyle \sum }}_{r=1}^{S_2}\frac{S_r^b}{y_{r0}^b})}\\ S.T.\left\{\begin{array}{c}\overline{x}\ge X\lambda \\ \overline{y^g}\le Y^g\lambda \\ \overline{y^b}\ge Y^b\lambda \\ \overline{x}\ge x_0,\overline{y^g}\le y_0,\overline{y^b}\ge y_0^b,\lambda >0\end{array}\right.\end{array}$$

(7)

2.3. Global Super-SBM-Undesired Model

The efficiency of different investigation periods could not be compared because the frontier planes were not at the same level. Pastor and Lovell [35] proposed the global benchmark technology (GBT) frontier plane construction method, which regarded each sample in different periods as a different DMU, and all DMUs conducted efficiency measurements with reference to the same frontier plane, making the results more comparable.

Global super-SBM-undesired model envelopes all temporal production potential sets, and the formula for production potential set $P^G$ is as follows:

$$P^{\prime G}=P^1\cup P^2\cup \cdots P^T$$

(8)

The global super-SBM-undesired model formula is shown as follows:

$$\begin{array}{l}{\sigma }^{*}=min\frac{\frac{1}{m}{{\displaystyle \sum }}_{t=1}^T{{\displaystyle \sum }}_{i=1}^m{\frac{\overline{x}}{x}}_{i0}}{\frac{1}{S_1+S_2}({{\displaystyle \sum }}_{t=1}^T{{\displaystyle \sum }}_{r=1}^g\frac{\overline{y^g}}{y_{r0}^g}+{{\displaystyle \sum }}_{T=1}^T{{\displaystyle \sum }}_{r=1}^b\frac{\overline{y^b}}{y_{r0}^b})}\\ S.T.\left\{\begin{array}{c}\overline{x}\ge {{\displaystyle \sum }}_{t=1,t\ne l}^{T}X{\lambda }^t\\ \overline{y^g}\le {{\displaystyle \sum }}_{t=1,t\ne l}^T{Y}^{gt}{\lambda }^t\\ \overline{y^b}\ge {{\displaystyle \sum }}_{t=1,t\ne l}^T{Y}^{bt}{\lambda }^t\\ \overline{x}\ge x_0,\overline{y^g}\le y_0,\overline{y^b}\ge y_0^b,{\lambda }^t>0\end{array}\right.\end{array}$$

(9)

2.4. Three-Stage SBM Model

The first stage: The super-SBM-undesired model and the global super-SBM-undesired model are used to calculate the CFE of sink-area and source-area, respectively. The initial efficiency, input redundancy $S^{-}$, desired output deficit $S^g$, and undesired output redundancy $S^b$ are obtained.

The second stage: The input and output redundancy analyzed in the first stage is affected by external environmental factors, random errors, and management factors. Fried et al. [29] found out the environmental variables and adjusted the input and output by constructing the SFA model. The regression equation is as follows:

$$S_{ij}^{\#}=f^i\left(z_j;{\beta }_i^{\#}\right)+v_{ij}^{\#}+{\mu }_{ij}^{\#}$$

(10)

where $\#$ denotes $-,g,b$. $S_{ij}^{\#}$ is the slack of the $j$ decision maker on $i$ inputs or outputs, assuming $K$ environmental variables, $z_j=\left[z_{1j},z_{2j},\cdots ,z_{kj}\right],j=1,2,\cdots n$, and ${\beta }_i$ is the parameter to be estimated. $v_{ij}+{\mu }_{ij}$ is the comprehensive error term; where $v_{ij}~iidN\left(0,{\sigma }_v^2\right)$ reflects statistical noise [36], and ${\mu }_{ij}\ge 0$ reflects management inefficiency, suppose ${\mu }_{ij}~iid{N}^{+}\left({\mu }^i,{\sigma }_{\mu }^2\right)$, i.e., truncated non-negative normal distribution at 0, which is usually assumed to follow semi-normal distribution ${\mu }_{ij}~iid{N}^{+}\left(0,{\sigma }_{\mu }^2\right)$ in empirical practice. In addition, it is assumed that $v_{ij}$ and ${\mu }_{ij}$ are independent of each other, and also independent of $K$ environment variables. Define $\gamma ={\sigma }_{\mu }^2/({\sigma }_{\mu }^2+{\sigma }_v^2)$; when $\gamma$ is close to 1, it means that the management factors dominate the inefficient DMUs; as $\gamma$ approaches 0, then random factors dominate. An estimation of the unknown parameters is carried out using the maximum likelihood, and the input and output data are adjusted. The adjustment formula is as follows:

$$x_{ij}^A=x_{ij}+\left[ma{x}_j\left\{z_j{\widehat{\beta }}_i^{-}\right\}-z_j{\widehat{\beta }}_i^{-}\right]+\left[ma{x}_j\left\{{\widehat{v}}_{ij}^{-}\right\}-{\widehat{v}}_{ij}^{-}\right]i=1,2,\cdots ,m;j=1,2,\dots n$$

(11)

$$y_{ij}^{gA}=y_{ij}^g+\left[ma{x}_j\left\{z_j{\widehat{\beta }}_{ij}^{\mathrm{g}}\right\}-z_j{\widehat{\beta }}_{ij}^{\mathrm{g}}\right]+\left[ma{x}_j\left\{{\widehat{v}}_{ij}^{\mathrm{g}}\right\}-{\widehat{v}}_{ij}^{\mathrm{g}}\right]i=1,2,\cdots ,s_1;j=1,2,\cdots n$$

(12)

$$y_{ij}^{bA}=y_{ij}^b+\left[ma{x}_j\left\{z_j{\widehat{\beta }}_{ij}^{\mathrm{b}}\right\}-z_j{\widehat{\beta }}_{ij}^{\mathrm{b}}\right]+\left[ma{x}_j\left\{{\widehat{v}}_{ij}^{\mathrm{b}}\right\}-{\widehat{v}}_{ij}^{\mathrm{b}}\right]i=1,2,\cdots ,s_2;j=1,2,\cdots n$$

(13)

$x_{ij}^A$ represents the adjusted input data, while $y_{ij}^{gA}$ and $y_{ij}^{bA}$ represent the adjusted desired and undesired output data, respectively. The first bracket means that all the DMUs are adjusted to the same environment, and the second bracket indicates that the statistical noise effect has been eliminated. The conditional estimator of ${\mu }_{ij}$ obtained is shown as follows:

$$\begin{array}{l}\widehat{E}\left({\mu }_{ij}{\mu }_{ij}+v_{ij}\right)={\sigma }_{*}\left[\frac{\varphi \left(\frac{{\epsilon }_i\lambda }{\sigma }\right)}{\mathsf{\Phi }\left(\frac{{\epsilon }_i\lambda }{\sigma }\right)}+\frac{{\epsilon }_i\lambda }{\sigma }\right] \\ {\sigma }_{*}^2=\frac{{\sigma }_{\mu }^2{\sigma }_v^2}{{\sigma }^2},{\epsilon }_i={\mu }_{ij}+v_{ij},{\sigma }^2={\sigma }_{\mu }^2+{\sigma }_v^2\end{array}$$

(14)

$\varphi (·)$ and $\mathsf{\Phi }(·)$ are the density function and the distribution function of standard normal distribution, respectively. The estimate of $v_{ij}$ obtained is shown as follows:

$$E\left[v_{ij}|{\mu }_{ij}+v_{ij}\right]=s_{ij}^{-}-z_j{\widehat{\beta }}_j-\widehat{E}\left[{\mu }_{ij}|{\mu }_{ij}+v_{ij}\right]$$

(15)

The third stage: Through the second stage of SFA analysis, the original input–output values are substituted by the adjusted input–output value. Again, the super-SBM-undesirable model and the global super-SBM-undesirable model are used to measure the CFE of the sink-area and source-area, respectively. The efficiency excluding the interference of environmental factors and random errors can be obtained, which can reflect the real management level of each DMU.

2.5. Global Malmquist–Luenberger Index

To further analyze the dynamic evolution of CFE in China, we considered that the geometric average of the Malmquist index is not transferable, which may result in a lack of a feasible solution for the linear programming. This paper constructs a global Malmquist–Luenberger index and further analyzes the internal driving factors of CFE. Pastor and Lovell [35] constructed the global Malmquist productivity index and defined the current production possibility set as $T^t=\left\{\left(x^t,y^t\right)|x^t\mathrm{produce}{y}^t\right\},t=1,2,\cdots ,T$; the global production possibility set is $T^G=\left\{T^1\cup T^2\cup \cdots \cup T^T\right\}$. The reference set of the global Malmquist productivity index contains data for all DMUs over time. Oh [37] constructed the GML index by combining a directional distance function, incorporating undesired outputs with global production possibility sets. Therefore, based on the super-SBM model and CRS assumption, the GML index is constructed as follows:

$$M^G\left(x^t,y^t,z^t,x^{t+1},y^{t+1},z^{t+1}\right)=\frac{D^G\left(x^{t+1},y^{t+1},z^{t+1}\right)}{D^G\left(x^t,y^t,z^t\right)}$$

(16)

The GML index can be further decomposed into EC and BPC. The decomposition is shown as follows:

$$\begin{array}{l}{M}^G\left(x^t,y^t,z^t,x^{t+1},y^{t+1},z^{t+1}\right)\\ =\frac{D^{t+1}\left(x^{t+1},y^{t+1},z^{t+1}\right)}{D^t\left(x^t,y^t,z^t\right)}\times \left\{\frac{D^G\left(x^{t+1},y^{t+1},z^{t+1}\right)}{D^{t+1}\left(x^{t+1},y^{t+1},z^{t+1}\right)}\times \frac{D^t\left(x^t,y^t,z^t\right)}{D^G\left(x^t,y^t,z^t\right)}\right\}\\ =\frac{T{E}^{t+1}\left(x^{t+1},y^{t+1},z^{t+1}\right)}{T{E}^t\left(x^t,y^t,z^t\right)}\times \left\{\frac{\frac{D^G\left(x^{t+1},y^{t+1},z^{t+1}\right)}{D^{t+1}\left(x^{t+1},y^{t+1},z^{t+1}\right)}}{\frac{D^G\left(x^t,y^t,z^t\right)}{D^t\left(x^t,y^t,z^t\right)}} \right\} \\ =EC\times \left\{\frac{BP{C}^{G,t+1}\left(x^{t+1},y^{t+1},z^{t+1}\right)}{BP{C}^{G,t+1}\left(x^t,y^t,z^t\right)}\right\}=EC\times BPC\end{array}$$

(17)

where $EC$ is measured by comparing the proximity of DMUs and the respective production front in different periods. $EC>1$ represents the improvement in technical efficiency, and $EC\le 1$ represents the decrease in technical efficiency. $BPC$ means the portion after the deduction of other factors, such as capital, labor, and production performance, reflecting the movement of the production front in different periods, and representing the speed of the technological frontier advancement of technology leaders. The GML index represents the ratio of CFE in period $t+1$ to that in period $t$. If $GML>1$, it means that the regional CFE grows from period $t$ to $t+1$, and vice versa, and it decreases.

2.6. Samples and Indicators

The three-stage SBM evaluation index comprises input, output, and external environment variables. Following the Cobb–Douglas production function, inputs in the production process mainly include labor, capital, and energy. After a comprehensive analysis of the existing literature and research content, this paper selects the evaluation indexes of CFE as follows. The research unit is based on the data of 30 provinces in China from 2010 to 2021 (excluding Tibet). The basic data come from the China Energy Statistical Yearbook, China Industrial Statistical Yearbook, China Fixed Asset Investment Statistical Yearbook, and the Statistical Yearbooks of each province. The carbon emission is calculated by using the IPCC method. With more sources of data for carbon emission factors, this paper is taken from the coal carbon emission coefficient of 0.7476 published by National Development and Reform Commission. To eliminate the influence of the data scale, the data of environmental variables are logarithms.

2.6.1. Input Variables

The coal flow network is a complex dynamic system with multi-body and multi-factor inputs and outputs. This paper sets up the CFE evaluation index system in the source-area and sink-area, respectively, based on the different flow functions assumed by different regions. However, there are no statistics on coal flow. Therefore, this paper borrows the method of “stripping coefficient” from the tourism industry to extract the data related to coal flow from the existing data [38].

For the source-area, as done by Zhang and Zhao [21], the ratio of the coal output volume to the coal production is used to characterize the stripping coefficient. The product of the source-area stripping coefficient and the number of people employed in the coal mining industry, the investment in fixed assets, and the energy consumption, respectively, were selected as the inputs in terms of labor, capital, and energy.

For the sink-area, considering that the flow process of coal is most related to the secondary industry, we selected the sink-area stripping coefficient multiplied by the number of employees in the secondary industry and the amount of fixed-asset investment in the energy industry as indicators of labor and capital inputs, characterizing the energy input by the number of coal inputs in each province. The sink stripping coefficient is $I_i/(I_i+P_i)$, where $I_i$ represents the coal input of region $i$ in a certain period, and $P_i$ represents the coal production of region $i$ in the same period.

2.6.2. Output Variable

Considering the accessibility and reasonableness of the data, the coal output and the stripping coefficient of the source-area multiplied by the gross industrial output value of the coal mining industry are used as the desired outputs of the source-area, and the CO₂ emission of the coal mining industry multiplied by the stripping coefficient is used as the non-desired output.

In terms of sink-area, the GDP of the secondary industry in each province is multiplied by the stripping coefficient of the sink-area as the desired output, and the non-desired output is expressed by multiplying the CO₂ emission of the secondary industry by the stripping coefficient of sink-area.

2.6.3. External Environment Variables

The external environment variables should be selected as factors that have an impact on the CFE, but they are not within the control range of the sample. In this paper, the external environment variables of the source-area are selected from five aspects, namely, the level of regional development (GDP), urbanization rate (Urban), degree of opening (Open), degree of governmental support (Gover), and environmental regulation factors (Envir). (1) The gross regional product is chosen to measure the level of regional development with the growth of the economy. On the one hand, it means that the infrastructure has been improved, and the rate of coal mining and transportation has been improved, which helps to improve the efficiency of coal flow; on the other hand, for rough economic development, the development of the economy brings more environmental pollution, so the carbon emissions have increased greatly. (2) The level of industrial development of an area is closely related to the process of urbanization, so the urbanization rate is used to represent the process of urbanization, which is equal to the ratio of the urban population to the total population. (3) One of the main features of fast economic growth is the constant development of foreign trade, and this paper measures the degree of openness by using the ratio between the total import and the GDP of each province. (4) It is difficult to quantify the degree of government intervention in economic development, including the government’s introduction of a variety of interventions in economic operation systems and policies. Therefore, in this paper, the ratio of fixed-assets investment to local industry fixed assets is used to measure the degree of government support. (5) The environment control is the ratio between the amount of investment completed in the control of industrial pollution and the value added by the industry. The government’s attention to environmental issues will help optimize and adjust the industry structure and improve the efficiency.

For the sink-area, the level of regional development (GDP), industrial structure (Indus), energy consumption structure (Energ), degree of openness (Open), and environmental regulation (Envir) are selected as environmental variables for sink-area. (1) The increase in the level of regional development has brought about an increase in science and technology, but has resulted in a rise in energy consumption, which affects the CFE of the sink-area. (2) The value added of the secondary industry as a proportion of GDP is used to represent the industrial structure. The economic development of most provinces relies heavily on the secondary industry, which is dominated by energy-intensive industries, and changes in the industrial structure will have a greater impact on CFE. (3) Energy consumption patterns shall be expressed as a proportion of coal consumption in primary energy consumption. It is well known that the heavy use of coal is a major factor in environmental degradation, such as the increase in pollutants in the atmosphere, such as SO₂, CO₂, and PM. Therefore, the ratio of coal consumption to primary energy consumption will have a direct influence on CFE. (4) Increased openness has brought advanced technology, equipment, and management experience, further improved the CFE, and reduced carbon emissions. (5) The government’s attention to the environmental issues has led to improvements in carbon emissions. The acronyms are described as shown in Abbreviations section.

3. Results

3.1. Results of the Regional Functional Division

For a more intuitive reflection of the roles played by different regions in the flow of coal, hierarchical maps were drawn using ArcGIS 10.2 (Figure 3). The images reveal that Shanxi, Shaanxi, Xinjiang, Guizhou, and Inner Mongolia are the main provinces responsible for coal production. The consumption of coal is primarily focused in the regions of East China and South China. In terms of geospatial distribution, it exhibits the feature of a “centralized source and decentralized sinking”. Based on the stratification map,

Table 1. Results of region division.

Type	Provinces
Source-area	Shanxi, Inner Mongolia, Guizhou, Shaanxi, Xinjiang
Sink-area	Beijing, Tianjin, Hebei, Liaoning, Jilin, Heilongjiang, Shanghai, Jiangsu, Zhejiang, Fujian, Jiangxi, Shandong, Henan, Hubei, Hunan, Guangdong, Guangxi, Hainan, Chongqing, Sichuan, Yunnan
Transit-area	Anhui, Gansu, Qinghai, Ningxia

presents the conclusive outcomes of the classification of source-area, sink-area, and transit-area.

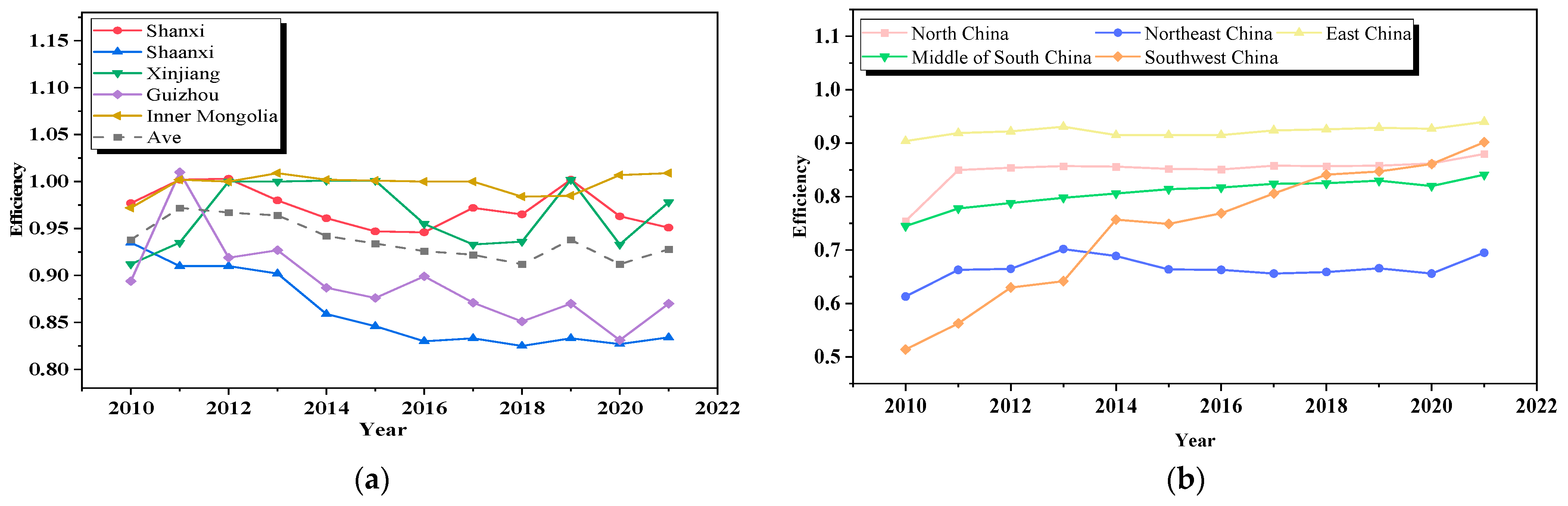
3.2. First Stage Analysis: Initial CFE Evaluation

Taking into account that there are only five DMUs in the source-area using the current production technology, this will distort the measured efficiency, and the efficiency measured under the global production technology is comparable in that period. According to Coelli and Rao [39], the CRS assumption is only made when dealing with an aggregate data choice. Therefore, under the CRS assumption in MatlabR2022a software, this stage employed the global super-SBM-undesired model and the super-SBM-undesired model to calculate the CFE in source-areas and sink-areas from 2010 to 2021, respectively. The results are shown in Figure 4.

For the source-area, between 2010 and 2021, the CFE shows a consistent increase, and the CFE of Xinjiang and Inner Mongolia are positioned at the forefront of efficiency in 2021. Remarkably, Inner Mongolia achieved a peak efficiency, registering a value of 1.011, the highest observed within the sample period. At the mean level, the CFE average stands at 0.758, and only Inner Mongolia’s CFE average reaches the efficiency frontier, with a value of 0.847, while Shaanxi lags behind with an efficiency value of 0.675. This shows that the gap in the CFE of the source-area is obvious; Inner Mongolia boasts abundant coal resources and garners great attention from national and local governments. It actively invests in coal mining and attracts professional talents and advanced technologies, leading to significant resource advantages. In contrast, other provinces heavily rely on extensive resource production, with the slow technological transformation of the coal industry severely constraining the enhancement of CFE, meaning the lagging provinces have a great potential for improvement [40].

In the sink-area, the CFE stands at 0.39 for the period 2010–2021, indicating a management inefficiency level of 61%. Notably, Beijing boasts the highest mean low-carbon mobility efficiency of 1.441, with Shanghai following closely at a mean efficiency of 1.116. Both regions consistently maintain an efficiency above 1 throughout the sample period, positioning them at the forefront of CFE. The three provinces with the lowest efficiency are Hebei, Heilongjiang, and Jilin. Significant variations in CFE among provinces may stem from environmental disparities across regions. The sink-area was divided into five regions, North, Northeast, East, middle of South, and Southwest China for further study of the regional differences.

Table 2. Regional division of sink-areas.

Region	Province
North China	Beijing, Tianjin, Hebei
Northeast China	Heilongjiang, Jilin, Liaoning
East China	Zhejiang, Jiangsu, Shanghai, Fujian, Jiangxi, Shandong
Middle of South China	Hubei, Hunan, Henan, Guangdong, Guangxi, Hainan
Southwest China	Chongqing, Sichuan, Yunnan

illustrates the results of the division. Figure 4b shows that the CFEs are higher in North China and East China. This result is consistent with previous research findings [41]. East China has a strong investment in independent innovation and R&D, which provide a good environment for improving CFE. The CFE in the middle of South China and Southwest China continue to decrease, while Northeast China is relatively stable but always at a lower level, and the efficiency gap between regions increases annually.

3.3. Second Stage Analysis: SFA Regression Evaluation

The redundancy resulting from each input slack variable and non-desired output indicator identified in stage I serves as the explanatory variable. Meanwhile, the source-area explanatory variables encompass the degree of openness, regional development level, urbanization rate, governmental support intensity, and environmental regulatory factors. The explanatory variables for the sink-area encompass the regional development level, industrial structure, energy consumption structure, degree of openness, and environmental regulation factors. Stage II involves the analysis through the SFA using Frontier 4.1, aimed at deriving the estimated coefficients and t-test values for each variable.

From

Table 3. SFA analysis results.

Variables	Source-Area				Sink-Area
	Labor	Financial	Energy	CO2	Labor	Financial	Energy	CO2
Constant	9.98 *** (7.04)	−6.75 ** (−2.21)	−3.88 *** (−3.81)	7.07 ** (2.48)	5.44 (0.08)	−201.93 *** (−2.88)	−507.36 *** (−3.54)	128.15 (1.22)
Open	−0.05 (−0.64)	−0.12 * (−1.65)	−0.41 (−1.37)	−0.84 *** (−3.54)	−1.67 (−0.72)	8.35 ** (2.47)	−16.18 * (−1.78)	−8.06 * (-1.88)
GDP	−1.14 *** (−5.54)	0.84 *** (3.55)	2.45 *** (4.09)	−0.15 (−0.25)	23.69 *** (7.41)	60.62 *** (18.22)	83.54 *** (13.16)	51.50 *** (12.38)
Envir	0.18 *** (4.07)	0.14 * (1.79)	0.41 * (1.69)	0.88 *** (5.72)	0.09 (0.07)	3.84 ** (2.40)	−0.23 (−0.07)	1.44 (0.90)
Gover	0.13 ** (2.47)	0.24 *** (3.00)	1.35 *** (6.00)	1.27 *** (7.54)	——	——	——	——
Urban	0.23 (0.54)	−0.42 (−0.46)	−4.94 *** (-3.56)	−1.20 (−0.93)	——	——	——	——
Indus	——	——	——	——	−41.71 *** (−3.92)	−83.49 *** (−6.13)	−42.7 (−1.06)	−125.51 *** (−6.97)
Energ	——	——	——	——	−6.93 ** (−2.14)	−12.24 ** (−2.40)	11.14 (1.51)	−6.81 (−1.19)
γ	0.98 *** (35.78)	0.98 *** (34.62)	0.60 *** (6.05)	0.99 *** (140.51)	0.95 *** (55.92)	0.97 *** (164.36)	0.92 *** (30.83)	0.96 *** (176.03)
Log likelihood	732,668,400	29.3	−57.76	−48.87	−1027.37	−1127.71	−1261.09	−1118.58
LR test	106.78 ***	35.46 ***	29.54 ***	70.27 ***	155.94 ***	239.87 ***	197.70 ***	280.77 ***

Note: Data in brackets denote t-statistics. *, **, and *** represent significant levels at 10%, 5%, and 1%, respectively.

, the existence of managerial inefficiency $u$ was determined by testing the hypothesis $H_0:{\sigma }_{u2}=0\mathrm{vs}.H_1:{\sigma }_{u2}$ through the $LR$ test [42]. The results show that the one-sided likelihood ratios of each slack variable pass the 1% significance test, and each of the gamma values is significantly close to 1, which indicates that managerial inefficiency dominates the composite error term. Therefore, it is feasible to apply the SFA to eliminate the effects of the external environment and random errors. Most of the regression coefficients of environmental variables on slack variables passed the 1% level of the significance test and a few passed the 5% or 10% level of the significance test.

(1)

Degree of openness: For the source-area, the degree of openness is strongly and negatively linked with the value of fixed-asset investment slack (10% significance level) and with CO₂ emissions (1% significance level). For sink-area, the degree of openness to GDP has a 5% significant positive correlation with fixed-asset investment and a 10% significant negative correlation with coal input and CO₂ emissions. Li [43] pointed out that the expansion of opening has, on the one hand, brought in numerous and new technologies, equipment, and management experience, which can effectively reduce the total amount of coal inputs, increase the use of clean energy, and enhance the efficiency of low-carbon flow; on the other hand, a large amount of capital has been spent on the advanced technologies and the learning of high-quality management experience. The prudent management and distribution of funds have a direct impact on the unutilized worth of investments in fixed assets;

(2)

Level of regional development: For the source-area, regional development has a significant positive correlation with fixed-asset investment and energy consumption slack; on the contrary, the level of regional development has a significant negative correlation with the relaxation of personnel input. For sink-area, GDP is significantly and positively correlated with all slack variables at 1%, indicating that as the level of development increases, there is also an increase in labor, fixed-asset investment, energy input, and redundancy in CO₂ emissions. Tang and Jiang [44] argue that the size of the economy is the primary factor behind the rise in carbon emissions. However, as regional development progresses, there will be a shift in industry structure, with labor-intensive sectors being replaced by technology-intensive sectors. Additionally, the energy industry will phase out outdated production capacity, reduce excess production capacity, and optimize production layout. These changes will lead to a decrease in labor inputs and an increase in coal redundancy [45]. The enhancement of regional development in resource-based provinces will stimulate employment and contribute to GDP growth primarily through increased labor input. This is consistent with the conclusion of Song et al. [46]. Moreover, fixed-asset investments commonly encounter delays and resistance arising from factors such as incomplete market information, policy uncertainties, and extended investment cycles. Consequently, this often culminates in an overinvestment scenario, where the level of investment surpasses market demand and exceeds available resources;

(3)

Environmental regulation factors: Environmental regulation has a significant positive correlation with source-area between input slack and CO₂ emission slack. This association is statistically significant at the 1% and 10% levels. For sink-area, environmental regulation has a 5% significant positive correlation with the value of fixed-asset investment slack and is not significant for several other items. Han and Niu [47] observed that as the ratio of investment in environmental pollution management to GDP increases, there is a corresponding increase in the relaxation variables of capital input and energy consumption, as well as an increase in the redundancy of capital input and energy consumption. The predominant factor can be attributed to the escalating proportion of investment directed towards pollution control within the coal industry. This strategic investment plays a vital role in facilitating advancements in industrial technology and hastening the transition towards environmentally friendly practices. As a result, there is a reduced dependence on high-carbon-emitting energy sources, leading to decreased energy consumption without compromising production levels. The advancement in industrial technology results in a lowered utilization of fixed assets and reduced investment in staff, thereby reducing capital expenditure. This improvement also enhances the efficiency of CO₂ emissions while sustaining current production [48]. The government, serving as the steward and enforcer of environmental legislation, has committed considerable resources to combat environmental pollution. However, the persistent deterioration in pollution issues suggests that the inputs have not yielded discernible benefits [49];

(4)

Degree of governmental support: The degree of government support is significantly and positively correlated with input slack of source-area, with statistical significance at the 1% and 5% levels. As government investment increases, there is a corresponding increase in redundancy in labor, capital, and energy. Although the government is investing more in the coal mining industry, it is not effectively directing the input funds, leading to inefficiency in fund utilization. The 1% significant positive connection between the regression coefficient of the CO₂ emission relaxation value and government investment indicates that government investment does not effectively contribute to reducing CO₂ emissions. Yadav et al. [50] pointed out that the government should strive to promote continuous support while prioritizing the efficient allocation of investment funds, ensuring that financial inputs effectively bolster carbon emission efficiency;

(5)

Urbanization rate: The level of urbanization has a 1% significant negative correlation with the amount of energy consumption slack in the source-area. Zhao et al. [51] suggest that as urbanization progresses, energy consumption in urban areas becomes more efficient and requires less energy compared to rural areas. Therefore, higher rates of urbanization yield advantages in terms of diminishing energy usage;

(6)

Industrial structure: At a 1% significance level, the industrial structure has a statistically significant and positive influence on the amount of labor input, fixed-asset input, and CO₂ emissions in the sink-area. This indicates that an increase in the percentage of value added by the secondary sector in the GDP leads to a rise in labor, fixed-asset investment, and total CO₂ emissions, which has a detrimental effect on the CFE. This is consistent with the conclusion of Lv et al. [52]. The main reason for this is that the goal of achieving “carbon neutrality” not only brings in new requirements for decreasing carbon emissions, but also sets up a new structure for integrating industrial transformation into the development strategy. Huang et al. [53] establish that industrial development exhibits a reliance on significant quantities of labor and physical resources for sustenance, while concurrently engendering environmental contamination. The enactment of industrial restructuring plans would result in a gradual transition in economic progress, shifting away from energy-intensive and pollution-intensive sectors towards energy-efficient and high-value-added businesses. This will significantly enhance the sink-area’s low-carbon CFE;

(7)

Energy consumption structure: The energy consumption structure has a negative correlation with the labor slack and fixed-asset investment slack of the sink-area. This correlation has been statistically tested and shown to be significant at the 5% level. These findings demonstrate that the large consumption of coal can reduce the capital and labor inputs, aligning with China’s historical pattern of economic growth. While increasing the proportion of coal consumption can decrease the excess of associated inputs, it also leads to a significant release of pollutants. Therefore, in order to enhance the low-carbon efficiency of coal, it is imperative to expedite the transformation and optimization of the energy structure.

In summary, it is unreasonable to ignore the impact of environmental factors and stochastic disturbances in stage I, and the resulting efficiency measurements are biased, so this paper utilizes Equations (10)–(15) to adjust the input–output variables.

3.4. Third-Stage Analysis: Actual CFE Evaluation

3.4.1. Stage III Results

Using the adjusted input–output data, the CFE of source-area and sink-area are re-measured based on the global super-SBM-undesired model and the super-SBM-undesired model, respectively.

From an overall perspective, the average CFE of the source-area during the sample period is 0.938, reaching a maximum value of 0.972 in 2011 and a minimum value of 0.912 in 2020 and 2018. The efficiency exhibits minor oscillations, with a pattern of initially increasing, then decreasing, and then stabilizing. From Figure 5a, the adjusted average flow efficiencies of Shanxi, Xinjiang, and Inner Mongolia all exceed 0.9, with Inner Mongolia consistently operating at the highest level of efficiency, surpassing 1 in most years. Both Guizhou and Shaanxi have efficiency levels that exceed 0.8. Inner Mongolia has consistently maintained stability in its production border, while Guizhou has experienced a slight reduction since hitting its peak in 2011. Meng et al. [54] pointed out that during the Eleventh Five-Year Plan period in 2010, the environmental condition of Guizhou province witnessed significant enhancement. However, the gradual decline in efficiency after 2011 might be attributed to Guizhou province’s proactive efforts in promoting urbanization and industry, resulting in substantial carbon emissions from energy-intensive sectors. The efficiency value of Xinjiang exhibits significant fluctuations and reaches its peak efficiency after 19 years. This achievement is closely linked to the successful execution of the “13th Five-Year Plan for the Implementation of the Work of the Autonomous Region on the Control of Greenhouse Gas Emissions” in Xinjiang.

The CFE for the sink-area in most provinces exhibits a noticeable and consistent increase from 2010 to 2021. Except for the year 2010 in Beijing, both Beijing and Guangdong consistently outperformed other provinces in terms of CFE by a margin of more than 1 throughout the period from 2010 to 2021. However, the CFE for the provinces of Hainan, Heilongjiang, and Yunnan are significantly lower compared to other provinces, with average efficiencies of 0.446, 0.583, and 0.604, respectively. The average real CFE for the five regions from 2010 to 2021 are shown in Figure 5b. The CFE in North and East China are considerably greater compared to other regions, suggesting that regional differences in efficiencies still exist due to the imbalance of development in Northeast and Southwest China, despite eliminating the effects brought about by external environmental variables. The comprehensive efficiency (CFE) in North China, Northeast China, the middle of South China, and Southwest China has exhibited a noticeable upward trajectory, suggesting that the internal management efficiency in these four regions is steadily improving. This result is consistent with previous research findings [55]. Meanwhile, East China has consistently maintained a higher level of efficiency, with a stable trend, and the disparities between regions are gradually diminishing.

3.4.2. Comparative Analysis of Stage I and Stage III

When comparing the CFE in stage I and stage III, it is evident that the efficiency of each region in the source-area has been enhanced. In Figure 6a, it is observed that the efficiency of the source-area has increased by over 15%. Specifically, the efficiency of Shanxi and Shaanxi has improved by 35% and 28%, respectively. These findings indicate that efficiency assessments, when not accounting for the impact of environmental factors and random disturbances, are underestimated.

During both stage I and stage III, Shaanxi’s efficiency is quite low. However, in stage III, the efficiency is much higher compared to stage I. This suggests that Shaanxi’s inefficiency is not just attributed to outdated management practices, but is also influenced by a less favorable external environment. The Shaanxi province is currently experiencing a phase of initial economic expansion, heavily reliant on factor resources. The proportion of resource-based sectors in the overall economy is over 50%, which is much higher compared to other provinces. Since 2010, Shaanxi province has significantly increased the size of its coal mining operations, leading to substantial economic growth but also causing significant environmental damage. The CFE in Shanxi is primarily influenced by the external environment. Shanxi is a significant energy-producing province, with raw coal production contributing to almost one-third of the national output. Coal transportation also accounts for approximately 20% of the country’s total. However, the excessive focus on coal efficiency and the neglect of coordinated development have resulted in the objective reality of environmental pollution, disregarding the cumulative consequences. Inner Mongolia and Xinjiang are relatively resilient to environmental influences.

The average CFE in the sink-area increases from 0.390 to 0.816 after adjustment, suggesting that external environmental factors enhance the level of redundancy in inputs and outputs, leading to a lower efficiency before adjustment. Based on Figure 6b, the efficiency of all provinces except Beijing and Shanghai have shown improvement. This indicates that environmental factors have a positive influence on Beijing and Shanghai. On the other hand, the inefficiencies observed in the other provinces during stage I can be attributed to unfavorable external conditions rather than solely their low level of internal management.

Figure 7 shows the trend of efficiency changes in each province. Specifically, the CFE of Shandong and Henan increased by 0.636 and 0.633, respectively, when eliminating environmental values and statistical noise. These values represent an improvement compared to the values before the exclusion. Shandong and Henan, being significant industrial hubs in China, face a substantial coal demand. However, these provinces possess limited reserves of coal resources, necessitating the importation of large quantities of coal from other provinces. This practice not only escalates transportation expenses and CO₂ emissions, but also the transfer of substandard coal with excessive sulfur and ash contents. In addition, there is an urgent need to optimize the industrial structure of the two provinces, as there are various projects that consume huge amounts of energy, emit high levels of pollutants, and have low efficiencies. After eliminating extraneous environmental factors and statistical fluctuations, the CFE of Hainan, Yunnan, and Heilongjiang provinces experienced respective increases of 0.137, 0.214, and 0.393. However, during stage I and stage III, the CFE of these three provinces remained at a low level. These three provinces are experiencing constraints on the CFE due to a combination of an adverse external environment and ineffective management levels. For instance, Hainan has made limited advancements in promoting the adoption of coal cleaning and transformation in crucial sectors like electricity and cement. Similarly, Heilongjiang intends to execute a project for the clean and efficient utilization of coal in the “14th Five-Year Plan” timeframe, suggesting that there is ample room for enhancement. The CFE of Beijing and Shanghai has decreased by 0.456 and 0.17, respectively, compared to stage I. In the past decade, Beijing’s coal consumption decreased significantly from 21.796 million tons in 2010 to under 1.5 million tons in 2021, reducing energy loss and pollution emissions. Shanghai’s energy consumption per unit of GDP in 2020 was 0.41 tons of standard coal, a 23.1% decrease from 2015, according to the Shanghai Municipal Bureau of Statistics. Similarly, the CO₂ emissions per unit of GDP were 0.88 tons, showing a decline of 25.4% from 2015. Shanghai has made tremendous progress in enhancing the CFE and reducing the intensity of CO₂ emissions, as indicated by these metrics [56].

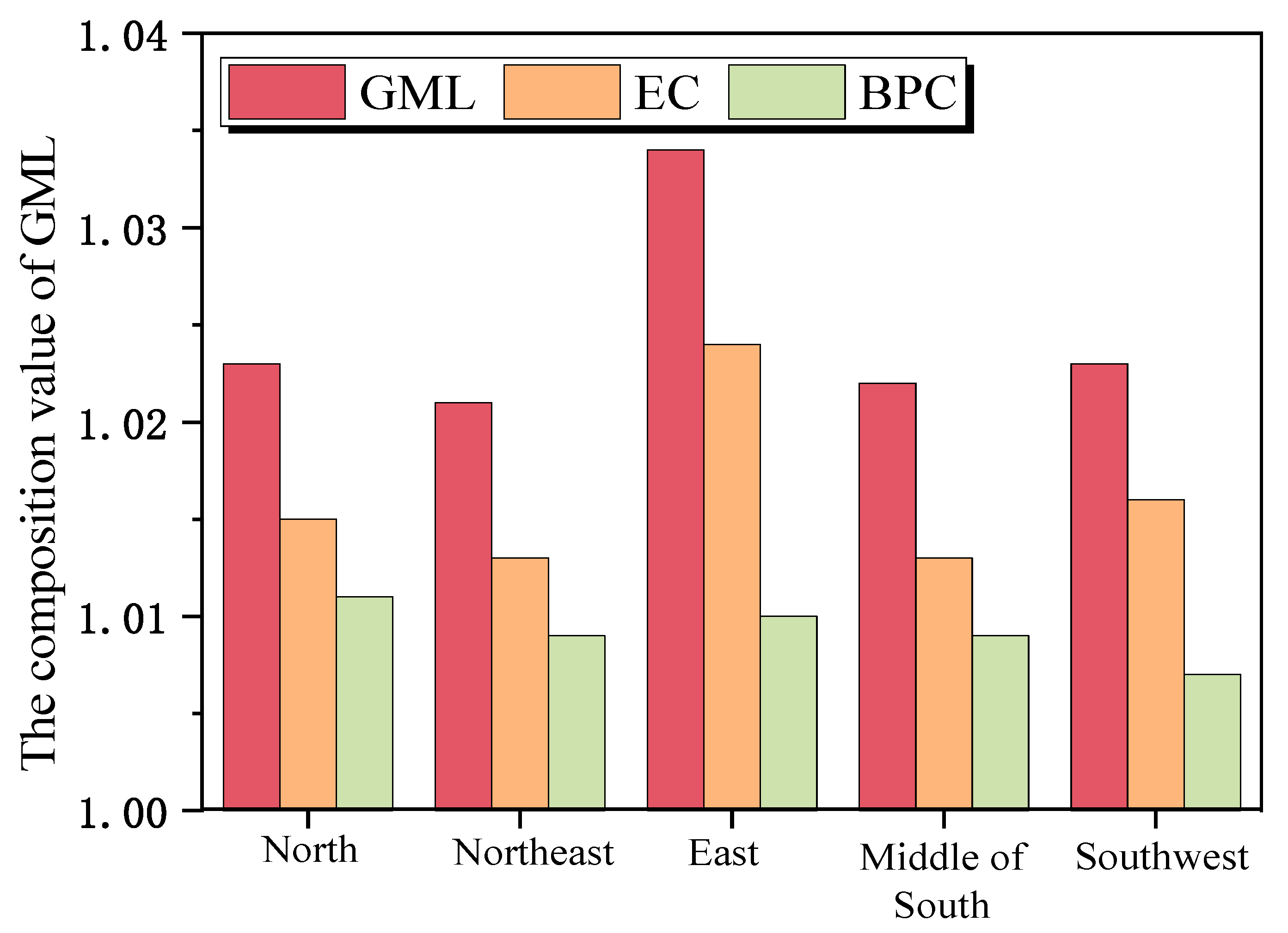
3.5. Dynamic CFE Evaluation

3.5.1. Dynamic CFE Growth Rate

The three-stage SBM is capable of quantifying the relative association between CFE and its front in each province, but it is static. This article employs the GML index model, which utilizes adjusted input–output data, to examine the dynamic fluctuations in efficiency and the underlying causes that drive its growth.

Table 4. Sub-annual GML index and decomposition.

Year	Source-Area			Sink-Area
	GML	EC	BPC	GML	EC	BPC
2010–2011	1.037	1.000	1.037	1.062	1.067	0.999
2011–2012	0.996	1.012	0.984	1.040	1.028	1.012
2012–2013	0.997	0.965	1.034	1.025	1.014	1.011
2013–2014	0.977	0.998	0.979	1.074	1.049	1.026
2014–2015	0.992	1.014	0.980	1.001	0.995	1.006
2015–2016	0.992	0.997	0.995	1.015	1.005	1.011
2016–2017	0.995	1.034	0.967	1.021	1.013	1.008
2017–2018	0.989	0.999	0.990	1.012	1.007	1.006
2018–2019	1.028	0.989	1.042	1.017	1.005	1.012
2019–2020	0.973	1.004	0.969	0.999	0.996	1.003
2020–2021	1.018	1.005	1.013	1.042	1.033	1.009
Average	0.999	1.002	0.999	1.028	1.019	1.009

indicates that the CFE of the source-area exhibits a declining pattern from 2010 to 2021. The GML indexes in 2010–2011 and 2018–2019 have increased significantly, reaching 1.037 and 1.028, respectively. This indicates a substantial improvement in the CFE in both 2011 and 2019. For sink-area, it can be seen that the average annual growth rate of CFE is 2.8% during 2010–2021, and except for the negative growth of efficiency during 2019–2020, the GML index is greater than 1 in all the other years and reaches the maximum during 2013–2014. The growth rate is 7.4%, indicating that the CFE is on an upward trend.

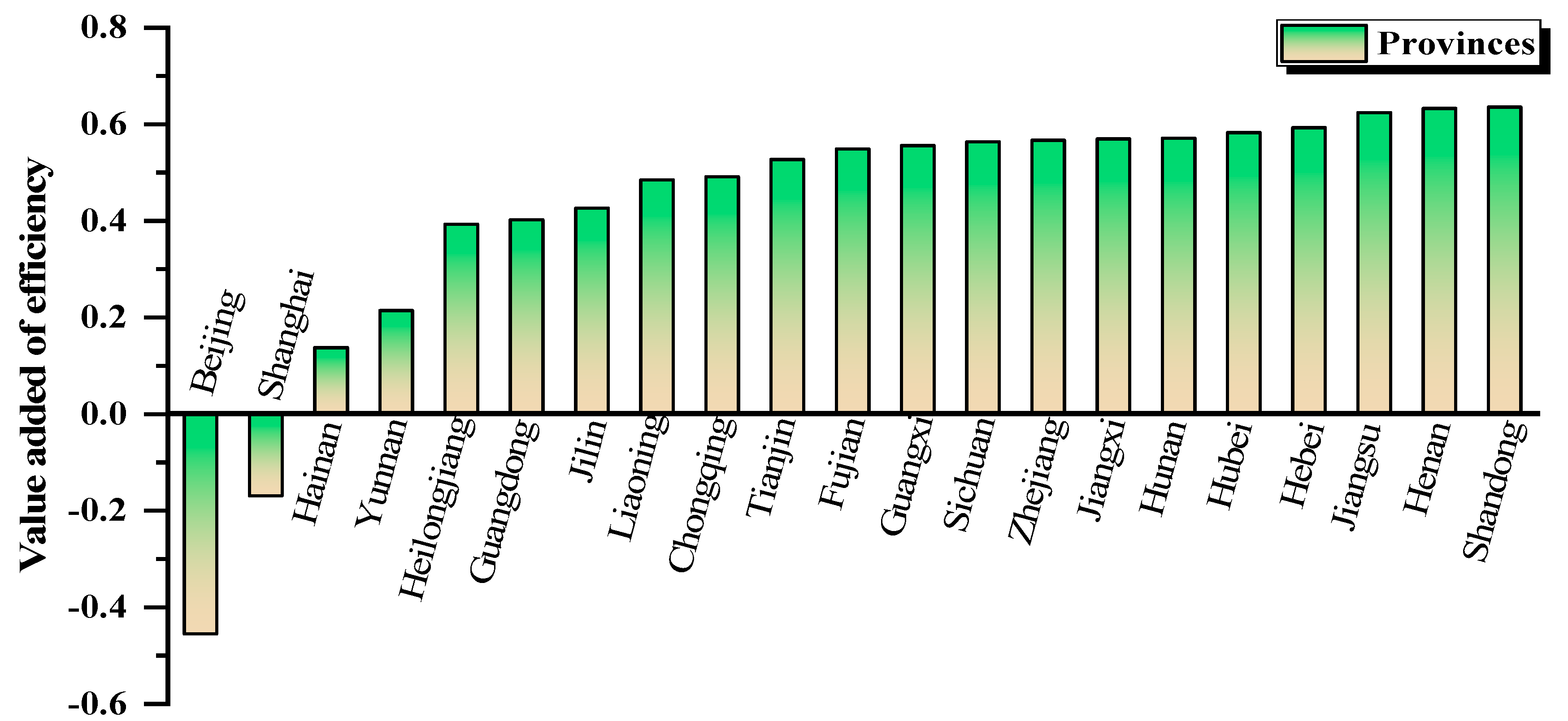
3.5.2. GML Index Component Changes and Regional Characteristics

From a yearly perspective, both in source-area and sink-area, the CFE shows a “W”-shaped fluctuation trend of “falling-rising-falling-rising”. From Figure 8, the trend of the GML index and the trend of the BPC index remain basically consistent, indicating that the changes in CFE in the source-area mainly come from the changes in the index of the BPC. However, the changing trend of the GML index is basically consistent with the changing trend of the EC, indicating that the change of the CFE in the sink-area mainly comes from the change of the EC.

From a regional perspective and in Figure 9, although all provinces have a GML index greater than 1, their intrinsic drivers are not the same, and the regional differences in the index of EC drivers are stronger than the BPC. The index of the BPC is always greater than 1 in all sample regions, with less regional variability, but the index of the BPC is slightly higher in North and East China than in other regions, suggesting that the BPC plays a greater role in efficiency improvement in North and East China. The index of the BPC in the Southwest is lower than in other regions, pointing to the need to focus on upgrading coal industry technology in the Southwest. For the index of EC, the Northeast region exhibits a slightly lower level of efficiency compared to other regions, leading to a slower enhancement of its CFE. This disparity may stem from the region’s focus on revitalizing its industrial foundations, as it faces ongoing difficulties and challenges, resulting in a lower economic growth rate. Additionally, the inefficient allocation of energy and other input factors has contributed to the sluggish improvement of its CFE [57].

4. Conclusions and Policy Suggestions

Coal resources play a crucial role in ensuring national energy security. As the concept of sustainable development becomes more prominent, it is imperative to expedite the establishment of an ecological civilization system for the coal industry. This includes developing a regional coal flow while adhering to carbon emission limitations. In this paper, the three-stage SBM model is used to evaluate China’s CFE by source-area and sink-area during the period of 2010–2021, and the internal driving factors of efficiency change are decomposed using the GML index. The empirical results show that after removing the effects of the external environment and random errors, most provinces are more efficient than before adjustment, suggesting that the poorer external environment causes CFE inefficiencies in all provinces except Beijing and Shanghai. In the decomposition factor, it is found that the changes in the CFE of the source-area mainly come from the changes in the BPC, while the sink-area mainly comes from the changes in EC. At the regional level, the regions with abundant resource endowment have a superior efficient performance. Finally, the external environmental factors have different effects on each slack, and the degree of government assistance and environmental regulation both have a beneficial influence on CFE. Based on the above discussion, this paper proposes suggestions for improving the CFE in China.

(1)

Enhance the external environment to optimize CFE at the provincial level. In the sink-area, provinces are characterized by an optimal industrial structure and elevated technological innovation, such as Beijing, Shanghai, and Guangdong. Inner Mongolia attains peak efficiency in the observed sample period for the source-area. Consequently, regional administrations should expedite economic restructuring, refine the economic development paradigm, and transition from energy- and pollution-intensive industries reliant on substantial capital and energy inputs to energy-efficient, high-value-added modern sectors;

(2)

The provincial government should delineate specific policies aimed at augmenting investment for securing coal flow. Fixed-asset investment and governmental backing wield significant influence in advancing regional economic and technological development. Augmenting investment in securing coal mining in the source-area facilitates the evolution and enhancement of coal-related enterprises, ensures the extraction and production of coal resources, and amplifies coal output and efficiency, thereby contributing to the overall enhancement of coal resource flow efficiency. Correspondingly, increased investment and expenditures in the sink-area serve to fortify the foundational support for optimizing industrial structures and the transition to high-tech industries, consequently elevating the utilization efficiency of coal resources.

This paper focuses on analyzing the CFE at the macro-provincial level. Given the significant geographical variations in coal flow patterns, a more effective approach to enhancing CFE in the future would involve examining it at the micro-level within individual firms or at the prefecture level in alignment with local coal resources. In order to enhance the quality of this study, considerations at more granular levels are recommended, potentially offering deeper insights and more targeted strategies to improve CFE practices.