Abstract
To figure out the primary factors that significantly impact the sustainability of highway routine maintenance management (HRMM), this paper examined 23 highway operating subsidiaries (evaluated decision-making units, DMUs) affiliated with Shaanxi Transportation Holding Group (STHG) in Shaanxi Province as an example. First, data envelopment analysis (DEA) was used to evaluate the performance of HRMM for each DMU. Subsequently, a truncated regression model was utilized to analyze the primary factors that impact the outcomes of HRMM. The conclusions indicated that except for the widely recognized input and output factors, there exist some uncontrollable factors that can affect HRMM efficiency, including the amount of natural dustfall, urbanization rate, tunnel length, and bridge length. These findings offer suggestions for STHG focusing on DMUs facing challenges with high dustfall and urbanization rate and long bridges and tunnels when allocating maintenance resources to improve HRMM efficiency and achieve sustainable highway maintenance management. Moreover, the methodology for analyzing uncontrollable factors can also serve as a valuable reference for other maintenance types or fields, contributing to the broader goal of promoting sustainability in transportation infrastructure development.
1. Introduction
With the growing travel demand, highway maintenance is facing grave challenges due to the long-term effects of environmental and traffic loading factors. In response to the above problem, highway agencies are increasingly focusing on the sustainability of highway maintenance, which refers to the application of environmentally friendly, efficient, and sustainable technologies and management practices to maintain and manage highway infrastructure assets, which can achieve the preservation and appreciation of highway assets while the reducing environmental impact and ensuring user safety. In recent years, numerous scholars have conducted research on the innovation of maintenance decision-making [1,2], maintenance management [3,4], maintenance assessment [5,6,7], and maintenance technology [8,9], which provide new development directions for sustainable highway maintenance.
Among the above sustainable maintenance aspects, this paper mainly focuses on performance evaluation in maintenance assessment. Performance evaluation aims to enhance the effectiveness of asset management practices, and it has been widely applied in areas such as corporate management [10], factory equipment maintenance [11], and manufacturing [12]. In the context of transportation asset management, corresponding standards and guidelines have been introduced [13,14,15,16]. Highways, as critical national infrastructure assets, attract significant attention from transportation departments regarding the final conditions and service levels. Transportation departments increasingly emphasize performance-based management in the maintenance and operation of highways to ensure an objective and scientifically-driven assessment [17], which plays an important role in sustainable highway asset management.
To objectively and fairly evaluate highway maintenance management (HMM), many scholars have integrated the concept of performance evaluation into management practices [18,19,20,21]. The fundamental content of performance evaluation is the measurement of efficiency, which can be achieved through two principal methodologies: stochastic frontier analysis (SFA, parametric approach) and data envelopment analysis (DEA, non-parametric approach). In contrast to SFA, DEA does not necessitate any parametric assumptions about the production frontiers and employs linear programming techniques to assess the relative efficiency of organizations, making it well suited to multi-input and multi-output problems. Since its inception, DEA has been employed extensively for performance evaluation in a multitude of fields, including higher education, healthcare, supply chain management, the defense sector, and transportation [22,23,24,25,26,27].
The asset management goal of highway management agencies is to attain optimal maintenance management results by minimizing the inputs of maintenance in order to maximize the generated maintenance benefits and achieve the sustainable development of highway infrastructures. In essence, this can be viewed as a process involving multiple inputs and multiple outputs. Based on this characteristic, DEA is one appropriate method to evaluate highway maintenance management performance (HMMP), which can be mainly classified into two aspects in existing studies: maintenance operations [28,29,30,31,32,33] or bridge maintenance [19,34,35,36,37].
It is noteworthy that highways are subject to a myriad of complex factors (i.e., climate, the natural environment, etc.) during operation, and these factors are objective and not under human control, which can be referred to as external factors or uncontrolled factors. Especially for routine maintenance, the fundamental type throughout the entire highway asset lifecycle, involving routine cleaning and minor repairs to ensure that highway assets are maintained at a high level, plays a significant role during the sustainable development of the operation period. Identifying the impact on highway routine maintenance management (HRMM) of uncontrollable factors is critical to improving highway routine maintenance management performance (HRMMP); however, few studies have focused on this problem.
Consequently, this paper intends to explore how uncontrollable factors affect HRMMP based on a case study of 23 highway operating subsidiaries affiliated with Shaanxi Transportation Holding Group (STHG) in Shaanxi Province so as to fulfill sustainable HRMM. First, in accordance with the principles of the DEA method’s evaluation indicators selection and considering the content and background of routine maintenance management work, input and output indicators were selected. Next, according to the characteristics of HRMM, the input-oriented DEA model was employed to calculate the routine maintenance management efficiency values of each subsidiary. Lastly, based on the obtained efficiency values, this paper utilized a truncated regression model to analyze the impact on HRMMP of potential uncontrollable factors, which explained the key aspects to be considered in sustainable HRMM.
2. Literature Review
2.1. Performance Evaluation of HMM
In the process of performance evaluation, the determination of evaluation subjects, indicators, and methods is important. For HMM, when selecting evaluation indicators, it is essential to consider the actual situation of the evaluation subject (i.e., operating agency or bridge), the relevant influencing factors, the main work contents, and the involved information comprehensively to ensure the comprehensiveness and scientific rationality of the indicators. Simultaneously, the selection of evaluation indicators will also depend on the characteristics of the evaluation method. It is required to satisfy the conditions of the evaluation model while objectively and accurately reflecting the substance of the evaluation subject. Table 1 reviews the partial research on the performance evaluation of HMM, indicating that scholars have various research contents and focuses based on evaluation indicators. The construction process and contents of evaluation indicators can provide a reference for the subsequent evaluation of HRMMP in this paper.

Table 1.
Review of performance evaluation of HMM.
2.2. Uncontrollable Factors Considered in Performance Evaluation of HMM
The maintenance and operation of highways are influenced by various factors, each with a specific impact to a greater or lesser extent. These factors, known as external, uncontrollable (used in this paper), or challenge factors, are objective and outside the control of decision makers (i.e., climate and location), whose impact must be considered in the performance evaluation of HMM [18,45]. Table 2 reviews the partial research on uncontrollable factors considered in the performance evaluation of HMM, which can inform the selection of the uncontrollable factors of HRMMP in the following parts.

Table 2.
Review of uncontrollable factors considered in performance evaluation of HMM.
2.3. Approaches to Deal with Uncontrollable Factors in DEA
As previously stated, uncontrollable factors have a significant impact on HMMP, particularly in performance evaluation using DEA. Uncontrollable factors may impact the ability of the decision-making unit (DMU) to increase outputs with a given number of inputs or limit the ability of the DMU to decrease inputs while maintaining a certain level of outputs. To address the above issues, there are two main types of approaches in past studies: one-stage approaches and multi-stage approaches [45]. One-stage approaches take uncontrollable factors into account when running a DEA model by refining the traditional DEA formula [47,48] or categorizing the uncontrollable factors of the DMU operation environment to compare the efficiency of DMUs in different environments [49,50]. Multi-stage approaches are carried out to explore the relevant effects by performing a regression analysis of uncontrollable factors based on the obtained DMU efficiency values [51,52,53]. The details and application situation of the above approaches can be found in the research of [45].
For the performance evaluation of HMM, one-stage approaches have been employed the most. One practice is to run the DEA model with and without considering the uncontrollable factors and analyze the impact of these factors on the HMMP by comparing the two results obtained [35,37]. Another one is to categorize the environment in which the DMU is located based on uncontrollable factors (i.e., climate and terrain condition) to capture their effects [28]. One disadvantage of the above approaches is that it is difficult to determine the specific quantitative impact of each factor on HMMP, making it challenging to use as a guide for decision-making. One study [46] provided an alternative method, two-stage bootstrapping regression, analyzing how uncontrollable factors affect the highway deterioration processes, which has inspired subsequent research. Through the above analysis, based on the characteristics of HRMM and DEA efficiency values, this paper opted for the regression method to explore the effects of uncontrollable factors on HRMMP.
2.4. Uncontrollable Factors Analysis of DEA Efficiency Values
The efficiency value obtained by DEA is a restricted dependent variable situation when analyzed as a dependent variable because it falls between 0 and 1 (). The traditional ordinary least squares (OLS) estimation method for regression, whether applied to the entire sample or a subsample after the discrete points have been excluded, results in inconsistent estimation due to the inclusion of the nonlinear term in the disturbance term [54]. Two primary methodologies are utilized to address the challenge of regression analysis of restricted dependent variables: the Tobit model and the truncated regression model.
- The Tobit method, introduced by Tobin in 1985, employs maximum likelihood estimation (MLE) to estimate censored regression models. Censored regression is one of the scenarios for a restricted dependent variable analysis. In the linear model , when censoring as for certain cases where or (where is a constant), this type of data is referred to as “censored data” [55].
- In the linear model , it is assumed that due to certain reasons, data can only be observed when (where is a constant). Therefore, when , no data regarding the variables are available, and this phenomenon is referred to as “truncation”. For instance, data can only be observed when is greater than c, resulting in a “left truncation” at .
In past studies, researchers have commonly employed the Tobit model to analyze the factors influencing DEA efficiency values [56,57,58,59,60]; however, the actual DEA efficiency value does not exhibit censoring issues and does not fall into the category of censored data. Considering the initial efficiency value as a whole and denoting the efficiency value in the worst state as , the application of the Tobit method implies that values are censored data within the data set; consequently, all values below are replaced by , as illustrated in Figure 1a. Nevertheless, for any evaluated DMU, the efficiency value will never be lower than in the worst state, much less reach or descend below 0. To put it another way, the scenario depicted in Figure 1a is not compatible with the actual DEA efficiency values. As shown in Figure 1b, the data in the range between 0 and are unobservable, which can be referred to as truncating at the left. Consequently, DEA efficiency values are more consistent with the truncated data, which can be processed by a truncated regression model [61,62,63,64].
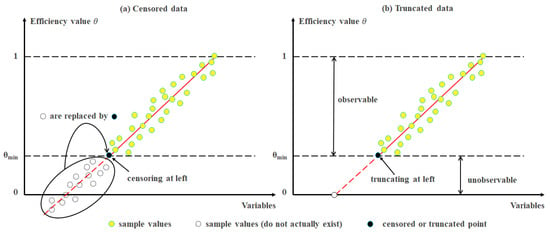
Figure 1.
Diagram of censored and truncated data (assuming a positive correlation between and variables): (a) censored data; (b) truncated data.
2.5. Knowledge Gap
The literature review above highlights the following two research gaps:
- The importance of routine maintenance in the preservation and appreciation of highway assets has been overlooked in studies that focus on overall highway maintenance or bridge maintenance, that is, there is a lack of research specifically focusing on HRMMP.
- Researchers often concentrate solely on the methods and conclusions of performance evaluation, neglecting to investigate the factors that influence HMMP, particularly in HRMMP. This lack of investigation hinders a more comprehensive understanding of maintenance management performance assessment and improvement.
Therefore, according to the characteristics of routine maintenance and management, this paper employed the DEA method to construct the performance evaluation indicators set and evaluated HRMMP. In addition, a truncated regression model was proposed to analyze the impact of uncontrollable factors on HRMMP, overcoming the shortcomings of the Tobit model.
3. Data Collection
STHG is primarily responsible for the investment, construction, and operation of highways within Shaanxi Province. It adopts a hierarchical management model of group–operation company–maintenance management subsidiary for HMM; the organizational structure and corresponding responsibilities are depicted in Figure 2.
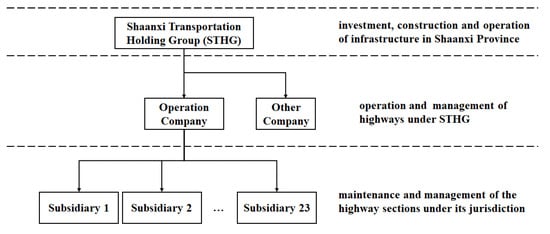
Figure 2.
Organizational structure and corresponding responsibilities of STHG.
In a previous study conducted by the authors, Shaanxi Province can be typically divided into three regions based on topography [65]: the Shaanbei plateau (northern Shaanxi), the Guanzhong plain (central Shaanxi), and the Shaannan mountains (southern Shannxi). There are 23 maintenance management subsidiaries (23 DMUs) responsible for the maintenance management of different road sections, the distribution of which is illustrated in Figure 3. The relative maintenance management data from 2020 to 2022 was provided by STHG, which involves the climate conditions, traffic, maintenance mileages, maintenance management resources, road conditions, etc., of each subsidiary, providing a strong foundation for the following research.
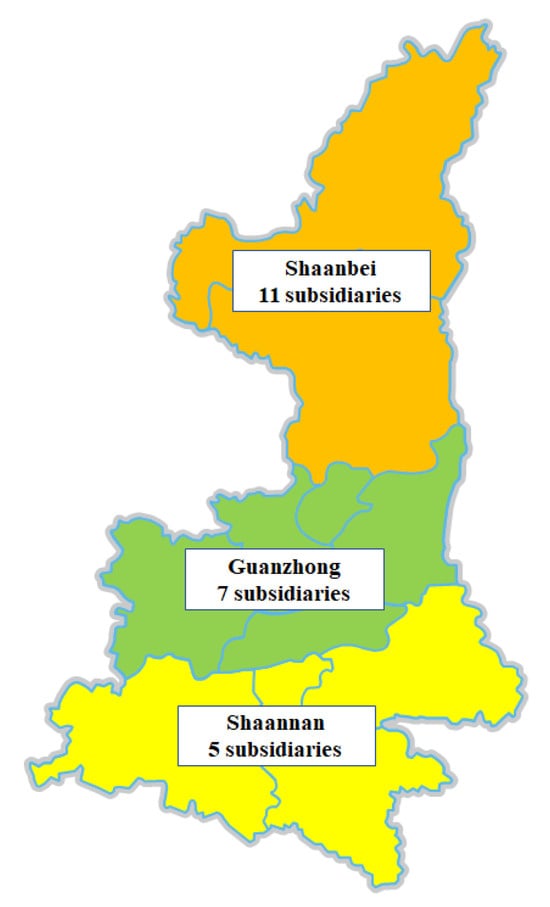
Figure 3.
Distribution of subsidiaries and regional divisions in Shaanxi Province.
4. Methodology
4.1. Input-Oriented DEA Model
Traditional DEA models consist of the Banker–Charnes–Cooper (BCC) model, which is based on variable returns to scale (VRS), and the Charness–Cooper–Rhodes (CCR) model, which is based on constant returns to scale (CRS). The efficiency obtained by the CCR model is known as combined technical efficiency (TE) because it incorporates scale efficiency (SE), while the efficiency obtained by the BCC model is pure technical efficiency (PTE). SE can be calculated by Equation (1).
SE = TE/PTE
CRS efficiency values reflect TE under a constant scale, highlighting the excellence of highway management agencies in terms of maintenance operation mechanisms and overall management levels. In contrast, VRS efficiency values indicate PTE under a variable scale, revealing whether there is redundancy in the maintenance management resources invested by highway management agencies. Moreover, the models mentioned above can be categorized as either input-oriented or output-oriented. From an input-oriented perspective, organizations usually want to keep the amount of input resources to a minimum while maintaining a constant level of output. From an output-oriented point of view, organizations strive to achieve more outputs while maintaining a constant level of input resources. Highway management agencies often have limited resources for maintenance, focusing on minimizing inputs while sustaining a certain level of maintenance performance; therefore, the input-oriented DEA model was selected to evaluate HRMMP, which is shown in Table 3.

Table 3.
Input-oriented DEA models.
4.2. Return to Scale (RTS)
The concept of returns to scale (RTS) is a crucial foundation in economics for analyzing the variations in production factors and outputs. With the ongoing evolution of DEA methodology, the application of RTS has been extended. When inputs and outputs vary in the same proportion, the evaluated DMU is in a CRS state. If the proportional change in output exceeds that of the input when increasing or the proportional change in output is less than that of the input when decreasing, the evaluated DMU is in an increasing returns to scale (IRS) state. Conversely, if the smaller proportional change in output exceeds that of the input when increasing or the proportional change in output when increasing is less than that of the input, the evaluated DMU is in a decreasing returns to scale (DRS) state. IRS and DRS fall under the VRS category.
There are the three following criteria to determine the RTS of DMU:
- When , the evaluated DMU satisfies CRS. Or else:
- When , the evaluated DMU satisfies IRS.
- When , the evaluated DMU satisfies DRS.
4.3. Truncated Regression Model
For a random variable y in the linear model , when it experiences truncation, the corresponding probability density function is altered. Let the initial probability density function be denoted as ; then, the conditional probability density function after left truncation at point c is represented by Equation (2) [54].
The area under the probability density function curve must sum to 1. Due to truncation, where data are unobservable at the left of point c, the probability density at the location of c is elevated to ensure that the area under the curve adds up to 1. This elevation continues until the entire area under the curve adds up to 1 [55]. For illustration, the impact of truncated data on the classical normal distribution’s probability density function is visually evident in Figure 4.
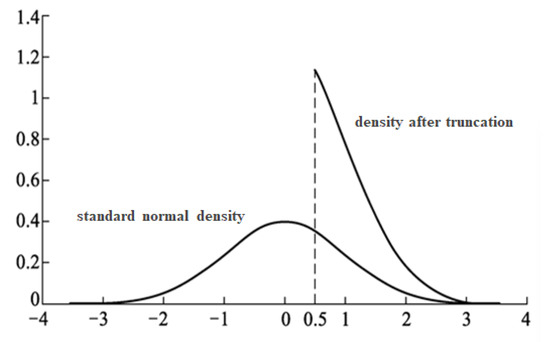
Figure 4.
Truncation effects under the standard normal distribution.
Then, the conditional expectation of the truncation distribution in the case of “left truncation” is calculated; the simplest case of the normal distribution is still used as an example.
For any real number , the inverse Mills’s ratio (IMR) is defined as , which is the density function of the standard normal divided by the area (referred to as the gray area, as illustrated in Figure 5) under the curve larger than . Consequently, can be obtained, as shown in Equation (3).
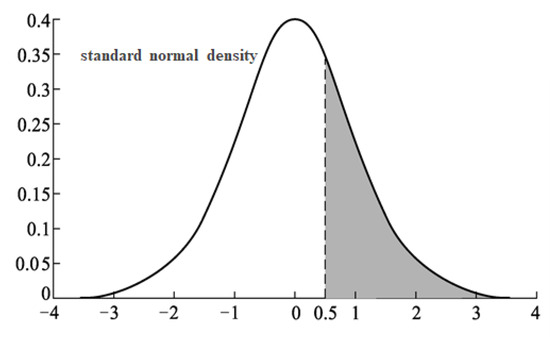
Figure 5.
Inverse Mills’s ratio (IMR).
For a general normal distribution , let , so that . Therefore, the conditional expectation in the case of a general normal distribution with truncation is shown in Equation (4).
Assume that , so that , and then Equation (5) can be obtained from Equation (4).
The sample data can only be observed in the case of left truncation (); if OLS is applied to estimate , the nonlinear term will be omitted and then included in the perturbation term. It can be seen that is a function of , and thus the inclusion of the nonlinear term in the perturbation term in the OLS regression leads to estimation bias.
To address the above problems, MLE is used to obtain a consistent estimate of the truncated regression. The initial probability density function for MLE of the regression model is shown in Equation (6).
The conditional probability that the sample data can be observed is shown in Equation (7), where the perturbation term obeys a normal distribution, that is, .
Then, the conditional density after truncation is shown in Equation (8).
The research frame in this study is shown in Figure 6.
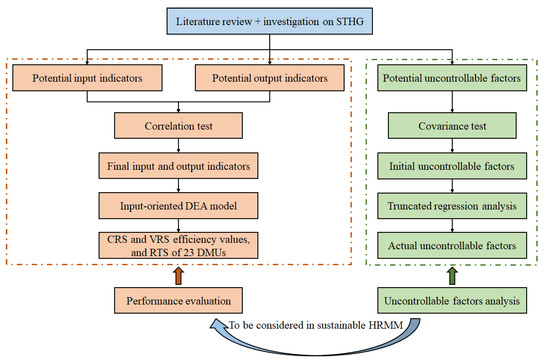
Figure 6.
Research frame.
5. Performance Evaluation
5.1. Selection of Potential Input and Output Indicators
Most organizations consider financial, material, and human resources as the three input factors in the performance evaluation process, and the results obtained through the transformation of inputs naturally become outputs. For the highway routine maintenance management process, financial input factors include the total maintenance costs, material input factors include maintenance materials and equipment other than contractors’ input, and human input factors include maintenance management personnel. Additionally, activities conducted by the maintenance management department, such as road inspections and road appearance improvements, which contribute to maintenance management, should also be considered. The output factors that require consideration primarily encompass maintenance mileage, traffic volume, various technical condition indices, user satisfaction, user costs, and so on.
By investigating the HRMM work and operational mechanisms of STHG, combined with Table 1, a compilation and summary were conducted to obtain the potential input and output indicators set illustrated in Table 4.

Table 4.
Potential evaluation indicators of HRMM.
5.2. Correlation Tests of Input and Output Indicators
The premise of DEA is that changes in input indicators should lead to positive proportional changes in output indicators [66]. Therefore, based on the availability and effectiveness of the data, the input and output indicators selected from Table 4 and data corresponding to STHG in the year 2022 are shown in Table 5. Spearman’s correlation tests were performed on the input and output data of 23 DMUs using the correlation analysis feature in the SPSS 26.0 software [67], as shown in Table 6.

Table 5.
Input and output indicators and maintenance data in the year 2022.

Table 6.
Results of Spearman’s rank correlation test for 2022 annual data.
Analyzing the results of the correlation analysis presented in Table 6, it is observed that MP and MC among the input indicators exhibited positive correlations with MM, AADT, and TSA among the output indicators. Conversely, ME and MA among the input indicators showed either no correlation or a negative correlation with MQI among the output indicators. These findings suggest that the initially identified input–output indicators, based on subjective significance, may not necessarily hold practical meaning in the analytical process. In consideration of the correlation analysis results, the revised selection of input indicators included MP and MC, while the output indicators consisted of MM, AADT, and TSA.
Building upon this analysis, a correlation test was conducted on the input and output data for each DMU from 2020 to 2022, and the results are presented in Table 7. Based on the outcomes shown in Table 7, the ultimate selection of the input indicators included MP and MC, while MM and TSA were chosen as the output indicators.

Table 7.
Results of Spearman’s rank correlation test for 2020–2022 annual data.
5.3. Determination of Efficiency Value and RTS
Based on the identified input and output indicators from the above analysis, the efficiency value of HRMMP for each DMU under the CCR and BCC scenarios was calculated, respectively, using the input-oriented DEA model, and the RTS of each DMU was determined; the results are presented in Table 8.

Table 8.
Efficiency value and RTS of each DMU in the year 2022.
According to Table 8, it can be observed that under the CCR model (CRS state), DMUs 11, 16, 19, 20, and 21 were on the efficiency frontier (). Furthermore, under the BCC model (VRS state), the DMUs on the efficiency frontier () included DMUs 2, 3, 12, and 22 in addition to those under the CRS state. For a DMU that is effective under a CRS state, it remains effective under a VRS state; however, effectiveness under a VRS state does not guarantee effectiveness under a CRS state. When a DMU is effective under both conditions, it is in a state of RTS with CRS, such as DMUs 11, 16, 19, 20, and 21. When the efficiency values under a CRS state and VRS state are not both 1, or when they are both not 1, there exist other RTS: IRS (DMU 2, 4, 8, 12, 13, 14, 15, 17, and 18) or DRS (DMU 1, 3, 5, 6, 7, 9, 10, 22, and 23). In summary, when the and values in Table 8 are not equal to 1, it indicates that the respective DMU is ineffective under a CRS state or VRS state.
Regarding the RTS, among the 23 DMUs, 5 operated under a CRS state. Additionally, nine DMUs experienced IRS, indicating an ongoing improvement in their maintenance management efficiency and an optimistic trend in efficiency development. On the other hand, nine DMUs faced DRS, suggesting a regression in their maintenance management efficiency. In comparison to the subsidiaries with IRS, those experiencing DRS may need to allocate more effort and intensify their optimization of input resource allocation in their later-stage management efforts.
6. Uncontrollable Factors Analysis
6.1. Selection of Potential Uncontrollable Factors
HRMMP is influenced by various uncontrollable factors, including natural conditions like climate and geography, maintenance history, years of operation, unexpected situations such as traffic accidents and natural disasters, and regional socio-economic development. Section 5.3 demonstrates significant variations in the HRMMP efficiency values among the 23 DMUs. It is unclear whether uncontrollable factors, in addition to their input resources, impact sustainable HRMM. To explore the problems, combined with Table 2 and the investigation into the HRMM work of STHG, the potential uncontrollable factors were analyzed as follows.
- Climate condition. When analyzing sustainable HRMM, it is important to consider the influence of climatic conditions, which can vary greatly. This study mainly focused on daily weather statistics in areas where each DUM is located, including the number of extreme weather days such as moderate-to-heavy rain days, snowy days, and hazy days. Additionally, the quantity of natural dustfall in the area was measured using the annual province-wide environmental quality status information provided by the Shaanxi Provincial Department of Ecology and Environment.
- Geographic location. The geographic location is mainly based on topography and geomorphology, which is reflected in this study by three main categories: the Shaanbei plateau, the Guanzhong plain, and the Shaannan mountains.
- Maintenance history. Maintenance history mainly refers to the data on corrective maintenance, preventive maintenance, emergencies, and special maintenance organized by each DMU of the specific road section from the opening of the operation to date, which was used to analyze the impact on HRMM.
- Years of operation. Years of operation refer to the service life of the road from the year of commissioning to the present.
- Emergencies. The data on emergencies mainly count the number of traffic accidents, landslides and mudslides, and other natural disasters that occurred during the statistical year of each DMU as analysis data.
- Regional characteristics. Regional characteristics primarily include population size, urbanization rate, and gross domestic product (GDP), as well as other indicators of socio-economic development in the regions where each DMU is located.
- Special asset type. Bridges and tunnels are considered special asset types that require more attention to routine maintenance than other asset types such as pavements and subgrades. This is due to the incalculable impact of damage to bridges and tunnels. The available data show that the length of bridges and tunnels managed by each DMU had significant variations, the impact of which on HRMMP cannot be ignored.
Based on the above analysis and available data, Table 9 summarizes the potential uncontrollable factors. In order to meet the requirements of the sample data volume in the truncated regression analysis, the efficiency values of each DMU from 2020 to 2022 were calculated. The data of the potential uncontrollable factors from Table 9 and the efficiency values of each DMU are listed in Table 10.

Table 9.
Potential uncontrollable factors of HRMM.

Table 10.
Potential uncontrollable factors data and efficiency values of each DMU.
6.2. Multicollinearity Test of Possible Uncontrollable Factors
Prior to commencing regression analysis, it is crucial to conduct multicollinearity tests on potential uncontrollable factors using the STATA 18.0 MP software and to exclude factors exhibiting high collinearity. Conventionally, factors with a variance inflation factor (VIF) exceeding 10 may suggest the presence of multicollinearity. To begin the regression analysis, considering the efficiency values of CRS or VRS from 2020 to 2022 as the dependent variable and various potential uncontrollable factors as independent variables, the VIF values for each potential uncontrollable factor were calculated. In this context, the regional factors underwent virtualization using the STATA software. Three dummy variables, namely r1 (Shaanbei), r2 (Guanzhong), and r3 (Shaannan), were generated. To address multicollinearity concerns, only r2 and r3 were included as indicators in the analysis.
The analysis results shown in Table 11 revealed notable multicollinearity issues among the factors of population, UR, and region (r2, r3). Although UR had a lower VIF value compared to population and region, due to multicollinearity concerns, it was still chosen in the truncated regression analysis. Advanced econometric studies suggest that when researchers prioritize the significance of the model and the factors under analysis, multicollinearity issues can be disregarded. The absence of multicollinearity interference may amplify the significance of initially significant factors, rendering them more pronounced. Hence, population and region were not taken into further consideration due to the fact that the inclusion of these two factors would not have augmented the significance of the model or the analyzed factors. Consequently, the initial identification of factors influencing the DEA efficiency values encompassed seven variables: weather, age, dustfall, BL, TL, GDP, and UR.

Table 11.
Covariance diagnosis results of uncontrollable factors.
6.3. Truncated Regression Analysis
From Section 6.2, the truncated regression model in this paper is shown in Equation (9):
where is the efficiency value of ith DMU in t year, is the interception, are estimated coefficients, = 1, 2, …, 23, and = 2020, 2021, 2022.
Integrating the preliminarily identified uncontrollable factors into the truncated regression analysis, distinct truncated regression models were formulated with CRS and VRS efficiency values as dependent variables. The distribution of the efficiency values is shown in Figure 7; considering the minimum CRS efficiency value of 0.317837901 and the minimum VRS efficiency value of 0.412463752, truncated regression analyses were performed with left truncation at 0.3 and 0.4, respectively. The outcomes are detailed in Table 12.
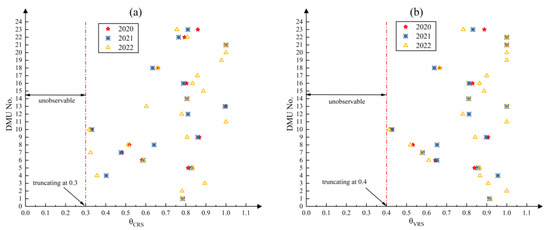
Figure 7.
The distribution of efficiency values: (a) CRS efficiency values; (b) VRS efficiency values.

Table 12.
Results of truncated regression analysis with θCRS and θVRS as the dependent variables.
6.3.1. Discussion of the Results in the Truncated Regression Analysis of θCRS
From Table 12, it is evident that the overall model had statistical significance, as indicated by Prob > = 0.0351, which is less than 0.05. This signifies the overall importance of the model. Upon examining the specific factors and their p > |z| values, only the dustfall variable demonstrated statistical significance, with a p-value less than 0.05. The coefficient associated with dustfall was 0.238089, indicating a positive correlation. Therefore, it was concluded that dustfall significantly influences CRS efficiency values, with a positive correlation existing between dustfall and CRS efficiency values.
This positive correlation implies the importance that each DMU places on the daily cleaning of highways. Natural dustfall significantly increases the daily cleaning burden of facilities along highways, such as dust settling on guardrails and signs. Timely cleaning is essential, as failure to do so could not only affect the aesthetics and functionality of these facilities but also potentially compromise the visibility guidance performance for drivers, posing safety concerns.
Therefore, in regions with higher levels of dustfall, it can be understood that corresponding DMUs place a greater emphasis on the cleanliness and environmental friendliness of highways. The stronger the commitment of managers to maintaining the cleanliness and environmental friendliness of roads, the more comprehensive and effective the related management measures become. This aligns with the principles outlined in emphasizing the promotion of green maintenance, urging a focus on ecological priorities, efficient resource utilization, carbon emission reduction, and the promotion of sustainable green development in highway maintenance work.
6.3.2. Discussion of the Results in the Truncated Regression Analysis of θVRS
From Table 12, it is evident that the overall model had statistical significance, as indicated by Prob > = 0.0061, which is less than 0.05, signifying the overall significance of the model. Examining the specific factors and their p > |z| values, TL, BL, dustfall, and UR all achieved statistical significance. All four indicators had a significant impact on the VRS efficiency values. Specifically, TL and dustfall exhibited positive correlations with VRS efficiency values, with correlation coefficients of 0.0051855 and 0.0255709, respectively. On the other hand, BL and UR showed negative correlations, with correlation coefficients of −0.0041227 and −0.012068, respectively.
- Tunnel length. Table 12 illustrates a positive correlation between the VRS efficiency values and TL, indicating that an increase in TL promotes the HRMMP of each DMU. Highway tunnels play a crucial role in reducing the distances between locations. With the continuous improvement of the highway network, the transportation department imposes higher standards for tunnel construction and maintenance. In addition to reducing distances, tunnels also enhance road technical status, transport capacity, and accident reduction. Due to the semi-enclosed structure of tunnels, traffic accidents inside can lead to challenging-to-extinguish fires. Despite research on flame-retardant pavement materials, the spatial structure remains a significant challenge for rescue operations in fire events. For example, the Qinling–Zhongnan Mountain Tunnel, with the longest mileage in China, has emergency rescue centers near it. Therefore, maintenance and repairs, especially routine maintenance, are crucial. In recent years, the transportation department has consistently enhanced the highway emergency support system, with a particular focus on ensuring the safety of those involved. The cleanliness of tunnel walls and signs inside affects drivers’ visual judgment after entering. The reflective performance of the film at the tunnel entrance and the integrity of the drainage trench cover are crucial for driver safety. Therefore, maintenance measures like daily inspections are implemented to prevent accidents. The highway management agency pays particular attention to tunnel maintenance, especially for long tunnels within its jurisdiction. Thus, an increase in tunnel length promotes improvements in HRMMP to a certain extent.
- Bridge length. Table 12 indicates a negative correlation between the VRS efficiency values and BL, that is, as the length of bridges managed by each DMU increases, HRMMP tends to decrease. In contrast to tunnels, subgrades, and pavements, bridges are subject to greater influence from natural environmental factors due to their suspended structures. Consequently, the requirements for both construction and maintenance are higher. For instance, expansion joints in bridges, affected by the natural environmental and geographical factors, coupled with the impact of vehicle loads, are prone to damage in components such as rubber seals, steel components, and concrete, requiring prompt repairs. The repair process involves challenges related to traffic disruption, safety precautions for maintenance workers, and time constraints. It is imperative that the drainage holes on the bridge deck and the drainage pipes on the bridge sides be cleared frequently to prevent blockages that could impede the drainage process. The most significant damage to bridges comes from water infiltration through expansion joints and cracks in the bridge deck surface, leading to the corrosion of steel reinforcements and damage to concrete. Therefore, regular and timely maintenance measures are required for bridge facilities. With an increase in the number and length of bridges, the difficulty of such routine maintenance also escalates. The results in this paper found that as the length of the bridges managed by each DMU increased, there was a slight downward trend in HRMMP.
- Amount of natural dustfall. As shown in Table 12, there was a positive correlation between the VRS efficiency values and dustfall, indicating that an increase in dustfall had a certain promoting effect on the HRMMP of each DMU. This observation aligns with the positive correlation relationship between the CRS efficiency values and dustfall shown in Table 12.
- Urbanization rate. As shown in Table 12, there was a negative correlation between the VRS efficiency values and UR, indicating that with an increase in UR, the HRMMP of each DMU gradually decreased. UR, as a key indicator measuring the level of urbanization in a region, is raised to promote the adjustment of the urban–rural economic structure and the healthy development of the national economy. In light of these considerations, the expansion of the urban population and the growth of the urban economy, driven by the rise in UR, have the effect of stimulating the development of secondary and tertiary industries. Consequently, highways become a critical bridge and link connecting urban and rural areas. From the perspective of individual residents, the increase in UR signifies a significant improvement in the standard of living. There is a continuous increase in per capita motor vehicle ownership and demand for outbound travel, contributing to the rise in transportation demand. From the logistics industry’s viewpoint, the upsurge in UR results in substantial demand for express delivery items. Meanwhile, industries like agricultural processing, planting, breeding, and tourism witness a continuous increase in the demand for materials and the flow of manufactured products. This illustrates that the development of urban and rural enterprises is inseparable from the crucial transportation channel provided by highways. The increase in UR simultaneously amplifies the transportation demand for highways, leading to a further increase in the difficulty of HRMM.
One noteworthy point from the analysis is the positive correlation between tunnel length and efficiency values, while there was a negative correlation between bridge length and efficiency values. The results may be attributed to the fact that bridges are typically structures that span bodies of water, valleys, or other features on roads, necessitating special attention being paid to stability and safety. Additionally, the structural complexity of bridges may require more frequent inspections and repairs, which can increase the difficulty of maintenance. Compared to bridges, tunnels are less affected by the external environment and are less susceptible to erosion and damage caused by natural factors. Moreover, the internal environment of tunnels is relatively closed, which facilitates the implementation of routine maintenance and the monitoring of its efficacy. Therefore, an increase in tunnel length may not have a significant negative impact on HRMMP.
To summarize, the HRMMP of each DMU was closely associated not only with its own input–output capacity but also with uncontrollable factors such as the amount of natural dustfall, urbanization rate, tunnel length, and bridge length managed by each DMU. When evaluating HRMMP, it is crucial to thoroughly consider these uncontrollable factors on the basis of performance ranking and identify reasonable solutions for performance improvement. When allocating maintenance resources, STHG (decision maker) should focus on DMUs with high dustfall, long bridges and tunnels, and high urbanization rates. For DMUs in a DRS state, it is necessary to implement appropriate resource reallocation and management optimization. For DMUs in an IRS state, it is possible to achieve higher outputs by increasing inputs in order to further improve productivity and performance.
7. Conclusions, Limitations, and Future Work
This study employed input-oriented DEA models to calculate HRMMP efficiency values for 23 maintenance management subsidiaries (23 DMUs) under STHG in 2022 and explored what should be considered in sustainable HRMM; the main contributions are as follows.
- This study evaluated the HRMMP of highway management agencies from the perspective of routine maintenance, which fills the gap of less attention being paid in the area of routine maintenance. The evaluation results revealed variations in the maintenance performance of 23 DMUs. Specifically, five DMUs were in a CRS state, nine DMUs were in a DRS state, and nine DMUs were in an IRS state.
- Most existing research on the performance evaluation of HMMP primarily focuses on outcomes, often overlooking uncontrollable factors. To explore the impact on sustainable HRMM, this study drew inspiration from uncontrollable factors impacting on HMMP in other research areas, utilizing the truncated regression analysis method to address the limitations of the Tobit model in previous studies. The data from 2020 to 2022 were utilized in the truncated regression analysis, with the dependent variables being the CRS and VRS efficiency values and the independent variables being various potential uncontrollable factors. The analysis identified the actual uncontrollable factors influencing HRMMP, including the amount of natural dustfall, urbanization rate, tunnel length, and bridge length managed by each DMU.
- It is evident that HRMMP is not only related to inputs and outputs but also influenced by uncontrollable factors; HRMMP efficiency has a positive correlation with the amount of natural dustfall and tunnel length, while it has a negative correlation with bridge length and the urbanization rate. Therefore, in the performance evaluation process, relying solely on results is insufficient. Instead, one should comprehensively consider potential uncontrollable factors, objectively analyze evaluation results, and provide a scientifically sound approach for improvement.
- According to the results of the evaluation of HRMMP and uncontrollable factors analysis, STHG (decision maker) should pay much attention to DMUs with high dustfall and urbanization rates and long bridges and tunnels when allocating maintenance resources so as to achieve sustainable HRMM. For DMUs in a DRS state, appropriate resource reallocation and management optimization should be carried out. For DMUs in an IRS state, higher outputs can be achieved by increasing inputs to further improve productivity and performance.
Considering the data limitations, this study did not incorporate factors such as maintenance history and traffic accidents. Future research can achieve a more comprehensive understanding of maintenance management by analyzing these aspects.
Author Contributions
Conceptualization, X.S. and Y.L.; data curation, X.S. and X.G.; formal analysis, X.S., X.G., and Y.L.; funding acquisition, X.S.; investigation, X.S. and Y.L.; methodology, X.S., X.G., Y.L., and X.W.; project administration, X.S.; resources, X.S. and Y.L.; software, X.G. and Y.L.; supervision, X.S. and X.W.; validation, X.S. and X.G.; visualization, X.G., Y.L., and X.W.; writing—original draft, X.S., X.G., and Y.L.; writing—review and editing, X.G. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Natural Science Basic Research Program of Shaanxi Province, No.2022 JM-307, the China Scholarship Council (202206560047), and the China Scholarship Council (202306560107).
Institutional Review Board Statement
This study does not require ethical approval.
Informed Consent Statement
This study does not involve humans.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors sincerely acknowledge the data support from Shaanxi Transportation Holding Group.
Conflicts of Interest
Author Yuhuan Li was employed by the company Xi’an Municipal Engineering Design & Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Cao, L.; Tan, T.; Hou, X.; Dong, Z. Decision-Making Optimization Model for the Targeted Sustainable Maintenance of a Complex Road Network. J. Clean. Prod. 2024, 434, 139891. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, D. Numerical Analysis of a Multi-Objective Maintenance Decision-Making Model for Sustainable Highway Networks: Integrating the GDE3 Method, LCA and LCCA. Energy Build. 2023, 290, 113096. [Google Scholar] [CrossRef]
- Xu, G.; Guo, F. Sustainability-Oriented Maintenance Management of Highway Bridge Networks Based on Q-Learning. Sustain. Cities Soc. 2022, 81, 103855. [Google Scholar] [CrossRef]
- Montoya-Alcaraz, M.; Mungaray-Moctezuma, A.; García, L. Sustainable Road Maintenance Planning in Developing Countries Based on Pavement Management Systems: Case Study in Baja California, México. Sustainability 2019, 12, 36. [Google Scholar] [CrossRef]
- Pan, Y.; Shang, Y.; Liu, G.; Xie, Y.; Zhang, C.; Zhao, Y. Cost-Effectiveness Evaluation of Pavement Maintenance Treatments Using Multiple Regression and Life-Cycle Cost Analysis. Constr. Build. Mater. 2021, 292, 123461. [Google Scholar] [CrossRef]
- Chen, L.-L.; Li, J.; Wang, Z.-F.; Wang, Y.-Q.; Li, J.-C.; Li, L. Sustainable Health State Assessment and More Productive Maintenance of Tunnel: A Case Study. J. Clean. Prod. 2023, 396, 136450. [Google Scholar] [CrossRef]
- Ma, L.; Cao, J.; Pan, Z.; Guo, L.; Zhang, H.; Ma, Y.; Yang, G.; Wang, H. Use of Condition-Based Valuation Approach to Evaluate the Maintenance Decision of Pavement Assets: A Case Study of Yunnan Province in China. Front. Energy Res. 2024, 11, 1346005. [Google Scholar] [CrossRef]
- Singh, R.; Sharma, R.; Vaseem Akram, S.; Gehlot, A.; Buddhi, D.; Malik, P.K.; Arya, R. Highway 4.0: Digitalization of Highways for Vulnerable Road Safety Development with Intelligent IoT Sensors and Machine Learning. Saf. Sci. 2021, 143, 105407. [Google Scholar] [CrossRef]
- Gong, F.; Cheng, X.; Chen, Y.; Liu, Y.; You, Z. 3D Printed Rubber Modified Asphalt as Sustainable Material in Pavement Maintenance. Constr. Build. Mater. 2022, 354, 129160. [Google Scholar] [CrossRef]
- Taticchi, P.; Tonelli, F.; Cagnazzo, L. Performance Measurement and Management: A Literature Review and a Research Agenda. Meas. Bus. Excell. 2010, 14, 4–18. [Google Scholar] [CrossRef]
- Kumar, U.; Galar, D.; Parida, A.; Stenström, C.; Berges, L. Maintenance Performance Metrics: A State-of-the-art Review. J. Qual. Maint. Eng. 2013, 19, 233–277. [Google Scholar] [CrossRef]
- Simões, J.M.; Gomes, C.F.; Yasin, M.M. A Literature Review of Maintenance Performance Measurement: A Conceptual Framework and Directions for Future Research. J. Qual. Maint. Eng. 2011, 17, 116–137. [Google Scholar] [CrossRef]
- GB/T 33172-2016; Asset Management—Overview, Principles and Terminology. SAC (Standardization Administration of the PRC): Beijing, China, 2016. Available online: https://www.55000.org.cn/overview-principles-terminology/ (accessed on 30 January 2024).
- GB/T 33173-2016; Asset Management—Management Systems—Requirements. SAC (Standardization Administration of the PRC): Beijing, China, 2016. Available online: https://www.55000.org.cn/asset-management-requirements/ (accessed on 30 January 2024).
- GB/T 33174-2016; Asset Management—Management Systems—Guidelines for the Application of GB/T 33173. SAC (Standardization Administration of the PRC): Beijing, China, 2016. Available online: https://www.55000.org.cn/2016-practice-guide/ (accessed on 30 January 2024).
- FTA (Federal Transit Administration) AASHTO Transportation Asset Management Guide. Available online: https://www.transit.dot.gov/regulations-and-programs/asset-management/aashto-transportation-asset-management-guide (accessed on 30 January 2024).
- Markow, M.J. Performance-Based Highway Maintenance and Operations Management; The National Academies Press: Washington, DC, USA, 2012. [Google Scholar]
- Adey, B.T.; García De Soto, B.; Senn, C. Evaluating the Operation and Routine Maintenance of Municipal Roads in Switzerland. Infrastruct. Asset Manag. 2017, 4, 96–108. [Google Scholar] [CrossRef]
- Patidar, V.; Labi, S.; Sinha, K.C.; Thompson, P.D.; Shirolé, A.; Hyman, W. Performance Measures for Enhanced Bridge Management. Transp. Res. Rec. J. Transp. Res. Board 2007, 1991, 43–53. [Google Scholar] [CrossRef]
- Qiu, L. Performance Measurement for Highway Winter Maintenance Operations. Ph.D. Thesis, University of Iowa, Iowa, IA, USA, 2008. [Google Scholar]
- Fu, X.; Li, Z.; Xu, G.; Cheng, Q. A Study on Evaluating lndex System of Highway Maintenance Modernization. Highway 2004, 49, 161–165. [Google Scholar]
- Fotova Čiković, K.; Martinčević, I.; Lozić, J. Application of Data Envelopment Analysis (DEA) in the Selection of Sustainable Suppliers: A Review and Bibliometric Analysis. Sustainability 2022, 14, 6672. [Google Scholar] [CrossRef]
- Jung, S.; Son, J.; Kim, C.; Chung, K. Efficiency Measurement Using Data Envelopment Analysis (DEA) in Public Healthcare: Research Trends from 2017 to 2022. Processes 2023, 11, 811. [Google Scholar] [CrossRef]
- Krmac, E.; Mansouri Kaleibar, M. A Comprehensive Review of Data Envelopment Analysis (DEA) Methodology in Port Efficiency Evaluation. Marit. Econ. Logist. 2023, 25, 817–881. [Google Scholar] [CrossRef]
- Pham Van, T.; Tran, T.; Trinh, T.; Phuong, T.; Hoang Ngoc, A.; Nghiem Thi, T.; La Phuong, T. Over Three Decades of Data Envelopment Analysis Applied to the Measurement of Efficiency in Higher Education: A Bibliometric Analysis. J. Effic. Responsib. Educ. Sci. 2022, 15, 251–265. [Google Scholar] [CrossRef]
- Rostamzadeh, R.; Akbarian, O.; Banaitis, A.; Soltani, Z. Application of DEA in Benchmarking: A Systematic Literature Review from 2003–2020. Technol. Econ. Dev. Econ. 2021, 27, 175–222. [Google Scholar] [CrossRef]
- Solana Ibáñez, J.; Caravaca Garratón, M.; Soto Meca, A. A Literature Review of DEA Efficiency Methodology in Defence Sector. Acad. Rev. Latinoam. Adm. 2020, 33, 381–403. [Google Scholar] [CrossRef]
- Fallah-Fini, S.; Triantis, K.P.; De La Garza, J.M. Performance Measurement of Highway Maintenance Operation Using Data Envelopment Analysis: Environmental Considerations. In Proceedings of the 2009 Industrial Engineering Research Conference, Miami, FL, USA, 1–3 June 2009; Host Publication: Miami, FL, USA, 2009. [Google Scholar]
- Lin, H.S.; Lin, J.D.; Chang, J.R. Performance of Maintenance and Management for Roads in HsinChu County, Taiwan. Adv. Mater. Res. 2013, 723, 861–868. [Google Scholar] [CrossRef]
- Ozbek, M.E.; De La Garza, J.M.; Triantis, K. Data and Modeling Issues Faced during the Efficiency Measurement of Road Maintenance Using Data Envelopment Analysis. J. Infrastruct. Syst. 2010, 16, 21–30. [Google Scholar] [CrossRef]
- Soemardi, B.W.; Fajri, A.R. Alternative Performance Measurement for Road Management Agencies Using Data Envelopment Analysis Method. J. Tek. Sipil 2013, 20, 161. [Google Scholar] [CrossRef]
- Wang, C. Discussion on the Construction of Performance Evaluation System for Highway Maintenance Management in Beijing. Highway 2007, 52, 123–128. [Google Scholar]
- Zhu, J.; Chen, Z.; Sun, L. Research of Performance Appraisal of Highway Maintenance Based on Assessment of the Assets Value. Highw. Eng. 2009, 34, 72–75. [Google Scholar]
- Ghahari, S.; Chen, S.; Labi, S. A Nonparametric Efficiency Methodology for Comparative Assessment of Infrastructure Agency Performance. Transp. Eng. 2021, 6, 100092. [Google Scholar] [CrossRef]
- Ozbek, M.E.; De La Garza, J.M.; Triantis, K. Efficiency Measurement of Bridge Maintenance Using Data Envelopment Analysis. J. Infrastruct. Syst. 2010, 16, 31–39. [Google Scholar] [CrossRef]
- Lad, V.H.; Patel, D.A.; Chauhan, K.A.; Patel, K.A. Data Envelopment Analysis for Efficiency Measurement of Bridge Resilience. Balt. J. Road Bridge Eng. 2022, 17, 189–212. [Google Scholar] [CrossRef]
- Zhang, Z.; Agbelie, B.R.; Labi, S. Efficiency Measurement of Bridge Management with Data Envelopment Analysis. Transp. Res. Rec. J. Transp. Res. Board 2015, 2481, 1–9. [Google Scholar] [CrossRef]
- Ravirala, V.; Grivas, D.A. State Increment Method of Life-Cycle Cost Analysis for Highway Management. J. Infrastruct. Syst. 1995, 1, 151–159. [Google Scholar] [CrossRef]
- Keoleian, G.; Kendall, A.; Chandler, R.; Helfand, G.; Lepech, M.; Li, V. Life-Cycle Cost Model for Evaluating the Sustainability of Bridge Decks. Available online: http://deepblue.lib.umich.edu/bitstream/2027.42/84802/1/KeoleianLCCApaperfinal.pdf (accessed on 7 April 2024).
- Zhu, J.; Chen, Z.; Sun, L. Construction of Index System of Performance Evaluation About Highway Maintenance. J. Tongji Univ. Sci. 2012, 40, 871–875. [Google Scholar]
- Du, J.; Wang, W.; Gao, X.; Hu, M.; Jiang, H. Sustainable Operations: A Systematic Operational Performance Evaluation Framework for Public–Private Partnership Transportation Infrastructure Projects. Sustainability 2023, 15, 7951. [Google Scholar] [CrossRef]
- Wang, L.-C.; Tsai, H.-Y. Evaluation of Highway Maintenance Performance Using Data Envelopment Analysis (DEA) in Taiwan. J. Mar. Sci. Technol. 2009, 17, 145–155. [Google Scholar] [CrossRef]
- Shakouri, R.; Salahi, M. Performance Measurement and Resource Sharing among Business Sub-Units in the Presence of Non-Discretionary Factors. J. Model. Manag. 2022, 17, 100–118. [Google Scholar] [CrossRef]
- Fallah-Fini, S.; Triantis, K.; Rahmandad, H.; De La Garza, J.M. Measuring Dynamic Efficiency of Highway Maintenance Operations. Omega 2015, 50, 18–28. [Google Scholar] [CrossRef]
- Ozbek, M.E. Development of a Comprehensive Framework for the Efficiency Measurement of Road Maintenance Strategies Using Data Envelopment Analysis. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2007. [Google Scholar]
- Fallah-Fini, S.; Triantis, K.; De La Garza, J.M.; Seaver, W.L. Measuring the Efficiency of Highway Maintenance Contracting Strategies: A Bootstrapped Non-Parametric Meta-Frontier Approach. Eur. J. Oper. Res. 2012, 219, 134–145. [Google Scholar] [CrossRef]
- Banker, R.D.; Morey, R.C. Efficiency Analysis for Exogenously Fixed Inputs and Outputs. Oper. Res. 1986, 34, 513–521. [Google Scholar] [CrossRef]
- Muñiz, M.; Paradi, J.; Ruggiero, J.; Yang, Z. Evaluating Alternative DEA Models Used to Control for Non-Discretionary Inputs. Comput. Oper. Res. 2006, 33, 1173–1183. [Google Scholar] [CrossRef]
- Banker, R.D.; Morey, R.C. The Use of Categorical Variables in Data Envelopment Analysis. Manag. Sci. 1986, 32, 1613–1627. [Google Scholar] [CrossRef]
- Ruggiero, J. On the Measurement of Technical Efficiency in the Public Sector. Eur. J. Oper. Res. 1996, 90, 553–565. [Google Scholar] [CrossRef]
- Ray, S.C. Resource-Use Efficiency in Public Schools: A Study of Connecticut Data. Manag. Sci. 1991, 37, 1620–1628. [Google Scholar] [CrossRef]
- Ruggiero, J. Non-Discretionary Inputs in Data Envelopment Analysis. Eur. J. Oper. Res. 1998, 111, 461–469. [Google Scholar] [CrossRef]
- Xue, M.; Harker, P.T. Overcoming the Inherent Dependency of DEA Efficiency Scores A Bootstrap Approach. Available online: https://core.ac.uk/download/pdf/6649882.pdf (accessed on 7 April 2024).
- Greene, W. Econometric Analysis, 8th ed.; Pearson: New York, NY, USA, 2018; pp. 958–964. [Google Scholar]
- Chen, Q. Advanced Econometrics and Stata Applications; Higher Education Press: Beijing, China, 2014; pp. 211–213. [Google Scholar]
- Li, H.; Yan, G. Research on the Operation Efficiency and Influencing Factors of Basic Pension Insurance Fund for Urban Workers in China—Based on DEA-Tobit Model. Adv. Appl. Math. 2022, 11, 7574–7582. [Google Scholar] [CrossRef]
- Li, J. The Performance Evaluation of Listed Pharmaceutical Companies and the Influencing Factors: A Study Based on DEA-Malmquist-Tobit Model. Stat. Appl. 2023, 12, 985–997. [Google Scholar] [CrossRef]
- Li, J.; Ding, J. Analysis of Spatiotemporal Changes, Influencing Factors, and Coupling Coordination Degree of Urban Human Settlements Efficiency: A Case Study of Megacities and Supercities in China. J. Urban Plan. Dev. 2024, 150, 05023044. [Google Scholar] [CrossRef]
- Tian, Z.; Chen, X.; Yu, L. Does the Urban Rail Transit Line Type Affect the Operational Efficiency? A Study Based on the DEA-Tobit Method. In Proceedings of the 22nd COTA International Conference of Transportation Professionals, Changsha, China, 8–11 July 2022; American Society of Civil Engineers: Reston, VA, USA; pp. 1004–1012.
- Xue, L.; Zhao, S. Evaluating and Analyzing the Operation Efficiency of Urban Rail Transit Systems in China Using an Integrated Approach of DEA Model, Malmquist Productivity Index, and Tobit Regression Model. J. Transp. Eng. Part Syst. 2021, 147, 04021061. [Google Scholar] [CrossRef]
- Ananda, J. Evaluating the Performance of Urban Water Utilities: Robust Nonparametric Approach. J. Water Resour. Plan. Manag. 2014, 140, 04014021. [Google Scholar] [CrossRef]
- Chowdhury, H.; Zelenyuk, V. Performance of Hospital Services in Ontario: DEA with Truncated Regression Approach. Omega 2016, 63, 111–122. [Google Scholar] [CrossRef]
- Güngör-Demirci, G.; Lee, J.; Keck, J. Performance Assessment of a California Water Utility by Data Envelopment Analysis. In Proceedings of the World Environmental and Water Resources Congress 2017, Sacramento, CA, USA, 18 May 2017; American Society of Civil Engineers: Reston, VA, USA; pp. 549–561.
- Lin, C. Exploring Performance and Corporate Governance of the China’s Silicon Semiconductor Industry- a Two-Stage Meta-Frontier DEA and a Truncated Model. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Wu, X.; Shi, X.; Li, Y.; Gong, X. Estimation of Annual Routine Maintenance Cost for Highway Tunnels. Adv. Civ. Eng. 2022, 2022, 5374461. [Google Scholar] [CrossRef]
- Su, H.; Liu, A. A study on the efficiency and influencing factors of scientific research in inter-provincial universities under “Double First-Class” construction: Based on DEA-Tobit model. J. Chongqing Univ. Sci. Ed. 2020, 26, 107–118. [Google Scholar]
- Dalgaard, P. Introductory Statistics with R, 2nd ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).