Understanding the Impact of Seismic Hazard and Climate Conditions on Multi Criteria–Based Retrofitting of Existing Buildings
Abstract
1. Introduction
2. Methodology
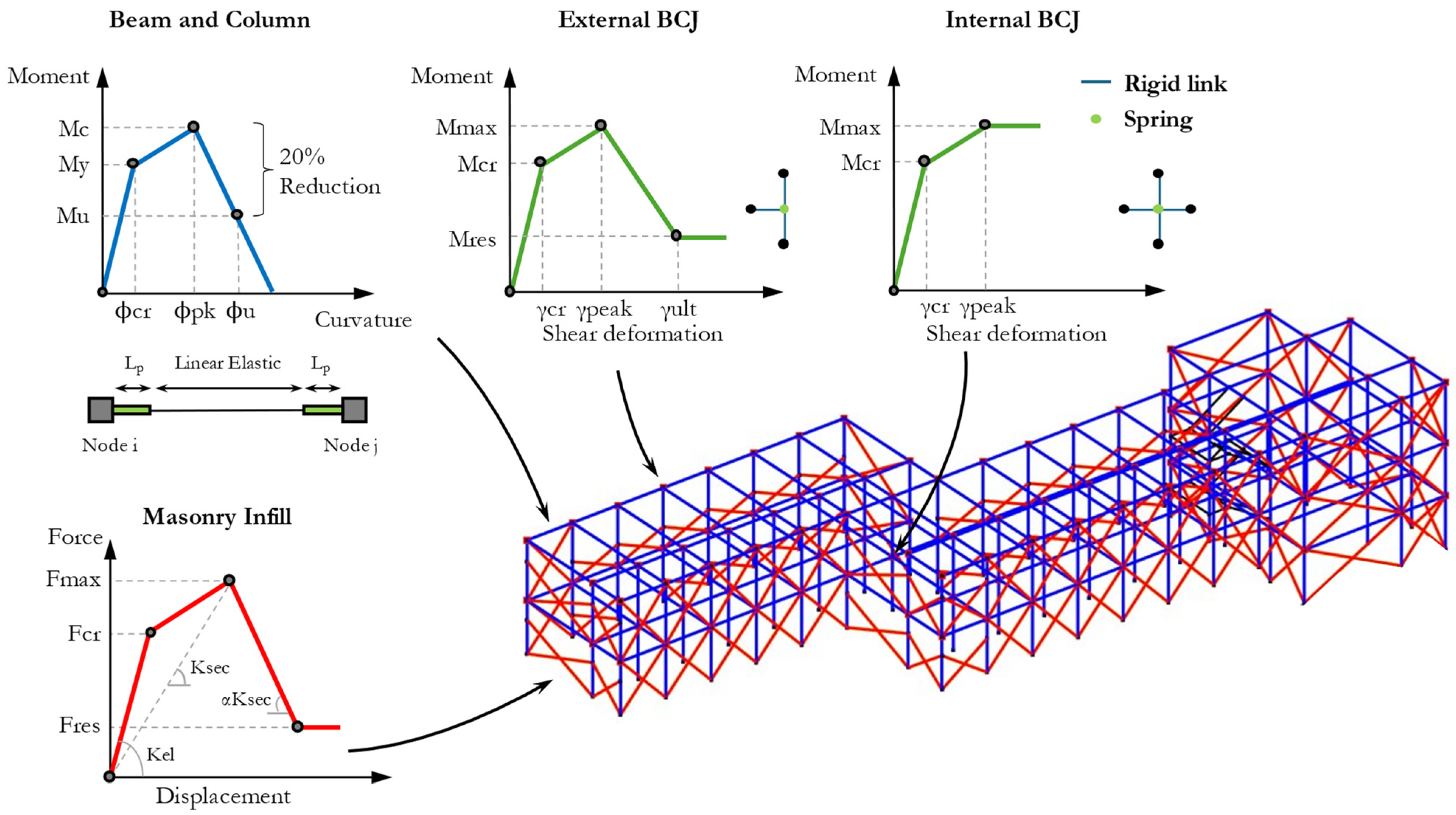
2.1. Detailed Approach
2.2. Simplified Approach
3. Application to a Case-Study Building
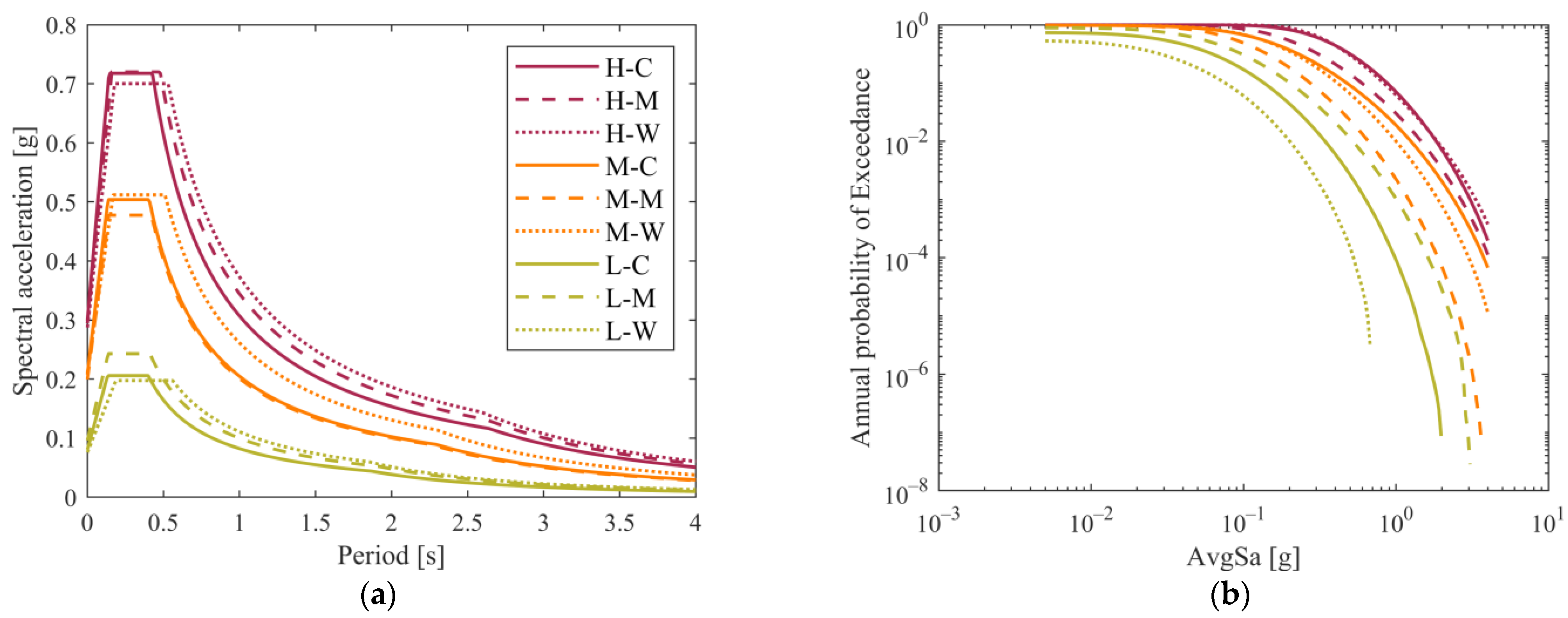
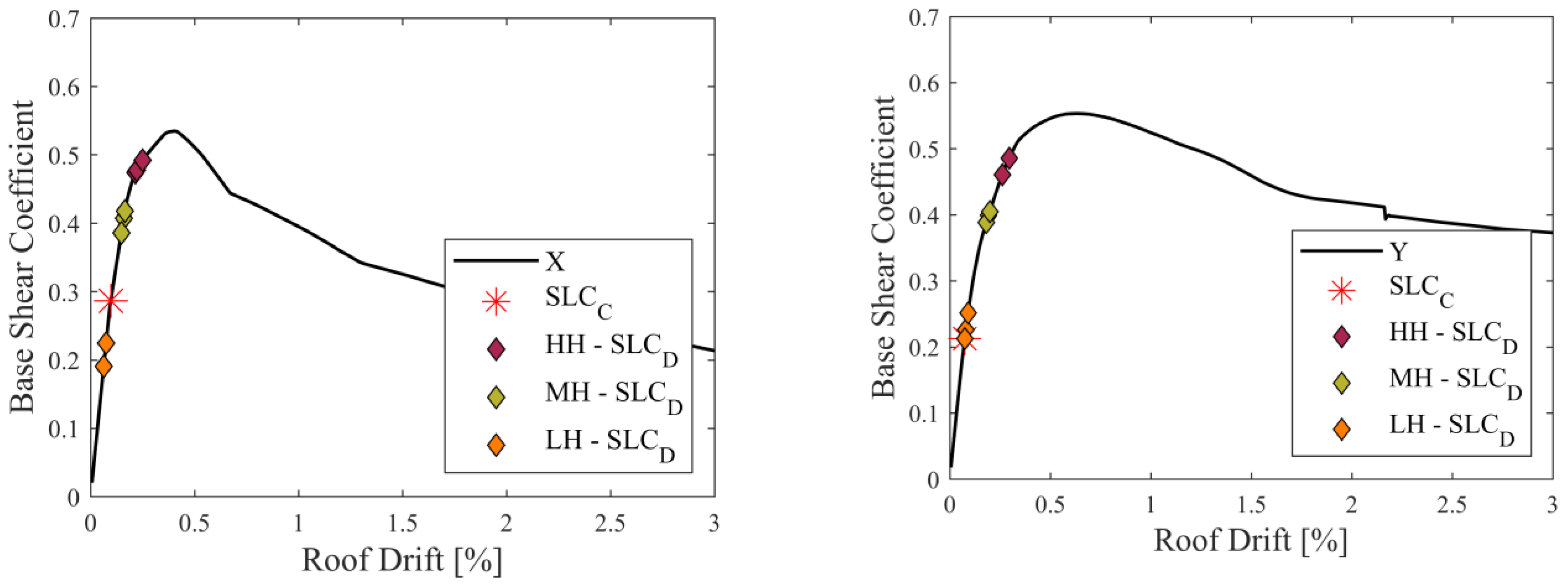
3.1. Preliminary Seismic Assessment
- The shear force demand exceeds the shear capacity of one or more of the beam or column elements;
- The chord rotation of one or more of the plastic hinges in the beam, column, or wall elements exceeds the collapse limit state deformation limits;
- The shear deformation in one or more of the beam–column joints (BCJs) exceeds 0.02 rad.
3.2. Seismic Retrofit Interventions
- -
- S1: local strengthening with carbon FRP (CFRP);
- -
- S2: global strengthening with concentric steel braces;
- -
- S3: CFRP strengthening combined with concentric steel braces;
- -
- S4: CFRP strengthening combined with viscous dampers.
3.3. Energy Retrofit Interventions
- -
- E1: roof insulation and installation of efficient LEDs and thermostatic valves on radiators;
- -
- E2: intervention E1 coupled with external wall insulation with expanded polystyrene (EPS) panels;
- -
- E3: intervention E2 coupled with installation of efficient windows, floor insulation, condensing boiler, lighting control system, and photovoltaic panels.
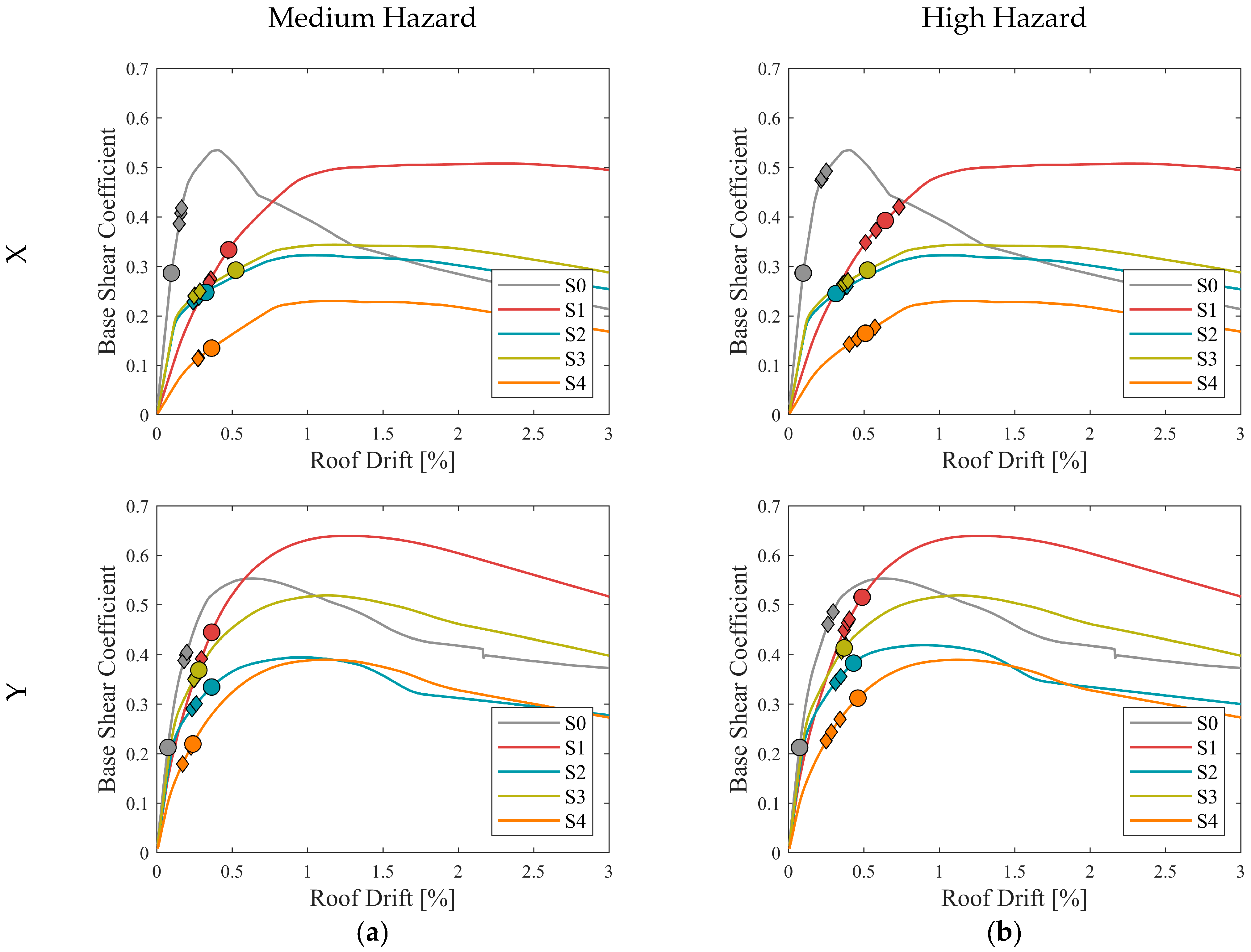
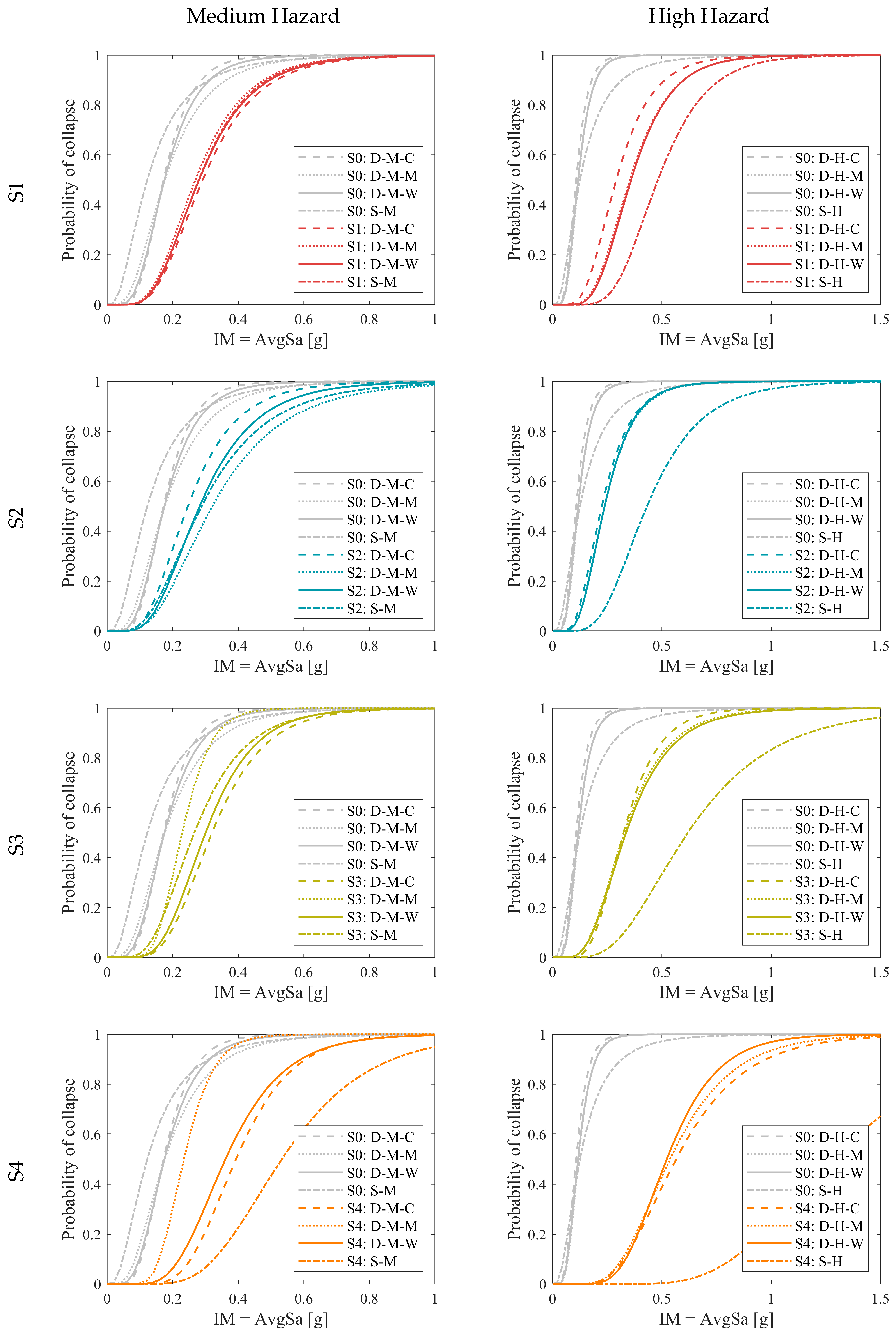
3.4. Post-Intervention Seismic Assessment
3.4.1. Annual Probability of Failure
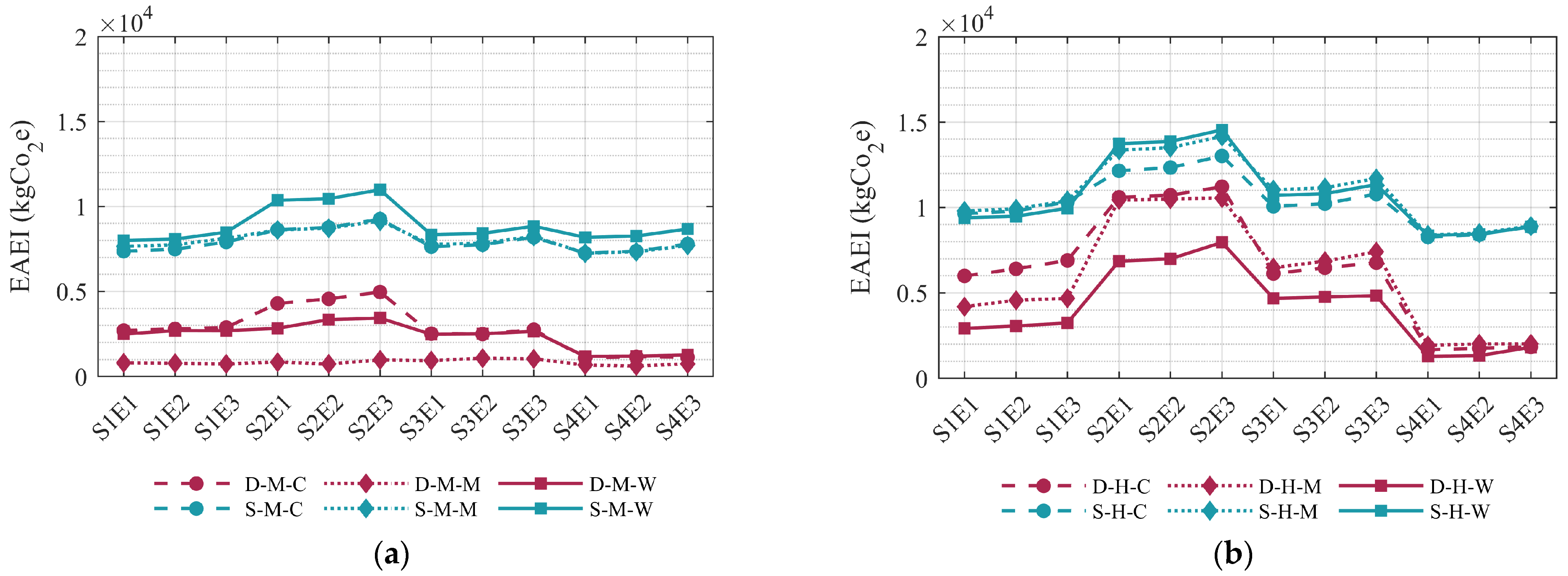
3.4.2. Expected Annual Losses (EAL) and Expected Annual Environmental Impacts (EAEI)
3.5. Post-Intervention Energy Assessment
4. Discussion
4.1. Decision Variable Assemblance
4.2. Ranking of the Retrofit Alternatives
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Comission Communication from the Commission to the European Parliament; the Council; the European Economic and Social Committee; the Committee of the Regions. The European Green Deal; ESDN Office: Vienna, Austria, 2020. [Google Scholar]
- Ministero dell’Ambiente e della Sicurezza Energetica. Piano Nazionale Integrato per l’Energia e per il Clima. 2023. Available online: https://www.mase.gov.it/pagina/ministero (accessed on 8 April 2024).
- Pohoryles, D.; Bournas, D.; Da Porto, F.; Santarsiero, G.; Triantafillou, G.; Oliveira, D.; Jelle, B. Technologies for the Combined Seismic and Energy Upgrading of Existing Buildings; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar] [CrossRef]
- Gkatzogias, K.; Crowley, H.; Veljkovic, A.; Pohoryles, D.; Norlén, H.; Tsionis, G.; Bournas, D. Prioritising EU Regions for Building Renovation: Seismic Risk, Energy Efficiency, Socioeconomic Vulnerability—REEBUILD: Integrated Techniques for the Seismic Strengthening and Energy Efficiency of Existing Buildings; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar] [CrossRef]
- Gkatzogias, K.; Pohoryles, D.A.; Romano, E.; Bournas, D.A. Integrated Seismic and Energy Renovation of Buildings; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar] [CrossRef]
- Pohoryles, D.A.; Bournas, D.A.; Da Porto, F.; Santarsiero, G.; Triantafillou, T. Overview of Combined Seismic and Energy Upgrading Technologies for Existing Buildings; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar] [CrossRef]
- Mucedero, G.; Monteiro, R. An integrated regional prioritisation framework for seismic and energy-efficiency performance upgrading of residential buildings. Int. J. Disaster Risk Reduct. 2024, 103, 104341. [Google Scholar] [CrossRef]
- Asadi, E.; Salman, A.M.; Li, Y. Multi-criteria decision-making for seismic resilience and sustainability assessment of diagrid buildings. Eng. Struct. 2019, 191, 229–246. [Google Scholar] [CrossRef]
- Caterino, N.; Iervolino, I.; Manfredi, G.; Cosenza, E. Multi-Criteria Decision Making for Seismic Retrofitting of RC Structures. J. Earthq. Eng. 2008, 12, 555–583. [Google Scholar] [CrossRef]
- Requena-García-Cruz, M.V.; Morales-Esteban, A.; Durand-Neyra, P.; Estêvão, J.M.C. An index-based method for evaluating seismic retrofitting techniques. Application to a reinforced concrete primary school in Huelva. Earth Its Atmos. 2019, 14, e0215120. [Google Scholar] [CrossRef] [PubMed]
- Clemett, N.; Carofilis, W.; Gabbianelli, G.; O’Reilly, G.J.; Monteiro, R. Optimal Combined Seismic and Energy Efficiency Retrofitting for Existing Buildings in Italy. J. Struct. Eng. 2023, 149, 04022207. [Google Scholar] [CrossRef]
- Caruso, M.; Pinho, R.; Bianchi, F.; Cavalieri, F.; Lemmo, M.T. Integrated economic and environmental building classification and optimal seismic vulnerability/energy efficiency retrofitting. Bull. Earthq. Eng. 2021, 19, 3627–3670. [Google Scholar] [CrossRef]
- Saler, E.; Gattesco, N.; da Porto, F. A new combined approach to prioritise seismic retrofit interventions on stocks of r.c. school buildings. Int. J. Disaster Risk Reduct. 2023, 93, 103767. [Google Scholar] [CrossRef]
- Couto, R.; Mucedero, G.; Bento, R.; Monteiro, R. On the Influence of Climate and Seismic Hazard Conditions in the Identification of Optimal Retrofitting Strategies for RC Buildings. COMPDYN Proc. 2023, 2070–2084. [Google Scholar] [CrossRef]
- Caruso, M.; Couto, R.; Pinho, R.; Monteiro, R. Decision-making approaches for optimal seismic/energy integrated retrofitting of existing buildings. Front. Built Environ. 2023, 9, 1176515. [Google Scholar] [CrossRef]
- Mucedero, G.; Couto, R.; Clemett, N.; Monteiro, R. Implications of masonry infill—Related uncertainty on the optimal seismic retrofitting of existing buildings. In Proceedings of the 14th International Conference on Applications of Statistics and Probability in Civil Engineering, ICASP14, Dublin, Ireland, 9–13 July 2023; pp. 1–8. [Google Scholar]
- Carofilis, W.; Clemett, N.; Gabbianelli, G.; O’Reilly, G.; Monteiro, R. Influence of Parameter Uncertainty in Multi-Criteria Decision-Making When Identifying Optimal Retrofitting Strategies for RC Buildings. J. Earthq. Eng. 2023, 27, 1769–1794. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Direct Estimation of Seismic Demand and Capacity of Multidegree-of-Freedom Systems through Incremental Dynamic Analysis of Single Degree of Freedom Approximation. J. Struct. Eng. 2005, 131, 589–599. [Google Scholar] [CrossRef]
- Baltzopoulos, G.; Baraschino, R.; Iervolino, I.; Vamvatsikos, D. SPO2FRAG: Software for seismic fragility assessment based on static pushover. Bull. Earthq. Eng. 2017, 15, 4399–4425. [Google Scholar] [CrossRef]
- Dolšek, M.; Fajfar, P. IN2—A Simple Alternative for IDA. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- FEMA P-58-1. Seismic Performance Assessment of Buildings: Volume 1—Methodology; FEMA: Washington, DC, USA, 2018; Volume 1, p. 344. [Google Scholar] [CrossRef]
- Ramirez, C.M.; Miranda, E. Building-Specific Loss Estimation Methods & Tools for Simplified Performance-Based Earthquake Engineering; Rep. No. 171; Stanford University: Stanford, CA, USA, 2009. [Google Scholar]
- Mucedero, G.; Perrone, D.; Monteiro, R. Generalised Storey Loss Functions for Seismic Loss Assessment of Italian Residential Buildings. J. Earthq. Eng. 2024, 28, 451–474. [Google Scholar] [CrossRef]
- Perrone, G.; Cardone, D.; O’Reilly, G.J.; Sullivan, T.J. Developing a Direct Approach for Estimating Expected Annual Losses of Italian Buildings. J. Earthq. Eng. 2022, 26, 1–32. [Google Scholar] [CrossRef]
- Nettis, A.; Gentile, R.; Raffaele, D.; Uva, G.; Galasso, C. Cloud Capacity Spectrum Method: Accounting for record-to-record variability in fragility analysis using nonlinear static procedures. Soil Dyn. Earthq. Eng. 2021, 150, 106829. [Google Scholar] [CrossRef]
- Cosenza, E.; Del Vecchio, C.; Di Ludovico, M.; Dolce, M.; Moroni, C.; Prota, A.; Renzi, E. The Italian guidelines for seismic risk classification of constructions: Technical principles and validation. Bull. Earthq. Eng. 2018, 16, 5905–5935. [Google Scholar] [CrossRef]
- FEMA P-58-3. Seismic Performance Assessment of Buildings: Volume 3—Performance Assessment Calculation Tool (PACT); FEMA: Washington, DC, USA, 2012. [Google Scholar]
- Applied Technology Council (ATC). Seismic Evaluation and Retrofit of Concrete Buildings; Rep. No. ATC-40 1–2; ATC: Redwood City, CA, USA, 1996. [Google Scholar]
- Jalayer, F.; Ebrahimian, H.; Miano, A.; Manfredi, G.; Sezen, H. Analytical fragility assessment using unscaled ground motion records. Earthq. Eng. Struct. Dyn. 2017, 46, 2639–2663. [Google Scholar] [CrossRef]
- Peres, R.; Couto, R.; Sousa, I.; Castro, J.; Bento, R. Modelling and evaluation of brittle shear effects on the seismic performance and loss assessment of RC buildings. Eng. Struct. 2023, 275, 115–230. [Google Scholar] [CrossRef]
- O’Reilly, G.J.; Perrone, D.; Fox, M.; Monteiro, R.; Filiatrault, A. Seismic assessment and loss estimation of existing school buildings in Italy. Eng. Struct. 2018, 168, 142–162. [Google Scholar] [CrossRef]
- Prota, A.; Di Ludovico, M.; Vecchio, C.; Menna, C. Progetto DPC-ReLUIS 2019–2021 WP5: Interventi di Rapida Esecuzione a Basso Impatto ed Integrati. 2020. Available online: https://www.reluis.it/doc/DPC-RELUIS-2019-2021-WP5/Interventi-Caso%20studio%202%20cemento%20armato.pdf (accessed on 8 April 2024).
- Mucedero, G.; Perrone, D.; Brunesi, E.; Monteiro, R. Numerical modelling and validation of the response of masonry infilled rc frames using experimental testing results. Buildings 2020, 10, 182. [Google Scholar] [CrossRef]
- McKenna, F.; Scott, M.H.; Fenves, G.L. Nonlinear Finite-Element Analysis Software Architecture Using Object Composition. J. Comput. Civ. Eng. 2010, 24, 95–107. [Google Scholar] [CrossRef]
- Scott, M.H.; Fenves, G.L. Plastic hinge integration methods for force-based beam-column elements. J. Struct. Eng. 2006, 132, 244–252. [Google Scholar] [CrossRef]
- Mucedero, G.; Perrone, D.; Monteiro, R. Infill Variability and Modelling Uncertainty Implications on the Seismic Loss Assessment of an Existing RC Italian School Building. Appl. Sci. 2022, 12, 12002. [Google Scholar] [CrossRef]
- O’Reilly, G.J. Performance-Based Seismic Assessment and Retrofit of Existing RC Frame Buildings in Italy. 2016. Available online: https://www.researchgate.net/publication/317746246_Performance-Based_Seismic_Assessment_and_Retrofit_of_Existing_RC_Frame_Buildings_in_Italy (accessed on 8 April 2024).
- Carofilis, W.; Gabbianelli, G.; Monteiro, R. Assessment of Multi-Criteria Evaluation Procedures for Identification of Optimal Seismic Retrofitting Strategies for Existing RC Buildings. J. Earthq. Eng. 2022, 26, 5539–5572. [Google Scholar] [CrossRef]
- MIT NTC 2018: D.M. del Ministero delle Infrastrutture e dei Trasporti del 17/01/2018. Aggiorna-Mento delle Norme Tecniche per le Costruzioni. 2018. (In Italian). Available online: https://www.gazzettaufficiale.it/eli/id/2018/2/20/18A00716/sg (accessed on 8 April 2024).
- Fajfar, P. A Nonlinear Analysis Method for Performance-Based Seismic Design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- O’Reilly, G.J.; Sullivan, T.J. Modeling Techniques for the Seismic Assessment of the Existing Italian RC Frame Structures. J. Earthq. Eng. 2019, 23, 1262–1296. [Google Scholar] [CrossRef]
- Decreto Ministeriale DM n. 58/2020. In Linee Guida per la Classificazione del Rischio Sismico delle Costruzioni; Ministero dell’Istruzione e del Merito: Rome, Italy, 2020.
- Calvi, G.M. Choices and criteria for seismic strengthening. J. Earthq. Eng. 2013, 17, 769–802. [Google Scholar] [CrossRef]
- Economico, I.M.D.S. Decreto interministeriale 26 Giugno 2015, Applicazione delle metodologie di calcolo delle prestazioni energetiche e definizione delle prescrizioni e dei requisiti minimi degli edifici; Italian Government: Rome, Italy, 2015. [Google Scholar]
- Carofilis, W.; Perrone, D.; O’Reilly, G.J.; Monteiro, R.; Filiatrault, A. Seismic retrofit of existing school buildings in Italy: Performance evaluation and loss estimation. Eng. Struct. 2020, 225, 111243. [Google Scholar] [CrossRef]
- Clemett, N.; Carofilis, W.; O’Reilly, G.J.; Gabbianelli, G.; Monteiro, R. Optimal seismic retrofitting of existing buildings considering environmental impact. Eng. Struct. 2022, 250, 113391. [Google Scholar] [CrossRef]
- GEM The OpenQuake-engine User Manual. Global Earthquake Model (GEM) Open—Quake Manual for Engine Version 3.7.0. 2019. Available online: https://www.globalquakemodel.org/product/openquake-engine (accessed on 8 April 2023).
- Ancheta, T.D.; Darragh, R.B.; Stewart, J.P.; Seyhan, E.; Silva, W.J.; Chiou, B.S.-J.; Wooddell, K.E.; Graves, R.W.; Kottke, A.R.; Boore, D.M.; et al. NGA-West2 Database. Earthq. Spectra 2014, 30, 989–1005. [Google Scholar] [CrossRef]
- O’Reilly, G.J.; Sullivan, T.J. Quantification of modelling uncertainty in existing Italian RC frames. Earthq. Eng. Struct. Dyn. 2018, 47, 1054–1074. [Google Scholar] [CrossRef]
- Mucedero, G.; Perrone, D.; Monteiro, R. Epistemic uncertainty in poorly detailed existing frames accounting for masonry infill variability and RC shear failure. Earthq. Eng. Struct. Dyn. 2022, 51, 3755–3778. [Google Scholar] [CrossRef]
- Gencturk, B.; Elnashai, A.S. Development and application of an advanced capacity spectrum method. Eng. Struct. 2008, 30, 3345–3354. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. Evaluation of NSP to Estimate Seismic Deformation: SDF Systems. J. Struct. Eng. 2000, 126, 482–490. [Google Scholar] [CrossRef]
- FEMA-P-58-4. Seismic Performance Assessment of Buildings Volume 4—Methodology for Assessing Environmental Impacts; FEMA: Washington, DC, USA, 2018; Volume 4, p. 122. [Google Scholar]
- Couto, R.; Mucedero, G.; Bento, R.; Monteiro, R. A practice-oriented approach for the seismic and energy performance upgrading of existing buildings. J. Earthq. Eng. 2024; in press. [Google Scholar]
- O’Reilly, G.J.; Nafeh, A.M.B.; Shahnazaryan, D. Simplified tools for the risk assessment and classification of existing buildings. Procedia Struct. Integr. 2023, 44, 1744–1751. [Google Scholar] [CrossRef]
- Edilclima EC700 Calcolo Prestazioni Energetiche Degli Edifici—Versione 11. 2022. Available online: https://www.infobuild.it/prodotti/progettazione-termotecnica/ (accessed on 8 May 2023).





| Group | Decision Variables | Weight | |
|---|---|---|---|
| Economic | C1 | Installation cost | 0.15 |
| C2 | Expected annual costs (EAC) | 0.19 | |
| Environmental | C3 | Expected life-cycle environmental impacts (LCEI) | 0.18 |
| Social | C4 | Annual probability of failure (APF) | 0.14 |
| C5 | Duration of works | 0.13 | |
| C6 | Architectural impact | 0.06 | |
| Technical | C7 | Need for specialized labour/design knowledge | 0.05 |
| C8 | Required intervention at the foundations | 0.10 | |
| City | ID | Coordinates | Level of Seismicity | PGA (SLV) [g] | Climatic Zone | Heating Degree Days (HDD) |
|---|---|---|---|---|---|---|
| Città di Castello | H-C | 43.4700° N, 12.2314° E | High (H) | 0.30 | Cold (C) | 2347 |
| Isola del Gran Sasso d’Italia | H-M | 42.5056° N, 13.6592° E | 0.29 | Moderate (M) | 2038 | |
| Catania | H-W | 37.5013° N, 15.0742° E | 0.29 | Warm (W) | 833 | |
| Vicenza | M-C | 45.5455° N, 11.5354° E | Medium (M) | 0.21 | Cold (C) | 2371 |
| Serravalle Pistoiese | M-M | 43.9059° N, 10.8330° E, | 0.20 | Moderate (M) | 2010 | |
| Cirò Marina | M-W | 39.368° N, 17.128° E | 0.21 | Warm (W) | 845 | |
| Alessandria | L-C | 44.9073° N, 8.6117° E | Low (L) | 0.08 | Cold (C) | 2559 |
| Genova | L-M | 44.4056° N, 8.9463° E | 0.10 | Moderate (M) | 1435 | |
| Agrigento | L-W | 37.3089° N, 13.5858° E | 0.08 | Warm (W) | 729 |
| Direction | Low Hazard | Medium Hazard | High Hazard | ||||||
|---|---|---|---|---|---|---|---|---|---|
| L-C | L-M | L-W | M-C | M-M | M-W | H-C | H-M | H-W | |
| X | 135 | 115 | 140 | 55 | 58 | 54 | 39 | 40 | 39 |
| Y | 95 | 81 | 98 | 38 | 41 | 38 | 27 | 28 | 27 |
| Retrofit Alternative | Units | Medium Hazard | High Hazard | |
|---|---|---|---|---|
| S1 | Column wrap | m2 | 245.1 | 352.6 |
| Column bar | m | 2972 | 2972 | |
| Beam wrap | m2 | 177.8 | 256.2 | |
| Joint wrap | m2 | 138.2 | 186 | |
| S2 | Braced bays | Nr | 9 | 10 |
| S3 | Column wrap | m2 | 5.1 | 10.2 |
| Column bar | m | 272.0 | 272.0 | |
| Beam wrap | m2 | 11.7 | 31.22 | |
| Joint wrap | m2 | 45.5 | 45.5 | |
| Braced bays | Nr | 10 | 10 | |
| S4 | Column wrap | m2 | - | 10.2 |
| Column bar | m | - | 456 | |
| Beam wrap | m2 | - | 33.7 | |
| Joint wrap | m2 | 53.4 | 53.4 | |
| Viscous dampers | Nr | 36 | 36 | |
| Alt | Medium Hazard | High Hazard | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cold | Moderate | Warm | Cold | Moderate | Warm | |||||||
| C1 (EUR/m2) | C5 (Days) | C1 (EUR/m2) | C5 (Days) | C1 (EUR/m2) | C5 (Days) | C1 (EUR/m2) | C5 (Days) | C1 (EUR/m2) | C5 (Days) | C1 (EUR/m2) | C5 (Days) | |
| S1E1 | 529 | 38 | 525 | 38 | 507 | 38 | 867 | 60 | 881 | 61 | 871 | 63 |
| S1E2 | 589 | 38 | 568 | 38 | 543 | 38 | 927 | 60 | 925 | 61 | 908 | 63 |
| S1E3 | 753 | 42 | 692 | 42 | 671 | 42 | 1091 | 64 | 1048 | 65 | 1036 | 67 |
| S2E1 | 135 | 21 | 131 | 21 | 113 | 21 | 136 | 22 | 132 | 22 | 114 | 22 |
| S2E2 | 196 | 23 | 175 | 23 | 150 | 23 | 196 | 24 | 175 | 24 | 150 | 24 |
| S2E3 | 359 | 28 | 298 | 28 | 277 | 28 | 360 | 29 | 299 | 29 | 278 | 29 |
| S3E1 | 172 | 23 | 168 | 23 | 150 | 23 | 180 | 37 | 213 | 42 | 195 | 42 |
| S3E2 | 232 | 23 | 211 | 23 | 186 | 23 | 240 | 37 | 257 | 42 | 232 | 42 |
| S3E3 | 396 | 27 | 335 | 27 | 314 | 27 | 404 | 41 | 380 | 46 | 360 | 46 |
| S4E1 | 289 | 14 | 284 | 14 | 266 | 14 | 437 | 44 | 419 | 44 | 381 | 43 |
| S4E2 | 349 | 27 | 328 | 27 | 303 | 27 | 499 | 44 | 463 | 44 | 418 | 43 |
| S4E3 | 513 | 31 | 451 | 31 | 431 | 31 | 661 | 48 | 586 | 48 | 546 | 47 |
| Alt. | Dir. | Medium Hazard | High Hazard | ||||
|---|---|---|---|---|---|---|---|
| M-C | M-M | M-W | H-C | H-M | H-W | ||
| S1 | X | 120% | 123% | 95% | 120% | 108% | 99% |
| Y | 134% | 134% | 105% | 120% | 107% | 109% | |
| S2 | X | 92% | 95% | 73% | 63% | 55% | 50% |
| Y | 113% | 115% | 88% | 85% | 76% | 70% | |
| S3 | X | 122% | 125% | 96% | 82% | 73% | 68% |
| Y | 111% | 113% | 99% | 87% | 77% | 76% | |
| S4 | X | 125% | 128% | 97% | 117% | 105% | 96% |
| Y | 127% | 130% | 99% | 155% | 137% | 129% | |
| Hazard Level | Model | Fundamental Period [s] | M1* [%] | TGM | 0.2TGM–1.5TGM | |
|---|---|---|---|---|---|---|
| Longitudinal | Transverse | |||||
| Medium hazard | S0 | 0.235 | 0.267 | 38.0 | 0.25 | 0.05–0.38 |
| S1 | 0.561 | 0.454 | 39.3 | 0.50 | 0.10–0.76 | |
| S2 | 0.408 | 0.379 | 47.1 | 0.39 | 0.08–0.59 | |
| S3 | 0.405 | 0.379 | 46.1 | 0.39 | 0.08–0.59 | |
| S4 | 0.779 | 0.565 | 41.5 | 0.66 | 0.13–1.00 | |
| High hazard | S0 | 0.235 | 0.267 | 38.0 | 0.25 | 0.05–0.38 |
| S1 | 0.571 | 0.454 | 40.4 | 0.44 | 0.09–0.67 | |
| S2 | 0.407 | 0.373 | 44.0 | 0.39 | 0.08–0.60 | |
| S3 | 0.405 | 0.365 | 43.9 | 0.38 | 0.08–0.60 | |
| S4 | 0.785 | 0.563 | 41.4 | 0.59 | 0.12–0.90 | |
| Alt. | Param. | Medium Hazard | High Hazard | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M-C | M-M | M-W | H-C | H-M | H-W | ||||||||||||||
| % | Class | % | Class | % | Class | % | Class | % | Class | % | Class | ||||||||
| S1 | SI-LS | 120 | A+ | A+ | 123 | A+ | A+ | 95 | A | A | 120 | A+ | A | 108 | A+ | A | 99 | A | A |
| EAL | 0.46 | A+ | 0.48 | A+ | 0.52 | A | 0.61 | A | 0.61 | A | 0.64 | A | |||||||
| S2 | SI-LS | 92 | A | A | 95 | A | A | 73 | B | B | 63 | B | B | 55 | C | C | 50 | C | C |
| EAL | 0.49 | A+ | 0.51 | A | 0.59 | A | 0.80 | A | 0.82 | A | 0.60 | A | |||||||
| S3 | SI-LS | 111 | A+ | A+ | 113 | A+ | A+ | 96 | A | A | 82 | A | A | 73 | B | B | 68 | B | B |
| EAL | 0.46 | A+ | 0.46 | A+ | 0.50 | A | 0.63 | A | 0.67 | A | 0.65 | A | |||||||
| S4 | SI-LS | 125 | A+ | A+ | 128 | A+ | A+ | 97 | A | A | 117 | A+ | A | 105 | A+ | A | 96 | A | A |
| EAL | 0.42 | A+ | 0.43 | A+ | 0.47 | A+ | 0.52 | A | 0.54 | A | 0.52 | A | |||||||
| Alt. | PEC (kWh/m2) | Eq. CO2 (kgCO2e) | AEC (EUR) | Energy Class |
|---|---|---|---|---|
| E0 | 309 | 76,651 | 12,718 | E |
| E1 | 221.76 (−28%) | 52,476 (−32%) | 8765 (−31%) | D |
| E2 | 166.63 (−46%) | 40,716 (−47%) | 7121 (−44%) | C |
| E3 | 64.92 (−79%) | 14,982 (−80%) | 3109 (−76%) | A2 |
| Detailed | Simplified | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | M | W | C | M | W | |||||||||||||
| Alt | C2 | C3 | C4 | C2 | C3 | C4 | C2 | C3 | C4 | C2 | C3 | C4 | C2 | C3 | C4 | C2 | C3 | C4 |
| S1E1 | 9.5 | 25.4 | 1.22 | 10.4 | 43.2 | 0.36 | 13.5 | 52.7 | 1.30 | 15.3 | 29.2 | 1.19 | 18.0 | 48.2 | 0.25 | 18.9 | 56.3 | 1.38 |
| S1E2 | 9.5 | 21.6 | 1.28 | 9.6 | 35.3 | 0.33 | 12.5 | 42.5 | 1.31 | 15.2 | 25.3 | 1.19 | 17.4 | 40.4 | 0.25 | 18.0 | 46.1 | 1.38 |
| S1E3 | 8.8 | 14.8 | 1.20 | 7.4 | 18.0 | 0.31 | 9.9 | 21.4 | 1.28 | 14.8 | 18.7 | 1.19 | 15.6 | 23.4 | 0.25 | 15.7 | 25.2 | 1.38 |
| S2E1 | 9.0 | 23.5 | 1.14 | 9.5 | 41.1 | 0.26 | 14.2 | 51.8 | 1.95 | 16.8 | 28.9 | 1.33 | 17.1 | 46.2 | 0.35 | 18.8 | 54.8 | 1.49 |
| S2E2 | 9.3 | 19.9 | 1.40 | 8.7 | 33.2 | 0.19 | 13.5 | 41.7 | 2.08 | 16.8 | 25.0 | 1.33 | 16.4 | 38.4 | 0.35 | 17.9 | 44.6 | 1.49 |
| S2E3 | 8.6 | 13.1 | 1.39 | 6.7 | 16.1 | 0.30 | 11.1 | 20.8 | 2.18 | 16.5 | 18.5 | 1.33 | 14.6 | 21.4 | 0.35 | 15.6 | 23.8 | 1.49 |
| S3E1 | 8.7 | 22.4 | 0.93 | 9.7 | 40.3 | 0.28 | 12.5 | 49.6 | 0.96 | 15.3 | 26.9 | 1.37 | 17.2 | 45.4 | 0.32 | 18.2 | 53.4 | 1.56 |
| S3E2 | 8.6 | 18.4 | 0.95 | 9.2 | 32.6 | 0.37 | 11.4 | 39.3 | 0.92 | 15.2 | 23.0 | 1.37 | 16.6 | 37.6 | 0.32 | 17.2 | 43.3 | 1.56 |
| S3E3 | 8.0 | 11.7 | 0.96 | 6.9 | 15.3 | 0.32 | 8.9 | 18.3 | 0.98 | 14.9 | 16.5 | 1.37 | 14.8 | 20.6 | 0.32 | 14.9 | 22.4 | 1.56 |
| S4E1 | 8.6 | 21.8 | 0.53 | 10.7 | 40.5 | 0.30 | 12.3 | 49.0 | 0.46 | 16.2 | 26.8 | 0.11 | 17.9 | 45.2 | 0.006 | 18.8 | 53.3 | 0.17 |
| S4E2 | 8.5 | 17.9 | 0.54 | 9.9 | 32.6 | 0.27 | 11.3 | 38.7 | 0.49 | 16.1 | 22.9 | 0.11 | 17.3 | 37.4 | 0.006 | 17.9 | 43.1 | 0.17 |
| S4E3 | 7.8 | 11.1 | 0.54 | 7.9 | 15.4 | 0.31 | 8.5 | 17.5 | 0.44 | 15.8 | 16.4 | 0.11 | 15.4 | 20.4 | 0.006 | 15.6 | 22.2 | 0.17 |
| Detailed | Simplified | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | M | W | C | M | W | |||||||||||||
| Alt | C2 | C3 | C4 | C2 | C3 | C4 | C2 | C3 | C4 | C2 | C3 | C4 | C2 | C3 | C4 | C2 | C3 | C4 |
| S1E1 | 12.9 | 28.4 | 1.01 | 16.2 | 40.4 | 1.66 | 18.8 | 47.5 | 2.67 | 19.7 | 33.0 | 0.91 | 22.7 | 52.3 | 1.42 | 23.7 | 60.3 | 1.20 |
| S1E2 | 12.9 | 24.5 | 1.08 | 14.3 | 23.4 | 1.87 | 16.5 | 26.6 | 2.90 | 19.6 | 29.1 | 0.91 | 22.1 | 44.5 | 1.42 | 22.8 | 50.2 | 1.20 |
| S1E3 | 12.3 | 17.9 | 1.12 | 13.4 | 42.7 | 1.81 | 16.9 | 52.5 | 2.94 | 19.3 | 22.6 | 0.91 | 20.4 | 27.5 | 1.42 | 20.6 | 29.4 | 1.20 |
| S2E1 | 13.1 | 25.0 | 2.86 | 18.8 | 38.7 | 4.55 | 19.7 | 44.6 | 4.58 | 20.3 | 30.1 | 1.36 | 22.5 | 48.9 | 2.05 | 22.4 | 56.2 | 1.81 |
| S2E2 | 13.1 | 21.2 | 2.93 | 16.6 | 21.5 | 4.70 | 17.1 | 23.5 | 4.73 | 20.3 | 26.3 | 1.36 | 22.0 | 41.1 | 2.05 | 21.5 | 46.1 | 1.81 |
| S2E3 | 13.3 | 15.1 | 3.30 | 22.3 | 47.2 | 4.37 | 24.2 | 55.9 | 4.69 | 20.2 | 19.9 | 1.36 | 20.5 | 24.3 | 2.05 | 19.5 | 25.3 | 1.81 |
| S3E1 | 13.6 | 23.9 | 1.66 | 17.4 | 36.3 | 2.46 | 17.8 | 41.7 | 2.05 | 19.9 | 28.5 | 0.65 | 22.8 | 47.7 | 1.00 | 23.0 | 55.2 | 0.85 |
| S3E2 | 13.5 | 20.0 | 1.67 | 15.5 | 19.3 | 2.66 | 15.4 | 20.8 | 2.30 | 19.8 | 24.6 | 0.65 | 22.2 | 40.0 | 1.00 | 22.1 | 45.1 | 0.85 |
| S3E3 | 12.8 | 13.3 | 1.62 | 22.8 | 45.6 | 2.74 | 23.3 | 53.3 | 2.24 | 19.6 | 18.2 | 0.65 | 20.6 | 23.1 | 1.00 | 19.9 | 24.3 | 0.85 |
| S4E1 | 13.7 | 22.6 | 0.43 | 16.3 | 34.2 | 0.79 | 16.9 | 39.8 | 0.52 | 21.2 | 27.6 | 0.027 | 23.8 | 46.6 | 0.06 | 24.8 | 54.7 | 0.03 |
| S4E2 | 13.6 | 18.7 | 0.40 | 14.2 | 19.2 | 0.74 | 14.2 | 20.8 | 0.57 | 21.1 | 23.7 | 0.027 | 23.2 | 38.9 | 0.06 | 23.9 | 44.6 | 0.03 |
| S4E3 | 13.4 | 14.4 | 0.59 | 2.6 | 1.5 | 0.68 | 2.4 | 1.4 | 0.54 | 20.7 | 19.4 | 0.027 | 21.4 | 24.0 | 0.06 | 21.6 | 25.9 | 0.03 |
| Alt. | C6 (-) | C7 (-) | C8 (-) | |||||
|---|---|---|---|---|---|---|---|---|
| Medium Hazard | High Hazard | |||||||
| M-C | M-M | M-W | H-C | H-M | H-W | |||
| S1E1 | 0.023 | 0.084 | 5.9 | 6.2 | 7.0 | 6.1 | 5.7 | 5.7 |
| S1E2 | 0.023 | 0.084 | 5.9 | 6.2 | 7.0 | 6.1 | 5.7 | 5.7 |
| S1E3 | 0.023 | 0.084 | 5.9 | 6.2 | 7.0 | 6.1 | 5.7 | 5.7 |
| S2E1 | 0.056 | 0.013 | 10.9 | 11.3 | 12.5 | 16.5 | 16.5 | 16.5 |
| S2E2 | 0.056 | 0.013 | 10.9 | 11.3 | 12.5 | 16.5 | 16.5 | 16.5 |
| S2E3 | 0.056 | 0.013 | 10.9 | 11.3 | 12.5 | 16.5 | 16.5 | 16.5 |
| S3E1 | 0.093 | 0.084 | 12.8 | 13.4 | 13.0 | 16.6 | 16.6 | 16.6 |
| S3E2 | 0.093 | 0.084 | 12.8 | 13.4 | 13.0 | 16.6 | 16.6 | 16.6 |
| S3E3 | 0.093 | 0.084 | 12.8 | 13.4 | 13.0 | 16.6 | 16.6 | 16.6 |
| S4E1 | 0.162 | 0.151 | 3.3 | 3.5 | 3.9 | 5.1 | 4.8 | 4.8 |
| S4E2 | 0.162 | 0.151 | 3.3 | 3.5 | 3.9 | 5.1 | 4.8 | 4.8 |
| S4E3 | 0.162 | 0.151 | 3.3 | 3.5 | 3.9 | 5.1 | 4.8 | 4.8 |
| Rank | Medium Hazard | High Hazard | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Detailed | Simplified | Detailed | Simplified | |||||||||
| C | M | W | C | M | W | C | M | W | C | M | W | |
| 1 | S3E3 | S2E3 | S3E2 | S4E1 | S4E1 | S4E1 | S3E3 | S4E3 | S4E2 | S4E2 | S4E2 | S4E2 |
| 2 | S4E3 | S2E2 | S4E1 | S4E2 | S4E2 | S4E2 | S4E3 | S4E2 | S4E1 | S3E3 | S4E3 | S4E1 |
| 3 | S4E2 | S3E3 | S2E1 | S4E3 | S4E3 | S2E1 | S4E2 | S3E3 | S4E3 | S4E3 | S4E1 | S4E3 |
| 4 | S3E2 | S2E1 | S3E1 | S2E2 | S2E2 | S2E2 | S3E2 | S4E1 | S3E2 | S3E2 | S3E3 | S3E2 |
| 5 | S4E1 | S3E2 | S4E2 | S2E3 | S2E1 | S4E3 | S3E1 | S3E2 | S3E3 | S4E1 | S3E2 | S3E1 |
| 6 | S3E1 | S4E3 | S3E3 | S2E1 | S2E3 | S3E1 | S4E1 | S2E3 | S3E1 | S3E1 | S3E1 | S3E3 |
| 7 | S2E3 | S3E1 | S2E2 | S3E2 | S3E2 | S3E2 | S2E3 | S3E1 | S2E2 | S2E3 | S2E3 | S2E2 |
| 8 | S2E2 | S4E1 | S2E3 | S3E1 | S3E3 | S2E3 | S2E2 | S2E2 | S2E1 | S2E2 | S2E2 | S2E1 |
| 9 | S2E1 | S4E2 | S4E3 | S3E3 | S3E1 | S3E3 | S2E1 | S2E1 | S2E3 | S2E1 | S2E1 | S2E3 |
| 10 | S1E3 | S1E3 | S1E3 | S1E3 | S1E3 | S1E1 | S1E3 | S1E3 | S1E2 | S1E3 | S1E3 | S1E2 |
| 11 | S1E2 | S1E2 | S1E1 | S1E2 | S1E2 | S1E2 | S1E1 | S1E1 | S1E1 | S1E2 | S1E2 | S1E1 |
| 12 | S1E1 | S1E1 | S1E2 | S1E1 | S1E1 | S1E3 | S1E2 | S1E2 | S1E3 | S1E1 | S1E1 | S1E3 |
| Medium Hazard | High Hazard | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Detailed | Simplified | Detailed | Simplified | ||||||||
| C | M | W | C | M | W | C | M | W | C | M | W |
| S1E1 | S1E1 | S1E1 | S1E1 | S1E1 | S1E1 | S1E1 | S1E1 | S1E1 | S1E1 | S1E1 | S1E1 |
| S1E2 | S1E2 | S1E2 | S1E2 | S1E2 | S1E2 | S1E2 | S1E2 | S1E2 | S1E2 | S1E2 | S1E2 |
| S1E3 | S1E3 | S1E3 | S1E3 | S1E3 | S1E3 | S1E3 | S1E3 | S1E3 | S1E3 | S1E3 | S1E3 |
| S2E1 | S2E1 | S2E1 | S2E1 | S2E1 | S2E1 | S2E1 | S2E1 | S2E1 | S2E1 | S2E1 | S2E1 |
| S2E2 | S2E2 | S2E2 | S2E2 | S2E2 | S2E2 | S2E2 | S2E2 | S2E2 | S2E2 | S2E2 | S2E2 |
| S2E3 | S2E3 | S2E3 | S2E3 | S2E3 | S2E3 | S2E3 | S2E3 | S2E3 | S2E3 | S2E3 | S2E3 |
| S3E1 | S3E1 | S3E1 | S3E1 | S3E1 | S3E1 | S3E1 | S3E1 | S3E1 | S3E1 | S3E1 | S3E1 |
| S3E2 | S3E2 | S3E2 | S3E2 | S3E2 | S3E2 | S3E2 | S3E2 | S3E2 | S3E2 | S3E2 | S3E2 |
| S3E3 | S3E3 | S3E3 | S3E3 | S3E3 | S3E3 | S3E3 | S3E3 | S3E3 | S3E3 | S3E3 | S3E3 |
| S4E1 | S4E1 | S4E1 | S4E1 | S4E1 | S4E1 | S4E1 | S4E1 | S4E1 | S4E1 | S4E1 | S4E1 |
| S4E2 | S4E2 | S4E2 | S4E2 | S4E2 | S4E2 | S4E2 | S4E2 | S4E2 | S4E2 | S4E2 | S4E2 |
| S4E3 | S4E3 | S4E3 | S4E3 | S4E3 | S4E3 | S4E3 | S4E3 | S4E3 | S4E3 | S4E3 | S4E3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Couto, R.; Mucedero, G.; Bento, R.; Monteiro, R. Understanding the Impact of Seismic Hazard and Climate Conditions on Multi Criteria–Based Retrofitting of Existing Buildings. Sustainability 2024, 16, 4318. https://doi.org/10.3390/su16104318
Couto R, Mucedero G, Bento R, Monteiro R. Understanding the Impact of Seismic Hazard and Climate Conditions on Multi Criteria–Based Retrofitting of Existing Buildings. Sustainability. 2024; 16(10):4318. https://doi.org/10.3390/su16104318
Chicago/Turabian StyleCouto, Rita, Gianrocco Mucedero, Rita Bento, and Ricardo Monteiro. 2024. "Understanding the Impact of Seismic Hazard and Climate Conditions on Multi Criteria–Based Retrofitting of Existing Buildings" Sustainability 16, no. 10: 4318. https://doi.org/10.3390/su16104318
APA StyleCouto, R., Mucedero, G., Bento, R., & Monteiro, R. (2024). Understanding the Impact of Seismic Hazard and Climate Conditions on Multi Criteria–Based Retrofitting of Existing Buildings. Sustainability, 16(10), 4318. https://doi.org/10.3390/su16104318









