Abstract
The I–V curve serves as an effective representation of the inherent nonlinear characteristics describing typical photovoltaic (PV) panels, which are essential for achieving sustainable energy systems. Over the years, several PV models have been proposed in the literature to achieve the simplified and accurate reconstruction of PV characteristic curves as specified in the manufacturer’s datasheets. Based on their derivation, PV models can be classified into three distinct categories: circuit-based, analytical-based, and empirical-based models. However, an extensive analysis of the accuracy of the reconstructed curves for different PV models at the maximum power point (MPP) has not been conducted at the time of writing this paper. The IEC EN 50530 standard stipulates that the absolute errors within the vicinity of MPP should always be less than or equal to 1%. Therefore, this review paper conducts an in-depth analysis of the accuracy of PV models in reconstructing characteristic curves for different PV panels. The limitations of existing PV models were identified based on simulation results obtained using MATLAB and performance indices. Additionally, this paper also provides suggestions for future research directions.
1. Introduction
Over the past three decades, there has been a rapid increase in global energy demand for residential and commercial purposes [1]. Although conventional fossil fuel energy sources such as the burning of coal and natural gas have dominated the energy markets due to their high energy density, the combustion of these fuels results in the release of carbon dioxide (CO) and other greenhouse gases into the atmosphere, thereby contributing to climate change and other environmental issues [2]. As a result, countries all over the world are enacting laws and policies aimed at ensuring a smooth energy transition to cleaner and more sustainable energy such as solar, wind, ocean, and biomass [3].
Photovoltaic cells (PV) are tools used for the effective and sustainable conversion of the abundant and radiant light energy from the sun into electrical energy [4,5,6,7,8]. In its basic form, a PV is an interconnection of multiple solar cells aimed at achieving maximum energy output (see Figure 1). In recent years, there has been significant progress in the fabrication of high-efficiency solar cells [9,10,11,12,13], with multijunction solar cells now approaching 50% efficiency [14]. Nonetheless, most PV panels used in the industry typically have conversion efficiencies between 17 and 20% [15,16,17].
Figure 1.
Classification of photovoltaic technologies [18,19,20,21].
The PV characteristic curve, which is widely known as the I–V curve, is the representation of the electrical behavior describing a solar cell, PV module, PV panel, or an array under different ambient conditions, which are usually provided in a typical manufacturer’s datasheet. Due to several constraints such as the cost of equipment, the exact replication of the specific ambient conditions required for the reconstruction of the I–V curve is quite a challenge for researchers all over the world. To address this challenge, several alternative methods, known as PV models, have been developed to achieve a simplified and accurate representation of these nonlinear characteristics.
A PV model can be simply described as a mathematical representation of the electrical behavior of PV panels for simulating and predicting the performance of PV panels [22] in commercial software environments such as MATLAB/SIMULINK, PSIM, etc. [23,24,25,26]. Following the approach utilized in the derivation of their mathematical equations, PV models can be broadly categorized into circuit-based, analytical-based, and empirical-based models.
Due to the in-depth understanding of the experimental behavior of PV panels across different ambient conditions, the equivalent-circuit-based models were first developed. These equivalent circuits are a combination of several electrical components including diode(s) and resistors [27,28,29,30,31,32]. By applying circuit analysis, an implicit characteristic equation describing the typical I–V curve has been derived, which varies in mathematical complexity and relies heavily on an accurate estimation of the fitting parameters [33,34,35,36,37,38,39,40].
To ease the complexity of these implicit circuit-based models, analytical-based PV models have been proposed, which decouple the exponential function in the widely used single-diode model [41]. In essence, these analytical-based models are a series of interconnected equations that are used for the domain conversion of the exponent into simple algebraic equations [42,43]. Although these PV models offer explicit equations of the I–V curve, they are still somewhat dependent on the fitting parameters of the circuit-based models.
Recently, empirical-based models have emerged as another alternative for the effective modeling and simulation of PV panels. These empirical models, which often involve curve fitting, are based on observed unique graphical characteristics between the typical I–V curve and the underlying mathematical equation, describing a wide range of similar shapes [42,43,44,45]. In comparison to the circuit-based and analytical-based models, the fitting parameters of the empirical-based models are completely independent of the physical representation of the PV panel.
In practical PV installations, the performance of any PV panel, regardless of its cell material, can be effectively evaluated from the accurate reconstruction of its PV characteristic curves. Hence, the IEC EN 50530 standard provides a set of design requirements and conditions establishing an interconnected relationship between the maximum power point (MPP) of the typical PV characteristic curves (i.e., I–V and P–V), the incident irradiance on the PV panel, the open circuit voltage, and the short-circuit current point, respectively. This standard specifies that for any PV simulator, the power output should not deviate by more than 1% within the range of of the voltage at MPP , as compared to the rated conditions of the predetermined characteristic curve of the simulator [46] (see Appendix A).
Thus, this review paper aims to:
- Provide a comprehensive summary of some of the widely used PV models in literature.
- Evaluate the accuracy of these models at MPP in accordance with the IEC EN 50530 standard.
- Identify limitations in existing photovoltaic (PV) models and propose potential research directions in this field with the aim of advancing toward energy sustainability.
The structure of the paper is as follows. Section 2 discusses the theoretical and mathematical derivations of the equivalent-circuit-based models for PV panels. By decoupling the exponent term in the characteristic equation describing the single-diode model, several approximate PV models have been derived and are carefully examined in Section 3. Next, Section 4 examines the empirical-based models, which are completely independent of the electrical parameters of the PV panel. In accordance with the IEC EN 50530 standard, a comprehensive evaluation of the accuracy of these PV models is carried out in Section 5. Finally, based on these simulation results, possible research directions and conclusions are provided in Section 5.4 and Section 6, respectively.
2. Equivalent-Circuit-Based Models
Equivalent-circuit-based models remain one of the most widely utilized approaches for representing the behavioral characteristics of the I–V curve. These models utilize conversion principles that describe a typical PV panel and can be classified based on the number of its diode components as single-diode, double-diode, or triple-diode models, as shown in Figure 2.
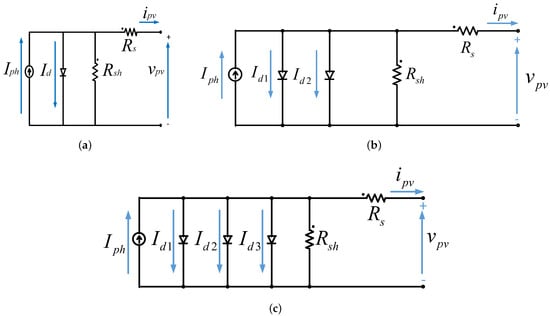
Figure 2.
Equivalent circuit-based representation for photovoltaic (PV) panels: (a) single-diode, (b) double-diode, (c) triple-diode.
2.1. Single-Diode Model
The single-diode model, consisting of a single-diode component and five electrical parameters, is one of the most basic representations of the inherent nonlinear characteristics of PV panels. By applying circuit theories to Figure 2a, an implicit mathematical equation known as the typical I–V characteristic equation has been defined as [47,48]
where is the PV output current (A), is the PV output voltage (V), is the photovoltaic current (A), is the saturation current of the diode (A), is the ideality factor, while , , and N are the series resistance (), parallel resistance (), and number of cells in a series string inside the panel, respectively. The thermal voltage has also been defined mathematically as , where k is the Boltzmann constant, defined as J/K, and q is the elementary charge, C.
By carrying out further circuit analysis, a mathematical correlation can be established between and the incident ambient condition of the solar cell (irradiance, G, and temperature, T) as [49,50]
where all the terms in (2) are defined such that is the short-circuit current at standard test conditions (STCs) K W/m) while is the temperature coefficient of .
Likewise, in (1) can, therefore, be further expressed as [51,52]
where is the open-circuit voltage at STCs and is the temperature coefficient of .
2.2. Double-Diode Model
In practice, the diode ideality is a function of the voltage across the solar cells. Due to its simplicity, the single-diode model assumes a constant value as defined by in (1). To account for the recombination effect in the space charge region, researchers proposed the introduction of an extra diode component in parallel, as shown in Figure 2b. Likewise, by applying circuit analysis, an upgraded characteristic equation describing the I–V can be expressed as [53,54,55,56]
where , , and remain as defined in Section 2.1, while , , , and are the reverse combination current and diode ideality for each diode component.
2.3. Triple-Diode Model
Based on the conversion principle, the triple-diode model has also been proposed, as shown in Figure 2c, with the third diode element accounting for the recombination effects in the defect region of the solar cell [57]. Hence, by applying circuit analysis, the I–V characteristic equation has been defined as [53,58,59,60,61]
where the , , and are as defined in Section 2.1. While and typically range between 1 and 2 [62,63,64,65,66,67,68], the estimated value for is usually greater than 2 and less than 5 for commercial solar cells [69].
By obtaining the numerical solutions to Equations (1), (4), and (5) the reconstruction of the I–V curve can be achieved as shown by the blue curve in Figure 3. According to basic circuit analysis [55], the instantaneous output power flowing through the circuits in Figure 2 can be defined mathematically as
which is also illustrated by the red curve in Figure 3. Regardless of the incident ambient condition of the PV panel, the I–V curve consists of four key points, i.e., open circuit voltage , short-circuit current , voltage at maximum power point , and current at maximum power point .
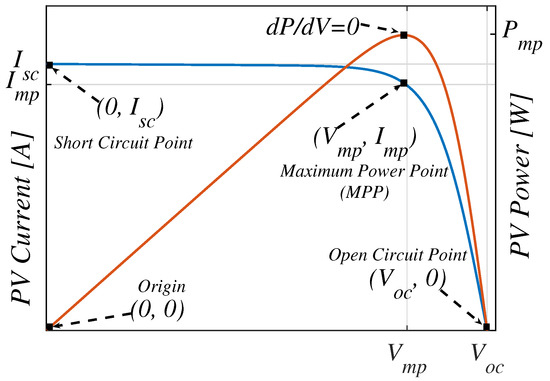
Figure 3.
Typical PV characteristic curves as specified in the manufacturer’s datasheet at standard test conditions (STCs).
3. Approximate PV Models
Finding a numerical solution for the full range enumeration of the I–V characteristic equation in the single-diode model (as described in (1)) can be a challenging task due to its exponential function. To simplify this task, approximate PV model (PVM) equations have been proposed and implemented in the literature.
These approximate PVM equations can be classified into two types based on their structure: iteration-based and analytical-based. Iteration-based PVM equations are derivative equations of (1), which are obtained after applying datasheet constraints under specified conditions [70,71,72,73,74,75]. Analytical-based PVM equations, on the other hand, are a series of explicit interconnected equations obtained after the transformation of the exponent in (1) into separate domains for performance analysis.
3.1. Approximation Using the Lambert W Function and the Asymptotic Formula
The Lambert W function is a popular method used to approximate (1) due to its ease of substitution. Essentially, it expresses (1) as an asymptotic formula such that [76,77]
with
where , , , and is the natural logarithm of x, thereby establishing a mathematical correlation with numerical solutions to both branches of (i.e., positive and negative branches). However, the basic Lambert W method (also known as Haley’s method [78,79]) does not express as simple elementary equations. Therefore, obtaining data point solutions for these equations is challenging and time consuming.
Several modifications and improvements have been proposed in the literature to tackle this challenge. Ref. [80] proposed obtaining numerical solutions to (7) by utilizing Taylor’s series expansion of , as defined in [81] such that
where , , and . Similarly, ref. [82] also presented a simple analytical-based approximation of based on [83]
where is a constant regardless of the cell material of the PV module.
Another simple and fast approximation technique for was introduced by [84,85] such that
where is the natural logarithm of x. Other methods include using the exact closed-form using Maple software [86], Marine Predator algorithm [87], Hybrid analytical [88], and Hessian function [82].
3.2. Other Analytical-Based PVM Equations
Based on the fixed points of the I–V curve as described in Figure 3 and the assumption that for any PV module, [89,90], introduced the three-point model, which decomposes (1) into
Since the estimated value for is usually high for silicon modules, we can assume that and , in (12), are valid. Therefore, we can rewrite the equation as
With the valid assumption that for any PV module , the exponent in (13) can be approximated as . Hence, this equation can be rewritten using a simplified polynomial expression as
where the model coefficients for the equation are , , and .
References [91,92] in his separate papers suggested utilizing the Padé approximant and Taylor’s series expansion to decouple its exponent function. Accordingly, ref. [91] proposed a Padé approximant model based on [93] which defined an approximation of a function as
where , are the polynomials of the degree , respectively. With the Padé approximant of the exponential function written as
where and from (1). Hence, by taking such that , (1) can, therefore, be rewritten as
By taking , , , , (17b) can, therefore, be rewritten as a cubic equation as
On the other hand, ref. [92] suggested applying the Taylor’s series expansion such that
where . Thus, (19) can also be rewritten as a cubic equation
where , , , .
Therefore, to obtain the roots to (18) and (20), the Shengjin’s formula as derived in [94,95] is used. Hence, if we take , , , and , the positive roots can be obtained such that
where , . Hence, the I–V curve can, therefore, be reconstructed using
where is the approximation of the current .
Although the I–V curve can be computed through two approaches—the I-approach, which calculates the values of with known values of , and the V-approach, which computes the value of with known values of —it is important to note that there is also an independent variation in the diode voltage from to . Thus, an upgraded two-port equivalent-circuit-based network was proposed by [96] (see Figure 4), which explicitly expresses the equations as follows:
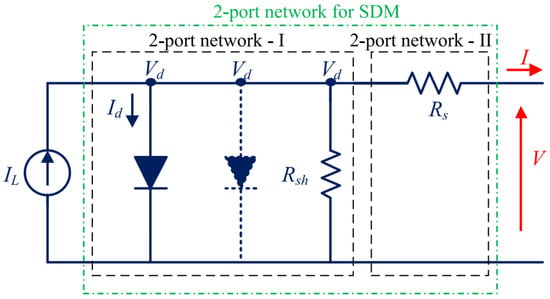
Figure 4.
The single-diode model (SDM)/double-diode model (DDM) equivalent circuit with two 2-port networks [96].
Since the output current from the 2-port network-I is the same as the input current to the 2-port network-II in Figure 4, an explicit equation for the computation of the I–V curve is defined as
Likewise, the two-parameter model, which was first introduced in [97], but popularized by [98,99,100], requiring only two fitting parameters was derived as
where the fitting parameters are computed using
while can be solved using the negative branch of the Lambert W function.
4. Empirical-Based PV Models
4.1. Three-Coefficient Model
Due to the computational burden often associated with analytical-based PV models including fitting parameter estimation, several other methods have also been proposed in the literature. Ref. [101] suggested that the nonlinear characteristic of the I–V curve can be reconstructed using
where A, B, and C are the parameters to be adjusted. By utilizing the key point values of the I–V curve under STCs as provided in the manufacturer’s datasheet, these coefficients can be easily determined using
4.2. Bézier Curve-Based Model
The Bézier curve (see Figure 5a) is one of the widely used tools in computer graphics design for creating parametric curves [102,103,104]. In simple terms, these curves are constructed using an nth-order Bernstein polynomial function which has been defined mathematically as [44,102,105]
where are the control points along the curve, with .
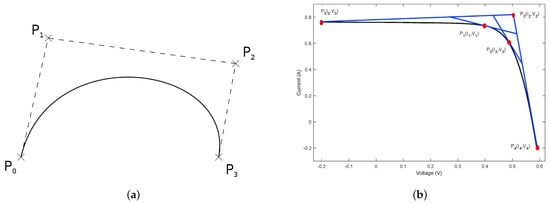
Figure 5.
(a) Cubic Bézier curve with four control points. (b) Subdivision construction of a cubic Bézier for the typical I–V curve [44].
To reconstruct the I–V characteristic curve using this curve, refs. [44,106,107] suggested defining the number of control points along the typical I–V curve as shown in Figure 5b with and , , , , and . Since the coordinates of the control points are tangents to the key points of the I–V curve, as specified in the manufacturer’s datasheet, the endpoints and are the and , and the other three control points are to be determined.
While [106] suggested determining these points using the estimated electrical parameters (i.e., , and ), ref. [107] proposed utilizing the key points of the I–V curve. On the other hand, [44] suggested using the De Casteliju algorithm, as presented in [108].
4.3. Superellipse-Based Model
The superellipse is a geometric curve that is similar to the Bézier curve and retains its intercept values at both ends regardless of any distortions in its overall shape (as shown in Figure 6) [42,109,110]. The equation that explicitly describes the curve in Figure 6b has been derived as
while A and B are the intercepts and m and n are its fitting parameters.
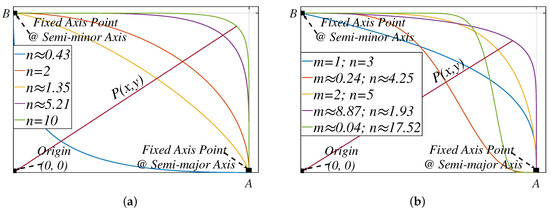
Figure 6.
Superellipse with varying parameter values [41]: (a) single-shaped, (b) double-shaped.
Based on the theoretical and mathematical relationship between Figure 3 and Figure 6b, several explicit equations describing the reconstruction of the PV characteristic curve have been derived as [41,94,111,112,113,114]
where is the output current of the superellipse model and is the output voltage of the superellipse model.
Various techniques have been proposed in the literature for extracting these fitting parameters. One such technique, as described in [114], involves initially determining fitting parameters through trial and error. These fitting parameters can then be further fine-tuned by calculating the correlation coefficients. On the other hand, ref. [113], and its subsequent papers such as [94,111,112], utilizes the estimated electrical parameters of the single-diode model. In [41], the datasheet constraints were incorporated into Equation (31a) to derive a two-dimensional equation. The optimal fitting parameters of the model are obtained by computing the roots of this equation using numerical optimization algorithms [43,115,116]. Regardless of the method used, these fitting parameters remain constant.
5. Comparative Evaluation and Further Discussion
This section gives a detailed evaluation of the accuracy of 20 distinct PVM methods, as categorized in Table 1, at MPP in accordance with the IEC EN 50530 standard. First, the theoretical and mathematical equations describing the IEC EN 50530 standard were discussed in Section 5.1. Then, the fitting parameters were extracted for the six different PV panels used for analysis in this paper (see Table 2). Finally, the full range of the I–V curve is reconstructed and evaluated within the vicinity of MPP in Section 5.3, while the observed research trends from these analyses are outlined in Section 5.4.

Table 1.
Classification of the 17 PVM equations used in this paper.

Table 2.
PV panel specifications used in this paper.
5.1. Criteria for Evaluating Model Accuracy
As explained in Section 1, the IEC EN 50530 standard, as published by the European Committee for Electrotechnical Standardization (CENELEC), stipulates that the maximum deviation of the output power should always be less than or equal to 1%. To quantify the accuracy of the PV simulator, the absolute error between the approximate and the reference datasheet curves is computed. Following conventional numerical analysis [125], the absolute error across the full range of the I–V curves can, therefore, be expressed as
where the subscript s represents the measured values of the approximate curves, and r denotes the data values for the reference model. However, to compute the accumulated absolute error within the stipulated of , which can be interpreted mathematically as the region in the I–V curve in which , a definite integral [126] is introduced such that
Furthermore, to ensure that these error calculations, regardless of the behavior of the PV panel, are normalized across the entire voltage range, a scaling factor defined as the total width of the voltage range, i.e., is introduced. Hence, the simplified equation for computing the absolute error at MPP for the I–V curve in accordance with the IEC EN 50530 standard is defined mathematically as [41,127,128]
In real PV applications, beyond providing actual information about the power output of the PV panel, the P–V curve detects and illustrates any potential amplification of error in the voltage source segment of the I–V curve [129]. Hence, by applying a similar theoretical and mathematical derivation process, the absolute error at MPP for the P–V curve has also been defined as [41,127,128]
where the integrals in (34) and (35) are computed in this paper by utilizing the trapezoidal rule [130,131].
5.2. Parameter Convergence
In this paper, the fitting parameters of the PV models were extracted using the different parameter extraction techniques as defined in the relevant literature. While the electrical parameters of the single-diode model were extracted through the utilization of the existing datasheet information [117], the triple-diode model parameters were extracted using the grasshopper optimization algorithm (GOA) [58]. On the other hand, due to the assumption that , ref. [64] proposed a simple and fast approach for estimating the electrical parameters of the double-diode model with and , where .
Since the PV panels (see Table 2) utilized in this analysis are the same as the reference papers, the fitting electrical parameters were easily obtained, as clearly outlined in Table 3 and Table 4. It is important to re-emphasize that since the analysis is carried out at STCs, the fitting parameters of both the approximate PV models (obtained as derivatives of the electrical parameters) and the empirical models (extracted by utilizing the key points of the I–V curve) were all obtained after a one-time computation, as clearly outlined in Table 4 and Table 5.

Table 3.
Electrical parameters for the equivalent-circuit-based models for the KC200GT PV panel.

Table 4.
Parameter extraction of circuit-based and analytical-based PV models for 6 different PV panels.

Table 5.
Parameter extraction of empirical-based PV models for 6 different PV panels.
5.3. Accuracy Evaluation Using the IEC EN 50530 Standard
5.3.1. Comparison of the Equivalent-Circuit-Based Models
To reconstruct the full range of the I–V characteristic curve from the to the point, equivalent-circuit-based models can be represented either using their piecewise circuit representation or by designing their implicit equations in MATLAB/Simulink. In this paper, the PV characteristic curves were effectively reconstructed using the electrical parameters of the KC200GT PV panel (see Table 3) in MATLAB and designed mathematically in Simulink, as defined by (1), (4), and (5).
Previously, emphasis had solely been placed on the reconstruction of the I–V curve. As shown in Figure 7, by increasing the number of diode components in the equivalent-circuit-based models, the absolute current error () within the vicinity of the MPP decreases. While the I–V curve provides key information about the PV panel (i.e., , , , and ), the P–V curve provides actual information about the power output of the PV panel.
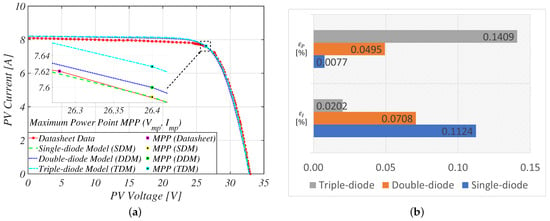
Figure 7.
Comparison of the reconstructed characteristic curves for the KC200GT PV panel using the equivalent-circuit-based models: (a) I–V curve, (b) accuracy evaluation at MPP.
Hence, in accordance with the IEC EN 50530 standard, the absolute power error () in the reconstructed P–V curve increases with the number of diode components, as shown in Figure 7b and outlined in Table 6. The increase in can be attributed to several factors, including the amplification of the error in the voltage source segment of the I–V curve [129]. Other potential factors include the assumption that [64] for the double-diode model and the sensitivity of the parameter extraction algorithm (i.e., grasshopper position strategy [58]) applied to the triple-diode model.

Table 6.
Comparison of the three equivalent-circuit-based models for KC200GT PV panel within the vicinity of MPP.
5.3.2. Comparison of the Approximate PV Models
In Section 3, we explain that the approximate PVM equations are explicit derivatives of the typical I–V characteristic equation describing the single-diode model. By applying the fitting parameters extracted from Table 4 and Table 5 to the 10 distinct approximate PVM equations (see Table 1), the full-range reconstruction of the I–V characteristic curve can be easily achieved. In this analysis, the 10 PVM equations were written in a .m file in MATLAB R2023b, and then subsequently compared with the reference datasheet curves.
The simulation results indicate that, except for the PC/PA05 PV panel, four PVM approximations—Padé approximant [91], Barry analytical expansion [82], two-parameter model [96], and Taylor’s series expansion [92] (see Figure 8 and Figure 9)—maintained a 1% absolute error threshold near the MPP for multi-crystalline PV panels, as summarized in Table 7 and Table 8. However, more traditional approximate PVM equations like fixed-point iteration [122], MATLAB (Haley’s) [78,79], Newton–Raphson [121], and the Wintzki approximation [84,123] exhibited low accuracy near the MPP, with more than double the specified threshold. While for the Trina Solar TSM-245 PC/PA05 PV panel the two-parameter model yielded accurate results, as described by Figure 10, other analytical-based PVM equations had low model accuracy at the MPP, with exceeding 8% for the Padé approximant [91], hybrid explicit expansion [80], and Taylor’s series expansion [92] (see Table 9).
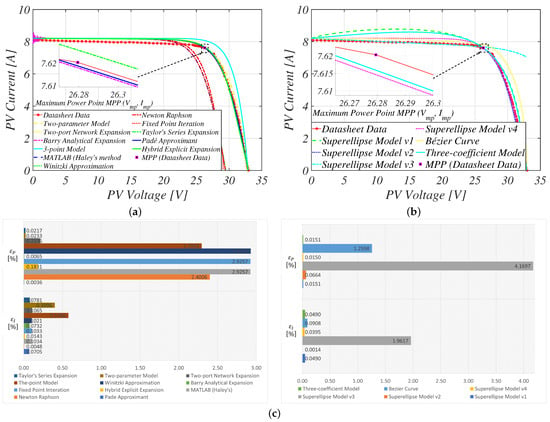
Figure 8.
Comparison of the reconstructed characteristic curves for the KC200GT PV panel: (a) approximate PV models (b) empirical-based PV models (c) accuracy evaluation at MPP.
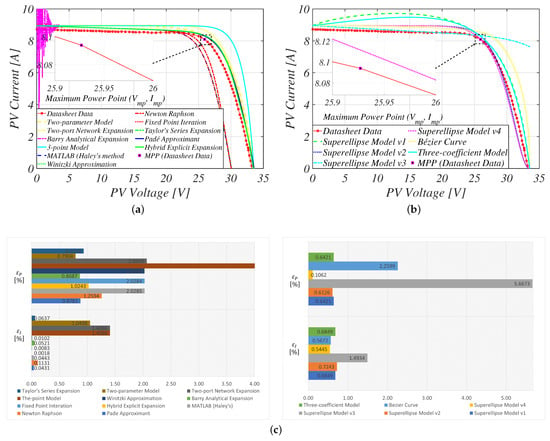
Figure 9.
Comparison of the reconstructed characteristic curves for the Alfa Solar Pyramid54-215 PV panel: (a) approximate PV models; (b) empirical-based PV models; (c) accuracy evaluation at MPP.

Table 7.
Comparison of 17 different PVM equations for KC200GT PV panel within the vicinity of MPP.

Table 8.
Comparison of 17 different PVM equations for Pyramid54-215 PV panel within the vicinity of MPP.
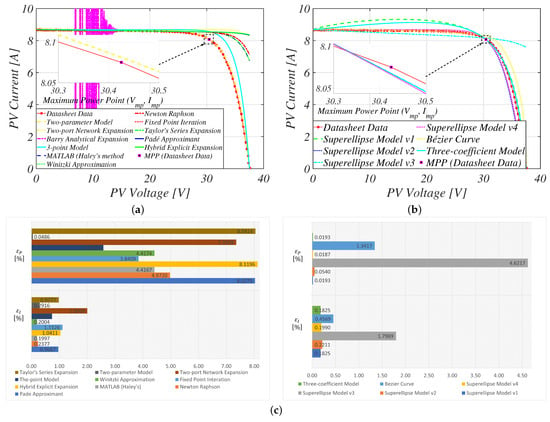
Figure 10.
Comparison of the reconstructed characteristic curves for the Trina Solar TSM-245 PC/PA05 PV panel: (a) approximate PV models; (b) empirical-based PV models; (c) accuracy evaluation at MPP.

Table 9.
Comparison of 17 different PVM equations for TSM-245 P/PA05 PV panel within the vicinity of MPP.
The accuracy of approximate PVM equations for monocrystalline PV panels remains high near the MPP (see Figure 11 and Figure 12), except for more traditional approximate PVM equations, as summarized in Table 10 and Table 11. As explained in Section 3, the accuracy of these approximate models depends on accurate parameter estimation in their initial domain model (i.e., single diode) before decoupling or parameterization.
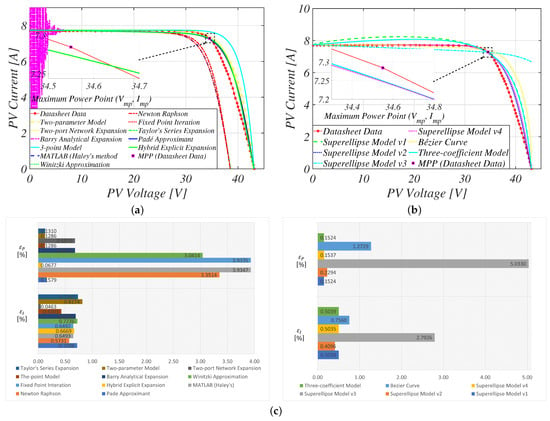
Figure 11.
Comparison of the reconstructed characteristic curves for the Sanyo HIT H250-E01 PV panel: (a) approximate PV models; (b) empirical-based PV models; (c) accuracy evaluation at MPP.
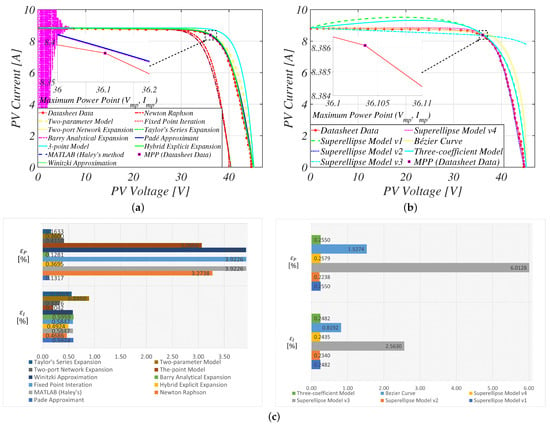
Figure 12.
Comparison of the reconstructed characteristic curves for the Canadian CS6X-300M PV panel: (a) approximate PV models; (b) empirical-based PV models; (c) accuracy evaluation at MPP.

Table 10.
Comparison of 17 different PVM equations for HIT H250-E01 PV panel within the vicinity of MPP.

Table 11.
Comparison of 17 different PVM equations for CS6X-300M PV panel within the vicinity of MPP.
With the rapid progress of the use of nanomaterials for PV panels, analyzing the model accuracy of this type of PV panel becomes important. Hence, the thin-film P-LE0055 PV panel is used. By reconstructing the I–V curve, we can determine the model’s accuracy (see Figure 13). Among the approximate PVM equations, Padé approximant [91], hybrid explicit expansion [80], two-parameter model [99,124], and Taylor’s series expansion [92] were highly accurate, meeting the stipulated maximum absolute errors as summarized in Table 12. However, the accuracy of the other approximate PVM equations was still relatively low. In particular, for the two-port network expansion [96] and three-point model [89,90] was extremely high.
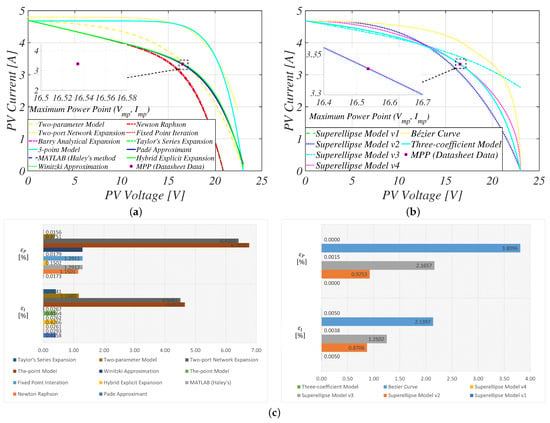
Figure 13.
Comparison of the reconstructed characteristic curves for the Kaneka P-LE0055 PV panel: (a) approximate PV models; (b) empirical-based PV models; (c) accuracy evaluation at MPP.

Table 12.
Comparison of 17 different PVM equations for P-LE0055 PV panel within the vicinity of MPP.
5.3.3. Comparison of the Empirical-Based Models
As detailed in Section 4, empirical-based PV models are mathematically explicit equations derived from the unique curve-fitting similarities with the I–V characteristic curve. By applying the fitting parameters extracted from the six PV panels, as outlined in Table 5, to their respective PVM equations, the full-range reconstructions of the I–V characteristic curve are obtained, as illustrated in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. Regardless of their specifications or cell materials, empirical-based PV models consistently achieve higher model accuracy within the vicinity of MPP, except for [118,119,120], as outlined in Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12. This higher accuracy is expected since these explicit equations are entirely independent of the physical meaning or representation of the nonlinear behavior describing the typical PV panel.
5.4. Research Trends
This review paper performs a comprehensive and in-depth analysis of some of the most widely used PV models in the literature, including circuit-based, analytical-based, and empirical-based models. Based on these analyses, the following conclusions and future research trends were noted:
- Equivalent-circuit-based PV models: For practitioners with prior experience in both the electrical behavior and conversion principles describing a PV panel, circuit-based models offer a more inclusive representation of the nonlinear characteristics of the I–V curve. However, to improve model accuracy, more research is needed to identify simple and effective techniques for accurately estimating the electrical parameters of PV panels.
- Analytical-based PV models: Since the explicit equations describing these PV models are derivatives from the conventional circuit-based model (single-diode), the model accuracy of the current approximate PVM equations in the literature is still dependent on the basic five electrical parameters. Nonetheless, the novelty and major contributions in this research will always lie in the relative simplification of the equation used for the reconstruction of the I–V curve.
- Empirical-based PV models: One of the main limitations of curve-fitting PV models is that they do not fully consider the specific characteristics of the PV panel. However, these models are very useful because they are relatively simple and easy to use for reconstructing the PV characteristic curve. While many equations could potentially generate a similar shape to the I–V curve, a hybrid model that combines the advantages of both circuit-based and empirical-based models would provide a better understanding of both the static and dynamic characteristics of the PV panel.
6. Conclusions
PV modeling is an essential tool employed by researchers and technicians in the field of sustainable energy for the effective performance evaluation of both the static and dynamic characteristics of typical PV panels. This review paper conducted a comprehensive analysis of the accuracy of the reconstructed I–V curves using various categories of PV models. The accuracy of each model was evaluated across different PV panels, including crystalline and thin-film, under the IEC EN 50530 standard.
While circuit-based models provide a more inclusive representation of the inherent nonlinear characteristics of PV panels, the accuracy of these models, specifically the double-diode and triple-diode models, heavily depends on the parameter extraction techniques and the initial conditions or assumptions made before computation. Despite the simplification of the explicit equation describing the approximate I–V curve, the accuracy of existing analytical-based PV models still depends on the accurate estimation of the electrical parameters of the single-diode model.
On the other hand, empirical-based PV models, which are curve-fitting derivatives of the graphical characteristics of the I–V curve and require fewer fitting parameters, achieve higher accuracy within the vicinity of the MPP. Additionally, this review paper provided insights into possible research trends in the field, including the suggestion of a hybrid model that combines the strengths of circuit-based and empirical-based PV models.
Author Contributions
Conceptualization, T.N.O., S.-H.H. and S.-J.C.; methodology, T.N.O.; validation, T.N.O.; investigation, T.N.O.; writing—original draft preparation, T.N.O.; writing—review and editing, T.N.O. and S.-J.C.; supervision, S.-J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Regional Innovation Strategy (RIS) through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (MOE) (2021RIS-003).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A. IEC EN 50530 Standard—Overall Efficiency of Grid Connected Photovoltaic Inverters
The accurate emulation of the nonlinear behavior of PV systems is crucial for testing and validating PV inverters. Central to this emulation is ensuring that a PV simulator’s current/voltage characteristics adhere to a predefined standard, ensuring reliable performance across diverse conditions. The IEC EN 50530 standard [46] establishes a criterion stipulating that for any reconstructed I–V characteristic curve, regardless of the PV panel’s specifications and cell material (see Table A1, “the current/voltage characteristic must not deviate by more than 1% in power within the voltage range of to concerning the predetermined characteristic at rated conditions”).

Table A1.
General requirements on the simulated I–V characteristic of the PV generator.
Table A1.
General requirements on the simulated I–V characteristic of the PV generator.
| cSi-Technology | Thin-Film Technology | Tolerance | |
|---|---|---|---|
| 0.95 | 0.98 | ||
| 0.8 | 0.72 | ||
| 0.9 | 0.8 |
References
- Nejat, P.; Jomehzadeh, F.; Taheri, M.M.; Gohari, M.; Majid, M.Z.A. A global review of energy consumption, CO2 emissions and policy in the residential sector (with an overview of the top ten CO2 emitting countries). Renew. Sustain. Energy Rev. 2015, 43, 843–862. [Google Scholar] [CrossRef]
- Metz, B.; Davidson, O.; De Coninck, H.; Loos, M.; Meyer, L. IPCC Special Report on Carbon Dioxide Capture and Storage; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Bouich, A.; Pradas, I.G.; Khan, M.A.; Khattak, Y.H. Opportunities, Challenges, and Future Prospects of the Solar Cell Market. Sustainability 2023, 15, 15445. [Google Scholar] [CrossRef]
- Afolayan, M.; Olayiwola, T.; Nurudeen, Q.; Ibrahim, O.; Madugu, I. Performance Evaluation of Soiling Mitigation Technique for Solar Panels. Arid. Zone J. Eng. Technol. Environ. 2020, 16, 685–698. [Google Scholar]
- Parida, B.; Iniyan, S.; Goic, R. A review of solar photovoltaic technologies. Renew. Sustain. Energy Rev. 2011, 15, 1625–1636. [Google Scholar] [CrossRef]
- Sampaio, P.G.V.; González, M.O.A. Photovoltaic solar energy: Conceptual framework. Renew. Sustain. Energy Rev. 2017, 74, 590–601. [Google Scholar] [CrossRef]
- Singh, G.K. Solar power generation by PV (photovoltaic) technology: A review. Energy 2013, 53, 1–13. [Google Scholar] [CrossRef]
- Lazaroiu, A.C.; Gmal Osman, M.; Strejoiu, C.V.; Lazaroiu, G. A Comprehensive Overview of Photovoltaic Technologies and Their Efficiency for Climate Neutrality. Sustainability 2023, 15, 16297. [Google Scholar] [CrossRef]
- Mahmood, A.; Irfan, A.; Wang, J.L. Molecular level understanding of the chalcogen atom effect on chalcogen-based polymers through electrostatic potential, non-covalent interactions, excited state behaviour, and radial distribution function. Polym. Chem. 2022, 13, 5993–6001. [Google Scholar] [CrossRef]
- Mahmood, A.; Hu, J.Y.; Xiao, B.; Tang, A.; Wang, X.; Zhou, E. Recent progress in porphyrin-based materials for organic solar cells. J. Mater. Chem. A 2018, 6, 16769–16797. [Google Scholar] [CrossRef]
- Mehboob, M.Y.; Hussain, R.; Adnan, M.; Irshad, Z.; Khalid, M. Impact of π-linker modifications on the photovoltaic performance of rainbow-shaped acceptor molecules for high performance organic solar cell applications. Phys. B Condens. Matter 2022, 625, 413465. [Google Scholar] [CrossRef]
- Khalid, M.; Murtaza, S.; Bano, M.; Shafiq, I.; Jawaria, R.; Ataulapa, A. Role of extended end-capped acceptors in non-fullerene based compounds towards photovoltaic properties. J. Photochem. Photobiol. A Chem. 2024, 448, 115292. [Google Scholar] [CrossRef]
- Tang, J.; Ni, H.; Peng, R.L.; Wang, N.; Zuo, L. A review on energy conversion using hybrid photovoltaic and thermoelectric systems. J. Power Sources 2023, 562, 232785. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory Interactive Best Research-Cell Efficiency Chart. 2023. Available online: https://www.nrel.gov/pv/interactive-cell-efficiency.html (accessed on 13 December 2023).
- Schultz, O.; Preu, R.; Glunz, S. Silicon solar cells with screenprinted front side metallization exceeding 19% efficiency. In Proceedings of the 22nd European Photovoltaic Solar Energy Conference and Exhibition, Milan, Italy, 3–7 September 2007; Volume 3, p. 7. [Google Scholar]
- Richter, A.; Hermle, M.; Glunz, S.W. Reassessment of the limiting efficiency for crystalline silicon solar cells. IEEE J. Photovoltaics 2013, 3, 1184–1191. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Kawasaki, H.; Yoshida, W.; Irie, T.; Konishi, K.; Nakano, K.; Uto, T.; Adachi, D.; Kanematsu, M.; Uzu, H.; et al. Silicon heterojunction solar cell with interdigitated back contacts for a photoconversion efficiency over 26%. Nat. Energy 2017, 2, 17032. [Google Scholar] [CrossRef]
- Gobichettipalayam Shanmugam, S.K.; Sakthivel, T.S.; Gaftar, B.A.; Iyyappan, P.; Sathyamurthy, R. Modeling and simulation of single-and double-diode PV solar cell model for renewable energy power solution. Environ. Sci. Pollut. Res. 2022, 29, 4414–4430. [Google Scholar] [CrossRef] [PubMed]
- Hernández-López, D.; Oña, E.R.d.; Moreno, M.A.; González-Aguilera, D. SunMap: Towards Unattended Maintenance of Photovoltaic Plants Using Drone Photogrammetry. Drones 2023, 7, 129. [Google Scholar] [CrossRef]
- Nayak, J.; Thalla, H.; Ghosh, A. Efficient maximum power point tracking algorithms for photovoltaic systems with reduced number of sensors. Process. Integr. Optim. Sustain. 2022, 7, 191–213. [Google Scholar] [CrossRef]
- Eiffert, P. Building-Integrated Photovoltaic Designs for Commercial and Institutional Structures: A Sourcebook for Architects; DIANE Publishing: Collingdale, PA, USA, 2000. [Google Scholar]
- Bader, S.; Ma, X.; Oelmann, B. One-diode photovoltaic model parameters at indoor illumination levels—A comparison. Sol. Energy 2019, 180, 707–716. [Google Scholar] [CrossRef]
- Pranith, S.; Bhatti, T. Modeling and parameter extraction methods of PV modules. In Proceedings of the 2015 International Conference on Recent Developments in Control, Automation and Power Engineering (RDCAPE), Noida, India, 12–13 March 2015; pp. 72–76. [Google Scholar]
- Vinod; Kumar, R.; Singh, S.K. Solar photovoltaic modeling and simulation: As a renewable energy solution. Energy Rep. 2018, 4, 701–712. [Google Scholar] [CrossRef]
- Pendem, S.R.; Mikkili, S. Modeling, simulation and performance analysis of solar PV array configurations (Series, Series–Parallel and Honey-Comb) to extract maximum power under Partial Shading Conditions. Energy Rep. 2018, 4, 274–287. [Google Scholar] [CrossRef]
- Pongratananukul, N.; Kasparis, T. Tool for automated simulation of solar arrays using general-purpose simulators. In Proceedings of the 2004 IEEE Workshop on Computers in Power Electronics, Urbana, IL, USA, 15–18 August 2004; pp. 10–14. [Google Scholar]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Jena, D.; Ramana, V.V. Modeling of photovoltaic system for uniform and non-uniform irradiance: A critical review. Renew. Sustain. Energy Rev. 2015, 52, 400–417. [Google Scholar] [CrossRef]
- Lei, W.; He, Q.; Yang, L.; Jiao, H. Solar photovoltaic cell parameter identification based on improved honey badger algorithm. Sustainability 2022, 14, 8897. [Google Scholar] [CrossRef]
- Ellithy, H.H.; Taha, A.M.; Hasanien, H.M.; Attia, M.A.; El-Shahat, A.; Aleem, S.H. Estimation of parameters of triple diode photovoltaic models using hybrid particle swarm and Grey wolf optimization. Sustainability 2022, 14, 9046. [Google Scholar] [CrossRef]
- Yuan, S.; Ji, Y.; Chen, Y.; Liu, X.; Zhang, W. An Improved Differential Evolution for Parameter Identification of Photovoltaic Models. Sustainability 2023, 15, 13916. [Google Scholar] [CrossRef]
- Aribia, H.B.; El-Rifaie, A.M.; Tolba, M.A.; Shaheen, A.; Moustafa, G.; Elsayed, F.; Elshahed, M. Growth Optimizer for Parameter Identification of Solar Photovoltaic Cells and Modules. Sustainability 2023, 15, 7896. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Gu, Q. A comprehensive survey on meta-heuristic algorithms for parameter extraction of photovoltaic models. Renew. Sustain. Energy Rev. 2021, 141, 110828. [Google Scholar] [CrossRef]
- Ridha, H.M.; Hizam, H.; Mirjalili, S.; Othman, M.L.; Ya’acob, M.E.; Ahmadipour, M. Parameter extraction of single, double, and three diodes photovoltaic model based on guaranteed convergence arithmetic optimization algorithm and modified third order Newton Raphson methods. Renew. Sustain. Energy Rev. 2022, 162, 112436. [Google Scholar] [CrossRef]
- Gu, Z.; Xiong, G.; Fu, X. Parameter Extraction of Solar Photovoltaic Cell and Module Models with Metaheuristic Algorithms: A Review. Sustainability 2023, 15, 3312. [Google Scholar] [CrossRef]
- Satria, H.; Syah, R.B.; Nehdi, M.L.; Almustafa, M.K.; Adam, A.O.I. Parameters Identification of Solar PV Using Hybrid Chaotic Northern Goshawk and Pattern Search. Sustainability 2023, 15, 5027. [Google Scholar] [CrossRef]
- Vais, R.I.; Sahay, K.; Chiranjeevi, T.; Devarapalli, R.; Knypiński, Ł. Parameter Extraction of Solar Photovoltaic Modules Using a Novel Bio-Inspired Swarm Intelligence Optimisation Algorithm. Sustainability 2023, 15, 8407. [Google Scholar] [CrossRef]
- Ginidi, A.; Ghoneim, S.M.; Elsayed, A.; El-Sehiemy, R.; Shaheen, A.; El-Fergany, A. Gorilla troops optimizer for electrically based single and double-diode models of solar photovoltaic systems. Sustainability 2021, 13, 9459. [Google Scholar] [CrossRef]
- Ali, H.H.; Ebeed, M.; Fathy, A.; Jurado, F.; Babu, T.S.; Mahmoud, A.A. A New Hybrid Multi-Population GTO-BWO Approach for Parameter Estimation of Photovoltaic Cells and Modules. Sustainability 2023, 15, 11089. [Google Scholar] [CrossRef]
- Rezk, H.; Olabi, A.; Wilberforce, T.; Sayed, E.T. A Comprehensive Review and Application of Metaheuristics in Solving the Optimal Parameter Identification Problems. Sustainability 2023, 15, 5732. [Google Scholar] [CrossRef]
- Olayiwola, T.N.; Choi, S.J. Superellipse model: An accurate and easy-to-fit empirical model for photovoltaic panels. Sol. Energy 2023, 262, 111749. [Google Scholar] [CrossRef]
- Olayiwola, T.N.; Choi, S.J. Fast IV Curve Approximation Technique for Photovoltaic Panels using Superellipse. In Proceedings of the KIPE Power Electronics Conference, Jeju, Republic of Korea, 5–7 May 2022; p. 7. [Google Scholar]
- Olayiwola, T.N.; Choi, S.J. Effective Approximation of the Photovoltaic Characteristic Curves using a Double-shaped Superellipse. In Proceedings of the 2023 11th International Conference on Power Electronics and ECCE Asia (ICPE 2023-ECCE Asia), Jeju, Republic of Korea, 22–25 May 2023; pp. 2443–2448. [Google Scholar]
- Louzazni, M.; Al-Dahidi, S. Approximation of photovoltaic characteristics curves using Bézier Curve. Renew. Energy 2021, 174, 715–732. [Google Scholar] [CrossRef]
- Olayiwola, T.N.; Choi, S.J. Long-term Aging Pattern Characterization for Photovoltaic Panels using the Superellipse Model. In Proceedings of the KIPE Power Electronics Conference, Jeju, Republic of Korea, 22–25 May 2023; p. 12. [Google Scholar]
- IEC 50530; Overall Efficiency of Grid Connected Photovoltaic Inverters. International Electrotechnical Commission: Geneva, Switzerland, 2008.
- Castaner, L.; Silvestre, S. Modelling Photovoltaic Systems Using PSpice; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Lindholm, F.A.; Fossum, J.G.; Burgess, E.L. Application of the superposition principle to solar-cell analysis. IEEE Trans. Electron Devices 1979, 26, 165–171. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Power Electronics and Control Techniques for Maximum Energy Harvesting in Photovoltaic Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Suntio, T.; Messo, T.; Puukko, J. Power Electronic Converters: Dynamics and Control in Conventional and Renewable Energy Applications; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Luque, A.; Hegedus, S. Handbook of Photovoltaic Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Messenger, R.A.; Abtahi, A. Photovoltaic Systems Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Ćalasan, M.; Aleem, S.H.A.; Zobaa, A.F. A new approach for parameters estimation of double and triple diode models of photovoltaic cells based on iterative Lambert W function. Sol. Energy 2021, 218, 392–412. [Google Scholar] [CrossRef]
- Bana, S.; Saini, R. A mathematical modeling framework to evaluate the performance of single diode and double diode based SPV systems. Energy Rep. 2016, 2, 171–187. [Google Scholar] [CrossRef]
- Nishioka, K.; Sakitani, N.; Uraoka, Y.; Fuyuki, T. Analysis of multicrystalline silicon solar cells by modified 3-diode equivalent circuit model taking leakage current through periphery into consideration. Sol. Energy Mater. Sol. Cells 2007, 91, 1222–1227. [Google Scholar] [CrossRef]
- Kraiem, H.; Touti, E.; Alanazi, A.; Agwa, A.M.; Alanazi, T.I.; Jamli, M.; Sbita, L. Parameters identification of photovoltaic cell and module models using modified social group optimization algorithm. Sustainability 2023, 15, 10510. [Google Scholar] [CrossRef]
- Steingrube, S.; Breitenstein, O.; Ramspeck, K.; Glunz, S.; Schenk, A.; Altermatt, P.P. Explanation of commonly observed shunt currents in c-Si solar cells by means of recombination statistics beyond the Shockley-Read-Hall approximation. J. Appl. Phys. 2011, 110, 014515. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Alsaidan, I.; Abdelaziz, A.Y.; Muyeen, S. Parameter estimation of three diode photovoltaic model using grasshopper optimization algorithm. Energies 2020, 13, 497. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; El-Fergany, A.; Elsayed, A.M. Optimal parameters extraction of photovoltaic triple diode model using an enhanced artificial gorilla troops optimizer. Energy 2023, 283, 129034. [Google Scholar] [CrossRef]
- Allam, D.; Yousri, D.; Eteiba, M. Parameters extraction of the three diode model for the multi-crystalline solar cell/module using Moth-Flame Optimization Algorithm. Energy Convers. Manag. 2016, 123, 535–548. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M.; Duck, B.C.; Nadarajah, M. An improved wind driven optimization algorithm for parameters identification of a triple-diode photovoltaic cell model. Energy Convers. Manag. 2020, 213, 112872. [Google Scholar] [CrossRef]
- Tsai, H.L. Insolation-oriented model of photovoltaic module using Matlab/Simulink. Sol. Energy 2010, 84, 1318–1326. [Google Scholar] [CrossRef]
- Saloux, E.; Teyssedou, A.; Sorin, M. Explicit model of photovoltaic panels to determine voltages and currents at the maximum power point. Sol. Energy 2011, 85, 713–722. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H. Simple, fast and accurate two-diode model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2011, 95, 586–594. [Google Scholar] [CrossRef]
- Sheriff, M.; Babagana, B.; Maina, B. A study of silicon solar cells and modules using PSPICE. World J. Appl. Sci. Technol. 2011, 3, 124–130. [Google Scholar]
- Nema, R.; Nema, S.; Agnihotri, G. Computer simulation based study of photovoltaic cells/modules and their experimental verification. Int. J. Recent Trends Eng. 2009, 1, 151–156. [Google Scholar]
- Ishaque, K.; Salam, Z.; Taheri, H.; Syafaruddin. Modeling and simulation of photovoltaic (PV) system during partial shading based on a two-diode model. Simul. Model. Pract. Theory 2011, 19, 1613–1626. [Google Scholar] [CrossRef]
- Patel, H.; Agarwal, V. MATLAB-based modeling to study the effects of partial shading on PV array characteristics. IEEE Trans. Energy Convers. 2008, 23, 302–310. [Google Scholar] [CrossRef]
- Khanna, V.; Das, B.; Bisht, D.; Singh, P. A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew. Energy 2015, 78, 105–113. [Google Scholar] [CrossRef]
- Batzelis, E. Non-iterative methods for the extraction of the single-diode model parameters of photovoltaic modules: A review and comparative assessment. Energies 2019, 12, 358. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Salvini, A. Identification of the one-diode model for photovoltaic modules from datasheet values. Sol. Energy 2014, 108, 432–446. [Google Scholar] [CrossRef]
- Laudani, A.; Mancilla-David, F.; Riganti-Fulginei, F.; Salvini, A. Reduced-form of the photovoltaic five-parameter model for efficient computation of parameters. Sol. Energy 2013, 97, 122–127. [Google Scholar] [CrossRef]
- ALQahtani, A.H. A simplified and accurate photovoltaic module parameters extraction approach using matlab. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Helsinki, Finland, 19–21 June 2012; pp. 1748–1753. [Google Scholar]
- Lineykin, S.; Averbukh, M.; Kuperman, A. An improved approach to extract the single-diode equivalent circuit parameters of a photovoltaic cell/panel. Renew. Sustain. Energy Rev. 2014, 30, 282–289. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Ruppert Filho, E. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Batzelis, E.I.; Anagnostou, G.; Chakraborty, C.; Pal, B.C. Computation of the Lambert W function in photovoltaic modeling. In ELECTRIMACS 2019: Selected Papers; Springer: Berlin/Heidelberg, Germany, 2020; Volume 1, pp. 583–595. [Google Scholar]
- Weisstein, E.W. Lambert W-Function. 2002. Available online: https://mathworld.wolfram.com/LambertW-Function.html (accessed on 12 May 2022).
- Moler, C. Cleve’s Corner: Cleve Moler on Mathematics and Computing. The Lambert W Function. 2013. Available online: https://blogs.mathworks.com/cleve/2013/09/02/the-lambert-w-function/ (accessed on 15 May 2022).
- Batzelis, E.I.; Routsolias, I.A.; Papathanassiou, S.A. An explicit PV string model based on the lambert W function and simplified MPP expressions for operation under partial shading. IEEE Trans. Sustain. Energy 2013, 5, 301–312. [Google Scholar] [CrossRef]
- Corless, R.M.; Jeffrey, D.J.; Knuth, D.E. A sequence of series for the Lambert W function. In Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation, Vancouver, BC, Canada, 28–31 July 1997; pp. 197–204. [Google Scholar]
- Moshksar, E.; Ghanbari, T. A model-based algorithm for maximum power point tracking of PV systems using exact analytical solution of single-diode equivalent model. Sol. Energy 2018, 162, 117–131. [Google Scholar] [CrossRef]
- Barry, D.; Parlange, J.Y.; Li, L.; Prommer, H.; Cunningham, C.; Stagnitti, F. Analytical approximations for real values of the Lambert W-function. Math. Comput. Simul. 2000, 53, 95–103. [Google Scholar] [CrossRef]
- Batzelis, E.I.; Papathanassiou, S.A. A method for the analytical extraction of the single-diode PV model parameters. IEEE Trans. Sustain. Energy 2015, 7, 504–512. [Google Scholar] [CrossRef]
- Borsch-Supan, W. On the Evaluation of the Function. J. Res. NBS 1961, 65. Available online: https://nvlpubs.nist.gov/nistpubs/jres/65B/jresv65Bn4p245_A1b.pdf (accessed on 10 December 2022).
- Jain, A.; Kapoor, A. Exact analytical solutions of the parameters of real solar cells using Lambert W-function. Sol. Energy Mater. Sol. Cells 2004, 81, 269–277. [Google Scholar] [CrossRef]
- Ridha, H.M. Parameters extraction of single and double diodes photovoltaic models using Marine Predators Algorithm and Lambert W function. Sol. Energy 2020, 209, 674–693. [Google Scholar] [CrossRef]
- Elyaqouti, M.; Arjdal, E.; Ibrahim, A.; Abdul-Ghaffar, H.; Aboelsaud, R.; Obukhov, S.; Diab, A.A.Z. Parameters identification and optimization of photovoltaic panels under real conditions using Lambert W-function. Energy Rep. 2021, 7, 9035–9045. [Google Scholar]
- Mehta, H.K.; Panchal, A.K. PV Panel Performance Evaluation via Accurate V–I Polynomial with Efficient Computation. IEEE J. Photovoltaics 2021, 11, 1519–1527. [Google Scholar] [CrossRef]
- Ishibashi, K.i.; Kimura, Y.; Niwano, M. An extensively valid and stable method for derivation of all parameters of a solar cell from a single current-voltage characteristic. J. Appl. Phys. 2008, 103, 094507. [Google Scholar] [CrossRef]
- Lun, S.X.; Du, C.J.; Yang, G.H.; Wang, S.; Guo, T.T.; Sang, J.S.; Li, J.P. An explicit approximate I–V characteristic model of a solar cell based on padé approximants. Sol. Energy 2013, 92, 147–159. [Google Scholar] [CrossRef]
- Lun, S.X.; Du, C.J.; Guo, T.T.; Wang, S.; Sang, J.S.; Li, J.P. A new explicit I–V model of a solar cell based on Taylor’s series expansion. Sol. Energy 2013, 94, 221–232. [Google Scholar] [CrossRef]
- Wang, X.; Zhuo, F.; Li, J.; Wang, L.; Ni, S. Modeling and Control of Dual-Stage High-Power Multifunctional PV System in d-Q-o Coordinate. IEEE Trans. Ind. Electron. 2012, 60, 1556–1570. [Google Scholar] [CrossRef]
- Das, A.K. An explicit J–V model of a solar cell using equivalent rational function form for simple estimation of maximum power point voltage. Sol. Energy 2013, 98, 400–403. [Google Scholar] [CrossRef]
- Fan, S. A new extracting formula and a new distinguishing means on the one variable cubic equation. Nat. Sci. J. Hainan Teach. Coll. 1989, 2, 91. [Google Scholar]
- Mathew, L.E.; Panchal, A.K. An exact and explicit PV panel curve computation assisted by two 2-port networks. Sol. Energy 2022, 240, 280–289. [Google Scholar] [CrossRef]
- Josephs, R. Solar Cell Array Design Handbook; NASA: Washington, DC, USA, 1976.
- Xiao, W.; Dunford, W.G.; Capel, A. A novel modeling method for photovoltaic cells. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; Volume 3, pp. 1950–1956. [Google Scholar]
- Bellini, A.; Bifaretti, S.; Iacovone, V.; Cornaro, C. Simplified model of a photovoltaic module. In Proceedings of the 2009 Applied Electronics: International Conference, Pilsen, Czech Republic, 9–10 September 2009; pp. 47–51. [Google Scholar]
- Tayyan, A.A. A simple method to extract the parameters of the single-diode model of a PV system. Turk. J. Phys. 2013, 37, 121–131. [Google Scholar] [CrossRef]
- Akbaba, M.; Alattawi, M.A. A new model for I–V characteristic of solar cell generators and its applications. Sol. Energy Mater. Sol. Cells 1995, 37, 123–132. [Google Scholar] [CrossRef]
- Mortenson, M.E. Mathematics for Computer Graphics Applications; Industrial Press Inc.: New York, NY, USA, 1999. [Google Scholar]
- Ueda, E.K.; Sato, A.K.; Martins, T.; Takimoto, R.Y.; Rosso, R.S.U.; Tsuzuki, M. Curve approximation by adaptive neighborhood simulated annealing and piecewise Bézier curves. Soft Comput. 2020, 24, 18821–18839. [Google Scholar] [CrossRef]
- Aihua, M.; Jie, L.; Jun, C.; Guiqing, L. A new fast normal-based interpolating subdivision scheme by cubic Bézier curves. Visual Comput. 2016, 32, 1085–1095. [Google Scholar] [CrossRef]
- Al-kufi, M.A.H.J.; Kadhim, O.N.; Razaq, E.S. Simulate a first-order Bézier curve in image encoding. J. Phys. Conf. Ser. 2020, 1530, 012080. [Google Scholar] [CrossRef]
- Szabo, R.; Gontean, A. Photovoltaic cell and module IV characteristic approximation using Bézier curves. Appl. Sci. 2018, 8, 655. [Google Scholar] [CrossRef]
- Shi, N.; Lv, Y.; Zhang, Y.; Zhu, X. Linear fitting Rule of I–V characteristics of thin-film cells based on Bezier function. Energy 2023, 278, 127997. [Google Scholar] [CrossRef]
- Delgado, J.; Peña, J. Geometric properties and algorithms for rational q-Bézier curves and surfaces. Mathematics 2020, 8, 541. [Google Scholar] [CrossRef]
- Gielis, J. A generic geometric transformation that unifies a wide range of natural and abstract shapes. Am. J. Bot. 2003, 90, 333–338. [Google Scholar] [CrossRef]
- Gardner, M. Mathematical Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American; American Mathematical Society: Providence, RL, USA, 1977. [Google Scholar]
- Das, A.K. Analytical derivation of explicit J–V model of a solar cell from physics based implicit model. Sol. Energy 2012, 86, 26–30. [Google Scholar] [CrossRef]
- Das, A.K. Analytical derivation of equivalent functional form of explicit J–V model of an illuminated solar cell from physics based implicit model. Sol. Energy 2014, 103, 411–416. [Google Scholar] [CrossRef]
- Das, A.K. An explicit J–V model of a solar cell for simple fill factor calculation. Sol. Energy 2011, 85, 1906–1909. [Google Scholar] [CrossRef]
- Saetre, T.O.; Midtgård, O.M.; Yordanov, G.H. A new analytical solar cell I–V curve model. Renew. Energy 2011, 36, 2171–2176. [Google Scholar] [CrossRef]
- Petković, M.S.; Neta, B.; Petković, L.D.; Džunić, J. Multipoint methods for solving nonlinear equations: A survey. Appl. Math. Comput. 2014, 226, 635–660. [Google Scholar] [CrossRef]
- Arora, R.K. Optimization: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Şentürk, A. New method for computing single diode model parameters of photovoltaic modules. Renew. Energy 2018, 128, 30–36. [Google Scholar] [CrossRef]
- Karmalkar, S.; Haneefa, S. A physically based explicit J–V model of a solar cell for simple design calculations. IEEE Electron Device Lett. 2008, 29, 449–451. [Google Scholar] [CrossRef]
- Saleem, H.; Karmalkar, S. An analytical method to extract the physical parameters of a solar cell from four points on the illuminated J –V curve. IEEE Electron Device Lett. 2009, 30, 349–352. [Google Scholar] [CrossRef]
- Dash, D.; Roshan, R.; Mahata, S.; Mallik, S.; Mahato, S.; Sarkar, S. A compact JV model for solar cell to simplify parameter calculation. J. Renew. Sustain. Energy 2015, 7, 013127. [Google Scholar] [CrossRef]
- Uoya, M.; Koizumi, H. A calculation method of photovoltaic array’s operating point for MPPT evaluation based on one-dimensional Newton–Raphson method. IEEE Trans. Ind. Appl. 2014, 51, 567–575. [Google Scholar] [CrossRef]
- Rivera, E.I.O.; Peng, F.Z. Algorithms to estimate the temperature and effective irradiance level over a photovoltaic module using the fixed point theorem. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006; pp. 1–4. [Google Scholar]
- Winitzki, S. Uniform approximations for transcendental functions. In Proceedings of the Computational Science and Its Applications—ICCSA 2003: International Conference, Montreal, QC, Canada, 18–21 May 2003; Proceedings, Part I. pp. 780–789. [Google Scholar]
- Jenkal, S.; Kourchi, M.; Yousfi, D.; Benlarabi, A.; Elhafyani, M.L.; Ajaamoum, M.; Oubella, M. Development of a photovoltaic characteristics generator based on mathematical models for four PV panel technologies. Int. J. Electr. Comput. Eng. (IJECE) 2020, 10, 6101–6110. [Google Scholar] [CrossRef]
- Weisstein, E.W. Absolute Error. 2017. Available online: http://mathworld.wolfram.com/AbsoluteError.html (accessed on 14 December 2023).
- Apostol, T.M. One-Variable Calculus, with an Introduction to Linear Algebra; Wiley: Hoboken, NJ, USA, 1967. [Google Scholar]
- Park, J.Y.; Choi, S.J. A novel simulation model for PV panels based on datasheet parameter tuning. Sol. Energy 2017, 145, 90–98. [Google Scholar] [CrossRef]
- Park, J.Y.; Choi, S.J. A novel datasheet-based parameter extraction method for a single-diode photovoltaic array model. Sol. Energy 2015, 122, 1235–1244. [Google Scholar] [CrossRef]
- Wellawatta, T.R.; Choi, S.J. Small-signal stability analysis with approximated PV model for solar array simulator. IEEE Trans. Power Electron. 2022, 38, 1190–1203. [Google Scholar] [CrossRef]
- Johnson, S.G. Notes on the Convergence of Trapezoidal-Rule Quadrature. 2010. Available online: https://math.mit.edu/~stevenj/trapezoidal.pdf (accessed on 14 December 2023).
- Mysovskikh, I. Trapzium formula. In Encyclopedia of Mathematics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).