Controlling Industrial Air-Pollutant Emissions under Multi-Factor Interactions Based on a Developed Hybrid-Factorial Environmental Input–Output Model
Abstract
1. Introduction
1.1. Importance and Motivation
1.2. Literature Review
1.3. Objective and Contribution
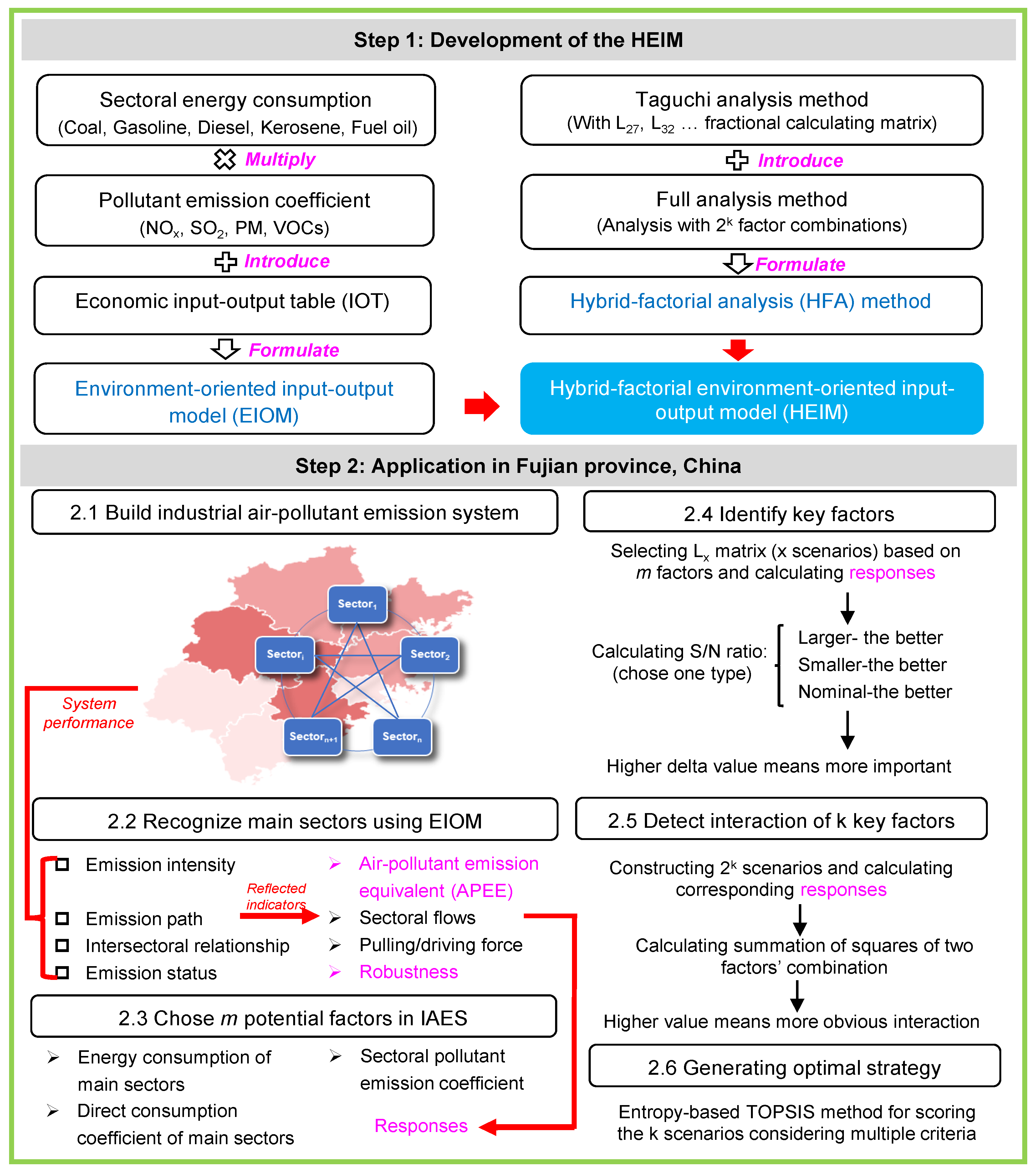
2. Methodology
2.1. Environmental Input–Output Model
2.2. Hybrid-Factorial Analysis
2.2.1. Taguchi Analysis
- (1)
- Larger the better (i.e., selected when the target maximizes the response).
- (2)
- Smaller the better (i.e., selected when the target minimizes the response).
- (3)
- Nominal the better (i.e., selected when the target is the response itself and the S/N ratio is based on the standard deviation only).where Yi is the response value of the ith computation; n is the number of computations; Y0 is the mean of all response values.
2.2.2. Full Factorial Analysis
3. Case Study
3.1. Statement of Problem
3.2. Data Collection
3.3. Scenario Design
4. Result and Discussion
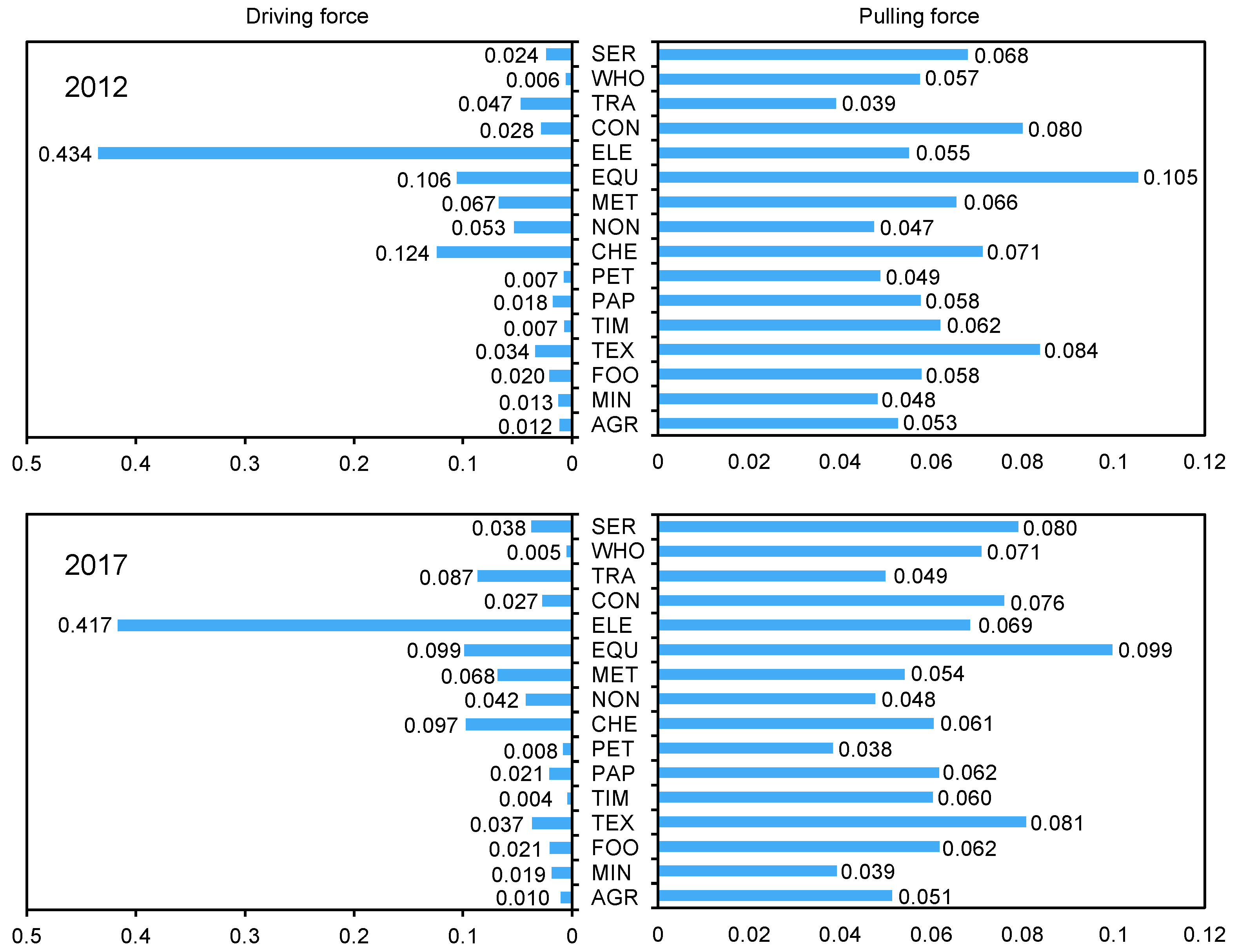
4.1. Air Pollutant Emissions
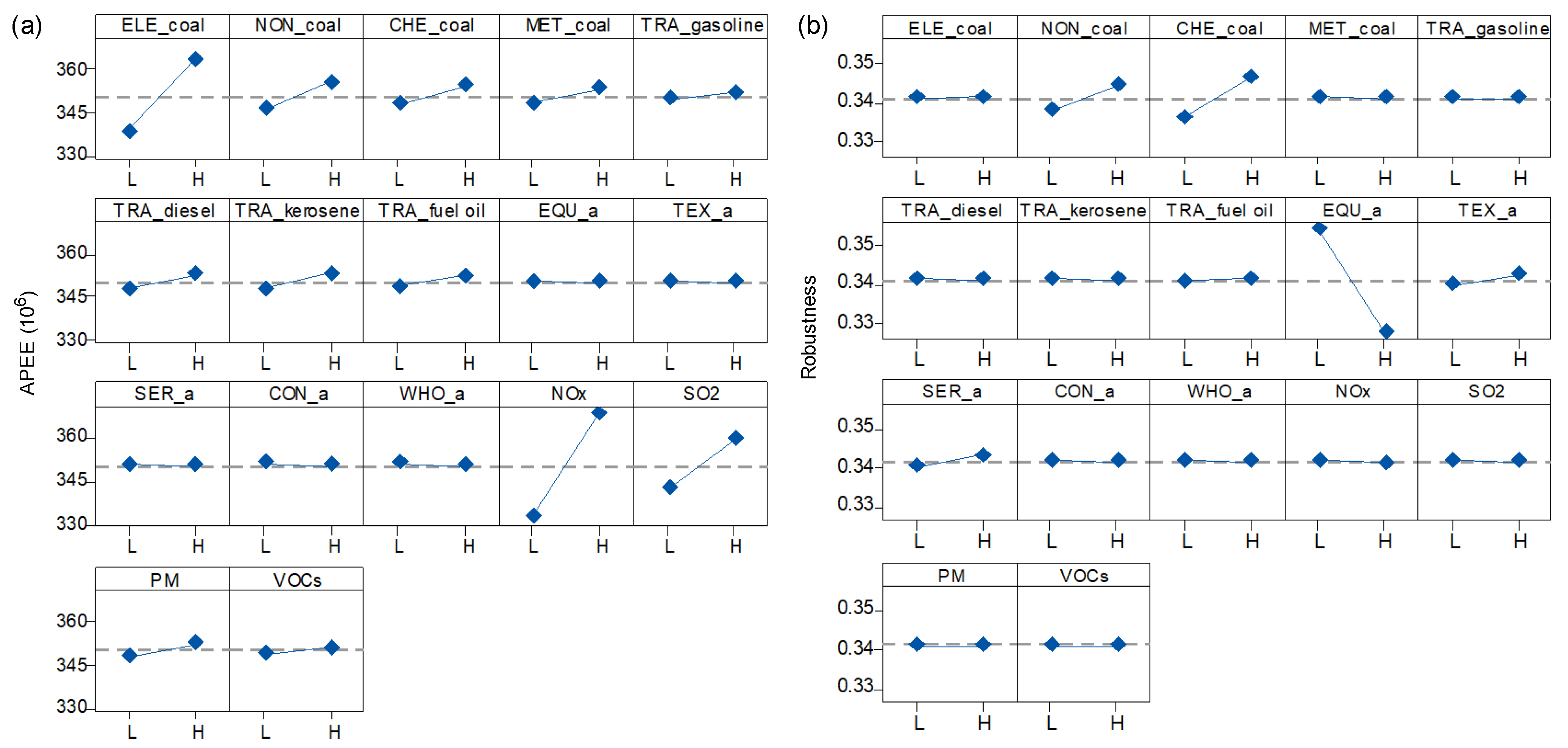
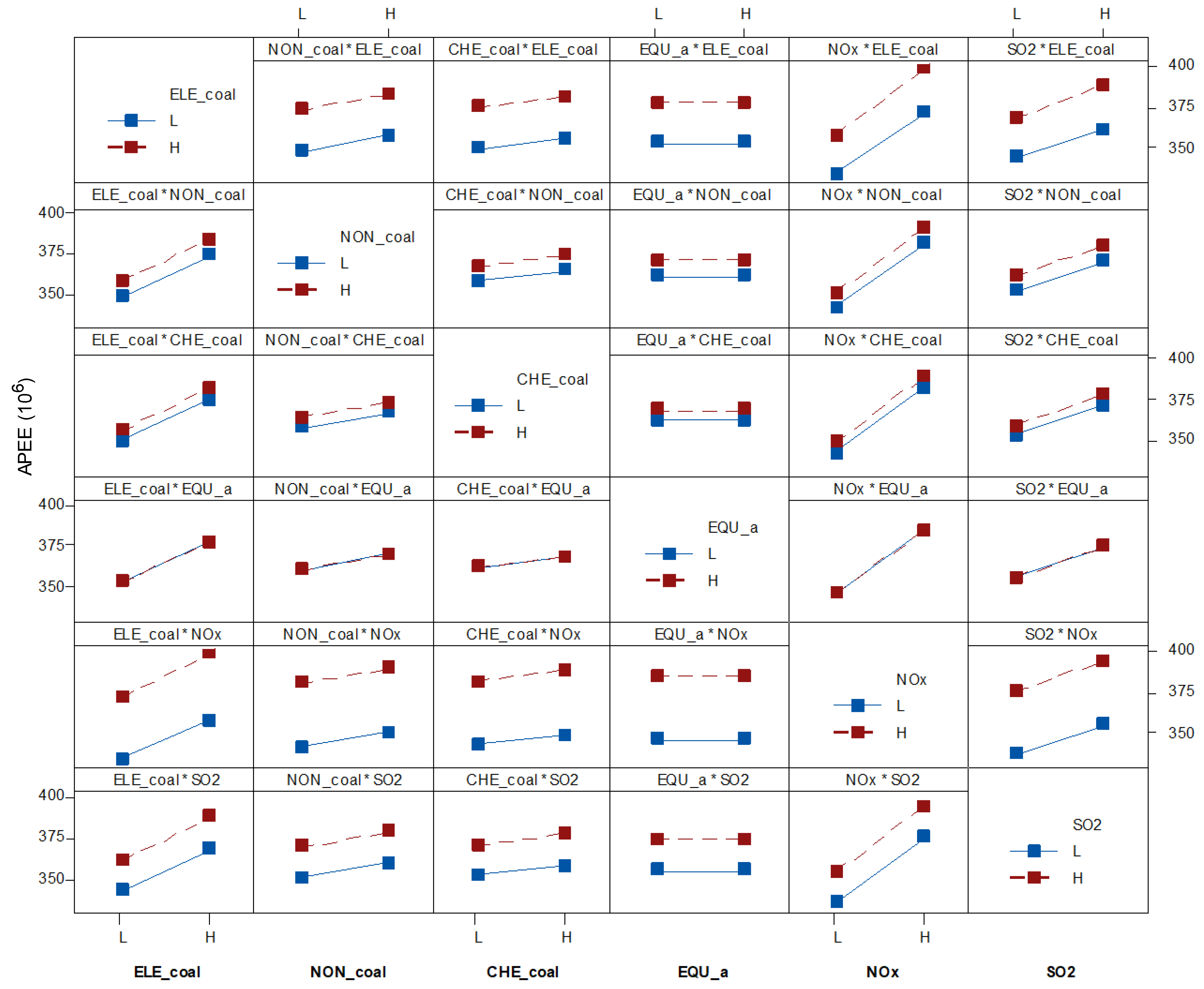
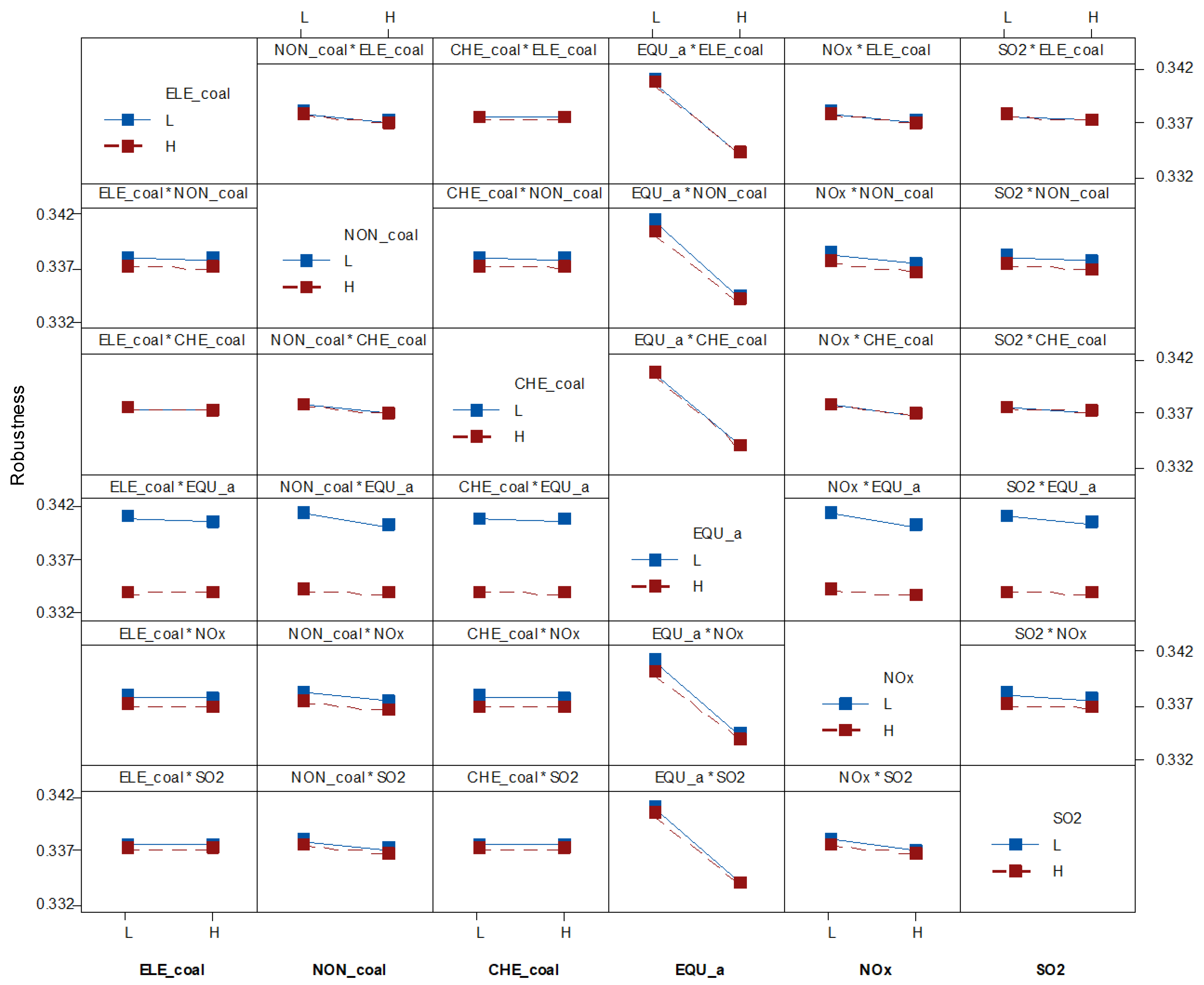
4.2. Identification of Key Factors
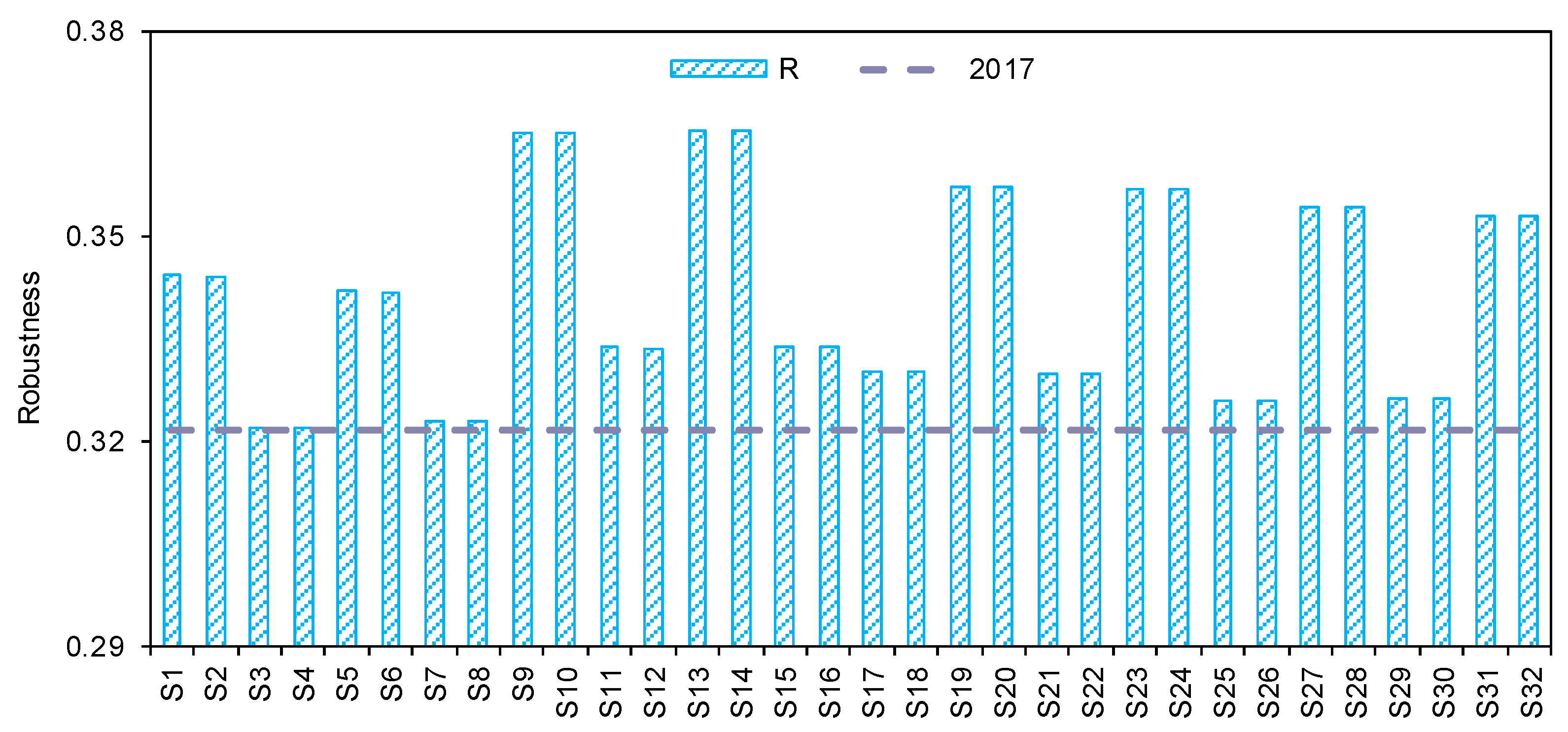
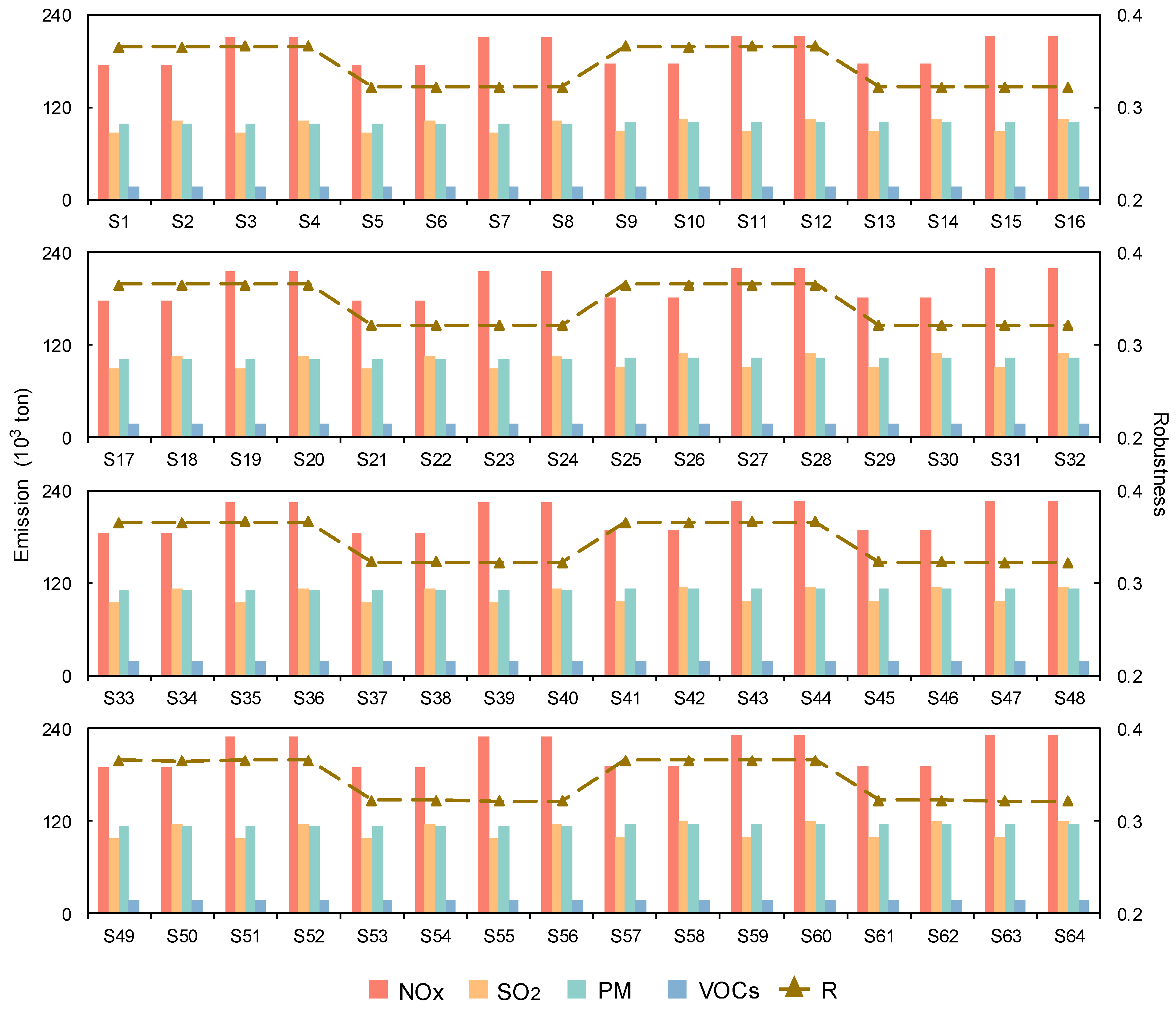
4.3. Determination of Optimal Strategies
4.4. Policy Implication
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, G.; Jia, Y.; Su, B.; Xiu, J. Environmental regulation, economic development and air pollution in the cities of China: Spatial econometric analysis based on policy scoring and satellite data. J. Clean. Prod. 2021, 328, 129496. [Google Scholar] [CrossRef]
- National Bureau of Statistics. China Statistics Yearbook; China Statistics Press: Beijing, China, 2016.
- Li, X.; Li, Y. A multi-scenario ensemble simulation and environmental input-output model for identifying optimal pollutant- and CO2-emission mitigation scheme of Guangdong province. J. Clean. Prod. 2020, 262, 121413. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, S.; Xing, J.; Wang, Y.; Chen, W.; Ding, D.; Wu, Y.; Wang, S.; Duan, L.; Hao, J. Progress of Air Pollution Control in China and Its Challenges and Opportunities in the Ecological Civilization Era. Engineering 2020, 6, 1423–1431. [Google Scholar] [CrossRef]
- Health Effects Institute. Global Burden of Disease-Major Air Pollution Sources—A Global Approach. 2018. Available online: https://www.healtheffects.org/research/ (accessed on 30 October 2021).
- Zhou, L.; Tang, L. Environmental regulation and the growth of the total-factor carbon productivity of China’s industries: Evidence from the implementation of action plan of air pollution prevention and control. J. Environ. Manag. 2021, 296, 113078. [Google Scholar] [CrossRef] [PubMed]
- Perera, F.; Ashrafi, A.; Kinney, P.; Mills, D. Towards a fuller assessment of benefits to children’s health of reducing air pollution and mitigating climate change due to fossil fuel combustion. Environ. Res. 2018, 172, 55–72. [Google Scholar] [CrossRef]
- Zaidi, S.A.H.; Zafar, M.W.; Shahbaz, M.; Hou, F. Dynamic linkages between globalization, financial development and carbon emissions: Evidence from Asia Pacific Economic Cooperation countries. J. Clean. Prod. 2019, 228, 533–543. [Google Scholar] [CrossRef]
- Guan, Y.; Huang, G.; Liu, L.; Zhai, M.; Xu, X. Measurement of air-pollution inequality through a three-perspective accounting model. Sci. Total. Environ. 2019, 696, 133937. [Google Scholar] [CrossRef]
- Sundar, S.; Mishra, A.K.; Shukla, J.B. Effects of Mitigation Options on the Control of Methane Emissions Caused by Rice Paddies and Livestock Populations to Reduce Global Warming: A Modeling Study and Comparison with Environmental Data. J. Environ. Inform. 2021, 38. [Google Scholar] [CrossRef]
- Ou, J.; Meng, J.; Zheng, J.; Mi, Z.; Bian, Y.; Yu, X.; Liu, J.; Guan, D. Demand-driven air pollutant emissions for a fast-developing region in China. Appl. Energy 2017, 204, 131–142. [Google Scholar] [CrossRef]
- Mi, Z.; Zheng, J.; Meng, J.; Zheng, H.; Li, X.; Coffman, D.; Woltjer, J.; Wang, S.; Guan, D. Carbon emissions of cities from a consumption-based perspective. Appl. Energy 2018, 235, 509–518. [Google Scholar] [CrossRef]
- Klemeš, J.J.; Varbanov, P.S.; Walmsley, T.G.; Jia, X. New directions in the implementation of Pinch Methodology (PM). Renew. Sustain. Energy Rev. 2018, 98, 439–468. [Google Scholar] [CrossRef]
- Xu, X.; Huang, G.; Liu, L.; Guan, Y.; Zhai, M.; Li, Y. Revealing dynamic impacts of socioeconomic factors on air pollution changes in Guangdong Province, China. Sci. Total. Environ. 2019, 699, 134178. [Google Scholar] [CrossRef] [PubMed]
- Mozaffar, A.; Zhang, Y.-L.; Fan, M.; Cao, F.; Lin, Y.-C. Characteristics of summertime ambient VOCs and their contributions to O3 and SOA formation in a suburban area of Nanjing, China. Atmos. Res. 2020, 240, 104923. [Google Scholar] [CrossRef]
- Zwolińska, E.; Sun, Y.; Chmielewski, A.G.; Pawelec, A.; Bułka, S. Removal of high concentrations of NOx and SO2 from diesel off-gases using a hybrid electron beam technology. Energy Rep. 2020, 6, 952–964. [Google Scholar] [CrossRef]
- Li, R.; Chen, W.; Xiu, A.; Zhao, H.; Zhang, X.; Zhang, S.; Tong, D.Q. A comprehensive inventory of agricultural atmospheric particulate matters (PM10 and PM2.5) and gaseous pollutants (VOCs, SO2, NH3, CO, NOx and HC) emissions in China. Ecol. Indic. 2019, 107, 105609. [Google Scholar] [CrossRef]
- Kumar, A.; Hakkim, H.; Sinha, B.; Sinha, V. Gridded 1 km × 1 km emission inventory for paddy stubble burning emissions over north-west India constrained by measured emission factors of 77 VOCs and district-wise crop yield data. Sci. Total. Environ. 2021, 789, 148064. [Google Scholar] [CrossRef] [PubMed]
- Alcántara, V.; Padilla, E.; Piaggio, M. Nitrogen oxide emissions and productive structure in Spain: An input–output perspective. J. Clean. Prod. 2017, 141, 420–428. [Google Scholar] [CrossRef]
- Faridzad, A.; Banouei, A.A.; Banouei, J.; Golestan, Z. Identifying energy-intensive key sectors in Iran: Evidence from decomposed input-output multipliers. J. Clean. Prod. 2019, 243, 118653. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, W.; Fan, J.; Yu, J.; Zhao, H. Transfers of embodied PM2.5 emissions from and to the North China region based on a multiregional input-output model. Environ. Pollut. 2018, 235, 381–393. [Google Scholar] [CrossRef]
- Liu, Q.; Long, Y.; Wang, C.; Wang, Z.; Wang, Q.; Guan, D. Drivers of provincial SO2 emissions in China—Based on multi-regional input-output analysis. J. Clean. Prod. 2019, 238, 117893. [Google Scholar] [CrossRef]
- Li, Y.; Chen, B.; Fang, D.; Zhang, B.; Bai, J.; Liu, G.; Zhang, Y. Drivers of energy-related PM2.5 emissions in the Jing-Jin-Ji region between 2002 and 2015. Appl. Energy 2021, 288, 116668. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Feng, C.; Liang, S.; Liu, Y.; Du, H.; Jia, N. Understanding the industrial NOx and SO2 pollutant emissions in China from sector linkage perspective. Sci. Total. Environ. 2021, 770, 145242. [Google Scholar] [CrossRef]
- de Bortoli, A.; Agez, M. Environmentally-extended input-output analyses efficiently sketch large-scale environmental transition plans: Illustration by Canada’s road industry. J. Clean. Prod. 2023, 388, 136039. [Google Scholar] [CrossRef]
- Chaker, M.; Berezowska-Azzag, E.; Perrotti, D. Exploring the performances of urban local symbiosis strategy in Algiers, between a potential of energy use optimization and CO2 emissions mitigation. J. Clean. Prod. 2021, 292, 125850. [Google Scholar] [CrossRef]
- Mei, H.; Li, Y.P.; Lv, J.; Chen, X.J.; Lu, C.; Suo, C.; Ma, Y. Development of an integrated method (MGCMs-SCA-FER) for assessing the impacts of climate change: A case study of Jing-Jin-Ji region. J. Environ. Inform. 2021, 38, 145–161. [Google Scholar] [CrossRef]
- Allen, I.E. Statistics for Experimenters; John Wiley & Sons: New York, NY, USA, 1978. [Google Scholar]
- Wang, J.; Li, Y.; Sun, J.; Lin, Y. Analyzing urban forest coverage variation in Guangzhou-Foshan region using factorial analysis based multivariate statistical prediction models. For. Ecol. Manag. 2019, 432, 121–131. [Google Scholar] [CrossRef]
- Liu, L.R.; Huang, G.H.; Baetz, B.; Huang, C.Z.; Zhang, K.Q. A factorial ecologically-extended input-output model for analyzing urban GHG emissions metabolism system. J. Clean. Prod. 2018, 200, 922–933. [Google Scholar] [CrossRef]
- Zhang, K.; Meng, Z.; Liu, L. Factorial two-stage analyses of parameters affecting the oil–gas interface and miscibility in bulk phase and nanopores. J. Colloid Interface Sci. 2019, 555, 740–750. [Google Scholar] [CrossRef] [PubMed]
- Jia, Q.; Li, Y.; Huang, G. Analyzing variation of inflow from the Syr Darya to the Aral Sea: A Bayesian-neural-network-based factorial analysis method. J. Hydrol. 2020, 587, 124976. [Google Scholar] [CrossRef]
- Gabryelczyk, A.; Ivanov, S.; Bund, A.; Lota, G. Taguchi method in experimental procedures focused on corrosion process of positive current collector in lithium-ion batteries. Electrochim. Acta 2020, 360, 137011. [Google Scholar] [CrossRef]
- Leontief, W. Input-Output Economics; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Tang, M.; Hong, J.; Liu, G.; Shen, G.Q. Exploring energy flows embodied in China’s economy from the regional and sectoral perspectives via combination of multi-regional input–output analysis and a complex network approach. Energy 2019, 170, 1191–1201. [Google Scholar] [CrossRef]
- Borrett, S.R.; Scharler, U.M. Walk partitions of flow in Ecological Network Analysis: Review and synthesis of methods and indicators. Ecol. Indic. 2019, 106, 105451. [Google Scholar] [CrossRef]
- Su, M.; Zhang, M.; Lu, W.; Chang, X.; Chen, B.; Liu, G.; Hao, Y.; Zhang, Y. ENA-based evaluation of energy supply security: Comparison between the Chinese crude oil and natural gas supply systems. Renew. Sustain. Energy Rev. 2017, 72, 888–899. [Google Scholar] [CrossRef]
- Kharrazi, A.; Rovenskaya, E.; Fath, B.D.; Yarime, M.; Kraines, S. Quantifying the sustainability of economic resource networks: An ecological information-based approach. Ecol. Econ. 2013, 90, 177–186. [Google Scholar] [CrossRef]
- Fath, B.D.; Asmus, H.; Asmus, R.; Baird, D.; Borrett, S.R.; de Jonge, V.N.; Ludovisi, A.; Niquil, N.; Scharler, U.M.; Schückel, U.; et al. Ecological network analysis metrics: The need for an entire ecosystem approach in management and policy. Ocean Coast. Manag. 2019, 174, 1–14. [Google Scholar] [CrossRef]
- Özakın, A.N.; Kaya, F. Experimental thermodynamic analysis of air-based PVT system using fins in different materials: Optimization of control parameters by Taguchi method and ANOVA. Sol. Energy 2020, 197, 199–211. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Huang, G.; Fu, H.; Zhang, J.; Cheng, G. Identification of water quality management policy of watershed system with multiple uncertain interactions using a multi-level-factorial risk-inference-based possibilistic-probabilistic programming approach. Environ. Sci. Pollut. Res. 2017, 24, 14980–15000. [Google Scholar] [CrossRef]
- Lyu, X.D.; Fan, Y.R. Characterizing Impact Factors on the Performance of Data Assimilation for Hydroclimatic Predictions through Multilevel Factorial Analysis. J. Environ. Inform. 2021, 38, 68–82. [Google Scholar] [CrossRef]
- Fujian Provincial Bureau of Statistics. Statistical Yearbook of Fujian Province; China Statistics Press: Beijing, China, 2021.
- Yu, Z.X.; Cao, G.L.; An, W.H.; Meng, X.B. Scenarios prediction for emissions of SO2, NOx in the year of 2020 and 2030 in China. CHN J. Environ. Eng. 2017, 11, 2355–2362. [Google Scholar] [CrossRef]
- National Bureau of Statistics. China Energy Statistics Yearbook; China Statistics Press: Beijing, China, 2021.




| No. | Sector | Abbreviation |
|---|---|---|
| 1 | Agriculture, forestry, animal husbandry and fishery | AGR |
| 2 | Mining industry | MIN |
| 3 | Food, drink, tea Manufacturing and tobacco processing | FOO |
| 4 | Textile products | TEX |
| 5 | Timber processing | TIM |
| 6 | Paper products | PAP |
| 7 | Petroleum processing, coking and nuclear fuel processing | PET |
| 8 | Chemical products | CHE |
| 9 | Nonmetal minerals products | NON |
| 10 | Metal processing | MET |
| 11 | Equipment manufacturing | EQU |
| 12 | Electricity production and supply | ELE |
| 13 | Construction | CON |
| 14 | Transportation, storage and postal services | TRA |
| 15 | Wholesale, retail and accommodation | WHO |
| 16 | Service industry | SER |
| Sector | NOx | SO2 | ||||||||
| Coal | Gasoline | Diesel | Kerosene | Fuel Oil | Coal | Gasoline | Diesel | Kerosene | Fuel Oil | |
| AGR | (3.30, 3.75) | (9.70, 16.70) | (4.00, 5.77) | (3.58, 4.48) | (3.10, 3.50) | (3.80, 4.19) | (0.02, 0.10) | (0.70, 0.90) | (1.00, 2.24) | (8.00, 10.00) |
| MIN-EQU | (3.30, 4.30) | (3.27, 3.67) | (3.21, 3.67) | (3.27, 3.67) | (3.20, 3.60) | (3.20, 4.00) | (0.02, 0.10) | (0.70, 0.90) | (1.00, 2.24) | (8.00, 10.00) |
| ELE | (1.70, 2.70) | (3.27, 3.67) | (3.21, 3.41) | - | (3.00, 3.41) | (2.40, 3.20) | (0.02, 0.10) | (0.56, 0.70) | - | (6.00, 8.08) |
| CON | (5.25, 7.25) | (9.70, 16.70) | (3.27, 9.62) | - | - | (7.66, 9.86) | (0.02, 0.10) | (0.70, 0.90) | - | - |
| TRA | (5.25, 7.50) | (3.65, 9.36) | (12.66, 14.25) | (21.00, 27.40) | (21.00, 27.40) | (3.60, 4.19) | (0.02, 0.10) | (0.10, 0.10) | (1.00, 2.24) | (8.00, 10.00) |
| WHO, SER | (2.00, 3.70) | (9.70, 16.70) | (3.21, 5.77) | - | - | (3.60, 4.19) | (0.02, 0.10) | (0.70, 0.90) | - | - |
| Sector | PM | VOCs | ||||||||
| Coal | Gasoline | Diesel | Kerosene | Fuel Oil | Coal | Gasoline | Diesel | Kerosene | Fuel Oil | |
| AGR | (3.30, 3.71) | (1.30, 1.74) | (1.30, 1.74) | (0.60, 0.90) | (1.30, 1.74) | (0.45, 0.60) | (3.00, 3.37) | (3.00, 3.37) | (0.13, 0.15) | (3.00, 3.37) |
| MIN-EQU | (2.00, 2.50) | (0.10, 0.31) | (0.40, 0.50) | (0.60, 0.90) | (0.45, 1.03) | (0.18, 0.39) | (0.07, 0.10) | (0.12, 0.15) | (0.13, 0.15) | (0.15, 0.17) |
| ELE | (1.30, 2.06) | (0.10, 0.31) | (0.40, 0.50) | - | (0.45, 0.85) | (0.15, 0.18) | (0.07, 0.10) | (0.12, 0.13) | - | (0.12, 0.13) |
| CON | (3.30, 3.50) | (2.00, 2.09) | (2.00, 2.09) | - | - | (0.18, 0.60) | (3.00, 3.39) | (3.00, 3.39) | - | - |
| TRA | (3.30, 3.50) | (0.03, 0.04) | (1.00, 1.10) | (0.60, 0.90) | (0.45, 1.03) | (0.45, 0.60) | (3.00, 3.14) | (0.12, 0.15) | (0.13, 0.15) | (0.15, 0.17) |
| WHO, SER | (3.30, 3.50) | (0.13, 0.31) | (0.40, 0.50) | - | - | (0.45, 0.60) | (0.09, 0.10) | (0.12, 0.15) | - | - |
| Factors | Description | Level (L) | Level (H) |
|---|---|---|---|
| ELE_coal | Consumption of coal in ELE (106 ton) | 35.77 | 44.71 |
| NON_coal | Consumption of coal in NON (106 ton) | 6.68 | 8.35 |
| CHE_coal | Consumption of coal in CHE (106 ton) | 4.66 | 5.83 |
| MET_coal | Consumption of coal in MET (106 ton) | 3.54 | 4.43 |
| TRA_gasoline | Consumption of gasoline in TRA (106 ton) | 1.73 | 2.16 |
| TRA_diesel | Consumption of diesel in TRA (106 ton) | 2.09 | 2.61 |
| TRA_kerosene | Consumption of kerosene in TRA (106 ton) | 1.05 | 1.31 |
| TRA_fuel oil | Consumption of fuel oil in TRA (106 ton) | 0.62 | 0.78 |
| EQU_a | Direct consumption coefficient of EQU | 0.37 | 0.46 |
| TEX_a | Direct consumption coefficient of TEX | 0.34 | 0.43 |
| SER_a | Direct consumption coefficient of SER | 0.20 | 0.25 |
| CON_a | Direct consumption coefficient of CON | 0.01 | 0.01 |
| WHO_a | Direct consumption coefficient of WHO | 0.02 | 0.02 |
| NOx | NOx emission from unit energy (kg/ton) | * | * |
| SO2 | SO2 emission from unit energy (kg/ton) | * | * |
| PM2.5 | PM2.5 emission from unit energy (kg/ton) | * | * |
| VOCs | VOCs emission from unit energy (kg/ton) | * | * |
| Level | ELE_coal | NON_coal | CHE_coal | MET_coal | TRA_gasoline | TRA_diesel | TRA_kerosene | TRA_fuel oil | EQU_a |
| L | −170.533 | −170.745 | −170.778 | −170.800 | −170.830 | −170.798 | −170.792 | −170.812 | −170.864 |
| H | −171.194 | −170.983 | −170.949 | −170.928 | −170.898 | −170.929 | −170.935 | −170.915 | −170.864 |
| Delta | 0.661 | 0.238 | 0.171 | 0.128 | 0.068 | 0.131 | 0.143 | 0.103 | 0 |
| Rank | 2 | 4 | 5 | 8 | 11 | 7 | 6 | 10 | 17 |
| Level | TEX_a | SER_a | CON_a | WHO_a | NOx | SO2 | PM | VOCs | |
| L | −170.863 | −170.865 | −170.865 | −170.866 | −170.396 | −170.633 | −170.807 | −170.835 | |
| H | −170.865 | −170.863 | −170.863 | −170.862 | −171.332 | −171.095 | −170.921 | −170.892 | |
| Delta | 0.002 | 0.002 | 0.003 | 0.004 | 0.936 | 0.462 | 0.114 | 0.057 | |
| Rank | 15 | 16 | 14 | 13 | 1 | 3 | 9 | 12 |
| Level | ELE_coal | NON_coal | CHE_coal | MET_coal | TRA_gasoline | TRA_diesel | TRA_kerosene | TRA_fuel oil | EQU_a |
| L | −9.352 | −9.427 | −9.472 | −9.340 | −9.344 | −9.342 | −9.340 | −9.352 | −9.003 |
| H | −9.335 | −9.261 | −9.215 | −9.348 | −9.343 | −9.346 | −9.347 | −9.336 | −9.684 |
| Delta | 0.017 | 0.166 | 0.257 | 0.008 | 0.001 | 0.004 | 0.007 | 0.016 | 0.681 |
| Rank | 7 | 3 | 2 | 10 | 17 | 13 | 11 | 8 | 1 |
| Level | TEX_a | SER_a | CON_a | WHO_a | NOx | SO2 | PM | VOCs | |
| L | −9.373 | −9.377 | −9.341 | −9.336 | −9.335 | −9.342 | −9.343 | −9.343 | |
| H | −9.315 | −9.311 | −9.346 | −9.351 | −9.352 | −9.345 | −9.344 | −9.344 | |
| Delta | 0.058 | 0.066 | 0.005 | 0.015 | 0.017 | 0.004 | 0.001 | 0.002 | |
| Rank | 5 | 4 | 12 | 9 | 6 | 14 | 16 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yang, Y. Controlling Industrial Air-Pollutant Emissions under Multi-Factor Interactions Based on a Developed Hybrid-Factorial Environmental Input–Output Model. Sustainability 2023, 15, 7717. https://doi.org/10.3390/su15097717
Liu J, Yang Y. Controlling Industrial Air-Pollutant Emissions under Multi-Factor Interactions Based on a Developed Hybrid-Factorial Environmental Input–Output Model. Sustainability. 2023; 15(9):7717. https://doi.org/10.3390/su15097717
Chicago/Turabian StyleLiu, Jing, and Yujin Yang. 2023. "Controlling Industrial Air-Pollutant Emissions under Multi-Factor Interactions Based on a Developed Hybrid-Factorial Environmental Input–Output Model" Sustainability 15, no. 9: 7717. https://doi.org/10.3390/su15097717
APA StyleLiu, J., & Yang, Y. (2023). Controlling Industrial Air-Pollutant Emissions under Multi-Factor Interactions Based on a Developed Hybrid-Factorial Environmental Input–Output Model. Sustainability, 15(9), 7717. https://doi.org/10.3390/su15097717






