Utilization of Synthetic Steel Gases in an Additively Manufactured Reactor for Catalytic Methanation
Abstract
1. Introduction
2. Materials and Methods
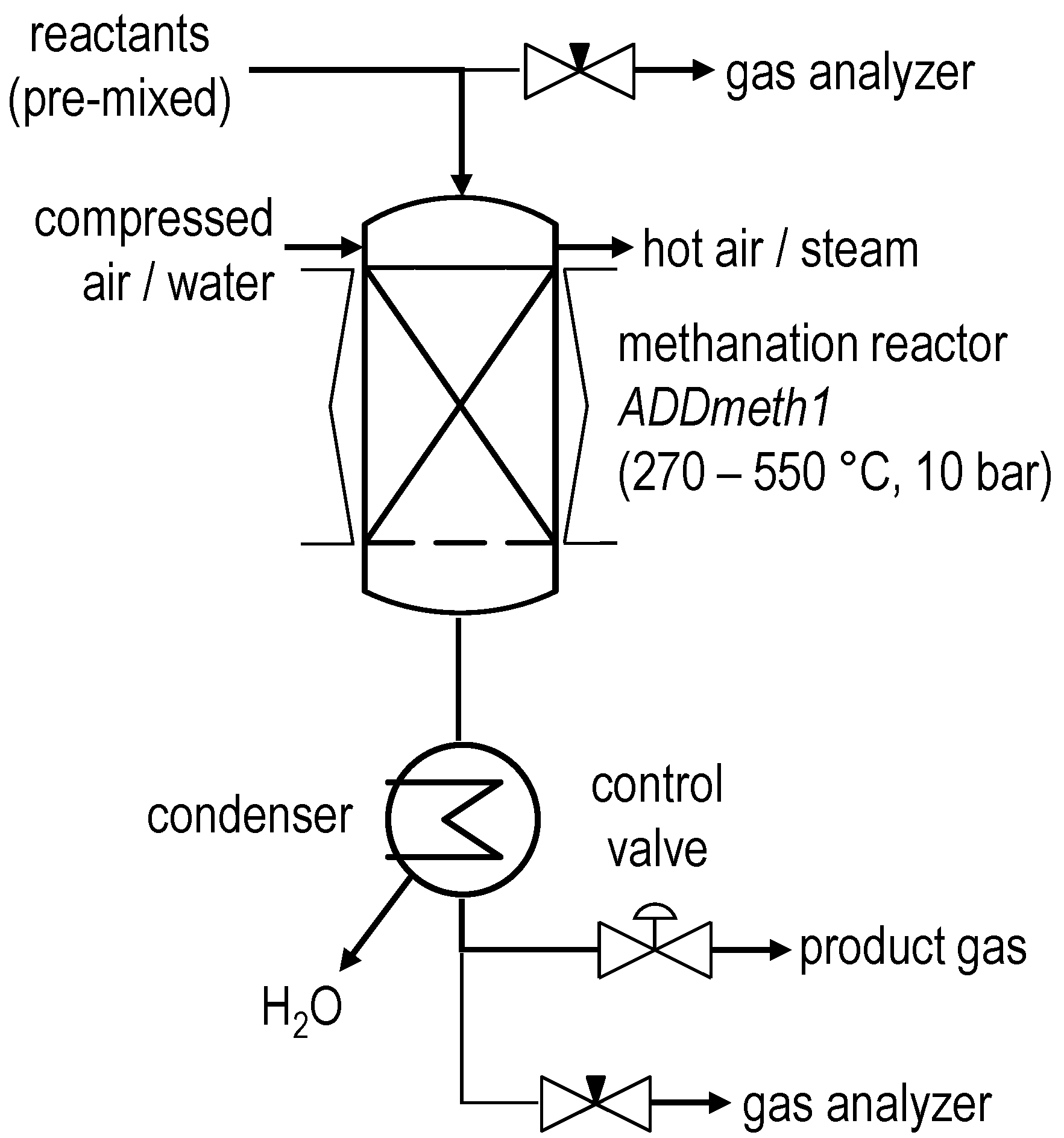
2.1. Experimental Setup
2.2. Process Parameters
2.3. Experimental Procedure
2.4. Simulation Model and Procedure
3. Results and Discussion
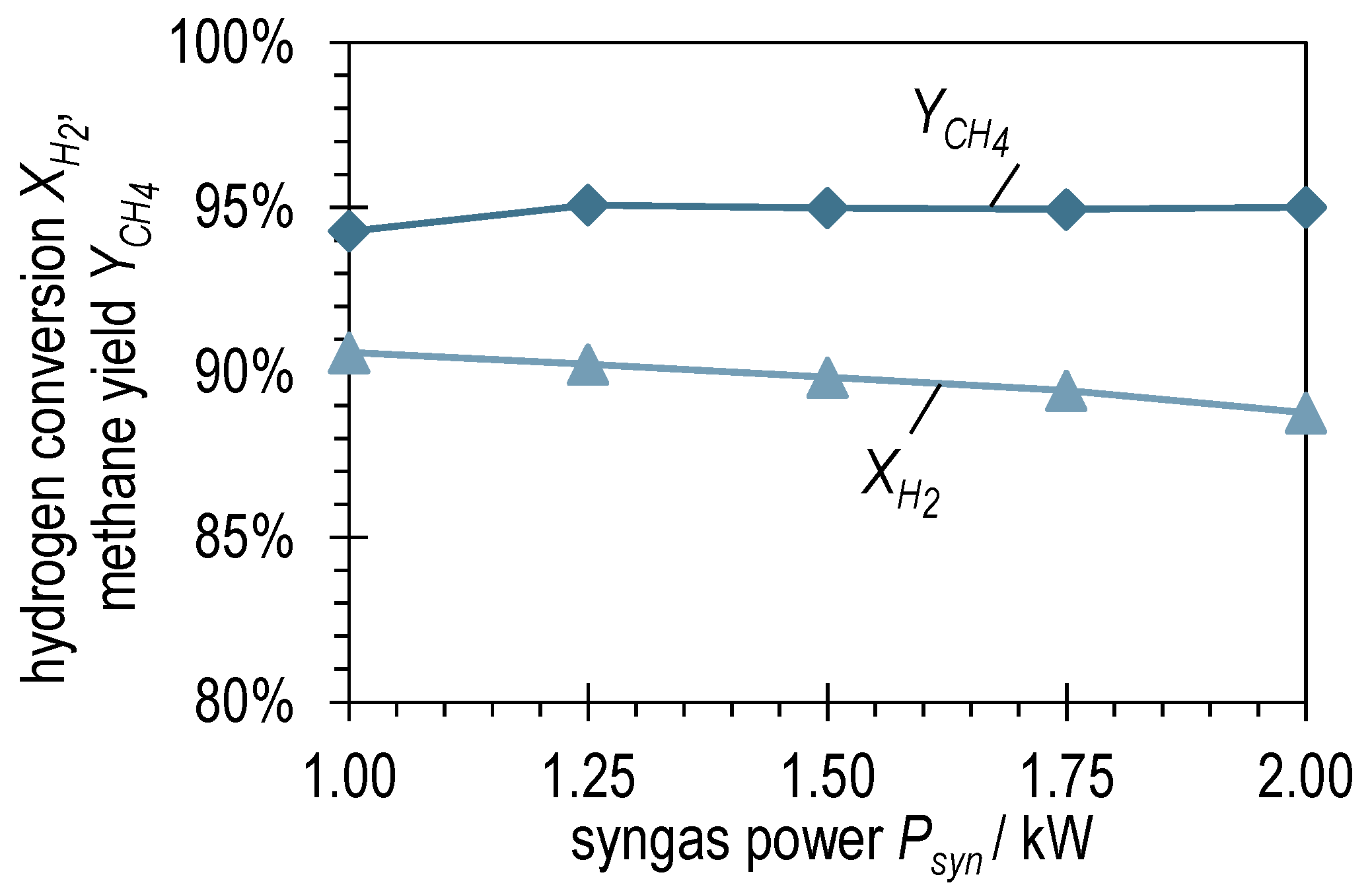
3.1. Experimental Variation of Syngas Power with BFG
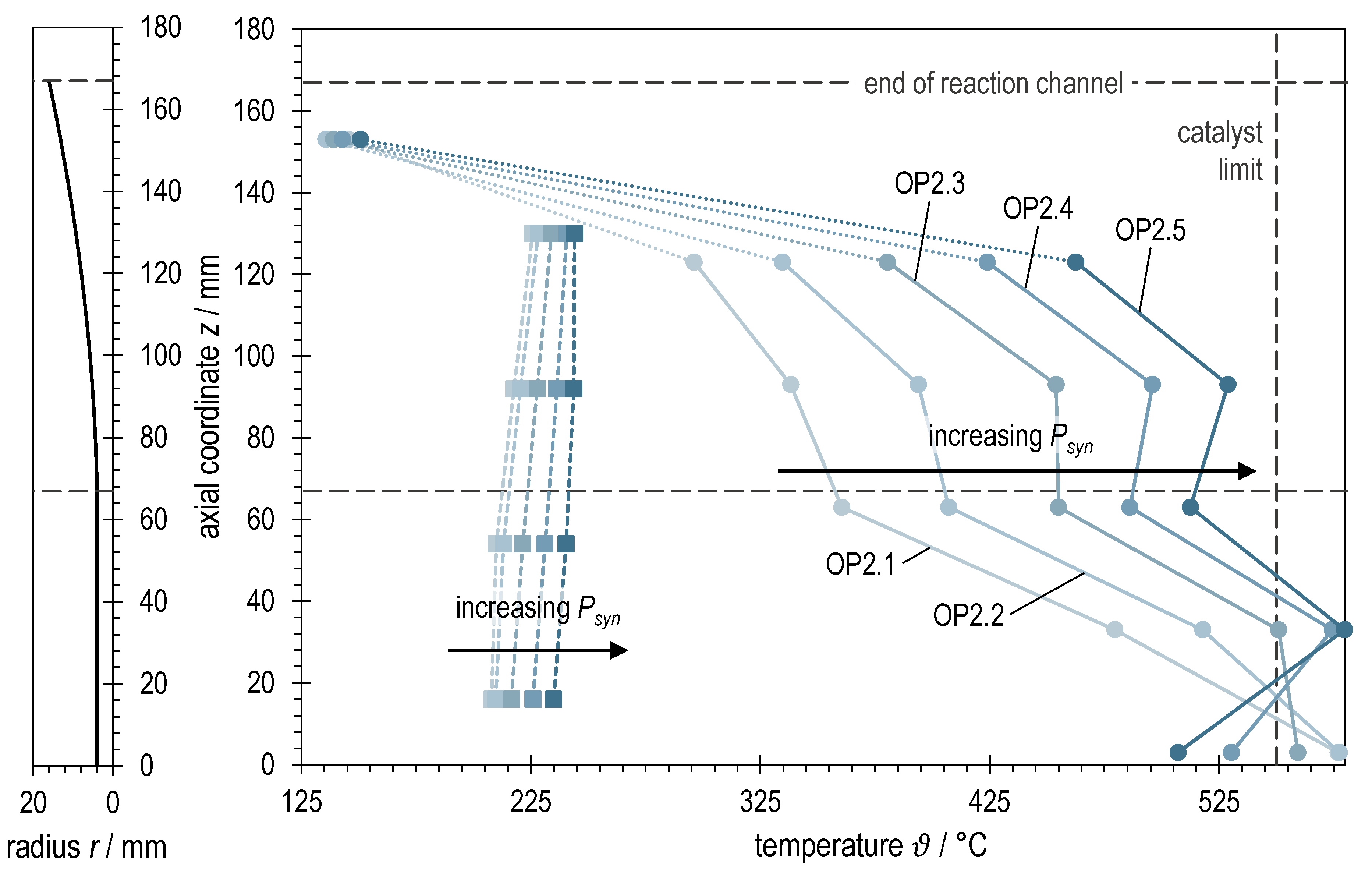
3.2. Experimental Variation of Syngas Power with BOFG
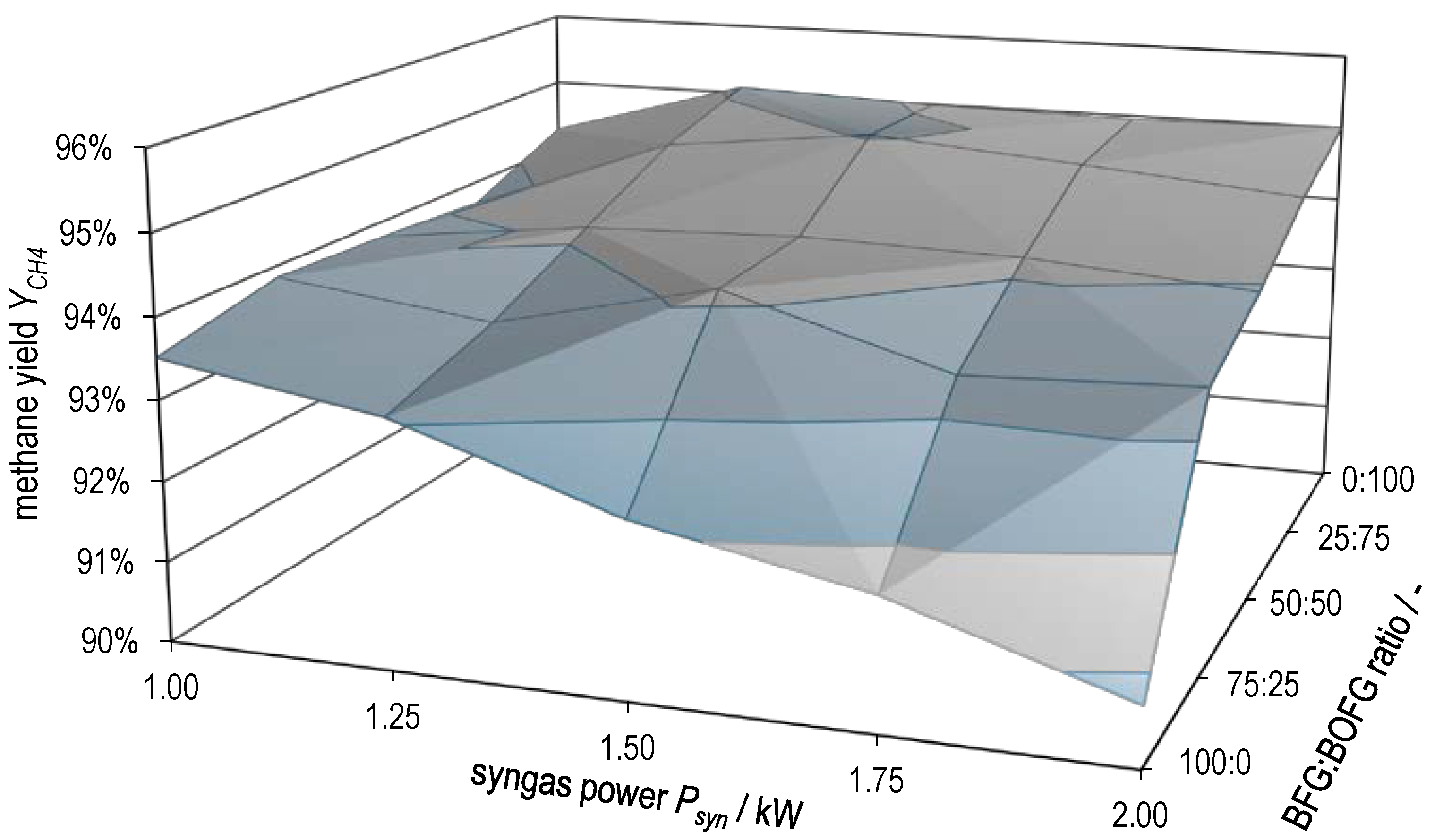
3.3. Experimental Variation of BFG/BOFG Ratio
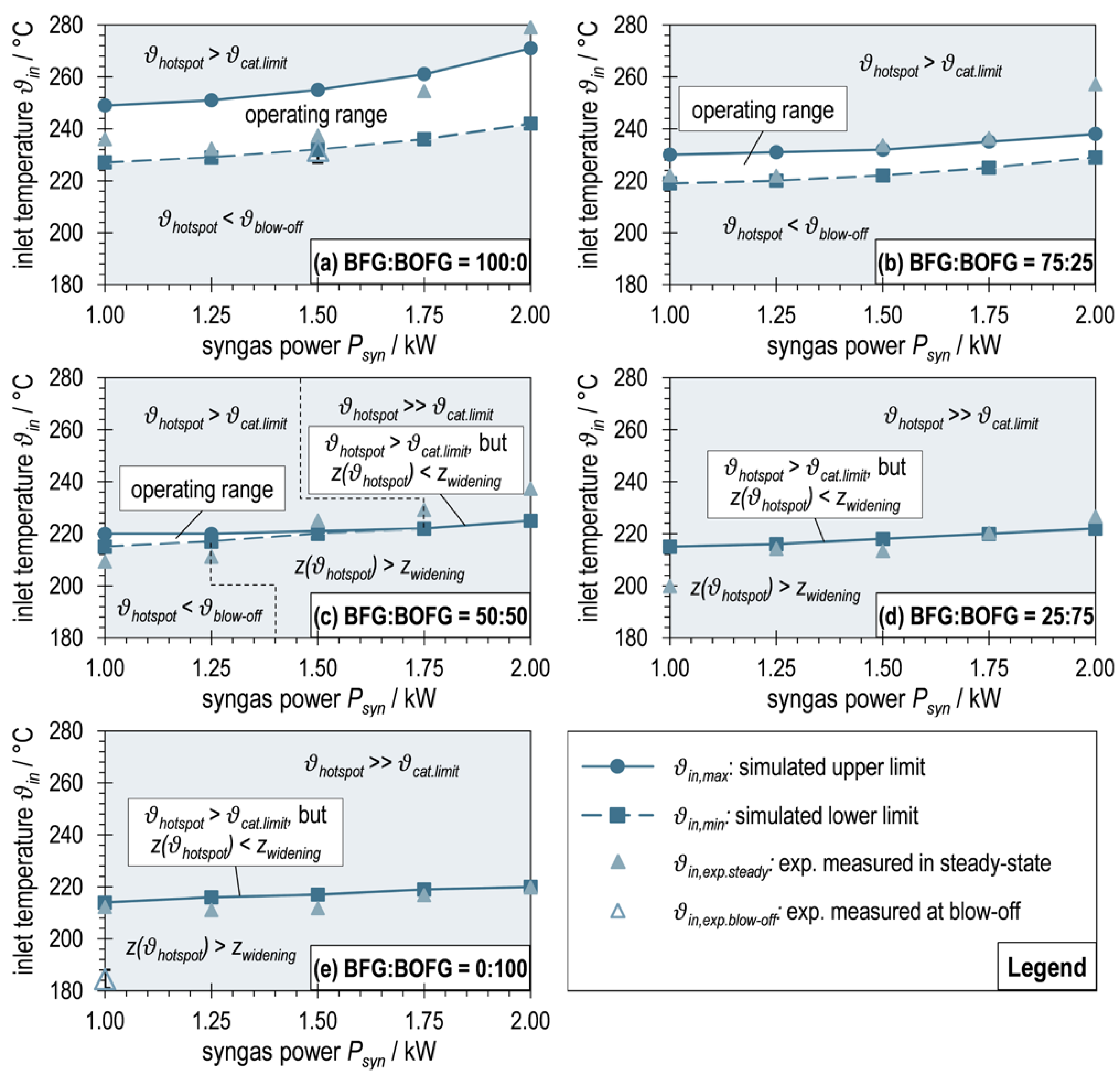
3.4. Simulated Operating Maps for Maximum and Minimum Inlet Temperatures of ADDmeth1
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Operating Point | H2 vol.% | CO2 vol.% | CO vol.% | CH4 vol.% | N2 vol.% | σH2 - | Psyn kW | GHSV h−1 |
|---|---|---|---|---|---|---|---|---|
| OP3.1 | 66.37 | 7.73 | 10.97 | 0.00 | 14.94 | 1.04 | 1.00 | 23,281 |
| OP3.2 | 1.25 | 29,088 | ||||||
| OP3.3 | 1.50 | 34,886 | ||||||
| OP3.4 | 1.75 | 40,717 | ||||||
| OP3.5 | 2.00 | 46,548 |
| Operating Point | H2 vol.% | CO2 vol.% | CO vol.% | CH4 vol.% | N2 vol.% | σH2 - | Psyn kW | GHSV h−1 |
|---|---|---|---|---|---|---|---|---|
| OP4.1 | 68.15 | 7.01 | 12.50 | 0.00 | 12.35 | 1.04 | 1.00 | 22,291 |
| OP4.2 | 1.25 | 27,829 | ||||||
| OP4.3 | 1.50 | 33,392 | ||||||
| OP4.4 | 1.75 | 38,961 | ||||||
| OP4.5 | 2.00 | 44,527 |
| Operating Point | H2 vol.% | CO2 vol.% | CO vol.% | CH4 vol.% | N2 vol.% | σH2 - | Psyn kW | GHSV h−1 |
|---|---|---|---|---|---|---|---|---|
| OP5.1 | 69.72 | 6.38 | 13.85 | 0.00 | 10.06 | 1.04 | 1.00 | 21,465 |
| OP5.2 | 1.25 | 26,831 | ||||||
| OP5.3 | 1.50 | 32,169 | ||||||
| OP5.4 | 1.75 | 37,537 | ||||||
| OP5.5 | 2.00 | 42,904 |
References
- European Commission. The European Green Deal; European Commission: Brussels, Belgium, 2019; Volume 53. [Google Scholar]
- IEA. Iron and Steel Technology Roadmap; OECD Publishing: Paris, France, 2020. [Google Scholar]
- World Steel Association. Steel Statistical Yearbook 2020 Concise Version; World Steel Association: Brussels, Belgium, 2020. [Google Scholar]
- IEA. Energy Technology Perspectives 2020—Special Report on Clean Energy Innovation; OECD Publishing: Paris, France, 2020. [Google Scholar]
- Osman, A.I.; Hefny, M.; Abdel Maksoud, M.I.A.; Elgarahy, A.M.; Rooney, D.W. Recent Advances in Carbon Capture Storage and Utilisation Technologies: A Review. Environ. Chem. Lett. 2021, 19, 797–849. [Google Scholar] [CrossRef]
- De Ras, K.; Van de Vijver, R.; Galvita, V.V.; Marin, G.B.; Van Geem, K.M. Carbon Capture and Utilization in the Steel Industry: Challenges and Opportunities for Chemical Engineering. Curr. Opin. Chem. Eng. 2019, 26, 81–87. [Google Scholar] [CrossRef]
- Uribe-Soto, W.; Portha, J.F.; Commenge, J.M.; Falk, L. A Review of Thermochemical Processes and Technologies to Use Steelworks Off-Gases. Renew. Sustain. Energy Rev. 2017, 74, 809–823. [Google Scholar] [CrossRef]
- Baker, R.W.; Freeman, B.; Kniep, J.; Huang, Y.I.; Merkel, T.C. CO2 Capture from Cement Plants and Steel Mills Using Membranes. Ind. Eng. Chem. Res. 2018, 57, 15963–15970. [Google Scholar] [CrossRef]
- He, X.; Chen, D.; Liang, Z.; Yang, F. Insight and Comparison of Energy-Efficient Membrane Processes for CO2 Capture from Flue Gases in Power Plant and Energy-Intensive Industry. Carbon Capture Sci. Technol. 2022, 2, 100020. [Google Scholar] [CrossRef]
- Cormos, C.C. Evaluation of Reactive Absorption and Adsorption Systems for Post-Combustion CO2 Capture Applied to Iron and Steel Industry. Appl. Therm. Eng. 2016, 105, 56–64. [Google Scholar] [CrossRef]
- Cormos, A.M.; Dinca, C.; Petrescu, L.; Andreea Chisalita, D.; Szima, S.; Cormos, C.C. Carbon Capture and Utilisation Technologies Applied to Energy Conversion Systems and Other Energy-Intensive Industrial Applications. Fuel 2018, 211, 883–890. [Google Scholar] [CrossRef]
- Yildirim, Ö.; Nölker, K.; Büker, K.; Kleinschmidt, R. Chemical Conversion of Steel Mill Gases to Urea: An Analysis of Plant Capacity. Chem. Ing. Tech. 2018, 90, 1529–1535. [Google Scholar] [CrossRef]
- Girod, K.; Lohmann, H.; Kaluza, S. Methanol Synthesis with Steel Mill Gases: Performance Investigations in an On-Site Technical Center. Chem. Ing. Tech. 2021, 93, 850–855. [Google Scholar] [CrossRef]
- Girod, K.; Lohmann, H.; Schlüter, S.; Kaluza, S. Methanol Synthesis with Steel-Mill Gases: Simulation and Practical Testing of Selected Gas Utilization Scenarios. Processes 2020, 8, 1673. [Google Scholar] [CrossRef]
- Hauser, A.; Wolf-Zoellner, P.; Haag, S.; Dettori, S.; Tang, X.; Mighani, M.; Matino, I.; Mocci, C.; Colla, V.; Kolb, S.; et al. Valorizing Steelworks Gases by Coupling Novel Methane and Methanol Synthesis Reactors with an Economic Hybrid Model Predictive Controller. Metals 2022, 12, 1023. [Google Scholar] [CrossRef]
- Hauser, A.; Weitzer, M.; Gunsch, S.; Neubert, M.; Karl, J. Dynamic Hydrogen-Intensified Methanation of Synthetic by-Product Gases from Steelworks. Fuel Process. Technol. 2021, 217, 106701. [Google Scholar] [CrossRef]
- Wolf-Zoellner, P.; Medved, A.R.; Lehner, M.; Kieberger, N.; Rechberger, K. In Situ Catalytic Methanation of Real Steelworks Gases. Energies 2021, 14, 8131. [Google Scholar] [CrossRef]
- Schöß, M.; Redenius, A.; Turek, T.; Güttel, R. Chemische Speicherung Regenerativer Elektrischer Energie Durch Methanisierung von Prozessgasen Aus Der Stahlindustrie. Chem. Ing. Tech. 2014, 86, 734–739. [Google Scholar] [CrossRef]
- Wolf-Zoellner, P.; Lehner, M.; Kieberger, N. Application-Based Catalytic Methanation of Steelworks Gases under Dynamic Operating Conditions. J. Clean. Prod. 2022, 371, 133570. [Google Scholar] [CrossRef]
- Matino, I.; Dettori, S.; Castellano, A.; Matino, R.; Mocci, C.; Vannocci, M.; Maddaloni, A.; Colla, V.; Wolff, A. Machine Learning-Based Models for Supporting Optimal Exploitation of Process Off-Gases in Integrated Steelworks. In Impact and Opportunities of Artificial Intelligence Techniques in the Steel Industry; Colla, V., Pietrosanti, C., Eds.; Springer: Cham, Switzerland, 2021; pp. 104–118. [Google Scholar]
- Matino, I.; Dettori, S.; Colla, V.; Rechberger, K.; Kieberger, N. Echo-State Neural Networks Forecasting Steelworks off-Gases for Their Dispatching in CH4 and CH3OH Syntheses Reactors. In Proceedings of the ESANN 2021 Proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 6–8 October 2021; pp. 317–322. [Google Scholar]
- Dettori, S.; Matino, I.; Iannino, V.; Colla, V.; Hauser, A.; Wolf-Zöllner, P.; Haag, S. Optimizing Methane and Methanol Production from Integrated Steelworks Process Off-Gases through Economic Hybrid Model Predictive Control. IFAC-PapersOnLine 2022, 55, 66–71. [Google Scholar] [CrossRef]
- Matino, I.; Dettori, S.; Zaccara, A.; Petrucciani, A.; Iannino, V.; Colla, V.; Bampaou, M.; Panopoulos, K.; Rechberger, K.; Kolb, S.; et al. Hydrogen Role in the Valorization of Integrated Steelworks Process Off-Gases through Methane and Methanol Syntheses. Matér. Tech. 2021, 109, 308. [Google Scholar] [CrossRef]
- Iannino, V.; Colla, V.; Mocci, C.; Matino, I.; Dettori, S.; Kolb, S.; Plankenbühler, T.; Karl, J. Multi-Agent Systems to Improve Efficiency in Steelworks. Matér. Tech. 2022, 109, 502. [Google Scholar] [CrossRef]
- Zaccara, A.; Petrucciani, A.; Matino, I.; Branca, T.A.; Dettori, S.; Iannino, V.; Colla, V.; Bampaou, M.; Panopoulos, K. Renewable VolumenHydrogen Production Processes for the Off-Gas Valorization in Integrated Steelworks through Hydrogen Intensified Methane and Methanol Syntheses. Metals 2020, 10, 1535. [Google Scholar] [CrossRef]
- Bampaou, M.; Panopoulos, K.; Seferlis, P.; Voutetakis, S.; Matino, I.; Petrucciani, A.; Zaccara, A.; Colla, V.; Dettori, S.; Annunziata Branca, T.; et al. Integration of Renewable Hydrogen Production in Steelworks Off-Gases for the Synthesis of Methanol and Methane. Energies 2021, 14, 2904. [Google Scholar] [CrossRef]
- Bampaou, M.; Panopoulos, K.; Seferlis, P.; Sasiain, A.; Haag, S.; Wolf-zoellner, P.; Lehner, M.; Rog, L.; Rompalski, P.; Kolb, S.; et al. Economic Evaluation of Renewable Hydrogen Integration into Steelworks for the Production of Methanol and Methane. Energies 2022, 15, 4650. [Google Scholar] [CrossRef]
- Remus, R.; Roudier, S.; Aguado Monsonet, M.A.; Sancho, L.D. Best Available Techniques (BAT) Reference Document for Iron and Steel Production; European Commission, Joint Research Centre: Seville, Spain, 2013; Volume BREF-IS. [Google Scholar]
- Strucks, P.; Failing, L.; Kaluza, S. A Short Review on Ni-Catalyzed Methanation of CO2: Reaction Mechanism, Catalyst Deactivation, Dynamic Operation. Chem. Ing. Tech. 2021, 93, 1526–1536. [Google Scholar] [CrossRef]
- Götz, M.; Lefebvre, J.; Mörs, F.; McDaniel Koch, A.; Graf, F.; Bajohr, S.; Reimert, R.; Kolb, T. Renewable Power-to-Gas: A Technological and Economic Review. Renew. Energy 2016, 85, 1371–1390. [Google Scholar] [CrossRef]
- Rönsch, S.; Schneider, J.; Matthischke, S.; Schlüter, M.; Götz, M.; Lefebvre, J.; Prabhakaran, P.; Bajohr, S. Review on Methanation—From Fundamentals to Current Projects. Fuel 2016, 166, 276–296. [Google Scholar] [CrossRef]
- Mills, G.A.; Steffgen, F.W. Catalytic Methanation. Catal. Rev. 1974, 8, 159–210. [Google Scholar] [CrossRef]
- Ridzuan, N.D.M.; Shaharun, M.S.; Anawar, M.A.; Ud-Din, I. Ni-Based Catalyst for Carbon Dioxide Methanation: A Review. Catalysts 2022, 12, 469. [Google Scholar] [CrossRef]
- Tan, C.H.; Nomanbhay, S.; Shamsuddin, A.H.; Park, Y.K.; Hernández-Cocoletzi, H.; Show, P.L. Current Developments in Catalytic Methanation of Carbon Dioxide—A Review. Front. Energy Res. 2022, 9, 795423. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, J.; Chu, M.; Yue, J.; Cui, Y.; Xu, G. Cooperation Between Active Metal and Basic Support in Ni-Based Catalyst for Low-Temperature CO2 Methanation. Catal. Lett. 2020, 150, 1418–1426. [Google Scholar] [CrossRef]
- Zhang, L.; Bian, L.; Li, Z.; Xia, R. The Promoter Action of CeO2 for the Ni/Al2O3-Catalyzed Methanation of CO2. Kinet. Catal. 2015, 56, 329–334. [Google Scholar] [CrossRef]
- Material Safety Data Sheet Nickel Tetracarbonyl (NiCO4). Available online: https://gestis.dguv.de/data?name=004260 (accessed on 17 April 2023).
- Neubert, M.F.W. Catalytic Methanation for Small-and Mid-Scale SNG Production|Katalytische Methanisierung für Die SNG Erzeugung in Kleinen Bis Mittleren Anlagengrößen; FAU Erlangen-Nürnberg: Erlangen, Germany, 2019. [Google Scholar]
- Kerfoot, D.G.E. Nickel. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH GmbH & Co. KGaA: Weinheim, Germany, 2000. [Google Scholar]
- Bengaouer, A.; Ducamp, J.; Champon, I.; Try, R. Performance Evaluation of Fixed-Bed, Millistructured, and Metallic Foam Reactor Channels for CO2 Methanation. Can. J. Chem. Eng. 2018, 96, 1937–1945. [Google Scholar] [CrossRef]
- Hauser, A.; Neubert, M.; Feldner, A.; Horn, A.; Grimm, F.; Karl, J. Design and Implementation of an Additively Manufactured Reactor Concept for the Catalytic Methanation. Appl. Sci. 2022, 12, 9393. [Google Scholar] [CrossRef]
- Kosaka, F.; Yamaguchi, T.; Ando, Y.; Mochizuki, T.; Takagi, H.; Matsuoka, K.; Kuramoto, K. Thermal Management of CO2 Methanation with Axial Staging of Active Metal Concentration in Ni-YSZ Tubular Catalysts. Int. J. Hydrogen Energy 2021, 46, 4116–4125. [Google Scholar] [CrossRef]
- Zimmermann, R.T.; Bremer, J.; Sundmacher, K. Load-Flexible Fixed-Bed Reactors by Multi-Period Design Optimization. Chem. Eng. J. 2022, 428, 130771. [Google Scholar] [CrossRef]
- Hervy, M.; Maistrello, J.; Brito, L.; Rizand, M.; Basset, E.; Kara, Y.; Maheut, M. Power-to-Gas: CO2 Methanation in a Catalytic Fluidized Bed Reactor at Demonstration Scale, Experimental Results and Simulation. J. CO2 Util. 2021, 50, 101610. [Google Scholar] [CrossRef]
- Tronconi, E.; Groppi, G.; Visconti, C.G. Structured Catalysts for Non-Adiabatic Applications. Curr. Opin. Chem. Eng. 2014, 5, 55–67. [Google Scholar] [CrossRef]
- Baena-Moreno, F.M.; González-Castaño, M.; Navarro De Miguel, J.C.; Miah, K.U.M.; Ossenbrink, R.; Odriozola, J.A.; Arellano-García, H. Stepping toward Efficient Microreactors for CO2 Methanation: 3D-Printed Gyroid Geometry. ACS Sustain. Chem. Eng. 2021, 9, 8198–8206. [Google Scholar] [CrossRef]
- Stiegler, T.; Meltzer, K.; Tremel, A.; Baldauf, M.; Wasserscheid, P.; Albert, J. Development of a Structured Reactor System for CO2 Methanation under Dynamic Operating Conditions. Energy Technol. 2019, 7, 1900047. [Google Scholar] [CrossRef]
- Pérez, S.; Aragón, J.J.; Peciña, I.; Garcia-Suarez, E.J. Enhanced CO2 Methanation by New Microstructured Reactor Concept and Design. Top. Catal. 2019, 62, 518–523. [Google Scholar] [CrossRef]
- Neubert, M.; Hauser, A.; Pourhossein, B.; Dillig, M.; Karl, J. Experimental Evaluation of a Heat Pipe Cooled Structured Reactor as Part of a Two-Stage Catalytic Methanation Process in Power-to-Gas Applications. Appl. Energy 2018, 229, 289–298. [Google Scholar] [CrossRef]
- Try, R.; Bengaouer, A.; Baurens, P.; Jallut, C. Dynamic Modeling and Simulations of the Behavior of a Fixed-Bed Reactor-Exchanger Used for CO2 Methanation. AIChE J. 2018, 64, 468–480. [Google Scholar] [CrossRef]
- Schlereth, D.; Hinrichsen, O. A Fixed-Bed Reactor Modeling Study on the Methanation of CO2. Chem. Eng. Res. Des. 2014, 92, 702–712. [Google Scholar] [CrossRef]
- Moioli, E.; Gallandat, N.; Züttel, A. Parametric Sensitivity in the Sabatier Reaction over Ru/Al2O3-Theoretical Determination of the Minimal Requirements for Reactor Activation. React. Chem. Eng. 2019, 4, 100–111. [Google Scholar] [CrossRef]
- Liu, D.M.; Tuan, W.H.; Chiu, C.C. Thermal Diffusivity, Heat Capacity and Thermal Conductivity in Al2O3Ni Composite. Mater. Sci. Eng. B 1995, 31, 287–291. [Google Scholar] [CrossRef]
- Pushnov, A.S. Calculation of Average Bed Porosity. Chem. Pet. Eng. 2006, 42, 14–17. [Google Scholar] [CrossRef]
- Rönsch, S.; Köchermann, J.; Schneider, J.; Matthischke, S. Global Reaction Kinetics of CO and CO2 Methanation for Dynamic Process Modeling. Chem. Eng. Technol. 2016, 39, 208–218. [Google Scholar] [CrossRef]
- Neubert, M.; Widzgowski, J.; Rönsch, S.; Treiber, P.; Dillig, M.; Karl, J. Simulation-Based Evaluation of a Two-Stage Small-Scale Methanation Unit for Decentralized Applications. Energy Fuels 2017, 31, 2076–2086. [Google Scholar] [CrossRef]
- Elnashaie, S.S.E.H.; Elshishini, S.S. Modelling, Simulation and Optimization of Industrial Fixed Bed Catalytic Reactors. Topics in Chemical Engineering; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1993; Volume 7, ISBN 2-88124-883-7. [Google Scholar]
- Jess, A.; Wasserscheid, P. Chemical Technology—An Integral Textbook; Wiley-VCH: Weinheim, Germany, 2013; ISBN 978-3-527-30446-2. [Google Scholar]
- Levenspiel, O. Chemical Reaction Engineering; Wiley: Hoboken, NJ, USA, 1999; ISBN 978-0-471-25424-9. [Google Scholar]
- Gruber, M. Detaillierte Untersuchung Des Wärme-Und Stofftransports in Einem Festbett-Methanisierungsreaktor Für Power-to-Gas Anwendungen; Karlsruher Institut für Technologie (KIT): Karlsruhe, Germany, 2019. [Google Scholar]
- Gruber, M.; Wiedmann, D.; Haas, M.; Harth, S.; Loukou, A.; Trimis, D. Insights into the Catalytic CO2 Methanation of a Boiling Water Cooled Fixed-Bed Reactor: Simulation-Based Analysis. Chem. Eng. J. 2021, 406, 126788. [Google Scholar] [CrossRef]
- Burger, T.; Donaubauer, P.; Hinrichsen, O. On the Kinetics of the Co-Methanation of CO and CO2 on a Co-Precipitated Ni-Al Catalyst. Appl. Catal. B Environ. 2020, 119408. [Google Scholar] [CrossRef]
- Schmider, D.; Maier, L.; Deutschmann, O. Reaction Kinetics of CO and CO2 Methanation over Nickel. Ind. Eng. Chem. Res. 2021, 60, 5792–5805. [Google Scholar] [CrossRef]
- COMSOL Inc. CFD Module User’s Guide. Available online: https://doc.comsol.com/6.0/docserver/#!/com.comsol.help.cfd/html_CFDModuleManual.html (accessed on 13 October 2022).
- Vdi, E.V. (Ed.) Verein Deutscher Ingenieure VDI-Wärmeatlas, 11th ed.; Springer: Berlin/Heidelberg, Germay, 2013; ISBN 978-3-642-19980-6. [Google Scholar]
- COMSOL Inc. Chemical Reaction Engineering User’s Guide. Available online: https://doc.comsol.com/6.0/docserver/#!/com.comsol.help.chem/html_ChemicalReactionEngineeringModuleManual.html (accessed on 13 October 2022).






| BFG | BOFG | |||
|---|---|---|---|---|
| Min. | Max. | Mean | ||
| H2 | vol.% | 1 | 8 | 4.3 |
| CO | vol.% | 19 | 27 | 60.9 |
| CO2 | vol.% | 16 | 26 | 17.2 |
| N2 | vol.% | 44 | 58 | 15.5 |
| CH4 | vol.% | 0.1 | ||
| Operating Point | H2 vol.% | CO2 vol.% | CO vol.% | CH4 vol.% | N2 vol.% | σH2 - | Psyn kW | GHSV h−1 |
|---|---|---|---|---|---|---|---|---|
| OP1.1 | 64.34 | 9.24 | 8.54 | 0.00 | 17.88 | 1.04 | 1.00 | 24,616 |
| OP1.2 | 1.25 | 30,679 | ||||||
| OP1.3 | 1.50 | 36,775 | ||||||
| OP1.4 | 1.75 | 42,937 | ||||||
| OP1.5 | 2.00 | 49,035 |
| Operating Point | H2 vol.% | CO2 vol.% | CO vol.% | CH4 vol.% | N2 vol.% | σH2 - | Psyn kW | GHSV h−1 |
|---|---|---|---|---|---|---|---|---|
| OP2.1 | 71.13 | 5.81 | 15.05 | 0.00 | 8.01 | 1.04 | 1.00 | 20,773 |
| OP2.2 | 1.25 | 25,969 | ||||||
| OP2.3 | 1.50 | 31,142 | ||||||
| OP2.4 | 1.75 | 36,341 | ||||||
| OP2.5 | 2.00 | 41,545 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hauser, A.; Feldner, A.; Treiber, P.; Grimm, F.; Karl, J. Utilization of Synthetic Steel Gases in an Additively Manufactured Reactor for Catalytic Methanation. Sustainability 2023, 15, 7652. https://doi.org/10.3390/su15097652
Hauser A, Feldner A, Treiber P, Grimm F, Karl J. Utilization of Synthetic Steel Gases in an Additively Manufactured Reactor for Catalytic Methanation. Sustainability. 2023; 15(9):7652. https://doi.org/10.3390/su15097652
Chicago/Turabian StyleHauser, Alexander, Alexander Feldner, Peter Treiber, Fabian Grimm, and Jürgen Karl. 2023. "Utilization of Synthetic Steel Gases in an Additively Manufactured Reactor for Catalytic Methanation" Sustainability 15, no. 9: 7652. https://doi.org/10.3390/su15097652
APA StyleHauser, A., Feldner, A., Treiber, P., Grimm, F., & Karl, J. (2023). Utilization of Synthetic Steel Gases in an Additively Manufactured Reactor for Catalytic Methanation. Sustainability, 15(9), 7652. https://doi.org/10.3390/su15097652







