Abstract
Freight transportation in urban areas represents an essential activity from the standpoint of economic development; in recent years, the spread of e-commerce (also accelerated by COVID-19) has contributed to increasing the demand for freight distribution over short distances. In most cities, the approaches and measures are often based on new technologies. Nevertheless, today there are contexts wherein delivery operations represent critical tasks to be solved. Furthermore, low accessibility areas, such as small islands, present further problems due to their exclusive dependence on maritime links (and often low-reliability services). This paper tackles this topic, formulating and solving a distribution problem by linking shipping services with last-mile distribution operated by means of an automatic delivery service (parcel lockers). A test application is proposed by considering the small island of Lipari in the archipelago of the Aeolian islands (Sicily, Southern Italy). The results show that such a type of service could reduce the user’s waiting time when compared to traditional home deliveries.
1. Introduction
The freight distribution in urban areas is crucial for connecting the producers with the end consumers. Therefore, the e-market and energy use relationship is crucial for developing sustainable urban logistic plans. However, some aspects, such as urban sprawl across the territory or customer habits, can make the process inefficient. Additionally, the growth of e-commerce (about 20% in the last ten years, [1]) has contributed to increasing freight distribution over short distances, thus requiring approaches and measures able to minimize the impacts. This topic has been widely studied by numerous researchers who have highlighted the benefits and the critical issues connected to it [2,3,4,5], pointing out the appropriate measures to take [6] and the assessment procedures [7]. The measures range from governance (e.g., [8]) to infrastructural elements (e.g., [9]) to equipment/new technologies (e.g., [2,10]). As an example, urban distribution centers (UDCs) are an element that could contribute to the reduction of impacts [11], especially if combined with low/zero-emissions freight vehicles [12,13,14]. This may contribute to the reduction of traffic congestion (since, in general, the vehicles moving from UDCs are fewer and smaller [15]), positively impacting the environment and urban life. Still, the general pattern of home deliveries (i.e., the freight vehicles that move into the city to serve the final clients, [16]) remains unchanged. A further level of the problem is the need to deliver to geographically particular places (for example, places that are difficult to reach with a truck and/or with a low population). To overcome this, pick-up points (e.g., local shops where clients can pick up their parcels), drone services and parcel lockers (clients pick up the parcels themselves) can be valuable alternatives. Thus, quantitative study on the potential interest of consumers in applying automatic delivery strategies is necessary to capture consumers’ future intentions, not underrating desire and expectation and possible consequences connected with choices [17].
Commercial establishments (newsagents, tobacco shops, and bookshops) can be used as hub points, thus representing delivery–collection facilities. This solution overcomes shortfalls connected with missed deliveries, providing a flexible collection method that allows the customers to have the package delivered to a location of their choice (e.g., near home or near work). A possible disadvantage (but it does not necessarily happen) is the queue that the customer can find in the commercial establishment (which must carry out its primary activity in addition to acting as a pick-up point).
The use of drones to provide delivery services in city centers and in particular geographical areas (or low-populated zones) is a measure considered in various papers (e.g., [18,19,20]), which note that the integration of drones into logistic plans is, up until today, limited by technological limitations and financial costs.
Parcel lockers are a reliable alternative to reduce the problems of home delivery services, being an effective last-mile distribution strategy (mainly if located in attended areas). The goal of using a parcel locker [21] is to reduce the distance travelled by freight vehicles and provide consumers with a flexible time window to collect their purchases (the locker is equipped with an electronic lock whose variable code is known by the customer). However, this approach could limit the size and the type of freight to be delivered and require some initial investments. In the literature [22], a classification of the use of parcel lockers is provided by considering the owner of the locker (e.g., carriers, companies, public providers), and also by considering the potential demand (customers) of those who could use the locker [17,23]. Hence, locker size and location issues must be solved [24,25].
This work aims to answer the main question of how to combine last-mile delivery with parcel lockers and naval services to improve deliveries in small islands. The traditional door-to-door service is often characterized by the fact that the courier cannot guarantee high standards in terms of waiting time for the delivery (e.g., because smaller vehicles are needed or because the courier waits until the number of orders is sufficient to fill the freight vehicle). The situation is the same if the delivery is made to the customer or to a pick-up point.
The paper represents a first attempt to analyze the use of parcel lockers in low-accessibility and remote areas. Specifically, in the present case study, customers are located on a small island. Thus, the aim of the paper was to propose a method to integrate ferry services and last-mile distribution, while also providing a procedure to solve the problem. More in detail, the problem was formulated as a constrained combinatorial problem whose goal consisted in minimizing the delivery waiting time, with a customer-based approach. The implementation of a genetic algorithm allowed us to solve the problem; since the purpose of the paper was not the proposition of a new model solution, the application of a consolidated methodology was made to avoid the introduction of any source of error in solving such a nontrivial problem that has not been addressed so far.
To the authors’ knowledge, the integration between naval services and urban freight distribution with parcel lockers has not been treated in detail in other works.
The structure of the paper is organized as follows. Section 2 reports a literature review on parcel lockers. Section 3 reports the problem definition and the proposed solution procedure. Section 4 reports a test application based on a real case. Finally, in Section 5 and in Section 6, some concluding remarks are reported.
2. Literature Review
The literature on urban freight distribution ranges from simulation models [26,27,28,29,30] to optimization models [31,32,33], taking into account environmental and technological aspects [34,35,36] and distribution strategies [37,38,39,40]. Since the use of parcel lockers has emerged as one of the possible distribution strategies, the number, size and location of parcel lockers require attention [24].
As the first to study this, Yuen et al. [41] examined the determinants that influence customers to accept parcel lockers: it emerged that customers consider elements such as service reliability, time flexibility and privacy; furthermore, they are willing to use the lockers if the extra charges that result are low. Such costs include the collection of information on using parcel lockers, the study of the locker interface and the cost of traveling to the locker location. Mitrea et al. [42] estimated customers’ attitudes toward lockers, highlighting that the most relevant factors are related to the environmental sustainability of the lockers and the customers’ willingness to carry the parcels themselves. Tang et al. [43] pointed out how both location and reliability of services, as well as flexibility and low fares, positively influence customers’ intentions to use automatic delivery solutions. Similarly, from Lai et al. [44], results show that time savings, security and reliability are significant predictors in analyzing the customer’s perception of the parcel locker. An et al. [45] highlighted that a positive attitude towards new technology and innovation and the ease of use are determinant factors that motivate people to approach services offered by e-procurement. Most of the interest in this topic concerns the locker position, the optimization of the courier trips to the locker location, and the integration with the traditional last-mile distribution, considering both mobile (autonomous or not) and fixed parcel lockers. Therefore, not intending to be fully exhaustive, we consider some works dealing with parcel lockers in last-mile distribution below.
Mobile parcel lockers (autonomous or operated by a human driver) represent a novelty for which there are prototype vehicles or patents, [46]. Li et al. [47] implemented a two-echelon vehicle routing problem to optimize both the travel of mobile lockers and the courier travels to restock them. Schwerdfeger and Boysen [46] proposed a dynamic location problem to allocate mobile parcel lockers to minimize the number of lockers. Wang et al. [48] proposed using mobile parcel lockers to meet demand, thus minimizing the costs, and optimizing the locker locations and the routes followed by the lockers. Then, they solved the same problem similarly under stochastic demand [49].
Considering the parcel locker in a fixed position, Lachapelle et al. [50] proposed a method based on logistic regression to locate the parcel lockers in the study area by considering accessibility, population density and customer characteristics. Che et al. [51] proposed a multi-objective model (maximize the covered demand, minimize the overlap between catchment areas of different parcel lockers, maximize the load of each locker) to optimize the location of parcel lockers, implementing a heuristic procedure to solve the problem. Similarly, Lin et al. [52] formulated a parcel locker location problem from a logistics company’s perspective to maximize profit. The approach used a discrete choice model to predict the probability of using the parcel locker. Peppel and Spinler [53] developed a model to design the location of fixed parcel lockers by minimizing emissions and costs during delivery operations. Prandtstetter et al. [54] investigated the benefits of parcel lockers, considering in the model the travels of clients from home to the locker and the variation in pollutant emissions. Furthermore, Bonomi et al. [55] proposed a location problem to minimize the environmental impacts. In this approach, a vehicle can deliver either to the client’s home or to the parcel locker station. Enthoven et al. [56] proposed a two-echelon vehicle routing problem to minimize costs by optimizing locker location and routes to serve customers; in particular, in the first level, a truck travels from a depot to a locker location or to a satellite location: in the first case the customers themselves collect the order, in the latter the delivery is assigned to a light freight vehicle. Luo et al. [57] formulated a model to optimize the position of the locker stations and the number of lockers (minimizing the cost and maximizing customer accessibility). Orestein et al. [58] formulated a parcel delivery problem to optimize the number of vehicles and assign them the best route. Pan et al. [59] presented a model to design a delivery network with parcel lockers when more than one depot is available.
Gadheri et al. [60] crossed parcel locker services with crowd-shipping: specifically, multiple shippers use lockers as exchange points. The proposed heuristic procedure allowed the assignment of the delivery tasks to different stakeholders. Fessler et al. [61] presented some results of a test designed for placing parcel lockers in public transport stations; the experiment involved the passengers in the parcel delivery from one locker to another. Zhang et al. [62] proposed an approach wherein the parcel lockers are still an exchange point, and crowd shippers use public transport to deliver the parcel. dos Santos et al. [63] solved the same problem by considering a two-echelon approach wherein a crowd-shipper could support the courier. In this case, the parcels could also be transported there on off-peak hours, avoiding traffic congestion and reducing the impacts.
3. Problem Formulation and Methodology
The procedure presented in this section aimed to optimize the delivery process from the consumer’s perspective (contributing by increasing the social equity deriving from access to the digital market). The process foresees the use of an automatic delivery system in the context of a small island linked to the mainland by naval services only. First, however, it is necessary to make some clarifications:
- The problem was formulated in a time interval, and what happened outside of this interval was not considered;
- The empty trips of the parcel lockers (i.e., the return trips) were not considered;
- It was assumed that the couriers planned their activities in advance; thus the parcels to be delivered were at the port before the departure of the ferry;
- The approach was customer-oriented; thus, the costs of the couriers were not considered (in this paper it is considered that the monetary costs incurred by users do not suffer variations due to the improvement of the service).
3.1. The Problem
The problem consisted in serving a set D of customers following a customer-oriented approach (e.g., [64,65,66] which tried to minimize the lead time in receiving a parcel. It should be noted that this approach had the side effect of reducing the immobilization of parcels in the warehouse and optimizing the use of warehouse space.
The couriers delivered by using a set of parcel lockers L available at the port, and a generic locker ℓ with a capacity Cℓ. We defined a time interval τ; a set B of ferry trips was available; the generic trip i had a scheduled departure time tDi and a travel time tmi. Then, if a customer j ∈ D placed an order, the courier stored it in the depot at time tAj. The task was to send it together with other ones, minimizing customers’ waiting time. In this formulation, it was assumed that the parcel was available to the customer when it arrived at the destination port (i.e., the time spent by the customer travelling to the parcel locker was not considered). For convenience, if a customer received more than one delivery, he/she was inserted into the set D more than once.
The problem is formulated as a minimization problem (Equation (1)) subject to a set of constraints (Equations (2)–(7)):
subject to:
where:
- D is the set of customers;
- L is the set of lockers;
- B is the set of scheduled ferry trips;
- is the arrival time of the parcel addressed to client j at the courier;
- is the departure time of the ferry trip i;
- is the travel time of the ferry trip i;
- ts is a threshold value for customer waiting time;
- qj is the dimension (weight) of the parcel addressed to the customer j;
- Cℓ is the capacity of locker ℓ;
- rℓ is the load rate of the locker ℓ;
- xijℓ is a binary decision variable, equal to 1 if the locker ℓ containing the parcel coming to the user j is embarked on the ferry i; 0 otherwise.
The objective Function (1) minimizes the waiting time in receiving the parcel. It is defined as the difference between the instant in which the parcel is embarked on the ferry and the instant when it arrives at the courier depot; it also considers the travel time on the naval service. In Equation (1), the ferry travel time , to maintain the generality of the formulation, differs according to the naval service and the ferry type.
The Constraint (2) is on the locker capacity whereas Constraint (3) defines a utilization factor for each locker (to avoid under-loading parcel lockers). The Constraint (4) indicates that a customer j is served by only one locker ℓ. The Constraint (5) establishes the congruence between the arrival and departure time of the parcel. Constraint (6) indicates that the waiting time is less than a threshold value. Finally, Constraint (7) defines the domain of the variables.
3.2. The Solution Approach
Considering the aim to design a general procedure capable of solving large problems in a reasonable computing time, the choice falls on a heuristic procedure. Being heuristic, it allows solving the problem in a reduced amount of time, obtaining a solution which, although it may not be the optimal one, can be very close to it [67]. From the various heuristics available (such as tabu search, simulated annealing and ant colony), the approach proposed in this paper is a genetic algorithm (GA), a well-known heuristic used in many fields, both with discrete and continuous variables. Such an algorithm is a versatile approach able to solve discrete optimization problems; its structure allows it to code/encode the problem to apply the optimization operators. It generates the problem solution(s) by imitating the biological mechanisms of evolution. The generic workflow of the GA is reported in Figure 1. The initial population contains a set of feasible solutions, generated by a dedicated procedure (e.g., a constructive heuristic, a hungry algorithm or other ones). The number of solutions in the population is governed by a parameter N which defines the population size. The selection operator lets the analyst obtain a subset of solutions from a population and operate on this subset with the other operators. Various selection procedures are available, based on the goodness of fit (the fitness is usually a transformation of the solution cost). The crossover operator uses two parents to generate the offspring: as for biological entities, each parent provides a piece of code to be used in the generation of children (in general, the crossover can be repeated several times on the same pair of parents providing different children). A control parameter αc defines the number of solution pairs involved in the operation. The mutation operator is applied to generate further solutions by moving the elements in the solution from one position to another. A control parameter αm defines the number of solutions involved in the mutation. After applying the genetic operators, a new population of solutions is obtained (e.g., by replacing the parents with the children or using a selection operator). Finally, a test is performed to stop the procedure; generally, the test is on the number of iterations (it_max).
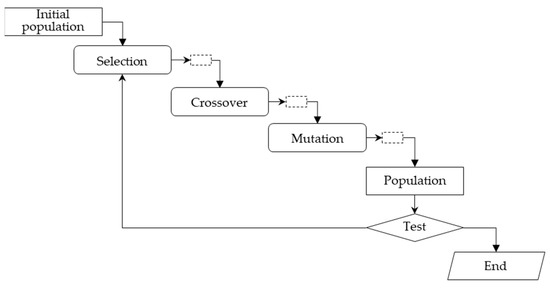
Figure 1.
Workflow of genetic algorithm.
In the proposed case study, the initial population is generated by a greedy algorithm, obtaining a set of feasible solutions. The selection operator is a stochastic universal sampling, considering the fitness as a transformation, based on a negative exponential function, of the solution cost. The crossover is an edge recombination crossover capable of preserving the order of elements in the solution. The mutation is a swap operator used to introduce variability into the population. Finally, the test is on the maximum number of iterations.
4. Application
The study area (Figure 2) was the island of Lipari, one of the Aeolian islands in the Tyrrhenian Sea. This choice appears plausible because this island is the largest (about 38 square kilometers) and the most populated (about 9800 inhabitants) of the Aeolian group; therefore, it attracts several parcels that justify this application. The study area was divided into 25 zones (Figure 3), following the subdivision proposed by the Italian institute of statistics, and data (e.g., population) are available for each zone. The most populated area is comprised of zones 1–9 (about 46% of the population resides there).
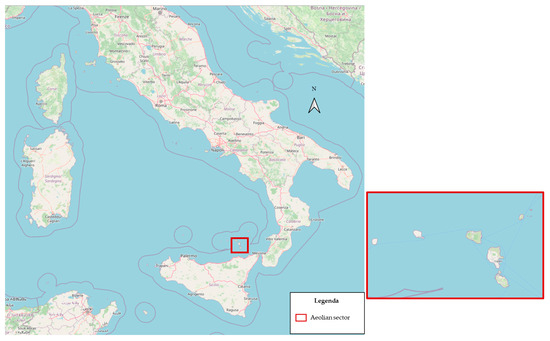
Figure 2.
Study area: Lipari Island (background map from OpenStreetMap).
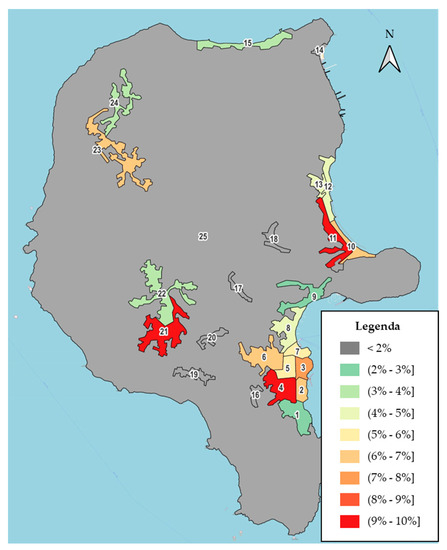
Figure 3.
Average deliveries per zone (background map from OpenStreetMap).
The number of parcels to be delivered for a given area represents an input value subjected to uncertainty for legal and privacy reasons. However, at an aggregate level, it was possible to obtain the online purchase rate of the population for each geographical area [68] and, considering the total amount of the population, it was possible to obtain an average value of online purchases. Following this reasoning, the average value was around 200 purchases per week (Figure 3).
4.1. Available Data
The application considered the use of parcel lockers in delivery operations, comparing the results with those obtainable by implementing a classic last-mile distribution with one or more small freight vehicles (laden weight less than 3.5 tons). The ferry trips connecting Lipari with Sicily and Italy are both with intermediate stops (to the other Aeolian islands) and direct (e.g., from Milazzo, Figure 4). At this stage, it was assumed that the delivery service was provided with direct trips, starting from the port of Milazzo. Under this assumption, the travel time was of 2.25 h. Furthermore, considering a time horizon τ of five days, the number of trips (from real scheduling) was 20. The time instant t = 0 was set at midnight of the first day and the other ones were calculated accordingly (all the values are in seconds). Table 1 reports the departure time of each ferry over the time horizon.
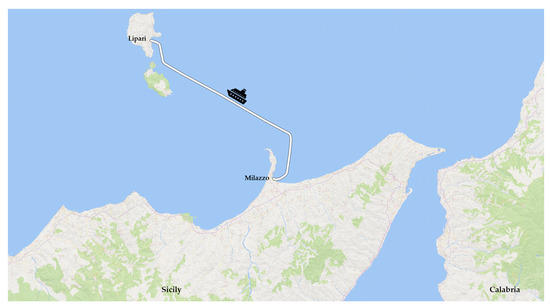
Figure 4.
Maritime link between Lipari and Sicily (background map from OpenStreetMap).

Table 1.
Ferry trips and departure time tDi (*).
In this preliminary test, it was assumed that there was one customer per zone, associating the entire quantity arriving in the zone with this customer. A total of 25 customers were then placed in the study area (Figure 5) and an average quantity qj (Table 2) was associated with each customer j (proportional to the population, according to the national statistical data [68]. Other data considered were the arrival time tAj of the parcel to the courier (randomly generated) and the client maximum waiting time ts (it was set at 48 h; note that the current delivery time guaranteed by couriers in this area is 72 h).
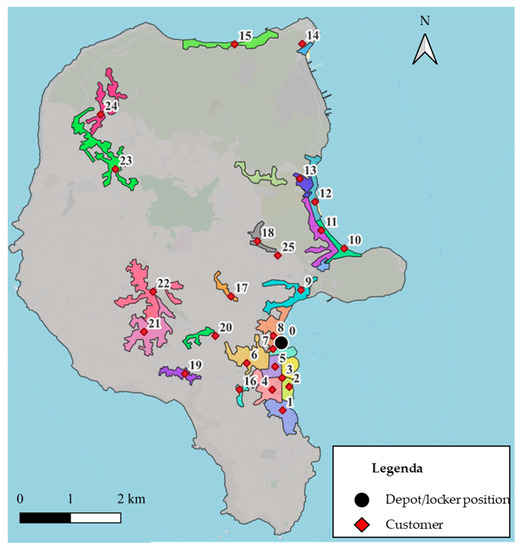
Figure 5.
Customer positions and characteristics (background map from OpenStreetMap).

Table 2.
Client id, quantity and parcel arrival time.
4.2. Parcel Lockers
The problem (1) was formulated in favor of the customers, in the sense that deliveries were organized in such a way as to minimize the waiting time. As reported in Section 3.2, the problem was solved with a genetic algorithm; the parameters used are reported in Table 3. The population size was of 30 individuals and the procedure was run for 1000 iterations, with a crossover rate of 60% and a mutation rate of 10%. Furthermore, it was assumed that all lockers had the same capacity C and must have been at least 70% filled (parameter r); this value is consistent with the average value of the load factor of vehicles in urban freight delivery [69].

Table 3.
Problem parameters.
A greedy algorithm generated the initial population, assigning the parcels to a ferry trip and considering the time constraints and locker capacity. For each solution i, the objective function Zi and a fitness value fi were calculated. The relationship between them is:
fi = exp(−β · Zi), with β > 0.
The selection operator is a stochastic universal sampling (SUS). It uses a random value for sampling and allows the selection of solutions with constant intervals. In contrast to other types of selection (for example, the roulette wheel) it also enables the selection of the worst elements of the population (e.g., an element with a high objective function), obtaining a more dispersed population. In this paper, the weight of a solution i was calculated as (note that the sum of wi is equal to 1):
By putting the values on a segment of unit length, each solution occupied a space proportional to the weight; thus, starting from a random offset, the procedure moved along the line with a regular step equal to 1/N (N is the number of elements in the population). Regarding the crossover, the approach used was an edge recombination crossover (ERX), capable of maintaining edge information; if two parcels were assigned to the same locker, the ERX tended to carry these parcels together (unless the constraints prevented it). The mutation was a swap procedure: a parcel was moved from one ferry trip to another within the constraints.
Since the GA is a heuristic procedure, a test is required to establish its stability. Thus, the optimal range of feasible solutions can be achieved by running the algorithm at different times. Figure 6 reports the results obtained from 30 runs; the objective function ranges from 1,366,589 s to 1,067,789 s, and the average value is equal to 1,250,542 s. Furthermore, the standard deviation is 84,588 (two orders of magnitude lower than the best-founded solution), and the ratio between the cost of the best and the worst solution is 0.73, indicating that the objective function values are quite stable with respect to the runs.
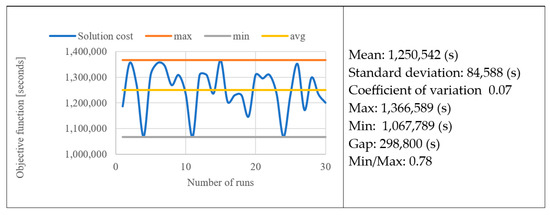
Figure 6.
Stability test for the genetic algorithm.
The test problem reached the best solution by using four different ferries and a single locker for each trip (Table 4). The locker load ranged from 60 (100% load rate) to 43 parcels (72% load rate). The average waiting time, evaluated as the difference between the instant when the parcel arrived at the courier depot and the instant when the parcel reached the harbour, was approximately 12 h.

Table 4.
The best-founded problem solution.
In the door-to-door delivery service, couriers had to respect the time constraints (5) and (6), to which other ones related to the driving time were added. In this scenario, they should have made at least two trips (using a vehicle with a capacity of 120 parcels, compatible with the characteristics of the study area and considering the time constraints). The vehicle routing problem (VRP) was defined by considering the port (indicated as depot in Figure 5) as the origin of each route performed by vehicles. To solve it, the VRP solver proposed by Erdogan [70] was used. Optimization was also considered in terms of distance travelled on the road network. As shown in Table 5, the use of the parcel lockers allowed the saving of 78.50 km over a time horizon of a week, or approximately 4000 km each year.

Table 5.
A possible solution for the vehicle routing problem.
If all customers made a trip solely to go to the locker, the balance (intended as the difference between the kilometers travelled by the courier and those travelled by clients) would be negative (that is, in terms of kilometers travelled, it would be better to use door-to-door distribution). Nevertheless, clients generally go to the locker during a trip chain (e.g., home–work travels), potentially making the balance positive [71,72]. It is remarkable that in a real-world situation, the lockers are often placed close to the workplace [73]. However, to evaluate this aspect, information on client behavior will be helpful.
Finally, the average waiting time for the clients was of 20.58 h (lower than the maximum guaranteed by the courier, but greater than the one found in the scenario with the parcel locker).
5. Discussion
This work has dealt with last-mile delivery for remote and disadvantaged areas, considering the case of small islands, where the services depend on ferries. The approach was developed considering the use of parcel lockers instead of the traditional door-to-door delivery service to overcome fragmentation, delivery failures and empty trips. The problem was formulated as an optimization problem (wherein the goal was minimizing customers’ waiting time) and solved with a genetic algorithm. A consolidated model was adopted to carry out the simulations, given that the purpose of the application was the analysis of the effects of the new logistic approach, before its real application in the field, and not the formulation of a new solution algorithm.
A test problem was generated by considering the island of Lipari (Aeolian archipelago, Tyrrhenian Sea, South Italy) as a study area. The freight to be delivered was estimated considering the population and the percentage of digital purchases in the area, using official data reported by the national statistical office. Considering a time horizon of five days, the area can be served by utilizing four parcel lockers, shipped on four different days, with an average waiting time for the customers of 11.86 h. If the same customers should be served with a traditional door-to-door service, the waiting time increases to 20.58 h; nowadays, the carriers’ companies guarantee shipments within 72 h of delivery to the area in question. These results demonstrate how introducing a parcel locker strategy could reduce the mean waiting time, thus increasing the service’s reliability. In this work, no assumptions have been made on how long the locker remains in port, and the service is simulated using four lockers.
6. Conclusions
The problem discussed in this paper relies on parcel lockers in last-mile freight distribution in very particular situations. In detail, the case of freight distribution in small islands has been addressed, where the last-mile distribution is connected with naval services. In a classic situation, the courier embarks on one or more freight vehicles which reach the island, and starts to travel to reach the users. It is a vehicle routing problem to whose constraints naval scheduling must be added: thus, the service is constrained by the timetable of ferries. In the proposed procedure, the introduction of parcel lockers relaxes, partly, the constraints, because the locker can remain on the island for more time than a vehicle without additional costs for the courier.
The proposed approach aims to contribute to the literature by integrating naval services and parcel lockers. Naturally, the research has some limitations: for example, the users’ demand has been analyzed in an aggregate way and it is not known whether users will accept the lockers. Therefore, future developments will be linked to the demand analysis and the design of a survey to understand the behavior of users regarding lockers. The analysis of the answers obtained will be useful; for example, in identifying the type of locker to use (e.g., fixed or mobile), where to position it (e.g., near inhabited areas or near workplaces) and in defining the possible policies to adopt in order to update the service.
Further development will consist in introducing constraints on the scheduling of the lockers and assessing the use of automated parcel lockers. Furthermore, other future development will focus on the application to a more extensive study area (in particular, all the Aeolian islands), quantifying the gain in pollutant emissions (this requires investigating the customers’ travel behavior), and the development of new solution procedures. Finally, the spreading of a on-field survey will be of interest to evaluate desire and expectation for different classes of stakeholders, thus evaluating the potential benefits and drawbacks of the introduction of such a service.
Author Contributions
Conceptualization, A.P., M.D.G. and O.M.B.; methodology, A.P.; software, A.P.; validation, M.D.G. and O.M.B.; formal analysis, A.P.; investigation, A.P. and O.M.B.; resources, M.D.G.; data curation, A.P.; writing—original draft preparation, A.P.; writing—review and editing, A.P., M.D.G. and O.M.B.; visualization, A.P., M.D.G. and O.M.B.; supervision, M.D.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding under “NAUSICA” (NAvi efficienti tramite l’Utilizzo di Soluzioni tecnologiche Innovative e low CArbon), under PON 2014-2020, project code: ARS01_00334.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request.
Acknowledgments
The authors wish to thank the reviewers for their suggestions, which were most useful in revising the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eurostat. E-Commerce Statistics for Individuals. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=E-commerce_statistics_for_individuals (accessed on 27 October 2022).
- Taniguchi, E.; Thompson, R.G.; Qureshi, A.G. Recent Developments and Prospects for Modeling City Logistics. In City Logistics 1; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2018; pp. 1–27. ISBN 978-1-119-42551-9. [Google Scholar]
- Russo, F.; Comi, A. A Classification of City Logistics Measures and Connected Impacts. Procedia-Soc. Behav. Sci. 2010, 2, 6355–6365. [Google Scholar] [CrossRef]
- Russo, F.; Comi, A. Investigating the Effects of City Logistics Measures on the Economy of the City. Sustainability 2020, 12, 1439. [Google Scholar] [CrossRef]
- Taniguchi, E. Concepts of City Logistics for Sustainable and Liveable Cities. Procedia-Soc. Behav. Sci. 2014, 151, 310–317. [Google Scholar] [CrossRef]
- Buldeo Rai, H.; Verlinde, S.; Macharis, C. City Logistics in an Omnichannel Environment. The Case of Brussels. Case Stud. Transp. Policy 2019, 7, 310–317. [Google Scholar] [CrossRef]
- Russo, F.; Comi, A. A Model System for the Ex-Ante Assessment of City Logistics Measures. Res. Transp. Econ. 2011, 31, 81–87. [Google Scholar] [CrossRef]
- Akgün, E.Z.; Monios, J.; Fonzone, A. Supporting Urban Consolidation Centres with Urban Freight Transport Policies: A Comparative Study of Scotland and Sweden. Int. J. Logist. Res. Appl. 2020, 23, 291–310. [Google Scholar] [CrossRef]
- Musolino, G.; Rindone, C.; Polimeni, A.; Vitetta, A. Planning Urban Distribution Center Location with Variable Restocking Demand Scenarios: General Methodology and Testing in a Medium-Size Town. Transp. Policy 2019, 80, 157–166. [Google Scholar] [CrossRef]
- Coppola, P.; Silvestri, F. Assessing the Impacts of E-Commerce on Future Urban Logistics Scenarios: Case Study of the City of Rome. Int. J. Transp. Econ. 2021, 48, 339–358. [Google Scholar]
- Teo, J.S.E.; Taniguchi, E.; Qureshi, A.G. Evaluation of Urban Distribution Centers Using Multiagent Modeling with Geographic Information Systems. Transp. Res. Rec. 2015, 2478, 35–47. [Google Scholar] [CrossRef]
- Juvvala, R.; Sarmah, S.P. Evaluation of Policy Options Supporting Electric Vehicles in City Logistics: A Case Study. Sustain. Cities Soc. 2021, 74, 103209. [Google Scholar] [CrossRef]
- Napoli, G.; Micari, S.; Dispenza, G.; Andaloro, L.; Antonucci, V.; Polimeni, A. Freight Distribution with Electric Vehicles: A Case Study in Sicily. RES, Infrastructures and Vehicle Routing. Transp. Eng. 2021, 3, 100047. [Google Scholar] [CrossRef]
- Polimeni, A.; Vitetta, A. Urban Transport Planning and Energy Resources: Electric Vehicle Routing with Reliable Link Travel Times. WIT Trans. Ecol. Environ. 2019, 238, 653–661. [Google Scholar]
- de Oliveira, L.K.; Macedo, A.D.R.; Sampaio, J.C.L.; de Oliveira, T.D.P.M.; de Oliveira, R.L.M.; Vieira, J.G.V. Challenges to Urban Freight Transport in Historical Cities: A Case Study for Sabará (Brazil). Transp. Res. Procedia 2019, 39, 370–380. [Google Scholar] [CrossRef]
- Russo, F.; Vitetta, A.; Polimeni, A. From Single Path to Vehicle Routing: The Retailer Delivery Approach. Procedia-Soc. Behav. Sci. 2010, 2, 6378–6386. [Google Scholar] [CrossRef]
- Belcore, O.M.; Polimeni, A.; Di gangi, M. Potential Demand for E-grocery Delivery Services: The effects of delivery attributes on consumers preferences. Transp. Res. Procedia. Forthcoming.
- Jung, H.; Kim, J. Drone Scheduling Model for Delivering Small Parcels to Remote Islands Considering Wind Direction and Speed. Comput. Ind. Eng. 2022, 163, 107784. [Google Scholar] [CrossRef]
- Hwang, J.; Kim, J.J.; Lee, K.-W. Investigating Consumer Innovativeness in the Context of Drone Food Delivery Services: Its Impact on Attitude and Behavioral Intentions. Technol. Forecast. Soc. Chang. 2021, 163, 120433. [Google Scholar] [CrossRef]
- Marinelli, M.; Caggiani, L.; Ottomanelli, M.; Dell’Orco, M. En Route Truck–Drone Parcel Delivery for Optimal Vehicle Routing Strategies. IET Intell. Transp. Syst. 2018, 12, 253–261. [Google Scholar] [CrossRef]
- Iannaccone, G.; Marcucci, E.; Gatta, V. What Young E-Consumers Want? Forecasting Parcel Lockers Choice in Rome. Logistics 2021, 5, 57. [Google Scholar] [CrossRef]
- Rohmer, S.; Gendron, B. CIRRELT-2020-11 A Guide to Parcel Lockers in Last Mile Distribution–Highlighting Challenges and Opportunities from an OR Perspective; Cirrelt: Montreal, QC, Canada, 2020. [Google Scholar]
- Rossolov, A. A Last-Mile Delivery Channel Choice by E-Shoppers: Assessing the Potential Demand for Automated Parcel Lockers. Int. J. Logist. Res. Appl. 2021, 1–23. [Google Scholar] [CrossRef]
- Deutsch, Y.; Golany, B. A Parcel Locker Network as a Solution to the Logistics Last Mile Problem. Int. J. Prod. Res. 2018, 56, 251–261. [Google Scholar] [CrossRef]
- Iwan, S.; Kijewska, K.; Lemke, J. Analysis of parcel lockers’ efficiency as the last mile delivery solution–the results of the research in Poland. Transp. Res. Procedia 2016, 12, 644–655. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Comi, A. Urban Freight Demand Forecasting: A Mixed Quantity/Delivery/Vehicle-Based Model. Transp. Res. Part E Logist. Transp. Rev. 2014, 65, 84–98. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Persia, L.; Polimeni, A. Agent-Based Simulation of Urban Goods Distribution: A Literature Review. Transp. Res. Procedia 2018, 30, 33–42. [Google Scholar] [CrossRef]
- Comi, A.; Nuzzolo, A.; Polimeni, A. Aggregate Delivery Tour Modeling through AVM Data: Experimental Evidence for Light Goods Vehicles. Transp. Lett. 2021, 13, 201–208. [Google Scholar] [CrossRef]
- Comi, A.; Savchenko, L. Last-Mile Delivering: Analysis of Environment-Friendly Transport. Sustain. Cities Soc. 2021, 74, 103213. [Google Scholar] [CrossRef]
- Castiglione, M.; Comi, A.; De Vincentis, R.; Dumitru, A.; Nigro, M. Delivering in Urban Areas: A Probabilistic-Behavioral Approach for Forecasting the Use of Electric Micromobility. Sustainability 2022, 14, 9075. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. A Heuristic Algorithm for the Symmetric and Asymmetric Vehicle Routing Problems with Backhauls. Eur. J. Oper. Res. 1999, 113, 528–543. [Google Scholar] [CrossRef]
- Özarık, S.S.; Veelenturf, L.P.; Woensel, T.V.; Laporte, G. Optimizing E-Commerce Last-Mile Vehicle Routing and Scheduling under Uncertain Customer Presence. Transp. Res. Part E Logist. Transp. Rev. 2021, 148, 102263. [Google Scholar] [CrossRef]
- Moccia, L.; Laporte, G. Improved Models for Technology Choice in a Transit Corridor with Fixed Demand. Transp. Res. Part B Methodol. 2016, 83, 245–270. [Google Scholar] [CrossRef]
- Muñoz-Villamizar, A.; Santos, J.; Montoya-Torres, J.R.; Velázquez-Martínez, J.C. Measuring Environmental Performance of Urban Freight Transport Systems: A Case Study. Sustain. Cities Soc. 2020, 52, 101844. [Google Scholar] [CrossRef]
- Heimfarth, A.; Ostermeier, M.; Hübner, A. A Mixed Truck and Robot Delivery Approach for the Daily Supply of Customers. Eur. J. Oper. Res. 2022, 303, 401–421. [Google Scholar] [CrossRef]
- Montoya-Torres, J.R.; Muñoz-Villamizar, A.; Vega-Mejía, C.A. On the Impact of Collaborative Strategies for Goods Delivery in City Logistics. Prod. Plan. Control 2016, 27, 443–455. [Google Scholar] [CrossRef]
- Antún, J.P.; Reis, V.; Macário, R. Strategies to Improve Urban Freight Logistics in Historical Centers: The Cases of Lisbon and Mexico City. In City Logistics 3; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2018; pp. 349–366. ISBN 978-1-119-42547-2. [Google Scholar]
- He, Z. The Challenges in Sustainability of Urban Freight Network Design and Distribution Innovations: A Systematic Literature Review. Int. J. Phys. Distrib. Logist. Manag. 2020, 50, 601–640. [Google Scholar] [CrossRef]
- Comi, A.; Polimeni, A. Freight transport and land use interaction: An analysis approach based on floating car data. Transp. Res. Procedia. forthcoming.
- Yuen, K.F.; Wang, X.; Ma, F.; Wong, Y.D. The Determinants of Customers’ Intention to Use Smart Lockers for Last-Mile Deliveries. J. Retail. Consum. Serv. 2019, 49, 316–326. [Google Scholar] [CrossRef]
- Mitrea, I.A.; Zenezini, G.; De Marco, A.; Ottaviani, F.M.; Delmastro, T.; Botta, C. Estimating E-Consumers’ Attitude Towards Parcel Locker Usage. In Proceedings of the 2020 IEEE 44th Annual Computers, Software, and Applications Conference (COMPSAC), Madrid, Spain, 13–17 July 2020; pp. 1731–1736. [Google Scholar]
- Tang, Y.M.; Chau, K.Y.; Xu, D.; Liu, X. Consumer Perceptions to Support IoT Based Smart Parcel Locker Logistics in China. J. Retail. Consum. Serv. 2021, 62, 102659. [Google Scholar] [CrossRef]
- Lai, P.L.; Jang, H.; Fang, M.; Peng, K. Determinants of Customer Satisfaction with Parcel Locker Services in Last-Mile Logistics. Asian J. Shipp. Logist. 2022, 38, 25–30. [Google Scholar] [CrossRef]
- An, H.S.; Park, A.; Song, J.M.; Chung, C. Consumers’ Adoption of Parcel Locker Service: Protection and Technology Perspectives. Cogent Bus. Manag. 2022, 9, 2144096. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Boysen, N. Optimizing the Changing Locations of Mobile Parcel Lockers in Last-Mile Distribution. Eur. J. Oper. Res. 2020, 285, 1077–1094. [Google Scholar] [CrossRef]
- Li, J.; Ensafian, H.; Bell, M.G.H.; Geers, D.G. Deploying Autonomous Mobile Lockers in a Two-Echelon Parcel Operation. Transp. Res. Part C Emerg. Technol. 2021, 128, 103155. [Google Scholar] [CrossRef]
- Wang, Y.; Bi, M.; Chen, Y. A Scheduling Strategy of Mobile Parcel Lockers for the Last Mile Delivery Problem. Promet-TrafficTransp. 2020, 32, 875–885. [Google Scholar] [CrossRef]
- Wang, Y.; Bi, M.; Lai, J.; Chen, Y. Locating Movable Parcel Lockers under Stochastic Demands. Symmetry 2020, 12, 2033. [Google Scholar] [CrossRef]
- Lachapelle, U.; Burke, M.; Brotherton, A.; Leung, A. Parcel Locker Systems in a Car Dominant City: Location, Characterisation and Potential Impacts on City Planning and Consumer Travel Access. J. Transp. Geogr. 2018, 71, 1–14. [Google Scholar] [CrossRef]
- Che, Z.H.; Chiang, T.A.; Luo, Y.J. Multiobjective Optimization for Planning the Service Areas of Smart Parcel Locker Facilities in Logistics Last Mile Delivery. Mathematics 2022, 10, 422. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, Y.; Lee, L.H.; Chew, E.P. Profit-Maximizing Parcel Locker Location Problem under Threshold Luce Model. Transp. Res. Part E Logist. Transp. Rev. 2022, 157, 102541. [Google Scholar] [CrossRef]
- Peppel, M.; Spinler, S. The Impact of Optimal Parcel Locker Locations on Costs and the Environment. Int. J. Phys. Distrib. Logist. Manag. 2022, 52, 324–350. [Google Scholar] [CrossRef]
- Prandtstetter, M.; Seragiotto, C.; Braith, J.; Eitler, S.; Ennser, B.; Hauger, G.; Hohenecker, N.; Schodl, R.; Steinbauer, M. On the Impact of Open Parcel Lockers on Traffic. Sustainability 2021, 13, 755. [Google Scholar] [CrossRef]
- Bonomi, V.; Mansini, R.; Zanotti, R. Last Mile Delivery with Parcel Lockers: Evaluating the Environmental Impact of Eco-Conscious Consumer Behavior. IFAC-PapersOnLine 2022, 55, 72–77. [Google Scholar] [CrossRef]
- Enthoven, D.L.J.U.; Jargalsaikhan, B.; Roodbergen, K.J.; uit het Broek, M.A.J.; Schrotenboer, A.H. The Two-Echelon Vehicle Routing Problem with Covering Options: City Logistics with Cargo Bikes and Parcel Lockers. Comput. Oper. Res. 2020, 118, 104919. [Google Scholar] [CrossRef]
- Luo, R.; Ji, S.; Ji, Y. An Active-Learning Pareto Evolutionary Algorithm for Parcel Locker Network Design Considering Accessibility of Customers. Comput. Oper. Res. 2022, 141, 105677. [Google Scholar] [CrossRef]
- Orenstein, I.; Raviv, T.; Sadan, E. Flexible Parcel Delivery to Automated Parcel Lockers: Models, Solution Methods and Analysis. EURO J. Transp. Logist. 2019, 8, 683–711. [Google Scholar] [CrossRef]
- Pan, S.; Zhang, L.; Thompson, R.G.; Ghaderi, H. A Parcel Network Flow Approach for Joint Delivery Networks Using Parcel Lockers. Int. J. Prod. Res. 2021, 59, 2090–2115. [Google Scholar] [CrossRef]
- Ghaderi, H.; Zhang, L.; Tsai, P.-W.; Woo, J. Crowdsourced Last-Mile Delivery with Parcel Lockers. Int. J. Prod. Econ. 2022, 251, 108549. [Google Scholar] [CrossRef]
- Fessler, A.; Cash, P.; Thorhauge, M.; Haustein, S. A Public Transport Based Crowdshipping Concept: Results of a Field Test in Denmark. Transp. Policy 2023, 134, 106–118. [Google Scholar] [CrossRef]
- Zhang, M.; Cheah, L.; Courcoubetis, C. Exploring the Potential Impact of Crowdshipping Using Public Transport in Singapore. Transp. Res. Rec. 2022, 2677, 173–189. [Google Scholar] [CrossRef]
- dos Santos, A.G.; Viana, A.; Pedroso, J.P. 2-Echelon Lastmile Delivery with Lockers and Occasional Couriers. Transp. Res. Part E Logist. Transp. Rev. 2022, 162, 102714. [Google Scholar] [CrossRef]
- Ling, T.K.; Lee, C.K.M.; Ho, W. The Analysis and Case Studies of Successful Express Logistics Companies. Int. J. Value Chain Manag. 2009, 3, 20–35. [Google Scholar] [CrossRef]
- Mikula, J.; Kulich, M. Solving the Traveling Delivery Person Problem with Limited Computational Time. Cent. Eur. J. Oper. Res. 2022, 30, 1451–1481. [Google Scholar] [CrossRef]
- Mishra, A.; Anning-Dorson, T. Dynamic Customer-Oriented Relational Capabilities: How Do They Impact Internationalizing Firm Performance? J. Serv. Theory Pract. 2022, 32, 843–871. [Google Scholar] [CrossRef]
- Dréo, J.; Siarry, P.; Pétrowski, A.; Taillard, E. Metaheuristics for Hard Optimization: Simulated Annealing, Tabu Search, Evolutionary and Genetic Algorithms, Ant Colonies,... Methods and Case Studies; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- ISTAT. Available online: http://Dati.Istat.It/Index.Aspx?QueryId=23002 (accessed on 18 November 2022).
- Thompson, R.G.; Taniguchi, E. City Logistics and Freight Transport. In Handbook of Logistics and Supply-Chain Management; Brewer, A.M., Button, K.J., Hensher, D.A., Eds.; Emerald Group Publishing Limited: Bingley, UK, 2017; Volume 2, pp. 393–405. ISBN 978-0-85724-563-2. [Google Scholar]
- Erdoğan, G. An Open Source Spreadsheet Solver for Vehicle Routing Problems. Comput. Oper. Res. 2017, 84, 62–72. [Google Scholar] [CrossRef]
- Hofer, K.; Flucher, S.; Fellendorf, M.; Schadler, M.; Hafner, N. Estimation of Changes in Customer’s Mobility Behaviour by the Use of Parcel Lockers. Transp. Res. Procedia 2020, 47, 425–432. [Google Scholar] [CrossRef]
- Belcore, O.M. Discrete Choice Model Assessing Attitudes Effects on Decisions: An Exploratory Modelling Approach, Based on Empirical Choice Observation to Analyse Households. Ph.D. Thesis, University of Reggio Calabria, Reggio Calabria, Italy, 2020. [Google Scholar]
- Schaefer, J.S.; Figliozzi, M.A. Spatial Accessibility and Equity Analysis of Amazon Parcel Lockers Facilities. J. Transp. Geogr. 2021, 97, 103212. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).