Scale Effects on Shear Strength of Rough Rock Joints Caused by Normal Stress Conditions
Abstract
1. Introduction
| Authors | Rock Types | Sample Size | Normal Stress (MPa) | Scale Effect |
|---|---|---|---|---|
| Azinfar et al. [13] | Silicon rubber | 25–2500 cm2 | 0.3, 0.8, 1.4 | O, N, P |
| Barton and Choubey [19] | Granite | 9.8 × 4.5, 45 × 50 cm | 0.1–2 | N |
| Bandis et al. [22] | plaster | 6–36 cm | 1 | N |
| Bahaaddini et al. [21] | Sandstone | 5–40 cm | 0.5 | N |
| Castelli et al. [23] | Cement | 100–400 cm2 | 0.75, 1.5, 3 | N |
| Fardin [24] | Concrete | 5 × 5–20 × 20 cm2 | 1, 2.5, 5, 10 | N |
| Hencher et al. [25] | Limestone | 44–531 cm2 | 0.0245 | O |
| Johansson [26] | Granite | 36, 400 cm2 | 1 | O |
| Ohnishi et al. [12] | Concrete | 100–1000 cm2 | 0.26–2.04 | P |
| Pratt et al. [14] | Quartz diorite | 60, 142–5130 cm2 | 3 | N |
| Ueng et al. [15] | Cement | 7.5–30 cm2 | 0.3, 0.6, 0.9 | O, N |
| Vallier et al. [27] | - | 10–200 cm | 2 | N |
| Yoshinaka et al. [17] | Granite | 20–9600 cm2 | 0.26–2.04 | N |
2. Synthetic Rock Model for Numerical Tests
2.1. Synthetic Rock Model Based on PFC2D
2.2. Calibration of Numerical Models
3. Validation of Synthetic Rock Models
3.1. Barton’s Shear Strength Model
3.2. Numerical Simulation Results
4. Configuration of Rock Samples for Scale Effect Investigations
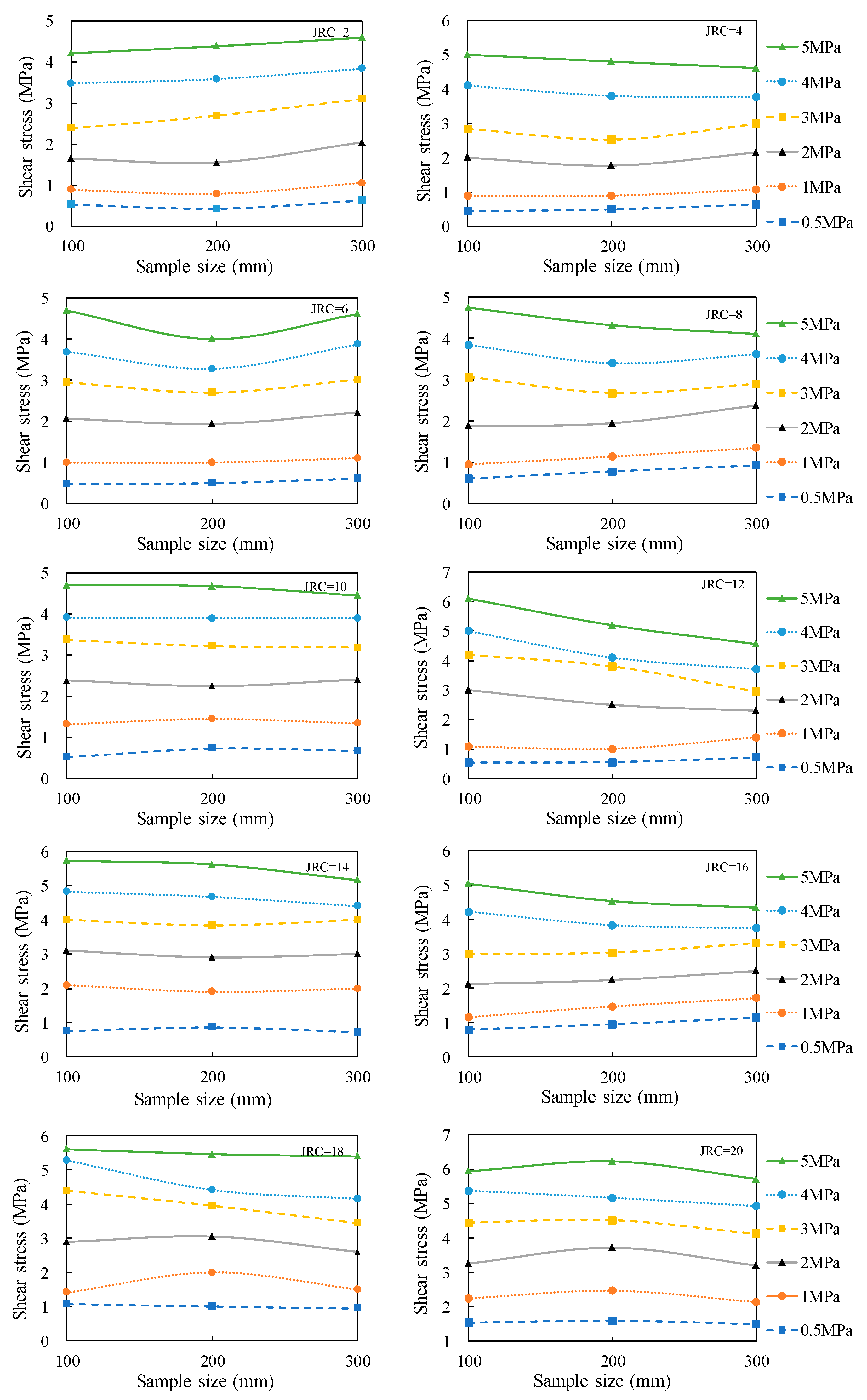
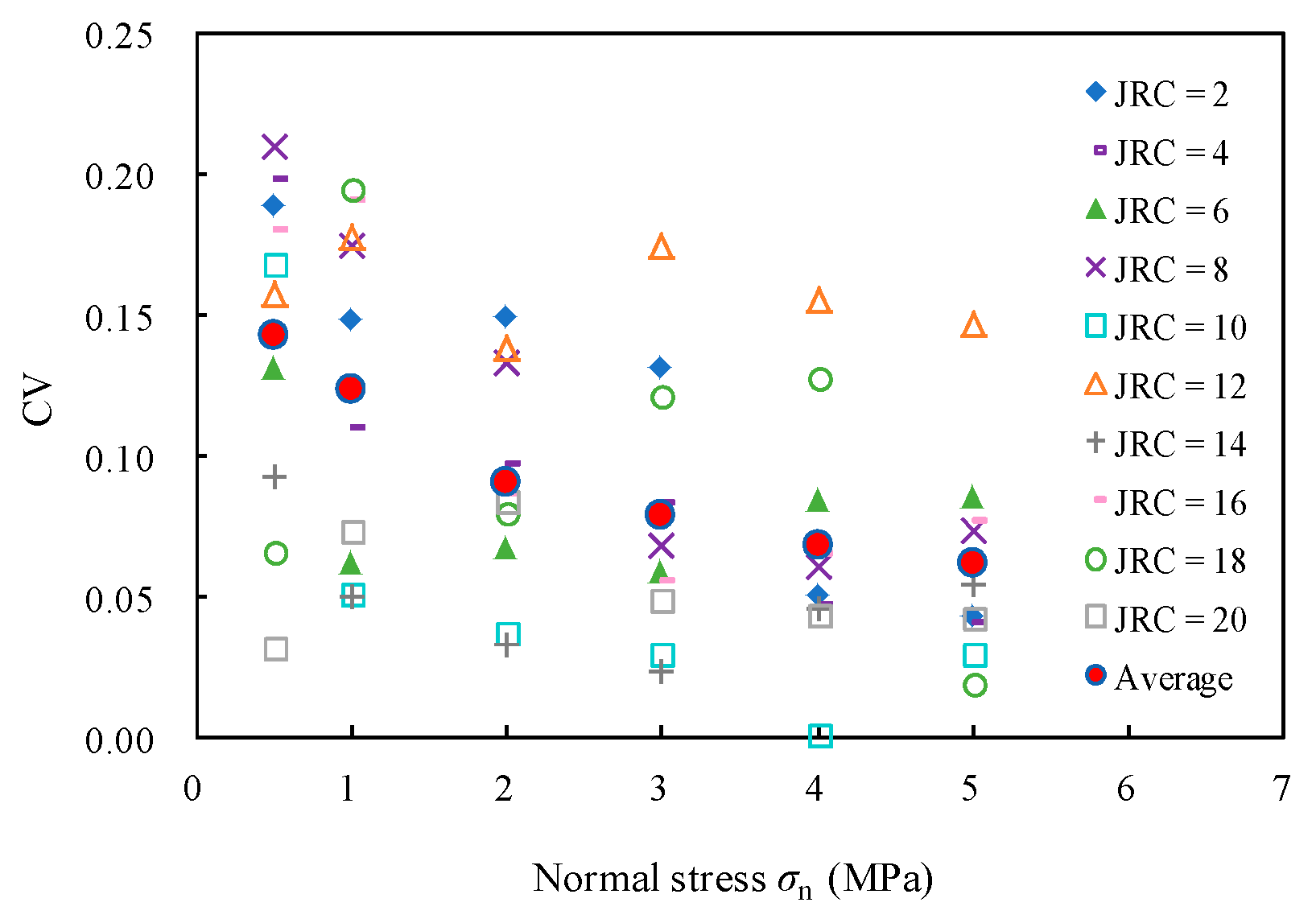
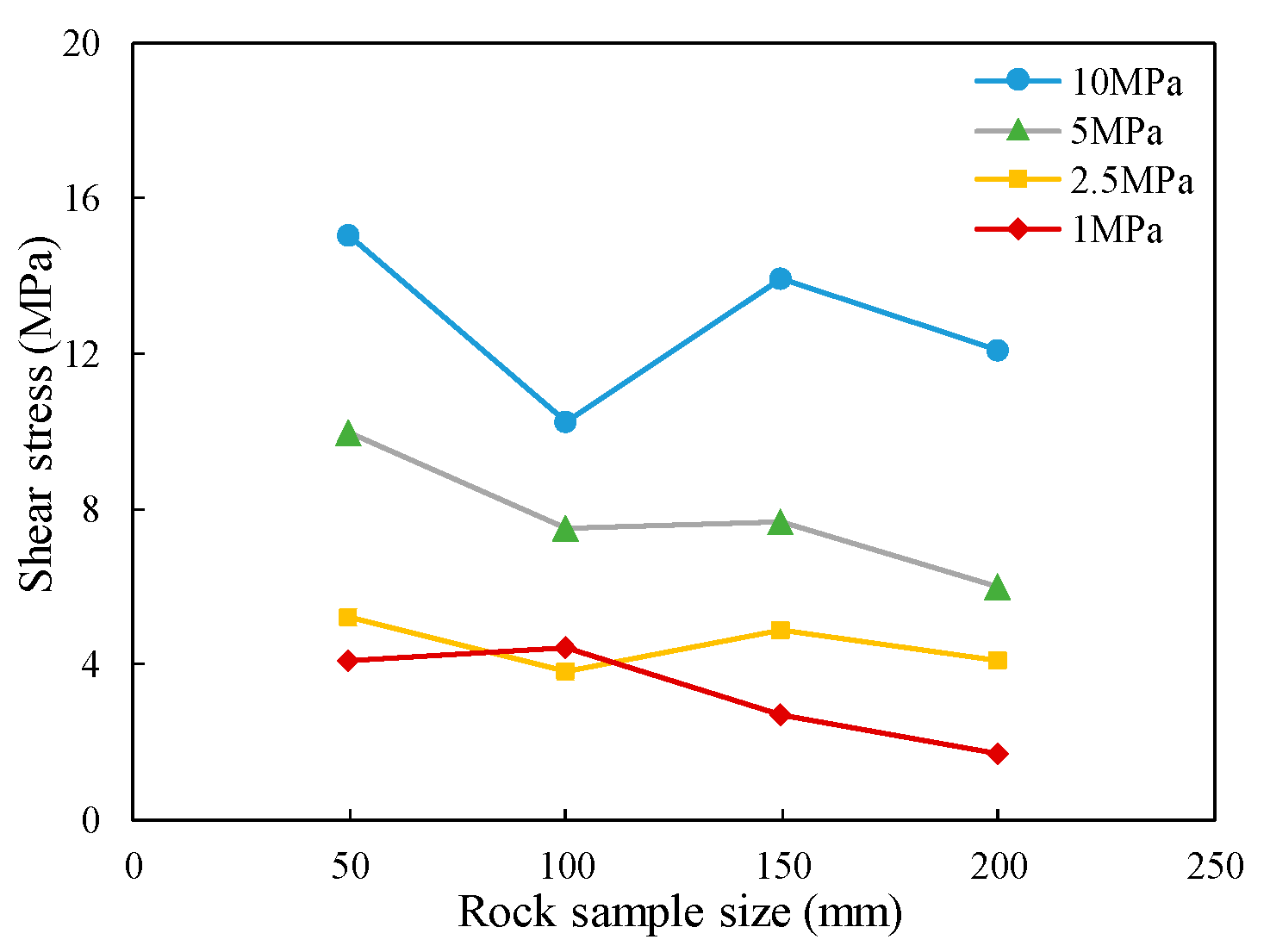
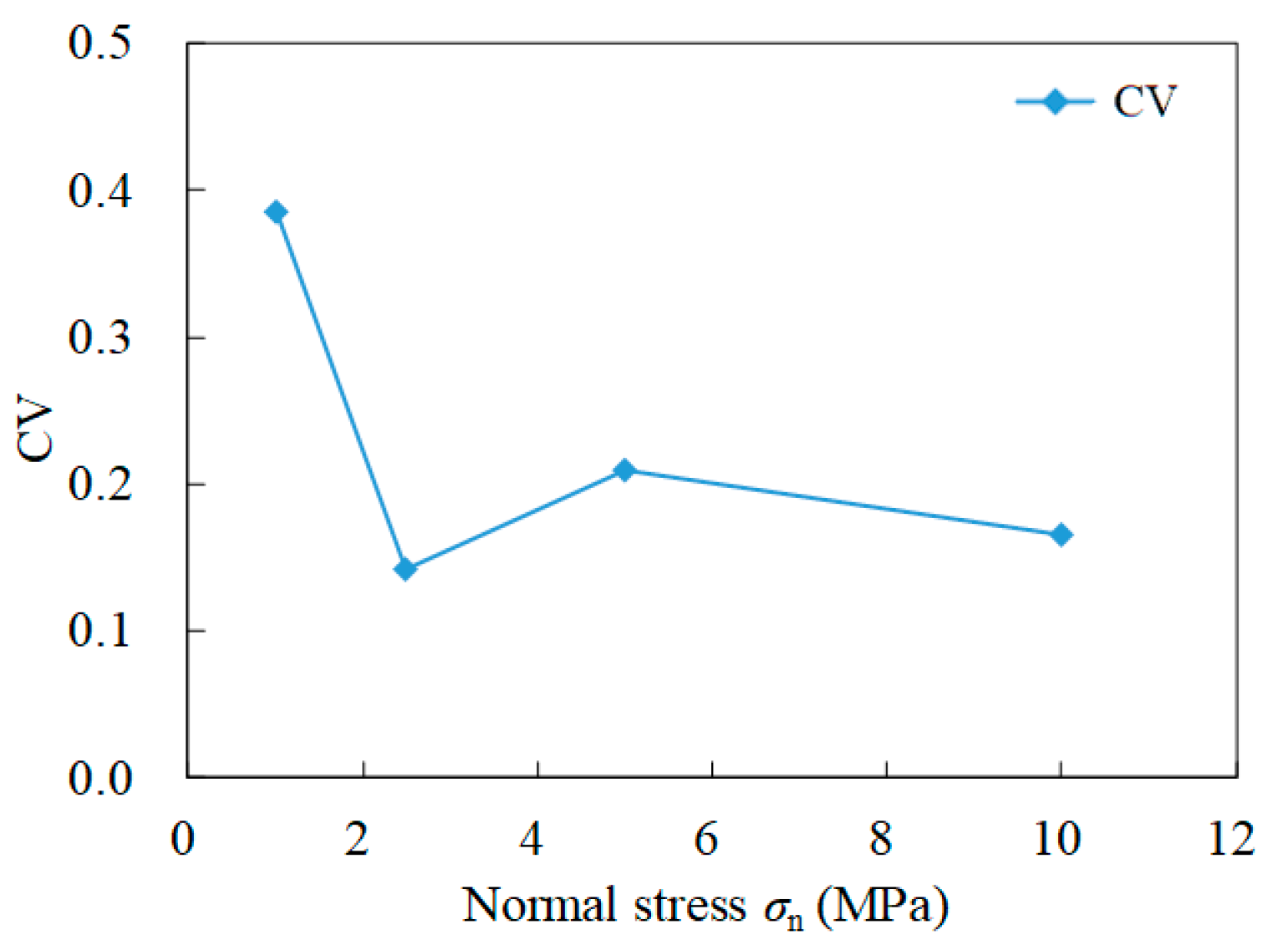
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, F.; Wang, S.; Yao, W.; Li, X.; Meng, F.; Xia, K. Effect of roughness on the shear behavior of rock joints subjected to impact loading. J. Rock Mech. Geotech. Eng. 2023, 15, 339–349. [Google Scholar] [CrossRef]
- Seungbeom, C.; Byungkyu, J.; Sudeuk, L.; Seokwon, J. Experimental Study on Hydromechanical Behavior of an Artificial Rock Joint with Controlled Roughness. Sustainability 2019, 11, 1014. [Google Scholar] [CrossRef]
- Seungbeom, C.; Sudeuk, L.; Hoyoung, J.; Seokwon, J. Development of a New Method for the Quantitative Generation of an Artificial Joint Specimen with Specific Geometric Properties. Sustainability 2019, 11, 373. [Google Scholar] [CrossRef]
- Yong, R.; Ye, J.; Li, B.; Du, S. Determining the maximum sampling interval in rock join roughness measurements using Fourier series. Int. J. Rock Mech. Min. Sci. 2018, 101, 77–78. [Google Scholar] [CrossRef]
- Hu, J.; Pan, H.; Liu, H.; Li, L.; Fan, H.; Liu, Q. Response of acoustic emission and vibration monitoring data during rock block collapse in the tunnel: Small-and large-scale experiments study. Tunn. Undergr. Space Technol. 2023, 137, 105121. [Google Scholar] [CrossRef]
- Li, S.; Huang, Q.; Hu, B.; Pan, J.; Chen, J.; Yang, J.; Yu, H. Mining Method Optimization of Difficult-to-Mine Complicated Orebody Using Pythagorean Fuzzy Sets and TOPSIS Method. Sustainability 2023, 15, 3692. [Google Scholar] [CrossRef]
- Hencher, S.; Richards, L. Assessing the shear strength of rock discontinuities at laboratory and field scales. Rock Mech. Rock Eng. 2015, 48, 883–905. [Google Scholar] [CrossRef]
- Buzzi, O.; Casagrande, D. A step towards the end of the scale effect conundrum when predicting the shear strength of large in situ discontinuities. Int. J. Rock Mech. Min. Sci. 2018, 105, 210–219. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Y.; Guo, H.; Liu, X.; Luo, Y.; Liu, Y. Relationship between Joint Roughness Coefficient and Statistical Roughness Parameters and Its Sensitivity to Sampling Interval. Sustainability 2022, 14, 13597. [Google Scholar] [CrossRef]
- Shen, J.; Shu, Z.; Cai, M.; Du, S. A shear strength model for anisotropic blocky rock masses with persistent joints. Int. J. Rock Mech. Min. Sci. 2020, 134, 104430. [Google Scholar] [CrossRef]
- Alejano, L.; Arzúa, J.; Bozorgzadeh, N.; Harrison, J. Triaxial strength and deformability of intact and increasingly jointed granite samples. Int. J. Rock Mech. Min. Sci. 2017, 95, 87–103. [Google Scholar] [CrossRef]
- Ohnishi, Y.; Herda, H.; Yoshinaka, R. Shear strength scale effect and the geometry of single and repeated rock joints. In Scale Effects in Rock Masses; CRC Press: Boca Raton, FL, USA, 1993; pp. 167–173. [Google Scholar]
- Azinfar, M.; Ghazvinian, A.; Nejati, H. Assessment of scale effect on 3D roughness parameters of fracture surfaces. Eur. J. Environ. Civ. Eng. 2019, 23, 1–28. [Google Scholar] [CrossRef]
- Pratt, H.; Black, A.; Brace, W. Friction and deformation of jointed quartz diorite. In Proceedings of the Third ISRM Congress, Denver, Colorado, 1–7 September 1974; pp. 306–310. [Google Scholar]
- Ueng, T.; Jou, Y.; Peng, I. Scale effect on shear strength of computer aided manufactured joints. J. Geoengin. 2010, 5, 29–37. [Google Scholar]
- Pirzada, M.; Roshan, H.; Sun, H.; Oh, J.; Bahaaddini, M. Effect of contact surface area on frictional behaviour of dry and saturated rock joints. J. Struct. Geol. 2020, 135, 104044. [Google Scholar] [CrossRef]
- Yoshinaka, R.; Yoshida, J.; Shimizu, T.; Arai, H.; Arisaka, S. Scale effect in shear strength and deformability of rock joints. In Proceedings of the 7th ISRM International Congress on Rock Mechanics, Aachen, Germany, 16–20 September 1991. [Google Scholar] [CrossRef]
- Leal, G. Some new essential questions about scale effects on the mechanics of rock mass joints. In Proceedings of the 10th ISRM Congress: Technology Roadmap for Rock Mechanics, Sandton, South Africa, 8–12 September 2003. [Google Scholar]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Min. Sci. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Giani, G.; Ferrero, A.; Passarello, G.; Reinaudo, L. Scale effect evaluation on natural discontinuity shear strength. Fract. Jt. Rock Masses 1992, 30, 447–452. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Hagan, P.; Mitra, R.; Hebblewhite, B. Scale effect on the shear behaviour of rock joints based on a numerical study. Eng. Geol. 2014, 181, 212–223. [Google Scholar] [CrossRef]
- Bandis, S.; Lumsden, A.; Barton, N. Experimental studies of scale effects on the shear behaviour of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 1–21. [Google Scholar] [CrossRef]
- Castelli, M.; Re, F.; Scavia, C.; Zaninetti, Z. Experimental evaluation of scale effects on the mechanical behavior of rock joints. In Proceedings of the ISRM Regional Symposium EUROCK 2001, Espoo, Finland, 4–7 June 2001; pp. 205–210. [Google Scholar]
- Fardin, N. Influence of structural non-stationarity of surface roughness on morphological characterization and mechanical deformation of rock joints. Rock Mech. Rock Eng. 2008, 41, 267–297. [Google Scholar] [CrossRef]
- Hencher, S.; Toy, J.; Lumsden, A. Scale dependent shear strength of rock joints. In Proceedings of the International Workshop in Scale Effects in Rock Masses, Lisbon, Portugl, 25 June 1993; Volume 93, pp. 233–240. [Google Scholar]
- Johansson, F. Influence of scale and matedness on the peak shear strength of fresh, unweathered rock joints. Int. J. Rock Mech. Min. Sci. 2016, 82, 36–47. [Google Scholar] [CrossRef]
- Vallier, F.; Mitani, Y.; Boulon, M.; Esaki, F. A shear model accounting scale effect in rock joints behavior. Rock Mech. Rock Eng. 2010, 43, 581–595. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Hagan, P.; Mitra, R.; Hebblewhite, B. Parametric study of smooth joint parameters on the shear behaviour of rock joints. Rock Mech. Rock Eng. 2015, 48, 923–940. [Google Scholar] [CrossRef]
- Huang, H.; Shen, J.; Chen, Q.; Karakus, M. Estimation of REV for fractured rock masses based on Geological Strength Index. Int. J. Rock Mech. Min. Sci. 2020, 126, 104–179. [Google Scholar] [CrossRef]
- Shen, J.; Zhan, S.; Karakus, M.; Zuo, J. Effects of flaw width on cracking behavior of single-flawed rock specimens. Bull. Eng. Geol. Environ. 2021, 80, 1701–1711. [Google Scholar] [CrossRef]
- Zhou, C.; Xu, C.; Karakus, M.; Shen, J. A systematic approach to the calibration of micro-parameters for the flat-jointed bonded particle model. Geomech. Eng. 2018, 16, 471–482. [Google Scholar] [CrossRef]
- Cundall, P.; Potyondy, D. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Chen, Y.; Sheng, B.; Xie, S.; Cao, R.; Wang, Y.; Zhao, Y.; Lin, H. Crack propagation and scale effect of random fractured rock under compression-shear loading. J. Mater. Res. Technol. 2023, 23, 5164–5180. [Google Scholar] [CrossRef]
- Wang, P.; Ren, F.; Miao, S.; Cai, M.; Yang, T. Evaluation of the anisotropy and directionality of a jointed rock mass under numerical direct shear tests. Eng. Geol. 2017, 225, 29–41. [Google Scholar] [CrossRef]
- Maqsood, Z.; Koseki, J.; Miyashita, Y.; Xie, J.; Kyokawa, H. Experimental study on the mechanical behaviour of bounded geomaterials under creep and cyclic loading considering effects of instantaneous strain rates. Eng. Geol. 2020, 276, 105774. [Google Scholar] [CrossRef]
- Swan, G.; Cook, J.; Bruce, S.; Meehan, R. Strain rate effects in Kimmeridge Bay shale. Int. J. Rock Mech. Min. Sci. 1989, 26, 135–149. [Google Scholar] [CrossRef]
- Maqsood, Z.; Koseki, J.; Ahsan, M.; Shaikh, M.; Kyokawa, H. Experimental study on hardening characteristics and loading rate dependent mechanical behaviour of gypsum mixed sand. Constr. Build. Mater. 2020, 262, 119992. [Google Scholar] [CrossRef]
- Liu, S.; Wang, W.; Cao, Y.; Li, H.; Shao, J. Numerical study of the influence of loading rate on fracture mechanism in elastoplastic rock-like materials with a modified phase-field model. Int. J. Rock Mech. Min. Sci. 2023, 162, 105309. [Google Scholar] [CrossRef]
- Barton, N.; Bandis, S. Some effects of scale on the shear strength of joints. Int. J. Rock Mech. Min. Sci. 1980, 17, 69–73. [Google Scholar] [CrossRef]


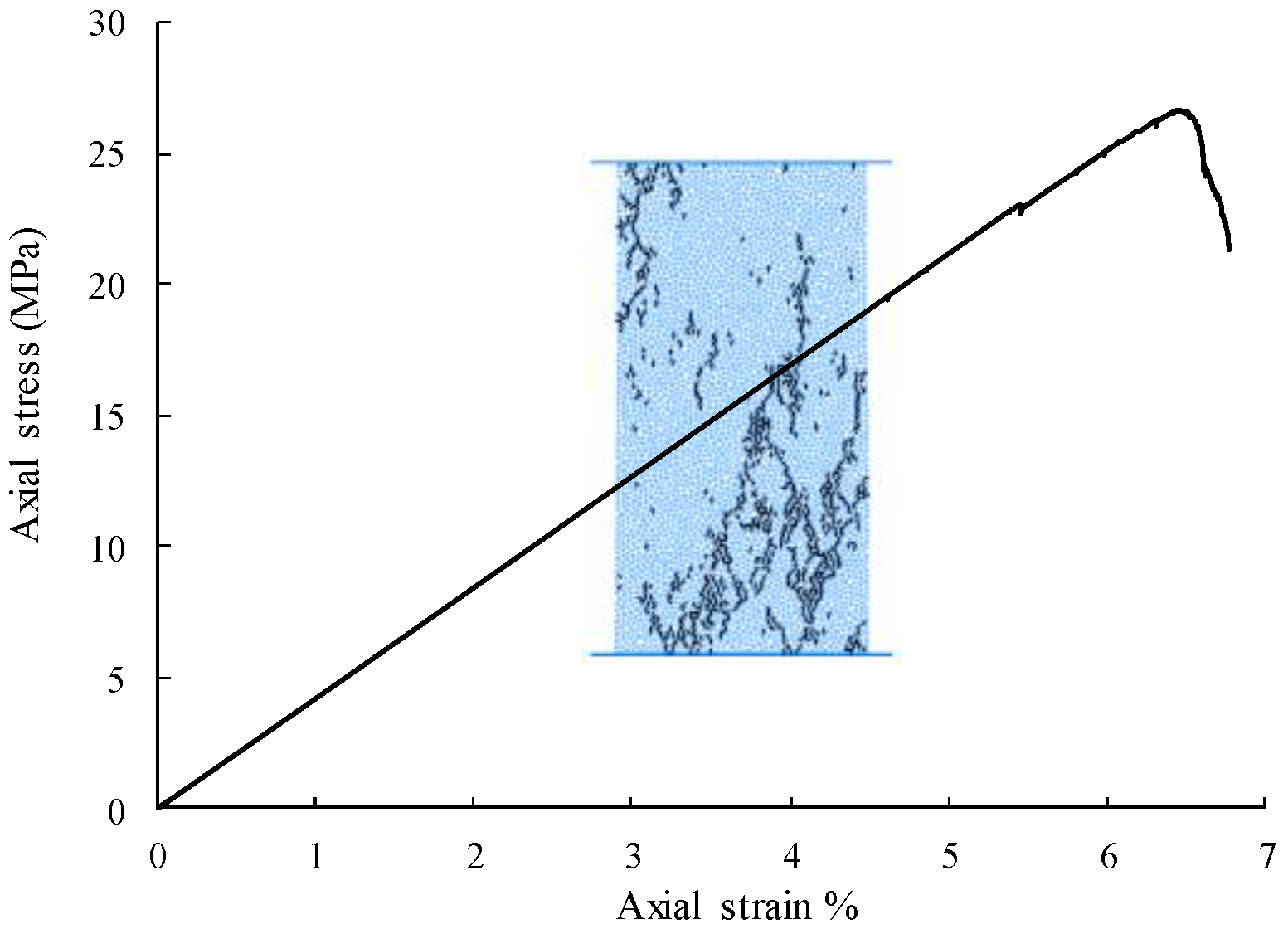
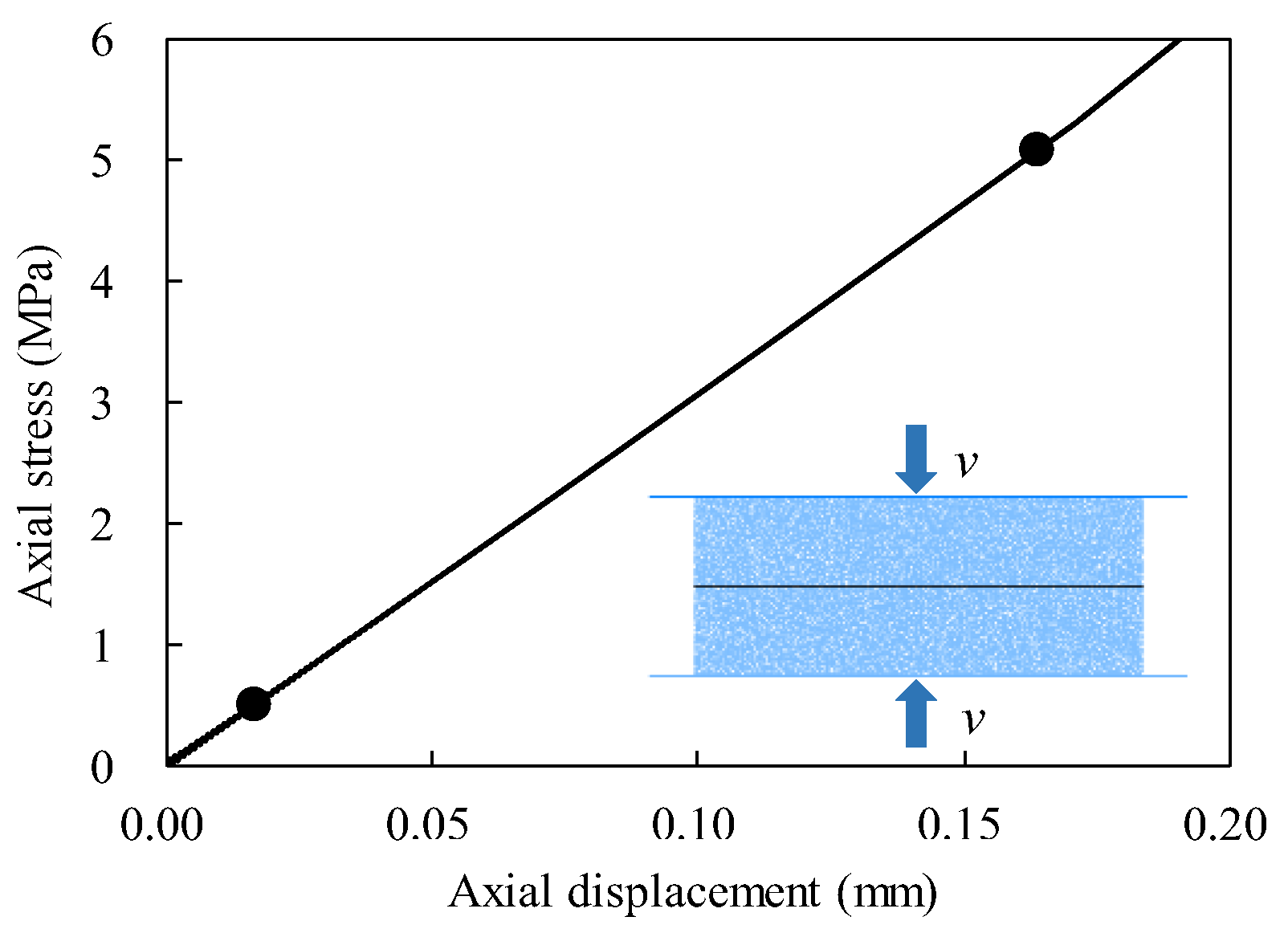
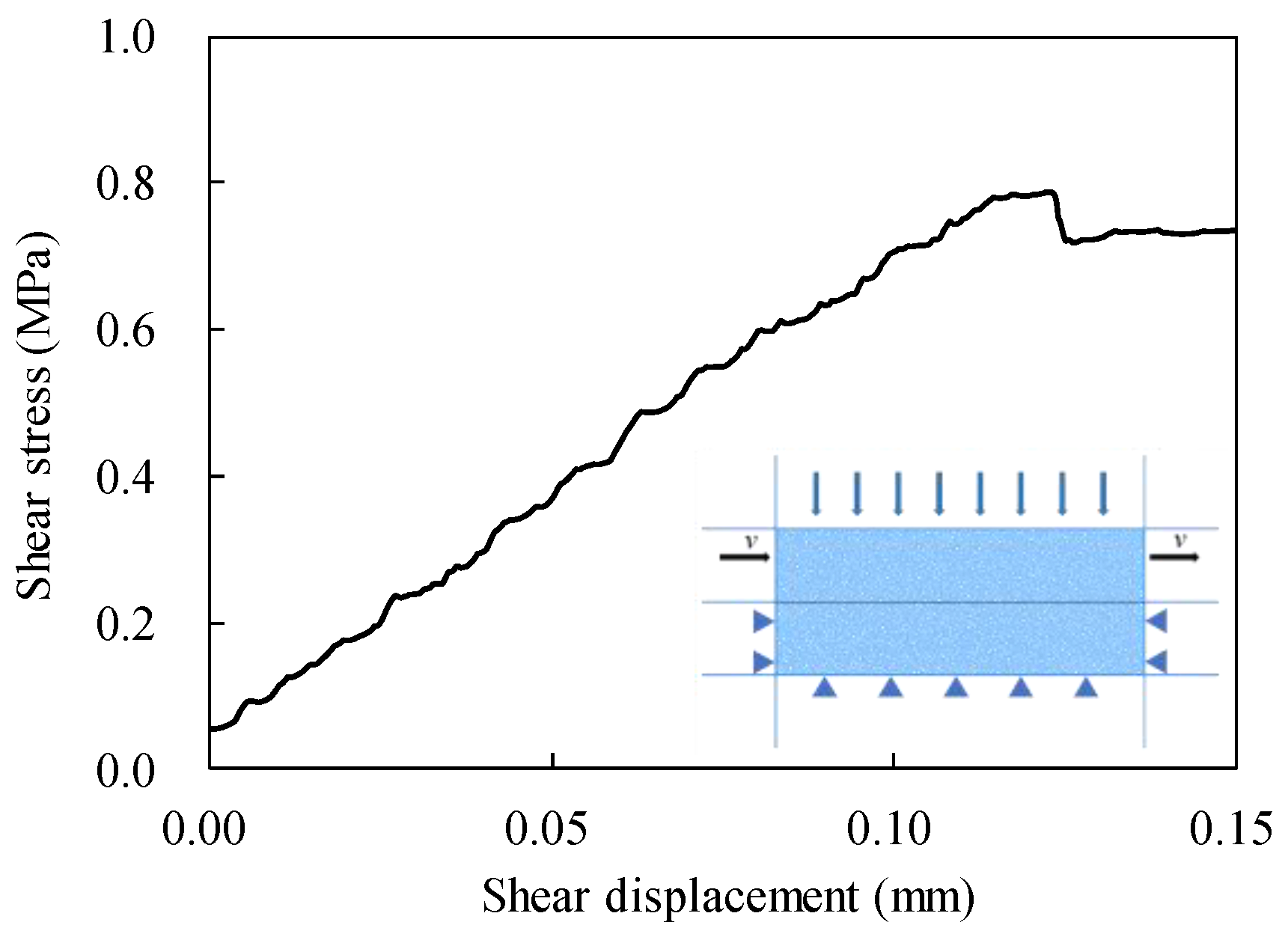





| Parameters | Values |
|---|---|
| Minimum particle radius: Rmin (mm) | 0.28 |
| Maximum particle radius: Rmax (mm) | 0.42 |
| Stiffness ratio: kn/ ks | 2.1 |
| Effective modulus: Ec (GPa) | 4.1 |
| Bond tensile strength: Tb (MPa) | 11.2 |
| Bond friction angle: Φb (°) | 35 |
| Cohesion: cb (MPa) | 11.2 |
| Friction coefficient: u | 0.2 |
| Porosity ratio: e | 0.16 |
| Properties | Parameters | Laboratory Test | PFC Model |
|---|---|---|---|
| Intact rock properties | UCS (MPa) | 27.40 | 27.40 |
| E (GPa) | 4.20 | 4.20 | |
| ν | 0.20 | 0.21 | |
| Joint properties | Kn (GPa/m) | 28.6 | 28.6 |
| Ks (GPa/m) | 6.40 | 6.40 | |
| φb (°) | 37.60 | 36.10 |
| JRC | Normal Stress σn (MPa) | |||||
|---|---|---|---|---|---|---|
| 0.5 | 1 | 2 | 3 | 4 | 5 | |
| 2 | P3 | P4 | P6 | P8 | P10 | P12 |
| 4 | P5 | P6 | P8 | P10 | N12 | N14 |
| 6 | P7 | P8 | P10 | P12 | P14 | N16 |
| 8 | P9 | P10 | P12 | N14 | N16 | N18 |
| 10 | P11 | P12 | P14 | N16 | N18 | N20 |
| 12 | P13 | P14 | N16 | N18 | N20 | N22 |
| 14 | N15 | N16 | N18 | N20 | N22 | N24 |
| 16 | P17 | P18 | P20 | P22 | N24 | N26 |
| 18 | N19 | P20 | N22 | N24 | N26 | N28 |
| 20 | N21 | N22 | N24 | N26 | N28 | N30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Sun, C.; Huang, H.; Chen, J.; Wu, C. Scale Effects on Shear Strength of Rough Rock Joints Caused by Normal Stress Conditions. Sustainability 2023, 15, 7520. https://doi.org/10.3390/su15097520
Shen J, Sun C, Huang H, Chen J, Wu C. Scale Effects on Shear Strength of Rough Rock Joints Caused by Normal Stress Conditions. Sustainability. 2023; 15(9):7520. https://doi.org/10.3390/su15097520
Chicago/Turabian StyleShen, Jiayi, Chenhao Sun, Huajie Huang, Jiawang Chen, and Chuangzhou Wu. 2023. "Scale Effects on Shear Strength of Rough Rock Joints Caused by Normal Stress Conditions" Sustainability 15, no. 9: 7520. https://doi.org/10.3390/su15097520
APA StyleShen, J., Sun, C., Huang, H., Chen, J., & Wu, C. (2023). Scale Effects on Shear Strength of Rough Rock Joints Caused by Normal Stress Conditions. Sustainability, 15(9), 7520. https://doi.org/10.3390/su15097520









