Theoretical and Experimental Study of Rotational Behaviour of Friction Pendulum Bearings

Abstract

Friction Pendulum Bearing (FPB for short) is a kind of widely used device to improve seismic capacities of building and bridge structures. Despite the considerable progress made in developing theoretical models to understand the mechanical behaviour of FPB, these models mostly focus on the horizontal movement behaviour and rarely on the rotational behaviour of FPB. However, rotational displacements of FPBs indeed will occur along with horizontal displacements in earthquakes and may affect the structural seismic performance. Motivated from these findings, a theoretical model of FPB that describes the rotational behaviour is established based on the moment balance theory in this paper. A set of rotational tests are carried out to validate the theoretical model, and comparisons of experimental and theoretical results show that they are in good agreement. The theoretical model developed in this paper will help understand the structural seismic performance more accurately in the case of rotations of FPBs.

1. Introduction

Earthquakes are one of the most devastating natural disasters faced by engineering structures. The end of an earthquake is generally synonymous with the enormous destruction of buildings, bridges, roads, etc. Those structural collapses are the main cause of mortality and economical loss after earthquakes [1,2]. The fatal consequences caused by earthquakes have aroused worldwide attention, especially in the civil engineering field. Nowadays, seismic protection is a crucial aspect to consider in structural design. During the last decades, many seismic protection techniques have been proposed and developed.

Among all these techniques, base isolation techniques such as Lead Rubber Bearings (LRBs), high damping seismic isolation rubber bearings, and Friction Pendulum Bearings (FPBs) have earned significant recognition as efficient seismic isolators for structures [3,4,5].

Friction Pendulum Bearing (FPB) are reputed to be very efficient at reducing the risk of damage and collapse for structures [6,7,8,9,10,11,12].

As presented in Figure 1, the FPB consists of two plates with concave surfaces and a slider to separate the two plates. The upper and lower concave surfaces have respective curvature radii $R_1$ and $R_2$ and friction coefficients of ${\mu }_1$ and ${\mu }_2$. The function of an FPB is to elongate the structural natural period beyond the predominant period of ground motions.

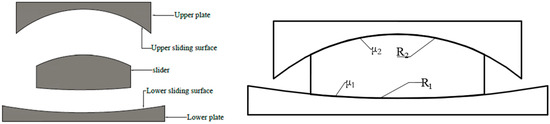
Figure 1. Sketch of an FPB cross-section.

The first concept of the FPB was presented by Jules Touallion in 1870, conceptualising a rolling ball bearing in his patent [13]. Since then, many prototypes of friction pendulum bearings have been invented, considering different curvature radii, curvature variation of concave surfaces, different friction coefficients of concave surfaces, different thicknesses of the slider, etc. Based on the force balance theory, many scholars have described the operation principle and force-displacement relationship of FPBs. Good fidelity with experimental results has been observed for the proposed theoretical models [14,15,16].

The main advantages of FPBs are the simplicity and efficacy of their principle, good re-centring capacity, and high energy dissipation capacity for both bridge and building structures [17,18,19,20,21,22].

The common aspect of aforementioned studies is that upper and lower plates of FPBs are assumed to remain horizontal, and the effect of a possible rotation of the two plates in earthquakes is neglected. This assumption may be acceptable if the upper and lower plates can only move in the horizontal direction, such as in the case when the base isolation technique is used for building structures. However, if FPBs are adopted in bridges with flexible piers for seismic isolation purpose, rotations of FPBs are inevitable.

Up until now, a few studies have concerned the issue of rotations of FPBs. Based on the kinematic constitutive model of the triple friction pendulum (TFP) bearing including rotations of lower and upper plates, Becker et al. investigated the effects of constant support rotation and flexible support on the TFP bearing seismic behaviour [23,24]. It is found that, when TFP bearings are subjected to constant rotations, the hysteresis loop is shifted to the positive shear direction, and the displacement capacity of the bearing decreases with the increase in the support rotation. Mosqueda et al. [25] made similar observations by including constant rotation of the plates to the restoring force formula. To minimize the effects of rotation on hysterical performance of FPBs, it is recommended to install the bearing plates to parts of the structure where rotations are less probable to occur.

However, only the influence of a constant rotation on the seismic performance is considered in these references. In this paper, the rotational behaviour of FPBs is described in a distinct way from the previous studies by considering variable rotation angle and moment. Formulas for restoring force and moment are derived based on the moment balance theory [26].

In addition, an experimental study on the rotational behaviour of FPB is conducted. The study includes four different specimens with different friction coefficient combinations of sliding surfaces under three different vertical loads. Experimental results are presented and compared to the theoretical predictions, and some conclusions are drawn.

2. Theoretical Study of the Rotational Behaviour of FPB

The initial state and rotational state of a typical FPB are presented in Figure 2.

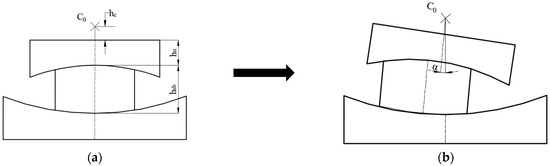
Figure 2. The initial state and rotational state of a typical FPB: (a) initial state; (b) rotational state.

It is assumed that the upper plate is rotated at an angle α, and the centre of rotation $C_0$ is located on the symmetric line of the upper plate; $h_c$ represents the vertical distance between $C_0$ and the top of the upper plate.

From the free body diagram shown in Figure 3, forces considered in the diagram are:

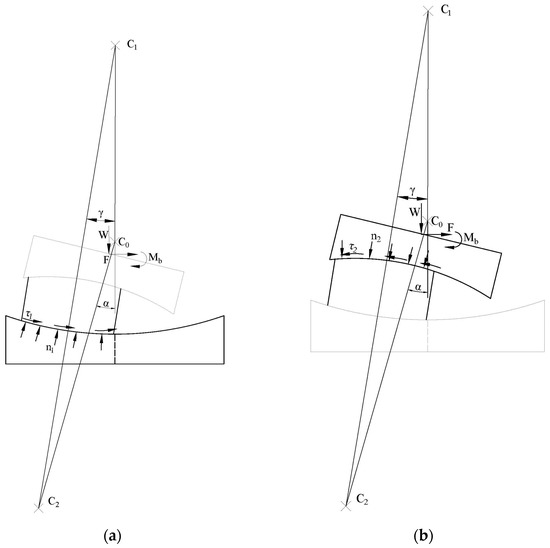
Figure 3. Free body diagram of FPB in rotation: (a) lower sliding surface free body diagram; (b) upper sliding surface free body diagram.

• The vertical load $W$;
• Rotation moment $M_b$ acting on the upper plate
• The horizontal restoring force $F$;
• The friction stresses acting on the lower and upper sliding surfaces, respectively ${\tau }_1$ and ${\tau }_2$;
• The normal stresses acting on the lower and upper sliding surfaces, respectively $n_1$ and $n_2$.

Setting the sum of the moment about points $C_1$ and $C_2$ to zero, the moment equilibrium equations could be written as

$${\displaystyle \sum M(C1)}=-W{h}_c\sin \alpha -F(|C_0{C}_1|+h_c\cos \alpha )-R_1{\displaystyle \int |\overrightarrow{{\tau }_1}|}dA+d_1{\displaystyle \int |\overrightarrow{n_1}|}dA+M_b=0$$

(1)

$${\displaystyle \sum M(C_2)}=W(R_2+h_u)\sin \alpha +F(R_2+h_u)\cos \alpha -R_2{\displaystyle \int |\overrightarrow{{\tau }_2}|}dA-d_2{\displaystyle \int |\overrightarrow{n_2}|}dA+M_b=0$$

(2)

where $h_u$ represents the minimum thickness of the upper plate as shown in Figure 2a.

Based on the geometry of Figure 3, the following relation can be obtained:

$$\frac{\sin \alpha }{R_e}=\frac{\sin \gamma }{R_2+h_u+h_c}=\frac{\sin (\alpha -\gamma )}{|C_0{C}_1|}$$

(3)

where $R_e=R_1+R_2-h_{sb}$, $h_{sb}$ represents the maximum thickness of the slider as shown in Figure 2a.

Horizontal displacements are far less than the curvature radii of the sliding surfaces, and the angles $\alpha$ and $\gamma$ are relatively small. Additionally, assuming the distribution of stresses on the concave surfaces is uniform, the resultants of normal forces of the concave surfaces and the radius of the concave surfaces are superposed; thus, the lever arm of the normal forces on the concave surfaces ($d_1$ and $d_2$) equals to zero. Therefore,

$$d_1{\displaystyle \int |\overrightarrow{n_1}|}dA=0$$

(4)

$$d_2{\displaystyle \int |\overrightarrow{n_2}|}dA=0$$

(5)

Considering the simplifications and assumptions made above, the following relations are obtained:

$${\displaystyle \sum M(C1)}=-W{h}_c\alpha -F(|C_0{C}_1|+h_c)-R_1{\displaystyle \int |\overrightarrow{{\tau }_1}|}dA+M_b=0$$

(6)

$${\displaystyle \sum M(C_2)}=W(R_2+h_u)\alpha +F(R_2+h_u)-R_2{\displaystyle \int |\overrightarrow{{\tau }_2}|}dA+M_b=0$$

(7)

$$\frac{\alpha }{R_e}=\frac{\gamma }{R_2+h_u+h_c}=\frac{\alpha -\gamma }{|C_0{C}_1|}$$

(8)

Combining Equations (6)–(8), equations of the moment $M_b$ and the restoring force $F$ can be determined as follows:

$$M_b=\frac{W(R_2+h_u)(R_2+h_u+h_c-R_e)}{R_e}\alpha +CS{T}_1$$

(9)

$$F=-\frac{W(R_2+h_u-h_c)}{R_e}\alpha +\frac{-{\mu }_1{R}_{1}W+{\mu }_2{R}_{2}W}{R_e}$$

(10)

where

$$CS{T}_1=({\mu }_1{R}_1{R}_2-{\mu }_2{R}^2+{\mu }_2{R}_2{R}_e+{\mu }_1{R}_1{h}_u-{\mu }_2{R}_2{h}_u)W/R_e\approx ({\mu }_1+{\mu }_2)R_1{R}_{2}W/R_e$$

(11)

From Equations (9)–(11), the following conclusions can be obtained:

(1)

Without any displacement before loading, the horizontal restoring force and moment are linear functions of the rotation angle α. It means that Equations (9) and (10) can be used more conveniently to compute the restoring force and moment of FPB from a zero initial state. It also means that simple connection elements of FEM software can be used to simulate rotational characteristics of FPB bearing.

(2)

From Equation (9), the rotational stiffness $k_{\alpha }$ of the FPB can be obtained by Equation (12). To keep the sign of $k_{\alpha }$ positive, the condition shown in Equation (13) must be satisfied.

$$k_{\alpha }=\frac{W(R_2+h_u)(R_2+h_u+h_{\mathrm{c}}-R_e)}{R_e}$$

(12)

$$R+h_u+h_c-R_e>0\iff h_c>R_e-R_2-h_u$$

(13)

(3)

From Equation (9), the values of $CS{T}_1$ and $h_u$ are relatively small compared to $R_1$ and $R_2$, and the sign of $CS{T}_1$ is determined by the three first terms of Equation (11), knowing that $R_2$ is inferior to $R_e$. Therefore, the initial value of the moment of FPB is generally positive. However, if $k_{\alpha }$ is negative and the FPB rotation angle is large enough, the moment will be negative.

(4)

Constant terms of $F$ and $M_b$ are only related to bearing parameters and the vertical load; they are independent of the location of the rotation centre. Therefore, the location of the rotation centre has only influence on the rotational stiffness of FPB. To reduce the moment and make the bearing rotate as flexibly as possible, it is suggested to use a smaller friction coefficient and make the difference between the curvature radii of the two concave surfaces as large as possible.

3. Experimental Study

An experimental study was conducted in the State Key Laboratory of Disaster Reduction in Civil Engineering of Tongji University to validate the proposed theoretical model of the rotational behaviour of FPBs.

3.1. Testing Device

The tests are carried out using a testing device composed by a moment applying system and a vertical load applying system as presented in Figure 4. One end of a rigid loading beam is placed between two identical FPB specimens symmetrically disposed with respect to the horizontal plane, and the vertical load is applied by the vertical load applying system; the other end of the loading beam is progressively vertically loaded to create a moment by displacement control mode.

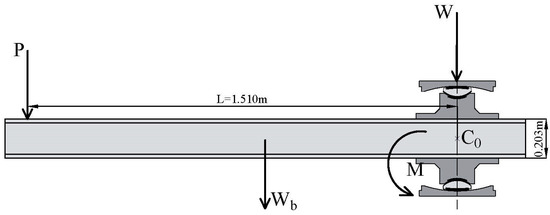
Figure 4. Testing device free body diagram.

3.2. Test Specimen and Loading Procedure

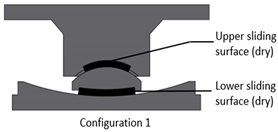
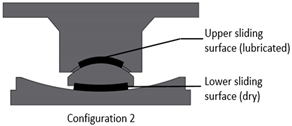
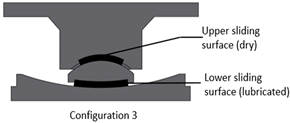
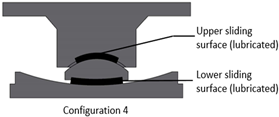
The FPB specimen used in the tests is illustrated in Figure 5. The tests are carried out according to the Chinese specifications on Friction Pendulum isolation bearing for highway bridges (JJT 852-2013) [27]. It consists of four different specimens with different friction coefficient combinations of sliding surfaces under three different vertical loads. Different friction coefficients are obtained by lubrication with silicone grease or non-lubrication. For each friction coefficient combination, three vertical loads of 20 kN, 30 kN, and 40 kN are loaded. The test cases are shown in Table 1. The friction coefficients are determined after each test case.

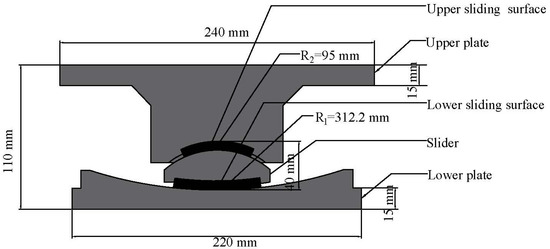
Figure 5. FPB specimen.

Table 1. Test cases.

Configuration	Vertical Load	Friction Coefficient
	20 kN 30 kN 40 kN	${\mu }_1={\mu }_2=0.0925$  ${\mu }_1={\mu }_2=0.0827$  ${\mu }_1={\mu }_2=0.0738$
	20 kN 30 kN 40 kN	${\mu }_1=0.0925$$, {\mu }_2=0.0759$  ${\mu }_1=0.0827$$, {\mu }_2=0.0764$  ${\mu }_1=0.0738$$, {\mu }_2=0.0706$
	20 kN 30 kN 40 kN	${\mu }_1=0.0759$$, {\mu }_2=0.0925$  ${\mu }_1=0.0671$$, {\mu }_2=0.0827$  ${\mu }_1=0.0618$$, {\mu }_2=0.0738$
	20 kN 30 kN 40 kN	${\mu }_1={\mu }_2=0.0759$  ${\mu }_1={\mu }_2=0.0671$  ${\mu }_1={\mu }_2=0.0618$

A photograph of the testing device is shown in Figure 6. Moment is applied by controlling the left actuator in displacement control mode at 30 mm/min velocity to rotate the specimens, and the reaction force is measured at each time increment until the vertical displacement of the loading point reaches $150 \mathrm{mm}$. The moment of a specimen is given by

$$M_{\theta }=\frac{Pl}{2}+\frac{W_{b}L}{4}$$

(14)

where P is the load applied by the actuator at each increment; L represents the lever arm (L = 1.510 m); and $W_b$ is the weight of the loading beam. For each test case, three identical tests are conducted, and the average value of moments are calculated for analysis.

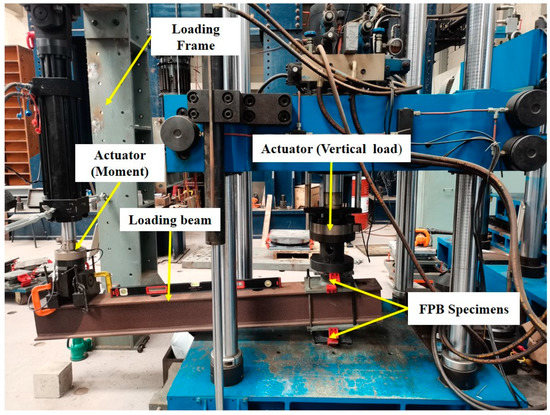
Figure 6. Photograph of the testing device.

The angle of rotation, $\alpha$, for each vertical displacement of the left actuator, $\delta$, is given by

$$\alpha =\arctan \frac{\delta }{L}$$

(15)

3.3. Comparison of Theoretical and Experimental Results

The moment–rotation angle curves from both the experimental data and theoretical model for each configuration are shown in Figure 7.

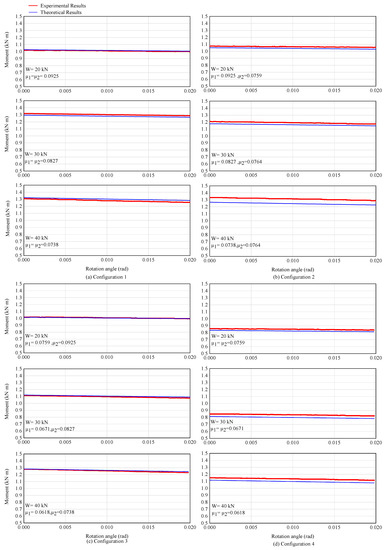
Figure 7. Experimental and theoretical results.

The comparisons of rotational stiffnesses from both the experimental data and theoretical model for each case are shown in Table 2. The theoretical model shows the ability to accurately describe the rotational behaviour of FPB. The predictions of the theoretical model are in very good agreement with the experimental results.

Table 2. Comparisons of Experimental and Theoretical rotational stiffness.

Configuration	Vertical Load (kN)	Experimental Rotational Stiffness (kN·m/rad)	Theoretical Rotational Stiffness (kN·m/rad)	Error
1	20	1.122	1.030	8%
	30	1.612	1.510	6%
	40	2.432	1.986	18%
2	20	0.941	1.030	−9%
	30	1.851	1.510	18%
	40	2.192	1.986	9%
3	20	1.203	1.030	14%
	30	1.872	1.510	19%
	40	2.423	1.986	18%
4	20	1.020	1.030	−1%
	30	1.428	1.510	−6%
	40	1.729	1.986	−15%

However, some errors are noted. From comparison of theoretical and experimental results, it is noticed that the theoretical model generally slightly underestimates the rotational stiffness of the bearing. The error between the experimental and theoretical results increases with the increase in the rotational angle.

4. Conclusions

This paper presents a theoretical model of FPB based on the moment balance theory. The model describes the rotational behaviour of friction pendulum bearings considering the variation of rotation angle. Additionally, extension to include the coupling of rotational and horizontal displacements in the mechanical model, not incorporated in this model, is suggested for future research.

An experimental study of the FPB rotational behaviour is conducted in order to validate the theoretical model. The experimental results show that the proposed theoretical model is accurate enough to describe the rotational behaviour of FPBs. The theoretical approach used in this paper is a powerful tool to describe the rotational behaviour of FPBs and can help to evaluate the structural performance in earthquakes in case of variable rotations of FPBs.