Wave Energy Convertor for Bilateral Offshore Wave Flows: A Computational Fluid Dynamics (CFD) Study
Abstract
1. Introduction
Objectives of the Study
- To analyze the modified CFT design’s ability to harness offshore wave energy resources effectively with a higher energy density environment.
- To conduct research on the performance of an augmented channel cross-flow turbine with considerably higher significant wave heights and wave periods in offshore conditions.
- To design and optimize a geographical location data-specific cross-flow-type turbine and enhance its performance using Commercial CFD code.
- To evaluate the flow field: pressure and velocity variation of the turbine in a range of efficiency conditions.
- To study the effect of nozzle shape and preliminary turbine design on the performance of the turbine efficiency when operating under bidirectional conditions.
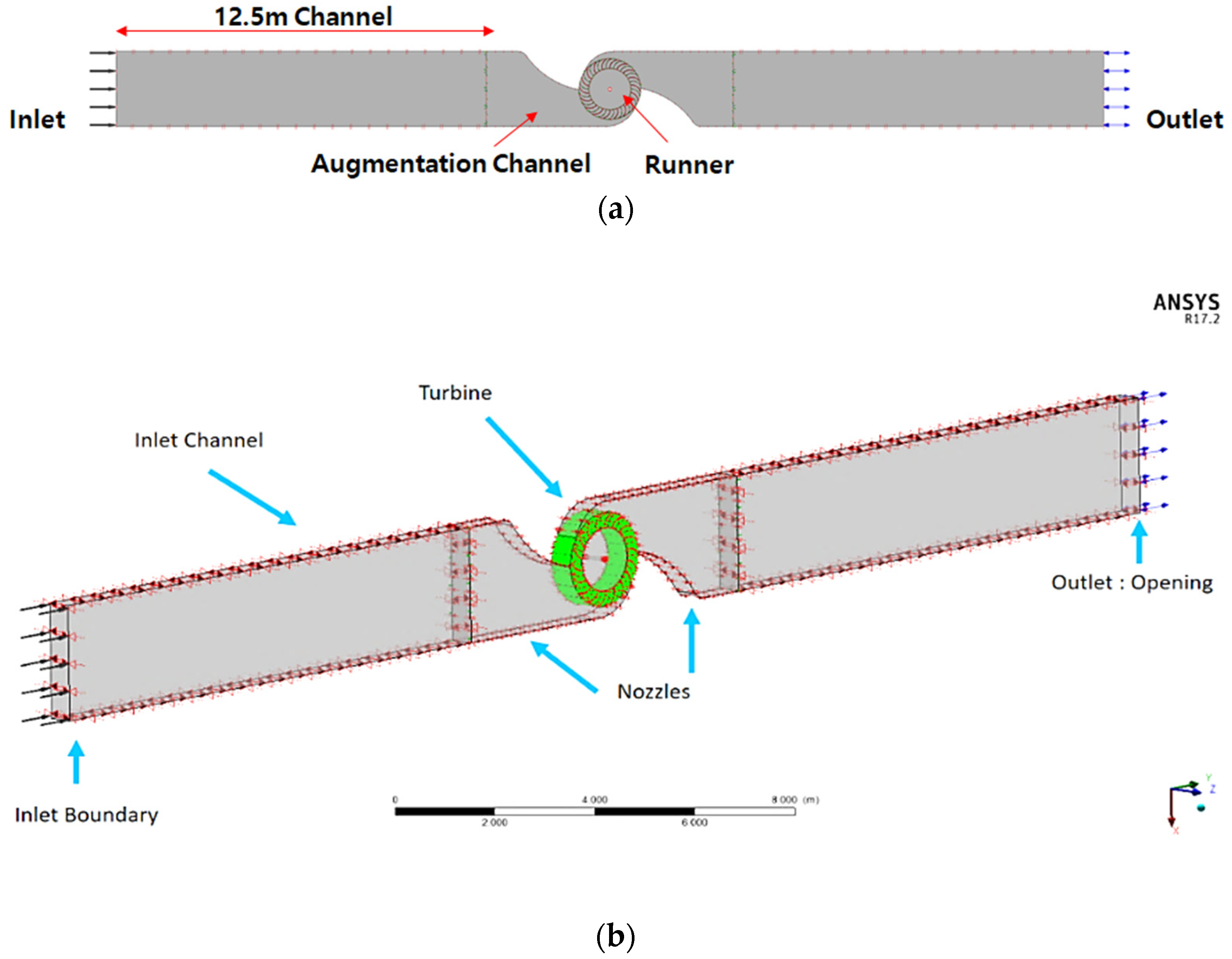
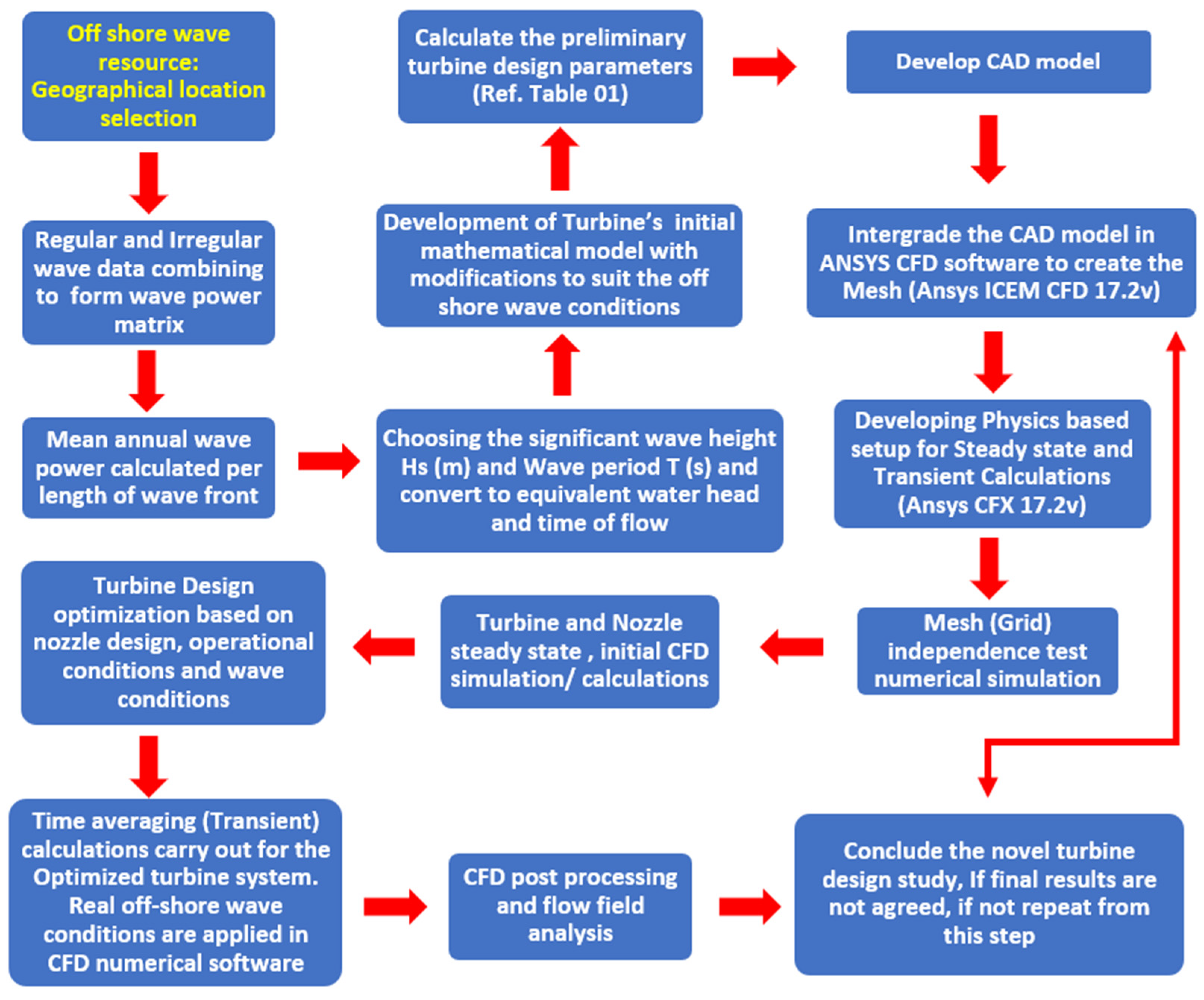
2. Materials and Methods
2.1. Offshore Wave Site Specification and Selection
Spectral Analysis
2.2. Design Condition of Turbine
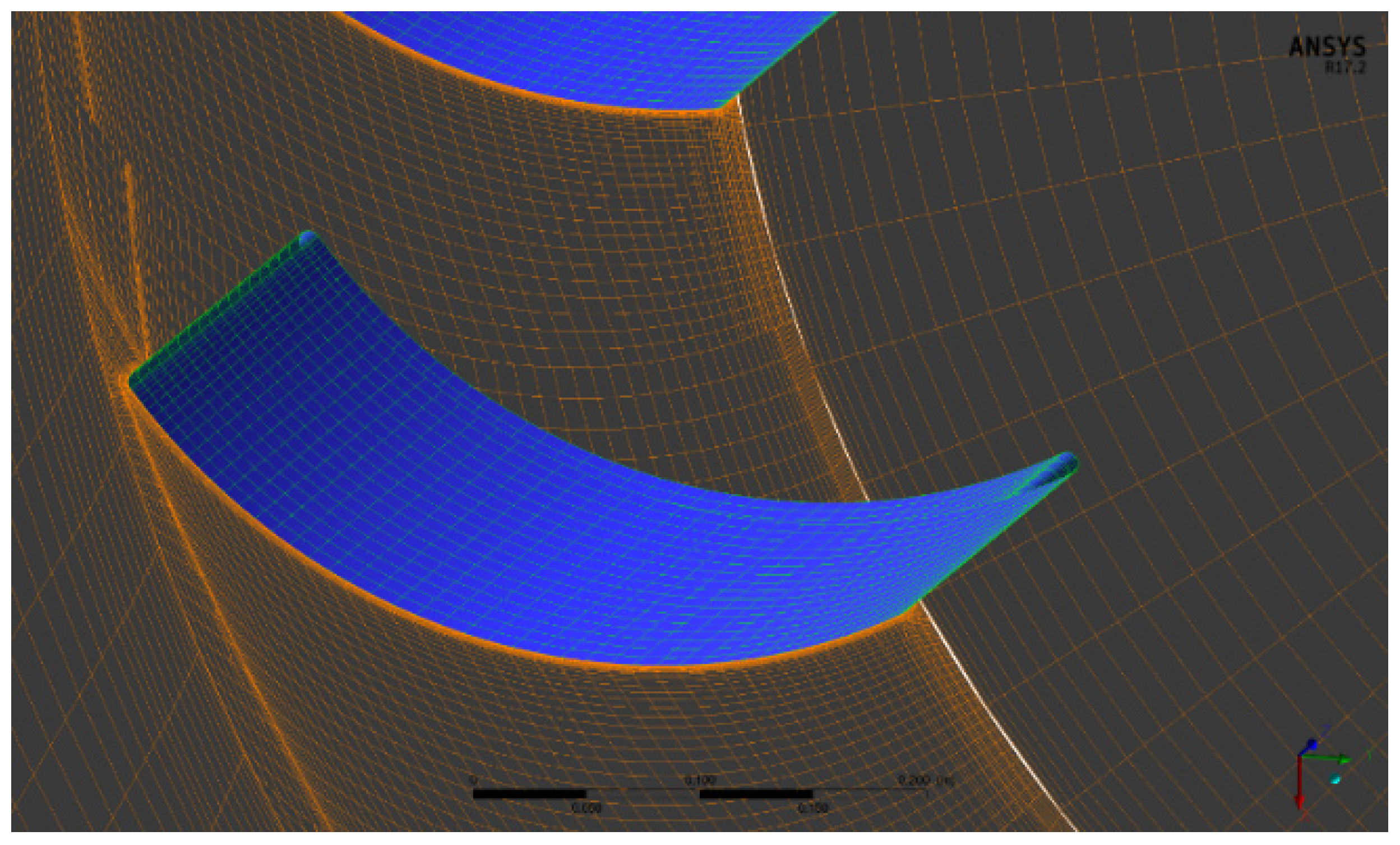
Mesh Generation
2.3. Turbine Optimization Numerical Setup (ANSYS CFX v. 17.2)
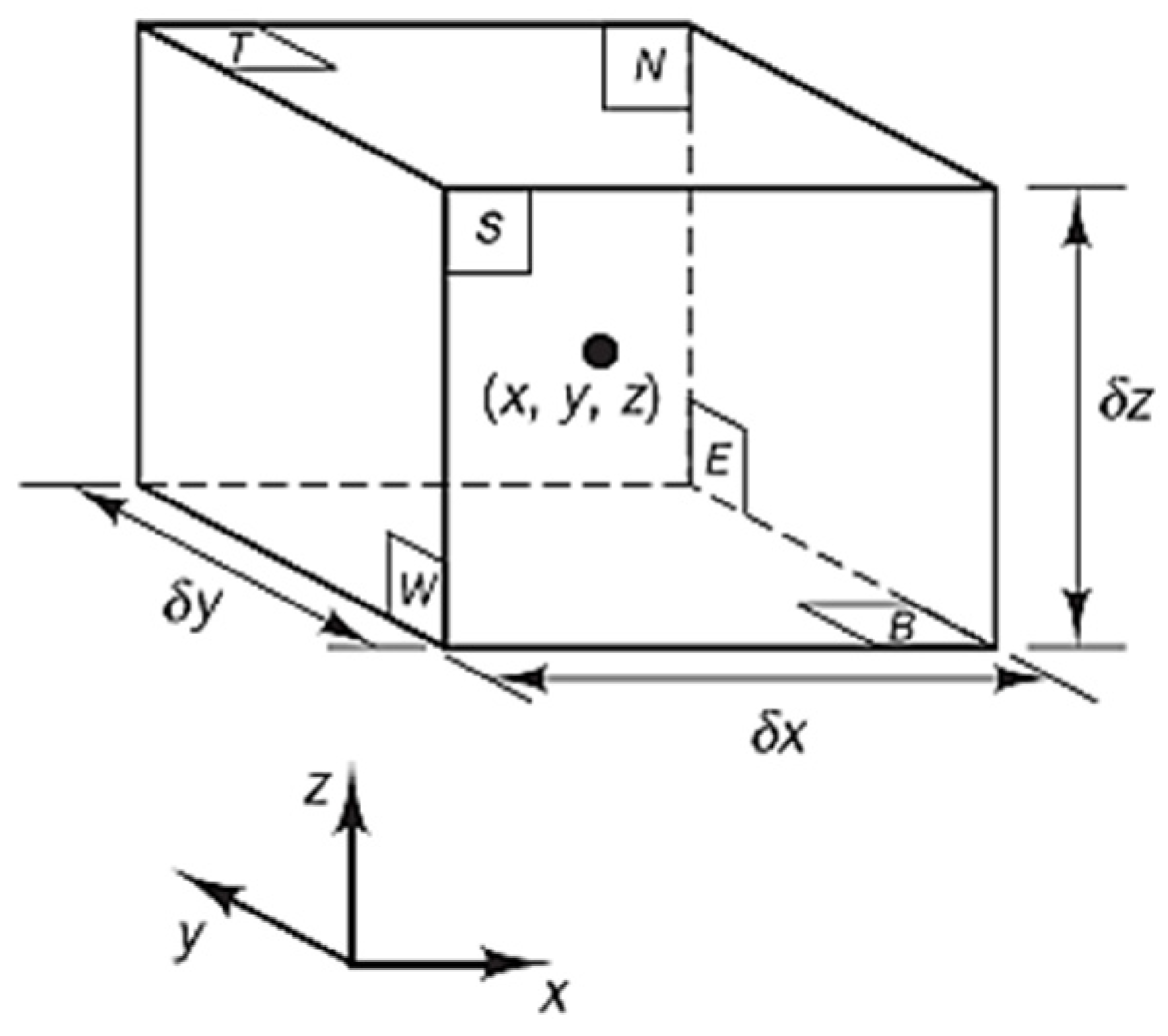
2.4. Governing Equations of CFD Code
CFD Code
3. Results and Discussion
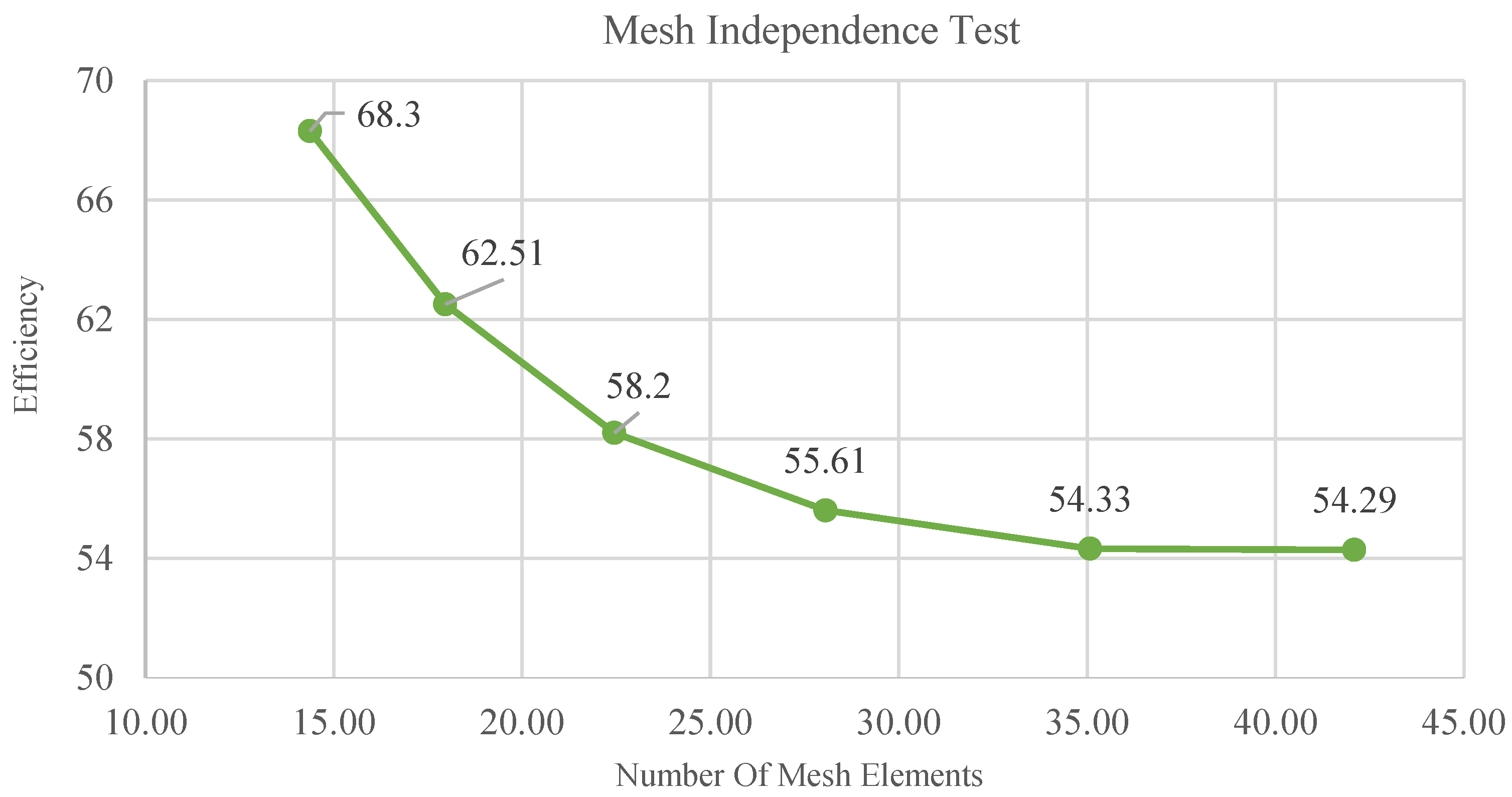
3.1. Mesh (Computational Grid) Independence Test
3.2. Base Turbine Performance
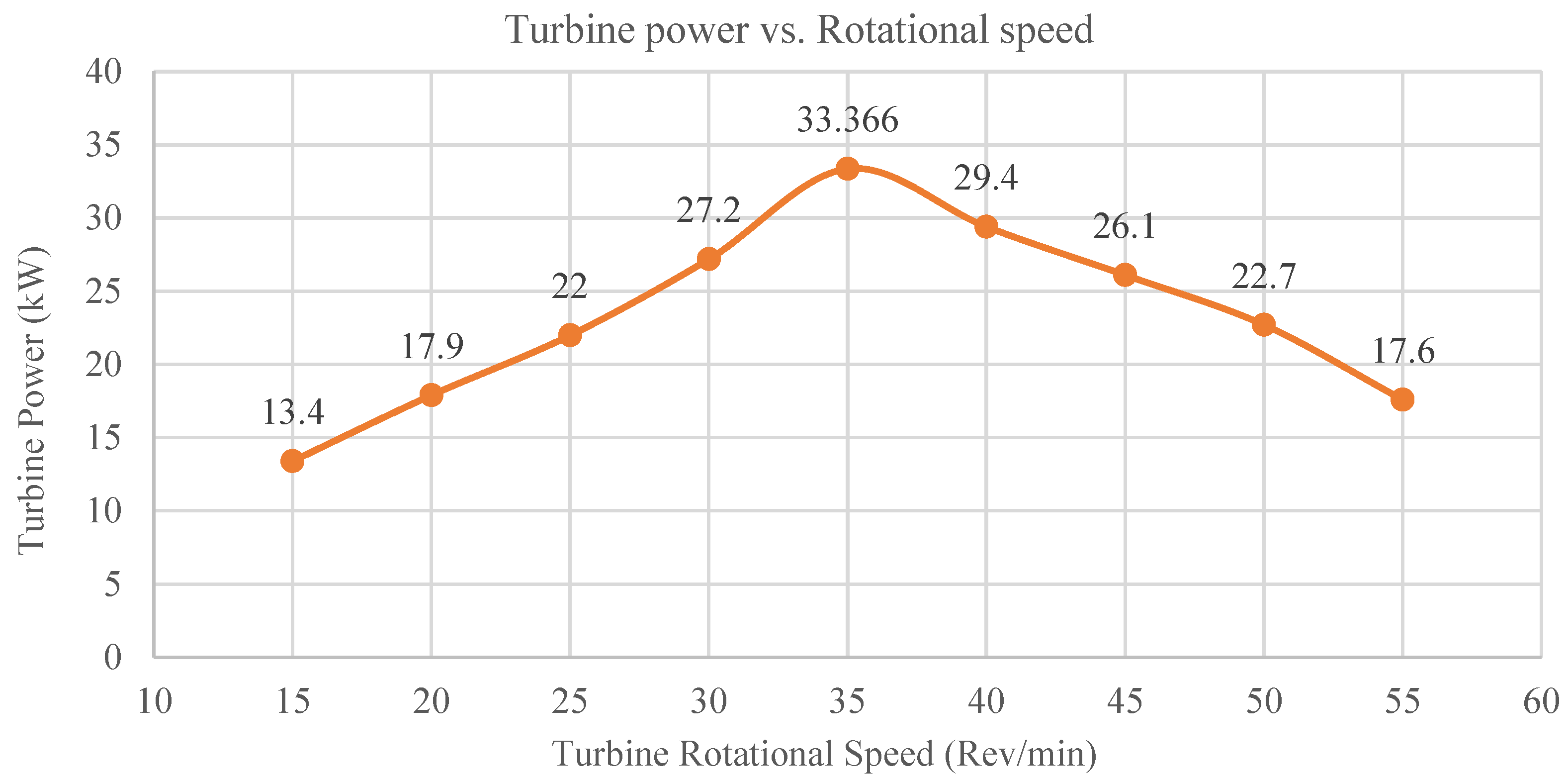
3.2.1. Turbine Performance Results and Analyses for Steady State
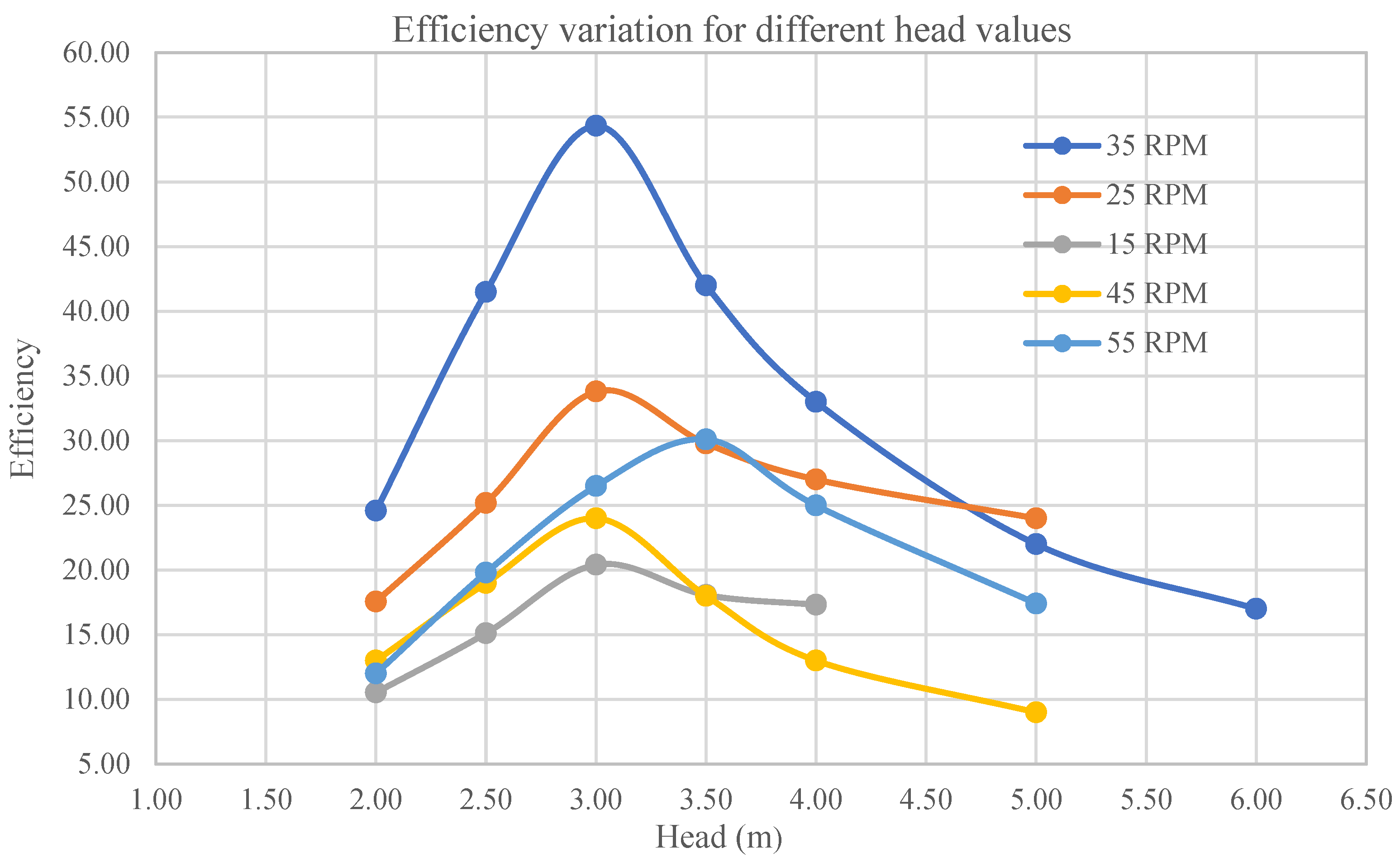
3.2.2. Geometric Modification Results: Nozzle Entry Arc Angle
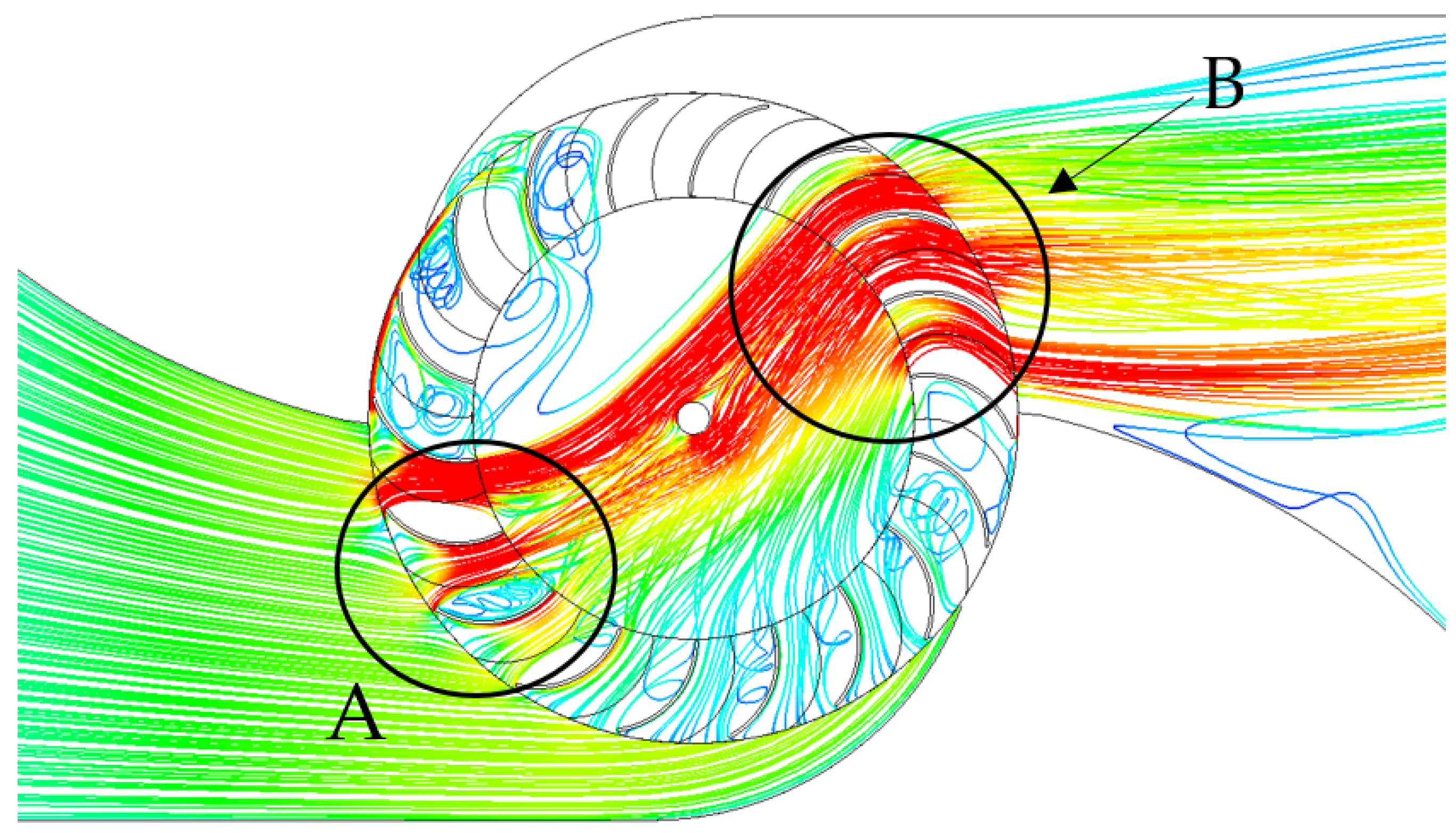
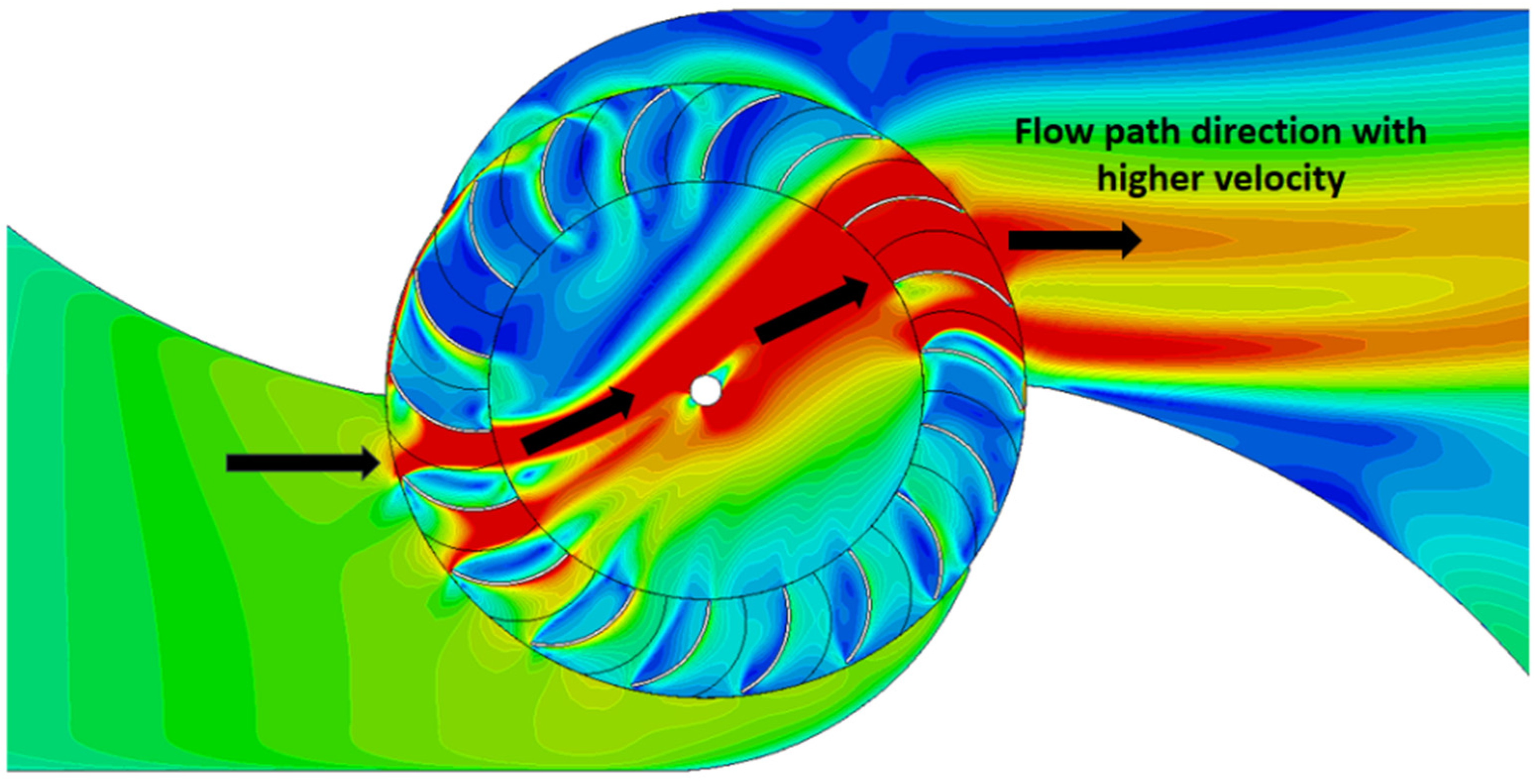
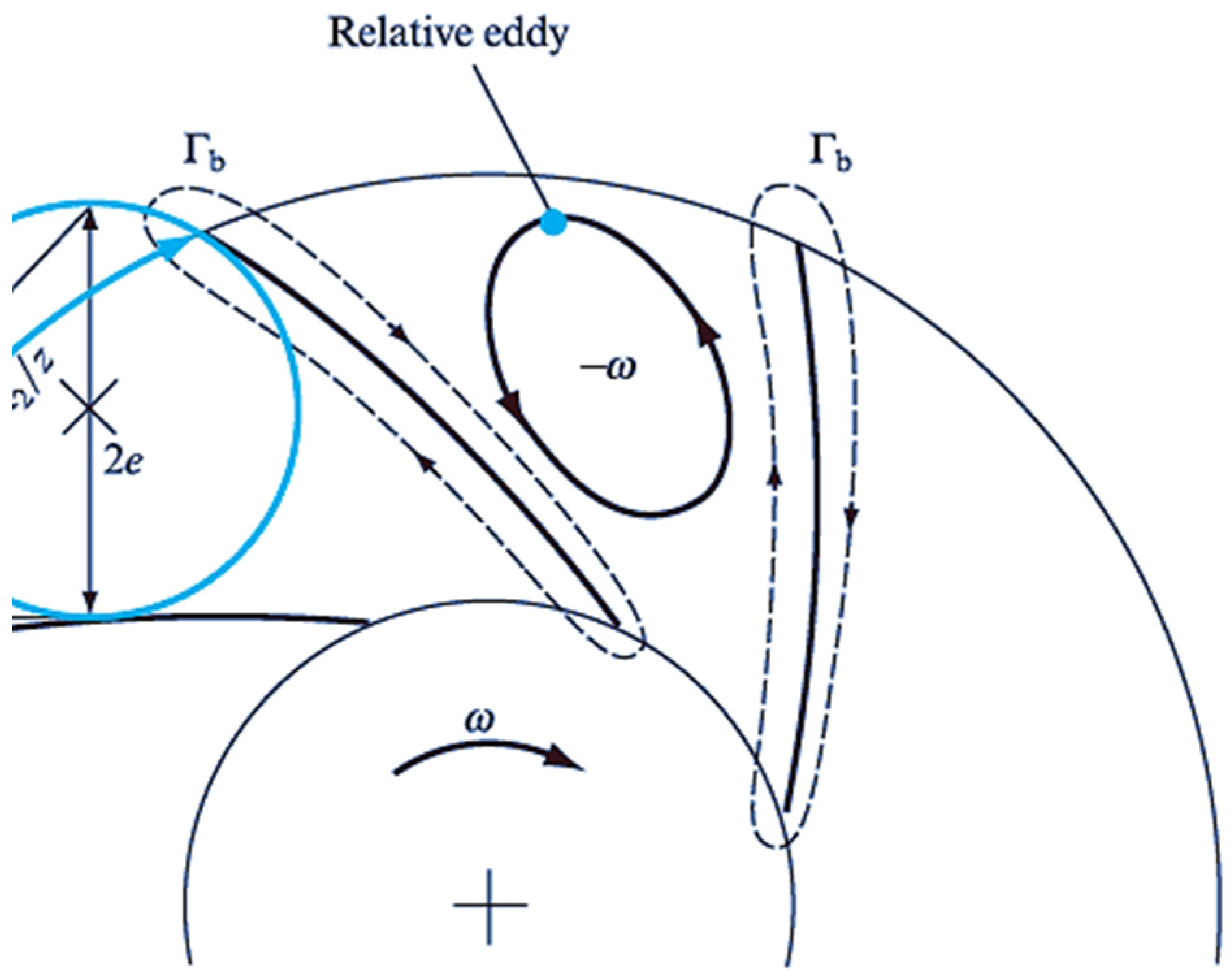
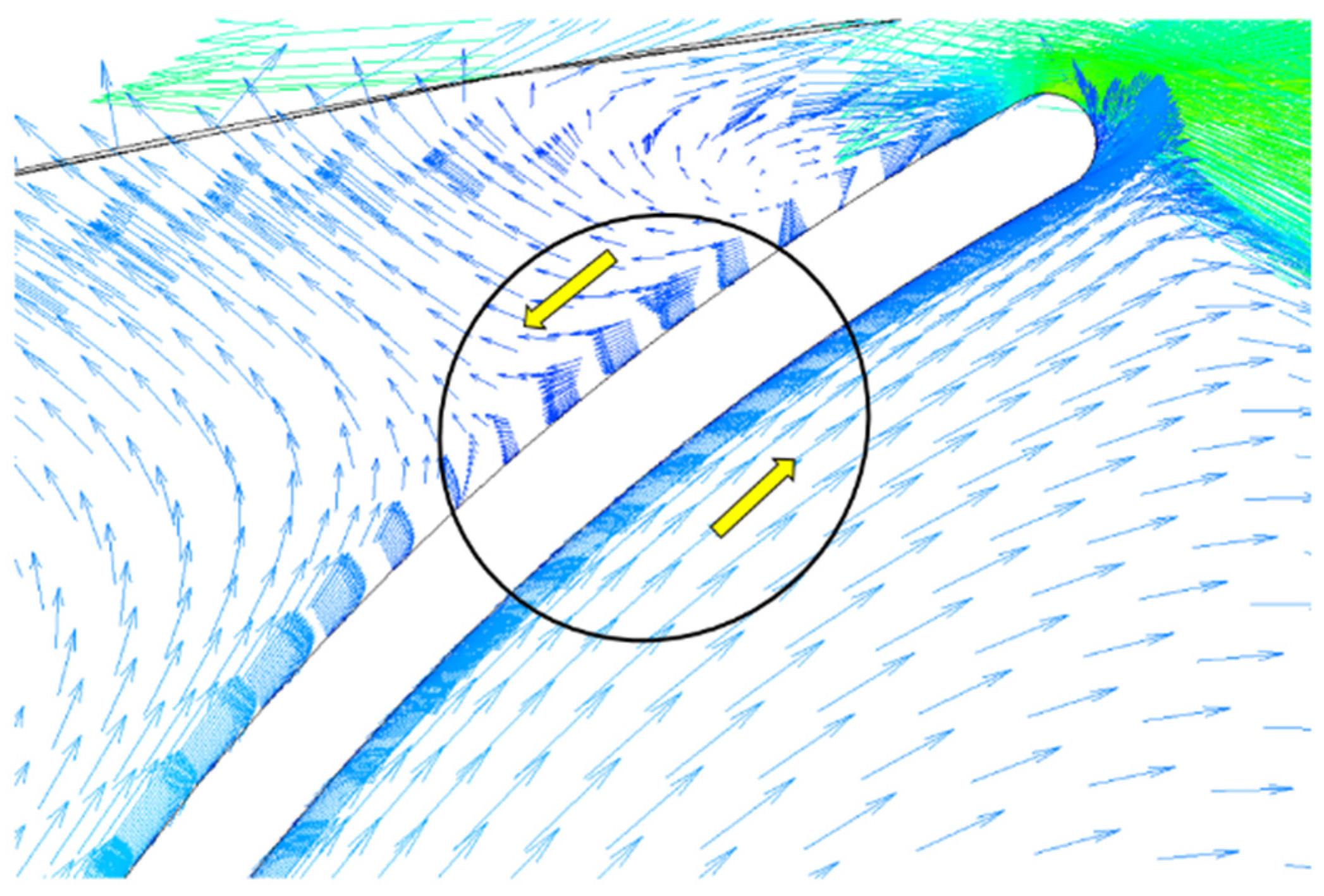
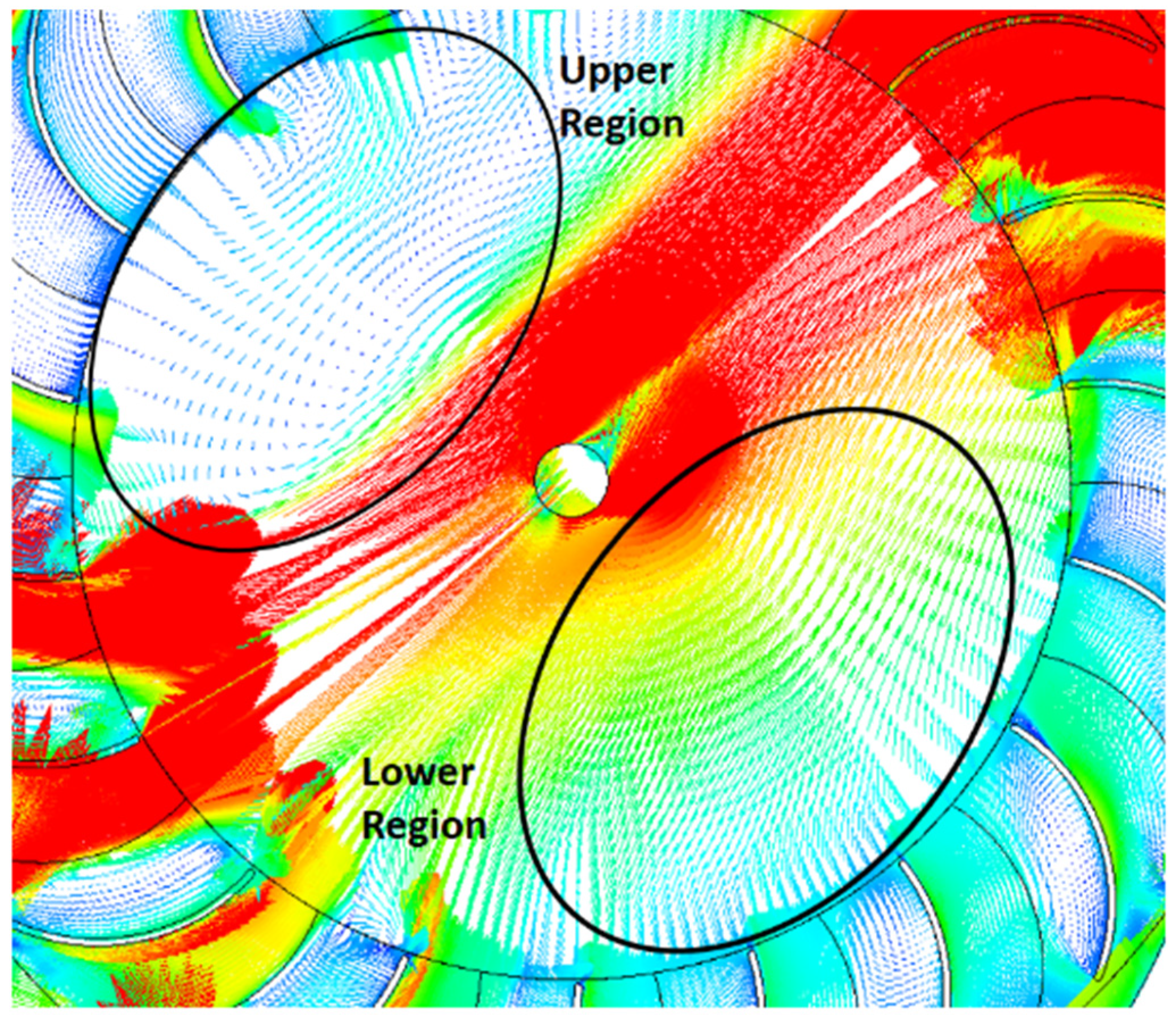
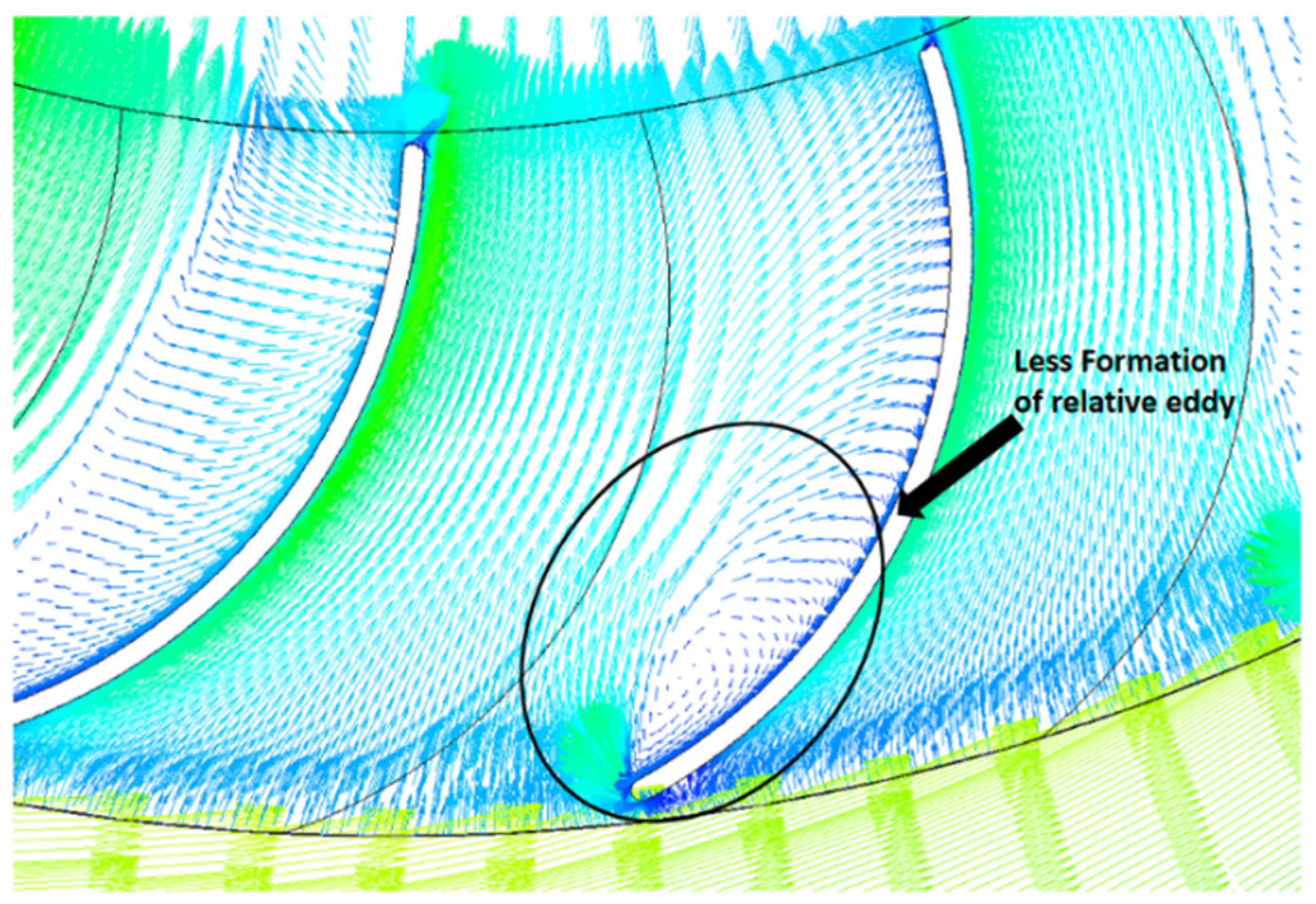
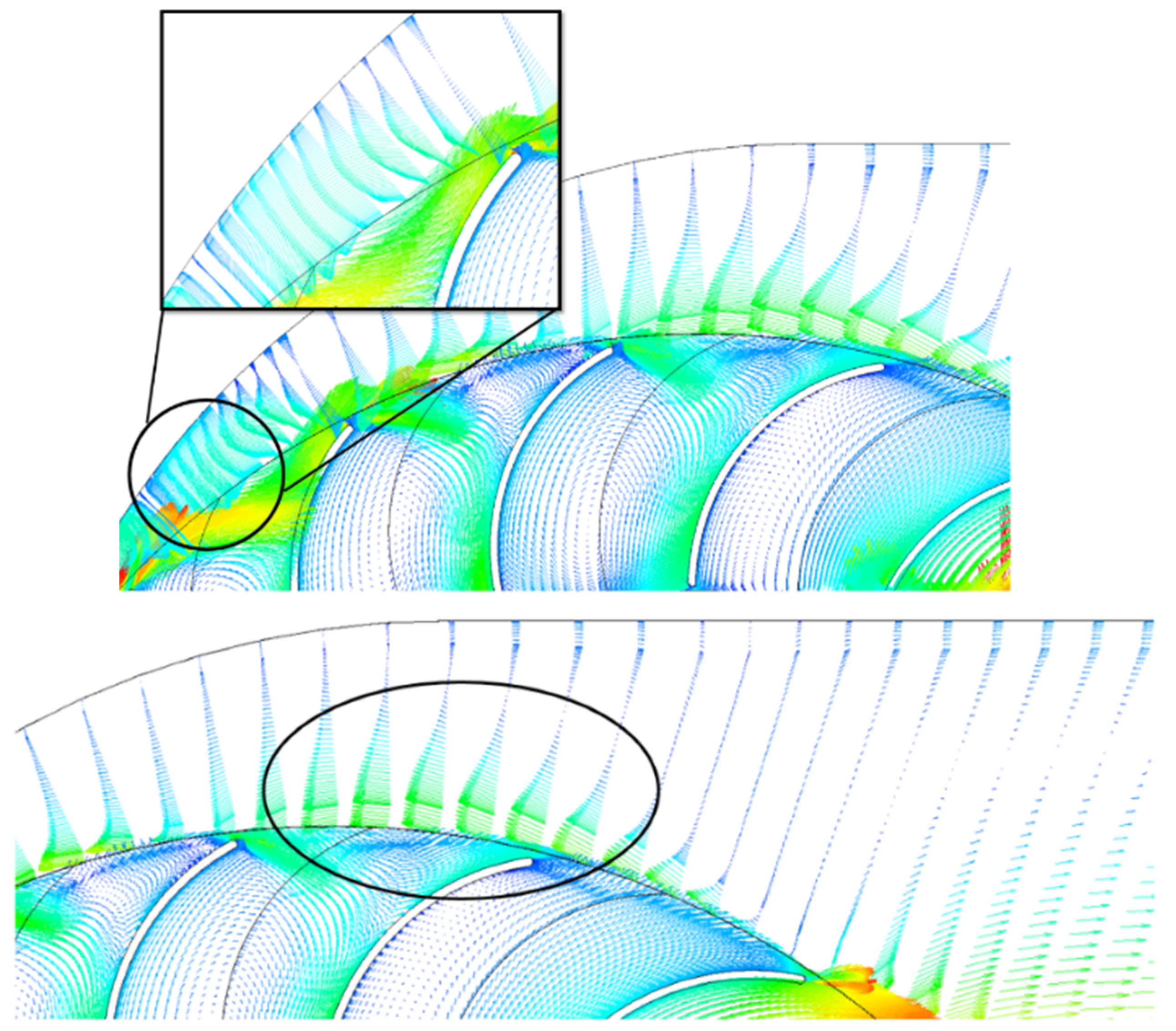
3.3. Flow Field Analysis of the Turbine
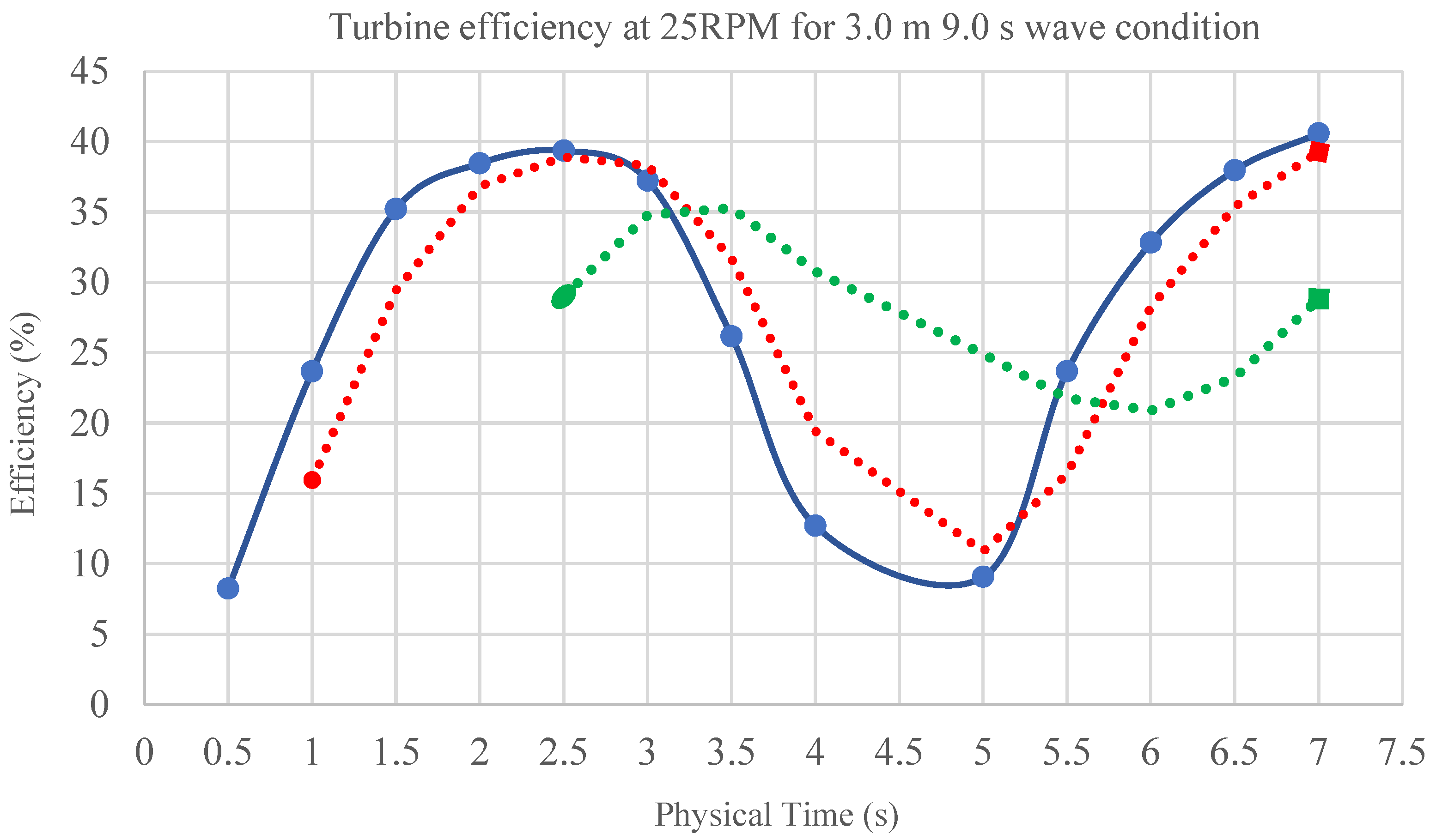
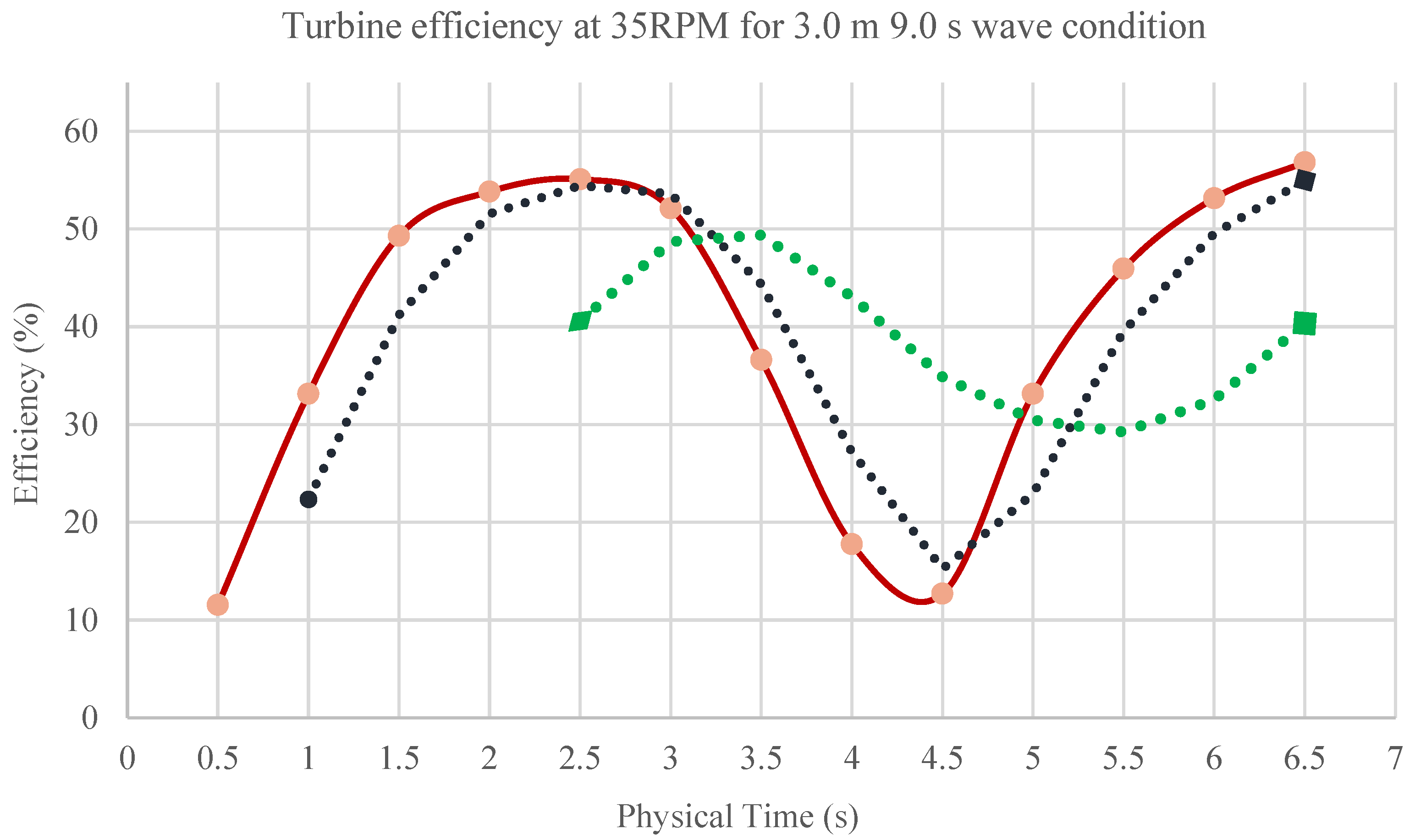
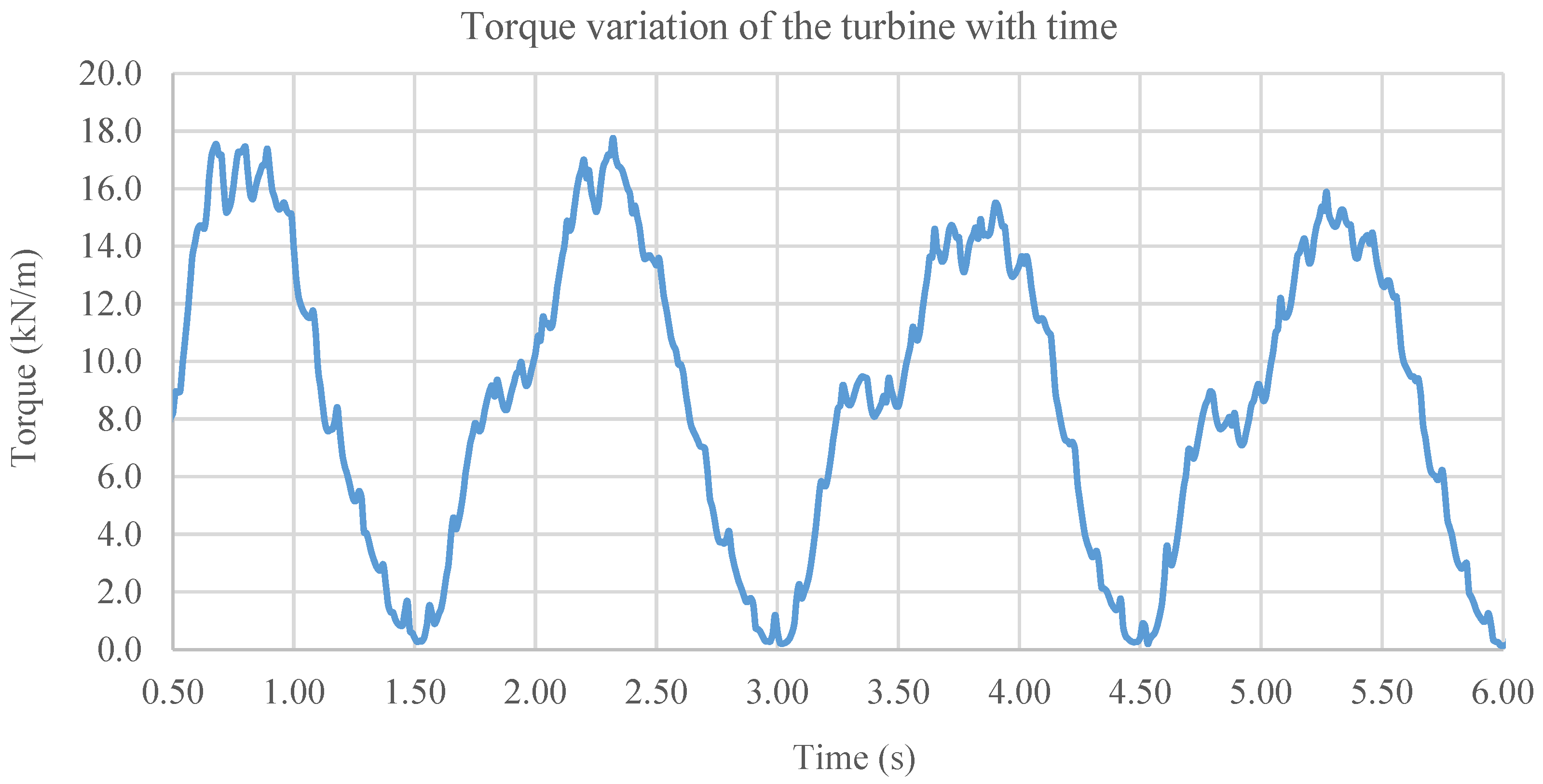
3.4. Transient Calculations Results and Bidirectional Flow Analysis
The Bidirectional Flow Results (Transient Simulation)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Title and Author | Date | Technology | Collection Method | Application | |
|---|---|---|---|---|---|
| Performance investigations of hybrid hydrokinetic turbine rotor with different system and operating parameters | Kamal, M., Saini, R. | 23 March | Current, Cross-Flow Turbine | Modeling | Hydrodynamics, Performance, Structural |
| Hybridized Vertical-Axis Underwater Current Power Turbine System Suitable for Low Underwater Current Velocities: A Report of Its Application and Potential in Nigeria | Agbakwuru, J., Arome, S. | 23 February | Current, Cross-Flow Turbine, Riverine | Field Data | Hybrid Devices, Performance |
| Numerical investigation on the performance of an innovative Airfoil-Bladed Savonius Hydrokinetic Turbine (ABSHKT) with deflector | Chaudhari, V., Shah, S. | 23 February | Current, Cross-Flow Turbine | Modeling | Performance |
| Performance parameters of lift-based vertical axis hydrokinetic turbines—A review | Reddy, K., Bhosale, A., Saini, R. | 22 December | Current, Cross-Flow Turbine | Review | Performance, Structural |
| The influence of material on the power performance of Savonius turbines in wind and water applications | Shamsuddin, M., Kamaruddin, N., Mohamed-Kassim, Z. | 22 December | Current, Cross-Flow Turbine, Riverine | Lab Data | Materials, Performance |
| Sea states influence on the behavior of a bottom mounted full-scale twin vertical axis tidal turbine | Moreau, M., Germain, G., Maurice, G. | 22 December | Current, Cross-Flow Turbine, Tidal | Field Data, Full Scale | Hydrodynamics, Performance |
| Performance analysis of novel V-shaped turbine blade profile by three-dimensional numerical investigations with varying overlap ratios for hydropower application | Shashikumar, C., Madav, V. | 22 December | Current, Cross-Flow Turbine, Riverine | Modeling | Performance, Structural |
| Optimization of semicircular blade profile of Savonius hydrokinetic turbine using artificial neural network | Rengma, T., Subbarao, P. | 22 November | Current, Cross-Flow Turbine | Modeling | Performance, Structural |
| Optimization of Hydrokinetic Swept Blades | Gemaque, M., Vaz, J., Saavedra, O. | 22 November | Current, Axial-Flow Turbine, Cross-Flow Turbine | Modeling | Performance, Structural |
| Power density capacity of tidal stream turbine arrays with horizontal and vertical axis turbines | Ouro, P., Dené, P., Garcia-Novo, P. | 22 September | Current, Axial-Flow Turbine, Cross-Flow Turbine, Tidal | Modeling | Array Effects, Performance |
| Performance enhancement of low speed current savonius tidal turbines through adding semi-cylindrical deflectors | Samadi, M., Hassanabad, M., Mozafari, A. | 22 September | Current, Cross-Flow Turbine, Tidal | Modeling | Hydrodynamics, Performance, Structural |
| Hydrodynamic performance of a mono-tangent backward-rotating impeller based on tidal current energy utilization | Wu, Z., Xu, Q., Ling, C-M. | 22 August | Current, Cross-Flow Turbine, Tidal | Modeling | Hydrodynamics, Performance |
| Performance and near-wake analysis of a vertical-axis hydrokinetic turbine under a turbulent inflow | Dhalwala, M., Bayram, A., Oshkai, P. | 22 August | Current, Cross-Flow Turbine, Tidal | Modeling | Hydrodynamics, Performance |
| Development of a Hydrokinetic Turbine Backwater Prediction Model for Inland Flow through Validated CFD Models | Niebuhr, C., Hill, C., Dijk, M. | 22 July | Current, Axial-Flow Turbine, Cross-Flow Turbine, Riverine | Modeling | Array Effects, Hydrodynamics, Performance |
| A review on modifications and performance assessment techniques in cross-flow hydrokinetic system | Kamal, M., Saini, R. | 22 June | Current, Cross-Flow Turbine | Review | Hydrodynamics, Performance, Structural |
| Field tests on model efficiency of twin vertical axis helical hydrokinetic turbines | Zhang, A., Liu, S., Ma, Y. | 22 May | Current, Cross-Flow Turbine, Tidal | Field Data, Modeling | Hydrodynamics, Performance |
| Numerical and Experimental Investigation of the Effect of Design Parameters on Savonius-Type Hydrokinetic Turbine Performance | Wu, K., Lo, K., Kao, R. | 22 March | Current, Cross-Flow Turbine | Lab Data, Modeling | Performance, Structural |
| Influence of blade numbers on start-up performance of vertical axis tidal current turbines | Sun, K., Yi, Y., Zhang, J. | 22 January | Current, Cross-Flow Turbine, Tidal | Modeling | Performance |
| A New Methodology for Smoothing Power Peaks Produced by Electricity Demand and a Hydrokinetic Turbine for a Household Load on Grid Using Supercapacitors | Arevalo, P., Tostado-Veliz, M., Jurado, F. | 21 December | Current, Axial-Flow Turbine, Cross-Flow Turbine, Riverine | Modeling | Grid Integration, Performance |
| Design optimization of a novel vertical augmentation channel housing a cross-flow turbine and performance evaluation as a wave energy converter | A.H Samitha Weerakoon, A., Kim, B-H., Cho, Y-J. | 21 December | Current, Cross-Flow Turbine, Wave, Oscillating Water Column | Lab Data, Modeling | Hydrodynamics, Performance |
| A comprehensive review on Crossflow turbine for hydropower applications | Anand, R., Jawahar, C., Bellos, E. | 21 November | Current, Cross-Flow Turbine | Review | Performance |
| Comparison of Sliding and Overset Mesh Techniques in the Simulation of a Vertical Axis Turbine for Hydrokinetic Applications | Lopez Mejia, O., Mejia, O., Escorcia, K. | 21 November | Current, Cross-Flow Turbine | Modeling | Hydrodynamics, Performance |
| Case study of a cross-flow hydrokinetic turbine in a narrow prismatic canal | Cacciali, L., Battisti, L., Dell’Anna, S. | 21 August | Current, Cross-Flow Turbine | Field Data | Performance |
| Turbine design dependency to turbulence: An experimental study of three scaled tidal turbines | Slama, M., Pinon, G., Hadi, C. | August 21 | Current, Cross-Flow Turbine, Tidal | Lab Data | Hydrodynamics, Performance, Structural |
| Numerical Study of the Dynamic Stall Effect on a Pair of Cross-Flow Hydrokinetic Turbines and Associated Torque Enhancement Due to Flow Blockage | Doan, M., Obi, S. | 21 August | Current, Cross-Flow Turbine | Lab Data, Modeling, Scale Device | Array Effects, Hydrodynamics, Performance |
| Lagrangian Vortex Computations of a Four Tidal Turbine Array: An Example Based on the NEPTHYD Layout in the Alderney Race | Slama, M., Bex, C., Pinon, G. | 21 June | Current, Cross-Flow Turbine, Tidal | Modeling | Array Effects, Performance |
| Experimental investigation on the characterization of self-starting capability of a 3-bladed Savonius hydrokinetic turbine using deflector plates | Salleh, M., Kamaruddin, N., Mohamed-Kassim, Z. | 21 May | Current, Cross-Flow Turbine | Lab Data, Modeling | Performance |
| Wind–Water Experimental Analysis of Small SC-Darrieus Turbine: An Approach for Energy Production in Urban Systems | Gharib-Yosry, A., Blanco-Marigorta, E., Fernández-Jiménez, A. | 21 May | Current, Cross-Flow Turbine | Lab Data | Hybrid Devices, Performance |
| Comprehensive experimental and numerical assessment of a drag turbine for river hydrokinetic energy conversion | Ramadan, A., Hemida, M., Abdel-Fadeel, W. | 21 May | Current, Cross-Flow Turbine, Riverine | Lab Data, Modeling | Performance, Structural |
| Cross-Flow Tidal Turbines with Highly Flexible Blades—Experimental Flow Field Investigations at Strong Fluid–Structure Interactions | Hoerner, S., Kösters, I., Vignal, L. | 21 February | Current, Cross-Flow Turbine, Oscillating Hydrofoil, Tidal | Lab Data | Hydrodynamics, Performance, Structural |
| Twin Marine Hydrokinetic Cross-Flow Turbines in Counter Rotating Configurations: A Laboratory-Scaled Apparatus for Power Measurement | Doan, M., Kai, Y., Obi, S. | 20 November | Current, Cross-Flow Turbine, Tidal | Lab Data, Scale Device | Hydrodynamics, Performance, Structural |
| Prediction of the fouling penalty on the tidal turbine performance and development of its mitigation measures | Song, S., Demirel, Y., Atlar, M. | October 20 | Current, Cross-Flow Turbine, Tidal | Modeling | Performance |
| Computational parametric analysis of the design of cross-flow turbines under constraints | Leguizamón, S., Avellan, F. | 20 October | Current, Cross-Flow Turbine, Tidal | Lab Data, Modeling | Performance |
| Effect of aspect ratio on cross-flow turbine performance | Hunt, A., Stringer, C., Polagye, B. | 20 September | Current, Cross-Flow Turbine | Lab Data | Performance, Structural |
| An experimental evaluation of blockage effects on the wake of a cross-flow current turbine | Ross, H., Polagye, B. | 20 August | Current, Cross-Flow Turbine | Lab Data, Scale Device | Array Effects, Performance |
| Experimental assessment of a 100 W prototype horizontal axis tidal turbine by towing tank tests | Alamian, R., Shafaghat, R., Amiri, H. | 20 August | Current, Cross-Flow Turbine, Tidal | Lab Data | Performance |
| An experimental assessment of analytical blockage corrections for turbines | Ross, H., Polagye, B. | 20 June | Current, Axial-Flow Turbine, Cross-Flow Turbine, Tidal | Lab Data | Hydrodynamics, Performance |
| MaRINET2 Tidal Energy Round Robin Tests: Performance Comparison of a Horizontal Axis Turbine Subjected to Combined Wave and Current Conditions | Gaurier, B., Ordonez-Sanchez, S., Facq, J. | 20 June | Current, Cross-Flow Turbine, Tidal | Lab Data | Performance |
| Torque coefficient analysis of a novel direct-drive parallel-stream counter-rotating darrieus turbine system | Janon, A. | 20 March | Current, Cross-Flow Turbine | Modeling | Materials, Performance, Structural |
| Large Eddy Simulations on Vertical Axis Hydrokinetic Turbines—Power coefficient analysis for various solidities | Guillaud, N., Balarac, G., Goncalvès, E. | 20 March | Current, Cross-Flow Turbine | Modeling | Hydrodynamics, Performance |
| Implications of biofouling on cross-flow turbine performance | Stringer, C., Polagye, B. | 20 February | Cross-Flow Turbine, Tidal | Lab Data | Performance |
| Numerical investigation of modal and fatigue performance of a horizontal axis tidal current turbine using fluid–structure interaction | Ullah, H., Hussain, M., Abbas, N. | 19 December | Current, Cross-Flow Turbine, Tidal | CFD Modeling | Performance |
| A review on technology, configurations, and performance of cross-flow hydrokinetic turbines | Saini, G., Saini, R. | 19 October | Current, Cross-Flow Turbine | FEA | Performance, Structural |
| Comparison of cross-flow turbine performance under torque-regulated and speed-regulated control | Polagye, B., Strom, B., Ross, H. | 19 July | Current, Cross-Flow Turbine | Lab Data | Control, Performance |
| Performance Optimization of a Kirsten–Boeing Turbine by A Metamodel Based on Neural Networks Coupled with CFD | Küppers, J., Metzger, J., Jensen, J. | 19 May | Current, Cross-Flow Turbine, Riverine | Lab Data, Modeling | Performance, Structural |
| Velocity and performance correction methodology for hydrokinetic turbines experimented with different geometry of the channel | Patel, V., Eldho, T., Prabhu, S. | 19 February | Current, Cross-Flow Turbine, Riverine | Lab Data, Modeling | Hydrodynamics, Performance |
| Research on the Hydrodynamic Performance of a Vertical Axis Current Turbine with Forced Oscillation | Ma, Y., Hu, C., Li, Y. | 18 November | Current, Cross-Flow Turbine | Modeling | Hydrodynamics, Performance |
| Novel Cyclic Blade Pitching Mechanism for Wind and Tidal Energy Turbine Applications | Rao, J., Diez, F. | 18 November | Cross-Flow Turbine | Modeling | Performance, Structural |
| Hydrodynamic Performance Analysis of the Vertical Axis Twin-Rotor Tidal Current Turbine | Ma, Y., Hu, C., Li, Y. | 18 November | Current, Cross-Flow Turbine | Modeling | Hydrodynamics, Performance, Structural |
| Validation of a Coupled Electrical and Hydrodynamic Simulation Model for a Vertical Axis Marine Current Energy Converter | Forslund, J., Goude, A., Thomas, K. | 18 November | Current, Cross-Flow Turbine | Modeling | Control, Performance |
| Field-testing of model helical-bladed hydrokinetic turbines for small-scale power generation | Talukdar, P., Kulkarni, V., Saha, U. | 18 November | Current, Cross-Flow Turbine | Field Data | Performance |
| Numerical Study of a Guide-Vane-Augmented Vertical Darrieus Tidal-Current-Turbine | Liu, Z., Wang, Z., Shi, H. | 18 October | Current, Cross-Flow Turbine | Modeling | Hydrodynamics, Performance, Structural |
| The effects of oblique waves and currents on the loadings and performance of tidal turbines | Martinez, R., Payne, G., Bruce, T. | 18 September | Current, Cross-Flow Turbine, Tidal | Lab Data, Scale Device | Performance |
| Experimental investigation of an innovative configuration for new marine current turbine | Hassanzadeh, R., Yaakob, O., Gholami, A. | 18 September | Current, Cross-Flow Turbine, Ocean Current | Lab Data | Performance, Structural |
| Numerical investigation of channel effects on a vertical-axis tidal turbine rotating at variable speed | Chen, B., Cheng, S., Su, T. | 18 September | Current, Cross-Flow Turbine, Tidal | Modeling | Hydrodynamics, Performance |
| Numerical Investigation of Contra Rotating Vertical-Axis Tidal-Current Turbine | Satrio, D., Utama, I., Mukhtasor | 18 June | Current, Cross-Flow Turbine | Modeling | Hydrodynamics, Performance, Structural |
| Impact of blade mounting structures on cross-flow turbine performance | Strom, B., Johnson, N., Polagye, B. | 18 May | Current, Cross-Flow Turbine | Lab Data | Performance, Structural |
| Performance of a horizontal axis marine current turbine– A comprehensive evaluation using experimental, numerical, and theoretical approaches | Rahimian, M., Walker, J., Penesis, I. | 18 April | Current, Cross-Flow Turbine, Tidal | Lab Data, Modeling, Scale Device | Performance |
| Multi-mode evaluation of power-maximizing cross-flow turbine controllers | Forbush, D., Cavagnaro, R., Donegan, J. | 17 December | Current, Cross-Flow Turbine | Field Data, Modeling, Full Scale | Control, Performance |
| Design and hydrodynamic analysis of horizontal axis tidal stream turbines with winglets | Ren, Y., Liu, B., Zhang, T. | 17 November | Current, Cross-Flow Turbine, Tidal | Lab Data, Modeling | Performance |
| Modeling of flow-induced stress on helical Savonius hydrokinetic turbine with the effect of augmentation technique at different operating conditions | Kumar, D., Sarkar, S. | 17 October | Current, Cross-Flow Turbine | Modeling | Hydrodynamics, Performance |
| Performance analysis of a Savonius hydrokinetic turbine having twisted blades | Kumar, A., Saini, R. | 17 August | Current, Cross-Flow Turbine | Modeling | Performance, Structural |
| A tuned actuator cylinder approach for predicting cross-flow turbine performance with wake interaction and channel blockage effects | Shives, M., Crawford, C., Grovue, S. | 17 June | Current, Cross-Flow Turbine | Modeling | Array Effects, Hydrodynamics, Performance, Power Take-Off |
| Impact of channel blockage on the performance of axial and cross-flow hydrokinetic turbines | Kinsey, T., Dumas, G. | 17 April | Current, Axial-Flow Turbine, Cross-Flow Turbine | Modeling | Performance |
| The influence of blade roughness on the performance of a vertical axis tidal turbine | Priegue, L., Stoesser, T. | 17 April | Current, Cross-Flow Turbine | Lab Data, Modeling | Hydrodynamics, Materials, Performance, Structural |
| Experimental investigations on Darrieus straight blade turbine for tidal current application and parametric optimization for hydro farm arrangement | Patel, V., Eldho, T., Prabhu, S. | 17 April | Current, Cross-Flow Turbine | Lab Data, Modeling, Scale Device | Array Effects, Hydrodynamics, Materials, Performance, Structural |
| Performance analysis of a vertical axis tidal turbine with flexible blades | Bouzaher, M., Guerira, B., Hadid, M. | 17 March | Current, Cross-Flow Turbine | Modeling | Performance, Structural |
| Performance characterization of a cross-flow hydrokinetic turbine in sheared inflow | Forbrush, D., Polagye, B., Thomson, J. | 16 December | Current, Cross-Flow Turbine | Field Data, Modeling | Performance, Structural |
| Experimental study on hydrodynamic characteristics of vertical-axis floating tidal current energy power generation device | Ma, Y., Li, T., Zhang, L. | 16 October | Current, Cross-Flow Turbine | Scale Device | Hydrodynamics, Mooring, Performance |
| Performance parameters of Savonius type hydrokinetic turbine—A Review | Kumar, A., Saini, R. | 16 October | Current, Cross-Flow Turbine, Riverine | CFD Modeling | Hydrodynamics, Performance, Structural |
| Experimental Study of a Reference Model Vertical-Axis Cross-Flow Turbine | Bachant, P., Wosnik, M., Gunawan, B. | 16 September | Current, Cross-Flow Turbine, Riverine | Lab Data, Modeling | Hydrodynamics, Performance |
| Design and test of 1/5th scale horizontal axis tidal current turbine | Liu, H., Zhou, H., Lin, Y. | 16 June | Current, Cross-Flow Turbine | Modeling, Scale Device | Hydrodynamics, Performance, Power Take Off |
| Physical testing of performance characteristics of a novel drag-driven vertical axis tidal stream turbine; with comparisons to a conventional Savonius | Harries, T., Kwan, A., Brammer, J. | 16 June | Current, Cross-Flow Turbine | Lab Data, Modeling | Hydrodynamics, Materials, Performance, Structural |
| Field performance assessment of a hydrokinetic turbine | Cavagnaro, R., Polagye, B. | 16 June | Current, Cross-Flow Turbine | Field Data, Lab Data | Hydrodynamics, Performance, Power Take-Off |
| Optimization of blade motion of vertical axis turbine | Ma, Y., Zhang, L., Zhang, Z. | 16 April | Current, Cross-Flow Turbine | Modeling | Performance, Structural |
| Numerical and experimental study of the 3D effect on connecting arm of vertical axis tidal current turbine | Guo, W., Kang, H., Chen, B. | 16 March | Current, Cross-Flow Turbine | Lab Data, Modeling | Hydrodynamics, Performance, Structural |
| Performance analysis of a horizontal axis 3-bladed Savonius type wave turbine in an experimental wave flume (EWF) | Tutar, M., Veci, I. | 16 February | Current, Cross-Flow Turbine | Lab Data | Performance |
| Effect of blade vortex interaction on performance of Darrieus-type cross flow marine current turbine | Wang, Y., Sun, X., Zhu, B. | 16 February | Current, Cross-Flow | Modeling | Hydrodynamics, Performance |
| Numerical investigation of laboratory tested cross-flow tidal turbines and Reynolds number scaling | Stringer, R., Hillis, A., Zang, J. | 16 January | Current, Cross-Flow Turbine | Modeling, Scale Device | Performance |
| Evaluation of Electromechanical Systems Dynamically Emulating a Candidate Hydrokinetic Turbine | Cavagnaro, R., Neely, J., Fa, F. | 16 January | Current, Cross-Flow Turbine | Modeling | Performance, Power Take-Off |
| Performance assessment of a vertical axis turbine in a marine current flume tank and CFD modelling | Rolland, S., Thatcher, M., Ellis, R. | 15 December | Current, Cross-Flow Turbine | Modeling, Test Center | Performance |
| Novel approach of bidirectional diffuser-augmented channels system for enhancing hydrokinetic power generation in channels | Elbatran, A., Yaakob, O., Ahmed, Y. | 15 November | Current, Cross-Flow Turbine | Modeling | Hydrodynamics, Performance |
| Numerical investigation of the influence of blade helicity on the performance characteristics of vertical axis tidal turbines | Marsh, P., Ranmuthugala, D., Penesis, I. | 15 September | Current, Cross-Flow Turbine | Modeling | Performance, Structural |
| Hydrokinetic energy harvesting by an innovative vertical axis current turbine | Fernandes, A., Rostami, A. | 15 September | Current, Cross-Flow Turbine | Lab Data, Modeling | Performance |
| Performance characterization and placement of a marine hydrokinetic turbine in a tidal channel under boundary proximity and blockage effects | Kolekar, N., Banerjee, A. | 15 June | Current, Axial-Flow Turbine, Cross-Flow Turbine | CFD Modeling | Hydrodynamics, Performance |
| Evaluating current power availability for energy conversion along the Southern Brazilian Shelf | Kinnus, E., Marques, W., Jung, B. | 15 June | Current, Cross-Flow Turbine | Field Data, Modeling | Performance |
| Performance measurements of cylindrical- and spherical-helical cross-flow marine hydrokinetic turbines, with estimates of exergy efficiency | Bachant, P., Wosnik, M. | 15 February | Current, Cross-Flow Turbine | Lab Data | Hydrodynamics, Performance |
| The effects of wave–current interaction on the performance of a model horizontal axis tidal turbine | Henriques, T., Tedds, S., Najafian, G. | 14 December | Current, Cross-Flow Turbine | Lab Data | Performance |
| Simulations of a vertical axis turbine in a channel | Goude, A., Agren, O. | 14 March | Current, Cross-Flow Turbine | Modeling | Performance |
| Research on the unsteady hydrodynamic characteristics of vertical axis tidal turbine | Zhang, X., Zhang, L., Wang, F. | 14 March | Current, Cross-Flow Turbine | Modeling | Control, Performance, Structural |
| Folding tidal turbine as an innovative concept toward the new era of turbines | Lam, W., Bhatia, A. | 13 December | Current, Cross-Flow Turbine | Modeling | Materials, Performance, Structural |
| Power measurement of hydrokinetic turbines with free-surface and blockage effect | Birjandi, A., Bibeau, E., Chatoorgoon, V. | 13 September | Current, Cross-Flow Turbine, Riverine | CFD Modeling | Hydrodynamics, Performance |
| Hydrodynamic performance of a vertical-axis tidal-current turbine with different preset angles of attack | Zhao, G., Yang, R., Liu, Y. | 13 April | Cross-Flow Turbine | Modeling, Scale Device | Hydrodynamics, Performance, Structural |
| Modeling and validation of a cross flow turbine using free vortex model and a modified dynamic stall model | Urbina, R., Peterson, M., Kimball, R. | 13 February | Current, Cross-Flow Turbine | CFD Modeling | Performance |
| Modeling passive variable pitch cross flow hydrokinetic turbines to maximize performance and smooth operation | Lazauskas, L., Kirke, B. | 12 September | Current, Cross-Flow Turbine | Modeling | Performance |
| The Tidal Stream Power Curve: A Case Study | Hardisty, J. | 12 May | Current, Cross-Flow Turbine, Tidal | Lab Data, Full Scale | Performance |
| Tests on ducted and bare helical and straight blade Darrieus hydrokinetic turbines | Kirke, B. | 11 November | Current, Cross-Flow Turbine | Field Data, Scale Device | Performance |
| Limitations of fixed pitch Darrieus hydrokinetic turbines and the challenge of variable pitch | Kirke, B., Lazauskas, L. | 11 March | Current, Cross-Flow Turbine | CFD Modeling | Performance |
| A design methodology for cross-flow water turbines | Zanette, J., Imbault, D., Tourabi, A. | 10 May | Current, Cross-Flow Turbine | Modeling | Performance, Structural |
| Recent TCP (Tidal Current Power) projects in Korea | Jo, C., Lee, K., Rho, Y. | 10 January | Current, Axial-Flow Turbine, Cross-Flow Turbine, Tidal | CFD Modeling | Performance, Power Take-Off |
| Efficiency and dynamic performance of Digital Displacement™ hydraulic transmission in tidal current energy converters | Payne, G., Kiprakis, A., Ehsan, M. | 7 March | Current, Cross-Flow Turbine, Tidal | CFD Modeling | Performance |
| Wave-current interactions in marine current turbines | Barltrop, N., Varyani, K., Grant, A. | 6 December | Current, Cross-Flow Turbine | Lab Data, Modeling | Performance |
| Dynamic Behaviour of the Patented Kobold Tidal Current Turbine: Numerical and Experimental Aspects | Coiro, D., De Marco, A., Nicolosi, F. | 5 March | Current, Cross-Flow Turbine | Lab Data, Modeling | Hydrodynamics, Performance |
References
- OPEC Reports Record Compliance with Output Cuts, Raises 2017 Oil Demand Growth Forecast. Available online: https://www.cnbc.com/2017/02/13/oil-demand-set-to-outdo-10-year-average-in-2017-opec.html (accessed on 17 September 2017).
- Aqua Facts. Available online: https://www.oceanicinstitute.org/aboutoceans/aquafacts.html (accessed on 8 February 2017).
- Bedard, R. Economic and social benefits from wave energy conversion marine technology. Mar. Technol. Soc. J. 2007, 41, 44–50. [Google Scholar] [CrossRef]
- Setoguchi, T.; Takao, M. Current status of self-rectifying air turbines for wave energy conversion. Energy Convers. Manag. 2006, 47, 2382–2396. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Henriques, J.C.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Linus Mofor (IRENA) Jarett Goldsmith and Fliss Jones (Garrad Hassan & Partners Ltd.). OCEAN ENERGY: Technology readiness, patents, Deployment status and outlook. Report: August 2020 (IRENA). Available online: www.irena.org (accessed on 14 August 2022).
- Adhikari, R.; Wood, D. The Design of High Efficiency Crossflow Hydro Turbines: A Review and Extension. Energies 2018, 11, 267. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, Z.; Zhang, X.; Xu, C. Review of CFD studies on axial-flow self-rectifying turbines for OWC wave energy conversion. Ocean. Eng. 2019, 175, 80–102. [Google Scholar] [CrossRef]
- Kaunda, C.S.; Kimambo, C.Z.; Nielsen, T.K. A numerical investigation of flow profile and performance of a low-cost Crossflow turbine. Int. J. Environ. Sci. Technol. 2014, 5, 275–296. [Google Scholar]
- Sammartano, V.; Aricò, C.; Carravetta, A.; Fecarotta, O.; Tucciarelli, T. Banki-Michell Optimal Design by Computational Fluid Dynamics Testing and Hydrodynamic Analysis. Energies 2013, 6, 2362–2385. [Google Scholar] [CrossRef]
- Choi, Y.-D.; Lim, J.-I.; Kim, Y.-T.; Lee, Y.-H. Performance and Internal Flow Characteristics of a Cross-Flow Hydro Turbine by the Shapes of Nozzle and Runner Blade. J. Fluid Sci. Technol. 2008, 3, 398–409. [Google Scholar] [CrossRef]
- Masuda, Y.; McCormick, M.E. Experiences in pneumatic wave energy conversion in Japan. In Utilization of Ocean Waves e Wave to Energy Conversion; Cormick, M.E.M., Kim, Y.C., Eds.; American Society of Civil Engineers: New York, NY, USA, 1986. [Google Scholar]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Weerakoon, A.H.S.; Young, H.-S.; Kim, W.-K.; Lee, Y.-H. Novel Tidal Energy Harnessing System Utilizing Quadruple Bi-directional Turbine Arrangement. In Proceedings of the 2020 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Gold Coast, Australia, 8 December 2020; p. 1, ISBN 978-1-6654-1974-1. [Google Scholar] [CrossRef]
- Alkhabbaz, A.; Yang, H.-S.; Weerakoon, A.H.S.; Lee, Y.-H. A novel linearization approach of chord and twist angle distribution for 10 kW horizontal axis wind turbine. Renew. Energy 2021, 178, 1398–1420. [Google Scholar] [CrossRef]
- Akimoto, H.; Tanaka, K.; Kim, Y.Y. Drag-type cross-flow water turbine for capturing energy from the orbital fluid motion in ocean wave. Renew. Energy 2015, 76, 196–203. [Google Scholar] [CrossRef]
- Mehr, G.; Durali, M.; Khakrand, M.H.; Hoghooghi, H. A novel design and performance optimization methodology for hydraulic Cross-Flow turbines using successive numerical simulations. Renew. Energy 2021, 169, 1402–1421. [Google Scholar] [CrossRef]
- Kim, K.-P.; Ahmed, M.R.; Lee, Y.-H. Efficiency improvement of a tidal current turbine utilizing a larger area of channel. Renew. Energy 2012, 48, 557–564. [Google Scholar] [CrossRef]
- Cooke, S.C.; Willden, R.H.J.; Byrne, B.W. The potential of cross-stream aligned sub-arrays to increase tidal turbine efficiency. Renew. Energy 2016, 97, 284–292. [Google Scholar] [CrossRef]
- Weerakoon, A.H.S.; Kim, B.-H.; Cho, Y.-J.; Prasad, D.D.; Ahmed, M.R.; Lee, Y.-H. Design optimization of a novel vertical augmentation channel housing a cross-flow turbine and performance evaluation as a wave energy converter. Renew. Energy 2021, 180, 1300–1314. [Google Scholar] [CrossRef]
- Sinagra, M.; Sammartano, V.; Aricò, C.; Collura, A.; Tucciarelli, T. Cross-flow Turbine Design for Variable Operating Conditions. Procedia Eng. 2014, 70, 1539–1548. [Google Scholar] [CrossRef]
- Babarit, A. A database of capture width ratio of wave energy converters. Renew. Energy 2015, 80, 610–628. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave energy potential along the Death Coast (Spain). Energy 2009, 34, 1963–1975. [Google Scholar] [CrossRef]
- Vanem, E. Joint statistical models for significant wave height and wave period in a changing climate. Mar. Struct. 2016, 49, 180–205. [Google Scholar] [CrossRef]
- Lee, U.-J.; Jeong, W.-M.; Cho, H.-Y. Estimation and Analysis of JONSWAP Spectrum Parameter Using Observed Data Around Korean Coast. J. Mar. Sci. Eng. 2022, 10, 578. [Google Scholar] [CrossRef]
- Tey, W.-Y.; Asako, Y.; Sidik, N.A.C.; Goh, R.-Z. Governing Equations in Computational Fluid Dynamics: Derivations and A Recent Review. Prog. Energy Environ. 2017, 1, 1–19. [Google Scholar] [CrossRef]
- Ransley, E.J.; Greaves, D.; Raby, A.; Simmonds, D.; Hann, M. Survivability of wave energy converters using CFD. Renew. Energy 2017, 109, 235–247. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Ringwood, J.V. High-fidelity numerical modelling of ocean wave energy systems: A review of computational fluid dynamics-based numerical wave tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef]
- Simonetti, I.; Cappietti, L.; Elsafti, H.; Oumeraci, H. Optimization of the geometry and the turbine induced damping for fixed detached and asymmetric OWC devices: A numerical study. Energy 2017, 139, 1197–1209. [Google Scholar] [CrossRef]
- Leijon, M.; Danielsson, O.; Eriksson, M.; Thorburn, K.; Bernhoff, H.; Isberg, J.; Sundberg, J.; Ivanova, I.; Sjöstedt, E.; Ågren, O.; et al. An electrical approach to wave energy conversion. Renew. Energy 2006, 31, 1309–1319. [Google Scholar] [CrossRef]
- Salter, S.H. Wave power. Nature 1974, 249, 720–724. [Google Scholar] [CrossRef]
- Douglas, J.F. Fluid Mechanics; Pearson/Prentice Hall: Hoboken, NJ, USA, 2005. [Google Scholar]
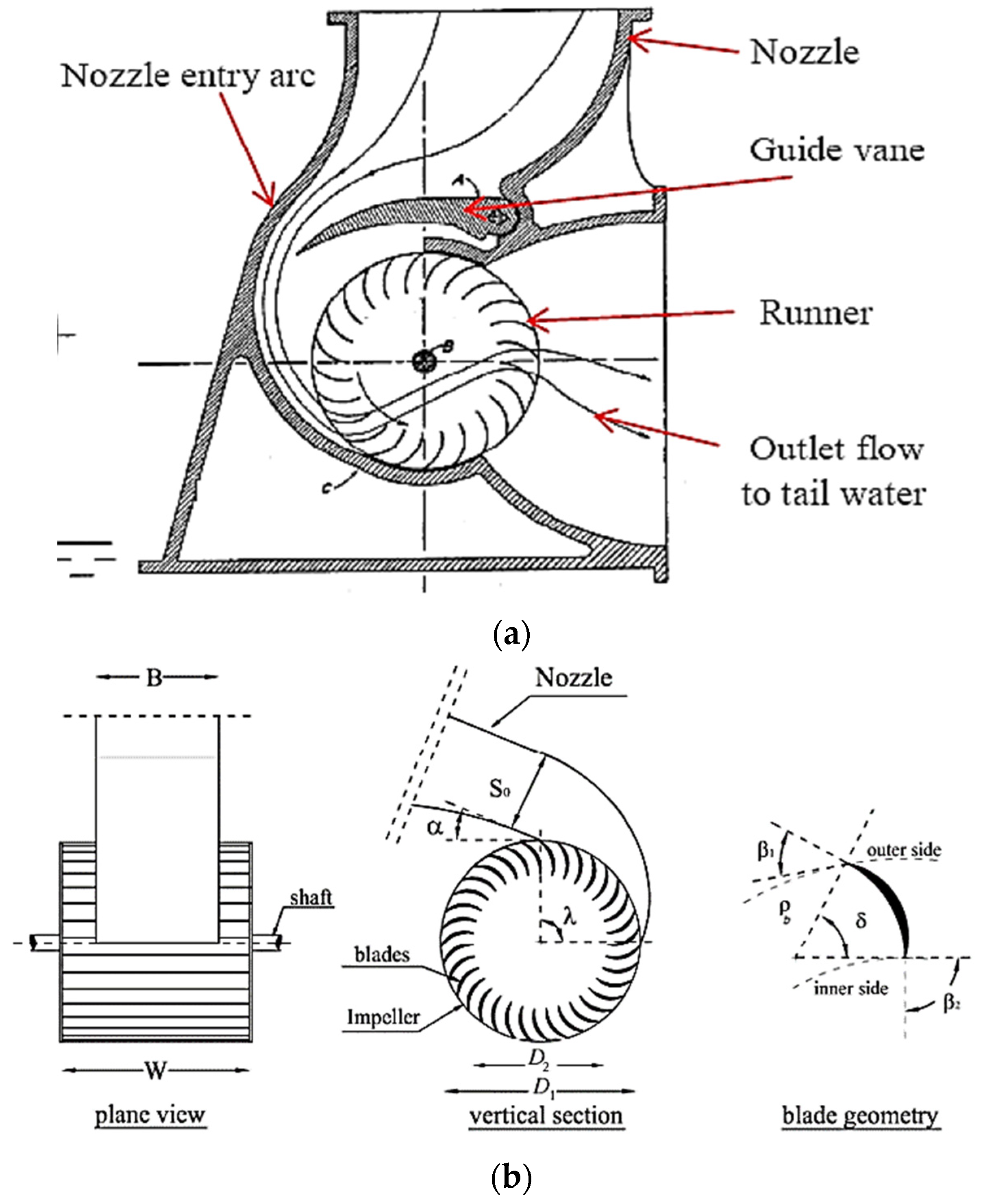




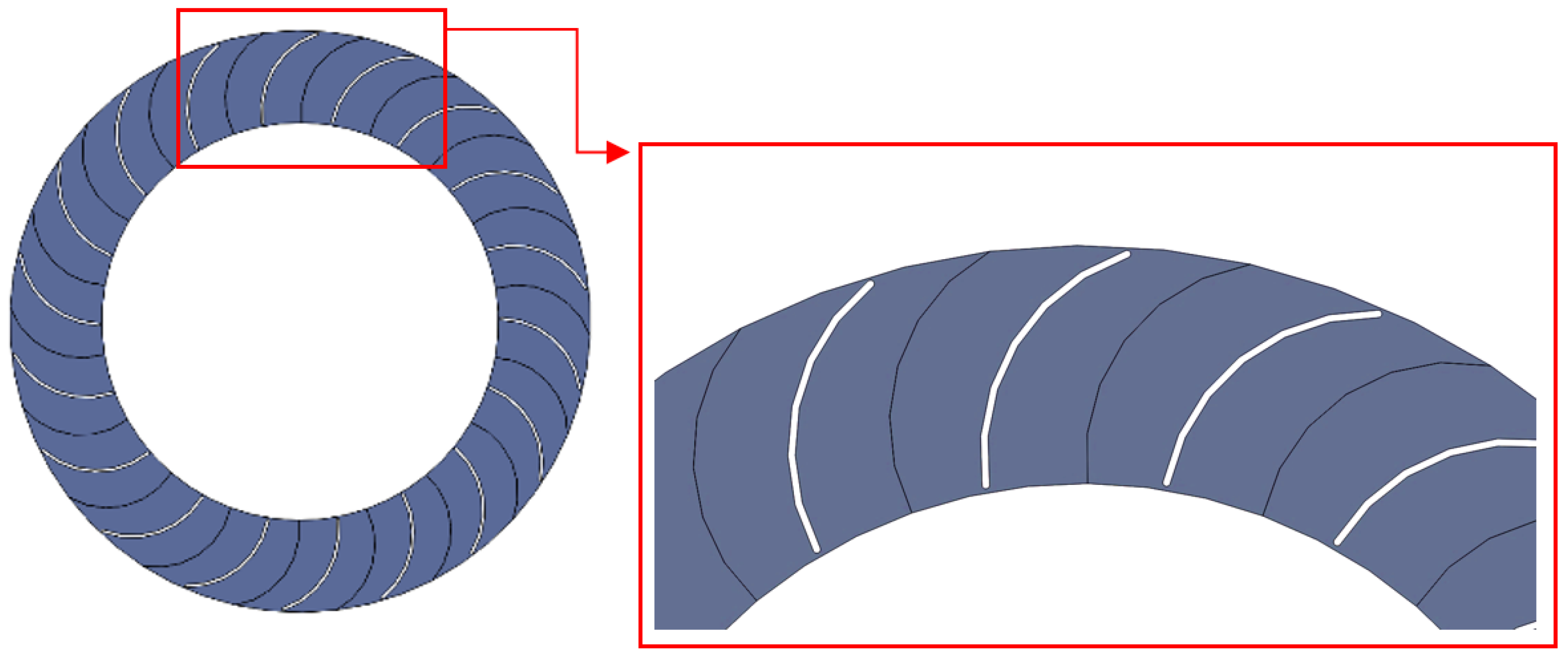
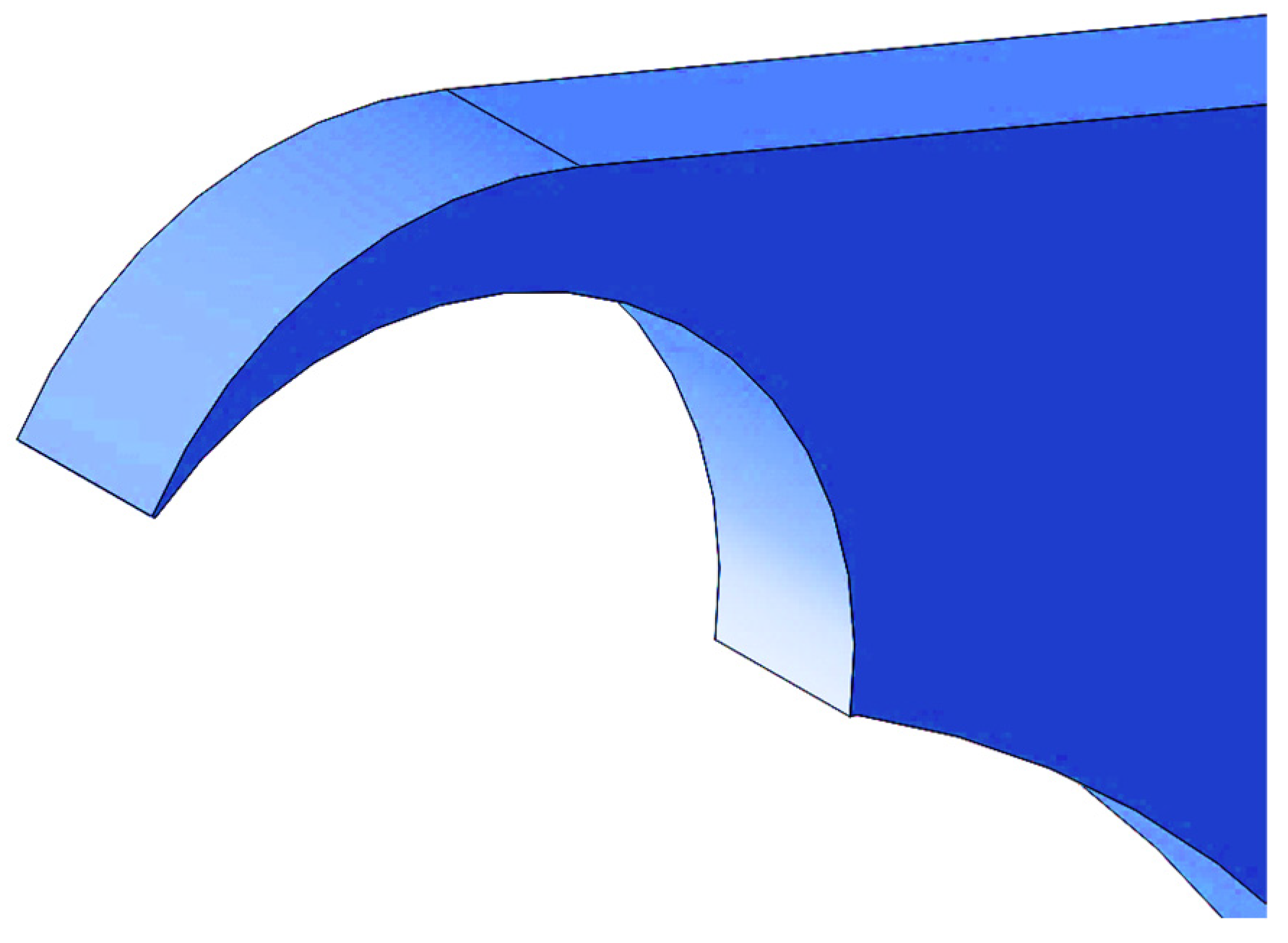














| Wave Specification Data | |
|---|---|
| Significant Wave Height (Hs) | 3.0 m |
| Peak Wave Frequency | 0.0177 Hz |
| Peak Wave Period | 9.0 s |
| Peak Frequency | 0.11 rad/s |
| Gamma Value | 3.3 |
| Turbine Design Parameters | |
|---|---|
| Designed Head (m) | 3 m |
| Flow Rate Q (m3/s) | 10 m3/s |
| Outer Diameter (D2) | 2.0 m |
| Inner Diam. (D1) | 1.36 m |
| Length/Width (L) | 7.5 m |
| N (RPM) | 35 RPM |
| Number of Blades (n) | 18 |
| Radial Rim Width (a) | 0.34 m |
| Blade Curvature (p) | 217.6 mm |
| Blade Span (t) | 0.348 m |
| Nozzle Entry Arc (λ) | 90~150 deg |
| Estimated Efficiency | 75% |
| Blade Angle | 16 deg |
| Entrance Angle | 30 deg |
| Exit Angle | 90 deg |
| Simulation Type | Steady State | Transient (Time Averaging) |
|---|---|---|
| Mesh Type | Hexahedral | Hexahedral |
| Number of Nodes | 3.56 million | 3.56 million |
| Time step | Automatic | 30 s |
| Turbulence model | Shea Stress Transport (SST) | Shea Stress Transport (SST) |
| Fluid Phase | Single Phase (Water) | Single Phase (Water) |
| Mesh Motion | Stationery | Moving |
| Inlet boundary | Wave inlet | Wave inlet |
| Outlet boundary | Opening | Opening |
| Turbine Rotational Speed | 20, 30, 35, 40, and 45 rpm | 25 and 35 rpm |
| Rotor–Stator Interface | Frozen Rotor | Transient Rotor Stator |
| Criterion | Numerical Value at BEP |
|---|---|
| Head | 3.00 m of Head |
| RPM | 35 RPM |
| Efficiency | 54.33% |
| Y+ Value | 3.14156 |
| Mass Flow Rate | 2025.56 kg/s |
| Extracted Power | 33.366 kW (0.5 m Width) |
| Real Scale Model Power | 500.49 kW |
| CFD Code | Efficiency |
| Ansys CFX | 54.33% |
| Star CCM+ | 52.38% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weerakoon, A.H.S.; Lee, Y.-H.; Assadi, M. Wave Energy Convertor for Bilateral Offshore Wave Flows: A Computational Fluid Dynamics (CFD) Study. Sustainability 2023, 15, 7152. https://doi.org/10.3390/su15097152
Weerakoon AHS, Lee Y-H, Assadi M. Wave Energy Convertor for Bilateral Offshore Wave Flows: A Computational Fluid Dynamics (CFD) Study. Sustainability. 2023; 15(9):7152. https://doi.org/10.3390/su15097152
Chicago/Turabian StyleWeerakoon, A. H. Samitha, Young-Ho Lee, and Mohsen Assadi. 2023. "Wave Energy Convertor for Bilateral Offshore Wave Flows: A Computational Fluid Dynamics (CFD) Study" Sustainability 15, no. 9: 7152. https://doi.org/10.3390/su15097152
APA StyleWeerakoon, A. H. S., Lee, Y.-H., & Assadi, M. (2023). Wave Energy Convertor for Bilateral Offshore Wave Flows: A Computational Fluid Dynamics (CFD) Study. Sustainability, 15(9), 7152. https://doi.org/10.3390/su15097152









