The Effect of Power Flow Entropy on Available Load Supply Capacity under Stochastic Scenarios with Different Control Coefficients of UPFC
Abstract
1. Introduction
- An index of improved power flow entropy is defined. It can not only quantify the equilibrium of the power flow distribution throughout the whole power system, but also reflects the degree of the branch loading rate.
- The adjustment of the control parameters of UPFC is taken into account during the calculating procedure of RPF herein, which makes the calculation result of ALSC under the influence of UPFC more reasonable.
- Taking LHS as the basis of the PPF method, and combining it with the RPF method, the probabilistic repeated power flow (PRPF) calculation method is proposed in this paper. Thus, the intrinsic relationship between the improved power flow entropy and the ALSC in stochastic scenarios is deeply analyzed.
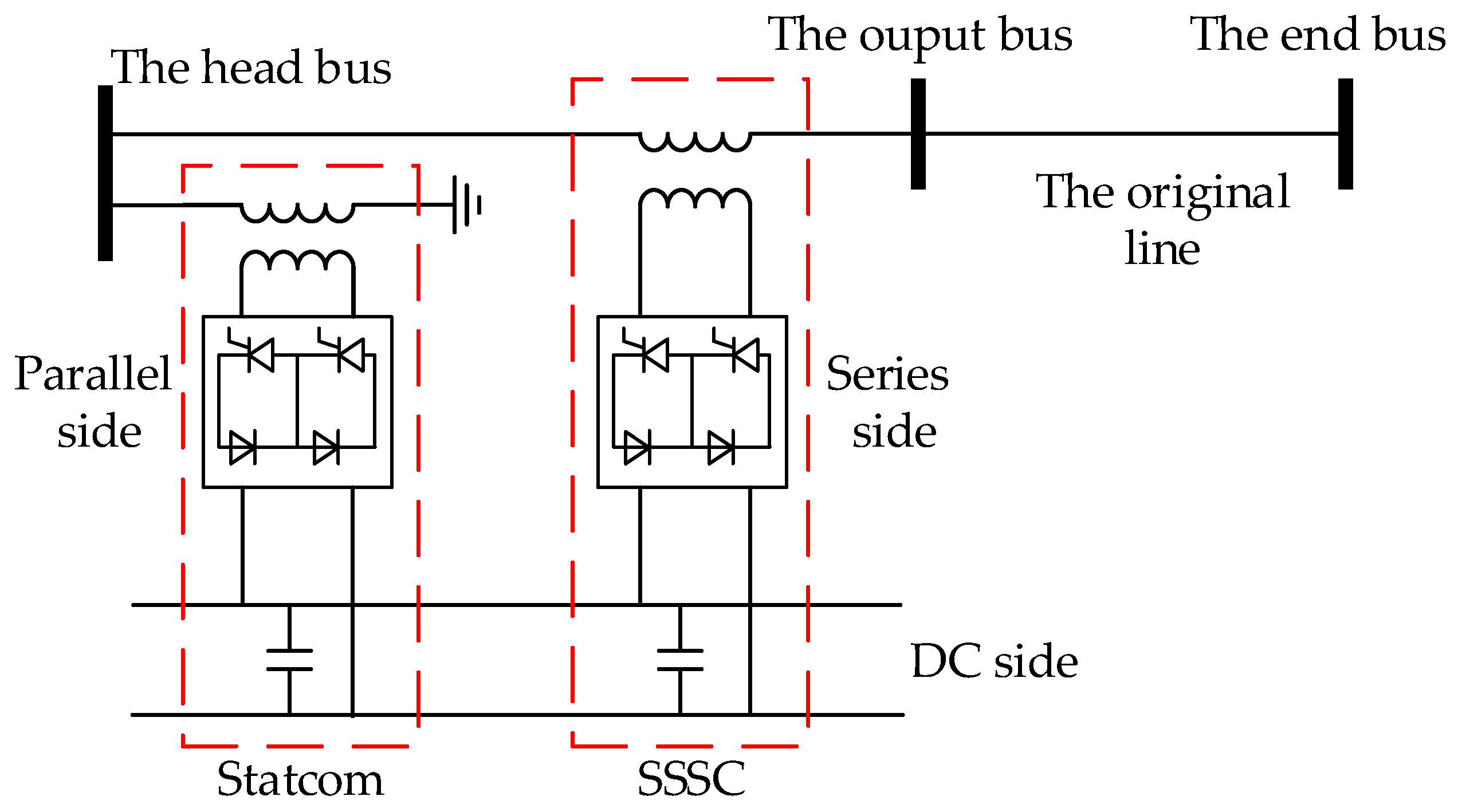
2. The Physical Model of UPFC
2.1. The Structure and Control Strategy of UPFC
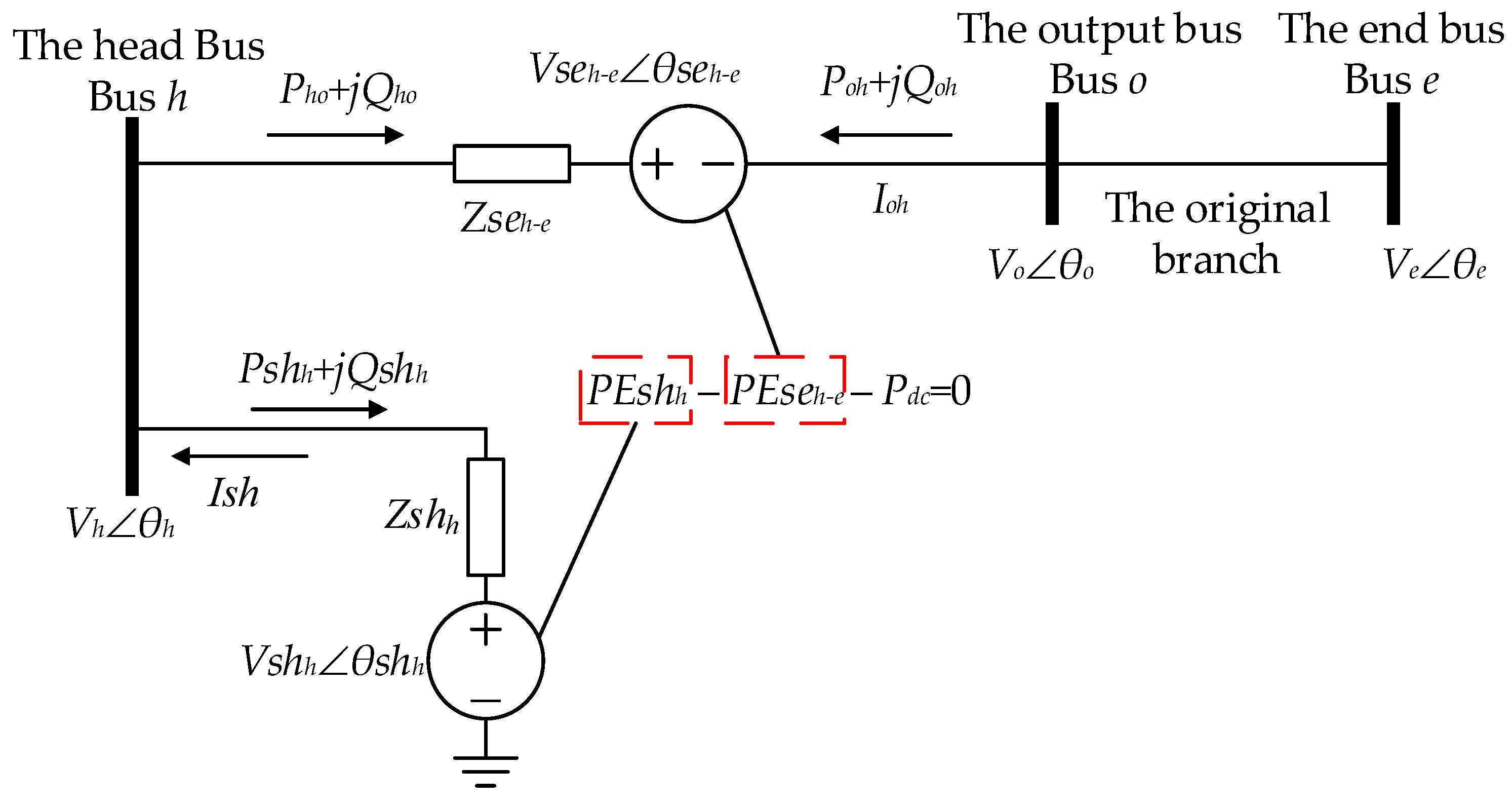
2.2. The Steady-State Model of UPFC
2.3. The Power Flow Calculation Method of AC System with UPFC
2.3.1. The Mismatch Equations of UPFC
2.3.2. The Mismatch Equations of the AC System
2.3.3. The Power Flow Calculation Method of the AC System with UPFC
3. The Basic Theories of LHS-MCS
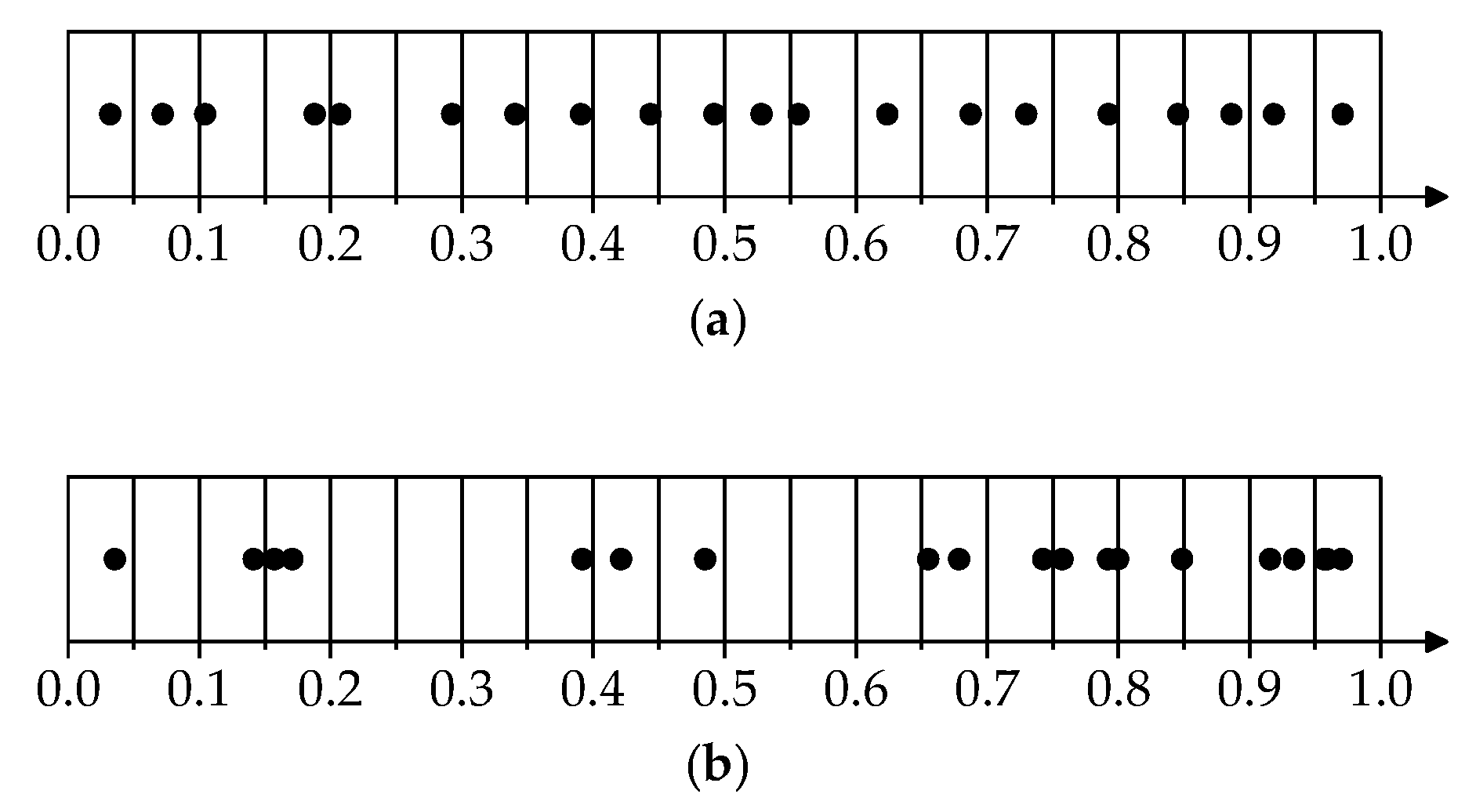
3.1. The Principles of the LHS Method
3.1.1. The Sampling
3.1.2. The Sorting
- Set the initial value of L; each row consists of a random permutation of the set of integers [1, 2, …, N].
- By using the Cholesky decomposition method to decompose the correlation coefficient matrix ρ, a lower trigonometric matrix D can be obtained, which satisfies .
- Obtain a sort matrix with a lower column correlation as . It is worth noting that the elements in may not be positive integers, so each row of data in can be arranged in order from largest to smallest and reassigned to positive integers ranging from 1 to N.
- Repeat steps 1 to 3 until the column correlation of L is less than a predetermined value. Then, according to the arrangement order, which can be represented in L, R is arranged to obtain the final sampling matrix.
3.2. The Procedure for LHS-MCS
4. Probabilistic Determination on the Power Flow Entropy and Available Load Supply Capability
4.1. Definition of Some Indices
4.1.1. Improved Power Flow Entropy
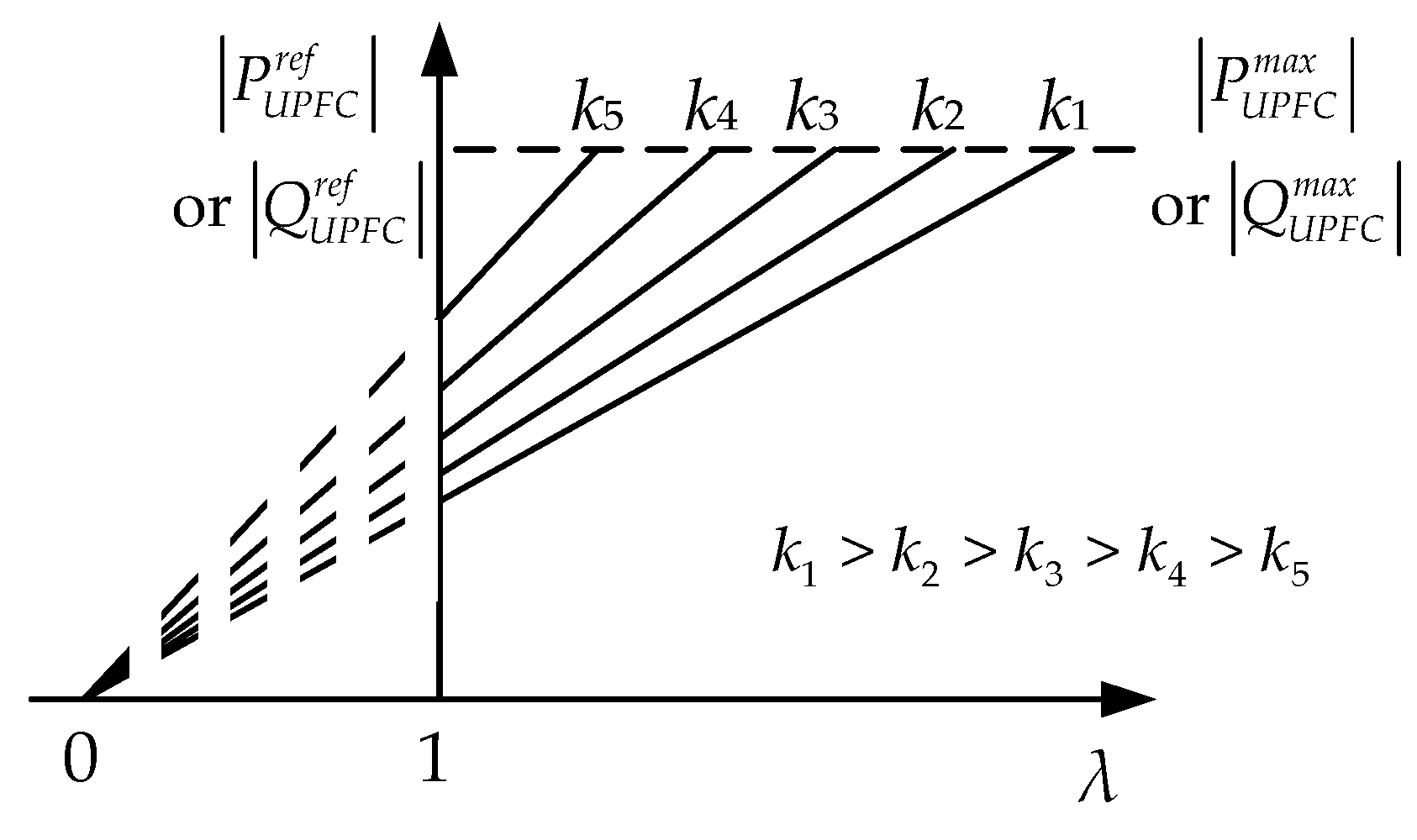
4.1.2. Available Load Supply Capability
4.2. The Repeated Power Flow
- Import basic system data. Set the initial values of h. Set At this time, the load of each bus is . The UPFC control parameters are and .
- Calculate the power flow of the system and determine whether the active power of each branch exceeds the capacity. If no, turn to step 3; if yes, turn to step 4.
- Perform , , , and . Then, go back to step 2.
- Perform , and order . Judge whether h is smaller than the convergence accuracy. If yes, go to Step 5; if no, go back to step 2.
- Perform other necessary calculations and give out the results.
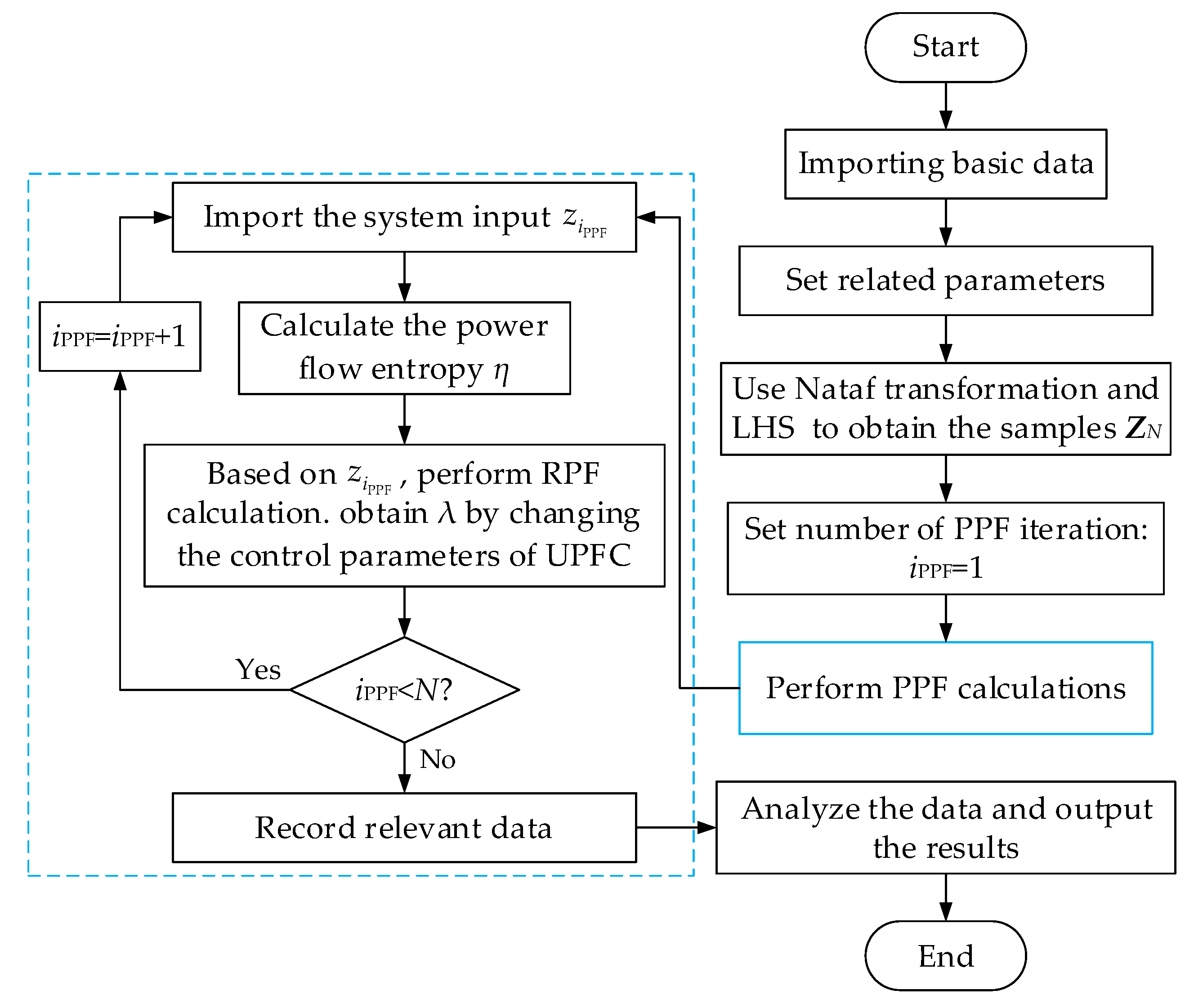
4.3. The Step of the PRPF
5. Test Results
5.1. The DPF Calculation of AC System with UPFC
5.1.1. Validity of the Proposed Model of UPFC
5.1.2. Robustness of the Proposed Algorithm
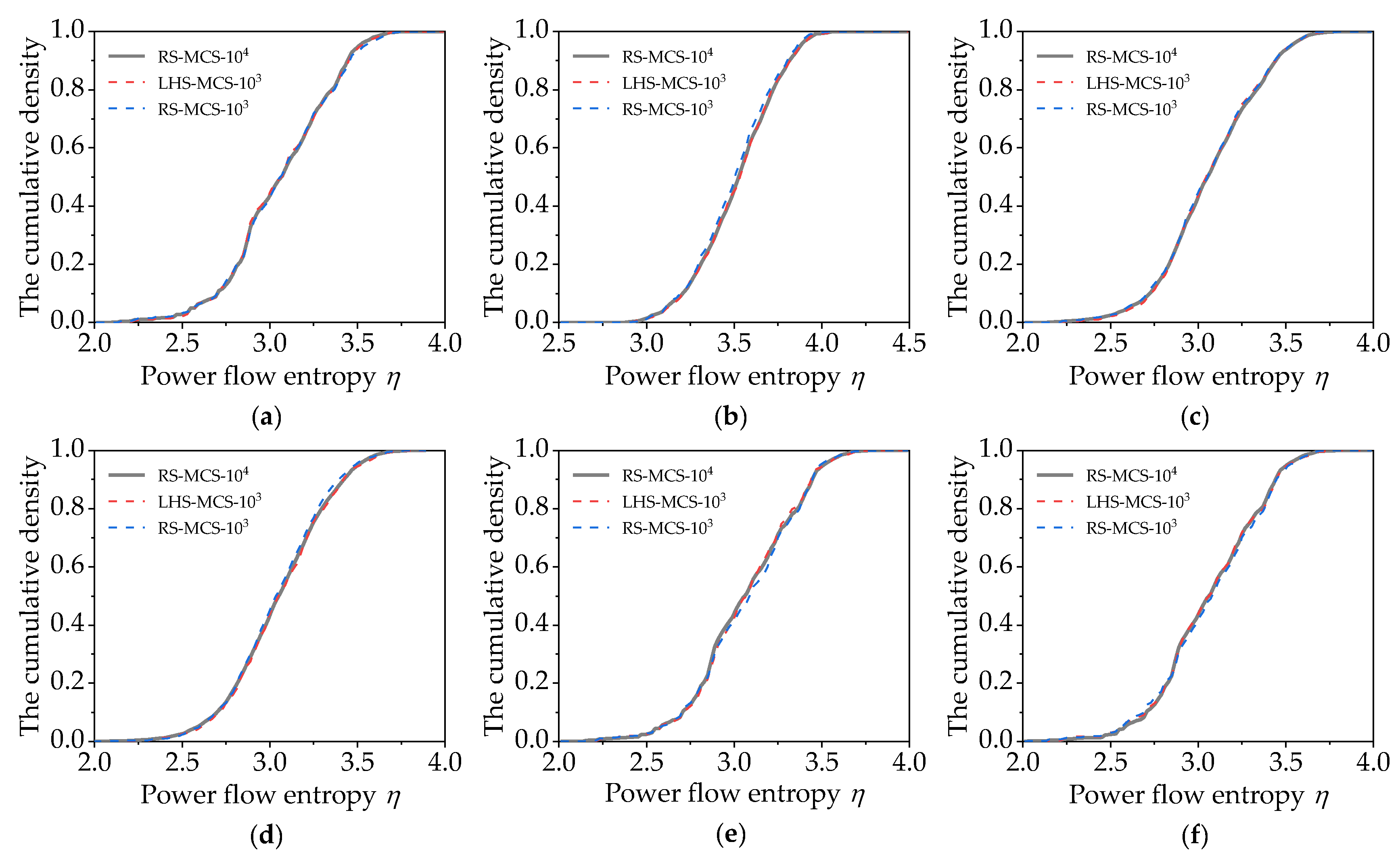
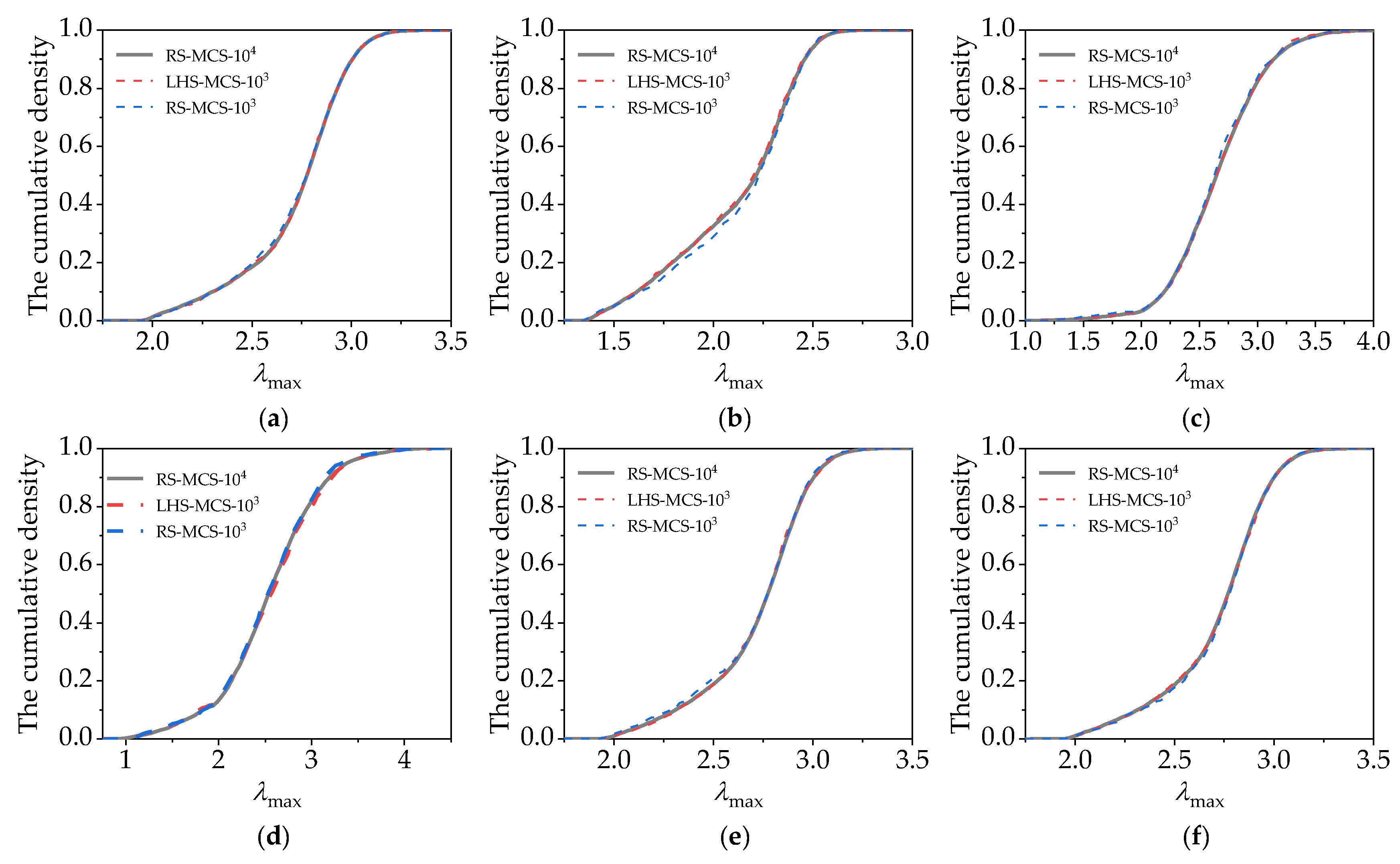
5.2. Tests of Combining LHS-MCS and Repeated Power Flow
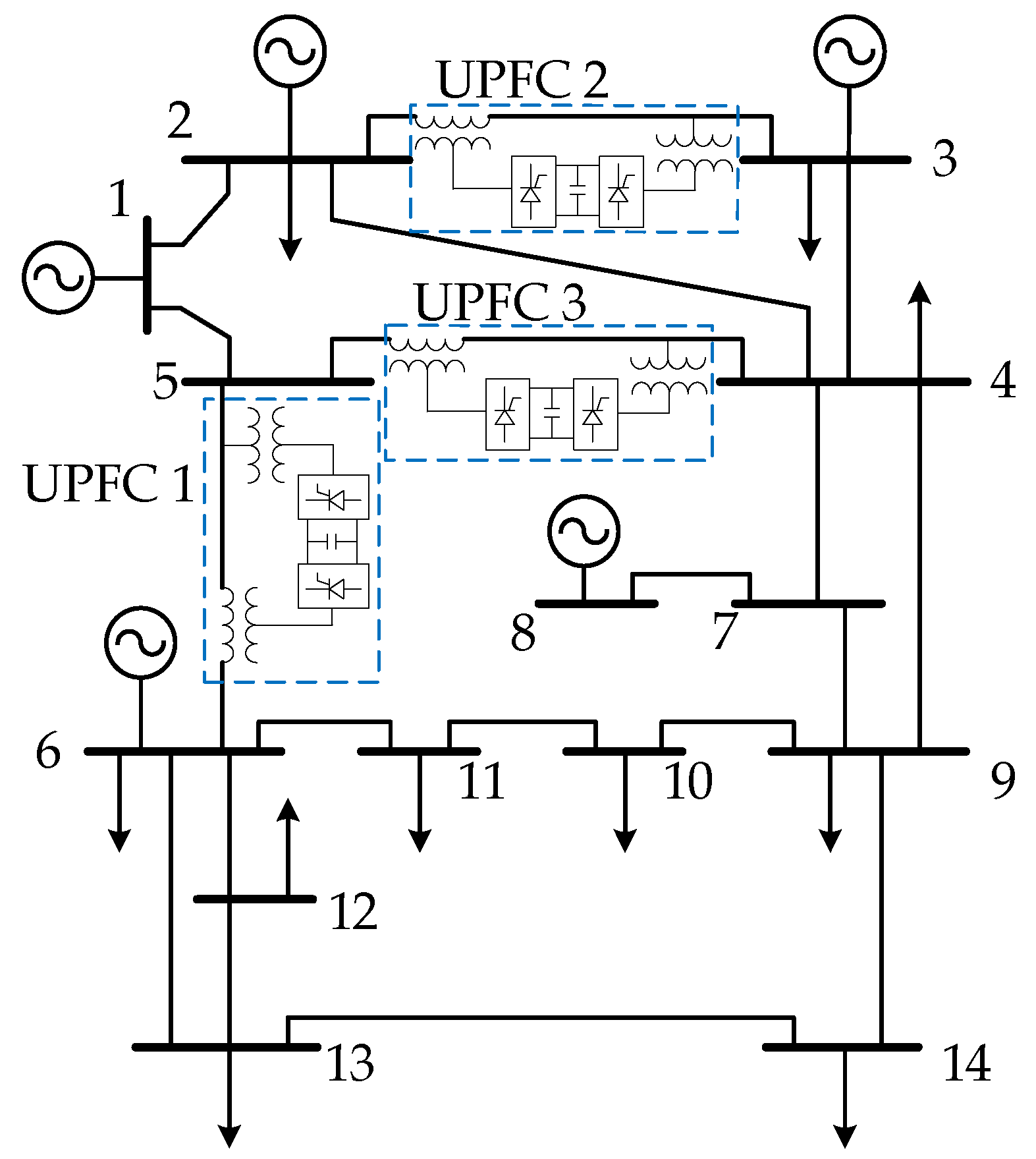
5.2.1. Test System under Study
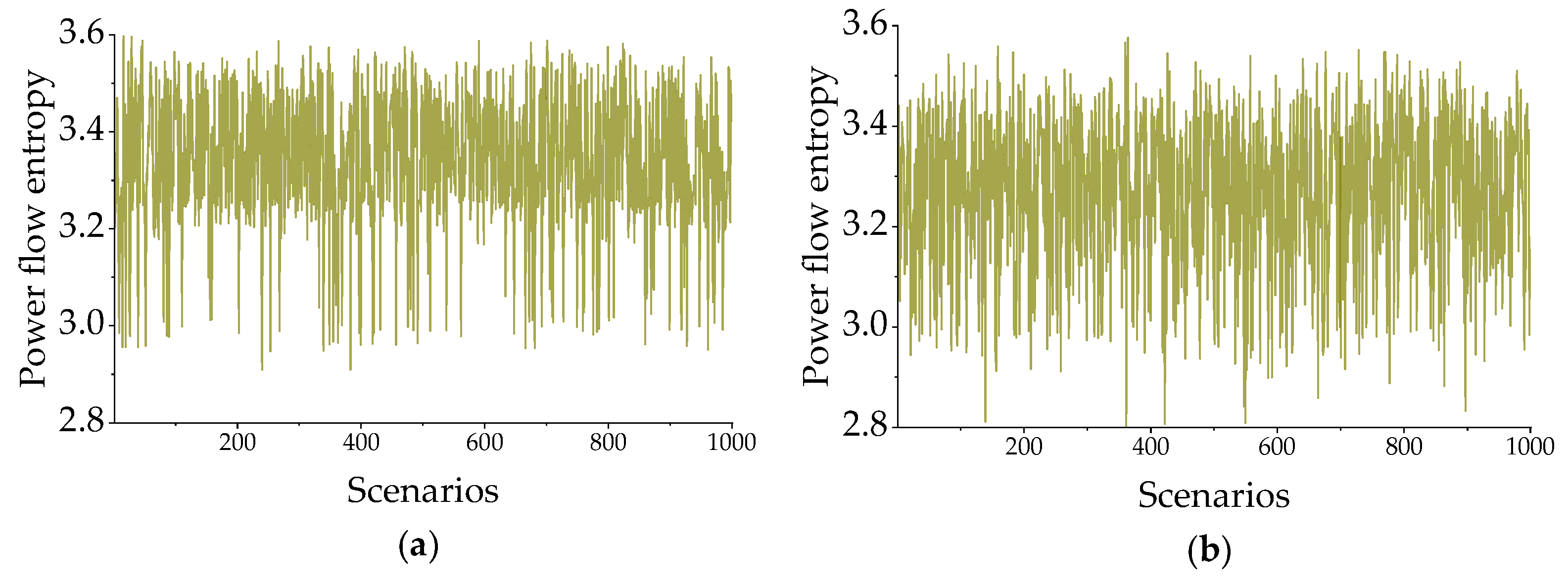
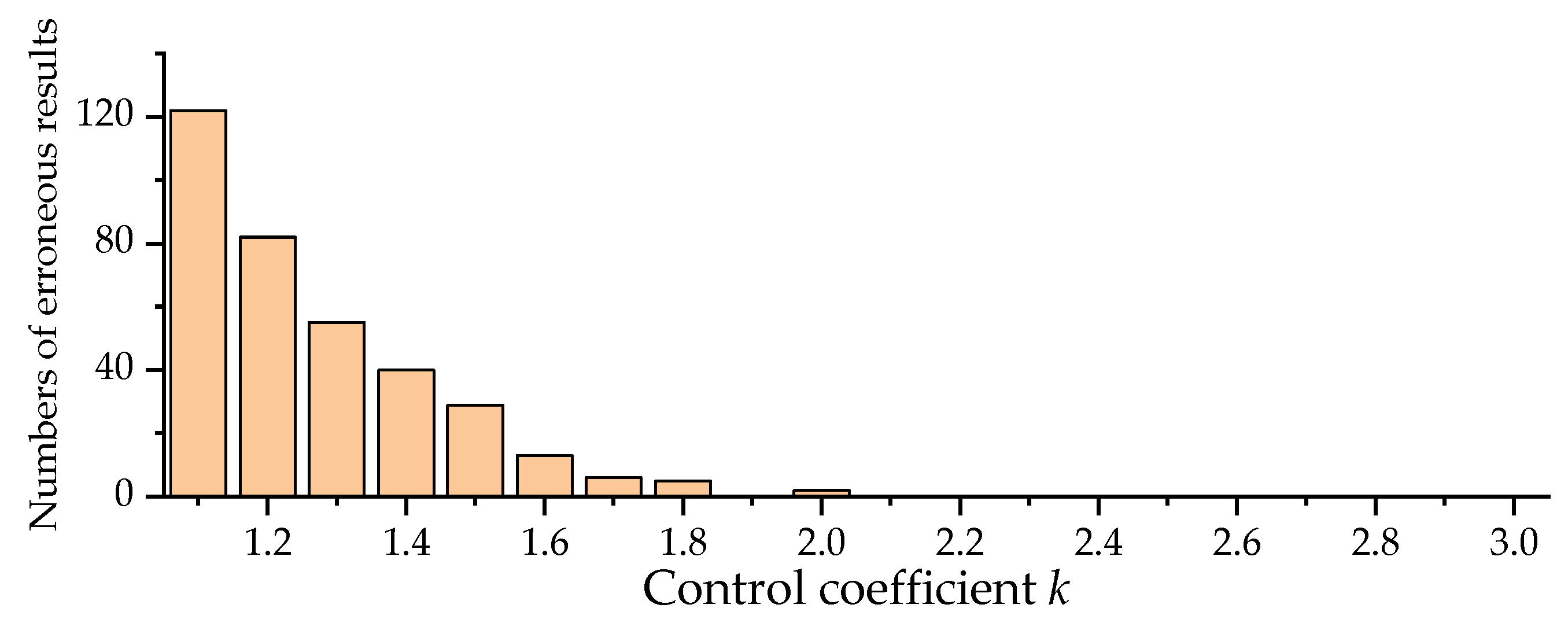
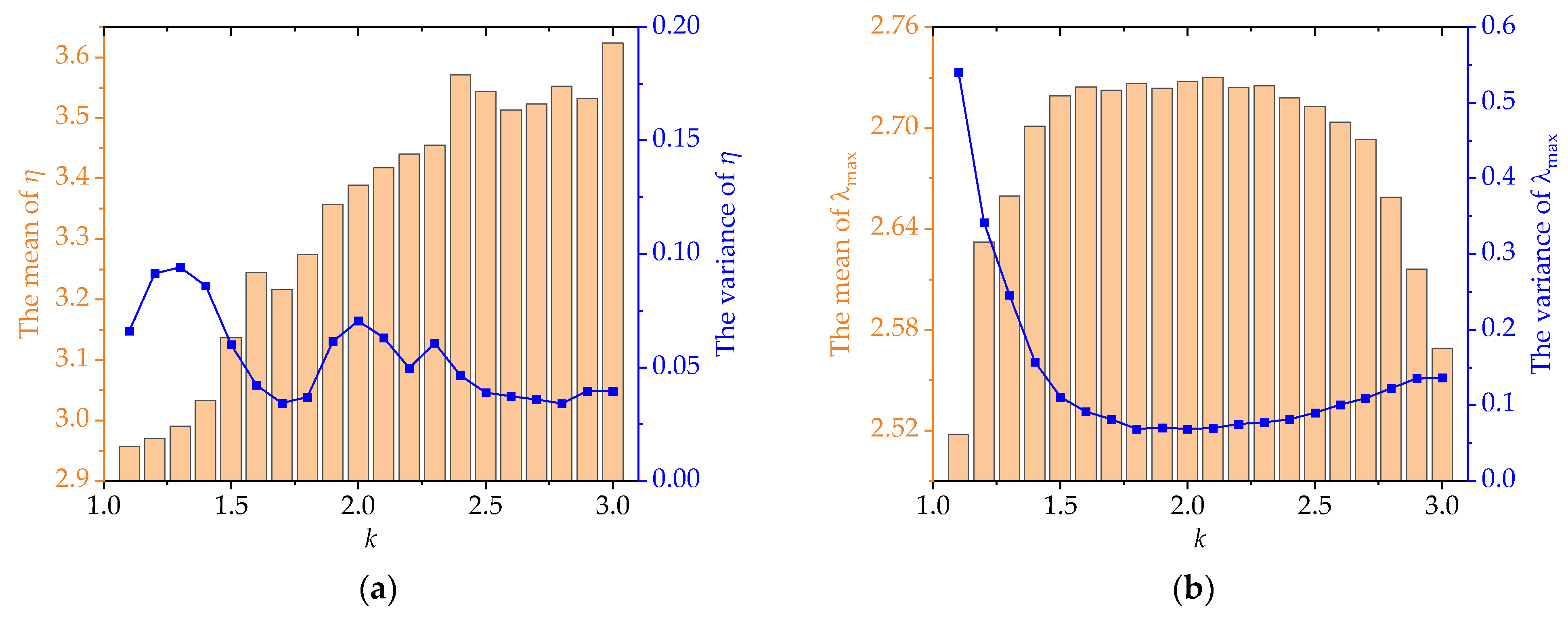
5.2.2. Analysis of the Results
5.3. The Positive Impact of UPFC on the System under Probabilistic Scenarios
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ali, M.A.; Kamel, S.; Hassan, M.H.; Ahmed, E.M.; Alanazi, M. Optimal Power Flow Solution of Power Systems with Renewable Energy Sources Using White Sharks Algorithm. Sustainability 2022, 14, 6049. [Google Scholar] [CrossRef]
- Borkowska, B. Probabilistic Load Flow. IEEE Trans. Power Appar. Syst. 1974, PAS-93, 752–759. [Google Scholar] [CrossRef]
- Chen, S.; Huang, Y.; Chen, Z. The improved probabilistic load flow method based on D-vine copulas and latin hypercube sampling in distribution network with multiple wind generators. IET Gener. Transmiss. Distrib. 2020, 14, 893–899. [Google Scholar] [CrossRef]
- Lin, C.F.; Bie, Z.H.; Pan, C.Q. Fast cumulant method for probabilistic power flow considering the nonlinear relationship of wind power generation. IEEE Trans. Power Syst. 2020, 35, 2537–2548. [Google Scholar] [CrossRef]
- Hashish, M.S.; Hasanien, H.M.; Ji, H.; Alkuhayli, A.; Alharbi, M.; Akmaral, T.; Turky, R.A.; Jurado, F.; Badr, A.O. Monte Carlo Simulation and a Clustering Technique for Solving the Probabilistic Optimal Power Flow Problem for Hybrid Renewable Energy Systems. Sustainability 2023, 15, 783. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, J.; Cheng, S. Probabilistic Load Flow Method Based on Nataf Transformation and Latin Hypercube Sampling. IEEE Trans. Sustain. Energy 2013, 4, 294–301. [Google Scholar] [CrossRef]
- Yu, H.; Chung, C.Y.; Wong, K.P.; Lee, H.W.; Zhang, J.H. Probabilistic Load Flow Evaluation with Hybrid Latin Hypercube Sampling and Cholesky Decomposition. IEEE Trans. Power Syst. 2009, 24, 661–667. [Google Scholar] [CrossRef]
- Shu, T. Probabilistic Power Flow Analysis for Hybrid HVAC and LCC-VSC HVDC System. IEEE Access 2019, 7, 142038–142052. [Google Scholar] [CrossRef]
- Miu, K.N.; Chiang, H.D. Electric distribution system load capability: Problem formulation, solution algorithm, and numerical results. IEEE Trans. Power Deliv. 2000, 15, 436–442. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, H.; Zhang, L.; Bazargan, M.; Yao, L. Probabilistic Evaluation of Available Load Supply Capability for Distribution System. IEEE Trans. Power Syst. 2013, 28, 3215–3225. [Google Scholar] [CrossRef]
- Luo, F. An evaluation method for power supply capability of urban electric power distribution system based on “N−1” simulation analysis of transformers. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009. [Google Scholar] [CrossRef]
- Augugliaro, A.; Dusonchet, L.; Favuzza, S.; Ippolito, M.G.; Riva Sanseverino, E. A simple method to assess loadability of radial distribution networks. In Proceedings of the 2005 IEEE Russia Power Tech, Petersburg, Russia, 27–30 June 2005. [Google Scholar] [CrossRef]
- Ou, Y.; Singh, C. Assessment of available transfer capability and margins. IEEE Trans. Power Syst. 2002, 17, 463–468. [Google Scholar] [CrossRef]
- Gravener, H.M.; Nwankpa, C. Available transfer capability and first order sensitivity. IEEE Trans. Power Syst. 1999, 14, 512–518. [Google Scholar] [CrossRef] [PubMed]
- Nan, L.; Liu, T.; He, C. Identification of transmission sections based on power grid partitioning. Int. Trans. Elect. Energ. Syst. 2019, 29, e2793. [Google Scholar] [CrossRef]
- Cai, D.; Shi, D.; Chen, J. Probabilistic load flow computation with polynomial normal transformation and Latin hypercube sampling. IET Gener. Transm. Distrib. 2013, 37, 474–482. [Google Scholar] [CrossRef]
- Wang, M.; Fan, Z.; Zhou, J.; Shi, S. Research on Urban Load Rapid Recovery Strategy Based on Improved Weighted Power Flow Entropy. IEEE Access 2021, 9, 10634–10644. [Google Scholar] [CrossRef]
- Li, C.; Xiao, L.; Cao, Y. Optimal allocation of multi-type FACTS devices in power systems based on power flow entropy. Power Syst. Clean Energy 2014, 2, 173–180. [Google Scholar] [CrossRef]
- Gyugyi, L.; Schauder, C.D.; Williams, S.L.; Rietman, T.R.; Torgerson, D.R.; Edris, A. The unified power flow controller: A new approach to power transmission control. IEEE Trans. Power Deliv. 1995, 10, 1085–1097. [Google Scholar] [CrossRef]
- Fuerte-Esquivel, C.R.; Acha, E.; Ambriz-Perez, H. A comprehensive Newton-Raphson UPFC model for the quadratic power flow solution of practical power networks. IEEE Trans. Power Syst. 2000, 15, 102–109. [Google Scholar] [CrossRef]
- Li, S.; Wang, T.; Zhang, H.; Wang, L.; Jiang, Y.; Xue, J. Sensitivity-based coordination to controllable ranges of UPFCs to avoid active power loop flows. Int. J. Electr. Power Energy Syst. 2020, 114, 1–13. [Google Scholar] [CrossRef]
- Wu, X.; Wang, R.; Wang, Y.; Wang, L. A Novel UPFC Model and its Convexification for Security-Constrained Economic Dispatch. IEEE Trans. Power Syst. 2022, 37, 4202–4213. [Google Scholar] [CrossRef]
- Jinjiao, L.; Yubo, Y.; Miao, J.; Peng, L.; Lei, G.; Chi, Z. Control System Performance research and measurement of Southern Suzhou 500kV power grid UPFC project. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018. [Google Scholar] [CrossRef]
- Gholipour, E.; Saadate, S. Improving of transient stability of power systems using UPFC. IEEE Trans. Power Deliv. 2005, 20, 1677–1682. [Google Scholar] [CrossRef]
- IMAN, R.L. Uncertainty and sensitivity analysis for computer modeling applications. In Proceedings of the Proceedings of the Winter Annual Meeting of ASME, Anaheim, CA, USA, 8–13 November 1992. [Google Scholar]
- Fang, C.; Ma, Z.; Wang, K.; Qin, B. Nataf Transformation based Probabilistic Energy Flow Calculation. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Xi’an, China, 21–24 October 2019. [Google Scholar] [CrossRef]





| The Active Control Variable | The Reactive Control Variable | |
|---|---|---|
| The parallel side | ― | The reactive power injection or the AC bus voltage amplitude |
| The series side | The active power | The reactive power |
| Branch | 1–2 | 1–5 | 2–3 | 2–4 | 2–5 | 3–4 | 4–5 |
| Pmax/p.u. | 3 | 1.5 | 1.5 | 1.5 | 2 | 1.5 | 2 |
| Branch | 4–7 | 4–9 | 5–6 | 6–11 | 6–12 | 6–13 | 7–8 |
| Pmax/p.u. | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Branch | 7–9 | 9–10 | 9–14 | 10–11 | 12–13 | 13–14 | |
| Pmax/p.u. | 1 | 1 | 1 | 1 | 1 | 1 |
| Parallel Side/p.u. | Series Side/p.u. | |
|---|---|---|
| UPFC1 | ||
| UPFC2 | ||
| UPFC3 |
| UPFC1 | Vse5-6 | θse5-6 | Vsh5 | θsh5 |
| 0.1580 | 1.6738 | 0.9950 | −0.0577 | |
| UPFC2 | Vse2-3 | θse2-3 | Vsh2 | θsh2 |
| 0.1529 | −2.4690 | 1.0231 | −0.0321 | |
| UPFC3 | Vse4-5 | θse4-5 | Vsh4 | θsh4 |
| 0.1008 | 2.2749 | 0.9395 | −0.0923 |
| Parallel Side/p.u. | Series Side/p.u. | |
|---|---|---|
| UPFC1 | ||
| UPFC2 | ||
| UPFC3 |
| Case | Modification |
|---|---|
| Case B1 | Basic case |
| Case B2 | Basic case but not including UPFC |
| Case B3 | Change the standard deviation of each load from 5% to 15% |
| Case B4 | Change the standard deviation of each load from 5% to 25% |
| Case B5 | Change the correlation coefficient between loads from 0.2 to 0.5 |
| Case B6 | Change the correlation coefficient between loads from 0.2 to 0.8 |
| Case B1 | Case B2 | Case B3 | Case B4 | Case B5 | Case B6 | |||
|---|---|---|---|---|---|---|---|---|
| η | Mean | LHS-MCS-103 | 1.87 × 10−4 | 3.29 × 10−4 | 1.63 × 10−3 | 2.33 × 10−3 | 4.49 × 10−4 | 6.44 × 10−4 |
| RS-MCS-103 | 7.98 × 10−3 | 5.03 × 10−3 | 2.59 × 10−3 | 3.51 × 10−3 | 3.04 × 10−3 | 1.61 × 10−3 | ||
| Variance | LHS-MCS-103 | 7.98 × 10−3 | 1.25 × 10−2 | 1.98 × 10−2 | 1.41 × 10−2 | 3.11 × 10−2 | 5.53 × 10−2 | |
| RS-MCS-103 | 5.30 × 10−2 | 4.17 × 10−2 | 7.85 × 10−3 | 6.12 × 10−2 | 1.64 × 10−2 | 1.00 × 10−1 | ||
| Mean | LHS-MCS-103 | 1.91 × 10−5 | 3.46 × 10−3 | 1.13 × 10−3 | 2.10 × 10−3 | 5.63 × 10−4 | 5.75 × 10−4 | |
| RS-MCS-103 | 1.81 × 10−3 | 8.73 × 10−3 | 6.65 × 10−3 | 6.88 × 10−3 | 4.62 × 10−3 | 2.61 × 10−3 | ||
| Variance | LHS-MCS-103 | 4.25 × 10−3 | 1.54 × 10−2 | 4.05 × 10−3 | 4.60 × 10−4 | 2.24 × 10−3 | 8.07 × 10−3 | |
| RS-MCS-103 | 2.37 × 10−1 | 4.06 × 10−2 | 2.02 × 10−2 | 1.67 × 10−2 | 6.89 × 10−2 | 2.91 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, Z.; Lou, Y.; Wang, J.; Li, Y.; Yang, K.; Peng, S.; Tang, J. The Effect of Power Flow Entropy on Available Load Supply Capacity under Stochastic Scenarios with Different Control Coefficients of UPFC. Sustainability 2023, 15, 6997. https://doi.org/10.3390/su15086997
Ou Z, Lou Y, Wang J, Li Y, Yang K, Peng S, Tang J. The Effect of Power Flow Entropy on Available Load Supply Capacity under Stochastic Scenarios with Different Control Coefficients of UPFC. Sustainability. 2023; 15(8):6997. https://doi.org/10.3390/su15086997
Chicago/Turabian StyleOu, Zhongxi, Yuanyuan Lou, Junzhou Wang, Yixin Li, Kun Yang, Sui Peng, and Junjie Tang. 2023. "The Effect of Power Flow Entropy on Available Load Supply Capacity under Stochastic Scenarios with Different Control Coefficients of UPFC" Sustainability 15, no. 8: 6997. https://doi.org/10.3390/su15086997
APA StyleOu, Z., Lou, Y., Wang, J., Li, Y., Yang, K., Peng, S., & Tang, J. (2023). The Effect of Power Flow Entropy on Available Load Supply Capacity under Stochastic Scenarios with Different Control Coefficients of UPFC. Sustainability, 15(8), 6997. https://doi.org/10.3390/su15086997






