The Spatiotemporal Dynamic Impact Mechanism of Soil Greenhouse Gases under Precipitation Based on Environmental Law
Abstract
1. Introduction
2. Model Design for Dynamic Analysis of Soil GHG under Precipitation
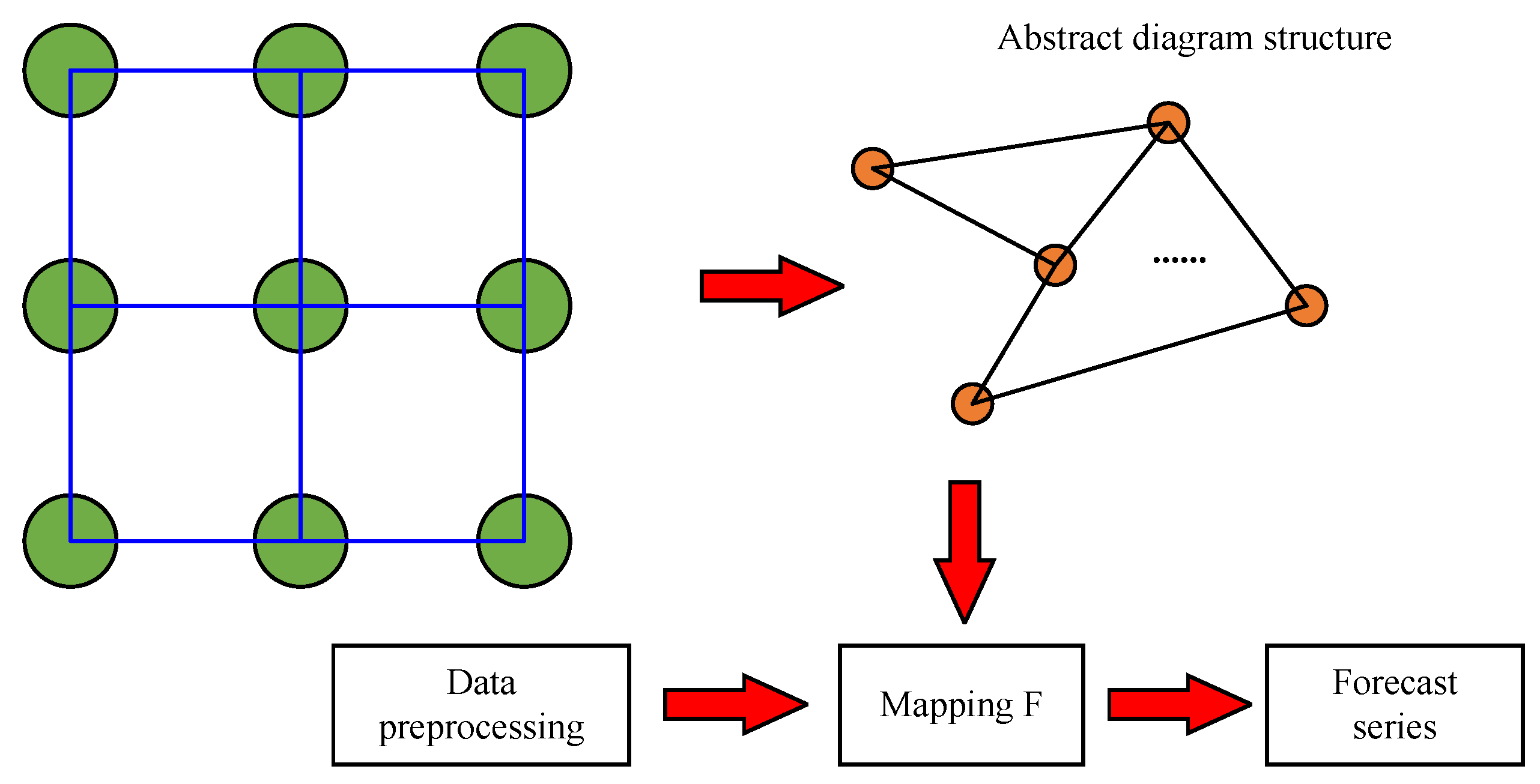
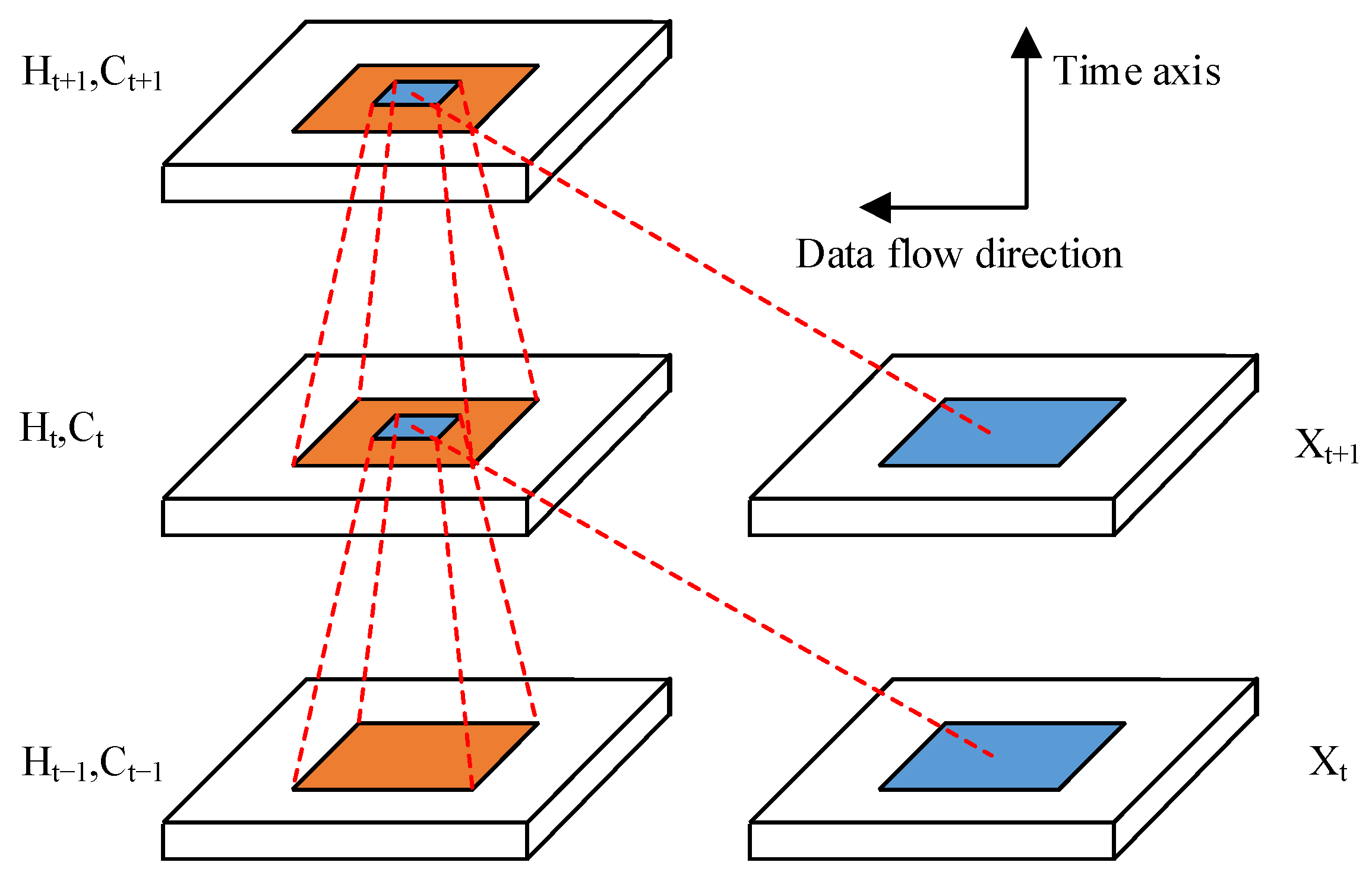
2.1. Model Construction for Characterizing the Dynamics of Soil GHG Fluxes
2.2. Construction of Spatiotemporal Variability Analysis Model for Soil GHG Flux
3. Results and Discussion
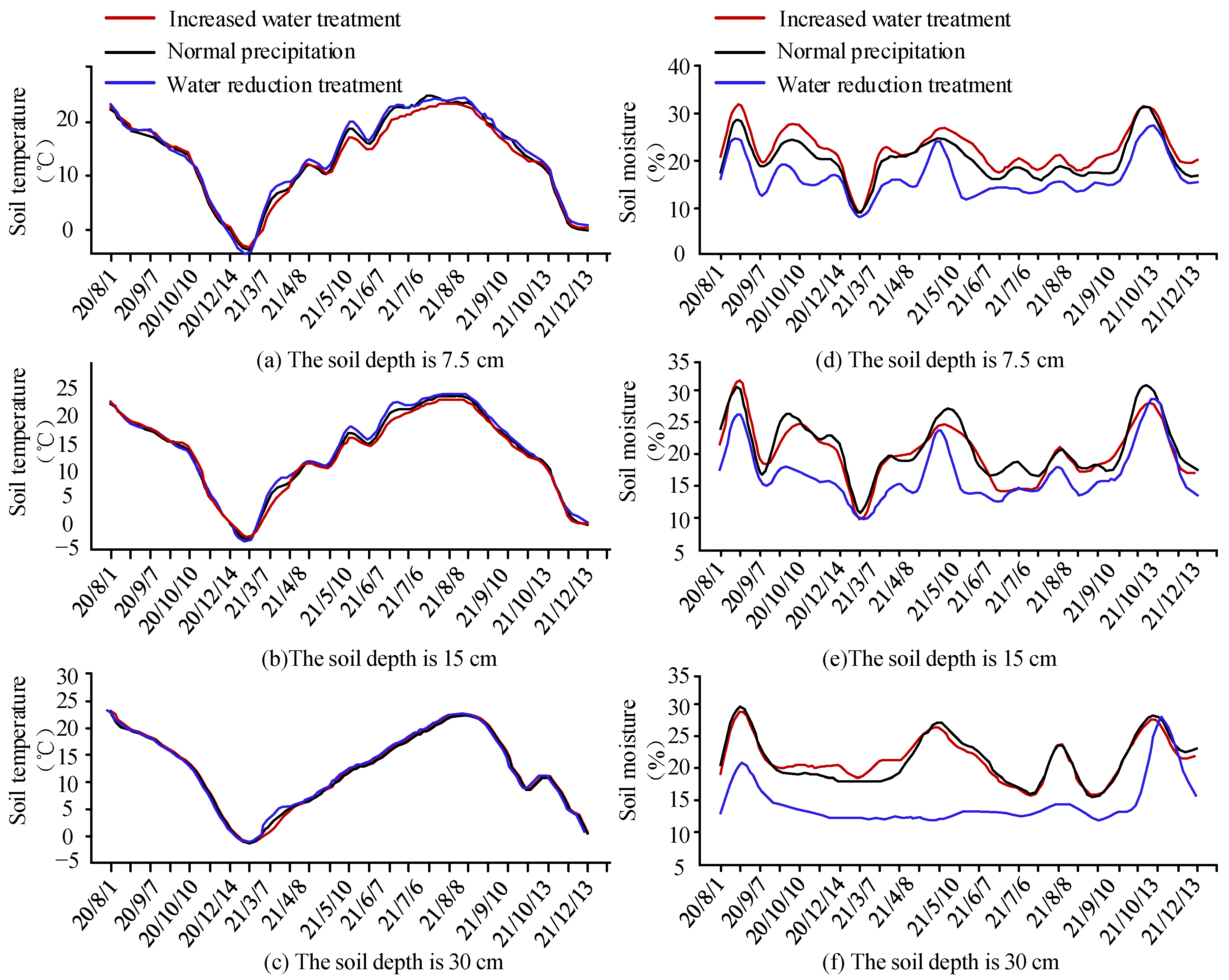
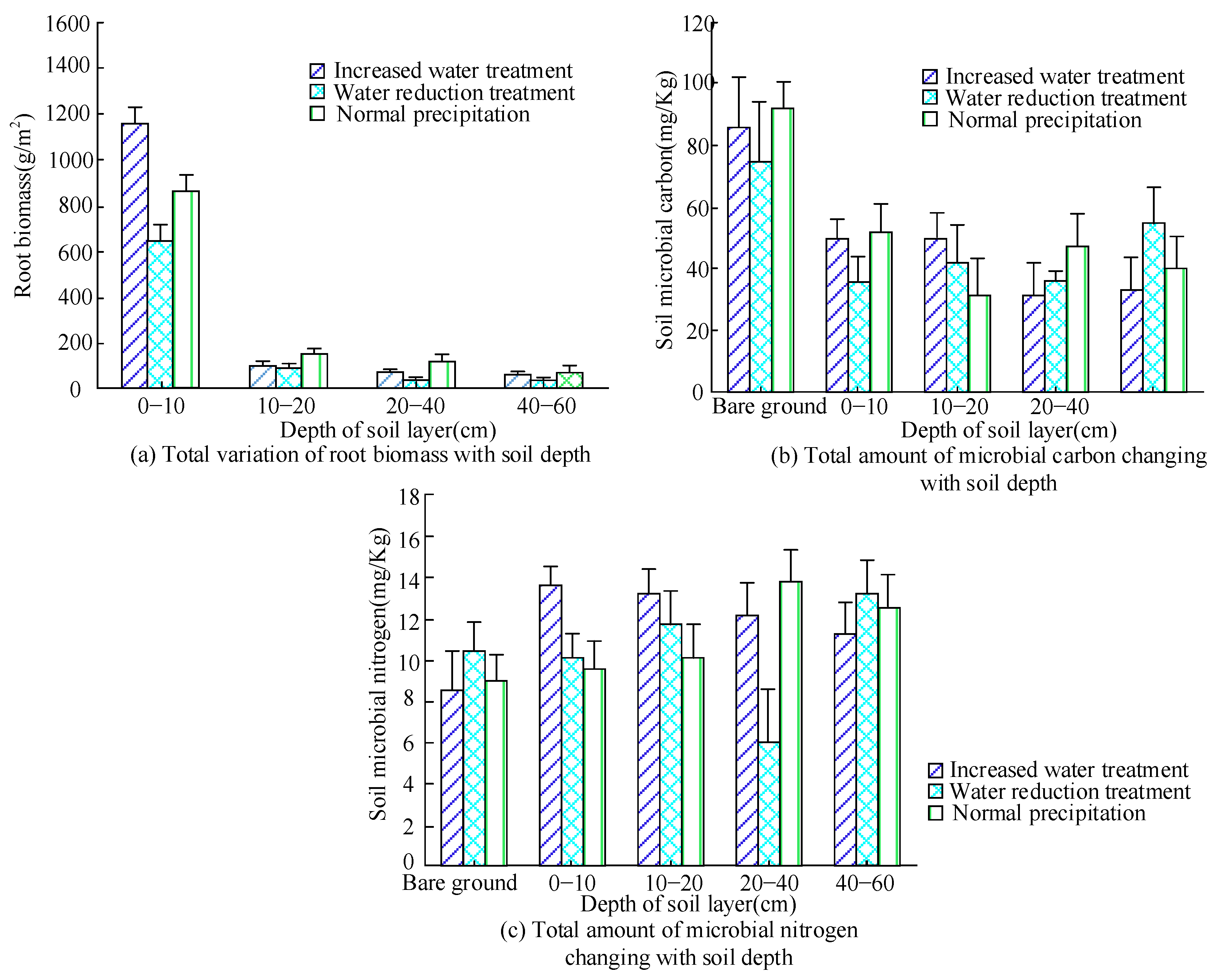
3.1. Influence of Abiotic Factors on GHG Fluxes in Grassland Soils under Precipitation
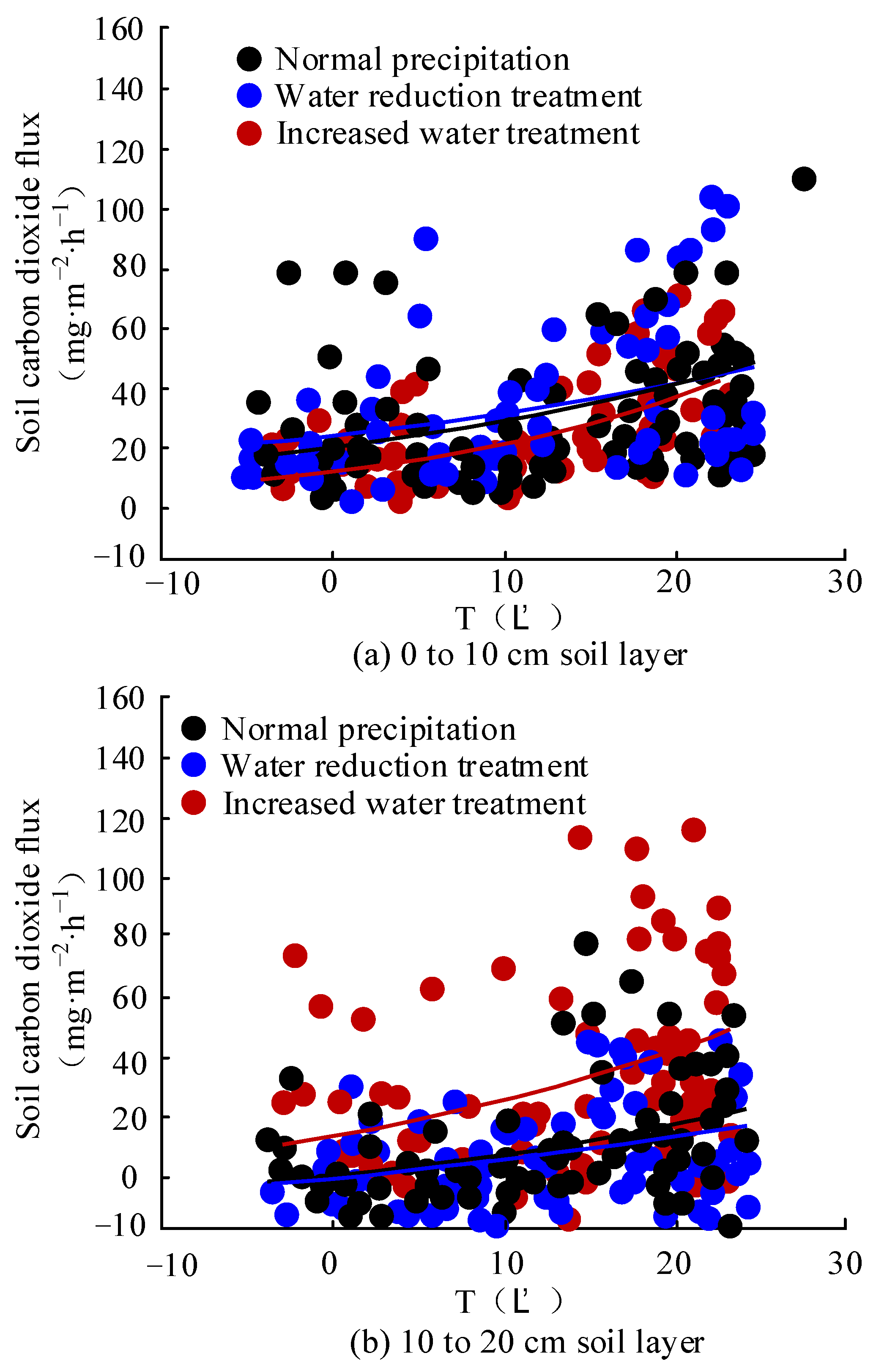
3.2. Effect of Biotic Factors on GHG Fluxes in Grassland Soils under Precipitation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smith, P.; Soussana, J.F.; Angers, D.; Schipper, L.; Chenu, C. How to measure, report and verify soil carbon change to realize the potential of soil carbon sequestration for atmospheric greenhouse gas removal. Glob. Chang. Biol. 2020, 26, 219–241. [Google Scholar] [CrossRef] [PubMed]
- Post, A.K.; Knapp, A.K. The importance of extreme rainfall events and their timing in a semi-arid grassland. J. Ecol. 2020, 108, 2431–2443. [Google Scholar] [CrossRef]
- Nissen, S.; Cretney, R. Retrofitting an emergency approach to the climate crisis: A study of two climate emergency declarations in Aotearoa New Zealand. Environ. Plan. C Politics Space 2022, 40, 340–356. [Google Scholar] [CrossRef]
- Rosenbach, M.; Barbieri, J.S. The Climate Crisis Affects Us All. JAMA Dermatol. 2023, 159, 23–24. [Google Scholar] [CrossRef] [PubMed]
- Tschakert, P. More-than-human solidarity and multispecies justice in the climate crisis. Environ. Politics 2022, 31, 277–296. [Google Scholar] [CrossRef]
- Elveny, M.; Jalil, A.T.; Davarpanah, A. CFD-based simulation to reduce greenhouse gas emissions from industrial plants. Chem. React. Eng. 2021, 19, 1179–1186. [Google Scholar] [CrossRef]
- Tan, L.; Ge, Z.; Zhou, X.; Li, S.H.; Li, X.Z.; Tang, J.W. Conversion of coastal wetlands, riparian wetlands, and peatlands increases greenhouse gas emissions: A global meta-analysis. Glob. Chang. Biol. 2020, 26, 1638–1653. [Google Scholar] [CrossRef]
- Søndergaard, M.; Nielsen, A.; Skov, C.; Baktoft, H.; Reitzel, K. Temporarily and frequently occurring summer stratification and its effects on nutrient dynamics, greenhouse gas emission and fish habitat use: Case study from Lake Ormstrup (Denmark). Hydrobiologia 2023, 850, 65–79. [Google Scholar] [CrossRef]
- Smith, M.D.; Blair, J.M.; Broderick, C.M.; Wilkins, K. Climate legacies determine grassland responses to future rainfall regimes. Glob. Chang. Biol. 2022, 28, 2639–2656. [Google Scholar] [CrossRef]
- Matos, I.S.; Menor, I.O.; Rifai, S.W. Deciphering the stability of grassland productivity in response to rainfall manipulation experiments. Ecol. Biogeogr. 2020, 29, 558–572. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, J.; Ao, Y.; Han, J.Y.; Guo, Z.H.H. Responses of soil N2O emissions and their abiotic and biotic drivers to altered rainfall regimes and co-occurring wet N deposition in a semi-arid grassland. Glob. Chang. Biol. 2021, 27, 4894–4908. [Google Scholar] [CrossRef]
- Griffin-Nolan, R.J.; Slette, I.J.; Knapp, A.K. Deconstructing precipitation variability: Rainfall event size and timing uniquely alter ecosystem dynamics. J. Ecol. 2021, 109, 3356–3369. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Wigneron, J.P.; Ciais, P.; Ballantyne, A.; Ogée, J. Asymmetric responses of ecosystem productivity to rainfall anomalies vary inversely with mean annual rainfall over the conterminous United States. Glob. Chang. Biol. 2020, 26, 6959–6973. [Google Scholar] [CrossRef]
- Shi, Y.; Ao, Y.; Sun, B.; Zhang, J.W.; Guo, Z.H.H. Productivity of Leymus chinensis grassland is co-limited by water and nitrogen and resilient to climate change. Plant Soil 2022, 474, 411–422. [Google Scholar] [CrossRef]
- Pastore, M.A.; Lee, T.D.; Hobbie, S.E.; Peter, B.R. Interactive effects of elevated CO2, warming, reduced rainfall, and nitrogen on leaf gas exchange in Plant. Cell Environ. 2020, 43, 1862–1878. [Google Scholar] [CrossRef]
- Rajamani, L.; Jeffery, L.; Höhne, N.; Hans, F.; Ganti, G.; Glass, A.; Geiges, A. National ‘fair shares’ in reducing greenhouse gas emissions within the principled framework of international environmental law. Clim. Policy 2021, 21, 983–1004. [Google Scholar] [CrossRef]
- Garske, B.; Stubenrauch, J.; Ekardt, F. Sustainable phosphorus management in European agricultural and environmental law. Rev. Eur. Comp. Int. Environ. Law 2020, 29, 107–117. [Google Scholar] [CrossRef]
- Ye, M. Building an enabling legal environment: Laws and policies on social enterprises in China. J. Asian Public Policy 2021, 14, 182–199. [Google Scholar] [CrossRef]
- Law, K.L.; Narayan, R. Reducing environmental plastic pollution by designing polymer materials for managed end-of-life. Nat. Rev. Mater. 2022, 7, 104–116. [Google Scholar] [CrossRef]
- Buns, M.A. Making a model: The 1974 Nordic Environmental Protection Convention and Nordic attempts to form international environmental law. Scand. J. Hist. 2023, 48, 93–115. [Google Scholar] [CrossRef]
- Howard, T.M. Regulatory resistance to environmental law in rural Australia: Land clearing, murder and the media. Local Environ. 2020, 25, 130–146. [Google Scholar] [CrossRef]
- Fang, Z.; Kong, X.; Sensoy, A.; Cui, X.; Cheng, F.C. Government’s awareness of environmental protection and corporate green innovation: A natural experiment from the new environmental protection law in China. Econ. Anal. Policy 2021, 70, 294–312. [Google Scholar] [CrossRef]
- Gschwend, P.; MacFarlane, J.; Jensen, D.; Soo, J.; Saparbaiuly, G.; Borrelli, R.; Vago, F. In situ equilibrium polyethylene passive sampling of soil gas VOC concentrations: Modeling, parameter determinations, and laboratory testing. Environ. Sci. Technol. 2022, 56, 7810–7819. [Google Scholar] [CrossRef] [PubMed]
- Haupenthal, A.; Brax, M.; Bentz, J.; Jungkunst, H.F.; Schützenmeister, K.; Kroener, E. Plants control soil gas exchanges possibly via mucilage. J. Plant Nutr. Soil Sci. 2021, 184, 320–328. [Google Scholar] [CrossRef]
- Samuel, T.D.; Farai, I.P.; Awelewa, A.S. Soil gas radon concentration measurement in estimating the geogenic radon potential in Abeokuta, Southwest Nigeria. J. Radiat. Res. Appl. Sci. 2022, 15, 55–58. [Google Scholar] [CrossRef]
- Bakhshian, S.; Romanak, K. DeepSense: A Physics-Guided Deep Learning Paradigm for Anomaly Detection in Soil Gas Data at Geologic CO2 Storage Sites. Environ. Sci. Technol. 2021, 55, 15531–15541. [Google Scholar] [CrossRef]
- Osterholt, L.; Kolbe, S.; Maier, M. A differential CO2 profile probe approach for field measurements of soil gas transport and soil respiration. J. Plant Nutr. Soil Sci. 2022, 185, 282–296. [Google Scholar] [CrossRef]
- Chamindu Deepagoda, T.K.K.; Clough, T.J.; Jayarathne, J.; Thomas, S.; Elberling, B. Soil-gas diffusivity and soil-moisture effects on N2O emissions from repacked pasture soils. Soil Sci. Soc. Am. J. 2020, 84, 371–386. [Google Scholar] [CrossRef]
- Eskander, S.M.S.U.; Fankhauser, S. Reduction in greenhouse gas emissions from national climate legislation. Nat. Clim. Chang. 2020, 10, 750–756. [Google Scholar] [CrossRef]
- Azadi, M.; Northey, S.A.; Ali, S.H.; Edraki, M. Transparency on greenhouse gas emissions from mining to enable climate change mitigation. Nat. Geosci. 2020, 13, 100–104. [Google Scholar] [CrossRef]
- Weech, S. Changing Climate, Changing Terrain: The Stasis Metaphor and the Climate Crisis. J. Tech. Writ. Commun. 2022, 52, 94–109. [Google Scholar] [CrossRef]
- Ziegler, F.; Jafarzadeh, S.; Skontorp, H.E.; Winther, U. Greenhouse gas emissions of Norwegian seafoods: From comprehensive to simplified assessment. J. Ind. Ecol. 2022, 26, 1908–1919. [Google Scholar] [CrossRef]
- Xu, X.; Sharma, P.; Shu, S.; Lin, T.; Ciais, P. Global greenhouse gas emissions from animal-based foods are twice those of plant-based foods. Nat. Food 2021, 2, 724–732. [Google Scholar] [CrossRef]
- Nicholson, S.R.; Rorrer, N.A.; Carpenter, A.C.; Beckham, G. Manufacturing energy and greenhouse gas emissions associated with plastics consumption. Joule 2021, 5, 673–686. [Google Scholar] [CrossRef]
- Zhai, H.; Xiong, W.; Li, F.; Yang, J.; Su, D.Y.; Zhang, Y.J. Prediction of cold rolling gas based on EEMD-LSTM deep learning technology. Assem. Autom. 2021, 42, 181–189. [Google Scholar] [CrossRef]
- Gambiroža, J.Č.; Mastelić, T.; Kovačević, T.; Čagalj, M. Predicting low-cost gas sensor readings from transients using long short-term memory neural networks. IEEE Internet Things J. 2020, 7, 8451–8461. [Google Scholar] [CrossRef]
- Shu, L.; Liu, Z.; Wang, K.; Zhu, N.N.; Yang, J. Characteristics and Classification of Microseismic Signals in Heading Face of Coal Mine: Implication for Coal and Gas Outburst Warning. Rock Mech. Rock Eng. 2022, 55, 6905–6919. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, L.; Hao, T.; Du, Y.; Shen, J.T. Multiple Sequence Long and Short Memory Network Model for Corner Gas Concentration Prediction on Coal Mine Workings. ACS Omega 2022, 7, 37980–37987. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, L.; Yao, D.; Wang, K.K.; Zhao, X.T.; Xu, W.X. Polluted gas quantitative detection in multi-gas sensor based on bidirectional long-short term memory network. Int. J. Model. Identif. Control. 2020, 36, 24–33. [Google Scholar] [CrossRef]
- Sun, J.; Tian, L.; Chang, J.; Kolomenskii, A.; Schuessler, H.A. Adaptively optimized gas analysis model with deep learning for near-infrared methane sensors. Anal. Chem. 2022, 94, 2321–2332. [Google Scholar] [CrossRef]
- Jung, H.T. The present and future of gas sensors. ACS Sens. 2022, 7, 912–913. [Google Scholar] [CrossRef] [PubMed]
- Dike, V.N.; Lin, Z.; Fei, K. Evaluation and multimodel projection of seasonal precipitation extremes over central Asia based on CMIP6 simulations. Int. J. Climatol. 2022, 42, 7228–7251. [Google Scholar] [CrossRef]
- Georgescu, M.; Broadbent, A.M.; Balling, R.C., Jr. Effect of increased greenhouse gas concentration on mean, extreme, and timing of precipitation over Arizona (USA). Int. J. Climatol. 2022, 42, 3776–3792. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, K.; Wu, Q. Seasonal precipitation and soil microbial community influence plant growth response to warming and N addition in a desert steppe. Plant Soil 2023, 482, 245–259. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, J.; Lambers, H. Intensified rainfall in the wet season alters the microbial contribution to soil carbon storage. Plant Soil 2022, 476, 337–351. [Google Scholar] [CrossRef]



| GHG | Processing Method | Root Biomass | Sample Size | Microbial Carbon | Microbial Nitrogen | Sample Size |
|---|---|---|---|---|---|---|
| CO2 | ALL | 0.101 | 96 | 0.047 | −0.094 | 192 |
| Increased water treatment | −0.138 | 32 | 0.197 | −0.141 | 64 | |
| Water reduction treatment | 0.417 | 32 | 0.03 | −0.055 | 64 | |
| Normal precipitation | 0.208 | 32 | 0.103 | −0.038 | 64 | |
| N2O | ALL | 0.35 * | 96 | 0.081 | −0.067 | 192 |
| Increased water treatment | 0.118 | 32 | 0.219 | −0.078 | 64 | |
| Water reduction treatment | 0.753 ** | 32 | 0.216 | 0.069 | 64 | |
| Normal precipitation | 0.456 | 32 | −0.158 | −0.049 | 64 | |
| CH4 | ALL | 0.059 | 96 | 0.057 | −0.157 | 192 |
| Increased water treatment | −0.175 | 32 | 0.075 | −0.159 | 64 | |
| Water reduction treatment | −0.187 | 32 | 0.172 | 0.079 | 64 | |
| Normal precipitation | 0.371 | 32 | 0.172 | −0.207 | 64 |
| Enzyme Type | GHG | ALL | Increased Water Treatment | Water Reduction Treatment | Normal Precipitation |
|---|---|---|---|---|---|
| BG | CO2 | 0.054 | −0.069 | 0.305 | −0.291 |
| CH4 | −0.047 | 0.027 | −0.082 | −0.142 | |
| N2O | 0.352 ** | 0.138 | 0.596 ** | −0.025 | |
| CBH | CO2 | 0.264 * | 0.241 | 0.337 | 0.144 |
| CH4 | 0.017 | 0.04 | −0.041 | 0.042 | |
| N2O | 0.366 ** | 0.264 | 0.423 * | 0.291 | |
| AP | CO2 | −0.144 | −0.191 | −0.02 | −0.212 |
| CH4 | −0.06 | 0.08 | −0.062 | −0.178 | |
| N2O | 0.089 | 0.009 | 0.217 | 0.024 | |
| LAP | CO2 | −0.071 | −0.161 | 0.163 | −0.398 * |
| CH4 | −0.044 | 0.073 | 0.042 | −0.339 | |
| N2O | 0.244 * | 0.025 | 0.453 * | −0.011 | |
| NAG | CO2 | −0.048 | −0.276 | 0.315 | −0.056 |
| CH4 | −0.128 | −0.119 | −0.026 | −0.164 | |
| N2O | 0.205 | -0.097 | 0.59 ** | 0.295 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhang, F. The Spatiotemporal Dynamic Impact Mechanism of Soil Greenhouse Gases under Precipitation Based on Environmental Law. Sustainability 2023, 15, 6959. https://doi.org/10.3390/su15086959
Zhang W, Zhang F. The Spatiotemporal Dynamic Impact Mechanism of Soil Greenhouse Gases under Precipitation Based on Environmental Law. Sustainability. 2023; 15(8):6959. https://doi.org/10.3390/su15086959
Chicago/Turabian StyleZhang, Wei, and Fang Zhang. 2023. "The Spatiotemporal Dynamic Impact Mechanism of Soil Greenhouse Gases under Precipitation Based on Environmental Law" Sustainability 15, no. 8: 6959. https://doi.org/10.3390/su15086959
APA StyleZhang, W., & Zhang, F. (2023). The Spatiotemporal Dynamic Impact Mechanism of Soil Greenhouse Gases under Precipitation Based on Environmental Law. Sustainability, 15(8), 6959. https://doi.org/10.3390/su15086959







