The Transient Unloading Response of a Deep-Buried Single Fracture Tunnel Based on the Particle Flow Method
Abstract
1. Introduction
2. Particle Flow Model of the Deep-Buried Single Fracture Tunnel
2.1. Contact Constitutive Model
2.2. Particle Flow Model
2.3. Working Condition Design
3. Numerical Calculation Results and Analysis
3.1. The Influence of Fracture Length on the Transient Unloading Effect of the Deep-Buried Tunnel
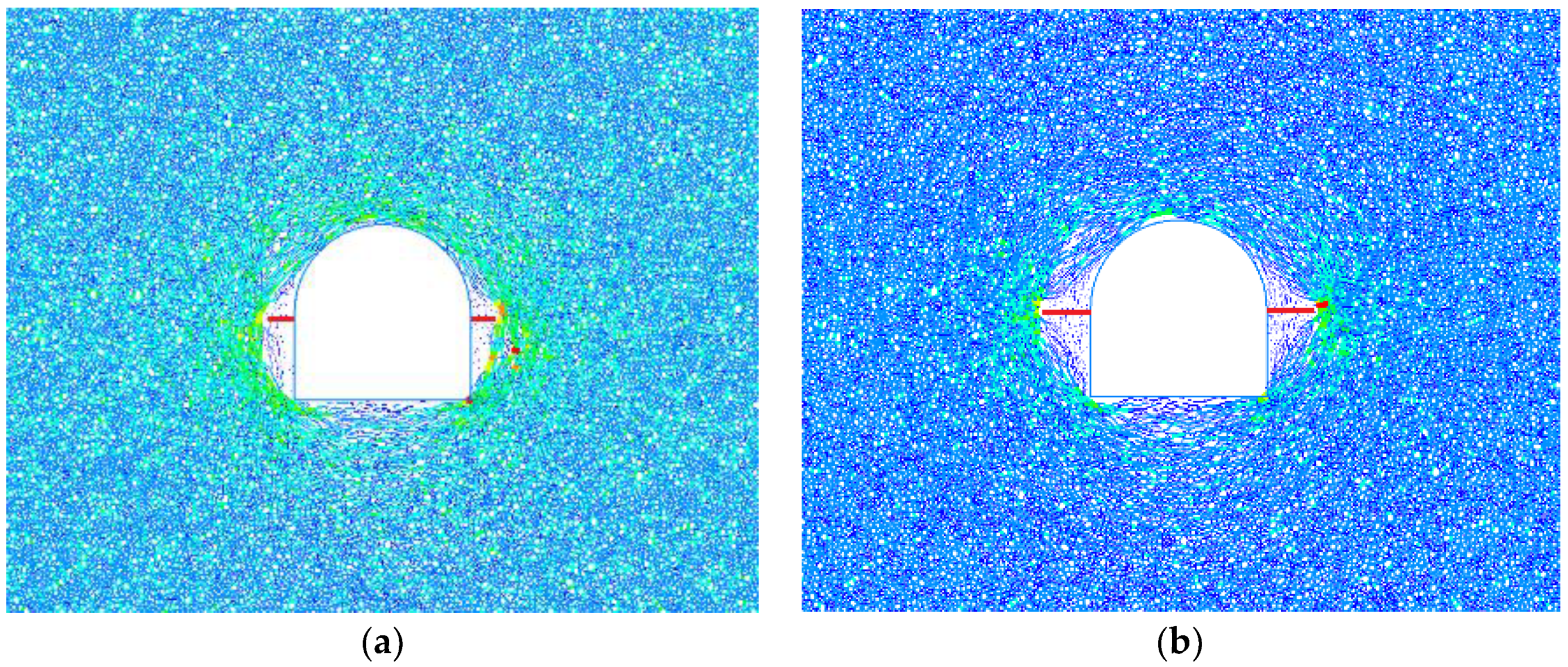
3.1.1. Stress Characteristic Analysis
3.1.2. Deformation Evolution Law
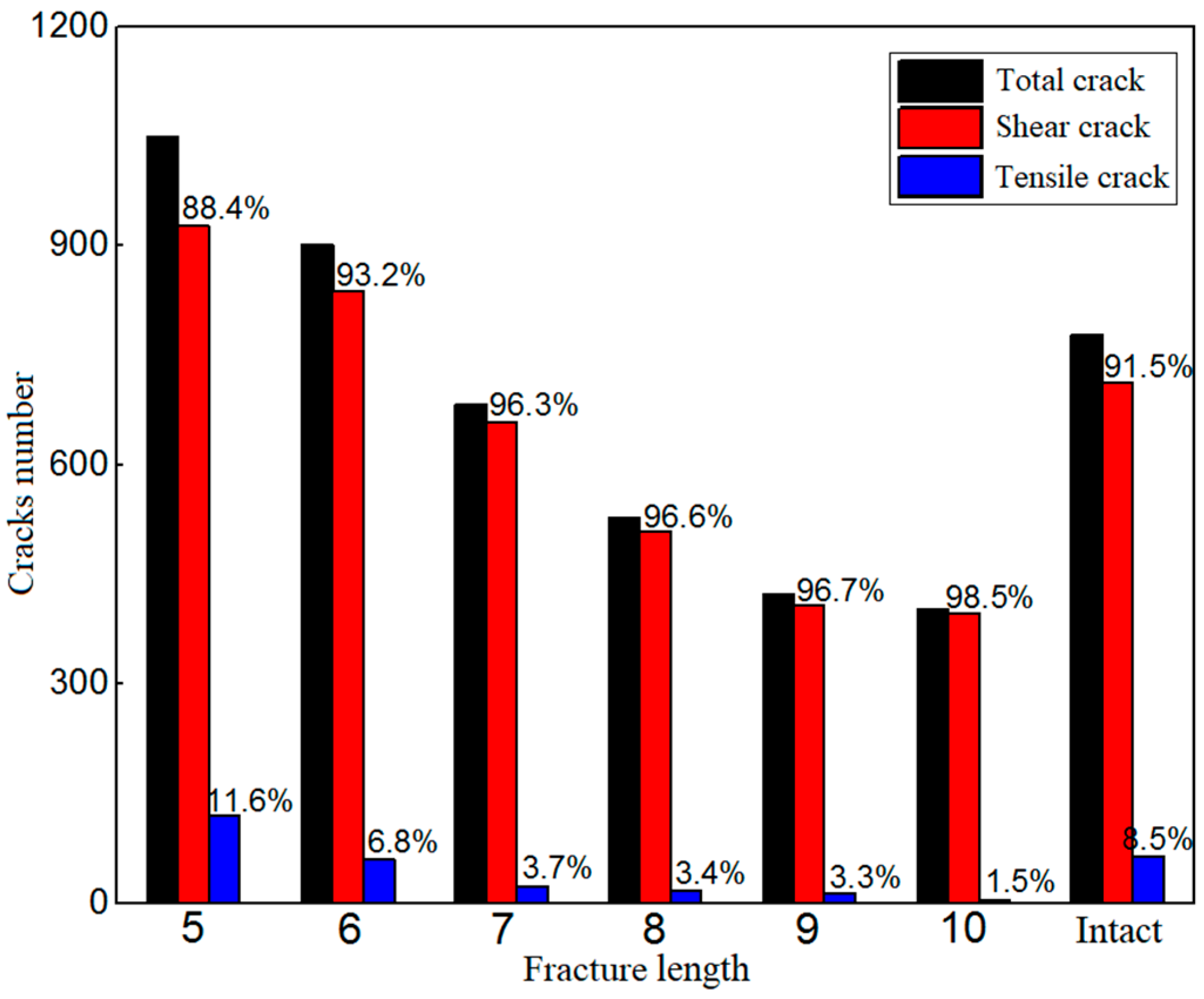
3.1.3. Fracture Propagation Law
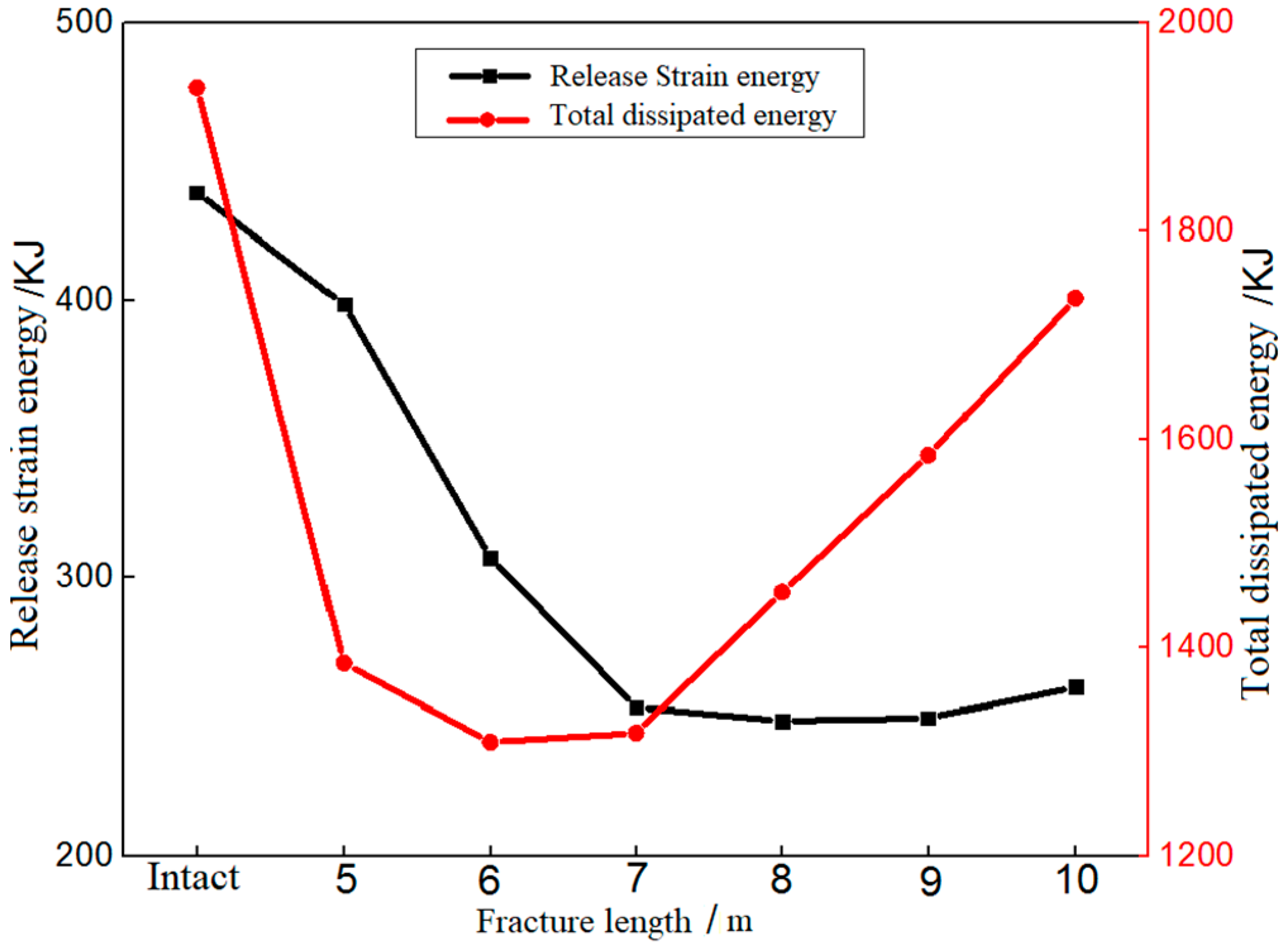
3.1.4. Energy Conversion Law
3.2. The Influence of the Fracture Inclination Angle on the Transient Unloading Effect of the Deep-Buried Tunnel
3.2.1. Stress Characteristic Analysis
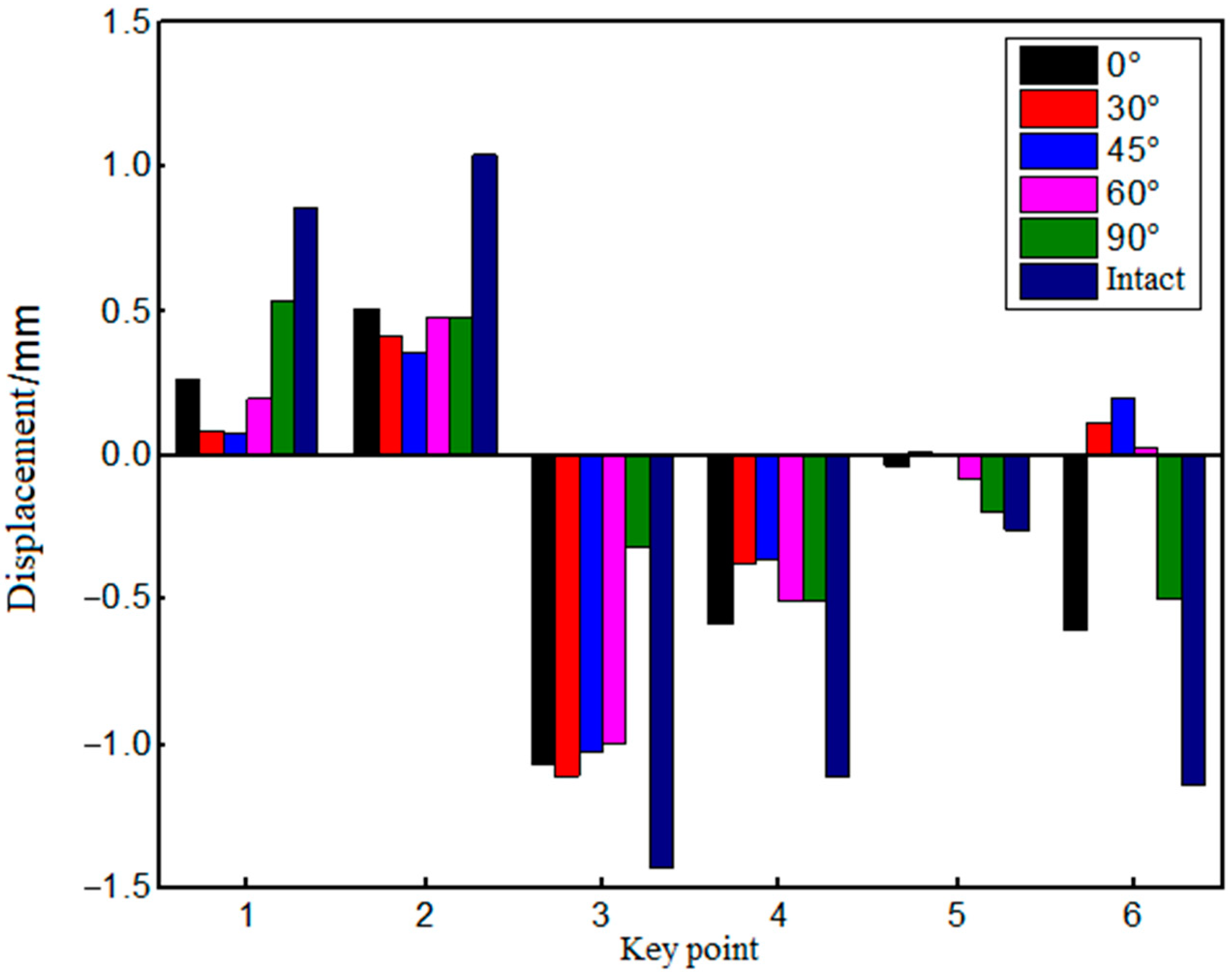
3.2.2. Deformation Evolution Law
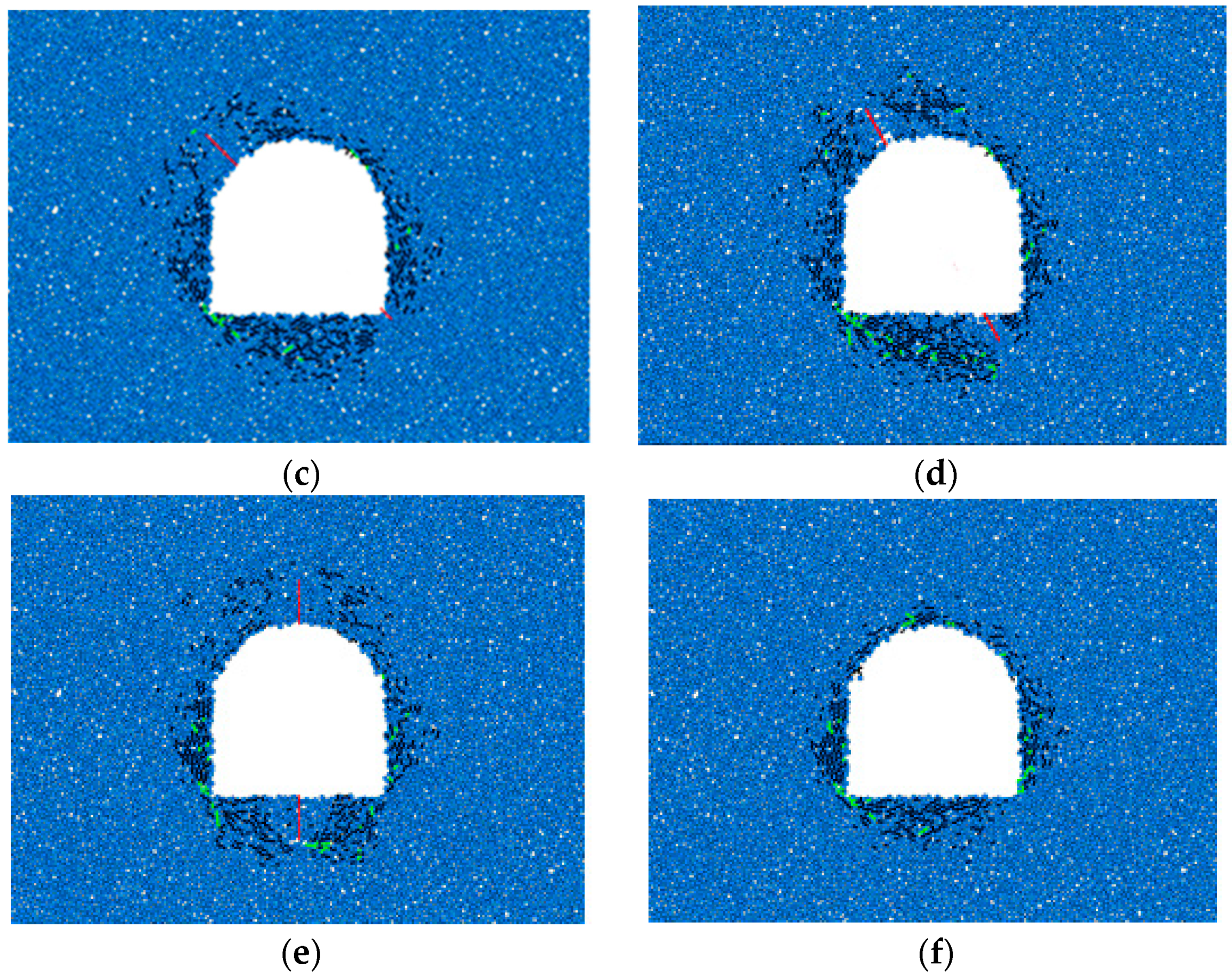
3.2.3. Fracture Propagation Law
3.2.4. Energy Conversion Law
4. Conclusions
- (1)
- The fracture has an important impact on the stress adjustment process of transient unloading in the deep-buried tunnel. The existence of fractures forces the stress adjustment area to change after tunnel excavation. In the surrounding rock of horizontal penetrating fractures with different lengths, the displacement of the vault is always greater than that of the bottom plate, but the difference decreases with the fracture length.
- (2)
- With the increase in the fracture length, the distance from the stress concentration at the fracture tip to the free surface gradually increases, and the damage range of the surrounding rock continues to expand. The distribution of mesocracks on the two sides of the tunnel gradually becomes sparse, the extended area gradually becomes larger, and the damaged area of the surrounding rock gradually migrates to the deep area.
- (3)
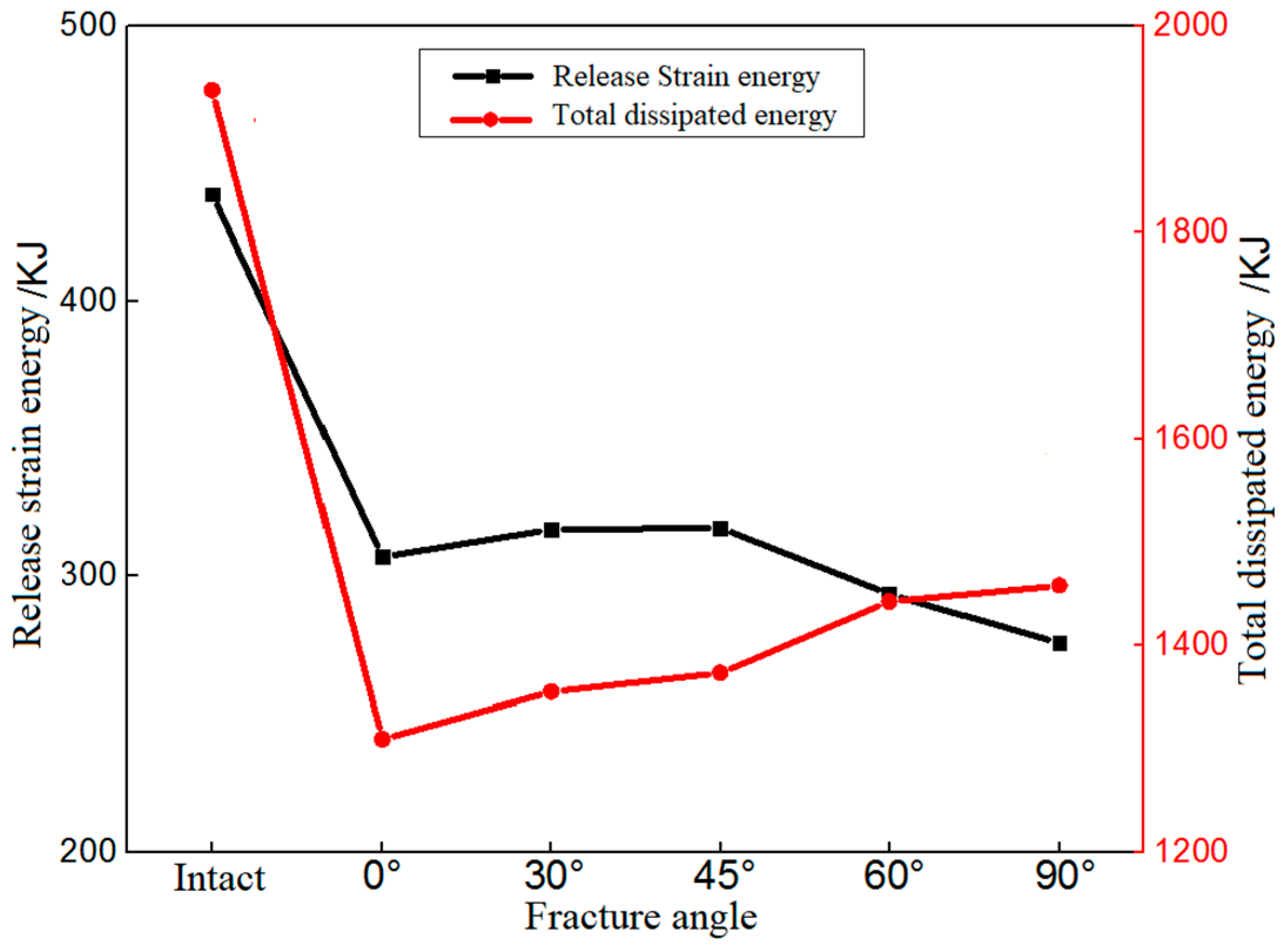
- With the increase in the fracture length, the total number of mesocracks shows a monotonic decreasing trend. With the increase in the fracture length, the released amount of strain energy during tunnel excavation shows a trend of first decreasing and then slowly increasing, while the total amount of dissipation energy first decreases and then increases rapidly.
- (4)
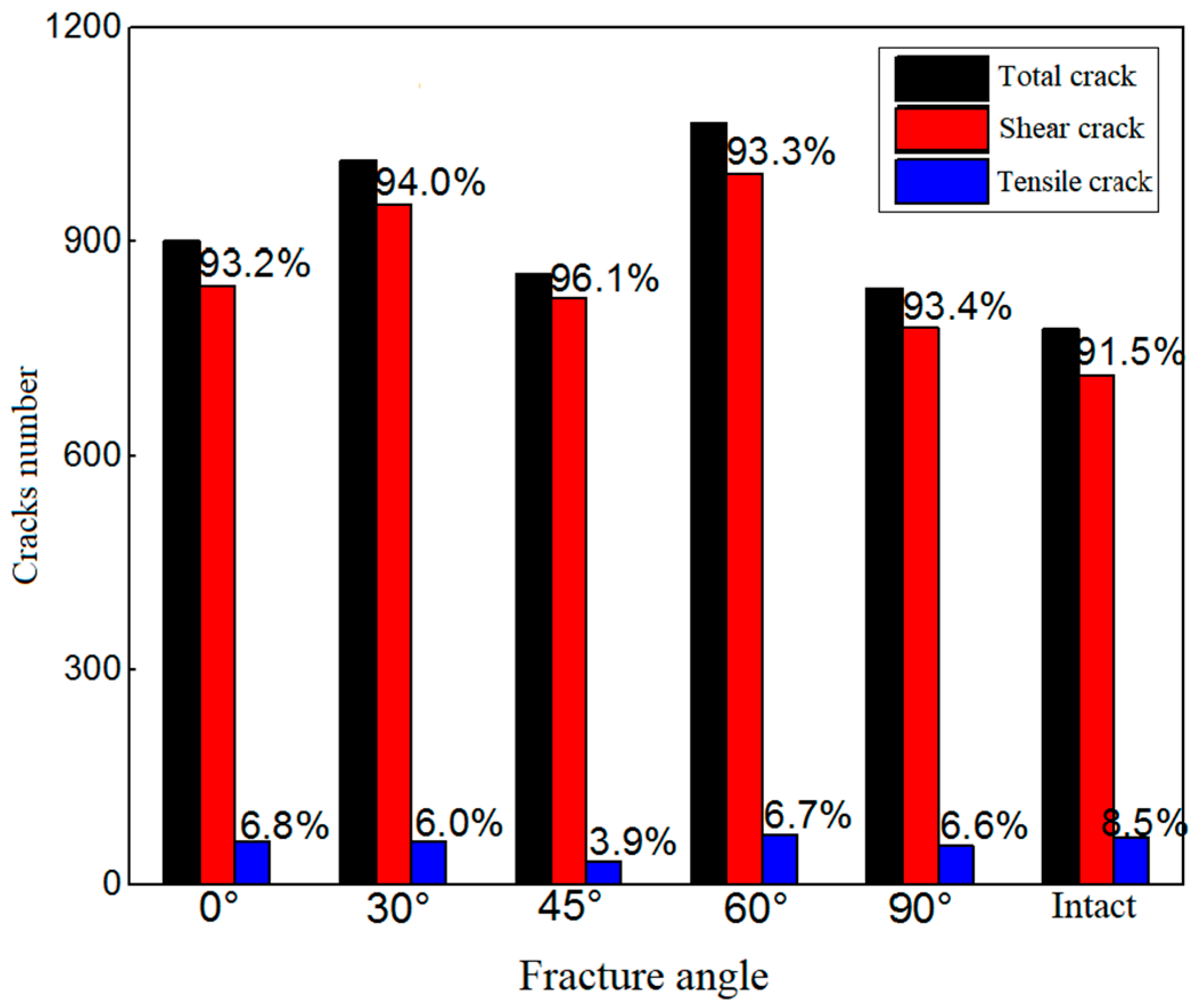
- Under different fracture angles, the number of mesocracks varies greatly. The total number of mesocracks in the 60° and 30° fractured surrounding rocks is greater, followed by the 0° fractured surrounding rock, and the total number of mesocracks in the 45° and 90° fractured surrounding rocks is relatively less. The proportion of compression-shear cracks shows a trend of increasing first and then decreasing with the increase in the fracture angle. However, the number of mesocracks in the fractured surrounding rocks is consistently higher than that in the complete surrounding rock. Under the 45° fractured surrounding rock, the proportion of compression-shear cracks reaches the maximum value of 96.1%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Petružálek, M.; Vilhelm, J.; Rudajev, V.; Lokajíček, T.; Svitek, T. Determination of the anisotropy of elastic waves monitored by a sparse sensor network. Int. J. Rock Mech. Min. Sci. 2013, 60, 208–216. [Google Scholar] [CrossRef]
- Wang, S.; Huang, L.; Li, X. Analysis of rockburst triggered by hard rock fragmentation using a conical pick under high uniaxial stress. Tunn. Undergr. Sp. Technol. 2020, 96, 103195. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, K.; Li, X.; Li, H.; Ma, G.; Zhao, J.; Zhou, Z.; Dai, F. Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials. Int. J. Rock Mech. Min. Sci. 2011, 49, 105–112. [Google Scholar] [CrossRef]
- Chen, D.; Wang, E.; Li, N. Analyzing the rules of fracture and damage, and the characteristics of the acoustic emission signal of a gypsum specimen under uniaxial loading. J. Geophys. Eng. 2017, 14, 780–791. [Google Scholar] [CrossRef]
- Liu, G.; Liu, Z.; Feng, J.; Song, Z.; Liu, Z. Experimental research on the ultrasonic attenuation mechanism of coal. J. Geophys. Eng. 2017, 14, 502–512. [Google Scholar] [CrossRef]
- Xie, H.; Peng, R.; Ju, Y.; Zhou, H. Energy analysis of rock failure. Chin. J. Rock Mech. Eng. 2005, 24, 2603–2608. [Google Scholar]
- Martin, C.; Christiansson, R. Estimating the potential for spalling around a deep nuclear waste repository in crystalline rock. Int. J. Rock Mech. Min. Sci. 2009, 46, 219–228. [Google Scholar] [CrossRef]
- Torano, J.; Rodríguez, R.; Diego, I.; Rivas, J.; Casal, M. FEM models including randomness and its application to the blasting vibrations prediction. Comput. Geotech. 2006, 33, 15–28. [Google Scholar] [CrossRef]
- Li, X.; Cao, W.; Tao, M.; Zhou, Z.; Chen, Z. Influence of unloading disturbance on adjacent tunnels. Int. J. Rock Mech. Min. Sci. 2016, 84, 10–24. [Google Scholar] [CrossRef]
- Cao, W.; Li, X.; Tao, M.; Zhou, Z. Vibrations induced by high initial stress release during underground excavations. Tunn. Undergr. Sp. Technol. 2016, 53, 78–95. [Google Scholar] [CrossRef]
- Huang, D.; Li, Y. Conversion of strain energy in triaxial unloading tests on marble. Int. J. Rock Mech. Min. Sci. 2014, 66, 160–168. [Google Scholar] [CrossRef]
- Huang, R.; Huang, D. Evolution of rock cracks under unloading condition. Rock Mech. Rock Eng. 2014, 47, 453–466. [Google Scholar] [CrossRef]
- Huang, D.; Guo, Y.; Cen, D.; Zhong, Z.; Song, Y. Experimental investigation on shear mechanical behavior of sandstone containing a pre-existing flaw under unloading normal stress with constant shear stress. Rock Mech. Rock Eng. 2020, 53, 3779–3792. [Google Scholar] [CrossRef]
- He, M.; Miao, J.; Feng, J. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions. Int. J. Rock Mech. Min. Sci. 2010, 47, 286–298. [Google Scholar] [CrossRef]
- Hogan, J.; Rogers, R.; Spray, J.; Boonsue, S. Dynamic fragmentation of granite for impact energies of 6–28. J. Eng. Fract. Mech. 2012, 79, 103–125. [Google Scholar] [CrossRef]
- Bobet, A.; Einstein, H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int. J. Rock Mech. Min. Sci. 1998, 35, 863–888. [Google Scholar] [CrossRef]
- Wong, R.; Tang, C.; Chau, K.; Lin, P. Splitting failure in brittle rocks containing pre-existing flaws under uniaxial compression. Eng. Fract. Mech. 2002, 69, 1853–1871. [Google Scholar] [CrossRef]
- Lee, H.; Jeon, S. An experimental and numerical study of fracture coalescence in pre-cracked specimens under uniaxial compression. Int. J. Solids Struct. 2011, 48, 979–999. [Google Scholar] [CrossRef]
- Fan, X.; Kulatilake, P.; Chen, X. Mechanical behavior of rock-like jointed blocks with multi-non-persistent joints under uniaxial loading: A particle mechanics approach. Eng. Geol. 2015, 190, 17–32. [Google Scholar] [CrossRef]
- Wang, X.; Tian, L. Mechanical and crack evolution characteristics of coal-rock under different fracture-hole conditions: A numerical study based on particle flow code. Environ Earth Sci. 2018, 77, 297. [Google Scholar] [CrossRef]
- Cundall, P.; Strack, O. Discussion: A discrete numerical model for granular assemblies. Géotechnique 1980, 30, 331–336. [Google Scholar] [CrossRef]
- Song, L.; Wang, G.; Wang, X.; Huang, M.; Xu, K.; Han, G.; Liu, G. The influence of joint inclination and opening width on fracture characteristics of granite under triaxial compression. Int. J. Geomech. 2022, 22, 04022031. [Google Scholar] [CrossRef]
- Potyondy, D.; Cundall, P. A bounded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Chen, H.; Lai, H.; Huang, M.; Wang, G.; Tang, Q. Failure mechanism and treatment measures of supporting structures at the portal for a shallow buried and asymmetrically loaded tunnel with small clear-distance. Nat. Hazards 2022, 114, 2283–2310. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, G.; Li, X.; Liu, T.; Qu, D.; Huang, J. Research on triaxial compression failure characteristics and meso-simulation of brittle gypsum material. Eur. J. Environ. Civ. Eng. 2002, 26, 5241–5258. [Google Scholar] [CrossRef]
- Zhou, C.; Xu, C.; Karakus, M.; Shen, J. A systematic approach to the calibration of micro-parameters for the flat-jointed bonded particle model. Geomech. Eng. 2018, 16, 471–482. [Google Scholar]
- Wang, G.; Song, L.; Liu, X.; Bao, C.; Lin, M.; Liu, G. Shear fracture mechanical properties and acoustic emission characteristics of discontinuous jointed granite. Rock Soil Mech. 2022, 43, 1533–1545. [Google Scholar]
- Song, L.; Zhang, D.; Wang, G.; Du, S.; Hu, G.; Han, G.; Liu, X. Evaluation method of local failure characteristics for joint based on white light scanning technology. Nat. Hazards 2022, 116, 97–110. [Google Scholar] [CrossRef]
- Soleiman Dehkordi, M.; Shahriar, K.; Moarefvand, P.; Gharouninik, M. Application of the strain energy to estimate the rock load in squeezing ground condition of Eamzade Hashem tunnel in Iran. Arab. J. Geosci. 2013, 6, 1241–1248. [Google Scholar] [CrossRef]
- Liu, X.; Wang, G.; Song, L.; Han, G.; Chen, W.; Chen, H. A new rockburst criterion of stress–strength ratio considering stress distribution of surrounding rock. B. Eng. Geol. Environ. 2023, 82, 29. [Google Scholar] [CrossRef]
- Niu, Y.; Hu, Y.; Wang, J. Cracking characteristics and damage assessment of filled rocks using acoustic emission technology. Int. J. Geomech. 2023, 23, 04023013. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, J.; Wang, X.; Hu, Y.; Zhang, J.; Zhang, R.; Hu, Z. Numerical study on cracking behaviors and fracture failure mechanism of flawed rock materials under uniaxial compression. Fatigue Fract. Eng. M 2023, 2023, 13983. [Google Scholar] [CrossRef]
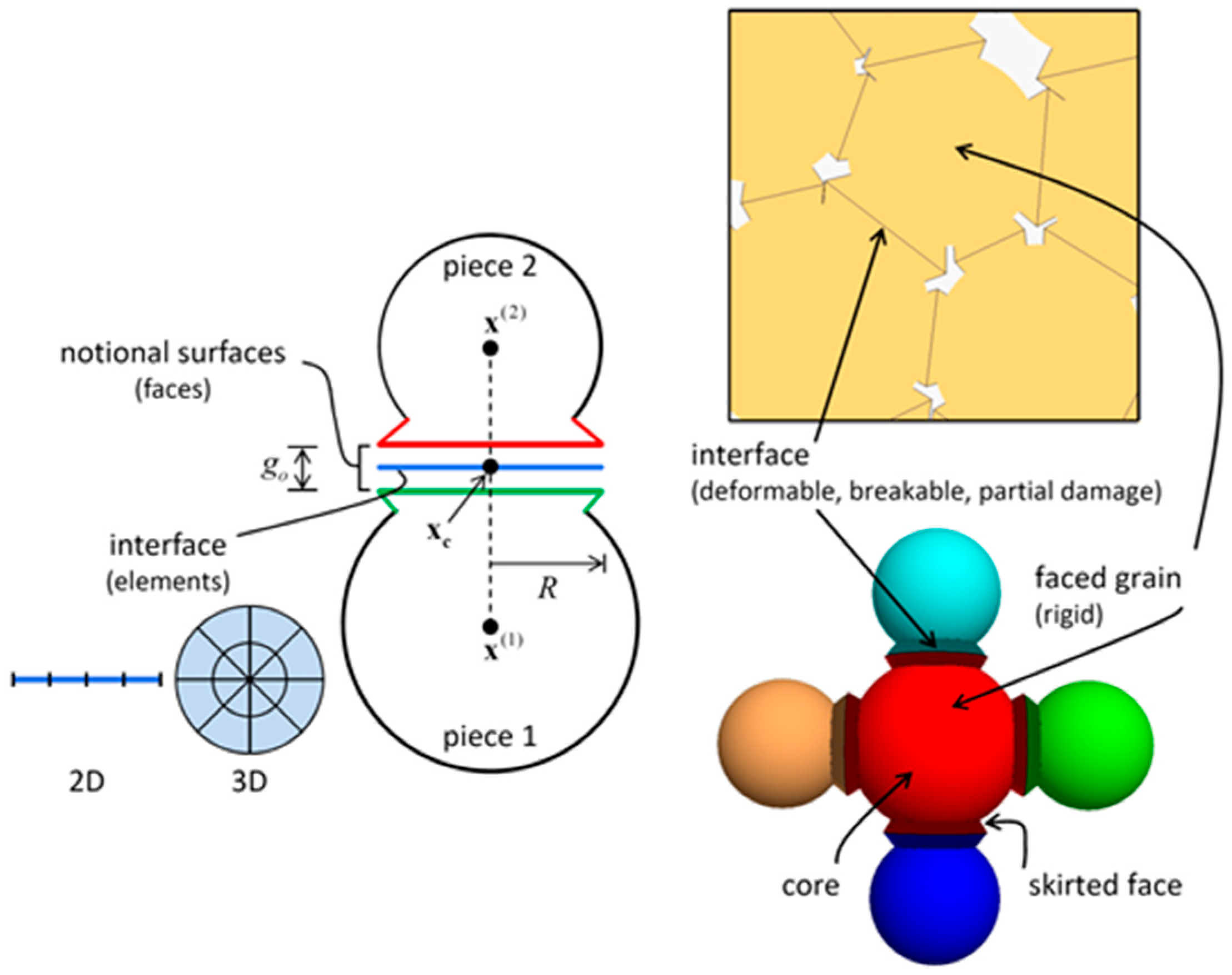










| λ | N | ρ/(kg/m3) | Rmax/Rmin | Rmin/mm | Ec/GPa | kn/ks | μ | σc/MPa | cc/MPa | ϕ/° |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 2500 | 1.66 | 45 | 10 | 2.38 | 0.55 | 2.5 | 10 | 21 |
| knj/GPa | ksj/GPa | μj | σcj/MPa | c/MPa | ϕ/° |
|---|---|---|---|---|---|
| 1 | 1 | 0.3 | 0 | 0 | 30 |
| Crack Length/m | Total Number of Cracks | Compression-Shear Crack | Tensile Crack | ||
|---|---|---|---|---|---|
| Number of Cracks | Proportion | Number of Cracks | Proportion | ||
| 5 | 1048 | 926 | 88.4% | 122 | 11.6% |
| 6 | 900 | 839 | 93.2% | 61 | 6.8% |
| 7 | 683 | 658 | 96.3% | 25 | 3.7% |
| 8 | 527 | 509 | 96.6% | 18 | 3.4% |
| 9 | 423 | 409 | 96.7% | 14 | 3.3% |
| 10 | 403 | 397 | 98.5% | 6 | 1.5% |
| Intact | 779 | 713 | 91.5% | 66 | 8.5% |
| Fracture Angle | Total Number of Cracks | Compression-Shear Crack | Tensile Crack | ||
|---|---|---|---|---|---|
| Number of Cracks | Proportion | Number of Cracks | Proportion | ||
| 0° | 900 | 839 | 93.2% | 61 | 6.8% |
| 30° | 1013 | 952 | 94.0% | 61 | 6.0% |
| 45° | 855 | 822 | 96.1% | 33 | 3.9% |
| 60° | 1066 | 995 | 93.3% | 71 | 6.7% |
| 90° | 835 | 780 | 93.4% | 55 | 6.6% |
| Intact | 779 | 713 | 91.5% | 66 | 8.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, G.; Wen, Z.; Wang, D.; Song, L.; Lin, M.; Chen, H. The Transient Unloading Response of a Deep-Buried Single Fracture Tunnel Based on the Particle Flow Method. Sustainability 2023, 15, 6840. https://doi.org/10.3390/su15086840
Liu X, Wang G, Wen Z, Wang D, Song L, Lin M, Chen H. The Transient Unloading Response of a Deep-Buried Single Fracture Tunnel Based on the Particle Flow Method. Sustainability. 2023; 15(8):6840. https://doi.org/10.3390/su15086840
Chicago/Turabian StyleLiu, Xiqi, Gang Wang, Zhijie Wen, Dongxing Wang, Leibo Song, Manqing Lin, and Hao Chen. 2023. "The Transient Unloading Response of a Deep-Buried Single Fracture Tunnel Based on the Particle Flow Method" Sustainability 15, no. 8: 6840. https://doi.org/10.3390/su15086840
APA StyleLiu, X., Wang, G., Wen, Z., Wang, D., Song, L., Lin, M., & Chen, H. (2023). The Transient Unloading Response of a Deep-Buried Single Fracture Tunnel Based on the Particle Flow Method. Sustainability, 15(8), 6840. https://doi.org/10.3390/su15086840








