Abstract
The walking time in metro stations is influenced by passenger flow with large fluctuation. Therefore, this paper proposes a method of station walking time calculation considering the influence of passenger flow: firstly, the time, entry, and exit direction and volume distribution characteristics of station passenger flow are analyzed, and the threshold of passenger flow that affects walking time is defined; then, an entry and exit walking time calculation model is established by five independent travel time chains and three station walking time constraints, and the transfer walking time is calculated based on the entry and exit walking time results; finally, the accuracy and validity of the walking time projection model are verified by using the calculation results. The results show that the calculation results are accurate and the validity of the model reaches 91.5%, and the constraint effect on walking time at station time is most obvious when the passenger flow reaches 3000 passengers per 30 min.
1. Introduction
In recent years, with the continuous improvement of the metro network, the metro has become one of the basic guaranteed facilities for the traffic operation of large cities in China. By the end of 2021, there were 283 [1] metro operating lines opened in 50 cities nationwide, with a total operating line length of 9206.8 km. Due to its on-time, fast, and comfortable features attracting a large number of passengers, the national urban metro completed 23.71 billion passenger trips in 2021, an increase of about 35% compared with 2020. At the same time, as more and more residents take metro as the preferred mode of transportation for daily travel, its share of public transportation is also growing. The share ratio of national metro passenger volume to total public transportation passenger volume has increased from 38.7% in 2020 to 43.4% in 2021, among which eight cities, namely Beijing, Shanghai, Guangzhou, Chengdu, Shenzhen, Nanjing, Nanning, and Hangzhou, have a share ratio of metro passenger volume to public transportation of more than 50%, which indicates that China’s demand for metro is growing and it is playing an extremely important role in the transportation of many big cities.
However, the huge passenger flow adds more challenges to the daily operation of the metro. Crowded carriages and waiting lounges, difficult walking facilities in and out of stations, and transfer lanes have led to a series of problems such as reduced efficiency, service level, and safety of passengers entering and exiting stations and transferring to and from stations. The study of walking time in metro stations is useful for operators to make preliminary assessments of the level of walking service in stations and improve station services. At the same time, passenger flow is the basis for developing and coordinating operation plans, and walking time, as a highly variable part of the travel time chain, is an important basis for improving the accuracy of passenger flow allocation. Finally, for companies providing passenger path planning, such as Baidu, Gaode, and other route planning companies, they need to use walking time parameters to improve the reference time for path planning, and thus provide more accurate planning services.
In the past, walking time was usually obtained by manual investigation. Du et al. and Zhao [2,3] designed a sampling survey method based on the influencing factors of passenger walking distance and walking speed to investigate the travel time of transfer passengers at transfer stations, and obtained the conclusion that the transfer travel time approximately obeys lognormal distribution; Zhou et al. [4] obtained the relationship between the transfer walking speed and passenger volume of different types of facilities by investigating the data of station passenger flow and facility types, and finally calculated the transfer time model parameters using the curve fitting method. With the accumulation of AFC data, scholars found that the data records of a large number of passengers’ travel details can provide enough evidence to mine potential passenger behaviors, which provides the possibility of walk time imputation. Among the methods of using AFC data mining, scholars have mainly studied from the perspective of reducing the unknown quantity by combining travel time chains, which are mainly divided into three categories. One is to obtain part of the data through manual survey. Sun et al. [5] proposed a method based on splitting travel time into timestamps of each constituent element and studied by combining travel time in AFC with partial data from field survey. Zhou et al. [6] extrapolated the station walk time of all stations by manually investigating the access walk time of a station based on the travel time chain relationship of each combination in the transportation network. The second is to use the train operation diagram to derive the exit walking time data. Tong et al. [7] designed a sampling survey method to investigate the travel time of transfer passengers in two directions of the Chongqing Metro transfer station. After verifying that the transfer travel time obeys normal distribution or lognormal distribution, the maximum likelihood estimation method is used to estimate the transfer travel time parameters in other directions. Scholars [8,9,10] argue that most passengers do not stay in the station after arrival, so the difference between the arrival time of the train and the departure time of the passenger can be used to project the departure walking time of the passenger. Paul et al. [11] found upon calculating walking time ratios for access, exit, and transfer based on manual research, and after matching exit walking times with train schedules using AFC transaction data, that the ratios were used to derive walking times for access and transfer. Similar, Eltved et al. [12] put forward an estimation of transfer time distribution from bus station to train platform based on the matching of smart card data and vehicle automatic positioning data. Yan [13], based on the assumption that passengers’ arrival obeys uniform distribution, calculates the distribution of passengers’ outbound travel time by using train arrival data and passengers’ outbound time, and calculates the distribution parameters of inbound travel time by using OD travel time without transfer after the train departure interval is known. Third, the variables were reduced by combining travel time chain components. Wu [14] divided the travel time into two components: fixed on-train time and random access and exit plus waiting time, and assumed that all ODs obeyed the same normal distribution to find the mean and variance of the random time component, and then, by inputting the in/out station and first station waiting time distributions, deriving the transfer time distribution. Based on the assumption of equal walking time in and out of stations with similar station layouts, Liang [15] and Jia et al. [16] used the travel time of passengers without waiting for trains in ODs with unique transfer paths to derive the walking time in and out of stations at different times, and verified that the walking time in and out of stations obeyed a normal distribution. Zhao [17] calculated the minimum access and exit walking time of each station by selecting the minimum travel time between ODs, considering that the waiting time is zero at this time, and based on the constraint that the sum of access walking time of all stations in the whole metro network is equal to the sum of exit walking time, the minimum access and exit walking time of each station is calculated using the Nanjing Metro, and then the minimum transfer walking time is found.
Furthermore, passenger flow is often considered an important influencing factor in walk time studies. Zeng et al. [18] believes that there is an interactive relationship between traffic objects. Harris [19], after collecting the walking time of passenger flow in London urban rail stations using the tracking survey method, studied the walking time of passengers under different passenger flows by constructing a passenger walking simulation model. Lam et al. [20] studied the pedestrian flow characteristics of different pedestrian facilities in Hong Kong, and conducted a study on the effects of different facility locations and through-flow on walking time based on three elements of traffic flow. Feng et al. [21] drew the relationship curve between passenger flow speed and density in the Beijing subway collecting-distributing area and upstairs. Wang et al. [22] studied the relationship between walking speed and passenger flow for pedestrian facilities such as upward stairs and downward stairs in one-way transfer passages in urban rail stations in Shanghai. Li et al. [23] studied the relationship between passenger flow and walking time per unit time in one-way transfer stations in Shanghai based on the relationship between passenger flow and walking time and fitted the correlation function between passenger flow and walking time. Therefore, this section investigates the distribution characteristics of passenger flow at stations and quantifies the effect of passenger flow density on walking time.
To sum up, in the study of the estimation method of walking time, it is proposed to split the components of travel time and calculate the rest time on the basis of obtaining some data, which provides a theoretical basis for the split of travel time in this paper. At the same time, in order to reduce the unknown variables in the composition of travel time, reasonable assumptions are usually made on waiting time or walking time in and out of the station, which also provides reference for the treatment of travel time composition in this paper. It is worth noting that although the calculation of travel time is simplified based on the minimum travel time, it cannot reflect the influence of passenger flow on travel time. At the same time, when studying the influence of passenger flow on travel time, we can find that there is a great correlation between travel time and passenger flow per unit time. It is necessary to consider the influence of passenger flow when calculating station travel time, but the cost of manual investigation is high. This paper will use AFC data to quantify this influence. Based on the summary and analysis of the above literature, this paper will propose a method for projecting walking time in stations considering the influence of passenger flow density. Under the premise of known train departure interval and on-train time, a walking time projection model is constructed based on multi-station combination passenger travel time chain splitting and the influence of station passenger flow density on walking time, and finally an example analysis is conducted. The details are as follows:
- (1)
- Travel time chain analysis. Usually, the travel time chain consists of walking time in and out of the station, waiting time, and on-board time, and for the travel time that requires transfer, this also includes transfer walking time and transfer waiting time. Python crawler technology can obtain the train departure interval and on-train time from the official website, which provides the basic data for the following walking time model construction.
- (2)
- Influence of passenger flow density. The walking time in the same station is mainly affected by the density of passenger flow, and there is a spatial and temporal unevenness in the distribution of passenger flow in the station. On this basis, the influence of passenger flow on walking time at stations is analyzed to determine the threshold value of passenger flow, which provides judgment data for the following walking time model constraints.
- (3)
- Design of walking time projection method. Based on the multi-station combination of passenger travel time chain splitting to initially build a regression model, and combined with the impact of passenger flow density to add walking time constraints to solve the problem of unsatisfactory rank of the model, so as to obtain the walking time imputation model.
- (4)
- Example validation. Based on the swipe data of the top five lines of daily average passenger flow in Guangzhou in 2018, the example validation analysis is conducted and the model is verified in terms of the accuracy of the results and the validity of the constraints.
2. Metro Passenger Time Chain Analysis
2.1. Passenger Travel Time Chain Building
The travel chain of metro passengers can usually be described as follows: passengers walk to the waiting hall to wait for the train to arrive after swiping the card at the access gate, then take the train until they reach the destination station, and then walk from the waiting hall to the exit gate to swipe the card, and the trip is over. If passengers need to transfer, they should get off at the transfer station and walk to the waiting hall of the transfer line, wait for the train to arrive again, and finally get off at the destination station and walk to the exit to swipe their cards.
Looking at the entire travel process, we can divide the passenger’s travel chain into six parts: walking in at the origin station, waiting for the train at the origin station, riding the train, walking at the transfer station, waiting for the train at the transfer station, and walking out at the terminal station. Therefore, the passenger’s travel time consists of access walking time, access waiting time, on-train time, transfer walking time, transfer waiting time, and exit walking time (Figure 1).
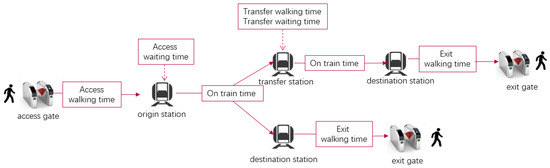
Figure 1.
Metro passenger travel time chain diagram.
It is calculated as shown in Equation (1):
where = the travel time of the passenger from station to station j; = the access walking time of the passenger at station ; = the passenger’s waiting time at station ; = the passenger’s on-train time from station to station ; = the transfer walking time of the passenger at station , if no transfer this value is 0; = the passenger’s on-train time from station to station , if no transfer this value is 0; = the exit walking time of the passenger at station . The above values are in seconds.
2.2. Component Element Analysis
In the metro passenger travel chain, there exist some elements that can be calculated by obtaining data, such as the passenger’s OD pair travel time, the passenger’s OD pair on-train time, and the passenger station waiting time.
The passenger’s OD pair travel time. Since the automatic fare collection (AFC) system records and uploads the specific transaction information data of a passenger’s one-way trip when riding the metro, the travel time of a passenger’s OD pair can be obtained by using keyword segment data, such as access station, exit station, access swipe moment, and exit swipe moment from the AFC data, which is calculated as in Equation (2):
Passenger’s OD pair on-train time. Since the train travels at a stable speed, the passenger’s on-train time can be considered as a fixed value even if the train is late, and the on-train time of Guangzhou Metro OD pairs can be crawled from the Baidu Map API platform using web crawler technology.
Passenger station waiting time. Since the arrival of passengers at stations follows a uniform distribution, the waiting time of passengers is related to the departure interval of trains, which is half of the departure interval. Therefore, the average waiting time of passengers can be calculated by crawling the departure interval of trains.
In summary, after subtracting the accessible components, the total walking time of passengers is calculated as in Equations (3) and (4):
3. Impact of Station Passenger Flow on Walking Time
3.1. Metro Traffic Data Selection and Pre-Processing
The subway data set used in this paper includes the subway credit card data records from 23 April 2018 to 11 May 2018. Because passenger flow is the main influencing factor of travel time, the greater the passenger flow, the more obvious the influence of passenger flow density on walking time. Therefore, this paper selects the top five lines (Line 1, Line 2, Line 3, North Extension Line of Line 3, and Line 5) of the Guangzhou Metro as the research object.
There are inevitably anomalies in the data, which affect the accuracy of the walk time and therefore need to be processed. Pre-processing of AFC data consists of three main steps as follow:
Step 1: Clean up the missing data of keywords. In this paper, we select four fields: access station, exit station, access swipe time, and exit swipe time as the key fields. If the key fields are missing, it is not possible to ask passengers to OD the travel time, so we clean this kind of data.
Step 2: Clean up the non-operating time data. Since the AFC data is recorded in all the entry and exit data, the data of maintenance personnel entering and exiting the station during non-operating hours is also recorded and needs to be cleaned.
Step 3: Clean up unreasonable data. According to the official regulations of the Guangzhou Metro, staying in the subway for more than 270 min is regarded as abnormal, and a fine will be imposed. Therefore, this paper thinks that the data exceeding this threshold is unreasonable and should be excluded.
3.2. Analysis of the Relationship between Station Passenger Flow and Walking Time
It has been mentioned in the introduction above that the travel time is often influenced by passenger flow, and this section will quantify the influence of passenger flow on the travel time.
3.2.1. Distribution Characteristics of Passenger Flow in Time and at Access and Exit Stations
The top six stations of daily average passenger flow of the Guangzhou Metro were selected as the research object, and the distribution of passenger flow was analyzed from the perspective of different time periods and different directions of access and exit of passenger flow. At the same time, due to the different travel purposes and the different characteristics of travel time, the study is divided into two parts from the date type: working day and weekend.
Through the comparison of Figure 2a,b, it can be seen that the time distribution of passenger flow is different. On weekdays, the travel time is mainly concentrated at 8:00 and 18:00 in the morning and evening peaks, and the peak can reach more than 6000 people per 30 min. Meanwhile, on weekends, the passenger travel time is scattered, with the largest number of people traveling around 18:00, but the peak only reaches about 4000 people per 30 min.
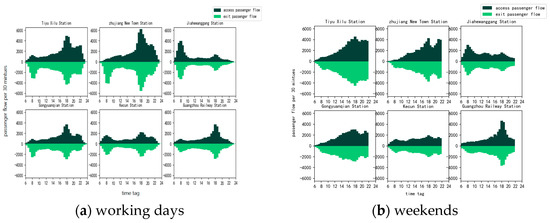
Figure 2.
Passenger flow time and access and exit distribution.
In addition, the imbalance between inbound and outbound stations is different: the distribution of passenger flow in and out of the station is more balanced on weekends, but the imbalance between inbound and outbound stations at the same time on weekdays is more obvious. For example, at Zhujiang New Town Station, commuters mainly arrive during the morning rush hour, and the inbound passenger flow at the station is much larger than the outbound passenger flow during the morning rush hour, with the largest difference of 3523 passengers. During the evening rush hour, as commuters return to their places of residence, the passenger flow at the exit is greater than that at the entrance, with a maximum difference of 1168 passengers.
3.2.2. Total Distribution Characteristics of Passenger Flow at All Stations
The top five stations of daily average passenger flow of the Guangzhou Metro are selected as the research object, and the cumulative frequency distribution of passenger flow in and out of stations is plotted, and the results are shown in Figure 3.
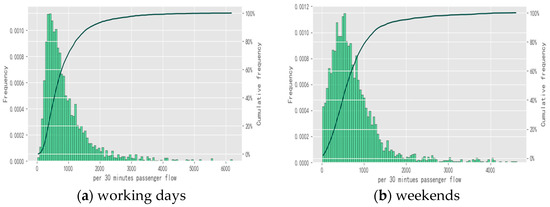
Figure 3.
Cumulative distribution of station passenger flow per 30 min access and exit.
It can be found that, whether on weekdays or weekends, the passenger flow in most stations is concentrated within 1500 passengers every 30 min, which can be considered as the general operation hours of the station, where the density of passengers in the station is low and the walking time is less influenced by the passenger flow. Therefore, this paper will quantify the relationship between the two and find the threshold of passenger flow that significantly affects the walking time, so as to provide a basis for judging the walking time constraint of the model.
3.2.3. Identify Passenger Flow Thresholds That Affect Walking Time
Due to the uneven distribution characteristics of station passenger flow at different time periods and in different environments in and out of the station, the walking time may vary at different time periods and in different directions in and out of the station within the same station. Xie [24], through a simulation study of passenger flow and walking time in the Changsha Metro Wanjiali square station, found that when the passenger access volume reaches 6000 passengers per hour, the walking time of passengers will increase with the increase of passenger flow due to the restricted area of the station. In this paper, the initial threshold value of passenger flow is set to 3000 passengers per 30 min for calculation with reference to this value. To further verify the reasonableness of this value, the validity of the results of more than 1500, 2000, 2500, 3500, and 4000 thresholds are compared in units of 500 passengers. (Unit: passenger per 30 min).
4. Method of Calculating the Walking Time of Passengers in the Station
4.1. Model Construction Ideas
4.1.1. Construction of Walking Time Models for Multi-Site Combinations
As we can see from the previous analysis, there are two unknown parts in an OD travel chain without transfer: access walking time and exit walking time. Therefore, for a group of OD pairs (one equation) with two stations (two unknown variables), there are infinitely many solutions, which is not consistent with the actual situation. However, the stations in the subway network are not independent, there is a link between stations and stations, which means that this feature can be used to select the same group of OD pairs into the station or out of the station for combined calculation. For example: two stations exist in two OD pairs (two equations, four variables), the number of variables is greater than the number of equations, so there are still infinite solutions; if we add a station, three stations exist in six OD pairs (six equations, six stations). Theoretically, there is a solution that best fits the actual situation (see Figure 4).
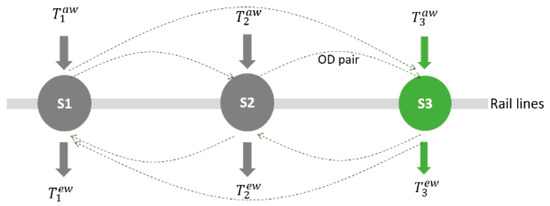
Figure 4.
Selection of walking time calculation model for multi-station combination.
4.1.2. Adding Constraints to Solve the Model Discontent Rank Problem
To verify whether the model has a solution and is unique at this point, the system of equations is transformed into a system of matrix equations with AX = B. It is found that the rank of the coefficient matrix is five. If the rank of the coefficient matrix is less than the number of variables, the equation cannot obtain the solution of the system of equations. In order to solve the situation where the model exists with insufficient rank, two perspectives are taken from adding variables or constraints.
(1) Adding variables:
The relationship between the number of variables and the rank of the coefficient matrix was observed by continuously increasing the number of stations, as shown in Table 1.

Table 1.
The number of model variables and the rank of the coefficient matrix.
From Table 1, we can find that the rank of the coefficient matrix is always one less than the number of variables no matter how many stations are added.
(2) Adding constraints:
In the study on passenger walking time, some scholars have assumed the mean value of walking time in and out of stations. Zhao [15] assumed that the access walking time of passengers is approximately equal to the exit walking time of passengers in the entire metro network based on the case of “zero waiting” (i.e., passengers do not need to wait for trains when arriving at stations). Based on the “zero-waiting” scenario, Liang [15] argues that for two stations with similar physical structures, the access walking time of passengers is equal to the exit walking time of passengers. Some scholars have also studied from the perspective of walking time distribution. Based on the similar walking distance of stations with similar station structures, Liu [25] argues that the access walking time and exit walking time of passengers in the same station are independently and identically distributed. The above studies mainly make assumptions from the physical distance of stations. In contrast, the walking time of passengers in the station is not only determined by the walking distance in the station, but also influenced by the passenger flow situation in the station. The analysis in Section 3.2 shows that there is an uneven flow of passengers in and out of the station, so the constraint that “the sum of the access walking time of all stations is equal to the sum of the exit walking time” is only valid in specific cases, such as free flow.
In summary, this paper will adopt a walking time constraint that takes into account the influence of passenger flow to make the coefficient matrix full rank. When the flow of passengers in and out of the station is large, it will obviously affect the outbound walking time, so such stations need to be excluded from the constraint equation, i.e., for the stations where the walking time in and out of the station is less affected by the flow of passengers, the sum of the walking time in the station is equal to the sum of the walking time out of the station, which is calculated as Equation (5):
where is the station, where both access and exit stations are less affected by passenger flow.
4.1.3. Calculation of Transfer Walking Time
From the analysis of the travel time chain in Section 2, it can be seen that for the travel time chain containing transfer, there are three unknown times of access walking time, outbound walking time, and transfer walking time. The access walking time and exit walking time of each station can be obtained by using the walking time projection model of multi-station combination. Therefore, for the travel time chain including transfer, only one unknown part of the transfer walking time remains and can be calculated directly. Since the transfer walking time at a transfer station is not related to the number of transfers in a single travel chain, the travel time data for only one transfer can be directly selected for calculation to avoid complicated calculations.
4.2. Design of Calculating Equations
For the calculation of walking time in and out of stations, the OD travel time data without transfers can be used to construct a model based on Equations (3) and (5) for the five sets of OD linearly independent travel time chains composed of three stations, and add the station walking constraint equation considering the influence of passenger flow to form a complete derivation model, where in Equation (3) is 0 because no transfer is required.
The existence of a solution to the model is again verified when the rank of the coefficient equation in the model is equal to the rank of the augmentation matrix and is equal to the number of variables, and a unique solution to the equation exists.
After obtaining the station entry and exit walking times, the OD that requires only one transfer is selected to calculate the transfer walking time, as Equation (6):
4.3. Selection Stations for Model
4.3.1. To Access and Exit Walking Time Model
The steps for selecting stations are as follows:
Step 1: Selecting three stations on the same line.
Step 2: Determine if there exists at least one station among the three where both incoming and outgoing walking times are unaffected by passenger flow.
Step 3: If it does not exist, return to Step 1; if it exists, continue.
Step 4: Determine if at least five OD walk time data exist for six sets of ODs.
Step 5: If it does not exist, return to Step 1; if it exists, continue.
Step 6: Input five linearly independent OD walking time data and three stations in the station that are not affected by passenger flow into the regression model of access and exit walking time, and output the results.
According to the above, for a line with N stations, there are at most (N − 1)(N − 2) possible combinations of solution results for each station. In the study of Qin et al. [26], it is mentioned that the location entropy is used as the basis to judge the traffic intensity. In this study, because the average value is used as the waiting time, when the data volume is large, the value is more accurate. However, due to the small data volume, some ODs may be biased. Therefore, in order to improve the representativeness and accuracy of the experimental results, this paper chooses the transaction data volume as the weight to carry out the weighted average on the experimental results of multiple combinations.
4.3.2. To Transfer Walking Time Calculation
In the calculation of transfer walking time, when selecting ODs with only one transfer, the OD travel time chain only leaves the transfer walking time unknown and can be calculated directly. Similarly, in a transfer station there also exists multiple groups of OD data, and the calculation results of multiple ODs are also taken to be averaged with the amount of transaction data as the weight.
5. Example Validation Analysis
The above calculation method is applicable to all metro stations. In this paper, the lines with high passenger flow in the Guangzhou Metro are selected as the research objects, and there are 87 stations in 5 lines, among which 7 stations are interchange stations in the research line network. The operation period, 6:00–23:59, is divided into 38 time periods labeled by 30 min as a unit time, so theoretically, there are a total of 3306 research objects. Due to the low number of OD trips in some time periods, the final result of 2547 valid station time periods is obtained.
5.1. Accuracy Validation of Model Results
This subsection will verify whether the results of the model are correct. Since the transfer walking time in the station walking time has a reference value in the route planning, it can be compared with the calculated transfer walking time by crawling this data to evaluate whether the results of the model in this paper are accurate. It will also be verified from two date types: working day and weekend.
Analysis of the mean transfer walking time results. Taking the walking time at the Gongyuanqian transfer station as an example, the OD travel data for only one transfer (and the transfer station was Gongyuanqian) were used to derive the transfer walking time for each time period at this station, and the calculation results of weekdays are shown in Table 2.

Table 2.
Gongyuanqian Station transfer walking time by period on weekdays.
For weekdays, a total of 24 time periods were obtained by calculating the average transfer walking time, which is 45.94 s. Using the Baidu map to check the walking time and walking distance of the transfer station, the walking length is 71 m and the walking time is 1 min, because the time accuracy is 1 min, so it may include 0–59 s, and 45.94 s is in the interval, so it can be considered that the walking time has reference. For weekends, due to the small amount of data, only six periods of data are obtained, but from the average value of the data in six periods, the walking time in Gongyuanqian Station on weekends is 39.12 s, which is also accurate. However, there are not enough data from the weekend result for feature distribution analysis. Therefore, the results of working days are distributed and verified below, but it does not mean that the results of weekends are unreliable.
Analysis of the results of transfer walking time distribution. The results were analyzed using SPSS to obtain frequency histograms, as shown in Figure 5.
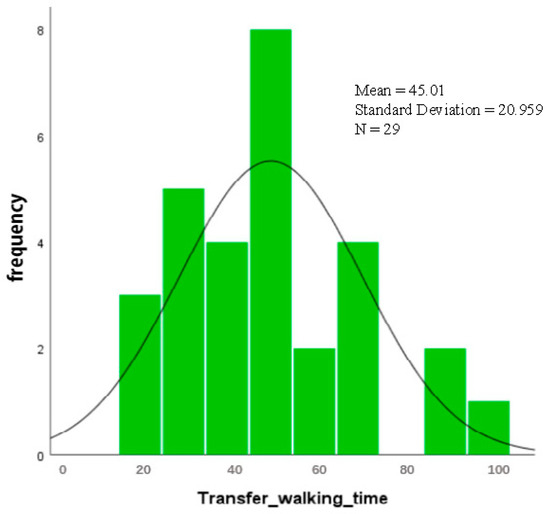
Figure 5.
Gongyuanqian Station transfer walking time frequency histogram.
According to the histogram, it is estimated that the station transfer walking time may obey normal distribution. Using SPSS to further the KS normal test for the park front transfer walking time, the results show that the significance level is 0.2, which is greater than 0.5, so it can be considered to obey normal distribution, further drawing a Q-Q diagram (see Figure 6). The graph scatter and straight line better match also verifies its normal distribution. This result is consistent with the existing walking time. The results are consistent with the results of existing studies on walking time distribution, which also note the reasonableness of the results.
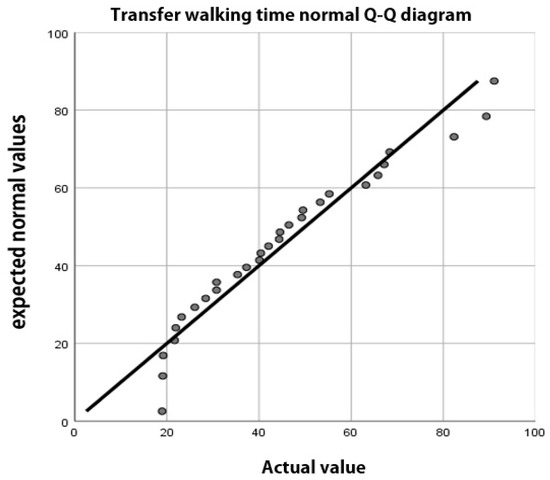
Figure 6.
Gongyuanqian Station transfer walking time Q-Q diagram.
5.2. Model Validity Verification
5.2.1. Model Validity Verification
Because the stations with large passenger flow are excluded from the constraints, it is necessary to verify the validity of the results of such stations.
Validation idea: Screening the data of stations with access or exit passenger flow greater than 3000 passengers per 30 min; classifying the data into “access passenger flow greater than exit passenger flow” and “access passenger flow less than exit passenger flow” according to the amount of access or exit passenger flow. If the direction is the same, the hypothesis is considered valid, and the proportion of validity is calculated and averaged for the two types of results.
The applicability of the results of the station during the heavy passenger flow period on weekdays and weekends is verified below. The calculation results are as follows:
As can be seen from Table 3, for weekdays, there are 29 station periods in the first category that have a high level of access passenger flow, and 83% of them have walking differences in the same direction as the passenger flow difference. In the second category, there are four station periods and the walking differences in the station periods are in the same direction as the passenger flow difference. In other words, on average, 91.5% of the station periods have walking variation in the same direction as the passenger flow, so it is reasonable to assume that the passenger flow density has an impact on the walking time in the station. At the same time, the average delay value for the first category is 44.54 s; the average delay value for the second category is 113.66 s. The lower delay value for the impact of access passenger flow may be due to the fact that the passenger flow is buffered from the short-time accumulation of passenger flow by actions such as flow restriction and security checks before entering the station.

Table 3.
Model validation results.
However, for weekends, the average effective rate is 0.625, which may be caused by the small amount of weekend data. From the perspective of passenger flow, it can be seen that even in the case of large passenger flow, passenger flow basically does not delay the travel time.
5.2.2. Comparison of the Effectiveness of Multiple Passenger Flow Thresholds
In the model, station walking time constraints need to be evaluated based on passenger flow period thresholds. In this section, we select several large passenger flow thresholds, such as 1500, 2000, 2500, 3000, 3500, 4000, etc., as the basis for judgment and compare the effectiveness of the thresholds on the model constraints (unit: passenger per 30 min). The validity results of different passenger flow thresholds on weekdays are as follows:
As can be seen from Table 4, the validity of the constraints increases with the increase of the threshold value of large passenger flow, but the time slots of the stations that satisfy the conditions decrease with the increase of the threshold value. When the threshold value of large passenger flow reaches 3000 passengers/30 min, the accuracy of the constraints increases most obviously, and the accuracy rate reaches 92%. If the threshold value of passenger flow continues to increase, although the accuracy rate is increasing, the change is not much and the stations can satisfy too few time slots, which cannot well reflect the impact of actual passenger flow on walking time. Therefore, this paper considers that “when the station passenger flow access or exit reaches 3000 passengers per 30 min, it will have an impact on the walking time” has some reference significance. At the same time, when the same verification is carried out on weekends, although the efficiency is low, the same trend can be obtained, so I will not repeat it here.

Table 4.
Results of comparing the effectiveness of multiple passenger flow thresholds.
6. Discussion
This study mainly focuses on the travel demand and travel experience of subway passengers, which is of great significance from the perspective of sustainable development. First of all, by optimizing subway operation and planning, traffic congestion and air pollution can be reduced, thus promoting the sustainable development of the city. Secondly, by optimizing the design and improvement of subway stations, passengers’ travel efficiency and experience can be improved, thus encouraging people to use public transport and reducing the use of personal cars, and thus reducing the carbon emissions and energy consumption of the city. In addition, the research results can also provide data support for the formulation of urban transportation planning and public policies, so as to better achieve the goal of urban sustainable development.
Therefore, sustainability factors can be considered in the future. For example, we could study how to reduce the impact on the environment and improve the sustainability of the subway by optimizing its operation and planning.
7. Conclusions
In this paper, based on metro passenger travel time data, we propose a method to derive station walking time without manual investigation by crawling the relevant data through Python. The method considers the influence of passenger flow on passenger walking time, and validates the model in terms of result accuracy and constraint validity. This result verifies the property that passenger in-station walking time obeys normal distribution, and also finds that when the passenger flow reaches 3000 passengers per 30 min, the degree of influence of passenger flow on walking time is more obvious. In addition, for working days, the influence of passenger flow on walking time at the exit is greater than that at the entrance. For weekends, the impact is not significant, which may be because the distribution of passenger flow on weekends is relatively scattered, and a large number of outbound passengers will not leave in a short time as on working days.
Author Contributions
Conceptualization, L.Z. (Liang Zou) and S.H.; methodology, S.H.; software, S.H. and L.Z. (Lingxiang Zhu); validation, S.H.; formal analysis, L.Z. (Lingxiang Zhu); Writing—original draft preparation, S.H.; Writing—review and editing, L.Z. (Liang Zou). All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by Open Research Fund Program of Guangdong Key Laboratory of Urban Informatics (Optimization of Bus Dispatching Passenger Flow Matching Considering Vehicle Behavior Characteristics) and Shenzhen University Liyuan Challenge Panfeng Project (Calculation of pedestrian time distribution in subway stations based on reasonable itinerary). This paper is supported by Shenzhen Municipal Science and Technology Innovation Committee (Grant No. JCYJ20170818142947240).
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Annual Statistics and Analysis Report of Urban Rail Transit in 2021. Available online: https://www.camet.org.cn/xhfb/9935 (accessed on 9 April 2023).
- Du, P.; Liu, C.; Liu, Z. Research on the travel time law of passengers in urban rail passage. J. Transp. Syst. Eng. Inf. Technol. 2009, 9, 103–109. [Google Scholar]
- Zhao, Y. Research on Urban Rail Transit Transfer Considering Service Level. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2011. [Google Scholar]
- Zhou, Y.; Yao, L.; Gong, Y.; Chen, Y. Time prediction model of subway transfer. SpringerPlus 2016, 5, 44. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Xu, R. Rail transit travel time reliability and estimation of passenger route choice behavior: Analysis using automatic fare collection data. Transp. Res. Rec. 2012, 2275, 58–67. [Google Scholar] [CrossRef]
- Zhou, F.; Shi, J.; Xu, R. Estimation method of path-selecting proportion for urban rail transit based on AFC data. Math. Probl. Eng. 2015, 2015, 350397. [Google Scholar] [CrossRef]
- Tong, Y.; Wang, X.; Pan, M.; Li, Z.; Jin, B. Estimation on the transfer walking time in the subway station based on mathematical statistics. Technol. Econ. Areas Commun. 2016, 18, 7–11. [Google Scholar]
- Zhang, L.; Hao, Y.; Hu, H. Estimation method of outbound travel time of urban rail passengers based on ATS and AFC data. Int. J. Comput. Intell. Appl. 2020, 10, 164–169. [Google Scholar]
- Zhu, W.; Fan, W.; Wei, J.; Fan, W.D. Complete estimation approach for characterizing passenger travel time distributions at rail transit stations. J. Transp. Eng. Part A Syst. 2020, 146, 04020050. [Google Scholar] [CrossRef]
- Li, W.; Yan, X.; Li, X.; Yang, J. Estimate passengers’ walking and waiting time in metro station using smart card data (scd). IEEE Access 2020, 8, 11074–11083. [Google Scholar] [CrossRef]
- Paul, E.C. Estimating Train Passenger Load from Automated Data Systems: Application to London Underground. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, UK, 2010. [Google Scholar]
- Eltved, M.; Lemaitre, P.; Petersen, N.C. Estimation of transfer walking time distribution in multimodal public transport systems based on smart card data. Transp. Res. Part C Emerg. Technol. 2021, 132, 103332. [Google Scholar] [CrossRef]
- Yan, Z. Research on Passenger Flow Allocation Method of Urban Rail Transit Network Based on AFC Data. Master’s Thesis, Southeast University, Nanjing, China, 2020. [Google Scholar]
- Wu, L. Research on Passenger Travel Path Matching and Impact of Unexpected Events in Rail Transit Network Based on AFC Data. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Liang, D. Research on the Estimation Method of Stranded Passenger Flow under the Interruption of Urban Rail Train Operation. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
- Jia, H.F.; Sang, H.; Luo, Q.Y.; Yang, J.L.; Miao, H.Z. A cooperative evacuation strategy for mass passenger flow in urban rail transit transfer stations. Int. J. Mod. Phys. C 2021, 32, 2150007. [Google Scholar]
- Zhao, J. Research on Collaborative Optimization of Rail Transit Schedules. Master’s Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Zeng, J.; Qian, Y.; Yin, F.; Zhu, L.; Xu, D. A multi-value cellular automata model for multi-lane traffic flow under lagrange coordinate. Comput. Math. Organ. Theory 2022, 28, 178–192. [Google Scholar] [CrossRef]
- Harris, N.G. Modelling walk link congestion and the prioritisation of congestion relief. Traffic Eng. Control 1991, 32, 78–80. [Google Scholar]
- Lam WH, K.; Morrall, J.F.; Ho, H. Pedestrian flow characteristics in Hong Kong. Transp. Res. Rec. 1995, 1487, 56–62. [Google Scholar]
- Feng, C.; Qibing, W.U.; Zhang, H.; Sanbing, L.I.; Liang, Z.H. Relationship analysis on station capacity and passenger flow: A case of Beijing subway line 1. J. Transp. Syst. Eng. Inf. Technol. 2009, 9, 93–98. [Google Scholar]
- Wang, Z.; Rong, S.; Gao, W. Analysis of walking time functions of passengers in shanghai rail transit stations. Urban Mass Transit 2010, 13, 57–60. [Google Scholar]
- Li, Y.; Sun, Y.; Wan, H.; Pu, Q. Evaluation method of passenger flow pressure in rail transit station interchange channels. Urban Mass Transit 2020, 23, 106–109,144. [Google Scholar]
- Xie, J.; Yang, K.; Zhang, Y.; Zhang, H.; Xie, Y. Simulation of Changsha Metro Wanjiali square Station Hall and Passenger Flow Optimization. J. Transp. Syst. Eng. Inf. Technol. 2021, 21, 275–281. [Google Scholar]
- Liu, Y. Research on Rail Traffic Passenger Flow Allocation Method Based on AFC Data. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Qin, X.; Qian, Y.; Zeng, J.; Wei, X. Accessibility and Economic Connections between Cities of the New Western Land–Sea Corridor in China—Enlightenments to the Passageway Strategy of Gansu Province. Sustainability 2022, 14, 4445. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).