Performance of Statistical and Intelligent Methods in Estimating Rock Compressive Strength
Abstract
1. Introduction
2. Methodology
2.1. Laboratory Tests
2.2. Random Forest Algorithm (RFA)
2.3. Gaussian Process Regression Based on Squared Exponential Kernel (GPR-SEK)
2.4. The SVM-RBF
2.5. K Nearest Neighbor Algorithm (KNNA)
2.6. ANFIS and FMP-ANN
2.7. Performance Evaluation of Results
3. Results and Discussion
3.1. Geomechanical Properties of Samples
3.2. Petrographic Features
3.3. Influence of Independent Variables on the UCS
3.4. Evaluation of Previous Emperical Relationships
3.5. Multiple Linear Regression (MPLR)
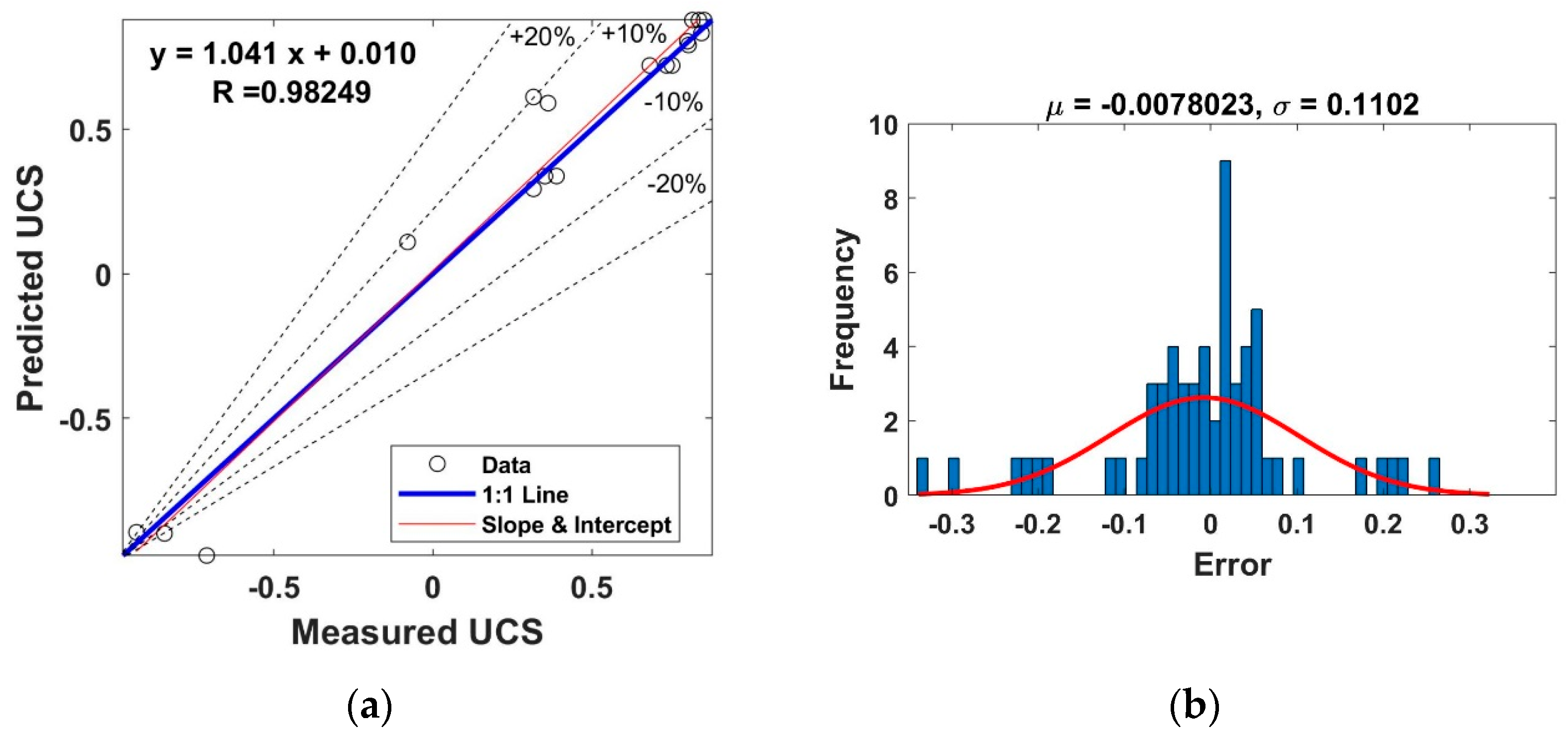
3.6. The Results of Modeling Using RFA and GPR-SEK Methods
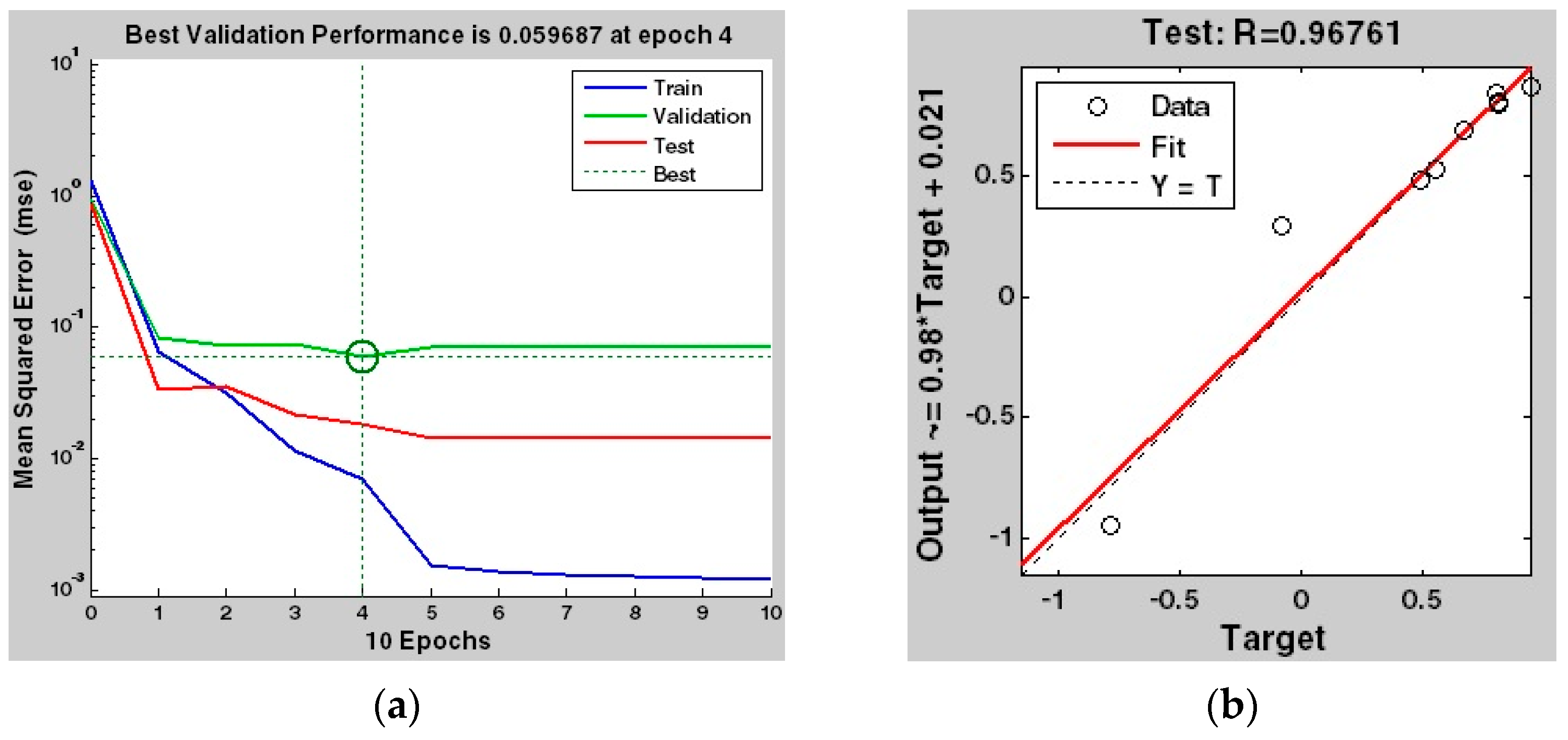
3.7. The FMP-ANN Results
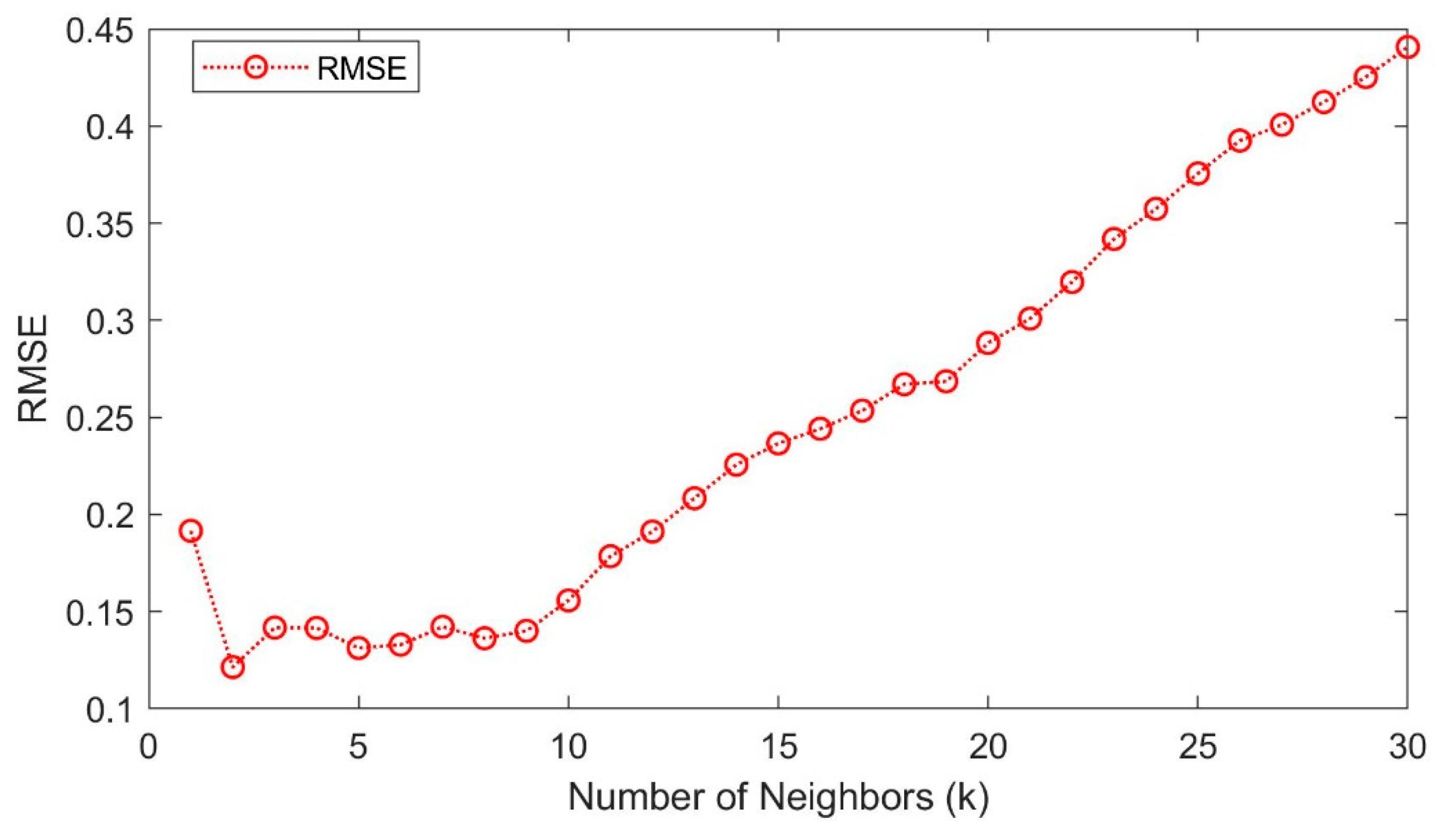
3.8. The KNNA Results
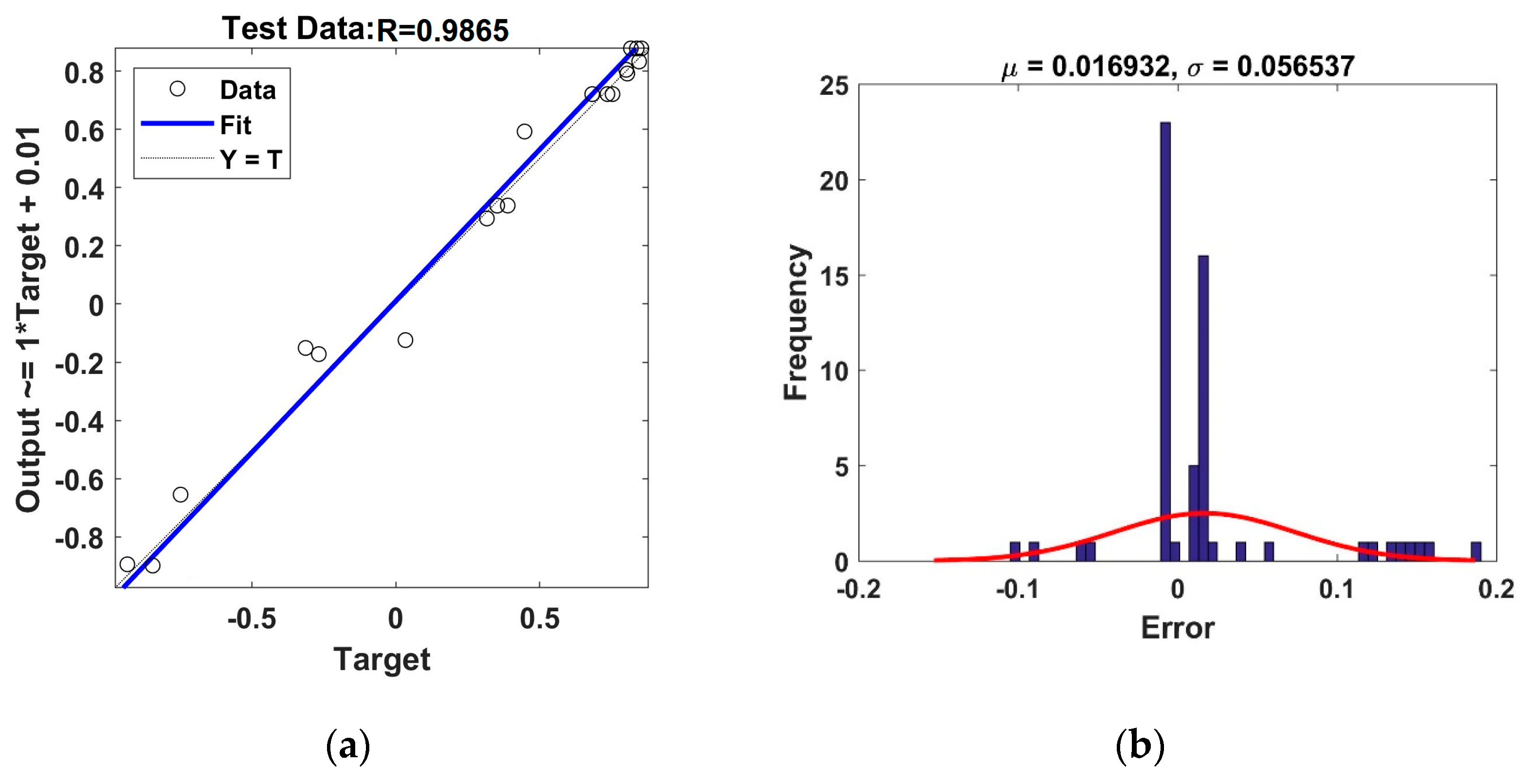
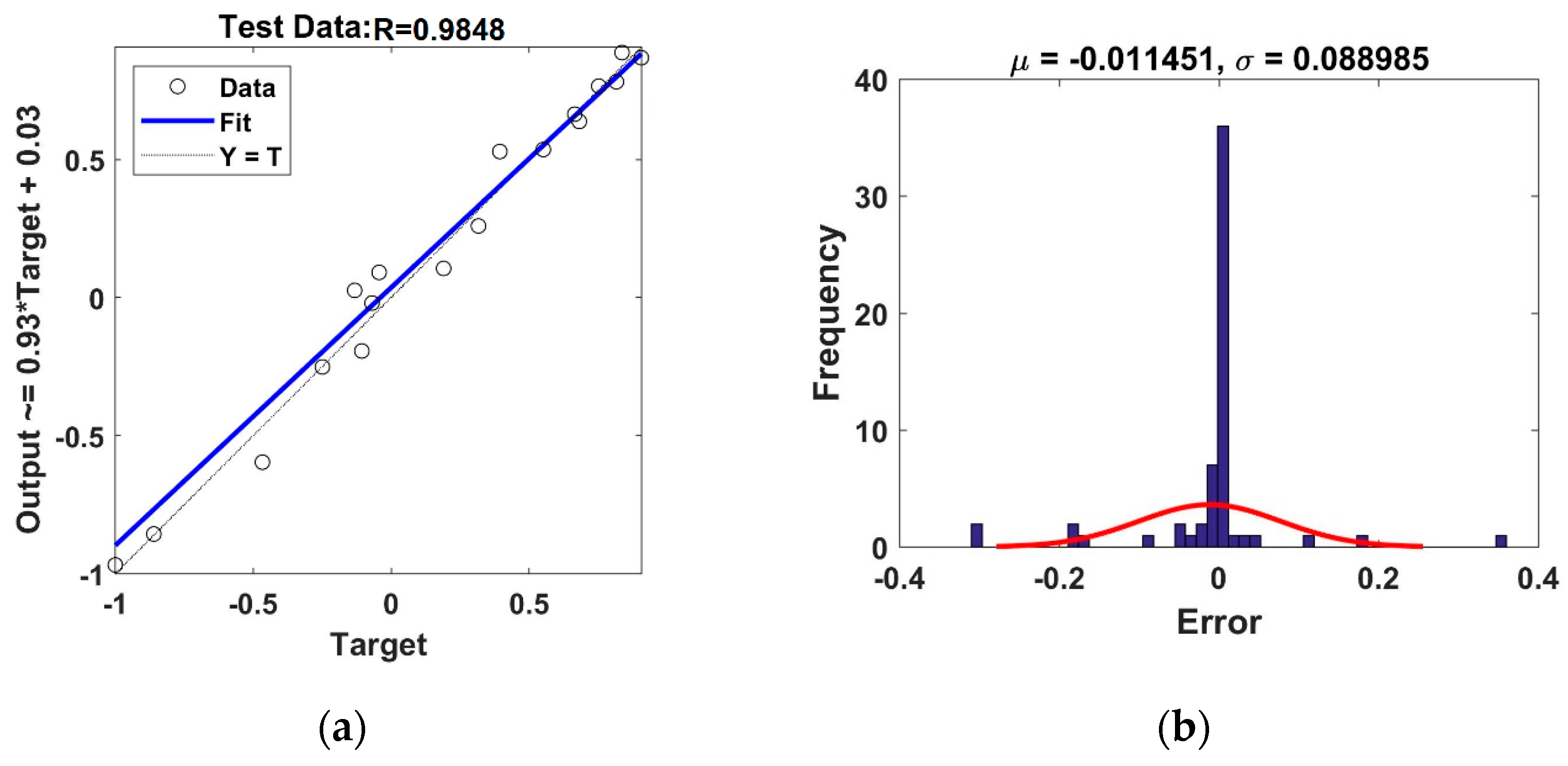
3.9. Results of SVM Method for Estimating UCS
3.10. Results of ANFIS Method for Estimating UCS
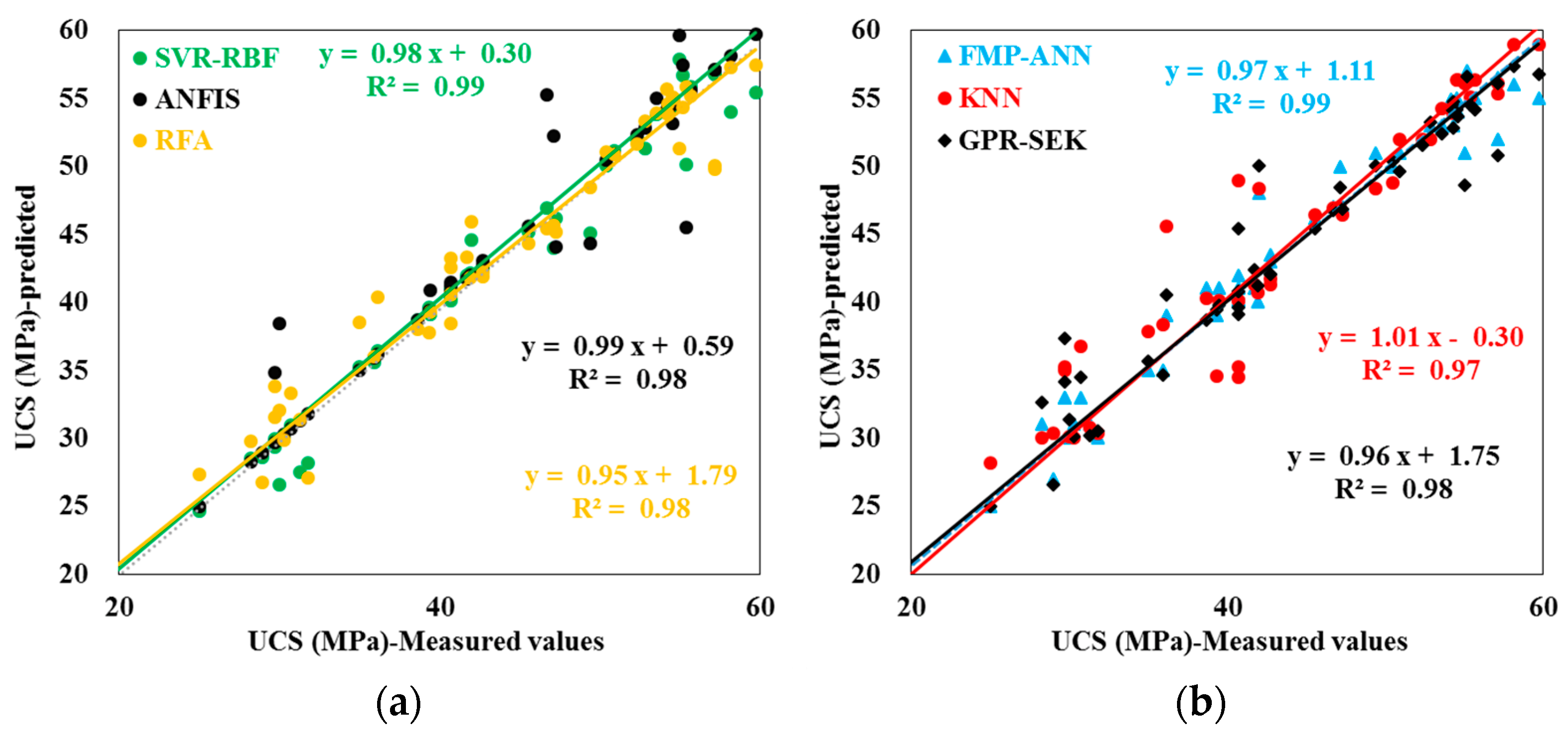
3.11. Evaluation of the Used Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, H.Q.; Zeng, Y.Y.; Lan, Y.F.; Zhou, X.P. Analysis of the excavation damaged zone around a tunnel accounting for geo-stress and unloading. Int. J. Rock Mech. Min. Sci. 2014, 69, 59–66. [Google Scholar] [CrossRef]
- Yang, H.Q.; Xing, S.G.; Wang, Q.; Li, Z. Model test on the entrainment phenomenon and energy conversion mechanism of flow-like landslides. Eng. Geol. 2018, 239, 119–125. [Google Scholar] [CrossRef]
- Edet, A. Correlation between Physico-mechanical Parameters and Geotechnical Evaluations of Some Sandstones along the Calabar/Odukpani–Ikom–Ogoja Highway Transect, Southeastern Nigeria. Geotech. Geol. Eng. 2018, 36, 135–149. [Google Scholar] [CrossRef]
- Abdi, Y.; Khanlari, G.R. Estimation of mechanical properties of sandstones using P-wave velocity and Schmidt hardness. New Find. Appl. Geol. 2019, 13, 33–47. [Google Scholar]
- Ajalloeian, R.; Mansouri, H.; Baradaran, E. Some carbonate rock texture effects on mechanical behavior, based on Koohrang tunnel data, Iran. Bull. Eng. Geol. Environ. 2017, 76, 295–307. [Google Scholar] [CrossRef]
- Madhubabu, N.; Singh, P.K.; Kainthola, A.; Mahanta, B.; Tripathy, A.; Singh, T.N. Prediction of compressive strength and elastic modulus of carbonate rocks. Measurement 2016, 88, 202–213. [Google Scholar] [CrossRef]
- Wen, L.; Luo, Z.Q.; Yang, S.J.; Guang, Y.Q.; Wang, W. Correlation of Geo-Mechanics Parameters with Uniaxial Compressive Strength and P-Wave Velocity on Dolomitic Limestone Using a Statistical Method. Geotech. Geol. Eng. 2018, 37, 1079–1094. [Google Scholar] [CrossRef]
- Aladejare, A.E. Evaluation of empirical estimation of uniaxial compressive strength of rock using measurements from index and physical tests. J. Rock Mech. Geotech. Eng. 2020, 12, 256–268. [Google Scholar] [CrossRef]
- Lawal, A.I.; Kwon, S.; Aladejare, A.E.; Oniyide, G.O. Prediction of the static and dynamic mechanical properties of sedimentary rock using soft computing methods. Geomech. Eng. 2022, 28, 313–324. [Google Scholar]
- Lawal, A.I.; Olajuyi, S.I.; Kwon, S.; Aladejare, A.E.; Edo, T.M. Prediction of blast-induced ground vibration using GPR and blast-design parameters optimization based on novel grey-wolf optimization algorithm. Acta Geophys. 2021, 69, 1313–1324. [Google Scholar] [CrossRef]
- Momeni, E.; Dowlatshahi, M.B.; Omidinasab, F.; Maizir, H.; Armaghani, D.J. Gaussian processregression technique to estimate the pile bearing capacity. Arab. J. Sci. Eng. 2020, 45, 8255–8267. [Google Scholar] [CrossRef]
- Gao, W.; Karbasi, M.; Hasanipanah, M.; Zhang, X.; Guo, J. Developing GPR model for forecasting the rock fragmentation in surface mines. Eng. Comput. 2018, 34, 339–345. [Google Scholar] [CrossRef]
- Dao, D.V.; Adeli, H.; Ly, H.B.; Le, L.M.; Le, V.M.; Le, T.T.; Pham, B.T. A sensitivity and robustness analysis of GPR and ANN for high-performance concrete compressive strength prediction using a Monte Carlo simulation. Sustainability 2020, 12, 830. [Google Scholar] [CrossRef]
- Barham, W.S.; Rabab’ah Aldeeky, S.R.; Al Hattamleh, O.H. Mechanical and Physical Based Artificial Neural Network Models for the Prediction of the Unconfined Compressive Strength of Rock. Geotech. Geol. Eng. 2020, 38, 4779–4792. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mamou, A.; Maraveas, C.; Roussis, P.C.; Siorikis, V.G.; Skentou, A.D.; Asteris, P.G. Predicting the unconfined compressive strength of granite using only two non-destructive test indexes. Geomech. Eng. 2021, 25, 317–330. [Google Scholar]
- Kwak, N.S.; Ko, T.Y. Machine learning-based regression analysis for estimating Cerchar abrasivity index. Geomech. Eng. 2022, 29, 219–228. [Google Scholar]
- Gül, E.; Ozdemir, E.; Sarıcı, D.E. Modeling uniaxial compressive strength of some rocks from turkey using soft computing techniques. Measurement 2021, 171, 108781. [Google Scholar] [CrossRef]
- Alizadeh, S.M.; Iraji, A.; Tabasi, S.; Ahmed, A.A.A.; Motahari, M.R. Estimation of dynamic properties of sandstones based on index properties using artificial neural network and multivariate linear regression methods. Acta Geophys. 2022, 70, 225–242. [Google Scholar] [CrossRef]
- Rastegarnia, A.; Teshniz, E.S.; Hosseini, S.; Shamsi, H.; Etemadifar, M. Estimation of punch strength index and static properties of sedimentary rocks using neural networks in south west of Iran. Measurement 2018, 128, 464–478. [Google Scholar] [CrossRef]
- McElroy, P.D.; Bibang, H.; Emadi, H.; Kocoglu, Y.; Hussain, A.; Watson, M.C. Artificial neural network (ANN) approach to predict unconfined compressive strength (UCS) of oil and gas well cement reinforced with nanoparticles. J. Nat. Gas Sci. Eng. 2021, 88, 103816. [Google Scholar] [CrossRef]
- Wang, M.; Wan, W.; Zhao, Y. Prediction of the uniaxial compressive strength of rocks from simple index tests using a random forest predictive model. C. R. Méc. 2020, 348, 3–32. [Google Scholar] [CrossRef]
- Matin, S.S.; Farahzadi, L.; Makaremi, S.; Chelgani, S.C.; Sattari, G.H. Variable selection and prediction of uniaxial compressive strength and modulus of elasticity by random forest. Appl. Soft Comput. 2018, 70, 980–987. [Google Scholar] [CrossRef]
- Gamal, H.; Alsaihati, A.; Elkatatny, S.; Haidary, S.; Abdulraheem, A. Rock strength prediction in real-time while drilling employing random forest and functional network techniques. J. Energy Resour. Technol. 2021, 143, 093004. [Google Scholar] [CrossRef]
- Umrao, R.K.; Sharma, L.K.; Singh, R.; Singh, T.N. Determination of strength and modulus of elasticity of heterogenous sedimentary rocks: An ANFIS predictive technique. Measurement 2018, 126, 194–201. [Google Scholar] [CrossRef]
- Hudaverdi, T. Prediction of flyrock throw distance in quarries by variable selection procedures and ANFIS modelling technique. Environ. Earth Sci. 2022, 81, 281. [Google Scholar] [CrossRef]
- Yesiloglu-Gultekin, N.; Gokceoglu, C.; Sezer, E.A. Prediction of uniaxial compressive strength of granitic rocks by various nonlinear tools and comparison of their performances. Int. J. Rock Mech. Min. Sci. 2013, 62, 113–122. [Google Scholar] [CrossRef]
- Yesiloglu-Gultekin, N.; Gokceoglu, C.A. Comparison Among Some Non-linear Prediction Tools on Indirect Determination of Uniaxial Compressive Strength and Modulus of Elasticity of Basalt. J. Nondestruct. Eval. 2022, 41, 10. [Google Scholar] [CrossRef]
- Fathipour-Azar, H. Machine learning-assisted distinct element model calibration: ANFIS, SVM, GPR, and MARS approaches. Acta Geotech. 2022, 17, 1207–1217. [Google Scholar] [CrossRef]
- Azimian, A. Application of statistical methods for predicting uniaxial compressive strength of limestone rocks using nondestructive tests. Acta Geotech. 2017, 12, 321–333. [Google Scholar] [CrossRef]
- Aliyu, M.M.; Shang, J.; Murphy, W.; Lawrence, J.A.; Collier, R.; Kong, F.; Zhao, Z. Assessing the uniaxial compressive strength of extremely hard cryptocrystalline flint. Int. J. Rock Mech. Min. Sci. 2019, 113, 310–321. [Google Scholar] [CrossRef]
- Selçuk, L.; Nar, A. Prediction of uniaxial compressive strength of intact rocks using ultrasonic pulse velocity and rebound-hammer number. Q. J. Eng. Geol. Hydrogeol. 2016, 49, 67–75. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Ali, H.F.H.; Abdulhamid, S.N.; Ibrahim, H.H.; Noori, K.M.G. Dynamic prediction models of rock quality designation in tunneling projects. Transp. Geotech. 2021, 27, 100497. [Google Scholar]
- Xu, C.; Amar, M.N.; Ghriga, M.A.; Ouaer, H.; Zhang, X.; Hasanipanah, M. Evolving support vector regression using Grey Wolf optimization; forecasting the geomechanical properties of rock. Eng. Comput. 2020, 38, 1819–1833. [Google Scholar] [CrossRef]
- Ceryan, N. Application of support vector machines and relevance vector machines in predicting uniaxial compressive strength of volcanic rocks. J. Afr. Earth Sci. 2014, 100, 634–644. [Google Scholar] [CrossRef]
- Trott, M.; Matthew, L.; Lindsay, H.; Daniel, L.M. Random forest rock type classification with integration of geochemical and photographic data. Appl. Comput. Geosci. 2022, 15, 100090. [Google Scholar] [CrossRef]
- Barzegar, R.; Sattarpour, M.; Nikudel, M.R.; Moghaddam, A.A. Comparative evaluation of artificial intelligence models for prediction of uniaxial compressive strength of travertine rocks, case study: Azarshahr area, NW Iran. Model. Earth Syst. Environ. 2016, 2, 76. [Google Scholar] [CrossRef]
- Mohamad, E.T.; Armaghani, D.J.; Momeni, E.; Abad, S. Prediction of the unconfined compressive strength of soft rocks: A PSO-based ANN approach. Bull. Eng. Geol. Environ. 2015, 74, 745–757. [Google Scholar] [CrossRef]
- Singh, R.; Umrao, R.K.; Ahmad, M.; Ansari, M.K.; Sharma, L.K.; Singh, T.N. Prediction of geomechanical parameters using soft computing and multiple regression approach. Measurement 2017, 99, 108–119. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Bardhan, A.; Samui, P.; Hu, J.W.; Zarzoura, F. Computational intelligence approaches for estimating the unconfined compressive strength of rocks. Arab. J. Geosci. 2023, 16, 37. [Google Scholar] [CrossRef]
- Teymen, A.; Mengüç, E.C. Comparative evaluation of different statistical tools for the prediction of uniaxial compressive strength of rocks. Int. J. Min. Sci. Technol. 2020, 30, 785–797. [Google Scholar] [CrossRef]
- Salehin, S. Investigation into engineering parameters of marls from Seydoon dam in Iran. J. Rock Mech. Geotech. Eng. 2017, 9, 912–923. [Google Scholar] [CrossRef]
- Aldeeky, H.; Al Hattamleh, O. Prediction of engineering properties of basalt rock in Jordan using ultrasonic pulse velocity test. Geotech. Geol. Eng. 2018, 36, 3511–3525. [Google Scholar] [CrossRef]
- Kahraman, S. Evaluation of simple methods for assessing the uniaxial compressive strength of rock. Int. J. Rock Mech. Min. Sci. 2001, 38, 981–994. [Google Scholar] [CrossRef]
- Uyanık, O.; Sabbağ, N.; Uyanık, N.A.; Öncü, Z. Prediction of mechanical and physical properties of some sedimentary rocks from ultrasonic velocities. Bull. Eng. Geol. Environ. 2019, 78, 6003–6016. [Google Scholar] [CrossRef]
- Kılıç, A.; Teymen, A. Determination of mechanical properties of rocks using simple methods. Bull. Eng. Geol. Environ. 2008, 67, 237–244. [Google Scholar] [CrossRef]
- ASTM D2938-95; Standard Test Method for Unconfined Compressive Strength of Intact Rock Core Specimens. ASTM International: West Conshohocken, PA, USA, 2002.
- ISRM. Rock Characterization Testing and Monitoring; Brown, E.T., Ed.; ISRM Suggested Methods; Pergamon Press: Oxford, UK, 1981; Volume 211. [Google Scholar]
- ASTM D5731; Standard Test Method for Determination of the Point Load Strength Index of Rock. ASTM International: West Conshohocken, PA, USA, 2002.
- ASTM D2845; Test Methods for Ultra Violet Velocities Determination. ASTM International: West Conshohocken, PA, USA, 1983.
- Folk, R.L. Petrology of Sedimentary Rocks; Hemphill: Austin, TX, USA, 1974; 600p. [Google Scholar]
- Dunham, R.J. Classification of Carbonate Rocks According to Depositional Textures; American Association of Petroleum Geologists: Tulsa, OK, USA, 1962; pp. 108–121. [Google Scholar]
- Zhou, J.; Huang, S.; Qiu, Y. Optimization of random forest through the use of MVO, GWO and MFO in evaluating the stability of underground entry-type excavations. Tunn. Undergr. Space Technol. 2022, 124, 104494. [Google Scholar] [CrossRef]
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning. In Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by Random Forest. R News 2002, 2, 18–22. [Google Scholar]
- Harris, J.; Grunsky, E.C. Predictive lithological mapping of Canada’s North using Random Forest classification applied to geophysical and geochemical data. Comput. Geosci. 2015, 80, 9–25. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112, 607p. [Google Scholar]
- Zhu, B.; Zhong, Q.; Chen, Y.; Liao, S.; Li, Z.; Shi, K.; Sotelo, M.A. A Novel Reconstruction Method for Temperature Distribution Measurement Based on Ultrasonic Tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 2352–2370. [Google Scholar] [CrossRef]
- Raja, M.N.A.; Jaffar, S.T.A.; Bardhan, A.; Shukla, S.K. Predicting and validating the load-settlement behavior of large-scale geosynthetic-reinforced soil abutments using hybrid intelligent modeling. JRMGE 2023, 15, 773–788. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998; p. 736. [Google Scholar]
- Fallah, M.; Pirali Zefrehei, A.R.; Hedayati, S.A.; Bagheri, T. Comparison of temporal and spatial patterns of water quality parameters in Anzali Wetland (southwest of the Caspian Sea) using Support vector machine model. Casp. J. Environ. Sci. 2021, 19, 95–104. [Google Scholar]
- Kookalani, S.; Cheng, B. Structural Analysis of GFRP Elastic Gridshell Structures by Particle Swarm Optimization and Least Square Support Vector Machine Algorithms. J. Civ. Eng. Mater. Appl. 2021, 5, 12–23. [Google Scholar]
- Yang, H.; Wang, Z.; Song, K. A new hybrid grey wolf optimizer-feature weighted-multiple kernel-support vector regression technique to predict TBM performance. Eng. Comput. 2020, 38, 2469–2485. [Google Scholar] [CrossRef]
- Yang, H.; Song, K.; Zhou, J. Automated Recognition Model of Geomechanical Information Based on Operational Data of Tunneling Boring Machines. Rock Mech. Rock Eng. 2022, 55, 1499–1516. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 3, pp. 731–739. [Google Scholar]
- Tharwat, A.; Ghanem, A.M.; Hassanien, A.E. Three different classifiers for facial age estimation based on k-nearest neighbor. In Proceedings of the 2013 9th International Computer Engineering Conference (ICENCO), Giza, Egypt, 28–29 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 55–60. [Google Scholar]
- Aghighi, F.; Aghighi, H.; Ebadati, O.M. Evaluation of the efficiency of SVM and KNN Classification algorithms to extract urban effects from LiDAR cloud points. In Second International Conference on Knowledge-Based Research in Computer Engineering & Information Technology, Tehran, Iran, 30 September 2016; Majlisi University: Mobarakeh, Iran, 2017. (In Persian) [Google Scholar]
- Saed, S.A.; Kamboozia, N.; Ziari, H.; Hofko, B. Experimental assessment and modeling of fracture and fatigue resistance of aged stone matrix asphalt (SMA) mixtures containing RAP materials and warm-mix additive using ANFIS method. Mater. Struct. 2021, 54, 225. [Google Scholar] [CrossRef]
- Sobhani, B.; Safarianzengir, V. Monitoring and prediction of drought using TIBI fuzzy index in Iran. Casp. J. Environ. Sci. 2020, 18, 237–250. [Google Scholar]
- Jang, J.S.R. ANFIS: Adaptive network based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Moshahedi, A.; Mehranfar, N.A. Comprehensive Design for a Manufacturing System using Predictive Fuzzy Models. J. Res. Sci. Eng. Technol. 2021, 9, 1–23. [Google Scholar] [CrossRef]
- Mokhberi, M.; Khademi, H. The use of stone columns to reduce the settlement of swelling soil using numerical modeling. J. Civ. Eng. Mater. Appl. 2017, 1, 45–60. [Google Scholar] [CrossRef]
- Rastegarnia, A.; Lashkaripour, G.R.; Sharifi Teshnizi, E.; Ghafoori, M. Evaluation of engineering characteristics and estimation of dynamic properties of clay-bearing rocks. Environ. Earth Sci. 2021, 80, 621. [Google Scholar] [CrossRef]
- Mikaeil, R.; Esmaeilzade, A.; Shaffiee Haghshenas, S. Investigation of the Relationship Between Schimazek’s F-Abrasiveness Factor and Current Consumption in Rock Cutting Process. J. Civ. Eng. Mater. Appl. 2021, 5, 47–55. [Google Scholar]
- Keykhah, H.; Dahan Zadeh, B. Stability Analysis of Upstream Slope of Earthen Dams Using the Finite Element method Against Sudden Change in the Water Surface of the Reservoir, Case Study: Ilam Earthen Dam in Ilam Province. J. Civ. Eng. Mater. Appl. 2018, 2, 24–30. [Google Scholar]
- Taheri, S.; Ziad, H. Analysis and Comparison of Moisture Sensitivity and Mechanical Strength of Asphalt Mixtures Containing Additives and Carbon Reinforcement. J. Civ. Eng. Mater. Appl. 2021, 5, 1–8. [Google Scholar]
- Sobhani, J.; Jafarpour, F.; Firozyar, F.; Pourkhorshidi, A.R. Simulated C3A Effects on the Chloride Binding in Portland Cement with NaCl and CaCl2 Cations. J. Civ. Eng. Mater. Appl. 2022, 6, 41–54. [Google Scholar]
- Liu, B.; Yang, H.; Karekal, S. Effect of water content on argillization of mudstone during the tunneling process. Rock Mech. Rock Eng. 2020, 53, 799–813. [Google Scholar] [CrossRef]
- Guo, Y.; Luo, L.; Wang, C. Research on Fault Activation and Its Influencing Factors on the Barrier Effect of Rock Mass Movement Induced by Mining. Appl. Sci. 2023, 13, 651. [Google Scholar] [CrossRef]
- Yang, H.Q.; Li, Z.; Jie, T.Q.; Zhang, Z.Q. Effects of joints on the cutting behavior of disc cutter running on the jointed rock mass. Tunn. Undergr. Space Technol. 2018, 81, 112–120. [Google Scholar] [CrossRef]
- Peng, J.; Xu, C.; Dai, B.; Sun, L.; Feng, J.; Huang, Q. Numerical Investigation of Brittleness Effect on Strength and Microcracking Behavior of Crystalline Rock. Int. J. Geomech. 2022, 22, 4022178. [Google Scholar] [CrossRef]
- Ghavami, S.; Rajabi, M. Investigating the Influence of the Combination of Cement Kiln Dust and Fly Ash on Compaction and Strength Characteristics of High-Plasticity Clays. J. Civ. Eng. Mater. Appl. 2021, 5, 9–16. [Google Scholar]
- Xiao, D.; Hu, Y.; Wang, Y.; Deng, H.; Zhang, J.; Tang, B.; Li, G. Wellbore cooling and heat energy utilization method for deep shale gas horizontal well drilling. Appl. Therm. Eng. 2022, 213, 118684. [Google Scholar] [CrossRef]
- Rastegarnia, A.; Lashkaripour, G.R.; Ghafoori, M.; Farrokhad, S.S. Assessment of the engineering geological characteristics of the Bazoft dam site, SW Iran. Q. J. Eng. Geol. Hydrogeol. 2019, 52, 360–374. [Google Scholar] [CrossRef]
- Kurtulus, C.; Bozkurt, A.; Endes, H. Physical and mechanical properties of serpentinized ultrabasic rocks in NW Turkey. Pure Appl. Geophys. 2012, 169, 1205–1215. [Google Scholar] [CrossRef]
- Yagiz, S.; Sezer, E.A.; Gokceoglu, C. Artificial neural networks and nonlinear regression techniques to assess the influence of slake durability cycles on the prediction of uniaxial compressive strength and modulus of elasticity for carbonate rocks. Int. J. Numer. Anal. Methods Géoméch. 2012, 36, 1636–1650. [Google Scholar] [CrossRef]
- Shirnezhad, Z.; Azma, A.; Foong, L.K.; Jahangir, A.; Rastegarnia, A. Assessment of water resources quality of a karstic aquifer in the Southwest of Iran. Bull. Eng. Geol. Environ. 2021, 80, 71–92. [Google Scholar] [CrossRef]
- Shayesteh, A.; Ghasemisalehabadi, E.; Khordehbinan, M.W.; Rostami, T. Finite element method in statistical analysis of flexible pavement. J. Mar. Sci. Technol. 2017, 25, 15. [Google Scholar]
- Rustamovich Sultanbekov, I.; Yurievna Myshkina, I.; Yurievna Gruditsyna, L. Development of an application for creation and learning of neural networks to utilize in environmental sciences. Casp. J. Environ. Sci. 2020, 18, 595–601. [Google Scholar]
- Tabatabaei, M.; Salehpour Jam, A. Optimization of sediment rating curve coefficients using evolutionary algorithms and unsupervised artificial neural network. Casp. J. Environ. Sci. 2017, 15, 385–399. [Google Scholar]
- Hecht-Nielsen, R. Kolmogorov’s mapping neural network existence theorem. In Proceedings of the International Conference on Neural Networks, San Diego, CA, USA, 21–24 June 1987; IEEE Press: New York, NY, USA, 1987; Volume 3, pp. 11–14. [Google Scholar]
- Hush, D. Classification with neural networks: A performance analysis. In Proceedings of the IEEE International Conference on Systems Engineering, Fairborn, OH, USA, 24–26 August 1989; IEEE: Piscataway, NJ, USA, 1989; pp. 277–280. [Google Scholar]
- Ripley, B.D. Statistical Aspects of Neural Networks; Barndorff-Nielsen, O.E., Jensen, J.L., Kendall, W.S., Eds.; Networks and Chaos–Statistical and Probabilistic Aspects; Chapman and Hall: London, UK, 1993; pp. 40–123. [Google Scholar]
- Paola, J.D. Neural Network Classification of Multispectral Imagery; The University of Arizona: Tucson, AZ, USA, 1994. [Google Scholar]
- Wang, C. A Theory of Generalization in Learning Machines with Neural Application. Ph.D. Thesis, The University of Pennsylvania, Philadelphia, PA, USA, 1994. [Google Scholar]
- Kaastra, I.; Boyd, M. Designing a neural network for forecasting financial and economic time series. Neurocomputing 1996, 10, 215–236. [Google Scholar] [CrossRef]
- Kanellopoulos, I.; Wilkinson, G.G. Strategies and best practice for neural network image classification. Int. J. Remote Sens. 1997, 18, 711–725. [Google Scholar] [CrossRef]
- Kavyanifar, B.; Tavakoli, B.; Torkaman, J.; Mohammad Taheri, A.; Ahmadi Orkomi, A. Coastal solid waste prediction by applying machine learning approaches (Case study: Noor, Mazandaran Province, Iran). Casp. J. Environ. Sci. 2020, 18, 227–236. [Google Scholar]
- Rashidi Tazhan, O.; Pir Bavaghar, M.; Ghazanfari, H. Detecting pollarded stands in Northern Zagros forests, using artificial neural network classifier on multi-temporal lansat-8 (OLI) imageries (case study: Armarde, Baneh). Casp. J. Environ. Sci. 2019, 17, 83–96. [Google Scholar]
- Dianati Tilaki, G.A.; Ahmadi Jolandan, M.; Gholami, V. Rangelands production modeling using an artificial neural network (ANN) and geographic information system (GIS) in Baladeh rangelands, North Iran. Casp. J. Environ. Sci. 2020, 18, 277–290. [Google Scholar]
- Zhan, C.; Dai, Z.; Soltanian, M.R.; De Barros, F.P. Data-Worth Analysis for Heterogeneous Subsurface Structure Identification With a Stochastic Deep Learning Framework. Water Resour. Res. 2022, 58, e2022WR033241. [Google Scholar] [CrossRef]
- Vapnik, V.; Chervonenkis, A. The necessary and sufficient conditions for consistency in the empirical risk minimization method. Pattern Recognit. Image Anal. 1991, 1, 283–305. [Google Scholar]
- Nguyen, H. Support vector regression approach with different kernel functions for predicting blast-induced ground vibration: A case study in an open-pit coal mine of Vietnam. SN Appl. Sci. 2019, 1, 283. [Google Scholar] [CrossRef]
- Al-Anazi, A.F.; Gates, I.D. Support vector regression to predict porosity and permeability: Effect of sample size. Comput. Geosci. 2012, 39, 64–76. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Opposition-based firefly algorithm for earth slope stability evaluation. China Ocean Eng. 2014, 28, 713–724. [Google Scholar] [CrossRef]
- Zhou, J.; Shen, X.; Qiu, Y.; Shi, X.; Khandelwal, M. Cross-correlation stacking-based microseismic source location using three metaheuristic optimization algorithms. Tunn. Undergr. Space Technol. 2022, 126, 104570. [Google Scholar] [CrossRef]


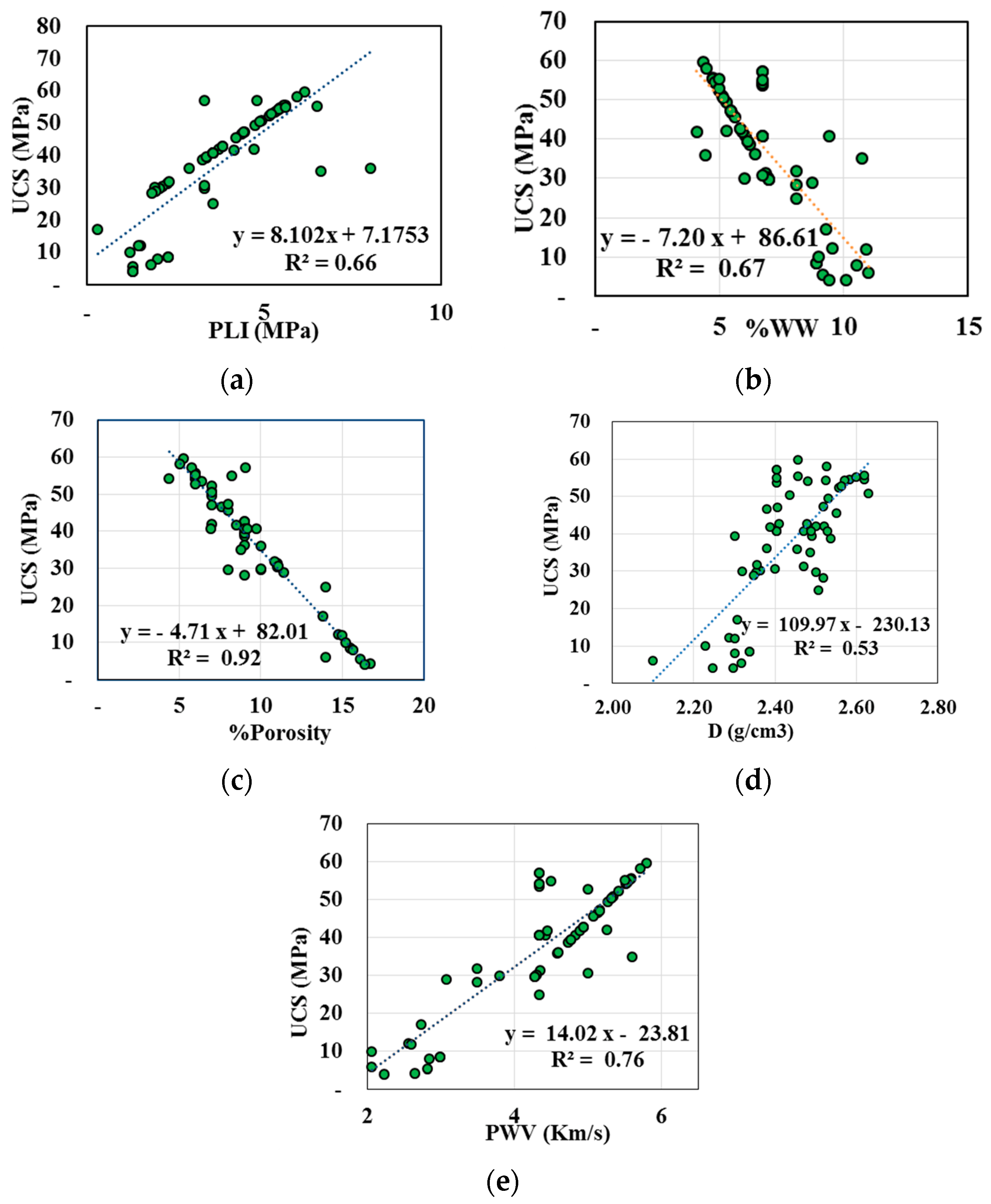
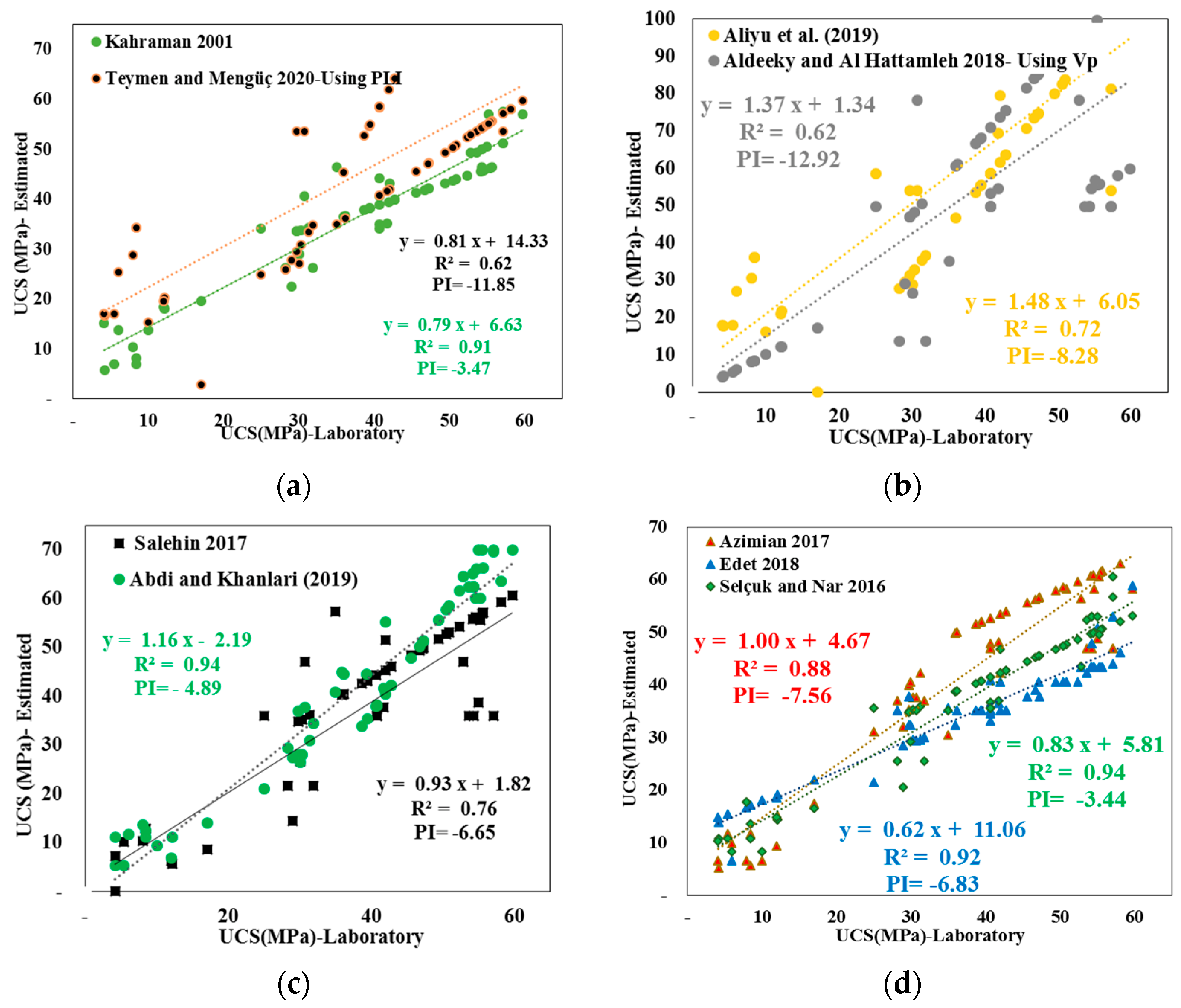
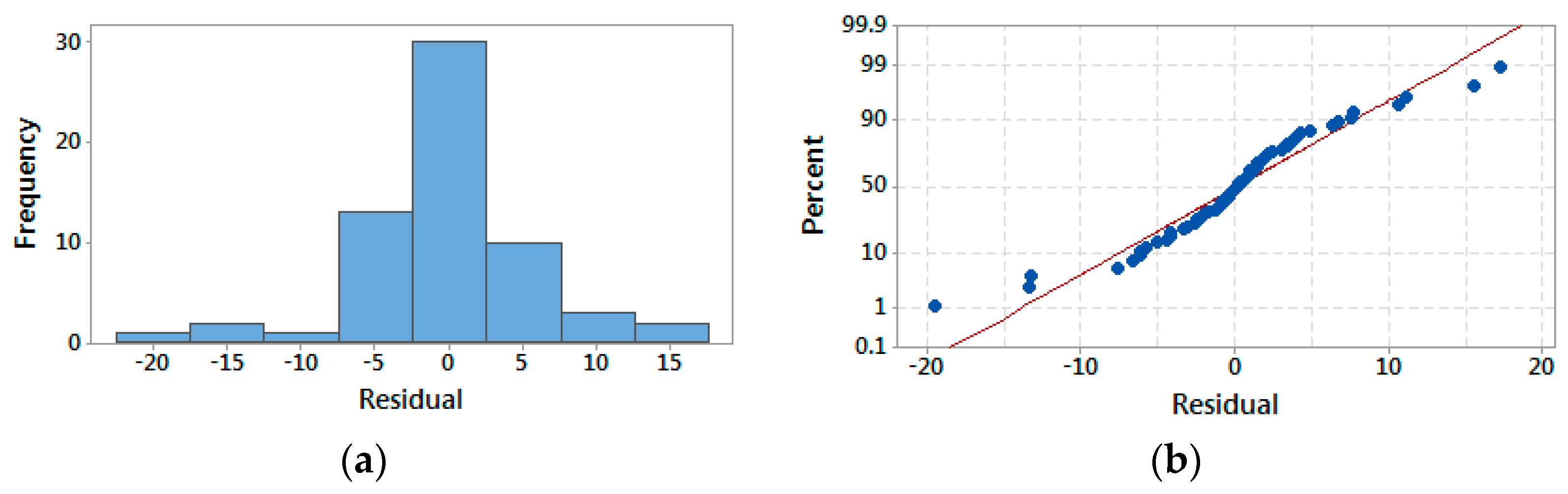

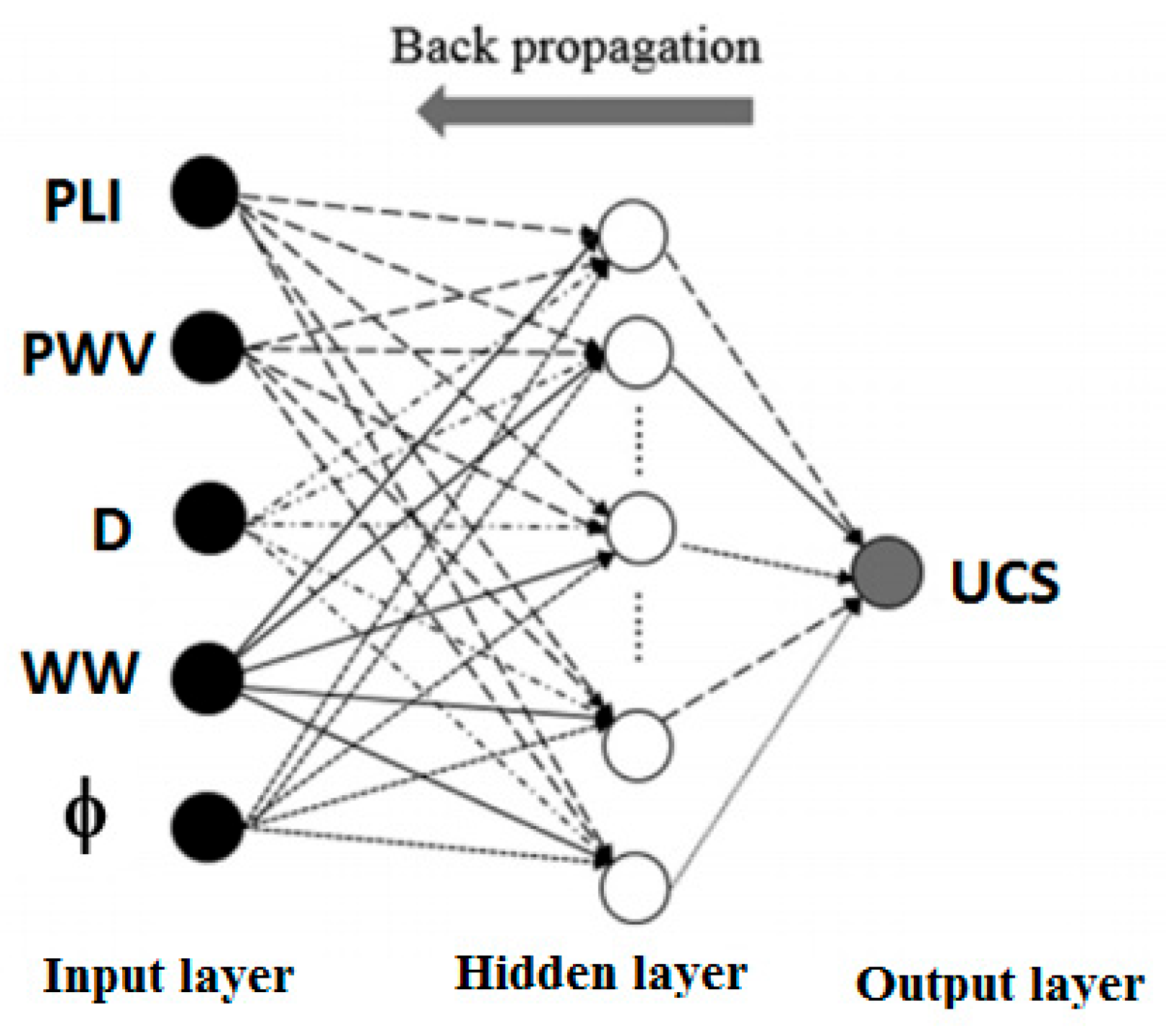
| Equation | Reference | Lithology |
|---|---|---|
| UCS = 12.29PLI1.233 | Teymen and Mengüç [40] | Various Rocks |
| UCS = −37.82 + (0.017PWV) | Salehin [41] | Sedimentary Rocks |
| UCS = 0.043PWV − 136.8 | Aldeeky and Al Hattamleh [42] | Basalt Rocks |
| UCS = 17.6PLI + 13.5 | Aliyu et al. [30] | Sedimentary Rocks |
| UCS = 14.3PLI | Aladejare [8] | Sedimentary Rocks |
| UCS = 9.95PWV(1.21) | Kahraman [43] | Sedimentary rocks |
| Wen et al. [7] | Limestone | |
| UCS = −5.10 + 110.79 | Edet [3] | Sandstone |
| UCS = 0.025PWV − 8.619 | Azimian [29] | Limestone |
| UCS = 6.6PWV1.6 | Uyanık et al. [44] | Sedimentary rocks |
| UCS = 22.18PWV − 30.32 | Selcuk and Nar [31] | Various Rocks |
| UCS = 0.041PWV − 15.40 | Abdi and Khanlari [4] | Sandstones |
| UCS = 2.304(PWV)2.43 | Kılıç and Teyman [45] | Various Rocks |
| UCS = 10 − 5D16.7 | Aladejare [8] | Sedimentary rocks |
| Test | Standards and References | Descriptions |
|---|---|---|
| UCS | ISRM [47] | A constant loading rate of 0.7 MPa per second was applied to the samples. The amount of deformation was recorded using the corresponding gauge in the UCS test. |
| Point load index (PLI) | ASTM D5731 [48] | This test was done on irregular and cylindrical samples. Then the PLI was calculated. |
| Compressional wave velocity test | ASTM D2845 [49] | With a ½ MHz frequency |
| Porosity (), density(D) and water absorption by weight (WW) | ISRM [47] | The total porosity () of specimens was measured using the method of saturation and immersion way. Density was computed from the ratio of mass to sample volume. |
| Petrography | Folk [50], Dunham [51] | For classifying the samples using thin section images. |
| Properties | Density (g/cm3) | PLI (MPa) | Water Absorption (%) | Porosity (%) | UCS (MPa) | Es (GPa) | PWV (km/s) | |
|---|---|---|---|---|---|---|---|---|
| Statistics | ||||||||
| Average | 2.43 | 3.75 | 6.81 | 9.44 | 37.54 | 14.95 | 4.38 | |
| Std. Dev. | 0.11 | 1.66 | 1.87 | 3.35 | 16.49 | 5.30 | 1.03 | |
| Kurtosis | 0.13 | (0.58) | (0.50) | (0.41) | (0.58) | (0.51) | (0.38) | |
| Skewness | (0.42) | 0.09 | 0.70 | 0.79 | (0.71) | (0.62) | (0.78) | |
| Min. | 2.10 | 0.31 | 4.08 | 4.36 | 4.12 | 3.00 | 2.06 | |
| Max. | 2.63 | 8.00 | 11.00 | 16.72 | 59.72 | 22.90 | 5.79 | |
| Specimens | 65 | 65 | 65 | 65 | 65 | 65 | 65 | |
| Equation | R2 | RMSE (MPa) | MAPE% | VAF % | PI | DWS | ANOVA Results | Eq. No. |
|---|---|---|---|---|---|---|---|---|
| UCS = 5.03PWV − 1.735 + 2.667PLI | 0.88 | 1.10 | 1.08 | 87.85 | 0.66 | 1.93 | F-value = 79.37 p-value = 0.00 | (18) |
| Term | Coefficients | T-Value | Significant Level (Sig.) | VIF (Variance Inflation Factor) |
|---|---|---|---|---|
| Constant | −32.1 | −1.34 | 0.187 | - |
| PWV | 5.03 | 2.44 | 0.018 | 7.58 |
| D | 21.4 | 1.82 | 0.074 | 3.02 |
| WW | 0.281 | 0.35 | 0.728 | 3.81 |
| −1.735 | −3.97 | 0.000 | 3.64 | |
| PLI | 2.667 | 3.05 | 0.003 | 3.77 |
| References | Neuron Numbers Calculated for This Study | Equations |
|---|---|---|
| Hecht-Nielsen [90] | 3 | ≤ |
| Hush [91] | 3 | |
| Ripley [92] | 3 | |
| Paola [93] | 11 | |
| Wang [94] | 1 | /3 |
| Kaastra and Boyd [95] | 2 | |
| Kanellopoulos and Wilkinson [96] | 1 |
| Function | Description | Kernel Function Type |
|---|---|---|
| This kernel is widely used in image processing, where d is the degree of the polynomial. | Polynomial kernel (PK) | |
| This kernel is used for general purposes. It is used when there is no prior knowledge about the data. In condition, parameter is used. | Radial basis function (RBF) | |
| - | Linear kernel (LK) |
| Kernel Function | Optimal Values of Parameters | Test Period | Train Period | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t | d | c | RMSE | R2 | PI | MAPE | RMSE | R2 | PI | MAPE | |||
| PK | 1.72 | 280.01 | 4 | - | 12.12 | 0.08 | 0.97 | 1.87 | 2.86 | 0.07 | 0.98 | 1.84 | 2.81 |
| RBF | 0.02 | - | - | 1.10 | 27 | 0.06 | 0.99 | 1.90 | 2.82 | 0.06 | 0.99 | 1.90 | 2.80 |
| LK | 0.45 | - | - | - | 0.90 | 0.09 | 0.96 | 1.83 | 2.84 | 0.09 | 0.97 | 1.81 | |
| FIS Generation Method | GENFIS4 |
|---|---|
| Influence radius | 0.60 |
| Number of epochs | 500 |
| Error goal | 0.00 |
| Type | Sugeno |
| Rules | 4 |
| Number of membership functions (MFs) | 6 |
| Input MF type | Gauss MF |
| Output MF type | Linear |
| APPROACHES | MAPE% | R2 | RMSE | VAF% | PI |
|---|---|---|---|---|---|
| RFA | 9.27 | 0.98 | 0.09 | 97.63 | 1.87 |
| SVM-RBF | 2.83 | 0.99 | 0.06 | 98.96 | 1.92 |
| ANFIS | 2.98 | 0.98 | 0.09 | 97.86 | 1.87 |
| KNNA | 8.44 | 0.97 | 0.11 | 97.25 | 1.83 |
| GPR-SEK | 6.63 | 0.98 | 0.09 | 97.45 | 1.86 |
| FMP-ANN | 4.66 | 0.99 | 0.24 | 98.36 | 1.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Altalbawy, F.M.A.; Gasmalla, T.A.S.; Al-Khafaji, A.H.D.; Iraji, A.; Syah, R.B.Y.; Nehdi, M.L. Performance of Statistical and Intelligent Methods in Estimating Rock Compressive Strength. Sustainability 2023, 15, 5642. https://doi.org/10.3390/su15075642
Zhang X, Altalbawy FMA, Gasmalla TAS, Al-Khafaji AHD, Iraji A, Syah RBY, Nehdi ML. Performance of Statistical and Intelligent Methods in Estimating Rock Compressive Strength. Sustainability. 2023; 15(7):5642. https://doi.org/10.3390/su15075642
Chicago/Turabian StyleZhang, Xuesong, Farag M. A. Altalbawy, Tahani A. S. Gasmalla, Ali Hussein Demin Al-Khafaji, Amin Iraji, Rahmad B. Y. Syah, and Moncef L. Nehdi. 2023. "Performance of Statistical and Intelligent Methods in Estimating Rock Compressive Strength" Sustainability 15, no. 7: 5642. https://doi.org/10.3390/su15075642
APA StyleZhang, X., Altalbawy, F. M. A., Gasmalla, T. A. S., Al-Khafaji, A. H. D., Iraji, A., Syah, R. B. Y., & Nehdi, M. L. (2023). Performance of Statistical and Intelligent Methods in Estimating Rock Compressive Strength. Sustainability, 15(7), 5642. https://doi.org/10.3390/su15075642











