Abstract
It has been observed from previous large earthquakes that weakening the structural foundation can reduce the damage of the structure itself by allowing a rocking motion to release the seismic energy, and this seismic design philosophy is gradually applied to new constructions. In this paper, a simplified model of the motion process of a rigid rocking block is proposed, the rocking motion equation of rigid rocking block is derived, and the parameter analysis is carried out. It was found that the height–width ratio and damping have a great impact on the rocking response of the structure. On this basis, combined with the Winkler foundation model, the equation of motion of the rigid rocking block considering the flexibility of the foundation is established. Through the analysis of an example, it is found that damping plays an important role in the overturning resistance of high-rise buildings and the soil elastic coefficient has a greater impact on the higher structure.
1. Introduction
Based on the aim of sustainable development during urban regeneration, we are increasingly concerned about whether a structure can be used effectively and sustainably. It has been found that many buildings that can be preserved from ancient times benefit from their own rocking motion when they encounter external vibration, such as the Yingxian wooden tower [1] in China and the Aphaia temple in Greece [2]. These structures weaken the connection between themselves and the foundation, release vibration energy through their own rocking under external excitation, reduce the damage of the structure itself, and achieve sustainability.
For the early study of rocking motion, people did not directly observe the partial lifting of buildings, but started from some smaller and more intuitive structures or furniture. The first person who systematically studied the problem of shaking and overturning of rigid blocks and the good performance of some obviously unstable structures under strong ground vibration was Housner [3]. In the Chile earthquake in May 1960, Houser observed that a few elevated water tanks designed with a special construction similar to a hinge joint at the bottom were almost intact after the earthquake, while other reinforced concrete elevated water tanks that seemed more stable were seriously damaged. From this, he proposed a theoretical model of the rigid rocking block (as shown in Figure 1), started the analysis and research of it, and analyzed the rocking behavior of the rigid rocking block when excited by the base. In 1978, Meek [4] carried out structural analysis through the simplified single mode model of rocking core tube and found that the rocking core tube can significantly reduce the dynamic response of the structure. The greater the height–width ratio, the more significant the reduction effect of the dynamic response. In 1983, Psycharis and Jennings [5] conducted a linear analysis of the rocking response of a rigid block on a viscoelastic foundation. In 1985, Yim and Chopra [6] carried out research on the condition that the bottom of the flexible structure is allowed to lift, and gave the corresponding linear analysis method.
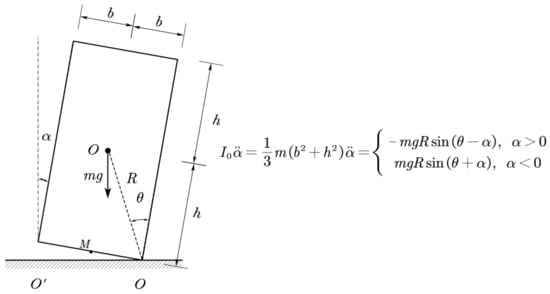
Figure 1.
Rigid rocking block and its motion equation.
Taniguchi’s research [7] in 2002 found that a rocking motion is a nonlinear problem, and even simple harmonic excitation can produce many kinds of rocking motion. In 2003, Jeong [8] conducted research on undamped rocking structures and found that periodic motion and mixed motion are the main dynamic responses of such structures. In 2004, Kuraffia [9] found that the earthquake damage of structures can be reduced with the structural lifting and rocking motion by studying the rocking structures with post-tensioned tendons. In 2008, Palmeri and Makris [10] analyzed the nonlinear moment of the momentum equation and found that the main factors affecting the motion of the rocking block were the structural size, structural shape, height–width ratio, stiffness and damping of the foundation, and energy loss in the collision process.
To create a sustainable and well-performing structural form that can rock to release the energy input from the outside, the rationality of its assumptions in design must be fully considered to ensure its long-term stability in practical use. The soil–structure interaction (SSI) has long been a hot topic in earthquake engineering. At present, we usually calculate the dynamic characteristics of the structure based on the assumption of a rigid foundation. Considering the soil–structure interaction, the dynamic characteristics of the structure system will be changed [11,12,13,14]. In the past, designers usually thought that the interaction effect of soil and structure would make the structure safer and ignored the interaction effect of the soil and structure to develop a more conservative design. However, a large number of studies show that the soil–structure interaction is not always conservative [15]. In some cases, the SSI effect cannot be ignored [16,17,18].
An actual earthquake disaster shows that the interaction between the soil and the structure may cause the actual natural period of the structure to be larger than the calculated value. Due to the wrong calculation of the structural period, the seismic period of the structure is consistent with the site seismic period in the actual earthquake, resulting in significant amplification of the building response and major damage (the Gediz earthquake in 1970, the Mexico City earthquake in 1985, the Adana Ceyhan earthquake in 1998, etc.) [19]. George Mylonakis [20] summarized the disadvantages of the soil–structure interaction with the structure, including increasing the natural vibration period of the structure, increasing the seismic response of the structure, and increasing the ductility demand of the structure.
The research on the analytical solution of the simplified model of the soil–structure dynamic interaction originated from the Boussinesq problem, in which Lamb [21] used the transformation integral method to study the reaction of an elastic half space surface under a vertical load in 1904. By 1936, Reissner [22] had analyzed and studied the vibration problem of a rigid circular foundation on the surface of an elastic half space, and integrated the solution given by Lamb, which was considered as the official start of the study of soil–structure dynamic interactions. In the 1950s, many researchers obtained the transient and steady analytical solutions of the translational, rotational, and torsional vibrations of circular and rectangular foundations under stress boundary conditions. By the mid-1960s, Parmelee [23] had initially revealed the basic law of inertial dynamic interaction. After that, with the continuous improvement of computer performance, the finite element method has been used more often in the research of SSI systems. However, even today, the analytic calculation method still has the advantages of fast calculation and a clear concept. At present, the Winkler foundation model [24] is the most popular analytical method; additionally, the elastic foundation beam method and the elastic continuum method [25] are also widely used.
At present, we are not sure if SSI effect will affect the structure with a rocking motion, which also restricts the practical engineering application of rocking structures to a certain extent. For a structure that can rock and relax with a certain degree of constraint, the problem of horizontal sliding hardly occurs, but bottom lifting, settlement, and structural overturning due to overall rotation cannot be ignored. In this paper, based on the simplified analysis model of the rocking block on the rigid ground proposed by Housner and the linear differential equation derived by Psycharis and Jennings, the geometric nonlinear motion equation of the two-spring rigid rocking block model is deduced and analyzed, and the influence of the key parameters on the lifting, rotation, and overturning of the rocking block is analyzed. Then, combined with the Winkler foundation model, the comprehensive response of the rigid rocking block considering the foundation flexibility is studied. The results of the above analysis can provide a reference for the design of structures with a rocking motion.
2. Two-Spring Rocking Block Model
2.1. Model Introduction
For structures with rocking properties, such as self-centering frames and rocking wall frame structures, they cannot be directly simplified as rocking blocks because the relationship between them and the ground is not a simple contact, but a buffer to avoid direct impact is set at the column bottom or at the bottom of the wall. When we assume that this buffer is elastic and damped, without considering the sliding of the rigid block relative to the base and the fact that the entire base cannot bear the tension, if the displacement of the rigid block moving upward is greater than the displacement due to its own gravity (that is, when the pressure on the spring is zero, the rigid block and the spring are separated), the movement of the uniform rigid block is shown in Figure 2.
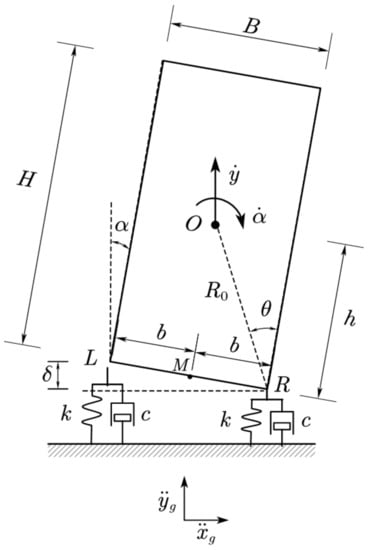
Figure 2.
Two-spring rocking block model.
The size of the rigid rocking block is . It can be seen from theoretical mechanics that when the center of mass of the block rotates beyond the vertical position of the long side, the rigid block will overturn, and the overturning angle has the relationship seen in Equation (1).
where , represent the width and height of the two-dimensional rocking block, respectively; and represent half the width and half the height , respectively; and represents the distance from the corners of the rocking block to the geometric center .
Assume that the rigid block has only two degrees of freedom: vertical and rotation. It can rotate around points L and R, but once it contacts the left or right spring supports, the contact point will only allow vertical movement. When the displacement is small, the rigid block is in continuous contact with the two supports L and R throughout the movement. If the mass of the rigid block is , when the vertical lifting of its side exceeds the displacement of the support spring due to the dead weight of the rigid block , separation occurs and the block is supported only on the other side. Therefore, a rigid block has four motion states:
- Complete contact at the L point and R point;
- Only contacts the L point;
- Only contacts the R point (corresponding to the motion state in Figure 2);
- The rigid block is separated from the two points and moves freely.
Since the rigid block will not be constrained after it is separated from both supports, it will be in a completely free motion state, so this situation should be avoided. Therefore, the first three motion states are mainly studied here.
In Housner’s model, energy dissipates when the rigid block contacts and collides with the rigid foundation, which will reduce the amplitude of each shaking until it finally stops. However, after the introduction of elastic bearings, energy dissipation will not occur automatically, and an energy dissipation mechanism must be introduced manually. Therefore, a new damper is introduced [5], whose damping constant . Tt is connected in a series at the top of spring and damper . Because of its large damping coefficient, the damper is essentially equivalent to a rigid link, which does not affect the response of the system, except in the case of collision. At the moment of impact, we assume that the rigid damper is locked, as shown in Figure 3b, for a short period of time , the damper is moved , then the rigid damper unlocks. During this period, the spring and damper are not activated, and the response is only affected by the rigid damper. Due to the effect of this damper, the velocity of point L is reduced. After , the impact buffer is unlocked, which has no impact on the response of the system thereafter.
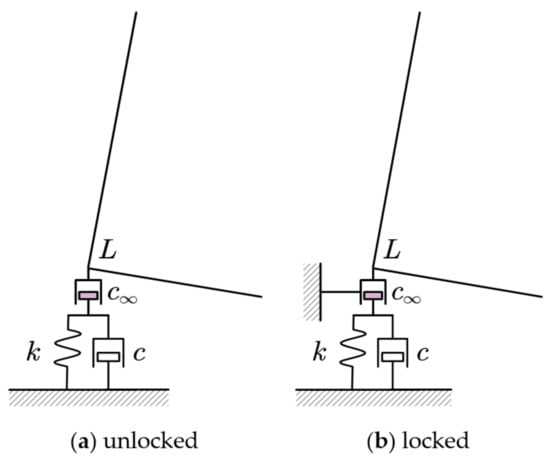
Figure 3.
Imposed impact damper.
Assume that and is a constant and the preset collision energy dissipation mechanism has a significant impact on the speed, but not on the displacement; then the calculation of the velocity relationship and energy loss is as seen in Equations (2) and (3).
where , , , correspond to the vertical speed and rotation angular speed before and after the collision, b is half of the width of the rigid block, and , correspond to the inertia moments of the rigid block around point O and point M, respectively. According to Psycharis and Jenning’s research, 1, is a parameter related to the physical characteristics of the rocking block itself and it can be calculated as Equation (4).
where , denoting the shape factor of the rigid block. For a rectangular block (), Equation (4) is then simplified to . Therefore, there is a limit overturning angle , as Equation (5).
When the rigid block is too short and wide, , , the rocking will not occur after collision, therefore the rocking block cannot be set too short.
In most practical cases, only a rocking motion occurs and neither support is separated from the frame, and the value of the coefficient of restitution is close to . Therefore, the rocking response is only related to the overturning angle and the frequency of the rigid block itself. The frequency can be calculated as Equation (6).
The spring support is assumed to be a viscoelastic Kelvin–Voigt model, that is, the spring stiffness and the damping coefficient of the viscous damper are defined as Equation (7).
The vertical frequency coefficient and damping coefficient both depend on the vertical stiffness of the supported elastic cushion. To facilitate the analysis, the scale factor is defined as Equation (8).
2.2. Motion Equation of Full Contact
When both ends of the rigid block are in contact with the spring, the force analysis is as shown in Figure 4.
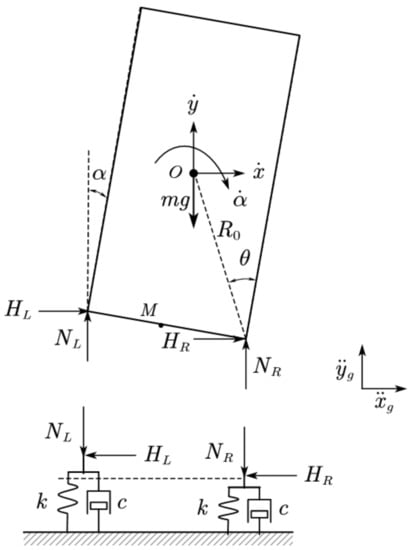
Figure 4.
Force analysis of a rigid block in full contact.
The corresponding motion equation is shown in Equation (9).
and are the horizontal and vertical accelerations of the center of the rigid block, respectively; and are the vertical reactions of the left and right bearings, respectively; and are the horizontal reaction force of the left and right supports, respectively; and are the time history of horizontal component and vertical component of ground acceleration, respectively; is the acceleration of gravity; and the other characters have the same meanings as above.
Assume that the vertical component of the bearing () is , and the upward displacement and velocity are and . The stress relationship is shown in Equation (10).
As the rigid block is in a full-contact state, both ends of the support shall meet the requirements . Since the bearing is assumed to be free from any tension, the first bearing will be separated from the rigid block when and .
Under the assumption above, the rigid block is not allowed to slide, so in fact, the whole system has only two degrees of freedom. For convenience, the vertical displacement and rotation angle of the center of the rigid block are selected. In addition, in the full-contact state, the displacement of a point on the rigid block is actually the superposition of the vertical displacement and the rotation displacement around the bottom center point M. According to the motion theorem of the center of mass, the expression of the displacement at the center of mass can be deduced as Equation (11).
Combined with Equations (7)–(11), the second-order nonlinear differential equation of a rigid block in full-contact motion is finally obtained as Equation (12).
2.3. Motion Equation of a Rigid Body with One Side Detached
As described in Section 2.2, when the upward displacement of the rigid block is greater than its sinking due to its own weight and upward velocity , the left side will be separated from the support, and only the right side will bear the force, as shown in Figure 5b. At this time, the dynamic equation can be obtained according to the force balance conditions shown in Equation (13).
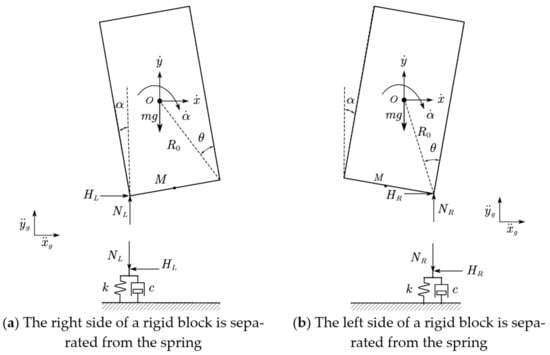
Figure 5.
Force analysis of a rigid block after separation on one side.
The corresponding displacement relation is shown in Equation (14).
Combining Equations (7), (8), (10), (13), and (14), the equation of motion after the left end separation is obtained. Through a similar process, the equation when the right end is separated can be obtained. By combining the two, the equation expression when only one side is stressed can be obtained as Equation (15).
The opposite signs in the equation denote that the rocking block rotates left or right.
2.4. Parameter Analysis
According to geometric analysis, the maximum rotation angle interval where the rigid block never separates during movement is , and the can be calculated as Equation (16).
The suffered unit excitation in the x-direction of the model is shown in Equation (17) and Figure 6.
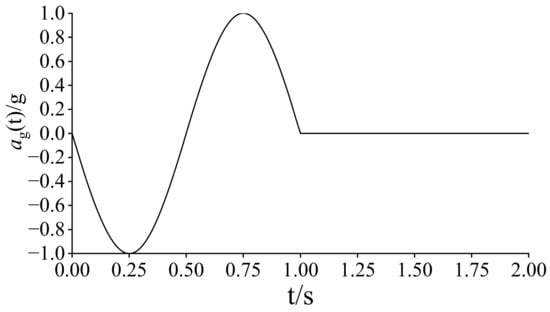
Figure 6.
Input excitation.
Suppose that the kinetic energy recovery coefficient of the rigid rocking block is always , the effects of different height width ratios (), different sizes (), different spring stiffness (), and different damping () on the response of the rigid block are analyzed. In order to facilitate the analysis, the clockwise rotation angle and vertical displacement of the two parameters of the response are normalized and divided by the overturning angle of the rigid block itself and the displacement generated under the self-weight condition, respectively.
The response of the structure within 10s is solved by numerical integration programmed in Matlab, and the response results are shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. In order to indicate the separation of one end of the rigid block from the spring, the rotation angle when one side of the rigid block is separated is marked in the figure (two brown horizontal solid lines). In Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, indicates the lifting of one side of the rigid rocking block, indicates that the rigid block rotates counterclockwise and inclines to the left, means that the rotation angle has exceeded the overturning angle of the rigid block itself, and the subsequent response becomes meaningless, so the overturning time occurs at the mark in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15.
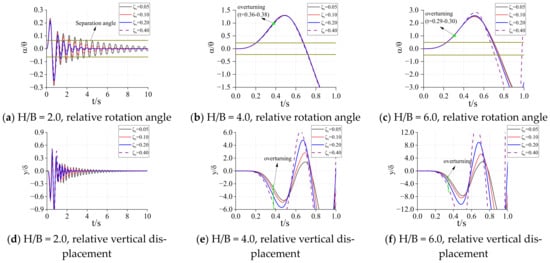
Figure 7.
= 1.0, = 10. Relative rotation angle and vertical displacement.
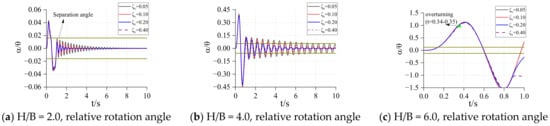
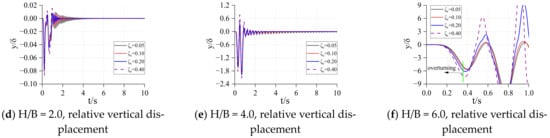
Figure 8.
= 1.0, = 20. Relative rotation angle and vertical displacement.
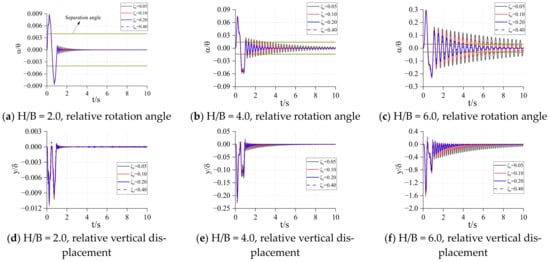
Figure 9.
= 1.0, = 40. Relative rotation angle and vertical displacement.
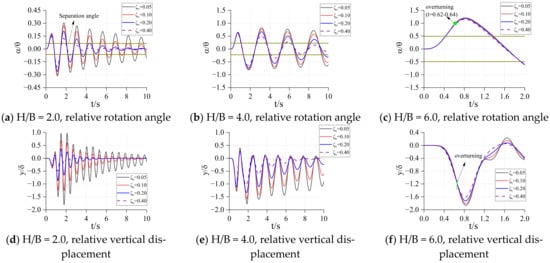
Figure 10.
= 5.0, = 10. Relative rotation angle and vertical displacement.
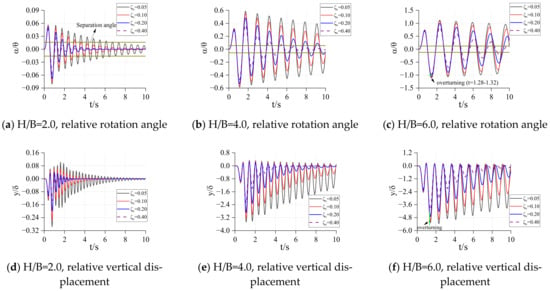
Figure 11.
= 5.0, = 20. Relative rotation angle and vertical displacement.
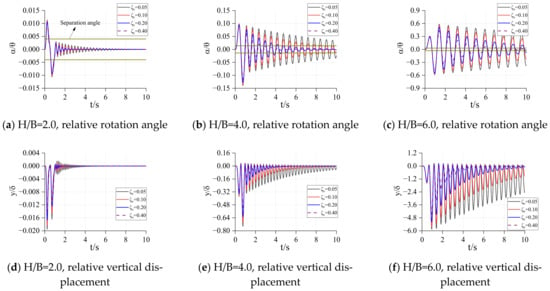
Figure 12.
= 5.0, = 40. Relative rotation angle and vertical displacement.
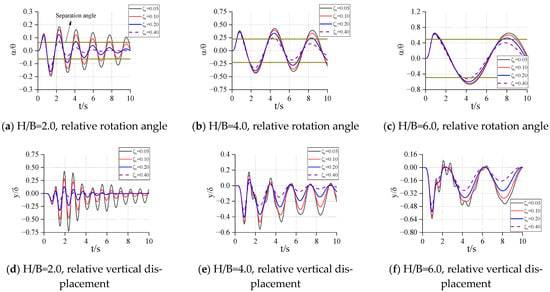
Figure 13.
= 10.0, = 10. Relative rotation angle and vertical displacement.
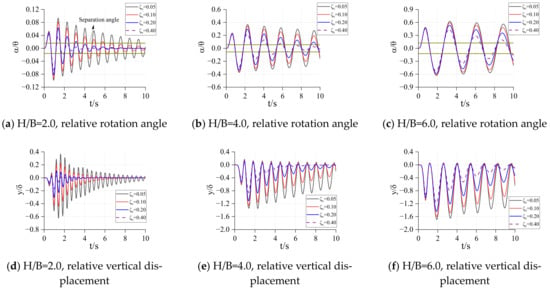
Figure 14.
= 10.0, = 20. Relative rotation angle and vertical displacement.
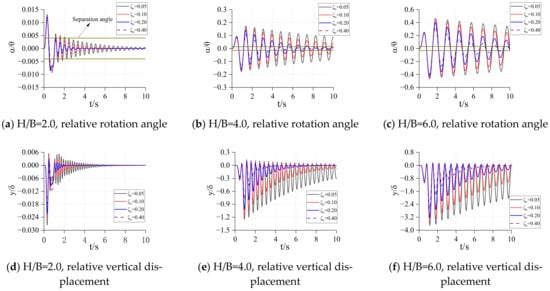
Figure 15.
= 10.0, = 40. Relative rotation angle and vertical displacement.
In Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, each figure is the response of the structure with different height–width ratios under a fixed rigid block size and spring stiffness. It can be found from these figures that when the size of the rigid block and the stiffness coefficient of the bottom spring are determined, its relative rotation response and relative vertical displacement response increase with the increase of the height–width ratio of the rigid block. When the size of the rigid block is big and the stiffness coefficient of the spring are small, the rigid block may overturn in a very short time under excitation. With the increase of the height–width ratio, the overturning time will be shorter and shorter, and the occurrence of this overturn does not change with the different damping of the structure. When the spring stiffness at the bottom of the structure is large, the overturning response may occur after the end of excitation ( in Figure 11).
From the comparison between the figures, when the height–width ratio of the rigid block and the stiffness coefficient of the spring are determined, it takes longer for the structure to become stable under the damping effect, as the size of the structure increases. When the height–width ratio is small, the response of the relative rotation angle and vertical displacement of the rigid block decrease with the increase of the size of the rigid block. When the height–width ratio is large, the response of the structure increases first, and then decreases as the size of the structure increases. This shows that for a structure with a larger height–width ratio, increasing the structure size may increase the response. In general, as the size of the structure increases, the possibility of overturning decreases and the occurrence time becomes later.
When the height–width ratio and size of the rigid block are determined, with the increase of the stiffness of the spring, the relative angular response and displacement response of the rigid block decrease. If the structure will overturn, the time point of overturning will be delayed. However, the subsequent response of the rigid block will gradually increase, or even exceed the initial response. At this time, the damping can well reduce the subsequent response amplitude of the rigid block. When the damping is large, the rigid block can be stabilized in a very short time.
3. Winkler Foundation Model
In order to consider the flexibility of the foundation under the rigid rocking block, the two-dimensional model of the Winkler foundation was used to simulate the foundation soil. The parameters of the Winkler foundation model are essentially the same as those of the two-spring models. The difference is that the bottom is replaced with a uniformly distributed damper and a spring in parallel. The stiffness and damping of each spring are and , respectively. The displacement generated under the dead weight of the rigid block is . The model diagram is shown in Figure 16.
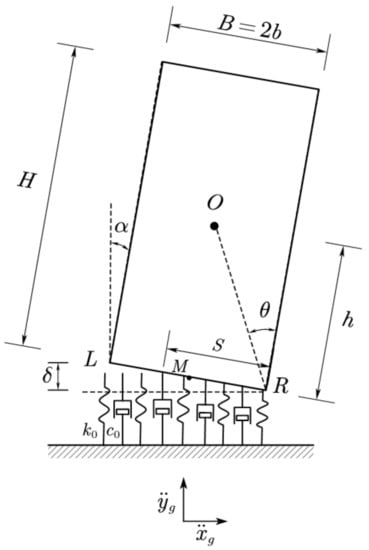
Figure 16.
Winkler foundation model.
Assuming that the displacement and rotation angle are relatively small, the motion equation under a full-contact state is shown in Equation (18).
where , denoting the moment of inertia of the rigid block to the bottom midpoint M. When the left end is raised, the motion equation is shown in Equation (19).
where
It can be seen from the equation above that the equations of motion of the system are uncoupled during the full contact process, and they can be solved directly. When one side of the rigid block is separated, the equations are coupled and highly nonlinear due to geometric complexity. The contact length with the bottom foundation changes with and , which makes the problem more complicated.
4. Rigid Rocking Body Model on Winkler Foundation
4.1. Combination of Two Models
The two-spring rigid rocking block model was combined with the Winkler foundation model. The foundation cushion cap plate acts as a rigid body on the Winkler foundation, and then the two-spring rigid rocking blocks act on the cushion cap plate. The combined model is shown in Figure 17.
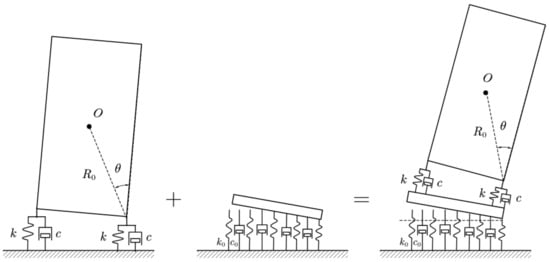
Figure 17.
Rigid rocking block model on a Winkler foundation.
When analyzing the motion response of the upper rigid rocking block, first take the upper part as a whole, input excitation from the Winkler foundation model to obtain the response result of the upper whole and the response of the bottom foundation plate , then input the response of the bottom foundation cap plate as a new excitation into the two-spring foundation model to obtain the response of the upper structure , and finally combine the two reactions to obtain the total response of the structure shown in Equation (20).
4.2. Equivalent 3D Frame to 2D Rigid Block
A two-dimensional rigid block model was used in the previous analysis; however, the actual structure is a three-dimensional frame. Therefore, the 3D model should be equivalent to the 2D rigid block before the case analysis. The schematic diagram of the equivalent process is shown in Figure 18.
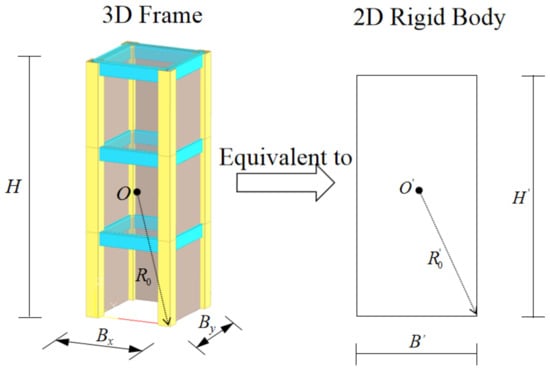
Figure 18.
Equivalence of 3D frames.
In the 2D and 3D models, and both denote the distance from the geometric center of the model to the contact point between the bottom of the structure and the foundation. The difference is that, since most of the frame is hollow, the mass cannot be expressed by the original apparent volume calculation and must be appropriately reduced, and the shape coefficient will also change. The plane of the frame is equivalent to the two-dimensional rigid body model, and the equivalent parameters can be calculated by Equations (21)–(23).
where refers to the mass of the ith component (beam, column, floor, infilled wall, etc.) of the frame; and respectively refer to the moment of inertia of the ith component around its shape-center and around point O; refers to the distance from point O to the shape-center of the ith component; refers to the space proportion; and refers to the volume of the ith component of the frame.
To simplify the calculation, assume that , the slab thickness is taken as 0.12 m, and the infill wall thickness is taken as 0.15 m. Table 1 shows the shape factor of the rigid block and the actual space proportions in several different cases, in which the parameter unit of the frame is m.

Table 1.
Shape factor and space ratio in several cases.
It can be seen that for common frame structures, the value is far less than the value of the rectangular block (), and the actual space of the structure accounts for less than 20% of the total space. Therefore, it is necessary to adjust the coefficient of the simplified two-dimensional block.
4.3. Analysis of Numerical Examples
On the basis of the foregoing derivation, this section will analyze the free response of the rocking structure and the response under the action of seismic waves. Considering the three-story and six-story rocking frame structures with a structural width of 4 m, the parameters after equivalence are shown in Table 2.

Table 2.
Equivalent parameters of the frame.
The height of the base cushion cap is taken as 1/20 of the main structure, and the scale factors are taken as 20, 40, and 60. The damping ratio of the selected system is 0.10, and the damping ratio of the soil is taken as 0.20.
4.3.1. Influence of Soil Elasticity and Structural Spring Stiffness on Structural Rotation Response
Under the conditions that the initial rotation angle of the structure is 0.10 rad, the response of the rotation angle and vertical displacement of the structure under different soil properties were studied. The results are shown in Figure 19 and Figure 20.
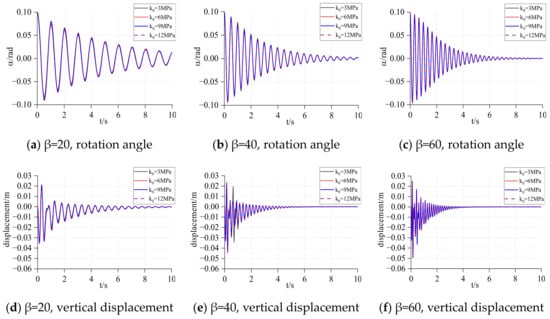
Figure 19.
Rotation and displacement of the three-story frame.
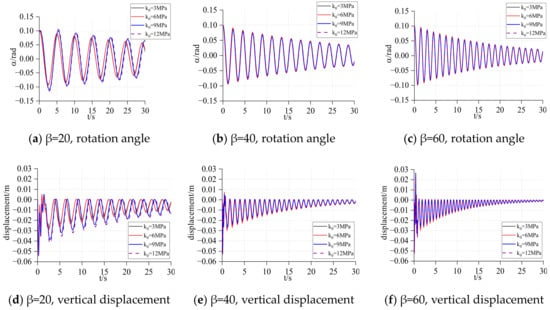
Figure 20.
Rotation and displacement of the six-story frame.
It can be found from Figure 19 that the rotation and vertical displacement responses of the three-story structure are affected very little by . However, in Figure 20, for a six-story structure, when the spring stiffness of the Winkler foundation is small (), the maximum response of the structure increases with the increase of , but with the increase of the base spring stiffness ( increase), almost no longer has a large impact on the structural rotation and vertical displacement response.
Comparing the different of the same structure, we can determine the rotation response of the structure or the vertical displacement response of the structure. Its impact on the initial response is very small, but it has a great impact on the subsequent response. With the increase of the spring stiffness at the bottom of the structure, the attenuation of the rotation response and the vertical displacement response of the structure becomes faster, but the maximum response of the vertical displacement of the structure also increases.
Comparing different structures in the same and , it can be found that the response attenuation speed of the three-story structure is obviously faster than that of the six-story structure, and the peak value of its rotation and vertical displacement response is also smaller than that of the six-story structure.
4.3.2. Effect of Different Bottom Spring Stiffness of a Rocking Structure on the Response of the Structure under Ground Motion
Since the influence of foundation stiffness on the structural response is not particularly obvious, one soil stiffness () was selected, and then the seismic record of TCU128 that occurred in Jiji, Taiwan in 1999 was input into the system. The time history of the motion and the corresponding Fourier spectrum is shown in Figure 21, taking 30–60 s for analysis.

Figure 21.
Time history and acceleration response spectrum of TCU128.
The overturning angles of the three-story and six-story frames are and , respectively. The response of the two frames under different base spring stiffness was studied, and the results are shown in Figure 22 and Figure 23.
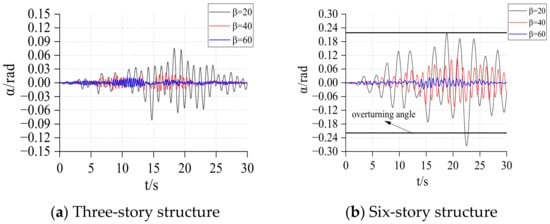
Figure 22.
Rotation response of frames under TCU128.
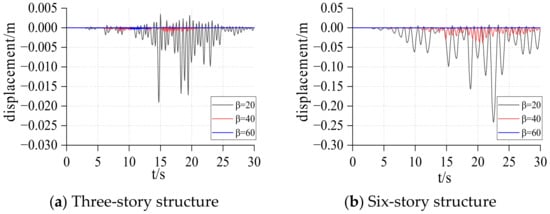
Figure 23.
Displacement response of frames under TCU128.
Comparing the responses of the three-story structure and six-story structure, it can be found that the response of the three-story structure is far less than that of the six-story structure, and with the increase of the base spring stiffness, the rotation and vertical displacement responses of the structure decrease significantly. This means that for a rocking structure, reducing the height of the structure or increasing the stiffness of the base spring will greatly reduce the response of the structure. Therefore, when weakening the connection between the bottom of the structure and the foundation, it is necessary to consider that the weakening degree should not be too large, otherwise it will produce a huge response. For the three-story structure, the structure will not overturn during the entire event, and the structure remains stable. For the six-story structure, when the spring stiffness at the base is small (), the six-story structure will overturn during the event, and increasing the spring stiffness of the base can effectively reduce the response of the structure, thus avoiding the occurrence of overturning.
5. Conclusions
In this paper, the theoretical model of the motion of the rigid rocking block is deduced and the parameters are analyzed based on the previous motion model of the rigid rocking block. After that, by combining with the Winkler foundation model, the motion equation of the rigid rocking block considering the flexibility of the foundation is derived, and the parameter analysis is conducted with the example of a three-story frame and a six-story frame. The main conclusions are as follows.
- (1)
- The damping of the spring support has little effect on the initial response of the rocking block but has a great effect on the subsequent response. The increase of damping can effectively reduce the subsequent response of the rocking structure.
- (2)
- The structure size and height–width ratio have great influence on the response of the rocking block, and increasing the size can effectively prevent the overturning of the rocking block.
- (3)
- When the spring stiffness of the base is small, the soil elastic coefficient has a greater impact on the higher story structure.
- (4)
- Under the same conditions, the attenuation speed of the response of the three-story is faster than that of the six-story’s.
- (5)
- For the three-story rocking frame model, the change of the soil elastic coefficient within a certain range () has no obvious effect on its initial rotation response. However, for the six-story model, when the spring stiffness of the base is small (), the larger is, the greater its response is. When becomes larger, the influence of becomes less obvious.
Author Contributions
Conceptualization, P.L. and Z.Z.; methodology, D.H. and P.L.; writing—original draft preparation, P.L. and D.H.; writing—review and editing, D.H. and P.L. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support from the National Natural Science Foundation of China (51978524) is highly appreciated.
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, T.T. Exploration on the Origin of Architectures Murals—Analysis on Geographical Features of Song, Liao and Jin Dynasty in Shanxi. Adv. Mater. Res. 2014, 838–841, 2870–2874. [Google Scholar] [CrossRef]
- Makris, N.; Vassiliou, M.F. Planar Rocking Response and Stability Analysis of an Array of Ffree-standing Columns Capped with a Freely Supported Rigid Beam. Earthq. Eng. 2012, 45, 31–39. [Google Scholar]
- Housner, G.W. The Behavior of Inverted Pendulum Structures During Earthquakes. B. Seismo. Soc. Am. 1963, 53, 403417. [Google Scholar] [CrossRef]
- Meek, J.W. Dynamic Response of Tipping Core Buildings. Earthq. Eng. Struct. Dyn. 1978, 6, 437–454. [Google Scholar] [CrossRef]
- Psycharis, I.N.; Jennings, P.C. Rocking of Slender Rigid Bodies Allowed to Uplift. Earthq. Eng. Struct. Dyn. 1983, 11, 57–76. [Google Scholar] [CrossRef]
- Chopra, A.K.; Yim, S.C.S. Simplified Earthquake Analysis of Structures with Foundation Uplift. J. Struct. Eng. 1985, 111, 906–930. [Google Scholar] [CrossRef]
- Taniguchi, T. Non—Linear Response Analyses of Rectangular Rigid Bodies Subjected to Horizontal and Vertical Ground Motion. Earthq. Eng. Struct. Dyn. 2002, 31, 1481–1500. [Google Scholar] [CrossRef]
- Jeong, M.Y.; Suzuki, K.; Yim, S.C.S. Chaotic Rocking Behavior of Freestanding Objects with Sliding Motion. J. Sound. Vib. 2003, 262, 1091–1112. [Google Scholar] [CrossRef]
- Kuraffia, Y.C.; Shen, Q. Posttensioned Hybrid Coupled Walls under Lateral Loads. J. Struct. Eng. 2004, 130, 297–309. [Google Scholar]
- Palmeri, A.; Makris, N. Response Analysis of Rigid Structures Rocking on Viscoelastic Foundation. Earthq. Eng. Struct. Dyn. 2008, 37, 1039–1063. [Google Scholar] [CrossRef]
- Veletsos, A.S.; Meek, J.W. Dynamic Behaviour of Building-foundation Systems. Earthq. Eng. Struct. Dyn. 1974, 3, 121–138. [Google Scholar] [CrossRef]
- Bielak, J. Dynamic Behaviour of Structures with Embedded Foundations. Earthq. Eng. Struct. Dyn. 1974, 3, 259–274. [Google Scholar] [CrossRef]
- Kim, S.; Stewart, J.P. Kinematic Soil-Structure Interaction from Strong Motion Recordings. J. Geotech. Geoenviron. Eng. 2003, 129, 323–335. [Google Scholar] [CrossRef]
- Mylonakis, G.; Nikolaou, S.; Gazetas, G. Footings under Seismic Loading: Analysis and Design Issues with Emphasis on Bridge Foundations. Soil Dyn. Earthq. Eng. 2006, 26, 824–853. [Google Scholar] [CrossRef]
- Veletsos, A.S.; Prasad, A.M.; Tang, Y. Design Approaches for Soil-Structure Interaction; NCEER: Buffalo, NY, USA, 1988. [Google Scholar]
- Chopra, A.K.; Gutierrez, J.A. Earthquake Response Analysis of Multistorey Buildings including Foundation Interaction. Earthq. Eng. Struct. Dyn. 1974, 3, 65–77. [Google Scholar] [CrossRef]
- Novak, M. Effect of Soil on Structural Response to Wind and Earthquake. Earthq. Eng. Struct. Dyn. 1974, 3, 79–96. [Google Scholar] [CrossRef]
- Constantinou, M.C.; Kneifat, M.C. Dynamics of Soil-base-isolated Structure Systems. J. Struct. Eng. 1988, 114, 211–221. [Google Scholar] [CrossRef]
- Hamza, G.; Pala, M. On the Resonance Effect by Dynamic Soil-structure Interaction: A Revelation Study. Nat. Hazards 2014, 72, 827–847. [Google Scholar]
- Mylonakis, G.; Gazetas, G. Seismic Soil-Structure Interaction: Beneficial or Detrimental. J. Earthq. Eng. 2000, 4, 277–301. [Google Scholar] [CrossRef]
- Lamb, H. On the Propagation of Tremors over the Surface of an Elastic Solid. Philo. Trans. Roy Soc. Ser. A 1904, 203, 1–42. [Google Scholar]
- Reissner, E. Stationäre, axialsymmetrische, durch eineschütte lndeMasse erregte Schwingungeneines homogenen elastischen Halbraumes. Ing. Archiv. 1936, 7, 381–396. [Google Scholar] [CrossRef]
- Parmelee, R.A. Building Foundation Interaction Effects. J. Eng. Mech. Div. 1967, 93, 131–152. [Google Scholar] [CrossRef]
- Clelland, B.M.; Focht, J.A. Soil Modulus for Laterally Loaded Piles. Transactions 1958, 123, 1049–1086. [Google Scholar]
- Yan, B.; Wang, Z.Q.; Wang, J.J. Review of Winkler Foundation Beam Model on Pile-soil Interaction Research Area. Build. Struct. 2011, 41, 1363–1368. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).