Parameters Identification of Solar PV Using Hybrid Chaotic Northern Goshawk and Pattern Search
Abstract
1. Introduction
2. Proposed Procedure
2.1. Northern Goshawk Optimization
| Algorithm 1. Pseudo-code of northern goshawk optimization algorithm. |
| Determine the NGO population size (N) and the number of iterations (T) |
| Initialization of the position of northern goshawk randomly based on Equation (1) |
| Calculate the objective function of the population |
| For t = 1:T |
| For I = 1:N |
| Phase 1: prey identification (exploration phase) |
| Select a random prey using Equation (4) |
| For j = 1:m |
| Calculate new status of the jth dimension using Equation (5) |
| End |
| Update the ith population member using Equation (6) |
| Phase 2: tail and chase operation (exploitation phase) |
| Update R using Equation (7) |
| For j = 1:m. |
| Calculate new status of the jth dimension using Equation (8) |
| End |
| Update the ith population member using Equation (9) |
| End |
| Update best candidate solution |
| End |
| Output best solution obtained by NGO |
2.2. Chaotic Northern Goshawk Optimization
2.3. Pattern Search (PS)
2.4. Chaotic Northern Goshawk Optimization—Pattern Search (CNGPS)
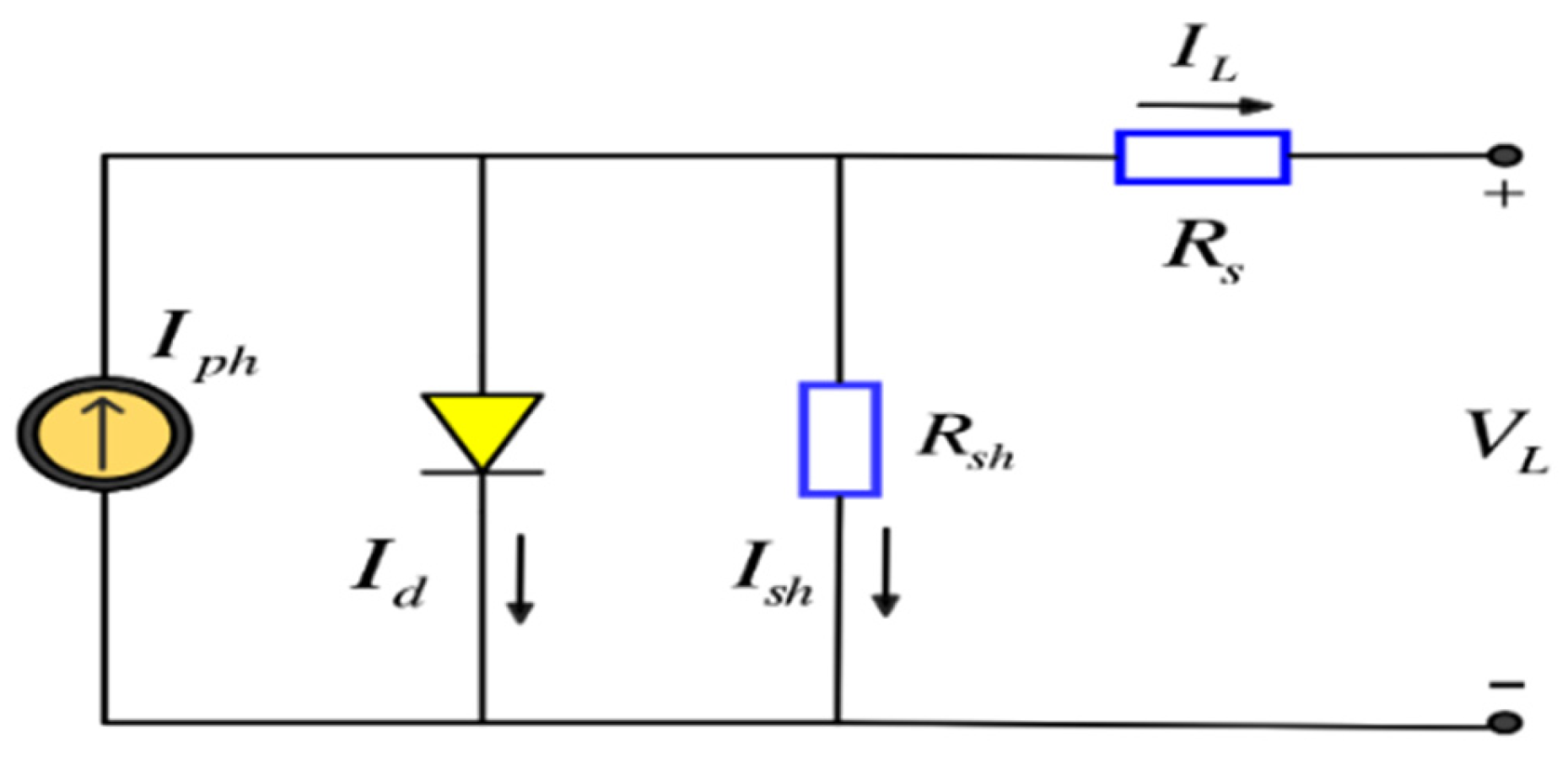
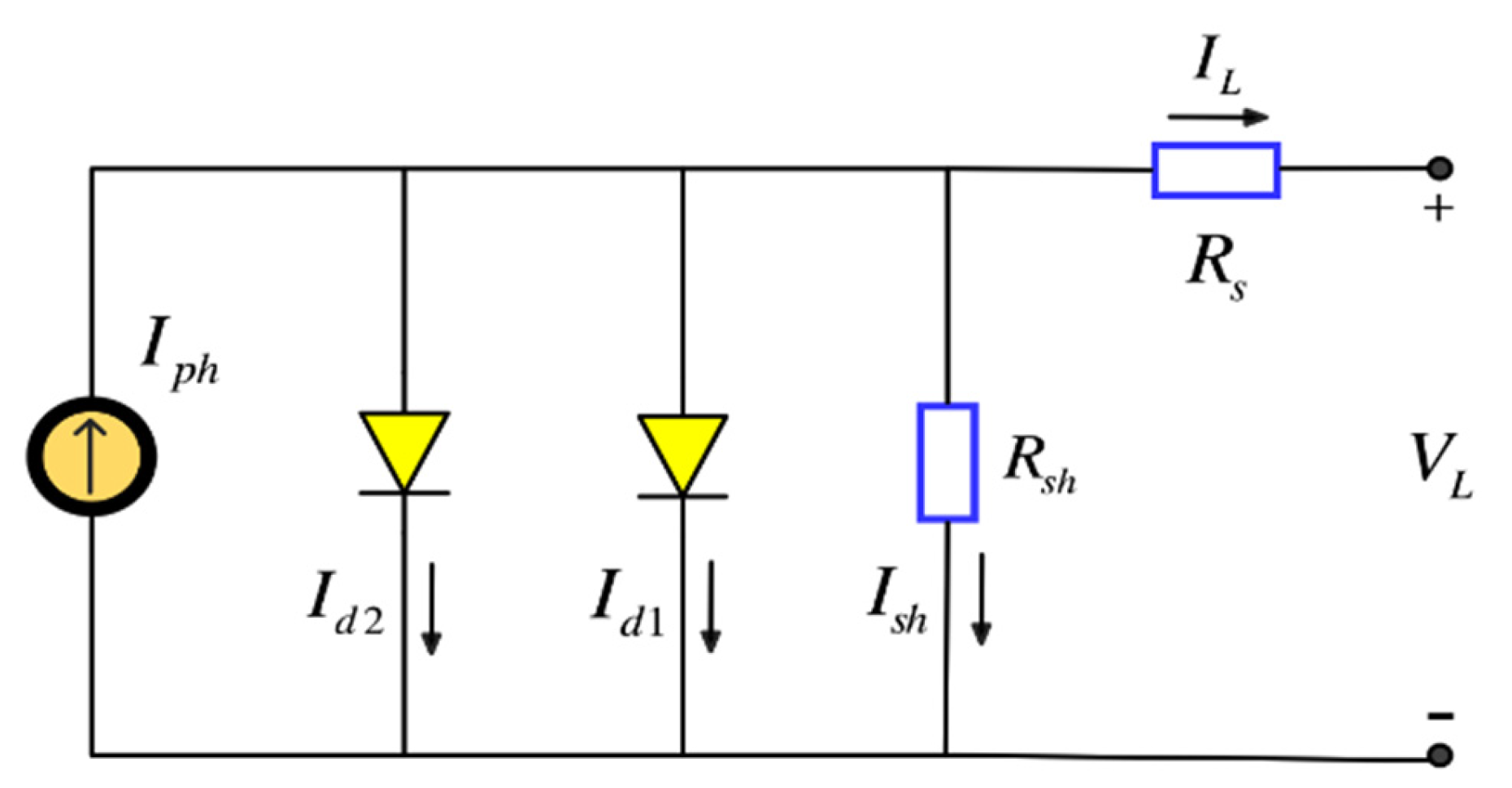
3. PV Models and Problem Formulation
3.1. SDM
3.2. DDM
3.3. TDM
3.4. Objective Function
- For SDM:
- For DDM:
- For TDM:
4. Results and Analysis
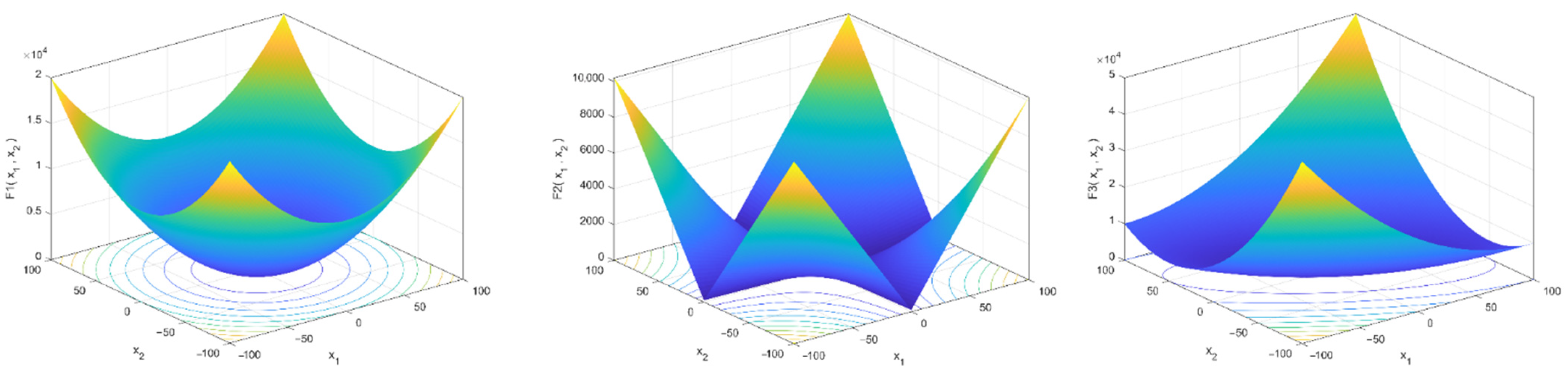
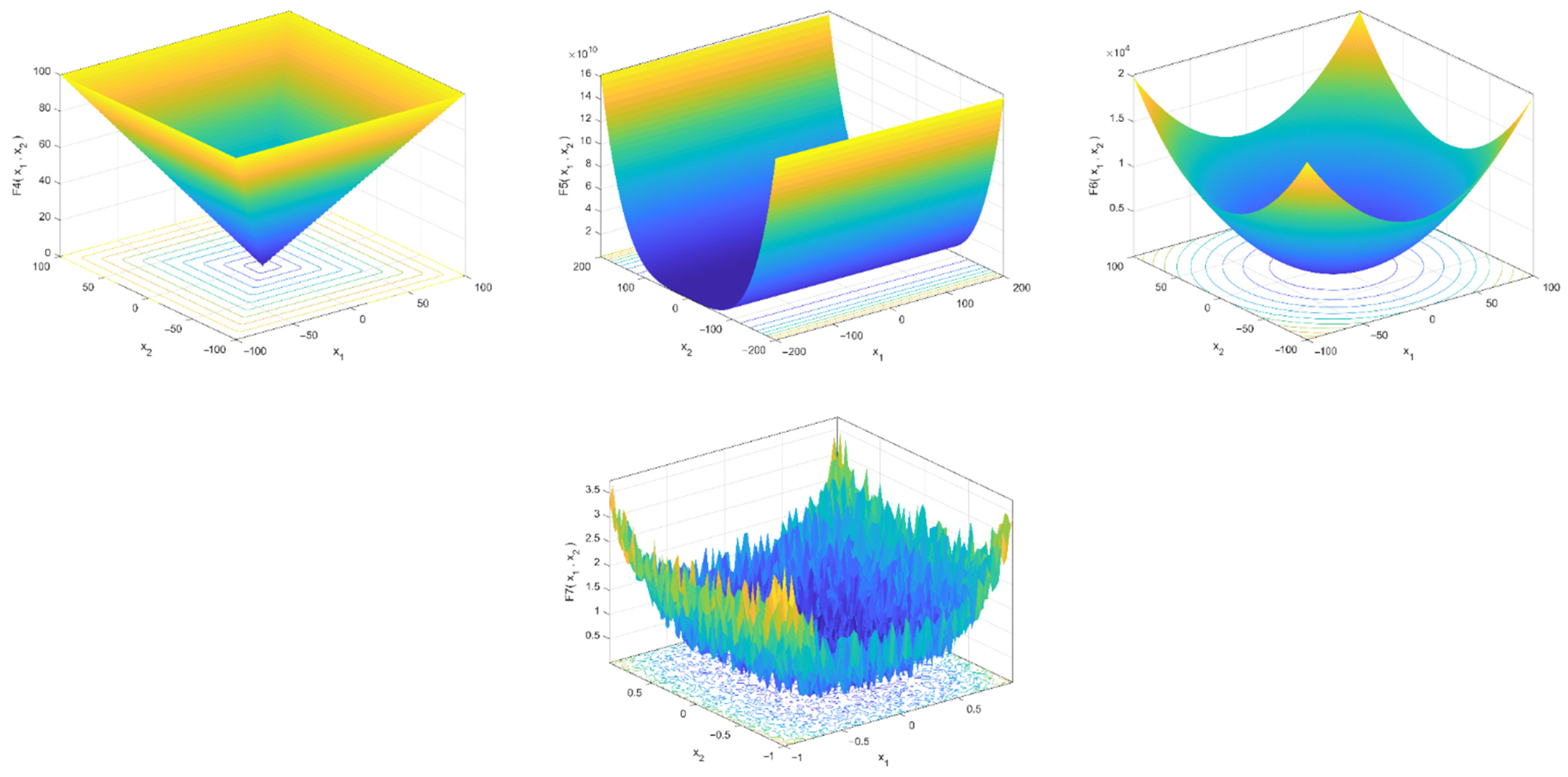
4.1. Proposed Method for Benchmark Functions
4.2. Simulation of CNGPS on Three Models
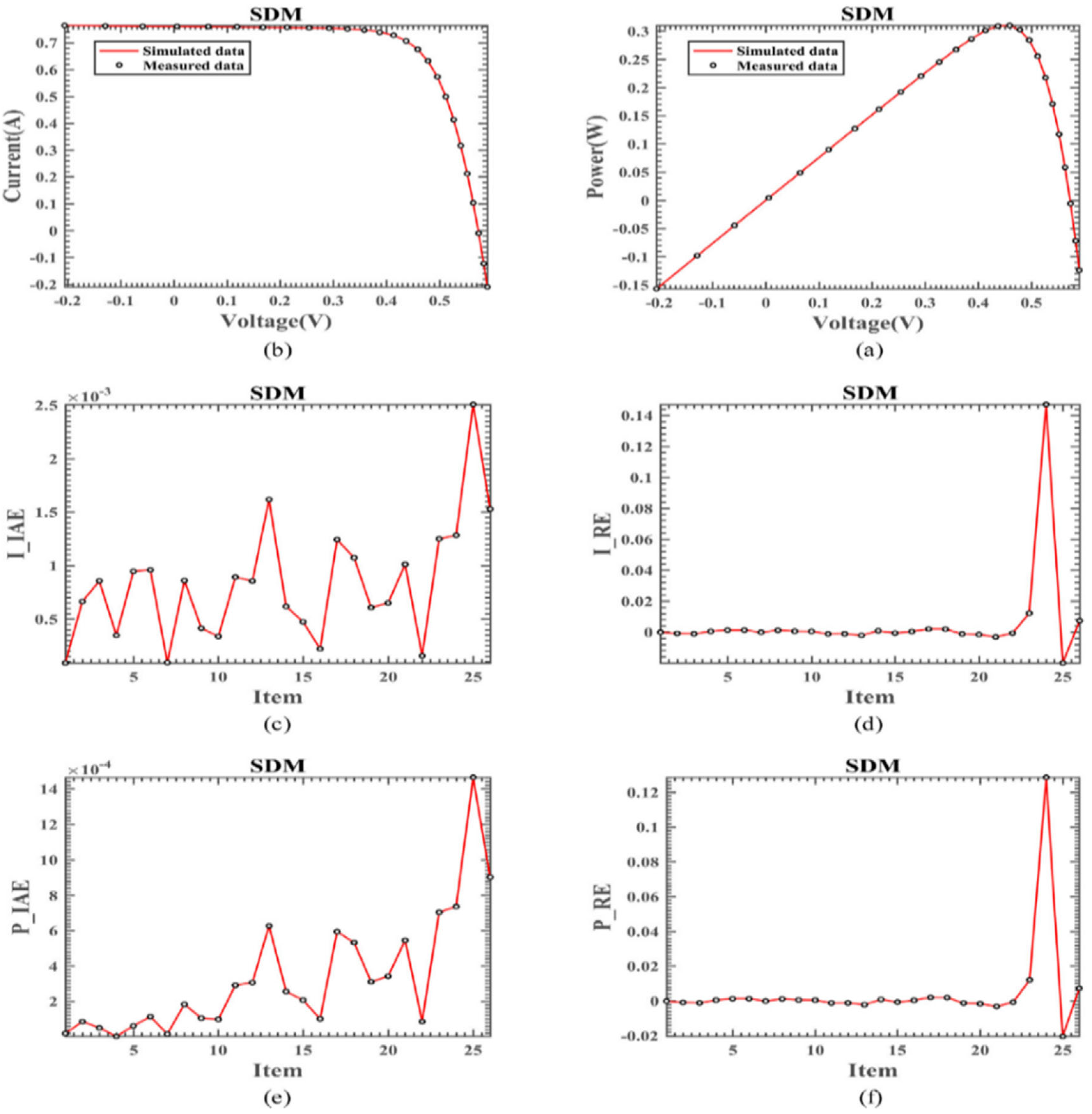
4.2.1. Results on the SDM
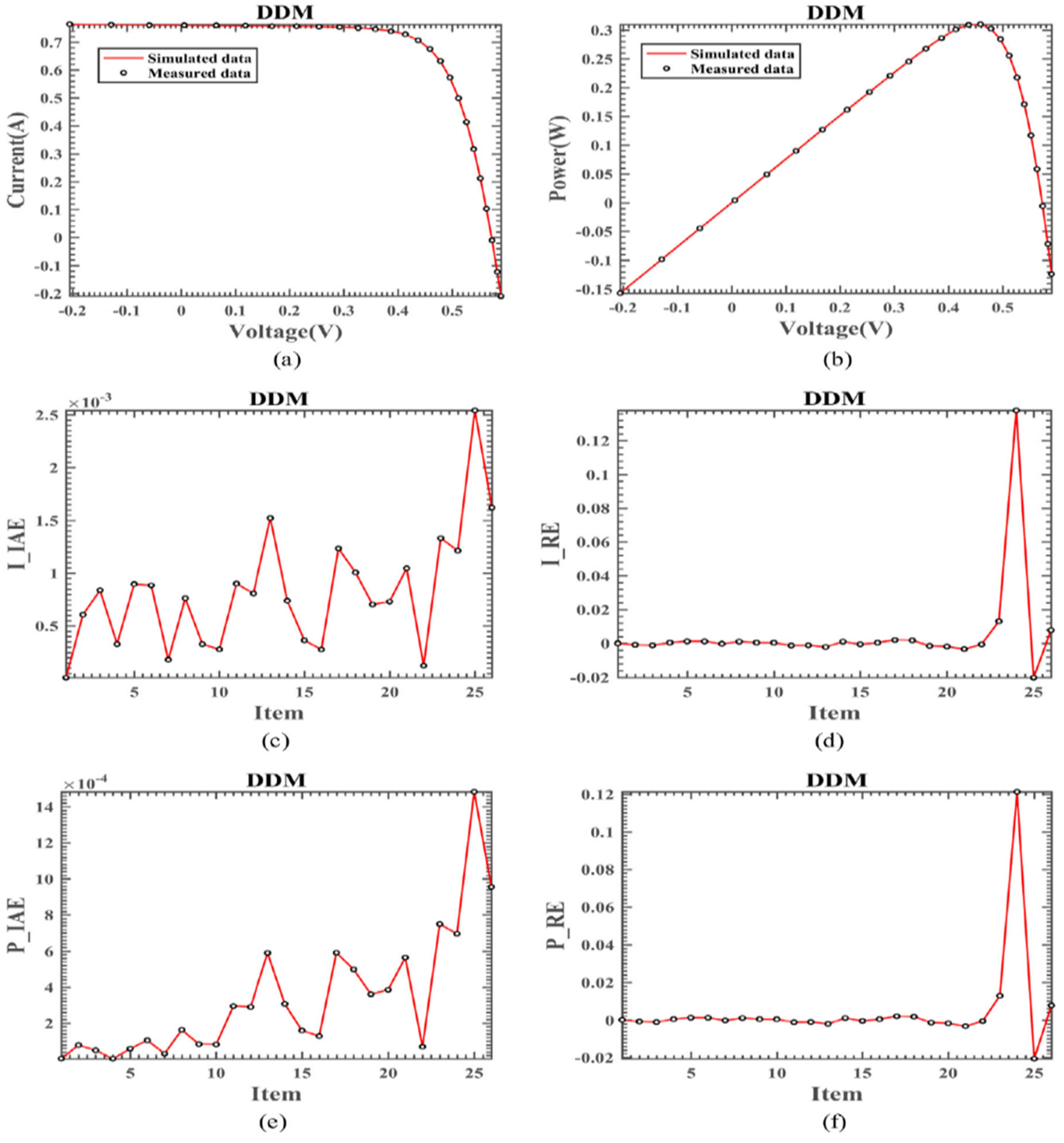
4.2.2. Results on the DDM
4.2.3. Experiment on TDM
4.2.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, B.; Yu, T.; Shu, H.; Zhang, Y.; Chen, J.; Sang, Y.; Jiang, L. Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renew. Energy 2017, 119, 577–589. [Google Scholar] [CrossRef]
- Oliva, D.; Cuevas, E.; Pajares, G. Parameter identification of solar cells using artificial bee colony optimization. Energy 2014, 72, 93–102. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.; Qu, B.; Chen, X.; Wang, H. Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Convers. Manag. 2017, 150, 742–753. [Google Scholar] [CrossRef]
- Siecker, J.; Kusakana, K.; Numbi, B. A review of solar photovoltaic systems cooling technologies. Renew. Sustain. Energy Rev. 2017, 79, 192–203. [Google Scholar] [CrossRef]
- Yao, S.; Yang, L.; Shi, S.; Zhou, Y.; Long, M.; Zhang, W.; Cai, S.; Huang, C.; Liu, T.; Zou, B. A Two-in-One Annealing Enables Dopant Free Block Copolymer Based Organic Solar Cells with over 16% Efficiency. Chin. J. Chem. 2023, 41, 672–678. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, L.; Cheng, S.; Lin, P.; Wu, Y.; Lin, W. Intelligent fault diagnosis of photovoltaic arrays based on optimized kernel extreme learning machine and I-V characteristics. Appl. Energy 2017, 204, 912–931. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Chen, H.; Jiao, S.; Wang, M.; Heidari, A.A.; Zhao, X. Parameters identification of photovoltaic cells and modules using diversification-enriched Harris hawks optimization with chaotic drifts. J. Clean. Prod. 2019, 244, 118778. [Google Scholar] [CrossRef]
- Yu, K.; Chen, X.; Wang, X.; Wang, Z. Parameters identification of photovoltaic models using self-adaptive teaching-learning-based optimization. Energy Convers. Manag. 2017, 145, 233–246. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; El-Shafie, A.; Eslami, M. A survey on meta-heuristic global optimization algorithms. Res. J. Appl. Sci. Eng. Technol. 2011, 3, 569–578. [Google Scholar]
- Khajehzadeh, M.; Taha, M.R.; El-Shafie, A.; Eslami, M. Search for critical failure surface in slope stability analysis by gravitational search algorithm. Int. J. Phys. Sci. 2011, 6, 5012–5021. [Google Scholar]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. PSS and TCSC Damping Controller Coordinated Design Using GSA. Energy Procedia 2012, 14, 763–769. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Efficient gravitational search algorithm for optimum design of retaining walls. Struct. Eng. Mech. 2013, 45, 111–127. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Damping controller design for power system oscillations using hybrid GA-SQP. Int. Rev. Electr. Eng. 2011, 6, 888–896. [Google Scholar]
- Eslami, M.; Shareef, H.; Mohamed, A. Optimization and coordination of damping controls for optimal oscillations damping in multi-machine power system. Int. Rev. Electr. Eng. 2011, 6, 1984–1993. [Google Scholar]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. A New Hybrid Firefly Algorithm for Foundation Optimization. Natl. Acad. Sci. Lett. 2013, 36, 279–288. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Multi-objective optimization of foundation using global-local gravitational search algorithm. Struct. Eng. Mech. 2014, 50, 257–273. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Multi-objective optimisation of retaining walls using hybrid adaptive gravitational search algorithm. Civ. Eng. Environ. Syst. 2013, 31, 229–242. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Optimal location of PSS using improved PSO with chaotic sequence. In Proceedings of the International Conference on Electrical, Control and Computer Engineering 2011 (InECCE), Kuantan, Malaysia, 21–22 June 2011; pp. 253–258. [Google Scholar]
- Zagrouba, M.; Sellami, A.; Bouaïcha, M.; Ksouri, M. Identification of PV solar cells and modules parameters using the genetic algorithms: Application to maximum power extraction. Sol. Energy 2010, 84, 860–866. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Perth, WA, Australia; Volume 4, pp. 1942–1948. [Google Scholar]
- Liang, J.; Ge, S.; Qu, B.; Yu, K.; Liu, F.; Yang, H.; Wei, P.; Li, Z. Classified perturbation mutation based particle swarm optimization algorithm for parameters extraction of photovoltaic models. Energy Convers. Manag. 2019, 203, 112138. [Google Scholar] [CrossRef]
- El-Naggar, K.; AlRashidi, M.; AlHajri, M.; Al-Othman, A. Simulated Annealing algorithm for photovoltaic parameters identification. Sol. Energy 2012, 86, 266–274. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Parameter identification for solar cell models using harmony search-based algorithms. Sol. Energy 2012, 86, 3241–3249. [Google Scholar] [CrossRef]
- Rajasekar, N.; Kumar, N.K.; Venugopalan, R. Bacterial Foraging Algorithm based solar PV parameter estimation. Sol. Energy 2013, 97, 255–265. [Google Scholar] [CrossRef]
- Awadallah, M.A. Variations of the bacterial foraging algorithm for the extraction of PV module parameters from nameplate data. Energy Convers. Manag. 2016, 113, 312–320. [Google Scholar] [CrossRef]
- Guo, L.; Meng, Z.; Sun, Y.; Wang, L. Parameter identification and sensitivity analysis of solar cell models with cat swarm optimization algorithm. Energy Convers. Manag. 2016, 108, 520–528. [Google Scholar] [CrossRef]
- Li, S.; Gu, Q.; Gong, W.; Ning, B. An enhanced adaptive differential evolution algorithm for parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 205, 112443. [Google Scholar] [CrossRef]
- Alam, D.; Yousri, D.; Eteiba, M. Flower Pollination Algorithm based solar PV parameter estimation. Energy Convers. Manag. 2015, 101, 410–422. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Shi, D.; He, Y. Parameter extraction of solar photovoltaic models using an improved whale optimization algorithm. Energy Convers. Manag. 2018, 174, 388–405. [Google Scholar] [CrossRef]
- Yang, X. Firefly Algorithms for Multimodal Optimization. Stoch. Algorithms Found. Appl. 2009, 5792, 169–178. [Google Scholar]
- Beigi, A.M.; Maroosi, A. Parameter identification for solar cells and module using a Hybrid Firefly and Pattern Search Algorithms. Sol. Energy 2018, 171, 435–446. [Google Scholar] [CrossRef]
- Sarjila, R.; Ravi, K.; Edward, J.B.; Kumar, K.S.; Prasad, A. Parameter Extraction of Solar Photovoltaic Modules Using Gravitational Search Algorithm. J. Electr. Comput. Eng. 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Long, W.; Cai, S.; Jiao, J.; Xu, M.; Wu, T. A new hybrid algorithm based on grey wolf optimizer and cuckoo search for parameter extraction of solar photovoltaic models. Energy Convers. Manag. 2019, 203, 112243. [Google Scholar] [CrossRef]
- Allam, D.; Yousri, D.; Eteiba, M. Parameters extraction of the three diode model for the multi-crystalline solar cell/module using Moth-Flame Optimization Algorithm. Energy Convers. Manag. 2016, 123, 535–548. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Gupta, J.; Nijhawan, P.; Ganguli, S. Parameter extraction of solar PV cell models using novel metaheuristic chaotic tunicate swarm algorithm. Int. Trans. Electr. Energy Syst. 2021, 31, e13244. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Noroozi, M.; Mohammadi, H.; Efatinasab, E.; Lashgari, A.; Eslami, M.; Khan, B. Golden Search Optimization Algorithm. IEEE Access 2022, 10, 37515–37532. [Google Scholar] [CrossRef]
- Gu, Z.; Xiong, G.; Fu, X. Parameter Extraction of Solar Photovoltaic Cell and Module Models with Metaheuristic Algorithms: A Review. Sustainability 2023, 15, 3312. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Seheimy, R.A.; Xiong, G.; Elattar, E.; Ginidi, A.R. Parameter identification of solar photovoltaic cell and module models via supply demand optimizer. Ain Shams Eng. J. 2022, 13, 101705. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubálovský, Š.; Trojovský, P. Northern Goshawk Optimization: A New Swarm-Based Algorithm for Solving Optimization Problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Dolan, E.D.; Lewis, R.M.; Torczon, V. On the Local Convergence of Pattern Search. SIAM J. Optim. 2003, 14, 567–583. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; El-Shafie, A. Reliability analysis of earth slopes using hybrid chaotic particle swarm optimization. J. Cent. South Univ. 2011, 18, 1626–1637. [Google Scholar] [CrossRef]
- El-Dabah, M.A.; El-Sehiemy, R.A.; Hasanien, H.M.; Saad, B. Photovoltaic model parameters identification using Northern Goshawk Optimization algorithm. Energy 2023, 262, 125522. [Google Scholar] [CrossRef]
- Olabi, A.G.; Rezk, H.; Abdelkareem, M.A.; Awotwe, T.; Maghrabie, H.M.; Selim, F.F.; Rahman, S.M.A.; Shah, S.K.; Zaky, A.A. Optimal Parameter Identification of Perovskite Solar Cells Using Modified Bald Eagle Search Optimization Algorithm. Energies 2023, 16, 471. [Google Scholar] [CrossRef]
- Beşkirli, A.; Dağ, İ. Parameter extraction for photovoltaic models with tree seed algorithm. Energy Rep. 2023, 9, 174–185. [Google Scholar] [CrossRef]
- Garip, Z. Parameters estimation of three-diode photovoltaic model using fractional-order Harris Hawks optimization algorithm. Optik 2023, 272, 170391. [Google Scholar] [CrossRef]
- Yaghoubi, M.; Eslami, M.; Noroozi, M.; Mohammadi, H.; Kamari, O.; Palani, S. Modified Salp Swarm Optimization for Parameter Estimation of Solar PV Models. IEEE Access 2022, 10, 110181–110194. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Y.; Zhang, Y.; Shang, W.-L.; Yang, Z.; Feng, W. Parameters identification of photovoltaic models using a differential evolution algorithm based on elite and obsolete dynamic learning. Appl. Energy 2022, 314, 118877. [Google Scholar] [CrossRef]
- Arandian, B.; Eslami, M.; Khalid, S.A.; Khan, B.; Sheikh, U.U.; Akbari, E.; Mohammed, A.H. An Effective Optimization Algorithm for Parameters Identification of Photovoltaic Models. IEEE Access 2022, 10, 34069–34084. [Google Scholar] [CrossRef]
- Yu, S.; Chen, Z.; Heidari, A.A.; Zhou, W.; Chen, H.; Xiao, L. Parameter identification of photovoltaic models using a sine cosine differential gradient based optimizer. IET Renew. Power Gener. 2022, 16, 1535–1561. [Google Scholar] [CrossRef]
- Eslami, M.; Akbari, E.; Sadr, S.T.S.; Ibrahim, B.F. A novel hybrid algorithm based on rat swarm optimization and pattern search for parameter extraction of solar photovoltaic models. Energy Sci. Eng. 2022, 10, 2689–2713. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, P.; Heidari, A.A.; Chen, H.; Turabieh, H.; Mafarja, M. Random reselection particle swarm optimization for optimal design of solar photovoltaic modules. Energy 2021, 239, 121865. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.; Liang, X.; Xu, M.; Tang, M.; Cai, S. Parameters estimation of photovoltaic models using a novel hybrid seagull optimization algorithm. Energy 2022, 249, 123760. [Google Scholar] [CrossRef]
- Abbassi, A.; Ben Mehrez, R.; Touaiti, B.; Abualigah, L.; Touti, E. Parameterization of photovoltaic solar cell double-diode model based on improved arithmetic optimization algorithm. Optik 2022, 253, 168600. [Google Scholar] [CrossRef]
- Bo, Q.; Cheng, W.; Khishe, M.; Mohammadi, M.; Mohammed, A.H. Solar photovoltaic model parameter identification using robust niching chimp optimization. Sol. Energy 2022, 239, 179–197. [Google Scholar] [CrossRef]
- Ridha, H.M.; Hizam, H.; Mirjalili, S.; Othman, M.L.; Ya’Acob, M.E.; Ahmadipour, M. Parameter extraction of single, double, and three diodes photovoltaic model based on guaranteed convergence arithmetic optimization algorithm and modified third order Newton Raphson methods. Renew. Sustain. Energy Rev. 2022, 162, 112436. [Google Scholar] [CrossRef]
- Song, S.; Wang, P.; Heidari, A.A.; Zhao, X.; Chen, H. Adaptive Harris hawks optimization with persistent trigonometric differences for photovoltaic model parameter extraction. Eng. Appl. Artif. Intell. 2022, 109, 104608. [Google Scholar] [CrossRef]
- Abbassi, A.; Ben Mehrez, R.; Bensalem, Y.; Abbassi, R.; Kchaou, M.; Jemli, M.; Abualigah, L.; Altalhi, M. Improved Arithmetic Optimization Algorithm for Parameters Extraction of Photovoltaic Solar Cell Single-Diode Model. Arab. J. Sci. Eng. 2022, 47, 10435–10451. [Google Scholar] [CrossRef]
- Yu, S.; Heidari, A.A.; Liang, G.; Chen, C.; Chen, H.; Shao, Q. Solar photovoltaic model parameter estimation based on orthogonally-adapted gradient-based optimization. Optik 2021, 252, 168513. [Google Scholar] [CrossRef]
- Kenward, R.E. Goshawk Hunting Behaviour, and Range Size as a Function of Food and Habitat Availability. J. Anim. Ecol. 1982, 51, 69–80. [Google Scholar] [CrossRef]
- AlRashidi, M.; AlHajri, M.; El-Naggar, K.; Al-Othman, A. A new estimation approach for determining the I–V characteristics of solar cells. Sol. Energy 2011, 85, 1543–1550. [Google Scholar] [CrossRef]
- Jordehi, A.R. Parameter estimation of solar photovoltaic (PV) cells: A review. Renew. Sustain. Energy Rev. 2016, 61, 354–371. [Google Scholar] [CrossRef]
- Niu, Q.; Zhang, H.; Li, K. An improved TLBO with elite strategy for parameters identification of PEM fuel cell and solar cell models. Int. J. Hydrogen Energy 2014, 39, 3837–3854. [Google Scholar] [CrossRef]
- Chen, X.; Yu, K.; Du, W.; Zhao, W.; Liu, G. Parameters identification of solar cell models using generalized oppositional teaching learning based optimization. Energy 2016, 99, 170–180. [Google Scholar] [CrossRef]






| Ref. | Objective Function | Algorithm | Type of Solar Cell | Remarks |
|---|---|---|---|---|
| [46] | RMSE | IMFOL | SDM DDM PV module | Appropriate levels of accuracy and robustness |
| [47] | RMSE | mBES | TDM | Low optimal fitness values |
| [48] | RMSE | TSA | PV module | Fast convergence, low fitness values |
| [49] | RMSE | FCHHHO | SDM DDM TDM | Superior performance, accuracy and robustness |
| [50] | RMSE | MSSA | SDM DDM PV module | Improved performance, avoiding local optimum |
| [51] | RMSE | DOLADE | SDM DDM PV Module | Great competition in terms of accuracy, reliability, and computational efficiency |
| [52] | RMSE | ITSA | SDM DDM PV Module | Higher convergence accuracy, better stability |
| [53] | RMSE | SDGBO | SDM DDM TDM PV Module | Enhance performance, capability to identify unknown parameters of PV models |
| [54] | RMSE | ARSO | SDM DDM PV Module | Accuracy, reliability, and convergence speed |
| [55] | RMSE | PSOCS | SDM DDM PV Module | High accuracy, enhanced exploration performance |
| [56] | RMSE SIAE | HSOA | SDM DDM PV module | Superior solution quality, convergence and reliability |
| [57] | RMSE NRMSD | IAOA | DDM | High level of reliability, accuracy, and effectiveness |
| [58] | RMSE | RN-ChOA | SDM DDM TDM PV Module | Better performance in estimating parameters of PV model |
| [59] | RMSE | GCAOAEmNR | SDM DDM TDM | Accuracy, stability, and convergence rate |
| [60] | RMSE | ADHHO | SDM DDM TDM PV Module | Proposed model can reasonably simulate output performance of PV and can be used as trustworthy method for extraction of unknown parameters of solar PV systems |
| [61] | RMSE NRMSD | IAOA | SDM | High level of reliability, accuracy, and effectiveness |
| [62] | RMSE | OLGBO | SDM DDM TDM PV Module | The OLGBO can be a fast, promising, reliable, and feasible optimization method for dealing with unknown parameter identification problems in PV models |
| Function | Name | Range | n (Dim) | |
|---|---|---|---|---|
| Sphere function | 0 | 30 | ||
| Schwefel’s problem 2.22 | 0 | 30 | ||
| Schwefel’s problem 1.2 | 0 | 30 | ||
| Schwefel’s problem 2.22 | 0 | 30 | ||
| Generalized Rosenbrock’s function | 0 | 30 | ||
| Step function | 0 | 30 | ||
| Quartic function with noise | 0 | 30 |
| Function | Name | Range | n (Dim) | |
|---|---|---|---|---|
| Generalized Schwefel’s problem 2.26 | 428.9829 × n | 30 | ||
| Generalized Rastrigin’s function | 0 | 30 | ||
| 0 | 30 | |||
| Ackley’s function | 0 | 30 | ||
| Generalized penalized function | 0 | 30 | ||
| Generalized penalized function | 0 | 30 |
| F | Index | CNGPS | NGO | PSO | FA | MVO | SSA | TSA |
|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 0.00 | 2.42 × 10−97 | 4.98 × 10−9 | 7.11 × 10−3 | 2.81 × 10−1 | 3.29 × 10−7 | 8.31 × 10−56 |
| Std. | 0.00 | 7.22 × 10−97 | 1.40 × 10−8 | 3.21 × 10−3 | 1.11 × 10−1 | 5.92 × 10−7 | 1.02 × 10−58 | |
| F2 | Mean | 0.00 | 1.16 × 10−52 | 7.29 × 10−4 | 4.34 × 10−1 | 3.96 × 10−1 | 1.9111 | 8.36 × 10−35 |
| Std. | 0.00 | 2.55 × 10−52 | 1.84 × 10−3 | 1.84 × 10−1 | 1.41 × 10−1 | 1.6142 | 9.86 × 10−35 | |
| F3 | Mean | 0.00 | 7.84 × 10−81 | 1.40 × 10 | 1.66 × 103 | 4.31 × 10 | 1.50 × 103 | 1.51 × 10−14 |
| Std. | 0.00 | 3.49 × 10−80 | 7.13 | 6.72 × 102 | 8.97 | 707.05 | 6.55 × 10−14 | |
| F4 | Mean | 0.00 | 4.57 × 10−46 | 6.00 × 10−1 | 1.11 × 10−1 | 8.80 × 10−1 | 2.44 × 10−5 | 1.95 × 10−5 |
| Std. | 0.00 | 9.98 × 10−46 | 1.72 × 10−1 | 4.75 × 10−2 | 2.50 × 10−1 | 1.89 × 10−5 | 4.49 × 10−4 | |
| F5 | Mean | 7.22 × 10−8 | 2.80 × 10 | 4.93 × 10 | 7.97 × 10 | 1.18 × 102 | 136.56 | 28.4 |
| Std. | 0.00 | 2.42 × 10−97 | 4.98 × 10−9 | 7.11 × 10−3 | 2.81 × 10−1 | 3.29 × 10−7 | 8.31 × 10−56 | |
| F6 | Mean | 0.00 | 7.22 × 10−97 | 1.40 × 10−8 | 3.21 × 10−3 | 1.11 × 10−1 | 5.92 × 10−7 | 1.02 × 10−58 |
| Std. | 0.00 | 1.16 × 10−52 | 7.29 × 10−4 | 4.34 × 10−1 | 3.96 × 10−1 | 1.9111 | 8.36 × 10−35 | |
| F7 | Mean | 0.00 | 2.55 × 10−52 | 1.84 × 10−3 | 1.84 × 10−1 | 1.41 × 10−1 | 1.6142 | 9.86 × 10−35 |
| Std. | 0.00 | 7.84 × 10−81 | 1.40 × 10 | 1.66 × 103 | 4.31 × 10 | 1.50 × 103 | 1.51 × 10−14 |
| Index | CNGPS | NGO | PSO | FA | MVO | SSA | TSA | |
| F8 | Mean | –1.25× 104 | –1.01 × 104 | –6.01 × 103 | –5.85 × 103 | –6.92 × 103 | –7.46 × 103 | –7.89 × 103 |
| Std. | 0.00 | 1.70 × 103 | 1.30 × 103 | 1.61 × 103 | 9.19 × 102 | 634.67 | 599.26 | |
| F9 | Mean | 0.00 | 0.00 | 4.72 × 10 | 1.51 × 10 | 1.01 × 102 | 55.45 | 151.45 |
| Std. | 0.00 | 0.00 | 1.03 × 10 | 1.25 × 10 | 1.89 × 10 | 18.27 | 35.87 | |
| F10 | Mean | 8.88 × 10−16 | 8.77 × 10−16 | 3.86 × 10−2 | 4.58 × 10−2 | 1.15 | 2.84 | 2.409 |
| Std. | 0.00 | 0.00 | 2.11 × 10−1 | 1.20 × 10−2 | 7.87 × 10−1 | 6.58 × 10−1 | 1.392 | |
| F11 | Mean | 0.00 | 0.00 | 5.50 × 10−3 | 4.23 × 10−3 | 5.74 × 10−1 | 2.29 × 10−1 | 0.0077 |
| Std. | 0.00 | 0.00 | 7.39 × 10−3 | 1.29 × 10−3 | 1.12 × 10−1 | 1.29 × 10−1 | 0.0057 | |
| F12 | Mean | 1.57 × 10−32 | 1.25 × 10−1 | 1.05 × 10−2 | 3.13 × 10−4 | 1.27 | 6.82 | 6.373 |
| Std. | 2.88 × 10−48 | 5.41 × 10−2 | 2.06 × 10−2 | 1.76 × 10−4 | 1.02 | 2.72 | 3.458 | |
| F13 | Mean | 1.35 × 10−32 | 1.99 | 4.03 × 10−1 | 2.08 × 10−3 | 6.60 × 10−2 | 21.31 | 2.897 |
| Std. | 2.95 × 10−48 | 2.51 × 10−1 | 5.39 × 10−1 | 9.62 × 10−4 | 4.33 × 10−2 | 16.99 | 0.643 |
| Parameter | Lower Limit | Upper Limit |
|---|---|---|
| Iph(A) | 0 | 1 |
| Isd1, Isd2, Isd3, Isd (μA) | 0 | 1 |
| Rs(Ω) | 0 | 0.5 |
| Rsh(Ω) | 0 | 100 |
| n1, n2, n3,n | 1 | 2 |
| Algorithm | Max | Min | Mean | Std |
|---|---|---|---|---|
| CNGPS | 9.86027 × 10−4 | 9.86021 × 10−4 | 9.86022 × 10−4 | 1.12317 × 10−9 |
| NGO | 1.56519 × 10−3 | 9.88767 × 10−4 | 1.19734 × 10−3 | 1.59523 × 10−4 |
| TSA | 1.45946 × 10−3 | 9.86126 × 10−4 | 1.08655 × 10−3 | 1.25814 × 10−4 |
| SSA | 2.45685 × 10−3 | 1.02799 × 10−3 | 2.37701 × 10−3 | 1.70656 × 10−4 |
| PSO | 1.45946 × 10−3 | 9.90726 × 10−4 | 1.08655 × 10−3 | 1.25814 × 10−4 |
| MVO | 1.30477 × 10−2 | 1.63882 × 10−3 | 3.66904 × 10−3 | 2.71439 × 10−3 |
| FA | 1.80225 × 10−3 | 1.02787 × 10−3 | 1.34978 × 10−3 | 1.91189 × 10−4 |
| Method | Iph (A) | Isd (A) | Rs (Ω) | Rsh (Ω) | n | RMSE | Sig |
|---|---|---|---|---|---|---|---|
| CNGPS | 0.760775 | 3.23021 × 10−7 | 0.0363771 | 53.7185 | 1.48118 | 9.86021× 10−4 | ∼ |
| NGO | 0.760776 | 3.22978 × 10−7 | 0.0363775 | 53.7101 | 1.48117 | 9.88767 × 10−4 | + |
| TSA | 0.760775 | 3.23021 × 10−7 | 0.0363771 | 53.7186 | 1.48118 | 9.86126 × 10−4 | + |
| SSA | 0.760980 | 3.21318 × 10−7 | 0.0362752 | 49.1335 | 1.48078 | 1.02799 × 10−3 | + |
| PSO | 0.770684 | 7.78089 × 10−7 | 0.0358563 | 30.4120 | 1.57304 | 9.90726 × 10−4 | + |
| MVO | 0.760833 | 3.16023 × 10−7 | 0.0364796 | 53.0828 | 1.47898 | 1.63882 × 10−3 | + |
| FA | 0.760776 | 3.19527 × 10−7 | 0.0364149 | 53.4137 | 1.48009 | 1.02787 × 10−3 | + |
| Item | Measured Data | Simulated Current Data | Simulated Power Data | ||||
|---|---|---|---|---|---|---|---|
| V (V) | I (A) | Isim (A) | IAE_I (A) | P (W) | Psim (W) | IAE_P (W) | |
| 1 | −0.26 | 0.7640 | 0.764088 | 8.7704 × 10−5 | −0.15716 | −0.1571728 | 1.8041 × 10−5 |
| 2 | −0.13 | 0.7620 | 0.762663 | 6.6309 × 10−4 | −0.09838 | −0.0984598 | 8.5604 × 10−5 |
| 3 | −0.06 | 0.7605 | 0.761355 | 8.5531 × 10−4 | −0.04472 | −0.0447677 | 5.0292 × 10−5 |
| 4 | 0.0057 | 0.7605 | 0.760154 | 3.4601 × 10−4 | 0.004335 | 0.0043329 | 1.9723 × 10−6 |
| 5 | 0.0646 | 0.7600 | 0.759055 | 9.4479 × 10−4 | 0.049096 | 0.0490350 | 6.1034 × 10−5 |
| 6 | 0.1185 | 0.7590 | 0.758042 | 9.5765 × 10−4 | 0.089942 | 0.0898280 | 1.1348 × 10−4 |
| 7 | 0.1678 | 0.7570 | 0.757092 | 9.1654 × 10−5 | 0.127025 | 0.1270400 | 1.5380 × 10−5 |
| 8 | 0.2132 | 0.7570 | 0.756141 | 8.5864 × 10−4 | 0.161392 | 0.1612093 | 1.8306 × 10−4 |
| 9 | 0.2545 | 0.7555 | 0.755087 | 4.1313 × 10−4 | 0.192275 | 0.1921696 | 1.0514 × 10−4 |
| 10 | 0.2924 | 0.7540 | 0.753664 | 3.3612 × 10−4 | 0.220470 | 0.2203713 | 9.8282 × 10−5 |
| 11 | 0.3269 | 0.7505 | 0.751391 | 8.9097 × 10−4 | 0.245338 | 0.2456297 | 2.9126 × 10−4 |
| 12 | 0.3585 | 0.7465 | 0.747354 | 8.5385 × 10−4 | 0.267620 | 0.2679264 | 3.0611 × 10−4 |
| 13 | 0.3873 | 0.7385 | 0.740117 | 1.6172 × 10−3 | 0.286021 | 0.2866474 | 6.2635 × 10−4 |
| 14 | 0.4137 | 0.7280 | 0.727382 | 6.1777 × 10−4 | 0.301174 | 0.3009180 | 2.5557 × 10−4 |
| 15 | 0.4373 | 0.7065 | 0.706973 | 4.7265 × 10−4 | 0.308952 | 0.3091591 | 2.0669 × 10−4 |
| 16 | 0.4590 | 0.6755 | 0.675280 | 2.1985 × 10−4 | 0.310055 | 0.3099536 | 1.0091 × 10−4 |
| 17 | 0.4784 | 0.6320 | 0.630758 | 1.2417 × 10−3 | 0.302349 | 0.3017548 | 5.9404 × 10−4 |
| 18 | 0.4960 | 0.5730 | 0.571928 | 1.0716 × 10−3 | 0.284208 | 0.2836765 | 5.3153 × 10−4 |
| 19 | 0.5119 | 0.4990 | 0.499607 | 6.0702 × 10−4 | 0.255438 | 0.2557488 | 3.1073 × 10−4 |
| 20 | 0.5265 | 0.4130 | 0.413649 | 6.4879 × 10−4 | 0.217445 | 0.2177861 | 3.4159 × 10−4 |
| 21 | 0.5398 | 0.3165 | 0.317510 | 1.0101 × 10−3 | 0.170847 | 0.1713920 | 5.4526 × 10−4 |
| 22 | 0.5521 | 0.2120 | 0.212155 | 1.5494 × 10−4 | 0.117045 | 0.1171307 | 8.5542 × 10−5 |
| 23 | 0.5633 | 0.1035 | 0.102251 | 1.2487 × 10−3 | 0.058302 | 0.0575982 | 7.0339 × 10−4 |
| 24 | 0.5736 | −0.0100 | −0.008718 | 1.2825 × 10−3 | −0.005736 | −0.0050004 | 7.3562 × 10−4 |
| 25 | 0.5833 | −0.1230 | −0.125507 | 2.5074 × 10−3 | −0.071746 | −0.0732085 | 1.4626 × 10−3 |
| 26 | 0.5900 | −0.2100 | −0.208472 | 1.5277 × 10−3 | −0.123900 | −0.1229987 | 9.0133 × 10−4 |
| Algorithm | Max | Min | Mean | Std |
|---|---|---|---|---|
| CNGPS | 9.87761 × 10−4 | 9.82508 × 10−4 | 9.85251 × 10−4 | 1.27917 × 10−6 |
| NGO | 2.43158 × 10−3 | 9.85467 × 10−4 | 1.53577 × 10−3 | 4.15711 × 10−4 |
| TSA | 9.31141 × 10−3 | 1.73608 × 10−3 | 4.25210 × 10−3 | 2.31125 × 10−3 |
| SSA | 1.43838 × 10−3 | 9.83532 × 10−4 | 1.13956 × 10−3 | 1.78691 × 10−4 |
| PSO | 2.48306 × 10−3 | 1.06254 × 10−3 | 1.47935 × 10−3 | 3.01999 × 10−4 |
| MVO | 1.68606 × 10−3 | 9.89404 × 10−4 | 1.15083 × 10−3 | 1.88651 × 10−4 |
| FA | 1.99227 × 10−3 | 9.83832 × 10−4 | 1.05121 × 10−3 | 1.90533 × 10−4 |
| Algorithm | Iph(A) | Isd1(A) | Rs(Ω) | Rsh(Ω) | n1 | Isd2(A) | n2 | RSME | Sig |
| CNGPS | 0.76078 | 6.9844 × 10−7 | 0.036715 | 55.370 | 1.9999 | 2.3182 × 10−7 | 1.4535 | 9.82508 × 10−4 | ∼ |
| NGO | 0.76047 | 3.4174 × 10−7 | 0.037050 | 58.052 | 1.9101 | 2.3812 × 10−7 | 1.4546 | 9.85467 × 10−4 | + |
| TSA | 0.71684 | 1.0000 × 10−6 | 0.036840 | 84.676 | 2.0000 | 5.8794 × 10−7 | 1.5439 | 1.73608 × 103 | + |
| SSA | 0.76083 | 2.1636 × 10−7 | 0.036828 | 54.557 | 1.4475 | 6.4258 × 10−7 | 1.9525 | 9.83532 × 10−4 | + |
| PSO | 0.76084 | 6.5779 × 10−7 | 0.033321 | 84.745 | 1.5563 | 1.8922 × 10−10 | 1.8273 | 1.06254 × 10−3 | + |
| MVO | 0.76083 | 5.7427 × 10−7 | 0.036739 | 55.185 | 1.9097 | 2.1647 × 10−7 | 1.4435 | 9.89404 × 10−4 | + |
| FA | 0.76035 | 2.5315 × 10−7 | 0.036842 | 53.800 | 1.4654 | 6.9214 × 10−8 | 1.6940 | 9.83832 × 10−4 | + |
| Item | Measured Data | Simulated Current Data | Simulated Power Data | ||||
|---|---|---|---|---|---|---|---|
| V (V) | I (A) | Isim (A) | IAE_I (A) | P (W) | Psim (W) | IAE_P (W) | |
| 1 | −0.2057 | 0.7640 | 0.763983 | 1.6588 × 10−5 | −0.157155 | −0.1571514 | 3.4121 × 10−6 |
| 2 | −0.1291 | 0.7620 | 0.762604 | 6.0410 × 10−4 | −0.098374 | −0.0984522 | 7.7989 × 10−5 |
| 3 | −0.0588 | 0.7605 | 0.761338 | 8.3770 × 10−4 | −0.044717 | −0.0447667 | 4.9257 × 10−5 |
| 4 | 0.0057 | 0.7605 | 0.760174 | 3.2621 × 10−4 | 0.004335 | 0.0043330 | 1.8594 × 10−6 |
| 5 | 0.0646 | 0.7600 | 0.759108 | 8.9232 × 10−4 | 0.049096 | 0.0490384 | 5.7644 × 10−5 |
| 6 | 0.1185 | 0.7590 | 0.758121 | 8.7858 × 10−4 | 0.089942 | 0.0898374 | 1.0411 × 10−4 |
| 7 | 0.1678 | 0.7570 | 0.757189 | 1.8861 × 10−4 | 0.127025 | 0.1270562 | 3.1649 × 10−5 |
| 8 | 0.2132 | 0.7570 | 0.756244 | 7.5639 × 10−4 | 0.161392 | 0.1612311 | 1.6126 × 10−4 |
| 9 | 0.2545 | 0.7555 | 0.755177 | 3.2270 × 10−4 | 0.192275 | 0.1921926 | 8.2127 × 10−5 |
| 10 | 0.2924 | 0.7540 | 0.753722 | 2.7765 × 10−4 | 0.220470 | 0.2203884 | 8.1184 × 10−5 |
| 11 | 0.3269 | 0.7505 | 0.751399 | 8.9913 × 10−4 | 0.245338 | 0.2456324 | 2.9393 × 10−4 |
| 12 | 0.3585 | 0.7465 | 0.747301 | 8.0144 × 10−4 | 0.267620 | 0.2679076 | 2.8732 × 10−4 |
| 13 | 0.3873 | 0.7385 | 0.740011 | 1.5107 × 10−3 | 0.286021 | 0.2866061 | 5.8508 × 10−4 |
| 14 | 0.4137 | 0.7280 | 0.727247 | 7.5305 × 10−4 | 0.301174 | 0.3008621 | 3.1154 × 10−4 |
| 15 | 0.4373 | 0.7065 | 0.706853 | 3.5030 × 10−4 | 0.308952 | 0.3091056 | 1.5319 × 10−4 |
| 16 | 0.4590 | 0.6755 | 0.675211 | 2.8946 × 10−4 | 0.310055 | 0.3099216 | 1.3286 × 10−4 |
| 17 | 0.4784 | 0.6320 | 0.630761 | 1.2392 × 10−3 | 0.302349 | 0.3017559 | 5.9285 × 10−4 |
| 18 | 0.4960 | 0.5730 | 0.571995 | 1.0053 × 10−3 | 0.284208 | 0.2837094 | 4.9861 × 10−4 |
| 19 | 0.5119 | 0.4990 | 0.499706 | 7.0614 × 10−4 | 0.255438 | 0.2557996 | 3.6147 × 10−4 |
| 20 | 0.5265 | 0.4130 | 0.413734 | 7.3367 × 10−4 | 0.217445 | 0.2178308 | 3.8628 × 10−4 |
| 21 | 0.5398 | 0.3165 | 0.317546 | 1.0462 × 10−3 | 0.170847 | 0.1714114 | 5.6474 × 10−4 |
| 22 | 0.5521 | 0.2120 | 0.212123 | 1.2300 × 10−4 | 0.117045 | 0.1171131 | 6.7906 × 10−5 |
| 23 | 0.5633 | 0.1035 | 0.102163 | 1.3367 × 10−3 | 0.058302 | 0.0575486 | 7.5298 × 10−4 |
| 24 | 0.5736 | −0.0100 | −0.008792 | 1.2082 × 10−3 | −0.005736 | −0.0050429 | 6.9305 × 10−4 |
| 25 | 0.5833 | −0.1230 | −0.125543 | 2.5434 × 10−3 | −0.071746 | −0.0732295 | 1.4836 × 10−3 |
| 26 | 0.5900 | −0.2100 | −0.208371 | 1.6284 × 10−3 | −0.123900 | −0.1229392 | 9.6076 × 10−4 |
| Method | Max | Min | Mean | std |
|---|---|---|---|---|
| CNGPS | 1.4385 × 10−3 | 9.8249× 10−4 | 1.08848× 10−3 | 1.52726× 10−4 |
| NGO | 4.8644 × 10−3 | 9.8256 × 10−4 | 1.27573 × 10−3 | 1.97125 × 10−4 |
| TSA | 5.5563 × 10−2 | 1.4814 × 10−3 | 9.2738 × 10−3 | 1.1422 × 10−2 |
| SSA | 6.3369 × 10−1 | 3.0098 × 10−2 | 5.3167 × 10−2 | 1.41972 × 10−2 |
| PSO | 1.9304 × 10−3 | 1.0301 × 10−3 | 1.1310 × 10−3 | 2.2646 × 10−4 |
| MVO | 2.4031 × 10−3 | 1.1167 × 10−3 | 1.5250 × 10−3 | 3.1907 × 10−4 |
| FA | 7.4451 × 102 | 2.2916 × 10−2 | 4.9223 × 10−2 | 1.1877 × 10−2 |
| Method | CNGPS | NGO | TSA | SSA | PSO | MVO | FA |
|---|---|---|---|---|---|---|---|
| Iph (A) | 0.760782 | 0.760781 | 0.765642 | 0.792467 | 0.760815 | 0.760763 | 0.760650 |
| Isd1 (A) | 2.28420 × 10−7 | 3.07069 × 10−7 | 1.74707 × 10−7 | 1.95578 × 10−7 | 8.51528 × 10−10 | 4.02028 × 10−7 | 3.80608 × 10−7 |
| Isd2 (A) | 7.26329 × 10−7 | 5.42394 × 10−7 | 9.57003 × 10−9 | 7.67869 × 10−7 | 2.71697 × 10−7 | 4.28194 × 10−7 | 1.64373 × 10−7 |
| Isd3 (A) | 4.91844 × 1015 | 2.14569 × 10−7 | 3.68999 × 10−7 | 1.74886 × 10−7 | 3.31786 × 10−7 | 5.46206 × 10−7 | 6.04885 × 10−7 |
| Rs (Ω) | 0.0368917 | 0.0368200 | 0.0365547 | 0.0533244 | 0.0366112 | 0.0359268 | 0.036813 |
| Rsh (Ω) | 55.3988 | 55.7599 | 36.6203 | 12.0785 | 57.6676 | 75.5573 | 62.4033 |
| n1 | 1.45190 | 1.99999 | 1.42543 | 1.85770 | 1.73659 | 1.51261 | 1.85961 |
| n2 | 1.99999 | 1.99999 | 1.45788 | 1.63053 | 1.99189 | 1.98739 | 1.42802 |
| n3 | 1.99926 | 1.44670 | 2.00000 | 1.55133 | 1.48587 | 1.94060 | 1.91769 |
| RMSE | 9.82490 × 10−4 | 9.82560 × 10−4 | 1.4814 × 10−3 | 0.0300982 | 1.03013 × 10−3 | 1.1167 × 10−3 | 0.022916 |
| Sig | ∼ | + | + | + | + | + | + |
| Item | Measured Data | Simulated Current Data | Simulated Power Data | ||||
|---|---|---|---|---|---|---|---|
| V (V) | I (A) | Isim (A) | IAE_I (A) | P (W) | Psim (W) | IAE_P (W) | |
| 1 | −0.2057 | 0.7640 | 0.7639834 | 1.6588 × 10−5 | −0.15716 | −0.157151 | 3.4121 × 10−6 |
| 2 | −0.1291 | 0.7620 | 0.7626041 | 6.0410 × 10−4 | −0.09837 | −0.098452 | 7.7989 × 10−5 |
| 3 | −0.0588 | 0.7605 | 0.7613377 | 8.3770 × 10−4 | −0.04472 | −0.044767 | 4.9257 × 10−5 |
| 4 | 0.0057 | 0.7605 | 0.7601738 | 3.2621 × 10−4 | 0.004335 | 0.0043330 | 1.8594 × 10−6 |
| 5 | 0.0646 | 0.7600 | 0.7591077 | 8.9232 × 10−4 | 0.049096 | 0.0490384 | 5.7644 × 10−5 |
| 6 | 0.1185 | 0.7590 | 0.7581214 | 8.7858 × 10−4 | 0.089942 | 0.0898374 | 1.0411 × 10−4 |
| 7 | 0.1678 | 0.7570 | 0.7571886 | 1.8861 × 10−4 | 0.127025 | 0.1270562 | 3.1649 × 10−5 |
| 8 | 0.2132 | 0.7570 | 0.7562436 | 7.5639 × 10−4 | 0.161392 | 0.1612311 | 1.6126 × 10−4 |
| 9 | 0.2545 | 0.7555 | 0.7551773 | 3.2270 × 10−4 | 0.192275 | 0.1921926 | 8.2127 × 10−5 |
| 10 | 0.2924 | 0.7540 | 0.7537224 | 2.7765 × 10−4 | 0.220470 | 0.2203884 | 8.1184 × 10−5 |
| 11 | 0.3269 | 0.7505 | 0.7513991 | 8.9913 × 10−4 | 0.245338 | 0.2456324 | 2.9393 × 10−4 |
| 12 | 0.3585 | 0.7465 | 0.7473014 | 8.0144 × 10−4 | 0.267620 | 0.2679076 | 2.8732 × 10−4 |
| 13 | 0.3873 | 0.7385 | 0.7400107 | 1.5107 × 10−3 | 0.286021 | 0.2866061 | 5.8508 × 10−4 |
| 14 | 0.4137 | 0.7280 | 0.7272470 | 7.5305 × 10−4 | 0.301174 | 0.3008621 | 3.1154 × 10−4 |
| 15 | 0.4373 | 0.7065 | 0.7068503 | 3.5030 × 10−4 | 0.308952 | 0.3091056 | 1.5319 × 10−4 |
| 16 | 0.4590 | 0.6755 | 0.6752105 | 2.8946 × 10−4 | 0.310055 | 0.3099216 | 1.3286 × 10−4 |
| 17 | 0.4784 | 0.6320 | 0.6307608 | 1.2392 × 10−3 | 0.302349 | 0.3017559 | 5.9285 × 10−4 |
| 18 | 0.4960 | 0.5730 | 0.5719947 | 1.0053 × 10−3 | 0.284208 | 0.2837094 | 4.9861 × 10−4 |
| 19 | 0.5119 | 0.4990 | 0.4997061 | 7.0614 × 10−4 | 0.255438 | 0.2557996 | 3.6147 × 10−4 |
| 20 | 0.5265 | 0.4130 | 0.4137337 | 7.3367 × 10−4 | 0.217445 | 0.2178308 | 3.8628 × 10−4 |
| 21 | 0.5398 | 0.3165 | 0.3175462 | 1.0462 × 10−3 | 0.170847 | 0.1714114 | 5.6474 × 10−4 |
| 22 | 0.5521 | 0.2120 | 0.2121230 | 1.2300 × 10−4 | 0.117045 | 0.1171131 | 6.7906 × 10−5 |
| 23 | 0.5633 | 0.1035 | 0.1021633 | 1.3367 × 10−3 | 0.058302 | 0.0575486 | 7.5298 × 10−4 |
| 24 | 0.5736 | −0.0100 | −0.008792 | 1.2082 × 10−3 | −0.00574 | −0.0050429 | 6.9305 × 10−4 |
| 25 | 0.5833 | −0.1230 | −0.125543 | 2.5434 × 10−3 | −0.07175 | −0.0732295 | 1.4836 × 10−3 |
| 26 | 0.5900 | −0.2100 | −0.208372 | 1.6284 × 10−3 | −0.12390 | −0.1229392 | 9.6076 × 10−4 |
| Algorithm | Max | Min | Mean | Std | |
|---|---|---|---|---|---|
| SDM | CNGPS | 9.8602× 10−4 | 9.8602× 10−4 | 9.8602× 10−4 | 1.1231× 10−9 |
| NGO | 1.56529 × 10−3 | 9.8877 × 10−4 | 1.19734 × 10−3 | 1.5952 × 10−4 | |
| TSA | 1.4595 × 10−3 | 9.8613 × 10−4 | 1.08655 × 10−3 | 1.2581 × 10−4 | |
| SSA | 2.4569 × 10−3 | 1.0278 × 10−3 | 2.37701 × 10−3 | 1.7066 × 10−4 | |
| PSO | 1.4595 × 10−3 | 9.9073 × 10−4 | 1.08655 × 10−3 | 1.2584 × 10−4 | |
| MVO | 1.3048 × 10−2 | 1.6389 × 10−3 | 3.66904 × 10−3 | 2.7140 × 10−3 | |
| FA | 1.8023 × 10−3 | 1.0279 × 10−3 | 1.34978 × 10−3 | 1.9119 × 10−4 | |
| DDM | CNGPS | 9.8777× 10−4 | 9.8251× 10−4 | 9.8525× 10−4 | 1.2792× 10−6 |
| NGO | 2.4316 × 10−3 | 9.8547 × 10−4 | 1.5358 × 10−3 | 4.1571 × 10−4 | |
| TSA | 9.3214 × 10−3 | 1.7361 × 10−3 | 4.2531 × 10−3 | 2.3113 × 10−3 | |
| SSA | 1.4384 × 10−3 | 9.8133 × 10−4 | 1.1386 × 10−3 | 1.7869 × 10−4 | |
| PSO | 2.4831 × 10−3 | 1.0635 × 10−3 | 1.4774 × 10−3 | 3.0199 × 10−4 | |
| MVO | 1.6961 × 10−3 | 9.8941 × 10−4 | 1.1518 × 10−3 | 1.8861 × 10−4 | |
| FA | 1.9823 × 10−3 | 9.8383 × 10−4 | 1.0512 × 10−3 | 1.9053 × 10−4 | |
| TDM | CNGPS | 1.4385× 10−3 | 9.8249× 10−4 | 1.0885× 10−3 | 1.5272× 10−4 |
| NGO | 4.8645 × 10−3 | 9.8256 × 10−4 | 1.2757 × 10−3 | 1.9712 × 10−4 | |
| TSA | 5.5563 × 10−2 | 1.4814 × 10−3 | 9.2738 × 10−3 | 1.1422 × 10−2 | |
| SSA | 6.3369 × 10−1 | 3.0098 × 10−2 | 5.3167 × 10−2 | 1.41972 × 10−2 | |
| PSO | 1.9304 × 10−3 | 1.0301 × 10−3 | 1.1310 × 10−3 | 2.2646 × 10−4 | |
| MVO | 2.4031 × 10−3 | 1.1167 × 10−3 | 1.5250 × 10−3 | 3.1907 × 10−4 | |
| FA | 7.4451 × 10−2 | 2.2916 × 10−2 | 4.9223 × 10−2 | 1.1877 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satria, H.; Syah, R.B.Y.; Nehdi, M.L.; Almustafa, M.K.; Adam, A.O.I. Parameters Identification of Solar PV Using Hybrid Chaotic Northern Goshawk and Pattern Search. Sustainability 2023, 15, 5027. https://doi.org/10.3390/su15065027
Satria H, Syah RBY, Nehdi ML, Almustafa MK, Adam AOI. Parameters Identification of Solar PV Using Hybrid Chaotic Northern Goshawk and Pattern Search. Sustainability. 2023; 15(6):5027. https://doi.org/10.3390/su15065027
Chicago/Turabian StyleSatria, Habib, Rahmad B. Y. Syah, Moncef L. Nehdi, Monjee K. Almustafa, and Abdelrahman Omer Idris Adam. 2023. "Parameters Identification of Solar PV Using Hybrid Chaotic Northern Goshawk and Pattern Search" Sustainability 15, no. 6: 5027. https://doi.org/10.3390/su15065027
APA StyleSatria, H., Syah, R. B. Y., Nehdi, M. L., Almustafa, M. K., & Adam, A. O. I. (2023). Parameters Identification of Solar PV Using Hybrid Chaotic Northern Goshawk and Pattern Search. Sustainability, 15(6), 5027. https://doi.org/10.3390/su15065027






