Ordering Technique for the Maximum Power Point Tracking of an Islanded Solar Photovoltaic System
Abstract
:1. Introduction
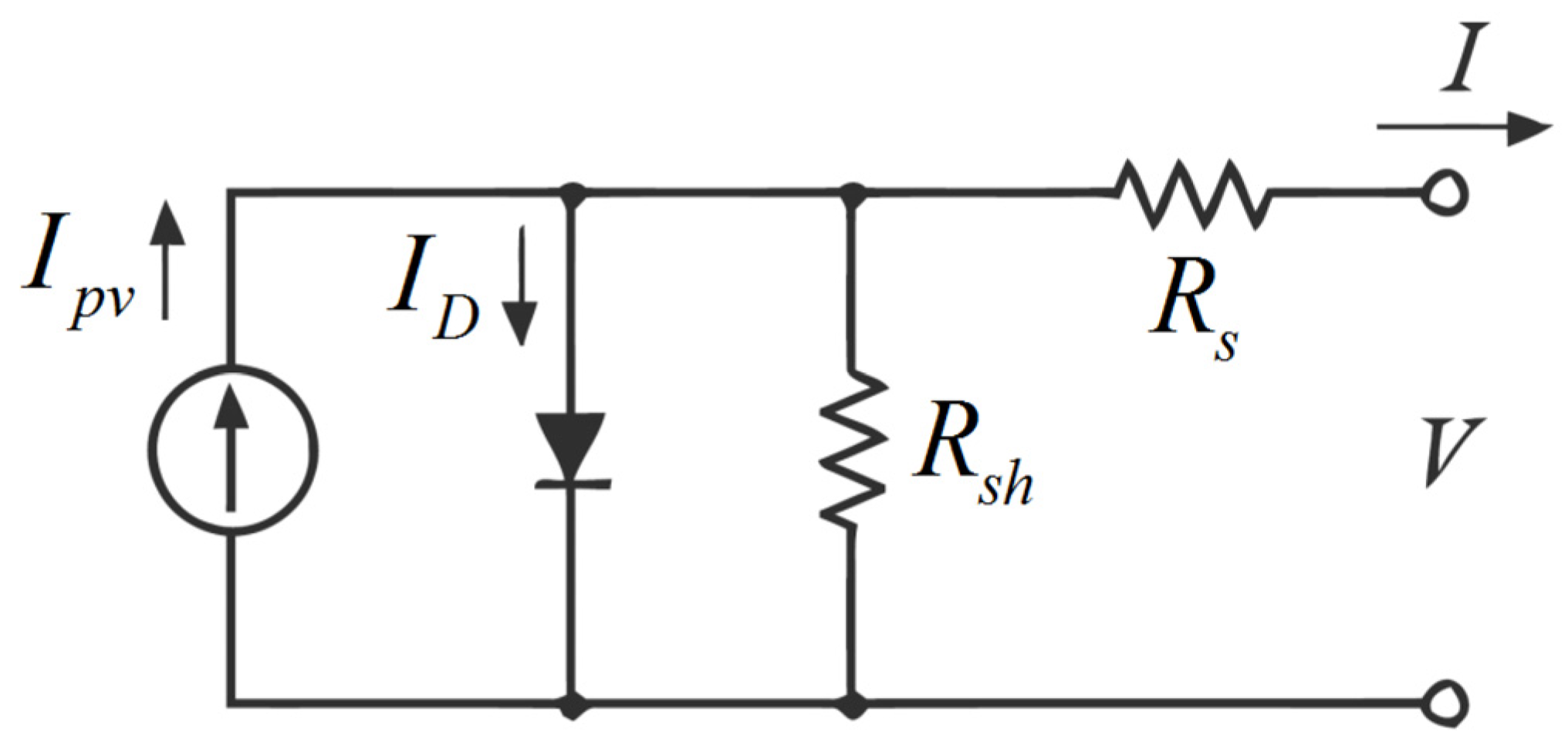
2. Modeling of Solar Photovoltaic Cell
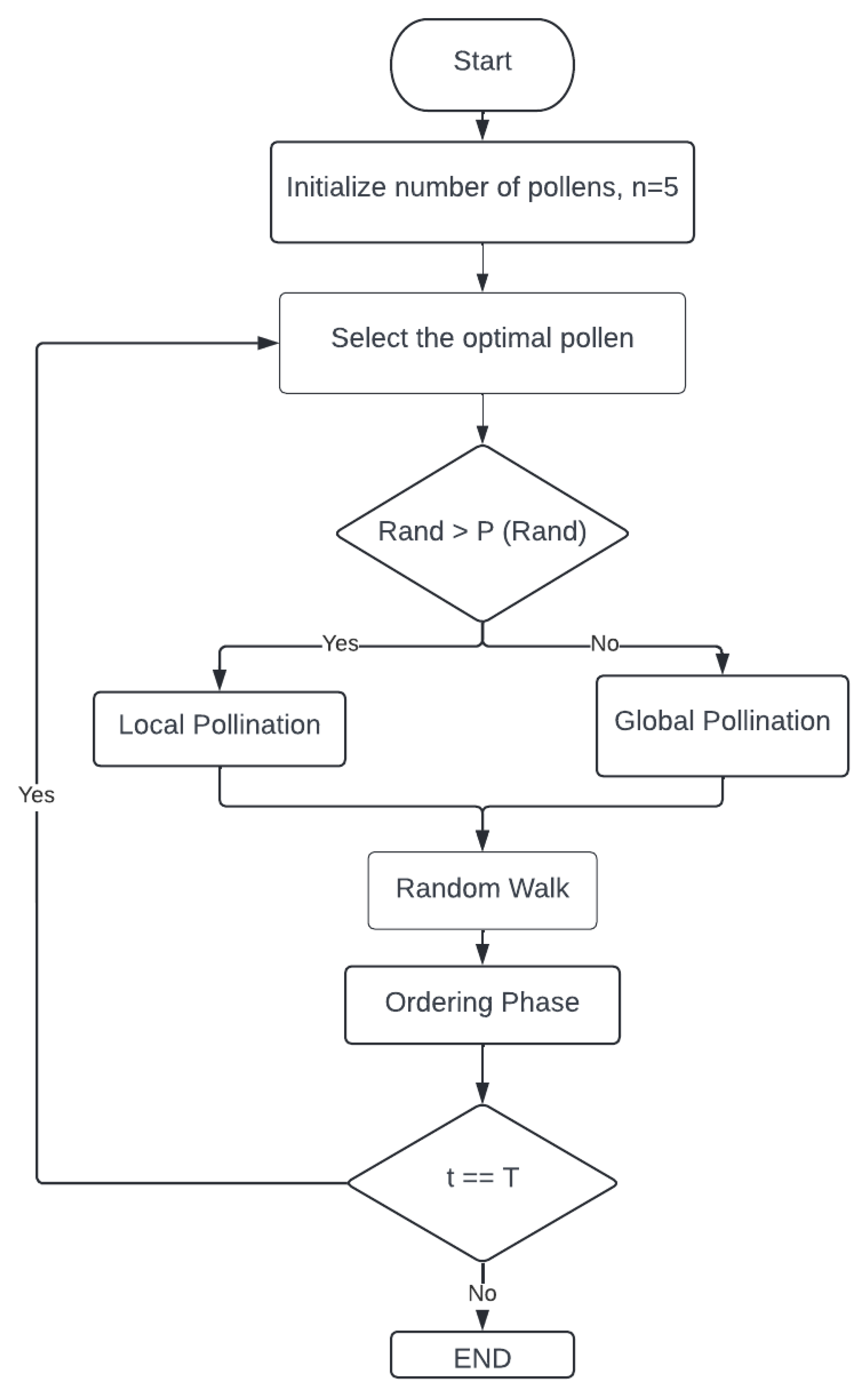
3. Flower Pollination Algorithm
4. Problem Formulation
5. Proposed Data Arrangement Technique
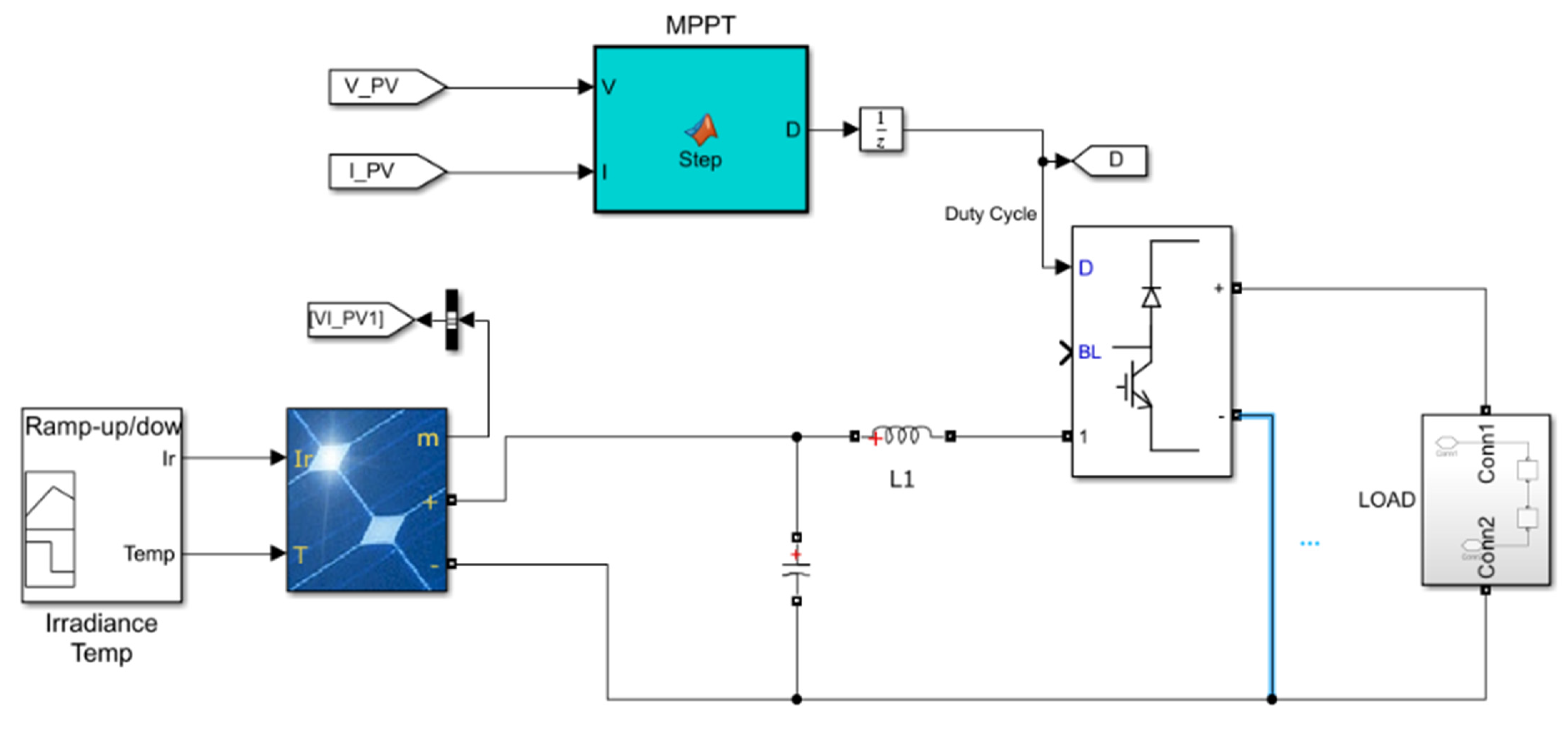
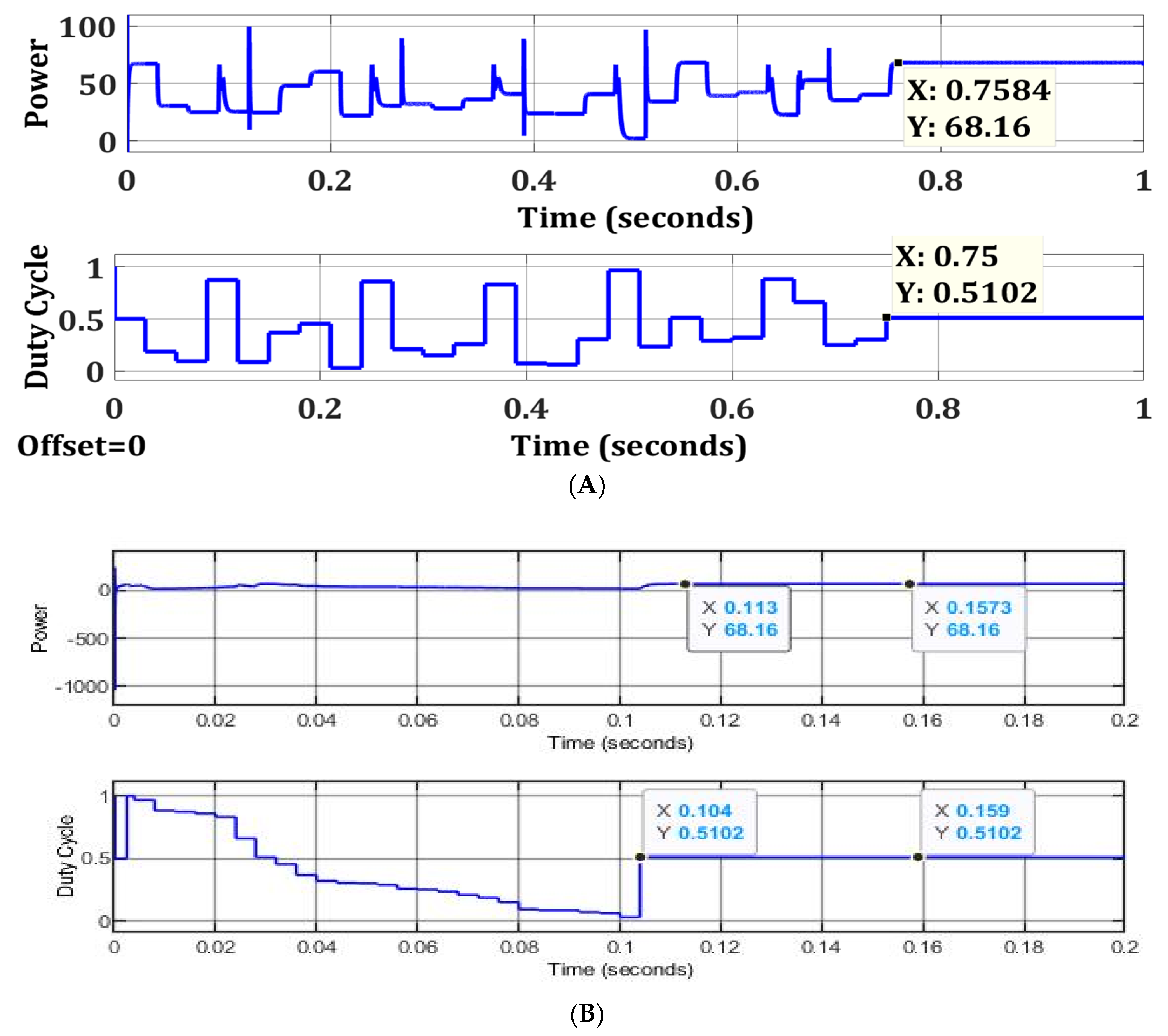
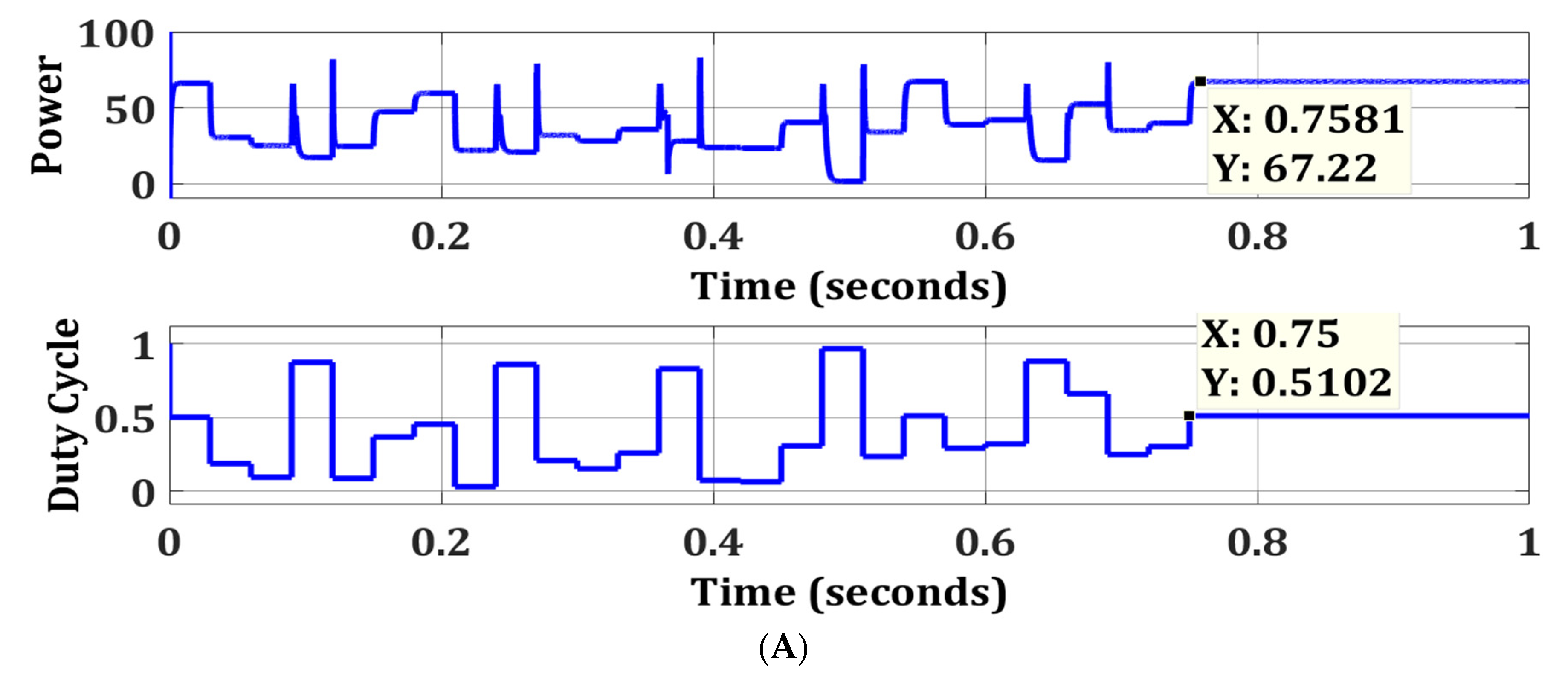
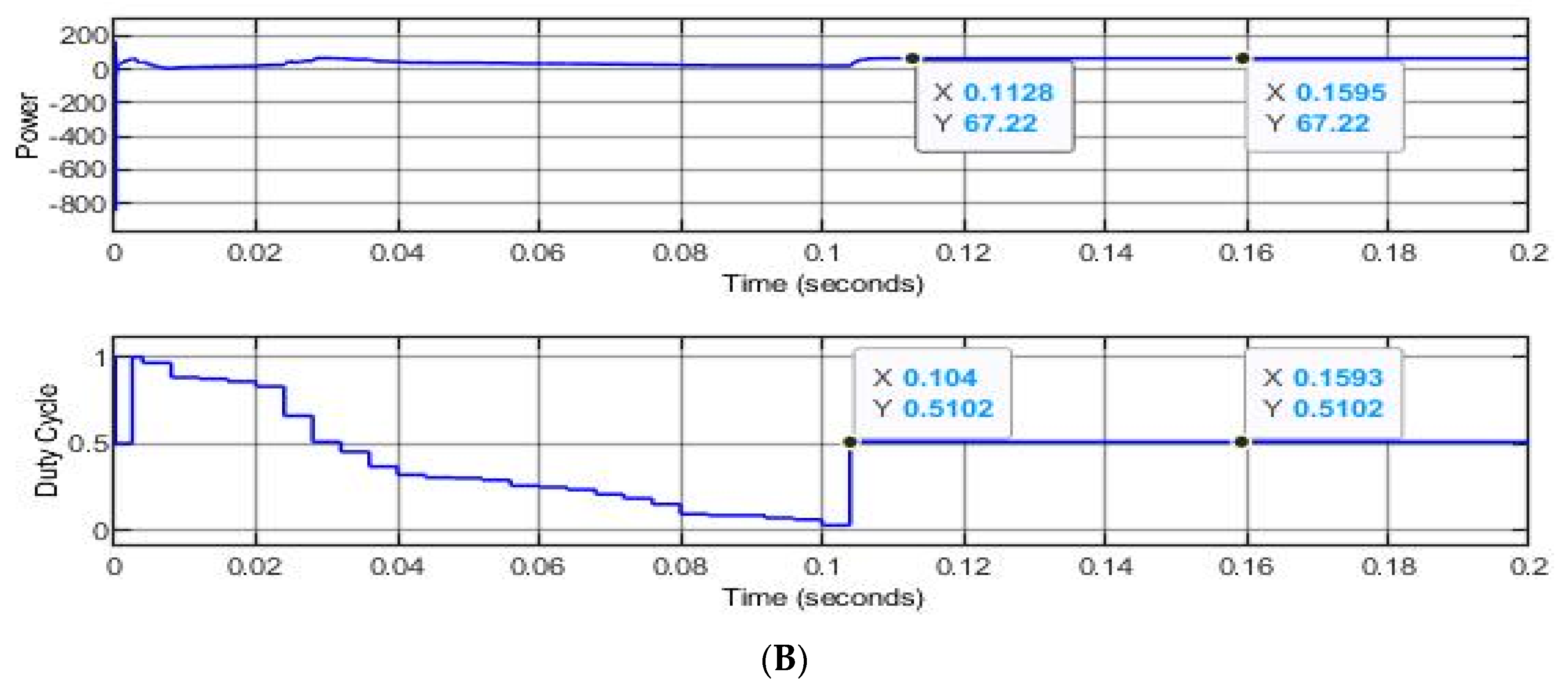
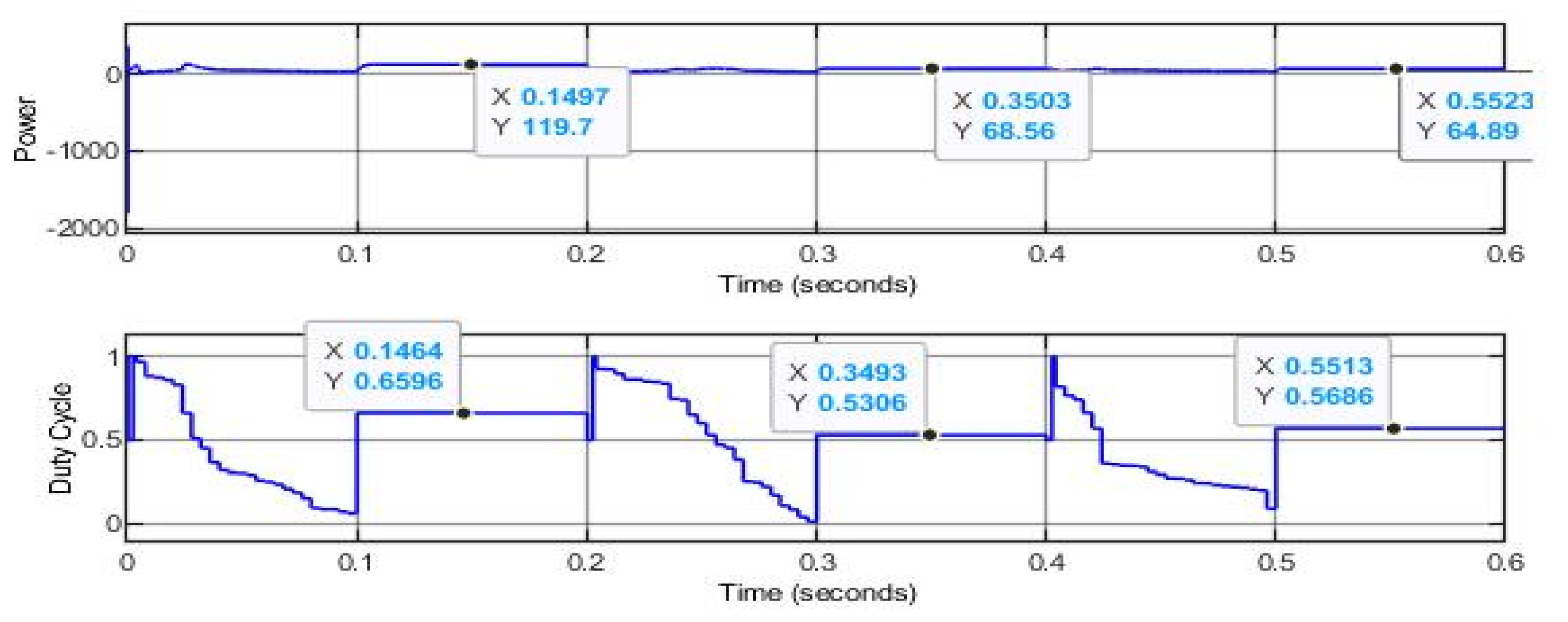
6. Simulation and Results
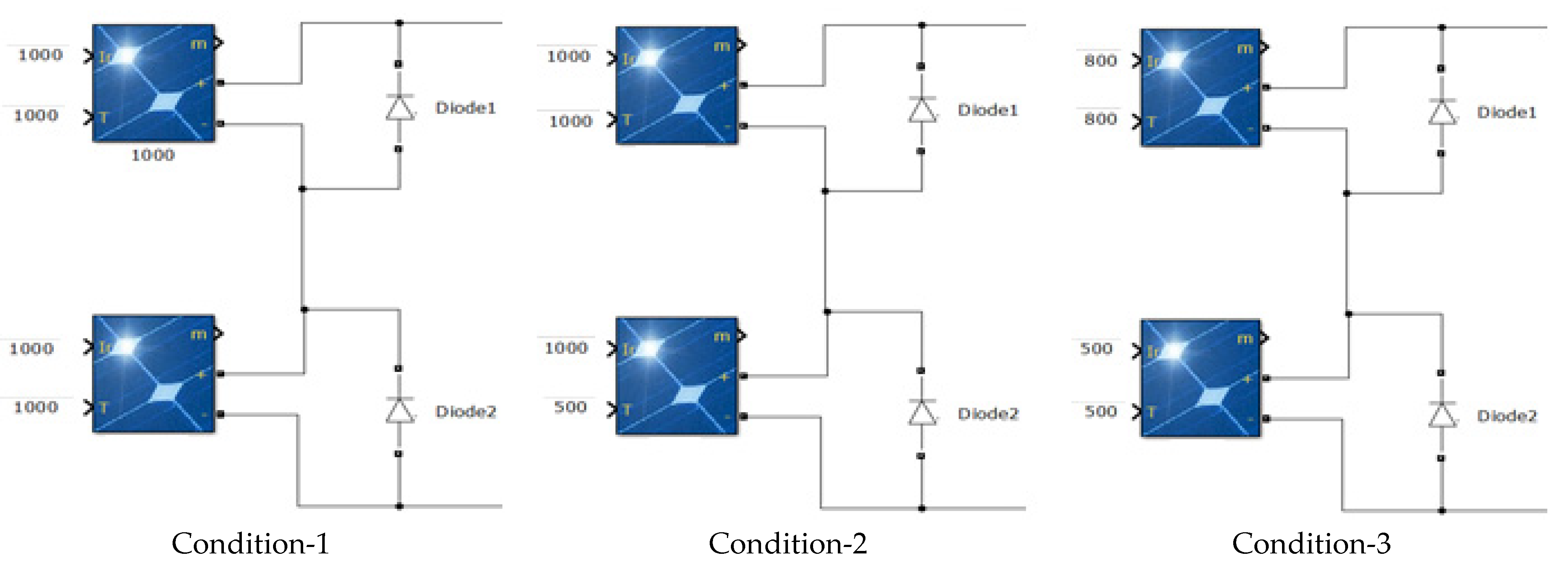
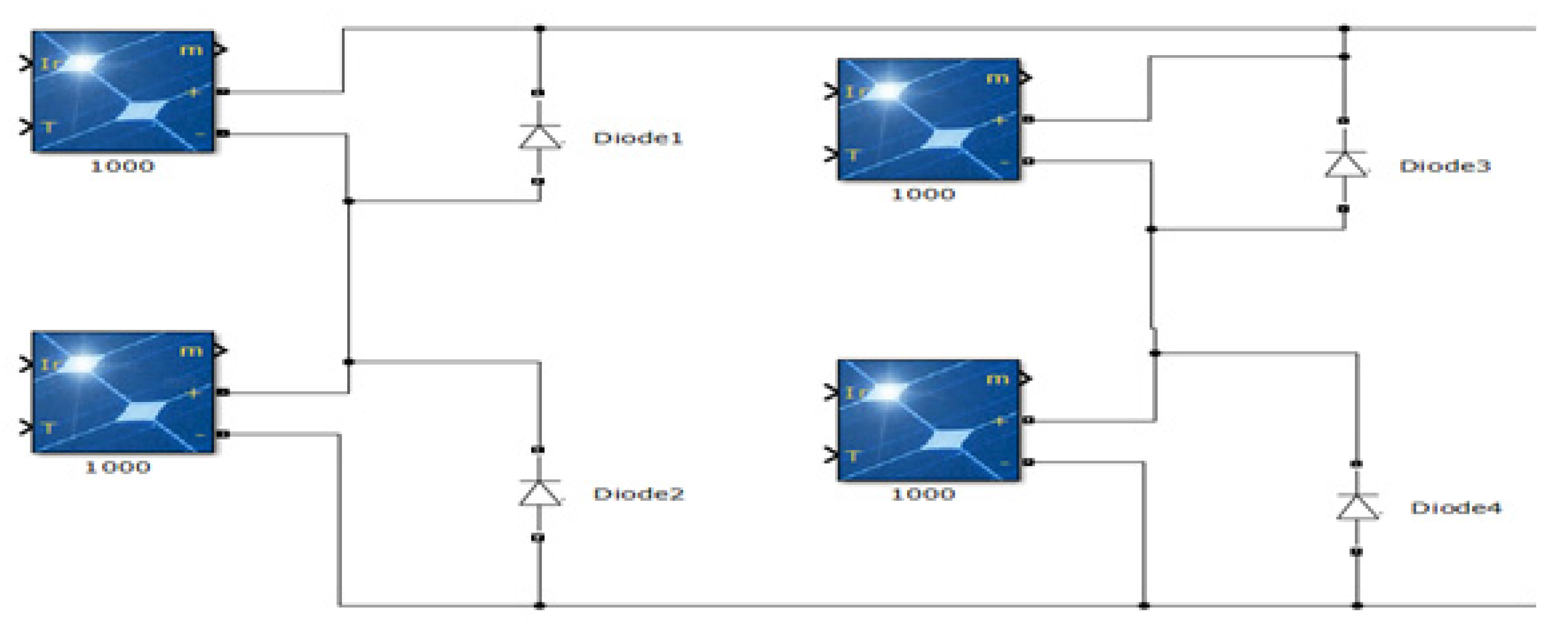
6.1. S Solar Photovoltaic System
6.2. S2P Solar Photovoltaic System
7. Discussion
8. Conclusions
9. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Awan, M.M.A.; Javed, M.Y.; Asghar, A.B.; Ejsmont, K. Economic integration of renewable and conventional power sources—A case study. Energies 2022, 15, 2141. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Huide, F.; Xuxin, Z.; Lei, M.; Tao, Z.; Qixing, W.; Hongyuan, S. A comparative study on three types of solar utilization technologies for buildings: Photovoltaic, solar thermal and hybrid photovoltaic/thermal systems. Energy Convers. Manag. 2017, 140, 1–13. [Google Scholar] [CrossRef]
- Afzal Awan, M.M.; Mahmood, T. A novel ten check maximum power point tracking algorithm for a standalone solar photovoltaic system. Electronics 2018, 7, 327. [Google Scholar] [CrossRef]
- Awan, M.M.A.; Mahmood, T. Modified flower pollination algorithm for an off-grid solar photovoltaic system. Mehran Univ. Res. J. Eng. Technol. 2022, 41, 95–105. [Google Scholar] [CrossRef]
- Başoğlu, M.E. A fast GMPPT algorithm based on PV characteristic for partial shading conditions. Electronics 2019, 8, 1142. [Google Scholar] [CrossRef]
- Feroz Mirza, A.; Mansoor, M.; Ling, Q.; Khan, M.I.; Aldossary, O.M. Advanced variable step size incremental conductance MPPT for a standalone PV system utilizing a GA-tuned PID controller. Energies 2020, 13, 4153. [Google Scholar] [CrossRef]
- Awan, M.M.A.; Javed, M.Y.; Asghar, A.B.; Ejsmont, K. Performance optimization of a ten check MPPT algorithm for an off-grid solar photovoltaic system. Energies 2022, 15, 2104. [Google Scholar] [CrossRef]
- Awan, M.M.A. A Technical Review of MPPT Algorithms for Solar Photovoltaic System: SWOT Analysis of MPPT Algorithms. Sir Syed Univ. Res. J. Eng. Technol. 2022, 12, 98–106. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of perturb and observe MPPT algorithm implementation techniques for PV pumping applications. IEEE Trans. Sustain. Energy 2011, 3, 21–33. [Google Scholar] [CrossRef]
- Jately, V.; Azzopardi, B.; Joshi, J.; Sharma, A.; Arora, S. Experimental Analysis of hill-climbing MPPT algorithms under low irradiance levels. Renew. Sustain. Energy Rev. 2021, 150, 111467. [Google Scholar] [CrossRef]
- Jately, V.; Arora, S. Performance investigation of Hill-Climbing MPPT techniques for PV systems under rapidly changing environment. In Intelligent Communication, Control and Devices, Proceedings of ICICCD 2017; Springer: Singapore, 2018; pp. 1145–1157. [Google Scholar]
- Jately, V.; Bhattacharya, S.; Azzopardi, B.; Montgareuil, A.; Joshi, J.; Arora, S. Voltage and current reference based MPPT under rapidly changing irradiance and load resistance. IEEE Trans. Energy Convers. 2021, 36, 2297–2309. [Google Scholar] [CrossRef]
- Debnath, A.; Olowu, T.O.; Parvez, I.; Dastgir, M.G.; Sarwat, A. A novel module independent straight line-based fast maximum power point tracking algorithm for photovoltaic systems. Energies 2020, 13, 3233. [Google Scholar] [CrossRef]
- Awan, M.M.A. Strategic Perturb and Observe Algorithm for Partial Shading Conditions: SP&O Algorithm for PSC. Sir Syed Univ. Res. J. Eng. Technol. 2022, 12, 26–32. [Google Scholar]
- Awan, M.M.A.; Awan, F.G. Improvement of maximum power point tracking perturb and observe algorithm for a standalone solar photovoltaic system. Mehran Univ. Res. J. Eng. Technol. 2017, 36, 501–510. [Google Scholar] [CrossRef]
- Jately, V.; Arora, S. November. An efficient hill-climbing technique for peak power tracking of photovoltaic systems. In Proceedings of the 2016 IEEE 7th Power India International Conference (PIICON), Bikaner, India, 25–27 November 2016; pp. 1–5. [Google Scholar]
- Tiwari, R.; Krishnamurthy, K.; Neelakandan, R.B.; Padmanaban, S.; Wheeler, P.W. Neural network based maximum power point tracking control with quadratic boost converter for PMSG—Wind energy conversion system. Electronics 2018, 7, 20. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Fang, G.; Zhang, B.; Wen, H.; Tang, H.; Fu, L.; Chen, X. An advanced maximum power point tracking method for photovoltaic systems by using variable universe fuzzy logic control considering temperature variability. Electronics 2018, 7, 355. [Google Scholar] [CrossRef]
- Settles, M.; Soule, T. June. Breeding swarms: A GA/PSO hybrid. In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, Prague, Czech Republic, 25–27 August 2005; pp. 161–168. [Google Scholar]
- Sharma, A.; Sharma, A.; Jately, V.; Averbukh, M.; Rajput, S.; Azzopardi, B. A novel TSA-PSO based hybrid algorithm for GMPP tracking under partial shading conditions. Energies 2022, 15, 3164. [Google Scholar] [CrossRef]
- Zhang, P.; Sui, H. Maximum power point tracking technology of photovoltaic array under partial shading based on adaptive improved differential evolution algorithm. Energies 2020, 13, 1254. [Google Scholar] [CrossRef]
- Pilakkat, D.; Kanthalakshmi, S. Single phase PV system operating under Partially Shaded Conditions with ABC-PO as MPPT algorithm for grid connected applications. Energy Rep. 2020, 6, 1910–1921. [Google Scholar] [CrossRef]
- Awan, M.M.A.; Mahmood, T. Optimization of maximum power point tracking flower pollination algorithm for a standalone solar photovoltaic system. Mehran Univ. Res. J. Eng. Technol. 2020, 39, 267–278. [Google Scholar] [CrossRef]
- Figueiredo, S.; e Silva, R.N.A.L. Hybrid MPPT technique PSO-P&O applied to photovoltaic systems under uniform and partial shading conditions. IEEE Lat. Am. Trans. 2021, 19, 1610–1617. [Google Scholar]
- Awan, M.M.A.; Awan, M.J. Adapted flower pollination algorithm for a standalone solar photovoltaic system. Mehran Univ. Res. J. Eng. Technol. 2022, 41, 118–127. [Google Scholar] [CrossRef]
- Mousa, H.H.; Youssef, A.R.; Mohamed, E.E. Variable step size P&O MPPT algorithm for optimal power extraction of multi-phase PMSG based wind generation system. Int. J. Electr. Power Energy Syst. 2019, 108, 218–231. [Google Scholar]
- Balaji, V.; Fathima, A.P. Enhancing the maximum power extraction in partially shaded PV arrays using hybrid salp swarm perturb and observe algorithm. Int. J. Renew. Energy Res. (IJRER) 2020, 10, 898–911. [Google Scholar]
- Zhang, S.; Wang, T.; Li, C.; Zhang, J.; Wang, Y. June. Maximum power point tracking control of solar power generation systems based on type-2 fuzzy logic. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 770–774. [Google Scholar]
- Miyatake, M.; Veerachary, M.; Toriumi, F.; Fujii, N.; Ko, H. Maximum power point tracking of multiple photovoltaic arrays: A PSO approach. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 367–380. [Google Scholar] [CrossRef]

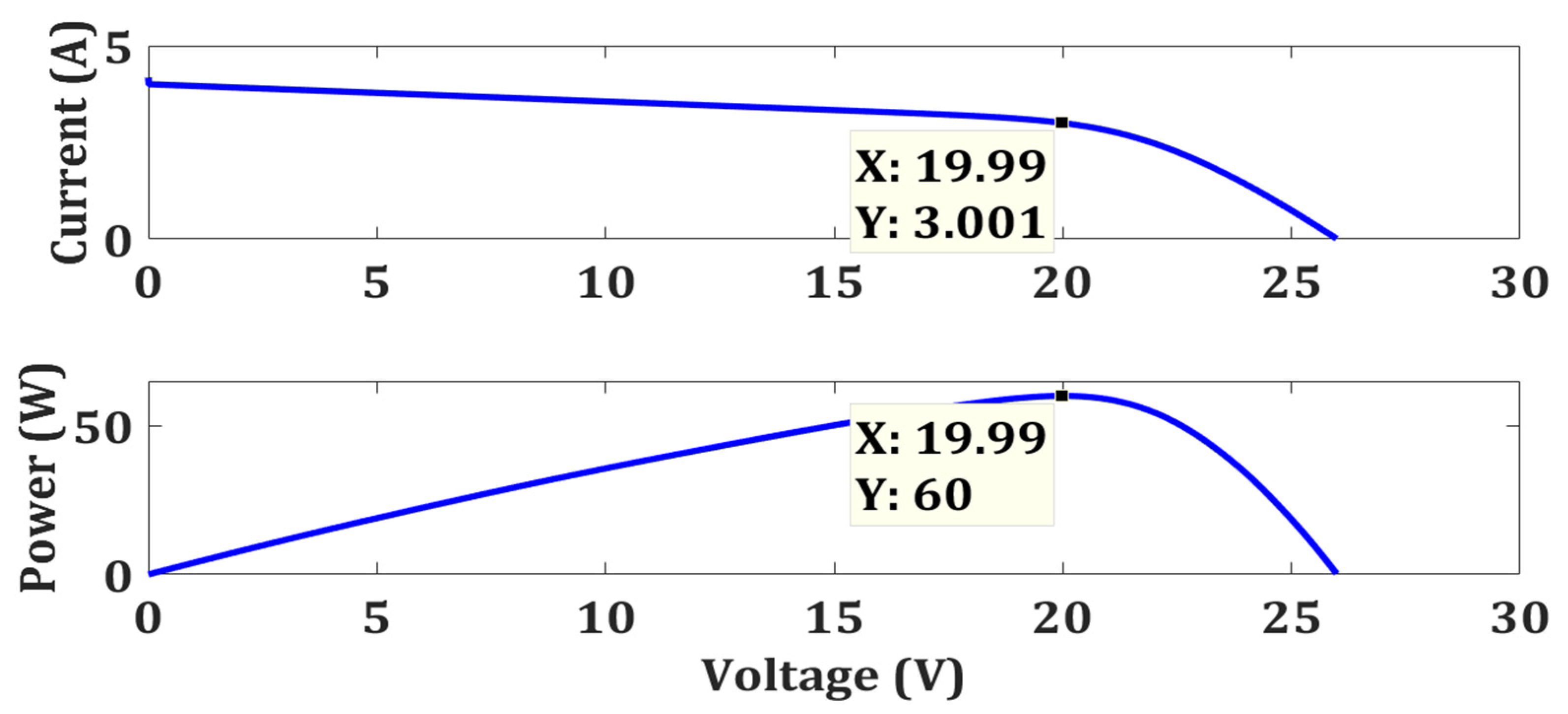
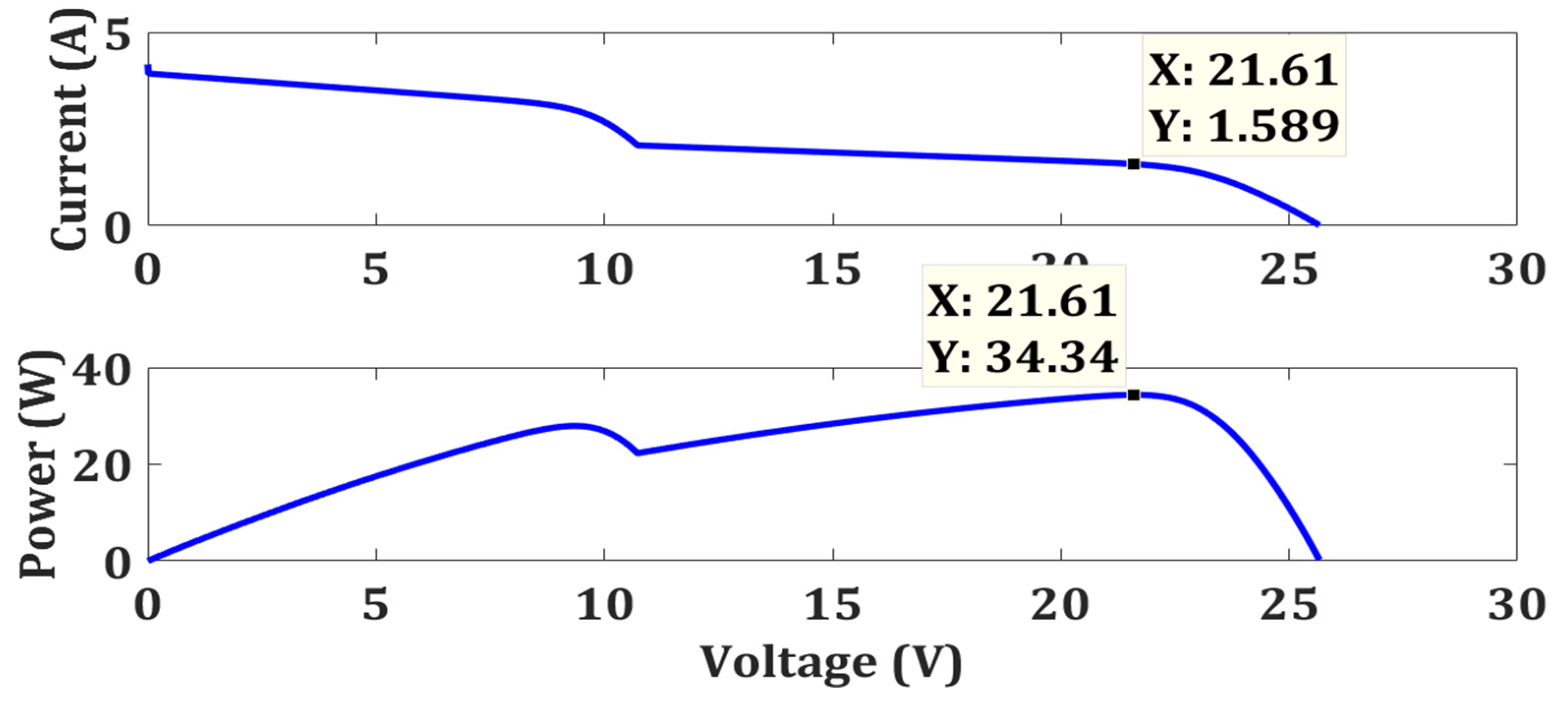
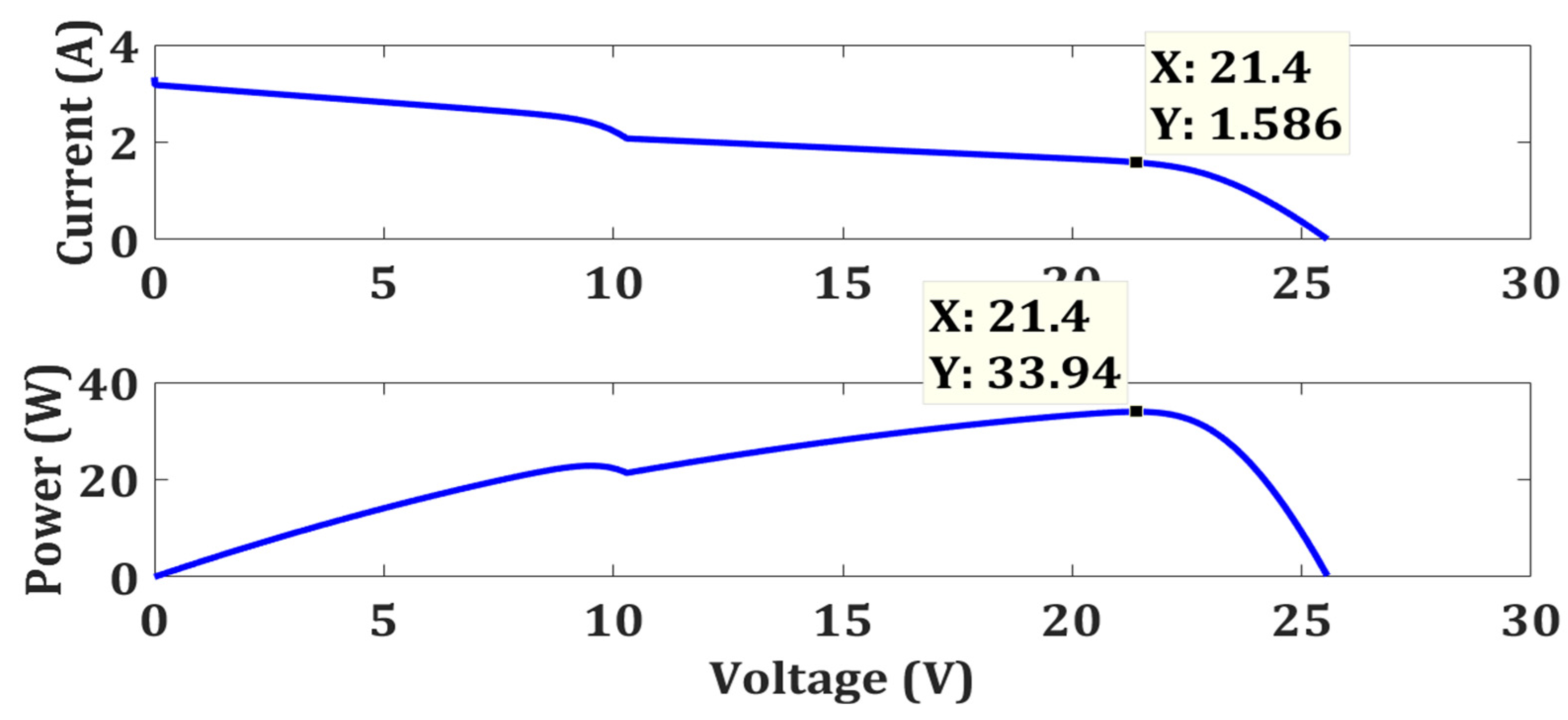
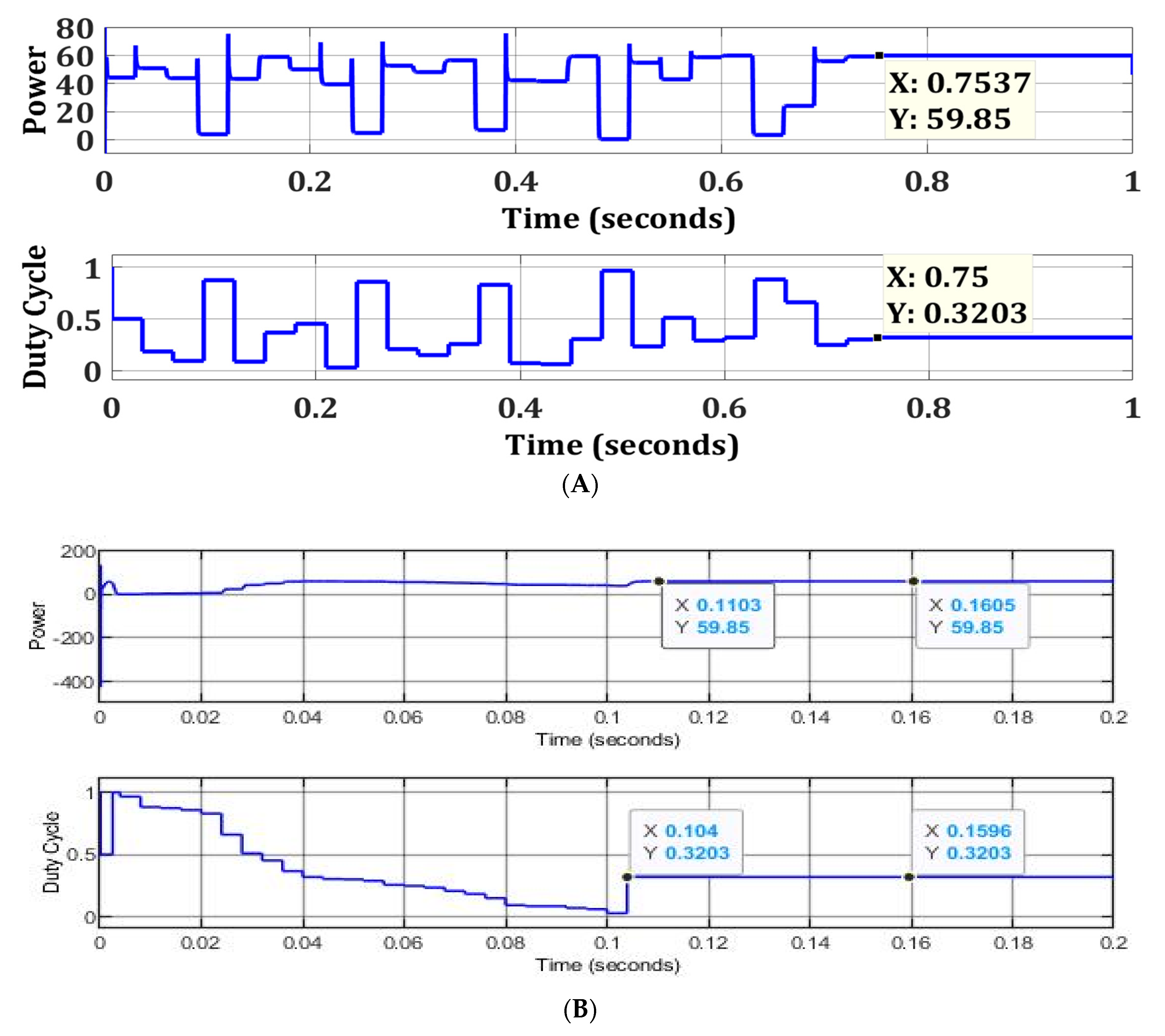
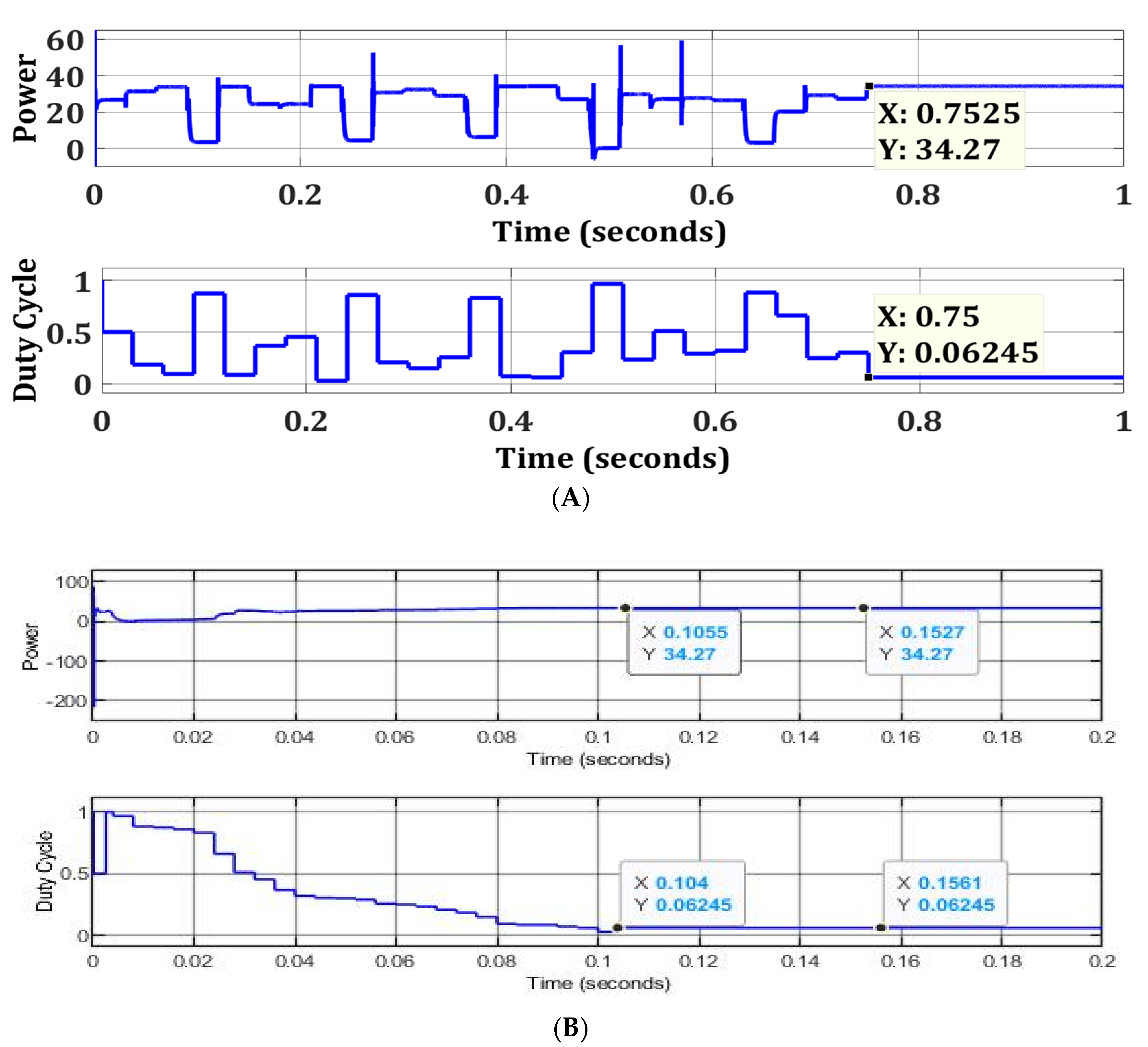
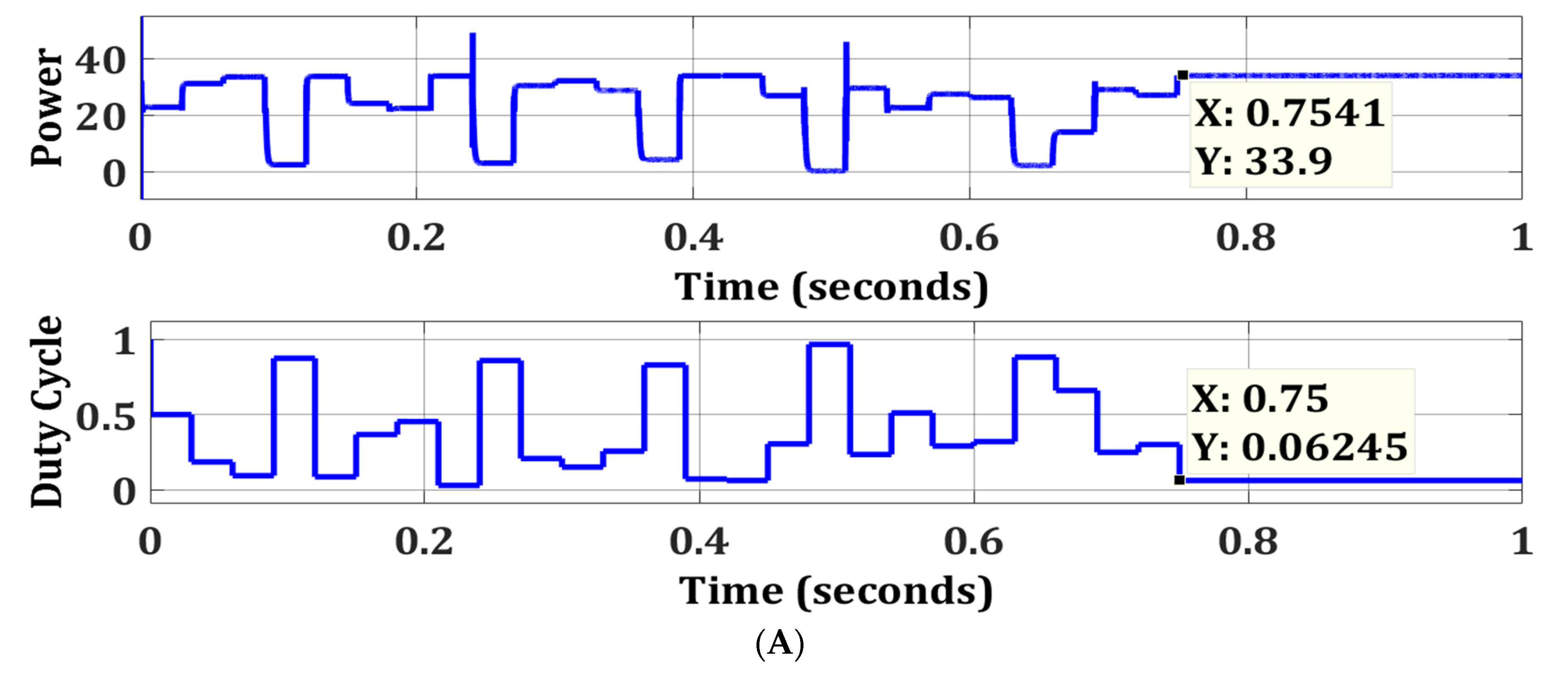
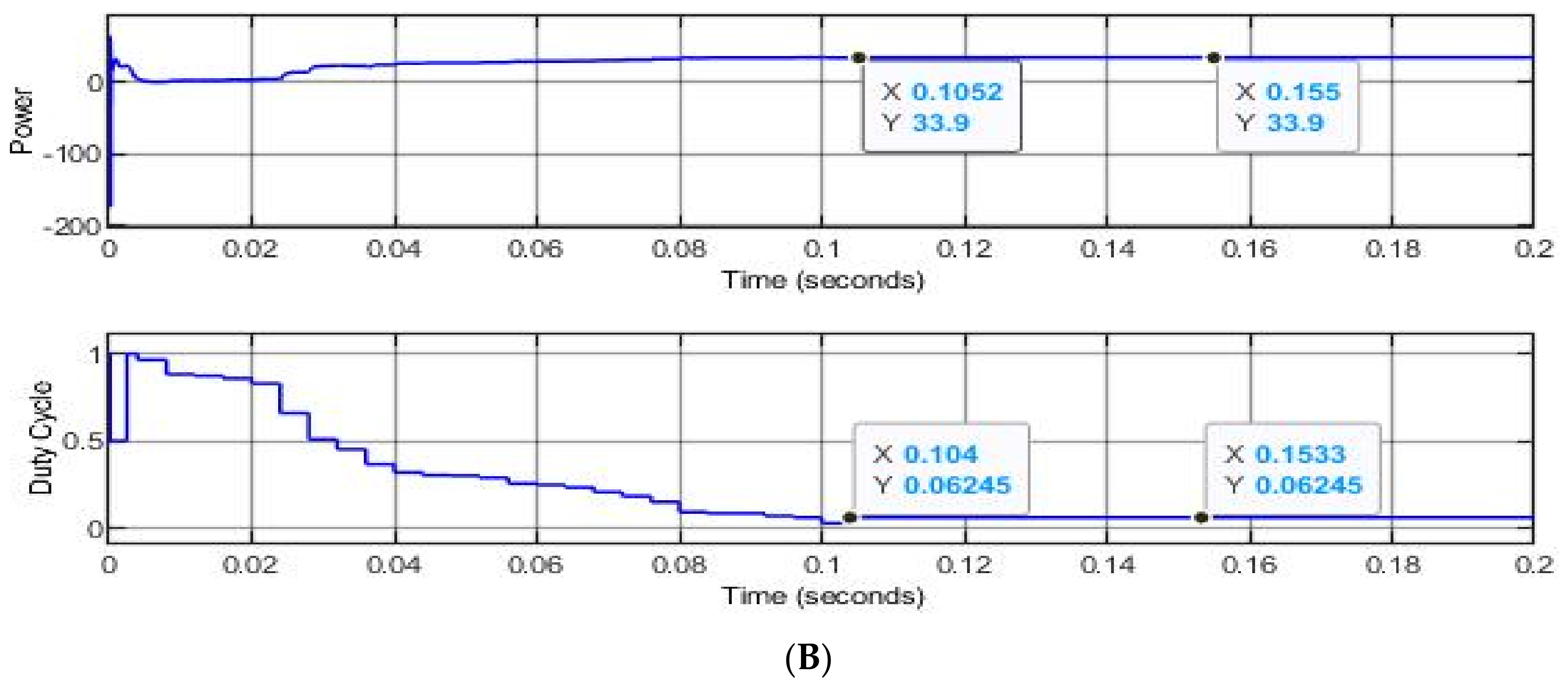
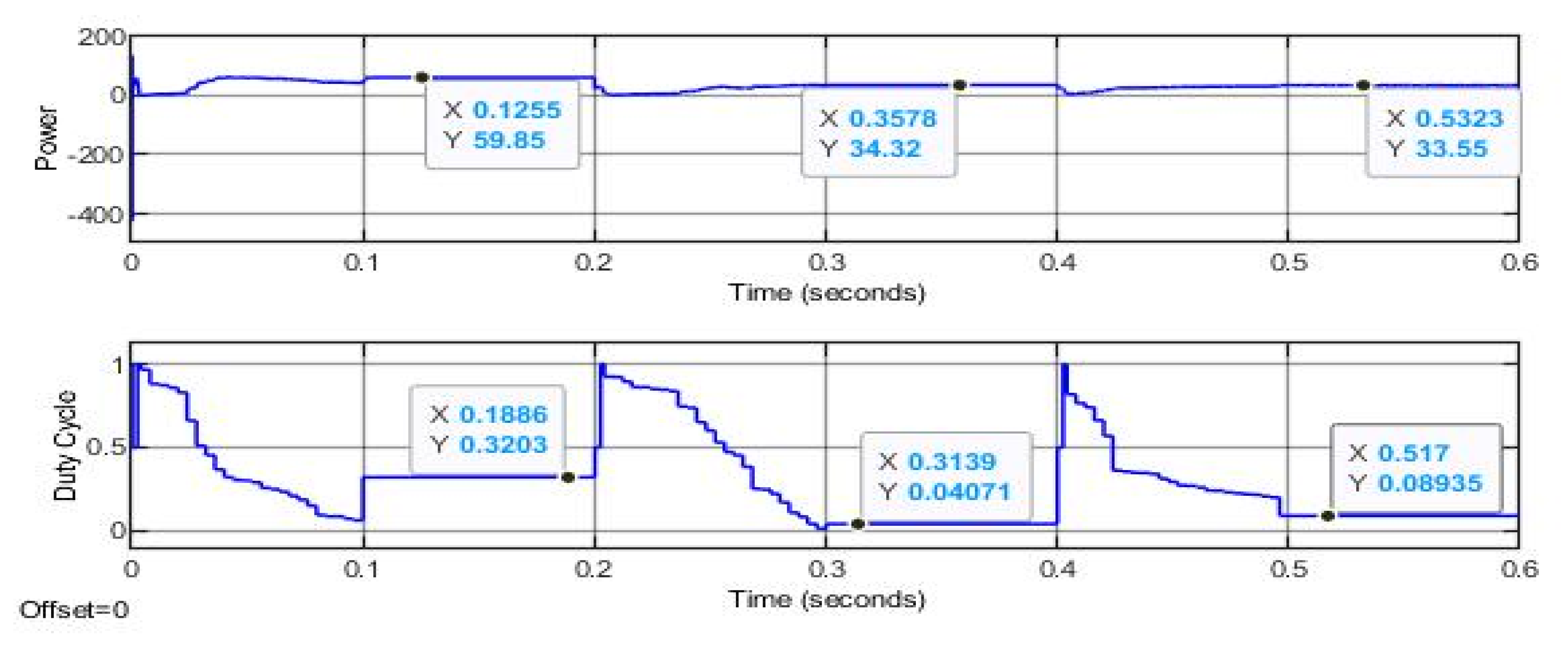

| Partial Shading | MPPT Algorithms | Power Output (W) | Rated Power (W) | Efficiency (%) | Tracking Speed (s) | Improvement in Tracking Speed (%) |
|---|---|---|---|---|---|---|
| Zero Shading | FPA | 59.85 | 60 | 99.75 | 0.7537 | 85.4 |
| OFPA | 59.85 | 99.75 | 0.1103 | |||
| Weak Partial Shading | FPA | 34.27 | 34.34 | 99.8 | 0.7525 | 86 |
| OFPA | 34.27 | 99.8 | 0.1055 | |||
| Strong Partial Shading | FPA | 33.9 | 33.94 | 99.88 | 0.7541 | 86 |
| OFPA | 33.9 | 99.88 | 0.1052 |
| Partial Shading | Algorithms | Power Output (W) | Rated Power (W) | Efficiency (%) | Tracking Speed (s) | Improvement in Tracking Speed (%) |
|---|---|---|---|---|---|---|
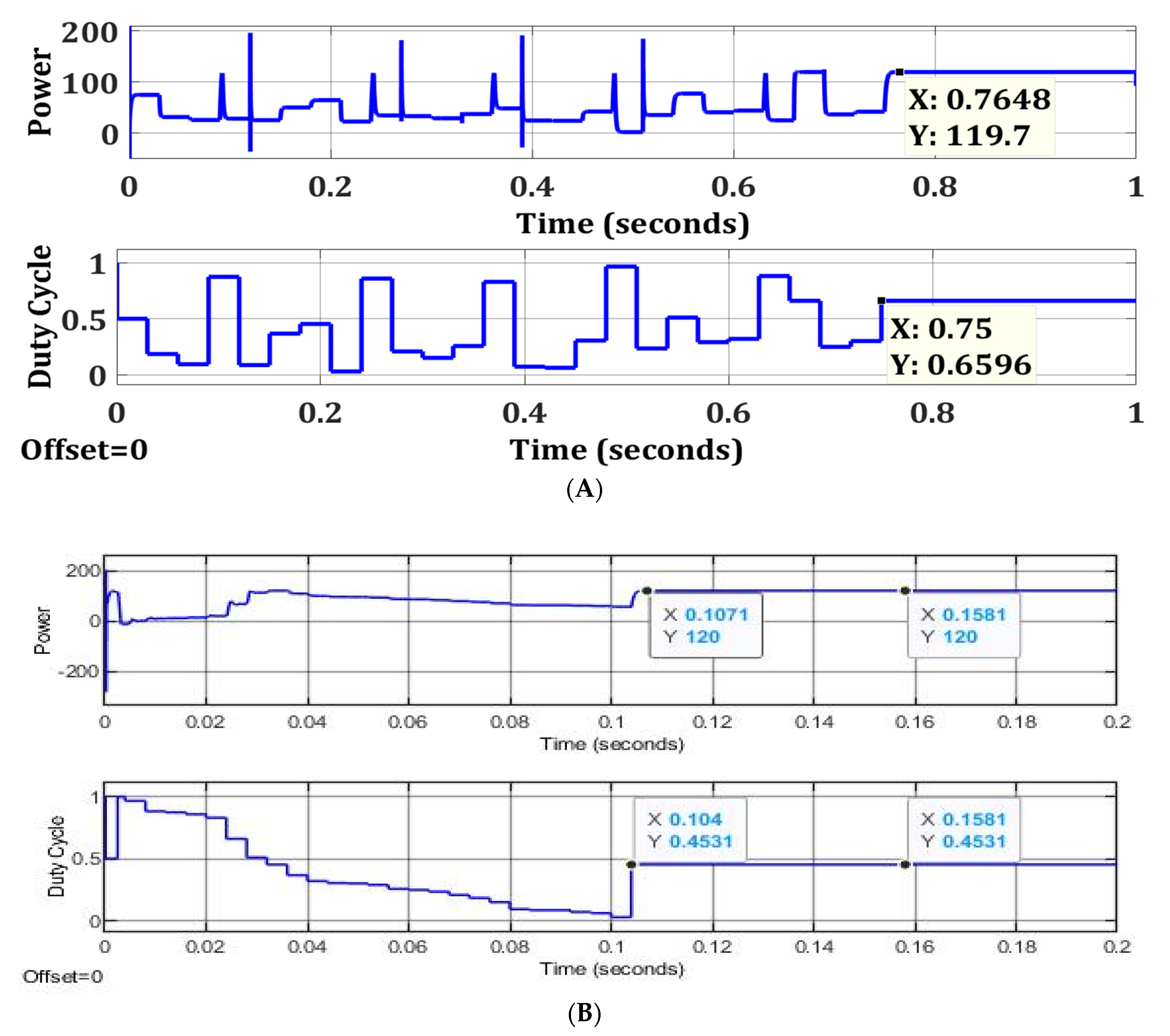
| Zero Shading | FPA | 119.7 | 120 | 99.75 | 0.7648 | 86 |
| OFPA | 120 | 100 | 0.1071 | |||
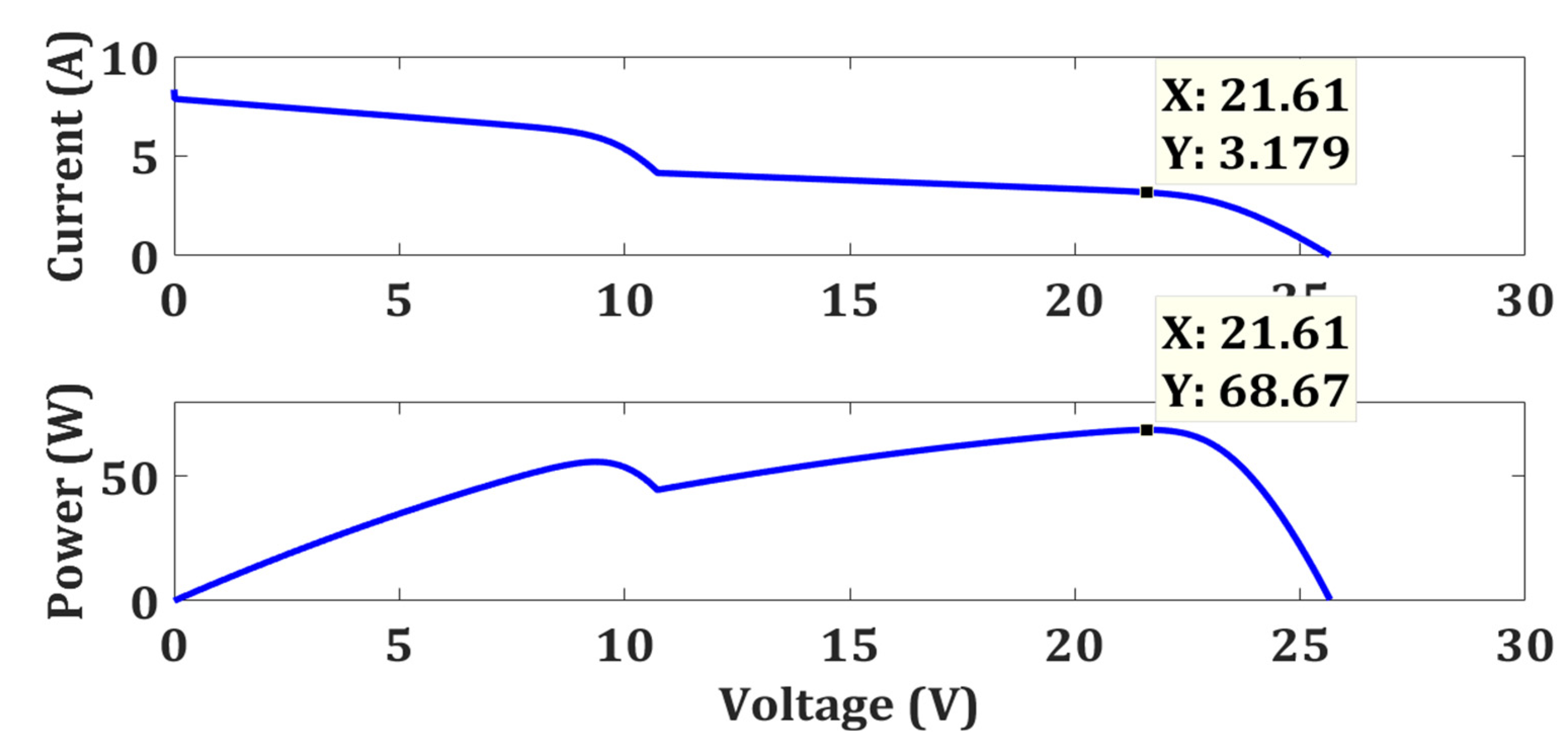
| Weak Partial Shading | FPA | 68.16 | 68.67 | 99.26 | 0.7584 | 85.10 |
| OFPA | 68.16 | 99.26 | 0.113 | |||
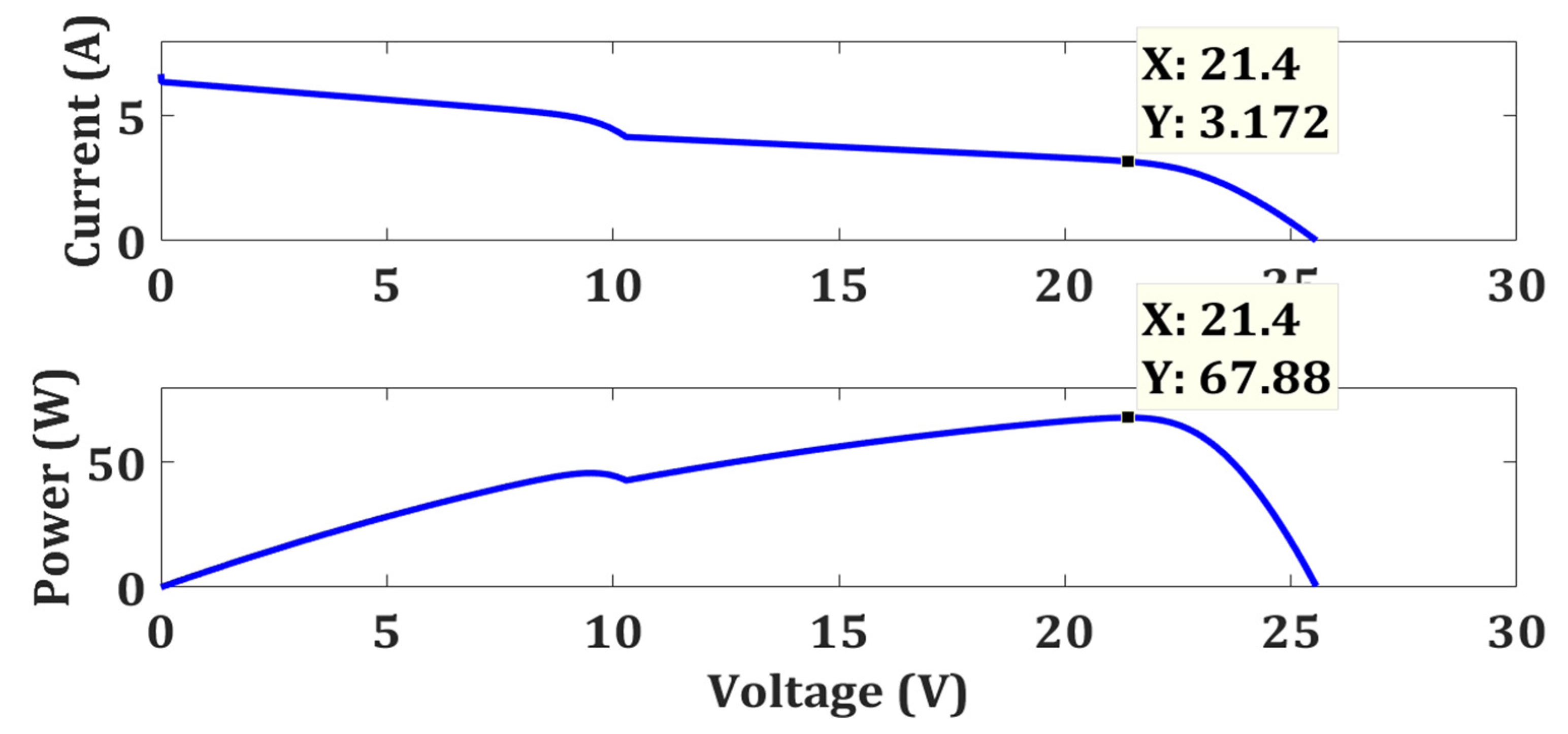
| Strong Partial Shading | FPA | 67.22 | 67.88 | 99.02 | 0.7581 | 85.02 |
| OFPA | 67.22 | 99.02 | 0.1128 |
| Sr. No. | Parameters | P&O [27,28] | Fuzzy [29] | PSO [30] | FPA [24] | Ordered FPA | |
|---|---|---|---|---|---|---|---|
| Algorithms | |||||||
| 1 | Steady State Oscillations | High | Low | Zero | Zero | Zero | |
| 2 | Tracking Speed | Low | Adequate | Adequate | Fast | FASTEST | |
| 3 | Procedural Complications | Less | High | Reasonable | Reasonable | Nil | |
| 4 | Memorizing Necessity | Few | Large | Few | Few | FEW | |
| 5 | Computational Complications | Zero | High | Average | Average | No | |
| 6 | Implementation | Cheap | Costly | Costly | Costly | Costly | |
| 7 | Performance in PSC | N/A | Good | Good | Good | EXCELLENT | |
| 8 | Module Dependent | Yes | Yes | No | No | No | |
| 9 | Efficiency | Fail | Low under PSC | Effective | Effective | Exciting | |
| 10 | Structure | Simple | Complex | Complex | Complex | Simple | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awan, M.M.A.; Asghar, A.B.; Javed, M.Y.; Conka, Z. Ordering Technique for the Maximum Power Point Tracking of an Islanded Solar Photovoltaic System. Sustainability 2023, 15, 3332. https://doi.org/10.3390/su15043332
Awan MMA, Asghar AB, Javed MY, Conka Z. Ordering Technique for the Maximum Power Point Tracking of an Islanded Solar Photovoltaic System. Sustainability. 2023; 15(4):3332. https://doi.org/10.3390/su15043332
Chicago/Turabian StyleAwan, Muhammad Mateen Afzal, Aamer Bilal Asghar, Muhammad Yaqoob Javed, and Zsolt Conka. 2023. "Ordering Technique for the Maximum Power Point Tracking of an Islanded Solar Photovoltaic System" Sustainability 15, no. 4: 3332. https://doi.org/10.3390/su15043332
APA StyleAwan, M. M. A., Asghar, A. B., Javed, M. Y., & Conka, Z. (2023). Ordering Technique for the Maximum Power Point Tracking of an Islanded Solar Photovoltaic System. Sustainability, 15(4), 3332. https://doi.org/10.3390/su15043332










