Abstract
Blasting is essential for breaking hard rock in opencast mines and tunneling projects. It creates an adverse impact on flyrock. Thus, it is essential to forecast flyrock to minimize the environmental effects. The objective of this study is to forecast/estimate the amount of flyrock produced during blasting by applying three creative composite intelligent models: equilibrium optimizer-coupled extreme learning machine (EO-ELM), particle swarm optimization-based extreme learning machine (PSO-ELM), and particle swarm optimization-artificial neural network (PSO-ANN). To obtain a successful conclusion, we considered 114 blasting data parameters consisting of eight inputs (hole diameter, burden, stemming length, rock density, charge-per-meter, powder factor (PF), blastability index (BI), and weathering index), and one output parameter (flyrock distance). We then compared the results of different models using seven different performance indices. Every predictive model accomplished the results comparable with the measured values of flyrock. To show the effectiveness of the developed EO-ELM, the result from each model run 10-times is compared. The average result shows that the EO-ELM model in testing (R2 = 0.97, RMSE = 32.14, MAE = 19.78, MAPE = 20.37, NSE = 0.93, VAF = 93.97, A20 = 0.57) achieved a better performance as compared to the PSO-ANN model (R2 = 0.87, RMSE = 64.44, MAE = 36.02, MAPE = 29.96, NSE = 0.72, VAF = 74.72, A20 = 0.33) and PSO-ELM model (R2 = 0.88, RMSE = 48.55, MAE = 26.97, MAPE = 26.71, NSE = 0.84, VAF = 84.84, A20 = 0.51). Further, a non-parametric test is performed to assess the performance of these three models developed. It shows that the EO-ELM performed better in the prediction of flyrock compared to PSO-ELM and PSO-ANN. We did sensitivity analysis by introducing a new parameter, WI. Input parameters, PF and BI, showed the highest sensitivity with 0.98 each.
1. Introduction
Surface mining is basically for breaking in situ rock, construction activities, and excavation; blasting is the most popular method throughout the globe [1,2,3]. Blasting is a system consisting of interaction between explosives and rock [4]. Blast design, properties of explosives, and rock mass are primarily the existing critical parameters for blasting and its performance [5,6]. Standard operating procedures are adopted for blast execution [7,8]. Desired blast fragmentation throw and shape muck pile affect the efficiency of loading equipment [9]. Blast fragmentation is also crucial for loading equipment and downstream operation of hauling and crushing [10,11]. Hence, these parameters are called favorable parameters [12,13], whereas flyrock, ground vibration, air overpressure, and dust affect the environment [7,14]. Therefore, these parameters are known as unfavorable parameters [8,15].
Flyrock is a geotechnical issue based on various rock mass properties. Various studies have been carried out to resolve geotechnical issues. Failure in geotechnical structure was studied with a multiscale work analysis approach [16]. An impressive micromechanical modeling (MM) framework was proposed by utilizing the discrete element method (DEM) and the micro-mechanical (MM) model [17]. The impact of flow direction vis-a-vis gravity direction on suffusion in geotechnical structures or slopes was resolved using the pioneering computational fluid dynamic-discrete element method (CFD-DEM) [18]. Further, the CFD-DEM model was helpful in investigating the particle shape effect and various levels of transmission at the macro- and micro-behavior levels during suffusion [19,20]. The CFD-DEM method played a significant role in the investigation of seepage in the underwater tunnel face [21]. The novel multi-scale approach, by deploying the smoothed particle hydrodynamics (SPH) method, was found to be efficient in computational analysis to understand granular collapse [22]. A possible solution for several engineering and industrial processes was found by developing DEM for irregular 3D particle shapes [23]. An algorithm was developed to accomplish 3D realistic stones of irregular geometries at random for specified samples with quantitative adjustable control [24]. In the convention of blasting safety criteria, defining frequency characteristics of blasting is of practical significance. A computational method associated with the wavelet frequency domain parameter or a main frequency band was proposed [25]. The innovative liquid carbon dioxide rock-breaking technology was found to be safer than explosive blasting. This technology needs further investigation to show that this technology is more efficient than traditional non-explosive techniques [26].
Flyrock has also been considered as an incidental or haphazard, exorbitant throw of rock pieces originating from blasting operations. Rock fragments from blasting may be thrown beyond the expected normal distance. This may result in a serious hazard to people working around the mines or severe danger to the property and machinery near the blasting site [27,28,29]. There are several causes of flyrock: usage of types of explosives, improper blast design, or explicit or uncertain conditions of the rock mass. Flyrock accidents are caused by poor security or blast management practices [30,31,32]. During the last decade, several researchers have developed many computational methods concurrently to forecast flyrock due to blasting [33].
Various researchers have pointed out that ANN, which is a branch of artificial intelligence (AI), is suitable for forecasting engineering problems [34,35]. For decades, many researchers had used ANN as a prediction method for flyrock distance [36,37,38]. However, ANN has some limitations, including slow learning speed and it falls into local minima due to the use of a gradient-based optimizer [39]. Furthermore, a specific ANN model for the prediction of flyrock is not available. On the other hand, the boundary condition of ANN models depends upon the variation in data sets [31]. Further, despite significant learning cycles on the same data set, there may be a marginal improvement in prediction performance. ANN models can easily find out the significance and sensitivity of input parameters [31]. As stated in the literature, various metaheuristic optimization algorithms (MOAs) could be deployed to forecast flyrock created by blasting due to the MOA’s higher efficiency and to avoid the limitation of ANN. Some of the researchers compared ANN with other models, such as the ICA-coupled ANN model, which provided better performance as compared to ANN for the prediction of flyrock [40]. Furthermore, ANFIS showed superior performance as compared to ANN [41,42]. The PSO algorithm provided a powerful equation to predict flyrock due to blasting [43]. Gene expression programming (GEP) and the firefly algorithm (FA) were used to compare the results of flyrock prediction [44]. Further, hybrid algorithms were developed using optimization algorithms and ANN. MOAs provide a powerful ability to search for the best local solution from global optima. Therefore, MOA’s estimated biases and weights of ANN can improve the prediction task of flyrock. The hybrid model, PSO-ANN, was developed for the prediction of flyrock [45]. The results of two different hybrid models, genetic algorithm-based ANN (GA-ANN) and recurrent fuzzy neural network (RFNN-GA), were compared with ANN to predict flyrock [46]. The results of three hybrid models, ICA-ANN, PSO-ANN, and GA-ANN, were compared to predict flyrock [47].
In recent years, one of the most exciting areas of study is machine learning (ML) [48]. In general, ML describes the ways of making predictions about and learning from data. As a subcategory of artificial intelligence, ML mainly aims at proposing and developing algorithms that can learn automatically from data.
Specifically, AI seeks to identify the objects existing in the neighboring areas and predict how the environment behaves in ways to make informed decisions. As a result, the ML techniques have a higher tendency to predict instead of estimate. For instance, it discusses the way researchers can make use of data obtained from an interferometry experiment to predict the interference pattern that would be seen under a variety of conditions. Furthermore, ML-based methods are mostly used to address high-dimensional problems of a higher complexity compared to the problems that may generally arise during a conventional statistics course [49]. The capability of generating and analyzing large data sets has dramatically increased during the last three decades. Such ‘‘big data’’ revolution has been prompted due to an exponential upsurge in computation capacities and memory, which is recognized as Moore’s law. The ML models SVM [50,51] and ORLEM [52] were used by researchers for the prediction of flyrock due to blasting. In this research work, three hybrid models: PSO-ANN, PSO-ELM, and EO-ELM, are developed for the prediction of flyrock and their results are compared.
2. Models for the Prediction of Flyrock
Numerous researchers have proposed various approaches for flyrock prediction, which includes empirical, semi-empirical, and mathematical models.
2.1. Empirical Models for the Prediction of Flyrock
Various empirical models were developed by several researchers, mainly for blast production, which depend upon blast design and/or rock mass properties. Figure 1 shows a schematic diagram of flyrock, which may result in face burst, cratering, and rifting. Face burst results when geological discontinuities or planes of weakness exist. Cratering happens due to the escape of gases in the stemming zone due to back breaks or weak rock. Furthermore, it may be caused due to incorrect delay sequence (back rows firing first as compared to front rows). Rifting is due to stemming release with air pulse and associated with air blast. Inadequate stemming length and inappropriate stemming material are the causes of rifting [53].
Various empirical equations were developed by several researchers for flyrocks, which occur in numerous sizes and shapes. The prediction of maximum flyrock was recommended based on a factor of safety and hole diameter [54]. Further, the relationship between the ratio of stemming length to burden was established to maximum flyrock distance [55].
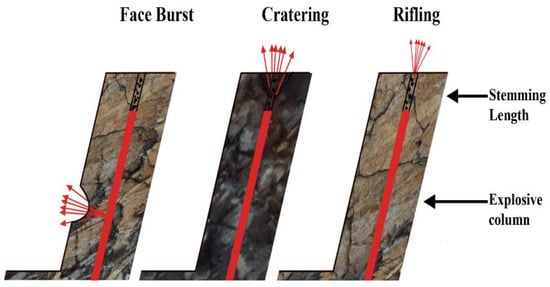
Figure 1.
Schematic diagram of a mechanism of flyrock [56].
Researchers developed equations for flyrock prediction for the calculation of initial velocity based on the scaled burden method [57,58]. As per the equation, a charge per m and burden are the key parameters of face burst, as face burst increases with the increase in charge per m or decrease in burden. Furthermore, stemming length or charging per m are the key parameters of cratering. Flyrocks increase due to cratering, with the increase in charge per m or decrease in stemming length. Similarly, rifting depends upon a charge per m, burden, and drill hole angle. Flyrock increase, with the increase in charge per m or decrease in burden and rifting, is minimum in cases of vertical drill hole angle.
Flyrock prediction was developed based on blast design parameters (burden, stemming length, linear charge concentration, and specific charge) and rock mass properties (unconfined compressive strength and RQD) [58]. The empirical equation was established based on blast design parameters (stemming length, hole depth, burden, and spacing) and rock mass property (rock mass rating) for the prediction of flyrock [39]. These equations do not consider rock mass properties of tropically weathered rock. Various researchers have reported that empirical equations for the prediction of flyrock may be suitable for a particular site only and are not accurate [40,59].
2.2. Mathematical Models for the Prediction of Flyrock
Various researchers developed mathematical models for the prediction of flyrock. To estimate flyrock range, Lundborg [60] adopted a semi-empirical method to analyze the relationship between rock velocity and charge diameter. In terms of crater blasting in granite blocks, these authors introduced the relationship between the beginning velocity of the flyrock fragment, its size, and throw [61]. Two expressions were derived by Chiapetta (1983) in the case of distance that may be traveled by flyrock (Chiapetta RF, 1983). Furthermore, a relation was established by Roth (1979) to find out the flyrock travel range. According to this approach, all of the measurements were done on the flyrock range and the most important variable was to estimate the flyrock velocity at the beginning. Roth applied Gurney’s proposed equation to compute the velocity at the beginning of the fragments thrown around through an explosion [61]. The limitation of mathematical equations is that their prediction is not accurate due to their being site-specific and having limited data input.
2.3. Semi-Empirical Trajectory Physics-Based Models for the Prediction of Flyrock
In semi-empirical trajectory physics-based models, the focus is on the beginning velocity of flyrock; therefore, they are most desired. One of the models developed by St. George and Gibson was modified by Little and Blair [62]. These models generally suffer from inexplicity in defining the velocity of detonation and the density of the explosive, which is applied to determine the blast-hole pressure and effects. The impact time applied to these equations is determined based on experimental observation instead of real monitoring.
2.4. Artificial Intelligence Techniques
Blasting is one of the major operations that causes several adverse environmental effects, such as generation of fines, ground vibrations, fumes, air blast, dust, and flyrock [44]. So, it is necessary to control these adverse effects while performing blasting operations [63]. During the last decade, various researchers have applied artificial intelligence (AI) techniques for the prediction, minimization, or optimization of these environmental effects. In recent years, ML is one of the trending methods. ML may be defined as computer algorithms that can improve automatically based on the nature of the signal or feedback provided to the learning system. It is divided into three categories, namely, reinforcement, unsupervised, and supervised learning. In “supervised learning”, the model is trained based on provided inputs and their desired outputs and the goal is to learn the pattern by mapping input to output. In “Unsupervised learning”, the model is trained based on provided inputs only where labels were not given so that it may find structure in the input on its own. In the case of “Reinforcement learning”, the model gets across with a dynamic environment to perform a certain goal and after performing this goal it obtains feedback that is equivalent to rewards, which the model attempts to maximize. ANN is one of the most significant algorithms of ML. ANN is a parallelly distributed system that epitomizes the neural network of the human brain to create information processing models by composing different networks and connections [64]. It has the advantages of self-organizing, adaptive, and real-time learning features that enable it to overcome the defects of traditional logic-based AI in handling unstructured information and intuition [65]. During 1992–1997, Vladimir Vapnik with colleagues developed support-vector machine (SVM) models at AT&T Bell Laboratories. SVM is one of the models of supervised learning that have associated learning algorithms to analyze data for regression or classification.
Despite intended flexibility in singleton AI models, the previous studies indicate that these algorithms may fail to deliver expected results and may experience poor generalization capability. The reason for this is that they may become stuck in a locally optimal solution due to the use of stochastic selection or gradient-based learning algorithms of learning parameters [66,67]. To get the precise result and to perform the tasks adequately, a hybrid combination of soft computing techniques may be used as it uses data pre-processing techniques or metaheuristic optimization approaches to solve those problems [65,67]. Furthermore, the metaheuristic approach coupled with the ML model may enhance the ML model’s performance as it may adequately reach the local solution from the global best solution [64,67].
The ANFIS model is a hybrid model developed with ANN and fuzzy interface system (FIS). Various researchers have used the ANFIS model for the prediction of flyrock due to blasting [68]. The results are highly promising, and comparative analysis suggests that the proposed modeling approach outperforms ANNs and other traditional time series models in terms of computational speed, forecast errors, efficiency, peak flow estimation, etc. It was observed that the ANFIS model preserves the potential of the ANN approach fully, and eases the model building process.
Zhou [69] utilized PSO and ANN techniques to minimize flyrock due to blasting [68]. PSO-ANN was found better as compared to the ANN model. ICA, GA, extreme learning machine (ELM), and biography-based optimization (BBO) have been applied for the prediction of various geotechnical issues by many researchers. Murlidhar [70] reviewed the ANN-GA [69], ANN-PSO [71], and ANN- ICA models. Each of these hybrid models provided better accuracy as compared to single models [42]. Murlidhar [72] have applied PSO-ELM, BBO-ELM, and ELM models to predict flyrock due to blasting [73].
ELM has insufficient generalization ability in dealing with the samples due to the random initialization of parameters, and PSO uses the individuals sharing information in the group to move the whole group to evolve from disorder to obtain the optimal solution [74]. PSO-ELM takes advantage of PSO to search for global optimal solutions and ELM to quickly deal with the nonlinear relationship [70]. In other words, PSO-ELM uses the PSO algorithm to optimize the input weight matrix and the hidden layer bias in ELM to obtain an optimal network [75,76,77,78]. Therefore, the PSO-ELM model provides better performance as compared to the singleton ELM model. Similarly, the BBO-ELM model provides better performance as compared to the singleton ELM model because the hybrid model provides the advantage of both BBO and ELM models [72]. Hence, in this paper, the authors decided to compare three hybrid models: PSO-ANN, PSO-ELM, and EO-ELM.
3. Background of Model
3.1. Extreme Learning Machine (ELM)
The ELM was introduced by Guang-Bin Huang (2004) [79] for feedforward neural networks. It consists of one hidden layer with multiple hidden nodes and their parameters do not require the tuning of input weights. In ELM, output weights of hidden nodes are generally learned only in one step that result in the learning of a linear model. ELM has a very high generalization capability and is considerably faster than the feedforward neural network (back-propagation algorithm (BP). This is because of the dependency among parameters of the different layers in a feedforward neural network. Due to these dependencies, one is obliged to adjust all of the parameters (weights and biases). So, several iterative learning steps are required to improve the learning performance of the feedforward network. For these reasons, ELM has been widely applied for classification, regression, sparse approximation compression, clustering, future learning, and many more.
Essence of ELM
The hidden layer’s parameters do not require tuning of input weights. “Randomness” is one of the ways to implement ELM other than semi-randomness, which is considered in many traditional methods. In ELM, the hidden layer’s mapping follows the rules of ridge regress theory [80], universal approximation, and neural network generalization theory [81]. Figure 2 shows the mapping of input space and feature space. ELM has the ability that may bridge the current gaps among linear systems, neural networks, matrix theories, SVM, random projection, Fourier series, and others.
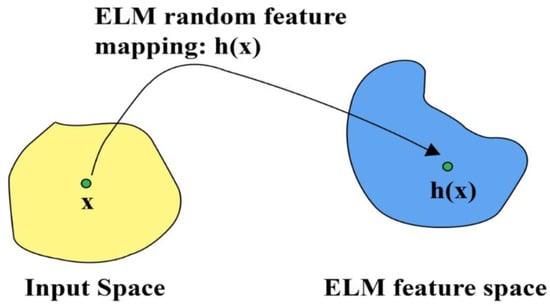
Figure 2.
Mapping of input space and feature space.
The following steps need to be performed if a model consists of a particular number of hidden notes, node output function, and certain training set:
- Randomly assign the hidden node’s parameter
- Calculate the output matrix of the hidden layer
- Compute the output weights.
ELM is one of the ML algorithms which is free from tuning and works on the above-mentioned steps. It consists of hidden nodes with high importance and has a high-speed learning process.
3.2. Artificial Neural Network
The idea of an ANN is derived from the biological neural architecture where a very large number of biological neurons are interconnected through the links. It is an information processing model that is similar to the structure of neural networks present in the human brain in both structure and functions. It mimics the biological neural architecture in two ways: (i) the learning process is used by the network to acquire the knowledge from its surroundings and (ii) the acquired knowledge is stored by the synaptic weights (interconnection strength). An ANN consists of a network of interconnected processing units, which is capable of ‘learning’ to ‘recognize’ a complex input pattern, and predict the output pattern thereof. For this, the neural network is first ‘trained’ to analyze the input patterns and recognize the output that results from these inputs. The network is then able to recognize similarities in new input patterns and can predict the output. This property of a neural network makes it very useful for noisy (inexact) data to be interpolated and outputs predicted in terms of patterns that are already ‘known’ to it. This makes neural networks a ready replacement for older statistical techniques, such as linear regressing, multi-variable regression, and autocorrelation, etc. Even outputs that were previously not apparent to non-experts become recognizable, making the neural network a virtual expert. To solve different problems an ANN can be designed using the following three fundamental components:
- Transfer Function
- Network Architecture
- Learning Law.
3.3. Equilibrium Optimization
The Equilibrium Optimizer (EO) was developed based on a generic mass balance equation [82]. The EO algorithm is designed with a high level of search capability from exploratory and exploitative systems to randomly change solutions and prevent local minima. In the Equilibrium Optimization (EO) algorithm, the equilibrium state (optimal result) is finally achieved through equilibrium candidates or best so-far solutions through search agents randomly [83]. If EO is compared with many metaheuristic algorithms, EO starts the optimization process based on the initial population. The construction of the initial concentrations is based on several dimensions and particles in the search space with consistent random initialization. Particles with their concentrations are known as search agents, corresponding to particles and positions in the PSO algorithm. During the process of optimization in the initial period, there is no awareness and understanding about the equilibrium state. In the beginning, equilibrium candidates are identified by updating concentrations randomly to fit solutions. During the whole optimization process, based on different experimentation and case studies four best-so-far particles are identified and another particle is the concentration of arithmetical mean of the aforesaid four particles. Exploration capability is based on best-so-far particles while exploitation capability is based on the average value. In several engineering problems, the generation rate can be expressed as a function of time [84]. In the case of EO, selecting an appropriate generation rate as well as updating concentrations randomly enhances EO’s exploratory performance during the initial irritation and exploitation search in the final iterations. Thus, EO supports from beginning to end the complete optimization process and avoids local minima. Exploration and exploitation processes are balanced to obtain adaptive values for monitoring parameters resulting in a significant reduction in the movement of particles. To study the efficiency and effectiveness of EO, quantitative and qualitative metrics were endorsed. The EO algorithm showed higher efficiency (i.e., shorter computational time or limited iterations) in achieving optimal or close to optimal solutions with specific or most of the problems examined. The EO algorithm is undoubtedly a better algorithm as compared to the metaheuristic algorithms, such as GA and PSO, or the recently developed algorithms, such as GWO, GA, and GSA. The performance of EO is statistically comparable with SHADE and LSHADE-SPACM algorithms.
3.4. Particle Swarm Optimization (PSO)
The particle swarm optimization algorithm was first introduced by Kennedy and Eberhart (1995) [85]. To start operation, this algorithm distributes a set of entities (particles, each of which stands for a feasible solution) randomly in the search space. An objective function is considered as the determining factor of the swarm’s goal. The fitness of every entity/particle is determined by the value that is correspondent to the objective function. Figure 3 shows a standard flow chart of a PSO.
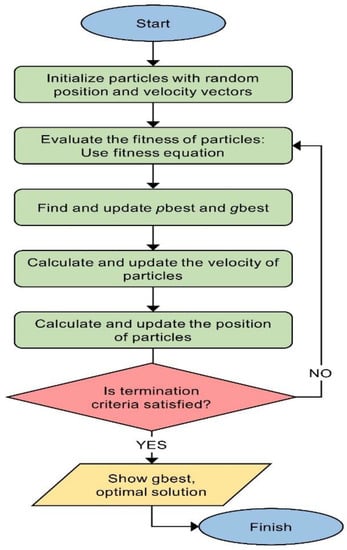
Figure 3.
Standard flow chart of PSO [85].
The PSO algorithm uses a random or stochastically selected population. The first step in the process is to select a population of particles or solutions and iterate the solutions until an optimum is reached. Each particle is assigned a value and then updated as per the ‘gbest’ fitness for two outstanding values. The solutions higher than ‘gbest’ fitness values are chosen and the ‘gbest’ fitness factors are updated. Subsequently, wherever the fitness of the particle is better or higher than that of ‘pbest’, the corresponding parameters of ‘pbest’ are updated. The process would then enter the second phase, where the particles would be examined again.
3.5. Case Study and Data Collection
Basalt, granite, and limestone are common rocks for manufacturing aggregates in the construction industry of Thailand. Figure 4 shows potential rock resources of aggregates in different locations of Thailand. Small aggregate quarries produce less than 15,000 cubic meters per month. On the other hand, large aggregate quarries produce up to 150,000 cubic meters per month [86]. Vast quarries of limestone are used to supply limestone to manufacture Portland cement in factories situated 100 km from Thailand. The selected limestone quarry is an aggregate limestone quarry. Figure 5 shows photographs of an aggregate limestone quarry. Figure 6 shows the blasted muck pile of the face. During a blasting operation, flyrock is generated, which is concerning. In the selected quarry, the input parameters consisting of hole diameter, burden, stemming length, rock density, explosives charge per meter, powder factor, blast ability index, weathering index, and flyrock distance for 114 blasting events were collected. Figure 4 shows the location of the limestone quarry. Table 1 shows the details of all input parameters. The weathering index is site-specific. Based on weathering index, the blast input parameters are decided. Hence, sensitivity analysis of parameters is compared with weathering index.
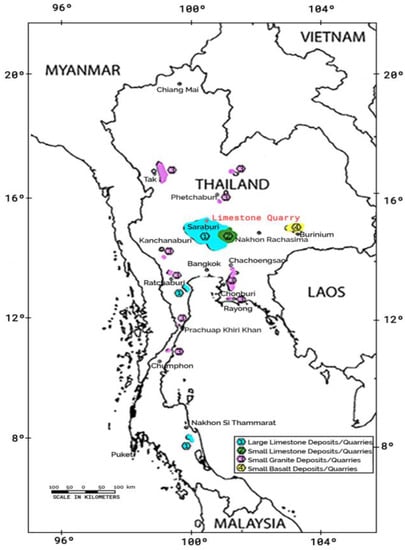
Figure 4.
Location map of Thailand quarry [86].

Figure 5.
Limestone quarry face at Thailand.

Figure 6.
Blasted stone muck pile at quarry face.

Table 1.
Input and output parameters.
Weathering index (WI) is a new parameter introduced based on rock mass properties, such as water absorption (%), porosity (%), and point load index. Maximum values of water absorption and porosity are obtained for completely weathered granite. The maximum value of the point load index is obtained for fresh rock. At each blasting site, samples are collected, and each rock mass property is compared with the maximum value. The average of these ratios is known as the WI.
4. Model Development
4.1. Hybridization of PSO-ANN
The PSO algorithm was developed as a bird swarm simulation by Kennedy and Eberhart. Swarm intelligence is the capability of an individual bird to deal with the previous experiences of the whole swarm. In PSO, the decision-making process is essential, and it can be made based on the following:
- Personal experiences of individuals that give their best results.
- Experiences of other individuals that give the best results of the entire swarms.
Several researchers tried to enhance the generalization capabilities and performance of ANNs by using PSO algorithms because PSO is one of the robust global search methods that can enhance the performance capacity of ANN by adjusting its bias and weight of it. Furthermore, in the case of the local minimum, ANNs can increase the probability of convergence and, at that time, the PSO is likely to obtain the global minimum. Consequently, the developed PSO-ANN model acquires the search properties of both the ANN and PSO models. So, in the case of the PSO-ANN model, the PSO searches for the global minimum and then exploits towards the local solution, which can be employed by the ANN to find the best results in the search space [87].
In a learning procedure for PSO-ANN, it starts with random assignment of weights and biases of a group of random particles. After this step the PSO-ANN model is trained based on the assigned weights and biases and then, at each iteration, the error is calculated between the predicted and actual value. After that, the calculated error is reduced by changing the particle position. By changing the particle position the best solution is selected and accordingly a new error is achieved. This complete learning process continues unless or until the termination criteria are fulfilled.
4.2. Hybridization of PSO-ELM
Based on theory, Huang et al. [88] demonstrated the performance capability of ELM as a universal approximation, and the ability to engage many activation functions. Several researchers utilize ELM due to well-known features, such as fast learning capability and adequate ability to generalize, the same is deployed for prediction methods [79,89]. The generalizing ability of ELM is further enhanced by merging it with some other methods [90,91]. Several researchers from recent decades have successfully combined a nature-based/inspired algorithm to optimize the ELM model. Mohapatra et al. [92] designed a hybrid model consisting of the cuckoo search algorithm and ELM to classify medical data. The stability analysis of the photovoltaic interactive microgrid was carried out with a firefly algorithm by Satapathy et al. [93]. The evaluation of the aging degree of the insulated gate bipolar transistor was done with a whale optimization algorithm and ELM by Li et al. [94]. Figueiredo and Ludermir [95] studied the different topology of PSO—Global, Local, Von Neumann, Wheel, and Four Clusters—and showed, depending upon the problem, suitable topology, which need to be selected for the best PSO-ELM performance. Many researchers have used PSO-ELM for prediction in various engineering problems. PSO-ELM forecasting models were used to predict the regional groundwater depth [96]. The PSO-ELM approach was used for predicting landslide displacement interval [97]. The PSO-ELM model was deployed for predicting stabilized aggregate bases [98]. The PSO-ELM model was deployed to predict the vibration of the ground caused by the process of blasting [99]. Thus, from various research studies, an optimized version of ELM with other algorithms outperformed individual ELM accuracy levels in prediction jobs. ELM models generally get trapped in local minima because the initialization process is stochastic for the network input weights and hidden biases [100]. Various researchers have applied a combination of PSO and ELM to various areas reliably [101]. During the current study, to the best of our information/knowledge, the PSO-ELM model is developed for the first time to predict the flyrock caused by blasting. The flow chart of PSO-ELM is shown in Figure 7.
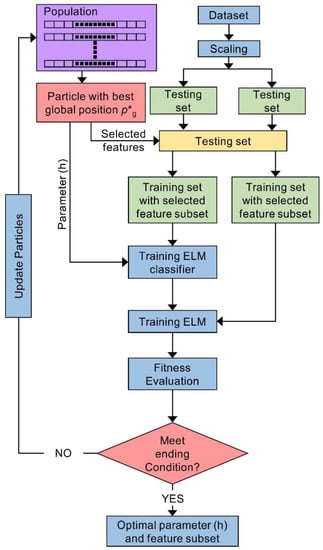
Figure 7.
Flow chart of PSO–ELM.
4.3. Hybridization of EO-ELM
This study proposes a new combination of hybrid ML models, called EO-ELM, where the EO optimizes the ELM learning parameters to find an optimal configuration of ELM for the prediction of flyrock. Here, the concentrations of EO are ELM learning parameters. The RMSE is considered an objective function for EO. The best equilibrium candidate found by EO is considered as the optimal configuration of ELM for prediction tasks.
In EO-ELM, initially, all particles do not know the solution space. The collaboration of five equilibrium candidates helps the concentration updating process of particles. At initial periods of iteration, the equilibrium candidates are diverse and the exponential term (F) produces large random numbers, which help particles to cover the entire solution space. Similarly, during the end period of iterations, particles are surrounded by equilibrium candidates which are in the optimum position with similar configurations. At these moments, the exponential term produces a lower value of random numbers, which helps fine-tune candidate solutions. The algorithm of EO-ELM is shown in the following Algorithm 1.
| Algorithm 1: The algorithm of EO-ELM. Exponential term (F), λ is a turnover rate and defined as a random vector in between 0 and 1, a2 is used to control the exploitation task. a1 is used to control the exploration task, component consequences the direction of intensification and diversification of particles, r is defined as a random vector in between 0 and 1, generation rate (G), r1, and r2 denote the random values between 0 and 1. GCP is called generation rate control parameter |
| 1. Select training and testing dataset 2. Begin ELM training 3. Set hidden units of ELM 4. Obtain the number of input weights and hidden biases 5. Initialize the populations (P) 6. Initialize the fitness of four equilibrium candidates 7. Assignment of EO parameters value (a1 = 2, a2 = 1, GP = 0.5) 8. for it = 1 to maximum iteration number do 9. for i = 1 to P do 10. Estimate the fitness of the ith particle 11. if fitness () < fitness () 12. Replace fitness () with fitness () and with 13. elseif fitness () < fitness () & fitness () < fitness () 14. Replace fitness () with fitness () and with 15. elseif fitness () < fitness () & fitness () < fitness () & fitness () < fitness () 16. Replace fitness () with fitness () and with 17. elseif fitness () < fitness () & fitness () < fitness () & fitness () < fitness () & fitness () < fitness () 18. Replace fitness () with fitness () and with 19. end if 20. end for 21. = 22. (Equilibrium pool) 23. Allocate 24. for i = 1 to P do 25. Random generation of vectors and 26. Random selection of equilibrium candidate from equilibrium pool 27. Evaluate 28. Evaluate 29. Evaluate 30. Evaluate 31. (Concentration update) 32. end for 33. end for 34. Set ELM optimal input weights and hidden biases using 35. Obtain output weights 36. ELM testing |
4.4. Model Verification and Evaluation
One of the most important aspects of the model development process is model verification and evaluation, as it is necessary to understand the behavior of the model to check the evolution of the model towards acquiring the accurate result and to know whether the quality of the test model is excellent or not. To fulfil the desired, a training set is used to train the developed models and a different testing set is used to verify the model development. To evaluate the reliability of the developed model, seven different evaluation matrices, namely determination coefficient (R|2), root mean square error (RMSE), variance account factor (VAF), mean absolute error (MAE), Nash–Sutcliffe efficiency (NSE), mean absolute percentage error (MAPE), and a-20 index (A20), were used to define the relation between the actual and predicted value. Out of these evaluation matrices, the RMSE shows the standard deviation of the error between the actual and predicted values. The MAPE shows the error value percentage with the original data; having 0% MAPE shows the perfect model. The NSE value is a normalized statistic and is used to measure the goodness of fit of the model. Similarly, in the case of MAE, the goodness of the model increases with a decrease in the value of MAE. Further, R2 indicates the correlation between the actual and predicted values. The closer the value is to 1, the more perfect the model (1). Similarly, if the value of A20 is closer to 1, this shows a perfect prediction model (2). VAF shows the ratio of error variance to the measured data variance. The calculation formulas for different evaluation matrices are as follows:
5. Results and Discussion
The objective of this study was to predict the flyrock distance. Therefore, crucial blast design parameters were selected as input parameters (hole diameter, burden, rock density, stemming length, charge per meter, powder factor, blastability index, and weathering index). After that, the PSO-ELM, PSO-ANN, and EO-ELM models were developed and used for the prediction of flyrock. When data are split into train and test sets, it always becomes a challenging task to develop a generalized data-driven model. This work used 80% and 20% data split ratios for train and test data, respectively. These split data are used to test and compare the performance of the developed models.
To prove the model’s effectiveness with the split dataset, a 10-times average run of three models is checked and compared. An average run of optimization-coupled ML models is useful to check the randomness in problem-solving for the optimal parameter set of optimization algorithms. Table 2 shows the optimal parameter set of metaheuristic algorithms, which are initially set by heat and trial method.

Table 2.
Optimal parameter values of metaheuristic algorithms for eight hidden neurons in ELM.
During training, 500 iterations are set for each optimization-coupled ML model. The convergence plot of RMSE vs. iteration count is plotted and shown in Figure 8. Figure 8 shows faster (around 200 iterations) and better convergence ability of the EO-ELM compared to the PSO-ELM and PSO-ANN. The PSO-ELM and PSO-ANN become stuck in a local solution with premature convergence (Figure 8). Furthermore, the PSO-ANN may have an improper learning rate and overfitting issues due to the use of stochastic selection or gradient-based learning algorithms. As gradient-based learning algorithms intend to reach the minimum training error, but do not consider the magnitude of weights and only uses differentiable activation functions; due to this, they have less generalization performance [102]. In spite of this, other models use ELM, which is extremely fast and can train SLFNs using non-differentiable activation function to reach the solutions in a straightforward way without having issues, such as local minimum, improper learning rate, and overfitting. It tends to reach the smallest training error including the smallest norm of weights; due to this, it has the better generalization performance [102].
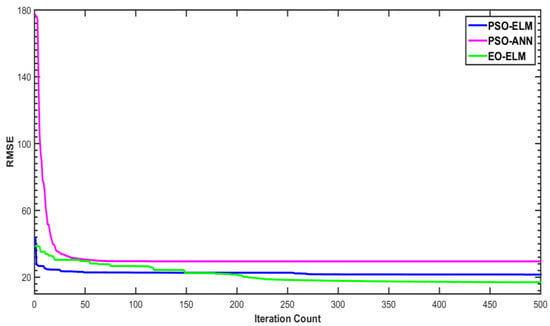
Figure 8.
Convergence plot of three models (training period).
The training phase scatter diagrams for the EO-ELM, PSO-ANN, and PSO-ELM are shown in Figure 9, Figure 10 and Figure 11, respectively. It is apparent from Figure 9, Figure 10 and Figure 11 that the EO-ELM (Figure 9) predicts flyrock values more accurately compared to the PSO-ANN (Figure 10) and PSO-ELM (Figure 11). The testing phase scatter diagrams for the EO-ELM, PSO-ANN, and PSO-ELM are shown in Figure 12, Figure 13 and Figure 14, respectively. It is evident that the EO-ELM (Figure 12) predicts the test flyrock data better compared to the PSO-ANN (Figure 13) and PSO-ELM (Figure 14). Table 3 shows linear equations of the predicted and measured values for the EO-ELM, PSO-ANN, and PSO-ELM for training and testing data, respectively.
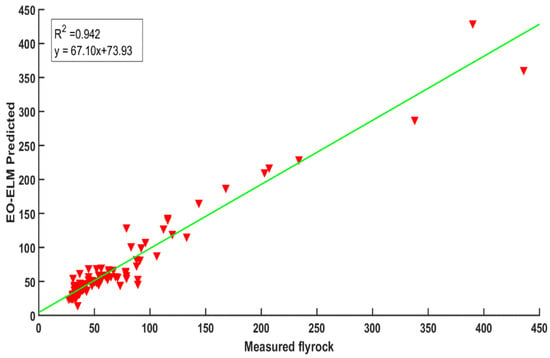
Figure 9.
Comparison of predicted flyrock with the EO-ELM vs. measured flyrock.
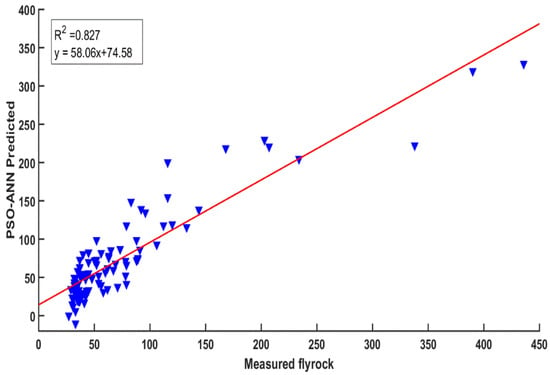
Figure 10.
Measured flyrock and predicted values of flyrock with the PSO-ANN for training data.
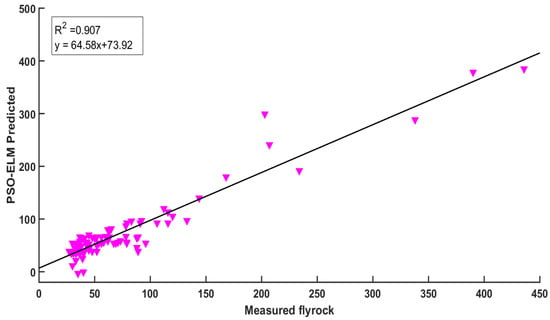
Figure 11.
Measured flyrock and predicted values of flyrock with the PSO-ELM for training data.
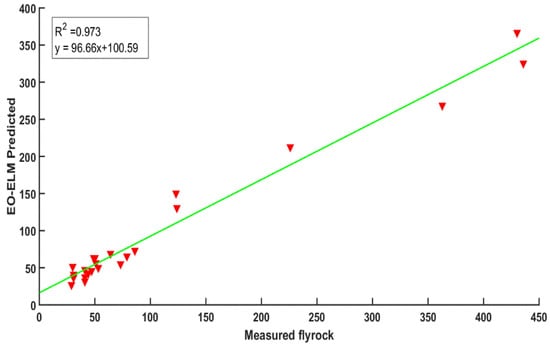
Figure 12.
Comparison of measured flyrock vs. the EO-ELM prediction for testing data.
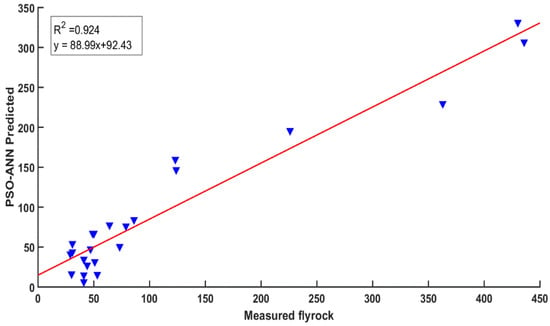
Figure 13.
Comparison of measured flyrock vs. the PSO-ANN prediction for testing data.
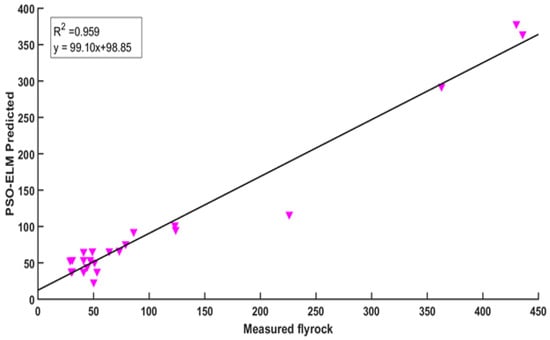
Figure 14.
Comparison of measured flyrock vs. the PSO-ELM prediction for testing data.

Table 3.
Linear equations for predicted and measured values for the EO-ELM, PSO-ANN, and PSO-ELM for training and testing data.
Table 4 shows the better prediction efficiency of the EO-ELM in the training and testing period compared to the PSO-ANN and PSO-ELM in terms of seven matrices. In the testing period, the developed EO-ELM (R2 = 0.97, RMSE = 34.82, MAE = 20.3, MAPE = 17.60, NSE = 0.978, VAF = 97.88, A20 = 0.65) performed better compared to the PSO-ELM (R2 = 0.959, RMSE = 35.7 MAE = 23.53, MAPE = 21.84, NSE = 0.96, VAF = 95.79, A20 = 0.56) and PSO-ANN (R2 = 0.924, RMSE = 48.12, MAE = 31.68, MAPE = 24.25, NSE = 0.93, VAF = 92.89, A20 = 0.35). Furthermore, for better representation in terms of model deviations, the receiver operating characteristic (ROC) curve was drawn. It is evident that all of the models capture the good relationship in the prediction of flyrock during training (Figure 15) and minimum deviation was found for the EO-ELM followed by the PSO-ELM and PSO-ANN. Amongst the models, the EO-ELM shows comparatively lesser deviation during the training period. During the testing period, a similar pattern was observed, the EO-ELM shows the minimum deviations followed by the PSO-ELM and PSO-ANN (Figure 16).

Table 4.
Comparison of three models in terms of seven matrices.
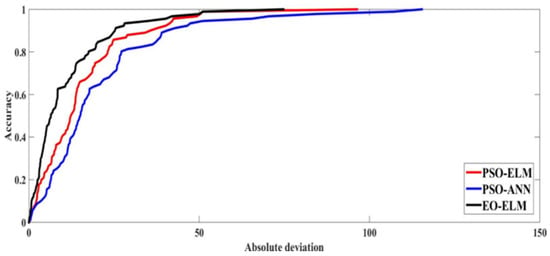
Figure 15.
Diagram of REC for training dataset.
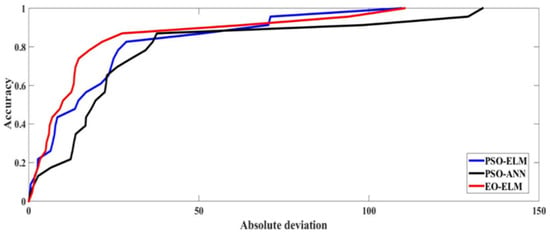
Figure 16.
Diagram of REC for testing dataset.
5.1. Average Performance of Models
Table 5 shows the average results for the 10-times run of three models. The EO-ELM shows the best average prediction performance compared to the PSO-ELM and PSO-ANN in terms of all matrices (Table 5). Figure 17a shows the most generalized performance of the EO-ELM (training phase) at each of the runs (10-times) compared to the PSO-ELM and PSO-ANN. Figure 17b shows that the EO-ELM has the best average convergence rate compared to the PSO-ELM and PSO-ANN.

Table 5.
Comparison of average results for 1-times run of models.
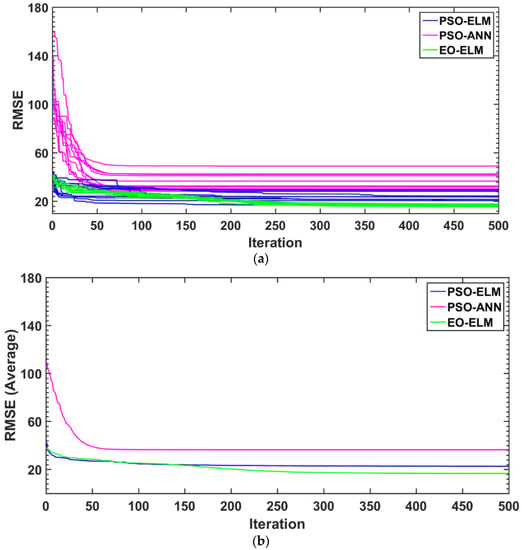
Figure 17.
Convergence of the models for (a) 10 runs, and (b) average of 10 runs.
5.2. Anderson–Darling (A–D) Test
A non-parametric test called the A–D test was performed to assess the normality of all three models [68]. The p-values for the PSO-ELM, PSO-ANN, and EO-ELM models are less than the significance level of 0.05 (Table 6). Table 6 shows that the EO-ELM is the best performing model in estimating flyrock.

Table 6.
Comparison of average results for 10-times run of models.
5.3. Sensitivity Analysis
Sensitivity analysis of parameters, with respect to the weathering index, was carried out as shown in Figure 18. It showed the corresponding relationship of the parameter with respect to the measured flyrock distance based on the cosine amplitude. The application of this method was based on expressing all data pairs in a common Z-space. The following equation defines a data array Z based on data pairs of each input and output:
whereas, zi is a vector of length m in array Z, that as Equation (9):
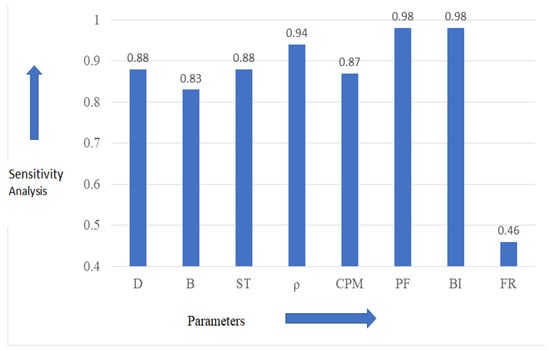
Figure 18.
Sensitivity analysis of parameters with respect to weathering index.
Each point required m-coordinates for describing completely by training each of these data pairs in m dimensional space. The results were achieved as all of the points were in the spaced pair. The following equation shows the strength of relation (rij) between the data set Zi and Zj as Equation (10):
The input parameters were selected, which were most sensitive, to apply to various prediction models and identify the best model suitable for comparing the predicted value and the measured value of flyrock distance.
6. Conclusions
This study uses three hybrid models: the EO–ELM, PSO–ANN, and PSO-ELM to predict flyrock. Out of these three hybrid models, the EO-ELM is proposed and the rest were used to validate the performance of the proposed model. The seven different matrices (R2, RMSE, MAPE, NSE, MAE, VAF, and A20) are used for comparing the efficacy of the developed model. The developed EO-ELM model performed better compared to PSO-the ELM and PSO-ANN in predicting flyrock (Table 4). Further, all models were run 10-times and average results are shown in Table 5. It was observed that the EO-ELM model outperformed the PSO-ELM and PSO-ANN in average results. Furthermore, the 10-times run of the EO-ELM model showed better convergence capability (Figure 17) than the other two. Further, the A–D test showed that the EO-ELM model has better performance efficiency compared to the PSO-ELM and PSO-ANN. A sensitivity analysis was done introducing a new parameter, WI. The PF and BI showed the highest sensitivity with 0.98 each (Figure 18).
The limitation of this study is that this study was carried out for a particular limestone mine in Thailand. Therefore, the obtained results may not be suitable for other geological settings, i.e., in granite or other quarries. So, there is a need of further research by considering non controllable parameters of the blastability index, WI. On the other hand, by refining the controllable parameters, accuracy of the prediction of flyrock can be improved. There are a large number of mines near to the limestone mine under study and if large data sets are collected, further reliability of the prediction models can be improved through future research. The number of input parameters is eight. However, future studies of the prediction of flyrock can be done by limiting to five influential input parameters. The use of the latest technology, such as the video recording of flyrock with drones, will add value for future research. Furthermore, the wavelet frequency domain parameter or innovative liquid carbon dioxide rock-breaking technology are recent technologies used for blasting. Thus, there is a need to develop a new technology alternative to blasting.
Author Contributions
Conceptualization, E.T.M., R.M.B., D.K. and B.R.; methodology, R.M.B. and R.K.; software, R.K., D.K. and B.R.; formal analysis, R.M.B. and D.K.; resources, E.T.M. and R.M.B.; data curation, R.M.B.; writing—original draft, E.T.M., R.M.B., D.K., BR., M.M.S.S., S.K. and R.K.; writing—review and editing, R.MB., E.T.M., RK., M.M.S.S. and D.K.; supervision, E.T.M., D.K. and B.R.; funding acquisition, M.M.S.S. All authors have read and agreed to the published version of the manuscript.
Funding
The research is partially funded by the Ministry of Science and Higher Education of the Russian Federation under the strategic academic leadership program ‘Priority 2030’ (Agreement 075-15-2021-1333 dated 30 September 2021).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Authors are thankful to Edy Toonizam Mohamad, Dean of Department of Civil Engineering, Universiti Teknologi Malaysia for encouragement for this research. Authors are also thankful to Vitaly Sergeev, Centre of Peter the Great St. Petersburg Polytechnic University, 195251 St. Petersburg, Russia for guidance and supervision of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bhandari, S. Engineering Rock Blasting Operations. Available online: https://www.osti.gov/etdeweb/biblio/661808 (accessed on 3 September 2022).
- Roy, P.P. Rock Blasting: Effects and Operations; IBH Publishing: New Delhi, India; Oxford, UK, 2005. [Google Scholar]
- Mohamad, E.T.; Yi, C.S.; Murlidhar, B.R.; Saad, R. Effect of Geological Structure on Flyrock Prediction in Construction Blasting. Geotech. Geol. Eng. 2018, 36, 2217–2235. [Google Scholar] [CrossRef]
- Li, H.B.; Zhao, J.; Li, J.R.; Liu, Y.Q.; Zhou, Q.C. Experimental studies on the strength of different rock types under dynamic compression. Int. J. Rock Mech. Min. Sci. 2004, 41, 68–73. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T.N. Prediction of blast-induced ground vibration using artificial neural network. Int. J. Rock Mech. Min. Sci. 2009, 46, 1214–1222. [Google Scholar] [CrossRef]
- Raina, A.K.; Murthy, V.M.S.R.; Soni, A.K. Estimating flyrock distance in bench blasting through blast induced pressure measurements in rock. Int. J. Rock Mech. Min. Sci. 2015, 76, 209–216. [Google Scholar] [CrossRef]
- Bhatawdekar, R.M.; Edy, M.T.; Danial, J.A. Building information model for drilling and blasting for tropically weathered rock. J. Mines Met. Fuels 2019, 67, 494–500. [Google Scholar]
- Mohamad, E.T.; Murlidhar, B.R.; Armaghani, D.J.; Saad, R.; Yi, C.S. Effect of Geological Structure and Blasting Practice in Fly Rock Accident at Johor, Malaysia. J. Teknol. 2016, 78. [Google Scholar] [CrossRef]
- Sastry, V.R.; Chandar, K.R. Assessment of objective based blast performance: Ranking system. In Measurement and Analysis of Blast Fragmentation; CRC Press: New Delhi, India, 2009; pp. 13–17. [Google Scholar]
- Kanchibotla, S.S.; Valery, W.; Morrell, S. Modelling fines in blast fragmentation and its impact on crushing and grinding. In Explo ’99—A Conference on Rock Breaking; The Australasian Institute of Mining and Metallurgy: Kalgoorlie, Australia, 1999; pp. 137–144. [Google Scholar]
- Armaghani, D.J. Rock fragmentation prediction through a new hybrid model based on imperial competitive algorithm and neural network. Smart Constr. Res. 2018, 2, 1–12. [Google Scholar] [CrossRef]
- Thornton, D.; Kanchibotla, S.S.; Brunton, I. Modelling the Impact of Rockmass and Blast Design Variation on Blast Fragmentation. Fragblast 2002, 6, 169–188. [Google Scholar] [CrossRef]
- Cunningham, C.V.B. The Kuz-Ram fragmentation model–20 years on. In Brighton Conference Proceedings; European Federation of Explosives Engineer: Brighton, UK, 2005; Volume 2005, pp. 201–210. [Google Scholar]
- Venkatesh, H.S.; Bhatawdekar, R.M.; Adhikari, G.R.; Theresraj, A.I. Assessment and Mitigation of Ground Vibrations and Flyrock at a Limestone Quarry. 1999, pp. 145–152. Available online: https://www.academia.edu/34145884/ASSESSMENT_AND_MITIGATION_OF_GROUND_VIBRATIONS_AND_FLYROCK_AT_A_LIMESTONE_QUARRY (accessed on 3 September 2022).
- Raina, A.K.; Chakraborty, A.K.; Choudhury, P.B.; Sinha, A. Flyrock danger zone demarcation in opencast mines: A risk based approach. Bull. Eng. Geol. Environ. 2011, 70, 163–172. [Google Scholar] [CrossRef]
- Xiong, H.; Yin, Z.Y.; Nicot, F. A multiscale work-analysis approach for geotechnical structures. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1230–1250. [Google Scholar] [CrossRef]
- Xiong, H.; Yin, Z.Y.; Nicot, F. Programming a micro-mechanical model of granular materials in Julia. Adv. Eng. Softw. 2020, 145, 102816. [Google Scholar] [CrossRef]
- Xiong, H.; Yin, Z.Y.; Zhao, J.; Yang, Y. Investigating the effect of flow direction on suffusion and its impacts on gap-graded granular soils. Acta Geotech. 2021, 16, 399–419. [Google Scholar] [CrossRef]
- Xiong, H.; Wu, H.; Bao, X.; Fei, J. Investigating effect of particle shape on suffusion by CFD-DEM modeling. Constr. Build. Mater. 2021, 289, 123043. [Google Scholar] [CrossRef]
- Chen, F.; Xiong, H.; Wang, X.; Yin, Z. Transmission effect of eroded particles in suffusion using CFD-DEM coupling method. Acta Geotech. 2022, 1–20. [Google Scholar] [CrossRef]
- Fu, Y.; Zeng, D.; Xiong, H.; Li, X.; Chen, Y. Seepage effect on failure mechanisms of the underwater tunnel face via CFD-DEM coupling. Comput. Geotech. 2020, 121, 103449. [Google Scholar] [CrossRef]
- Xiong, H.; Yin, Z.Y.; Nicot, F.; Wautier, A.; Marie, M.; Darve, F.; Veylon, G.; Philippe, P. A novel multi-scale large deformation approach for modelling of granular collapse. Acta Geotech. 2021, 16, 2371–2388. [Google Scholar] [CrossRef]
- Wang, X.; Yin, Z.Y.; Xiong, H.; Su, D.; Feng, Y.T. A spherical-harmonic-based approach to discrete element modeling of 3D irregular particles. Int. J. Numer. Methods Eng. 2021, 122, 5626–5655. [Google Scholar] [CrossRef]
- Wang, X.; Yin, Z.Y.; Zhang, J.Q.; Xiong, H.; Su, D. Three-dimensional reconstruction of realistic stone-based materials with controllable stone inclusion geometries. Constr. Build. Mater. 2021, 305, 124240. [Google Scholar] [CrossRef]
- Chen, G.; Li, Q.-Y.; Li, D.-Q.; Wu, Z.-Y.; Liu, Y. Main frequency band of blast vibration signal based on wavelet packet transform. Appl. Math. Model. 2019, 74, 569–585. [Google Scholar] [CrossRef]
- Li, Q.-Y.; Chen, G.; Luo, D.-Y.; Ma, H.-P.; Liu, Y. An experimental study of a novel liquid carbon dioxide rock-breaking technology. Int. J. Rock Mech. Min. Sci. 2020, 128, 104244. [Google Scholar] [CrossRef]
- Hudaverdi, T.; Akyildiz, O. A new classification approach for prediction of flyrock throw in surface mines. Bull. Eng. Geol. Environ. 2019, 78, 177–187. [Google Scholar] [CrossRef]
- Kecojevic, V.; Radomsky, M. Flyrock phenomena and area security in blasting-related accidents. Saf. Sci. 2005, 43, 739–750. [Google Scholar] [CrossRef]
- Bajpayee, T.S.; Rehak, T.R.; Mowrey, G.L.; Ingram, D.K. Blasting injuries in surface mining with emphasis on flyrock and blast area security. J. Saf. Res. 2004, 35, 47–57. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, G.R. Studies on Flyrock at Limestone Quarries. Rock Mech. Rock Eng. 1999, 32, 291–301. [Google Scholar] [CrossRef]
- Raina, A.K.; Murthy, V.M.S.R.; Soni, A.K. Flyrock in bench blasting: A comprehensive review. Bull. Eng. Geol. Environ. 2014, 73, 1199–1209. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Amnieh, H.B. A Fuzzy Rule-Based Approach to Address Uncertainty in Risk Assessment and Prediction of Blast-Induced Flyrock in a Quarry. Nat. Resour. Res. 2020, 29, 669–689. [Google Scholar] [CrossRef]
- Bhatawdekari, R.M.; Danial, J.A.; Edy, T.M. A review of prediction of blast performance using computational techniques. In Proceedings of the ISERME 2018 International Symposium on Earth Resources Management & Environment, Thalawathugoda, Sri Lanka, 24 August 2018. [Google Scholar]
- Sharma, L.K.; Vishal, V.; Singh, T.N. Developing novel models using neural networks and fuzzy systems for the prediction of strength of rocks from key geomechanical properties. Measurement 2017, 102, 158–169. [Google Scholar] [CrossRef]
- Koohmishi, M. Assessment of strength of individual ballast aggregate by conducting point load test and establishment of classification method. Int. J. Rock Mech. Min. Sci. 2021, 141, 104711. [Google Scholar] [CrossRef]
- Monjezi, M.; Bahrami, A.; Varjani, A.Y.; Sayadi, A.R. Prediction and controlling of flyrock in blasting operation using artificial neural network. Arab. J. Geosci. 2011, 4, 421–425. [Google Scholar] [CrossRef]
- Ghasemi, E.; Amini, H.; Ataei, M.; Khalokakaei, R. Application of artificial intelligence techniques for predicting the flyrock distance caused by blasting operation. Arab. J. Geosci. 2014, 7, 193–202. [Google Scholar] [CrossRef]
- Dehghani, H.; Ataee-Pour, M. Development of a model to predict peak particle velocity in a blasting operation. Int. J. Rock Mech. Min. Sci. 2011, 48, 51–58. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mahdiyar, A.; Hasanipanah, M.; Faradonbeh, R.S.; Khandelwal, M.; Amnieh, H.B. Risk Assessment and Prediction of Flyrock Distance by Combined Multiple Regression Analysis and Monte Carlo Simulation of Quarry Blasting. Rock Mech. Rock Eng. 2016, 49, 3631–3641. [Google Scholar] [CrossRef]
- Marto, A.; Hajihassani, M.; Armaghani, D.J.; Mohamad, E.T.; Makhtar, A.M. A Novel Approach for Blast-Induced Flyrock Prediction Based on Imperialist Competitive Algorithm and Artificial Neural Network. Sci. World J. 2014. [Google Scholar] [CrossRef] [PubMed]
- Jahed Armaghani, D.; Hajihassani, M.; Monjezi, M.; Mohamad, E.T.; Marto, A.; Moghaddam, M.R. Application of two intelligent systems in predicting environmental impacts of quarry blasting. Arab. J. Geosci. 2015, 8, 9647–9665. [Google Scholar] [CrossRef]
- Trivedi, R.; Singh, T.N.; Gupta, N. Prediction of Blast-Induced Flyrock in Opencast Mines Using ANN and ANFIS. Geotech. Geol. Eng. 2015, 33, 875–891. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Armaghani, D.J.; Amnieh, H.B.; Majid, M.Z.A.; Tahir, M.M.D. Application of PSO to develop a powerful equation for prediction of flyrock due to blasting. Neural Comput. Appl. 2017, 28, 1043–1050. [Google Scholar] [CrossRef]
- Faradonbeh, R.S.; Armaghani, D.J.; Amnieh, H.B.; Mohamad, E.T. Prediction and minimization of blast-induced flyrock using gene expression programming and firefly algorithm. Neural Comput. Appl. 2018, 29, 269–281. [Google Scholar] [CrossRef]
- Kumar, N.; Mishra, B.; Bali, V. A Novel Approach for Blast-Induced Fly Rock Prediction Based on Particle Swarm Optimization and Artificial Neural Network. In Proceedings of International Conference on Recent Advancement on Computer and Communication; Springer: Berlin/Heidelberg, Germany, 2018; Volume 34, pp. 19–27. [Google Scholar] [CrossRef]
- Rad, H.N.; Bakhshayeshi, I.; Jusoh, W.A.W.; Tahir, M.M.; Foong, L.K. Prediction of Flyrock in Mine Blasting: A New Computational Intelligence Approach. Nat. Resour. Res. 2020, 29, 609–623. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Fallah, A.; Armaghani, D.J.; Azizi, A.; Mohamad, E.T. Three hybrid intelligent models in estimating flyrock distance resulting from blasting. Eng. Comput. 2019, 35, 243–256. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Zaharakis, I.; Pintelas, P. Supervised machine learning: A review of classification techniques. Emerg. Artif. Intell. Appl. Comput. Eng. 2007, 160, 3–24. [Google Scholar]
- Blum, A.L.; Langley, P. Selection of relevant features and examples in machine learning. Artif. Intell. 1997, 97, 245–271. [Google Scholar] [CrossRef]
- Amini, H.; Gholami, R.; Monjezi, M.; Torabi, S.R.; Zadhesh, J. Evaluation of flyrock phenomenon due to blasting operation by support vector machine. Neural Comput. Appl. 2012, 21, 2077–2085. [Google Scholar] [CrossRef]
- Rad, H.N.; Hasanipanah, M.; Rezaei, M.; Eghlim, A.L. Developing a least squares support vector machine for estimating the blast-induced flyrock. Eng. Comput. 2018, 34, 709–717. [Google Scholar] [CrossRef]
- Lu, X.; Hasanipanah, M.; Brindhadevi, K.; Amnieh, H.B.; Khalafi, S. ORELM: A Novel Machine Learning Approach for Prediction of Flyrock in Mine Blasting. Nat. Resour. Res. 2020, 29, 641–654. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Tonnizam Mohamad, E.; Hajihassani, M.; Alavi Nezhad Khalil Abad, S.V.; Marto, A.; Moghaddam, M.R. Evaluation and prediction of flyrock resulting from blasting operations using empirical and computational methods. Eng. Comput. 2016, 32, 109–121. [Google Scholar] [CrossRef]
- Ghasemi, E.; Sari, M.; Ataei, M. Development of an empirical model for predicting the effects of controllable blasting parameters on flyrock distance in surface mines. Int. J. Rock Mech. Min. Sci. 2012, 52, 163–170. [Google Scholar] [CrossRef]
- Gupta, R.N. Surface Blasting and Its Impact on Environment. Impact of Mining on Environment; Ashish Publishing House: New Delhi, India, 1980; pp. 23–24. [Google Scholar]
- Little, T.N. Flyrock risk. In Proceedings EXPLO; 2007; pp. 3–4. [Google Scholar]
- Richards, A.; Moore, A. Flyrock control-by chance or design. In Proceedings of the Annual Conference on Explosives and Blasting Technique; International Society for Environmental Ethics (ISEE), 2004; Volume 1, pp. 335–348. [Google Scholar]
- Trivedi, R.; Singh, T.N.; Raina, A.K. Prediction of blast-induced flyrock in Indian limestone mines using neural networks. J. Rock Mech. Geotech. Eng. 2014, 6, 447–454. [Google Scholar] [CrossRef]
- Zhou, J.; Aghili, N.; Ghaleini, E.N.; Bui, D.T.; Tahir, M.M.; Koopialipoor, M. A Monte Carlo simulation approach for effective assessment of flyrock based on intelligent system of neural network. Eng. Comput. 2020, 36, 713–723. [Google Scholar] [CrossRef]
- Lundborg, N.; Persson, A.; Ladegaard-Pedersen, A.; Holmberg, R. Keeping the lid on flyrock in open-pit blasting. Eng. Min. J. 1975, 176, 95–100. [Google Scholar]
- Roth, J. A Model for the Determination of Flyrock Range as a Function of Shot Conditions; National Technical Information Service: Alexandria, VA, USA, 1979. [Google Scholar]
- Stojadinović, S.; Pantović, R.; Žikić, M. Prediction of flyrock trajectories for forensic applications using ballistic flight equations. Int. J. Rock Mech. Min. Sci. 2011, 48, 1086–1094. [Google Scholar] [CrossRef]
- Bui, X.-N.; Nguyen, H.; Le, H.-A.; Bui, H.-B.; Do, N.-H. Prediction of Blast-induced Air Over-pressure in Open-Pit Mine: Assessment of Different Artificial Intelligence Techniques. Nat. Resour. Res. 2020, 29, 571–591. [Google Scholar] [CrossRef]
- Kasabov, N.; Scott, N.M.; Tu, E.; Marks, S.; Sengupta, N.; Capecci, E.; Othman, M.; Doborjeh, M.G.; Murli, N.; Hartono, R.; et al. Evolving spatio-temporal data machines based on the NeuCube neuromorphic framework: Design methodology and selected applications. Neural Netw. 2016, 78, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Hajihassani, M.; Armaghani, D.J.; Marto, A.; Mohamad, E.T. Ground vibration prediction in quarry blasting through an artificial neural network optimized by imperialist competitive algorithm. Bull. Eng. Geol. Environ. 2015, 74, 873–886. [Google Scholar] [CrossRef]
- Roy, B.; Singh, M.P. An empirical-based rainfall-runoff modelling using optimization technique. Int. J. River Basin Manag. 2020, 18, 49–67. [Google Scholar] [CrossRef]
- Roy, B.; Singh, M.P.; Singh, A. A novel approach for rainfall-runoff modelling using a biogeography-based optimization technique. Int. J. River Basin Manag. 2021, 19, 67–80. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, M.P.; Roy, B.; Shahid, A.H. A Comparative Assessment of Metaheuristic Optimized Extreme Learning Machine and Deep Neural Network in Multi-Step-Ahead Long-term Rainfall Prediction for All-Indian Regions. Water Resour. Manag. 2021, 35, 1927–1960. [Google Scholar] [CrossRef]
- Zhou, J.; Koopialipoor, M.; Murlidhar, B.R.; Fatemi, S.A.; Tahir, M.M.; Armaghani, D.J.; Li, C. Use of Intelligent Methods to Design Effective Pattern Parameters of Mine Blasting to Minimize Flyrock Distance. Nat. Resour. Res. 2020, 29, 625–639. [Google Scholar] [CrossRef]
- Murlidhar, B.R.; Armaghani, D.J.; Mohamad, E.T. Intelligence Prediction of Some Selected Environmental Issues of Blasting: A Review. Open Constr. Build. Technol. J. 2020, 14, 298–308. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Hasanipanah, M.; Mahdiyar, A.; Majid, M.Z.A.; Amnieh, H.B.; Tahir, M.M.D. Airblast prediction through a hybrid genetic algorithm-ANN model. Neural Comput. Appl. 2018, 29, 619–629. [Google Scholar] [CrossRef]
- Murlidhar, B.R.; Kumar, D.; Armaghani, D.J.; Mohamad, E.T.; Roy, B.; Pham, B.T. A Novel Intelligent ELM-BBO Technique for Predicting Distance of Mine Blasting-Induced Flyrock. Nat. Resour. Res. 2020, 29, 4103–4120. [Google Scholar] [CrossRef]
- Faradonbeh, R.S.; Hasanipanah, M.; Amnieh, H.B.; Armaghani, D.J.; Monjezi, M. Development of GP and GEP models to estimate an environmental issue induced by blasting operation. Environ. Monit. Assess. 2018, 190, 351. [Google Scholar] [CrossRef]
- Anand, A.; Suganthi, L. Forecasting of Electricity Demand by Hybrid ANN-PSO Models. In Deep Learning and Neural Networks: Concepts, Methodologies, Tools, and Applications; IGI Global: Hershey, PA, USA, 2020; pp. 865–882. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Hajihassani, M.; Mohamad, E.T.; Marto, A.; Noorani, S.A. Blasting-induced flyrock and ground vibration prediction through an expert artificial neural network based on particle swarm optimization. Arab. J. Geosci. 2014, 7, 5383–5396. [Google Scholar] [CrossRef]
- Cai, W.; Yang, J.; Yu, Y.; Song, Y.; Zhou, T.; Qin, J. PSO-ELM: A Hybrid Learning Model for Short-Term Traffic Flow Forecasting. IEEE Access 2020, 8, 6505–6514. [Google Scholar] [CrossRef]
- Zeng, J.; Roy, B.; Kumar, D.; Mohammed, A.S.; Armaghani, D.J.; Zhou, J.; Mohamad, E.T. Proposing several hybrid PSO-extreme learning machine techniques to predict TBM performance. Eng. Comput. 2021, 1–17. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Kumar, D.; Zarzoura, F.; Roy, B.; Hu, J.W. A wavelet—Particle swarm optimization—Extreme learning machine hybrid modeling for significant wave height prediction. Ocean Eng. 2020, 213, 107777. [Google Scholar] [CrossRef]
- Cui, D.; Huang, G.-B.; Liu, T. ELM based smile detection using Distance Vector. Pattern Recognit. 2018, 79, 356–369. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 2000, 42, 80. [Google Scholar] [CrossRef]
- Bartlett, P.L. The sample complexity of pattern classification with neural networks: The size of the weights is more important than the size of the network. IEEE Trans. Inf. Theory 1998, 44, 525–536. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Nazaroff, W.W.; Alvarez-Cohen, L. Environmental Engineering Science; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Guo, Z. Review of indoor emission source models. Part 1. Overview. Environ. Pollut. 2002, 120, 533–549. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Tangchawal, S. Planning and Evaluation for Quarries: Case Histories in Thailand; IAEG2006: Nottingham, UK, 2006. [Google Scholar]
- Jahed Armaghani, D.; Shoib, R.S.N.S.B.R.; Faizi, K.; Rashid, A.S.A. Developing a hybrid PSO–ANN model for estimating the ultimate bearing capacity of rock-socketed piles. Neural Comput. Appl. 2017, 28, 391–405. [Google Scholar] [CrossRef]
- Huang, G.-B.; Chen, L.; Siew, C.-K. Universal Approximation Using Incremental Constructive Feedforward Networks with Random Hidden Nodes. IEEE Trans. Neural Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Tsang, E.C.C.; Zhu, J. Training an extreme learning machine by localized generalization error model. Soft Comput. 2018, 22, 3477–3485. [Google Scholar] [CrossRef]
- Mohapatra, P.; Chakravarty, S.; Dash, P.K. An improved cuckoo search based extreme learning machine for medical data classification. Swarm Evol. Comput. 2015, 24, 25–49. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. An experimental investigation of three new hybrid wind speed forecasting models using multi-decomposing strategy and ELM algorithm. Renew. Energy 2018, 123, 694–705. [Google Scholar] [CrossRef]
- Satapathy, P.; Dhar, S.; Dash, P.K. An evolutionary online sequential extreme learning machine for maximum power point tracking and control in multi-photovoltaic microgrid system. Renew. Energy Focus 2017, 21, 33–53. [Google Scholar] [CrossRef]
- Li, L.-L.; Sun, J.; Tseng, M.-L.; Li, Z.-G. Extreme learning machine optimized by whale optimization algorithm using insulated gate bipolar transistor module aging degree evaluation. Expert Syst. Appl. 2019, 127, 58–67. [Google Scholar] [CrossRef]
- Figueiredo, E.M.N.; Ludermir, T.B. Effect of the PSO Topologies on the Performance of the PSO-ELM. In Proceedings of the 2012 Brazilian Symposium on Neural Networks, Curitiba, Brazil, 20–25 October 2012; pp. 178–183. [Google Scholar] [CrossRef]
- Liu, D.; Li, G.; Fu, Q.; Li, M.; Liu, C.; Faiz, M.A.; Khan, M.I.; Li, T.; Cui, S. Application of Particle Swarm Optimization and Extreme Learning Machine Forecasting Models for Regional Groundwater Depth Using Nonlinear Prediction Models as Preprocessor. J. Hydrol. Eng. 2018, 23. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, H.; Wen, T.; Ma, J. A hybrid intelligent approach for constructing landslide displacement prediction intervals. Appl. Soft Comput. 2019, 81, 105506. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Kumar, D.; Samui, P.; Gabr, A.R.; Hu, J.W.; Jin, X.; Roy, B. Particle Swarm Optimization Algorithm-Extreme Learning Machine (PSO-ELM) Model for Predicting Resilient Modulus of Stabilized Aggregate Bases. Appl. Sci. 2019, 9, 3221. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Kumar, D.; Samui, P.; Hasanipanah, M.; Roy, B. A novel approach for forecasting of ground vibrations resulting from blasting: Modified particle swarm optimization coupled extreme learning machine. Eng. Comput. 2021, 37, 3221–3235. [Google Scholar] [CrossRef]
- Li, G.; Kumar, D.; Samui, P.; Nikafshan Rad, H.; Roy, B.; Hasanipanah, M. Developing a New Computational Intelligence Approach for Approximating the Blast-Induced Ground Vibration. Appl. Sci. 2020, 10, 434. [Google Scholar] [CrossRef]
- Cao, J.; Lin, Z.; Huang, G.-B. Self-Adaptive Evolutionary Extreme Learning Machine. Neural Process. Lett. 2012, 36, 285–305. [Google Scholar] [CrossRef]
- Chen, S.; Shang, Y.; Wu, M. Application of PSO-ELM in electronic system fault diagnosis. In Proceedings of the 2016 IEEE International Conference on Prognostics and Health Management (ICPHM), Ottawa, ON, Canada, 20–22 June 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; pp. 985–990. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).