Missing Structural Health Monitoring Data Recovery Based on Bayesian Matrix Factorization
Abstract
:1. Introduction
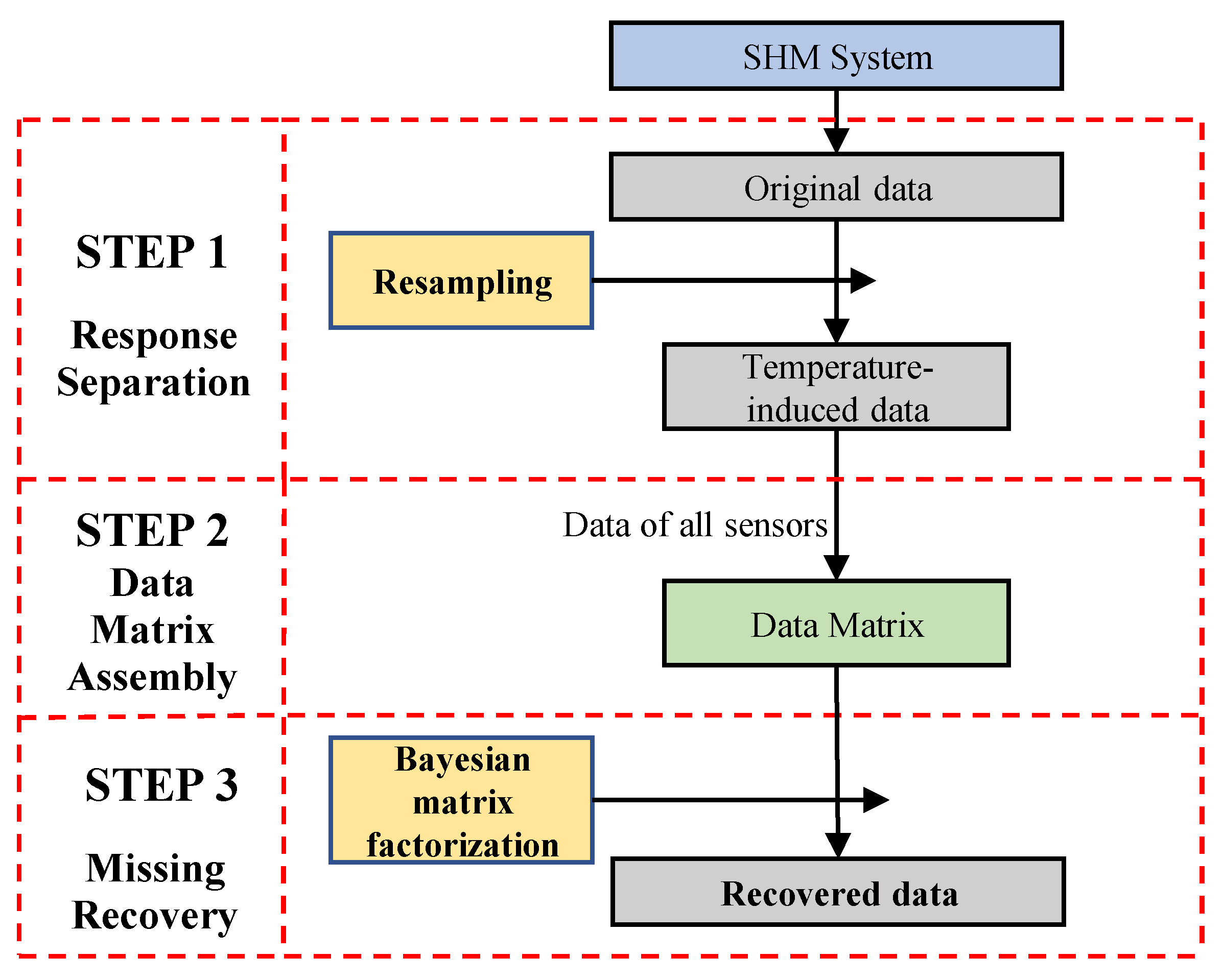
2. Methodology
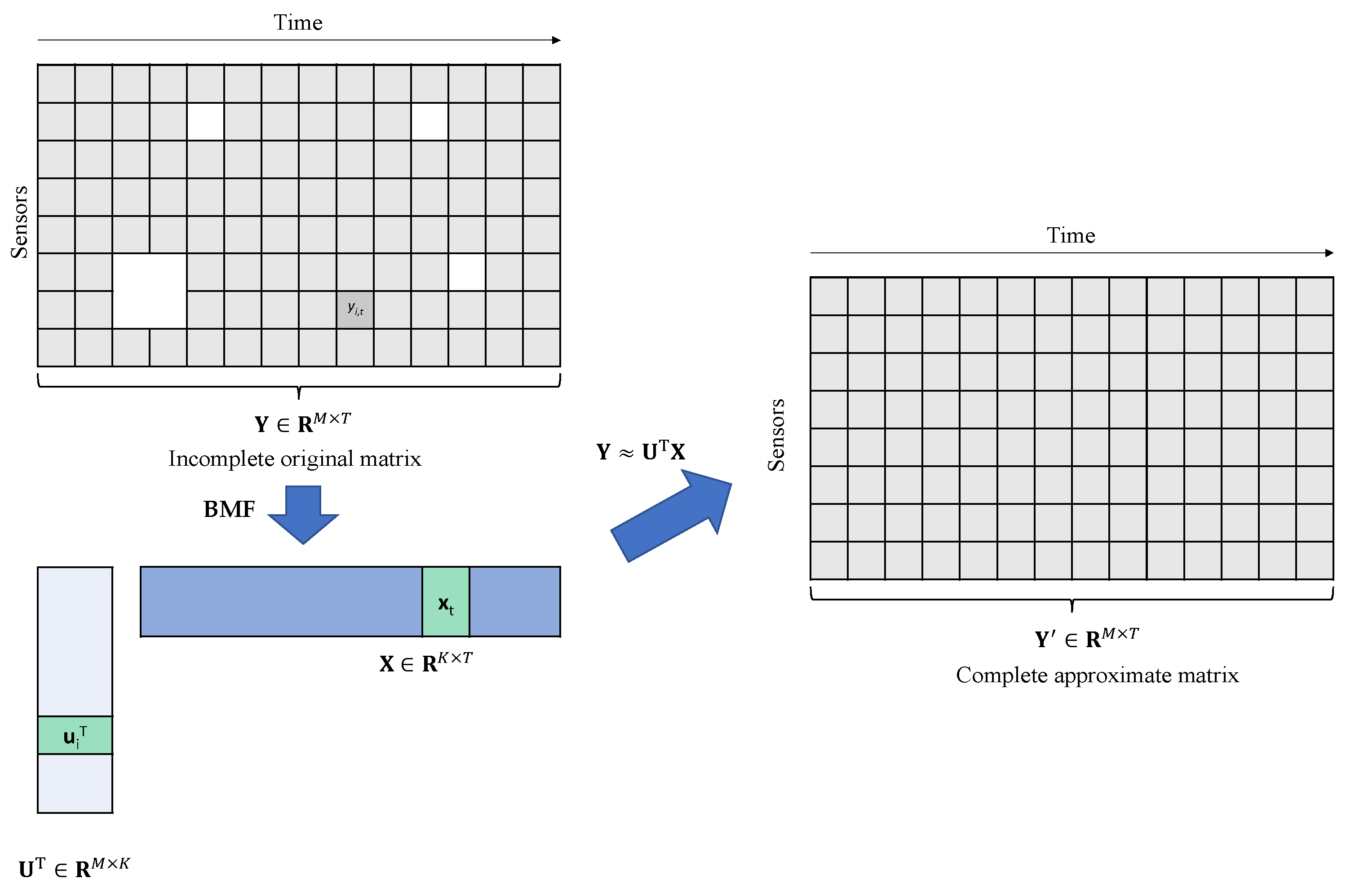
2.1. Problem Introduction
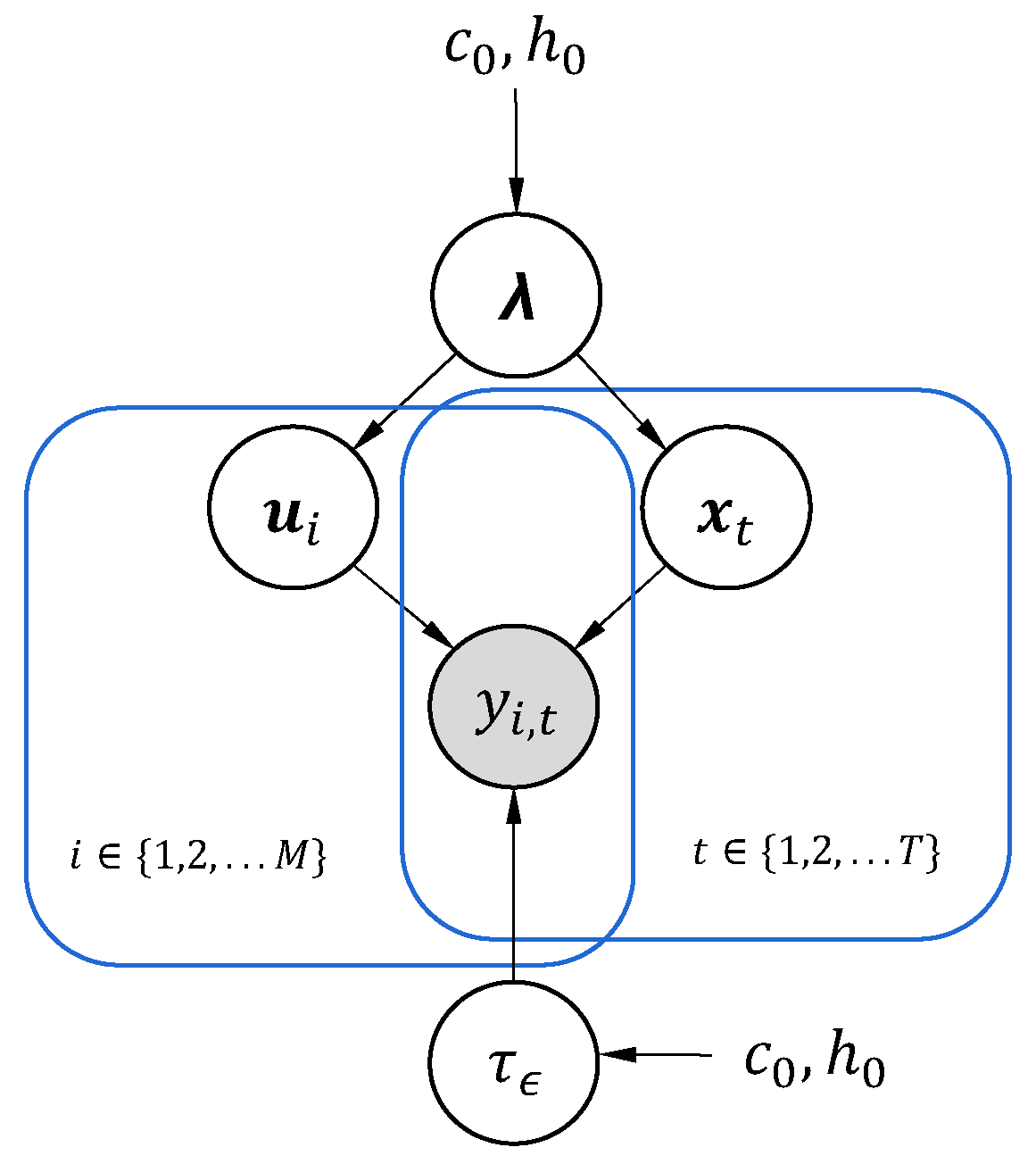
2.2. Bayesian Hierarchical Model for Matrix Factorization
2.3. Setting Priors for Parameters and Hyperparameters
2.4. Gibbs Sampling for Bayesian Matrix Factorization
2.4.1. Sampling Spatiotemporal Feature and
2.4.2. Sampling
2.4.3. Sampling Hyperparameter λ
3. Experimental Verification
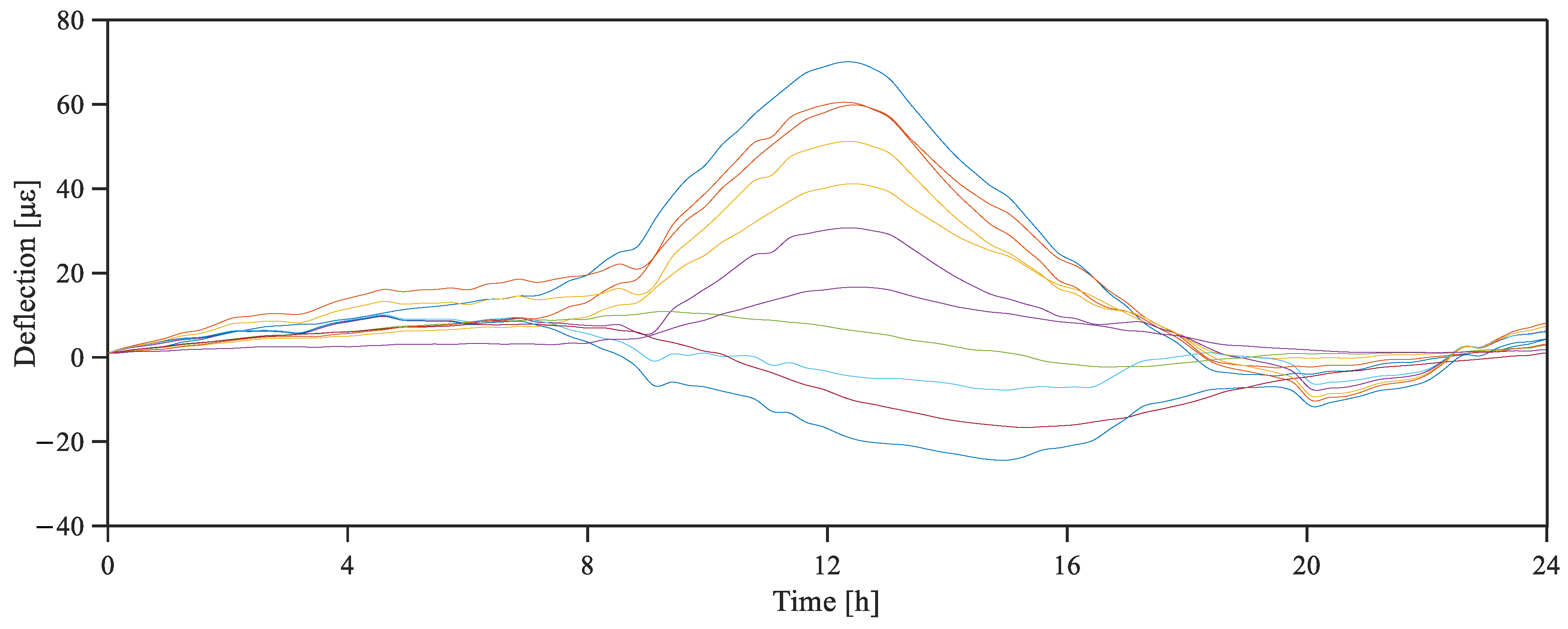
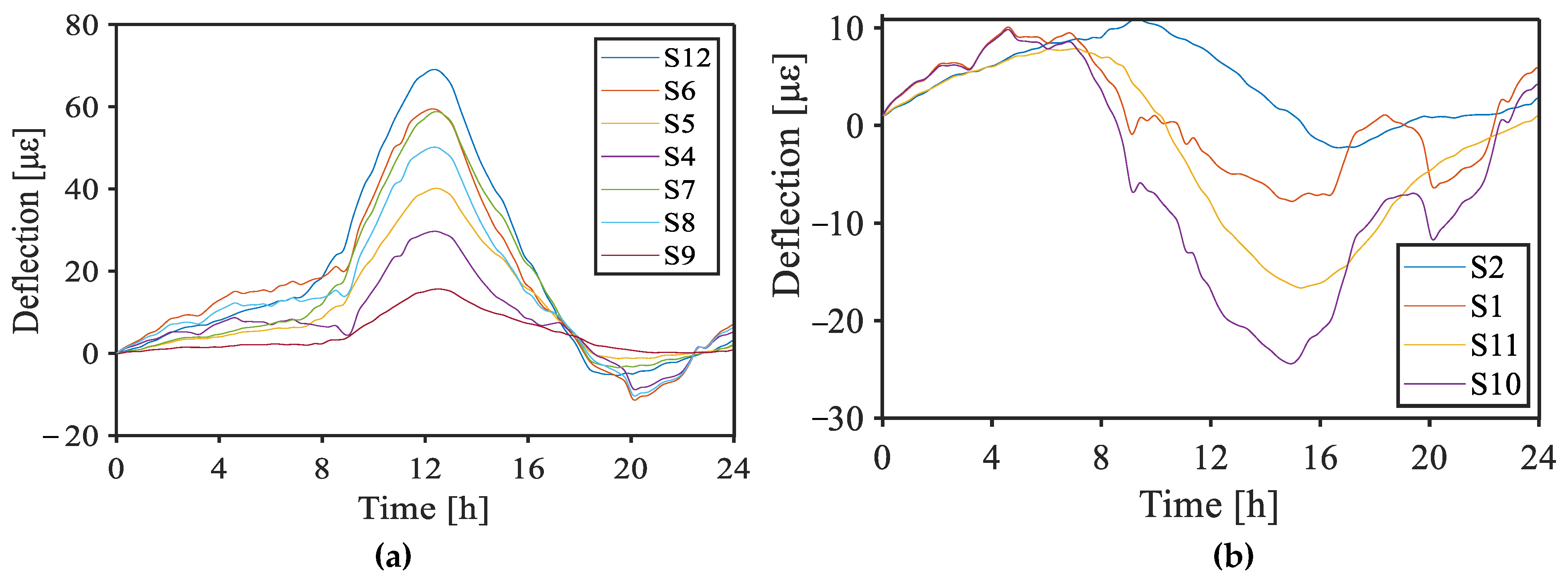
3.1. Bridge Introduction
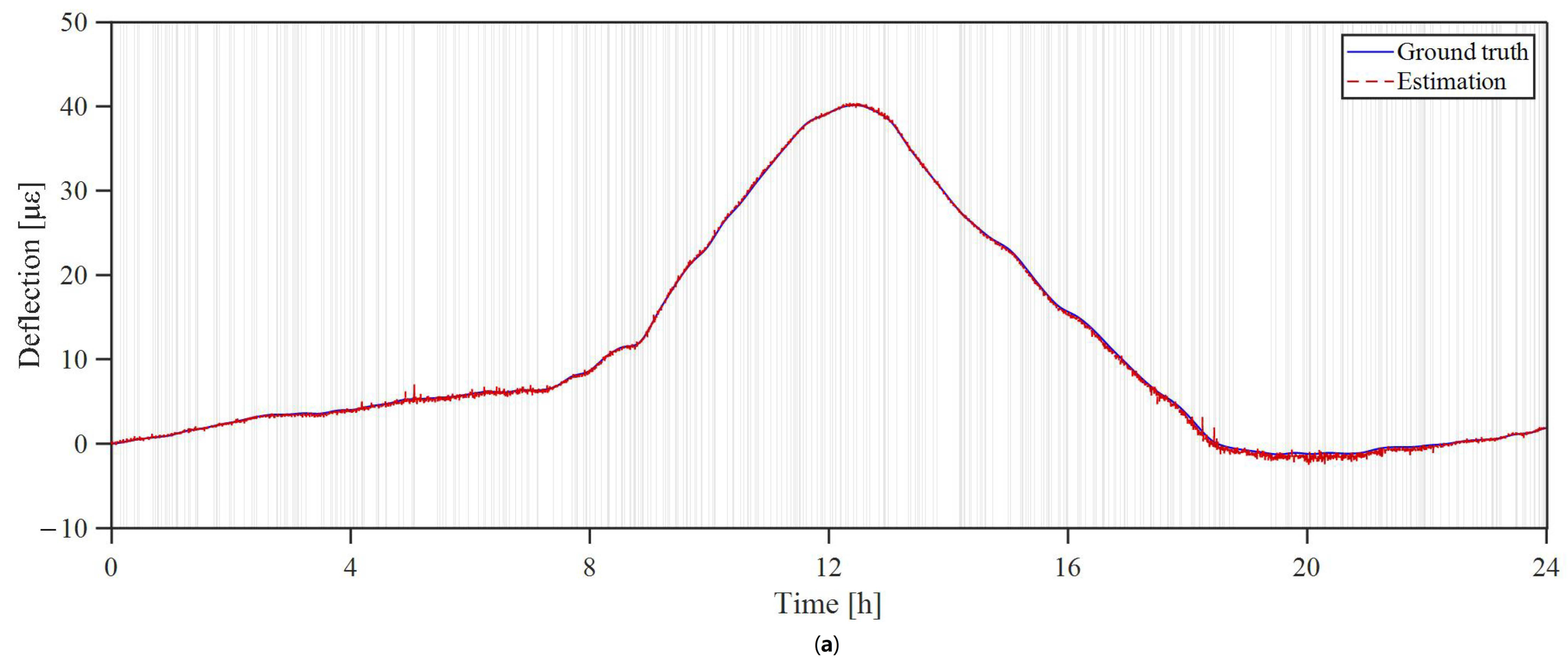
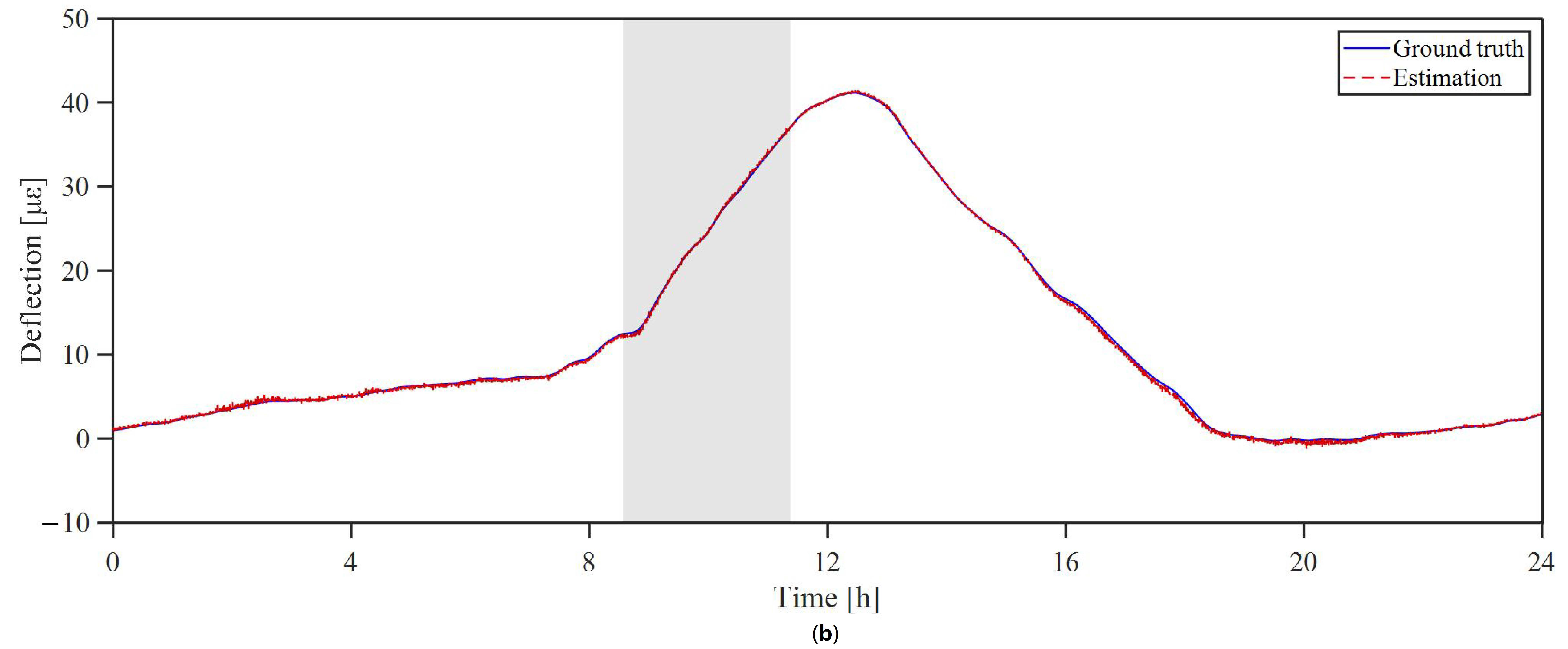
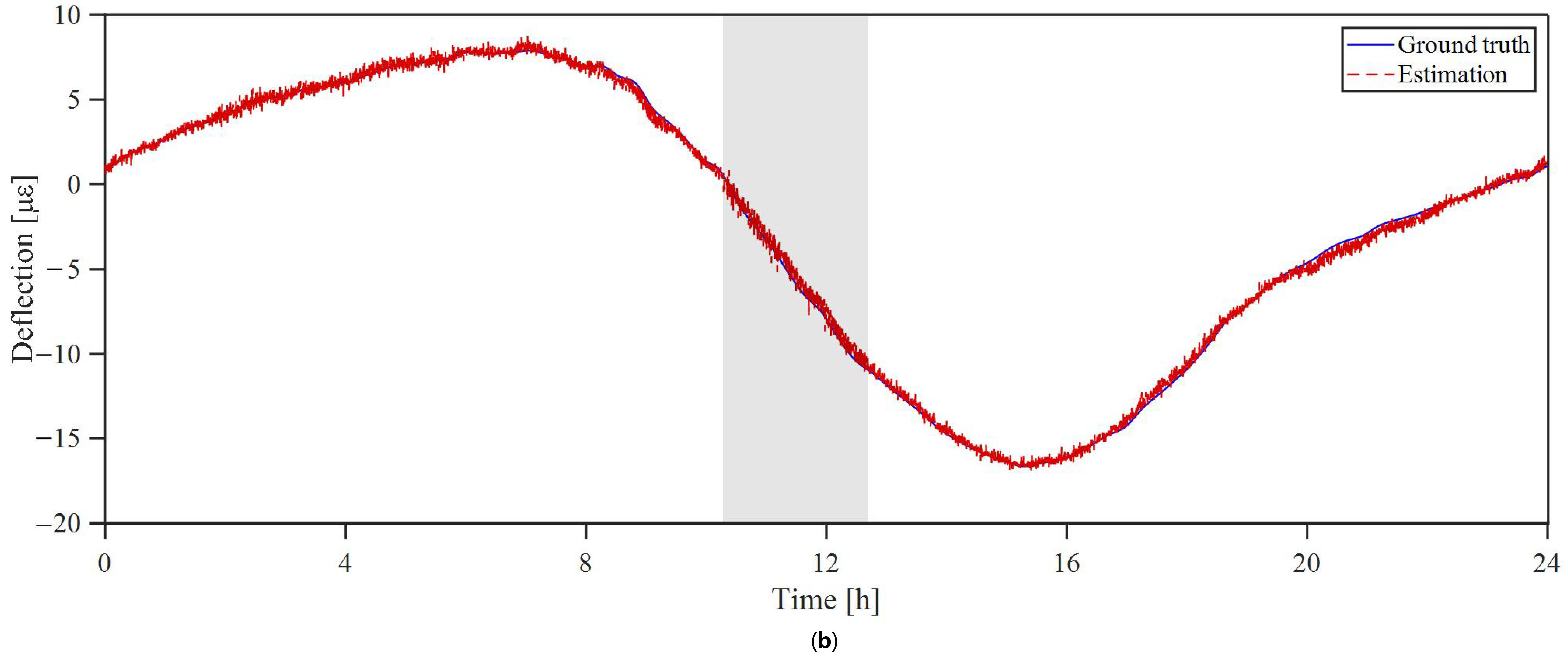
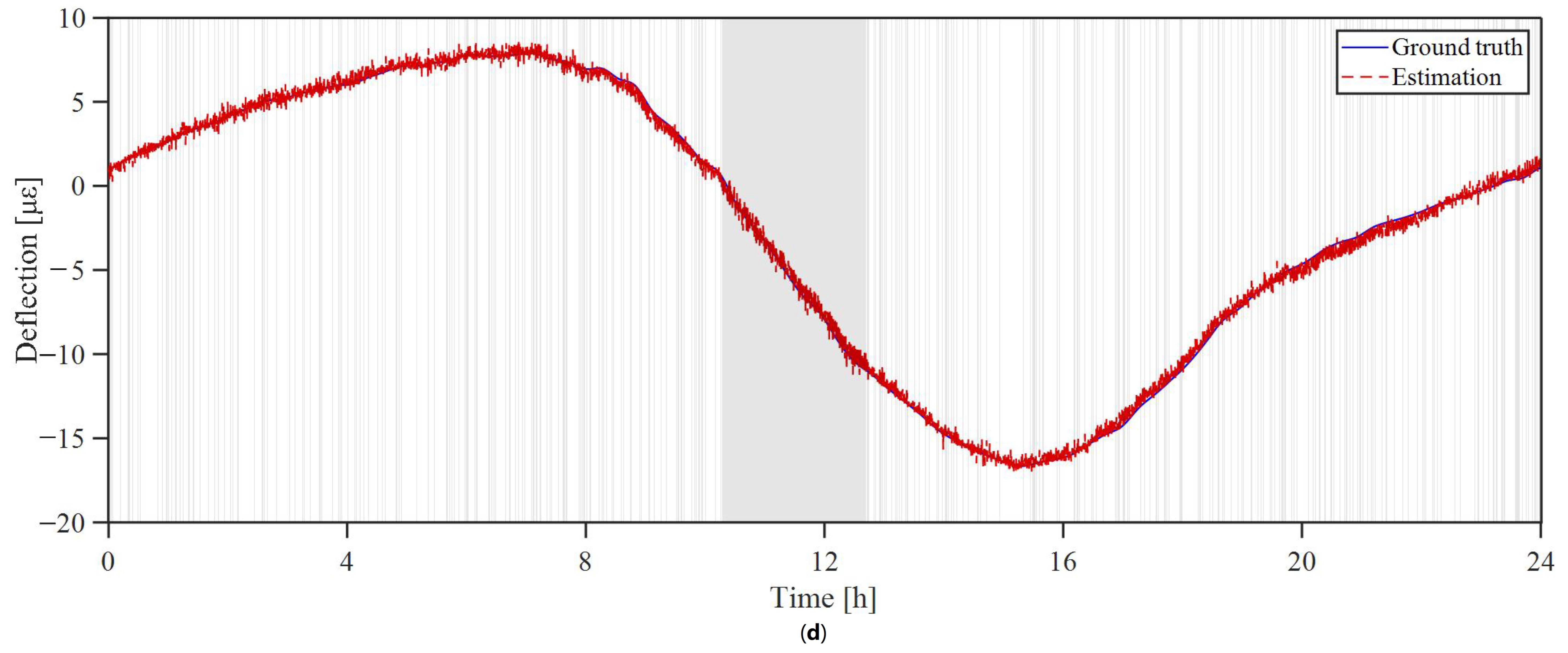
3.2. Missing-Data Recovery Result
3.3. Analysis of Rank
3.4. Comparison with Support Vector Machine
3.5. Comparison with K-Nearest Neighbor
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, L.; Shang, Z.; Xia, Y.; Bhowmick, S.; Nagarajaiah, S. Review of Bridge Structural Health Monitoring Aided by Big Data and Artificial Intelligence: From Condition Assessment to Damage Detection. Eng. Struct. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- Jiang, H.; Wan, C.; Yang, K.; Ding, Y.; Xue, S. Continuous Missing Data Imputation with Incomplete Dataset by Generative Adversarial Networks-Based Unsupervised Learning for Long-Term Bridge Health Monitoring. Struct. Health Monit. Int. J. 2021, 21, 14759217211021942. [Google Scholar] [CrossRef]
- Marcantonio, V.; Monarca, D.; Colantoni, A.; Cecchini, M. Ultrasonic waves for materials evaluation in fatigue, thermal and corrosion damage: A review Mechanical. Syst. Signal Process. 2019, 120, 32–42. [Google Scholar] [CrossRef]
- Jeong, S.; Ferguson, M.; Hou, R.; Lynch, J.; Sohn, H.; Law, K.H. Sensor Data Reconstruction Using Bidirectional Recurrent Neural Network with Application to Bridge Monitoring. Adv. Eng. Inform. 2019, 42, 100991. [Google Scholar] [CrossRef]
- Liu, H.; Ding, Y.; Zhao, H.; Wang, M.; Geng, F.F. Deep Learning-Based Recovery Method for Missing Structural Temperature Data Using LSTM Network. Struct. Monit. Maint. 2020, 7, 109–124. [Google Scholar]
- Rautela, M.; Gopalakrishnan, S. Ultrasonic guided wave based structural damage detection and localization using model assisted convolutional and recurrent neural networks. Expert Syst. Appl. 2020, 167, 114189. [Google Scholar] [CrossRef]
- Wan, H.-P.; Ni, Y.-Q. Bayesian multi-task learning methodology for reconstruction of structural health monitoring data. Struct. Health Monit. 2018, 18, 1282–1309. [Google Scholar] [CrossRef]
- Chen, Z.; Li, H.; Bao, Y. Analyzing and modeling inter-sensor relationships for strain monitoring data and missing data imputation: A copula and functional data-analytic approach. Struct. Health Monit. 2018, 18, 1168–1188. [Google Scholar] [CrossRef]
- Rabcan, J.; Levashenko, V.; Zaitseva, E.; Kvassay, M.; Subbotin, S. Non-destructive diagnostic of aircraft engine blades by Fuzzy Decision Tree. Eng. Struct. 2019, 197, 109396. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, Q.; Li, X.; Liu, J. A Survey on Tensor Techniques and Applications in Machine Learning. IEEE Access 2019, 7, 162950–162990. [Google Scholar] [CrossRef]
- Nie, X.; Yin, Y.; Sun, J.; Liu, J.; Cui, C. Comprehensive Feature-Based Robust Video Fingerprinting Using Tensor Model. IEEE Trans. Multimed. 2016, 19, 785–796. [Google Scholar] [CrossRef]
- Hu, W.R.; Tao, D.; Zhang, W.; Xie, Y.; Yang, Y.H. The Twist Tensor Nuclear Norm for Video Completion. Ieee Trans. Neural Netw. Learn. Syst. 2017, 28, 2961–2973. [Google Scholar] [CrossRef] [PubMed]
- Xie, K.; Wang, L.; Wang, X.; Xie, G.; Wen, J.; Zhang, G.; Cao, J.; Zhang, D. Accurate Recovery of Internet Traffic Data: A Sequential Tensor Completion Approach. IEEE/ACM Trans. Netw. 2018, 26, 793–806. [Google Scholar] [CrossRef]
- Zheng, C.; E, H.; Song, M.; Song, J. CMPTF: Contextual Modeling Probabilistic Tensor Factorization for recommender systems. Neurocomputing 2016, 205, 141–151. [Google Scholar] [CrossRef]
- Ren, P.; Chen, X.; Sun, L.; Sun, H. Incremental Bayesian matrix/tensor learning for structural monitoring data imputation and response forecasting. Mech. Syst. Signal Process. 2021, 158, 107734. [Google Scholar] [CrossRef]
- Salehi, H.; Burgueño, R. Emerging artificial intelligence methods in structural engineering. Eng. Struct. 2018, 171, 170–189. [Google Scholar] [CrossRef]
- Bahadori, M.T.; Yu, Q.; Liu, Y. Fast Multivariate Spatiotemporal Analysis via Low Rank Tensor Learning. In Proceedings of the 28th Conference on Neural Information Processing Systems (NIPS), Montreal, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Yue, Z.-X.; Ding, Y.-L.; Zhao, H.-W. Deep Learning-Based Minute-Scale Digital Prediction Model of Temperature-Induced Deflection of a Cable-Stayed Bridge: Case Study. J. Bridg. Eng. 2021, 26, 05021004. [Google Scholar] [CrossRef]
- Chen, X.; He, Z.; Wang, J. Spatial-temporal traffic speed patterns discovery and incomplete data recovery via SVD-combined tensor decomposition. Transp. Res. Part C Emerg. Technol. 2018, 86, 59–77. [Google Scholar] [CrossRef]
- Liang, P.P.; Liu, Z.; Tsai, Y.-H.H.; Zhao, Q.; Salakhutdinov, R.; Morency, L.-P. Learning Representations from Imperfect Time Series Data via Tensor Rank Regularization. In Proceedings of the 57th Annual Meeting of the Association-for-Computational-Linguistics (ACL), Florence, Italy, 28 July–2 August 2019; pp. 1569–1576. [Google Scholar]
- Sun, J.; Zhang, J.; Gu, Y.; Huang, Y.; Sun, Y.; Ma, G. Prediction of permeability and unconfined compressive strength of pervious concrete using evolved support vector regression. Constr. Build. Mater. 2019, 207, 440–449. [Google Scholar] [CrossRef]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]







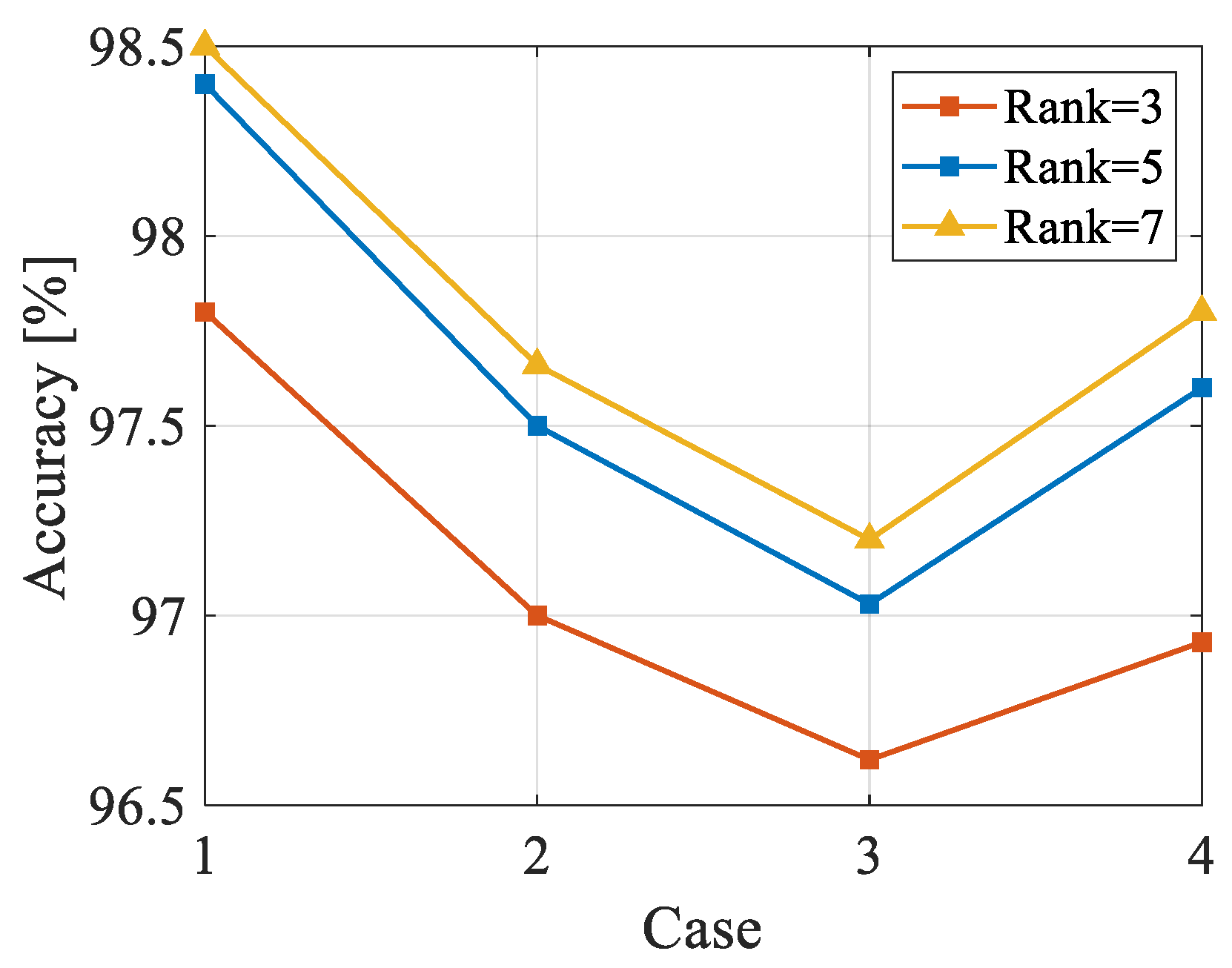



| Case | Missing Type | |
|---|---|---|
| 1 | 10% | RM |
| 2 | 10% | SM |
| 3 | 20% | SM |
| 4 | 10%SM + 10%RM | MM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Jiao, S.; Hu, Q.; Wang, Z.; Xia, Z.; Ding, Y.; Yi, L. Missing Structural Health Monitoring Data Recovery Based on Bayesian Matrix Factorization. Sustainability 2023, 15, 2951. https://doi.org/10.3390/su15042951
Sun S, Jiao S, Hu Q, Wang Z, Xia Z, Ding Y, Yi L. Missing Structural Health Monitoring Data Recovery Based on Bayesian Matrix Factorization. Sustainability. 2023; 15(4):2951. https://doi.org/10.3390/su15042951
Chicago/Turabian StyleSun, Shouwang, Sheng Jiao, Qi Hu, Zhiwen Wang, Zili Xia, Youliang Ding, and Letian Yi. 2023. "Missing Structural Health Monitoring Data Recovery Based on Bayesian Matrix Factorization" Sustainability 15, no. 4: 2951. https://doi.org/10.3390/su15042951
APA StyleSun, S., Jiao, S., Hu, Q., Wang, Z., Xia, Z., Ding, Y., & Yi, L. (2023). Missing Structural Health Monitoring Data Recovery Based on Bayesian Matrix Factorization. Sustainability, 15(4), 2951. https://doi.org/10.3390/su15042951






