Design of Tunnel Initial Support in Silty Clay Stratum Based on the Convergence-Confinement Method
Abstract
1. Introduction
2. Engineering Survey
3. Determination of the Key Curves of CCM
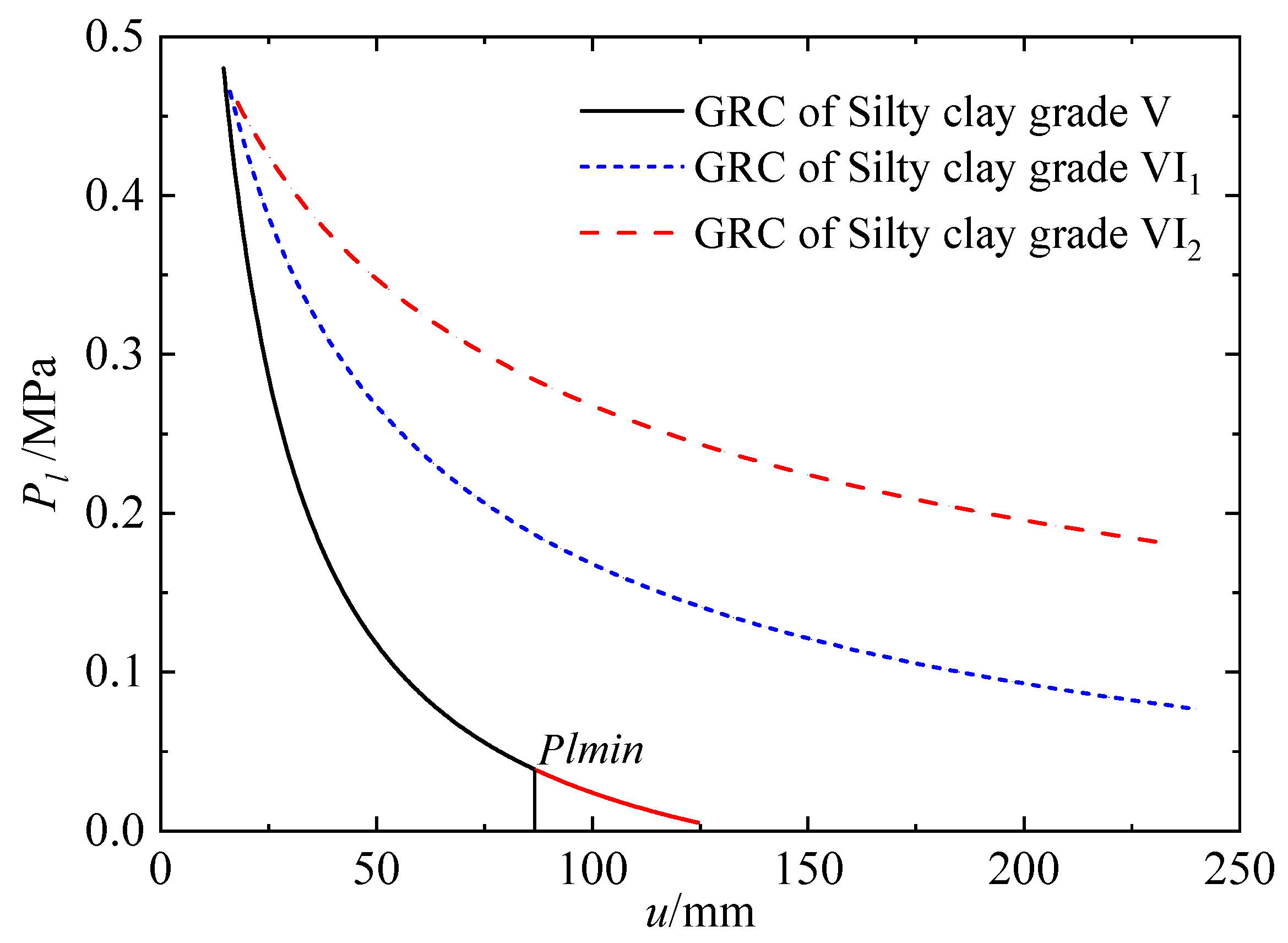
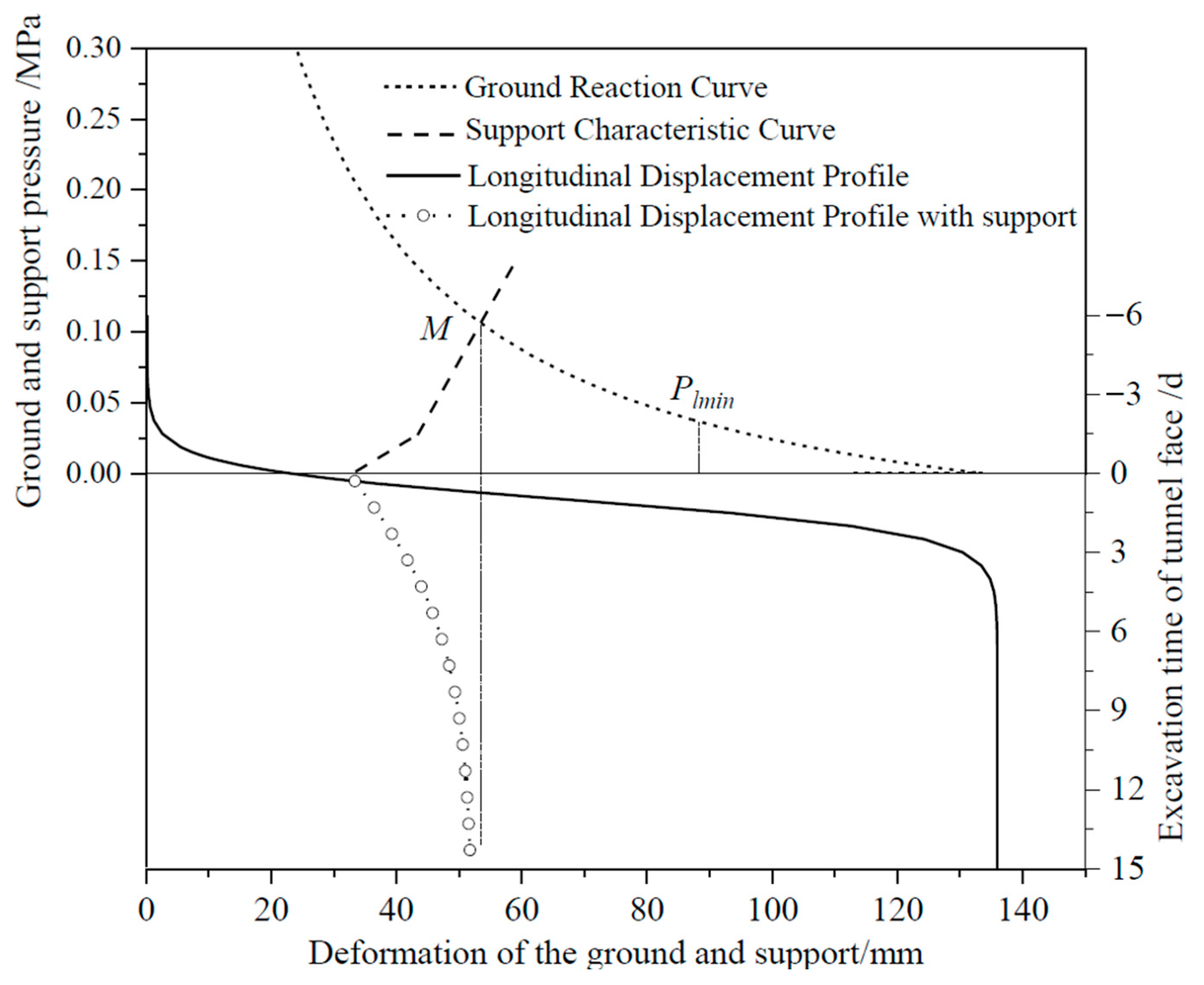
3.1. Ground Reaction Curve
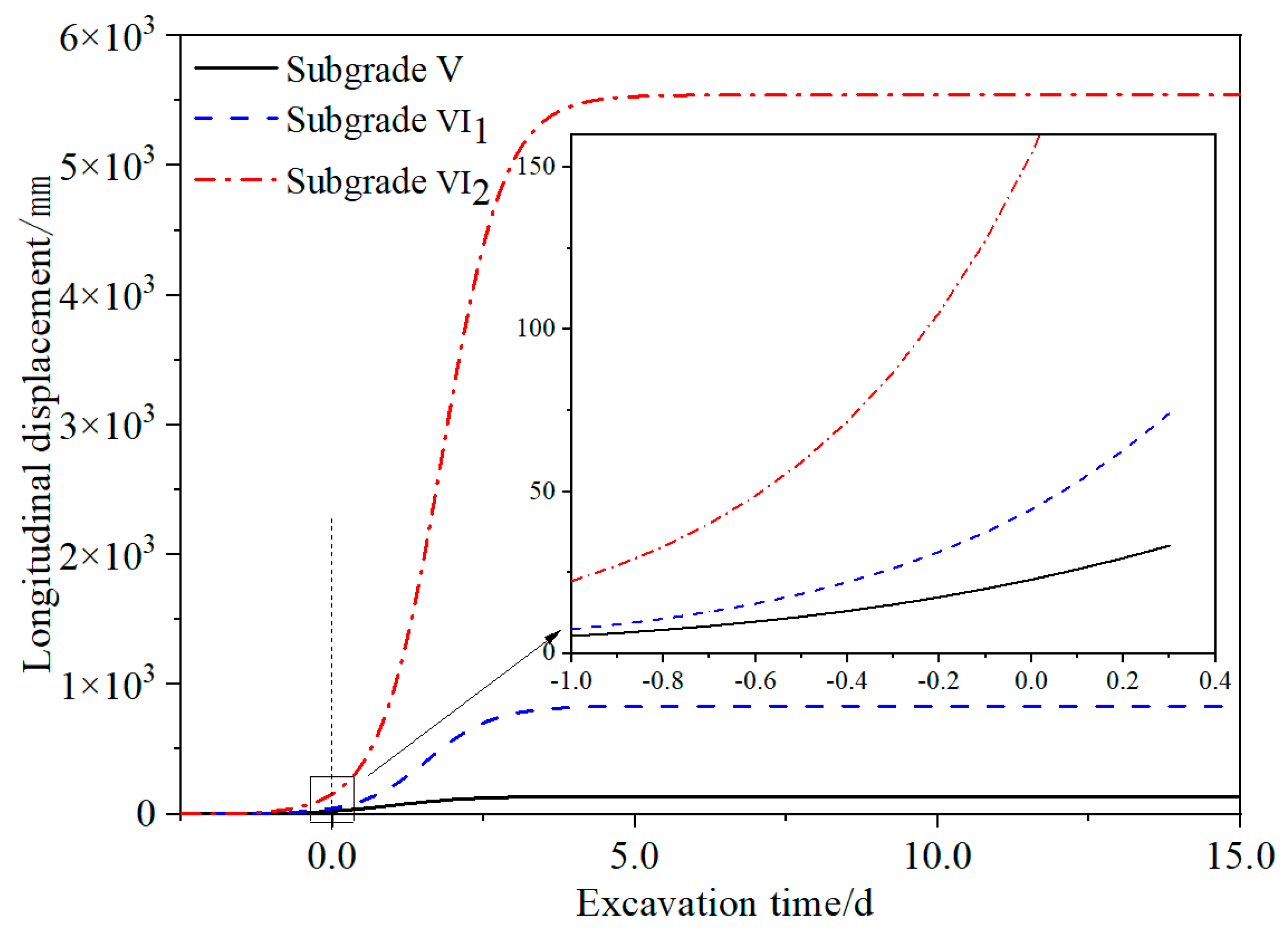
3.2. Longitudinal Displacement Profile
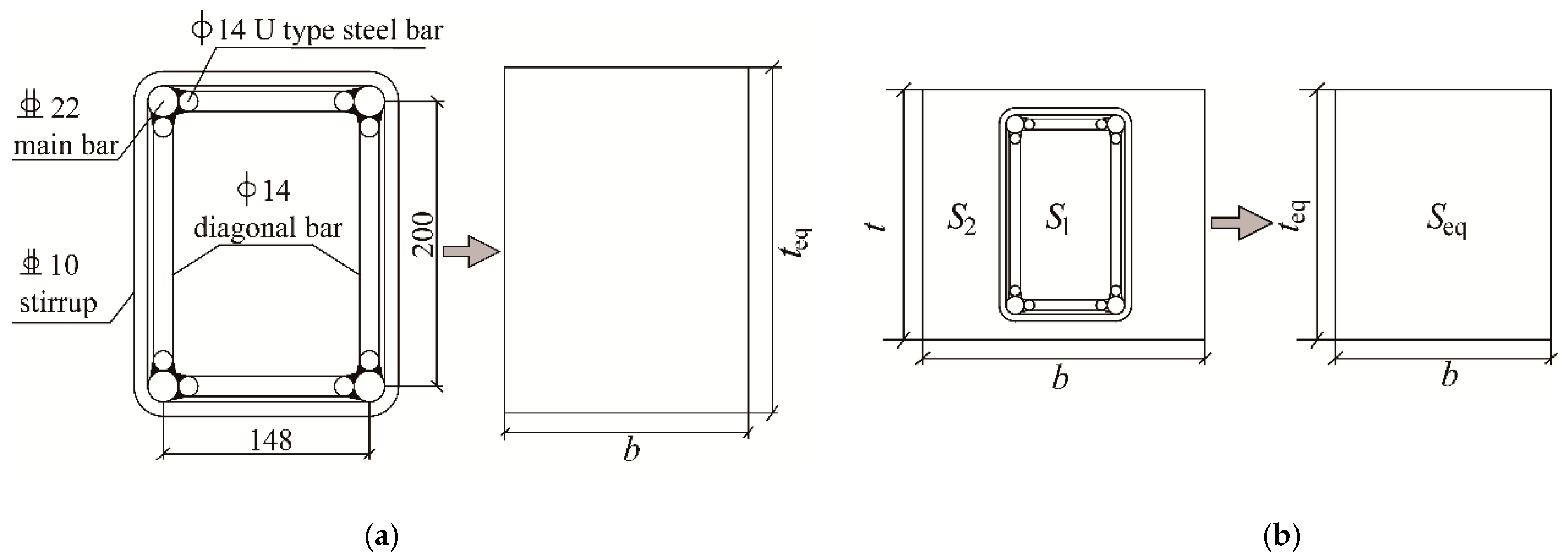
3.3. Support Characteristic Curve
- (a)
- Steel grille acts as support alone:
- (b)
- Steel grid and spray concrete are combined to support:
4. Support Scheme Design
4.1. Safety Factor of the Permitted Displacement
4.2. Optimization of Supporting Time
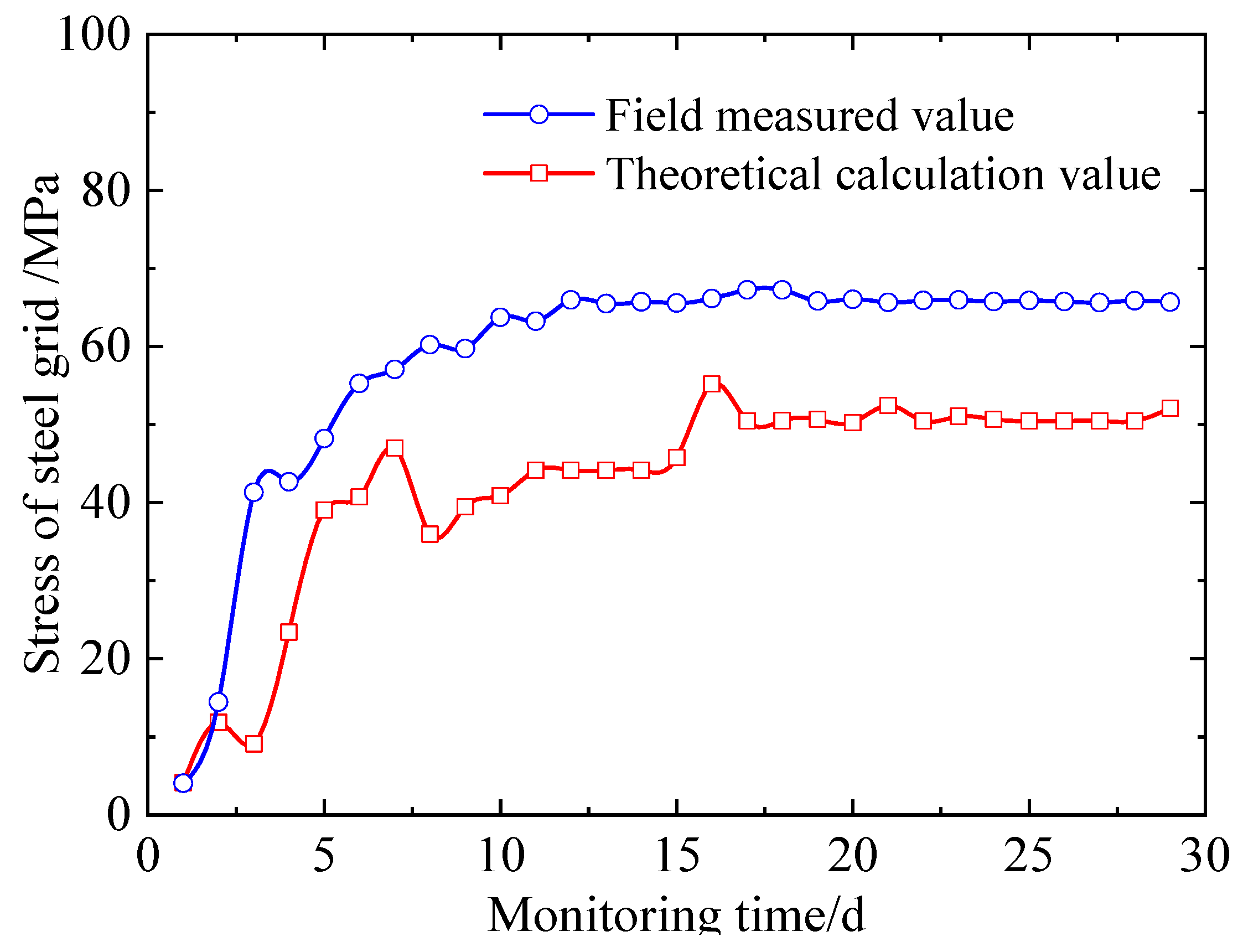
5. Discussion
6. Conclusions
- (1)
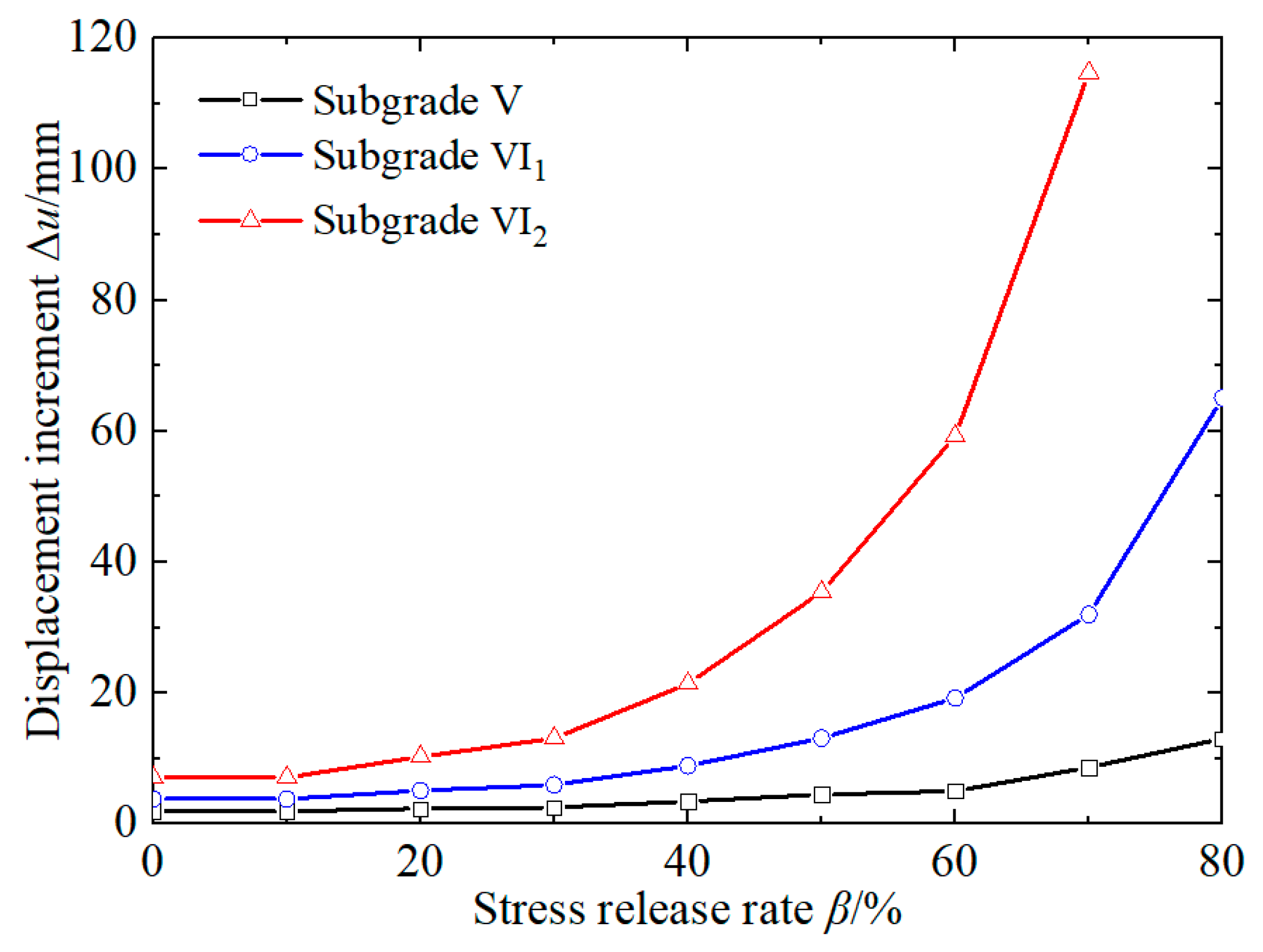
- The stress release ratio of the surrounding rock in the silty clay stratum is approximately 78–90% when the supporting structure and surrounding rock displacement are coordinated and stable under the current excavation and support conditions. The surrounding rock displacement began at one time diameter of the tunnel in front of the tunnel face. Under the condition of subgrade V in the silty clay stratum, the displacement before installing the supporting structure is approximately 33.28 mm, which belongs to the nonmonitorable portion, accounting for 64% of the total displacement of the surrounding rock. After installation of the supporting structure, the coordinated displacement is approximately 18.45 mm, which belongs to the monitorable portion, accounting for 36% of the total displacement.
- (2)
- Based on the convergence–confinement method, the longitudinal displacement law of silty clay under different subgrade conditions is determined by the hyperbolic tangent function. Then, the stress release law and displacement law of the surrounding rock under support are further determined. In the existing supporting design, the permitted displacement is 16.31 mm, and the maximum supporting force is 0.221 MPa when the steel grid support alone. The permitted displacement is 25.63 mm, and the maximum supporting force is 1.897 MPa for the combined support of the steel grid and spray concrete.
- (3)
- For the condition of subgrade V in a silty clay stratum, the safety factor of the permitted displacement is approximately 2.91, which can ensure tunneling stability. It is suggested that initial support should be carried out within 1 m after face advancement. For the surrounding rock of subgrade VI1, the safety factor of the permitted displacement is 1.40. The initial support must be carried out 1 m ahead of the tunnel face. Therefore, it is suggested to adopt advanced small conduits to ensure the safety and quality of construction. For the condition of subgrade VI2, the surrounding rock must be supported 4 m ahead of the tunnel face, and the advanced pipe shed or deep hole grouting reinforcement can be considered. The treatment effect of the relevant schemes still needs to be further studied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Su, Y.H.; Xiao, F. Research on quantification optimization of tunnel self-stability based on catastrophe theory. Highw. Eng. 2020, 45, 63–67. [Google Scholar] [CrossRef]
- Li, S.C.; Yan, Q.; Xie, C.; Wu, J. The mechanical behavior of composite supports of steel-grid in loess tunnel. Chin. J. Rock Mech. Eng. 2017, 36, 446–456. [Google Scholar]
- Zhang, Z.; Xu, T.; Cao, G.; Liu, X. Distribution Features of the Minimum Rock Cover Thickness of the Surrounding Rock Self-Stability of the Metro Tunnel in the Soil-Rock Dualistic Stratum. Adv. Civ. Eng. 2020, 2020, 8840043. [Google Scholar] [CrossRef]
- Tanoli, A.Y.; Yan, B.; Xiong, Y.-L.; Ye, G.-L.; Khalid, U.; Xu, Z.-H. Numerical analysis on zone-divided deep excavation in soft clays using a new small strain elasto–plastic constitutive model. Undergr. Space 2021, 7, 19–36. [Google Scholar] [CrossRef]
- Kang, Y.; Liu, Q.; Xi, H.; Gong, G. Improved compound support system for coal mine tunnels in densely faulted zones: A case study of China’s Huainan coal field. Eng. Geol. 2018, 240, 10–20. [Google Scholar] [CrossRef]
- Li, W.; Yang, N.; Yang, B.; Ma, H.; Li, T.; Wang, Q.; Wang, G.; Du, Y.; Zhao, M. An improved numerical simulation approach for arch-bolt supported tunnels with large deformation. Tunn. Undergr. Space Technol. 2018, 77, 1–12. [Google Scholar] [CrossRef]
- Wang, C.; Li, G.; Gao, A.; Shi, F.; Lu, Z.; Lu, H. Optimal pre-conditioning and support designs of floor heave in deep roadways. Geomech. Eng. 2018, 4, 429–437. [Google Scholar]
- Iasiello, C.; Torralbo, J.C.G.; Fernández, C.T. Large deformations in deep tunnels excavated in weak rocks: Study on Y-Basque high-speed railway tunnels in northern Spain. Undergr. Space 2021, 6, 636–649. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Engen, M. The support characteristic curve for blocked steel sets in the convergence-confinement method of tunnel support design. Tunn. Undergr. Space Technol. 2017, 69, 233–244. [Google Scholar] [CrossRef]
- Fenner, R. Untersuchungen zur Erkenntnis des Gebirgsdruckes, Gluckauf, Study of Ground Pressures. Tech. Transl. 1938, 515, 691–696. [Google Scholar]
- Pacher, F. Deformationsmessungen im Versuchsstollen als Mittel zur Erforschung des Gebirgsverhaltens und zur Bemessung des Ausbaues, Grundfragen auf dem Gebiete der Geomechanik/Principles in the Field of Geomechanics. In Proceedings of the 14th Symposium of the Austrian Regional Group of the International Society for Rock Mechanics, Ottawa, ON, Canada, 24–25 September 1964; Springer: Berlin, Heidelberg, 1964. [Google Scholar] [CrossRef]
- Ladanyi, B. Use of the Long-Term Strength Concept in the Determination of Ground Pressure on Tunnel Linings. In Proceedings of the Third Congress of the International Society for Rock Mechanics on Advances in Rock Mechanics, Washington, DC, USA, 1–7 September 1974. [Google Scholar]
- Eisenstein, Z.; Branco, P. Convergence—Confinement method in shallow tunnels. Tunn. Undergr. Space Technol. 1991, 6, 343–346. [Google Scholar] [CrossRef]
- Bukaçi, E.; Korini, T.; Periku, E.; Allkja, S.; Sheperi, P.; Sharra, L.; Barko, O. Factor of safety and probability of failure using convergence-confinement method for tunnels in rock. In Proceedings of the Geo-Environment and Construction European Conference in Geo-Environment and Construction, Tirana, Albania, 26–28 November 2015. [Google Scholar]
- Basirat, R.; Hassani, R.; Mahmoodian, N. Forepoling Design in Weak Medium based on the Convergence-Confinement Method. In Proceedings of the International Conference on Civil Engineering, Singapore, 1–3 May 2016. [Google Scholar] [CrossRef]
- Sadeghiyan, R.; Hashemi, M.; Moloudi, E. Determination of longitudinal convergence profile considering effect of soil strength parameters. Int. J. Rock Mech. Min. Sci. 2016, 82, 10–21. [Google Scholar] [CrossRef]
- Brown, E.T.; Bray, J.W.; Ladanyi, B.; Hoek, E. Ground Response Curves for Rock Tunnels. J. Geotech. Eng. 1983, 109, 15–39. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Fairhurst, C. Application of the Convergence-Confinement method of tunnel design to rock masses that satisfy the Hoek-Brown failure criterion. Tunn. Undergr. Space Technol. 2000, 15, 187–213. [Google Scholar] [CrossRef]
- Daemen, J.J.K. Tunnel Support Loading Caused by Rock Failure; Research Report No. MRD-3-75; University of Minnesota: Minneapolis, MN, USA, 1975. [Google Scholar]
- Lee, Y.-J. Determination of tunnel support pressure under the pile tip using upper and lower bounds with a superimposed approach. Géoméch. Eng. 2016, 11, 587–605. [Google Scholar] [CrossRef]
- Dias, D. Convergence-confinement approach for designing tunnel face reinforcement by horizontal bolting. Tunn. Undergr. Space Technol. 2011, 26, 517–523. [Google Scholar] [CrossRef]
- Vu, M.N.; Broere, W.; Bosch, J.W. Structural Analysis for Shallow Tunnels in Soft Soils. Int. J. Géoméch. 2017, 17, 04017038. [Google Scholar] [CrossRef]
- Cui, L.; Zheng, J.-J.; Zhang, R.-J.; Lai, H.-J. A numerical procedure for the fictitious support pressure in the application of the convergence–confinement method for circular tunnel design. Int. J. Rock Mech. Min. Sci. 2015, 78, 336–349. [Google Scholar] [CrossRef]
- Mousivand, M.; Maleki, M.; Nekooei, M.; Mansoori, M.R. Application of Convergence–Confinement Method in Analysis of Shallow Non-circular Tunnels. Geotech. Geol. Eng. 2017, 35, 1185–1198. [Google Scholar] [CrossRef]
- Mousivand, M.; Maleki, M. Constitutive Models and Determining Methods Effects on Application of Convergence–Confinement Method in Underground Excavation. Geotech. Geol. Eng. 2017, 36, 1707–1722. [Google Scholar] [CrossRef]
- Vlachopoulos, N.; Diederichs, M.S. Appropriate Uses and Practical Limitations of 2D Numerical Analysis of Tunnels and Tunnel Support Response. Geotech. Geol. Eng. 2014, 32, 469–488. [Google Scholar] [CrossRef]
- Bin, L.; Taiyue, Q.; Wang, Z.; Longwei, Y. Back analysis of grouted rock bolt pullout strength parameters from field tests. Tunn. Undergr. Space Technol. 2012, 28, 345–349. [Google Scholar] [CrossRef]
- Liu, F.; Yao, S.; Zhang, J.; Wang, Y.-Q. Field measurements of aerodynamic pressures in high-speed railway tunnels. Tunn. Undergr. Space Technol. 2018, 72, 97–106. [Google Scholar] [CrossRef]
- Miranda, T.; Dias, D.; Pinheiro, M.; Eclaircy-Caudron, S. Methodology for real-time adaptation of tunnels support using the observational method. Géoméch. Eng. 2015, 8, 153–171. [Google Scholar] [CrossRef]
- Yang, S.-R.; Huang, W.-H. Permanent Deformation and Critical Stress of Cohesive Soil under Repeated Loading. Transp. Res. Rec. J. Transp. Res. Board 2007, 2016, 23–30. [Google Scholar] [CrossRef]
- Ma, K.; Zhang, J.; Xu, J.; Chen, X.; Ren, Z.; Feng, J. The influence mechanism of water content on the tunnel stability in the silty clay layer. Chin. J. Rock Mech. Eng. 2022, 43, 1–12. [Google Scholar]
- Estabragh, A.; Parsaei, B.; Javadi, A. Laboratory investigation of the effect of cyclic wetting and drying on the behaviour of an expansive soil. Soils Found. 2015, 55, 304–314. [Google Scholar] [CrossRef]
- Wang, D.-Y.; Tang, C.-S.; Cui, Y.-J.; Shi, B.; Li, J. Effects of wetting–drying cycles on soil strength profile of a silty clay in micro-penetrometer tests. Eng. Geol. 2016, 206, 60–70. [Google Scholar] [CrossRef]
- Wang, Z.; Li, W.; Li, S.; Qiu, W.; Ding, W. Development of an Optimum Forepole Spacing (OFS) determination method for tunnelling in silty clay with a case study. Tunn. Undergr. Space Technol. 2018, 74, 20–32. [Google Scholar] [CrossRef]
- Liu, K.; Li, S.; Ding, W.; Hou, M.; Gong, Y.; Li, H. Pre-supporting mechanism and supporting scheme design for advanced small pipes in the silty clay layer. Tunn. Undergr. Space Technol. 2020, 98, 103259. [Google Scholar] [CrossRef]
- Horpibulsuk, S.K.; Rachan, R.L.; Chinkulkijniwat, A.; Raksachon, Y.; Suddeepong, A. Analysis of strength development in cement-stabilized silty clay from microstructural considerations. Constr. Build. Mater. 2010, 24, 2011–2021. [Google Scholar] [CrossRef]
- Jia, D.; Shi, F.; Zheng, G.; Xu, S.H.; An, L. Elastic modulus of soil used in numerical simulation of deep foundation pits. Chin. J. Geotech. Eng. 2008, 30, 155–158. [Google Scholar]
- Zhao, Y. Study on Deformation Mechanism and Control Technology of Weak Rock Surrounding Tunnel. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2012. [Google Scholar]
- Sun, J. Study and Application on Key Technology of Tunnel Structure Design; China Communications Press Co., Ltd.: Beijing, China, 2014. [Google Scholar]
- Zhang, P.F. Study on Approximate Building Method of Ground Reaction Curve for Non-Circular Underground Caverns. Master’s Thesis, Hunan University, Changsha, China, 2015. [Google Scholar]
- Li, W.J.; Zhu, Y.Q. Tunnel Mechanics; China Machine Press: Beijing, China, 2013. [Google Scholar]
- Qi, M.S. Study on Rheological Properties of Soft Rock with Large Deformation and its Application in Tunnel Engineering. Ph.D. Thesis, Tongji University, Shanghai, China, 2006. [Google Scholar]
- Sun, J.; Wang, B.J. Finite Element Analysis of Underground Structures; Tongji University Press: Shanghai, China, 1988. [Google Scholar]
- Zheng, Y.R. Stability Analysis and Design Theory of Surrounding Rock of Underground Engineering; China Communications Press Co., Ltd.: Beijing, China, 2012. [Google Scholar]
- TB10753–2010; Standard for Constructional Quality Acceptance of High-speed Railway Tunnel Engineering. Railway Engineering Technology Standards Institute China Railway Publishing House: Beijing, China, 2010.
- Qiao, L.; Liu, J.; Li, S.; Wang, Z.C.; Jiang, Y.Y.; Wang, Z.H. Study of spatial effect of excavation face for underground facility and its application. Rock Soil Mech. 2014, 35, 481–487. [Google Scholar]
- Carranza-Torres, C.; Diederichs, M. Mechanical analysis of circular liners with particular reference to composite supports. For example, liners consisting of shotcrete and steel sets. Tunn. Undergr. Space Technol. 2009, 24, 506–532. [Google Scholar] [CrossRef]
- Guan, B.S. Introduction to Tunnel Mechanics; Southwest Jiaotong University Press: Chengdu, China, 1993. [Google Scholar]
- Su, Y.; Su, Y.; Zhao, M.; Vlachopoulos, N. Tunnel Stability Analysis in Weak Rocks Using the Convergence Confinement Method. Rock Mech. Rock Eng. 2020, 54, 559–582. [Google Scholar] [CrossRef]
- Hu, S.M. Research on Safety of Initial Support in Metro Regional Tunnel Based on Convergence-confinement Method. J. China Railw. Soc. 2015, 37, 117–121. [Google Scholar]

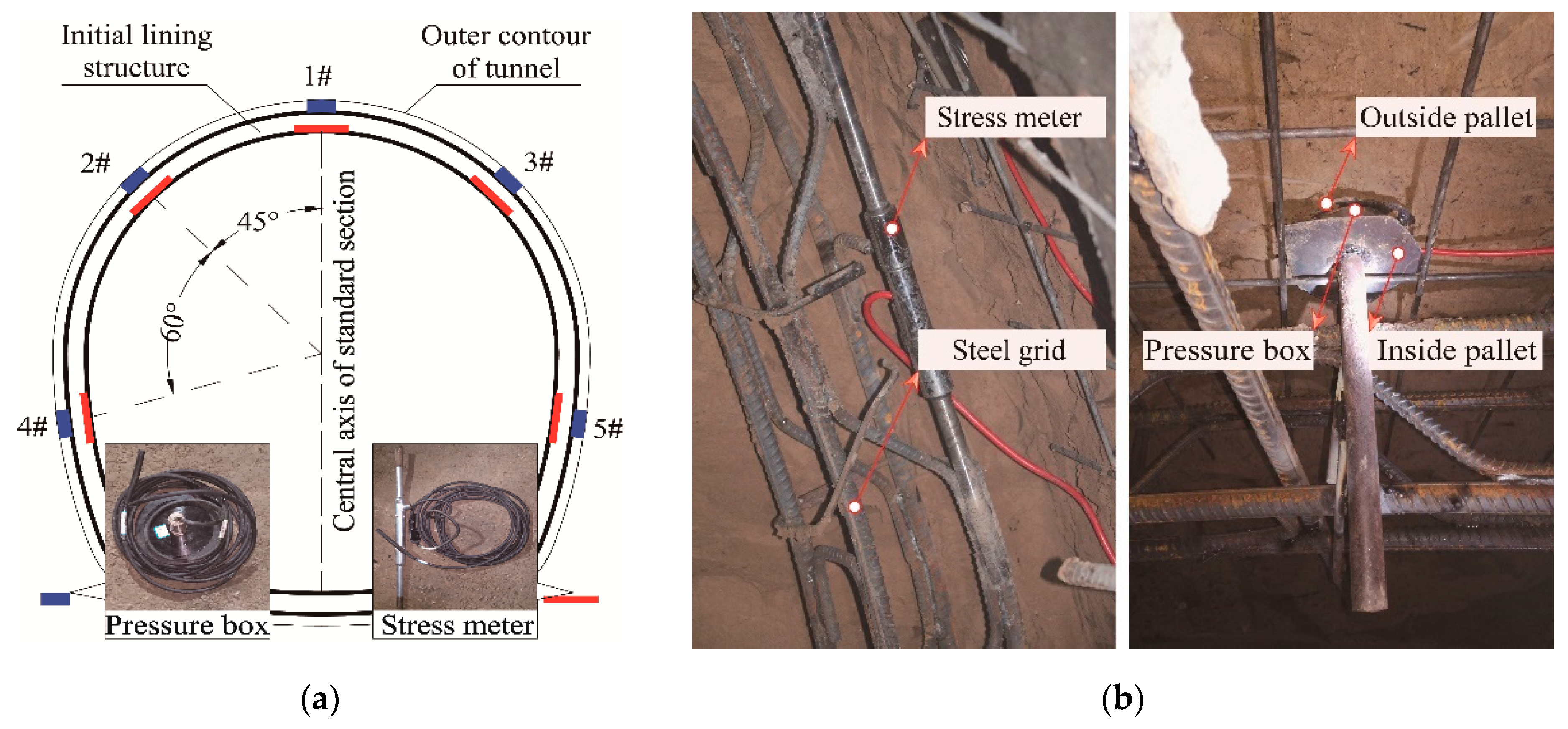


| Parameters | Void Ratio, e | Density, G (cm3) | Water Content, w (%) | Plastic Limit, wP (%) | Liquid Index, IL | Cohesion, cs (kPa) | Friction Angle, φs (°) | Poisson’s Ratio, μs | Young Modulus, Es (MPa) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Subgrade | ||||||||||
| V | 0.6–0.7 | 1.95 | 21–24 | 18.5–22.4 | 0.05–0.25 | 40 | 20 | 0.33–0.35 | 80 | |
| VI1 | 0.7–0.8 | 1.90 | 24–29 | 0.25–0.75 | 25 | 19 | 0.35–0.38 | 50 | ||
| VI2 | 0.8–0.9 | 1.85 | 30–34 | 0.75–1 | 20 | 18 | 0.38–0.43 | 30 | ||
| Subgrade | a1 | b1 | S0 (m) | SSE | R2 |
|---|---|---|---|---|---|
| V | 1.720 | 3.028 | 0.136 | 1.53 × 10−6 | 0.9999 |
| VI1 | 1.983 | 4.708 | 0.832 | 0.0045 | 0.9993 |
| VI2 | 2.118 | 5.448 | 5.543 | 0.3667 | 0.9990 |
| Section Number | Initial Measurement Time, (d) | Measured Final Value, (mm) | a2 | b2 | (mm) | (mm) | SSE | R2 |
|---|---|---|---|---|---|---|---|---|
| ① | 1 | 6.565 | 0.1701 | –6.794 | 9.581 | 16.146 | 7.88 × 10−6 | 0.9362 |
| ② | 1 | 6.225 | 0.2118 | –9.956 | 8.972 | 15.197 | 2.52 × 10−5 | 0.8353 |
| ③ | 3 | 6.352 | 0.1781 | –1.069 | 8.762 | 15.114 | 9.27 × 10−6 | 0.8841 |
| ④ | 3 | 6.671 | 0.1954 | –2.123 | 9.461 | 16.132 | 5.07 × 10−6 | 0.9377 |
| ⑤ | 3 | 5.553 | 0.1613 | –5.499 | 9.854 | 15.407 | 5.52 × 10−6 | 0.9099 |
| ⑥ | 1 | 6.567 | 0.1029 | –6.732 | 8.673 | 15.240 | 8.58 × 10−6 | 0.8952 |
| ⑦ | 2 | 5.547 | 0.1519 | –7.291 | 8.965 | 14.512 | 4.86 × 10−5 | 0.8136 |
| ⑧ | 2 | 6.894 | 0.1551 | –7.982 | 8.423 | 15.317 | 8.95 × 10−5 | 0.8566 |
| Average value | - | 6.297 | 0.1658 | –5.931 | 9.086 | 15.383 | - | - |
| Section Number | Position 1# | Position 2# | Position 3# | Position 4# | Position 5# | Average Value |
|---|---|---|---|---|---|---|
| ① | 0.035 | 0.036 | 0.089 | 0.034 | 0.074 | 0.0536 |
| ② | 0.063 | 0.066 | 0.113 | 0.161 | 0.108 | 0.1022 |
| ③ | 0.044 | 0.129 | 0.212 | 0.073 | 0.076 | 0.1068 |
| ④ | 0.108 | 0.133 | 0.09 | 0.094 | 0.072 | 0.0994 |
| ⑤ | 0.103 | 0.021 | 0.05 | 0.104 | 0.095 | 0.0746 |
| ⑥ | 0.028 | 0.084 | 0.065 | 0.027 | 0.026 | 0.046 |
| ⑦ | 0.086 | 0.066 | 0.077 | 0.022 | 0.028 | 0.0558 |
| ⑧ | 0.029 | 0.062 | 0.047 | 0.074 | 0.034 | 0.0492 |
| Steel Grid | Spray Concrete | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Eseq/GPa | As/cm2 | Is/m4 | σs′/MPa | tseq/m | Ec/GPa | μc | tc/cm | Leqc/(GPa) | Pmc/MPa |
| 1.52 | 15 | 9.78 × 10−6 | 2.92 | 0.28 | 20 | 0.2 | 25 | 0.52 | 1.85 |
| Support Form | Support Stiffness (GPa) | Permitted Displacement (mm) | Maximum Support Force (MPa) |
|---|---|---|---|
| Steel grid | 0.0440 | 16.31 | 0.221 |
| Steel grid-spray concrete | 0.5845 | 25.63 | 1.897 |
| Subgrade | umax (mm) | uin (mm) | ueq (mm) | Fs |
|---|---|---|---|---|
| V | 87 | 33.28 | 51.73 | 2.91 |
| VI1 | 100 * | 74.14 | 92.59 | 1.40 |
| VI2 | 100 * | 271.60 | 290.05 | <1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Zhao, W.; Li, J.; Ding, W. Design of Tunnel Initial Support in Silty Clay Stratum Based on the Convergence-Confinement Method. Sustainability 2023, 15, 2386. https://doi.org/10.3390/su15032386
Liu K, Zhao W, Li J, Ding W. Design of Tunnel Initial Support in Silty Clay Stratum Based on the Convergence-Confinement Method. Sustainability. 2023; 15(3):2386. https://doi.org/10.3390/su15032386
Chicago/Turabian StyleLiu, Keqi, Wen Zhao, Jiaxiang Li, and Wantao Ding. 2023. "Design of Tunnel Initial Support in Silty Clay Stratum Based on the Convergence-Confinement Method" Sustainability 15, no. 3: 2386. https://doi.org/10.3390/su15032386
APA StyleLiu, K., Zhao, W., Li, J., & Ding, W. (2023). Design of Tunnel Initial Support in Silty Clay Stratum Based on the Convergence-Confinement Method. Sustainability, 15(3), 2386. https://doi.org/10.3390/su15032386






