Detection Framework of Abrupt Changes and Trends in Rainfall Erosivity in Three Gorges Reservoir, China

Highlights

What are the main findings?

• Variations in the form of trends and abrupt changes are distinguished.

What is the implication of the main finding?

• Using the single-test method produced large uncertainty. Trend tests were performed separately from abrupt change tests to assess the long-term changes in rainfall erosivity series, which would result in the wrong conclusion.

Abstract

Rainfall erosivity is commonly used to estimate the probability of soil erosion caused by rainfall. The accurate detection of temporal changes in rainfall erosivity and the identification of abrupt changes and trends are important for understanding the physical causes of variation. In this study, a detection framework is introduced to identify temporal changes in rainfall erosivity time series as follows: (i) The significance of time series variation of rainfall erosivity is assessed based on the Hurst coefficient and divided into three levels: None, medium, and high. (ii) The detection of abrupt changes (Mann–Kendall, Moving T, and Bayesian tests) and trends (Spearman and Kendall rank correlation tests) of variate series and the correlation coefficient between the variation component and the original series is calculated. (iii) The modified series is obtained by preferentially eliminating the variation component (trend or change point) with larger correlation coefficients. (iv) We substituted the modified series into steps i to iii until the correlation coefficient was not significant. This framework is used to analyze the variation of rainfall erosivity in the Three Gorges Reservoir, China. The results showed that by using traditional methods, both an increasing trend and an upward change point were observed in Zigui station. However, after the upward change point was deducted from the annual rainfall erosivity series R(t), the resultant R_m(t) showed no statistically significant trend. Trend analysis should be performed considering the existence of an abrupt change to assess the long-term changes in rainfall erosivity series; otherwise, it would result in the wrong conclusion. In addition, the change points detected in the R_m(t) varied with the methods. Compared with the single-test method, the proposed framework can effectively reduce uncertainty.

1. Introduction

Global warming and intensive human activities have exacerbated and triggered extreme rainfall events, increasing the risk of water and soil loss and environmental deterioration [1,2,3]. Rainfall erosivity (R factor), in the Universal Soil Loss Equation (USLE) [4] and the Revised USLE (RUSLE) [5], is used worldwide to assess and predict the potential of rainfall to cause erosion [6]. Understanding the variation of rainfall erosivity is critical for sediment yield modeling and land use management. After the construction and operation of the Three Gorges Dam, the seasonal distribution of precipitation changed, and non-stationary changes such as the change point and trend have been found on the watershed scale [7,8]. Thus, determining how to diagnose the physical causes of variation and evaluate the significance levels of complex variability in rainfall erosivity series are important issues in the Three Gorges Reservoir (TGR) area.

Temporal variations in rainfall erosivity have been extensively studied by scholars, both on basin and region scales. A number of test methods have been used to detect the abrupt changes or trends of rainfall erosivity. For the trend cases, Nunes et al. [9] investigated the precipitation and erosivity in southern Portugal by using Spearman’s rank correlation and found increasing trends in precipitation erosivity during autumn and summer. Fenta et al. [10] complemented the least-squares regression with the Kendall’ tau test in rainfall erosivity trends analysis. By adopting the Mann–Kendall test and Theil and Sen’s method, Wang et al. [11] found that rainfall erosivity in the source region of the Three rivers showed an upward trend. For the abrupt change cases, the non-parametric Mann–Kendall test was employed to test abrupt changes in rainfall erosivity [12,13]. Traditional statistical methods such as the moving T/F test [14,15], the rank sum test [16], Bayesian analysis [17], and the Pettitt test method [18] are regularly used for abrupt change detection. Regarding the nonlinear and nonstationary rainfall erosivity, Lü et al. [19] used the heuristic segmentation method in abrupt change detection.

In detecting the trends and abrupt changes in rainfall erosivity series, accurate detection is very essential to soil erosion prediction, sediment management, and conservation planning. Although there are many methods for detecting temporal variations in rainfall erosivity, as discussed above, each method has its advantages and weaknesses, and they may not be able to reasonably identify the variations [20,21,22]. For example, the Bayesian analysis method is applicable when the data follow the exponential family distribution [23]. Gocic and Trajkovic [24] reported that the Mann–Kendall test is not suitable for time series with multiple abrupt changes. The parametric tests, such as moving T and F tests, would result in unreliable results when the observed data do not meet the assumptions [25,26]. Non-parametric tests, such as the Kendall test [27] and Spearman test [28], are usually proposed to detect trends but cannot quantify the statistical significance. Generally, the application of a single method to describe the temporal variation is reasonably difficult to identify, and results are highly influenced by the methods used [22]. Previous research studies have focused on spatial-temporal variation in rainfall erosivity, but few have studied whether these changes really exist.

This paper proposes a framework using Hurst and correlation coefficients as indicators to improve detection accuracy and perform significance grading. The proposed framework is applied to analyze the variation of rainfall erosivity in the Three Gorges Reservoir, China. The aim of this study is to (1) analyze the spatial distribution of annual precipitation/rainfall erosivity in the TGR area and (2) provide a scientific basis for accurate analysis of rainfall erosivity.

2. Methods

2.1. Methodological Framework

A detection framework is introduced to identify the temporal changes of rainfall erosivity (in Figure 1). Firstly, as shown in Table 1, the Hurst coefficient (H) is used to quantitatively characterize the long-term correlation of the time series [29,30], which is evaluated for rainfall erosivity time series, and the significance levels of H value are graded into three levels: None, medium, and high. Secondly, the abrupt changes and trends are detected for variate series. The correlation coefficient method is employed to confirm the effectiveness of the correlation coefficient index. The significance levels of abrupt changes and trends of rainfall erosivity series are also divided into three ranks: None, medium, and high. Thirdly, according to the principle of the maximum correlation coefficient, the change point or trend with the largest correlation coefficient is selected for its best interpretation of the impacts of changes. Finally, we removed the variation component (change point or trend) and larger correlation coefficients and substitute the modified series into steps one to three until the correlation coefficient is not significant.

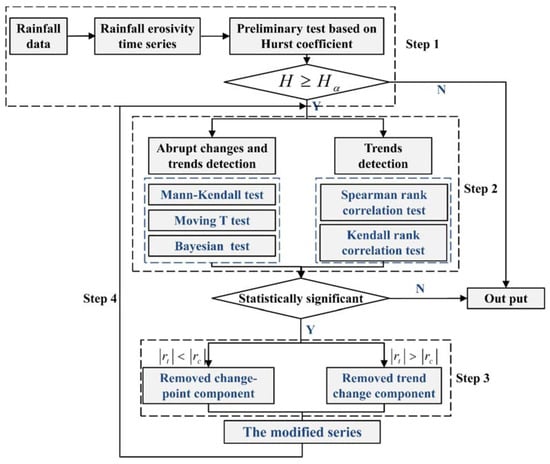
Figure 1. The framework of temporal changes identification for rainfall erosivity time series.

Table 1. Hurst coefficient H of significance level classification for temporal variations in rainfall erosivity time series.

Correlation Coefficient r(t)	Hurst Coefficient H	Significance Level
0 ≤ r(t) < r95%	0.5 ≤ H <0.673	None
r95% ≤ r(t) < r99%	0.673 ≤ H <0.717	Medium
r99% ≤ r(t) ≤ 1.0	0.717 ≤ H ≤ 1.0	High

2.2. The Correlation Coefficient Method for Trend Detection

In the trend detection procedure, supposing that the rainfall erosivity series $\left\{R_t,t=1,2,\cdot \cdot \cdot ,\right.\left.n\right\}$ has a significant trend, the original series is given as follows:

$$R_t=a+bt+{\eta }_t\begin{array}{cc}& \left(t=1,2,\cdots ,n\right)\end{array}$$

(1)

where a and b are parameters, ${\eta }_t$ is the residual term, and $\overline{R}$ and $\overline{t}$ are the average values of R_t and t. Then, the correlation coefficient r_t between the rainfall erosivity series R_t and t is estimated by:

$$r_t=\frac{{\displaystyle \sum _{i=1}^n\left(R_i-\overline{R}\right)\left(t-\overline{t}\right)}}{{\displaystyle \sum _{i=1}^n{\left(R_i-\overline{R}\right)}^2}{\displaystyle \sum _{i=1}^n{\left(t-\overline{t}\right)}^2}}$$

(2)

If the r_t value is positive, it indicates that the R factor has an increasing trend and vice versa. In this study, r values at 95% and 99% confidence levels are taken as the thresholds, and the significance levels of trend changes are divided into three levels: None, medium, and high (Table 2).

Table 2. Correlation coefficient r of significance level classification for trends in rainfall erosivity time series.

Correlation Coefficient r	Significance Level
0≤ |r| <r95%	None trend
r95% ≤ |r| < r99%	Medium trend
r99% ≤ |r| ≤ 1.0	High trend

2.3. The Correlation Coefficient Method for Abrupt Changes Detection

In order to obtain the correlation coefficient between the abrupt change component and the original series R_t, we divided R_t into two parts, R_a and R_b, according to the position of the change point τ_i, and the corresponding average values are given as follows:

$$\overline{R_a}=(R_1+R_2+\cdots R_{\tau i})/{\tau }_i$$

(3)

$$\overline{R_b}=(R_{{\tau }_i+1}+R_{{\tau }_i+2}+\cdots R_n)/\left(n-{\tau }_i\right)$$

(4)

$$\overline{R}=(R_1+R_2+\cdots R_n)/n$$

(5)

where $\overline{R_a}$, $\overline{R_b}$, and $\overline{R}$ are the average values of R_a, R_b, and R_t with the size of τ_i, n-τ_i, and n, respectively. A new series C_t is generated as follows:

$$C_t=\left\{\begin{array}{cc}\overline{R_a}\hfill & \hfill t=1,2,\cdot \cdot \cdot ,{\tau }_i\\ \overline{R_b}\hfill & \hfill t={\tau }_i+1,{\tau }_i+2,\cdot \cdot \cdot ,n\end{array}\right.$$

(6)

where C_t reflects the change point component in R_t. The average values of C_t are given as follows:

$$\overline{C}=\left(C_1+C_2+...,+C_n\right)/n$$

(7)

The correlation coefficient r_i between R_t and C_t is given by [31]:

$$r_i=\pm \sqrt{\frac{{({\displaystyle \sum _{t=1}^n{R}_t{C}_t-n\overline{R}\overline{C}})}^2}{({\displaystyle \sum _{t=1}^n{R}_t^2-n{\overline{R}}^2})({\displaystyle \sum _{t=1}^n{C}_t^2-n{\overline{C}}^2})}}$$

(8)

Let ${\tau }_1,{\tau }_2,\cdot \cdot \cdot ,{\tau }_m$ be the change points obtained by the selected methods, the correlation coefficients of which are $r_1,r_{}{}_2,\cdot \cdot \cdot ,r_{}{}_m$, respectively. For the purpose of detecting abrupt changes in rainfall erosivity, correlation coefficients r are calculated by Equation (8), and we analyzed which significance levels (Table 3) they belonged to and chose the position τ with the maximum correlation coefficient r_max as the jump-point.

Table 3. Coefficient r of significance level classification for abrupt changes in rainfall erosivity time series.

Correlation Coefficient r	Significance Level
0 ≤ |r| < r95%	No abrupt change
r95% ≤ |r| < r99%	Medium abrupt change
r99% ≤ |r| ≤ 1.0	High abrupt change

In this study, the moving T (MMT), Mann–Kendall (MKT), and Bayesian (BYS) tests are selected for abrupt change detection. Spearman rank correlation coefficients and Kendall correlation tests are employed to detect trends. The correlation coefficient and Hurst coefficient values at 95% and 99% confidence levels are taken as the thresholds.

3. Detection of Trends and Abrupt Changes in Rainfall Erosivity

3.1. Study Area and Data Source

The Three Gorges Reservoir (TGR) area is located between 106°16′ E–111°28′ E and 28°56′ N–31°44′ N and covers an area of approximately 5.8 × 10⁴ km² (Figure 2). This region has a complex geomorphic type with elevation varying from 43 to 2724 m. Three water levels, namely, a power generation and navigation level (November–February), irrigation and navigation level (March–May), and flood control level (June–September), could be classified from winter to monsoon season [32]. The weather in TGR is a subtropical monsoonal climate, with average annual precipitation ranging from 1000 to 1800 mm. Purple soil is the dominant type of soil, including rapidly weathered Jurassic rocks characterized by high erosion. The land cover primarily consists of secondary vegetation and agricultural fields [33].

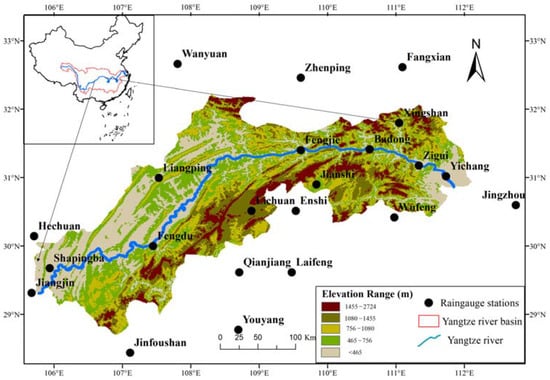
Figure 2. Distribution of meteorological stations in the TGR region.

Daily precipitation data from 1961 to 2014 at 22 national meteorological stations in/surrounding the TGR were gathered and are listed in Table 4. Eleven meteorological stations were in the TGR area and eleven meteorological stations were surrounding the TGR area for spatial interpolation of precipitation and rainfall erosivity, with the principle that stations were from Hubei province or Chongqing city and the maximum distance from the stations to the TGR area was not more than 80 km. All the selected data were gathered from the National Meteorological Information Center of China and had been through quality control, with the criteria that the missing data were less than 5% and both normality and homogeneity of the data were testified. The 22 selected meteorological stations had not lost data since the 1960s.

Table 4. The information on the meteorological stations in/surrounding the TGR.

Station	E	P	R	Station	E	P	R
Shapingba a	259.6	1056.9	5146.0	Hechuan b	231.2	1089.9	5454.3
Jiangjin a	256.3	986.6	4266.1	Jinfoushan b	1905.9	1021.7	4256.5
Fengdu a	290.4	1001.3	4200.5	Wanyuan b	674.0	1215.1	8758.5
Liangping a	454.5	1237.1	5783.6	Zhenping b	995.8	972.4	4157.9
Lichuan a	1074.1	1237.1	5783.6	Fangxian b	426.9	785.1	2728.9
Fengjie a	299.8	1069.9	5517.7	Jingzhou b	31.8	1026.3	5534.8
Jianshi a	609.2	1359.4	8331.9	Wufeng b	619.9	1300.6	7220.7
Badong a	334.0	1030.9	5121.3	Enshi b	457.1	1383.2	8067.7
Xingshan a	336.8	932.6	4075.6	Laifeng b	502.8	1286.4	6892.8
Zigui a	295.5	1038.7	4962.5	Qianjiang b	786.9	1138.3	5323.7
Yicang a	256.5	1086.4	5749.8	Youyang b	826.5	1298.2	6876.9
Mean a	406.1	1094.2	5358.1
Standard deviation a	234.1	123.1	1120.8

E is the elevation (m), P is the annual average precipitation (mm), R is the annual average rainfall erosivity (MJ mm hm⁻² h⁻² a⁻¹), ^a Stations in the TGR, ^b Stations surrounding the TGR.

3.2. Rainfall Erosivity Estimation Method

Rainfall erosivity was calculated for the 54-year daily rainfall data provided by 22 meteorological stations using the equation put out by Zhang et al. [34]. This equation was derived from the model originally proposed by Richardson et al. [35]. This equation was applied to the First National Water Conservancy Survey of China and worked well in humid climate areas. The mean annual precipitation for all 11 stations in the TGR during 1961–2014 was 1128.44 mm. The model can be applied in the TGR area, and the equations for the calculation are as follows:

$$R_i=\lambda {\displaystyle \sum _{j=1}^m{\left(D_j\right)}^{\mu }}$$

(9)

$$\mu =0.8363+\frac{18.144}{P_{d12}}+\frac{24.455}{P_{y12}}$$

(10)

$$\lambda =21.586{\mu }^{-7.1891}$$

(11)

where R_i is the rainfall erosivity of i-th half of the months in the year, MJ mm hm⁻² h⁻¹. D_j is the erosive rainfall on day j, and the threshold value of erosive precipitation is larger than 12 mm [36]. $\lambda$ and $\mu$ are empirical parameters. P_d12 and P_y12 are the mean values of daily and annual rainfall (≥12 mm).

3.3. Variations in Precipitation and Erosivity

The mean annual precipitation for the 11 meteorological stations in the TGR was 1094.2 mm (Table 4). The maximum value was 1359.3 mm in Jianshi in the south-central TGR, while the lowest value was 932.6 mm in Xingshan in the northeastern TGR. The distribution of mean annual rainfall erosivity presented a pattern of low ends and a high middle from the northeast to southwest TGR (Figure 3), and the maximum value was found in Jianshi (8331.9 MJ mm hm⁻² h⁻¹ a⁻¹) in the south-central TGR, followed by three stations having values over 5700 MJ mm hm⁻² h⁻¹ a⁻¹ (Liangping, Lichuan, and Yicang).

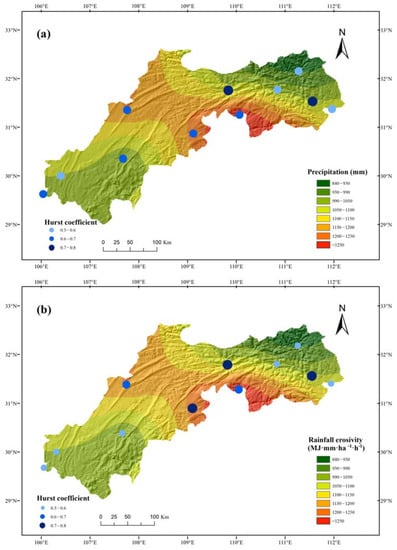
Figure 3. Spatial distribution of annual precipitation/rainfall erosivity and Hurst coefficient over the TGR: (a) Precipitation (mm) and (b) rainfall erosivity (MJ·mm·ha⁻¹·h⁻¹).

The average value of the Hurst coefficient at all 11 stations in the TGR was 0.628 and the standard deviation was 0.10. The spatial distribution of the Hurst coefficient is shown in Figure 3b. According to the thresholds of the Hurst coefficient H, 63.6% of all 11 stations were categorized as having no variation in annual rainfall erosivity (H < 0.673). Lichuan (H = 0.702) and Jianshi (H = 0.681) were classified as having weak variation (0.673 ≤ H < 0.717). Strong variation (H ≥ 0.717) in annual rainfall erosivity was found in Zigui (H = 0.786) and Fengjie (H = 0.721). A similar variation distribution was observed in precipitation (Figure 3a). The H value of precipitation varied between 0.425 and 0.817 with an average of 0.613. Nine stations (9/11, 81.8%) showed no variation, with two (Zigui and Fengjie) statistically significant at the 99% confidence level. The median Hurst coefficient of precipitation was 0.624 larger than the median H for rainfall erosivity (0.596). The data distribution (the ‘cloud’), raw data (the ‘rain’), and box-plots for the H value of precipitation and rainfall erosivity are shown in Figure 4. A unimodal distribution was observed in the H values of both precipitation and rainfall erosivity.

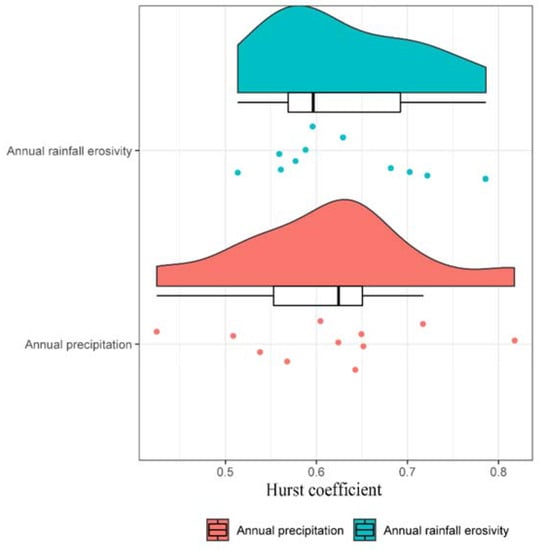
Figure 4. Raincloud plots and boxplots for the Hurst coefficient of annual rainfall erosivity and annual precipitation.

3.4. Five Quintiles in Erosive Rainfall

In order to analyze the causes of changes in rainfall erosivity, all precipitation (≥12 mm) in flood (May–September) and non-flood seasons (January–April, October–December) for all 11 stations in the TGR were divided into quintiles, with five groups (Q1: Zero to twenty percent, Q2: Twenty to forty percent, Q3: Forty to sixty percent, Q4: Sixty to eighty percent, and Q5: Eighty to a hundred percent). According to the 24-h precipitation classification criteria of the China Meteorological Administration, for the flood season, all moderate precipitation (10–25 mm) was in Q1, Q2, and Q3, and all heavy precipitation (25–50 mm) and torrential precipitation (50–100 mm) were in Q4 and Q5. For the no-flood season, all the moderate precipitation (10–25 mm) was in Q1, Q2, Q3, and Q4, and all the heavy precipitation (25–50 mm) and torrential precipitation (50–100 mm) were in Q5 (Table 5).

Table 5. Median standard deviation of erosive rainfall for five quintiles, and the maximum values of flood and no-flood seasons at Zuigui station.

	Flood Season (mm)					No-Flood Season (mm)
Statistics	20%	40%	60%	80%	Max	20%	40%	60%	80%	Max
Median of each criteria	15.1	19.2	25.3	41.0	192.3	13.5	15.7	19.2	24.9	93.3
Standard deviation of each criteria	0.2	0.5	1.1	2.7	34.6	0.4	0.5	0.9	0.8	16.5

The median values of five quintiles in erosive rainfall were similar at different stations in the same season but varied widely from flood season to no-flood season. The median H values of five quintiles in flood season ranged from 0.591 to 0.637, showing an order of Q2 > Q1 > Q4 > Q5 > Q3 (Figure 5a). In addition, approximately 45% of all 11 stations for Q1, 27% for Q2, 9% for Q3, 18% for Q4, and 27% for Q5 were categorized as having significant variations in erosive rainfall (H ≥ 0.673). The H values of Q3 and Q4 showed a unimodal distribution, and the distributions of the other quintiles were relatively flat. During no-flood season, the median H value varied between 0.603 and 0.676, with an average of 0.642. The median for Q1 was 1.01–1.12 times larger than the other quintiles. The H values of Q5 and Q3 showed a unimodal distribution, and the distributions of the other three quintiles were relatively flat (Figure 5b).

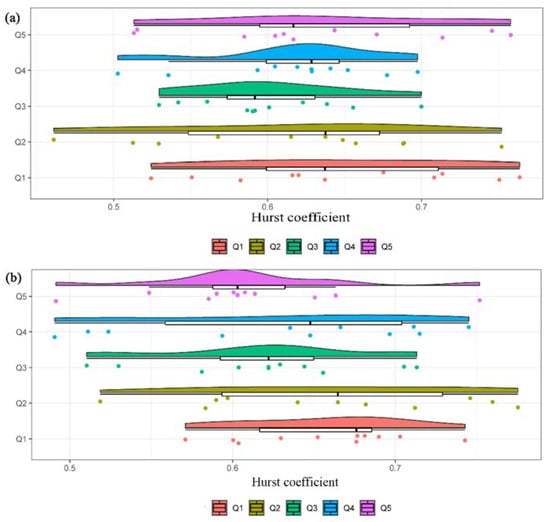
Figure 5. Raincloud plots and boxplots for the Hurst coefficient of the erosive rainfall amounts during flood season (a) and no-flood season (b).

3.5. Trends and Abrupt Changes Analysis for Zigui Station

According to the results of the Hurst test, the maximum value of H was 0.786 in Zigui station (the head area of TGR), which was categorized as having a strong variation in annual rainfall erosivity. Therefore, Zigui station was chosen to perform trends and change points research for annual rainfall erosivity during the period of 1961-2014. The results are presented in Table 6. Both the Spearman rank correlation coefficient and the Kendall correlation test showed an upward trend in rainfall erosivity. The correlation coefficient r_t between the rainfall erosivity series and trend components was estimated by Equation (2). r_t (0.317) showed a weak significance level. MTT, MKT, and BYS found the same upward change point in 1997. The correlation coefficient r_a between rainfall erosivity series and abrupt change components was estimated by Equation (8). The r_a value was 0.470, 1.48 times larger than the correlation coefficient of trends. According to the principle of the maximum correlation coefficient, the change point in 1997 was selected as the best interpretation of the impacts of changes in the rainfall erosivity series. The mean value of the annual rainfall erosivity series R(t) before and after 1997 were 4266.2 and 6478.1 MJ mm hm⁻² h⁻¹ a⁻¹, respectively (Figure 6). The expression of change point components C(t) was generated as follows:

$$C(t)=\left\{\begin{array}{cc}0\hfill & \hfill t\le 1997\\ 2211.8 \hfill & \hfill t>1997\end{array}\right.$$

(12)

Table 6. Abrupt change and trend detection for the annual rainfall erosivity series R(t) of Zuigui.

Time Series	Detection of Temporal Variations	Methods	Results	Hurst/Correlation Coefficient	Comprehensive Results	Classification of Temporal Variations
R(t)	Preliminary test	Hurst coefficient	+	0.785	+	High
	Trend change	Spearman	+	0.317	+	Weak trend change
		Kendall	+
	Abrupt change	Moving t test	1997 (+)	0.470	1997 (+) ↑	High abrupt change
		Mann-kendall	1997 (+)
		Bayesian	1997 (+)

Note: + represent significance at 0.05 significant levels; ↑ represents abrupt change is the upward change point.

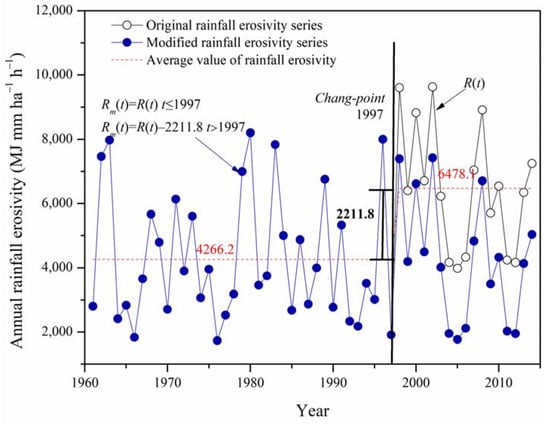
Figure 6. Change point in annual rainfall erosivity time series of Zigui station.

Thus, the modified rainfall erosivity series R_m(t) was given as follows:

$$R_m(t)=\left\{\begin{array}{cc}R\left(t\right)\hfill & \hfill t\le 1997\\ R\left(t\right)-2211.8 \hfill & \hfill t>1997\end{array}\right.$$

(13)

In order to find out all the variation components of the original series, we used the proposed framework (Steps 2–4) to test change points and trends of the modified rainfall erosivity series R_m(t). The results in Table 7 indicated that no significant trends in R_m(t) have been detected. The correlation coefficient between R_m(t) and its abrupt change components showed an order of MTT (0.228) = BYS (0.228) > MKT (0.091). R_m(t) did not exhibit a significant change point. Hence, there were no trend changes in Zigui station during the period 1961–2014, but an upward change point in 1997 was found.

Table 7. Temporal variation detection for the modified rainfall erosivity series.

Time Series	Detection of Temporal Variations	Methods	Results	Hurst/Correlation Coefficient	Comprehensive Results	Classification of Temporal Variations
Rm(t)	Trend change	Spearman	-	-	-	Not significant
		Kendall	-
	Abrupt change	Moving t test	1963 (−)	0.228		Not significant
		Mann-kendall	1978 (−)	0.091	-
		Bayesian	1963 (−)	0.228

Note: − represents no statistical significance.

4. Discussion

4.1. Performance of the Detection Framework

Variations in the form of trends and abrupt changes are hard to distinguish in statistical tests [37,38]. This study presented a four-step framework for detecting trends and abrupt changes based on Hurst and correlation coefficients. The detection of trends and change points suggested that the annual rainfall erosivity in Zigui has a weak increasing trend and a strong upward change point (Table 6). This result was in agreement with previous studies that rainfall erosivity increased in humid areas [11,39]. Generally, trend tests were performed separately from abrupt change tests to assess the long-term variations in time series [13]. However, after the upward change point was deducted from R(t), the resultant R_m(t) showed no statistically significant trend (Table 7). Similar studies were reported by Wang et al. [11] using the relative trend index (RT) and annual rainfall erosivity data in Qingshuihe station in the SRTR during the period of 1961–2012, and no significant trends were observed. Instead, when considering abrupt changes, an increasing trend was found in Qingshuihe station for the latest period of 1993–2012, generating new explanations of variations in rainfall erosivity. Interpretations of rainfall erosivity series are sensitive to the selection of statistical methods or models. Thus, a clear distinction between trends and abrupt changes is important to understand the physical causes or the variation in rainfall erosivity. In addition, the abrupt changes detected in the R_m(t) series varied with the methods. As shown in Table 7, both MTT and BYS found the same change point in 1963, while the change point obtained from MKT was in 1978. It is difficult to reasonably identify the change points with a single-test method [22] (Xie et al., 2019). Through this framework, the most reliable variation components can be extracted, which is an effective method to reduce uncertainty.

4.2. Possible Causes for The Rainfall Erosivity Changes

Temporal characteristics in rainfall erosivity are directly affected by changes in erosive rainfall events [40,41]. Yigzaw et al. [42] reported that a 4%⁻¹ increase in extreme precipitation was found after the dam construction. An increase in precipitation was also observed in the TGR areas [19,43]. During the operation of the Three Gorges Dam, the waterway of TGR reached 660 km, with a water area of 1084 km². Significant changes in land use and evaporation will lead to regional weather patterns change [44]. Hossain et al. [45] showed that dam construction can improve the convective effective potential energy, which may increase the chance of precipitation.

In addition, influenced by climate warming, the amount of precipitation and the number of extreme precipitation events showed an increasing trend in most areas [1]. During 1959–2013, the amount of extreme precipitation (daily rainfall amount > 95th percentile) in TGR increased by 6.48% per 1 °C [19]. Generally, precipitation intensity is related to raindrop kinetic energy, which has a great influence on potential erosivity [46]. At Zigui station, which is near the TGD, a significant linear relationship between rainfall erosivity and Q5 was found in both flood (R² = 0.81) and no-flood (R² = 0.67) seasons (Figure 7). Therefore, the possible causes for the variation in rainfall erosivity are attributed to an increase in rainfall intensity and duration.

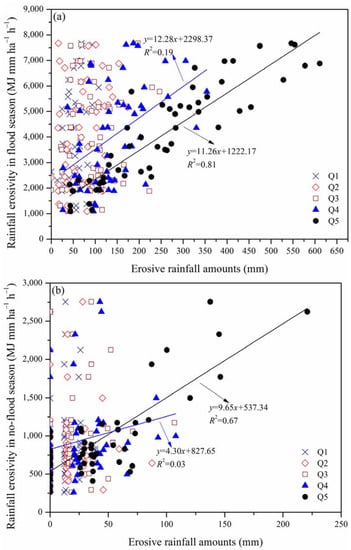
Figure 7. Relationship between rainfall erosivity and erosive rainfall amounts at Zigui station during flood season (a) and no-flood season (b).

5. Conclusions

In this study, we proposed a detection framework for trends and abrupt changes in rainfall erosivity based on Hurst and correlation coefficients. Firstly, the Hurst coefficient was applied to detect the variations in rainfall erosivity at three ranks: None, medium, and high. Secondly, the correlation coefficient between variations (trends or abrupt changes) and the original series was estimated at three levels: None, medium, and high. Thirdly, the variation component of the maximum correlation coefficient was removed to obtain a modified series. Fourthly, we substituted the modified series into steps one to three until the correlation coefficient was not significant. This framework was used to analyze the variation of rainfall erosivity in the Three Gorges Reservoir, China. Conclusions are drawn as follows:

• The distribution of average annual rainfall erosivity showed a pattern of low ends and a high middle from the northeast to southwest TGR. The values of the Hurst coefficient showed no significant variation in annual rainfall erosivity time series for 7 stations, 63.6% of all 11 stations in the TGR, with 2 stations (Lichuan and Jianshi) having weak variation and 2 stations (Zigui and Fengjie) having strong variation.
• An increasing trend and an upward change point in rainfall erosivity were observed in Zigui using traditional methods. However, after the upward change point was deducted from the annual rainfall erosivity series R(t), the resultant R_m(t) showed no statistically significant trend. This finding revealed that trend tests were performed separately from abrupt change tests to assess the long-term changes in rainfall erosivity series, which may lead to the wrong conclusion. In addition, the abrupt changes detected in the R_m(t) series varied with the methods.
• At Zigui station, a significant linear relationship between rainfall erosivity and Q5 was found in both flood and no-flood seasons. The increase in heavy precipitation with a high intensity and long duration led to variations in rainfall erosivity.

Further research should analyze the impact of extreme rainfall events on erosion, and more research should aim for the quantitative description and classification of the changes in rainfall erosivity, especially the impact of hydrological periodical fluctuation.