Hierarchical Multimodal Hub Location Problem with Carbon Emissions

Abstract

The increasing demand for multimodal freight transportation makes the expansion of new secondary hubs necessary. The carbon tax has also received attention from various sectors due to the development requirements of green transportation. Therefore, this study proposed a multimodal transport hub location problem, where carbon emissions are specifically considered to achieve green strategic planning. A mixed integer non-linear programming model was formulated to determine the location of newly-built secondary hubs, the distribution of cargo flow and the modes of the transportation links. A tangible adaptive genetic algorithm (AGA) is designed to effectively search for the optimal solution. The result of the secondary hub location based on Ningbo Port shows that the additional secondary hub brought a 41.46% increase in cargo flow, a 2.2% saving in transportation time and a 2.35% saving in total cost. Furthermore, the sensitivity analysis of the carbon tax reveals that a higher carbon tax increases the transport time, and more secondary hubs are needed to reduce the average cargo transport volume and save the total cost.

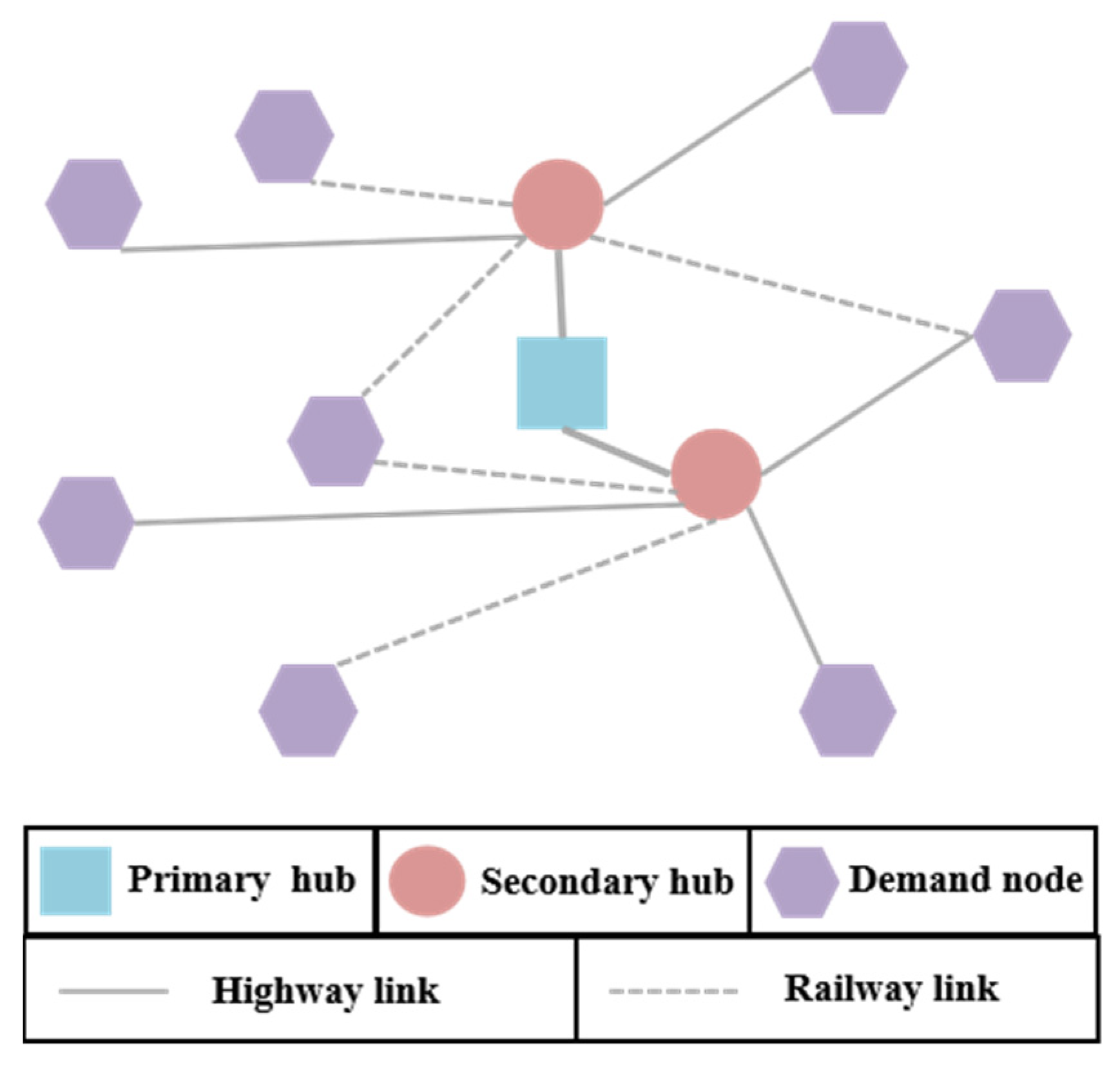
1. Introduction

The global transportation system is confronted with environmental challenges. According to the 2016 Climate Conference of the Parties (COP22), around 6.5 million deaths are directly or indirectly related to the air pollution each year. Furthermore, as reported in International Energy Agency 2018, the emissions from transportation sector account for 25% in global emissions, which is expected to reach 30% by 2030 and to approach 50% by 2050 if no key measures are undertaken. Moreover, among various transportation modes, road transportation has accounted for more than 70% of the total transportation volume for many years. However, its carbon emission intensity is 4 times that of railway transportation and 10 times that of waterway transportation. Therefore, optimizing the transport structure has become one of the important means of deep emission reduction in the transport sector. Many countries and agencies intend to develop multimodal transportation networks to reduce carbon emissions and contribute to achieving carbon peaking and carbon neutral statuses as soon as possible [1]. In addition, multimodal transport can help reduce costs and improve efficiency by combining the advantages of multiple transport modes, which is also the focus of government departments and logistics enterprises. As an intensive and efficient modern intermodal transport organization mode, multimodal transport can help promote the supply-side structural reform of China’s transportation. It is also an important way to promote the high-quality development of transport and the sustainability of logistics activities [2].

A typical multimodal transportation network is a hub-and-spoke transportation network, where the hub represents several hub nodes for gathering materials, and the spoke represents the transportation paths formed by the outward radiation from the hubs connected at the center. In the network, goods that need to be delivered are first collected at branch offices. The cargo processing operations, such as loading, unloading, sorting, etc., are carried out at hub facilities. These hub facilities are consolidation and dissemination centers. In hubs, cargos from different origins but similar destinations are collected together and re-routed according to their destinations. A package arriving at a hub can travel directly to its destination, if the destination branch office has a connection with this hub, or travel to the hub to which the destination is allocated. Due to managerial reasons, each branch office usually requires the coordination between different transportation modes. The transportation flow of the current multimodal transport network is mostly from the primary hub to the secondary hub, and then to the demand city. However, based on the actual survey, it is found that there are two outstanding problems in this two-layer transport network. First, with the development of the economy, some secondary hubs in the transport network struggle to meet the growing demand for freight transportation due to limitations of the capacity and the hub location. The material handling capacity of the whole network is obviously limited for this reason. Secondly, the transportation distance from some secondary hubs to the demand cities is too long, which makes it impossible to meet users’ variable demands promptly and the growing freight demand of primary hubs. Therefore, it is imperative to build new secondary hubs to expand the transportation network. Most of the existing research on hub location is based on a new multimodal transport network, while the expansion of new secondary hubs based on the existing multimodal transport network is more suitable for practical applications. Furthermore, the consideration of carbon emissions is believed to further promote the development of green transportation and expand the research on low-carbon optimization at the strategic level. Thus, in this study, we focused on the hierarchical multimodal hub location problem with carbon emissions based on a typical hub-and-spoke network. The problem aims to expand secondary hubs on the original intermodal network and decide their locations, the modes of the transportation links and the distribution of cargo flow, with the objective of minimizing transport time, transport cost and carbon emission cost. The main contributions of this study are summarized as follows.

• A mixed integer non-linear programming (MINLP) novel model is proposed to simultaneously optimize the location of newly-built secondary hubs (i.e., secondary hubs) and the modes of the transportation links while considering practical issues, such as cargo handling capacity, cargo clearing and carbon emission;
• Due to the complexity of the study problem (consisting of sets of potential secondary hubs and transportation modes), a tangible adaptive genetic algorithm (AGA) is developed to solve the problem efficiently;
• Based on the proposed model and the case study from real world, the result and sensitivity analyses investigate the relationship between some important input parameters and output variables, which may help decision makers to further assess its performance.

The remainder of this paper is organized as follows. Section 2 provides an overview of the related work from existing research. Section 3 introduces the background information and states the formulation of the proposed model. The developed AGA is detailed in Section 4. Section 5 covers the case study from the real world, where the experimental results and sensitivity analysis are discussed. Section 6 provides a discussion of the implications and limitations of the study. Section 7 concludes our work and discusses some possible directions for future study.

2. Literature Review

The hub location problem is an important branch of the transportation network, which has attracted the attention of many scholars. For the classical hub-and-spoke networks, its hub location problem was first proposed by O’kelly [3]. In addition, two heuristic algorithms based on the enumeration method were designed to solve this problem [4]. O’kelly and Lao [5] also developed a zero-one linear programming model to solve the transportation mode selection of hub-and-spoke multimodal networks. Campbell [6,7] realized the single allocation and multi allocation between hubs and demand nodes based on the study of O’kelly et al., and defined four discrete hub location problems: the P-hub median problem, the uncapacitated hub location problem, the P-hub center problem and the hub covering problem. Scholars have conducted extensive research based on the model proposed by Campbell [8,9,10,11,12,13]. Some studies have expanded the hub location problem by, for example, considering capacity constraints [14], budget constraints [15], dual decision-makers [16], traffic congestion [17], etc., to achieve more practical applications. Other researches focused on the exploration of solutions to hub location problems, such as analytic hierarchy process (AHP) decision-making [18], multi-criteria decision-making [19], improved or hybrid methods based on genetic algorithm [14,20], tabu search algorithm [21], benders decomposition [15] and other meta heuristics.

The introduction of hub nodes in multimodal transport network was first proposed by Slack and has been proved to improve the efficiency and reduce the cost of freight transport [22]. Therefore, the hub location problem of multimodal transport has become particularly fundamental and important. He et al. [23] developed an improved MIP heuristic, which combines branch-and-bound, Lagrangian relaxation and linear programming relaxation to obtain competitive results for the intermodal hub location problem. Considering the multi-cycle scenario and the uncertainty of freight demand, Benedyk et al. [24] proposed a scenario-based mixed integer dynamic capacitated intermodal facility location model, which aims to minimize the total cost of transportation, congestion, handling, empty container repositioning and investment cost, to help decision-makers with national or regional intermodal facility investment planning. Rothenbacher et al. [25] developed an arc-based model to solve the hub location problem of the road–rail intermodal transport network, and designed a branch-and-price-and-cut algorithm. Zhang et al. [26] applied road–rail intermodal transportation to the supply chain design of forest-delivered biofuel, and established a mixed integer programming model for strategic and tactical decisions, including the location decision of storage yards. They also verified the effectiveness and economy of road–rail multimodal transport compared with single transport mode through a case study. Fortuhi and Huynh [27] addressed a multi-period intermodal transport expansion location problem by modeling a robust path-based mixed integer program and developing a hybrid simulated annealing algorithm. Fazayeli et al. [28] integrated the freight transport route optimization into the intermodal location problem, taking into account both the time windows and uncertain demands of customers. A mixed integer fuzzy mathematical model was proposed and solved by a two-stage genetic algorithm. Kumar et al. [29] evaluated the sustainability of multimodal transport candidate locations from five dimensions of society, technology, economy, environment and politics through the TOPSIS method, and verified the proposed framework through the dedicated freight corridor of India. Real et al. [30] optimized the location of the hub and the fleet size of heterogeneous vehicle when designing multimodal transport network, and proposed two algorithms based on the adaptive large neighborhood search as solution methods. Zukhruf et al. [31] presented an integrated restoration model for a multimodal transportation network disrupted by a catastrophic disaster, which determined the road network and multimodal terminals to be restored. In addition, the model was solved by the designed particle swarm optimization and greedy heuristic algorithm.

With the development of green transportation, some scholars also pay attention to carbon emissions in the research of multimodal transport. Sedehzadeh et al. [32] proposed a multi-modal tree hub location problem considering energy consumption, and constructed a double objective function model including energy consumption and cost. A triangular fuzzy approach is adopted to cope with the uncertainty of parameters, and a multi-objective imperialist competitive algorithm is designed to obtain the Pareto-optimal solution of the model. According to the emission limit of freight orders through intermodal transportation network, Heinold et al. [33] proposed a MIP formulation to make decisions on the optimized order routing, transportation mode selection and emission allocation. Wang et al. [34] presented an integrated production and distribution model for multimodal transport considering the uncertain delay of marine arrival, and designed an improved multiple heterogeneous coded genetic algorithm. They also analyzed the impact of different operation strategies on carbon emissions. Qi et al. [35] studied a multi-commodity flow service selection problem under the Belt and Road Initiative and multimodal transport, and formulated a mathematical model considering the transportation costs, in-transit inventory costs and carbon emission costs. The case study showed the impact of carbon emissions on route selection. Wang et al. [36] regarded the energy consumption and emission reduction as one of the efficiency evaluation indicators of multimodal transport, and decide the route selection of multimodal transport based on the evaluation results. Demir et al. [37] considered environmental factors in intermodal freight transportation planning, developed a bi-objective model to minimize costs and carbon emissions simultaneously, and obtained the Pareto optimal solution of the model through the ε-constraint method.

From the above studies, fewer scholars have studied multimodal networks similar to this study, where new secondary hubs were established to extend the original network. Moreover, in addition to Sedehzadeh et al. [32], most studies consider carbon emission factors at the operational level (such as the routing problem) of multimodal transport, rather than at the strategic level (such as the location problem). In addition, most optimization objective functions are formulated to explore the impact between economic cost and carbon emission cost. However, little attention has been paid to the impact of carbon emissions on time efficiency pursued by customers. Therefore, in this study, we focused on siting new secondary hubs based on existing multimodal networks. Strategic location problem takes into account carbon emission factors. In addition, transportation time and total cost, including carbon emission cost, are comprehensively considered in the objective function. Our study makes up for the environment-friendly multimodal transport strategic planning. In addition, genetic algorithm has shown good performance in solving various facility location problems [38,39,40], and has also been selected as the solution heuristic for this study. Combined with the characteristics of the research problem, an adaptive genetic algorithm is designed to solve the proposed hierarchical multimodal hub location problem.

3. Methodology

In this section, the optimization problem of planning a hierarchical multimodal hub-and-spoke network is discussed. Then, the assumptions acquired for formulating the mixed integer non-linear problem (MINLP) are presented, followed by a discussion of the formulation of the objective functions and associated constraints.

3.1. Problem Description

As is shown in Figure 1 and Figure 2, the hierarchical multimodal hub-and-spoke network consists of two types of hubs (e.g., primary hubs and secondary hubs), transportation links (e.g., highway and railway modes) and several demand nodes. The cargo is firstly operated in the primary hub, then distributed and delivered to the secondary hubs. Finally, the cargo is delivered from secondary hubs to the demand nodes. The imported cargo should be cleared at the primary hub or secondary hub once the demands of all nodes (excluding the primary hub) have been satisfied. Note that the secondary hub can be built at a set of certain demand nodes (seen as candidate secondary hubs). Each demand node can be connected to more than one secondary hub. As depicted in Figure 1 and Figure 2, the existing intermodal network can be optimized through building some new secondary hubs to remove some redundant transportation links, further decreasing the total cost and transportation time. Thus, based on the existing hierarchical multimodal hub-and-spoke network, we introduce a cost-minimizing hub covering optimization problem, in which the location of newly-built secondary hubs, the hubs to clear the cargo and the modes of the transportation links are jointly optimized. It provides comprehensive multimodal hub-and-spoke network design with higher efficiency and lower cost for decision-makers.

3.2. Model Assumption

The proposed model is developed to jointly optimize the location of newly-built secondary hubs, the hubs to clear the cargo and modes of transportation links for the existing hierarchical multimodal hub-and-spoke network. The assumptions needed for formulating the model are shown below.

• A set of nodes (including primary hubs, secondary hubs and demand nodes) are given;
• Only a set of certain demand nodes can be selected as candidate secondary hubs.
• There is no direct connection between demand node and primary hub;
• The demand of all nodes should be cleared at one hub (e.g., primary hub or secondary hub).

3.3. Notations

The hierarchical multimodal hub location problem was denoted on a graph $G\left(N,A\right)$, where $N$ denotes all nodes and $A$ denotes all transportation links. All sets, parameters and variables are listed in

Table 1. Definition of sets.

Sets	Definition
$ND$	Set of demand nodes
$NF$	Set of primary hubs
$NP$	Set of the existing secondary hubs
$N$	Set of all nodes, $ND\cup NF\cup NP=N$
$NS$	Set of candidate secondary hubs, $NS\subset ND$
$M$	Set of transportation modes, $m\in M=\left\{highway;railway\right\}$

,

Table 2. Definition of parameters.

Parameter	Definition
$D_{ijm}$	Transportation distance between nodes $i$ and $j$ using transportation mode $m$, $i,j\in N$, $m\in M$
$d_i$	Demand of node $i$, $i\in ND$
$W_i$	Cargo clearing capacity of primary hub $i$, $i\in NF$
$w_i^L$	Cargo clearing speed of hub $i$, $i\in NF\cup NP\cup NS$
$C_m^L$	Unit cargo handling cost using transportation mode $m$, $m\in M$
$C_m^T$	Unit transportation cost using transportation mode $m$, $m\in M$
$C_i^C$	Unit cost for building secondary hubs, $i\in NS$
$C_{ijm}^T$	Unit transportation cost between nodes $i$ and $j$ using transportation mode $m$, $i,j\in N$,$m\in M$,$C_{ijm}^T=C_m^T\times D_{ijm}$
$l$	Number of newly-built secondary hubs
$v_m$	Speed of transportation mode $m$, $m\in M$
$t_m^L$	Unit cargo handling time using transportation mode $m$, $m\in M$
$t_{ijm}^T$	Transportation time between nodes $i$ and $j$ using transportation mode $m$, $i,j\in N$,$m\in M$,$t_{ijm}^T=D_{ijm}/v_m$
$R_i$	Cargo clearing capacity of secondary hub $i$, $i\in NP\cup NS$
$e_i$	$e_i=1$, node $i$ is an existing secondary hub; $e_i=0$, otherwise, $i\in ND$
$CC$	Carbon emission tax
${\alpha }_m$	Unit transportation carbon emission tax of transportation mode $m$, $m\in M$
${\epsilon }_{im}$	Unit cargo handling carbon emission using transportation mode $m$ at secondary hub $i$, $i\in NP\cup NF\cup NS$,$m\in M$
$MM$	A sufficiently large number

and

Table 3. Definition of variables.

Variables	Definition
$x{1}_{ij}$	$x{1}_{ij}=1$, $\left(i,j\right)$ link is routed using highway; $x{1}_{ij}=0$, otherwise, $i\in N$,$j\in ND$
$x{2}_{ij}$	$x{2}_{ij}=1$, $\left(i,j\right)$ link is routed using railway; otherwise, $x{2}_{ij}=0$,$i\in N$,$j\in ND$
$w_{ijm}$	Total cargo delivered from node $i$ to node $j$ using transportation mode $m$, $i\in N$,$j\in ND$,$m\in M$
$h_i$	$h_i=1$, demand node $i$ is selected to build secondary hub; $h_i=0$, otherwise, $i\in NS$
${\gamma }_{ikj}$	${\gamma }_{ikj}=1$, $\left(i,k\right)$ link (primary hub-demand node) is routed through secondary hub $j$; ${\gamma }_{ikj}=0$, otherwise, $i\in NF$, $k\in ND$, $j\in NF\cup NP\cup NS$
${\rho }_{ikj}$	${\rho }_{ikj}=1$, cargo from primary hub $i$ to demand node $k$ is cleared at hub $j$, ${\rho }_{ikj}=0$, otherwise, $i\in NF$, $k\in ND$, $j\in NF\cup NP\cup NS$

.

3.4. Model Formulation

3.4.1. Objective Function

In this study, the objective is to minimize the total time and total cost consumed in the network. The total time is calculated in Equation (1), which consists of three terms. Equation (2) represents the total time consumed for cargo clearing at primary hubs and secondary hubs. The total time for cargo handling is calculated in Equation (3). The total transportation time is formulated in Equation (4).

$$\min T=T1+T2+T3$$

(1)

$$T1={\displaystyle \sum _{i\in NF}{\displaystyle \sum _{k\in ND}{\displaystyle \sum _{m\in M}{\displaystyle \sum _{j\in NP\cup NS}\frac{w_{ikm}}{w_j^L}\times {\rho }_{ijk}}}}}+{\displaystyle \sum _{i\in NF}{\displaystyle \sum _{k\in ND}{\displaystyle \sum _{m\in M}\frac{w_{ikm}}{w_i^L}\times {\rho }_{iki}}}}$$

(2)

$$T2={\displaystyle \sum _{i\in NF\cup NP\cup NS}{\displaystyle \sum _{k\in ND}{\displaystyle \sum _{m\in M}{t}_m^L\times w_{ikm}}}}$$

(3)

$$T3={\displaystyle \sum _{i\in N}{\displaystyle \sum _{k\in ND}{\displaystyle \sum _{m\in M}{t}_{ikm}^T\times \left(x{1}_{ik}+x{2}_{ik}\right)}}}$$

(4)

The total cost consumed in the network is formulated in Equation (5), which consists of five terms. Equation (6) sums the total handling cost. Total transportation cost is calculated in Equation (7). Equation (8) represents the total cost for building secondary hubs. The total transportation carbon emission cost is formulated in Equation (9). Equation (10) calculates the total cargo handling carbon emission cost.

$$\min C=C1+C2+C3+C4+C5$$

(5)

$$C1={\displaystyle \sum _{i\in NF\cup NP\cup NS}{\displaystyle \sum _{k\in ND}{\displaystyle \sum _{m\in M}{C}_m^L\times w_{ikm}}}}$$

(6)

$$C2={\displaystyle \sum _{i\in N}{\displaystyle \sum _{k\in ND}{\displaystyle \sum _{m\in M}{C}_{ikm}^T\times w_{ikm}}}}$$

(7)

$$C3={\displaystyle \sum _{i\in NS}\left(C_i^C\times h_i\right)}$$

(8)

$$C4={\displaystyle \sum _{i\in N}{\displaystyle \sum _{j\in ND}{\displaystyle \sum _{m\in M}{e}^{{}_m}\times D_{ijm}\times w_{ijm}}}}$$

(9)

$$C5={\displaystyle \sum _{i\in NF\cup NP\cup NS}{\displaystyle \sum _{k\in ND}{\displaystyle \sum _{m\in M}q\times {\epsilon }_{im}\times w_{ikm}}}}$$

(10)

3.4.2. Constraints

The associated constraints are formulated as follows.

$${\rho }_{ikj}\le {\gamma }_{ikj},\forall i\in NF,j\in NS\cup NP,k\in ND$$

(11)

$${\displaystyle \sum _{i\in NF}{\displaystyle \sum _{j\in NP\cup NS}\left({\rho }_{iki}+{\rho }_{ikj}\right)}}=1,\forall k\in ND$$

(12)

$${\rho }_{ikj}\le h_j+e_j,\forall i\in NF,k\in ND,j\in NP\cup NS$$

(13)

$${\gamma }_{ikj}\le h_j+e_j,\forall i\in NF,k\in ND,j\in NP\cup NS$$

(14)

$${\displaystyle \sum _{k\in ND}{\displaystyle \sum _{m\in M}{w}_{ikm}}\le W_i},\forall i\in NF$$

(15)

$${\displaystyle \sum _{i\in NF}\left({\displaystyle \sum _{m\in M}{w}_{ikm}\ge d_k\times {\gamma }_{iki}}\right)},\forall k\in ND$$

(16)

$${\displaystyle \sum _{j\in NP\cup NS}\left({\displaystyle \sum _{m\in M}{w}_{jkm}\ge {\displaystyle \sum _{i\in NF}{d}_k\times {\gamma }_{ikj}}}\right)},\forall k\in ND$$

(17)

$${\displaystyle \sum _{i\in NF}{\displaystyle \sum _{m\in M}{w}_{ijm}}}=d_j+{\displaystyle \sum _{k\in ND}{\displaystyle \sum _{m\in M}{w}_{ikm}}},\forall j\in NP\cup NS$$

(18)

$${\displaystyle \sum _{i\in NF}{\displaystyle \sum _{m\in M}{w}_{ijm}}}\le R_j,\forall j\in NP\cup NS$$

(19)

$${\displaystyle \sum _{j\in NS}{h}_j}=l$$

(20)

$$h_k\le 1-e_k,\forall k\in ND$$

(21)

$$x{1}_{ik}+x{2}_{ik}=1,\forall i\in N,k\in ND$$

(22)

$$x{1}_{ik}+x{2}_{ik}\le {\displaystyle \sum _{m\in M}{w}_{ikm}}\times MM,\forall i\in NF\cup NP\cup NS,k\in ND,m\in M$$

(23)

$${\displaystyle \sum _{m\in M}{w}_{ikm}}\le \left(x{1}_{ik}+x{2}_{ik}\right)\times MM,\forall i\in NF\cup NP\cup NS,k\in ND,m\in M$$

(24)

$$x{1}_{jk},x{2}_{jk},e_j,h_i,{\gamma }_{ikj},{\rho }_{ikj}\in \left(0,1\right),\forall i\in NF,r,j\in N,k\in ND,m,n\in M$$

(25)

$$w_{ikm}\ge 0,\forall i\in N,k\in ND,m\in M$$

(26)

Equation (11) ensures that the demand of node $i$ can be cleared at secondary hub $j$ only if the $\left(i,k\right)$ link (primary hub-demand node) is routed through secondary hub $j$. Equation (12) restricts that the demand of node $i$ can be cleared only once. Equations (13) and (14) ensure that the demand of node $i$ can be cleared at node $j$ only if node $j$ is the secondary hub. Equation (15) represents that the total cargo delivered from the primary hub $i$ to the demand nodes is always less than the cargo clearing capacity of the primary hub $i$. Equations (16) and (17) ensure that all demand nodes can be satisfied by the hubs. Equation (18) calculates the total cargo of the secondary hub $j$. Equation (19) restricts that the total cargo of the secondary hub $j$ should be within its cargo handling capacity. The number of newly-built secondary hubs is treated as an exogenous parameter in Equation (20). Equation (20) ensures that the secondary hubs can only be built at demand nodes. Equation (21) restricts that only one type of transportation mode can be used to deliver the cargo between two nodes. Equations (23) and (24) ensure that $\left(i,k\right)$ flow is routed only if one type of transportation mode is selected to deliver the cargo between two nodes. Equation (25) is formulated to ensure that the binary variables are either 0 or 1, while Equation (26) is to restrict that the total cargo flow from node $i$ to node $j$ using transportation mode $m$ is non-negative.

4. Solution Algorithm

The proposed model consisting of seven binary decision variables is combinatorial, for which the solution can be optimized with commercial solvers only for small cases. Hence, a tangible adaptive genetic algorithm (AGA) is developed to search the solution. AGA is expected to improve the traditional GA by adaptively adjusting the crossover and mutation probabilities. In addition, a real number coding method was designed to jointly optimize the location of newly-built secondary hubs, the hubs to clear the cargo and the modes of the transportation links. The flow chart of the proposed AGA is illustrated in Figure 3. The AGA starts by randomly initializing a group of the population. Each individual in the population is tested by the constraints’ sorting and has a fitness value. Then, the evolution process is applied to search for the optimal solution. A group of individuals pass through tournament selection, crossover, mutation and fitness evaluation, which are discussed next. Note that in the proposed AGA, the crossover rate and mutation rate are reset in every iteration. This process is repeated until the stopping criteria is met.

4.1. Initialization

4.1.1. Chromosome Coding

As is shown in Figure 4, there is a sample network containing seven nodes besides one primary hub, among which 1, 2, 3, 4, 5, 6, 7 8 are demand nodes (1 and 2 are selected as the candidate secondary hubs, while 7 and 8 are the existing secondary hubs). The number of newly-built secondary hubs is set as one. Thus, the sample chromosome can be divided into three parts, which consists of seven demand nodes including two candidate secondary hubs, two existing secondary hubs and five demand nodes. The first part is to select the best location of newly-built secondary hubs from candidate hubs. The second part is to choose the transportation modes for links and the third part is to select the hubs to clear the cargo. Each gene contains two terms. The upper one is real-coded, representing the node in the network. The lower one is randomly initialized between 0 and 1 to assist the genetic process.

4.1.2. Chromosome Decoding

The decoding process is illustrated in Figure 5. In step 1, two randomly initialized numbers for two candidate secondary hubs are compared with 0.5 in the first part. If it is larger than 0.5, the corresponding node will be selected to build the new secondary hub. Step 2 is to select the transportation node. Seven randomly initialized numbers for seven nodes are compared with 0.5 in the second part. If it is larger than 0.5, the railway is employed to its in-flow link. If not, the highway is employed. Step 3 and 4 are to allocate demand nodes and secondary hubs, which are discussed next. Step 5 is to select the hubs to clear the cargo of all nodes. Similar to step 2, seven randomly initialized numbers for seven nodes are compared with 0.5 in the third part. If it is larger than 0.5, the cargo of the corresponding node is cleared at the primary hub. If not, the corresponding cargo is cleared at secondary hubs.

Figure 6 details steps 3 and 4. The node allocating process starts from demand node $i=1$. If demand node $i$ is selected to build the new secondary hub, secondary hub $i$ will be allocated to the primary hub. If not, we will find secondary hub $j$ which is the closest to demand node $i$. If the remaining cargo handling capacity of secondary hub $j$ is larger than the cargo demand of node $i$, node $i$ will be allocated to hub $j$. If not, $j=j+1$. Then, the remaining cargo handling capacity of secondary hub $j$ is updated. This process is repeated until all demand nodes are allocated.

4.1.3. Population Initialization

The chromosome length is determine based on the number of candidate hubs, the number of demand cities and the number of existing secondary hubs. A reasonable population size ($popsize$) is set based on the length of the chromosome, and $popsize$ individuals are randomly generated. All individuals must satisfy relevant constraints after chromosome decoding.

4.2. Fitness Evaluation

In order to evaluate the fitness of each individual, two contrary objectives (e.g., total time T and total cost C) in the proposed model are normalized by Equation (27). $f_1$, $f_1^{\max }$ and $f_1^{\min }$ denote the fitness, maximum fitness and minimum fitness of total time T, respectively. $f_2$, $f_2^{\max }$ and $f_2^{\min }$ represent the fitness, maximum fitness and minimum fitness of total cost C, respectively. ${\omega }_T$ and ${\omega }_C$ are the weights of total time and total cost, respectively.

$$F={\omega }_T\times \frac{f_1-f_1^{\min }}{f_1^{\max }-f_1^{\min }}+{\omega }_C\times \frac{f_2-f_2^{\min }}{f_2^{\max }-f_2^{\min }}$$

(27)

4.3. Selection

Tournament selection is employed to yield new population in the proposed AGA, which is detailed as follows.

Step 1: N is set as the number of the selected individuals in each iteration;

Step 2: N individuals are selected from the population. The individual with the highest fitness is kept while the rest N-1 individuals are put back to the population;

Step 3: Step 2 is repeated until the number of kept individuals reaches the preset population size.

4.4. Crossover and Mutation

Multi-point crossover and single-point mutation are employed in the proposed AGA. In each iteration, the crossover rate $p_c$ and mutation rate $p_m$ are adjusted by the hyperbolic function, which is a probabilistic nonlinear method to adjust parameters [41,42]. As shown in Equations (28) and (29), $f_{avg}$ denotes average fitness of the individual in each iteration. $A$ is an exogenous auxiliary adaptive parameter. A larger $A$ indicates more probability of crossover and mutation in the genetic process.

$$p_c=\{\begin{array}{l}\frac{p_{c\max }-p_{c\min }}{1+\exp (A\frac{2(f_{avg}-f)}{f_{avg}-f_{\min }-1})}+p_{c\min },f\le f_{avg}\\ p_{c\max },f>f_{avg}\end{array}$$

(28)

$$p_m=\{\begin{array}{l}\frac{p_{m\max }-p_{m\min }}{1+\exp (A\frac{2(f_{avg}-f)}{f_{avg}-f_{\min }-1})}+p_{m\min },f\le f_{avg}\\ p_{m\max },f>f_{avg}\end{array}$$

(29)

4.5. Stopping Criterion

Setting a maximum number of iterations is a common algorithm termination criterion. In this study, the AGA terminates when it iterates for $gen$ times; otherwise, it continues to iterate to find the optimal solution.

5. Case Study

In this section, we employ a generalized hierarchical multimodal hub-and-spoke network based on the real logistics network from China (see Figure 7), for which the proposed model and AGA are applied to jointly determine the optimal location of newly-built secondary hubs, the hubs to clear the cargo and the modes of the transportation links. The study network consists of 16 cities, which are detailed as follows.

• All nodes: Ningbo, Chongqing, Chengdu, Nanchang, Huhhot, Beijing, Zhengzhou, Changsha, Kunming, Xi’an, Wuhan, Lanzhou, Urumqi, Xuzhou, Bengbu, Wuhu;
• Primary hub: Ningbo;
• Existing secondary hubs: Chongqing, Chengdu, Nanchang;
• Candidate hubs: Huhhot, Beijing, Zhengzhou, Changsha, Kunming, Xi’an, Lanzhou, Urumqi (the number of newly-built secondary hubs is set as two).

The detailed data are shown in the Appendix A. Demand, capacity and speed of cargo clearing and fixed costs for building new hubs are listed in

Table A1. Demand, capacity and speed of freight clearing and fixed costs for building new hubs.

	Ningbo Port	Chongqing	Chengdu	Nanchang	Changsha	Zhengzhou	Xi’an	Hohhot	Lanzhou	Kunming	Beijing	Urumqi	Wuhan	Wuhu	Bengbu	Xuzhou
Demand $d_i$ (105 ton)	——	3690	3011	2025	2073	3449	2591	1772	1859	1940	1856	1885	2787	1787	1910	1927
Cargo clearing capacity $R_i$ (105 ton)	80,000	15,000	14,000	12,000	13,000	9000	8000	8000	7000	7000	8000	9000	——	——	——	——
Cargo clearing speed $w_i^L$ (105 ton/h)	10	10	8	8	13	11	8	8	8	8	8	8	——	——	——	——
Fixed cost of building new hubs $C_i^C$ (106 yuan)	——	——	——	——	400	500	400	600	400	500	400	500	——	——	——	——

. In addition, the freight demand in each node city comes from “Chinese national logistics statistics report 2019”. Highway and railway link transportation distances are listed in

Table A2. Highway link distance D_ij (km).

	Ningbo Port	Chongqing	Chengdu	Nanchang	Hohhot	Beijing	Zhengzhou	Changsha	Kunming	Xi’an	Lanzhou	Urumqi	Wuhan	Wuhu	Bengbu	Xuzhou
Ningbo Port	0	1808	2072	696	1896	2472	1128	1048	2320	1528	2152	4056
Chongqing	1808	0	309	1222	1679	2982	1178	901	827	711	975	2982	1604	1408	1370	1478
Chengdu	2072	309	0	1448	1671	2995	1187	1186	850	712	956	2855	1831	1635	1596	1540
Nanchang	696	1222	1448	0	1729	2529	851	343	1673	1097	1719	3626	495	484	572	743
Huhhot	1896	1679	1671	1729	0	1721	893	1675	2431	967	1057	2292	1859	1545	1356	1141
Beijing	2472	2982	2995	2529	1721	0	1888	2657	3742	2279	2669	3947	2474	2212	2014	1800
Zhengzhou	1128	1178	1187	851	893	1888	0	818	1938	480	1093	3000	1062	699	475	366
Changsha	1048	901	1186	343	1675	2657	818	0	1312	977	1598	3523	811	813	818	989
Kunming	2320	827	850	1673	2431	3742	1938	1312	0	1473	1662	3572	2086	2044	2025	2184
Xi’an	1528	711	712	1097	967	2279	480	977	1473	0	631	2527	1442	1060	921	833
Lanzhou	2152	975	956	1719	1057	2669	1093	1598	1662	631	0	1907	2052	1669	1534	1434
Urumqi	4056	2982	2855	3626	2292	3947	3000	3523	3572	2527	1907	0	3986	3578	3445	3343
Wuhan		1604	1831	495	1859	2474	1062	811	2086	1442	2052	3986	0	394	606	757
Wuhu		1408	1635	484	1545	2212	699	813	2044	1060	1669	3578	394	0	241	424
Bengbu		1370	1596	572	1356	2014	475	818	2025	921	1534	3445	606	241	0	187
Xuzhou		1478	1540	743	1141	1800	366	989	2184	833	1434	3343	757	424	187	0

and

Table A3. Railway link distance D_ij railway (km).

	Ningbo Port	Chongqing	Chengdu	Nanchang	Huhhot	Beijing	Zhengzhou	Changsha	Kunming	Xi’an	Lanzhou	Urumqi	Wuhan	Wuhu	Bengbu	Xuzhou
Ningbo Port	0	1950	2333	935	2128	2530	1218	1133	2616	1604	2280	4094
Chongqing	1950	0	306	1437	1815	3580	1262	817	995	771	868	2889	1578	1609	1999	1733
Chengdu	2333	306	0	1511	1961	3336	1400	1123	1112	971	828	2781	2065	1747	2018	1702
Nanchang	935	1437	1511	0	2203	2696	975	419	1902	1386	1927	3854	505	460	593	817
Huhhot	2128	1815	1961	2203	0	1955	1312	2210	2810	1064	1144	2727	2280	2193	1637	1473
Beijing	2530	3580	3336	2696	1955	0	2085	2877	4472	2453	3099	5062			2075
Zhengzhou	1218	1262	1400	975	1312	2085	0	898	2485	511	1187	3114	1186	743	513	349
Changsha	1133	817	1123	419	2210	2877	898	0	1587	1265	2085	4012	865	849	854	1247
Kunming	2616	995	1112	1902	2810	4472	2485	1587	0	1723	1863	3816	2348	2374	2498	2659
Xi’an	1604	771	971	1386	1064	2453	511	1265	1723	0	676	2603	1583	1140	1024	883
Lanzhou	2280	868	828	1927	1144	3099	1187	2085	1863	676	0	1953	2259	1816	1700	1536
Urumqi	4094	2889	2781	3854	2727	5062	3114	4012	3816	2603	1953	0	4055	3857	3627	3463
Wuhan		1578	2065	505	2280	2851	1186	865	2348	1583	2259	4055	0	443	752	916
Wuhu		1609	1747	460	2193	2408	743	849	2374	1140	1816	3857	443	0	309	309
Bengbu		1999	2018	593	1637	2075	513	854	2498	1024	1700	3627	752	309	0	164
Xuzhou		1733	1702	817	1473	1904	349	1247	2659	883	1536	3463	916	473	164	0

, respectively. The developed AGA is implemented in MATLAB 2016a on a personal laptop (Intel Core i5, 4.00 GB, 1.80 GHz).

5.1. Input Parameters

Some model input parameters to evaluate transportation cost and time are obtained by the survey. The unit railway and highway cost are set as 0.145 yuan·km⁻¹ and 0.45 yuan·km⁻¹, respectively. The transportation speed of railway and highway are set as 60 km·h⁻¹ and 100 km·h⁻¹, respectively. The unit cargo handling speed in the hub and green gas emission cost for different transportation mode are illustrated in

Table 4. Unit cargo handling speed in the hub and CARBON cost.

	Unit Cargo Handling Speed in the Hub(kg·h−1)	Unit CARBON Cost (yuan·kg−1)
Highway	0.2 × 10−2	1500
Railway	0.18 × 10−2	1700

. The carbon emission tax CC is set as 12,000 yuan·kg⁻¹. The unit carbon emission of transportation and cargo handling in the hub for different transportation modes are listed in

Table 5. Unit CARBON emission during transportation and cargo handling in the hub.

	Unit CARBON Emission during Transportation ${\mathit{\alpha }}_{\mathit{m}}$ (kg/ton·km−1)	Unit CARBON Emission during Cargo Operation ${\mathit{\epsilon }}_{\mathit{i}\mathit{m}}$ (kg/ton·km−1)
Highway	7.96 × 10−5	1.56 × 10−4
Railway	2.8 × 10−6	1.56 × 10−4

.

Regarding the developed AGA, the input parameters are determined experimentally in terms of the study case and illustrated in

Table 6. Input AGA parameters setting.

Parameters	Value
Population size ($popsize$)	50
Generation ($gen$)	200
Weight of time (${\omega }_T$)	0.3
Weight of cost (${\omega }_C$)	0.7
Auxiliary adaptive parameter	9.903438
Tournament selection size ($N$)	2
Minimum crossover probability ($p_{c\min }$)	0.8
Maximum crossover probability ($p_{c\max }$)	0.95
Minimum mutation probability ($p_{m\min }$)	0.01
Maximum mutation probability ($p_{m\max }$)	0.05

. In order to highlight the concept of sustainability, the weight of cost is set as 0.7 in the weighted comprehensive goal because it includes carbon emission costs. In addition, the weight of time is set as 0.3.

5.2. Algorithm Performance Analysis

The performance of AGA was analyzed by comparing its solution results with those of GA. Ten simulation runs were executed so that the randomness of GA and AGA results may be assessed. It can be seen from

Table 7. Comparison of the solution results of GA and AGA.

	Avg (105 million)	Best (105 million)	Gap (%)	Time (s)
GA	5.419	5.407	0.22	39.52
AGA	5.397	5.393	0.07	39.89
GAP(%)	-	0.26	-	-

that the deviation between the optimal solution (Best) and the average solution (Avg) of AGA is only 0.07%, which shows the good stability of AGA. In addition, the AGA obtained a better solution than the GA, with a gap of 0.26%. The average computation time of AGA is 39.89 s. Moreover, the objective value found by GA and AGA over iteration is illustrated in Figure 8. The results suggest that AGA is more efficient because AGA converges significantly quicker than GA. The adaptive adjustment of genetic parameters by AGA improves the convergence accuracy and accelerates its convergence speed. Combined with Table 7 and Figure 8, it can be considered that AGA has shown good performance in solving the multimodal transport network hub location in this study.

5.3. Result Analysis

The detailed results of the optimized network are compared with those of the existing network. The corresponding outputs are illustrated in Figure 9 and Figure 10 and

Table 8. Flow distribution of the existing network.

Hubs	Transportation Mode between Primary Hub and Secondary Hubs (m)	Flow between Primary Hub and Secondary Hubs ${\mathit{w}}_{\mathit{i}\mathit{j}\mathit{m}}$ (104 ton)	Demand Nodes	Transportation Mode between Secondary Hubs and Demand Nodes	Flow ${\mathit{w}}_{\mathit{i}\mathit{j}\mathit{m}}$ (104 ton)
Chongqing	Highway	15,000	Chongqing	/	3690
			Huhhot	Highway	1772
			Zhengzhou	Railway	3449
			Changsha	Highway	2073
			Kunming	Railway	1940
			Xi’an	Railway	2076
Chengdu	Highway	7562	Chengdu	/	3011
			Xi’an	Highway	515
			Lanzhou	Railway	1859
			Urumqi	Railway	1885
			Xuzhou	Railway	292
Nanchang	Highway	12,000	Nanchang	/	2025
			Beijing	Railway	1856
			Wuhan	Highway	2787
			Wuhu	Highway	1787
			Bengbu	Highway	1910
			Xuzhou	Railway	1635

,

Table 9. Flow distribution of optimized network.

	Hubs	Transportation Mode between Primary Hub and Secondary (m)	Flow between Primary Hub and Secondary Hubs ${\mathit{w}}_{\mathit{i}\mathit{j}\mathit{m}}$ (104 ton)	Demand Nodes	Transportation Mode between Hubs and Spokes $\mathit{x}{1}_{\mathit{i}\mathit{j}}/\mathit{x}{2}_{\mathit{i}\mathit{j}}$	Flow ${\mathit{w}}_{\mathit{i}\mathit{j}\mathit{m}}$ (104 ton)
Existing secondary hubs	Chongqing	Railway	5630	Chongqing	/	3690
				Kunming	Railway	1940
	Chengdu	Highway	4896	Chengdu	/	3011
				Urumqi	Railway	1885
	Nanchang	Railway	12,509	Nanchang	/	2025
				Changsha	Highway	2073
				Wuhan	Highway	2787
				Wuhu	Railway	1787
				Bengbu	Railway	1910
				Xuzhou	Highway	1927
Newly built secondary hubs	Zhengzhou	Highway	9000	Zhengzhou	/	3449
				Beijing	Railway	695
				Xuzhou	Highway	1923
				Huhhot	Railway	1772
	Xi’an	Railway	4450	Xi’an	/	2591
				Lanzhou	Railway	1859

,

Table 10. Comparison between optimized and existing networks for cargo operated in the secondary hubs.

Secondary Hubs (Existing/Newly-Built)	Chongqing	Chengdu	Nanchang	Zhengzhou	Xi’an
Optimized network	5630	4896	12,509	9000	4450
Existing network	15,000	7562	12,000	-	-

and

Table 11. Comparison between optimized and existing networks for transportation cost and time.

	Optimized Network	Existing Network	Gap
Total time (h)	13,170	13,466	2.20%
Total cost (yuan)	5.43 × 107	5.56 × 107	2.35%

.

The flow distribution scenarios of different networks are depicted in Figure 8 and Figure 9 and listed in Table 8 and Table 9. Comparing Figure 9 with Figure 10, we can see that two newly-built secondary hubs are located at Zhengzhou and Xi’an in the optimized network. Thus, the cargo flow originating from the primary hub can be shared by more secondary hubs. It is also found that more cargo is delivered by railway in the optimized network. It could be explained by Equation (10) that since the carbon emission cost is considered in the objective, the optimized network is more likely to employ the transportation mode with low carbon emission.

Further comparing Table 8 with Table 9, we can observe that some links are modified. It is worth noting that the existing network contains some detouring links (e.g., Ningbo-Nanchang-Beijing and Ningbo-Chongqing-Xi’an) due to the lack of enough secondary hubs. In the optimized network, those detouring links are adjusted to Ningbo-Zhengzhou-Beijing and Ningbo-Xi’an, respectively. This indicates that the links in the network might also be optimized by the proposed model.

Table 10 lists the total cargo operated in secondary hubs. It can be observed that in the optimized network, the cargo operated in the secondary hubs generally decreases while only that in Nanchang slightly increases (4.2%). This indicates that the proposed model might help distribute the cargo flow and prevent the cargo from concentrating in one secondary hub.

Table 11 shows the comparison of transportation cost and time between optimized networks and existing networks. It is observed that both total time and cost of the optimized network decrease (2.2% and 2.35%). This indicates that the extra cost incurred by building new secondary hubs is lower than the cost reduced by less transportation distance and carbon emission, further demonstrating the economic benefit and operational efficiency of the optimized network.

5.4. Carbon Emission Tax Analysis

A sensitivity analysis was conducted to explore the relation between carbon emission and the optimized results. The value of the carbon emission tax is varied within a certain range. The corresponding outputs are shown in Figure 11 and Figure 12.

Figure 11 shows that as the carbon emission tax increases, the total time slightly increases, while the total cost excluding the carbon emission cost substantially decreases. It can be explained by Equations (5)–(10) why the increase of carbon emission tax may lead to more railway links (with lower carbon emission, transportation cost and speed) employed in the optimized network.

In order to explore how the carbon emission affects the optimization of the secondary hubs, Equation (20) is eliminated from the model. Thus, the number of newly-built secondary hubs is not preset and will be also optimized in the model. It can be seen from Figure 12 that the increase of carbon emission tax results in more secondary hubs deployed in the optimize network. Thus, the average cargo flow through secondary hubs decreases, which indicates that the deployment of the secondary hubs is sensitive to the carbon emission tax.

6. Discussion

The model proposed in this paper effectively solves the problem of extending secondary hubs in the existing network consisting of primary hub, secondary hub and demand side. The model has the potential to be reproduced for solving the network expansion siting and traffic distribution problems in all similar three-level networks. In practice, this study will make a great contribution to the expansion of the waterless ports as the secondary hub has the capacity to support the construction of the port’s collection and distribution system and to strengthen the port’s agglomeration and radiation capacity. Furthermore, this study can provide a relevant theoretical basis for the research on the location of distribution centers in the three-level logistics distribution network, where goods are usually transported from the warehouse to the distribution center and then to the customer point.

Moreover, the consideration of carbon emissions in the model and the corresponding carbon tax sensitivity analysis results provide insights to government departments and managers of multimodal transport companies:

(1) For government departments, the regulation of carbon tax will directly affect the network structure of freight transportation. For the decarbonized and stable development of national freight transportation, government departments should actively encourage transportation companies to expand their hub network. Reasonable transportation hub layout and well-developed hub channel will promote multimodal transport enterprises to adopt low-carbon transportation mode;

(2) For the managers of transportation enterprises, this study brought new inspiration from the perspective of low carbon. The consideration of carbon emission cost can increase the transportation time and affect the efficiency of freight transportation. From the perspective of the demand customer, managers need to build more hubs to mitigate the impact of low-carbon and inefficient transportation modes on customers. Therefore, how to balance the interests of enterprises and customers is worth thinking about by managers.

The model assumptions proposed in this study also make the model have some limitations in practical application. The secondary hub is usually located at the intersection of the railway and the highway in the inland economic center city. It is a natural logistics hub with convenient cargo handling, temporary storage and transportation. This study only focused on the functions of the secondary hubs for collecting and distributing goods and customs declaration; it ignored the hub channel between them. The transportation modes and networks among the primary hub, secondary hub and demand points are also relatively simple. In practice, there are various ways to transfer from the primary hub to the demand cities, such as multiple transfers through the secondary hub, transfer between the demand cities, etc. When the primary hub is close to the demand city, goods can also be directly transported from the primary hub to the demand city. Combining various real-world scenarios, the proposed model needs to be extended to further meet the complex traffic network environment.

7. Conclusions

This study proposes a hierarchical multimodal transport hub location problem to expand the existing network. An innovative mixed integer nonlinear model considering carbon emissions is developed to determine the optimal location of new-built secondary hubs and the optimal transportation mode among hubs. From the perspective of logistics enterprises and customers, the minimization of total transportation cost and the minimization of transportation time are considered, respectively, and the double objective optimization is achieved by weighting method. The proposed model provides a potential reproducibility capability for the similar three-level network of “primary hubs—secondary hubs—demand cities” in different regions. A tangible adaptive genetic algorithm (AGA) is designed to solve the proposed model effectively. AGA showed better convergence performance than traditional GA and is expected to be applied to solve larger scale cases. The case study of Ningbo Port in China shows that the located secondary hubs significantly improved the current multimodal transport network. The new-built hubs have been proven to improve cargo handling capacity. Two additional hubs can handle 41.46% more cargo flow than the original network. Moreover, these new-built hubs achieve 2.35% transportation cost savings and 2.2% transportation time savings. The sensitivity analysis of carbon tax also provides the government and enterprises with insightful opinions from the perspective of low-carbon transportation. The government’s regulation of carbon tax can directly affect the network structure of cargo transportation. A higher carbon tax would prompt enterprises to choose a low-carbon transportation mode or open more secondary hubs to reduce the transit time for goods.

For further research, it would be interesting to continue the study with the created model and application. In this study, only highway and railway transportation modes are considered. In practice, other transportation modes may be required according to the characteristics of goods. In addition, in the complex transportation network, secondary hubs are connected, and some demand cities are also connected. Thus, the proposed hub location model will be further expanded to accommodate various hybrid hub-and-spoke networks. The location–routing problem of multimodal transport networks will also be studied to explore the impact of route optimization on hub location decision. In addition, some exact solution algorithms or other heuristic algorithms will be explored to find more efficient solutions for the hub location combination optimization problem.