Analysis and Dissolution of Potential Contradictions in Thematic Lessons from a Cultural-Historical Activity Theory Perspective
Abstract
:1. Introduction
2. Literature Review and Framework
2.1. TL
2.2. LS
2.3. CHAT and Its Revealed Contradictions
2.4. This Study
- What are the potential contradictions in a TLAS according to CHAT?
- What measures can be adopted to dissolve those potential contradictions?
- How are those contradictions dissolved as the lesson proceeds?
3. Research Design
3.1. Setting and Participants
3.2. Procedure
3.3. Data Collection and Analysis
4. Research Process and Results
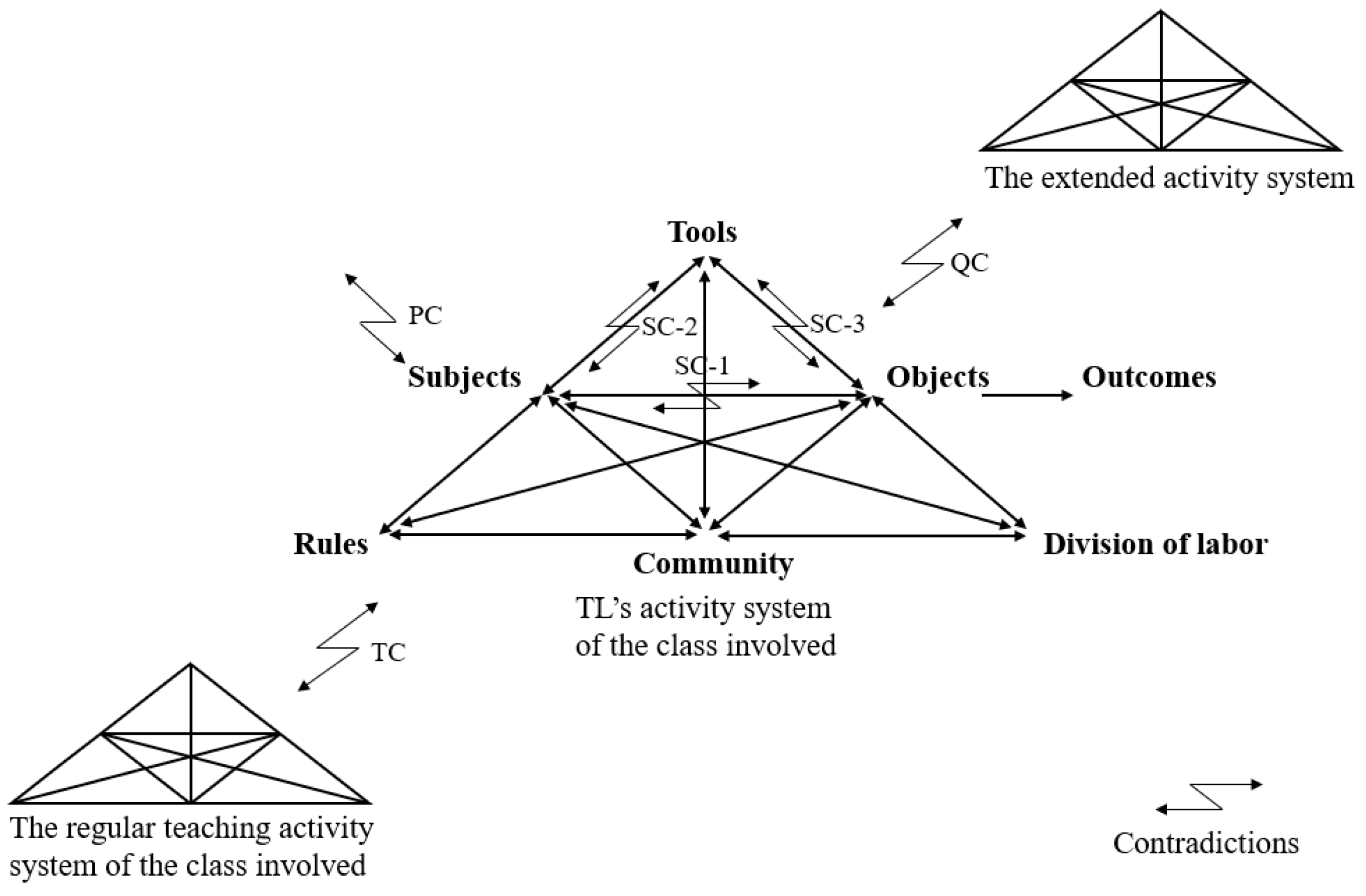
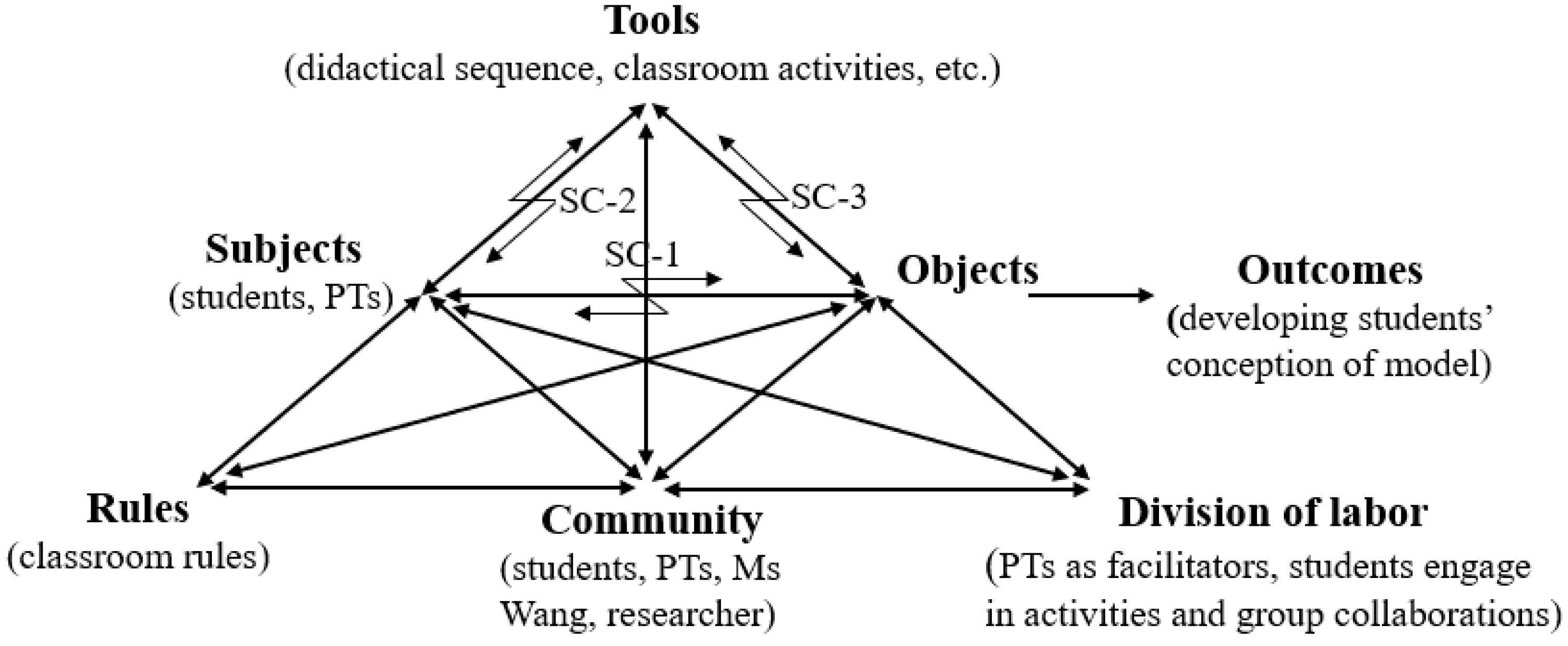
4.1. Analysis of Potential Contradictions
4.1.1. Primary Contradictions
I don’t know if they have any previous experience in teaching, and if they can successfully establish a positive interaction with students in a short period; after all, such TL is more open and lively compared to regular teaching. In addition, I was concerned that students would not take these lessons seriously when facing these new faces.
Nonetheless, I think they are capable of dealing with these difficulties; after all, they are graduate students in mathematics education and have better knowledge than I do about the theory of mathematics education, the TL mentioned in the curriculum standard, and the knowledge about PM. In addition, they are young and creative, and I feel confident that they are competent in teaching such novel sessions.
4.1.2. Secondary Contradictions
I think that the establishment of positive interaction between the prospective teachers and the students that I just mentioned would not yet be particularly challenging since I believe that they (i.e., the prospective teachers) are psychologically prepared and also, I believe, they have the experience and ability to work with students. However, as teachers, these graduate students need to learn about students’ learning status to design an achievable goal for them accordingly. In this process, how much do these graduate students know about the textbooks? How much do they know about the students? Do they have a clear idea of the lesson plan to achieve the goals? I’m not so sure about that, so I think those difficulties and challenges are probably the ones that need the most attention.
Your Conceived Didactical Sequence for the TL is fun and will be engaging for the students. The students in this class are currently in seventh grade, and they are very active, and curious and enjoy hands-on activities and teamwork in the classroom. They have already learned preparatory knowledge such as the concepts of triangles, quadrilaterals, and polygons, and they have recently learned about translations, rotations, and folding before your PM-themed lessons, all of which can prepare them for this TL. In addition, students have many experiences with PM in their lives. So, the students probably won’t have much difficulty understanding this concept. However, when exploring the single PM and combined PM, inevitably, the formula for the sum of the interior angles of polygons (including triangles) will be involved, whereas they have not learned this formula so far. So, I think students may encounter difficulties just after stage (b), which presents a challenge to your lesson plan.
Yes, students have learned about linear equations with two unknowns in the second semester of sixth grade and about finding integer solutions to a linear equation with two unknowns, so I think this is unlikely to be a difficult area for them. The biggest difficulty lies in the exploration of the formulas for the sum of the interior angles of triangles and the sum of the interior angles of polygons, and I think students need to be allowed to explore and discover.
I think your emphasis on interaction in the classroom is appealing to students, and the group work and presentations are also attractive. As far as I know, students enjoy a lively classroom, and personally, I love to provide students with opportunities to interact and discuss in my daily teaching. If there are any contradictions to be figured out, I think it might appear in the teaching design.
According to your provided Conceived Didactical Sequence, I think the current approach is clear and logical. You have followed a teaching process from special to general, starting with the exploration of single PMs of such common geometric figures as regular triangles and squares, and gradually transitioning to exploring single PMs with special geometric figures such as regular pentagons and regular hexagons, a process of exploration accessible to the students. Also, it’s good that you followed a logical progression from single PM to combined PM. For the fact that both an arbitrary triangle and an arbitrary quadrilateral can be used as the basic figure to construct single PMs, I am not sure if they are easily acceptable, so I suggest you invest more time in the class. In addition, I would recommend that you leave out the consideration of constructing PMs using regular pentagons and a special rhombus; after all, this is not well aligned with the previous theme (i.e., constructing combined PMs with two regular polygons as the basic figures), as well as it would increase students’ learning burden. Lastly, as students have just finished the chapter on translation, rotation, and folding, for which PM is an extended learning material, I think you might consider introducing relevant elements involved in a life or in artwork to establish a connection between this chapter’s knowledge and PM.
Probably still lies in exploring the formula for the sum of the interior angles of polygons and applying this formula to analyze which figures are available as the basic one to construct PMs, which I think is challenging for students.
Compared to the (potential) contradictions between the subject and the tools, I think the (potential) ones between the tools and the objects are not as prominent.
Probably because we conceived the tools concerning the objects (including the outcomes), which ensured a theoretically coherent relationship between the tools and the objects. In other words, we designed the lessons based on the objects, so they appear to be harmonious. But still, we would appreciate some advice from you.
Yes, your intention to develop students’ comprehensive skills and modeling concepts is fine in terms of the teaching design alone. However, returning to my previous opinion, would the students be able to cope with the challenging tasks involved (i.e., the contradictions with the tools)? Let’s talk back to the relationship between your design and your objects. It’s good that your design runs through a theme from the very beginning to end, with logic and progression. I’m not sure if you place a particular emphasis on mathematical modeling in the classroom, but I don’t think this is a good idea. Because what the curriculum standard requires of middle school students is modeling concepts, not something like the rigorous mathematical modeling at the college level.
4.1.3. Tertiary and Quaternary Contradictions
If I understood correctly, the tertiary contradictions are about the conflicts between the TL you will be conducting and the regular teaching. I don’t think there are any conflicts because the current curriculum standard also advocates TL as well, and our school has already introduced similar open-ended, exploratory programs like that in the after-school service courses, where students enjoyed them.
No problem, because this is our partnership project, the weekly after-school service hours can be used to carry out it, and this TL will exactly enrich the after-school service courses.
I think there is probably not a problem because all the classes are teaching at the same pace and your sessions for this class will not affect the pace…… I feel that if we work well on this project, other classes will also be interested in joining your project.
4.1.4. The Overall Picture of the Contradictions Focused upon in this Study
4.2. Pedagogical Considerations for Those Contradictions
4.2.1. Setting Moderate Learning Objects
Hi everyone, after the three vivid and interesting sessions about PM, we have learned about its concept, explored its principles, conditions, etc., and experienced its beauty. Now, let’s work together to apply this acquired knowledge!
There are two kinds of regular polygons (regular m-sides and regular n-sides, respectively) with a number of x and y. Please construct a mathematical model of combined PM using them as the basic figures, draw a pattern of PM based on your model, and find an example of this pattern in real life (either a photo you shot or material obtained from the Internet), and finally form a research report.
4.2.2. Creating Sustainable Exploratory Learning Environments Featuring Progressive Didactical Sequence and Coherent Activities
4.2.3. Scaffolding Necessary Knowledge for Students to Model Mathematically
4.2.4. Situating Students in an Interactive, Communicative, and Cooperative Classroom Environment
4.3. The Observed Dissolution of Those Contradictions
4.3.1. Episode 1
PT-Xin: Guys, let’s look at the floor under our feet first, then at the five pictures on the screen (the first one is the ceiling of the classroom, the second is a nice mural, the third is an artwork by Maurits Cornelis Escher, the fourth is a designed pattern for the floor of a shopping mall, and the fifth is a pattern decorating a wall). What characteristics do they have in common? Please communicate and discuss within each group and share your findings later.
……
Students: All these patterns are pieced together.
PT-Xin: With what?
Student: They are formed by joining several smaller figures together at one point.
PT-Xin: What are the characteristics of these smaller figures?
Student: They are the same.
PT-Xin: So, is the whole pattern made up of one or several figures of the same size and shape?
Student: Yes.
PT-Xin: So, if we look again, what do the figures look like at those joints?
Student: The joints are seamless.
PT-Xin: Good. These figures are pieced together without slits or overlaps, which we call a PM. Could any student define it based on these characteristics?
Student: A pattern that is pieced together with the same figure without either slits or overlaps is called a PM.
PT-Xin: Good, please sit down. Then a PM can be defined as a pattern made by piecing together one, or several, basic figures without either overlaps or slits. Do you know any other examples of PMs in our lives?
Student: The floor, the ceiling, or putting desks together to form a conference table.
Student: And honeycomb.
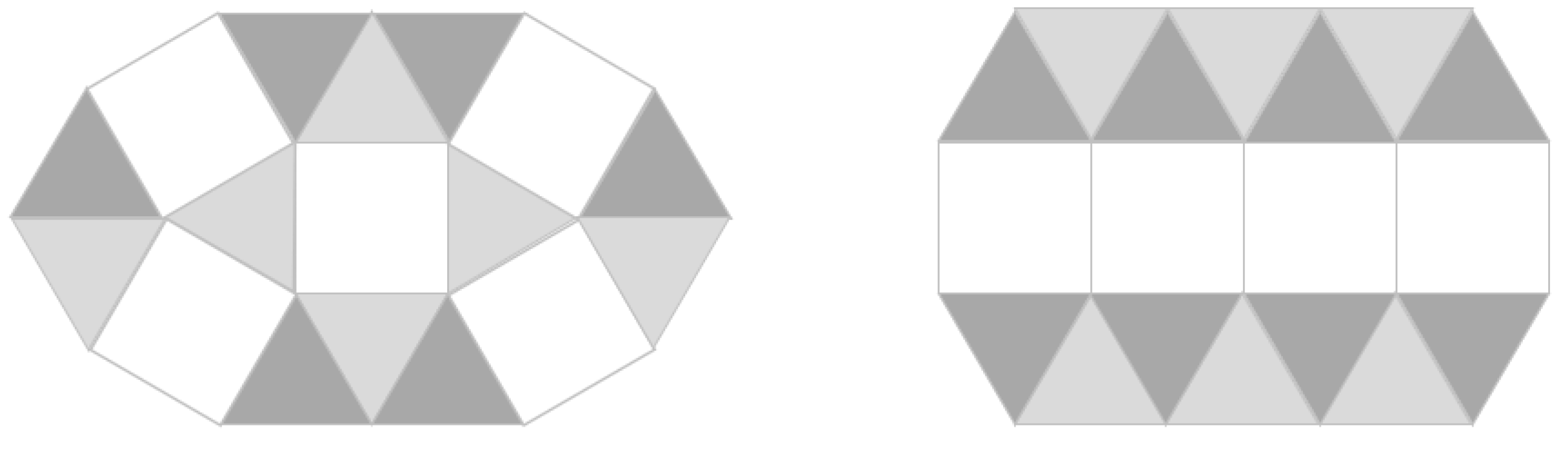
PT-Xin: Good, everyone seems to find math from life well. Here, please look at these three patterns on the board again (see Figure 3). Which of them is the PM?
Student: The first is not, because there is an overlap; the second is not, because there is a gap, and the third is.
PT-Xin: Good. When judging whether a pattern is a PM or not, we can draw on its three characteristics. Let’s observe the previous five patterns and the third one here. What are the basic figures that construct these PMs? How can the whole pattern be viewed as constructed from this or these basic figures? Relate this to what we have learned earlier about translation, rotation, and folding.
PT-Xin: Well. We can find that PM can be considered as getting from a basic figure or several basic figures by translation, rotation, and/or folding, which is the nature of PM. So, can all figures be used as basic figures to construct a PM, and if not, which ones can? Here, we start from the simplest case and consider using one figure as the basic one to construct a PM, and, following the principle of moving from the particular to the general, we first choose the case of a regular polygon to explore.
……
4.3.2. Episode 2
PT-Tang: Through the hands-on game earlier, we find that one can use a regular triangle and a square as the basic figures to construct a PM. For example, three regular triangles and two squares are available. Can you explain the mathematical rationale for that?
Student: This is because when piecing them together, the angles of the three regular triangles add up to 180 degrees and the angles of the two squares add up to 180 degrees.
PT-Tang: Excellent, that satisfies the definition of PM. We just discovered this through a hands-on game, and now we’ve confirmed it mathematically. In other words, 60 × 3 + 90 × 2 is exactly equal to 360. I noticed you all constructed very creative patterns, and altogether two patterns of PMs were provided (see Figure 4). Next, I have a question, can we only use three regular triangles and two squares to construct a PM, are there any other ways? Can it only be three regular triangles and two squares? Can it be four regular triangles and three squares? Can it be two regular triangles and two squares? Can you mathematically solve this problem?
Student: Build an equation.
PT-Tang: Okay, how do we do it?
Student: Suppose the number of the regular triangles is x and the number of the squares is y. Then 60x + 90y = 360.
PT-Tang: Is that correct? Can this equation be solved? Have you ever learned this equation?
Student: Yes, a linear equation with two unknowns.
PT-Tang: How do we solve this equation?
Student: First simplify it to get 2x + 3y = 12, then we can get the solutions.
PT-Tang: I feel that this equation has countless sets of solutions. For example, if x equals -1, y equals 14/3. So, what exactly should we seek for a solution to this equation?
Student: Positive integers.
PT-Tang: Excellent, why should we seek positive integer solutions?
Student: Because non-positive integers don’t work.
PT-Tang: Why don’t they work?
Student: The number of figures cannot be zero, because if x is zero then there is only one figure. And of course, it cannot ever be a negative number.
PT-Tang: Good, now we are clear that we have to find positive integer solutions to this equation (60x + 90y) = 360, right? How do we find it?
Students: Just try them one by one.
PT-Tang: Where can we start trying?
Student: Start with 1, but simplify it first, we can simplify it to 2x + 3y = 12.
PT-Tang: With x equal to 1, can we calculate the solution for y? What is it?
Student: 10/3
PT-Tang: Is it fine if y = 10/3?
Student: No.
PT-Tang: Next, it’s time to use 2 regular triangles, right? Let’s see how many squares it needs.
Student: 8/3.
……
PT-Tang: x = 6, y = 0, which are both integers, does this set of solutions work?
Student: No.
PT-Tang: Why not?
Student: They cannot be zero.
PT-Tang: Yes. Since we are constructing a combined PM with two regular polygons, neither of them can be zero in number. Do we need to continue to try further down?
Student: No.
PT-Tang: Why not? Because if x is equal to 7, y must be a negative number, right? So, we’ve just found all the positive integers for this equation. How many cases have we found that are available?
Students: Only the third case.
PT-Tang: OK, that means we found a general way to solve the problem of constructing a PM using two regular polygons as the basic figure. We just need to know the degree of each interior angle of each regular polygon, and we can suppose the number of them separately. Can anyone build a generalized equation?
Student: αx + βy = 360.
PT-Tang: What solutions should we find about α and β?
Student: The positive integer solutions.
……
5. Discussion
6. Conclusions
7. Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haataja, E.; Moreno-Esteva, E.G.; Salonen, V.; Laine, A.; Toivanen, M.; Hannula, M.S. Teacher's visual attention when scaffolding collaborative mathematical problem solving. Teach. Teach. Educ. 2019, 86, 102877. [Google Scholar] [CrossRef]
- Nieminen, J.H.; Chan, M.C.E.; Clarke, D. What affordances do open-ended real-life tasks offer for sharing student agency in collaborative problem-solving? Educ. Stud. Math. 2022, 109, 115–136. [Google Scholar] [CrossRef]
- Yao, J.-X.; Guo, Y.-Y. Core competences and scientific literacy: The recent reform of the school science curriculum in China. Int. J. Sci. Educ. 2018, 40, 1913–1933. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Q.; Du, X.; Liu, J. Chinese mathematics curriculum reform in the twenty-first century. In The 21st-Century Mathematics Education in China; Cao, Y., Leung, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 53–72. [Google Scholar]
- Cai, J.; Jiang, C. An Analysis of Problem-Posing Tasks in Chinese and US Elementary Mathematics Textbooks. Int. J. Sci. Math. Educ. 2016, 15, 1521–1540. [Google Scholar] [CrossRef]
- Pratama, I.G.D.J.; Dantes, N.; Yudiana, K. Thematic learning plan with a nature of science learning model in the fourth grade of elementary school. Int. J. Elem. Educ. 2020, 4, 447–453. [Google Scholar]
- China Ministry of Education. Mathematics Curriculum Standards for Compulsory Education (2022 Edition); Beijing Normal University Press: Beijing, China, 2022. (In Chinese) [Google Scholar]
- Lewis, C. How does lesson study improve mathematics instruction? ZDM 2016, 48, 571–580. [Google Scholar] [CrossRef]
- Willems, I.; Bossche, P.V.D. Lesson Study effectiveness for teachers’ professional learning: A best evidence synthesis. Int. J. Lesson Learn. Stud. 2019, 8, 257–271. [Google Scholar] [CrossRef]
- Huang, X.; Huang, R.; Huang, Y.; Wu, C.; Wanner, C.A. Lesson study and its role in the implementation of curriculum reform in China. In Theory and Practices of Lesson Study in Mathematics: An International Perspective; Huang, R., Ed.; Springer: New York, NY, USA, 2019; pp. 229–254. [Google Scholar]
- Huang, R.; Gong, Z.; Han, X. Implementing mathematics teaching that promotes children’ understanding through theory-driven lesson study. ZDM 2016, 48, 425–439. [Google Scholar] [CrossRef]
- Qi, C.; Liu, X.; Wang, R.; Zhang, J.; Fu, Y.; Huang, Q. Contradiction and its solutions in the mathematics teacher–researcher partnership: An activity theory perspective. ZDM 2022, 3, 639–652. [Google Scholar] [CrossRef]
- Qi, C.; Lai, M.Y.; Liu, L.; Zuo, S.; Liang, H.; Li, R. Examining teachers’ learning through a project-based learning lesson study: A case study in China. Int. J. Lesson. Learn. S. 2023, 1, 106–119. [Google Scholar] [CrossRef]
- Huang, R.; Han, X. Developing mathematics teachers’ competence through parallel lesson study. Int. J. Lesson Learn. Stud. 2015, 4, 100–117. [Google Scholar] [CrossRef]
- Huang, X.; Huang, R.; Lai, M.Y. Exploring teacher learning process in Chinese lesson study: A case of representing fractions on a number line. Int. J. Lesson Learn. Stud. 2021, 11, 121–132. [Google Scholar] [CrossRef]
- Tamura, T.; Uesugi, Y. Involving students in lesson study: A new perspective. Int. J. Lesson Learn. Stud. 2019, 9, 139–151. [Google Scholar] [CrossRef]
- Engeström, Y. Expansive learning at work: Toward an activity theoretical reconceptualization. J. Educ. Work 2001, 14, 133–156. [Google Scholar] [CrossRef]
- Handal, B.; Bobis, J. Teaching mathematics thematically: Teachers’ perspectives. Math. Educ. Res. J. 2004, 16, 3–18. [Google Scholar] [CrossRef]
- Putnam, R.T.; Borko, H. What do new views of knowledge and thinking have to say about research on teacher learning? Educ. Res. 2000, 29, 4–15. [Google Scholar] [CrossRef]
- Chen, Y.-T. The effect of thematic video-based instruction on learning and motivation in e-learning. Int. J. Phys. Sci. 2012, 7, 957–965. [Google Scholar] [CrossRef]
- Chronaki, A. Teaching math through theme-based resources: Pedagogic style, theme’ and math’ in lessons. Educ. Stud. Math. 2000, 42, 141–163. [Google Scholar] [CrossRef]
- Huang, R.; Takahashi, A.; De Ponte, J. Theory and Practices of LS in Mathematics: An International Perspective; Springer: New York, NY, USA, 2019. [Google Scholar]
- Huang, R.; Kimmins, D.; Winters, J.; Rushton, G. Does a technology assisted lesson study approach enhance teacher learning while eliminating obstacles of traditional lesson study? Contemp. Issues Technol. Teach. Educ. (CITE J.) 2020, 20, 618–659. [Google Scholar]
- Lamb, P.; Ko, P.Y. Case studies of lesson and learning study in initial teacher education programs. Int. J. Lesson. Learn. Stud. 2016, 5, 78–83. [Google Scholar] [CrossRef]
- Huang, R.; Shimizu, Y. Improving teaching, developing teachers and teacher educators, and linking theory and practice through lesson study in mathematics: An international perspective. ZDM 2016, 48, 393–409. [Google Scholar] [CrossRef]
- Huang, R.; Barlow, A.T.; Haupt, M.E. Improving core instructional practice in mathematics teaching through lesson study. Int. J. Lesson Learn. Stud. 2017, 6, 365–379. [Google Scholar] [CrossRef]
- Cheung, W.M.; Wong, W.Y. Does lesson study work? Int. J. Lesson Learn. Stud. 2014, 3, 137–149. [Google Scholar] [CrossRef]
- Lewis, C.; Perry, R. Lesson Study to Scale Up Research-Based Knowledge: A Randomized, Controlled Trial of Fractions Learning. J. Res. Math. Educ. 2017, 48, 261–299. [Google Scholar] [CrossRef]
- Chen, X. Theorizing Chinese lesson study from a cultural perspective. Int. J. Lesson Learn. Stud. 2017, 6, 283–292. [Google Scholar] [CrossRef]
- Huang, R.; Fang, Y.; Chen, X. Chinese lesson study: An improvement science, a deliberate practice, and research methodology. Int. J. Lesson Learn. Stud. 2017, 6, 270–282. [Google Scholar] [CrossRef]
- Huang, X.; Lai, M.Y.; Huang, R. Teachers’ learning through an online lesson study: An analysis from the expansive learning perspective. Int. J. Lesson Learn. Stud. 2021, 10, 202–216. [Google Scholar] [CrossRef]
- Engeström, Y.; Sannino, A. Studies of expansive learning: Foundations, findings and future challenges. Educ. Res. Rev. 2010, 5, 1–24. [Google Scholar] [CrossRef]
- Galleguillos, J.; Borba, M.d.C. Expansive movements in the development of mathematical modeling: Analysis from an Activity Theory perspective. ZDM 2017, 50, 129–142. [Google Scholar] [CrossRef]
- Salloum, S.; BouJaoude, S. Understanding Interactions in Multilingual Science Classrooms through Cultural-Historical Activity Theory (CHAT): What Do Contradictions Tell Us? Int. J. Sci. Math. Educ. 2020, 19, 1333–1355. [Google Scholar] [CrossRef]
- Qi, C.; Cao, C.; Huang, R. Teacher learning through collaboration between teachers and researchers: A case study in China. Int J of Sci and Math Educ. 2023, 1, 93–112. [Google Scholar] [CrossRef]
- Engeström, Y. Learning by Expanding: An Activity-Theoretical Approach to Developmental Research, 2nd ed; Cambridge University Press: New York, NY, USA, 2015. [Google Scholar]
- Rittle-Johnson, B.; Koedinger, K.R. Designing Knowledge Scaffolds to Support Mathematical Problem Solving. Cogn. Instr. 2005, 23, 313–349. [Google Scholar] [CrossRef]
- Ma, L. Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States; Routledge: New York, NY, USA, 2010. [Google Scholar]
- Nunes, T.; Bryant, P.; Evans, D.; Gottardis, L.; Terlektsi, M.-E. The cognitive demands of understanding the sample space. ZDM 2014, 46, 437–448. [Google Scholar] [CrossRef]
- Pu, S.; Sun, X.; Li, Y. How do Chinese teachers acquire and improve their knowledge through intensive textbook studies. In How Chinese Acquire and Improve Mathematics Knowledge for Teaching? Li, Y., Huang, R., Eds.; Brill Sense: Leiden, The Netherlands, 2018; pp. 165–184. [Google Scholar]
- China Ministry of Education. Mathematics Curriculum Standards for Compulsory Education (Trial Edition); Beijing Normal University Press: Beijing, China, 2001. (In Chinese) [Google Scholar]
- Wong, J.L. Searching for good practice in teaching: A comparison of two subject-based professional learning communities in a secondary school in Shanghai. Comp. A J. Comp. Int. Educ. 2010, 40, 623–639. [Google Scholar] [CrossRef]
- Xue, E.; Li, J. What is the value essence of “double reduction” (Shuang Jian) policy in China? A policy narrative perspective. Educ. Philos. Theory 2023, 55, 787–796. [Google Scholar] [CrossRef]
- Niss, M.; Blum, W. The Learning and Teaching of Mathematical Modelling; Routledge: New York, NY, USA, 2020. [Google Scholar]

| Session | The Didactical Sequence and Activities Involved |
|---|---|
| 1 | A-1: Observe floors, artwork, etc., and summarize the concept and types of PM (including single PM and combined PM). A-2: Students provide other examples of applications of PM and analyze how it is formed by basic shapes. A-3: Students study PM with a mathematical perspective and are guided to start their exploration by constructing a single PM using a regular polygon as the basic figure. A-4: Students explore and discuss whether a single PM can be constructed using a regular triangle, square, regular pentagon, and regular hexagon as basic figures by playing games. A-5: Through group communication, students analyze the conditions for constructing a single PM using a regular polygon as the basic figure with a mathematical model (Model 1). A-6: Through group communication, students mathematically explain which regular polygons can be used as basic figures to construct a single PM. A-7: Through group collaboration, students draw a pattern of a single PM constructed using a certain regular polygon as the basic figure. |
| 2 | A-8: Students recall the concept of PM and the mathematical model of constructing a single PM using a regular polygon as the basic figure. A-9: Students are guided to move on to constructing a combined PM using two regular polygons as basic figures. A-10: Through games, students explore whether a regular triangle and square can be used as basic figures to construct a combined PM. A-11: Through group communication, students mathematically explain why a combined PM can be constructed using a regular triangle and square as basic figures. A-12: By seeking integer solutions to linear equations with two unknowns, students find all possible cases for constructing a combined PM using a regular triangle and square as basic figures. A-13: Through group communication, students build the mathematical model (Model 2) for constructing a combined PM using two regular polygons as basic figures. A-14: Through group collaboration, students explore all possible cases of constructing a combined PM using a regular triangle and regular hexagon as basic figures. A-15: Students try to construct a combined PM using a regular octagon and another regular polygon as basic figures. |
| 3 | A-16: Students are guided to move to the general case to consider whether only regular polygons can be used as basic figures to construct single PMs. A-17: Through games and collaboration, students discover that any triangle and any quadrilateral can be used as basic figures to construct single PMs (which can be viewed as Model 3). A-18: The teacher shows the patterns of constructing single PMs using certain non-regular pentagons as basic figures to arouse students’ impressions of the charm of PMs. A-19: Students observe irregular figures, and the teacher guides them to construct a PM using translations, rotations, and folding, as well as to draw beautiful patterns. A-20: Students systematically review the contents of these three sessions and are guided to summarize the exploration process of explaining problems in life with mathematical models. |
| 4 | A-21: Group presentations of research reports (the teacher provides a template for the research report; the report takes one week to complete collaboratively). |
| No. of Sides | 3 | 4 | 5 | 6 | 7 | … | N |
|---|---|---|---|---|---|---|---|
| Q2 |  |  |  |  |  | … | |
| Q3 | 180° | 360° | 540° | 720° | 900° | … | (n−2)180° |
| Q4 | 60° | 90° | 108° | 120° | 900°/7 | … | (n−2)180°/n |
| Q5 | yes | yes | no | yes | no | … | yes |
| Q7 | 6 | 4 | - | 3 | - | - | - |
| Q8 |  |  | - | 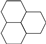 | - | - | - |
| Question Chain. Q1: What is the sum of the interior angles of a triangle? Q2: How can the problem of the sum of the interior angles of polygons be transformed into the problem of the sum of the interior angles of triangles? Q3: How to calculate the sum of the interior angles of a polygon? Q4: If this polygon is a regular one, what is the degree of its every interior angle? Q5: How do you determine if you can construct a single PM using this regular polygon as the basic figure? Why? Q6: Why can’t a regular polygon with more than six sides be used as the basic figure to construct a single PM? Q7: If a certain regular polygon can be used as the basic figure to construct a single PM, how many such regular polygons are needed at least? Q8: If a certain regular polygon can be used as the basic figure to construct a single PM, what does the pattern of this PM look like? | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Qi, C. Analysis and Dissolution of Potential Contradictions in Thematic Lessons from a Cultural-Historical Activity Theory Perspective. Sustainability 2023, 15, 16931. https://doi.org/10.3390/su152416931
He S, Qi C. Analysis and Dissolution of Potential Contradictions in Thematic Lessons from a Cultural-Historical Activity Theory Perspective. Sustainability. 2023; 15(24):16931. https://doi.org/10.3390/su152416931
Chicago/Turabian StyleHe, Shengqing, and Chunxia Qi. 2023. "Analysis and Dissolution of Potential Contradictions in Thematic Lessons from a Cultural-Historical Activity Theory Perspective" Sustainability 15, no. 24: 16931. https://doi.org/10.3390/su152416931
APA StyleHe, S., & Qi, C. (2023). Analysis and Dissolution of Potential Contradictions in Thematic Lessons from a Cultural-Historical Activity Theory Perspective. Sustainability, 15(24), 16931. https://doi.org/10.3390/su152416931





