Optimal Positioning of Mobile Cranes on Construction Sites Using Nonlinear Programming with Discontinuous Derivatives
Abstract
1. Introduction
2. Optimization Problem Formulation
| subject to: | ||||
| (DNLP) | ||||
3. Optimization Model Formulation
3.1. Objective Function
3.2. Duration Constraints
3.3. Positioning Constraints
3.4. Bounds on Degrees of Freedom of Movement and Stop Positions
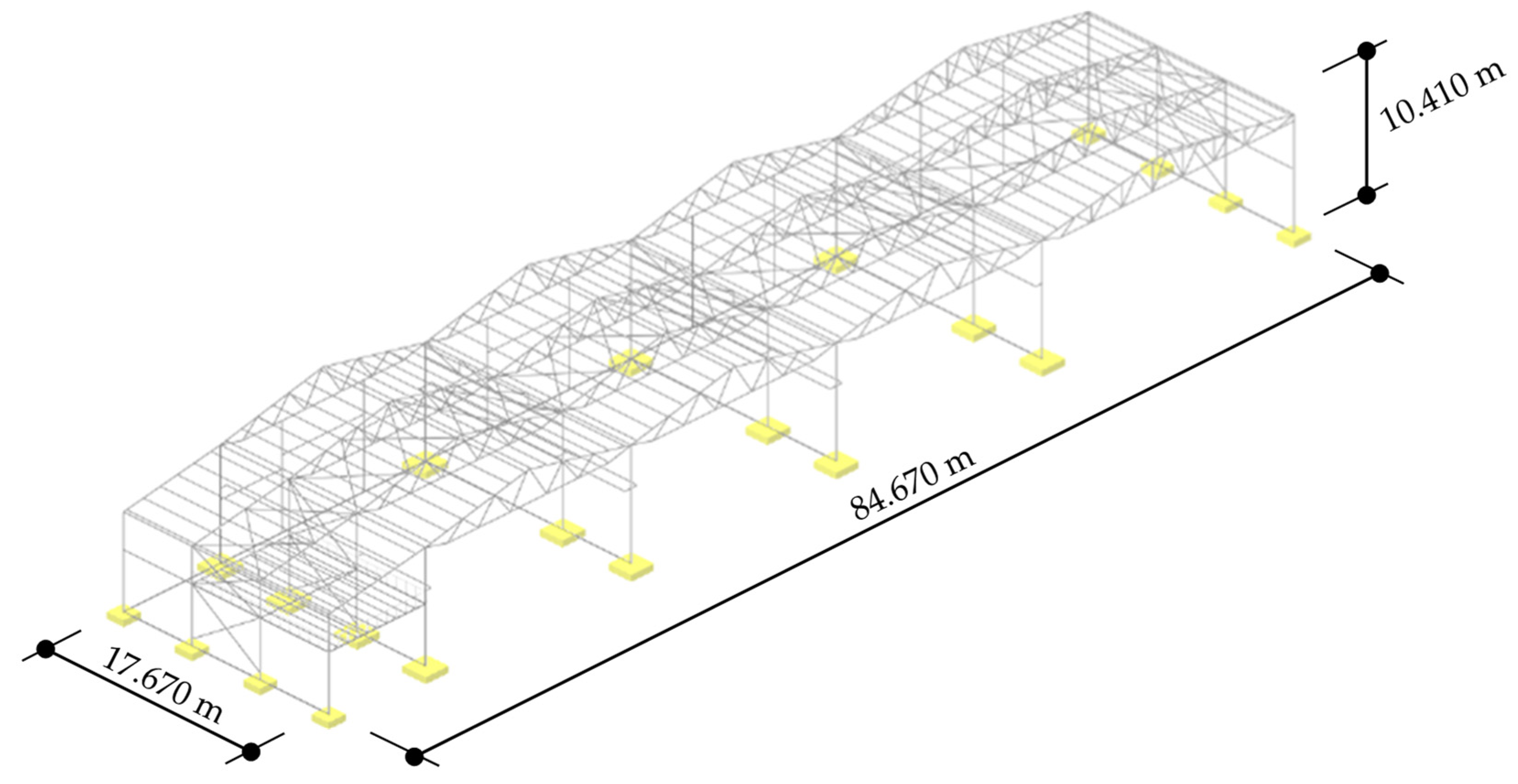
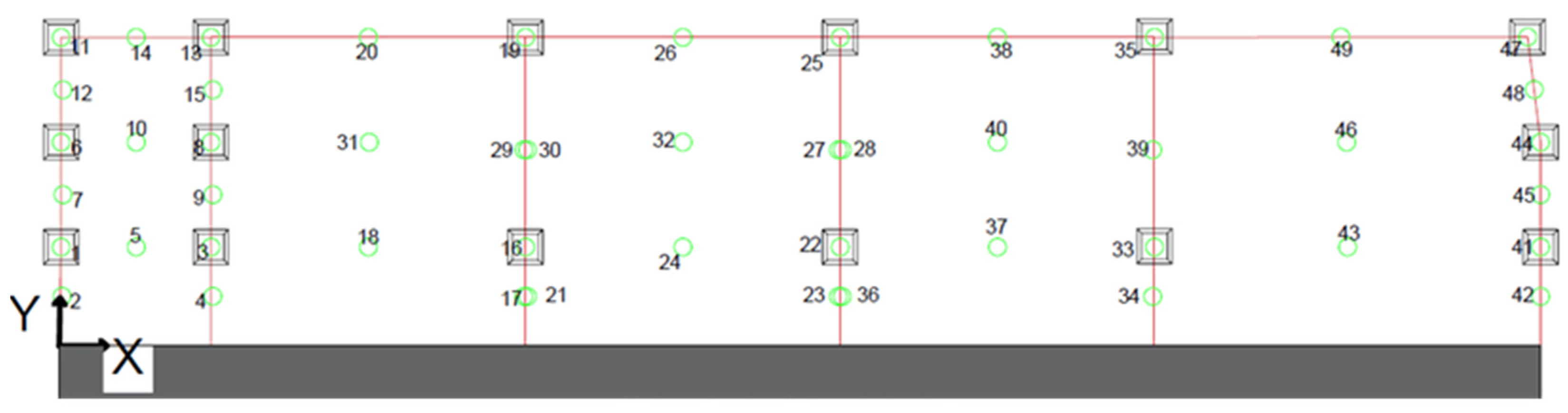
4. Application Example
4.1. General Information
4.2. Input Data
4.3. Optimization Setup
4.4. Optimization Results
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DNLP | nonlinear programming with discontinuous derivatives |
| GAMS | general algebraic modeling system |
| GRG | generalized reduced gradient method |
Appendix A
| Notations | |
| Indices and Sets | |
| for components requiring crane movement to the next stop | |
| for all crane stops | |
| Parameters | |
| extra cost of mobile crane independent of the rental duration [currency unit] | |
| minimum mobile crane chassis travel distance between stops prior to component transport [m] | |
| maximum mobile crane chassis travel distance between stops prior to component transport [m] | |
| horizontal distance between the demand and supply locations for the component transport [m] | |
| duration of verification and positioning of component assemblies [h] | |
| duration required to reach the maximum mobile crane boom extension [h] | |
| duration of the mobile crane dismantling [h] | |
| duration of the component’s fitment [h] | |
| duration of the component’s hooking to the crane lifting device [h] | |
| duration of preparing the mobile crane for operation [h] | |
| duration of the mobile crane setup [h] | |
| duration of the component’s unhooking from the crane lifting device [h] | |
| duration required to extend the mobile crane boom horizontally in the radial direction for the component transport [h] | |
| mobile crane chassis travel velocity [m/h] | |
| velocity of vertical lifting with the mobile crane winch [m/h] | |
| angular velocity of the mobile crane boom lift [rad/h] | |
| mobile crane slew velocity [rad/h] | |
| minimum x-coordinate of the mobile crane at the stop [m] | |
| maximum x-coordinate of the mobile crane at the stop [m] | |
| x-coordinate of the demand location for the component [m] | |
| x-coordinate of the supply location for the component [m] | |
| minimum y-coordinate of the mobile crane at the stop [m] | |
| maximum y-coordinate of the mobile crane at the stop [m] | |
| y-coordinate of the demand location for the component [m] | |
| y-coordinate of the supply location for the component [m] | |
| height difference between the demand and supply locations for the component [m] | |
| z-coordinate of the demand location for the component [m] | |
| z-coordinate of the supply location for the component [m] | |
| minimum vertical angle to which the mobile crane boom can be raised [rad] | |
| maximum vertical angle to which the mobile crane boom can be raised [rad] | |
| probability that the horizontal radial and tangential movements of components will be performed simultaneously | |
| probability that the horizontal and vertical movements of components will be performed simultaneously | |
| maximum mobile crane boom extension [m] | |
| Variables | |
| total cost of mobile crane usage [currency unit] | |
| rental cost of mobile crane, including any discount [currency unit] | |
| mobile crane chassis travel distance between stops prior to component transport [m] | |
| crane boom length when installing the component [m] | |
| horizontal distance between the demand location and the mobile crane for the component transport [m] | |
| horizontal distance between the supply location and the mobile crane for the component transport [m] | |
| duration of the mobile crane rental [h] | |
| duration of the component assembly cycle [h] | |
| duration of movement an empty crane lifting device from the demand location to the next supply location [h] | |
| duration of the component’s horizontal movement [h] | |
| duration of the rise of the component from the supply location to the demand location [h] | |
| duration of the mobile crane chassis’ travel between stops prior to component transport [h] | |
| duration of the component’s vertical movement [h] | |
| duration of the work procedure with the component [h] | |
| duration required to rotate the mobile crane boom horizontally in the radial direction for the component transport [h] | |
| duration of the component’s horizontal movement in the tangential direction [h] | |
| duration of the component’s horizontal movement in the radial direction [h] | |
| x-coordinate of the mobile crane at the stop [m] | |
| y-coordinate of the mobile crane at the stop [m] | |
| total vertical change in the crane lifting device position for transporting the component with a winch [m] | |
| vertical change in the crane lifting device position due to the boom angle change for the component transport [m] | |
| vertical angle of the mobile crane boom when installing the component [rad] | |
| horizontal angle between the demand and supply locations for the component transport [rad] | |
References
- Špak, M.; Mandičák, T.; Spišáková, M.; Verčimák, D. Risk management on concrete structures as a tool for the control of construction efficiency. Sustainability 2023, 15, 9577. [Google Scholar] [CrossRef]
- Azami, R.; Lei, Z.; Hermann, U.; Zubick, T. A predictive analytics framework for mobile crane configuration selection in heavy industrial construction projects. Buildings 2022, 12, 960. [Google Scholar] [CrossRef]
- Kayhani, N.; Taghaddos, H.; Mousaei, A.; Behzadipour, S.; Hermann, U. Heavy mobile crane lift path planning in congested modular industrial plants using a robotics approach. Autom. Constr. 2021, 122, 103508. [Google Scholar] [CrossRef]
- Lin, X.; Chen, S.; Guo, H.; Guo, Z. Developing a robotic system for construction truck crane. In Lecture Notes in Operations Research, Proceedings of the 27th International Symposium on Advancement of Construction Management and Real Estate (CRIOCM 2022), Hong Kong, China, 5–6 December 2022; Li, J., Lu, W., Peng, Y., Yuan, H., Wang, D., Eds.; Springer: Singapore, 2023; pp. 11–23. [Google Scholar] [CrossRef]
- Guo, H.; Zhou, Y.; Pan, Z.; Lin, X. Automated lift planning methods for mobile cranes. Autom. Constr. 2021, 132, 103982. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.Y.; Wu, D.; De Gao, S. Collision-free path planning for mobile cranes based on ant colony algorithm. Key Eng. Mater. 2011, 467–469, 1108–1115. [Google Scholar] [CrossRef]
- Bagheri, S.M.; Taghaddos, H.; Mousaei, A.; Shahnavaz, F.; Hermann, U. An A-Star algorithm for semi-optimization of crane location and configuration in modular construction. Autom. Constr. 2021, 121, 103447. [Google Scholar] [CrossRef]
- Gwak, H.-S.; Lee, H.-C.; Choi, B.-Y.; Mi, Y. GA-based optimization method for mobile crane repositioning route planning. Appl. Sci. 2021, 11, 6010. [Google Scholar] [CrossRef]
- Lin, K.L.; Haas, C.T. Multiple heavy lifts optimization. J. Constr. Eng. Manag. 1996, 122, 354–362. [Google Scholar] [CrossRef]
- Kaneshige, A.; Terashima, K.; Suzuki, M.; Yin, R. Autonomous mobile crane system considering obstacle recognition and optimal path planning. Nihon Kikai Gakkai Ronbunshu C Hen/Trans. Japan Soc. Mech. Eng. Part C 1998, 64, 487–494. [Google Scholar] [CrossRef][Green Version]
- Mousaei, A.; Taghaddos, H.; Marzieh Bagheri, S.; Hermann, U. Optimizing heavy lift plans for industrial construction sites using Dijkstra’s algorithm. J. Constr. Eng. Manag. 2021, 147, 04021160. [Google Scholar] [CrossRef]
- Huang, C.; Wong, C.K.; Tam, C.M. Optimization of tower crane and material supply locations in a high-rise building site by mixed-integer linear programming. Autom. Constr. 2011, 20, 571–580. [Google Scholar] [CrossRef]
- Nadoushani, Z.S.M.; Hammad, A.W.A.; Akbarnezhad, A. Location optimization of tower crane and allocation of material supply points in a construction site considering operating and rental costs. J. Constr. Eng. Manag. 2017, 143, 04016089. [Google Scholar] [CrossRef]
- Briskorn, D.; Dienstknecht, M. Mixed-integer programming models for tower crane selection and positioning with respect to mutual interference. Eur. J. Oper. Res. 2019, 273, 160–174. [Google Scholar] [CrossRef]
- Dasović, B.; Galić, M.; Klanšek, U. Active BIM approach to optimize work facilities and tower crane locations on construction sites with repetitive operations. Buildings 2019, 9, 21. [Google Scholar] [CrossRef]
- Ji, Y.; Leite, F. Optimized planning approach for multiple tower cranes and material supply points using mixed-integer programming. J. Constr. Eng. Manag. 2020, 146, 04020007. [Google Scholar] [CrossRef]
- Zhou, C.; Dai, F.; Xiao, Z.; Liu, W. Location optimization of tower cranes on high-rise modular housing projects. Buildings 2023, 13, 115. [Google Scholar] [CrossRef]
- Hammad, A.W.; Rey, D.; Akbarnezhad, A.; Haddad, A. Integrated mathematical optimisation approach for the tower crane hook routing problem to satisfy material demand requests on-site. Adv. Eng. Inform. 2023, 55, 101885. [Google Scholar] [CrossRef]
- Peng, B.; Flager, F.L.; Wu, J. A method to optimize mobile crane and crew interactions to minimize construction cost and time. Autom. Constr. 2018, 95, 10–19. [Google Scholar] [CrossRef]
- Žnidarič, M.; et al. Hal 1 Extension. Detailed Design. Project No.: 21-001; Progrin d.o.o.: Radenci, Slovenia, 2021. (In Slovene) [Google Scholar]
- Raynar, K.A.; Smith, G.R. Intelligent positioning of mobile cranes for steel erection. Comput. Aided Civ. Infrastruct. Eng. 1993, 8, 67–74. [Google Scholar] [CrossRef]
- Jeong, W.; Chang, S.; Son, J.; Yi, J.-S. BIM-integrated construction operation simulation for just-in-time production management. Sustainability 2016, 8, 1106. [Google Scholar] [CrossRef]
- GAMS General Algebraic Modeling System. Available online: https://www.gams.com/ (accessed on 21 October 2023).
- Drud, A.S. CONOPT—A large-scale GRG code. ORSA J. Comput. 1994, 6, 207–216. [Google Scholar] [CrossRef]






| Parameters | Input Values |
|---|---|
| Cost parameters | |
| Rental cost of mobile crane | |
| Extra cost of mobile crane | |
| Parameters of operations durations | |
| Duration of preparing the mobile crane for operation | |
| Duration of the mobile crane setup | |
| Duration of the mobile crane dismantling | |
| Duration needed to reach the maximum mobile crane boom extension | |
| Probability parameters | |
| Coefficient of concurrent horizontal radial and tangential movements | |
| Coefficient of concurrent horizontal and vertical movements | |
| Parameters from mobile crane technical specifications | |
| Mobile crane chassis travel velocity | |
| Mobile crane angular velocity of boom lift | |
| Mobile crane slew velocity | |
| Mobile crane winch’s vertical lifting velocity | |
| Minimum vertical angle of the mobile crane boom | |
| Maximum vertical angle of the mobile crane boom | |
| Minimum horizontal slew angle of the mobile crane boom | |
| Maximum horizontal slew angle of the mobile crane boom | |
| Minimum length of the mobile crane boom | |
| Maximum length of the mobile crane boom | |
| Minimum total vertical change in the crane lifting device position | |
| Maximum total vertical change in the crane lifting device position | |
| Limiting parameters for crane positioning, movements, and maneuvers | |
| Minimum mobile crane chassis travel distance between stops | |
| Maximum mobile crane chassis travel distance between stops | |
| Minimum x-coordinate of the mobile crane at the stop | |
| Maximum x-coordinate of the mobile crane at the stop | |
| Minimum y-coordinate of the mobile crane at the stop | |
| Maximum y-coordinate of the mobile crane at the stop | |
| Minimum z-coordinate of the mobile crane at the stop | |
| Maximum z-coordinate of the mobile crane at the stop |
| 1 | 0.000 | 0.063 | 0.025 | 0.367 | 0.110 | 39.400 | 5.650 | 10.400 | 8.200 | 0.000 | 40.000 |
| 2 | 0.167 | 0.063 | 0.060 | 0.367 | 0.160 | 39.400 | 2.830 | 10.400 | 8.200 | 0.000 | 40.000 |
| 3 | 0.167 | 0.063 | 0.025 | 0.367 | 8.680 | 39.400 | 5.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 4 | 0.167 | 0.063 | 0.060 | 0.367 | 8.780 | 39.400 | 2.820 | 10.400 | 8.200 | 0.000 | 34.200 |
| 5 | 0.167 | 0.063 | 0.060 | 0.367 | 4.390 | 39.400 | 5.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 6 | 0.167 | 0.063 | 0.025 | 0.367 | 0.110 | 39.400 | 11.650 | 10.400 | 8.200 | 0.000 | 40.000 |
| 7 | 0.167 | 0.063 | 0.060 | 0.367 | 0.210 | 39.400 | 8.650 | 10.400 | 8.200 | 0.000 | 40.000 |
| 8 | 0.167 | 0.063 | 0.025 | 0.367 | 8.680 | 39.400 | 11.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 9 | 0.167 | 0.063 | 0.060 | 0.367 | 8.780 | 39.400 | 8.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 10 | 0.167 | 0.063 | 0.060 | 0.367 | 4.390 | 39.400 | 11.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 11 | 0.167 | 0.063 | 0.025 | 0.367 | 0.110 | 39.400 | 17.650 | 10.400 | 8.200 | 0.000 | 40.000 |
| 12 | 0.167 | 0.063 | 0.060 | 0.367 | 0.210 | 39.400 | 14.650 | 10.400 | 8.200 | 0.000 | 40.000 |
| 13 | 0.167 | 0.063 | 0.025 | 0.367 | 8.680 | 39.400 | 17.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 14 | 0.167 | 0.063 | 0.060 | 0.367 | 4.390 | 39.400 | 17.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 15 | 0.167 | 0.063 | 0.060 | 0.367 | 8.780 | 39.400 | 14.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 16 | 0.167 | 0.063 | 0.025 | 0.367 | 26.680 | 39.400 | 5.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 17 | 0.167 | 0.063 | 0.060 | 0.367 | 26.570 | 39.400 | 2.820 | 10.400 | 8.200 | 0.000 | 34.200 |
| 18 | 0.167 | 0.063 | 0.060 | 0.367 | 17.680 | 39.400 | 5.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 19 | 0.167 | 0.063 | 0.025 | 0.367 | 26.680 | 39.400 | 17.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 20 | 0.167 | 0.063 | 0.060 | 0.367 | 17.680 | 39.400 | 17.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 21 | 0.167 | 0.063 | 0.060 | 0.367 | 26.780 | 39.400 | 2.820 | 10.400 | 8.200 | 0.000 | 34.200 |
| 22 | 0.167 | 0.063 | 0.025 | 0.367 | 44.680 | 39.400 | 5.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 23 | 0.167 | 0.063 | 0.060 | 0.367 | 44.680 | 39.400 | 2.820 | 10.400 | 8.200 | 0.000 | 34.200 |
| 24 | 0.167 | 0.063 | 0.060 | 0.367 | 35.680 | 39.400 | 5.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 25 | 0.167 | 0.063 | 0.025 | 0.367 | 44.680 | 39.400 | 17.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 26 | 0.167 | 0.063 | 0.060 | 0.367 | 35.680 | 39.400 | 17.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 27 | 0.167 | 0.063 | 0.060 | 0.367 | 44.570 | 39.400 | 11.210 | 10.400 | 8.200 | 0.000 | 34.200 |
| 28 | 0.167 | 0.063 | 0.060 | 0.367 | 44.780 | 39.400 | 11.210 | 10.400 | 8.200 | 0.000 | 34.200 |
| 29 | 0.167 | 0.063 | 0.060 | 0.367 | 26.570 | 39.400 | 11.210 | 10.400 | 8.200 | 0.000 | 34.200 |
| 30 | 0.167 | 0.063 | 0.060 | 0.367 | 26.780 | 39.400 | 11.210 | 10.400 | 8.200 | 0.000 | 34.200 |
| 31 | 0.167 | 0.063 | 0.060 | 0.367 | 17.730 | 39.400 | 11.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 32 | 0.167 | 0.063 | 0.060 | 0.367 | 35.680 | 39.400 | 11.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 33 | 0.167 | 0.063 | 0.025 | 0.367 | 62.680 | 39.400 | 5.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 34 | 0.167 | 0.063 | 0.060 | 0.367 | 62.570 | 39.400 | 2.820 | 10.400 | 8.200 | 0.000 | 34.200 |
| 35 | 0.167 | 0.063 | 0.025 | 0.367 | 62.680 | 39.400 | 17.650 | 10.400 | 8.200 | 0.000 | 34.200 |
| 36 | 0.167 | 0.063 | 0.060 | 0.367 | 44.780 | 39.400 | 2.820 | 10.400 | 8.200 | 0.000 | 34.200 |
| 37 | 0.167 | 0.063 | 0.060 | 0.367 | 53.680 | 39.400 | 5.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 38 | 0.167 | 0.063 | 0.060 | 0.367 | 53.680 | 39.400 | 17.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 39 | 0.167 | 0.063 | 0.060 | 0.367 | 62.570 | 39.400 | 11.210 | 10.400 | 8.200 | 0.000 | 34.200 |
| 40 | 0.167 | 0.063 | 0.060 | 0.367 | 53.680 | 39.400 | 11.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 41 | 0.167 | 0.063 | 0.025 | 0.367 | 84.780 | 39.400 | 5.650 | 10.400 | 8.200 | 0.000 | 40.000 |
| 42 | 0.167 | 0.063 | 0.060 | 0.367 | 84.780 | 39.400 | 2.820 | 10.400 | 8.200 | 0.000 | 40.000 |
| 43 | 0.167 | 0.063 | 0.060 | 0.367 | 73.720 | 39.400 | 5.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 44 | 0.167 | 0.063 | 0.025 | 0.367 | 84.780 | 39.400 | 11.650 | 10.400 | 8.200 | 0.000 | 40.000 |
| 45 | 0.167 | 0.063 | 0.060 | 0.367 | 84.780 | 39.400 | 8.650 | 10.400 | 8.200 | 0.000 | 40.000 |
| 46 | 0.167 | 0.063 | 0.060 | 0.367 | 73.660 | 39.400 | 11.650 | 10.400 | 10.410 | 0.000 | 34.200 |
| 47 | 0.167 | 0.063 | 0.025 | 0.367 | 84.020 | 39.400 | 17.670 | 10.400 | 8.200 | 0.000 | 40.000 |
| 48 | 0.167 | 0.063 | 0.060 | 0.367 | 84.400 | 39.400 | 14.660 | 10.400 | 8.200 | 0.000 | 40.000 |
| 49 | 0.167 | 0.063 | 0.060 | 0.367 | 73.340 | 39.400 | 17.660 | 10.400 | 10.410 | 0.000 | 34.200 |
| Optimization Solver | Objective Value [c. u.] | CPU Time [s] |
|---|---|---|
| CONOPT/LINDO/MSNLP/OQNLP | 2591.6325 | 0.156/0.905/9.937/11.934 |
| IPOPT | 2596.2831 | 0.248 |
| SNOPT | 2591.7477 | 0.234 |
| Minimum Total Cost of Mobile Crane Usage: | |||||||
| 1 | 0.573 | 3.231 | 0.000 | –7.380 | |||
| 2 | 0.553 | 3.313 | 0.000 | 7.504 | |||
| 3 | 0.745 | 3.276 | 0.000 | 13.434 | Mobile crane stop positions: | ||
| 4 | 0.721 | 3.386 | 0.000 | 7.584 | |||
| 5 | 0.538 | 3.250 | 0.000 | 5.372 | |||
| 6 | 0.586 | 3.232 | 0.000 | 9.794 | |||
| 7 | 0.590 | 3.142 | 0.000 | 8.360 | |||
| 8 | 0.761 | 3.247 | 0.000 | 12.735 | |||
| 9 | 0.765 | 3.157 | 0.000 | 8.312 | |||
| 10 | 0.556 | 3.238 | 0.000 | 4.764 | |||
| 11 | 0.548 | 3.408 | 0.000 | 7.947 | |||
| 12 | 0.581 | 3.321 | 0.000 | 9.209 | |||
| 13 | 0.714 | 3.481 | 0.000 | 11.909 | |||
| 14 | 0.502 | 3.440 | 0.000 | 4.484 | |||
| 15 | 0.749 | 3.368 | 0.000 | 15.030 | |||
| 16 | 1.332 | 3.684 | 0.000 | 18.132 | |||
| 17 | 1.274 | 3.916 | 0.000 | 7.672 | |||
| 18 | 1.072 | 3.375 | 0.000 | 7.742 | |||
| 19 | 1.271 | 4.027 | 0.000 | 10.843 | |||
| 20 | 1.036 | 3.632 | 0.000 | 7.155 | |||
| 21 | 1.278 | 3.932 | 0.000 | 11.523 | |||
| 22 | 1.208 | 5.860 | 0.000 | 7.431 | |||
| 23 | 1.167 | 5.663 | 0.000 | 7.674 | |||
| 24 | 1.423 | 5.137 | 0.000 | 12.789 | |||
| 25 | 1.163 | 5.740 | 0.000 | 5.773 | |||
| 26 | 1.339 | 5.050 | 0.000 | 12.295 | |||
| 27 | 1.237 | 6.232 | 0.000 | 7.221 | |||
| 28 | 1.230 | 6.233 | 16.090 | 8.127 | |||
| 29 | 0.835 | 6.271 | 0.000 | 1.315 | |||
| 30 | 0.843 | 6.270 | 0.000 | 8.388 | |||
| 31 | 0.376 | 6.272 | 0.000 | –2.569 | |||
| 32 | 1.152 | 6.204 | 0.000 | 29.092 | |||
| 33 | 1.153 | 3.418 | 0.000 | 8.219 | |||
| 34 | 1.120 | 3.602 | 0.000 | 7.720 | |||
| 35 | 1.109 | 3.709 | 0.000 | 8.035 | |||
| 36 | 1.317 | 5.253 | 0.000 | 10.693 | |||
| 37 | 1.394 | 3.904 | 0.000 | 10.968 | |||
| 38 | 1.313 | 4.254 | 0.000 | 9.812 | Notation: | ||
| 39 | 1.177 | 3.276 | 0.000 | 6.712 | – | building component, | |
| 40 | 1.439 | 3.561 | 0.000 | 12.734 | – | vertical angle of the mobile crane boom | |
| 41 | 0.476 | 3.223 | 0.000 | −13.107 | when installing the component, | ||
| 42 | 0.451 | 3.301 | 0.000 | 7.290 | – | horizontal angle between the supply and | |
| 43 | 0.768 | 3.278 | 0.000 | 19.257 | demand locations for the component, | ||
| 44 | 0.489 | 3.230 | 0.000 | −0.805 | – | mobile crane chassis travel distance | |
| 45 | 0.489 | 3.145 | 0.000 | 8.226 | between stops prior to component | ||
| 46 | 0.784 | 3.251 | 0.000 | 18.475 | transport, | ||
| 47 | 0.486 | 3.402 | 0.000 | −1.357 | – | total vertical change in the crane lifting | |
| 48 | 0.494 | 3.316 | 0.000 | 8.493 | device position for transporting the | ||
| 49 | 0.749 | 3.494 | 0.000 | 17.476 | component with a winch. | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hozjan, M.; Klanšek, U. Optimal Positioning of Mobile Cranes on Construction Sites Using Nonlinear Programming with Discontinuous Derivatives. Sustainability 2023, 15, 16889. https://doi.org/10.3390/su152416889
Hozjan M, Klanšek U. Optimal Positioning of Mobile Cranes on Construction Sites Using Nonlinear Programming with Discontinuous Derivatives. Sustainability. 2023; 15(24):16889. https://doi.org/10.3390/su152416889
Chicago/Turabian StyleHozjan, Matjaž, and Uroš Klanšek. 2023. "Optimal Positioning of Mobile Cranes on Construction Sites Using Nonlinear Programming with Discontinuous Derivatives" Sustainability 15, no. 24: 16889. https://doi.org/10.3390/su152416889
APA StyleHozjan, M., & Klanšek, U. (2023). Optimal Positioning of Mobile Cranes on Construction Sites Using Nonlinear Programming with Discontinuous Derivatives. Sustainability, 15(24), 16889. https://doi.org/10.3390/su152416889







