Prediction of CO2 Emissions Related to Energy Consumption for Rural Governance
Abstract
:1. Introduction
2. Related Works
3. Construction of CE Prediction Model for Air Governance in Industrialized Rural Areas
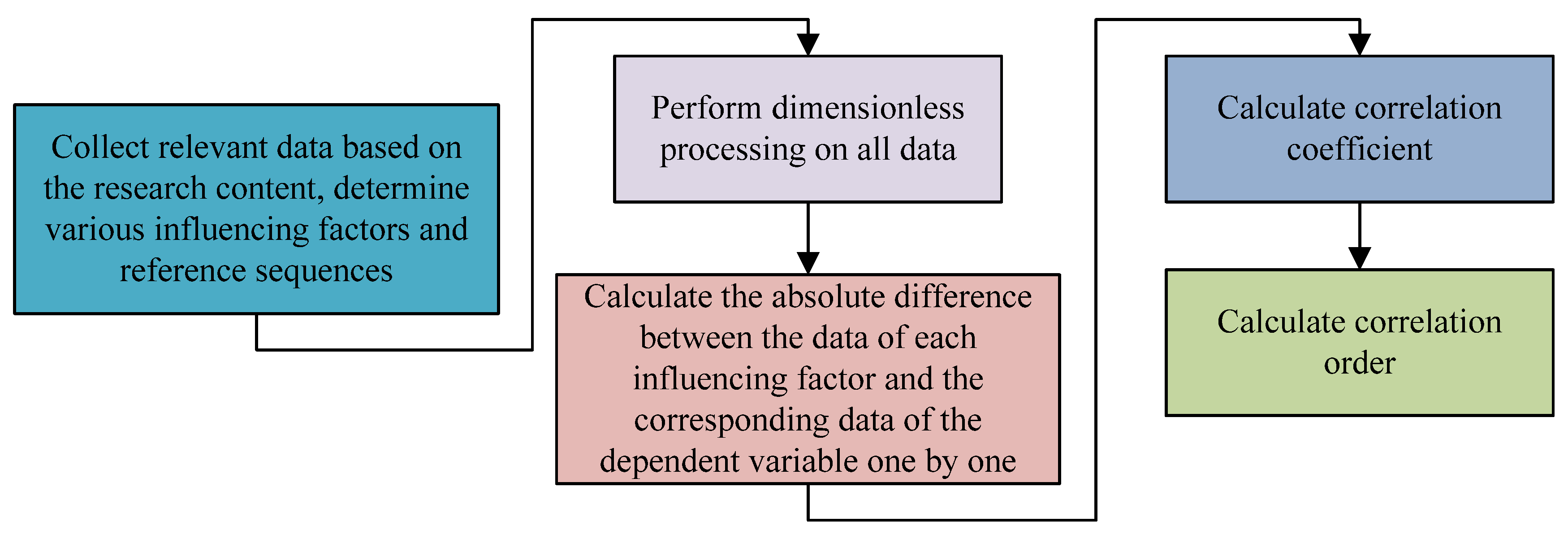
3.1. Calculation of CE in Industrialized Rural Areas and Analysis of Influencing Factors
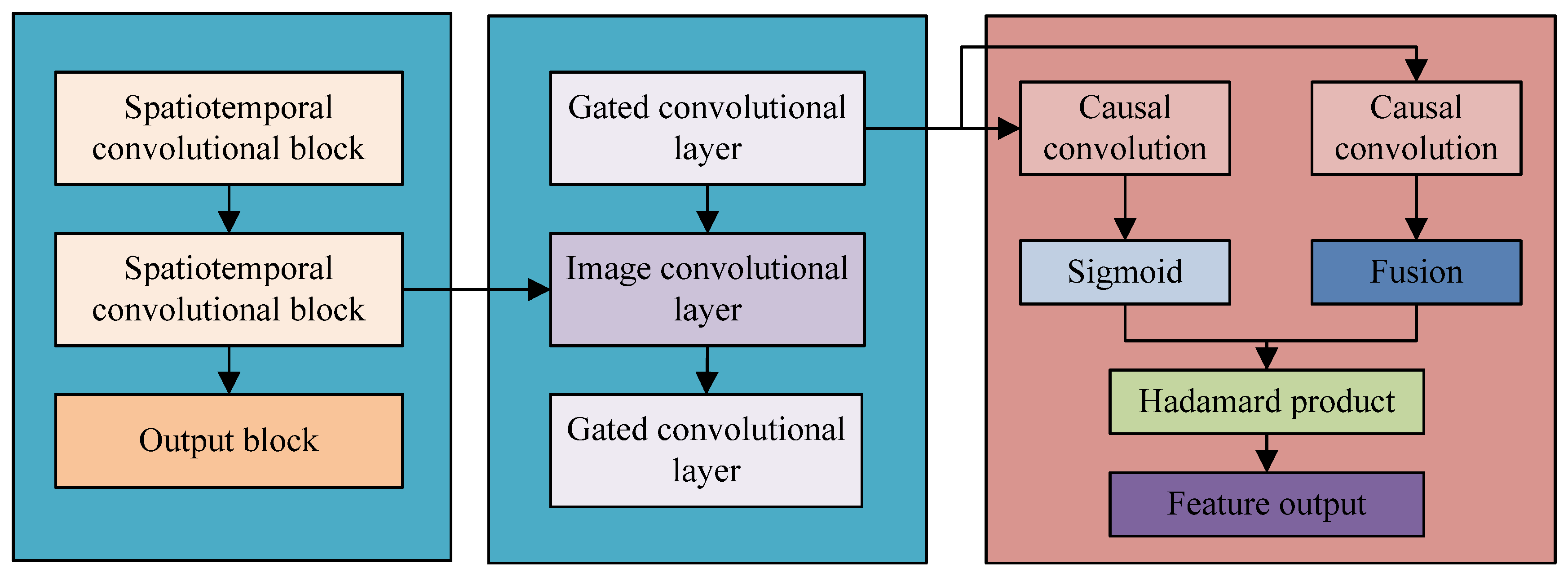
3.2. Construction of CO2 Emission Prediction Model Based on Deep Learning Network
4. Utility Analysis of CE Prediction Model in Industrialized Rural Areas Based on Deep Learning Networks
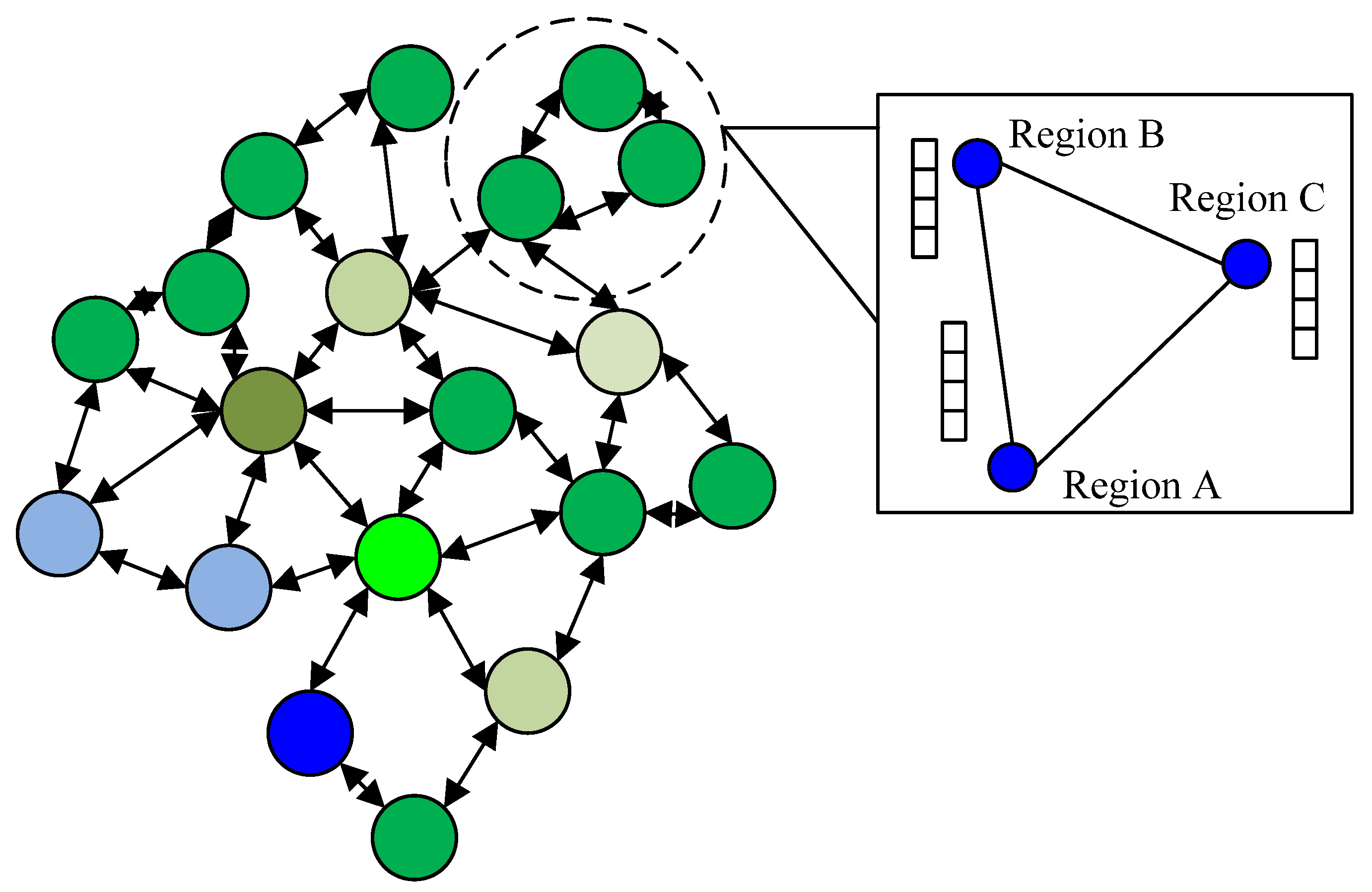
4.1. Analysis of Correlation Results of CE-Influencing Factors in Industrialized Rural Areas
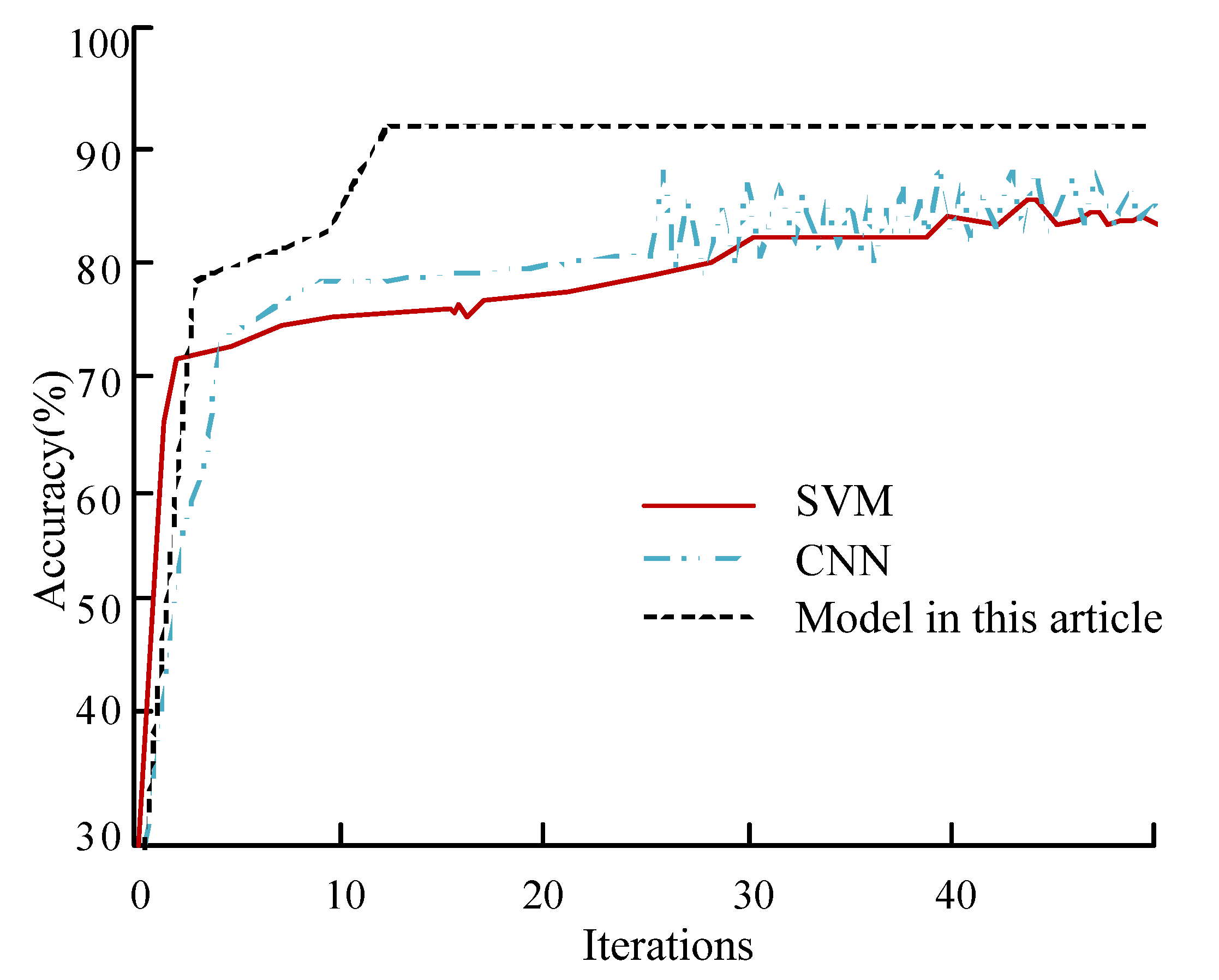
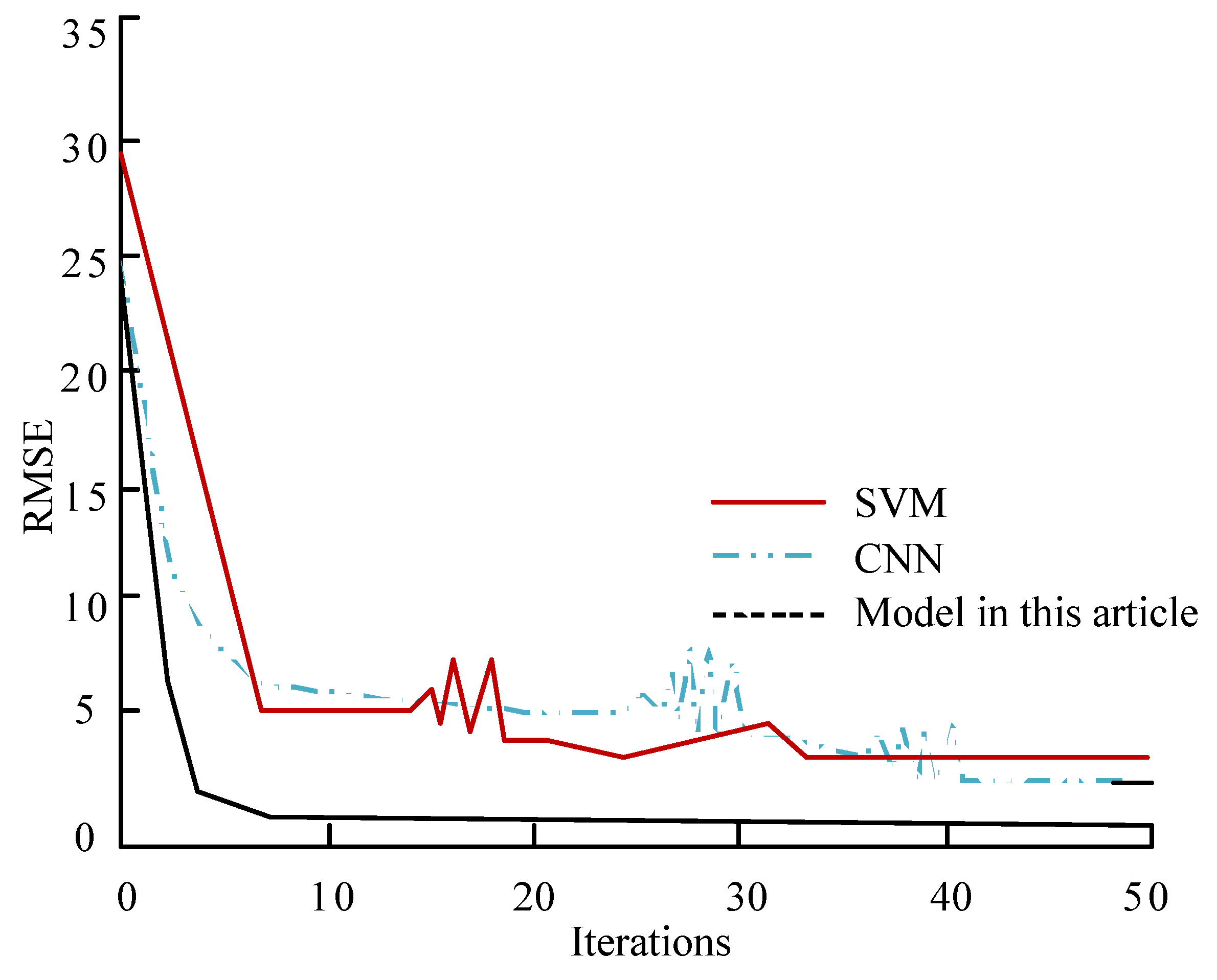
4.2. Effectiveness Analysis of CE Prediction Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duarte, A.J.; Malheiro, B.; Arnó, E.; Perat, I.; Silva, M.F.; Fuentes-Durá, P.; Guedes, P.; Ferreira, P. Engineering education for sustainable development: The European project semester approach. IEEE Trans. Educ. 2020, 63, 108–117. [Google Scholar] [CrossRef]
- Mai, V.; Vanderborght, B.; Haidegger, T.; Khamis, A.; Bhargava, N.; Boesl, D.B.O.; Gabriels, K.; Jacobs, A.; Moon, A.; Murphy, R.; et al. The role of robotics in achieving the united nations sustainable development goals—The experts’ meeting at the 2021 IEEE/RSJ IROS workshop. IEEE Robot. Autom. Mag. 2022, 29, 92–107. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, S.L.; Rong, B.; Kadoch, M. Intelligent reflective surface based 6g communications for sustainable energy infrastructure. IEEE Wirel. Commun. 2021, 28, 49–55. [Google Scholar] [CrossRef]
- Pao, H.T.; Fu, H.C.; Tseng, C.L. Forecasting of CO2 emissions, energy consumption and economic growth in China using an improved grey model. Energy 2012, 41, 400–409. [Google Scholar] [CrossRef]
- Ding, T.; Jia, W.H.; Shahidehpour, M.; Han, O.Z.; Sun, Y.G.; Zhang, Z.Y. Review of optimization methods for energy hub planning, operation, trading, and control. IEEE Trans. Sustain. Energy 2022, 13, 1802–1818. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Yang, Z.; Li, G.Q. Coordinating flexible demand response and renewable uncertainties for scheduling of community integrated energy systems with an electric vehicle charging station: A bi-level approach. IEEE Trans. Sustain. Energy 2021, 12, 2321–2331. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Xu, Y.; Yang, H.M.; Dong, Z.Y.; Zhang, R. Optimal whole-life-cycle planning of battery energy storage for multi-functional services in power system. IEEE Trans. Sustain. Energy 2020, 11, 2077–2086. [Google Scholar] [CrossRef]
- Xu, D.; Wu, Q.W.; Zhou, B.; Li, C.B.; Bai, L.; Huang, S. Distributed multi-energy operation of coupled electricity, heating, and natural gas networks. IEEE Trans. Sustain. Energy 2020, 11, 2457–2469. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.N.; Yang, Z. Optimal scheduling of isolated microgrids using automated reinforcement learning-based multi-period forecasting. IEEE Trans. Sustain. Energy 2022, 13, 159–169. [Google Scholar] [CrossRef]
- Brown, D. Towards a comparative research agenda on in situ urbanisation and rural governance transformation. Int. Dev. Plan. Rev. 2021, 43, 289–320. [Google Scholar] [CrossRef]
- Bhuvana, M.; Vasantha, S. Assessment of rural citizens satisfaction on the service quality of common service centers (CSCs) of e-governance. J. Crit. Rev. 2020, 7, 302–305. [Google Scholar] [CrossRef]
- Yaacoub, E.; Alouini, M.S. A key 6g challenge and opportunity—Connecting the base of the pyramid: A survey on rural connectivity. Proc. IEEE 2020, 108, 533–582. [Google Scholar] [CrossRef]
- Yaacoub, E.; Alouini, M.S. Efficient Fronthaul and Backhaul Connectivity for IoT Traffic in Rural Areas. IEEE Internet Things Mag. 2021, 4, 60–66. [Google Scholar] [CrossRef]
- Kirikkaleli, D.; Adebayo, T.S. Do public-private partnerships in energy and renewable energy consumption matter for consumption-based carbon dioxide emissions in India? Environ. Sci. Pollut. Res. 2021, 28, 30139–30152. [Google Scholar] [CrossRef] [PubMed]
- Dong, K.Y.; Dong, X.C.; Jiang, Q.Z. How renewable energy consumption lower global CO2 emissions? Evidence from countries with different income levels. World Econ. 2020, 43, 1665–1698. [Google Scholar] [CrossRef]
- Murad, M.W.; Alam, M.M.; Noman, A.H.M.; Ozturk, I. Dynamics of technological innovation, energy consumption, energy price and economic growth in Denmark. Environ. Prog. Sustain. Energy 2019, 38, 22–29. [Google Scholar] [CrossRef]
- Wei, Z.Q.; Wei, K.K.; Liu, J.C. Decoupling relationship between carbon emissions and economic development and prediction of carbon emissions in Henan Province: Based on Tapio method and STIRPAT model. Environ. Sci. Pollut. Res. 2023, 30, 52679–52691. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.N.; Wei, X.X.; Xiao, J.Y.; Liu, Z.H.J.; Xu, Y.; Tian, Y. Energy consumption and emission mitigation prediction based on data center traffic and PUE for global data centers. Glob. Energy Int. 2020, 3, 272–282. [Google Scholar] [CrossRef]
- Adame, M.F.; Connolly, R.M.; Turschwell, M.P.; Lovelock, C.E.; Fatoyinbo, T.; Lagomasino, D.; Goldberg, L.A.; Holdorf, J.; Friess, D.A.; Sasmito, S.D.; et al. Future carbon emissions from global mangrove forest loss. Glob. Chang. Biol. 2021, 27, 2856–2866. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Du, Y. Impact of technological innovation on CO2 emissions and emissions trend prediction on ‘New Normal’ economy in China. Atmos. Pollut. Res. 2019, 10, 152–161. [Google Scholar] [CrossRef]
- Ran, Q.Y.; Bu, F.B.; Razzaq, A.; Ge, W.F.; Peng, J.; Yang, X.D.; Xu, Y. When will China’s industrial carbon emissions peak? Evidence from machine learning. Environ. Sci. Pollut. Res. 2023, 30, 57960–57974. [Google Scholar] [CrossRef] [PubMed]
- Lv, T.G.; Hu, H.; Xie, H.L.; Zhang, X.M.; Wang, L.; Shen, X.Q. An empirical relationship between urbanization and carbon emissions in an ecological civilization demonstration area of China based on the STIRPAT model. Environ. Dev. Sustain. 2023, 25, 2465–2486. [Google Scholar] [CrossRef]
- Jin, I. Probability of achieving NDC and implications for climate policy: CO-STIRPAT approach. J. Econ. Anal. 2023, 2, 82–97. [Google Scholar] [CrossRef]
- Pan, G.S.; Gu, W.; Lu, Y.P.; Qiu, H.F.; Lu, S.; Yao, S. Optimal planning for electricity-hydrogen integrated energy system considering power to hydrogen and heat and seasonal storage. IEEE Trans. Sustain. Energy 2020, 11, 2662–2676. [Google Scholar] [CrossRef]
- Hu, J.J.; Liu, X.T.; Shahidehpour, M.; Xia, S.W. Optimal operation of energy hubs with large-scale distributed energy resources for distribution network congestion management. IEEE Trans. Sustain. Energy 2021, 12, 1755–1765. [Google Scholar] [CrossRef]
- Li, Z.W.; Cheng, Z.P.; Liang, J.; Si, J.K.; Dong, L.H.; Li, S.H. Distributed event-triggered secondary control for economic dispatch and frequency restoration control of droop-controlled ac microgrids. IEEE Trans. Sustain. Energy 2020, 11, 1938–1950. [Google Scholar] [CrossRef]
- Lu, R.Z.; Ding, T.; Qin, B.Y.; Ma, J.; Fang, X.; Dong, Z.Y. Multi-stage stochastic programming to joint economic dispatch for energy and reserve with uncertain renewable energy. IEEE Trans. Sustain. Energy 2020, 11, 1140–1151. [Google Scholar] [CrossRef]
- Yu, D.M.; Ebadi, A.G.; Jermsittiparsert, K.; Jabarullah, N.H.; Vasiljeva, M.V.; Nojavan, S. Risk-constrained stochastic optimization of a concentrating solar power plan. IEEE Trans. Sustain. Energy 2020, 11, 1464–1472. [Google Scholar] [CrossRef]
- Guo, Z.J.; Wei, W.; Chen, L.J.; Dong, Z.Y.; Mei, S.W. Impact of energy storage on renewable energy utilization: A geometric description. IEEE Trans. Sustain. Energy 2021, 12, 874–885. [Google Scholar] [CrossRef]
- Hua, H.C.; Qin, Z.M.; Dong, N.Q.; Qin, Y.C.; Ye, M.J.; Wang, Z.D.; Chen, X.Y.; Cao, J.W. Data-driven dynamical control for bottom-up energy internet system. IEEE Trans. Sustain. Energy 2022, 13, 315–327. [Google Scholar] [CrossRef]
- Zheng, Y.; Song, Y.; Huang, A.D.; Hill, D.J. Hierarchical optimal allocation of battery energy storage systems for multiple services in distribution systems. IEEE Trans. Sustain. Energy 2020, 11, 1911–1921. [Google Scholar] [CrossRef]
- Ge, L.J.; Liu, H.X.; Yan, J.; Zhu, X.S.; Zhang, S.; Li, Y.Z. Optimal integrated energy system planning with dg uncertainty affine model and carbon emissions charges. IEEE Trans. Sustain. Energy 2022, 13, 905–918. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Qiu, J.; Tao, Y.C.; Zhao, J.H. Carbon-oriented operational planning in coupled electricity and emission trading markets. IEEE Trans. Power Syst. 2020, 35, 3145–3157. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, X.; Sun, Y.X.; Qiu, J. Carbon emission flow oriented tri-level planning of integrated electricity–hydrogen–gas system with hydrogen vehicles. IEEE Trans. Ind. Appl. 2021, 58, 2607–2618. [Google Scholar] [CrossRef]
- Bao, J.B.; He, D.B.; Luo, M.; Choo, K.K.R. A survey of blockchain applications in the energy sector. IEEE Syst. J. 2021, 15, 3370–3381. [Google Scholar] [CrossRef]
- Yang, L.F.; Luo, J.Y.; Xu, Y.; Zhang, Z.R.; Dong, Z.Y. A distributed dual consensus admm based on partition for dc-dopf with carbon emission trading. IEEE Trans. Ind. Inform. 2020, 16, 1858–1872. [Google Scholar] [CrossRef]
- Cheng, Y.H.; Zhang, N.; Zhang, B.S.; Kang, C.Q.; Xi, W.M.; Feng, M.S. Low-Carbon operation of multiple energy systems based on energy-carbon integrated prices. IEEE Trans. Smart Grid 2020, 11, 1307–1318. [Google Scholar] [CrossRef]
- Patterson, D.; Gonzalez, J.; Hölzle, U.; Le, Q.; Liang, C.; Munguia, L.M.; Rothchild, D.; So, D.R.; Texier, M.; Dean, J. The carbon footprint of machine learning training will plateau, then shrink. Computer 2022, 55, 18–28. [Google Scholar] [CrossRef]
- Yan, M.Y.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A.; Gurung, N.; Zheng, H.H.; Ogunnubi, O.; Vukojevic, A.; Paaso, E.A. Blockchain for transacting energy and carbon allowance in networked microgrids. IEEE Trans. Smart Grid 2021, 12, 4702–4714. [Google Scholar] [CrossRef]
- Huang, W.J.; Zhang, N.; Cheng, Y.H.; Yang, J.W.; Wang, Y.; Kang, C.Q. Multienergy networks analytics: Standardized modeling, optimization, and low carbon analysis. Proc. IEEE 2020, 108, 1411–1436. [Google Scholar] [CrossRef]
- Li, R.; Wang, Q.; Liu, Y.; Jiang, R. Per-capita carbon emissions in 147 countries: The effect of economic, energy, social, and trade structural changes. Sustain. Prod. Consum. 2021, 27, 1149–1164. [Google Scholar] [CrossRef]
- Li, Y.; Yang, X.; Ran, Q.; Wu, H.T.; Irfan, M.; Ahmad, M. Energy structure, digital economy, and carbon emissions: Evidence from China. Environ. Sci. Pollut. Res. 2021, 28, 64606–64629. [Google Scholar] [CrossRef] [PubMed]
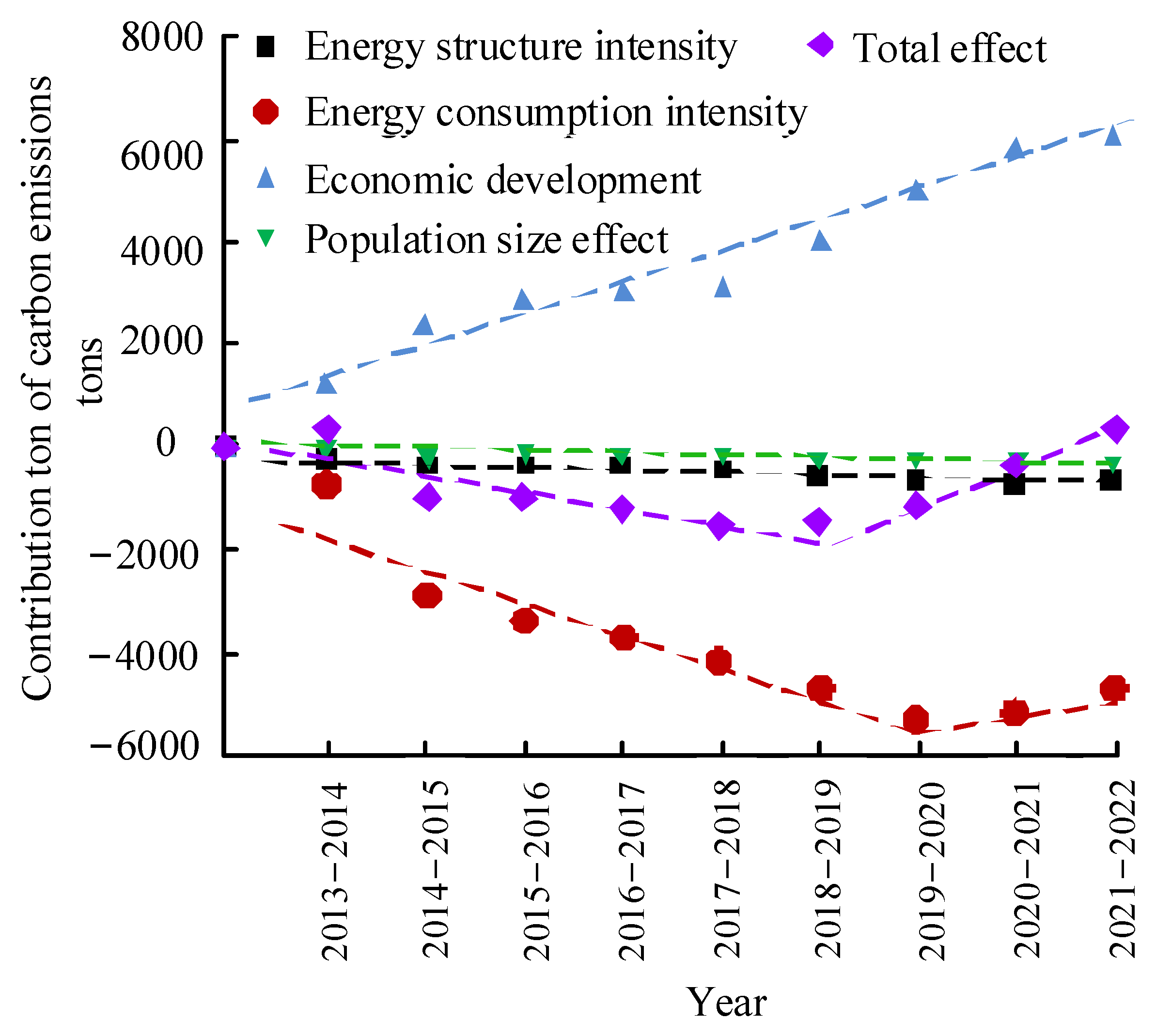

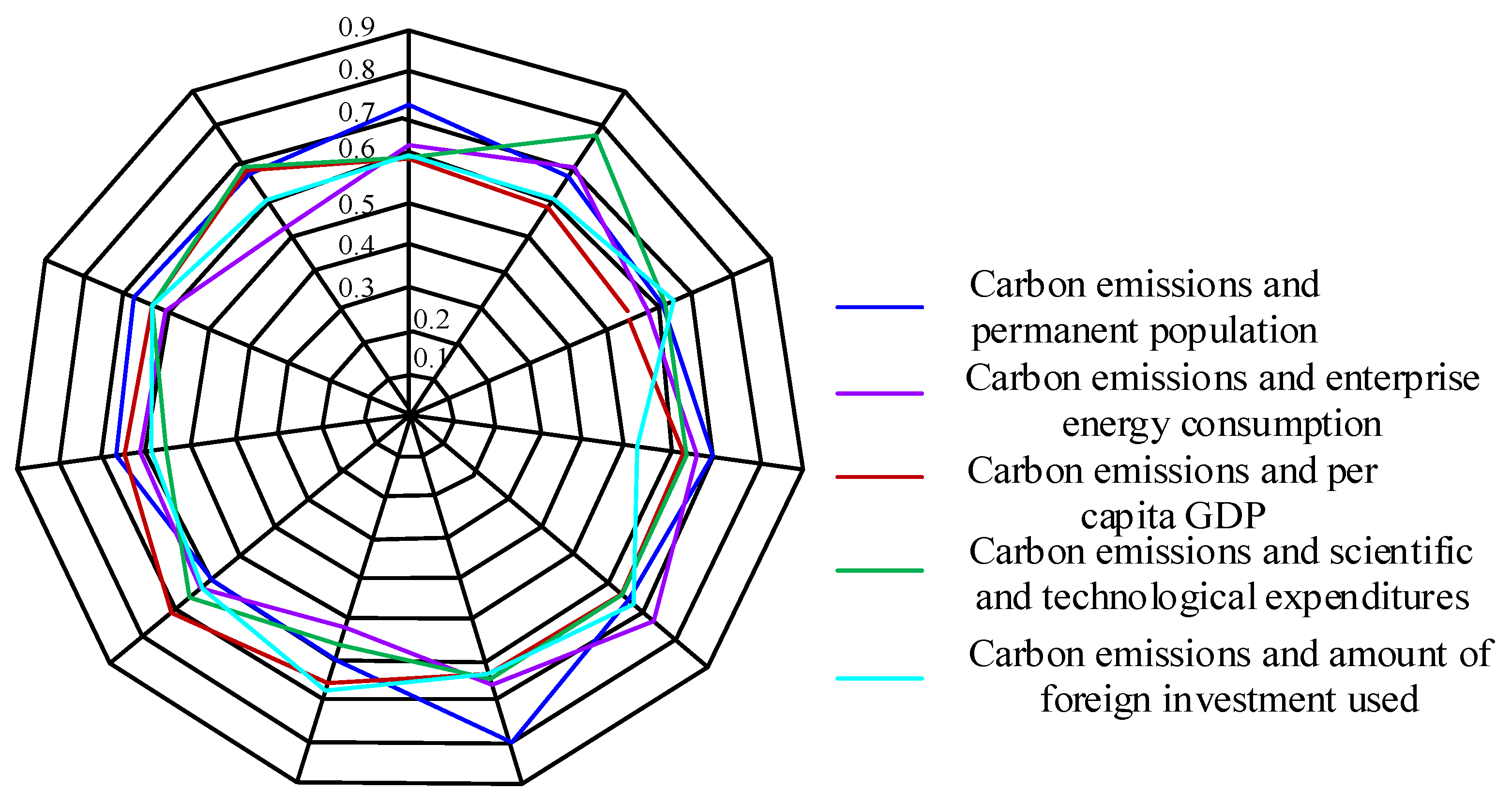
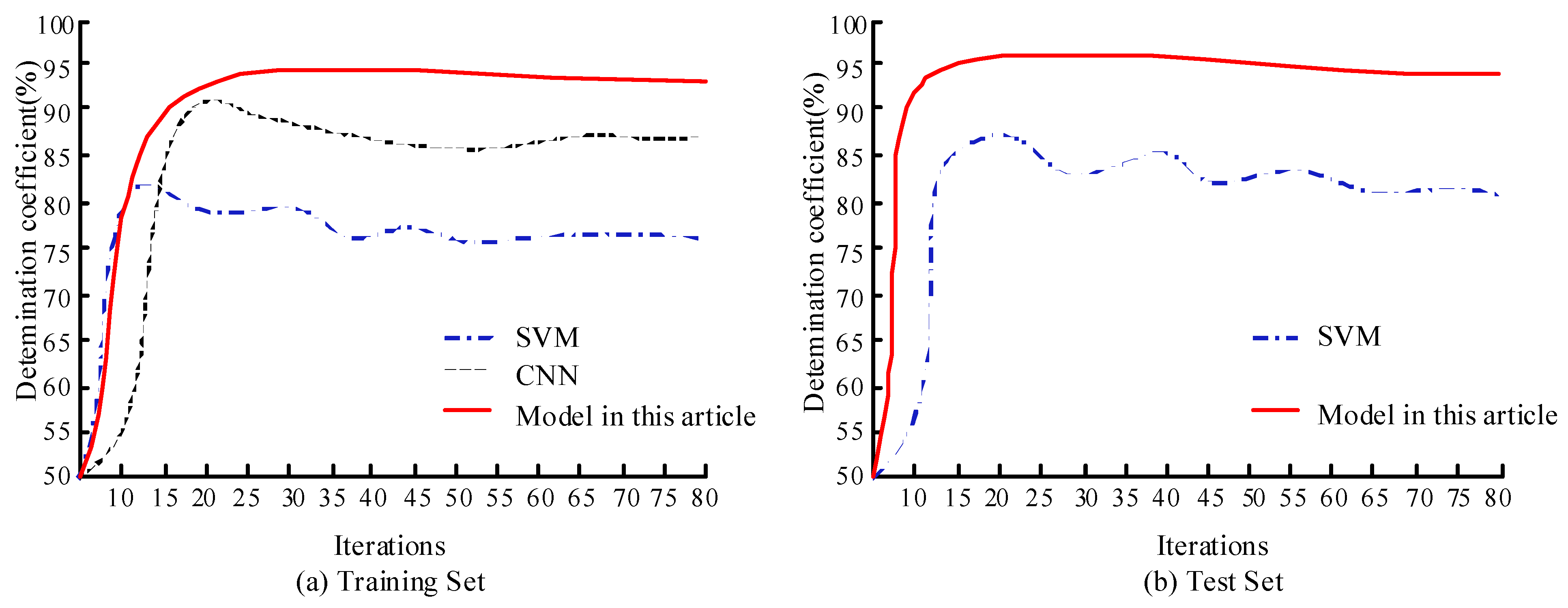
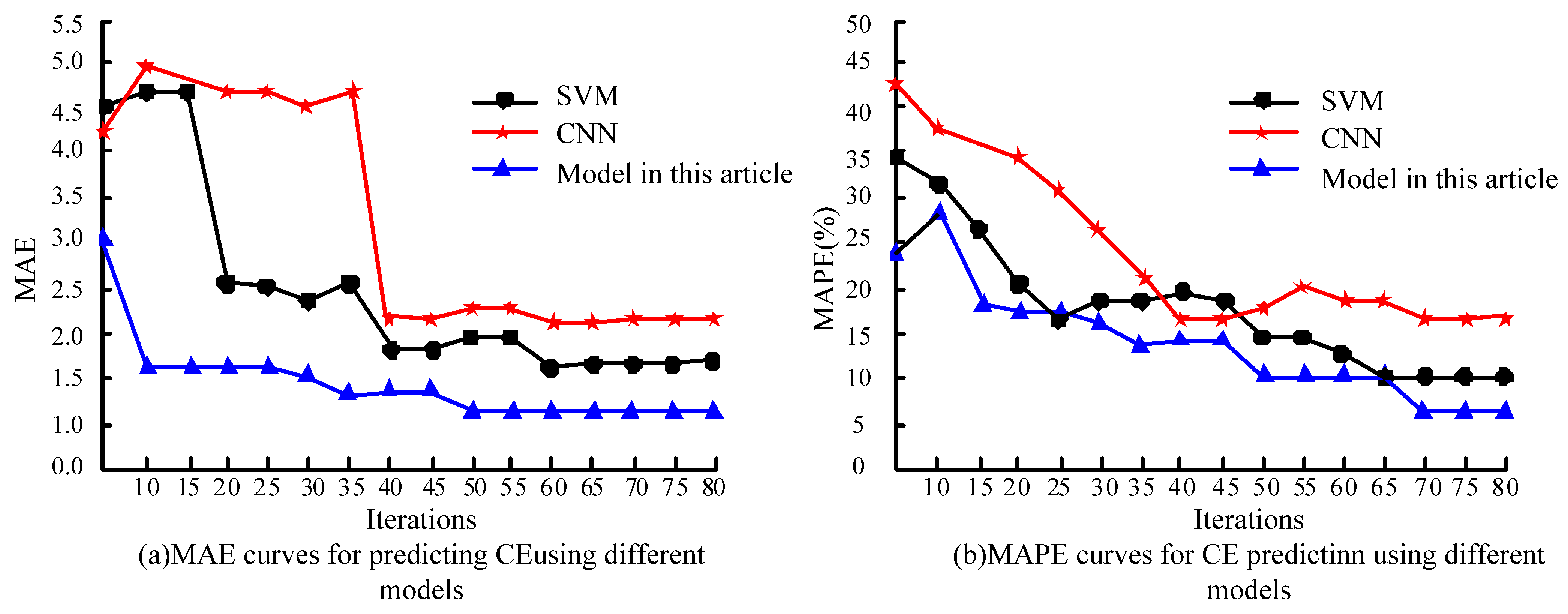
| Number | Energy Type | Conversion Coefficient of Standard Coal (kg Standard coal/kg) | CE Coefficient (ton of Carbon/ton) |
|---|---|---|---|
| 1 | Raw coal | 0.71 | 2.02 |
| 2 | Washed coal | 0.90 | 2.46 |
| 3 | Coke | 0.97 | 3.08 |
| 4 | Crude oil | 1.43 | 3.09 |
| 5 | Gasoline | 1.47 | 2.99 |
| 6 | Kerosene | 1.47 | 3.10 |
| 7 | Diesel oil | 1.46 | 3.16 |
| 8 | Fuel oil | 1.43 | 3.24 |
| 9 | Liquefied petroleum gas | 1.71 | 3.17 |
| 10 | Natural gas | 1.33 | 21.87 |
| Type | Influence Factor | Unit | Definition |
|---|---|---|---|
| 1 | Population | Ten million | The total number of people living in a certain area or group |
| 2 | GDP | CNY trillion | The final result of production activities of all permanent units in a country (or region) within a certain period of time |
| 3 | Urbanization rate | % | The proportion of urban population to the total population (including agriculture and non-agriculture) |
| 4 | Total industrial output value | CNY trillion | The total amount of products produced within a certain period of time |
| 5 | Labor productivity | % | The efficiency of products produced by workers during the reporting period |
| 6 | Number of people engaged | Ten thousand people | Total number of people engaged in production and operation |
| 7 | EC | 100 million tons | The energy resources consumed in the production process that exist in their original form in nature and are not processed or converted |
| Region | GDP | Population Size | Urbanization Rate | Energy Consumption | Energy Type |
|---|---|---|---|---|---|
| Zhao Wang Zhuang Zhen Lu Er Gang Cun, Laiyang City, Yantai City, Shandong Province | 0.0129 | 0.0187 | 0.3025 | 0.0503 | 0.6467 |
| Pan Shi Dian Zhen Hu Shan Cun, Haiyang City, Yantai City, Shandong Province | 0.0163 | 0.1472 | 0.4975 | 0.1056 | 0.8801 |
| Fang Yuan Jie Dao Mou Jia Cun, Haiyang City, Yantai City, Shandong Province | 0.0091 | 0.0449 | 0.4827 | 0.0368 | 0.9309 |
| Liu Ge Zhuang Zhen Liu Ge Zhuang Cun, Haiyang City, Yantai City, Shandong Province | 0.0174 | 0.1680 | 0.0253 | 0.0207 | 0.6936 |
| Guo Cheng Zhen Qian Kuang Cun, Haiyang City, Yantai City, Shandong Province | 0.0005 | 0.0121 | 0.2714 | 0.0253 | 0.6128 |
| Liu Ge Zhuang Zhen Fang Li Cun, Haiyang City, Yantai City, Shandong Province | 0.0178 | 0.0616 | 0.2911 | 0.0378 | 0.6923 |
| Industrial Functions | Year | Moran’s I | p-Value | Z-Score | Industrial Functions | Year | Moran’s I | p-Value | Z-Score |
|---|---|---|---|---|---|---|---|---|---|
| Industrial CE | 2014 | 0.114 | <0.05 | 6.3122 | Living CE | 2014 | 0.385 | <0.05 | 21.9918 |
| 2016 | 0.3 | <0.05 | 8.3658 | 2016 | 0.31 | <0.05 | 8.7669 | ||
| 2018 | 0.263 | <0.05 | 7.5172 | 2018 | 0.436 | <0.05 | 11.834 | ||
| 2020 | 0.048 | <0.05 | 1.7253 | 2020 | 0.354 | <0.05 | 13.7516 | ||
| 2022 | 0.045 | >0.05 | 1.4006 | 2022 | 0.202 | <0.05 | 7.5203 | ||
| Building CE | 2014 | 0.19 | <0.05 | 11.1912 | Public CE | 2014 | −0.152 | <0.05 | −10.7103 |
| 2016 | 0.331 | <0.05 | 9.802 | 2016 | −0.429 | <0.05 | −12.0519 | ||
| 2018 | 0.134 | <0.05 | 3.7417 | 2018 | −0.401 | <0.05 | −11.5734 | ||
| 2020 | −0.065 | <0.05 | −3.0851 | 2020 | −0.33 | <0.05 | −13.3907 | ||
| 2022 | 0.03 | >0.05 | 0.8669 | 2022 | −0.43 | <0.05 | −14.2779 | ||
| Commercial CE | 2014 | 0.011 | >0.05 | −0.0584 | CE from the transportation industry | 2014 | 0.171 | <0.05 | 10.1696 |
| 2016 | 0.08 | <0.05 | 2.252 | 2016 | 0.205 | <0.05 | 6.1525 | ||
| 2018 | 0.166 | <0.05 | 4.7099 | 2018 | 0.273 | <0.05 | 8.0469 | ||
| 2020 | 0.353 | <0.05 | 14.4168 | 2020 | 0.325 | <0.05 | 13.795 | ||
| 2022 | 0.356 | <0.05 | 11.6346 | 2022 | 0.285 | <0.05 | 9.9201 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Cheng, J.; Li, L. Prediction of CO2 Emissions Related to Energy Consumption for Rural Governance. Sustainability 2023, 15, 16750. https://doi.org/10.3390/su152416750
Yu X, Cheng J, Li L. Prediction of CO2 Emissions Related to Energy Consumption for Rural Governance. Sustainability. 2023; 15(24):16750. https://doi.org/10.3390/su152416750
Chicago/Turabian StyleYu, Xitao, Jianhong Cheng, and Liqiong Li. 2023. "Prediction of CO2 Emissions Related to Energy Consumption for Rural Governance" Sustainability 15, no. 24: 16750. https://doi.org/10.3390/su152416750
APA StyleYu, X., Cheng, J., & Li, L. (2023). Prediction of CO2 Emissions Related to Energy Consumption for Rural Governance. Sustainability, 15(24), 16750. https://doi.org/10.3390/su152416750






