Two-Way Slab Punching Shear Resistance: Experimental Insights into Basalt-FRP Bar as Flexural Reinforcement

Abstract

This study seeks to experimentally evaluate the punching shear performance of two-way concrete slabs reinforced with conventional steel and basalt fiber-reinforced polymer (basalt-FRP) bars subjected to punching loading condition. Basalt-FRP bars offer high tensile strength and corrosion resistance but are understudied in two-way concrete slabs concerning punching shear. This study aims to fill this gap, with key implications for future structural design considerations. To achieve the objectives of the study, six large-scale square slabs were fabricated and subjected to a concentric load until failure. The parameters of the experiment included are the type of reinforcement used (either basalt-FRP or steel), the percentage of basalt-FRP used (ranging from 0.88% to 1.77%), the size of the basalt-FRP bars used (either 16 or 12 mm), and the concrete’s compressive strength (25, 30, and 35 MPa). The findings from the tests showed that incorporating basalt-FRP bars with one-quarter equivalent axial stiffness ($\rho \left(E_f/E_s\right)$) to that of steel significantly enhanced the punching shear resistance of flat slabs, achieving approximately 65% of the capacity observed in steel-reinforced control sample. Moreover, increasing the amount of basalt-FRP bar reinforcement to half of the equivalent axial stiffness of steel had a substantial effect in improving shear strength, reaching approximately 89% of the capacity observed in the steel-reinforced specimen and concurrently reducing deflection during the failure. Additionally, the reinforcement type and concrete compressive strength played a crucial role in determining the ultimate load, failure modes, and crack propagation patterns. The study reveals discrepancies between experimental results and existing models for punching shear in FRP-reinforced slabs. Certain prevalent models prove to be conservative in their estimates, while others offer more accurate predictions, indicating the need for comprehensive model refinement. The investigation found that one model, encompassing the majority of variables affecting punching shear, exhibited the highest level of precision, with a slight adjustment recommended to enhance its accuracy further. This study suggests a sustainable, more durable way to reinforce concrete in bridges and high-rise buildings, potentially improving construction efficiency, enhanced service life, and potential updates to building codes.

1. Introduction

Over the years, concrete flat slabs have gained popularity in modern construction due to their cost-effectiveness, reduced story height, and ease of construction. However, the performance of flat slabs is often challenged by a punching shear, a critical structural failure mechanism that occurs at the slab–column connection. Traditionally, steel bars have been used as reinforcement to improve the punching shear capacity of concrete slabs. Despite their effectiveness, steel bars are susceptible to corrosion, thereby limiting the durability of the structure [1].

In this regard, basalt fiber-reinforced polymer (basalt-FRP) bars have emerged as a promising alternative to steel bars for enhancing the punching shear capacity of flat slabs. Their high tensile strength and resistance to corrosion make them a subject of increasing academic studies [2,3]. These FRP bars not only possess high tensile strength and excellent resistance to corrosion, but also offer multiple inherent advantages, such as low density, favorable tensile behavior, and electrical and magnetic neutrality. Furthermore, their minimal susceptibility to corrosion and easy integration into concrete structures make them an increasingly attractive option for both researchers and practitioners [4]

Several studies have examined the structural behavior of FRP-reinforced concrete two-way slabs using glass or carbon FRPs and their impact on punching shear capacity, contributing to current design guidelines. These studies have been instrumental in shaping existing design guidelines, such as ACI 440.1R-15, CSA S806-12 [1,2,3,4,5,6,7,8]. However, less attention has been given to other types of FRP bars, such as basalt fiber-reinforced polymer (basalt-FRP), which offer a balanced combination of mechanical properties and economic viability [9].

Basalt-FRP bars have recently gained popularity among the many types of FRP materials due to their improved mechanical qualities, environmental sustainability, and cost-effectiveness [10,11,12,13,14,15,16].There are still challenges associated with the use of basalt-FRP bars as reinforcement in RC slabs, such as the lack of design guidelines. Therefore, further research is needed to investigate the punching shear behavior of two-way RC slabs reinforced with basalt-FRP bars and to update design guidelines for their safe and reliable use [17,18,19]. These standards and codes have not incorporated research on the use of basalt-FRP bars for enhancing the punching shear resistance in two-way slabs.

In an earlier study by Elgabbas et al. (2016), the researchers examined concrete bridge-deck slabs reinforced with basalt-FRP bars and supported the effectiveness of basalt-FRP reinforcement, particularly when subjected to conditions similar to North American slab-on-girder bridge decks, and found that these slabs surpassed Canadian design load requirements [10]. Subsequently, Zheng et al. (2018) focused on the environmental benefits and the structural integrity of bridge deck slabs made of self-compacting concrete (SCC) and reinforced with basalt-FRP bars, noting that punching shear was the dominant failure mode [12]. In a 2020 study, Wang et al. highlighted the enhanced post-cracking rigidity and energy efficiency found in basalt-FRP grid-reinforced slabs [11]. In the same year, Xu and Hou proposed using basalt-FRP bars in ultra-high performance concrete (UHPC) slabs, which displayed better ductility despite a lower ultimate capacity compared to steel-reinforced slabs [14]. Most recently, in 2022, Shill et al. compared slabs reinforced with basalt-FRP, CFRP, and steel, finding that basalt-FRP-reinforced slabs exhibited superior ductility and a more gradual decrease in load capacity beyond the peak load [15]. Despite these valuable contributions, there remains an apparent gap in the literature: a lack of comprehensive research focusing solely on the punching shear capacity of full-scale two-way flat slabs reinforced with basalt-FRP bars.

Given this research gap, the primary objective of the present study is to experimentally evaluate the punching shear performance of two-way concrete slabs reinforced with basalt-FRP bars and compare them with those using conventional steel reinforcement. This study is imperative, as it aims to provide experimental insights into the role of basalt-FRP bars as flexural reinforcement in two-way slabs, thereby filling a significant void in the existing literature. The experiment scrutinizes various parameters, including the type of reinforcement used (basalt-FRP versus steel), the percentage and size of basalt-FRP bars, and the concrete’s compressive strength, offering a comprehensive understanding of their influence on punching shear behavior. In addition to that, it offers implications for more durable and cost-effective construction. The results could influence building codes and promote the use of sustainable materials in structures such as high-rise buildings and bridges.

To achieve these objectives, this study employs a combination of experimental and computational methods. Experimental tests on six full-scale two-way flat slabs reinforced with basalt-FRP bars were carried out to assess the punching shear behavior under a concentric load condition. Subsequently, these test results were compared against existing analytical design formulas. The findings indicate a significant impact in punching shear resistance when basalt-FRP bars are used. Further, it was found that the type of reinforcement, reinforcement ratio, bar size, and the concrete’s compressive strength played critical roles in determining the slabs’ ultimate load, failure modes, and crack propagation patterns. Alarmingly, our experimental data revealed noticeable discrepancies when compared with predictions based on existing design equations, underscoring the need for revisiting and possibly adjusting these models for enhanced accuracy and reliability.

This study faces a set of limitations that should be acknowledged when interpreting its findings. Experimentally, the scope of the work is circumscribed by the availability of specialized lab equipment and logistical challenges in sourcing basalt-FRP bars from abroad. These factors introduce both time and budget constraints that further restrict the study to a focus on short-term loading conditions, leaving the important area of long-term material behavior unexplored.

2. Experimental Program

2.1. Overview of Test Specimens

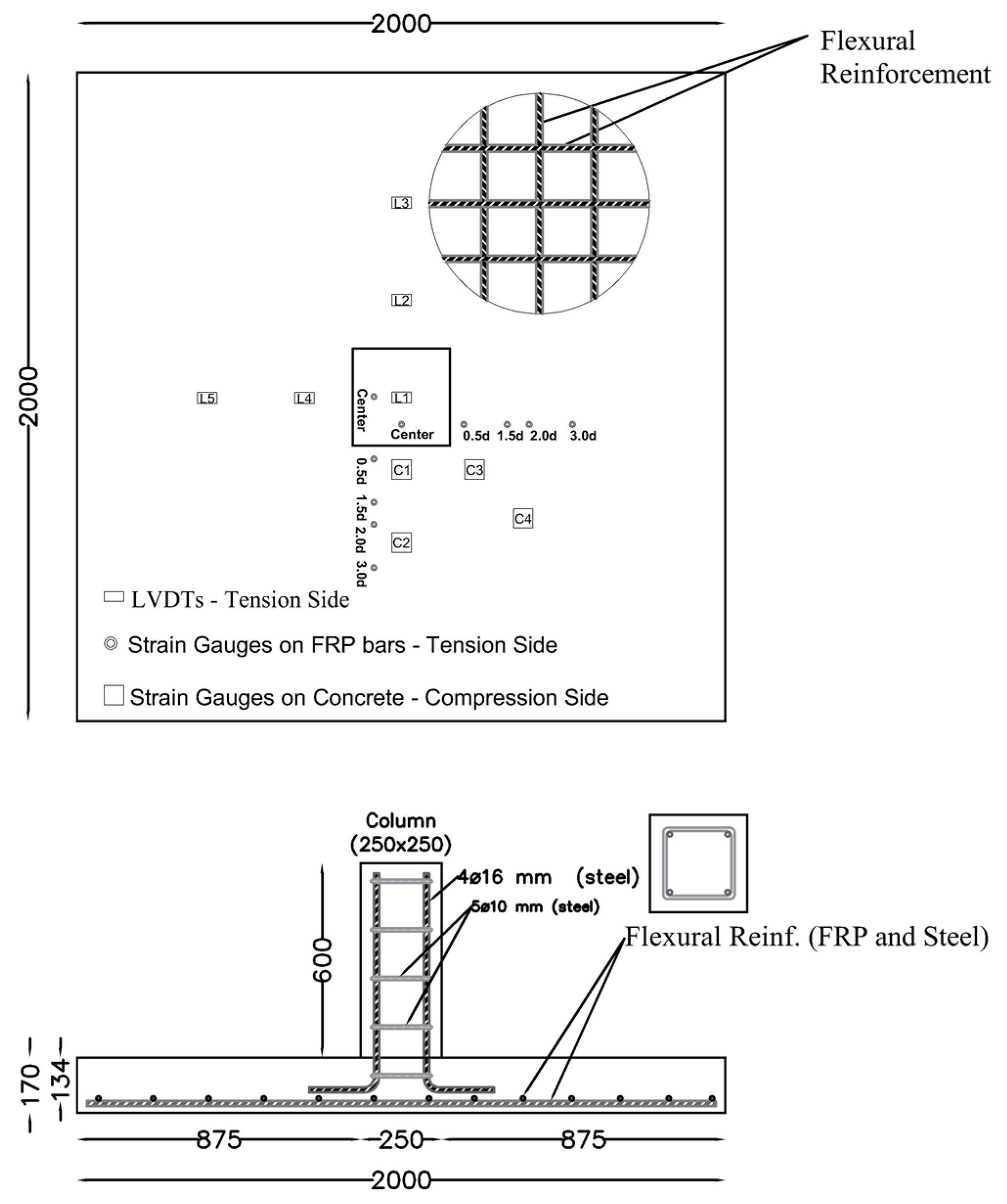
As part of a thorough Ph.D. study, the investigators selected six samples from a set of 17 slab-column specimens, all of which featured reinforcement using both steel and basalt-FRP bars. The targeted focus of the study is on reinforcement type and amount, bar size, and concrete compressive strength. The specimens were designed to replicate independent interior connections between slabs and columns. The selection of the slab thickness aimed to mimic the commonly employed flat slabs in a randomly chosen prototype multi-story, multi-bay reinforced concrete building. In developing the dimensions of the test specimens, it was aimed to balance real-world applicability with the constraints of the experimental setup. Each specimen measured 2000 × 2000 mm and was based on the analysis of a prototype multi-story, multi-bay concrete building. The prototype featured square columns of 250 × 250 mm, equally spaced at a distance of L = 5 m (centerline-to-centerline) in both directions. The column extended 600 mm above the top surface of the slabs. Figure 1 illustrates the typical shape and reinforcement arrangement of these test specimens. This size was specifically selected to represent the zone of negative moments around an interior column, defined by lines of contra-flexure assumed to be at a distance of 0.2 ℓ from the column centerline. These dimensions were chosen due to the limitations of available laboratory instruments and tools, yet they also served to mimic structural scenarios that are commonly found in medium-sized commercial and residential buildings.

The test samples were organized into two separate groups. Group I featured three basalt-FRP-RC slabs with reinforcement ratios that varied between 0.88% and 1.71% alongside a steel-reinforced specimen as a reference sample. All specimens within this series exhibited a cylindrical concrete compressive strength of 29.8 MPa. Group 2 includes two specimens, each with a distinct concrete compressive strength and reinforced with 12 mm basalt-FRP bar size. The specimens in this group displayed cylindrical concrete compressive strengths of 21.1 MPa and 34.6 MPa, respectively. Based on previous studies, key variables, such as reinforcement type, ratio, bar size, and concrete compressive strength, have been proven to be critical for investigation, as they yield varying outcomes in punching shear capacity. See

Table 1. Specimen details.

Specimen	Thickness mm	Reinf. Spacing mm	Effective Depth—d mm	Reinf. Material	Tens. Reinf. Size mm	$\mathbf{Reinf}. \mathbf{Ratio}, \mathit{\rho }\mathit{\%}$	${\mathit{f}}_{\mathit{c}}^{\mathit{\prime }}$ MPa
S16(0.88)	170	170	134	Steel	16	0.88	29.8
B16(0.88)	170	170	134	Basalt	16	0.88	29.8
B16(1.77)	170	85	134	Basalt	16	1.77	29.8
B12(0.88)	170	95	138	Basalt	12	0.88	29.8
S16(0.88)–C35	170	95	138	Basalt	12	0.88	34.6
S16(0.88)–C25	170	95	138	Basalt	12	0.88	21.1

.

2.2. Materials Used in This Study

The study utilized standard-weight, ready-mixed concrete with varying strengths to cast the specimens, targeting compressive strengths of 25, 30, and 35 MPa. The concrete mixture included Portland cement and had a maximum aggregate size of 19 mm, see

Table 2. Concrete mix proportions.

Ingredient	$\mathbf{Mix} \mathbf{Proportions}, \mathbf{k}\mathbf{g}/{\mathbf{m}}^3$
	$25 \mathbf{M}\mathbf{P}\mathbf{a}$	$30 \mathbf{M}\mathbf{P}\mathbf{a}$	$35 \mathbf{M}\mathbf{P}\mathbf{a}$
Cement	317	355	410
Sand	699	674	750
Gravel	1207	1173	1100
Water	184	181	175

. Simultaneously with the testing of the slab specimens, tests were conducted on cylinders in accordance with ASTM C39 [20] on the same day. The concrete’s real compressive strength was found by calculating the mean result from conducting compressive tests on standard cylinders with dimensions measuring 100 × 200 mm. The outcomes are presented in

Table 3. Concrete’s actual compressive strength mix proportions.

	$\mathbf{Cylindrical} \mathbf{Concrete} \mathbf{Compressive} \mathbf{Strength} {\mathit{f}}_{\mathit{c}}^{\mathit{\prime }}\left(\mathbf{M}\mathbf{p}\mathbf{a}\right)$
Target	$25$	$30$	$35$
Actual	21.1	29.8	34.6

.

The ordinary steel bars utilized in the reference sample and the column stud were acquired locally and evaluated in compliance with the ASTM standard [21]. The basalt-FRP bars were all purchased from Sichuan Jumeisheng New Material Technology Co., Ltd., Dazhou, China. The manufacturer also supplied the technical datasheet, and the test results for basalt-FRP were in accordance with the Chinese Standard GBT228-2002 [22].

Table 4. Properties of steel and basalt-FRP bars in terms of mechanical characteristics.

Bar Size, mm	Reinforcement Materials	$\mathbf{Tensile} \mathbf{Strength} (\mathbf{M}\mathbf{P}\mathbf{a}$)	$\mathbf{Modulus} \mathbf{of} \mathbf{Elasticity} (\mathbf{G}\mathbf{P}\mathbf{a}$)	Ultimate Elongation (%)
16	Steel	595.5	200	16.1
16	Basalt-FRP	978.6	48.26	2.06
12	Basalt-FRP	977.2	48.0	2.08

lists all the required characteristics of the conventional steel and basalt-FRP bars.

For this study, basalt-FRP bars from Sichuan Jumeisheng New Material Technology Co., Ltd. were selected for their established tensile strength and environmental resistance, aligning with the research goals. The choice of supplier for basalt-FRP bars was motivated by their demonstrated uniformity in material properties. The concrete used was a reputable, local ready-mixed company previously validated and accepted by other researchers, ensuring both quality and consistency. It is worth noting that the specific mix design of the concrete plays a role; a mix with a different aggregate size or cement type may react differently under load, subsequently affecting the punching shear capacity. It can be noted that changes in material sources could impact the punching shear capacity, thereby affecting the study’s generalizability and interpretive scope. Figure 2 shows the specimens preparation steps.

2.3. Experimental Arrangement and Instrumentation

Following the material selection, experimental setup was outlined, emphasizing the accuracy and reliability of the measuring instruments to validate the generated data.

Figure 1 provides a visual depiction of the experimental test arrangement. To induce punching failure in the two-way slab specimens, a 2000 KN testing machine was employed. The load was applied concentrically to the column-stud with the assistance of a hydraulic jack, utilizing a 200 mm steel plate to uniformly distribute the load across the surface of the column. The specimens were supported at their extremities by an I-shaped steel section resting on four steel columns. To create simply supported conditions, a 50 mm steel rod was placed over the I-steel section, as it is the case in a counter-flexure point in a flat slab.

2.4. Steps in the Testing Procedure

The test setup was prepared by positioning the simply supported slab specimen horizontally on the testing rig, using I-shaped steel sections and a 50 mm steel rod as supports placed at the slab’s edges. The supports were evenly distributed, and the slab was level. To ensure uniform load distribution over the entire column surface, a $20 \mathrm{m}\mathrm{m}$ steel plate was positioned atop the column region for load application. A hydraulic jack was employed to apply the concentrated load centrally onto the column-stud through the steel plate, maintaining a steady and controlled load application rate of $0.2 \mathrm{k}\mathrm{N}$ per second during the test. Figure 3 provides an overall depiction of the test setup.

The monitoring and data collection process included the placement of 5 LVDTs, 10 steel strain gauges for reinforcement in perpendicular orientations within the slab, and 4 concrete strain gauges on the upper surface of the sample. To provide a more localized understanding of the slab’s deformation characteristics, the first LVDT was located at the mid-span. Additionally, two LVDTs were equally spaced between the origin and the mid-span LVDT. Specifically, these were positioned at 0.3 m and 0.6 m from the origin along orthogonal axis. This symmetrical arrangement allowed for capturing deflection profiles at three equidistant points leading up to the mid-span, thereby enabling a comprehensive analysis of the slab’s structural behavior under applied loads. Ten steel strain gauges were used in total for the flexural reinforcement, with their placement carefully calibrated along two principal axis to capture strain profiles, thereby providing a multi-directional understanding of the material behavior. The strain gauges were situated at calculated distances of mid-span, 0.5 d, 1.5 d, 2 d, and 3 d from the column face, along both orthogonal axes. To capture the peak compression strain within the concrete, an additional set of four electrical strain gauges was strategically affixed to the top surface of the slab, positioned approximately 25 mm away from the column face; this placement is critical for quantifying the maximum compressive stresses that develop in the slab, especially on the compression side nearest to the column support.

LVDTs and strain gauges were used for accurate measurement of displacements and strains, respectively. Prior to testing, LVDTs were calibrated using a 0.01 mm-accurate digital caliper under expert supervision. Any discrepancies between LVDT and caliper readings were rectified through immediate recalibration. Strain gauges, recognized for their precision, were also utilized to enhance measurement reliability. This rigorous approach to instrumentation calibration ensured the credibility of our findings. A data-acquisition device was employed to periodically record load and displacement data throughout the test. Figure 1 displays the positioning of the strain gauges and LVDTs.

To ensure the validity and reliability of the experimental outcomes, control measures and baseline tests were performed for the study. For control measures, specific variables, such as the quality of the concrete, curing time, and environmental factors, were maintained consistently across all test specimens to isolate the effects of basalt-FRP reinforcement on shear capacity. Instrument calibration was also routinely verified at different stages of the experiment to ensure measurement accuracy. Additionally, a reference slab reinforced with conventional steel was tested to serve as a baseline. This baseline test offered a standard point of comparison, enabling a more detailed assessment of the performance enhancements attributable to basalt-FRP-reinforced slabs.

3. Results and Discussion

3.1. Failure Modes and Cracking Characteristics

The results of the experimental program have revealed that all the analyzed slabs exhibited brittle failure modes, characterized by punching shear cracks in the vicinity of the column. Similar patterns of cracking were observed on the tension face of the specimens at the point of failure. The initiation and subsequent propagation of cracks were consistent across all the tested slabs, starting from the corners of the columns at vertical cracking loads identified in Figure 4. These observations align with the findings from previous studies [1,15,23]. As the load increased, radial cracks formed near the column, expanding towards the supports in all directions. Notably, circumferential cracks emerged when the failure load reached approximately 40 to 55%, linking the radial cracks across all slab–column connections.

The slab S16(0.88), reinforced with steel bars, presented fewer cracks upon failure than the slabs reinforced with basalt-FRP bars despite failing under greater vertical loads. This may be due to the elevated cracking load associated with steel reinforcement, which seems to delay crack initiation. In comparing slabs with similar reinforcement ratios (0.88%), those reinforced with basalt-FRP bars showed accelerated crack growth and non-uniform crack distribution compared to their steel-reinforced counterpart.

It is worth noting that the reinforcement ratio had a significant impact on crack propagation. A lower ratio resulted in a more distributed pattern of cracks, as observed in slab B16(0.88) compared to B16(1.77). Notably, some concrete peeled off from the tension face of B16(0.88) near the punching surface. This phenomenon is likely due to the decreased stiffness of the slab reinforced with the 0.88 reinforcement ratio that corresponds with a decline in the reinforcement ratio as compared to B16(1.77). This suggests that the reinforcement ratio plays a vital role in the failure characteristics and that optimizing the ratio could lead to improved performance. In addition, the use of smaller bars (12 mm) in specimen B12(0.88) resulted in more localized stress points, and thus, a higher degree of distributed cracking, possibly due to a larger contact surface between the bars and adjacent concrete. Finally, specimens B12(0.88), B12(0.88)–C35, and B12(0.88)–C25, representing different concrete compressive strengths, exhibited analogous failure surfaces in their respective modes of failure and crack patterns.

The findings reveal that the brittle nature of the failure mechanism is consistent regardless of the type and ratio of reinforcement used, different basalt-FRP bar sizes, and concrete compressive strength. On the other hand, the initiation and progression of cracks were influenced by the material type (i.e., basalt-FRP vs. steel) as well as the size and ratio of the basalt-FRP bars employed. This has important implications for both design considerations and theoretical models of flat slabs reinforced with basalt-FRP bars. In addition to that, given the brittle nature of the observed failure modes, potential mitigation strategies should be considered. One approach might involve using a hybrid system of steel and FRP bars to leverage the benefits of both materials, such as enhanced ductility and corrosion resistance [24]. Another option is to experiment with varying reinforcement ratios to balance strength and ductility, as prior research suggests that a higher reinforcement ratio can improve ductility [25,26]. By acknowledging the impact of the material choice and reinforcement ratio on failure characteristics, the study aims to contribute to safer and more effective construction practices, potentially influencing future building codes.

3.2. Punching Shear Strength

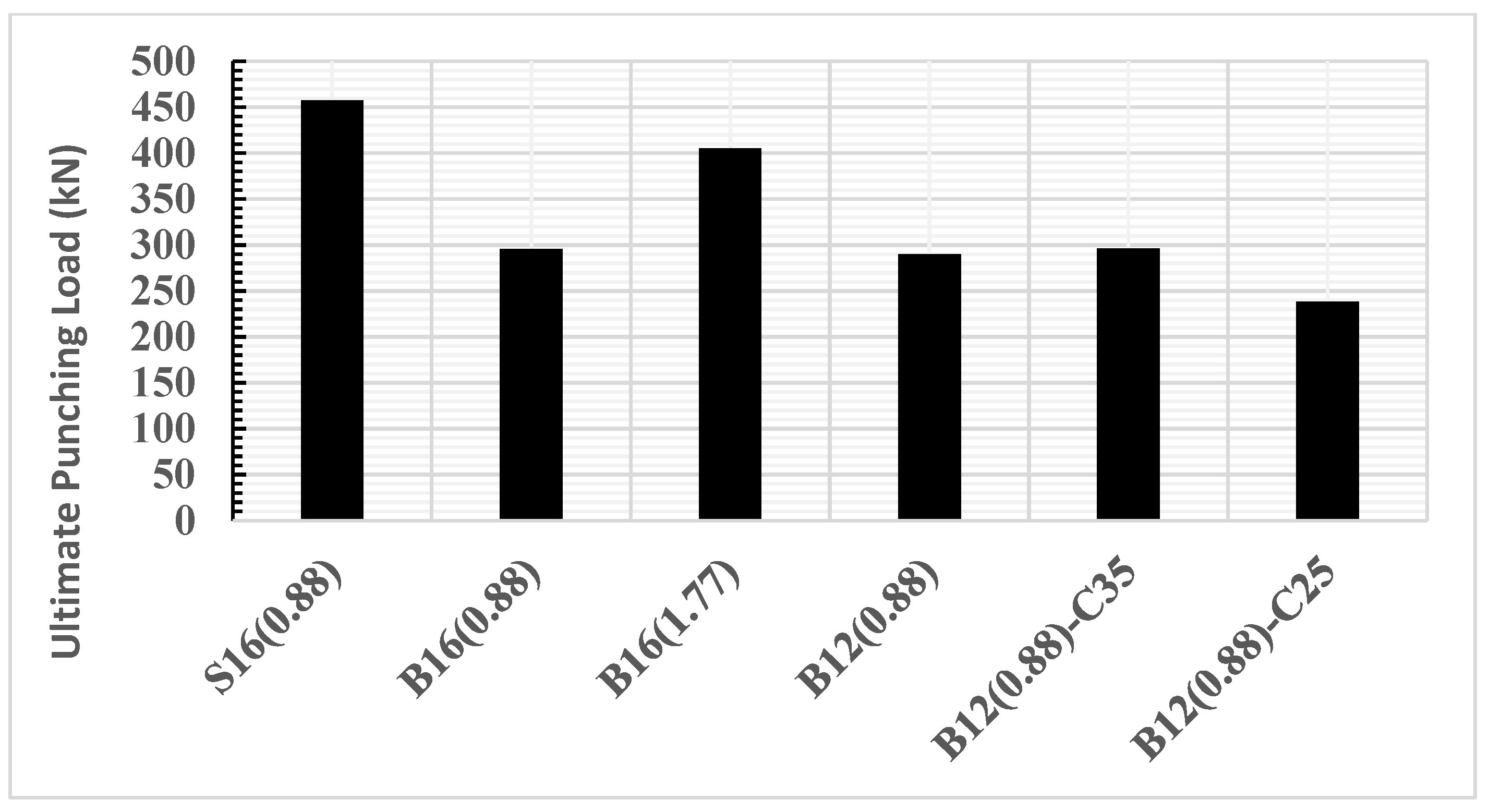
The evaluation of the experimental results from all six specimens listed in

Table 5. Test results.

Specimen ID	$\mathit{\rho }\left({\mathit{E}}_{\mathit{f}}/{\mathit{E}}_{\mathit{s}}\right)\mathit{\%}$	${\mathit{V}}_{\mathit{c}\mathit{r}}\left(\mathbf{k}\mathbf{N}\right)$	${∆}_{\mathit{c}\mathit{r}}\left(\mathbf{m}\mathbf{m}\right)$	${\mathit{V}}_{\mathit{u}}\left(\mathbf{k}\mathbf{N}\right)$	${∆}_{\mathit{u}}\left(\mathbf{m}\mathbf{m}\right)$	$\mathbf{Max}. \mathbf{Reinf}. \mathbf{Strain}, {\mathit{\epsilon }}_{\mathit{u}}\left(\mathit{\mu }\mathit{\epsilon }\right)$	$\mathbf{Max}. \mathbf{Conc}. \mathbf{Strain}, {\mathit{\epsilon }}_{\mathit{c}}\left(\mathit{\mu }\mathit{\epsilon }\right)$	$\mathbf{Post}-\mathbf{Cracking} \mathbf{Stiffness}$ $(\mathbf{k}\mathbf{N}/\mathbf{m}\mathbf{m})$
S16(0.88)	0.88	91.2	1.3	457.3	16.5	3421	−627	26.7
B16(0.88)	0.21	94.4	1.95	295.5	25.9	9033	−773	9.8
B16(1.77)	0.43	108.9	1.38	405.2	16.9	4277	−669	19.6
B12(0.88)	0.21	99.1	1.37	290.1	24.8	8148	−1081	8.4
B12(0.88)–C35	0.21	108.7	1.24	295.8	24.5	7684	−1383	8.6
B12(0.88)–C25	0.21	75.3	1.12	238.1	25.6	6229	−597	8.0

Note: $V_{cr}$ is the cracking load, ${∆}_{cr}$ the cracking load deflection, $V_u$ is the ultimate punching load, ${∆}_u$ is the maximum deflection.

reveals a significant correlation between parameters, such as the reinforcement type, reinforcement ratio, bar size, concrete compressive strength, and maximum punching shear capacity. When comparing S16(0.88) and B16(0.88), which have identical properties except for the type of reinforcement, a significant drop of about 35.3% in the punching shear capacity is observed when transitioning from steel bars to basalt-FRP bars, indicating steel’s superior contribution to shear strength. This is primarily due to basalt-FRP’s lower modulus of elasticity. In both steel and basalt-FRP slabs in this study, the dominant failure mode is punching shear, resulting from concrete crushing that occurs before the reinforcement reaches its yielding point. Therefore, the ultimate tensile strength of the rebar is not a determining factor for the cracking load values in this failure mode. See Figure 5.

The impact of the reinforcement ratio is evident when comparing B16(0.88) and B16(1.77). Despite sharing the same reinforcement type, bar size, and compressive strength, the higher reinforcement ratio of B16(1.77) compared to B16(0.88) led to an increase in the punching shear capacity of approximately 37.1%. This underscores the importance of the reinforcement ratio in boosting shear resistance. The decrease in punching shear resistance in basalt-FRP bar-reinforced slabs compared to steel-reinforced slabs is primarily due to three factors, as found in previous research findings [27]. The first factor is the lower dowel action of basalt-FRP bars, leading to a less effective transmission of shear stresses. Furthermore, the decreased modulus of elasticity of basalt-FRP bars leads to a diminished uncracked compression zone, consequently reducing the effective stress transmission area. Lastly, the interaction between basalt-FRP bars and the concrete matrix is less efficient than with steel, potentially leading to premature de-bonding and reduced shear capacity.

The influence of the bar size can be observed in the comparison between B16(0.88) and B12(0.88), both having similar properties except for the bar size. Here, the shift from 16 mm to 12 mm bars for basalt-FRP leads to a slight decrease in the shear capacity of 1.8%, suggesting that a larger bar size offers relatively improved performance for the ultimate capacity. Although this change was minor, it could potentially be attributed to the lower modulus of elasticity associated with the 12 mm basalt-FRP bars, as detailed in Table 4. Additionally, a smaller cross-sectional area might inherently possess a lower load-bearing capacity, affecting the slab’s resistance to punching shear. On the other hand, the specimen B12(0.88) exhibited a higher cracking load and lower cracking deflection as compared to B16(0.88), potentially owing to reduced stress concentrations facilitated by the smaller bar diameter and closer spacing. This indicates the good performance of basalt-FRP 12 mm bar diameter in serviceability conditions. Thus, while the bar diameter had a limited impact on the ultimate capacity of the slabs, it significantly influenced the performance under serviceability conditions.

The variation in compressive strength observed between B12(0.88), B12(0.88)–C35, and B12(0.88)–C25—all reinforced with 12 mm basalt-FRP bars and a ratio of 0.88 but with differing compressive strengths—leads to a range of shear capacities. Lower compressive strength in B12(0.88)–C25 (21.2 MPa), results in a 17.9% reduction in shear capacity compared to B12(0.88) (30 MPa). Conversely, increasing the compressive strength to 35 MPa in B12(0.88)–C35 elevates the shear capacity by 1.9% compared to B12(0.88), illustrating the complex relationship between concrete compressive strength and shear capacity. This can be explained by several mechanical considerations. Higher compressive strength generally leads to a stiffer stress–strain curve, affecting stress distribution around critical shear areas. Enhanced cohesive and adhesive properties within the concrete matrix at higher compressive strengths can result in better bonding with the basalt-FRP bars, indirectly influencing shear capacity. Furthermore, stronger concrete optimizes the effective use of the slab’s effective depth, contributing to enhanced shear resistance. Finally, increased resistance to micro-cracking in stronger concrete can delay shear-related failures [1]. These mechanical aspects offer a foundational understanding of the observed variations in shear capacity with changes in concrete compressive strength.

3.3. Load–Deflection

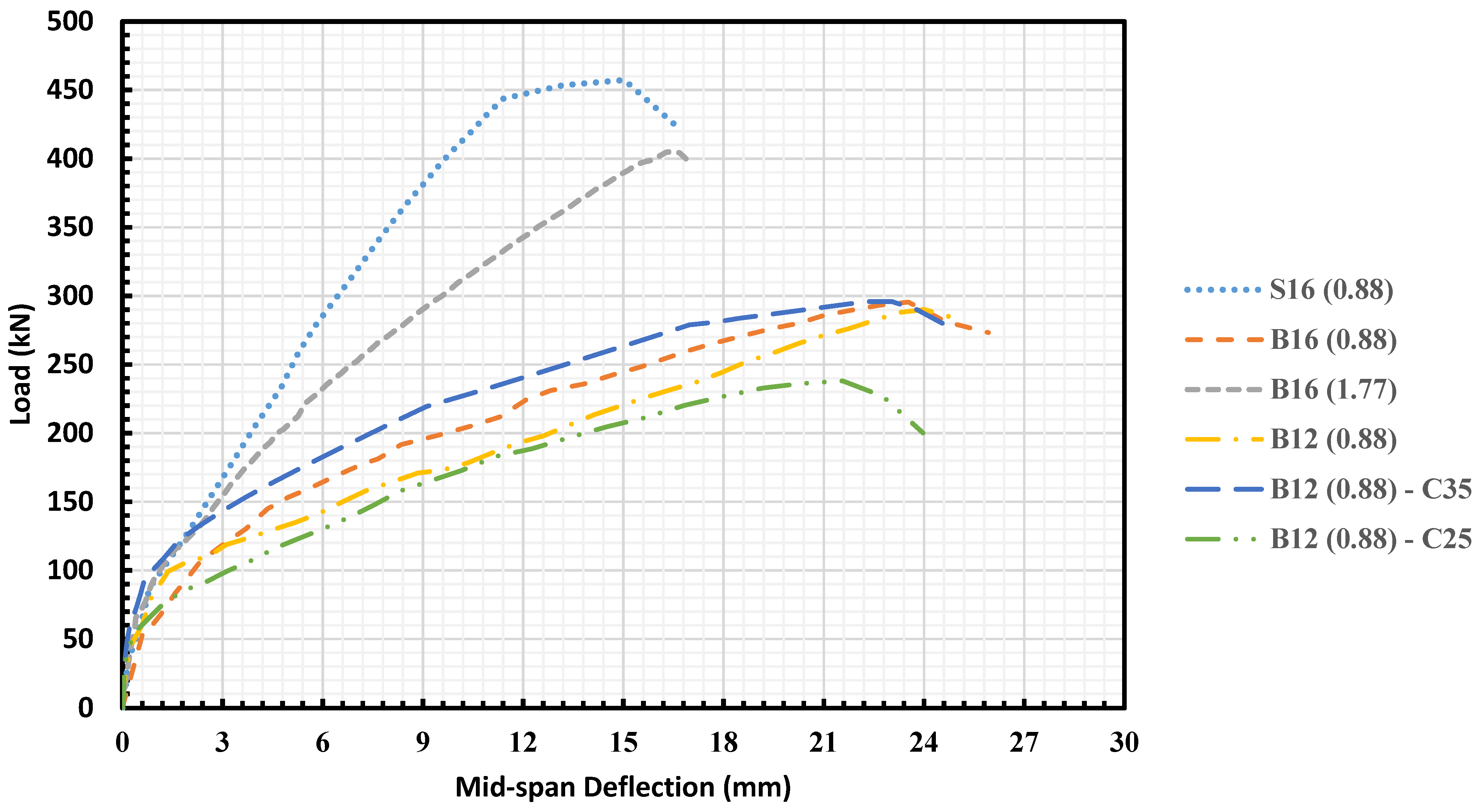
Figure 6 demonstrates the load–deflection curves for the tested specimens measured from an LVDT located at the mid-span of the slabs. Observations from the load–deflection curves reveal that all test samples exhibit a linear and quite comparable behavior during the uncracked stage of loading, also referred to as the initial stiffness ($K_i$), a stage that is uncracked and primarily dependent on the mechanical properties of the concrete material. However, the analysis of post-cracking stiffness ($K_p$) across the tested specimens reveals notable variations arising from different reinforcement configurations, including material type, reinforcement ratio, bar size, and concrete compressive strength. This stage is dependent on the axial stiffness of the type of reinforcement used in the samples.

The load–deflection curves pertaining to steel and basalt-FRP bars show significant differences as the steel-reinforced specimen showed a magnificent increase in its loading capacity up to failure as compared to basalt-FRP bar-reinforced slabs. This is profoundly related to the incomparable stiffness exhibited by steel bars, with $\rho \left(E_f/E_s\right)$ values of 0.88% for S16(0.88) and a mere 0.21% for B16(0.88). Nevertheless, it is evident that increasing the reinforcement ratio for specimen B16(1.77), where $\rho \left(E_f/E_s\right)$ is 0.43%, has a substantial influence on its load–deflection profile and degree of deformation. This highlights the critical role of the modulus of elasticity in determining both the punching shear resistance and the deformability of slabs exposed to punching loads. This observation aligns with findings from [25]. Furthermore, B16(0.88) and B12(0.88), B12(0.88)–C35, and B12(0.88)–C25, which had similar stiffness in terms of axial reinforcement, exhibit a decrease in post-cracking stiffness of approximately 63.3% and 68.3%, 67.8%, and 70.15%, respectively, compared to S16(0.88). In contrast, B16(1.77), demonstrates a substantial increase in post-cracking stiffness of around 50.1%, indicating enhanced stiffness due to the increased reinforcement ratio as compared to B16(0.88). It can be noted that all the slabs reinforced with 12 mm basalt-FRP bars B12(0.88), B12(0.88)–C35, B12(0.88)–C25 showed a reduced post-cracking stiffness as compared to B16(0.88) specimen reinforced with 16 mm basalt-FRP bars of approximately 13.6%, 12.1%, and 18.5%, respectively. Reduced post-cracking stiffness in basalt-FRP-reinforced slabs impacts both stress distribution and crack propagation. A lower stiffness leads to localized shear stresses around the column, making the slab prone to brittle punching shear failure. It also accelerates the rate of crack growth, depleting the structure’s energy-absorbing capacity more rapidly. These observations challenge traditional design assumptions based on ductile failure mechanisms, necessitating the development of material-specific design equations and higher safety factors. In essence, the diminished post-cracking stiffness calls for revised safety and design guidelines to ensure the structural integrity and performance of basalt-FRP-reinforced slabs.

The comparative analysis of deflection in the steel-reinforced slab S16(0.88) and the basalt-FRP-reinforced slabs (B16(0.88), B12(0.88), B12(0.88)–C35, B12(0.88)–C25) does indeed showcase significant differences due to material properties and the reinforcement ratio. The increase in the ultimate deflection in the case of B16(0.88) and B12(0.88) are 25.3% and 24.1%, respectively, compared to S16(0.88). This can indeed be owing to the comparatively lower modulus of elasticity of the basalt-FRP bars. This characteristic effectively diminishes the slab’s moment of inertia of the slabs, leading to greater deflections under identical loads.

The case of B16(1.77) provides a particularly striking illustration of the impact of the reinforcement ratio on the ultimate deflection. Despite being reinforced with basalt-FRP bars, it showed a decrease in ultimate deflection of 25. 3% in comparison to B16(0.88) due to its higher reinforcement ratio of 1.78%. Notably, B16(1.77) had a similar ultimate deflection to the steel-reinforced S16(0.88), even though its reinforcement ratio was twice as high. The specimens B16(0.88), B12(0.88), and B12(0.88)–C35, which have similar reinforcement ratios, underwent identical ultimate deflections. The ultimate deflection of B12(0.88)–C25, which had a lower compressive strength, displayed a higher ultimate deflection of 25.6 mm at the same load level of other specimens. This suggests that a reduction in compressive strength significantly influences the ultimate deflection. Incorporating the practical implications of the load–deflection findings, it is evident that the material type and reinforcement ratio play pivotal roles in determining both the performance and safety in flat slab designs. While steel reinforcement provides superior resistance under a punching load, a higher reinforcement ratio in basalt-FRP-reinforced slabs can offer comparable benefits, offering a broader selection of material choices. Importantly, these differences mandate a design approach that considers not only load-bearing requirements, but also safety factors, thereby aligning theoretical research more closely with field application needs.

3.4. Reinforcement and Concrete Strains

Figure 7 illustrates how the applied axial load relates to the strains measured in both the flexural reinforcement at the midpoint and the concrete near the column on the compression side. Strain measurements were taken at various positions along the specimen spans. Following the initial development of cracks in all specimens, the concrete in the tension side failed, and a rapid escalation in the strain of both the reinforcement and the concrete was noted.

The specimens reinforced with basalt-FRP bars exhibited higher strain levels compared to the control specimen reinforced with steel. This is attributed to the lower elastic modulus inherent in basalt-FRP reinforcement. Specimen S16(0.88) demonstrated the lowest rate of strains in both the reinforcing bars (3421 µε) and the concrete (−627 µε) under identical load conditions. Despite its low strain levels, the observed value of the reinforcement strain was greater than the yield strain, suggesting that the steel bars had reached the yielding stage near the area affected by the punching shear. The maximum strain observed in reinforcing bars is in B16(0.88), which was equivalent to 44% of the ultimate tensile strain characteristic of the basalt-FRP bars. This indicates that the basalt-FRP bars remained intact and did not experience a fracture at the point of punching failure.

As the reinforcement ratio increased in specimen B16(1.77), there was a significant decrease of 53% and 13% in strain values observed in both the flexural reinforcement and concrete, respectively, at the same load level, as compared to B16(0.88). This is attributed to the axial stiffness of the reinforcing bars, which becomes the primary carrier of the tensile stresses. Therefore, the reinforcement ratio plays a crucial role for the post-cracking stiffness of the slabs. Moreover, it is worth noting that the dimensions of the bars had a substantial impact on the strain measurements observed in both the reinforcing bars and the concrete. This can be illustrated by comparing B16(0.88) with B12(0.88). Despite having comparable reinforcement ratios and concrete compressive strengths, the use of smaller-diameter basalt-FRP bars in B12(0.88) leads to diminished strains in the basalt-FRP bars and an increase in concrete strain. This can be attributed to the lessened stress concentration, which is enabled by the reduced bar diameter and closer spacing between the bars.

The compressive strength of concrete had a tremendous impact on the recorded strain measurements. The aforementioned phenomenon was observed in specimens B12(0.88), B12(0.88)–C35, and B12(0.88)–C25, wherein an escalation in the compressive strength of the concrete resulted in a reduction in both the strain experienced by the reinforcing bars and the strain experienced by the concrete itself. Nevertheless, a decrease in the compressive strength of concrete led to a significant rise in the strains experienced by both the basalt-FRP bars and the concrete material.

The maximum concrete strains in all tested specimens remained under the theoretical threshold for concrete crushing, which is 3500 µε. This indicates that the slabs failed due to punching shear, not flexural limitations.

The observed strain behavior in both the reinforcing bars and the concrete yields critical insights into structural integrity and failure mechanisms. Lower strains at increased reinforcement ratios indicate better stress distribution and enhanced structural resistance while higher strains in slabs with a lower basalt-FRP reinforcement ratio and lower concrete compressive strengths suggest compromised integrity and an increased risk of premature failure. These strain correlations are pivotal for calibrating computational failure models and for guiding material selection and reinforcement configurations in structural design. The study thereby emphasizes the need for material-specific design guidelines to optimize both performance and safety.

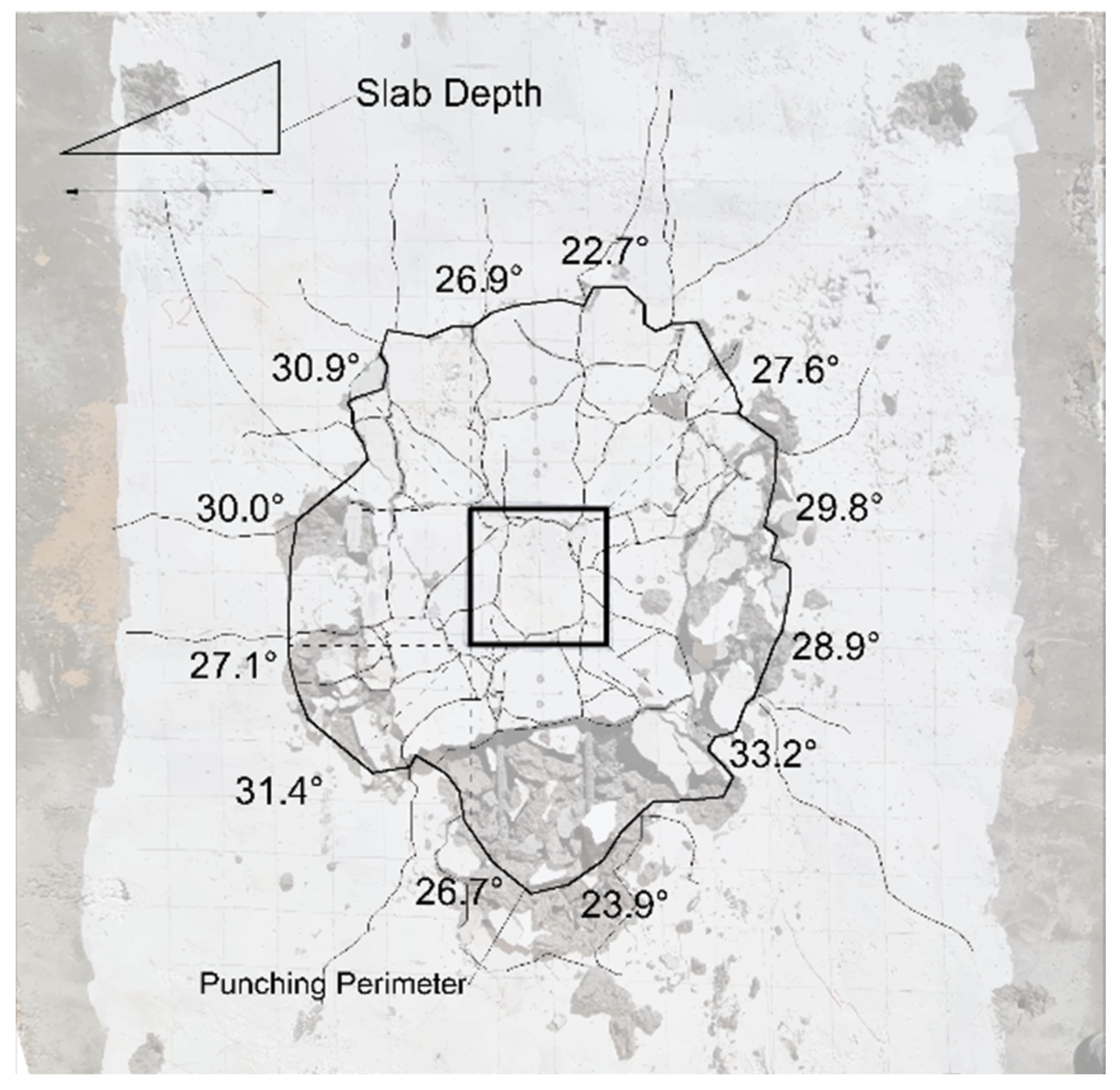
3.5. Punching Cone Angle and Critical Perimeter Distance

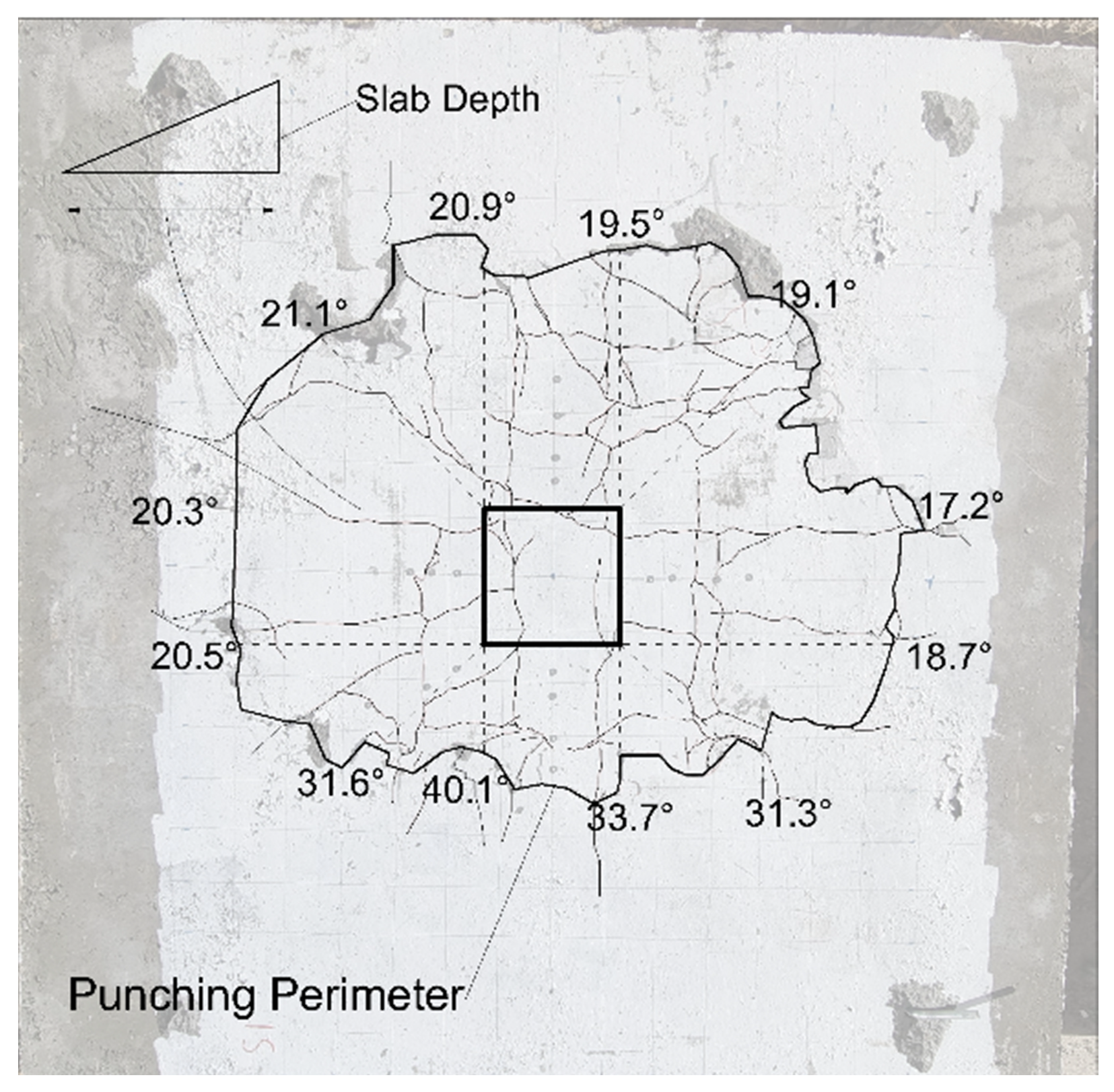
The punching shear surface as well as the calculated punching cone angles for the S16(0.88) and B16(0.88) specimens are shown visually in Figure 8 and Figure 9. The cone angles were measured at the intersection of the punched shear failure line with the vertical, horizontal, and 45-degree directions. The observed punching cone angles are listed in detail in

Table 6. Computed and mean punching cone angles along with the distance of the punching cone from the column’s corners.

Specimen ID	Average Punching Cone Angle	Critical Perimeter Distance
S16(0.88)	$24.5\pm 7.5$	$4.51 \mathrm{d}$
B16(0.88)	$28.3\pm 3.1$	$3.58 \mathrm{d}$
B16(1.77)	$26.7\pm 8.5$	$3.91 \mathrm{d}$
B12(0.88)	$27.2\pm 5.6$	$3.76 \mathrm{d}$
B12(0.88)–C35	$26.9\pm 5.8$	$3.81 \mathrm{d}$
B12(0.88)–C25	$27.2\pm 4.1$	$3.68 \mathrm{d}$

. The specimens exhibit distinct characteristics in terms of their punching shear behavior.

Specimen S16(0.88) displays an average punching cone angle of 24.5 ± 7.5 degrees and a critical punching perimeter distance of 4.51 times the effective depth ($d$). In comparison, specimens of basalt-FRP-reinforced slabs, all reinforced with 16 mm or 12 mm basalt-FRP bars, showcased larger average punching cone angles ranging from 26.7 to 28.3 degrees and smaller critical punching perimeter distances ranging from 3.58d to 3.91d. These specimens generally demonstrate more distributed failure mechanisms, suggesting a broader distribution of shear forces as compared to S16(0.88). Notably, B16(1.77) with a higher reinforcement ratio of 1.77 compared to B16(0.88) exhibits a relatively lower average punching cone angle and higher average critical shear perimeter, indicating better control of shear forces. In addition to that, the basalt-FRP-reinforced slabs with 12 mm bar size exhibited greater critical punching perimeter in comparison to B16(0.88), which have similar reinforcement ratio. This can be owing to the lower spacing of basalt-FRP specimens reinforced with 12 mm bars. Moreover, increasing the compressive strength of concrete showed a relative increase in critical punching perimeter and lower punching cone angles. The reason for this phenomenon may be attributed to the enhanced ductile characteristics observed in the samples fabricated using a higher concrete compressive strength. The results are consistent with the experimental program carried out by Hassan et al. [28].

The analysis on punching cone angles and critical perimeter distances reveals significant variations based on reinforcement type and ratio, bar size, and concrete compressive strength. Steel-reinforced slabs exhibited lower punching cone angles and longer critical perimeter distance of 4.51d, indicating a broader shear force distribution. Conversely, basalt-FRP-reinforced slabs presented higher punching cone angles and shorter critical distances of 3.75 d on average, suggesting a localized distribution of shear forces. Given that the critical location for the design coincides with the intersection point of the primary diagonal shear crack at the center depth of the slab, the results indicate that for steel-reinforced slabs, the critical section is situated at a distance of 2.25 times the slab’s effective depth from the column face. In the case of basalt-FRP-reinforced slabs, the critical section is positioned at a distance of 1.87 times the slab’s effective depth from the column face. These findings are pivotal for optimizing design models and guide material selection for enhanced structural safety against punching shear.

3.6. Predictions from the Existing Codes of Practice

Table 7. Existing design guidelines and models from the literature.

Design Models	Punching Shear Strength (MPa)	Remarks
ACI 440.1R-15 [17]	$v_c=\frac{4}{5}\sqrt{f_c^{\mathrm{\prime }}} \left(k\right)$ $k=\sqrt{2{\rho }_F{n}_F+{\left({\rho }_F{n}_F\right)}^2}-{\rho }_F{n}_F$ $n_F=\frac{E_f}{E_c}$	$b_{°} is at 0.5d$
CSA/S806-12 [18]	$v_c=\left(1+\frac{2}{{\beta }_c}\right)0.028\lambda {\varphi }_c{\left(E_F{\rho }_F{f}_c^{\mathrm{\prime }}\right)}^{1/3}$ $v_c=\left[\left(\frac{{\alpha }_{s}d}{b_{°,0.5d}}+0.19\right)\right]0.14\lambda {\varphi }_c{\left(E_F{\rho }_F{f}_c^{\mathrm{\prime }}\right)}^{1/3}$ $v_c=0.56\lambda {\varphi }_c{\left(E_F{\rho }_F{f}_c^{\mathrm{\prime }}\right)}^{1/3}$	$b_{°} is at 0.5d$
JSCE, 1997 [19]	$v_c={\beta }_d{\beta }_p{\beta }_r\frac{f_{pcd}}{{\gamma }_b}x\frac{1}{\alpha }$ ${\beta }_d=\sqrt[4]{1/d}\le 1.5$ ${\beta }_p=\sqrt[3]{100{\rho }_F{E}_f/E_s}\le 1.5$ ${\beta }_{r}1+[1/(1+0.25u/d)]$ $f_{pcd}=0.2\sqrt{f_c^{\mathrm{\prime }}}\le 1.2MPa$ $\alpha =1+1.5\left[\left(e_x+e_y\right)+\sqrt{b_x{b}_y}\right]$	$b_{°} is at 0.5d$
Matthys and Taerwe 2000 [5]	$v_c={\left(100{\rho }_F\frac{E_F}{E_s}{f}_c^{\mathrm{\prime }}\right)}^{1/3}x\frac{1.36}{d^{0.25}}$	$b_{°} is at 1.5d$
Ospina et al., 2003 [29]	$v_c=2.77{\left({\rho }_F{f}_c^{\mathrm{\prime }}\right)}^{1/3}x\sqrt{\frac{E_F}{E_s}}$	$b_{°} is at 1.5d$
El-Ghandour et al.,2003 [25]	$v_c=0.33\sqrt{f_c^{\mathrm{\prime }}}{\left(\frac{E_F}{E_s}\right)}^{1/3}$	$b_{°} is at 0.5d$
El-Gamal et al., 2005 [8]	$v_c=0.33\sqrt{f_c^{\mathrm{\prime }}}\alpha {\left(1.2\right)}^N$ $\alpha =0.62\sqrt[3]{{\rho }_F{E}_f}(1+\frac{8d}{b_{°}})$	$b_{°} is at 0.5d$ $N is the continuity$ $effect of the slab$

demonstrates the most common guidelines and models available in the design standards and the literature. The equations consider a whole range of parameters that have significant importance on the capacity of FRP-reinforced slabs in punching shear.

Table 8. Test to predict ultimate punching shear capacity ($V_{test}/V_{predicted})$.

			${\mathit{V}}_{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}/{\mathit{V}}_{\mathit{p}\mathit{r}\mathit{e}\mathit{d}\mathit{i}\mathit{c}\mathit{t}\mathit{e}\mathit{d}}$
Specimen ID	${\mathit{V}}_{\mathit{t}\mathit{e}\mathit{s}\mathit{t}}\left(\mathbf{k}\mathbf{N}\right)$	[17] ACI 440.IR, 2015	[18] (CSA, 2012)	[19] (JSCE,1997)	[5] (Matthys and Taerwe, 2000)	[29] (Opsina et al., 2003)	[25] (Ghandour et al., 2003)	[8] (El-Gamal et al., 2005)	Proposed Model
B16(0.88)	295.5	1.97	1.10	1.11	1.14	0.97	1.28	1.01	1.02
B16(1.77)	405.2	1.99	1.20	1.20	1.24	1.05	1.75	1.09	1.11
B12(0.88)	290.1	1.89	1.05	1.05	1.09	0.92	1.21	0.95	0.96
B12(0.88)–C35	295.8	1.85	1.02	0.99	1.06	0.89	1.15	0.90	0.91
B12(0.88)–C25	238.1	1.64	0.92	0.96	0.96	0.81	1.10	0.93	0.94
Mean		1.88	1.06	1.07	1.12	0.96	1.34	0.98	0.99
S.D		0.114	0.087	0.082	0.093	0.082	0.254	0.076	0.078

offers the ratio of experimentally measured punching capacities to the ones predicted using the provided codes and some existing equations from the literature. In this context, the reliability of current punching shear formulas is assessed by comparing their predicted results with the punching shear capacity determined through experimental testing.

Drawing upon the predicted values, it can be observed that all the employed equations consistently deliver trustworthy and prudent predictions. A deviation from this pattern is embodied in [17], which yields a ratio of 1.88 on average, and it is highly conservative, representing a deviation from this pattern. This could be attributed to the equation’s novel method of determining the neutral axis position solely through the utilization of the reinforcement ratio. This is emphasized in the study by Hassan et al. [28]. Moreover, it implies that shear forces are primarily countered by uncracked concrete, without considering the contributions of aggregate interlock and dowel action [30]. Another conservative equation is the one presented in [25], which resulted in a ratio of 1.34. This is owing to the influence of the reinforcement omitted from the equation. On the other hand, the models proposed in [5,18,19] and Ref. [29] produced consistent and conservative predictions for all the samples with a ratio of 1.06, 1.07, and 1.12 and 0.96, respectively, on average. These equations incorporate the axial rigidity inherent in the reinforcement as well as the effect of the dimensions, resulting in presumably greater precision. With a ratio of 0.98 on average and a standard deviation of 0.076, the equation from El-Gamal et al. [8], which is the modified version of the ACI318 equation, demonstrated highly satisfactory and accurate results in comparison to other models. This model relatively incorporates all the relevant factors that affect the capacity of flat slabs to withstand punching failure.

3.7. Proposed Model

The model introduced by El-Gamal et al. [8] has proven to be highly accurate when compared to other guidelines. A minor amendment to this model can make its mean value approach unity even more closely. This involves replacing the existing constant of 0.33 in the formula with 0.326 based on a trial and error approach. As a result, the modified equation is as follows:

$$v_c=0.326 \sqrt{f_c^{\prime }} \alpha {\left(1.2\right)}^N$$

This newly suggested equation, as depicted in Table 8, provides highly precise and dependable predictions with a mean value of 0.99 and a standard deviation of 0.078. The El-Gamal model for predicting the punching shear capacity in flat slabs is highly commendable for several key reasons. Its empirical validation and comprehensive inclusion of significant variables, such as the reinforcement ratio and modulus of elasticity of an FRP bar and the continuity effect (N), make it broadly applicable and reliable. The statistical robustness, indicated by a mean value close to unity and a low standard deviation, enhances its precision and unbiased nature. The model’s formula is straightforward and user-friendly, allowing for ease of computation even in less resource-intensive settings. Furthermore, its amendable nature—evidenced by the improvement achieved through a minor constant adjustment—demonstrates adaptability and a potential for future fine-tuning. Collectively, these factors, along with its strong theoretical foundation and academic validation, make the El-Gamal model a reliable and invaluable tool for both research and practical applications in structural engineering.

4. Conclusions

In conclusion, this study’s experimental results help enhance our understanding of the behavior of slab–column connections under punching shear in both steel-reinforced and basalt-FRP-reinforced concrete slabs. The observations from the conducted experiments reveal distinct failure modes, crack propagation patterns, and strain characteristics for the slabs under scrutiny. Significant findings include the following:

• All the slabs experienced punching shear failure, displaying radial and tangential cracks that appeared when the failure load reached approximately 40 to 55% of the maximum load.
• It was observed that steel-reinforced slabs demonstrated delayed crack initiation compared to those reinforced with basalt-FRP bars.
• The ultimate load-carrying capacity and the observed reinforcement and concrete strain and slabs’ mid-span deflection are significantly influenced by the reinforcement material, reinforcement ratio, bar size, and concrete compressive strength.
• The test results showed that introducing basalt-FRP bars with one-quarter equivalent axial stiffness ($\mathsf{\rho }\left({\mathrm{E}}_{\mathrm{f}}/{\mathrm{E}}_{\mathrm{s}}\right)$) to that of steel had a significant and positive influence on enhancing the punching shear capacity of two-way flat slabs, achieving roughly 65% of the capacity observed in the steel-reinforced sample. Furthermore, increasing the quantity of basalt-FRP bar reinforcement to half the equivalent axial stiffness of steel had a substantial impact on improving shear strength, reaching approximately 89% of the capacity seen in steel-reinforced sample while also reducing deflection during the failure. This study highlights the idea that the use of basalt-FRP bars as reinforcement can indeed yield positive results, offering a viable alternative to be used in slabs against punching shear failure.
• Lower elastic modulus in basalt-FRP bars resulted in higher strain values. The strain was reduced by 53% in flexural reinforcement and 13% in concrete when the reinforcement ratio was increased to 1.77%.
• Basalt-FRP-reinforced slab with higher reinforcement ratio (1.77%) showed an approximately 37.1% increase in the punching shear capacity compared to those with lower ratios (0.88%). Moreover, lower reinforcement ratios led to more distributed crack patterns, revealing a crucial role of the reinforcement ratio in controlling failure characteristics.
• A decrease in compressive strength of approximately 8.8 MPa led to a 17.9% reduction in shear capacity. However, higher compressive strength led to better bonding with the basalt-FRP bars and a stiffer stress–strain curve, contributing to enhanced shear resistance.
• The study highlights significant discrepancies among existing models for predicting punching shear capacity in flat slabs reinforced with FRP bars. Some models prove conservative due to unique methodologies or omissions (ACI 440.1R [17] and El-Ghandour et al. [25]) while others offer more consistent and comprehensive approaches (CSA [18], JSCE [19], Matthys and Taerwe [5], and Ospina et al. [29]). These differences call for further research and potential revisions to ensure precise structural engineering designs.
• The findings also highlight that a reduction in the compressive strength significantly influences the ultimate deflection of the slabs. This insight can inform the design and use of concrete structures in scenarios where significant deflection could cause operational issues or risk to structural integrity.
• Steel-reinforced slabs displayed lower punching cone angles (24.5 ± 7.5 degrees) and longer critical perimeter distances (4.51d), in contrast to basalt-FRP-reinforced slabs that showed higher angles (ranging from 26.7 to 28.3 degrees) and shorter distances (ranging from 3.58d to 3.91d). This suggests that steel-reinforced slab had broad stress distribution and basalt-FRP-reinforced slabs exhibited localized shear force concentration.
• Existing design guidelines and the literature models were used to predict the ultimate punching shear capacity. The predictions were compared with the experimental results, with some guidelines providing more accurate predictions than others. The model proposed by El-Gamal et al. [8] was found to be the most accurate, with a minor amendment proposed for even better accuracy. The El-Gamal model stands out for its empirical accuracy, comprehensive variable inclusion, and statistical robustness, making it both precise and reliable. Its straightforward formula allows for easy computation while its adaptability is shown by improvements through minor constant adjustments.
• The research provides practical insights into using basalt-FRP bars as a sustainable, durable alternative to steel in flat slabs. Its findings could influence material selection, update design codes, and inspire new construction techniques, making it highly relevant for real-world engineering and construction.
• The study faces limitations, including insufficient lab equipment for larger samples; challenges in sourcing costly basalt-FRP bars from abroad; a lack of tools for diverse loading conditions, such as cyclic loading; and time constraints that narrow the focus to short-term material behavior. These factors limited the study’s scope and generalizability.
• The conclusions of this study are derived from a limited number of specimens and therefore should be interpreted as preliminary insights into the punching shear capacity of flat slabs reinforced with basalt-FRP bars. Further research involving a more extensive range of specimens is essential to validate and expand upon these findings, enhancing their applicability in engineering practices and structural design.