1. Introduction
A holistic assessment of the sustainable development of infrastructure necessitates the consideration of different aspects, ranging from environmental to economic factors. In fact, Goal 9 of the 2030 Agenda for Sustainable Development of the United Nations [
1], emphasizes the need for ‘quality, reliable, sustainable’ infrastructure. Additionally, it discusses ‘affordable and equitable access’ to such infrastructure via the enhancement of related scientific research. It is fairly well established that human beings have been using lime-mortared brick masonry for centuries, across the world, dating back to ancient Rome and Greece [
2]. This makes masonry constructions a very commonly used, and, therefore, accessible, form of infrastructure. While different binders may be used in mortars, two of the most commonly used binding materials are lime and cement, which are often mixed together to obtain optimal performance [
3].
From the viewpoint of environmental impact, lime-based construction materials as well as a few other binders have been fairly well researched, typically via life cycle assessments (LCA) [
4,
5,
6,
7,
8]. LCA assesses sustainability through CO
2 emissions and the footprint of materials from their extraction to manufacturing, use in construction, and disposal. This also includes aspects related to the higher reutilization and recycling rates of lime-based construction materials, which can lead to decreased environmental pollution due to the otherwise necessary disposal of wastes. Yet, another important aspect affecting sustainability is serviceability behavior, durability, and reliability. Balanced decisions regarding the sustainability of construction materials can only be taken if their impact on mechanical performance at a structural level is well understood, which ultimately contributes to better serviceability behavior. In turn, improved serviceability behavior results in longer structural life cycles, and thus lower demand for natural materials and resources, thus contributing toward sustainability.
The focus of this research article, therefore, is on the mechanical performance of unreinforced brick masonry as a function of the type of mortar used in it, especially focusing on the presence of lime. The reason for this is that while lime/cement-mortared masonry is easily accessible and used across different geographical regions of the world, and there are existing studies that have focused on the environmental assessment of such materials [
4,
5,
6,
7,
8], there is still limited research that studies the effects of lime at the masonry level. As illustrated in the following text, most research has focused on the impacts at the mortar level.
One of the most significant aspects of mechanical performance is compressive strength. Masonry compressive strength depends on aspects such as the type of adopted unit, the stiffness of the mortar, and the unit–mortar bond [
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. Despite the fact that the strength of masonry is a result of the combination of the strength of the unit and of the mortar, the unit typically has a greater impact on the strength of the masonry. A study by Lima et al. [
21] indicates that in 10 mm and 15 mm thick mortar joints, a 150% increase in the strength of the mortar resulted in a 16% and 36% increase in masonry strength, respectively. Research conducted on concrete masonry prisms (both filled and unfilled ones), showed an increase of 35% in compressive strength stemming from a 250% increase in mortar strength [
22]. In another study, increasing the compressive strength of mortar in unfilled prisms by approximately 72% resulted in an increase of no more than 20% in the strength of the masonry [
23]. This means that the relationship between the strength of mortar and the strength of masonry is not linearly proportional, and the use of increasingly stronger mortars may not be effective in increasing the strength of masonry [
24,
25].
Notwithstanding the fact that mortar may not be the major contributor to the strength of masonry, it is an essential factor in determining its environmental impact [
26,
27,
28], deformation properties, as well as non-linear behavior [
29,
30,
31,
32]. Environmentally, lime tends to outperform cement in several areas, some of the most noteworthy being human health and ecosystem quality. In addition, the recycling potential of lime is, to some extent, superior to that of cement, as the former is biodegradable and fully recyclable [
23]. From the point of view of mechanical performance, especially focusing on deformation properties and non-linear behavior, it is also well established that an increase in the quantity of lime in the binder of a lime–cement mortar contributes to a lower value of mortar strength. With a reduction in mortar strength, the stress–strain behavior of masonry becomes significantly more non-linear [
24]. Yet, considerable experimental data on its E-modulus assume that masonry behaves linearly up to 33–50% of its maximum compressive strength [
22,
24]. Limited studies have been conducted to evaluate the E-modulus of masonry through cyclic compressive loading. Since data from cyclic loading tests are not accessible for determining its E-modulus, the correlation of compressive strength with the secant E-modulus of masonry is most commonly used to gauge its stiffness [
25]. Various global standards permit this, including the International Building Code (IBC) and Eurocode 6, both of which recommend the evaluation of Young’s modulus to be at least 700 to 1000 times higher than the compressive strength, respectively [
33,
34]. Other sources have reported considerable differences in these values, which can be anywhere between 80 and 1700 times the compressive strength [
25,
35,
36]. The structural weakness of unreinforced masonry in the face of out-of-plane loads is a well-established issue, particularly during earthquakes [
37,
38,
39]. Masonry’s low tensile strength has been known to be the main contributor to this vulnerability [
40,
41,
42]. Masonry is more resilient when subjected to bending forces perpendicular to the bed joints, as opposed to parallel to them. In the former case, the bond strength of head joints and the friction between them determine the resistance to compressive forces, while only the bond strength of bed joints contributes to resistance in the latter instance, as reported in [
42]. Eurocode 6 [
33] advises the use of the strength of mortar and the type of unit as indications to determine the values of characteristic flexural strength. Alternatively, experimental values stemming from four-point bending tests can also be employed [
43]. Researchers have been investigating how various types, combinations, and reinforcements of mortar and masonry units can impact flexural strength [
44,
45,
46,
47,
48,
49]. This includes cement composites and FRP laminates. Nevertheless, the authors are not aware of any studies looking into the effect that the lime content in mortar has on the flexural strength and other characteristics of masonry [
29,
43].
In addition, the shear bond strength between masonry materials is a crucial parameter and has been examined by various researchers [
10,
50]. To evaluate its value, an experiment was conducted utilizing couplet or triplet specimens, with the latter being more prevalent among them [
51,
52,
53]. Research has also been conducted to analyze the effect that pre-compression has on peak shear stress for brick masonry (wire-cut clay) and various cement mortars ranging from 10 to 30 MPa [
54]. Experiments were performed to measure the shear strength of a variety of lime–cement mortar and concrete blocks [
55]. The primary aim was to compare the relative strength of the mortar and unit. It was demonstrated that the strength of the mortar and the unit both contributed to improved cohesion as the amount of cement in the binder was increased. A different study corroborated the findings by analyzing lime–cement mortars with varying compositions (1:2:9, 1:1:6, and 4:1:12 cement:lime:sand) on different units, including molded clay brick, extruded clay brick, and concrete blocks in triplet specimens. The study concluded that the higher the cement content in the binder, the higher the shear strength across all kinds of units [
56]. However, no research has been conducted on the coefficient of friction with pre-compression applied, denoting a gap in current knowledge. The shear strength and coefficient of friction values recorded for lime–cement mortars were in the ranges of 0.07 to 1 MPa and 0.80 to 0.92 MPa, respectively [
55,
56]. Additionally, the initial shear strength of lime-based mortars varied from 0.15 to 0.43 MPa [
57].
This article examines the outcomes of experiments conducted on masonry specimens built with solid (frogged) molded clay bricks and three different mortar mixes (with 1:0:5, 1:1:6, and 1:2:9 as the volume ratios of cement:lime:sand). Specific attention was paid in this experimental campaign to pick mortar mix proportions that are already commonly used in the field by consulting with industry experts. A professional mason was hired to construct the masonry specimens as further illustrated in this article to ensure that the masonry was constructed in alignment with field practices, using workable mortars so that the conclusions of this research would be of practical value. An extensive and thorough experimental campaign was conducted to ensure repeatability. The properties of the masonry studied include compressive strength, flexural strength (parallel and normal to bed joints), the E-modulus via cyclic compression, and shear bond strength, including the parameters of cohesion and internal friction. All of these aspects when accounted for in totality directly align with Goal 11 of the 2030 Agenda for Sustainable Development of the United Nations, which focuses on ‘strengthening efforts to safeguard the world’s heritage’, as well as ‘building sustainable and resilient buildings utilizing local materials’.
3. Experimental Setup
The compressive strength of the masonry was evaluated in accordance with the guidelines specified in EN 1052-1 [
80]. Specimens for the experiment consisted of a single leaf of bricks, with a height of 450 mm (6 rows of bricks) and a width of 440 mm (2 bricks per row), as illustrated in
Figure 1. In order to evaluate the effectiveness of the specimens, they were allowed to cure for 90 days prior to testing. A hydraulic actuator with a load capacity of 1000 kN was utilized, resorting to the displacement control technique at a speed of 3 µm/s. To assess deformation in the specimens, four LVDTs were used in total. These were situated on the wider faces of each sample (2 at the front and 2 at the back), as illustrated in
Figure 1. The final compressive strength was determined by testing 3 masonry specimens for each type of mortar. Before testing, one masonry specimen for each mortar type was tested to confirm conditions such as the capacity of the actuator, the testing speed, and the value of cyclic loads to be applied to the specimens for E-modulus measurements. These specimens were not taken into account for the calculation of results.
With regard to flexural strength, the masonry specimens were tested in both directions (‘parallel’, referring to parallel to the bed joints, and ‘perpendicular’, referring to perpendicular to the bed joints) according to the recommendations of EN 1052-2 [
43] (
Figure 2). To conduct the tests, a 300 kN hydraulic actuator was used with displacement control at a rate of 3 µm/s. In both parallel and perpendicular cases, 2 LVDTs set up on either side of each specimen were used to measure the out-of-plane deformation. In the case of the parallel layout, the single-leaf specimens had 9 courses of bricks, with 2 bricks in each course. The size of each sample was measured as 670 mm in height and 440 mm in width (refer to
Figure 2). EN 1052-2 [
43] outlines the recommended dimensions of the length of a specimen in the direction of the span (l
s), the spacing between supports (l
1), and the distance between inner bearings (l
2) for the proper application of a load. The values adopted for this case were l
s = 670 mm, l
1 = 570 mm, and l
2 = 290 mm. For the perpendicular case, while the specimens were also single-leaf specimens, they featured 6 courses of bricks, with 4 bricks in each course. The dimensions of each sample were 890 mm in height and 440 mm in width (
Figure 2). In this case, l
s corresponded to 890 mm, while l
1 and l
2 were 790 mm and 380 mm, respectively.
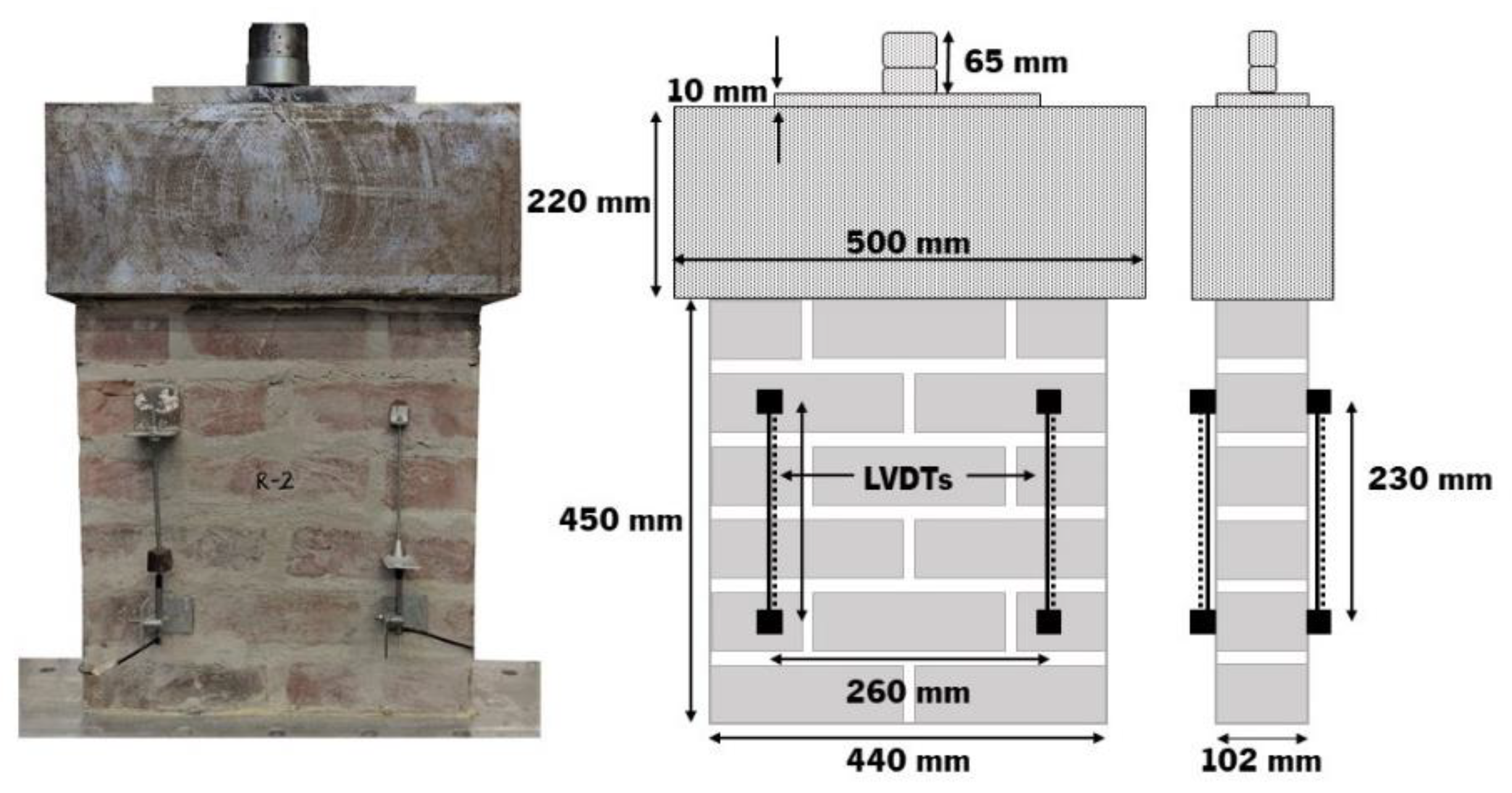
The shear bond strength of the samples was assessed per the guidelines of EN 1052-3 [
81]. Nine masonry specimens (triplets) were tested for each type of mortar, resulting in a total of twenty-seven specimens evaluated (
Figure 3). For each mortar, three specimens were tested for three levels of perpendicular pre-compression: 0.2 MPa, 0.6 MPa, and 1 MPa. A manually operated hydraulic pump was used, with a capacity of 100 kN to maintain a steady pre-compressive load. This load had an average maximum variation of ≤0.9 kN across the different tests. To apply the shearing load, an additional actuator with a 200 kN force and a sampling rate of 4 Hz was employed. This actuator was capable of providing the desired displacement control at 3 µm/s. Two LVDTs were positioned on either side of the specimen (front and back) so as to measure the amount of movement between the bricks and mortar joints (as seen in
Figure 3). This enabled the accurate measurement of the relative slip between bricks.
5. Conclusions
In the context of sustainability, while lime is often compared with cement and other binders through the lens of environmental impact, from a reliability/serviceability behavior standpoint, the impact of varying their ratio is often studied only at the mortar level. This study, however, primarily focused on their ratio’s impact on important mechanical properties at the masonry level. The influence of varying the lime–cement ratio on properties such as the cohesion, angles of internal friction, flexural strength, and E-modulus of masonry was assessed in a single, consistent experimental campaign, with an emphasis on the repeatability of the experiments and the use of mixes that are commonly used in the industry. The experimental results were also compared with the predictions/recommendations of Eurocode 6.
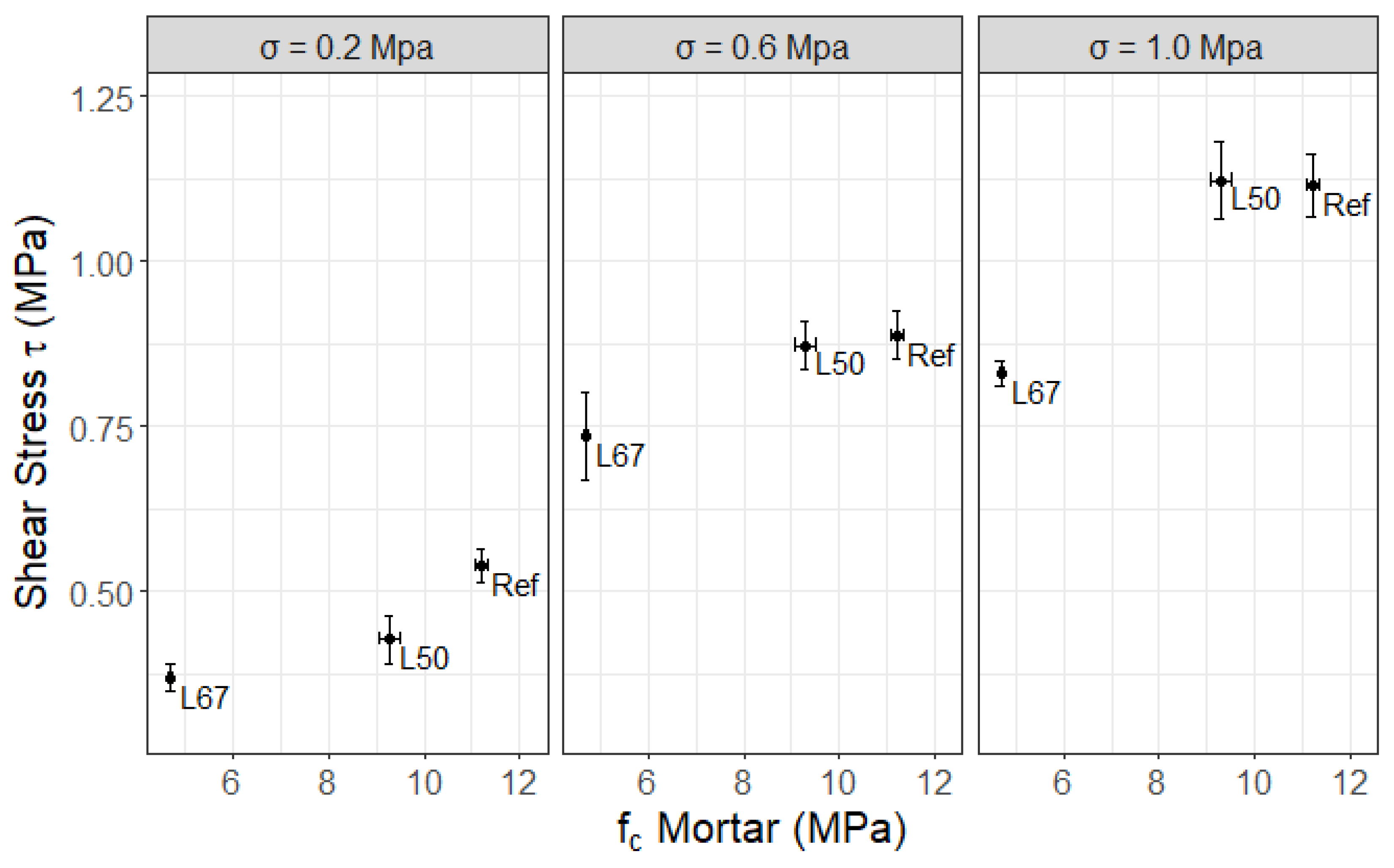
The results show that the effect of lime in the mortar on the mechanical properties of the masonry was not prominently evident. Three mortar mixes were tested in the experiments: L67 (1:2:9), L50 (1:1:6), and Ref (1:0:5).
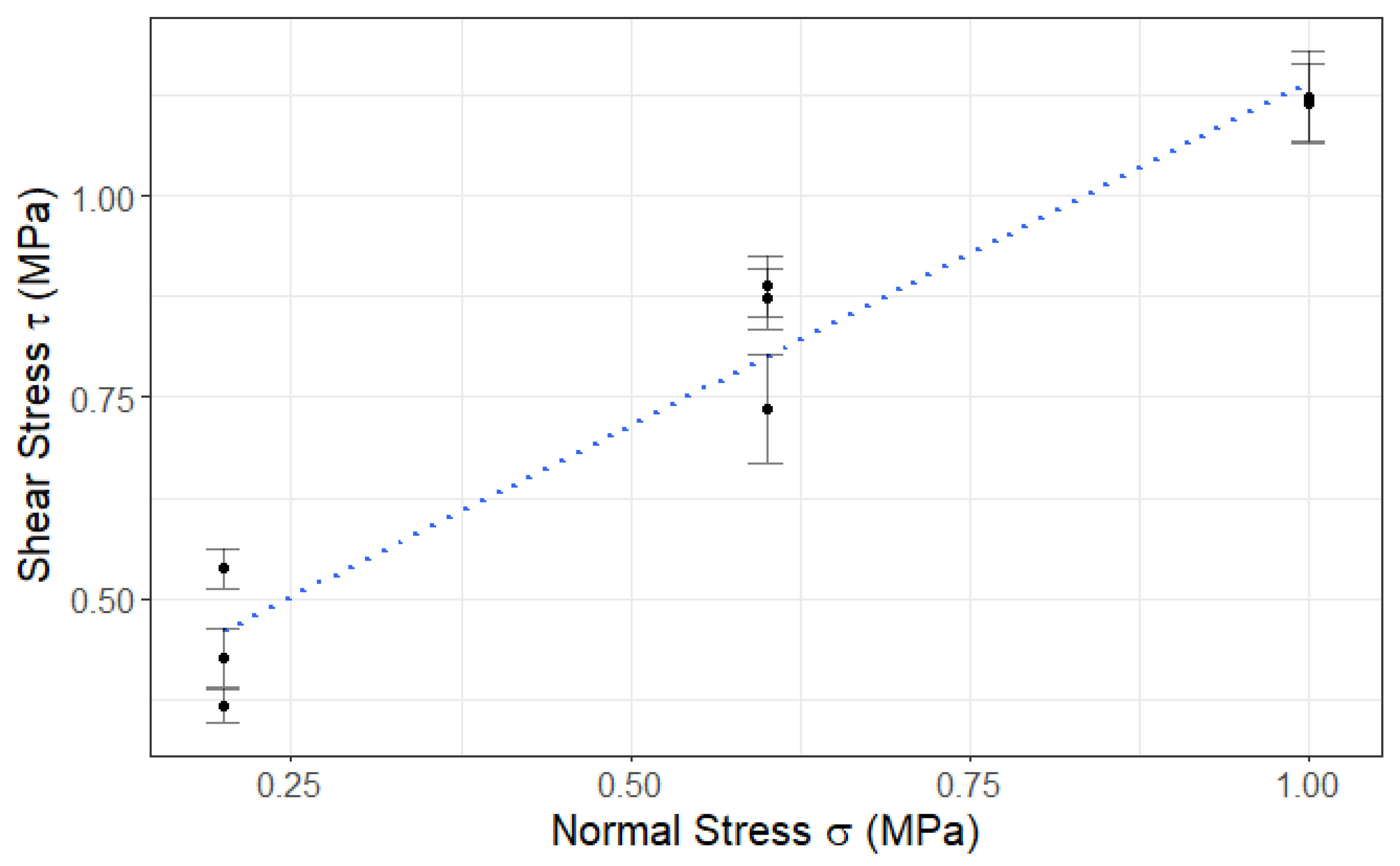
Increasing the quantity of lime in the binder led to a minor decrease in the compressive strength and E-modulus of the masonry. However, it resulted in a minor increase in the vertical deformation capacity of the masonry at peak load. The compressive strength of the masonry for all three mortars was found to range from 6.0 to 7.2 MPa, and the E-moduli ranged from 3.8 to 4.5 GPa. Furthermore, it was found that Eurocode 6 significantly overestimated (50–70%) the values of compressive strength. The flexural strength of the masonry was found to range from 0.1 to 1.2 MPa and was impacted by the strength of the mortar, rather than the presence of lime in the mortar. Among the mortar mixes tested, L67 had the lowest strength at the mortar level and led to the lowest values of masonry flexural strength in both parallel and perpendicular directions. L50 and Ref, both of which had similar mortar strengths, seemed to result in almost identical values as far as the flexural strength of the masonry was concerned. All of the obtained experimental values were higher than those in the guidelines of Eurocode 6, with one exception: L67 in the parallel direction had a characteristic value that was lower than 0.1 MPa. Finally, the strength of the mortar also had a direct impact on the coefficient of friction (0.58–0.87) of the masonry. It was not possible to discern a pattern that related mortar strength with cohesion (0.29–0.41 MPa). The data indicated that all measured cohesion values were higher than the values recommended by Eurocode 6.
The authors would like to acknowledge the need for testing more mixes prior to the generalization of the results. Furthermore, more units need to be tested in combination with the mixes tested herein to better understand the impact of the type of unit on the masonry, as well as the interaction of lime–cement mortars with different units such as stone and CMU blocks, specifically for shear bond strength. The authors hope that the results of the current research regarding the impact of lime on the mechanical performance of masonry will add to a more holistic understanding of sustainable constructions and the sustainable development of infrastructure and the preservation of the world’s heritage, as outlined in the 2030 Agenda for Sustainable Development by the UN.