Data-Driven-Based Eco Approach for Connected and Automated Articulated Trucks in the Space Domain
Abstract
1. Introduction
- Is able to overtake slow-moving vehicles in order to achieve sustainability and mobility.
- Is Able to efficiently optimize the travel duration approaching a signalized intersection.
- Achieves the trade-off between fuel saving and vehicle mobility.
- Improved computational efficiency and optimality for the articulated truck control.
2. Research Scope
- No more waiting for the slow-moving vehicle: The proposed eco approach controller can enable the CAV truck to automatically overtake the slow-moving vehicles when they impede the normal operation of the ego truck. The lane-changing and overtaking maneuvers reduce the chance of being obstructed and provides the opportunity for the ego truck to further improve fuel saving and mobility. It also enables the passengers on board to have a more comfortable experience.
- Highly efficient and optimal control for the articulated truck: One feature of the research is to solve the computational efficiency and optimality challenge that the nonlinear dynamic model adds to the control of the articulated truck. The research utilized data-driven-based Koopman operator theory to globally linearize the dynamic model of the articulated truck. The linearized dynamic model can support the highly efficient receding horizon control while ensuring the accuracy of the original model.
- Ecological but not slow: The proposed controller has the ability to balance fuel saving and travel speed. The controller is designed to optimize travel time together with fuel cost. Weights are ascribed to both optimized objectives. Therefore, the amount of mobility sacrificed to save fuel can be adjusted according to the user’s preference.
- Module 1: As indicated in Figure 1, the controlled area is defined as the communication range of roadside units. In this area, the information of signal timing and traffic conditions is collected by the roadside units and transmitted to the ego truck through vehicle-to-infrastructure (V2I) communication. The proposed eco approach system requires to be equipped with the following devices: (i) onboard GPS; (ii) on-board communication device; (iii) communication devices traffic lights; and (iv) roadside units supporting perception and V2I communication.
- Module 2: This module is activated when the central controller detects that the ego truck has just entered the controlled area. The state of the ego truck and the information collected in Module 1 are fed to the controller. Then, combining the stored dynamic model and the input information, the controller can optimize the travel duration and the vehicle trajectory for the improvement of sustainability and mobility.
- Module 3: The optimal trajectory generated from Module 2 is transmitted to the CAD truck as the control commands. Then, the CAV truck receives commands and adjusts its states accordingly.
3. Problem Formulation
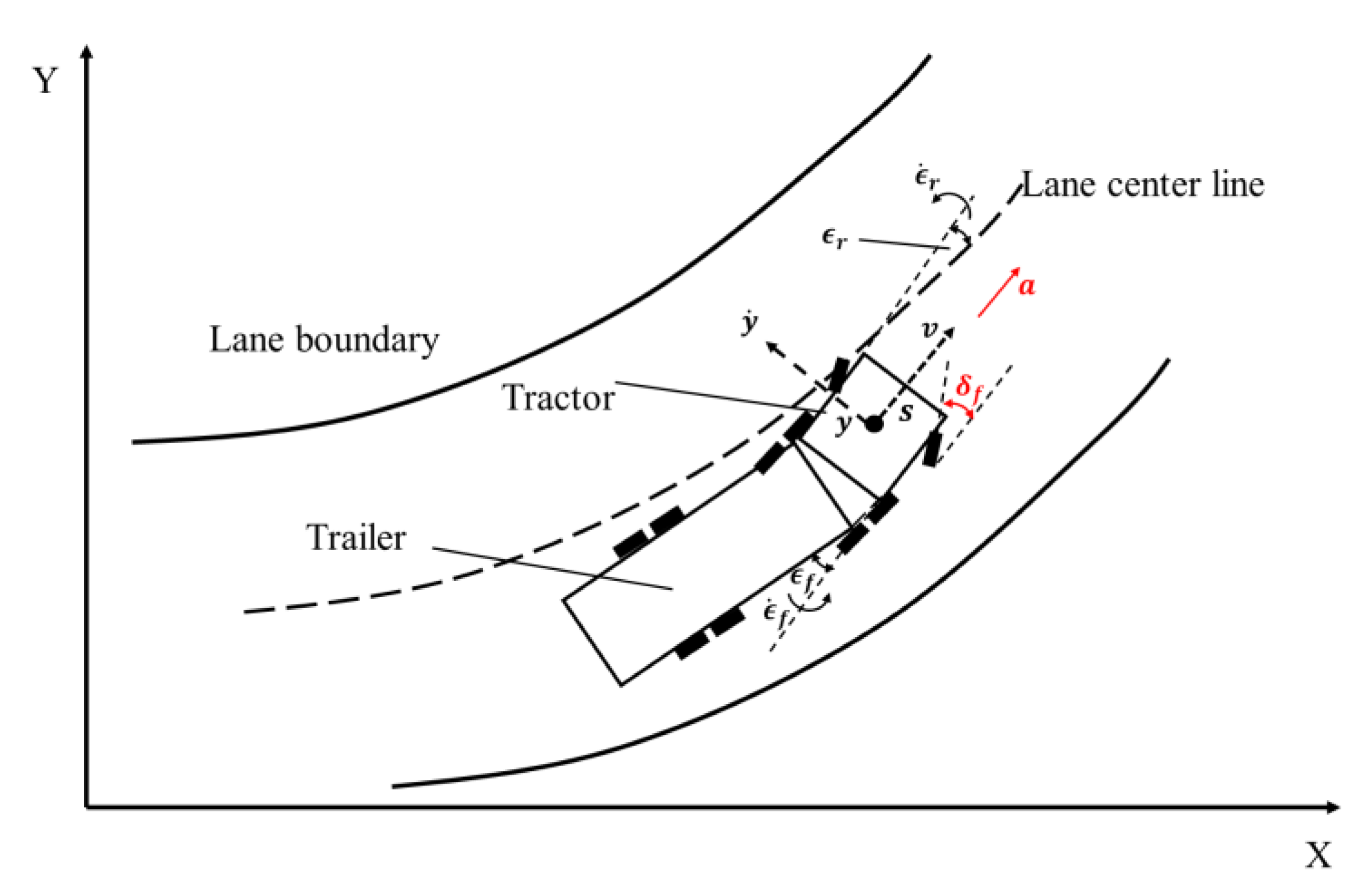
3.1. State and Control Input Definition
3.2. Koopman System Dynamics
3.3. Cost Function
3.4. Constraints
- (1)
- Speed limit: The speed limit constrains both the longitudinal speed (referred to as the slowness in the space domain) and the lateral speed. The longitudinal speed will never exceed the road speed limit and is greater than zero. The lateral speed should be constrained within a range to guarantee safety. The speed limit constraints are specified as:
- (2)
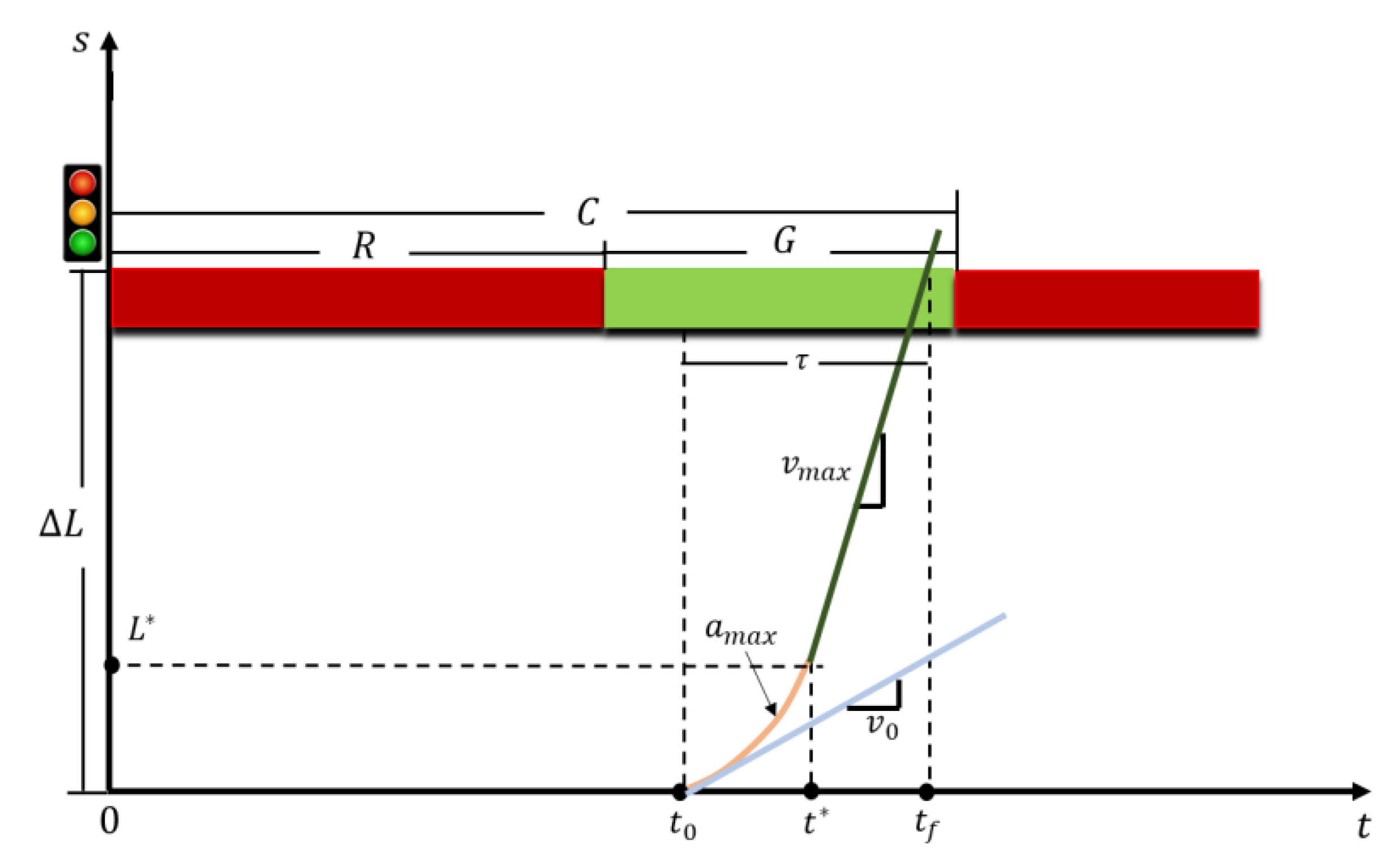
- Time constraints: As shown in Figure 3, time-related parameters are defined. C is the cycle length, R is the red light duration, and G is the green light duration. The amber light is considered as a part of the green light. is defined as the minimum travel duration for the ego truck to reach the stop bar from its current position. This time constraint guarantees that the terminal time is constrained by signal timing so that the ego truck is able to pass through the stop line before the end of the green light. Therefore, it would make a difference whether the ego truck passes the intersection during this current green or the next green.
- (3)
- Control input range: The control input, including the moderation and the steering angle, are in a reasonable value range where both the comfort and the vehicle performance are taken into consideration. This constraint is specified as:
- (4)
- Collision avoidance: This constraint ensures that the ego truck keeps a certain safe distance from the preceding vehicles on the road. In the space domain, headway is utilized to formulate this safety constraint. The detailed formulation of this constraint is shown as follows:where and , respectively, are referred to the time that the ego truck and the preceding vehicle spend on reaching the same position; and is the pre-setting value of the safe time headway.
- (5)
- Initial condition: The initial condition of the optimal control problem is formulated as follows:
4. Solution Method
| Algorithm 1: EDMD for the Koopman system dynamics |
| Input: a set of data collected by the simulation experiment; the observable ; the original model of the articulated truck g(xk, uk) |
| Output: the coefficient matrices and in the linearized system dynamics |
| 1. Use dataset and the truck model to achieve predicted data |
| 2. Use the observable to lift X, Y to , , where , |
| 3. Solve the least square problem: |
| 4. Obtain by calculating |
| Algorithm 2: Dynamic Programing for the optimal control problem |
| Input: linearized system dynamics , the weighting factors , , , , β4, the initial condition the constraint-related parameters |
| Output: control and state on each control step |
| 1. Discretize the optimal control problem, |
| 2. Calculate the weighting matrix and according to , , , and β4. is the weight of the quadratic term of states, is the weight of the coupling term of the states and control inputs: |
| 3. , |
| 4. , |
| 5. |
| 6. Initialization: set |
| Backward compute |
| 7. For kK-1 to 0 do |
| 8. |
| 9. End for |
| Forward compute the control law |
| 10. For k0 to K-1 do |
| 11. |
| 12. |
| 13. If any constraint is activated on the state at the k + 1 step, then |
| 14. Set the control input at the k + 1 state as the feasible control ufeasible |
| 15. Reset the control input |
| 16. End if |
| 17. End for |
5. Verification
5.1. Evaluation for Koopman System Dynamics
5.2. Evaluation for the Eco Approach Controller
5.2.1. Experiment Design
- (1)
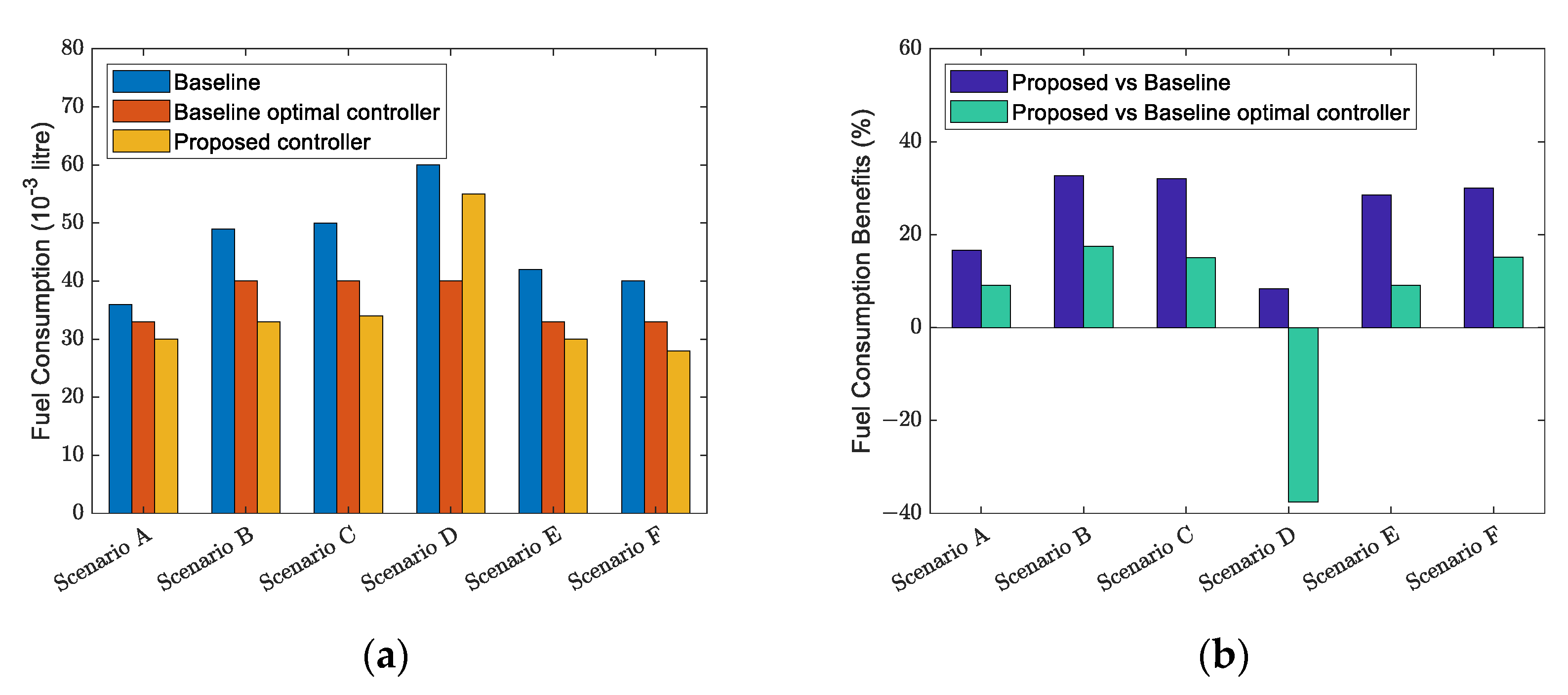
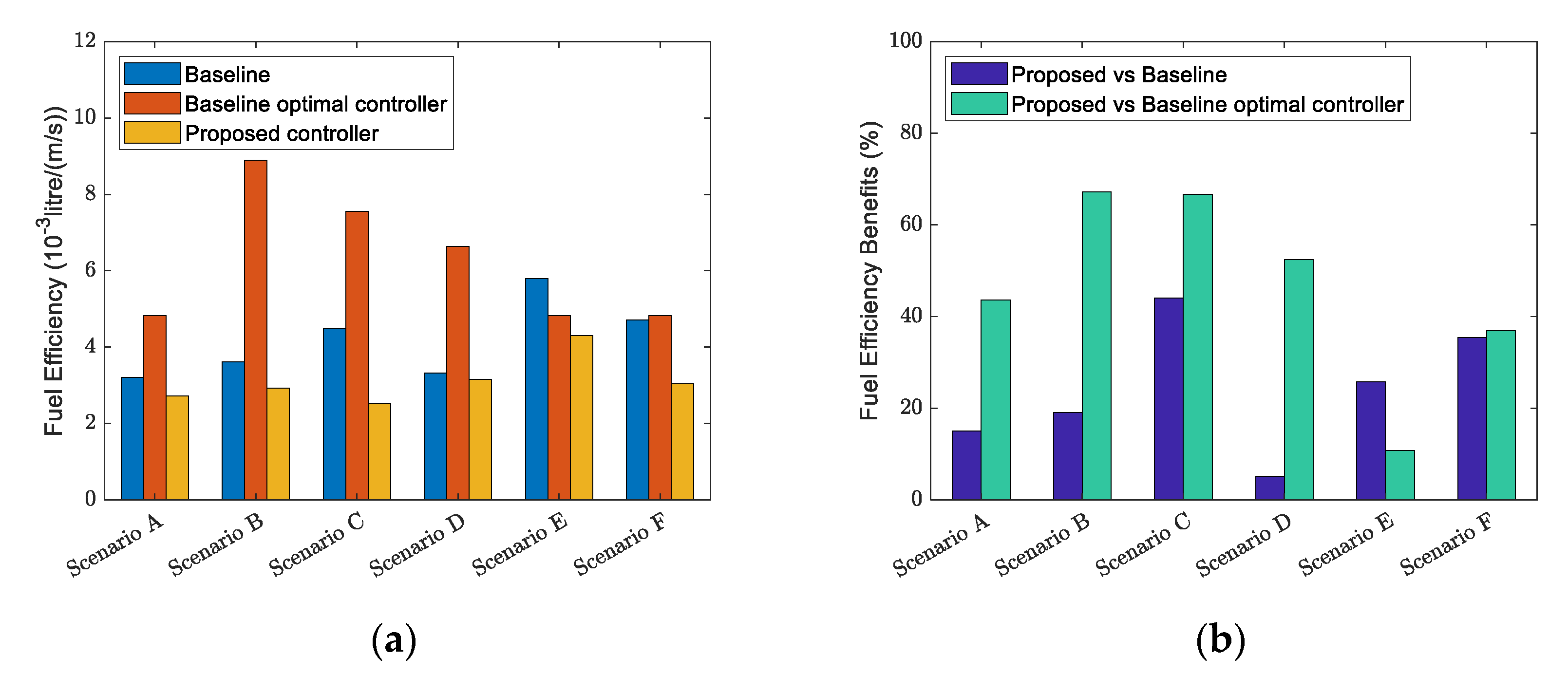
- Measurements of Effectiveness (MOE): Fuel consumption, average speed, and fuel efficiency were adopted as the MOE. Fuel consumption was calculated by the VT-micro model [50]. Averaged speed was utilized for measuring the mobility level of the ego truck. In addition, a new MOE, named fuel efficiency, was proposed to standardize the fuel cost over mobility. It was defined as the fuel consumption per unit averaged speed:where is the fuel efficiency, denotes the fuel consumption, and represents the average speed of the ego truck.
- (2)
- Controller types: The proposed eco approach controller was evaluated against two baseline controllers to demonstrate its advantage over human drivers and the benefit brought by the automated lane-changing and overtaking capability:
- Baseline: The ego truck is controlled by the human driver. In this case, a human-driven articulated truck cruises at a constant desired speed (20 m/s). The behavior of the human driver is simulated by the microscopic simulation software VISSIM. The VISSIM has a whole package of decision maker and controller that is able to mimic the behavior of human drivers (Widemann driver model). The parameters in the model adopt the default ones that can show the regular human driver behavior.
- Baseline optimal controller: In this case, only longitudinal automation is considered. Neither lane-changing nor overtaking maneuver exist. This optimal controller is borrowed from [51]. The parameters in the cost function are tuned in order for the controller to have the same performance as the proposed eco approach controller in the scenario where no lane changing occurs.
- Proposed controller: Both longitudinal and lateral automation are considered. The ego articulated truck has automated lane-changing and overtaking capabilities.
- (3)
- Parameter settings: The following settings were adopted in the simulation experiment, and the partial parameters are shown in Figure 5:
- The controlled area considers the DSRC communication range; thus, the controller is activated when the ego truck arrives at 300 m upstream of the signalized intersection.
- The control step in the space domain is 1 m.
- The cycle of the signal is 90 s.
- The road speed limit is 45 mph (about 20 m/s). and the initial speed of the ego truck is 10 m/s.
5.2.2. Sensitivity Analysis and Results
- Scenario A: the truck enters the controlled area at the beginning of the red signal (5 s after the red light starts).
- Scenario B: the truck enters the controlled area in the middle of the red signal (25 s after the red light starts).
- Scenario C: the truck enters the controlled area at the end of the red signal (35 s after the red light starts).
- Scenario D: the truck enters the controlled area at the beginning of the green signal (5 s after the green light starts).
- Scenario E: the truck enters the controlled area in the middle of the green signal (20 s after the green light starts).
- Scenario F: the truck enters the controlled area at the end of the green signal (30 s after the green light starts).
6. Conclusions and Future Research
- Koopman system dynamics is able to support the receding horizon optimization for the state of the articulated truck.
- The conventional eco approach system is disabled when a slow-moving vehicle impedes the ego vehicle. Under such circumstances, its performance might be worse than a regular human driver.
- Arrival time has a significant impact on the performance of the proposed controller.
- Most fuel savings are observed when the ego truck enters the controlled area in the middle or at the end of the red light duration.
- The benefits are the least when the ego truck’s arrival time is at the beginning of the green signal.
- The proposed controller might sacrifice fuel to achieve a better overall fuel efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- U.S. EPA. Sources of Greenhouse Gas Emissions. 2022. Available online: https://www.epa.gov/ghgemissions/sources-greenhouse-gas-emissions (accessed on 3 April 2022).
- IEA. Transport: Improving the Sustainability of Passenger and Freight Transport. 2022. Available online: https://www.iea.org/topics/transport (accessed on 3 April 2022).
- Barkenbus, J.N. Eco-driving: An overlooked climate change initiative. Energy Policy 2010, 38, 762–769. [Google Scholar] [CrossRef]
- Xiong, S.; Xie, H.; Tong, Q. The effects of an eco-driving assistance system for a city bus on driving style. IFAC Pap. 2018, 51, 331–336. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, J.; An, S.; Wang, M.; Park, B.B. Eco approaching at an isolated signalized intersection under partially connected and automated vehicles environment. Transp. Res. Part C Emerg. Technol. 2017, 79, 290–307. [Google Scholar] [CrossRef]
- Saerens, B.; Rakha, H.A.; Diehl, M.; Van den Bulck, E. A methodology for assessing eco-cruise control for passenger vehicles. Transp. Res. Part D Transp. Environ. 2013, 19, 20–27. [Google Scholar] [CrossRef]
- Park, S.; Rakha, H.; Ahn, K.; Moran, K. Predictive eco-cruise control: Algorithm and potential benefits. In Proceedings of the 2011 IEEE Forum on Integrated and Sustainable Transportation Systems, Vienna, Austria, 29 June–1 July 2011; pp. 394–399. [Google Scholar]
- Lin, Y.-C.; Nguyen, H.L.T. Development of an eco-cruise control system based on digital topographical data. Inventions 2016, 1, 19. [Google Scholar] [CrossRef]
- Schwickart, T.; Voos, H.; Hadji-Minaglou, J.-R.; Darouach, M. An efficient nonlinear model-predictive eco-cruise control for electric vehicles. In Proceedings of the 2013 11th IEEE International Conference on Industrial Informatics (INDIN), Bochum, Germany, 29–31 July 2013; pp. 311–316. [Google Scholar]
- Zhai, C.; Chen, C.; Zheng, X.; Han, Z.; Gao, Y.; Yan, C.; Luo, F.; Xu, J. Ecological Cooperative Adaptive Cruise Control for Heterogenous Vehicle Platoons Subject to Time Delays and Input Saturations. IEEE Trans. Intell. Transp. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, D.; Lan, J.; Xue, S.; Zhao, W.; Tian, D.; Zhou, Q.; Song, K. Eco-Driving of General Mixed Platoons with CAVs and HDVs. IEEE Trans. Intell. Veh. 2022, 1–14. [Google Scholar] [CrossRef]
- Lacombe, R.; Gros, S.; Murgovski, N.; Kulcsár, B. Distributed Eco-Driving Control of a Platoon of Electric Vehicles Through Riccati Recursion. IEEE Trans. Intell. Transp. Syst. 2022, 1–16. [Google Scholar] [CrossRef]
- Hao, P.; Wu, G.; Boriboonsomsin, K.; Barth, M.J. Eco-approach and departure (EAD) application for actuated signals in real-world traffic. IEEE Trans. Intell. Transp. Syst. 2018, 20, 30–40. [Google Scholar] [CrossRef]
- Xia, H.; Wu, G.; Boriboonsomsin, K.; Barth, M.J. Development and evaluation of an enhanced eco-approach traffic signal application for connected vehicles. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 296–301. [Google Scholar]
- Shao, Y.; Sun, Z. Eco-approach with traffic prediction and experimental validation for connected and autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1562–1572. [Google Scholar] [CrossRef]
- NOcOE. SPaT Challenge. 2019. Available online: http://transportationops.org/spatchallenge (accessed on 8 April 2022).
- Garcia, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Di Cairano, S. An industry perspective on MPC in large volumes applications: Potential Benefits and Open Challenges. IFAC Proc. Vol. 2012, 45, 52–59. [Google Scholar] [CrossRef]
- Forbes, M.G.; Patwardhan, R.S.; Hamadah, H.; Gopaluni, R.B. Model predictive control in industry: Challenges and opportunities. IFAC Pap. 2015, 48, 531–538. [Google Scholar] [CrossRef]
- Barth, M.; Mandava, S.; Boriboonsomsin, K.; Xia, H. Dynamic ECO-driving for arterial corridors. In Proceedings of the 2011 IEEE Forum on Integrated and Sustainable Transportation Systems, Vienna, Austria, 29 June–1 July 2011; pp. 182–188. [Google Scholar]
- Wu, X.; He, X.; Yu, G.; Harmandayan, A.; Wang, Y. Energy-optimal speed control for electric vehicles on signalized arterials. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2786–2796. [Google Scholar] [CrossRef]
- He, X.; Liu, H.X.; Liu, X. Optimal vehicle speed trajectory on a signalized arterial with consideration of queue. Transp. Res. Part C Emerg. Technol. 2015, 61, 106–120. [Google Scholar] [CrossRef]
- Lin, X.; Görges, D.; Liu, S. Eco-driving assistance system for electric vehicles based on speed profile optimization. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA), Juan Les Antibes, France, 8–10 October 2014; pp. 629–634. [Google Scholar]
- Hu, J.; Shao, Y.; Sun, Z.; Bared, J. Integrated vehicle and powertrain optimization for passenger vehicles with vehicle-infrastructure communication. Transp. Res. Part C Emerg. Technol. 2017, 79, 85–102. [Google Scholar] [CrossRef]
- Ard, T.; Guo, L.; Han, J.; Jia, Y.; Vahidi, A.; Karbowski, D. Energy-Efficient Driving in Connected Corridors via Minimum Principle Control: Vehicle-in-the-Loop Experimental Verification in Mixed Fleets. arXiv 2022, arXiv:2211.09658. [Google Scholar] [CrossRef]
- IEA. Tracking Transport 2021. 2022. Available online: https://www.iea.org/reports/tracking-transport-2021 (accessed on 3 April 2022).
- FHWA. Truck Platooning. 2021. Available online: https://highways.dot.gov/research/laboratories/saxton-transportation-operations-laboratory/Truck-Platooning (accessed on 8 April 2022).
- ACEA. EU Roadmap for Truck Platooning. 2017. Available online: https://www.acea.auto/publication/eu-roadmap-for-truck-platooning/ (accessed on 3 April 2022).
- Hu, J.; Zhang, Z.; Xiong, L.; Wang, H.; Wu, G. Cut through traffic to catch green light: Eco approach with overtaking capability. Transp. Res. Part C Emerg. Technol. 2021, 123, 102927. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Zhang, Y.; Sun, B.; Ma, W.; Hu, J. Motion planning algorithm under partially connected and automated environment. In Proceedings of the Transportation Research Board 98th Annual Meeting, Washington, DC, USA, 13–17 January 2019. [Google Scholar]
- Alexander, L.; Donath, M.; Hennessey, M.; Morellas, V.; Shankwitz, C. A Lateral Dynamic Model of a Tractor-Trailer: Experimental Validation; Minnesota Technical Report MN/RC-97/18; Minnesota Department of Transportation Office of Research Administration: St. Paul, MN, USA, 1996. [Google Scholar]
- Chen, Y.; Hereid, A.; Peng, H.; Grizzle, J. Enhancing the performance of a safe controller via supervised learning for truck lateral control. J. Dyn. Syst. Meas. Control 2019, 141, 101005. [Google Scholar] [CrossRef]
- Kumar, M.; Hildebrandt, A.-C.; Strauss, P.; Kraus, S.; Stiller, C.; Zimmermann, A. Lateral Trajectory Stabilization of an Articulated Truck during Reverse Driving Maneuvers. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 744–751. [Google Scholar]
- Tassa, Y.; Erez, T.; Smart, W. Receding horizon differential dynamic programming. Adv. Neural Inf. Process. Syst. 2007, 20, 1465–1472. [Google Scholar]
- Mauroy, A.; Susuki, Y.; Mezić, I. Koopman Operator in Systems and Control; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Koopman, B.O. Hamiltonian systems and transformation in Hilbert space. Proc. Natl. Acad. Sci. USA 1931, 17, 315–318. [Google Scholar] [CrossRef]
- Bevanda, P.; Sosnowski, S.; Hirche, S. Koopman operator dynamical models: Learning, analysis and control. Annu. Rev. Control 2021, 52, 197–212. [Google Scholar] [CrossRef]
- Brunton, S.L.; Budišić, M.; Kaiser, E.; Kutz, J.N. Modern Koopman theory for dynamical systems. arXiv 2021, arXiv:2102.12086. [Google Scholar] [CrossRef]
- Korda, M.; Mezić, I. Linear predictors for nonlinear dynamical systems: Koopman operator meets model predictive control. Automatica 2018, 93, 149–160. [Google Scholar] [CrossRef]
- Mauroy, A.; Goncalves, J. Linear identification of nonlinear systems: A lifting technique based on the Koopman operator. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 6500–6505. [Google Scholar]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A data–driven approximation of the koopman operator: Extending dynamic mode decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Williams, M.O.; Rowley, C.W.; Kevrekidis, G.I. A kernel-based approach to data-driven Koopman spectral analysis. arXiv 2014, arXiv:1411.2260. [Google Scholar]
- Li, M.; Wu, X.; He, X.; Yu, G.; Wang, Y. An eco-driving system for electric vehicles with signal control under V2X environment. Transp. Res. Part C Emerg. Technol. 2018, 93, 335–350. [Google Scholar] [CrossRef]
- Zhang, Y.; Cassandras, C.G. Decentralized optimal control of connected automated vehicles at signal-free intersections including comfort-constrained turns and safety guarantees. Automatica 2019, 109, 108563. [Google Scholar] [CrossRef]
- He, C.R.; Maurer, H.; Orosz, G. Fuel consumption optimization of heavy-duty vehicles with grade, wind, and traffic information. J. Comput. Nonlinear Dyn. 2016, 11, 061011. [Google Scholar] [CrossRef]
- Armijos, A.S.C.; Li, A.; Cassandras, C.G.; Al-Nadawi, Y.K.; Chalaki, B.; Moradi-Pari, E.; Hossein, N.M.; Tadiparthi, V. Cooperative Energy and Time-Optimal Lane Change Maneuvers with Minimal Highway Traffic Disruption. arXiv 2022, arXiv:2211.08636. [Google Scholar]
- Zhang, Y.; Bai, Y.; Wang, M.; Hu, J. Cooperative adaptive cruise control with robustness against communication delay: An approach in the space domain. IEEE Trans. Intell. Transp. Syst. 2020, 22, 5496–5507. [Google Scholar] [CrossRef]
- Chen, C.; Tomizuka, M. Modeling and Control of Articulated Vehicles. California PATH Research Report UCB-ITS-PRR-97-42; Institute of Transportation Studies: Berkeley, CA, USA, 1997. [Google Scholar]
- Bertsekas, D. Dynamic Programming and Optimal Control: Volume I; Athena Scientific: Nashua, NH, USA, 2012. [Google Scholar]
- Rakha, H.; Ahn, K.; Trani, A. Development of VT-Micro model for estimating hot stabilized light duty vehicle and truck emissions. Transp. Res. Part D Transp. Environ. 2004, 9, 49–74. [Google Scholar] [CrossRef]
- Hoogendoorn, S.; Hoogendoorn, R.; Wang, M.; Daamen, W. Modeling driver, driver support, and cooperative systems with dynamic optimal control. Transp. Res. Rec. 2012, 2316, 20–30. [Google Scholar] [CrossRef]




| Indices and Parameters | Meaning |
|---|---|
| The state vector of the system dynamics | |
| The time variable (s) | |
| Ego truck’s slowness (s/m) | |
| Ego truck’s lateral speed (m/s) | |
| Relative yaw angle rate of the tractor from the road centerline (rad/s) | |
| Relative yaw angle rate of the tractor and the trailer (rad/s) | |
| Lateral position of the tractor C.G. from the road centerline (m) | |
| Relative yaw angle of the tractor from the road centerline (rad) | |
| Relative yaw angle of the tractor and the trailer (rad) | |
| Ego truck’s longitudinal position (m) | |
| Ego truck’s longitudinal speed (m/s) | |
| Ego truck’s longitudinal acceleration (m/s2) | |
| The control input vector of the system dynamics | |
| Ego vehicle’s moderation (s/m2) | |
| Ego vehicle’s steering angle (rad) | |
| Koopman operator | |
| The real-value observable (a nonlinear base function) | |
| The system matrix of the Koopman system dynamics | |
| The control matrix of the Koopman system dynamics | |
| The current time detected by the on-board device (s) | |
| The terminal time when the ego truck passes through the stop line (s) | |
| The current longitudinal position of the ego truck (m) | |
| The longitudinal distance from the vehicle’s current position to the stop line (m) | |
| Ego vehicle’s desired lateral position (the preferred lane) (m) | |
| The cycle of the signal light (s) | |
| The duration of the green light (s) | |
| The duration of the red light (s) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, X.; Zhang, Z. Data-Driven-Based Eco Approach for Connected and Automated Articulated Trucks in the Space Domain. Sustainability 2023, 15, 1229. https://doi.org/10.3390/su15021229
Zhang X, Li X, Zhang Z. Data-Driven-Based Eco Approach for Connected and Automated Articulated Trucks in the Space Domain. Sustainability. 2023; 15(2):1229. https://doi.org/10.3390/su15021229
Chicago/Turabian StyleZhang, Xianhong, Xiaoyun Li, and Zihan Zhang. 2023. "Data-Driven-Based Eco Approach for Connected and Automated Articulated Trucks in the Space Domain" Sustainability 15, no. 2: 1229. https://doi.org/10.3390/su15021229
APA StyleZhang, X., Li, X., & Zhang, Z. (2023). Data-Driven-Based Eco Approach for Connected and Automated Articulated Trucks in the Space Domain. Sustainability, 15(2), 1229. https://doi.org/10.3390/su15021229





