Reliability Analysis of Nuclear Power Plant Electrical System Considering Common Cause Failure Based on GO-FLOW
Abstract
:1. Introduction
2. Reliability Modeling of Nuclear Power Plant Electrical Systems Based on the GO-FLOW Method
- (1)
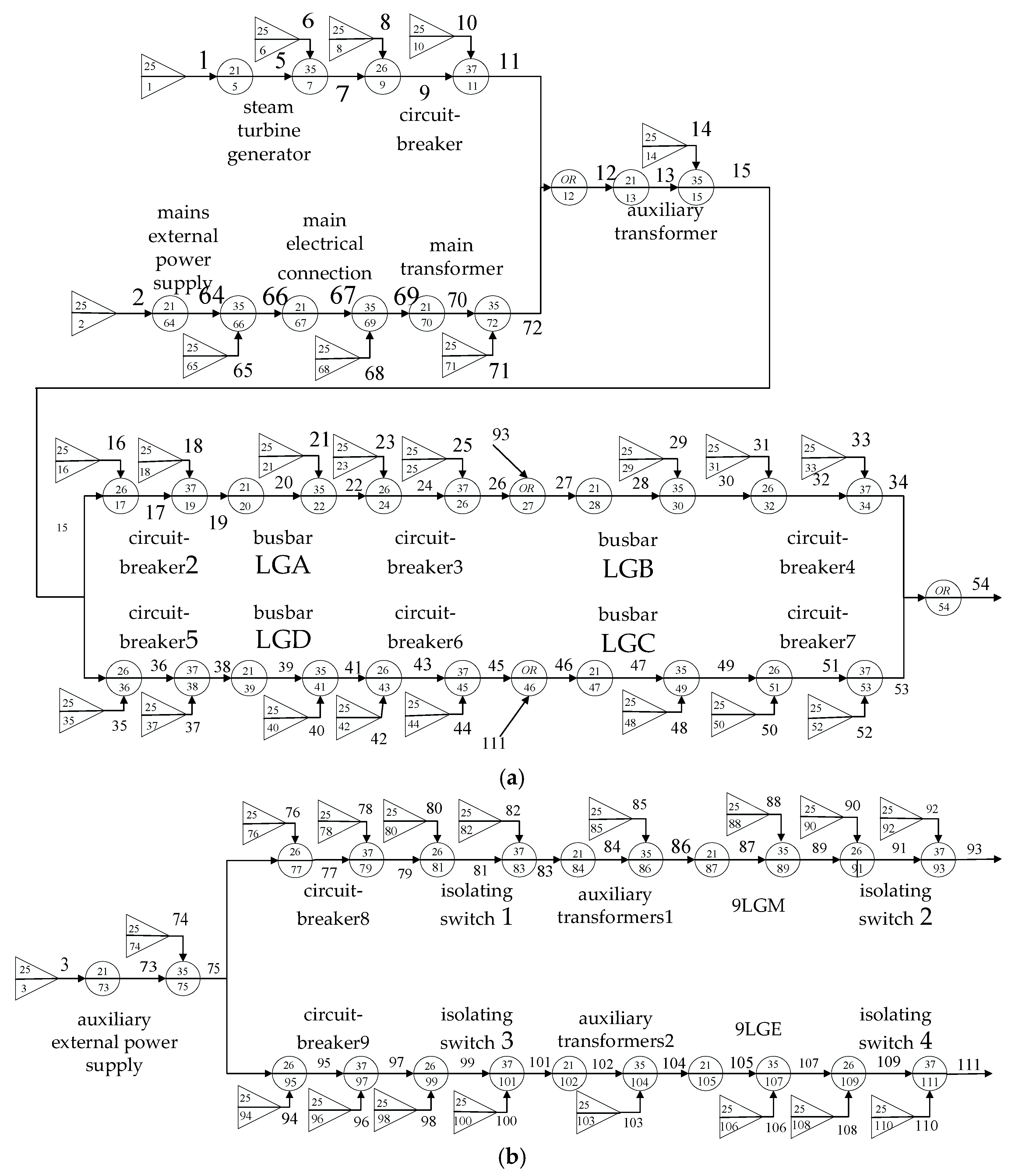
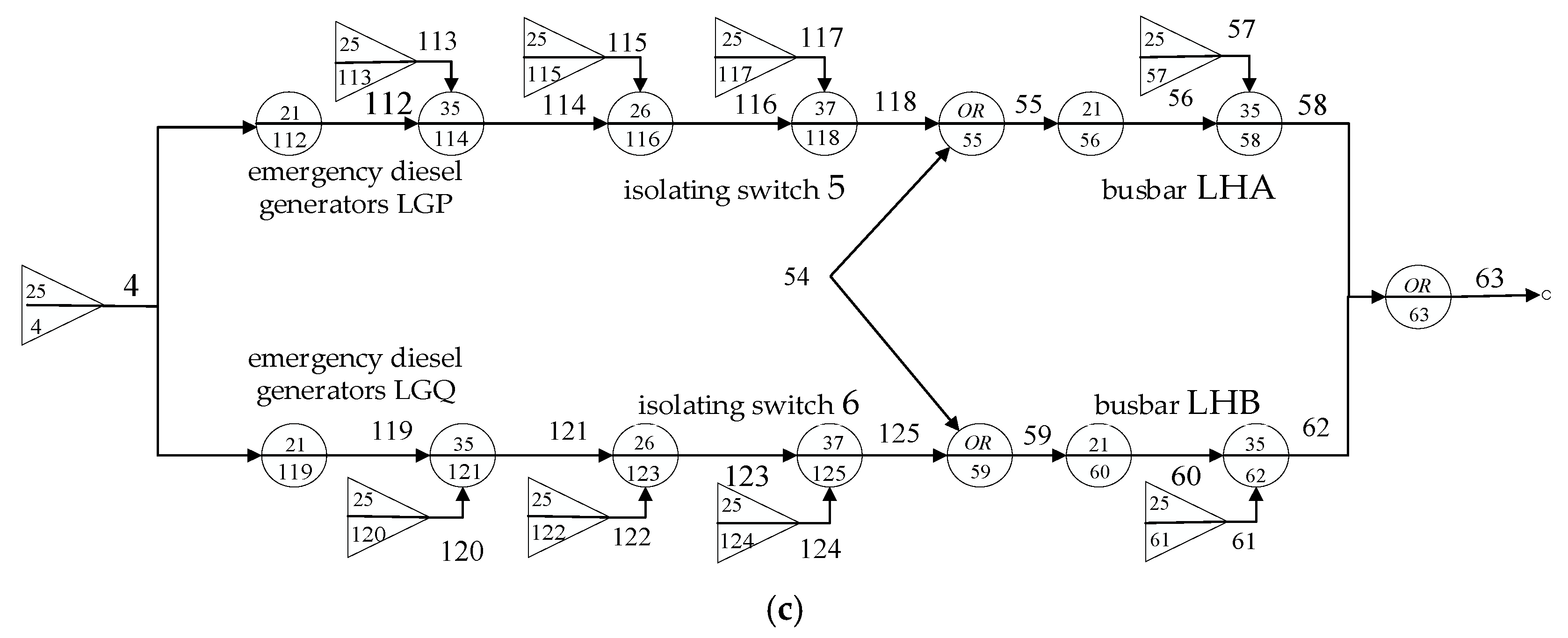
- Failure analysis of the external power supply system: In the GO-FLOW diagram of the external power supply system, signal flow 54 represents the entire external power supply system, and signal flows 34 and 53 represent the outputs of the two-way power supply of the external power supply system, respectively. The logical relationship of the two-way power supply outputs is indicated by OR gate operator 54, and when there is no power supply in the two-way power supply because of a loss of the external power supply system, this is called a LOOP event.
- (2)
- Analysis of the failure of the electrical system and plant-wide power failure: When the external power system of a nuclear power plant is lost, the external power system and the diesel generator relate to the contingency gate operators 55 and 59 in the diagram. Signal flow 58 and 62, respectively, represent the backup system two-way power supply output, with OR gate operator 63 representing the two-way power supply output of the logical relationship. The output signal 63 failure means that the two-way power supplies have no power supply output because of the nuclear power plant’s plant-wide power outage. This is called an SBO event.
3. A Common Fault Failure Analysis Method for Repairable Systems Based on the GO-FLOW Approach
3.1. Theoretical Basis of GO-FLOW Method to Deal with Common Fault Failure
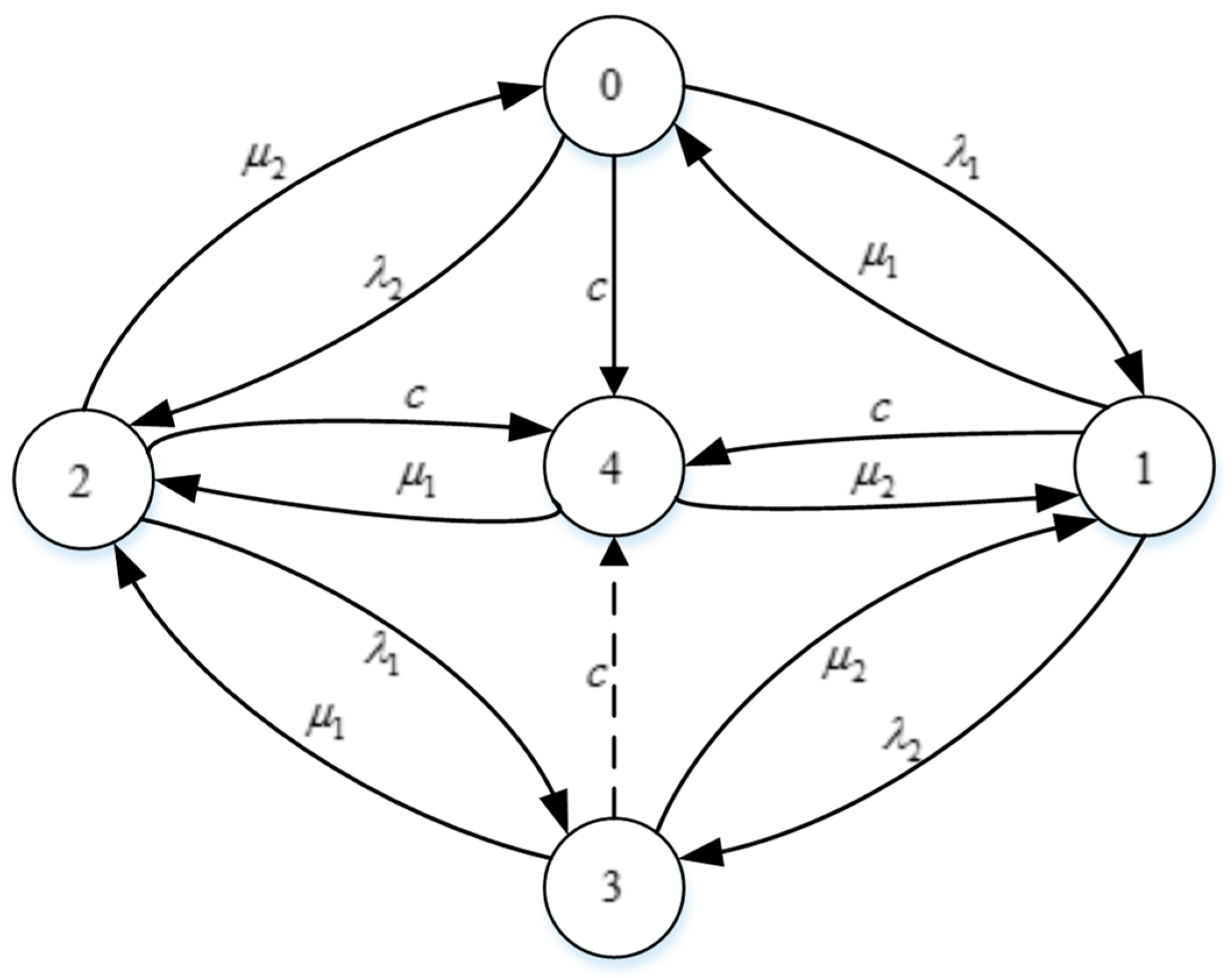
3.2. Model for Calculating the Probability of Co-Causal Failure of Repairable Systems
- State 0: Parts A and B are intact,
- State 1: Component A has failed, and component B is intact,
- State 2: Component A is intact, and component B has failed,
- State 3: Non-co-causal simultaneous failure of components A and B,
- State 4: Co-causal failure of components A and B.
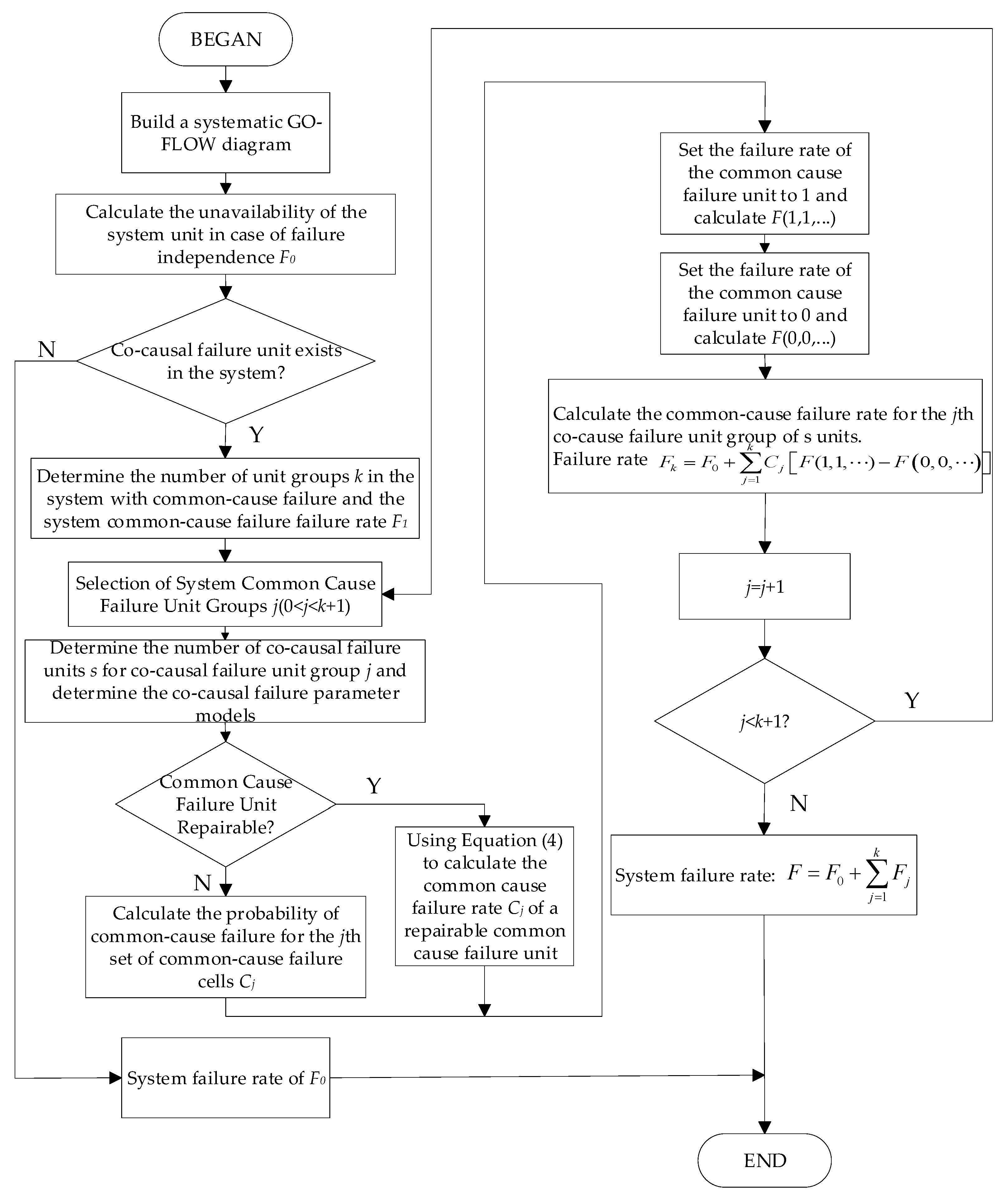
4. Reliability Analysis Process of Nuclear Power Plant Electrical Systems Based on GO-FLOW Method Considering Common Fault Failure
5. Example Analysis
5.1. Calculations Introduction
5.2. Reliability Analysis of Nuclear Power Plants’ External Power Supply System and Electrical System
- (1)
- Scene 1: The external power supply system in the case of shared signals.
- (2)
- Scene 2: The external power system when shared signals are not considered.
- (3)
- Scene 3: The electrical system not considering shared signals.
- (4)
- Scene 4: The electrical system considering shared signals.
- (1)
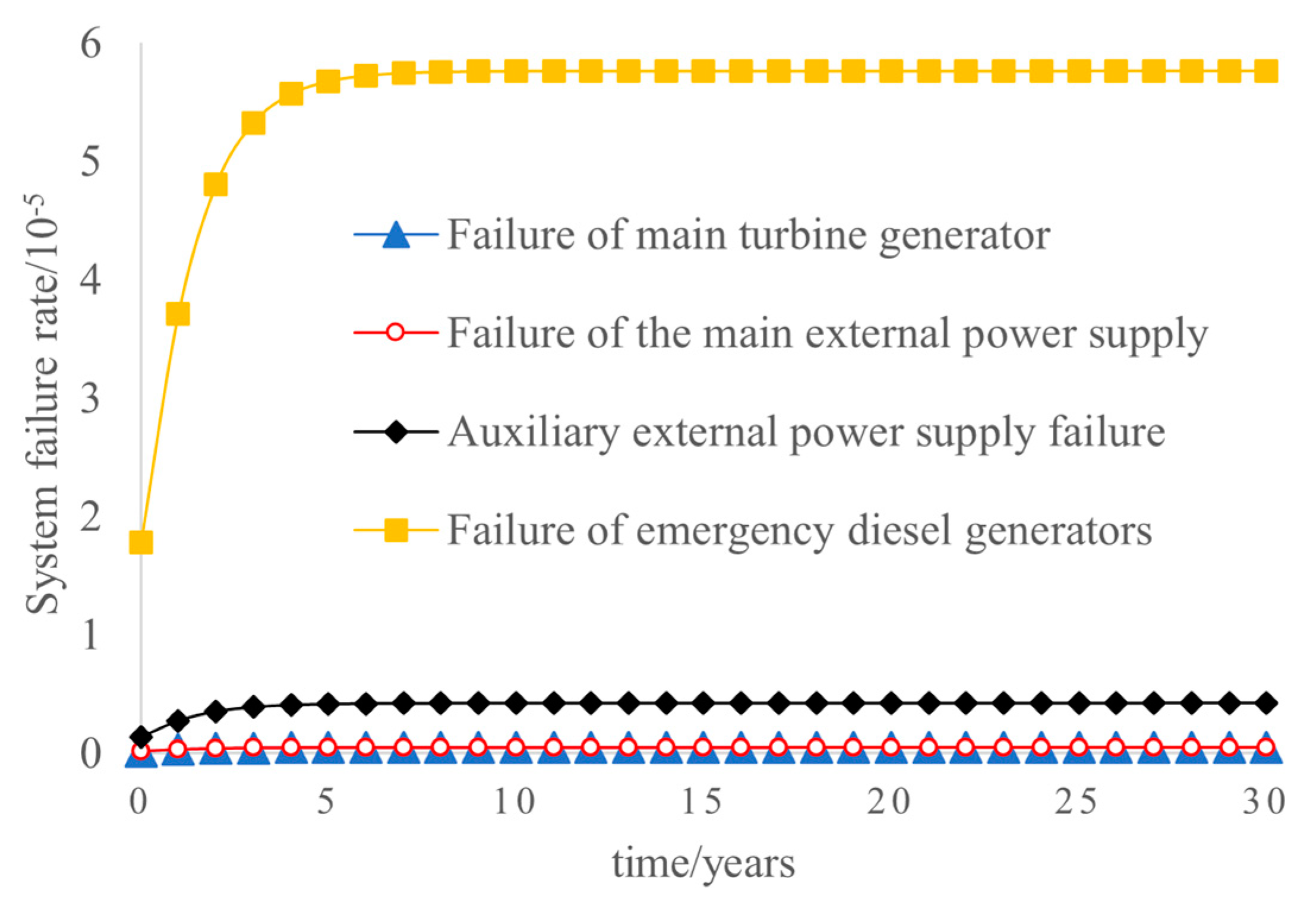
- For a nuclear power plant’s external power supply system, the system failure probability without considering the shared signals grows rapidly from 1.777503 × 10−5 at time point 0 to 5.760142 × 10−5 at time point 9, and is finally maintained at a relatively smooth state. The system failure rate considering the shared signal grows rapidly from 1.966868 × 10−5 at time point 0 to 6.048316 × 10−5 at time point 16, and is finally maintained at a relatively smooth state. For the nuclear power plant power supply system, the system failure probability without considering the shared signals is basically maintained near 0. The system failure rate considering the shared signals grows rapidly from 1.456204 × 10−5 at time point 0 to 4.721015 × 10−5 at time point 14, and is finally maintained at a relatively smooth state. In the early stage of the operation of the nuclear power plant, the failure probability of the external power system and the electrical system increases significantly with time, which is mainly caused by the increase in the failure probability of the equipment and components in the nuclear power plant as well as the connection between the nuclear power plant and the external power grid over time. However, after the 6th year of operation, the probability of failure of the external power system tends to level off, which is mainly caused by the high maintenance rate and regular overhaul of the equipment and components in the nuclear power plant as well as the connection between the nuclear power plant and the external power grid. Overall, the reliability of the external power supply system and the electrical system of the nuclear power plant is quite high.
- (2)
- Compared with the external power supply system, the electrical system has also added two emergency diesel generators to supply power to the emergency bus, resulting in the reliability of the electrical system of the nuclear power plant being two orders of magnitude higher than that of the external power supply system, and the data are in line with the design logic of gradual enhancement of the mitigation measures from the LOOP event to the SBO event.
- (3)
- The results after considering the shared signals are very different from the results without considering the shared signals. Therefore, it is necessary to consider the effect of shared signals for external power systems and electrical systems in nuclear power plants, as well as in redundant systems where special treatment of shared signals is necessary.
5.3. Analysis of the Impact of Single Power Supply Failure on the Reliability of Electrical Systems
5.4. Analysis of the Impact of Common Cause Failure Factors on the Reliability of Electrical Systems
- (1)
- Assuming that no common fault failure occurs at startup of auxiliary transformers 1 and 2, the runtime common cause failure is modeled using the β-factor model β = 0.1. Then, the common fault failure rate at operation is , and the common fault failure probability of the auxiliary transformer is calculated by applying Equation (4) as
- (2)
- Nuclear power units are equipped with emergency diesel generators, which are called EMP and EMQ. Assuming that the probability of startup failure of EMP and EMQ is and the common fault failure is modeled using a β-factor model with B = 0.05 at startup and A = 0.1 at operation, then the probability of initial success of the standby diesel generator EMP and EMQ after considering startup failure is Then, their initial common fault failure probability is , the common fault failure rate at operation is , and the common fault failure probability of the diesel generator is calculated by applying Equation (4) as
- (3)
- Applying the GO-FLOW method to first calculate the failure probability of the system that does not contain the common fault failure, and then calculate the failure probability of the system that contains the common fault failure according to Equation (4), the total unavailability change curve of the system is obtained, as shown in Figure 7.
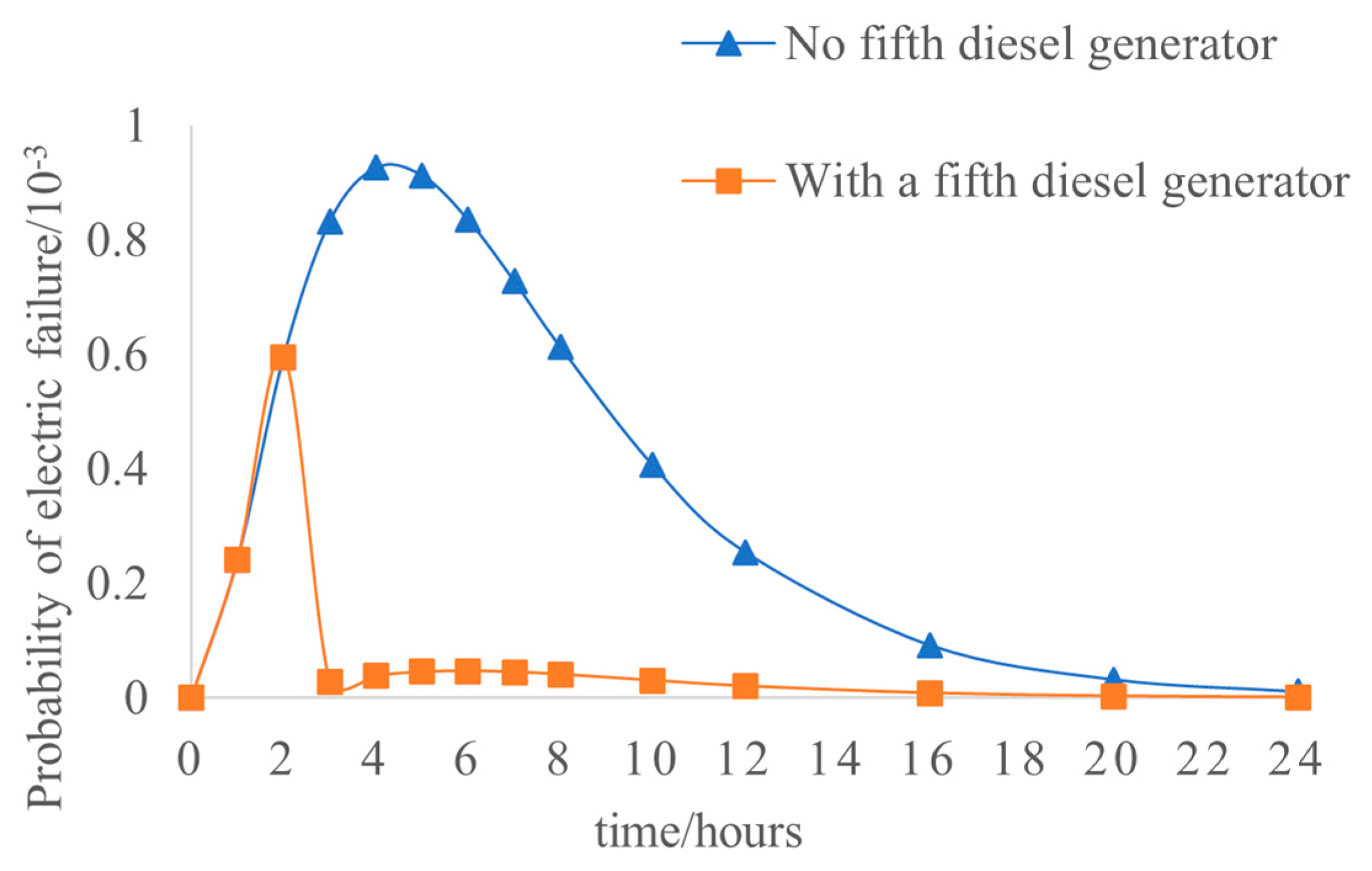
5.5. Analysis of the Impact of Additional Standby Units on the Reliability of the Electrical System
6. Conclusions
- (1)
- The constructed GO-FLOW model of the external power supply system, auxiliary power supply system, and standby power supply system of a nuclear power plant considers the multi-mode repairable component reliability parameter equivalence model and the improved quantitative calculation method of the common signaling system, which improves the accuracy of the reliability analysis of the electrical system of a nuclear power plant.
- (2)
- The group of common fault failure components has a greater impact on the overall reliability analysis of a nuclear power plant’s electrical system, and for redundant systems, common fault failure factors should be fully considered.
- (3)
- The addition of standby diesel generators can greatly reduce the probability of power outages and can effectively improve the reliability of the electrical system in nuclear power plants.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ying, Y.; Guo, J.; Zhao, J. Preliminary Analysis of Large Scale Blackout In Interconnected. Power Syst. Technol. 2003, 27, 8–11+16. [Google Scholar]
- Papazoglou, I.A. Mathematical Foundations of Event Trees. Reliab. Eng. Syst. Saf. 1998, 61, 169–183. [Google Scholar] [CrossRef]
- Leveson, N.G.; Stolzy, J.L. Safety Analysis Using Petri Nets. IEEE Trans. Softw. Eng. 1987, SE-13, 386–397. [Google Scholar] [CrossRef]
- Dugan, J.B.; Bavuso, S.J.; Boyd, M.A. Dynamic Fault-Tree Models for Fault-Tolerant Computer Systems. IEEE Trans. Reliab. 1992, 41, 363–377. [Google Scholar] [CrossRef]
- Maghraby HA, M.; Allan, R.N. Application of DC equivalents to the reliability evaluation of composite power systems. IEEE Trans. Power Syst. 1999, 14, 355–361. [Google Scholar] [CrossRef]
- Cojazzi, G. The DYLAM Approach for the Dynamic Reliability Analysis of Systems. Reliab. Eng. Syst. Saf. 1996, 52, 279–296. [Google Scholar] [CrossRef]
- Gao, S. Methods and Implementation of Dynamic Fault Tree Analysis. Master’s Thesis, Engineering in Control Science and Engineering Graduate School of National University of Defense Technology, Changsha, China, 2005. [Google Scholar]
- Acosta, C.; Siu, N. Dynamic Event Trees in Accident Sequence Analysis: Application to Steam Generator Tube Rupture. Reliab. Eng. Syst. Saf. 1993, 41, 135–154. [Google Scholar] [CrossRef]
- Huiyuan, J. Methods of Dynamic Fault Tree Analysis. Master’s Thesis, Engineering in Control Science and Engineering Graduate School of National University of Defense Technology, Changsha, China, 2002. [Google Scholar]
- Smidts, C. Probabilitic Dynamics: A Comparision between Continuous Event Trees and Discrete Tree Model. Realiability Eng. Syst. Saf. 1994, 44, 189–206. [Google Scholar] [CrossRef]
- Yanfeng, L. New Methods of Dynamic Fault Tree Analysis of Complex System and Its Application. Ph.D. Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2009. [Google Scholar]
- Okazaki, T.; Mitomo, N. The Use of the GO-FLOW Methodology to Investigate the Aging Effects in Nuclear Power Plants. In Proceedings of the International Conference on Probabilistic Safety Assessment and Management, PSAM8, New Orleans, LA, USA, 14–18 May 2006. [Google Scholar]
- Matsuoka, T. Reliability Analyses of a Self-Holding Type Relay System by a Dynamical Event Tree and the GO-FLOW Methodology. In Proceedings of the International Conference on Probabilistic Safety Assessment and Management, PSAM8, New Orleans, LA, USA, 14–18 May 2006. [Google Scholar]
- Zhe, L.; Zongxiang, L.; Jingquan, L. Reliability Analysis of Nuclear Power Plant Bus Systems Arrangement Based on GO Methodology. Nucl. Power Eng. 2010, 31, 69–73. [Google Scholar]
- Guangjiang, W.; Yong, W.; Yanlong, S. Reliability Analysis of Repairable System Based on GO-FLOW Methodology. Nucl. Power Eng. 2012, 33, 25–29. [Google Scholar]
- Faqing, Z. Probabilistic Safety Evaluation of Nuclear Power Plants; Shanghai Jiao tong University Press: Shanghai, China, 1996. [Google Scholar]
- Zupei, S.; Jia, G. GO methodology and improved quantification of system reliability. J. Tsinghua Univ. 1999, 42, 569–572. [Google Scholar]
- Jie, L. Research on the Principles and the ComputerAided Technology of the GO-FLOW. Master’s Thesis, Engineering in Control Science and Engineering Graduate School of National University of Defense Technology, Changsha, China, 2003. [Google Scholar]
- Vaurio, J.K. Is mapping a part of common cause failure quantification? Kerntechnik 2006, 71, 41–49. [Google Scholar] [CrossRef]
- Montague, D.F. A Methodology for Calculating the Expected Number of Failure of a System Undergoing a Phased Mission. Nucl. Sci. Eng. 1980, 74, 199–209. [Google Scholar] [CrossRef]
- Tian, L.; Jie, Z. Model and Method of Low Frequency Protector’s Synthesized Safety Risk Assessment for Nuclear Power Plant Connected to the Grid. Proc. CSEE 2017, 37, 696–705. [Google Scholar]
- Hongbing, S.; Jun, X.; Yuejin, T. Cause—Effect Analysis and Method of Risk Assessment for System Safety. China Saf. Sci. J. 1998, 8, 74–78. [Google Scholar]
- Lei, L. The Application and Improvement of GO-FLOW Methodology in the Reliability Analysis of System with High Redundancy. Master’s Thesis, Zhejiang University, Hangzhou, China, 2011. [Google Scholar]
- Yan-long, S.; Li-sheng, C.; Qi, C. Analysis of Continuously Maintained Complex Redundancy System with CCF Based on GO-FLOW Methodology. Nucl. Power Eng. 2009, 30, 70–75. [Google Scholar]
- Chaogui, W.; Jian-bing, G. Probabilistic Safety Assessment of Station Blackout Accident and 5th Emergency Diesel in Daya Bay NPP. Nucl. Power Eng. 2004, 25, 324–327. [Google Scholar]



| Unit Name | Malfunctions Number of Modes | Failure Frequency (Times/Year) | Average Repair Time (Hours) |
|---|---|---|---|
| main steam turbine generator | 1 | 1.500 | 7.300 × 10 |
| mains external power supply | 1 | 2.300 × 10−3 | 1.000 × 102 |
| auxiliary external power supply | 1 | 8.468 | 3.351 |
| emergency diesel generator | 1 | 1.743 × 102 | 5.000 |
| main transformer | 2 | 2.015 × 10−3 | 1.000 × 10 |
| 8.760 × 10−3 | 7.500 × 102 | ||
| auxiliary transformer | 2 | 5.694 × 10−3 | 1.000 × 10 |
| 8.760 × 10−3 | 4.000 × 102 | ||
| auxiliary transformers | 2 | 1.139 × 10−2 | 1.000 × 10 |
| 1.139 × 10−2 | 4.000 × 102 | ||
| main electrical connection | 1 | 2.059 × 10−2 | 1.060 × 102 |
| busbar | 2 | 3.679 × 10−3 | 5.000 × 10 |
| 4.643 × 10−4 | 7.200 × 10 | ||
| generator export circuit-breaker | 1 | 4.890 × 10−2 | 1.116 × 102 |
| circuit-breaker | 1 | 3.030 × 10−2 | 5.750 × 10 |
| isolating switch | 1 | 0 | 0 |
| Unit Name | Unit State | Frequency of Overhaul (Times/Year) | Overhaul Time (Hours) |
|---|---|---|---|
| main steam turbine generator | examine and fix (a motor) | 1.000 | 2.800 × 102 |
| main transformer | examine and fix (a motor) | 2.000 × 10−1 | 1.600 × 102 |
| main electrical connection | examine and fix (a motor) | 5.000 × 10−1 | 2.400 × 10 |
| circuit-breaker | examine and fix (a motor) | 7.872 × 10−1 | 8.100 × 10 |
| Unit Name | Equivalent Failure Rate | Equivalent Maintenance Rate | Average Probability of Success | Mean Failure Probability |
|---|---|---|---|---|
| main steam turbine generator | 2.50000 | 5.62260 × 10 | 0.957429 | 4.2571 × 10−3 |
| circuit-breaker 1 | 4.89000 × 10−2 | 7.84946 × 10 | 0.999377 | 6.2258 × 10−4 |
| auxiliary transformer | 1.44540 × 10−2 | 3.55572 × 10 | 0.999594 | 4.0633 × 10−4 |
| circuit-breaker 2 | 8.17500 × 10−1 | 1.09430 × 102 | 0.992585 | 7.4151 × 10−3 |
| busbar LGA | 4.14348 × 10−3 | 7.00386 × 102 | 0.999994 | 5.9160 × 10−6 |
| circuit-breaker 3 | 8.17500 × 10−1 | 1.09430 × 102 | 0.992585 | 7.4151 × 10−3 |
| busbar LGB | 4.14348 × 10−3 | 7.00386 × 102 | 0.999994 | 5.9160 × 10−6 |
| circuit-breaker 4 | 8.17500 × 10−1 | 1.09430 × 102 | 0.992585 | 7.4151 × 10−3 |
| circuit-breaker 5 | 8.17500 × 10−1 | 1.09430 × 102 | 0.992585 | 7.4151 × 10−3 |
| busbar LGD | 4.14348 × 10−3 | 7.00386 × 102 | 0.999994 | 5.9160 × 10−6 |
| circuit-breaker 6 | 8.17500 × 10−1 | 1.09430 × 102 | 0.992585 | 7.4151 × 10−3 |
| busbar LGC | 4.14348 × 10−3 | 7.00386 × 102 | 0.999994 | 5.9160 × 10−6 |
| circuit-breaker 7 | 8.17500 × 10−1 | 1.09430 × 102 | 0.992585 | 7.4151 × 10−3 |
| busbar LHA | 4.14348 × 10−3 | 7.00386 × 102 | 0.999994 | 5.9160 × 10−6 |
| busbar LHB | 4.14348 × 10−3 | 7.00386 × 102 | 0.999994 | 5.9160 × 10−6 |
| mains external power supply | 2.30000 × 10−3 | 8.76000 × 10 | 0.999974 | 2.6255 × 10−5 |
| main electrical connection | 7.50000 × 10−1 | 4.10625 × 102 | 0.998177 | 1.8232 × 10−3 |
| main transformer | 2.10775 × 10−1 | 4.78461 × 10 | 0.995614 | 4.3860 × 10−3 |
| auxiliary transformer | 8.46800 | 2.61414 × 103 | 0.996771 | 3.2288 × 10−3 |
| circuit-breaker 8 | 8.17500 × 10−1 | 1.09430 × 102 | 0.992585 | 7.4151 × 10−3 |
| isolating switch 1 | 0 | 1 | 0 | |
| auxiliary transformers 1 | 2.27760 × 10−2 | 4.27316 × 10 | 0.999467 | 5.3281 × 10−4 |
| 9LGM | 4.14348 × 10−3 | 7.00386 × 102 | 0.999994 | 5.9160 × 10−6 |
| isolating switch 2 | 0 | 1 | 0 | |
| circuit-breaker 9 | 8.17500 × 10−1 | 1.09430 × 102 | 0.992585 | 7.4151 × 10−3 |
| isolating switch 3 | 0 | 1 | 0 | |
| auxiliary transformers 2 | 2.27760 × 10−2 | 4.27316 × 10 | 0.999467 | 5.3281 × 10−4 |
| 9LGE | 4.14348 × 10−3 | 7.00386 × 102 | 0.999994 | 5.9160 × 10−6 |
| isolating switch 4 | 0 | 1 | 0 | |
| emergency diesel generator LGP | 1.74324 × 102 | 1.75200 × 103 | 0.909504 | 9.0496 × 10−2 |
| isolating switch 5 | 0 | 1 | 0 | |
| emergency diesel generator LGQ | 1.74324 × 102 | 1.75200 × 103 | 0.909504 | 9.0496 × 10−2 |
| isolating switch 6 | 0 | 1 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Sun, Y.; Zhao, J.; Dong, X.; Chen, C.; Wang, B.; Wu, H. Reliability Analysis of Nuclear Power Plant Electrical System Considering Common Cause Failure Based on GO-FLOW. Sustainability 2023, 15, 14071. https://doi.org/10.3390/su151914071
Wang Z, Sun Y, Zhao J, Dong X, Chen C, Wang B, Wu H. Reliability Analysis of Nuclear Power Plant Electrical System Considering Common Cause Failure Based on GO-FLOW. Sustainability. 2023; 15(19):14071. https://doi.org/10.3390/su151914071
Chicago/Turabian StyleWang, Zhijian, Yao Sun, Jie Zhao, Xuzhu Dong, Chen Chen, Bo Wang, and Haocheng Wu. 2023. "Reliability Analysis of Nuclear Power Plant Electrical System Considering Common Cause Failure Based on GO-FLOW" Sustainability 15, no. 19: 14071. https://doi.org/10.3390/su151914071
APA StyleWang, Z., Sun, Y., Zhao, J., Dong, X., Chen, C., Wang, B., & Wu, H. (2023). Reliability Analysis of Nuclear Power Plant Electrical System Considering Common Cause Failure Based on GO-FLOW. Sustainability, 15(19), 14071. https://doi.org/10.3390/su151914071







