Application of a Semi-Empirical Approach to Map Maximum Urban Heat Island Intensity in Singapore
Abstract
:1. Introduction
2. Study Area, Observational Data, and Urban Morphological Characteristics
3. Application of Diagnostic Equation Proposed in Theeuwes et al. [33]
- Different reference stations are used for the weather variables. and are mainly considered in the equation to determine the seasonal variability of weather conditions within the study period. Although similar day-to-day variability is expected at Changi compared to the rural site, the magnitude, particularly for wind speed, might vary.
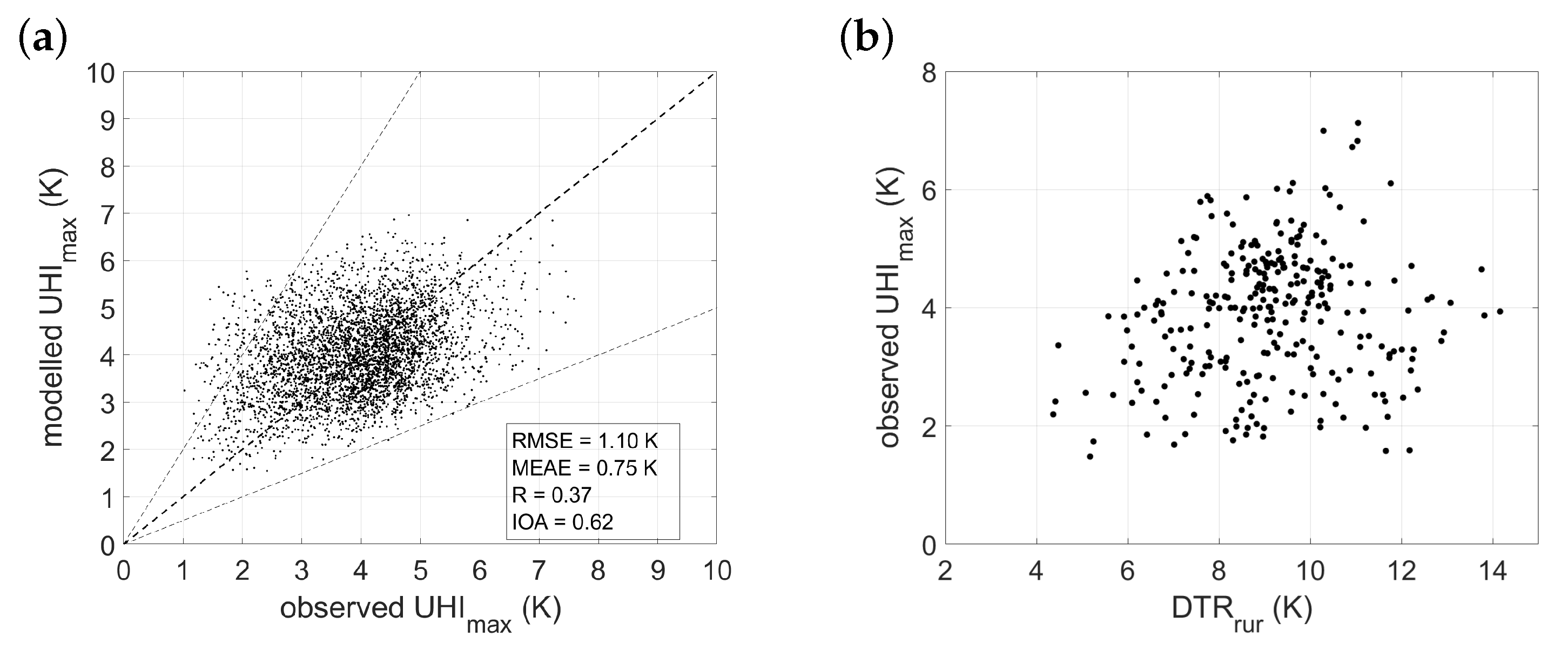
- The rural reference sites are characterized by different land cover types. LCZ D (low plants) is used in T17, but LCZ B (scattered trees) in the present study. DTR for the former is therefore likely larger since daytime air temperature will be higher over an open area, compared to a partially shaded area. This discrepancy could be responsible for the large scatter in Figure 2b, as compared to the strong relationship between UHImax and DTR observed in T17.
4. Development of the Model Equation for Singapore
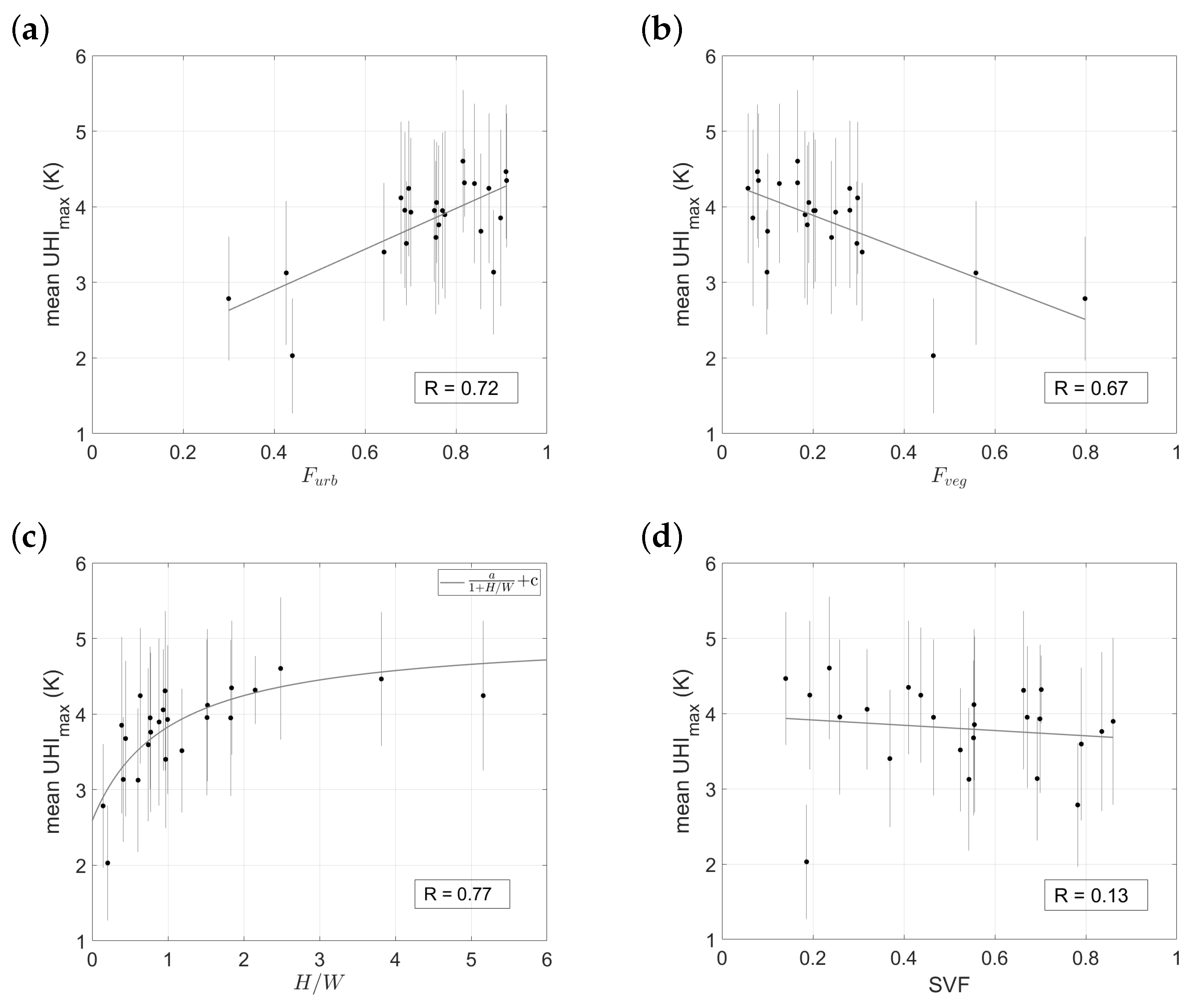
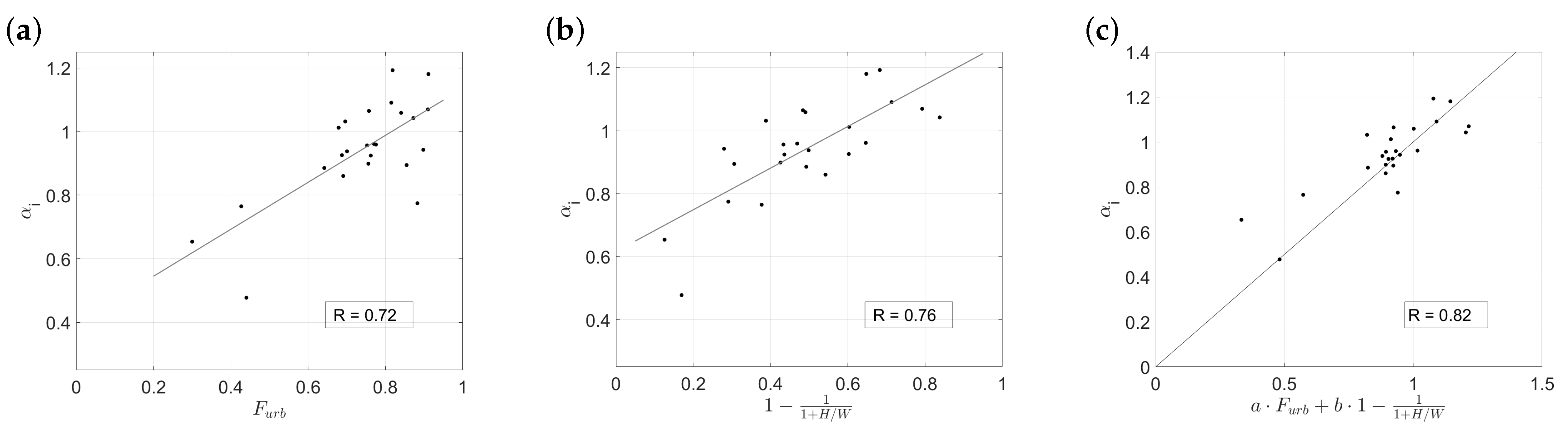
4.1. Selection of Independent Variables
4.1.1. Land Cover and Morphological Parameters
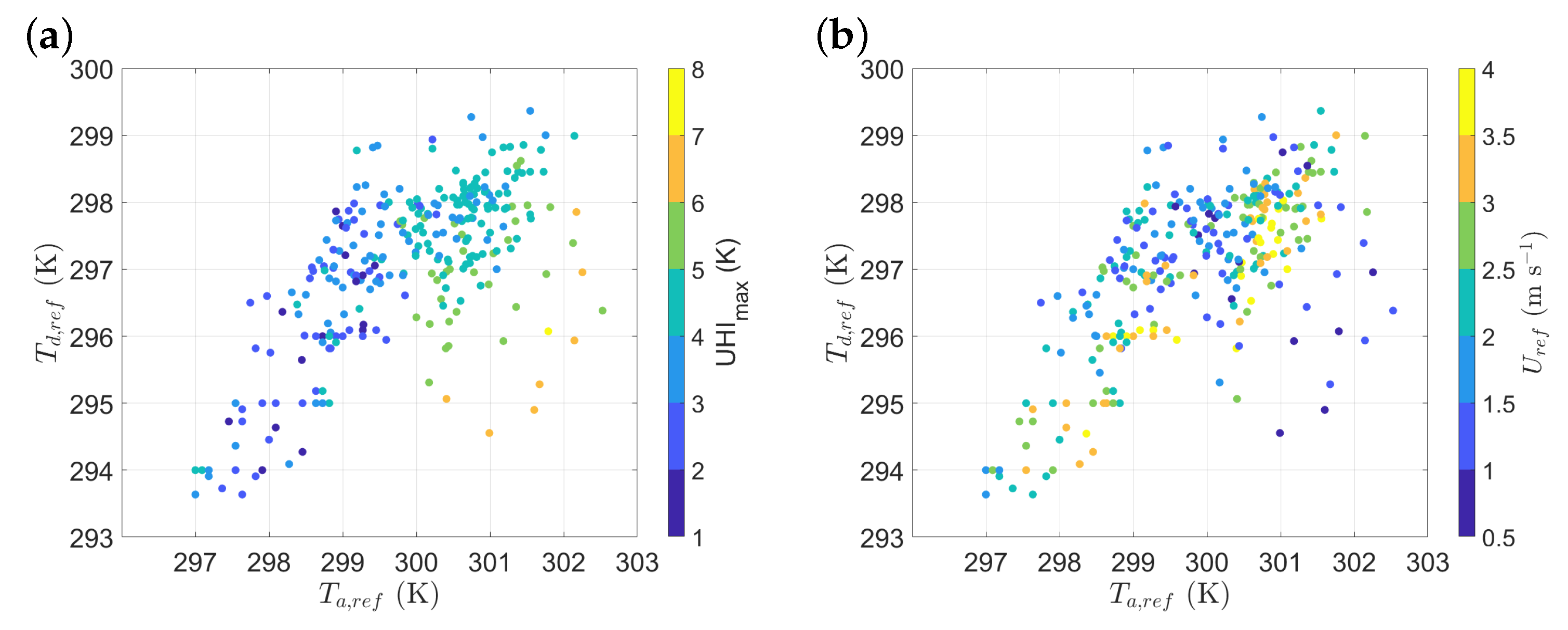
4.1.2. Meteorological Variables
4.2. Development of the Model Equation for Singapore
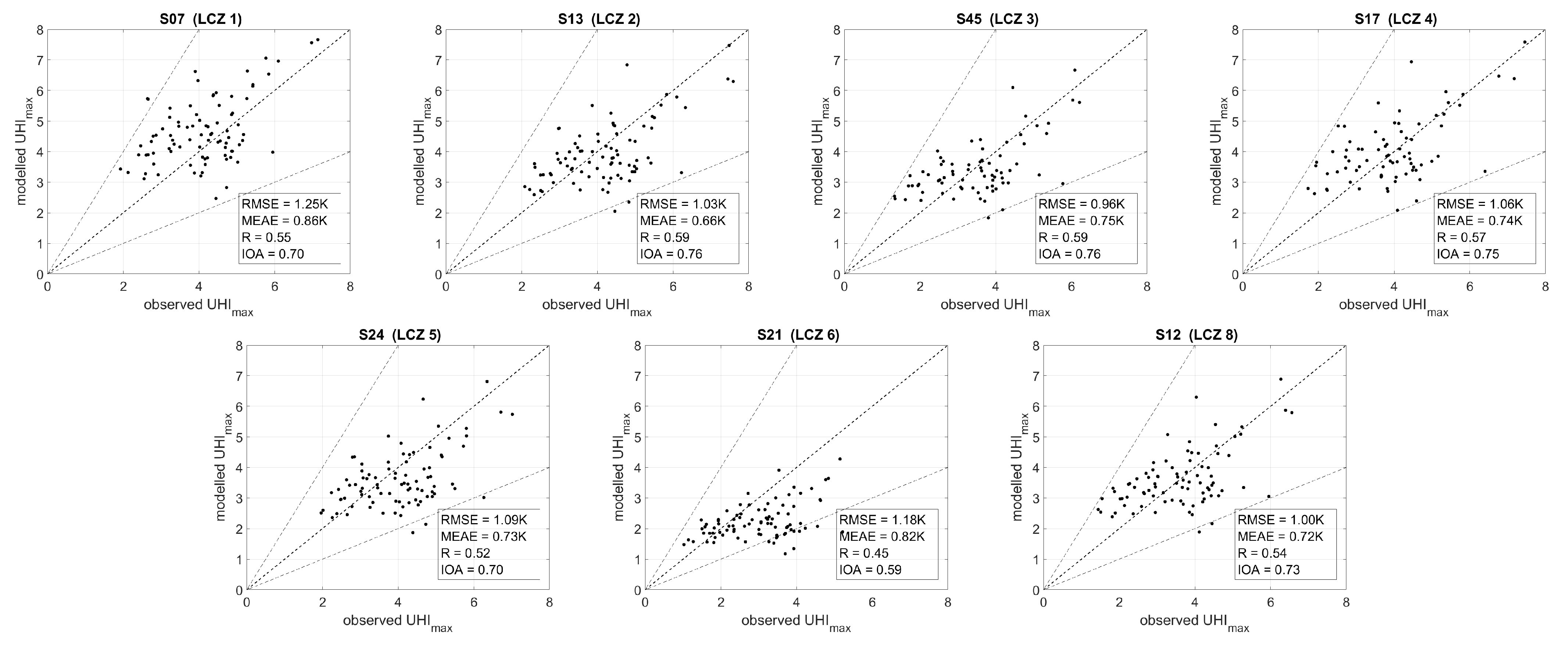
5. Model Evaluation
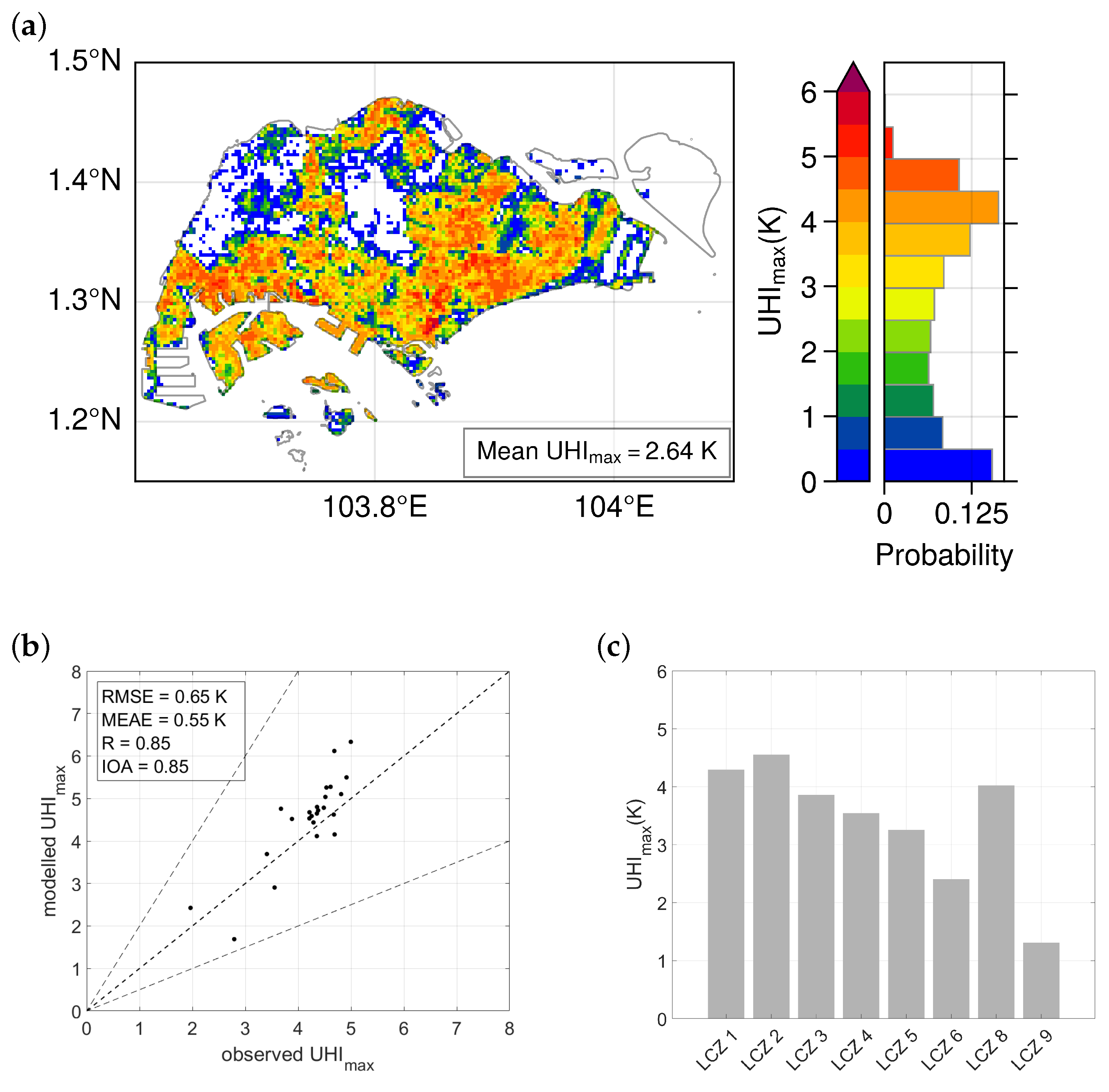
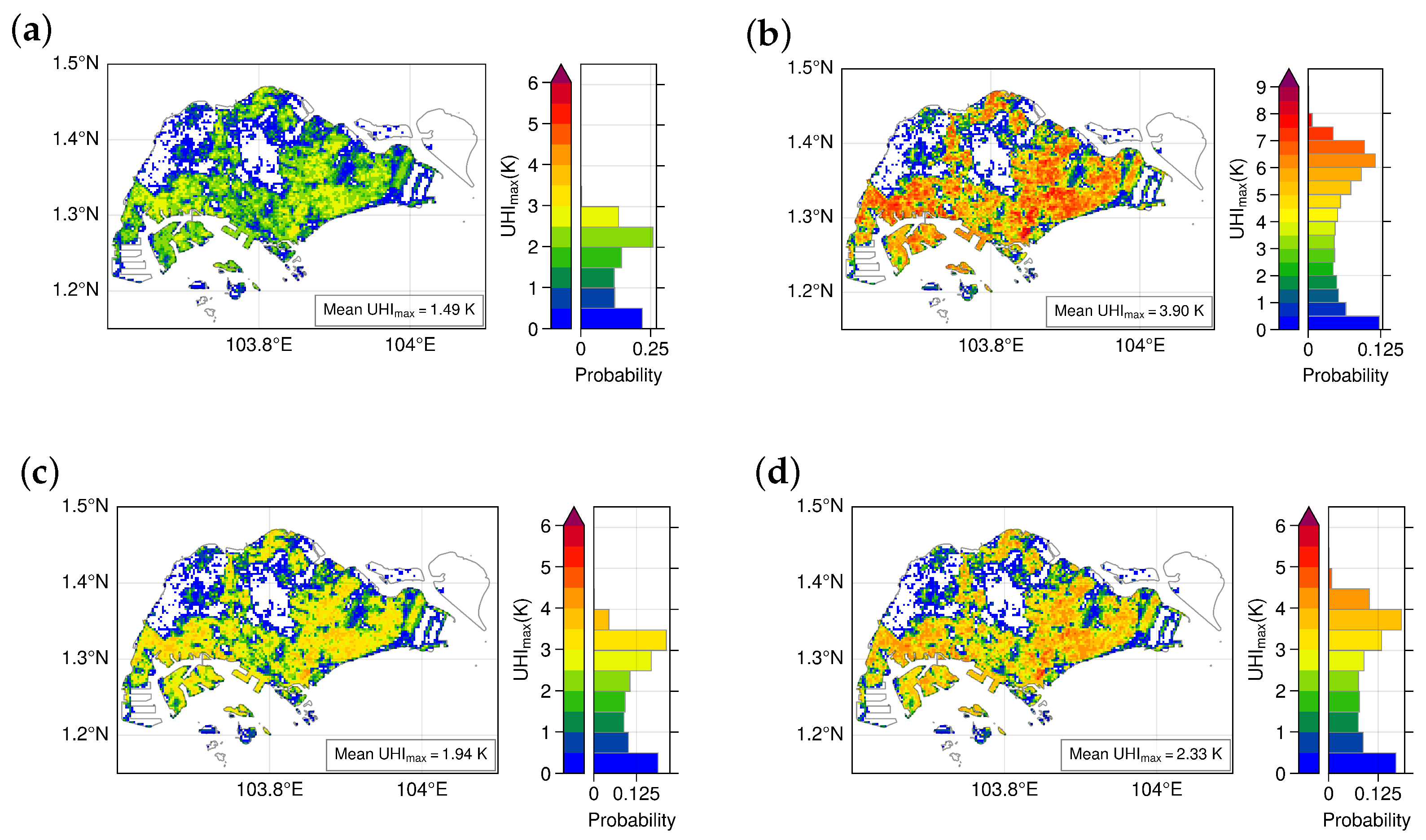
6. Mapping Spatial Patterns of UHImax Intensities
7. Summary and Conclusions
- Evaluation of the model adapted to Singapore (Equation (3)) shows overall good agreement with observations of daily UHImax for different dry weather conditions.
- Model performance shows a strong dependency of the estimated UHImax on wind speed. Best performance is reached for low wind speed (<2.5 m s−1 at the reference site). During these conditions, the model provides reliable estimations of UHImax with low errors (RMSE and MEAE < 1 K) and a high level of agreement with observations (R > 0.80).
- Estimates for UHImax tend to underpredict observed values over open low-rise areas (LCZ 6) (R < 0.5). The paucity of stations with low values (0.3–0.6), compared to the majority of stations that are placed in more densely built-up environments ( > 0.6), is one reason why the model is less robust over these open urban landscapes. Given nevertheless significant UHImax magnitudes over less developed urban spaces, we suggest increasing the placement of stations in these areas.
- The low prediction errors (RMSE < 1.2 K and MEAE < 1 K) obtained at every station and for different seasons in Singapore reveal that the accuracy of this simple semi-empirical equation might be comparable to the performance for dry weather conditions of more sophisticated numerical models (e.g., WRF or uSINGV), which include complex building effect parameterizations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
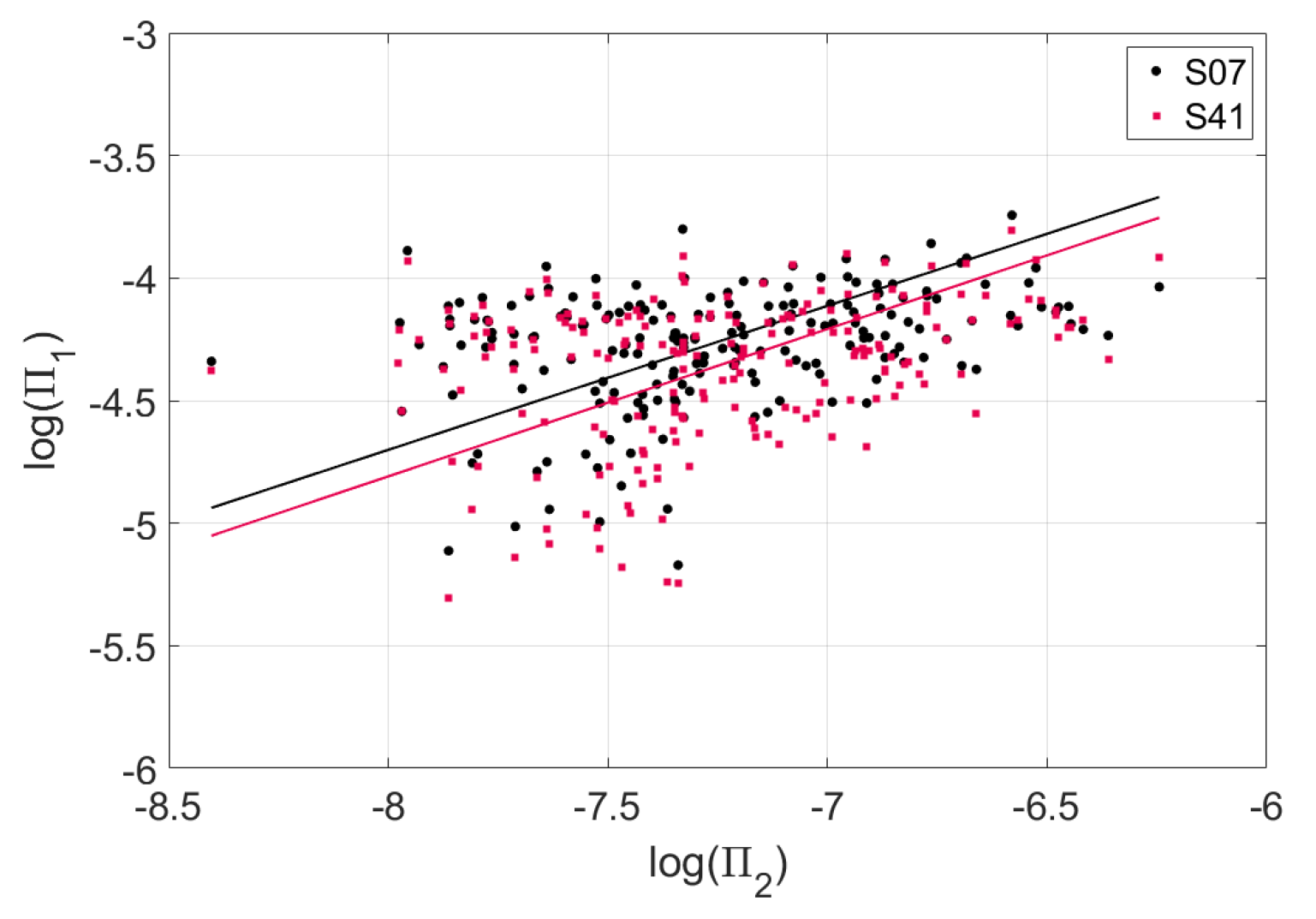
Appendix A. Calculation of the Dimensionless Π Variables
References
- Stewart, I.D. Why should urban heat island researchers study history? Urban Clim. 2019, 30, 100484. [Google Scholar] [CrossRef]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Rizwan, A.M.; Dennis, L.Y.; Chunho, L. A review on the generation, determination and mitigation of Urban Heat Island. J. Environ. Sci. 2008, 20, 120–128. [Google Scholar] [CrossRef] [PubMed]
- Steeneveld, G.J.; Koopmans, S.; Heusinkveld, B.; Van Hove, L.; Holtslag, A. Quantifying urban heat island effects and human comfort for cities of variable size and urban morphology in the Netherlands. J. Geophys. Res. Atmos. 2011, 116, D20. [Google Scholar] [CrossRef]
- Schatz, J.; Kucharik, C.J. Seasonality of the urban heat island effect in Madison, Wisconsin. J. Appl. Meteorol. Climatol. 2014, 53, 2371–2386. [Google Scholar] [CrossRef]
- Oke, T.R. The urban energy balance. Prog. Phys. Geogr. 1988, 12, 471–508. [Google Scholar] [CrossRef]
- Oke, T.R. Canyon geometry and the nocturnal urban heat island: Comparison of scale model and field observations. J. Climatol. 1981, 1, 237–254. [Google Scholar] [CrossRef]
- Unger, J. Intra-urban relationship between surface geometry and urban heat island: Review and new approach. Clim. Res. 2004, 27, 253–264. [Google Scholar] [CrossRef]
- Yuan, C.; Chen, L. Mitigating urban heat island effects in high-density cities based on sky-view factor and urban morphological understanding: A study of Hong Kong. Archit. Sci. Rev. 2011, 54, 305–315. [Google Scholar] [CrossRef]
- Zoulia, I.; Santamouris, M.; Dimoudi, A. Monitoring the effect of urban green areas on the heat island in Athens. Environ. Monit. Assess. 2009, 156, 275–292. [Google Scholar] [CrossRef]
- Oliveira, S.; Andrade, H.; Vaz, T. The cooling effect of green spaces as a contribution to the mitigation of urban heat: A case study in Lisbon. Build. Environ. 2011, 46, 2186–2194. [Google Scholar] [CrossRef]
- Konarska, J.; Holmer, B.; Lindberg, F.; Thorsson, S. Influence of vegetation and building geometry on the spatial variations of air temperature and cooling rates in a high-latitude city. Int. J. Climatol. 2016, 36, 2379–2395. [Google Scholar] [CrossRef]
- Freitas, E.D.; Rozoff, C.M.; Cotton, W.R.; Dias, P.L.S. Interactions of an urban heat island and sea-breeze circulations during winter over the metropolitan area of São Paulo, Brazil. Bound.-Layer Meteorol. 2007, 122, 43–65. [Google Scholar] [CrossRef]
- He, B.J.; Ding, L.; Prasad, D. Relationships among local-scale urban morphology, urban ventilation, urban heat island and outdoor thermal comfort under sea breeze influence. Sustain. Cities Soc. 2020, 60, 102289. [Google Scholar] [CrossRef]
- Skarbit, N.; Stewart, I.D.; Unger, J.; Gál, T. Employing an urban meteorological network to monitor air temperature conditions in the ‘local climate zones’ of Szeged, Hungary. Int. J. Climatol. 2017, 37, 582–596. [Google Scholar] [CrossRef]
- Stewart, I.D. A systematic review and scientific critique of methodology in modern urban heat island literature. Int. J. Climatol. 2011, 31, 200–217. [Google Scholar] [CrossRef]
- Arnds, D.; Böhner, J.; Bechtel, B. Spatio-temporal variance and meteorological drivers of the urban heat island in a European city. Theor. Appl. Climatol. 2017, 128, 43–61. [Google Scholar] [CrossRef]
- Giannaros, T.M.; Melas, D.; Daglis, I.A.; Keramitsoglou, I.; Kourtidis, K. Numerical study of the urban heat island over Athens (Greece) with the WRF model. Atmos. Environ. 2013, 73, 103–111. [Google Scholar] [CrossRef]
- Chen, F.; Yang, X.; Zhu, W. WRF simulations of urban heat island under hot-weather synoptic conditions: The case study of Hangzhou City, China. Atmos. Res. 2014, 138, 364–377. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Y.; Qian, Y. Simulation of urban climate with high-resolution WRF model: A case study in Nanjing, China. Asia-Pac. J. Atmos. Sci. 2012, 48, 227–241. [Google Scholar] [CrossRef]
- Salamanca, F.; Martilli, A.; Yagüe, C. A numerical study of the Urban Heat Island over Madrid during the DESIREX (2008) campaign with WRF and an evaluation of simple mitigation strategies. Int. J. Climatol. 2012, 32, 2372–2386. [Google Scholar] [CrossRef]
- Gutiérrez, E.; González, J.E.; Martilli, A.; Bornstein, R.; Arend, M. Simulations of a heat-wave event in New York City using a multilayer urban parameterization. J. Appl. Meteorol. Climatol. 2015, 54, 283–301. [Google Scholar] [CrossRef]
- Li, H.; Zhou, Y.; Wang, X.; Zhou, X.; Zhang, H.; Sodoudi, S. Quantifying urban heat island intensity and its physical mechanism using WRF/UCM. Sci. Total Environ. 2019, 650, 3110–3119. [Google Scholar] [CrossRef] [PubMed]
- Kusaka, H.; Chen, F.; Tewari, M.; Dudhia, J.; Gill, D.O.; Duda, M.G.; Wang, W.; Miya, Y. Numerical simulation of urban heat island effect by the WRF model with 4-km grid increment: An inter-comparison study between the urban canopy model and slab model. J. Meteorol. Soc. Jpn. 2012, 90, 33–45. [Google Scholar] [CrossRef]
- Sharma, A.; Fernando, H.J.; Hamlet, A.F.; Hellmann, J.J.; Barlage, M.; Chen, F. Urban meteorological modeling using WRF: A sensitivity study. Int. J. Climatol. 2017, 37, 1885–1900. [Google Scholar] [CrossRef]
- Bottyán, Z.; Unger, J. A multiple linear statistical model for estimating the mean maximum urban heat island. Theor. Appl. Climatol. 2003, 75, 233–243. [Google Scholar] [CrossRef]
- Hoffmann, P.; Krueger, O.; Schlünzen, K.H. A statistical model for the urban heat island and its application to a climate change scenario. Int. J. Climatol. 2012, 32, 1238–1248. [Google Scholar] [CrossRef]
- Straub, A.; Berger, K.; Breitner, S.; Cyrys, J.; Geruschkat, U.; Jacobeit, J.; Kuehlbach, B.; Kusch, T.; Philipp, A.; Schneider, A.; et al. Statistical modelling of spatial patterns of the urban heat island intensity in the urban environment of Augsburg, Germany. Urban Clim. 2019, 29, 100491. [Google Scholar] [CrossRef]
- Gardes, T.; Schoetter, R.; Hidalgo, J.; Long, N.; Marquès, E.; Masson, V. Statistical prediction of the nocturnal urban heat island intensity based on urban morphology and geographical factors—An investigation based on numerical model results for a large ensemble of French cities. Sci. Total Environ. 2020, 737, 139253. [Google Scholar] [CrossRef] [PubMed]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Hidalgo, J.; Masson, V.; Gimeno, L. Scaling the daytime urban heat island and urban-breeze circulation. J. Appl. Meteorol. Climatol. 2010, 49, 889–901. [Google Scholar] [CrossRef]
- Lee, T.W.; Lee, J.; Wang, Z.H. Scaling of the urban heat island intensity using time-dependent energy balance. Urban Clim. 2012, 2, 16–24. [Google Scholar] [CrossRef]
- Theeuwes, N.E.; Steeneveld, G.J.; Ronda, R.J.; Holtslag, A.A. A diagnostic equation for the daily maximum urban heat island effect for cities in northwestern Europe. Int. J. Climatol. 2017, 37, 443–454. [Google Scholar] [CrossRef]
- Zhang, X.; Steeneveld, G.J.; Zhou, D.; Duan, C.; Holtslag, A.A. A diagnostic equation for the maximum urban heat island effect of a typical Chinese city: A case study for Xi’an. Build. Environ. 2019, 158, 39–50. [Google Scholar] [CrossRef]
- Yao, L.; Yang, X.; Zhu, C.; Jin, T.; Peng, L.L.; Ye, Y. Evaluation of a Diagnostic equation for the daily maximum urban heat island effect. Procedia Eng. 2017, 205, 2863–2870. [Google Scholar] [CrossRef]
- Yang, X.; Yao, L.; Peng, L.L.; Jiang, Z.; Jin, T.; Zhao, L. Evaluation of a diagnostic equation for the daily maximum urban heat island intensity and its application to building energy simulations. Energy Build. 2019, 193, 160–173. [Google Scholar] [CrossRef]
- Chow, W.T.; Roth, M. Temporal dynamics of the urban heat island of Singapore. Int. J. Climatol. J. R. Meteorol. Soc. 2006, 26, 2243–2260. [Google Scholar] [CrossRef]
- Jin, H.; Cui, P.; Wong, N.H.; Ignatius, M. Assessing the effects of urban morphology parameters on microclimate in Singapore to control the urban heat island effect. Sustainability 2018, 10, 206. [Google Scholar] [CrossRef]
- Roth, M.; Sanchez, B.; Li, R.; Velasco, E. Spatial and temporal characteristics of near-surface air temperature across local climate zones in a tropical city. Int. J. Climatol. 2022, 42, 9730–9752. [Google Scholar] [CrossRef]
- Mughal, M.O.; Li, X.X.; Yin, T.; Martilli, A.; Brousse, O.; Dissegna, M.A.; Norford, L.K. High-resolution, multilayer modeling of Singapore’s urban climate incorporating local climate zones. J. Geophys. Res. Atmos. 2019, 124, 7764–7785. [Google Scholar] [CrossRef]
- DOS. Yearbook of Statistics Singapore 2019; Department of Statistics (DOS), Ministry of Trade & Industry: Singapore, 2019.
- Stewart, I.D.; Oke, T.R. Local climate zones for urban temperature studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Demuzere, M.; Bechtel, B.; Mills, G. Global transferability of local climate zone models. Urban Clim. 2019, 27, 46–63. [Google Scholar] [CrossRef]
- Middel, A.; Lukasczyk, J.; Maciejewski, R.; Demuzere, M.; Roth, M. Sky View Factor footprints for urban climate modeling. Urban Clim. 2018, 25, 120–134. [Google Scholar] [CrossRef]
- Simón-Moral, A.; Dipankar, A.; Roth, M.; Sánchez, C.; Velasco, E.; Huang, X.Y. Application of MORUSES single-layer urban canopy model in a tropical city: Results from Singapore. Q. J. R. Meteorol. Soc. 2020, 146, 576–597. [Google Scholar] [CrossRef]
- Li, R. Spatio-Temporal Dynamics of the Urban Heat Island in Singapore. Master’s Thesis, Department of Geography, National University of Singapore, Singapore, 2012. [Google Scholar]
- Yow, D.M. Urban heat islands: Observations, impacts, and adaptation. Geogr. Compass 2007, 1, 1227–1251. [Google Scholar] [CrossRef]
- Runnalls, K.; Oke, T. Dynamics and controls of the near-surface heat island of Vancouver, British Columbia. Phys. Geogr. 2000, 21, 283–304. [Google Scholar] [CrossRef]
- Sanchez, B.; Roth, M.; Simón-Moral, A.; Martilli, A.; Velasco, E. Assessment of a meteorological mesoscale model’s capability to simulate intra-urban thermal variability in a tropical city. Urban Clim. 2021, 40, 101006. [Google Scholar] [CrossRef]
- Zhu, W.; Yuan, C. Urban heat health risk assessment in Singapore to support resilient urban design—By integrating urban heat and the distribution of the elderly population. Cities 2023, 132, 104103. [Google Scholar] [CrossRef]
- Koopmans, S.; Ronda, R.; Steeneveld, G.J.; Holtslag, A.A.; Klein Tank, A.M. Quantifying the effect of different urban planning strategies on heat stress for current and future climates in the agglomeration of The Hague (The Netherlands). Atmosphere 2018, 9, 353. [Google Scholar] [CrossRef]
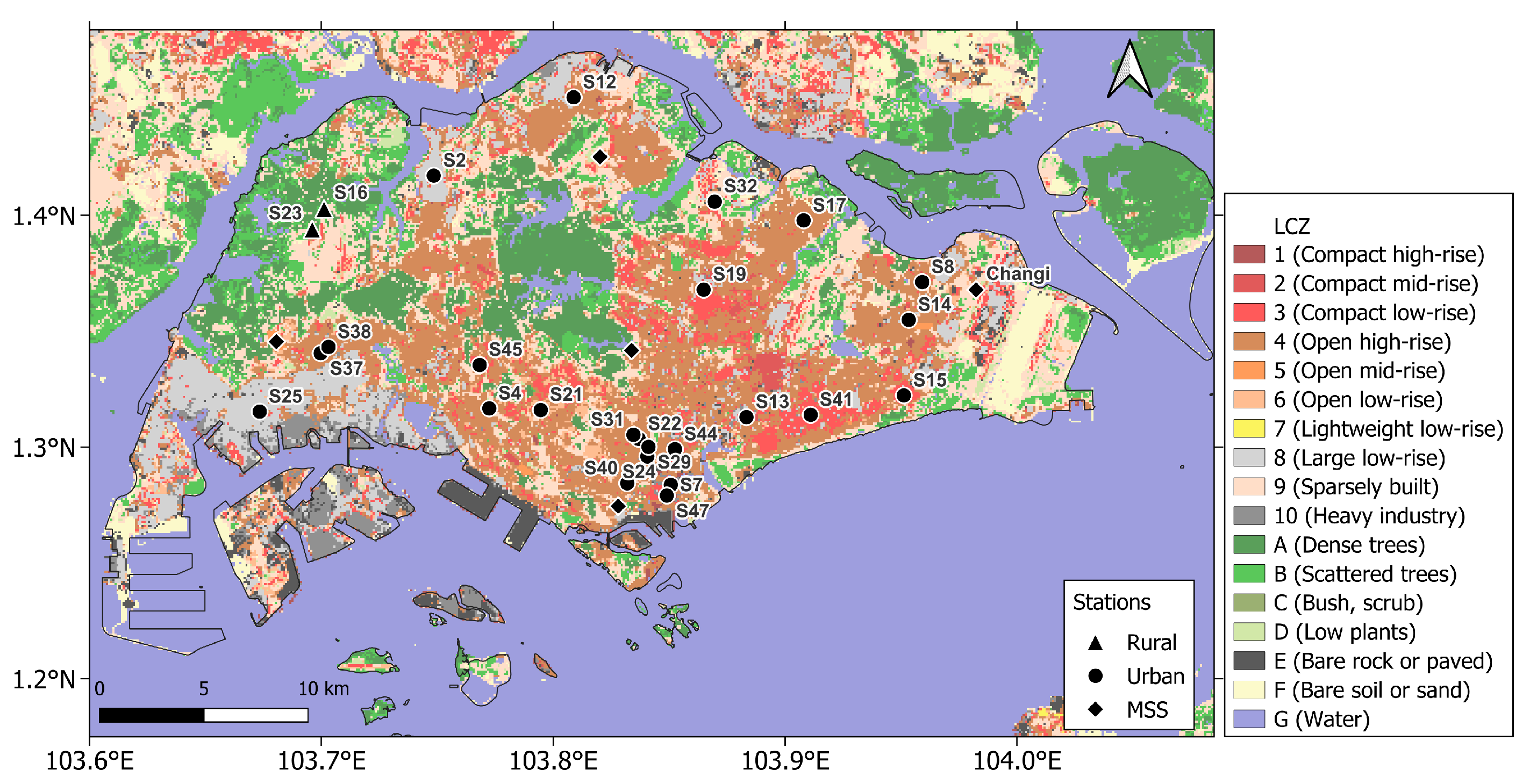


| Station ID | Lon (°) | Lat (°) | Local SVF | (300-m Average) | (300-m Average) | (300-m Average) | LCZ |
|---|---|---|---|---|---|---|---|
| Urban stations | |||||||
| S2 | 1.4171 | 103.7485 | 0.69 | 0.41 | 0.88 | 0.10 | 8 |
| S4 | 1.3167 | 103.7724 | 0.19 | 0.20 | 0.44 | 0.47 | A/4 |
| S7 | 1.2837 | 103.8507 | 0.19 | 5.16 | 0.87 | 0.06 | 1 |
| S8 | 1.3712 | 103.9591 | 0.37 | 0.97 | 0.64 | 0.31 | 4 |
| S12 | 1.4509 | 103.8088 | 0.55 | 0.44 | 0.85 | 0.10 | 8 |
| S13 | 1.3129 | 103.8833 | 0.66 | 0.96 | 0.84 | 0.13 | 2 |
| S14 | 1.3549 | 103.9533 | 0.32 | 0.94 | 0.76 | 0.19 | 4 |
| S15 | 1.3223 | 103.9512 | 0.67 | 0.76 | 0.75 | 0.20 | 3 |
| S17 | 1.3978 | 103.9080 | 0.47 | 1.83 | 0.77 | 0.20 | 4 |
| S19 | 1.3679 | 103.8649 | 0.84 | 0.77 | 0.76 | 0.19 | 3 |
| S21 | 1.3160 | 103.7946 | 0.54 | 0.61 | 0.43 | 0.56 | 6 |
| S22 | 1.3035 | 103.8369 | 0.24 | 2.49 | 0.82 | 0.17 | 1 |
| S24 | 1.2960 | 103.8406 | 0.55 | 1.52 | 0.68 | 0.30 | 5 |
| S25 | 1.3153 | 103.6734 | 0.56 | 0.39 | 0.90 | 0.07 | 8 |
| S29 | 1.3001 | 103.8411 | 0.52 | 1.18 | 0.69 | 0.30 | 4 |
| S31 | 1.3053 | 103.8346 | 0.70 | 2.15 | 0.82 | 0.17 | 3 |
| S32 | 1.4059 | 103.8696 | 0.78 | 0.14 | 0.30 | 0.70 | 6 |
| S37 | 1.3405 | 103.6997 | 0.70 | 0.99 | 0.70 | 0.25 | 4 |
| S38 | 1.3432 | 103.7031 | 0.26 | 1.52 | 0.69 | 0.28 | 4 |
| S40 | 1.2844 | 103.8319 | 0.44 | 0.63 | 0.70 | 0.28 | 5 |
| S41 | 1.3139 | 103.9110 | 0.86 | 0.88 | 0.78 | 0.18 | 3 |
| S44 | 1.2991 | 103.8525 | 0.41 | 1.84 | 0.91 | 0.09 | 1/2 |
| S45 | 1.3354 | 103.7683 | 0.79 | 0.74 | 0.76 | 0.24 | 3 |
| S47 | 1.2791 | 103.8490 | 0.14 | 3.81 | 0.91 | 0.09 | 1 |
| Rural stations1 | |||||||
| S16 | 1.4028 | 103.7012 | 0.66 | 0.01 | 0.08 | 0.9 | B |
| S23 | 1.3939 | 103.6961 | 0.83 | 0.01 | 0.07 | 0.9 | B |
| Dataset | IOA | RMSE (K) | MEAE (K) | R |
|---|---|---|---|---|
| Theeuwes et al. [33]—European cities | 0.91 | 0.58 | 0.81 | |
| Zhang et al. [34]—Xi’an (China) | 1.68 | 1.14 | 0.67 | |
| Yang et al. [36]—Nanjing (China) | 1.00 | 0.68 | ||
| Theeuwes et al. [33]—Singapore | 0.62 | 1.10 | 0.75 | 0.37 |
| Equation (3) for Singapore | 0.76 | 1.13 | 0.79 | 0.58 |
| Wind Speed Ranges | Test Period | Entire Period | ||||||
|---|---|---|---|---|---|---|---|---|
| IOA | R | RMSE | MEAE | IOA | R | RMSE | MEAE | |
| < 2.5 m s−1 | 0.86 | 0.76 | 0.95 | 0.64 | 0.81 | 0.66 | 0.99 | 0.68 |
| > 2.5 m s−1 | 0.49 | 0.31 | 1.33 | 1.03 | 0.70 | 0.50 | 1.18 | 0.84 |
| Case | IOA | R | RMSE (K) | MEAE (K) |
|---|---|---|---|---|
| ‘Ideal’ conditions | 0.85 | 0.85 | 0.65 | 0.55 |
| Lowest UHImax—5 February 2012 | 0.55 | 0.80 | 0.94 | 0.84 |
| Largest UHImax—19 June 2013 | 0.89 | 0.86 | 0.90 | 0.52 |
| mean UHImax for February | 0.82 | 0.83 | 0.57 | 0.55 |
| mean UHImax for June | 0.72 | 0.83 | 1.01 | 0.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanchez, B.; Roth, M.; Patel, P.; Simón-Moral, A. Application of a Semi-Empirical Approach to Map Maximum Urban Heat Island Intensity in Singapore. Sustainability 2023, 15, 12834. https://doi.org/10.3390/su151712834
Sanchez B, Roth M, Patel P, Simón-Moral A. Application of a Semi-Empirical Approach to Map Maximum Urban Heat Island Intensity in Singapore. Sustainability. 2023; 15(17):12834. https://doi.org/10.3390/su151712834
Chicago/Turabian StyleSanchez, Beatriz, Matthias Roth, Pratiman Patel, and Andrés Simón-Moral. 2023. "Application of a Semi-Empirical Approach to Map Maximum Urban Heat Island Intensity in Singapore" Sustainability 15, no. 17: 12834. https://doi.org/10.3390/su151712834
APA StyleSanchez, B., Roth, M., Patel, P., & Simón-Moral, A. (2023). Application of a Semi-Empirical Approach to Map Maximum Urban Heat Island Intensity in Singapore. Sustainability, 15(17), 12834. https://doi.org/10.3390/su151712834





